Simulation of calcium signaling in fine astrocytic processes: Effect of spatial properties on spontaneous activity

Abstract

Astrocytes, a glial cell type of the central nervous system, have emerged as detectors and regulators of neuronal information processing. Astrocyte excitability resides in transient variations of free cytosolic calcium concentration over a range of temporal and spatial scales, from sub-microdomains to waves propagating throughout the cell. Despite extensive experimental approaches, it is not clear how these signals are transmitted to and integrated within an astrocyte. The localization of the main molecular actors and the geometry of the system, including the spatial organization of calcium channels IP₃R, are deemed essential. However, as most calcium signals occur in astrocytic ramifications that are too fine to be resolved by conventional light microscopy, most of those spatial data are unknown and computational modeling remains the only methodology to study this issue. Here, we propose an IP₃R-mediated calcium signaling model for dynamics in such small sub-cellular volumes. To account for the expected stochasticity and low copy numbers, our model is both spatially explicit and particle-based. Extensive simulations show that spontaneous calcium signals arise in the model via the interplay between excitability and stochasticity. The model reproduces the main forms of calcium signals and indicates that their frequency crucially depends on the spatial organization of the IP₃R channels. Importantly, we show that two processes expressing exactly the same calcium channels can display different types of calcium signals depending on the spatial organization of the channels. Our model with realistic process volume and calcium concentrations successfully reproduces spontaneous calcium signals that we measured in calcium micro-domains with confocal microscopy and predicts that local variations of calcium indicators might contribute to the diversity of calcium signals observed in astrocytes. To our knowledge, this model is the first model suited to investigate calcium dynamics in fine astrocytic processes and to propose plausible mechanisms responsible for their variability.

Author summary

Astrocytes process information in the brain via calcium signals that can modulate neuronal communication. Astrocytic calcium signals are associated with brain functioning, including memory and learning, and are altered in the diseased brain. Astrocytic calcium signals display a huge spatio-temporal diversity, which mechanisms and functional roles are poorly understood. 80% of calcium signals occur in the gliapil, corresponding to astrocytic ramifications that are too thin to be detected by conventional light microscopy. Because of the small volumes at stake, we modeled astrocytic calcium signals in the gliapil with a stochastic spatially-explicit individual-based model. Our model successfully reproduces calcium signals that we measured in hippocampal astrocytic gliapil and sheds light to the importance of the localization of calcium sources. We predict that the diversity of calcium signals measured with fluorescent indicators might be partly due to local variations of the concentration of those indicators. We believe that this model will be useful to investigate the propagation of calcium signals within the sponge-like network of astrocytic processes, and eventually to better understand information processing in the brain.

Introduction

Astrocytes were first characterized as non-excitable cells of the central nervous system since, although they express voltage-gated channels [1], they do not exhibit electrical excitability [2]. Astrocytes excitability instead results from variations of cytosolic calcium concentration [3]. At the cellular level, those calcium signals emerge in astrocytes in response to synaptic activity and may cause the release of molecules called gliotransmitters such as glutamate, ATP, tumor necrosis factor-α, or D-serine, which can modulate synaptic transmission [4–7] and vasoconstriction/vasodilatation [8–11]. This close association of astrocytes to pre- and post- synaptic elements, both structurally and functionally, is referred to as tripartite synapse (see e.g. [12–15] for reviews on tripartite synapses and the associated controversies). On a larger scale, astrocytic calcium signals can modulate neuronal synchronization and firing pattern [16–18] and have been observed in vivo in response to external stimuli [19, 20]. Altogether, those observations disrupt the traditional view that allocates information processing in the brain to neurons only.

Cell culture, ex vivo and in vivo studies have demonstrated that astrocytes display both spontaneous calcium signals [19, 21–25] and neuronal activity-induced calcium signals [17, 20, 26]. Astrocytic calcium signals can be localized to synapses [4, 26–28], propagate along processes [29], lead to whole-cell events [30] or even propagate to other cells [31]. Whether this spatio-temporal variability of calcium signals is associated to different physiological functions and whether this could reflect signal integration from different neural circuits is still unknown.

Astrocytic calcium signals are considered to rely mainly on the IP₃R calcium channel pathway. Indeed, type-2 IP₃R calcium channel is enriched in astrocytes [32] and knocking-out IP₃R2 channels abolishes all calcium signals in astrocytic soma and roughly half of them in the cell processes [28]. The molecular origin of the IP₃R2-independent signals in processes remains a matter of debate, and could involve calcium fluxes through the plasma membrane [28] and/or other IP₃R channel subtypes [33]. In any case, astrocytes respond to G-protein-coupled receptor (GPCR) agonists with calcium transients [34, 35]. Binding of agonists to G_q/11-GPCRs activates IP₃ synthesis. In turn, binding of both IP₃ and calcium ions to IP₃R channels on the membrane of the endoplasmic reticulum (ER) triggers a calcium influx from the ER to the cytosol [36]. The initiation and propagation of calcium signals within astrocytes then relies on the so-called calcium-induced-calcium release (CICR) mechanism: an increase, even small, of the local calcium concentration increases IP₃R opening probability thus increasing the probability for local calcium concentration to rise further.

80% of the astrocyte calcium activity in vivo take place in the gliapil, which is mostly formed by astrocytic ramifications that cannot be spatially resolved by conventional light microscopy [37], yet account for 75% of the astrocytic volume [38]. According to electron microscopy studies, the perisynaptic astrocyte projections (PAPs) that belong to the gliapil could be as thin as 30-50nm in diameter [39, 40]. At this spatial scale, calcium signals are characterized by non-uniform spatial distributions composed of hotspots where calcium signals are more likely to occur and repeat [41, 42]. Those observations suggest the existence of subcellular spatial organizations responsible for the spatial distribution of calcium signal patterns. Understanding calcium signaling in PAPs, where astrocytes potentially regulate neuronal information processing, is crucial. However, only calcium signals in thicker processes, around 300nm in diameter, are within reach of current conventional imaging methods [40] and most studies on astrocytic calcium have focused on astrocytic soma and main processes, where characteristics and physiological roles of calcium signals are likely to differ from those of PAPs. Because of the small dimensions and volumes at stake, modeling is currently the only approach that can investigate calcium signal generation, transmission and the effect of spatial properties within PAPs.

Mathematical models of CICR-based signaling date back to the beginning of the 1990s (for recent reviews see e.g. [43–45]). The first IP₃R-mediated calcium signaling models assumed perfect mixing of the molecular species and deterministic kinetics (ordinary differential equations) and typically treated IP₃ concentration as a parameter [46–48]. In those models, calcium transients emerge as limit-cycle oscillations from a Hopf bifurcation (or a saddle-node on an invariant circle) beyond a critical value of the IP₃ concentration. The first astrocyte-specific calcium signaling models arose a decade later. In those models, the IP₃ concentration is usually a dynamical variable coupled to calcium but calcium transients still emerge through the Hopf-bifurcation scenario. Notably, those models focused on intercellular IP₃ transport within astrocyte networks via gap junctions [49, 50]. Stochastic models of IP₃R-mediated calcium signaling have also been proposed, that take into account the stochasticity associated with molecular interactions [51–54]. Yet, none of those studies accounts both for molecular species diffusion and stochasticity of the reactions taking place inside astrocytes, which is essential for modeling the stochastic effects associated with small volumes and the low copy number of molecules or ions involved in fine processes. Recently, individual-based modeling has been introduced to evaluate the impact of diffusive noise on IP₃R opening dynamics [55], but this simplified model disregarded IP₃ dynamics and restricted stochasticity to the vicinity of the IP₃Rs.

Here, we propose an IP₃R-mediated calcium signaling model adapted to the dynamics of CICR in small spatial volumes corresponding to thin PAPs. To account for the stochasticity inherent to small sub-cellular volumes and low copy numbers expected in fine processes, our model is both spatially explicit and particle-based: each molecule is described individually, diffuses in space through a random walk and reacts stochastically upon collision with reaction partners. The kinetics of IP₃R channels is accounted for with a simplified version of the 8-state Markov model on which most of the previous CICR models are based. In order to explore the range of dynamical behaviors that the model can display, we first focus on a 2D version of our model, that is less compute-intensive than the 3D version. Extensive simulations of the 2D model show that spontaneous calcium signals arise in the model via the interplay between the excitability of the system and its stochasticity. The model accounts for various forms of calcium signals (“blips” and “puffs”) and their frequency depends on the spatial organization of the IP₃R channels. In particular, we demonstrate that the co-localization of sources of calcium influx plays a crucial role in triggering an effect of IP₃R clustering on calcium signaling. Finally, as solute concentrations can hardly be defined in 2D, we use a 3D version of the model in order to compare it to experimental data. We show that the spontaneous calcium signals generated by the 3D model with realistic process volume and astrocytic calcium concentrations successfully reproduce the spontaneous calcium transients measured in calcium micro-domains with confocal microscopy in organotypic culture of hippocampal astrocytes. Our simulations predict that local variations of the concentration of calcium indicators such as GECIs might contribute to the diversity of calcium signals observed in astrocytes so that precise monitoring of their concentration should be performed. Our model therefore represents the first validated tool to investigate calcium signals in realistic small sub-cellular volumes such as in PAPs, where astrocytes and synapses communicate. This provides a crucial step towards a better understanding of the spatiotemporal response patterns of astrocytes to neuronal activity and beyond, towards astrocyte-neuron communication.

Results

Spontaneous oscillations in the model

We first analyzed our particle-based model for the CICR signaling system of Fig 1, with parameter values presented in Table 1. To that end, we compared Monte-Carlo simulations of the particle-based model in two dimensions with the corresponding Mean-Field and Gillespie’s SSA models (see Methods section). Those three models represent different levels of approximation: the Mean-Field model assumes deterministic kinetics and perfect mixing; the SSA model keeps the perfect mixing hypothesis but assumes stochastic kinetics while the particle-based model assumes stochastic kinetics but accounts for potential non-perfect mixing, i.e. diffusion effects. For comparison with SSA, we first considered perfect mixing of Ca²⁺ ions and IP₃ molecules in the particle-based model by setting the diffusion coefficients D_Ca = D_IP3 = ∞ (see Method section).

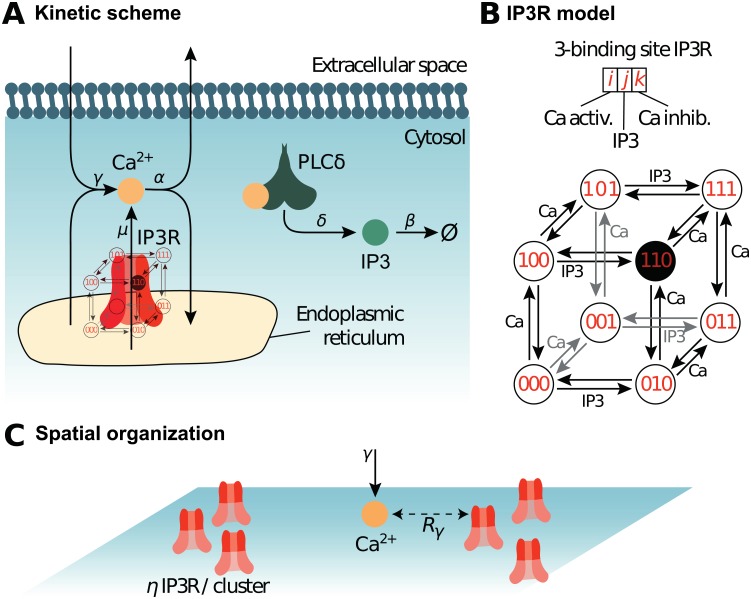
Fig 1. Reaction scheme and IP₃R model.

The biochemical processes included in the model are illustrated in (A). Cytosolic calcium can exit the cytosol to the extracellular space or the endoplasmic reticulum (ER) at a (total) rate α, lumping together the effects of ER and plasma membrane pumps. Likewise, Ca²⁺ can enter the cytosol from the extracellular space or from the ER via IP₃R-independent flow, with (total) rate γ, emulating calcium channels from the plasma membrane. When an IP₃R channel opens, calcium enters the cytosol through the channel at rate μ. Phospholipase Cδ (PLCδ), once activated by calcium binding, produces IP₃ at rate δ. Like Ca²⁺, IP₃ can bind the IP₃R channel and is removed with rate β. (B) Our model of the kinetics of the IP₃R channel is an 8-state Markov model adapted from [46, 56]. Each IP₃R channel monomer is associated with 3 binding sites, two calcium binding sites and one IP₃ binding site. Occupancy states are designated by a triplet {i, j, k} where i stands for the occupation of the first Ca binding site (i = 1 if bound, 0 else), j for that of the IP₃ binding site and k for the second Ca site. The first calcium binding site has higher affinity than the second. The open state is state {110}, where the first Ca and the IP₃ sites are bound but not the second Ca site. (C) Spatial parameters for the particle-based model. The $N_{{\text{IP}}_{\text{3}}\text{R}}I{P}_{\text{3}}R$ molecules are positioned within uniformly distributed clusters, with η IP₃R in each cluster. Hence η = 1 corresponds to uniformly distributed IP₃R (no clustering), while the degree of clustering increases with η (for constant total IP₃R number). To account for potential co-localization between IP₃R-dependent and IP₃R-independent calcium sources, the influx of IP₃R-independent calcium (at rate γ) occurs within distance R_γ of an IP₃R. Thus, low values of R_γ emulate co-localization between IP₃R-dependent and IP₃R-independent Ca²⁺ influx sources.

Table 1. Parameter values and initial conditions of the 2D model.

a.u: arbitrary unit. In 2d, by definition, a MC time unit is 100 Δt and one MC space unit is set by the interaction radius of IP₃R, i.e. $d_{{\text{IP}}_{\text{3}}\text{R}}=1.0\text{MC}$ space unit. δ, β, μ, γ, b₁, b₂ and b₃ are first order constants, in (MC time unit)⁻¹. Diffusion coefficients D_Ca and D_IP3 are expressed in (MC space unit)².(MC time unit)⁻¹ whereas α, a₁, a₂, a₃ are expressed in (MC space unit)².(MC time unit)⁻¹.

Parameter	Description	Value in 2d model
V	Cell volume	200 × 200 a.u.
IP3 dynamics
IP0	Initial IP3 number/conc.	15 molec.
DIP3	IP3 diffusion	10 a.u
Nplc	PLCδ number/conc.	1000 molec.
δ	PLCδ max rate	0.1 a.u
β	IP3 decay	0.01 a.u
Ca2+ dynamics
Ca0	Initial Ca2+ number/conc.	50 molec.
DCa	Ca2+ diffusion	varied
μ	Ca2+ flux through open IP3R	50 a.u
γ	cytosolic Ca2+ influx	50 a.u
α	Ca2+ decay rate	1.0 a.u
IP3R
$N_{{\text{IP}}_{\text{3}}\text{R}}$	IP3R number	1000 molec.
$d_{{\text{IP}}_{\text{3}}\text{R}}$	IP3R interact. distance	1 space unit
IP3R binding
a1	First Ca	1.0 a.u
a2	IP3	1.0 a.u
a3	Second Ca	0.1 a.u
IP3R dissociation
b1	First Ca	0.1 a.u
b2	IP3	0.1 a.u
b3	Second Ca	0.1 a.u

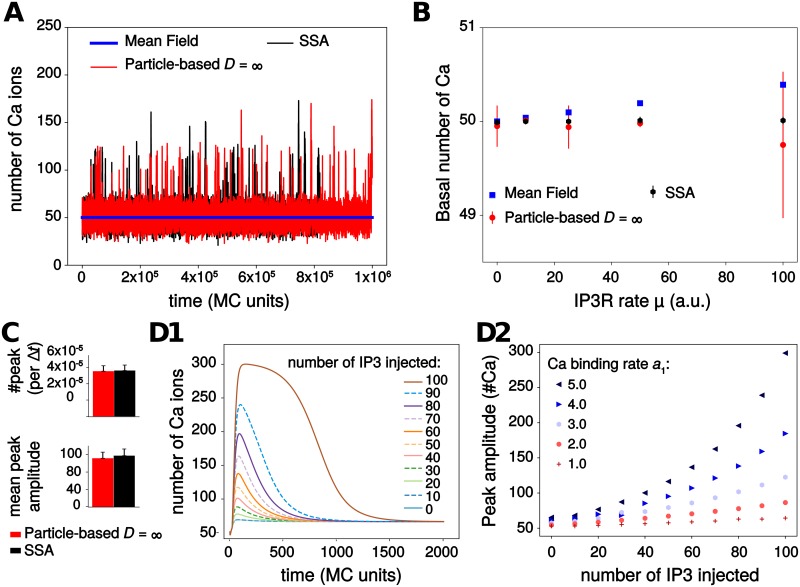
Fig 2A shows one simulation sample for each model. A first result is that the stochastic models (SSA and particle-based) do exhibit spontaneous calcium peaks with the parameters of this figure. On top of a background level of approximately 50 Ca²⁺ ions, with fluctuations of roughly ± 20 ions, large and fast peaks arise spontaneously with a total amplitude between 20 and 120 ions above the baseline. In strong opposition, the (deterministic) mean-field model does not show these oscillations: one gets a stationary trace, that systematically coincides with the baseline level of the stochastic traces (Fig 2B). Comparing the two stochastic models (SSA and particle-based) indicates that both display the same basal calcium level (Fig 2B) and the same frequency and mean peak amplitude (Fig 2C). Altogether, this suggests that stochasticity is necessary for spontaneous calcium signals to occur in this model.

Fig 2. Model exploration.

(A) Spontaneous transients are observed in simulations of the particle-based and the Gillespie’s SSA model but not in the Mean Field model. (B) The three models display the same basal calcium level when μ, the calcium influx rate through open IP₃R channels, increases. The higher variability in the stochastic models reflects the integer value of basal calcium (either 49 or 50, depending on simulations). (C) Quantification of calcium transients in the stochastic models (calcium peak frequency and mean peak amplitude). No significant difference between the two models was observed. (D) Excitability of the Mean-Field model: increasing quantities of exogenous IP₃ molecules were injected at time t = 20Δt, after model equilibration. The amplitude of the resulting calcium response (D1) was quantified depending on the amount of IP₃ injected and the value of the binding rate constant to the first calcium IP₃R site, a₁ (D2). Parameter values for the particle-based model: D_Ca = D_IP3 = ∞ (perfect mixing) and η = 1, R_γ = 200, i.e. no IP₃R channels clustering, and no co-localization of IP₃R with IP₃R-independent Ca²⁺ sources. For SSA and particle-based models, the figure shows the average ± standard deviation over 20 simulations.

We next searched for the dynamical mechanism that gives rise to those spontaneous peaks. A thorough numerical parameter exploration of the mean-field model failed to demonstrate the existence of Hopf bifurcations or of any other bifurcation that would generate limit-cycle oscillations in the model. This is a distinctive feature of our model, since spontaneous oscillations in the vast majority of IP₃R-mediated calcium signaling models arise from limit-cycle generating bifurcations [46–48]. This is however not unexpected since the simplifications made to derive our model significantly reduced its nonlinearity compared to these models, and the emergence of limit-cycle bifurcations demands strong nonlinearity. For instance, limit-cycle oscillations in the classical Li and Rinzel model [48] disappear when IP₃R opening needs less than three open monomers. However, our model retains enough nonlinearity to exhibit excitability. To demonstrate this, we used the mean-field model, waited until all concentrations reached their stationary state, and injected an increasing amount of exogenous IP₃ molecules. In response to this IP₃ injection, a calcium transient was obtained, before relaxation to the stationary state (Fig 2D). Fig 2D2 shows how the resulting transient amplitude depends on the amount of injected IP₃. For low values of IP₃R calcium binding rate (first site), a₁, the calcium response is basically linear with the number of injected IP₃: doubling the amount of IP₃ injected only doubles the amplitude of the calcium response. However, as a₁ increases, peak amplitude becomes a strongly nonlinear function of the number of IP₃ injected. With a₁ = 5 a.u. for instance, doubling the number of injected IP₃ from 50 to 100 results in an almost threefold increase of the calcium response. Therefore the mean-field model with large values of a₁ is an excitable system that amplifies the fluctuations of IP₃ in its calcium responses. We conclude that spontaneous calcium transients occur in the system of Fig 1 through the interplay of the stochasticity of the SSA or particle-based models and the underlying excitability of the system.

Transitions between calcium activity regimes

The experimental and modeling literature on intracellular calcium signals distinguishes two classes of localized calcium peaks: puffs and blips [57]. Blips refer to brief and weak peaks that correspond to the opening of a single IP₃R channel (or a single IP₃R channel tetramer), whereas puffs are longer and higher peaks resulting from the concerted opening of a group of nearby IP₃R channels (or tetramers thereof), via the calcium-induced calcium-release principle. We next examined whether our model was able to reproduce these observations.

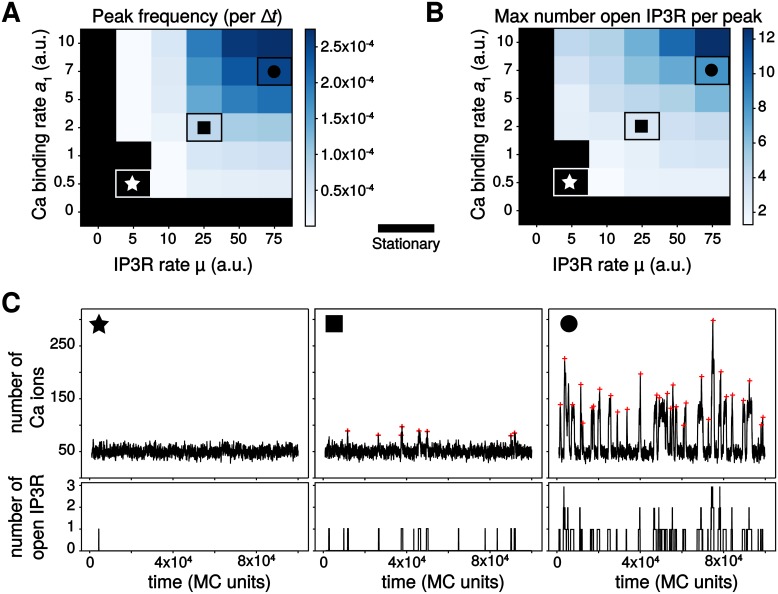
We carried out parameter exploration of the particle-based model in conditions of perfect mixing for mobile molecules (Ca and IP₃) and uniform spatial distribution of the immobile ones (PLCδ, IP₃R). As expected, we found that calcium peaks frequency depends on parameter values (Fig 3A). When the rate of calcium influx through open IP₃R channels μ or the binding rate constant to the first Ca IP₃R site a₁ are too small, the model does not exhibit calcium peaks at all, only fluctuations around a stationary state (Fig 3C★). This is in agreement with our analysis of the system excitability above, that evidenced excitability only for large enough values of a₁ (Fig 2D2). Note however that in the model, IP₃R openings do not necessarily lead to a calcium peak, especially for low values of both μ and a₁ (Fig 3C★). Spontaneous calcium transients are obtained in the particle-based model beyond threshold of (μ, a₁) values, with a peak frequency that increases with parameters values (Fig 3A). Inspection of the maximal number of open IP₃R per peak reveals that not only the frequency, but also the type of these transient signals changes with parameters values (Fig 3A): the less frequent signals are generally associated with a single open IP₃R per peak (Fig 3C◼), corresponding to blips, whereas the high-frequency spontaneous signals rely on the opening of 2 − 12 IP₃R in a peak (Fig 3C●), corresponding to puffs. In agreement with experimental observations [58, 59], calcium puffs in the particle-based model are characterized by higher peak amplitude and peak duration compared to blips. Taken together, these results show that our particle-based model not only reproduces the existence of spontaneous calcium peaks in conditions of low copy numbers, it is also able to reproduce the existence of different types of localized calcium transients, in agreement with experimental measurements.

Fig 3. The particle-based model produces different calcium activity regimes depending on parameter values.

Color-coded map of variation of the peak frequency, expressed as the number of calcium peaks per MC time step (A) and as the maximal number of IP₃R channel open per peak (B). The color scale is given for each map. The black area corresponds to the stationary regime. Note that the x and y-axis scales in (A) and (B) are not regularly spaced. The symbols ★, ◼ and ● locate parameter pairs that are illustrative of the three dynamical regimes shown in (C): stationary (★, μ = 5, a₁ = 0.5), blips (◼, μ = 25, a₁ = 2) and puffs (●, μ = 75, a₁ = 7). Red crosses show the locations of peaks from automatic detection. D_Ca = D_IP3 = ∞, η = 1, R_γ = 200.

Impact of calcium diffusion coefficient on calcium signals

A modeling study has demonstrated the necessity to account for the stochasticity inherent to calcium diffusion when modeling calcium signaling in small volumes [60]. We next investigated the impact of calcium diffusion on calcium dynamics in the particle-based model. In neurons or astrocytes, the amount of endogenous calcium buffers is large so that the diffusion distance of free calcium is believed to be very small. Many of the endogenous buffers are however mobile. Buffers can have a very significant effect on calcium dynamics because they decrease the diffusion distance and the effective diffusion coefficient of calcium ions [53, 54, 61–64]. Here, we have chosen not to include buffers explicitly in the model for the sake of model simplicity, but to account for their presence by decreasing the diffusion coefficient for calcium. Therefore, the latter is to be interpreted as an effective diffusion coefficient lumping together calcium buffering by mobile endogenous buffer and diffusion of these buffers. To confirm that explicit addition of buffers yields effects similar to a decrease of the Ca²⁺ diffusion coefficient, we have explicitly added endogenous buffer molecules to our 2D model in a subset of simulations, assigning a low coefficient of diffusion for buffers and high one for free calcium ions. These simulations confirmed the absence of significant difference between simulations obtained using fast calcium diffusion and slow explicit buffers on the one hand, and our reference model without buffers but with an effective lower D_Ca on the other hand (S1 Fig).

Moreover, several plasma membrane proteins, in particular the Na⁺-Ca²⁺ exchanger (NCX) have been observed to co-localize with ER proteins in neurons and astrocytes [65]. Such a co-localization of calcium signaling molecules might imply spatial organizations including raft-like micro-domains. This organization seems essential for calcium wave propagation in astrocytes [66]. Moreover, mGluR5-ER proteins co-clusters mediated by an interaction with Homer1 scaffold protein have been observed in astrocytic processes [67]. Homer1 is also known for increasing calcium activity in neurons by increasing IP₃R-mGluR5 proximity [68]. Those experimental studies suggest that several calcium sources are co-localized with ER proteins in astrocytes and that it might alter calcium dynamics. Such a co-localization could be crucial for calcium signaling, in particular in small volumes. We thus placed our study of the influence of calcium mobility on calcium signaling in a framework where calcium sources (IP₃R-dependent and IP₃R-independent) can co-localize.

To this end, the IP₃R-independent calcium influx in the cytosol (from e.g. plasma membrane transporters or channels) was made dependent on parameter R_γ, that sets the distance from IP₃R receptors within which new calcium ions are injected in the cytosol when they originate from IP₃R-independent fluxes (see Methods section). When R_γ = 0, the initial location of the new calcium ion is shared with an IP₃R channel whereas when R_γ increases, the injection positions of new calcium ions are increasingly uncorrelated from those of the IP₃R channels. When R_γ becomes as large as the size of the reaction surface (i.e. for R_γ = 100), the injection position of the new calcium ion is effectively independent of the positions of the IP₃R channels.

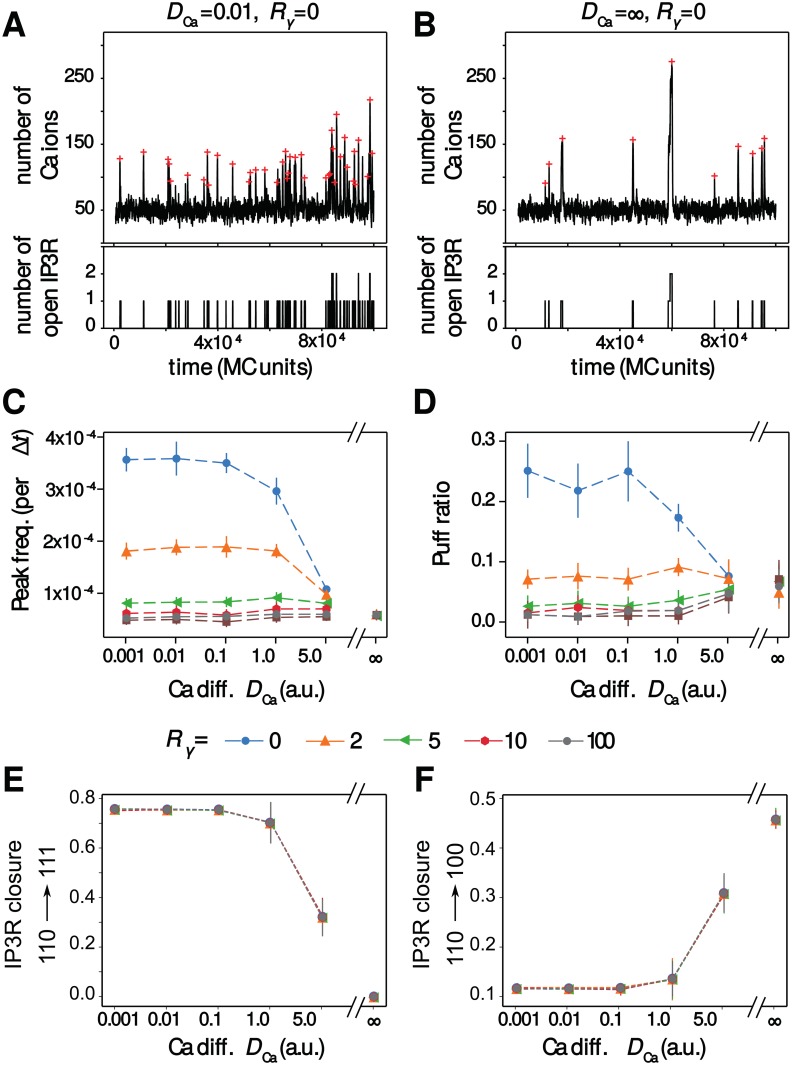
Our simulations show that the impact of the calcium diffusion coefficient is mainly visible when calcium sources are co-localized, i.e. for small values of R_γ. Fig 4A and 4B compare a representative simulation obtained when Ca²⁺ diffuses slowly (A) with a simulation obtained with perfectly-mixed calcium (B), in a case where the IP₃R receptors are not clustered (η = 1). Those representative simulations hint that the peak frequency is much larger with slow calcium, and suggests that slow calcium diffusion slightly favors the puff regime compared to perfect mixing. The systematic quantification of Fig 4C and 4D confirms these interpretations: when IP₃R-dependent and IP₃R-independent calcium sources are co-localized, i.e. for R_γ < 5, the value of D_Ca controls calcium transient frequency, as well as the probability to observe a puff. The effects are strong: for instance for R_γ = 0, decreasing D_Ca from 5 to 0.1 increases the frequency roughly threefold. However, when the IP₃R-independent influx was not co-localized with IP₃R channels (i.e. for R_γ ≥ 5), both the peak frequency and the type of signal were found not to depend on the calcium diffusion coefficient anymore. Those results suggest that calcium diffusion could control the frequency and type of calcium signals within astrocytes when IP₃R channels are co-localized with IP₃R-independent calcium sources.

Fig 4. Ca²⁺ diffusion modulates the temporal characteristics of the signals upon co-localization.

Representative simulations of the particle-based model showing both calcium trace and number of open IP₃R for co-localized calcium sources (R_γ = 0) in the case of slow calcium diffusion (A) or perfect-mixing of calcium (B). The red crosses show peak locations from automatic detection. The impact of calcium diffusion coefficient D_Ca on peak frequency (C) and the amount of puff (D) are shown for different values of the co-localization parameter R_γ: from R_γ = 0 (IP₃R are not clustered but co-localized with other calcium sources) to R_γ = 100 (IP₃R are neither clustered nor co-localized). The puff ratio quantifies the fraction of peaks that are puffs. (E) and (F) respectively present the probabilities that IP₃R closure results from binding of a Ca²⁺ to the inactivating site (probability to switch to state {111}, P_110−>111) or unbinding of an IP₃ (probability to switch to state {100}, P_110−>100) depending on D_Ca and on R_γ. Probability of closure due to Ca²⁺ unbinding from activating site, P_110−>010 can be deduced from 1 = P_110−>010 + P_110−>100+P_110−>111. Data are presented as mean ± standard deviation over 20 simulations. Lines are guide for the eyes. Note that the x-axis scale in (C), (D), (E) and (F) is not regularly spaced. Other parameters: η = 1 (no clustering), a₁ = 1 a.u, μ = 50 a.u.

Once open, i.e in state {110}, the IP₃R can switch to state {111} with probability P_110−>111, due to binding of Ca²⁺ to the inactivating site. Open receptors can also switch to state {100} (or {010}) with probability P_110−>100 (or P_110−>010, respectively), due to the unbinding of IP₃ (or of Ca²⁺, respectively) from the activating site. Fig 4E and 4F shows how the probabilities P_110−>111 and P_110−>100 vary with D_Ca and R_γ (P_110−>010 can be deduced from 1 = P_110−>010 + P_110−>100+P_110−>111). In contrast, R_γ has no significant effect on P_110−>111, P_110−>100 and P_110−>010 probabilities. The effect of the effective diffusion coefficient D_Ca is strong: when low, most of IP₃R closure is due to the binding of Ca²⁺ to the inhibiting site. As D_Ca increases, P_110−>111 decreases and in well-mixed conditions (D_Ca = ∞), IP₃R closure is always due to the stochastic unbinding of IP₃ and Ca²⁺. So, receptor closure is strongly dominated by binding of Ca²⁺ to the inactivating site when Ca²⁺ effective diffusion is slow, but mostly relies on unbinding from the activating sites for fast Ca²⁺ effective diffusion. This result illustrates that well-mixed simulations are not well-suited to study the self-inhibiting behaviour of IP₃R, i.e the fact that the Ca²⁺ influx resulting from the opening of a given IP₃R can subsequently shut down this very receptor. Therefore accounting for diffusion with spatial models appears necessary to the study of the dynamics of IP₃R at the single-receptor scale.

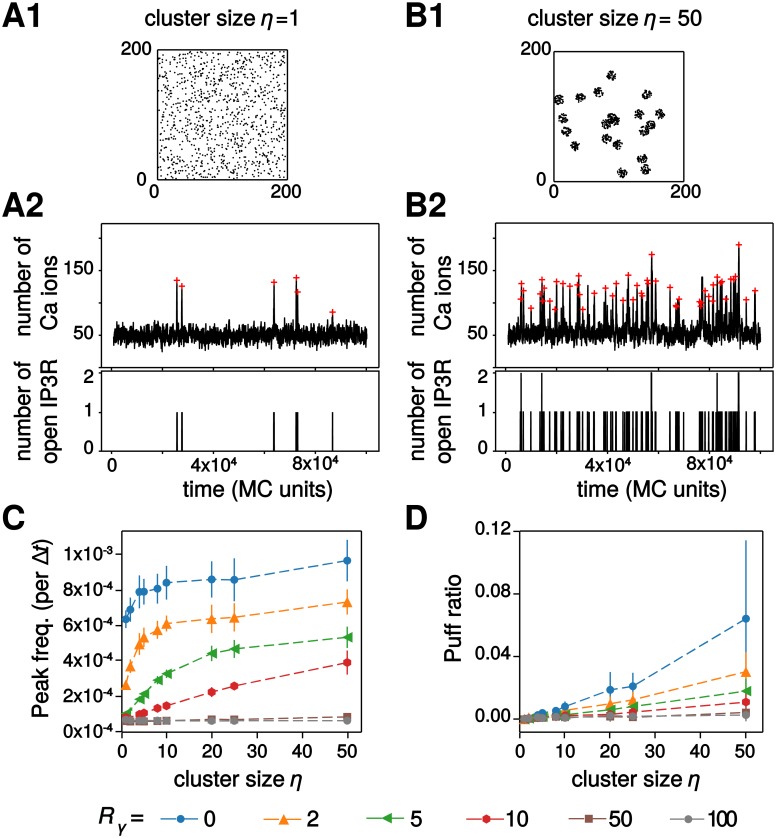
IP₃R clustering controls calcium signals when co-localized

Experimental data demonstrate that IP₃R in SH-SY5Y and COS7 cells are not uniformly distributed on the ER membrane but form clusters [58, 59]. We next investigated the impact of IP₃R clustering on calcium signal dynamics in our particle-based model. Simulations were performed with D_Ca = 0.1 and various amounts of co-localization between IP₃R channels and other calcium sources (parameter R_γ). Representative simulations for uniformly-distributed IP₃R channels (η = 1) and strongly clustered IP₃R (η = 50) are presented in Fig 5A and 5B. In these two examples, the IP₃R were weakly co-localized with the IP₃-independent calcium sources (i.e. R_γ = 10). These traces indicate that the frequency and type of calcium signal in this case is heavily dependent on the spatial distribution of IP₃R channels: clustered IP₃R seem to exhibit much larger peak frequency and slightly more frequent puffs. However, here again this effect is quite mitigated by the amount of co-localization between IP₃R channels and the IP₃R-independent calcium sources. In particular, the dynamical range of the modulation by IP₃R cluster size η (i.e. the ratio between the frequency at η = 50 and η = 1) is maximal for intermediate co-localizations (2 ≤ R_γ ≤ 10) but the calcium peak frequency is hardly dependent on η when co-localization is either very strong (R_γ < 2) or very weak (R_γ ≥ 50). Increasing clustering also tends to improve the emergence of puffs, although the effect is significant only for strong co-localization (R_γ ≤ 2, Fig 5D). We emphasize that in such cases of strong co-localization, the regime of calcium activity (puffs vs blips) changes by simply rearranging the spatial distribution of the IP₃R, without changing any of the kinetics parameters of the model.

Fig 5. IP₃R clustering modulates calcium signals when co-localized.

Representative simulations of the particle-based model with the corresponding IP₃R distribution over space, the calcium trace and number of open IP₃R for weakly co-localized calcium sources (R_γ = 10) in the case of uniform distribution of the IP₃R (A) or strongly clustered IP₃R (B) are illustrated. The red crosses show peak locations from automatic detection. The impact of IP₃R cluster size η on calcium peak frequency (C) and on the amount of puffs (D) are shown for different values of the cluster size: from η = 1 (IP₃R are not clustered) to η = 50 (strong clustering). Data are presented as mean ± standard deviation over 20 simulations. Lines are guide for the eyes. Other parameters: D_Ca = 0.1 a.u, a₁ = 1 a.u, μ = 50 a.u.

Taken together, these simulation results pinpoint the interplay between calcium source co-localization and the degree of IP₃R clustering as a crucial modulator of temporal characteristics of the calcium signals and of the signaling regime. In particular, they suggest that in the presence of certain amount of co-localization between IP₃R channels and other sources of calcium influx in the cytosol the spontaneous calcium peak frequency can have a large amplitude variation. Within this range of parameters, calcium peak frequency can be finely tuned by the geometry of the colocalization.

Simulations in a compartmentalized 3d geometry reproduce spontaneous calcium microdomains signals

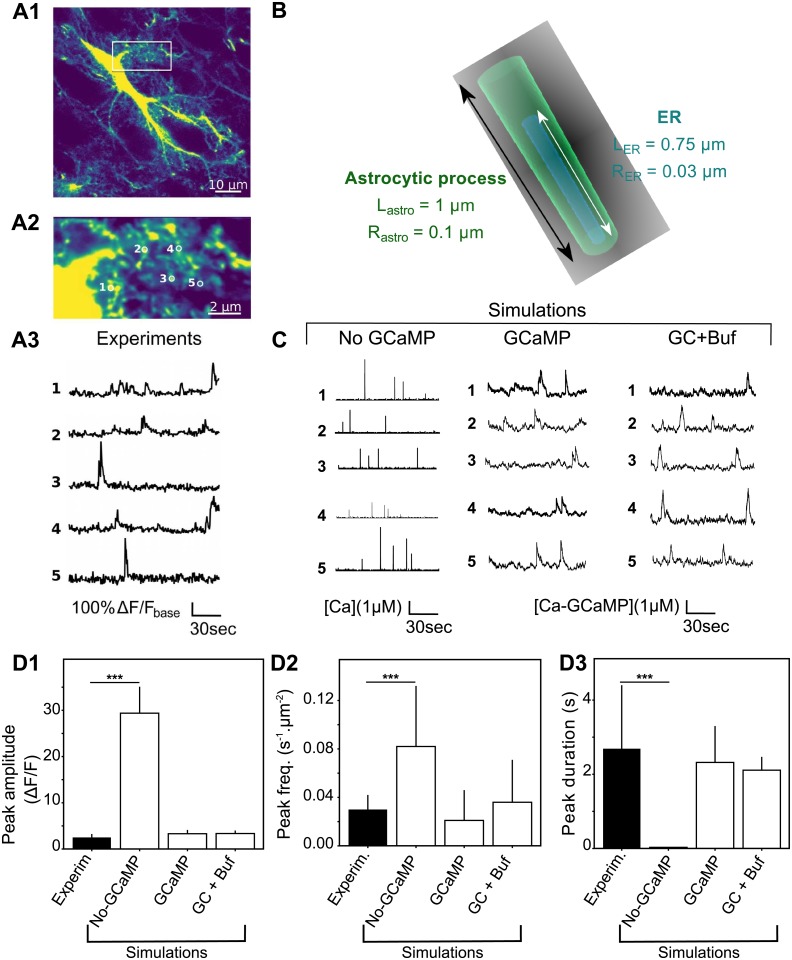
The above 2d simulations of the particle-based model have the advantage of a good computational efficiency, which makes them suitable for parametric studies with averaging over a number of Monte-Carlo simulations. However, the 2d setting does not facilitate the comparison of the copy number of molecules in the simulations with species concentrations as measured experimentally. Moreover, it is difficult to investigate with a 2d setting the impact of the fact that IP₃R channels are specifically localized at the surface of the ER membrane and not freely diffusing in the cytosol bulk. To tackle those questions, we carried out simulations of our model in a more refined three-dimensional setting (Fig 6), in which we could adjust more precisely molecule concentrations, reaction volume and cytosol compartmentalization to what is expected in fine astrocytic processes. We then compared our simulations to experimental measurements of calcium dynamics in microdomains of comparable dimensions in mice hippocampal organotypic culture (Fig 6A). We have chosen to use organotypic slices as they provide better optical access and sample stability, which, combined with confocal microscopy, enabled us to distinguish individual processes (resolution ≈ 200 nm VS ≈ 500 nm with two-photon microscopy in vivo). While this resolution is not enough to resolve the exact sizes of PAPs, it provides the most realistic calcium dynamics experimentally available for calcium transients occurring at fine astrocytic processes.

Fig 6. 3d model simulations in fine astrocyte processes successfully reproduce calcium microdomains signals.

(A) Experimental monitoring of the spontaneous local Ca²⁺ signals in astrocytic sponge-like processes. Panel A1 shows a ‘summed projection’ of a confocal time lapse image stack of a GCaMP6s-expressing astrocyte. Panel A2 illustrates magnification of the boxed region of panel A1. Panel A3 displays spontaneous calcium traces from the regions of interest shown in (A2). (B) The 3d geometry used for the 3D model is a cylinder of length L_astro = 1 μm and radius R_astro = 0.1 μm, with ER as a thinner cylinder inside. The interior volume is roughly 0.03 fL. (C) Representative simulations of calcium dynamics within the above cylinder with the “No-GCaMP”, “GCaMP” and “GC+Buf” simulations. The raw signal corresponds to cytosolic free calcium concentration for the “No-GCaMP” model and to calcium-bound GCaMP concentration for “GCaMP” and “GC+Buf” models. For all simulation types, parameter values were partly taken from the literature and partly adjusted for fitting calcium traces shown in A (reported in Table 2). (D) Quantitative comparisons of the spontaneous calcium signals measured experimentally (black bars) or simulated with the “No-GCaMP”, “GCaMP” or “GC+Buf” models (white bars). The compared quantities are peaks amplitude in terms of ΔF/F ratio (D1), their frequency (measured in min⁻¹ for each μm² area, D2) and duration (expressed as full width at half maximum, FWHM) D3. Significance is assigned by * for p ≤ 0.05, ** for p ≤ 0.01, *** for p ≤ 0.001.

As 80% of calcium activity occurs in astrocytic ramifications that cannot be resolved by optical microscopy [38], astrocytic calcium signaling models must take into account small volumes associated to it. For that purpose, we created the 3d structure mimicking one process geometry shown in Fig 6B. The reaction volume was chosen to match the range of sizes that are within reach of current imaging methods: a 1 μm-long cylinder of 100 nm radius (i.e. a volume around 0.03 fL), inside which we position a 0.75 μm-long cylindrical ER with a radius of 30 nm. In this 3d implementation, Ca²⁺ and IP₃ molecules diffuse in the bulk 3D space located between the external (plasma) membrane and that of the ER, while IP₃R molecules are distributed uniformly at random over ER membrane surface.

Our calcium imaging of calcium dynamics in fine astrocyte processes reveals the sponge-like structure of the processes Fig 6A1, with localized submicron calcium microdomains (regions of interest (ROI) in Fig 6A2) of size that can be less than 0.5μm². The corresponding calcium traces display infrequent (a few hundredths of Hz) peaks with average amplitude around 2 (ΔF/F) and typical duration of ≈ 2.7 seconds at FWHM (Fig 6A3 and 6D). Notice that these experimental traces correspond to spontaneous signals to the extent that they were measured in the absence of any neuronal or astrocytic stimulation. In particular, TTX application in this preparation did not alter peak frequency [69].

Our first noticeable result is that our model is able to reproduce the emergence of spontaneous calcium peaks of comparable frequency, duration and signal-to-noise ratio (Fig 6C). This result therefore indicates that spontaneous calcium signals can emerge in the fine processes even with a realistic basal calcium concentration of 83 ± 29 nM, which corresponds to only one to two calcium ions in the whole cylinder. Quantification of the free Ca²⁺ signal properties shows that signals are quantitatively and qualitatively different from experimental signals (Fig 6C and 6D, “No-GCaMP” simulations). Adding GCaMP6s to the model improved drastically both qualitatively and quantitatively the match between simulations and experimental data (Fig 6C and 6D, “GCaMP” and “GC+Buf” simulations), with no apparent difference between the “GCaMP” and the “GC+Buf” models. Note that our experimental statistics are tightly associated with the temporal sampling frequency used in the experiments (2 Hz) since very fast calcium events may be accessible only to higher sampling frequencies [38]. In particular, the experimental peak frequency measured might have been higher with better temporal resolution. Our spontaneous signals measured in organotypic hippocampal cultures are of the same order of magnitude as the ones measured in vivo [38, 70]. In any case, our results show that genetically encoded calcium indicators (GECIs), such as GCaMP6s, may change local calcium concentration, in particular close to open IP₃R channels, leading to an increased peak duration. Those results are in accordance with previous studies that demonstrate that calcium buffers, such as GECIs, modulate signal readout [53, 71].

Together these results demonstrate that our model, without any endogenous buffers, is enough to reproduce calcium signals within fine astrocytic processes in a quantitative way, making it a powerful tool to investigate calcium dynamics in the small volumes associated with PAPs.

Effect of GCaMP properties on calcium dynamics

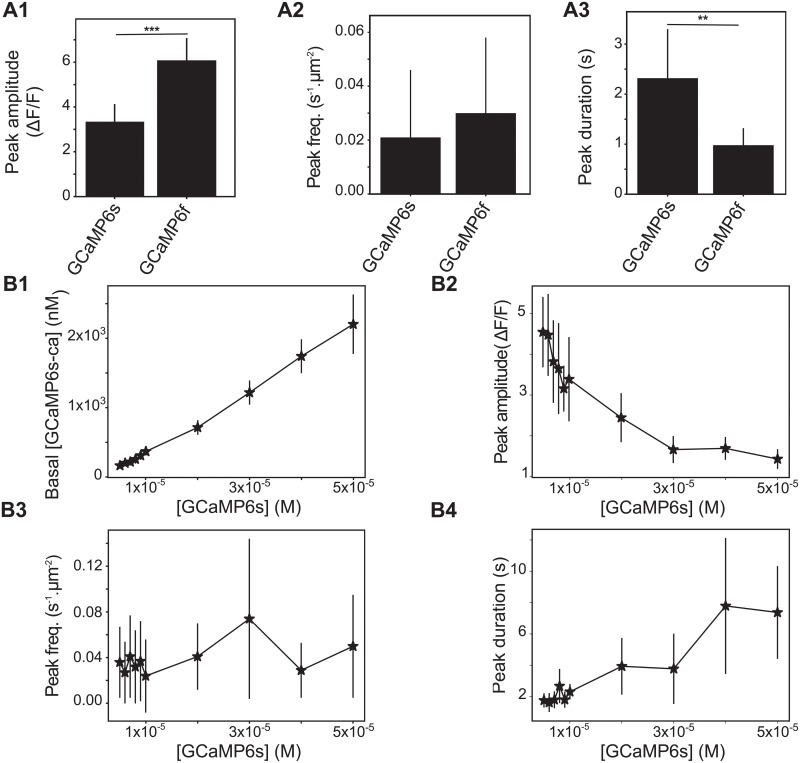
Because our “GCaMP” simulations revealed that the use of GECIs may change local calcium concentration and thus impact peak duration, we have next investigated the effect on calcium dynamics of several parameters defining GCaMP molecules: their kinetics and their concentration. We tested to what extent using different GECIs in our simulations impacted calcium dynamics. We compared the dynamics of [GCaMP6s-Ca] with those of [GCaMP6f-Ca]. Although the total concentration of GECIs in those two models is identical, GCaMP6f-Ca signals display higher amplitude and smaller duration than GCaMP6s-Ca signals (Fig 7A1 and 7A3). Those results are partially in agreement with experimental measurements [72] that have reported a similar decrease of peak duration when using GCaMP6f compared to GCaMP6s. However, experimental observations also included a decrease of the peak amplitude with GCaMP6f, that we do not observe. This discrepancy could be due to a higher fluorescence baseline of GCaMP6f-Ca in those experiments, leading to decreased ΔF/F ratio.

Fig 7. The kinetics and concentration of GECIs strongly influence calcium dynamics.

(A) Quantitative comparisons of the spontaneous calcium signals measured with “GCaMP6s” or “GCaMP6f” as fluorescent reporters. The compared quantities are peak amplitude in terms of ΔF/F ratio (A1), frequency (measured in min⁻¹ for each μm² area, A2) and duration (expressed as full width at half maximum, FWHM) (A3). (B) The impact of the concentration of GCaMP6s in the system on basal concentration of GCaMP-Ca (B1), on the GCaMP-Ca peak amplitude (B2), frequency (B3) and duration (B4) are shown for different values of [GCaMP6s]. Significance is assigned by * for p ≤ 0.05, ** for p ≤ 0.01, *** for p ≤ 0.001. Data are presented as mean ± standard deviation over 20 simulations. Lines are guide for the eyes.

As the concentration of GECIs cannot be controlled experimentally and is often not reported in calcium imaging studies, we have next investigated its effect on calcium signals (Fig 7B). Our simulations demonstrate that an increased GCaMP concentration in the cell results in a linear increase of basal GCaMP-Ca levels (Fig 7B1), with an unchanged basal concentration of free calcium. Increased [GCaMP] is associated with a decrease of GCaMP-Ca peak amplitude expressed in terms of ΔF/F ratio (Fig 7B2) and an increase of peak duration (Fig 7B4). Interestingly, varying [GCaMP] does not seem to have an impact on peak frequency (Fig 7B3), which is contradictory to Skupin et al’s results that have demonstrated a non-linear increase of the average signal period with the concentration of exogenous buffers [54]. However, Skupin et al studied whole-cell EGTA or BAPTA dynamics, which is fundamentally different from the local spontaneous GCaMP-Ca signals in the fine processes that we are modelling here. Local variations of cellular GCaMP concentration might thus yield variations of peak duration and amplitude, so that measuring cellular GCaMP concentration and its variations along the cellular compartments appears crucial to analyze calcium signals more accurately.

Discussion

Recent experimental reports suggested that the complete dependence of cytosolic calcium transients on IP₃R2 is only observed in the astrocyte cell body whereas calcium signals measured within astrocytic processes are a mix of IP₃R2-dependent and non-IP₃R2-dependent calcium signals [21, 28]. The identity, subtype and localization of the receptors responsible for non-IP₃R2-dependent calcium signals in astrocytes, in particular their processes, are still to be uncovered. However, our study sheds light on the importance of the localization of these various calcium sources. Our simulation results indeed indicate that when IP₃R channels are (even moderately) co-localized with IP₃R-independent calcium sources, e.g. plasma membrane calcium channels, the degree of IP₃R clustering and/or the mobility of the calcium buffers will have a strong impact on the frequency and amplitude of the spontaneous calcium signals. In particular, our simulations predict that two astrocyte processes expressing exactly the same repertoire of channels, pumps and receptors but in a different spatial organization (for instance various degrees of clustering or co-localization), can exhibit very different types and properties of spontaneous calcium events. This could result in significant variability of the calcium response of different processes, even from the same cell. Moreover, our results suggest that ‘puffs’ might reflect cellular sub-compartments in which calcium channels are co-localized, which increases the calcium response to a given stimulus. It would thus be interesting to investigate whether those co-localizations can be observed at specific locations, such as at neuron-astrocyte contact sites, or if they are randomly distributed within the cell.

During the past few years, fine astrocytic processes have been regarded as devoid of ER [73, 74]. This questions the validity of our model, in which the presence of ER-attached IP₃R in the process is crucial for spontaneous activity. We however note that a recent EM study has observed that ER dynamically ramified in astrocyte perivascular processes in vivo and detected contact sites between ER processes and plasma membrane, often positioned in apposition to neuronal synapses [75]. Such contiguous membranous juxtapositions would definitely validate the presence of ER in PAPs. Although dynamical ER remodeling has been reported in dissociated astrocyte culture [76], technical limitations have prevented direct investigation of ER localization within PAPs in vivo or in slices. To our knowledge, it is not even clear whether astrocytic ER is continuous or consists in several independent reservoirs. Super-resolution microscopy of cellular ER and mitochondrial dynamics and structure (resolution ≈ 100nm) has recently been developed and could help solve the controversy regarding the presence of ER in fine processes [77, 78]. Correlative super-resolution fluorescence imaging and electron microscopy approaches can yield a resolution of less than 50 nm (down to 10nm) [79], which is very promising avenue to PAPs ultrastructure investigation. ER-bound GECIs, OER-GCaMP6f, have been recently developed and, combined with the use of ER luminal calcium indicators such as G-CEPIA1_er [80], could help investigate the involvement of calcium channels on the ER membrane in calcium dynamics depending on subcellular localization in astrocytes [81]. In any case, since the IP₃R pathway is involved in calcium dynamics, further investigations regarding ER sub-cellular localization, sub-compartmentalization and dynamics are crucial for better understanding astrocyte information processing. Meanwhile, a straightforward extension of our computational model would be to simulate neuronal stimulation-triggered calcium dynamics.

IP₃Rs are thought to assemble as tetramers, and a recent experimental study suggested that the four subunits of the tetramer must be simultaneously bound to IP₃ for the tetramer to allow calcium influx, independently of cytosolic calcium or ATP concentrations [82]. Actually, the original IP₃R model predicted that subunit cooperativity for calcium binding is also necessary to fit experimental data of IP₃R dynamics [46, 48]. Even though the IP₃R binding sites for calcium have been characterized, their roles in IP₃R dynamics are still poorly understood [83]. The requirement for inter-subunit cooperativity, in which the 4 IP₃ binding sites should simultaneously be bound for the tetramer to open, is expected to hinder the emergence of spontaneous calcium events. In a subset of simulations, we have replaced our non-cooperative IP₃R model, in which the binding of a single IP₃ site is enough to open the monomer channel, with the cooperative model proposed by Bicknell and collaborators [84]. With 100 nM basal IP₃ and Ca²⁺ [85, 86], we could not produce spontaneous calcium signals in these conditions, even after a search of the parameter space to locate parameters allowing spontaneous activity with this cooperative model. This issue might reflect a general problem of the De Young Keizer model in discrete particle-based models with low copy number of particles. The De Young Keizer model is based on steady-state experimental data representing averages over time and over channel populations, which proved sufficient to reproduce experimental statistics such as the average open time or the steady-state open probability. However, this model might not be suited to describe behaviors at the level of individual channels and low copy number of particles. More recent models have been proposed that successfully reproduce the evolution with time of the open/close dynamics of a single IP₃R [87, 88]. In those models, the transition rates between different states of the IP₃R are not triggered by Ca²⁺ or IP₃ binding events but by complex continuous functions of their concentrations. We could not implement such complicated functions with a pure particle-based modeling strategy such as used here. Therefore, further investigations are needed to clarify the suitability of the De Young Keizer model in the context of particle-based spatially-explicit stochastic models. Alternatively, our results may be interpreted as casting doubts on the existence of spontaneous calcium signals in astrocytes when the basal IP₃ and Ca²⁺ concentrations are of the order of 100 nM. A number of studies have reported higher calcium concentration localized at the vicinity of calcium channels [89–91]. Such calcium microdomains, in the vicinity of IP₃R, could facilitate the emergence of spontaneous signals from cooperative IP₃Rs in thin processes.

On the other hand, experimental evidence for spontaneous calcium signals in astrocytes is still debated. Even in the absence of presynaptic neural activity, presynaptic axon terminals do probabilistically release neurotransmitter vesicles, generating so-called miniature EPSCs. Bafilomycin application has been used in several experimental studies to investigate the dependence of astrocytic calcium signals on EPSCs, because this inhibitor of V-ATPases inhibits miniature EPSCs by blocking the refill of presynaptic vesicles. However, the impact of bafilomycin bath application on the frequency of spontaneous calcium signals in astrocytes has proven variable (compare e.g. [92] and [93]). In our preparation, bath-application of bafilomycin strongly decreased peak frequency and amplitude [69]. As bafilomycin has a wide range of effects on calcium signaling that is independent of its effect on the refill of presynaptic neurotransmitter vesicles [94, 95], we cannot conclude whether those signals are triggered by EPSCs and further investigation is needed to decipher whether the “spontaneous” calcium signals reported in astrocyte processes are due to spontaneous release of presynaptic vesicles or rely on a synapse-independent mechanism inherent to the CICR system.

For simplicity, IP₃R clustering in our model was considered static during simulation time. Experimentally, though, IP₃R clustering might be highly dynamic [96, 97]. Several molecules can trigger IP₃R clustering, including IP₃ and calcium themselves [96, 97], through a mechanism that may include the lateral diffusion of IP₃R on the ER surface [97] or be independent from it [98]. Beyond this IP₃R classification into clustered and un-clustered populations, another approach is to quantify single IP₃R channels based on their mobility. A recent study on HeLa cells [41] indicates that calcium signals emerge most of the time from immobile IP₃R, which are found in apposition to ER-plasma membrane junctions, whereas the mobile IP₃R fraction would not be involved in calcium influx. Our simulation results, in agreement with previous IP₃R-mediated calcium models [99, 100], indicate that IP₃R clustering can lead to an increase of the frequency and amplitude of their calcium signals. This result is in contradiction with a previous modeling study that concluded in favor of a reduction of IP₃R channel activity upon IP₃R clustering [101]. This discrepancy might rely on the different modeling choices. In particular, the model in [101] incorporates a 5-state IP₃R model derived from Tu et al. [102, 103]. All of those modeling studies however agree that dynamical IP₃R clustering could be a mechanism used by astrocyte processes to modulate their calcium signals. This could provide astrocyte processes with a capacity for information processing plasticity.

In our model, the value of the rate constant for calcium binding on IP₃R changes the type of spontaneous dynamics (e.g. blips vs puffs) in addition to its characteristics (frequency, amplitude). Experimentally, several post-transcriptional mechanisms can modulate IP₃R affinity. For instance, phosphorylation of type-1 and -2 IP₃R by cAMP-activated PKA increases the affinity of IP₃R to calcium and IP₃ [104]. At a larger time scale, the sensitivity of IP₃R to calcium is encoded in a sequence of calcium sensor (Cas) region that differs depending on the IP₃R isoform [102, 105, 106]. Since multiple IP₃R isoforms seem to be involved in calcium signaling within astrocytic processes [33], they could assemble into a variety of homo- or hetero- IP₃R tetramers that would exhibit a range of calcium and IP₃ affinity.

In addition, immobile or weakly mobile endogenous calcium buffers are responsible for an effective intracellular calcium diffusion that is an order of magnitude slower than free calcium ions [107]. Our simulation results indicate that the value of the effective Ca²⁺ mobility also participates in the determination of the type and characteristics of the spontaneous events, thus confirming previous experimental [108] and modeling studies [53, 60, 62, 109, 110]. Although our simulations with both GCaMP and endogenous buffers,”GC+Buf”, overall displayed dynamics similar to the simulations without endogenous buffers (”GCaMP”), we note that, similarly to the effect of GCaMP concentration, increasing the concentration of endogenous buffers led to longer duration of the calcium signals. Those results are consistent with previous studies that have demonstrated significant effects of buffers [61] or of intra-cluster channel communication and coupling [53] on calcium dynamics. Endogenous calcium buffers display various kinetics and diffusion coefficients in astrocytes [111] and some of them are overexpressed in hippocampal and striatal astrocytes, possibly in a region-specific pattern [112], which could be involved in the regional variability of astrocytic calcium signals [113]. Our study shows that precisely accounting for the effects of GECIs and endogenous calcium buffers on calcium dynamics is crucial for better interpreting calcium signals in PAPs. Particular care should be taken when interpreting GCaMP-Ca signals as GCaMP concentration is rarely monitored although it could be partly responsible for the diversity of calcium signals observed in PAPs.

Therefore, in addition to the spatial organization of the Ca²⁺ channels, the differential expression of endogenous calcium buffers, including the fluorescent Ca²⁺ reporters, could also be potential determinants allowing a range of responsiveness and spatio-temporal characteristics of calcium signals in astrocyte processes.

To conclude, we have presented a spatially-explicit stochastic model to investigate intracellular calcium signaling based on CICR in small sub-cellular volumes. Recent studies proposed models for the simulation of astrocytic sodium [114] and calcium signals [74, 115, 116] in 3d with deterministic differential equation models that correspond to cellular volumes large enough to validate a law of large numbers. To our knowledge, our model is the first model suited to reproduce spontaneous calcium signals in the finest astrocyte processes, where low copy number and spatial localization effects are expected to be more prominent than in larger volumes. Our simulations demonstrate that low copy number of molecules can display dynamics that cannot be predicted by deterministic approaches and that spatial modelling is crucial to better understand the effect of molecular distributions and sub-compartments geometries on calcium dynamics. Since these fine processes are thought to be the place of initiation of neuron-astrocyte interactions, we believe that this model, combined with models of signal propagation between astrocytic compartments such as Savtchenko et al. [116], might be useful to investigate the initiation and spatiotemporal integration of calcium signals in the sponge-like network of astrocyte processes, a prerequisite to understand neuron-astrocyte communication.

Materials and methods

Modeling methods

Reaction scheme

The model considers cytosolic calcium and IP₃ dynamics in the framework of calcium-induced calcium release (CICR) signaling. The reaction scheme considered is shown in Fig 1 A. In short, we consider calcium fluxes between the cytosol and the extracellular space or the endoplasmic reticulum (ER), including via IP₃R channels. We also take into account the effect of phospholipase C δ (PLCδ), that, when activated by calcium, synthesizes IP₃. To derive simple models for this scheme, we made the following assumptions:

• We considered that the extracellular and ER calcium concentrations are constant during the simulation, as well as the electrical potentials across the plasma and ER membranes. In this case, calcium outflow from the cytosol to the ER or to the extracellular medium can be lumped into a single first-order rate α. Likewise, calcium entry from the extracellular medium or any IP₃R-independent Ca²⁺ influx from the ER can be considered constants, too. We lumped them into a single overall constant flux γ.

• PLCδ enzymes remain located in the cytosol (no translocation) and the amount of their substrate PIP2 is present everywhere in large excess. Under this condition, activated PLCδ produces IP₃ with constant rate δ.

IP₃R channels are gated both by calcium and IP₃, with a bell-shaped dependence of the open probability to calcium concentration [56]. To model their dynamics, we used the classical 8-state Markov model proposed in [46, 56], with two calcium binding sites, referred to as ‘Ca sites’, and one IP₃ binding site for each IP₃R (see Fig 1B). However we used the following simplifications:

• We considered that the binding or unbinding rate constant of a given binding site is independent from the occupancy state of the other sites (no intra-channel cooperativity). Under this assumption, the rate constant for calcium binding at the first calcium binding site, a₁, does not depend on whether the other two binding sites are bound or not. Thus, the rate constant for {000} + Ca → {100} has the same value as e.g. the reaction {011} + Ca → {111} (where the triplet notation corresponds to the one defined in Fig 1). Likewise, the rate constants for Ca²⁺ or IP₃ binding or unbinding to the three sites were considered independent from the other occupancy states.

• The open state is assumed to be state {110} (first Ca site and IP₃ bound, second Ca site free), as in [46, 56]. These latter models further assume inter-channel cooperativity, where IP₃R channels assemble as tetramers of which at least three monomers must be in the open state for calcium to be transferred. Here we neglected inter-channel cooperativity and considered that every single channel was open when in the open state i.e., as long as an IP₃R channel is open, it is assumed to inject calcium in the cytosol at constant rate μ.

Monte Carlo simulations of the spatially-explicit stochastic particle-based model

We first modeled the kinetic scheme described in Fig 1 with a lattice-free spatially-explicit stochastic particle-based model, referred to as “Particle-based” model below, in two spatial dimensions, with reflective boundary conditions. Each molecule of the system was explicitly modeled with its associated position in space. PLCδ and IP₃R molecules were considered immobile whereas Ca²⁺ and IP₃ molecules were mobile by diffusion. At the beginning of each Monte-Carlo (MC) simulation of this model, the space coordinates for each Ca²⁺, IP₃ and PLCδ molecules are chosen uniformly at random.

To determine the positions of the $N_{{\text{IP}}_{\text{3}}\text{R}}I{P}_{\text{3}}R$ molecules, we first chose the centers of $N_c=N_{{\text{IP}}_{\text{3}}\text{R}}/\eta I{P}_{\text{3}}R$ clusters uniformly at random in the reaction space, where η is the number of IP₃R per cluster (as illustrated in Fig 1C). For each cluster, we positioned η IP₃R molecules uniformly at random within a distance R_c of the cluster center, with $R_c=d_{I{P}_{3}R}\sqrt{\eta /0.91}$, where $d_{{\text{IP}}_{\text{3}}\text{R}}$ is the interaction distance of the IP₃R, i.e. the maximal distance between IP₃R center and a Ca²⁺ or IP₃ molecule below which binding can occur. According to this algorithm, η = 1 corresponds to randomly distributed independent IP₃R molecules (no clustering) whereas IP₃R molecules become increasingly clustered when η increases, with constant IP₃R density within the clusters and constant total IP₃R number in the reaction space.

Each MC stimulation step (of duration Δt) consists in iterating the following steps:

1. Diffusion. The position of each mobile molecule (Ca²⁺ and IP₃) is updated independently according to Brownian motion: $\mathbf{\text{r}}(t+\Delta t)=\mathbf{\text{r}}\left(t\right)+\sqrt{2D_i\Delta t}\xi$, where D_i, i = {Ca, IP3} is molecule i diffusion coefficient and ξ is a vector of i.i.d. Gaussian-distributed random numbers with zero mean and unit variance. In a subset of simulations, the new position of each mobile molecule was chosen at random in the reaction volume, i.e. r(t + Δt) = ζ were ζ is a vector of i.i.d. random numbers uniformly distributed in [0, L], with L the length of the spatial domain. We refer to this setting as “infinite” diffusion coefficients, D = ∞.

2. Binding. For each Ca²⁺ ion close enough to a PLCδ to react (i.e. when the distance between both is less than the interaction radius of PLCδ), a new IP₃ molecule is created with probability δΔt at the position of the PLCδ molecule. Likewise, each Ca²⁺ or IP₃ molecule close enough to an IP₃R molecule (i.e. within its interaction radius) can bind it depending on its occupancy state. If the IP₃ binding site is free, an IP₃ molecule binds with probability a₂Δt. If one of the Ca sites is free, a Ca²⁺ ion binds the free site with probability a₁Δt (first Ca site) or a₃Δt (second Ca site). If both Ca sites are free, binding occurs to the first site with probability a₁Δt and to the second one with probability (1 − a₁Δt)a₃Δt.

3. Unbinding. Each IP₃R molecule releases its bound Ca²⁺ or IP₃ molecules independently, with probability b₁Δt (first Ca site), b₂Δt (IP₃ site) and b₃Δt (second Ca site). Ca²⁺ or IP₃ molecules that bound the IP₃R at the previous (binding) step of the current time step do not unbind.

4. Removal. Free cytosolic Ca²⁺ and IP₃ molecules are removed from the cytosol with probability αΔt and βΔt, respectively. Ca²⁺ and IP₃ molecules that unbound from IP₃R at the previous (unbinding) step of the current time step are not removed.

5. Ca²⁺ Influx. For each IP₃R channel in the open state {110}, a new Ca²⁺ ion is created in the cytosol at the IP₃R position with probability μΔt. A new calcium ion can also be created in the cytosol with probability γΔt, mimicking Ca²⁺ influx from IP₃R-independent sources in the ER membrane or through the plasma membrane. Note that the position of this new calcium is not uniform over space but depends on parameter R_γ and works as follows: an IP₃R molecule is chosen (uniformly) at random and the new Ca²⁺ ion is positioned uniformly at random within distance R_γ of the chosen IP₃R. Therefore low values of R_γ emulate co-localization between IP₃R-dependent and IP₃R-independent Ca²⁺ influx sources, whereas the location of IP₃R-independent Ca²⁺ influx is uniform over the reaction volume when R_γ becomes as large as the volume side length.

Table 1 gives the parameter values used in our 2D simulations, including the initial numbers of Ca²⁺, PLCδ, IP₃ and IP₃R molecules.

Mean-field (MF) dynamics of the perfectly stirred model

With infinite diffusion, the dynamics of the system can be assumed to be perfectly stirred. With that mean-field (MF) assumption, the temporal dynamics of reaction scheme Fig 1 can be modeled using ordinary differential equations based on the mass-action law. IP₃R dynamics in these conditions can be described with seven ODEs that express the temporal dynamics of the concentration of IP₃R in state {ijk}, [ijk]:

$$\{\begin{array}{l}\text{d}[000]/\text{d}t=-\left(a_1[Ca]+a_2[IP3]+a_3[Ca]\right)[000]+b_1[100]+b_2[010]+b_3[001]\hfill \\ \text{d}[001]/\text{d}t=-\left(a_1[Ca]+a_2[IP3]+b_3\right)[001]+b_1[101]+b_2[011]+a_3[Ca][000]\hfill \\ \text{d}[010]/\text{d}t=-\left(a_1[Ca]+b_2+a_3[Ca]\right)[010]+b_1[110]+a_2[IP3][000]+b_3[011]\hfill \\ \text{d}[011]/\text{d}t=-\left(a_1[Ca]+b_2+b_3\right)[011]+b_1[111]+a_2[IP3][001]+a_3[Ca][010]\hfill \\ \text{d}[100]/\text{d}t=-\left(b_1+a_2[IP3]+a_3[Ca]\right)[100]+a_1[Ca][000]+b_2[110]+b_3[101]\hfill \\ \text{d}[101]/\text{d}t=-\left(b_1+a_2[IP3]+b_3\right)[101]+a_1[Ca][001]+b_2[111]+a_3[Ca][100]\hfill \\ \text{d}[110]/\text{d}t=-\left(b_1+b_2+a_3[Ca]\right)[110]+a_1[Ca][010]+a_2[IP3][100]+b_3[111]\hfill \end{array}$$ (1)

where [Ca] and [IP3] denote Ca²⁺ and IP₃ concentration, respectively. The concentration of the eighth occupancy state, {111} is obtained from conservation of the IP₃R, i.e. $\left[111\right]=N_{{\text{IP}}_3\text{R}}/V-\left(\left[000\right]+\left[001\right]+\left[010\right]+\left[011\right]+\left[100\right]+\left[101\right]+\left[110\right]\right)$. IP₃ dynamics in the mean-field model is given by:

$$\begin{array}{c}\hfill \mathrm{d}\left[IP3\right]/\mathrm{d}t=-a_2\left[IP3\right]\sum _{i=0}^1\sum _{k=0}^1\left[i0k\right]+b_2\sum _{i=0}^1\sum _{k=0}^1\left[i1k\right]+\delta \left[PLC\delta \right]\left[Ca\right]-\beta \left[IP3\right]\end{array}$$ (2)

where [PLCδ] = N_plc/V. Finally, the mean-field dynamics of the free Ca²⁺ is obtained with:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{d}\left[Ca\right]/\mathrm{d}t=& -(a_1\sum _{j=0}^1\sum _{k=0}^1\left[0jk\right]+a_3\sum _{i=0}^1\sum _{j=0}^1\left[ij0\right])\left[Ca\right]\hfill \\ & +b_1\sum _{j=0}^1\sum _{k=0}^1\left[1jk\right]+b_3\sum _{i=0}^1\sum _{j=0}^1\left[ij1\right]\hfill \\ & -\alpha \left[Ca\right]+\gamma +\mu \left[110\right]\hfill \end{array}\end{array}$$ (3)

For comparison with the output of the other models, the concentrations were transformed into numbers of molecules by multiplication by the reaction volume V.

Perfectly-stirred stochastic temporal dynamics (SSA)

For comparison, we also modeled the reaction scheme depicted in Fig 1 using Gillespie’s exact Stochastic Simulation Algorithm (SSA) that accounts for stochasticity due to low copy numbers and assumes perfect mixing of the reactants [117, 118]. Here, the dynamic variables are the number of Ca²⁺ and IP₃ molecules in the system, N_Ca and N_IP3 and the number of IP₃R channels in state {ijk}, N_ijk. The rates of all the reactions of the scheme of Fig 1 are then calculated according to mass-action laws like in the MF model of Eqs (1), (2) and (3). For instance, at reaction time t, the rate of reaction {001} + Ca → {101} is given by a₁/V N₀₀₁(t)N_Ca(t). The next reaction time τ is sampled from an exponential distribution with mean 1/R_T, where R_T is the sum of the reaction rates of all reactions. The next reaction to occur at time t + τ is chosen as an integer random variable with point probability given by the ratio of its rate to R_T. For instance, for the reaction illustrated above, the probability that this reaction is the one occurring at time t + τ is a₁/V N₀₀₁(t)N_Ca(t)/R_T. Finally, the variables are updated according to the chosen reaction. In the data presented below, we have modeled each receptor individually, i.e. for each receptor $l\in 0\dots N_{{\text{IP}}_3\text{R}}$, $N_{ijk}^l=1$ if receptor l is in state ijk, 0 else. If the illustration reaction described above on receptor l is chosen, this means $N_{001}^l(t+\tau )=N_{001}^l(t)-1$, N_Ca(t + τ) = N_Ca(t) − 1 and $N_{101}^l(t+\tau )=N_{101}^l(t)+1$. The other variables keep their values.

Realistic simulations in 3d astrocytic processes

In order to simulate calcium dynamics within a more refined 3d geometry with realistic volumes and concentrations, we built a model in STEPS (http://steps.sourceforge.net/). STEPS is a software for voxel-based stochastic reaction-diffusion simulations within complex 3d geometries that simulates stochastic chemical reaction-diffusion with a spatialized version of Gillespie’s SSA, usually referred to as the reaction-diffusion master equation (RDME). In RDME, space is partitioned into voxels inside which perfect mixing is assumed, while diffusion between adjacent voxels is modeled as first order reactions [119, 120]. STEPS uses a derivative of the SSA in tetrahedral voxels that allows for a better resolution than the cubic voxels mostly used in voxel-based models [121].

Geometry. The main advantage of STEPS in the context of the present study is its automatic handling of external and internal membranes [122]. Moreover, STEPS simulations can easily be parallelized [123], a crucial property given the computational burden of such compartmentalized 3d simulations. This allowed us to explicitly describe the presence of the ER membrane inside the 3d cell cytoplasm and the fact that IP₃R channels are located in the ER membrane. The geometry of the reaction volume consisted in a cylinder of length L_astro = 1 μm and radius R_astro = 0.1 μm. The ER was modeled as a second cylinder, internal, with length L_ER = 0.75 μm and radius R_ER = 0.03 μm. The resulting cytosolic volume (2.81 × 10⁻¹⁷ L) was meshed with 11345 tetrahedra of individual volume 2.48 × 10⁻²¹ L, thus ensuring the well-mixed subvolume condition [121].

Reactions. In this spatial configuration, we modeled the IP₃R-mediated calcium signaling kinetic scheme of Fig 1 with IP₃R channels positioned on the intracellular ER membrane and according to three model variants:

• A first variant, referred to as the “No-GCaMP” model, did not include fluorescent calcium indicators. In this 3d model, parameter values were taken, whenever possible, from the literature (Table 2). γ and α values were adjusted to yield basal calcium concentration around 120 nM [86, 124]. Likewise, β and μ were adjusted for a basal IP₃ concentration of 120nM [85]. Note that this value is based on recent, precise measurements of IP₃ concentration and differs by an order of magnitude from IP₃ concentration values routinely used in IP₃R-mediated calcium models [59, 125, 126]. IP₃R density on the ER surface has been measured from TIRF-microscopy analysis in cell cultures [89], reporting IP₃R cluster diameters of 0.3 μm at most, with up to 10 IP₃R per cluster. The ER surface area in our model is 0.69 μm². Ignoring the potential unclustered IP₃Rs [98], this represents a maximum of 4 clusters, thus at most 40 IP₃R. We thus set the number of IP₃R in our model to 50 channels on the ER surface. Finally, Ca²⁺ and IP₃ binding and dissociation constants to IP₃R were adjusted to fit our experimental data of calcium micro-domains in organotypic cultures of hippocampal astrocytes.

• A second variant of the 3d model, referred to as the “GCaMP”(=”GCaMP6s”) model, was obtained by adding GCaMP6s calcium indicators in the cytosol. GCaMP6s are ultrasensitive calcium indicators that fluoresce when bound to Ca²⁺. The fluorescence signal from experimental data indeed corresponds to the concentration of calcium-bound GCaMP6s, which can be quite different from free cytosolic Ca²⁺ trace. For this model, all the parameters were set to the same values as the “No-GCaMP” model, except those related to GCaMP that were taken from the available experimental literature and shown in Table 2. The parameters for GCaMP6f kinetics were taken from Chen et al. [72].

• A third variant of the 3d model, referred to as the “GC+Buf” model, was obtained by adding endogenous buffers to the “GCaMP” model. The kinetic scheme is presented in S2 Fig. Parameter values for calcium, IP₃, IP₃R and GCaMP dynamics were the same as the “GCaMP” model. Parameter values for endogenous buffers dynamics were taken from the literature [127] and are presented in S1 Table.

Table 2. Parameter values and initial conditions of the 3d model.

The parameter values for the 3d model listed here correspond to the “GCaMP” model. The parameter values for the “No-GCaMP” 3d model are the same except that GCaMP6s concentration equals 0 nM. In the “GCaMP6f” model variant, Gcamp_f = 1.05 × 10⁷ M⁻¹.s⁻¹ and Gcamp_b = 3.93s⁻¹. Parameter values in the 3d model have been adjusted to optimize the match with experimental data as described in the Methods section. Note that the values for calcium and IP₃ binding or unbinding to IP₃R, i.e. the a_i’s and b_j’s parameters below, are smaller in our model than in the literature, probably because our model is not cooperative. For GCaMP6s and GCaMP6f, we used the diffusion coefficient of calmodulin. The initial number of Ca²⁺ ions was adjusted so that the measured basal GCaMP6s-Ca concentration was around 300nM [86, 124].

Parameter	Description	Value in 3d GCaMP model	Reference
V	Cell volume	2.81 × 10−17 L	[128]
IP3 dynamics
IP0	Initial IP3 number/conc	3 molec. i.e 177 nM	[85]
DIP3	IP3 diffusion	280 μm2.s−1	[107]
Nplc	PLCδ number/conc.	1696 molec. i.e 100 μM	[129]
δ	PLCδ max rate	1 s−1	-
β	IP3 decay	1.2 × 10−4 s−1	-
Ca2+ dynamics
Ca0	Initial Ca2+ number/conc.	5 molec. i.e 295 nM	[86]
DCa	Ca2+ diffusion	13 μm2.s−1	[107]
μ	Ca2+ flux through open IP3R	6 × 103 s−1	-
γ	cytosolic Ca2+ influx	1.5 × 10−7 s−1	-
α	Ca2+ decay rate	30 s−1	-
GCaMP6s
CGCa	GCaMP6s conc.	169 molec. i.e 10 μM	[130, 131]
DGCaMP	GCaMP6s diffusion	50 μm2.s−1	[132]
Gcampf	GCaMP6s Ca binding rate	7.78 × 106 M−1.s−1	[72]
Gcampb	GCaMP6s-Ca dissociation rate	1.12 s−1	[72]
IP3R
$N_{{\text{IP}}_{\text{3}}\text{R}}$	IP3R number	50 molec.	[89]
$d_{{\text{IP}}_{\text{3}}\text{R}}$	IP3R interact. distance	1 mesh triangle	-
IP3R binding
a1	First Ca	1.2 × 106 M−1.s−1	-
a2	IP3	4.1 × 107 M−1.s−1	-
a3	Second Ca	1.6 × 104 M−1.s−1	-
IP3R dissociation
b1	First Ca	50 s−1	-
b2	IP3	400 s−1	-
b3	Second Ca	100 s−1	-

Simulations code

The code of our ODE, Gillespie, Particle-based and STEPS models is available on ModelDB [133] at http://modeldb.yale.edu/247694.

Peak detection and analysis

Automated peak detection from model simulations was based on the statistics of baseline calcium trace. A histogram of Ca²⁺ trace was built with a bin size of 0.25 ions and the mode of this histogram was used to define baseline calcium. A peak initiation corresponded to the time step where calcium trace overcame a peak threshold defined as baseline + nσ_Ca where σ_Ca is the standard deviation of the above histogram. The value of n varied between 2 and 4 and was set by hand for each simulation, depending on its signal/noise ratio. The peak was considered terminated when the calcium trace decreased again below peak threshold. This implies that in case of a second calcium peak starting before the first one terminated, both events were considered as being part of the same peak. Peak duration was defined as the full width at half maximum (FWHM). Peak amplitude was defined as the maximum number of calcium ions reached during the peak duration. In the 3D model, the peak amplitude A was rescaled to facilitate comparison with experimental data, using $\Delta F/F=\left(A-C_{a_{\text{baseline}}}\right)/C_{a_{\text{baseline}}}$, where $C_{a_{\text{baseline}}}$ is the basal calcium determined above. The number of IP₃R open per peak was defined as the maximum number of IP₃R open simultaneously during peak duration. Puffs were defined as calcium events resulting from the cooperation of more than one IP₃R. In our spatially-explicit simulations, a calcium signal was considered to be a puff if more than one IP₃R were open during the peak and if the average distance traveled by calcium within the duration of this peak was larger than the distance between the simultaneously open IP₃R molecules.

Experimental methods

All experiments were performed as described in [69]. We give below the main outlines of the methods. All experimental procedures were in accordance with the European Union and CNRS UMR5297 institutional guidelines for the care and use of laboratory animals (Council directive 2010/63/EU).

Organotypic hippocampal slice cultures

Organotypic hippocampal slices (Gähwiler type) were dissected from 5–7-d-old wild-type mice and cultured 5–8 week in a roller drum at 35°C, as previously described [134].

Viral infection

AAV9-GFAP-GCaMP6s [70] was injected by brief pressure pulses (40ms; 15 psi) into the stratum radiatum of 2-3-week old slices from Thy1-YFP-H (JAX:003782) mice 4-6 weeks prior to the experiment.

Image acquisition

For Ca²⁺ imaging, we used a custom-built setup based on an inverted microscope body (Leica DMI6000), as previously described in [135]. We used a 1.3 NA glycerol immersion objective equipped with a correction collar to reduce spherical aberrations and thereby allow imaging deeper inside brain tissue [136]. The excitation light was provided by a pulsed diode laser (l = 485 nm, PicoQuant, Berlin, Germany). The fluorescence signal was confocally detected by an avalanche photodiode (APD; SPCM-AQRH-14-FC; PerkinElmer). The spatial resolution of the setup was around 175 nm (in x-y) and 450 nm (z). Confocal time-lapse imaging (12.5 x 25 μm, pixel size 100 nm) was performed at 2Hz for 2.5 min in artificial cerebrospinal fluid containing 125 mM NaCl, 2.5 mM KCl, 1.3 mM MgCl₂, 2 mM CaCl₂, 26 mM NaHCO₃, 1.25 mM NaH₂PO₄, 20 mM D-glucose, 1 mM Trolox; 300 mOsm; pH 7.4. Perfusion rate was 2 mL/min and the temperature 32°C. Calcium traces are available at https://figshare.com/articles/Astrocytic_calcium_traces_from_organotypic_hippocampal_slices/8951006.

Image analysis

Spontaneous calcium events were detected and analyzed automatically by ImageJ plugin LC_Pro [137] and then manually verified using Igor Pro (Wavemetrics) [33].

Statistical analysis

For stochastic models, we generated 20 simulations (with different random numbers) and quantified these simulations as mean ± standard deviation over those 20 simulations. One-way ANOVA was performed to investigate the effect of a given parameter on calcium dynamics. Comparison between two simulation conditions were performed with unpaired Student T test if values followed a Gaussian distribution. Otherwise, a Mann-Whitney test was performed. The same method was applied to compare simulation to experimental results. Significance is assigned by * for p ≤ 0.05, ** for p ≤ 0.01, *** for p ≤ 0.001.

Supporting information

S1 Fig. Effect of adding buffers to the 2D particle-based model.

(A) Biochemical reactions and regulatory interactions modeled in the 2D particle-based model in which endogenous buffers (’Buf’) were added. Reactions are the same as the ones described in Fig 1, except that Buf particles were added. The binding rate and dissociation constant associated with the binding of Ca²⁺ to Buf correspond respectively to buf_f and buf_b. Different amounts of endogenous Ca²⁺ buffers were added to the model (500 or 2000), with the following diffusion coefficients: D_buf = 0.1 a.u and D_Ca = 0.8 a.u. Those simulations were compared to our reference model, which contains no Buf particles but in which D_Ca = 0.1 a.u, corresponding to an effective lower D_Ca. No significant difference between simulations with a number of Buf of 0, 500 or 2000 is observed regarding basal Ca²⁺ concentration (B), peak amplitude (C) or peak frequency (D). Note that we refer here to free Ca²⁺ peaks and not to Buf-Ca peaks. Simulating Ca²⁺ diffusion in our 2D model with a decreased effective coefficient of diffusion is thus equivalent to simulating endogenous buffers of slower diffusion with faster diffusion of free Ca²⁺.

(PDF)

S2 Fig. Reaction scheme of the 3D “GC+Buf” model.

This figure presents the biochemical reactions and regulatory interactions modeled in the endogenous buffers model, “GC+Buf”, in 3D. Reactions are the same as the ones described in Fig 1, except that new particles have been added: slow (CBs) and fast calbindin (CBf) as well as parvalbumin (PV), that can bind Ca²⁺ ions and diffuse, whether bound or not. Parameter values associated with this model are presented in S1 Table.

(PDF)

S1 Table. Parameter values and initial conditions associated to endogenous buffers in the 3D “GC+Buf” model.

Parameter values for the “GC+Buf” 3d model described in supplemental S2 Fig are the same as in “GCaMP” model, presented in Table 2. Parameter values associated with endogenous kinetics and diffusion were taken from a study that modeled calcium dynamics in dendrites [127]. Note that total endogenous buffer concentration in our model is 2 orders of magnitude lower than in this study.

(PDF)

Data Availability

The code of our ODE, Gillespie, Particle-based and STEPS models is available on ModelDB at https://senselab.med.yale.edu/modeldb/enterCode.cshtml?model=247694.

Funding Statement

The author(s) received no specific funding for this work.