Elucidating the Nuclear Quantum Dynamics of Intramolecular Double Hydrogen Transfer in Porphycene

Abstract

We address the double hydrogen transfer (DHT) dynamics of the porphycene molecule, a complex paradigmatic system in which the making and breaking of H-bonds in a highly anharmonic potential energy surface require a quantum mechanical treatment not only of the electrons but also of the nuclei. We combine density functional theory calculations, employing hybrid functionals and van der Waals corrections, with recently proposed and optimized path-integral ring-polymer methods for the approximation of quantum vibrational spectra and reaction rates. Our full-dimensional ring-polymer instanton simulations show that below 100 K the concerted DHT tunneling pathway dominates but between 100 and 300 K there is a competition between concerted and stepwise pathways when nuclear quantum effects are included. We obtain ground-state reaction rates of 2.19 × 10¹¹ s^–1 at 150 K and 0.63 × 10¹¹ s^–1 at 100 K, in good agreement with experiment. We also reproduce the puzzling N–H stretching band of porphycene with very good accuracy from thermostated ring-polymer molecular dynamics simulations. The position and line shape of this peak, centered at around 2600 cm^–1 and spanning 750 cm^–1, stem from a combination of very strong H-bonds, the coupling to low-frequency modes, and the access to cis-like isomeric conformations, which cannot be appropriately captured with classical-nuclei dynamics. These results verify the appropriateness of our general theoretical approach and provide a framework for a deeper physical understanding of hydrogen transfer dynamics in complex systems.

Introduction

In hydrogen and proton transfer reactions,¹ electronic polarization and anharmonicities of the potential energy surface (PES) cause a considerable coupling between different degrees of freedom in the system, leading to complex intra- and intermolecular vibrational energy transfer.² In addition, because of the light mass of hydrogen, nuclear quantum effects (NQEs) such as tunneling and zero-point energy (ZPE) can play a crucial role at remarkably high temperatures,³⁻⁷ and even heavy atoms (e.g., carbon or oxygen) can have an impact on hydrogen tunneling.^8,9 An accurate and quantitative description requires an all-atom, all-electron quantum simulation of these reactions and makes theoretical approaches based on empirical potentials and/or a dimensionality reduction of the PES, as well as a classical treatment of nuclear dynamics, inadequate.

Porphycene, the first synthesized structural isomer of free base porphyrin,¹⁰ has emerged as a unique example of intramolecular double hydrogen transfer (DHT) in a multidimensional anharmonic PES, where strong hydrogen bonds are formed in the molecular cavity.^11,12 Interest in this molecule has increased in recent years, especially due to results obtained from scanning probe microscopy. Those have shown how different external stimuli, such as light,¹³ heat,¹⁴ and force¹⁵ can control the DHT, establishing this molecule as a prototype for the manufacture of rapid optical molecular switches and logic gates.

The presence of strong hydrogen bonds results in a low reaction barrier and a high DHT rate at room temperature (k ≈ 10¹² s^–1)¹⁶ compared to those of other derivatives, e.g., porphine (k ≈ 10⁴ s^–1).¹⁷ The DHT reaction, which in this case connects the two degenerate trans tautomeric states (Figure 1), can occur through a stepwise or concerted mechanism. In the former case, the hydrogen atoms are transferred sequentially through an intermediate cis tautomeric state and the reaction pathway involves a first-order saddle point (SP1 in Figure 1). In the latter case, two hydrogen atoms are transferred in a correlated fashion without passing by a stable intermediate. This transfer can occur simultaneously through a second-order saddle point (SP2 in Figure 1), which is usually termed the synchronized mechanism.¹⁸ It is also well established that the tautomerization reaction in the porphycene molecule is a multidimensional process. The strong vibrational level dependence of the tunneling splittings^19,20 and the modification of the tautomerization rate upon deuteration of the peripheral hydrogens²¹ are two manifestations of the multidimensional nature of the tunneling process. At cryogenic temperatures in the gas phase (or in a helium droplet), the vibrational ground-state level exhibits a tunneling splitting of 4.4 cm^–1,^19,20,22 showing that trans–trans tautomerization takes place via coherent tunneling through the concerted mechanism.^23,24 Indeed, excellent agreement with the experimental values has been obtained considering only this pathway.²⁵ However, vibrational couplings to the environment or, at higher temperatures, couplings to the intramolecular vibrational modes lead to decoherence of the wave function such that the quantum state decays exponentially and the reaction dynamics can be described as a rate process.²⁶ In these cases, which are more relevant for biological or technological applications, it is not straightforward to clarify which mechanism governs the DHT reaction, how temperature affects the reaction rates, and the character of the vibrational modes that play a role.

Figure 1.

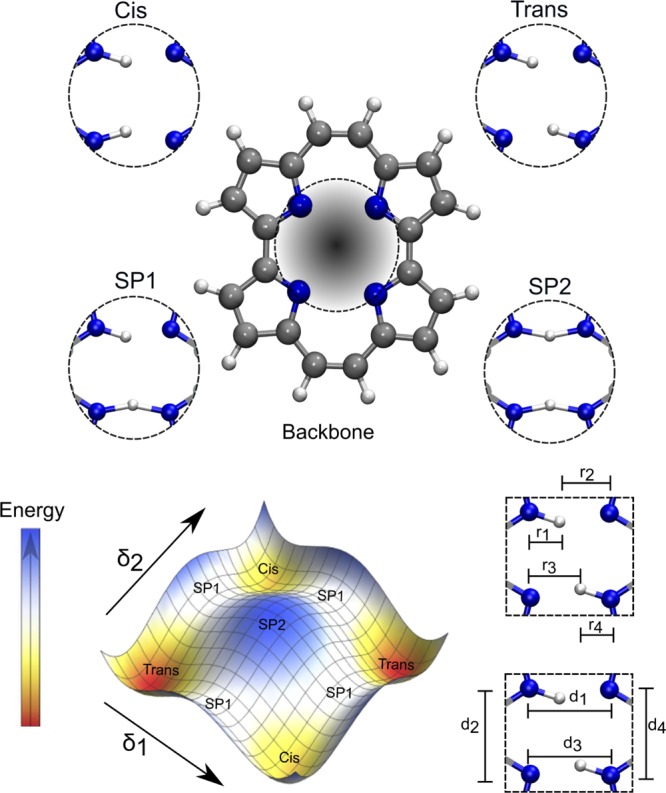
Characterization of the cis and trans isomers as well as a schematic two-dimensional (2D) potential energy surface (PES) of the porphycene molecule. SP1 and SP2 stand for first-order and second-order saddle points, respectively, and r and d are distances between atoms as marked in the figure. In the schematic 2D PES, δ₁ = r₁ – r₂ and δ₂ = r₃ – r₄.

Vibrational spectroscopy is a powerful tool that can shed light on nuclear dynamics and the PES. The hydrogen stretching vibrational band in this system serves as a fingerprint of hydrogen bonding and can exhibit extremely complex spectral features, such as a broadening and the emergence of satellite peaks. In porphycene, the characterization of the N–H stretching mode (ν_N–H) related to the trans–trans tautomerization has been particularly controversial, because of its apparent absence in the experimental Raman and infrared (IR) spectra, although theoretical calculations in the harmonic approximation predict a very intense band.²⁷ The broadening of ν_N–H in porphycene resulting from the intermode coupling has been examined by a classical nuclear dynamics approach,²⁷ but an agreement between simulations and experiment could not be fully achieved. This suggests that a strongly anharmonic PES, intermode couplings, and NQEs all play a decisive role in the static and dynamic properties of the inner hydrogen atoms of porphycene.

The situation outlined above has long hampered the elucidation of the hydrogen bonding structure and tautomerization dynamics in porphycene. Approximations to the quantum dynamics have been reported, but they relied on a dimensionality reduction of the system and thus neglected vibrational coupling to several modes.^24,28−30 Classical molecular dynamics simulations that included the full dimensionality of the system but neglected the quantum nature of the nuclei have been performed.^27,31 Imaginary-time path-integral simulations based on a semiempirical PES have been carried out to compute quantum statistical properties but did not use a methodology that could access the real-time dynamics of the system (e.g., rates or vibrational spectra).^32,33 To date, an atomistic full-dimensional study of the quantum dynamics in this system has not been presented.

Here we demonstrate that all-atom and all-electron quantum simulations of porphycene can fully reveal the equilibrium and dynamical properties of this molecule in the gas phase and explain a variety of experimental observations. Employing newly implemented and optimized ring-polymer instanton theory³⁴ and the recently proposed ring-polymer molecular dynamics coupled to colored noise thermostats,³⁵ we assess in detail the open questions regarding the hydrogen bonding geometry, the hydrogen transfer dynamics, and the nature of the ν_N–H band observed in the IR spectrum using a first-principles PES without resorting to any dimensionality reduction. We show that the hydrogen transfer mechanism in porphycene follows non-intuitive pathways at certain temperatures, which underlines the significance of NQEs and intramolecular vibrational coupling.

Results and Discussion

We first analyze the equilibrium properties of the porphycene molecule obtained from density functional theory (DFT-B3LYP+vdW) calculations and ab initio path-integral molecular dynamics (PIMD) simulations (see Methods). In Figure 2a, we show the free energy profile projected on the two hydrogen transfer coordinates δ₁ and δ₂ defined in Figure 1 for the PIMD simulation at 290 K. As expected, the trans isomer is the most energetically stable and the free energy barrier for hydrogen transfer is around 2 k_BT, in agreement with previous studies in which NQEs were also included.^32,33 For comparison, in the classical-nuclei ab initio molecular dynamics (MD) simulation at the same temperature, the hydrogen transfer reaction is a much rarer event with an effective barrier above 4 k_BT, as shown in the Supporting Information.

Figure 2.

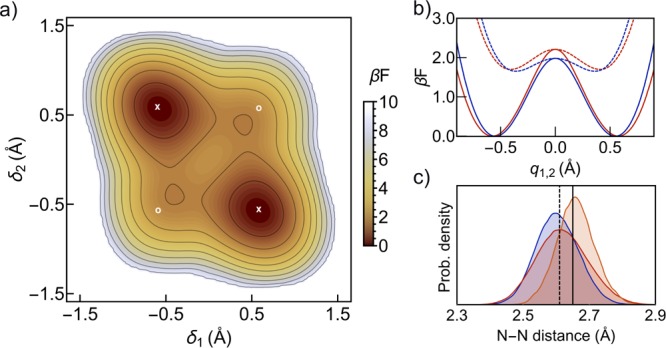
(a) Effective free energy profile of the porphycene molecule obtained from PIMD simulations at 290 K, projected on the δ₁ and δ₂ coordinates. The contour lines start at 0.75 k_BT and are separated by 1 k_BT. The x and o symbols mark the position of the trans and cis conformers, respectively, when optimized at the potential energy surface. We define “cis-like” conformations as those lying in the vicinity of (δ₁, δ₂) equal to (+0.4, +0.4) or (−0.4, −0.4). (b) Effective free energy projections along the q₁ (δ₁ = −δ₂) (solid lines) and q₂ (δ₁ = δ₂) (dashed lines) directions. Red and blue lines correspond to PIMD simulations at 290 and 100 K, respectively. (c) Nitrogen–nitrogen distance probability density obtained from PIMD simulations at 100 K (blue), PIMD simulations at 290 K (red), and MD simulation at 290 K (orange). Vertical lines indicate the minimum energy geometry values for the trans isomer (solid) and cis isomer (dashed).

The stationary points of the free energy surface can be assigned to the cis, trans, first-order saddle point (SP1), and second-order saddle point (SP2) states of the molecule. While the exact boundary value (b) to distinguish different states is arbitrary due to the non-negligible density at all values connecting both states within the PIMD simulations, the cis/trans population ratio is robust for reasonable values of 0.1 < b < 0.3, as shown in Figure S5. We calculate the trans population to be larger than the cis population by a factor 7. Note that these two-dimensional (2D) free energy surfaces are provided as a guide to understand this system. All our calculations are carried out in the full 3N-dimensional space.

The one-dimensional (1D) PIMD free energy projections along the q₁ and q₂ coordinates (defined along the lines δ₁ = −δ₂ and δ₁ = δ₂, respectively) are shown in Figure 2b at two temperatures, 290 and 100 K. These projections exhibit two interesting features. First, the effective energy difference between the wells, which within a first approximation would determine the cis and trans populations, does not change between 290 and 100 K. This means that in this temperature range only the lowest vibrational modes involving the N–H groups are populated and consequently the relative population is mostly governed by ZPE. The wells along q₂ (cis), however, are considerably softened toward the barrier when the temperature is reduced, while the wells along q₁ (trans) are not. This effectively increases the probability of cis conformations at lower temperatures. Second, decreasing the temperature has the surprising effect of decreasing the effective trans–trans free energy barrier by 10% and the cis–cis free energy barrier by 35%. This effect can be traced back to fluctuations in the cage dimensions. In Figure 2c, we show the probability density of the N–N distances, d₁ and d₃, defined in Figure 1. The quantum distribution at 290 K is broader and shifted to higher values in comparison to that at 100 K. The cage expansion at higher temperatures leads to an increase in the effective potential energy barrier for the hydrogen transfer reaction and is directly translated to the free energy profile. The smaller average N–N distances at lower temperatures correlate with an increased amount of cis-like conformations with respect to trans and are consistent with the strengthening of the hydrogen bonds observed from previous calculations on a reduced PES and NMR experiments.²⁹ In our PIMD simulations, we also observe that the average absolute value of the dipole projected along the H-bonded N atoms is 0.5 D, which is in contrast to the absent dipole moment of the trans minimum energy isomer. At the same time, it is also lower than the corresponding dipole of the cis minimum energy isomer (1.2 D). This observation is consistent with the observed N–N distance distribution shown in Figure 2c, which is centered closer to the N–N distance of the optimal cis isomer when considering quantum nuclei. In the classical-nuclei simulations, the cis-like geometries are not visited at all and the cage is much larger.

At this point, it is worth noting that a reduction of the effective free energy barrier along the chosen reaction coordinate does not necessarily result in an increase in the hydrogen transfer rate. Within transition-state theory (TST), a probabilistic term that depends on the effective barrier height is multiplied by a dynamical correction factor (also called the transmission coefficient). It has been shown that the dynamical factor can have a temperature dependence that is much stronger than the probabilistic one.³⁶ Consequently, rates and barrier heights are not always trivially correlated and the temperature dependence of the rate obtained based exclusively on free energy barriers should be treated with caution. In fact, for this system, it is experimentally observed that the rates decrease with decreasing temperatures²⁶ and this is also what we find in our full-dimensional calculations shown below.

We now examine the quantum dynamical aspects of the hydrogen transfer reactions, which we approximate with ring-polymer instanton theory^37,38 and thermostated ring-polymer molecular dynamics.³⁹ We locate two instanton pathways, namely, the one related to the trans–trans concerted pathway and the one related to the trans–cis (−trans) stepwise pathway. Each instanton is a uniquely defined path that best describes a tunneling mechanism in porphycene. With these pathways, we can compute the thermal rate as k = 2k_step + k_conc,²⁸ where k_step and k_conc are the rate constants corresponding to the concerted and stepwise mechanisms, respectively. The factor 2 takes into account the two possible cis intermediates. The ratios R_s = 2k_step/k and R_c = k_conc/k show the relative contribution of each pathway to the total observed double hydrogen transfer rate. The fact that we find two stable instanton pathways means that there are at least two independent pathways for the DHT. Even though we cannot guarantee that all possible DHT tunneling pathways are being considered, the symmetry of porphycene indicates that these should be the dominating (or the only) ones. Our best estimates for the DHT rates are listed in Table 1. These values are in good agreement with the experimental values measured in solution. Direct comparison between our gas-phase calculation and these results in certain condensed-phase environments is supported by the observation of negligible solvent dependency in experiments.^40,41 In other types of environments such as surfaces^42,43 or polymer matrices,⁴⁴ the rate depends more strongly on the environment. Larger porphycene derivatives show rate dependency in both isotropic⁴¹ and non-isotropic environments.⁴⁵

Table 1. Calculated Hydrogen Transfer Rates (k) Compared to Experimental k_exp Data from Reference (26), as Well as Tunneling Enhancement Factors (κ_tun), Contributions from the Concerted Path to the Rate R_c = k_conc/k, and Calculated Kinetic Isotope Effects (KIEs, k^HH/k^DD).

	T (K)	k (1011 s–1)	kexp (1011 s–1)	Rc	κtun	KIE
HH	150	2.190	1.62 ± 0.04	0.63	70
HH	100	0.630	1.09 ± 0.08	0.95	1135
DD	100	0.0025	0.03 ± 0.02	0.59	471	250

The tunneling enhancement factor, also reported in Table 1, is defined as κ_tun = k_inst/k_TST, where k ≡ k_inst is the rate obtained with the instanton method and k_TST is the rate obtained with the Eyring TST. As expected, tunneling effects thus increase the rates by almost 2 and 3 orders of magnitude at 150 and 100 K, respectively. More interestingly, at 150 K, the concerted and stepwise mechanisms make comparable contributions to the total rate, while at 100 K, the concerted path accounts for 95% of the rate. Note that if we neglect NQEs, the scenario is completely different: At both temperatures, the stepwise mechanism fully dominates.

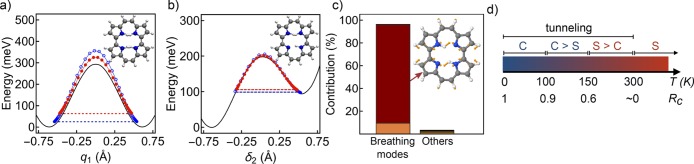
This result can be understood in terms of the mechanisms predicted by the instanton pathways. In panels a and b of Figure 3, we show the minimum energy path (MEP) for the concerted trans–trans path and the stepwise trans–cis path, respectively, at 150 and 100 K (black solid curves). The barrier for the concerted path is higher than that of the stepwise one. Analyzing the tunneling paths themselves, we note that the stepwise path requires that the initial trans geometry be thermally excited to an energy comparable to that of the intermediate cis geometry, which is ∼100 meV higher than the minimum, for tunneling to take place. From that point, the tunneling path follows quite closely the MEP and has essentially no temperature dependence between 100 and 150 K. In contrast, the concerted path enables tunneling at an energy close to the bottom of the well. The energy at which the system tunnels in this mechanism is temperature-dependent and is defined by instanton theory to give the optimal balance of the probability of barrier penetration and the probability of thermal excitation.³⁸ At 100 K, the tunneling path starts 25 meV above the minimum and reaches points above 350 meV. At 150 K, because more thermal energy is available, the path starts at 64 meV but does not reach such high values, keeping closer to the MEP.

Figure 3.

(a) Potential energies of different instanton imaginary-time slices along the trans–trans path at 100 K (empty blue circles) and 150 K (filled red circles). The black energy profile marks the ground-state potential energy surface, and the dashed lines mark the minimum energy of the intanton slices. (b) Same as in panel a for the trans–cis path. (c) Decomposition of the instanton turning point displacement of the trans–trans path into the mimimum energy trans geometry normal modes. The inset shows the breathing mode at 197 cm^–1 (2A_g) with the largest contribution. (d) Competition of different transfer mechanisms at different temperatures. C denotes the concerted mechanism, and S the stepwise mechanism. R_c is the contribution from the concerted path to the rate as defined in the title of Table 1.

At low temperatures, only the concerted mechanism is possible because there is not enough thermal energy available to reach the high-energy conformation at which the stepwise path takes place. The concerted mechanism presents a larger effective path length because two particles need to tunnel, and consequently, the microcanonical tunneling probability is always smaller than that for the stepwise case (see the Supporting Information). For this reason, increasing the available thermal energy strongly favors the stepwise mechanism. Indeed, above the crossover temperature of this system,⁴⁶T_c = ℏω*/2πk_B ≈ 300 K, where in most cases the contribution to the rate from classical hopping over the barrier becomes more important than tunneling, the stepwise mechanism is dominant. Previous evidence of the stepwise mechanism at 300 K from classical-nuclei molecular dynamics simulations reported in ref (31) benefits from this fact, but those simulations would not be able to predict the intricate balance between the two mechanisms at lower temperatures. Our calculated DHT mechanisms at different temperatures are summarized schematically in Figure 3d.

The competition of both mechanisms below T_c is compatible with some previous 2D model studies.²³ However, it goes against the common experimental interpretation that this reaction happens exclusively through the concerted path at any (low) temperature.^21,47 In particular, the lack of cis conformers observed in fluorescence anisotropy studies is treated as an indirect evidence for the concerted mechanism.^16,40 We propose that this is not a conclusive observation. The energy difference between the two isomers results in a very small cis population, and because of the low barrier height for the cis–trans reaction, any transient cis isomer will have a very short lifetime. Therefore, anisotropy measurements performed so far cannot rigorously confirm the mechanism in this particular scenario. Another possible experimental strategy for discerning the DHT mechanism is to monitor kinetic isotope effects (KIEs) upon substitution of two (DD) internal hydrogens by deuterium.¹⁷ However, because of the lack of well-defined ν_HH and ν_DD bands, it has been difficult to interpret and quantify the isotopic purity of any sample. The KIE can be easily accessed via our calculations, and we report in Table 1 the DHT rate and the KIE for the DD isotopologue of porphycene at 100 K. KIEs from instanton theory benefit from error cancellations⁴⁸ that make them typically more reliable than direct rate calculations. Nonetheless, our calculated KIE is 7 times higher than what was reported from experiments.²⁶ This discrepancy would be consistent with an error in the theoretical barrier width with respect to experiment, especially for the stepwise mechanism. Indeed, we are correcting the B3LYP+vdW barrier height with data from CCSD(T) but cannot correct the barrier width with the available data. Because the trans–trans pathway is symmetric and the trans–cis (stepwise) pathway is not, correcting only the barrier should work better for the former. The deuterium rate at 100 K involves a large fraction of the stepwise mechanism contribution and thus is prone to a larger error. From our simulations, we find that the DHT mechanism itself changes upon isotopic substitution, with deuteration strongly favoring the stepwise path as reflected by R_c. This situation is different for porphyrin, where there is no competition between the different pathways already for HH, such that it was possible to confirm the dominance of the stepwise mechanism from experiments.¹⁷

Our full-dimensional description allows us to go one step further and understand mode coupling in this DHT in more detail. We employ the normal mode decomposition proposed in ref (25) to analyze mode-specific contributions to tunneling splittings in porphycene. We take the trans isomer normal modes to decompose the displacement between the geometry from where the tunneling takes place (the instanton turning point) of the concerted path and the global minimum. Our decomposition, shown in Figure 3c, shows that >87% of the displacement is given by the breathing mode of the molecular cage at ∼200 cm^–1 (24 meV). The coupling of the concerted DHT to this low-energy mode implies a temperature dependence for this reaction rate at low temperatures that can look like an Arrhenius behavior, despite the massive contribution from tunneling. Therefore, we show that the concerted mechanism is related to the temperature dependence of the rate at low temperatures measured in refs (26) and (47), which is consistent with a barrier of 22 meV and the previous suggestion that this vibrational mode contributes to the DHT. A novel insight that we gain from our simulations is that we can unambiguously explain the origin of the activation barrier for the second thermally activated channel reported in ref (26). From Figure 3b, it is apparent that for the stepwise tunneling path to be activated, the cis conformer minimum energy needs to be reached. Detailed balance thus imposes an effective activation energy for this mechanism equal to the trans to cis energy difference. Our best estimate for this value is 107 meV [CCSD(T) with MP2 ZPE corrections], which matches the experimentally inferred activation barrier of 108 ± 9 meV.

The signature of anharmonic intermode coupling and quantum contributions in the DHT is directly reflected in the vibrational fingerprints that appear in an IR spectrum. We compare in Figure 4 the IR spectra obtained with the quantum harmonic approximation (QH), the (anharmonic) time-correlation formalism with classical-nuclei dynamics (CL) at 290 K, and the same formalism with the approximation to quantum-nuclei dynamics from TRPMD (QA) at the same temperature (see Methods). We also present the experimental IR spectrum reported in ref (27). Below 1700 cm^–1 this spectrum was measured for porphycene in a CS₂ solution and above 1700 cm^–1 for porphycene in a KBr matrix.

Figure 4.

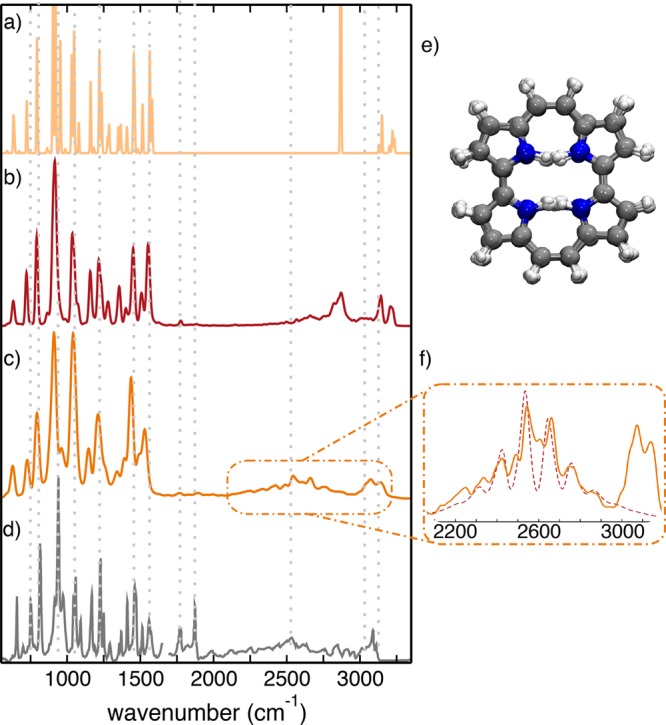
Porphycene IR spectra obtained through the (a) harmonic approximation, (b) Fourier transform of the dipole autocorrelation function from DFT-B3LYP+vdW trajectories with classical nuclei at 290 K, and (c) Fourier transform of the dipole autocorrelation function from DFT-B3LYP+vdW trajectories with quantum nuclei at 290 K from TRPMD. (d) Experimental spectra as reported in ref (27). Below 1700 cm^–1 this spectrum was measured for porphycene in a CS₂ solution and above 1700 cm^–1 for porphycene in a KBr matrix. The harmonic spectrum was artificially broadened with Gaussian functions for better visualization, and all of the theoretical spectra have a constant red-shift of 40 cm^–1. Dotted lines serve as guides to the eye. (e) Representative snapshots of the trajectory with quantum nuclei where all of the replicas are superimposed. (f) Close-up of the Fourier transform of the TRPMD IR spectrum in the N–H stretching mode region (orange) together with the adiabatic model (red dashed line) described in the text.

Our calculated QH and CL spectra are in good agreement with the theoretical simulations previously presented in ref (27). As discussed there, (classical-nuclei) anharmonicities play an important role in ν_N–H at ∼2900 cm^–1 (which can be easily assigned via normal mode analysis) and coupling to low-frequency vibrations considerably broadens the peak. However, the band is still present and shows a shape different from that of the experimentally measured spectrum at 290 K from ref (27). With the inclusion of NQEs, this peak is red-shifted by 300 cm^–1 and broadened, producing a very weak signal, remarkably similar to the experimental line shape. We observe a constant shift of only ≈40 cm^–1 between our simulations and experiment, which likely originates from the B3LYP+vdW PES. We corroborated the N −H stretch character of this peak by comparing spectra from hydrogenated and deuterated molecules (see Figure S9). The overtone peaks just below 2000 cm^–1 that were also observed in ref (27) are present in our CL and QA simulations, albeit with an intensity much lower than that of the experimental bands. This discrepancy in intensities could stem from the fact that both CL and QA spectra cannot capture quantum coherence. It could also stem from a particular enhancement of these bands due to the KBr matrix in experiment or to the laser power profile. To resolve this issue, comparison to gas-phase experimental spectra at lower temperatures would be desirable, but such data are not available. Overall, the results presented here show that NQEs are essential for quantitatively explaining the softening of the ν_N–H band and resolving its apparent absence from the experimental spectrum.^27,49

One can relate this line shape also to the N–N distance distributions shown in Figure 2c. The shorter N–N distances in the path-integral simulations point to a strengthening of the H-bonds, which is related to the mode softening (red-shift). Characterizing the strength of mode couplings and the fine structure of this band, however, requires a deeper analysis, especially due to the fact that, as shown in Figure 4e, the hydrogens are delocalized over the several energy wells.

We follow the approach suggested in ref (50) that provides a way of calculating IR line shapes for coupled low- and high-frequency vibrational modes, which we detail in the Supporting Information. We used the adiabatic model, including direct damping (relaxation of the high-frequency mode) and indirect damping (relaxation of the low-frequency mode that is coupled to the high-frequency one). The most relevant parameters of the model are the high-frequency (Ω) and low-frequency (ω) values as well as the strength of the coupling between them (α). As shown in Figure 4f, the agreement of the model with the TRPMD IR spectrum is good, especially for the fine structure of the mode. Because this model disregards hydrogen transfer and the DHT occurs on very long time scales compared to the N–H vibration, we safely conclude that DHT does not contribute to the line shape of this peak, similar to recent reports regarding the formic acid dimer.⁵¹ The parameters for the curve shown in Figure 4f are reported in the Supporting Information. We can obtain good agreement for 2680 cm^–1 < ω < 2750 cm^–1 and 100 cm^–1 < Ω < 115 cm^–1, with corresponding α values ranging from 0.70 to 0.85. The exact value of Ω most likely reflects an effective value that averages the coupling to several low-frequency cage vibration modes. The coupling parameter α is more than 1 order of magnitude larger than a simple evaluation in the strong anharmonic coupling theory⁵² based on harmonic modes, reflecting the enhancement of coupling due to anharmonic NQE. Notably, the ω values are very illuminating. They lie between the trans (2907 cm^–1) and cis (2680 cm^–1) harmonic frequency values. This shows the importance of visiting cis-like structures, which is only possible due to tunneling and ZPE contributions.

Conclusions

In this paper, we have presented a combination of techniques joining high-level density functional theory simulations and state-of-the-art path-integral-based approximations to nuclear quantum dynamics that provides a deep physical understanding of hydrogen transfer reactions. We validated the predictive power of our approach through comparison with experimental data.

In particular, we have shown that in an accurate potential energy surface, NQEs involved in hydrogen transfer events can qualitatively change the dynamical properties of the porphycene molecule. Our calculated full-dimensional ring-polymer instanton rate of DHT is in good agreement with experiment at different temperatures. From our simulations, we are able to quantitatively obtain the relative contribution from the stepwise and the concerted DHT mechanisms at any temperature. We conclude that both tunneling pathways make a similar contribution to the rate at 150 K and that only below 100 K does the concerted pathway become dominant. We corroborate that the skeletal low-frequency vibration that couples to the DHT coordinate leads to an Arrhenius-like temperature dependence for the rate, even when the DHT is dominated by tunneling. Additionally, we show that the contribution of the stepwise pathway down to low temperatures explains the second thermally activated reaction channel reported in experiments.

From the path-integral simulations, we have shown how NQEs can strengthen N–H···N bonds, modify the N–N distances, and shift peaks up to 300 cm^–1. The coupling and delocalization of the hydrogens within the cage explain the apparent absence of the N–H stretch band in the IR spectrum of this molecule, which had long puzzled researchers. The IR spectrum calculated from thermostated ring-polymer molecular dynamics yields an exquisite agreement with the experimental line shape of ν_N–H, even for the fine structure of the peak. We could reproduce this line shape with a simple model of coupled quantum harmonic oscillators, which allowed us to confirm that the coupling of this mode to low-frequency vibrations is enhanced when NQEs are included.

A shortcoming of increasing the complexity is that a detailed quantitative understanding of vibrational mode coupling can be compromised. Techniques like vibrational configuration interaction can, nevertheless, provide quantitative numbers even for rather complex molecules.⁵³ Techniques based on dynamics, however, do not give direct access to coupling coefficients without the application of other models.⁵⁴ The adiabatic model we employed in this work could give a qualitative explanation of the coupling and fine structure of the N–H stretching mode in the IR spectrum. Mode-specific experimental and theoretical techniques, like time-resolved 2D spectroscopy, would be necessary for a quantitative characterization of mode coupling at finite temperatures in high-dimensional systems. Nevertheless, the approaches presented here pave the way for addressing important problems in biology, related to enzymatic reactions through low-barrier H-bonds⁵⁵ and unusual fingerprints of N–H···N bonds in proteins,⁵⁶ and modeling functional materials that take advantage of hydrogen transfer events.⁵⁷⁻⁵⁹

Methods

We performed CCSD(T) calculations extrapolated to the infinite basis-set limit to obtain benchmarks for the energetics of local minima and saddle points of porphycene (see more details in the Supporting Information). We then compared less expensive exchange-correlation (xc) functionals within density functional theory (DFT) to these benchmarks and concluded that the B3LYP functional,⁶⁰ including pairwise van der Waals (vdW) corrections,⁶¹ presented the best agreement with our reference for both energetic and geometrical properties. We thus chose this functional to perform all further electronic structure calculations in this work. The Orca package⁶² was used to perform CCSD(T) simulations, and the FHI-aims⁶³ package for DFT simulations.

The nuclear degrees of freedom were sampled according to the B3LYP+vdW PES with MD and PIMD through the i-PI program^34,64 in connection with FHI-aims. The PIMD simulations were performed coupled to the colored noise PIGLET thermostat.⁶⁵ We were therefore able to use 6 and 12 beads for 290 and 100 K simulations, respectively.

Thermal rates were calculated with instanton rate theory.^37,38 The instanton path represents an approximation to the optimal tunneling pathway at a given temperature and can be determined for the full high-dimensional problem. We used the ring-polymer approach⁶⁶⁻⁶⁹ in which the path is discretized and represented by P beads in a harmonic ring polymer,⁷⁰ through our recent implementation in the i-PI code.³⁴ We include all 108 porphycene degrees of freedom in the path optimization. We have achieved convergence with 192 replicas at both 100 and 150 K (see the Supporting Information). This corresponds to a simulation involving, effectively, 7296 atoms with first-principles and on-the-fly force evaluations. We included a correction factor in the instanton action detailed in the Supporting Information, which linearly scales the action to match the CCSD(T) reference barrier, similar to that in ref (71).

Restarting an instanton calculation with a larger number of replicas can be computationally expensive due to the necessity of calculating all Hessians for the new amount of replicas. To overcome this bottleneck, we have derived and implemented in i-PI a ring-polymer expansion of the Hessian, given by 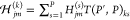, where P < P′ and H_jm^(s) is the jm matrix element of the Hessian corresponding to the sth original replica and 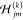is the jm matrix element of the Hessian corresponding to the kth expanded replica. The P′ × P matrix T(P′, P) is the same transformation matrix used in other contraction/expansion approaches and given in ref (72). We provide the derivation of this expression in the Supporting Information. This procedure completely removes the necessity of calculating any new Hessians during the optimization, after their calculation for the first ring-polymer geometry with a small number of beads (replicas).

The IR spectra were computed from the Fourier transform of the dipole autocorrelation function. The classical-nuclei correlation function was computed from four different 10 ps NVE trajectories. An approximation to the quantum correlation function was computed using thermostated ring-polymer molecular dynamics³⁹ coupled to generalized Langevin equation (TRPMD+GLE) thermostats, as described in ref (35). In this case, we ran 7 different 10 ps trajectories using 16 beads (see convergence tests in the Supporting Information) and computed the dipole for all beads. In all cases, the starting configurations were taken from uncorrelated thermalized structures and we used a 0.5 fs time step for the integration of the equations of motion.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b12471.

• Additional information regarding convergence tests, instanton rates, and simulations of vibrational spectra (PDF)

The authors declare no competing financial interest.