Abstract
It is widely recommended that any developed—diagnostic or prognostic—prediction model is externally validated in terms of its predictive performance measured by calibration and discrimination. When multiple validations have been performed, a systematic review followed by a formal meta-analysis helps to summarize overall performance across multiple settings, and reveals under which circumstances the model performs suboptimal (alternative poorer) and may need adjustment. We discuss how to undertake meta-analysis of the performance of prediction models with either a binary or a time-to-event outcome. We address how to deal with incomplete availability of study-specific results (performance estimates and their precision), and how to produce summary estimates of the c-statistic, the observed:expected ratio and the calibration slope. Furthermore, we discuss the implementation of frequentist and Bayesian meta-analysis methods, and propose novel empirically-based prior distributions to improve estimation of between-study heterogeneity in small samples. Finally, we illustrate all methods using two examples: meta-analysis of the predictive performance of EuroSCORE II and of the Framingham Risk Score. All examples and meta-analysis models have been implemented in our newly developed R package “metamisc”.
Keywords: Meta-analysis, aggregate data, evidence synthesis, systematic review, prognosis, validation, prediction, discrimination, calibration
1 Introduction
In medicine, many decisions require to estimate the risk or probability of an existing disease (diagnosis) or of developing a future outcome that yet has to occur (prognosis). Although having experience and intuition often provide excellent advice, it is increasingly common to quantify such diagnostic and prognostic probabilities through the use of prediction models. These models commonly combine information from multiple findings, such as from history taking, physical examination, and additional testing such as blood, imaging, elektrofysiology, and omics tests, to provide absolute outcome probabilities for a certain individual. Prediction models can, for instance, be used to inform patients and their treating physicians, to decide upon the administration of subsequent testing (diagnostic models) or treatments (prognostic models), or to identify participants for clinical trials.1,2 Well-known examples are the European system for cardiac operative risk evaluation (EuroSCORE) II to predict mortality after cardiac surgery3 and the Framingham Risk Score for predicting coronary heart disease.4
Over the past few decades, prediction modeling studies have become abundant in the medical literature. For the same disease, outcome or the target population, often numerous, sometimes hundreds, prediction models have been published.5 This practice is clearly undesirable for health-care professionals, guideline developers and patients, as it obfuscates which model to use in which context. More efforts are therefore needed to evaluate the performance of existing models in new settings and populations, and to adjust them if necessary.6 In contrast to redevelopment, validation and updating of prediction models allows to (more effectively) account for information already captured in previous studies, and thus to make better use of existing evidence and data at hand.7,8
The evaluation (and revision) of prediction models can be achieved by performing so-called external validation studies. In these studies, the original model is applied to new individuals whose data were not used in the model development. Model performance is then assessed by comparing the predicted and observed outcomes across all individuals, and by calculating measures of discrimination and calibration. Discrimination quantifies a model’s ability to distinguish individuals who experience the outcome from those who remain event free, while calibration refers to the agreement between observed outcome frequencies and predicted probabilities. Unfortunately, the interpretation of validation study results is often difficult, as changes in prediction model performance are likely to occur due to sampling error, differences in predictor effects, and/or differences in patient spectrum.9,10 Furthermore, because validation studies are often conducted using small and local data sets,11 they rarely provide evidence about a model’s potential generalizability across different settings and populations. For this reason, it may come as no surprise that for many developed prediction models, numerous authors have (re-)assessed the discrimination and calibration performance. Systematic reviews—ideally including a formal meta-analysis—are thus urgently needed to summarize their evidence and to better understand under what circumstances developed models perform adequately or require further adjustments.
Previous guidance for systematic reviews of prediction model studies mainly addressed formulation of the review aim, searching,12 critical appraisal (CHARMS)13 and data extraction of relevant studies. There is, however, little guidance on how to quantitatively synthesize the results of external validation studies. For this reason, we recently discussed meta-analysis methods to summarize and examine a model’s predictive performance across different settings and (sub)populations.14 These methods mainly focused on (diagnostic) prediction models with a binary outcome, and may therefore have limited value when reviewing (prognostic) models with a time-to-event outcome.
For this reason, we provide a comprehensive statistical framework to meta-analyze performance estimates of both diagnostic and prognostic prediction models, involving either binary or time-to-event outcomes. In particular, we discuss how to extract and restore relevant (and possibly missing) estimates of prediction model performance, and corresponding estimates of uncertainty. We also discuss how to obtain summary estimates of discrimination and calibration performance, even when none of the primary studies reported such estimates. Finally, we discuss the role and implementation of Bayesian methods for meta-analysis, and contrast their use with the more traditional frequentist methods. We illustrate all methods by reanalyzing the data from previously published reviews involving a prediction model with a binary3 and with a time-to-event4 outcome. All methods have been implemented in the R package “metamisc”, which is available from https://CRAN.R-project.org/package=metamisc.15 This package aims to facilitate meta-analysis of prediction model performance by integrating the proposed statistical methods for data extraction and evidence synthesis.
2 Motivating examples
We here focus on prediction models with either a binary or time-to-event outcome, as these are most common in the medical literature.16 Binary outcomes are typically used to represent the current (health) status of an individual, or to model events that occur within a relatively short period of time. Examples include the presence or absence of a particular disease, or death after surgery. Conversely, when the event times are of primary interest, binary outcomes need to be modeled together with the time after which they occurred. Examples of these so-called time-to-event outcomes include the time until the onset of breast cancer, the time until cardiovascular death, or the time until development of coronary heart disease (CHD).
We now introduce two motivating prognostic model examples—one for a binary and one for a time-to-event outcome—that will be used to illustrate the statistical methods that are required to extract relevant estimates of a model’s predictive performance from published studies and how to quantitatively summarize these. Details on the corresponding systematic reviews can be found in Table 1.
Table 1.
Population, intervention, comparison, outcome, timing and setting (PICOTS) of the empirical examples.
| EuroSCORE II | Framingham Risk Score | |
|---|---|---|
| Population | Patients undergoing coronary artery bypass grafting | General male poulation, free from CHD and not on treatment |
| Intervention | EuroSCORE II | Framingham Wilson |
| Comparator | Not applicable | Not applicable |
| Outcome | All-cause mortality | Fatal or non-fatal coronary heart disease (CHD) |
| Timing | Death within 30 days of operation or within the same hospital admission, predicted using preoperative conditions. | Initial CHD within 10 years |
| Setting | To inform considerations for the timing and choice of surgical intervention | To target individuals for the primary prevention of coronary disease |
In the first example, we meta-analyze the predictive performance of the European system for cardiac operative risk evaluation (EuroSCORE) II. This logistic regression model was developed using 16,828 adult patients from 43 countries to predict mortality after cardiac surgery.3 The corresponding prediction model equations are presented in Supporting Information 1.1. In a recent review,17 23 validations of EuroSCORE II were identified in which its predictive performance was examined in patients undergoing cardiac surgery. For each study, the number of patients, their mean age, and the proportion of female gender were extracted, as well as information on mortality, the concordance (c-) statistic, and the EuroSCORE II mean value. All data are available from the R package “metamisc”.
In the second example, we meta-analyze the predictive performance of the Framingham Risk Score developed by Wilson et al.4 This Cox proportional hazards regression model was developed in 1998 for predicting the 10-year risk of CHD in the general population free from CHD and not on treatment (Supporting Information 1.2). A recent systematic review identified 23 studies examining the performance of Framingham Wilson for predicting fatal or nonfatal CHD in male populations (Supporting Information 1.2).18 For each validation, estimates of model calibration and discrimination were extracted, as well as details on the study and population characteristics.
3 Data extraction and estimating unreported results to facilitate meta-analysis
The two most common statistical measures of predictive performance are described by discrimination and calibration. In a meta-analysis without access to individual participant data (IPD), we are reliant on extracting these performance measures from study publications. However, they are often poorly reported.11,16 We now discuss how to retrieve the necessary but not explicitly reported predictive performance estimates from the primary prediction model (validation) studies using other reported data.
3.1 Model discrimination
Discrimination refers to a prediction model’s ability to distinguish between subjects developing and not developing the outcome, and is often quantified by the concordance (c)-statistic, both for prediction models for binary outcomes as well as for time-to-event outcomes. The c-statistic is an estimated conditional probability that for any pair of a subject who experienced and a subject who did not experience the outcome, the predicted risk of an event is higher for the former. Although c-statistics are frequently reported in external validation studies, when missing they can also be calculated from other reported quantities. For instance, for prediction models with a binary outcome, the c-statistic is a reparameterization of Somer’s D,19 and can also be derived from the distribution of the linear predictor,20 Cohen’s effect size,20 or several correlation indices.21 An overview of relevant equations for this derivation of the c-statistic from other measures was previously presented.14
In this study, we compared two methods for estimating the c-statistic from reported information. Results in Supporting Information 2.2 indicate that accurate predictions can be obtained for c < 0.70 by using the standard deviation of the linear predictor. More accurate predictions (for c < 0.95) can be obtained if the mean and variance of the linear predictor are known for the affected and unaffected populations.
For prediction models with a time-to-event outcome, concordance is not uniquely defined and several variations of the c-statistic have been proposed.22,23 These variations typically adopt different strategies to account for ties or censoring, and may thus lead to different values for c. Although validation studies do not commonly report the definition and estimation method of presented c-statistics, Harrell’s version21 appears to be most widespread and recommended.22 Sometimes, discrimination is measured using Royston and Sauerbrei’s D index, usually referred to as the “D statistic”.24 This index quantifies prognostic separation of survival curves and is closely related to the standard deviation of the prognostic index, with Jinks et al. suggesting an equation to convert c values to D values based on empirical evidence25
| (1) |
It is also possible to convert D values to c values by making distributional assumptions with respect to the standard deviation of the prognostic index.26 The c-statistic can then be predicted as follows
| (2) |
where is the standard normal density function and where is used to describe infinitesimal increments of z (Leibniz’s notation). More information is provided in Supporting Information 2.2.
For prediction models including covariates with time-dependent effects and/or time-dependent covariates, concordance is often measured using time-dependent ROC curves.27 Again, several variations have been proposed that adopt different strategies to account for censoring. A recent study by Blanche et al. showed that these strategies perform similarly when censoring is independent,28 and are thus likely to yield comparable estimates of time-dependent concordance. However, when censoring depends on the predictor values, some ROC curve estimators are prone to substantial bias and may therefore contribute towards between-study heterogeneity in a meta-analysis.
Regarding the standard error of the c-statistic, when missing, it can be approximated from a combination of the reported c-statistic, the total sample size and the total number of events in the validation study. We here consider a method proposed by Newcombe to estimate the standard error of the c-statistic.29
| (3) |
with c the reported c-statistic, n the number of observed events, m the total number of non-events and . For prediction models with a time-to-event outcome, the equation above is applicable for estimating the standard error of Harrell’s c-statistic. As illustrated in Supporting Information 2, this method is fairly accurate for validation studies involving a binary or time-to-event outcome, as long as the total number of observed events is sufficiently large (above 10).
As we will discuss in the next section, it is important to transform estimates of the c-statistic and its standard error to the logit scale prior to meta-analysis.30 The logit c-statistic is simply given by , and its standard error can be approximated by applying the delta method.31 This then yields14
| (4) |
Alternatively, when the lower () and upper () boundary of the confidence interval of the c-statistic are available, it is preferred to derive the standard error of the logit c-statistic as follows (to preserve possible asymmetry around the c-statistic)32
| (5) |
where is the percentile of the Normal distribution. For instance, for a 95% confidence interval we have .
3.2 EuroSCORE II
Estimates for the c-statistic could be obtained for all 23 validations (Supporting Information 1.1). For four validations, equation (4) was used to approximate the standard error of the (logit) c-statistic. An example is given below.
Previously, Howell et al. assessed the predictive performance of EuroSCORE II in 933 high-risk patients.33 The observed in-hospital mortality was 9.7% (90 deaths). The reported c-statistic was 0.67; however, no information was provided on the corresponding standard error or confidence interval. We can derive the logit c-statistic as follows
Further, based on the reported information, we have n = 90, m = 843 and . This enables us to estimate the standard error of the logit c-statistic (equation 4)
3.3 Framingham
The c-statistic was only reported in 19/24 validations. In some cases, missing c-statistics could be restored by contacting the study authors (two validations). For these 21 estimates of the c-statistic, 10 studies provided the standard error and 11 studies required approximation of the standard error using Newcombe’s method (Supporting Information 1.2).
3.4 Model calibration
Calibration refers to a model’s accuracy of predicted probabilities, and is preferably reported graphically in so-called calibration plots. In these plots, expected outcome probabilities from the model are depicted against observed outcome frequencies in the validation dataset, often across tenths of predicted risk or for 4–5 risk groups over time (e.g. via Kaplan–Meier plots versus predicted survival). Calibration plots can also be constructed using smoothed loess curves, by directly regressing (transformations of) expected versus observed outcomes.
In order to summarize a model’s calibration performance across different validation studies, it is helpful to retrieve expected and observed outcome probabilities (e.g. across different risk strata), and to extract reported calibration measures. For prediction models for binary outcomes as well as for time-to-event outcomes, common measures are the calibration intercept and slope.34 The intercept is also known as calibration-in-the-large, and indicates whether predicted probabilities are, on average, too high (intercept below 0) or too low (intercept above 0). Conversely, the calibration slope quantifies whether predicted risks are, on average, too extreme (slope below 1) or too invariant (slope above 1).35
Unfortunately, extraction of calibration measures is often hampered by poor assessment and reporting.11,16 For instance, validation studies rarely present information on the calibration intercept and slope, or different studies report estimates for different risk strata or time horizons. However, it is common for validation studies to present information on the total number of observed (O) and expected (E) events, or the corresponding observed frequencies and . These quantities can then be used to calculate the total ratio, which provides a rough indication of the overall model calibration. In particular, the total ratio quantifies the averaged observed:expected ratio across the entire range of predicted risks, and is strongly related to calibration-in-the-large.14 Formulas for calculating the total O:E ratio and its standard error were recently presented (see also Supporting Information 3).14
For prediction models with a time-to-event outcome, it is important to be aware that some events are likely to be unobserved (e.g. due to drop-out). For this reason, extracted values for O (or ) should account for censoring (and thus be based on Kaplan–Meier estimates) as otherwise they cannot directly be compared to E (or ). Additional difficulties may arise when event rates are only available for shorter (or longer) follow-up times than intended for the review aim, as the applicability of calculated ratios may then be limited. This situation may, for instance, arise when a model developed to predict a 10-year risk has been validated for a five-year risk. Although it is possible to exclude such studies from the meta-analysis, an alternative strategy that does not discard information is to apply extrapolation by assuming a Poisson distribution (Supporting Information 3.2). When missing, the standard error of the total ratio can directly be derived from the total number of observed events.
Further, as we will discuss in the next section, estimates of the total ratio and its standard error should be transformed to the (natural) log scale prior to meta-analysis.30 Again, this can be achieved by applying the delta method36 or by transforming reported confidence intervals.32 The former strategy generally yields the following approximation14
| (6) |
Table 2 provides an overview of formula’s for calculating the total log ratio and its standard error for prediction models with a time-to-event outcome. Examples are provided in Supporting Information 3.3 and in our recent publication.14
Table 2.
Formulas for estimating the total ratio from other information in a primary study.
| What is reported? | Estimate for | Estimate for | Estimate for |
|---|---|---|---|
| Ot, Et | |||
| , Et, Nt | |||
| , Nt | |||
| , Nt | |||
| , Nl | |||
| , Nl |
The quantities Ot and Et represent the total number of observed (using Kaplan-Meier estimates) and expected events at time t. The corresponding observed and expected survival probabilities are given by and (). When Kaplan-Meier estimates are not available, it is still possible to approximate using the total number of observed events Ot during time t and the sample size Nt or, if drop-out is negligible, the original sample size N.
Although the total ratio is a useful measure to depict a model’s overall calibration, it is rarely sufficient to identify whether predicted risks are sufficiently accurate. In particular, substantial mis-calibration may still occur in some patient groups even when . For this reason, it is generally recommended to assess calibration performance separately for different subgroups. An example is given by a recent review on the performance of the additive EuroSCORE, where the total ratio was extracted for each distinct EuroSCORE value.14 These estimates can then be used to construct a (summary) calibration plot, which is more informative than a single summary estimate of the total ratio. Alternatively, when validation studies report (observed and predicted) event rates across different risk strata, it is possible to estimate a calibration slope of the observed-expected plot.35 A poor calibration slope usually reflects overfitting of the model in the development sample, but may also indicate lack of transportability.9 The calibration slope therefore may provide further insight into the potential generalizability of the model under review. Rather than estimating the slope for individual validations, we discuss in the next section how reported event rates across the primary studies can directly be used to obtain a summary estimate of the calibration slope and its standard error.
3.5 Example
Buitrago et al. analyzed the 10-year performance of the original Framingham coronary risk functions in nondiabetic patients.37 They reported the observed () and predicted () 10-year risk estimates in a table, as well as the total number of observed events (). Hence, we have
with
3.6 Framingham
Estimates for observed and expected 10-year CHD risk were directly available for 6/24 validations (Supporting Information 1.2). For some studies, ratios were derived from reported calibration plots, see for instance example 4 in the supporting information. For 10/24 validations, information was only available for 5 or 7.5 years of follow-up, and we therefore considered a sensitivity analysis where we extrapolated observed and expected event counts using a Poisson distribution. A total of 11 validations presented event rates for different risk strata (see, for instance, Figure S5). The corresponding calibration plots are depicted in Figures S2 and S3, and can be used to derive summary estimates of the calibration slope.
3.7 EuroSCORE II
The total number of observed and expected events was available for all 23 validations. Furthermore, because the EuroSCORE II model does not consider time-to-event, estimates for the total ratios and their standard error could directly be derived from extracted quantities for O and E (Supporting Information 1.1).
4 Meta-analysis
Once all relevant studies have been identified and corresponding results have been extracted, the retrieved estimates of model discrimination and calibration can be summarized into a weighted average to provide an overall summary of their performance. We here consider the situation where K studies () are available for meta-analysis and describe various meta-analysis approaches or models that can be implemented using a frequentist or a Bayesian estimation framework. All meta-analysis approaches or models have been implemented in the R package “metamisc”, which in turn makes use of the “metafor” package38 and the JAGS software39 to summarize (restored) estimates of model performance. Relevant examples and source code are available in Supporting Information 4.3.
4.1 Meta-analysis models
In general, two main types of meta-analysis models can be distinguished. In fixed effect meta-analysis models, all studies are considered to be equivalent, and variation in predictive performance measures across studies are assumed to arise by chance only. Accordingly, precision estimates of discrimination and calibration parameters are used to weight each study in the averaging of the model’s corresponding performance measures. In random effects meta-analysis models, it is assumed that variation in predictive performance measures across studies may not only appear due to chance, but is also prone to the (potential) presence of between-study heterogeneity. As a result, random effects models usually yield larger confidence intervals and assign study weights that are more similar to one another than those under fixed effect meta-analysis.40
Although both types of aforementioned meta-analysis models have limitations, and following the guidance of meta-analysis of interventions and diagnostic tests, we generally recommend the use of random effects models. In particular, discrimination and calibration performance are highly dependent on patient spectrum (case-mix variation) and therefore most likely to vary across validation studies.14 For instance, it is well known that a model’s discrimination performance tends to deteriorate when it is applied to populations or subgroups with a more homogeneous case-mix, as there is less separation of predicted risks across individuals.9,10,20,41,42 Between-study heterogeneity may also appear when reported performance estimates (such as c-statistics) are based on different definitions or estimation methods (e.g. adopt different criteria to account for ties or censoring).
4.2 Model discrimination
For random effects meta-analysis of the c-statistic (for either logistic or survival models), we have
| (Model \ 1) |
with the logit of the estimated c-statistic in the ith study. The logit transformation is applied to improve the validity of the Normality assumption, which is used to model variability around the summary c-statistic.30 After estimation of Model 1, the summary c-statistic is given by , which corresponds to . The extent of between-study heterogeneity is quantified by , the between-study standard deviation of the logit c-statistic.
4.3 Model calibration
Similarly, for random effects meta-analysis of the total ratio, as a measure of model calibration, we have
| (Model\ 2) |
with the natural log of the estimated ratio in the ith study, and its error variance. Again, a transformation is applied to improve the validity of the Normality assumption.30 Here, the summary ratio is given by . An important limitation of Model 2 is that continuity corrections are required when no events were observed or expected. This situation may, for instance, arise when validation studies are relatively small or when their event rate is much lower than in the development study.
One approach to avoid continuity corrections is to explicitly account for sampling error in the observed event rates by modelling the binomial likelihood directly in a one-stage random-effects model, where the within and between-study distributions are modelled in a single analysis43
| (Model \ 2^\ast) |
Alternatively, we may treat the total number of observed events as count data in a one-stage random-effects model43
| (Model \ 2^{\ast\ast}) |
where the summary ratio is again given by . Unfortunately, Model 2* and Model 2** may no longer be advantageous when some studies do not report Ei (or ) but provide estimates of the total ratio and its standard error. In such situations, continuity corrections can be avoided more effectively by considering study-specific likelihood functions. This approach is described in more detail below, and in Supporting Information 4.4.2.
Finally, if observed and expected event rates are available for different strata of predicted risk in the validation studies, it is possible to obtain a summary estimate of the calibration slope (Supporting Information 4.4.3). The one-stage random effects model below is a natural extension of Cox’ proposed regression model for describing agreement between predicted and observed probabilities35
| (Model\ 3) |
with Oij the number of observed events in subgroup j of study i, which is modeled according to a binomial distribution with event probability . For prediction models with a survival outcome, Oij and Nij represent quantities for specific (and same) time periods, and should be adjusted when drop-out occurred or when studies evaluated different time periods (e.g. by means of extrapolation). The summary estimate of the calibration slope is simply given by .
4.4 The frequentist approach for random effects meta-analysis
The parameters of the meta-analysis models above (Models 1 and 2) can be estimated by optimizing their corresponding (log-)likelihood function. This yields the well-known estimator of the meta-analysis summary44
where represents the study-specific estimates for the parameter of interest (e.g. the logit c-statistic or log ratio). In the standard DerSimonian and Laird approach, the heterogeneity parameter is estimated separately and subsequently inserted in the equations above.44,45 We recommend to use restricted maximum likelihood (REML) estimation to account for the simultaneous estimation of τ and μ. Note that for Model 2*, Model 2** and Model 3, estimates for μ and are analytically intractable and can only be derived jointly through iterative estimation procedures.
In line with previous recommendations,46,47 we propose to correct estimates of for potential bias when few studies are included in the meta-analysis. This can, for instance, be achieved using the method proposed by Hartung and Knapp
For all models, boundaries of the confidence interval (CI) can then be approximated using
with denoting the percentile of the Student-t distribution with K − 1 degrees of freedom, where α is usually chosen as 0.05, to give a 5% significance level and thus 95% confidence interval. The Student-t (rather than the Normal) distribution is chosen to account for the uncertainty in .
Finally, for meta-analysis of model discrimination and calibration, we recommend the calculation of an (approximate) 95% prediction interval (PI) to depict the extent of between-study heterogeneity.48 This interval provides a range for the predicted model performance in a new validation of the model. A 95% PI for the summary estimate in a new setting is approximately given as
where again the Student-t (rather than the Normal) distribution is used to help account for the uncertainty of . Recently, Partlett and Riley showed that this equation has poor coverage in many situations, and requires improvement.46 This motivates the Bayesian approach below.
4.5 The Bayesian approach for random effects meta-analysis
Generally speaking, in contrast to frequentist methods, Bayesian methods use formal probability models to express uncertainty about parameter values.49,50 This is particularly relevant when confronting sparse data, multiple comparisons, collinearity, or non-identification, and for deriving PI.51 Estimation problems are likely to occur in frequentist meta-analyses of prediction model performance, as validations of a specific model and thus existing evidence or data on predictive performance measures are often sparse. Furthermore, many frequentist estimation methods (including REML) sometimes fail to produce reliable confidence or prediction intervals. For instance, Partlett and Riley showed that the coverage of Hartung–Knapp confidence intervals based on REML estimation is too narrow for meta-analyses with less than five studies.46 Furthermore, when the heterogeneity is small and the study sizes are mixed, the Hartung–Knapp method produces confidence intervals that are too wide.46,47 Similarly, prediction intervals have poor coverage when the extent of heterogeneity is limited, when few (less than 5) studies are included, or when there are a mixture of large and small studies.46 For this reason, several authors have recommended the adoption of a Bayesian estimation framework,46,52,53 which more naturally accounts for all parameter uncertainty in the derivation of credibility and probability intervals.
An additional advantage of Bayesian meta-analysis models is that the distribution for modeling the within-study variation can be tailored to each validation study. This is, for instance, relevant when meta-analyzing the total ratio. In particular, a binomial distribution can be used for studies that report the total number of observed events, the total number of expected events and the total sample size (Model 2*). Conversely, a Poisson distribution can be used for studies that only report the total number of observed and expected events (Model 2**). Finally, a Normal distribution can be used for studies providing information on the total ratio and its standard error (Model 2). The corresponding likelihood functions are then linked together by constructing a shared parameter model through and (Supporting Information 4.4.2), also known as hierarchical related regression. Though this could be undertaken in a frequentist framework if the user writes their own likelihood (e.g. using SAS Proc NLMIXED), the Bayesian approach is more flexible and accounts for uncertainty more fully.
When adopting a Bayesian framework for meta-analysis, it is always important to specify appropriate prior distributions. In aforementioned meta-analysis models, prior distributions are needed for the unknown parameters , αi, and . It is generally recommended to be conservative when setting the spread of the prior, and to empirically justify prior assertions.54,55 For this reason, we here propose the use of non-informative prior distributions by assuming that , αi, . Further, because requires exponentiation and is often based on discrete likelihood functions, we here assume that . In line with previous recommendations,51,55 we consider empirically-based priors for and to rule out unreasonable values for these parameters and to allow for regularization when few studies are available for meta-analysis.54 Therefore, we retrieved heterogeneity estimates from more than 20 previously published meta-analyses (Supporting Information 4.1). Finally, we assume prior independence of μ and τ.51
Results in Supporting Information 4.2 demonstrate that for the logit c-statistic and the log ratio, it is unlikely that and, respectively, . Although no empirical data was identified for heterogeneity on the calibration slope, individual estimates usually do not exceed [0,2] and thus it is also unlikely that . For this reason, we propose the uniform distribution as functional form for modeling the prior,56–58 with .
Because the uniform distribution tends to unduly favor presence of heterogeneity in discrimination and calibration estimates across studies,58,59 we also consider a half Student-t distribution with location m, scale σ and ν degrees of freedom. Here, we set m = 0 and define σ equal to the largest empirical value of (to allow for more extreme values of heterogeneity than presented in Supporting Information 4.1). These hyper-parameter values allow to penalize the extent of between-study heterogeneity when the number of included validation studies is low. Further, we chose ν = 3 to ensure that the variance exists. Finally, we truncate samples for τ above 10 to rule out unreasonable values. The resulting priors are then given as and and . Results in Supporting Information 4.3 indicate that aforementioned priors allow for large, but realistic, values of between-study heterogeneity.
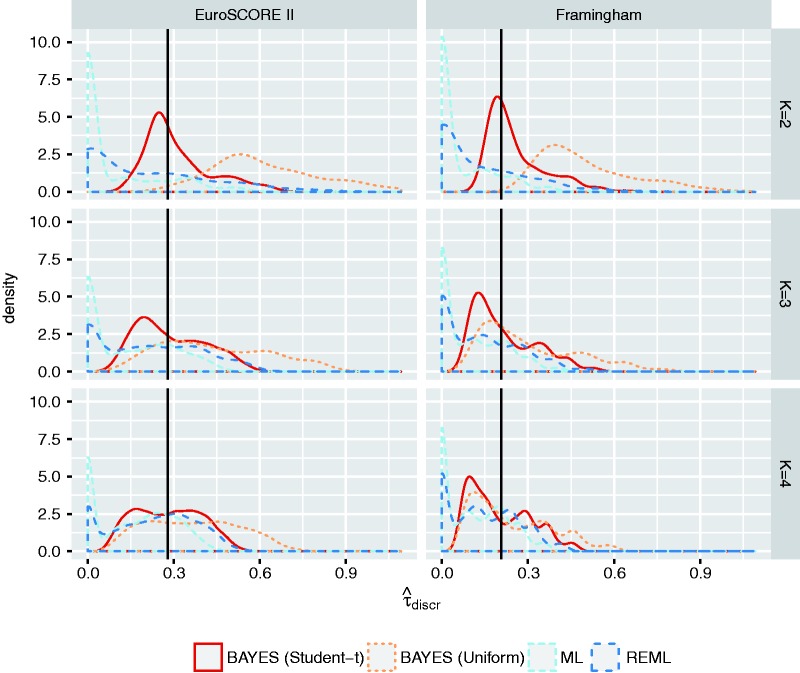
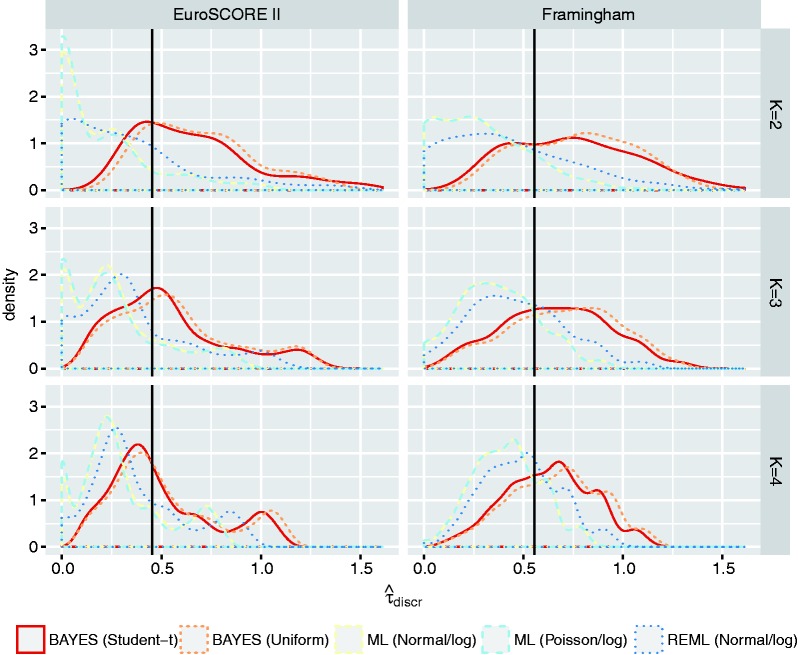
To evaluate the performance of the proposed prior distributions, we used the empirical example data to conduct a series of simulation studies where we varied the size of the meta-analysis (Supporting Information 4.5). Results in Figure 1 and Figure 2 suggest that the proposed priors substantially improve estimation of the between-study standard deviation when meta-analyses are relatively small. Researchers may, however, need to further tailor these priors to their own particular setting and example.
Figure 1.
Estimation of in small samples. Estimates of for meta-analyses with K validation studies. Results are based on meta-analyses for EuroSCORE II, and on meta-analyses for the Framingham Risk Score. For Bayesian meta-analysis models, represents the posterior median. The reference value (solid line) was obtained by adopting a Bayesian meta-analysis with uniform prior in the full set of 23 (for EuroSCORE II) or 21 (for the Framingham Risk Score) studies. Similar reference values were obtained for ML, REML and Bayes (Student-t). ML: Maximum likelihood estimation; REML: restricted maximum likelihood estimation; BAYES (Student-t): Bayesian estimation with ; BAYES (Uniform): Bayesian estimation with .
Figure 2.
Estimation of in small samples. Estimates of for meta-analyses with K validation studies. Results are based on meta-analyses for EuroSCORE II and on meta-analyses for the Framingham Risk Score. For Bayesian meta-analysis models, represents the posterior median. The reference value (solid line) was obtained by adopting a Bayesian meta-analysis with uniform prior in the full set of 23 (for EuroSCORE II) or 17 (for the Framingham Risk Score) studies. Similar reference values were obtained for ML, REML and Bayes (Student-t).
ML: maximum likelihood estimation; REML: restricted maximum likelihood estimation; BAYES (Student-t): Bayesian estimation with ; BAYES (Uniform): Bayesian estimation with .
To further highlight the potential advantages of Bayesian meta-analysis, we extended Model 3 to directly account for (1) sampling error in the number of expected events, (2) uncertainty due to the need for extrapolation and (3) uncertainty resulting from data transformations. The corresponding Model 3* is given in Supporting Information 4.4.3, and may help to conduct sensitivity analyses.
Finally, similar to a frequentist meta-analysis, uncertainty around summary estimates resulting from sampling error and/or heterogeneity can be formally quantified. In a Bayesian meta-analysis, the corresponding intervals are denoted as credibility and, respectively, prediction intervals. Boundaries for these intervals can directly be obtained by sampling from the posterior distribution.51 It is also possible to make probabilistic statements about future validation studies, such as the probability that the c-statistic will be above 0.7, or that the calibration slope will be between 0.9 and 1.1.
4.6 Empirical examples
All meta-analysis models have been implemented in the R-package “metamisc”. Convergence of Bayesian meta-analysis models was verified by evaluating the upper confidence limits of the potential scale reduction factor (values were considered as converged).60
4.7 EuroSCORE II
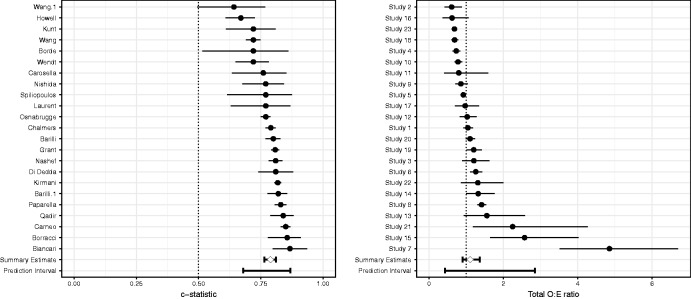
The estimates of all discussed meta-analysis models are presented in Table 3 and Supporting Information 5.1. As an example, a forest plot for the frequentist meta-analyses is depicted in Figure 3. For model discrimination, we found a summary c-statistic of 0.79 (95% CI 0.76 to 0.81; approximate 95% PI 0.68 to 0.87). For model calibration, we found a summary O:E ratio of 1.11 (95% CI 0.90 to 1.36; approximate 95% PI 0.43 to 2.85). Although similar results were obtained when implementing alternative link functions, estimates of between-study heterogeneity were often more precise when adopting a Bayesian estimation framework. Overall, the results suggest that, as expected, discrimination, and particularly calibration performance of EuroSCORE II substantially varied across studies. Although the average ratio was close to 1, predicted risks were systematically too high or too low in certain populations as revealed by the PI. The calibration slope could not be estimated for EuroSCORE II because subgroup-specific event rates were not extracted from the validation studies and the slope itself was not directly provided.
Table 3.
Meta-analysis estimates for the EuroSCORE II model.
| Performance | Estimation | Model | K | Summary | 95% CI | 95% PI |
|---|---|---|---|---|---|---|
| c-statistic | REML | Model 1 | 23 | 0.79 | 0.76–0.81 | 0.68–0.87 |
| Bayesiana | Model 1 | 23 | 0.79 | 0.76–0.81 | 0.68–0.89 | |
| Bayesianb | Model 1 | 23 | 0.79 | 0.77–0.81 | 0.68–0.87 | |
| Total ratio | REML | Model 2 | 23 | 1.11 | 0.90–1.36 | 0.43–2.85 |
| Bayesiana | Model 2* | 23 | 1.10 | 0.88–1.34 | 0.27–2.46 | |
| Bayesianb | Model 2* | 23 | 1.10 | 0.88–1.33 | 0.27–2.45 | |
| MLc | Model 2** | 23 | 1.09 | 0.90–1.33 | 0.44–2.67 | |
| Bayesiana | Model 2** | 23 | 1.10 | 0.88–1.33 | 0.29–2.45 | |
| Bayesianb | Model 2** | 23 | 1.10 | 0.88–1.33 | 0.30–2.45 | |
K: Number of studies included in the meta-analysis; REML: Restricted Maximum Likelihood; ML: Maximum Likelihood; CI: confidence (in case of REML) or credibility (for Bayesian models) interval; PI: (approximate) prediction interval
A uniform prior was used for modeling the between-study standard deviation.
A truncated Student-t distribution was used for modeling the between-study standard deviation.
REML estimation is not available for this type of model.
Figure 3.
Meta-analysis estimates for EuroSCORE II.
To illustrate the potential advantages of hierarchical related regression, we omitted information on the total sample size for seven studies. Model 2* could then only be applied to 16 studies, yielding a summary estimate for the total ratio of 1.17 (95% CI: 0.86 to 1.50). Conversely, when applying hierarchical related regressions, a binomial distribution was used for aforementioned 16 studies whereas a Poisson distribution was used for the remaining seven studies. The meta-analysis is then again based on 23 studies and yielded a summary estimate of 1.10 (with a 95% CI of 0.88 to 1.32).
4.8 Framingham
Results in Table 4 reveal substantial heterogeneity for the discrimination performance, with 95% PI ranging from 0.59 to 0.77 based on the frequentist approach. Although the 10-year predicted risk of CHD occurrence was usually too large (summary ), the calculated PI (0.2 to 1.8) indicates that predicted risks were too low for some of the validation studies. The summary estimate of the calibration slope was close to 1, indicating that predictions by the Framingham Risk Score were sufficiently scaled (despite being too high on average). Further, because most studies only reported calibration performance for five years follow-up, we conducted two sensitivity analyses where (1) studies with less than 10 years follow-up were excluded from the meta-analysis, and (2) where observed and expected event counts were extrapolated using a Poisson distribution. Results in Supporting Information 5.1 indicate that both strategies yielded similar summary estimates.
Table 4.
Meta-analysis estimates for the Framingham Risk Score.
| Performance | Estimation | Model | K | Summary | 95% CI | 95% PI |
|---|---|---|---|---|---|---|
| c-statistic | ML | Model 1 | 21 | 0.69 | 0.66–0.71 | 0.59–0.77 |
| REML | Model 1 | 21 | 0.69 | 0.66–0.71 | 0.59–0.77 | |
| Bayesiana | Model 1 | 21 | 0.69 | 0.66–0.71 | 0.59–0.78 | |
| Bayesianb | Model 1 | 21 | 0.69 | 0.66–0.71 | 0.59–0.77 | |
| Total ratio | ML | Model 2 | 17 | 0.60 | 0.46–0.79 | 0.20–1.84 |
| REML | Model 2 | 17 | 0.60 | 0.46–0.79 | 0.19–1.90 | |
| Bayesiana | Model 2* | 17 | 0.60 | 0.44–0.78 | 0.10–1.64 | |
| Bayesianb | Model 2* | 17 | 0.60 | 0.44–0.77 | 0.10–1.61 | |
| ML | Model 2** | 17 | 0.60 | 0.46–0.78 | 0.20–1.83 | |
| Bayesiana | Model 2** | 17 | 0.60 | 0.44–0.78 | 0.10–1.63 | |
| Bayesianb | Model 2** | 17 | 0.60 | 0.44–0.78 | 0.08–1.58 | |
| Calibration slope | ML | Model 3 | 11 | 1.03 | 0.94–1.12 | 0.93–1.13 |
| Bayesiana | Model 3 | 11 | 1.04 | 0.87–1.21 | 0.55–1.54 | |
| Bayesianb | Model 3 | 11 | 1.04 | 0.88–1.20 | 0.58–1.52 | |
K: Number of studies included in the meta-analysis; REML: Restricted Maximum Likelihood; ML: Maximum Likelihood; CI: confidence (in case of REML) or credibility (for Bayesian models) interval; PI: (approximate) prediction interval
A uniform prior was used for modeling the between-study standard deviation.
A truncated Student-t distribution was used for modeling the between-study standard deviation.
5 Investigating sources of heterogeneity
As applies to all types of meta-analysis, also for meta-analysis of prediction model studies, summary estimates of model performance may be of limited value in the presence of (substantial) between-study heterogeneity. Although we recommended the use of random effects models to evaluate the presence of heterogeneity, these models do not offer any insight about potential causes of this. For this reason, it is often helpful to investigate potential sources of heterogeneity in the predictive performance by performing a meta-regression or subgroup analysis.14,61 Common sources of heterogeneity are differences in study characteristics,62 differences in study quality, or differences in baseline risk across the validation studies.9,10 Heterogeneity may also arise when reported performance estimates are based on “improper” validations where certain predictors were neglected (e.g. due to missing data) or where various model parameters have been adjusted (e.g. intercept update).
5.1 Meta-regression models
We extend the presented meta-analysis models as follows to investigate sources of between-study heterogeneity.63 Let denote the (row)vector of covariates of study i including the constant term. Meta-regression considers the relation between the “predictor” and the performance estimate of the corresponding study. Hereby, it assumes that covariate effects are (roughly) linear on the meta-analysis scale. Similar to aforementioned random effects models, Normal distributions are used to account for the presence of sampling error and between-study heterogeneity. For instance, the marginal model for meta-regression of the logit c-statistic is given by
| (Model\ 1') |
To enhance estimation of covariate effects , it is recommended to center the covariates Xi around their respective means. Although meta-regression may help to identify sources of heterogeneity and poor model transportability, the power for this is often low. In addition, meta-regression may suffer from study-level confounding (also known as ecological bias) when analyzing aggregate patient (average) information.
5.2 Empirical examples
We used the R-package “metafor” to estimate the meta-regression models.
5.3 EuroSCORE II
In a meta-regression model (for discrimination), we examined whether heterogeneity was explained by one or more of the following: the spread of the prognostic index of EuroSCORE II in each validation study, whether the study was a multicentre study, whether the study included patients before 2010 (i.e. before EuroSCORE II was developed) and the spread of the age of the patients. The resulting meta-regression plots are depicted in Figure S14 (Supporting Information), and indicate that the summary c-statistic generally remains unaffected by changes in the distribution of the prognostic index or patient age. The p-value of the regression coefficients was all larger than 0.05. We therefore could not attribute heterogeneity in the c-statistic to these differences.
5.4 Framingham
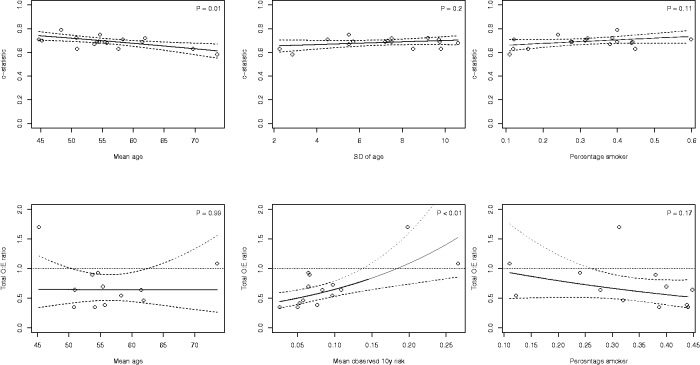
We examined whether heterogeneity for the Framingham Risk Score in male populations could be explained by differences in age distribution, smoking prevalence, and observed 10-year event rates. For instance, the mean age ranged from 41 to 74 across the included validations. Also the standard deviation of age substantially varied across the included validation studies (range: 2–13), further highlighting the presence of differences in patient spectrum. Results in Figure 4 indicate that the c-statistic of the Framingham Risk Score tended to decrease when validated in older (male) populations (p = 0.01). This can be explained by the narrower case-mix leading to more narrow separation, and thus lower c values. For the calibration performance, we found that under-estimation (i.e. ) notably occurred in low-risk populations (p < 0.01, Figure 4).
Figure 4.
Results from random-effects meta-regression models for the Framingham Risk Score (validations in male populations). Full lines indicate the bounds of the 95% confidence interval around the regression line. Dots indicate the included validation studies.
6 Conclusion
Quantitative synthesis of prediction model studies may help to better understand their potential generalizability and can be achieved by applying meta-analysis methods.14 In this paper, we discussed several common stumbling blocks when meta-analyzing the predictive performance of prediction models. In particular, substantial efforts are often needed to restore missing information from the primary studies and to harmonize the extracted performance statistics. In addition, estimates of a model’s predictive performance are likely to be affected by the presence of between-study heterogeneity. Finally, because validation studies of a certain prediction model are often sparse, traditional (frequentist) meta-analysis models may suffer from convergence issues and yield unreliable estimates of precision and between-study heterogeneity.64 For this reason, we presented several methods to overcome these deficiencies, and to obtain relevant summary statistics of prediction model performance even when the primary validation studies did not report such information. Furthermore, to facilitate the implementation of the presented methods, we created the open source R package metamisc which includes the empirical example data.15
We generally recommend the use of one-stage methods for summarizing the O:E ratio (here, Model 2* and Model 2**) and calibration slope (here, Model 3), as they use the exact likelihood. Further, adopting a Bayesian estimation framework may help to fully propagate the uncertainty resulting from estimating the within-study standard errors and the between-study standard deviation, which in turn may improve the coverage of calculated intervals. Future efforts should focus on comparing the presented meta-analysis methods in new empirical examples and simulation studies. Results from previous studies suggest that these methods are most likely to yield discordance when there is low between-study heterogeneity, when there are few studies for meta-analysis, or when studies are small or based on different sample sizes.46,65,66
Further work is also still needed to summarize the evidence on multiple, competing, prediction models that were compared head-to-head in validation studies. Another important issue arises when individual participant data (IPD) are available for one or more validation studies. Although it is possible to reduce these studies to relevant performance estimates and to adopt the meta-analysis methods presented in this article, more advanced (so-called one-stage) approaches exist to directly combine the IPD with published summary data.67 An additional advantage of IPD is that it becomes possible to adjust discrimination performance for (variation in) subject-level covariates, and thus to gain more understanding in sources of between-study heterogeneity.9,10,26,68 Finally, methods for meta-analyzing clinical measures of performance such as net benefit deserve further attention.
In summary, our empirical examples demonstrate that meta-analysis of prediction models is a feasible strategy despite the complex nature of corresponding studies. As developed prediction models are being validated increasingly often, and as the reporting quality is steadily improving, we anticipate that evidence synthesis of prediction model studies will become more commonplace in the near future. The R package “metamisc” is designed to facilitate this endeavor, and will be updated as new methods become available.
Supplemental Material
Supplemental Material for A framework for meta-analysis of prediction model studies with binary and time-to-event outcomes by Thomas PA Debray, Johanna AAG Damen, Richard D Riley, Kym Snell, Johannes B Reitsma, Lotty Hooft, Gary S Collins and Karel GM Moons in Statistical Methods in Medical Research
Acknowledgements
We gratefully acknowledge Ian White for sharing the algebraic expressions relating the c-statistic in terms of the standard deviation of the linear predictor (equation 2, and Supporting Information 2.2.1). Further, we thank Hans van Houwelingen for his reference to earlier work by D. R. Cox on the calibration slope.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The work leading to these results has received support from the Netherlands Organisation for Health Research and Development (91617050) and from the Cochrane Methods Innovation Funds Round 2 (MTH001F).
Supplemental material
Supplemental material for this article is available online.
References
- 1.Moons KGM, Royston P, Vergouwe Y, et al. Prognosis and prognostic research: what, why, and how? BMJ 2009; 338: b375–b375. [DOI] [PubMed] [Google Scholar]
- 2.Steyerberg EW, Moons KGM, van der Windt DA, et al. Prognosis Research Strategy (PROGRESS) 3: prognostic model research. PLoS Med 2013; 10: e1001381–e1001381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nashef SAM, Roques F, Sharples LD, et al. EuroSCORE II. Eur J Cardiothorac Surg 2012; 41: 734–744; discussion 744–745. [DOI] [PubMed] [Google Scholar]
- 4.Wilson PW, D’Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation 1998; 97: 1837–1847. [DOI] [PubMed] [Google Scholar]
- 5.Damen JAAG, Hooft L, Schuit E, et al. Prediction models for cardiovascular disease risk in the general population: systematic review. BMJ 2016; 353: i2416–i2416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Moons KGM, Kengne AP, Grobbee DE, et al. Risk prediction models: II. External validation, model updating, and impact assessment. Heart 2012; 98: 691–698. [DOI] [PubMed] [Google Scholar]
- 7.Debray TP, Koffijberg H, Nieboer D, et al. Meta-analysis and aggregation of multiple published prediction models. Stat Med 2014; 33: 2341–2362. [DOI] [PubMed] [Google Scholar]
- 8.Steyerberg EW, Borsboom GJJM, van Houwelingen HC, et al. Validation and updating of predictive logistic regression models: a study on sample size and shrinkage. Stat Med 2004; 23: 2567–2586. [DOI] [PubMed] [Google Scholar]
- 9.Debray TPA, Vergouwe Y, Koffijberg H, et al. A new framework to enhance the interpretation of external validation studies of clinical prediction models. J Clin Epidemiol 2015; 68: 279–289. [DOI] [PubMed] [Google Scholar]
- 10.Vergouwe Y, Moons KGM, Steyerberg EW. External validity of risk models: use of benchmark values to disentangle a case-mix effect from incorrect coefficients. Am J Epidemiol 2010; 172: 971–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Collins GS, de Groot JA, Dutton S, et al. External validation of multivariable prediction models: a systematic review of methodological conduct and reporting. BMC Med Res Methodol 2014; 14: 40–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Geersing GJ, Bouwmeester W, Zuithoff P, et al. Search filters for finding prognostic and diagnostic prediction studies in Medline to enhance systematic reviews. PLoS ONE 2012; 7: e32844–e32844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Moons KGM, de Groot JA, Bouwmeester W, et al. Critical appraisal and data extraction for systematic reviews of clinical prediction modelling studies: the CHARMS checklist. PLoS Med 2014; 11: e1001744–e1001744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Debray TPA, Damen JAAG, Snell KIE, et al. A guide to systematic review and meta-analysis of prediction model performance. BMJ 2017; 356: i6460–i6460. [DOI] [PubMed] [Google Scholar]
- 15.Debray T. metamisc: diagnostic and prognostic meta-analysis, https://CRAN.R-project.org/package=metamisc (accessed 1 January 2018).
- 16.Bouwmeester W, Zuithoff NPA, Mallett S, et al. Reporting and methods in clinical prediction research: a systematic review. PLoS Med 2012; 9: 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guida P, Mastro F, Scrascia G, et al. Performance of the European System for Cardiac Operative Risk Evaluation II: a meta-analysis of 22 studies involving 145,592 cardiac surgery procedures. J Thorac Cardiovasc Surg 2014; 148: 3049–3057.e1. [DOI] [PubMed] [Google Scholar]
- 18.Damen JAAG, Pajouheshnia R, Heus P, et al. Performance of the Framingham risk models and pooled cohort equations: a systematic review and meta-analysis. PLOS ONE 2018. Under review (submitted). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Newson R. Parameters behind nonparametric statistics: Kendalls tau, Somers D and median differences. Stata J 2002; 2: 45–64. [Google Scholar]
- 20.Austin PC, Steyerberg EW. Interpreting the concordance statistic of a logistic regression model: relation to the variance and odds ratio of a continuous explanatory variable. BMC Med Res Methodol 2012; 12: 82–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Harrell FE, Califf RM, Pryor DB, et al. Evaluating the yield of medical tests. JAMA 1982; 247: 2543–2546. [PubMed] [Google Scholar]
- 22.Lirette ST, Aban I. Quantifying predictive accuracy in survival models. J Nucl Cardiol 2015; 24: 1998–2003. DOI:10.1007/s12350-015-0296-z. [DOI] [PubMed] [Google Scholar]
- 23.Austin PC, Pencinca MJ, Steyerberg EW. Predictive accuracy of novel risk factors and markers: a simulation study of the sensitivity of different performance measures for the Cox proportional hazards regression model. Stat Methods Med Res 2015; 26: 1053–1077. DOI:10.1177/ 0962280214567141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Royston P, Sauerbrei W. A new measure of prognostic separation in survival data. Stat Med 2004; 23: 723–748. [DOI] [PubMed] [Google Scholar]
- 25.Jinks RC, Royston P, Parmar MKB. Discrimination-based sample size calculations for multivariable prognostic models for time-to-event data. BMC Med Res Methodol 2015; 15: 82–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.White IR, Rapsomaniki E. Emerging Risk Factors Collaboration. Covariate-adjusted measures of discrimination for survival data. Biom J 2015; 57: 592–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kamarudin AN, Cox T, Kolamunnage-Dona R. Time-dependent ROC curve analysis in medical research: current methods and applications. BMC Med Res Methodol 2017; 17: 53–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Blanche P, Dartigues JF, Jacqmin-Gadda H. Review and comparison of ROC curve estimators for a time-dependent outcome with marker-dependent censoring. Biom J 2013; 55: 687–704. [DOI] [PubMed] [Google Scholar]
- 29.Newcombe RG. Confidence intervals for an effect size measure based on the Mann-Whitney statistic. Part 2: asymptotic methods and evaluation. Stat Med 2006; 25: 559–573. [DOI] [PubMed] [Google Scholar]
- 30.Snell KI, Ensor J, Debray TP, et al. Meta-analysis of prediction model performance across multiple studies: which scale helps ensure between-study normality for the C -statistic and calibration measures? Stat Meth Med Res 2017, pp. 096228021770567–096228021770567. DOI:10.1177/0962280217705678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Oehlert GW. A note on the delta method. Am Stat 1992; 46: 27–27. [Google Scholar]
- 32.Altman DG, Bland JM. How to obtain the P value from a confidence interval. BMJ 2011; 343: d2304–d2304. [DOI] [PubMed] [Google Scholar]
- 33.Howell NJ, Head SJ, Freemantle N, et al. The new EuroSCORE II does not improve prediction of mortality in high-risk patients undergoing cardiac surgery: a collaborative analysis of two European centres. Eur J Cardiothorac Surg 2013; 44: 1006–1011; discussion 1011. [DOI] [PubMed] [Google Scholar]
- 34.Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology 2010; 21: 128–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cox DR. Two further applications of a model for binary regression. Biometrika 1958; 45: 562–565. [Google Scholar]
- 36.Dorfman R. A note on the method for finding variance formulae. Biometric Bull 1938; 1: 129–137. [Google Scholar]
- 37.Buitrago F, Calvo-Hueros JI, Can-Barroso L, et al. Original and REGICOR Framingham functions in a nondiabetic population of a Spanish health care center: a validation study. Ann Fam Med 2011; 9: 431–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Viechtbauer W. Conducting meta-analyses in R with the metafor package. J Stat Software 2010; 36: 1–48. DOI:10.18637/jss.v036.i03. [Google Scholar]
- 39.Plummer M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In: Proceedings of the 3rd international workshop on distributed statistical computing, Vienna, Austria, March 2003.
- 40.Borenstein M, Hedges LV, Higgins JPT, et al. A basic introduction to fixed-effect and random-effects models for meta-analysis. Res Synth Meth 2010; 1: 97–111. [DOI] [PubMed] [Google Scholar]
- 41.Kundu S, Mazumdar M, Ferket B. Impact of correlation of predictors on discrimination of risk models in development and external populations. BMC Med Res Methodol 2017; 17: 63–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nieboer D, van der Ploeg T, Steyerberg EW. Assessing discriminative performance at external validation of clinical prediction models. PLoS ONE 2016; 11: e0148820–e0148820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stijnen T, Hamza TH, Zdemir P. Random effects meta-analysis of event outcome in the framework of the generalized linear mixed model with applications in sparse data. Stat Med 2010; 29: 3046–3067. [DOI] [PubMed] [Google Scholar]
- 44.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trial 1986; 7: 177–188. [DOI] [PubMed] [Google Scholar]
- 45.Veroniki AA, Jackson D, Viechtbauer W, et al. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Res Synth Meth 2016; 7: 55–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Partlett C, Riley RD. Random effects meta-analysis: coverage performance of 95% confidence and prediction intervals following REML estimation. Stat Med 2017; 36: 301–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cornell JE, Mulrow CD, Localio R, et al. Random-effects meta-analysis of inconsistent effects: a time for change. Ann Intern Med 2014; 160: 267–270. [DOI] [PubMed] [Google Scholar]
- 48.Riley RD, Higgins JPT, Deeks JJ. Interpretation of random effects meta-analyses. BMJ 2011; 342: d549–d549. [DOI] [PubMed] [Google Scholar]
- 49.Greenland S. Bayesian perspectives for epidemiological research: I. Foundations and basic methods. Int J Epidemiol 2006; 35: 765–775. [DOI] [PubMed] [Google Scholar]
- 50.Spiegelhalter DJ. Evidence synthesis. In: Senn S and Barnett V (eds.) Bayesian approaches to clinical trials and health-care evaluation. Chichester, UK: John Wiley & Sons, Ltd, 2004, pp.267–303.
- 51.Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J R Stat Soc Ser A Stat Soc 2009; 172: 137–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bodnar O, Link A, Arendack B, et al. Bayesian estimation in random effects meta-analysis using a non-informative prior. Stat Med 2017; 36: 378–399. [DOI] [PubMed] [Google Scholar]
- 53.Turner RM, Jackson D, Wei Y, et al. Predictive distributions for between-study heterogeneity and simple methods for their application in Bayesian meta-analysis. Stat Med 2015; 34: 984–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Simpson D, Rue H, Riebler A, et al. Penalising model component complexity: a principled, practical approach to constructing priors. Stat Sci 2017; 32: 1–28. [Google Scholar]
- 55.Greenland S. Bayesian perspectives for epidemiological research. II. Regression analysis. Int J Epidemiol 2007; 36: 195–202. [DOI] [PubMed] [Google Scholar]
- 56.Burke DL, Bujkiewicz S, Riley RD. Bayesian bivariate meta-analysis of correlated effects: Impact of the prior distributions on the between-study correlation, borrowing of strength, and joint inferences. Stat Meth Med Res 2018; 27: 428–450. DOI: 10.1177/0962280216631361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lambert PC, Sutton AJ, Burton PR, et al. How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS. Stat Med 2005; 24: 2401–2428. [DOI] [PubMed] [Google Scholar]
- 58.Spiegelhalter D. Prior distributions. In: Senn S and Barnett V (eds.) Bayesian approaches to clinical trials and health-care evaluation. Chichester, UK: John Wiley & Sons, Ltd, 2004, pp.139–180.
- 59.Gelman A. Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayes Analys 2006; 1: 515–534. [Google Scholar]
- 60.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Stat Science 1992; 7: 457–472. [Google Scholar]
- 61.Pennells L, Kaptoge S, White IR, et al. Assessing risk prediction models using individual participant data from multiple studies. Am J Epidemiol 2013; 179: 621–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ban JW, Emparanza JI, Urreta I, et al. Design characteristics influence performance of clinical prediction rules in validation: a meta-epidemiological study. PLoS ONE 2016; 11: e0145779–e0145779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.van Houwelingen HC, Arends LR, Stijnen T. Advanced methods in meta-analysis: multivariate approach and meta-regression. Stat Med 2002; 21: 589–624. [DOI] [PubMed] [Google Scholar]
- 64.Austin PC. Estimating multilevel logistic regression models when the number of clusters is low: a comparison of different statistical software procedures. Int J Biostat 2010; 6: Article 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sidik K, Jonkman JN. A comparison of heterogeneity variance estimators in combining results of studies. Stat Med 2007; 26: 1964–1981. [DOI] [PubMed] [Google Scholar]
- 66.Langan D, Higgins JPT, Simmonds M. Comparative performance of heterogeneity variance estimators in meta-analysis: a review of simulation studies. Res Synth Meth 2017; 8: 181–198. DOI: 10.1002/jrsm.1198. [DOI] [PubMed] [Google Scholar]
- 67.Debray TPA, Moons KGM, van Valkenhoef G, et al. Get real in individual participant data (IPD) meta-analysis: a review of the methodology. Res Synth Meth 2015; 6: 239–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.van Klaveren D, Gnen M, Steyerberg EW, et al. A new concordance measure for risk prediction models in external validation settings. Stat Med 2016; 35: 4136–4152. DOI:10.1002/sim.6997. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Material for A framework for meta-analysis of prediction model studies with binary and time-to-event outcomes by Thomas PA Debray, Johanna AAG Damen, Richard D Riley, Kym Snell, Johannes B Reitsma, Lotty Hooft, Gary S Collins and Karel GM Moons in Statistical Methods in Medical Research