Fast and Slow Voltage-Dependent Dynamics of Magnesium Block in the NMDA Receptor: The Asymmetric Trapping Block Model

Abstract

The NMDA receptor (NMDAR) produces a long-lasting component of the glutamatergic EPSC in mammalian central neurons. The current through NMDARs is voltage dependent as a result of block by extracellular magnesium, which has recently been shown to give rise to a complex time dependence, with fast and slow components of responses to changes in membrane potential. Here, we studied the dynamics of block and unblock by measuring voltage step responses in conjunction with fast perfusion of agonist in nucleated patches isolated from rat cortical pyramidal neurons. We found that slow unblock shows a progressive onset during synaptic-like responses to brief pulses of agonist. Repolarizing briefly from +40 to -70 mV revealed that slow unblock is reestablished with a time constant of ∼5 msec at room temperature. Also, the time course of deactivation, in response to a pulse of agonist, slows twofold over the potential range -30 to +40 mV. An asymmetric “trapping block” model in which the voltage-independent closing rate constant of the blocked channel is approximately three times that of the unblocked channel accounts quantitatively for all of these phenomena and for responses to action potential waveform clamp. This model allows much more accurate prediction of NMDAR current in physiological conditions of magnesium concentration and changing membrane potential than previously possible. It suggests a positive allosteric link between occupation of the NMDAR pore by magnesium and closure of the permeation gate.

Introduction

Activation of NMDA receptors (NMDARs) produces a long-lasting component of glutamatergic EPSPs (Forsythe and Westbrook, 1988; Lester et al., 1990; Robinson et al., 1991; Stern et al., 1992), which might provide approximately half of the excitatory current in some cortical neurons during natural activity (Harsch and Robinson, 2000). The opening of the channel is controlled by a powerful voltage-dependent block by external magnesium ions (Mayer et al., 1984; Nowak et al., 1984), almost total at the resting potential, but half-removed at -20 mV. This depolarization-induced inward current could contribute strongly to excitability (Schiller et al., 2000) and may be the trigger for controlling long-term potentiation (McBain and Mayer, 1994).

Previously, detailed kinetic studies have been performed in nominally zero external [Mg²⁺] to best expose the activation of the NMDAR (for review, see Dingledine et al., 1999). The voltage dependence of magnesium block has generally been studied at equilibrium at a steady holding potential (Ascher and Nowak, 1988; Jahr and Stevens, 1990). Accordingly, computational studies of NMDAR function have assumed that NMDAR current has instantaneous voltage dependence (Pongrácz et al., 1992; Mel, 1993; Spruston et al., 1995; Lansner et al., 1998; Koch, 1999; Schiller et al., 2000), with the current level following the steady-state current-voltage relationship exactly, even during rapidly changing voltage.

However, a large fraction of NMDAR-mediated current actually unblocks quite slowly in the millisecond timescale (Spruston et al., 1995). Recently, we examined the unblock kinetics of NMDARs in detail (Vargas-Caballero and Robinson, 2003) to assess the functional significance of its timing. Using nucleated patches isolated from cortical pyramidal neurons, we found that unblock after large depolarizations from rest produces currents that have two major components, each contributing approximately half the current: a relatively fast component with a time constant of 1 msec or less and a slower component with a time constant of ∼10-15 msec at room temperature. These kinetics mean that the time course of physiological NMDAR current responses can be quite complex, such that it makes no contribution to the upstroke of somatic sodium action potentials (APs) while greatly exceeding steady-state predictions during repolarization, especially in burst firing driven by dendritic calcium APs. Thus, the nature of NMDAR slow unblock will strongly influence dendritic excitability, including the generation, failure, shape, and conduction speed of dendritic action potentials (Larkum et al., 2001) when NMDARs are activated.

A trapping-block kinetic scheme, in which agonist may unbind while magnesium still occupies its blocking site has been proposed as a model for NMDAR magnesium block (Benveniste and Mayer, 1995; Sobolevsky and Yelshansky, 2000). In this study, we show that the kinetics of the NMDAR during changing membrane potential can be reproduced accurately if an asymmetry in the trapping block is assumed, such that the closing rate constant when blocked is several times faster than when unblocked. This asymmetric trapping block (ATB) model accounts quantitatively for the complex voltage-dependent dynamics of NMDAR gating in physiological conditions.

Materials and Methods

Preparation. Using United Kingdom Home Office approved procedures, brains were removed from 8- to 16-d-old Wistar rats killed by cervical dislocation. Sagittal slices 300 μm thick were cut on a vibrating slicer (Campden Instruments, Leicester, UK; or model DTK-3000, Dosaka EM Co., Kyoto, Japan). During the slicing procedure, tissue was kept in the following ice-cold low-sodium solution (in mm): 254 sucrose, 2.5 KCl, 26 NaHCO₃, 10 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, and 1 MgCl₂. Slices were then incubated in Ringer solution at room temperature. The Ringer solution contained (in mm): 125 NaCl, 2.5 KCl, 25 NaHCO₃, 25 glucose, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, and 10 μm glycine. Both slicing and recording solutions were bubbled with a 95% O₂,5%CO₂ gas mixture to give a pH of 7.4.

Recording. For recording, a single slice was transferred to a recording chamber. The preparation was continuously perfused with oxygenated Ringer solution containing 100 nm tetrodotoxin (Sigma, St. Louis, MO) to block voltage-dependent Na channels. Recordings were performed at room temperature (20-23°C). Slices were viewed with an upright microscope (Olympus BW50WI; Olympus, London, UK) with a water-immersion objective (Olympus LUMPlanFI, 60×; numerical aperture, 0.90) and infrared differential interference contrast optics. Nucleated patch recordings were obtained using standard techniques (Hamill et al., 1981; Sather et al., 1992) from layer II/III cortical pyramidal cells in the occipital cortex. The shanks of pipettes used for nucleated patch recordings were coated with dental wax to reduce the pipette capacitance and heat-polished. Membrane potentials were corrected for prenulled liquid junction potential, which was measured directly (Neher, 1992). Recordings were made with an Axopatch 200A amplifier (Axon Instruments, Foster City, CA) in voltage-clamp mode; the built-in series resistance compensation circuitry was used in most recordings. Signals were filtered at 5 kHz (-3 dB; four-pole Bessel) and sampled with 12-bit resolution at 20 kHz. Pipettes were filled with a cesium-based solution that had the following composition (in mm): 20 phosphocreatine-Na₂, 4 Mg-ATP, 0.3 GTP, 50 Cs-methane sulfonate, 30 CsCl, 10 HEPES, and 10 BAPTA, balanced to pH 7.3 with CsOH.

Perfusion. To activate NMDAR currents, nucleated patches were perfused locally with the bath Ringer solution containing NMDA in concentrations between 20 and 500 μm. To perform fast steps of agonist concentration, two-barrel (θ) glass tubing, pulled to an outside diameter of 50 μm, was used to create parallel adjacent streams of agonist and control solutions with gravity-driven flow. The perfusion tubes were moved by a piezoelectric translator (Luigs and Neumann, Ratingen, Germany), switching perfusion of a nucleated patch from one stream to the other, within 1-4 msec.

Data analysis. NMDAR current responses to voltage steps were corrected for residual capacitative and background ionic currents by recording responses induced in Ringer solution alone or in Ringer with added agonist, 7-15 times at intervals of 5-10 sec, averaging and then subtracting the control from the agonist-induced ensemble average. For fitting of time constants, current responses were digitally filtered (Gaussian filter at 1 kHz cutoff frequency) and fitted by least squares. The step response of the digital filter, which dominated the total step response of the system, had a 10-90% rise time of 0.3 msec. Where indicated, recordings have been plotted without digital filtering to show the speed of current responses more accurately.

Modeling. Responses of kinetic models to step changes in voltage and agonist concentration were calculated using standard methods from kinetic theory (Cox and Miller, 1965; Colquhoun and Hawkes, 1977, 1995). Briefly, for a k-state process, if P is the k×k matrix of conditional probabilities of occupying state j given occupation of state i at t = 0, Q is the matrix of transition rates between states, ((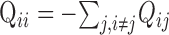)), the solution to the differential equation

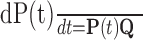1

is given by e^Qt, denoting the matrix exponential. For a particular vector p(0) of starting occupation probabilities, p(t) = p(0)e^Qt. For stationary Q, each element of p(t) is a sum of k-1 exponential terms with amplitudes and time constants that are obtained from the spectral expansion of Q. Matlab (MathWorks, Natick, MA) was used to write succinct programs for calculating these solutions. For simulations of spike generation, in which Q varies with the free membrane potential, equation 1 was solved numerically as part of a system of equations together with a three-conductance Hodgkin-Huxley type model for a cortical neuron (Lytton and Sejnowski, 1991) using a fourth-order variable time-step Runge-Kutta method (Matlab function ode45) or an Euler method and integration time step of 10 μsec.

Measured responses were fitted using the fminsearch function of Matlab to minimize the least-squares deviation of data from the model prediction. As described in Results, one or two rate constants at a time were varied as free parameters in this fit along with N (number of channels). The desensitization rate constant k_d (which was set equal to k′_d unless otherwise stated) was determined for each patch by fitting responses to agonist concentration steps at a constant holding potential. Other values of rate constants are given in Table 1. In fitting the data in Figure 2, we assumed a perfusion time course, which was a Gaussian-filtered step concentration change (Colquhoun and Sigworth, 1995), with a 10-90% rise time of 3.38 msec, which was determined as a free parameter in the fitting.

Table 1.

Rate constants used for OCB and STB models

kon Glutamate	5000 mm/sec
kon NMDA	2000 or 5000 mm−1sec−1
koff Glutamate	5.5 sec−1
koff NMDA	32.8 or 82 sec−1
kd High [agonist]	8.4 sec−1
kd Low [agonist]	1 sec−1
kr	1.8 sec−1
β	46.5 sec−1
α	91.6 sec−1
k+	610 exp(−V/17) mm−1sec−1
K−	5400 exp(V/47) sec−1

k_on for glutamate is taken from Clements and Westbrook (1991), k_on for NMDA (2000 mm/sec) from Benveniste and Mayer (1991) or as for glutamate (5000 mm⁻¹sec⁻¹), as described with the corresponding k_off values based on K_d values reported by Patneau and Mayer (1990). A k_on of 2000 mm⁻¹sec⁻¹ gave a better fit for brief pulses of high concentration agonist, whereas the difference was small for voltage steps applied during constant agonist concentration. Mg²⁺ -binding and -unbinding rate constants from Ascher and Nowak (1988) (V in mV). α, β, from Lester and Jahr (1992). Desensitization rate constant k_d was larger for simulations with high agonist concentrations (200 μm glutamate, 500 μm NMDA) than for those with low concentrations (5-10 μm glutamate, 25-30 μm NMDA). For experimental currents, k_r and k_d were fitted from the current decay at a constant voltage for each nucleated patch. In general, however, fitting only k_d as a free parameter produced satisfactory fits.

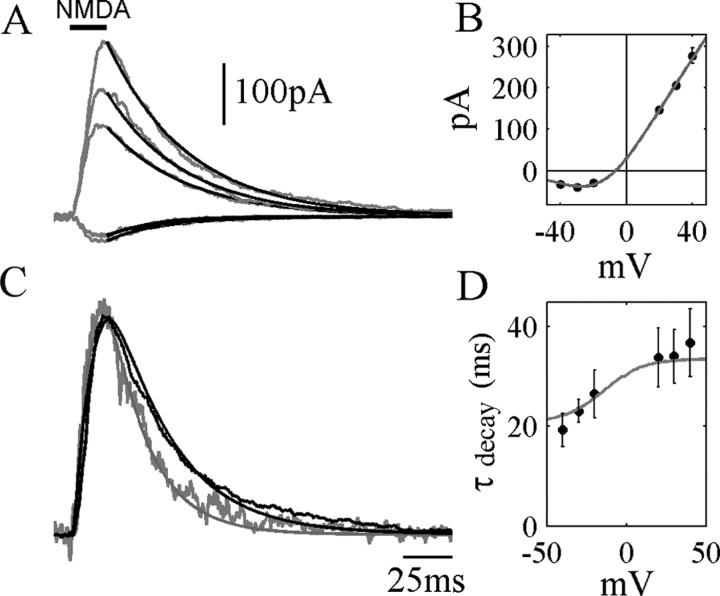
Figure 2.

Voltage dependence of deactivation. A, Single exponential fits to the decay phase of NMDA receptor currents in response to a 20 msec exposure to 500 μm NMDA. Holding potentials (from top to bottom): +40, +30, +20, -20, -40 mV. B, Current-voltage plot of peak NMDAR currents, fitted to a Boltzmann distribution for Mg²⁺ block. C, Currents at -40 and +40 mV in A, normalized to peak amplitude to allow comparison of time course. Smooth superimposed curves are the predictions of the ATB model (see as follows) with the following parameters: α′ = 270, β′ = 46, k_r = 1.8, k_d = k_d′= 8.4 (sec^-1), k_on = 2000 mm^-1sec^-1, k_off = 32.8 sec^-1. Agonist concentration time course was a Gaussian-filtered step with a 10-90% rise time of 3 msec. D, Circles represent the average (±SD) of single exponential fits to NMDAR current decay (500 μm NMDA, 20 msec perfusion, 5 nucleated patches), showing an increase in the decay time constant with membrane potential. Superimposed curve shows the time constant of single exponential fits to deactivation time course for the ATB model.

Results

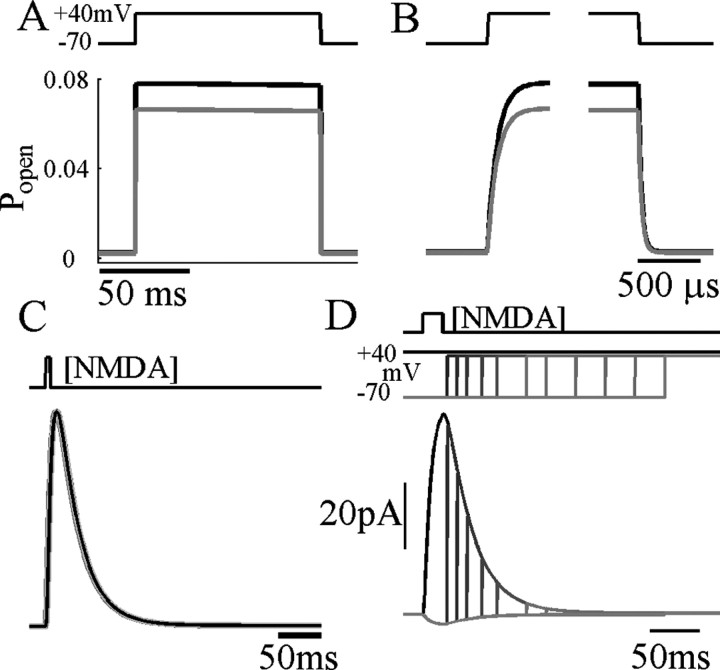
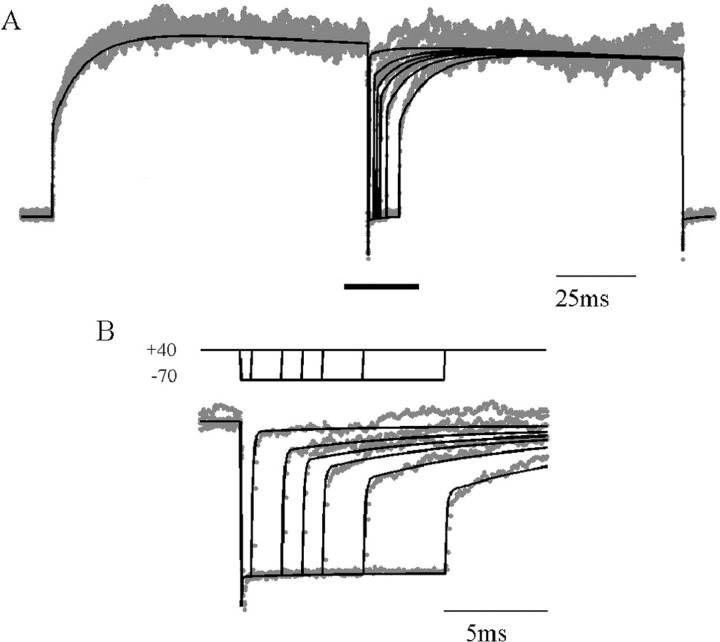
Figure 1A shows NMDAR current responses recorded in cortical pyramidal cell nucleated patches exposed to a 20 msec pulse of NMDA, in the presence of a physiological level (1 mm) of external [Mg²⁺]. When holding the potential at +40 mV (Fig. 1A, black trace), a large outward current is elicited, showing a fast activation, followed by a slower deactivation lasting ∼200 msec. At this potential, NMDARs are almost completely unblocked. If, instead, the membrane potential is held at -70 mV and stepped only briefly (for 5 msec) to +40 mV, only ∼50% of the full level of NMDAR current is uncovered (gray traces). In contrast, 5 msec depolarizations from 0 to +40 mV revealed >90% unblock of the current at +40 mV (Fig. 1B). This is a consequence of the slow unblocking fraction of NMDAR current described in Vargas-Caballero and Robinson (2003). Figure 1C shows a similar protocol for a family of different holding potentials in one patch, showing that the slow fraction of unblock, the proportion that fails to occur within 5 msec (3 msec for the trace at -70 mV), varies with the starting potential. Also, the slow unblock fraction is much larger during the deactivation phase than during the brief activation phase. The time course of slow unblock was unaffected by replacing cesium with potassium as the main intracellular monovalent cation (data not shown; five patches).

Figure 1.

Unblock has a large slow component. A, Current response to a brief pulse of NMDA (500 μm), while holding at +40 mV (black trace), compared with the responses to 5 msec depolarizing voltage steps to +40 mV from a holding potential of -70 mV (gray trace), with timing indicated at the top. B, Comparison of current obtained during continuous depolarization (black) and responses to voltage steps from 0 to +40 mV (gray), showing greatly reduced slow unblock. C, NMDAR unblock during 3 or 5 msec depolarizations from the potentials indicated by shades of gray at the top to +40 mV.

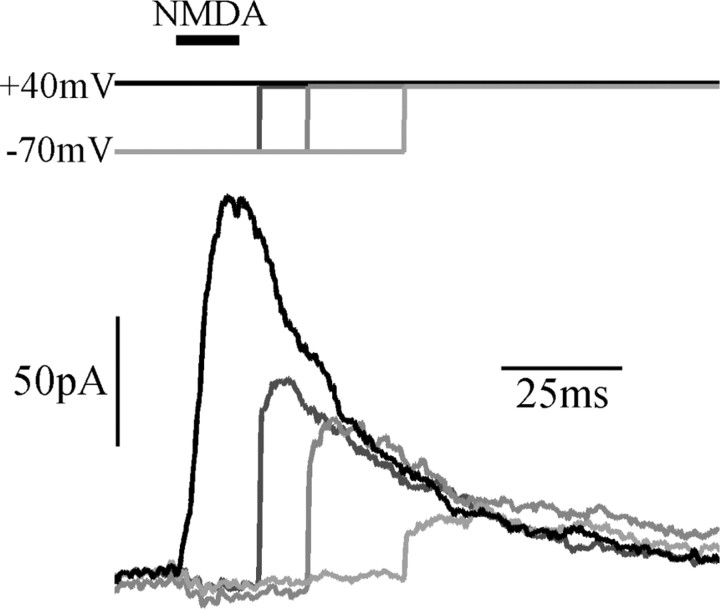
There is some disagreement in the literature about the voltage dependence of the deactivation or decay of the EPSC. Konnerth et al. (1990), D'Angelo et al. (1994), and Keller et al. (1991) report that the EPSC decay is slowed several-fold by depolarization over the physiological potential range, whereas Hestrin et al. (1990) found no dependence on voltage. Taking advantage of the excellent voltage-clamp and calcium-buffering conditions afforded by the nucleated patch technique, we examined the time course of deactivation at a number of different steady holding potentials (Fig. 2A). Superimposing the peak-normalized current responses (Fig. 2C) shows that deactivation is slowed distinctly with depolarization, although a clear dependence of deactivation time constant on voltage is only seen at negative potentials (Fig. 2D). If the membrane potential is stepped from -70 to +40 mV at various times after a pulse of NMDA (Fig. 3), the current returns with slow and fast components to a time course that does not overshoot the response recorded at +40 mV.

Figure 3.

Deactivation proceeds during block. Responses to a pulse of NMDA (500 μm), while holding at +40 mV, or stepping from -70 to +40 mV at the times indicated. Responses rejoin a similar time course of deactivation regardless of the point at when block is relieved, consistent with a trapping-block type of mechanism.

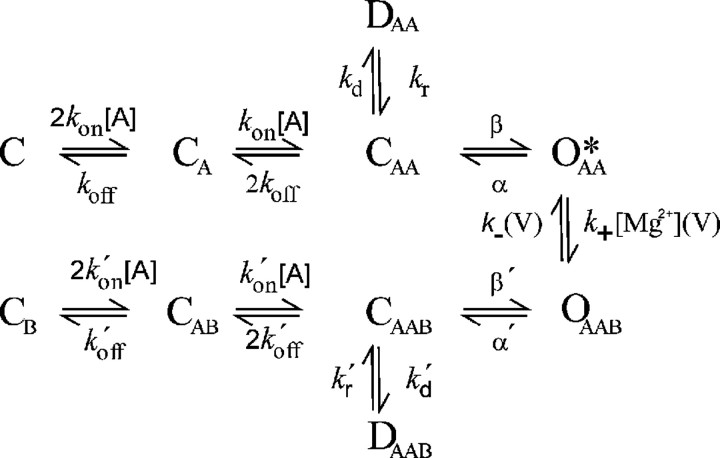
Can these voltage-dependent kinetics (the slow unblock and the voltage dependence of deactivation) be accounted for by the existing understanding of NMDAR gating? Models of activation and deactivation kinetics are based on studies performed in nominally magnesium-free conditions to remove the complication of block, whereas the kinetics of magnesium-blocking reactions near the open state have been studied using single-channel recording (Ascher and Nowak, 1988; Antonov and Johnson, 1999). The most widely accepted scheme for describing the kinetics of macroscopic NMDA currents in the presence of magnesium block is the trapping-block model (Benveniste and Mayer, 1995; Sobolevsky and Yelshansky, 2000) shown in Figure 4. The data in Figure 3 are compatible with this kind of mechanism, which allows deactivation to proceed even when channels are blocked at hyperpolarized potentials, unlike “foot in the door” open-channel block (Ascher and Nowak, 1988). So far, it has been assumed that the rates of corresponding transitions for the blocked and unblocked channels are the same, and we refer to this as the symmetrical trapping-block scheme (STB). In the version used here, the activation reactions of Lester and Jahr (1992) were combined with the voltage-dependent magnesium blocking and unblocking rates measured by Ascher and Nowak (1988). See Table 1 for values of rate constants.

Figure 4.

Trapping block kinetic scheme for the NMDA receptor. Activation and deactivation reactions are equivalent for the Mg-free (top half) and Mg-bound channel (bottom half). For STB, k′_x = k_x. The symbols C, O, and D represent the closed, open, and desensitized channels, respectively, bound to molecules of agonist (subscript A) or blocker (subscript B). The asterisk indicates the conducting open state.

The relaxation of open-channel probability of the STB model (see Modeling in Materials and Methods) after a step depolarization from -70 to +40 mV reached a steady-state value of ∼0.13 within several hundred microseconds (Fig. 5A,B) without any sign of the slow unblock phase observed experimentally. The STB model shows no voltage dependence of deactivation kinetics whatsoever (Fig. 5C), because deactivation proceeds equally quickly when the channel is blocked or unblocked. Accordingly, with depolarizing steps applied during the deactivation phase, the current returns rapidly along the same time course regardless of how long the receptors are held hyperpolarized. In the experimental finding (Fig. 3), the return of the current has a large slow component, whereas the STB model predicts an extremely rapid return. Thus, the STB scheme fails to account for the slow-unblocking response to depolarizing steps or for the voltage dependence of the deactivation phase. We also investigated a simple foot in the door open-channel block model (data not shown). This also failed to show slow unblock but also produced a large transient of channel opening during unblock and showed a delay in deactivation time course when holding at hyperpolarized potentials, neither of which were observed experimentally.

Figure 5.

STB scheme fails to predict slow unblock and voltage dependence of deactivation time course. Relaxation of NMDA-induced currents in the STB model during a voltage step from -70 to +40 mV, with timing indicated by the top trace. A, Black traces are responses to 3 μm glutamate, and gray traces are responses to 25 μm NMDA. B, Unblock and block transitions at an expanded time scale. [Mg²⁺]_o = 1 mm. Voltage steps were applied after allowing 800 msec equilibration with agonist. k_d was 1 sec^-1. For NMDA, k_on = 2000 mm^-1sec^-1, k_off = 32.8 sec^-1. See Table 1 for details of other rate constants used. C, D, Voltage dependence of deactivation. C, Normalized time course of deactivation of normalized responses of the STB model to 5 msec exposures to 500 μm NMDA while holding at any potential (all traces overlie exactly); there is no voltage dependence of the conductance transient. D, Voltage steps applied at variable times (indicated at top) during deactivation in the STB model. Current calculated from the open-channel probability and voltage assuming a reversal potential of -5 mV and a population of 100 channels, each with a conductance of 50 pS.

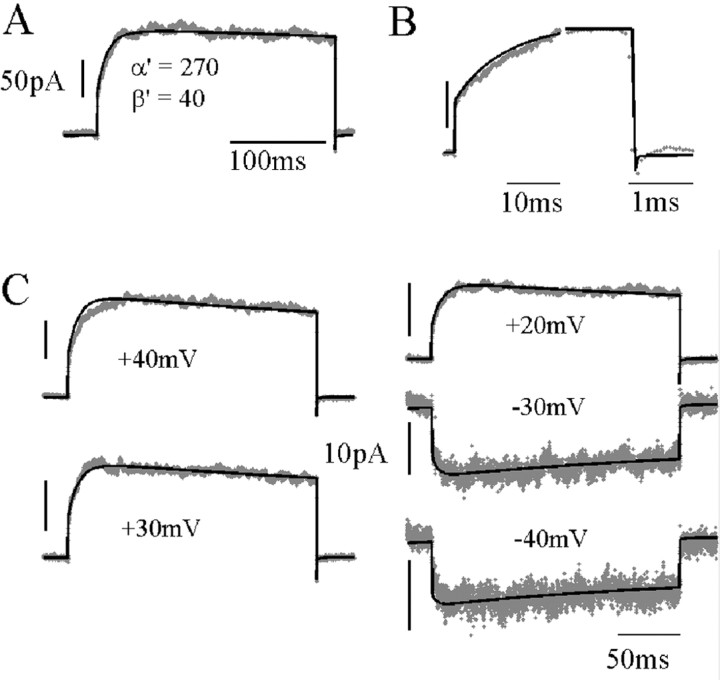
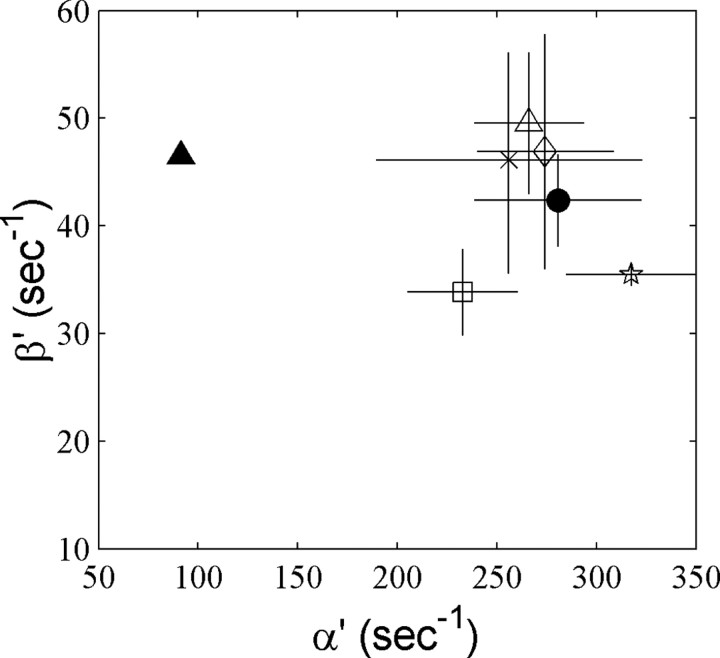
What is the simplest modification to the STB model that would satisfactorily account for NMDAR responses to voltage steps? What appears to be required is a slower flux of channels from blocked states with depolarization. We first investigated fitting of all rate constants as free parameters. However, although providing good fits, using so many parameters did not always result in reproducible modification of the same rate constants when fitting data from different sweeps or different patches. For example, sometimes the desensitization rate constants were greatly altered, but sometimes not. Instead, we chose to fix the well substantiated rate constants in the unblocked part of the model, as well as the blocking and unblocking reactions, and to ask what is the effect of varying individual rate constants between blocked states (see supplementary figures, available at www.jneurosci.org/cgi/content/full/24/27/6171/DC1). This showed that although slow unblocking kinetics can be produced by individually modifying other rate constants, only modification of α′ was able to produce the correct time constant and amplitude of the slow component. An α′:α ratio of ∼3 was sufficient to fit the observed time course, both of unblock and reblock (Fig. 6A,B), producing a slow component that accounted for between 40 and 50% of the total current amplitude. Figure 6C shows the fit to a family of both inward and outward current step responses with α′, β′, and N, the number of channels in the population, as free parameters. This allowed a good fit to the form of both unblock and reblock time course (including the small fast tail current) at all potentials. Figure 7 shows the extent by whichα′ andβ′ were altered fromα andβ to fit the voltage step responses by least-squares. α′ was consistently and significantly different, larger by a factor of ∼3 than α, whereas there was no significant difference between β′ and β. The ranges of values obtained in different fits were 205-308 sec^-1 for α′ and 28-57 sec^-1 for β′. Thus, increasing one voltage-independent rate constant, α′, several-fold was able to account for the different forms of block and unblock relaxations at potentials across the physiological range.

Figure 6.

ATB model fit to a family of voltage step responses during stationary NMDAR activation (25 μm). A, Current response to a voltage step (-70 to +40 mV) fitted to the ATB model with parameters as shown (n = 400; single-channel conductance, 50 pS; reversal potential, -5 mV). B, Expanded time scale of response in A to show the fit to fast responses of unblock and block. C, Current responses to voltage steps from -70 mV to the voltages indicated for each trace. Black lines show predictions using a constant α′ = 287 sec^-1 and β′ = 48.5 sec^-1 for all voltages, adjusting only the number of channels for each trace by least-squares (n = 253 ± 20), k_d and k′_d = 3 sec^-1, k_on = 5000 mm^-1sec^-1, k_off = 82 sec^-1. Calibration, 50 pA (outward currents); 10 pA (inward currents).

Figure 7.

Comparison of closing and opening rate constant fits for the ATB model. The fixed values of α and β (used for the Mg-free channel) are indicated by the filled triangle. Other symbols show least-squares fits of voltage step responses. Each symbol represents fits to different families of responses from the same nucleated patch, with the SD of fits to individual traces indicated, except for the filled circle where data for voltage steps from -70 to +40 mV were pooled from different experiments (n = 4). Averages and SDs are from best simultaneous fits of α′ and β′ for 6-10 leak-corrected averaged current responses.

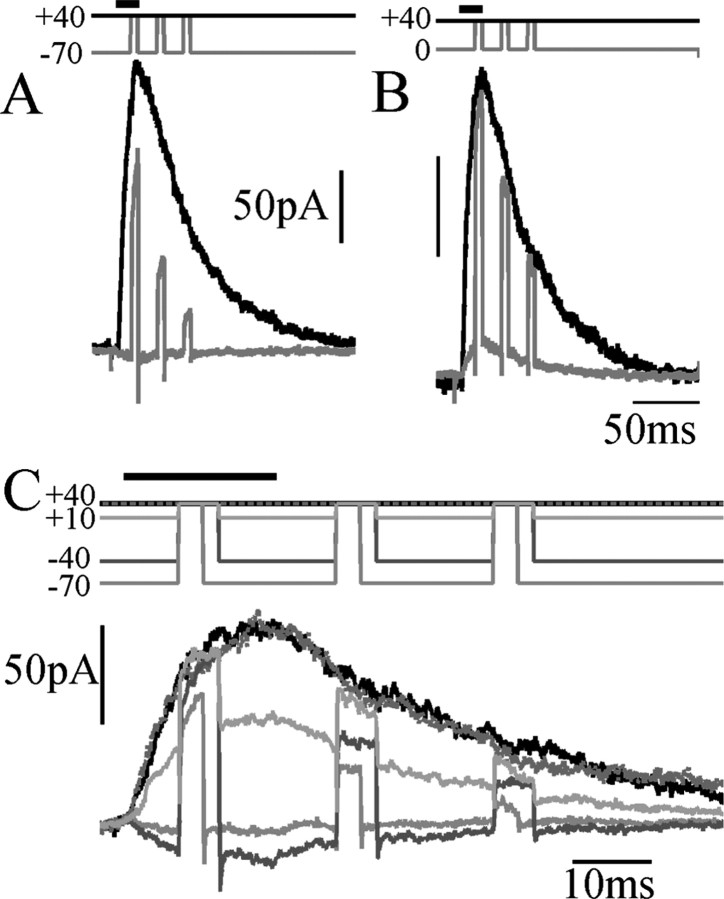
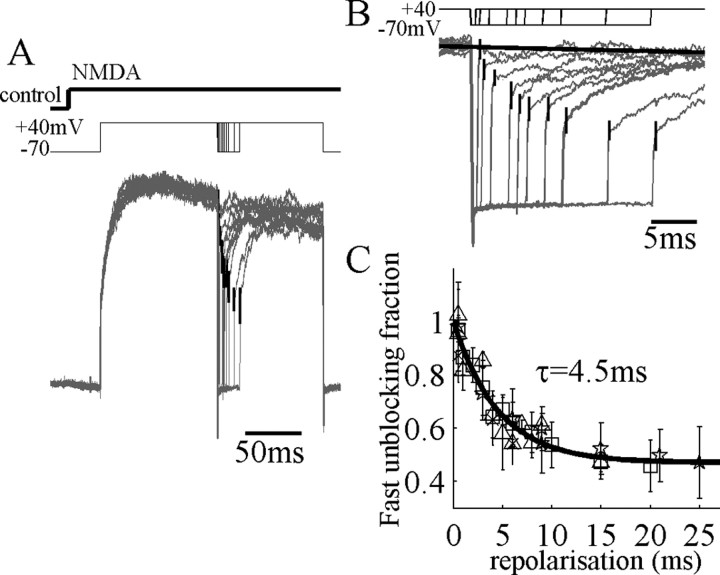
To test whether this ATB model can now explain responses to more complex voltage protocols, we decided to examine how unblock kinetics are changed after brief repolarizations of varying duration. During responses in maintained agonist concentration, unblock at +40 mV after repolarizations to -70 mV lasting only 1-2 msec showed no slow component (Fig. 8A,B). However, increasing the duration of repolarization showed a gradual return of the slow component with an average time constant of 4.5 msec (Fig. 8C). The ATB model with α′ obtained from fits to families of step depolarizations (as in Fig. 6) provided an excellent fit also to these data (Fig. 9). Brief repolarizations move channels predominantly into state O_AAB (Fig. 4), whereas longer repolarizations allow more channels to move to C_AAB or beyond, which then must unblock against the relatively high α′ rate constant. We also found that the ATB model could account accurately for the time course of currents during repolarization over the range of physiological potentials, including very slow components at potentials of approximately -40 to -10 mV (see supplementary figures, available at www.jneurosci.org/cgi/content/full/24/27/6171/DC1). The voltage dependence of deactivation, or NMDAR EPSC decay, was predicted correctly by the ATB model (Fig. 2C); at positive potentials, channels deactivate increasingly through the slower α transition instead of through the α′ transition. In addition, it reproduced the observation that there is less slow unblock early in a transient response (Fig. 1D), assuming that channels start from the closed unblocked state before the response.

Figure 8.

Recovery of slow-unblocking fraction during brief repolarizations. A, NMDAR currents evoked in a nucleated patch perfused with 60 μm NMDA as indicated at top. Currents are normalized by maximum amplitude, because some rundown occurred during recording. Leak subtracted currents showed a maintained activation after depolarization with a slight desensitization. Voltage steps from -70 to +40 mV were then applied to the patch, and brief repolarizations to -70 mV, lasting 0.5-25 msec, were applied as indicated. The fraction of NMDAR-current fast-unblock was measured at the corner of the fast and slow components as shown by the vertical bars, which indicate ensemble SD. B, Expanded time view of repolarizations in A. The maximum level of current at +40 mV is shown as a black solid line. C, Data from four nucleated patches showing the fraction of fast unblocking current normalized to the maximum level of the current. Recovery to the minimum amplitude of fast unblocking current (0.47) takes place with a time constant of 4.5 msec.

Figure 9.

Fit of ATB model to recovery of slow-unblocking fraction. A, Current responses recorded as in Figure 8. Superimposed black traces show fit to ATB model with α′ = 214 sec^-1, β′ = 40 sec^-1, k_d = 5 sec^-1, k_d′ = 5 sec^-1, k_on = 5000 mm^-1sec^-1, k_off = 82 sec^-1. B, Expanded time scale view for the segment indicated by the thick bar in A.

Because the model contains 10 states, the time course of relaxation of occupation probability for any of the states after voltage steps has nine exponential components. However, three of these components account for >97% of the probability of being in the open state for most physiological voltages; we designate their time constants as τ_fast, τ_slow-a, and τ_slow-b. In Figure 10, we show a portrait of NMDAR dynamics for voltage steps within the physiological range, using the ATB model (with α′ = 3α), plotting each time constant as a function of starting and finishing voltages and coloring the surfaces to indicate the amplitudes of the components.

Figure 10.

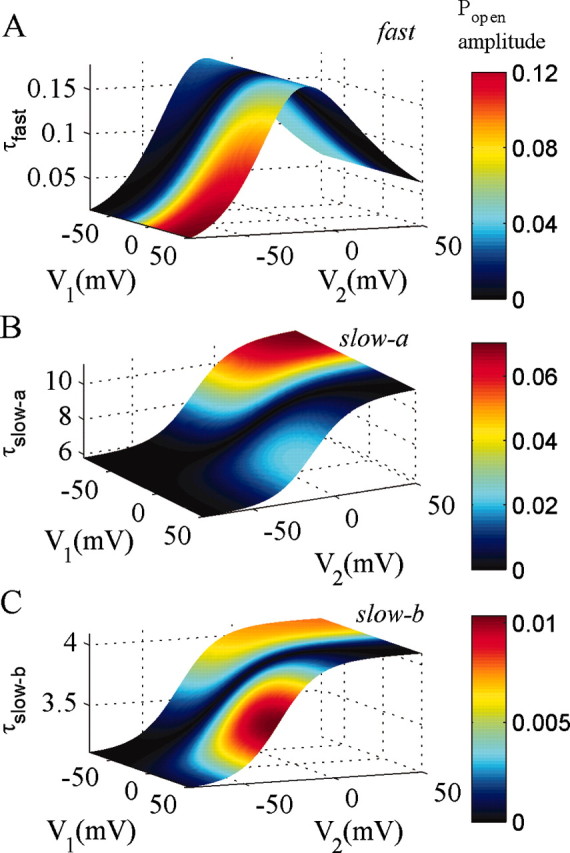
Principal exponential components of the ATB mechanism. Time constant and amplitude of three exponential components of open-channel probability in the ATB mechanism, which account for >97% of response amplitudes, are shown. α′ = 270 sec^-1 and β′= 46 sec^-1, k_on = 5000 mm^-1sec^-1, k_off = 82 sec^-1. Other rate constants as specified in Table 1 (25 μm NMDA). Time constant and amplitude are plotted as functions of the starting voltage (V₁) and the end voltage (V₂) for voltage steps. The time constants are independent of V₁, whereas the probability amplitude depends on both V₁ and V₂.

The fast component (Fig. 10A) accounts for most of the block after voltage steps from very depolarized to very hyperpolarized potentials, and τ_fast is <10 μsec. At -20 mV, the peak value of τ_fast is ∼150 μsec, but the amplitude is smaller, ∼30% of the total amplitude for a step from +50 to -20 mV. For depolarizing voltage steps from -70 to +40 mV, the fast component accounts for only 40% of the unblock. It would be difficult to directly measure even the slowest values of τ_fast in experiments, even by deconvolving the impulse response of the recording system (Kleppe and Robinson, 1999). However, values of ∼150 μsec would still limit charge influx during the upstroke of fast action potentials.

The “slow-a” component has a time constant between 6 and 10 msec in the physiological range of potentials. Its largest contribution is for depolarizing voltage steps from hyperpolarized potentials, where it accounts for up to half of the amplitude of the probability of being in the open state (P_open) (Fig. 10B). The probability amplitude of the slow-a component becomes smaller at more negative potentials (accounting for 30% for steps from -70 to -20 mV) but is large for voltage steps repolarizing from highly depolarized potentials to potentials in the range where maximal inward current flows through the channel (-40 to -10 mV). Thus, block is far from instantaneous at these potentials. This is relevant to the repolarizing phase of APs, explaining why NMDARs contribute more inward current than expected from the steady-state I-V relationship during this phase (Vargas-Caballero and Robinson, 2003). Finally, although smaller in amplitude than slow-a, the slow-b component can contribute up to 10% of the open probability amplitude, with time constants in the range of 3-4 msec, as seen in Figure 10C. Like slow-a, the slow-b component is largest for depolarizations to 0 and above and for repolarizations to -40 to -10 mV.

The ATB model successfully predicts the response of NMDARs to various voltage step protocols. Can it correctly account for the NMDAR current flowing during more complex, physiological waveforms of voltage? In our previous study (Vargas-Caballero and Robinson, 2003), we recorded NMDAR current in nucleated patches during membrane potential waveforms reflecting fast spikes and bursts of spikes associated with a slow plateau potential (Fig. 11A). In Figure 11B, the response of the best-fit ATB model is superimposed on this data. As seen in the time-expanded segments (Figure 11a-c), the ATB model fits the data in detail, during the upstroke, repolarization of fast action potential, outward phases of the current, and during maintained plateau potentials. Figure 11C shows the data in Figure 11B replotted as an instantaneous I-V relationship (black) with the ATB model prediction (light gray) and the measured steady-state I-V relationship (dark gray). Both data and model show a wide variation of inward and outward current levels. In the inward direction, the dynamics of the NMDAR result in both much more and much less current than expected from the steady-state I-V relationship, whereas outward current responses always fall short of the steady-state level, because the positive excursions of the membrane potential are so brief. We fitted the ATB model to current flowing during action potentials recorded at room temperature, because there is good information available on the rate constants of the model at room temperature. However, we also found a reasonable fit of currents recorded at near-physiological temperature (33°C) (Vargas-Caballero and Robinson, 2003) in response to somatic and dendritic APs by simply scaling up the Q matrix of the model by a factor of 3 to simulate the difference in temperature (data not shown).

Figure 11.

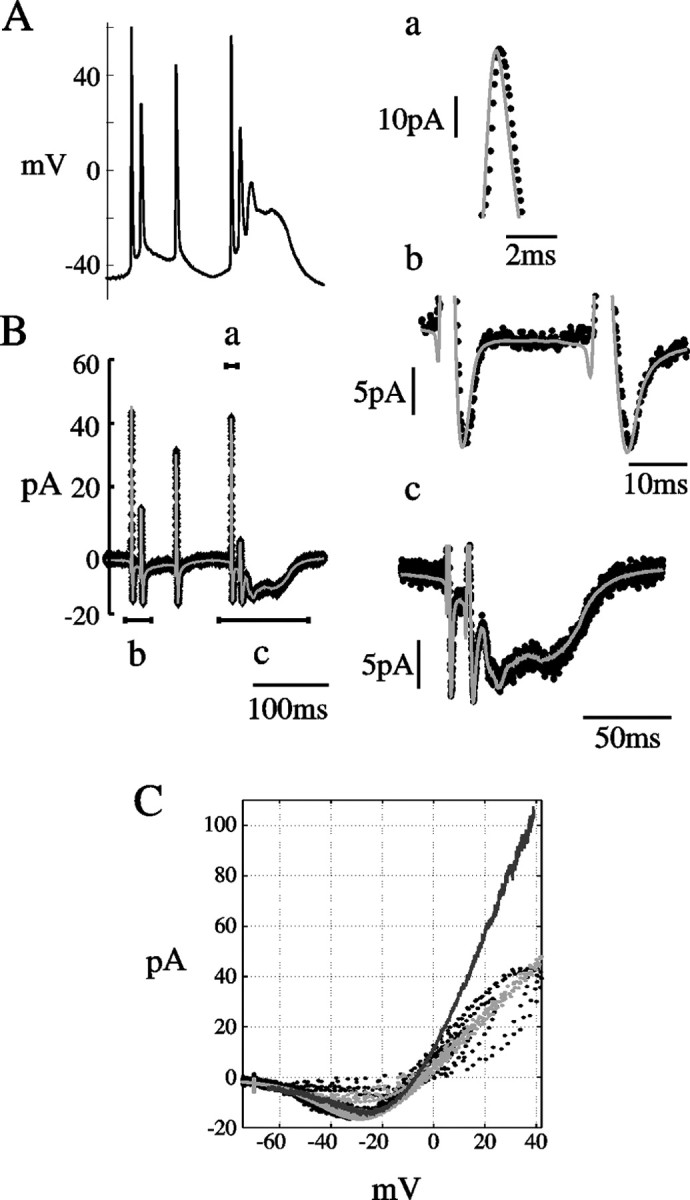
Fit of NMDAR current responses to AP waveform clamp at room temperature. ATB mechanism fit to NMDAR current during action potential waveforms. A, AP waveform recorded at room temperature (data from Vargas-Caballero and Robinson, 2003). B, Black trace shows leak-subtracted average NMDA current response to A in a maintained concentration of 25 μm NMDA. Superimposed gray trace is the best fit from the ATB model obtained by minimizing the squared deviation between fit and data with α′, β′, and N, the number of channels as free parameters. Best-fit values were α′ = 293, β′ = 43 sec^-1, and N = 920. k_on = 5000 mm^-1sec^-1, k_off = 82 sec^-1. Current segments labeled a, b, and c are shown in the corresponding panels at expanded time and current scales. C, Instantaneous current-voltage relationship from B. Recorded data shown in black, ATB fit in light gray, and for comparison, the steady-state I-V relationship measured by a slow (3 sec) ramp of membrane potential in dark gray.

Discussion

Explaining the voltage-dependent kinetics of the NMDAR

Previously, the activation and deactivation time course of NMDARs has almost exclusively been studied at a constant potential and in the absence of magnesium. This study fits voltage step responses of NMDARs in the presence of physiological levels of magnesium with a kinetic model of NMDAR gating. The slow voltage-dependent kinetics of NMDARs plays a major role in determining the trajectory of open-channel probability during physiological membrane potential transients (Vargas-Caballero and Robinson, 2003). The ATB model was constructed by combining the trapping-block scheme of Sobolevsky and Yelshansky (2000) with the voltage dependence of blocking reactions of Ascher and Nowak (1988) and adjusting a single rate constant (α′) to fit families of voltage step responses. Compellingly, it is then highly effective in explaining all the macroscopic current responses to voltage perturbations that we examined, including responses to natural waveforms. Sobolevesky and Yelshansky (2000) found that STB was able to account adequately for their concentration-jump data. By simulating their experiment (Sobolevesky and Yelshansky, 2000, their Fig. 8) in which magnesium is applied and removed during continuous receptor activation, we showed (see supplementary figures, available at www.jneurosci.org/cgi/content/full/24/27/6171/DC1) that the difference between ATB and STB under these circumstances is very small and unlikely to be resolved with the time course of their perfusion (20-30 msec time constant). Qian et al. (2002) argued that their finding, that direct measurements of the IC₅₀ for Mg block correspond well with values predicted from single-channel blocking events, implies that trapping block is symmetrical, that binding of magnesium does not influence the other gating reactions of the channel. We calculated the IC₅₀(V) relationship for the ATB model and found that indeed it falls below, by a factor of ∼1.8, the predicted IC₅₀ of their model. It is not presently possible to resolve this discrepancy, because we did not perform measurements of magnesium IC₅₀. However, as we have shown in Figure 5, an STB scheme is not able to reproduce slow unblock; an asymmetry is necessary.

The values of the slow-a time constant in our average best-fit model (Fig. 10) were lower than the values reported by Vargas-Caballero and Robinson (2003) for exponential fits to the slow component. This is likely to be related to the different perfusion technique and timing of the present study, in which we use continuous-flow fast perfusion and apply voltage steps within 50 msec in agonist solution, minimizing slow processes of desensitization.

Single-channel studies have recently led to different proposed models of activation of the channel. Popescu and Auerbach (2003) proposed a scheme to account for modal gating of single channels but assumed a foot-in-the-door magnesium block of open states rather than trapping block. In the model by Banke and Traynelis (2003), who investigated gating in the absence of magnesium, a single open state is used, as in the ATB model. However, they also used a more complicated sequence of closed states, reflecting additional permissive structural changes after completion of binding of agonists, as well as a second desensitized state. It should be readily possible in the future to extend such a model with an asymmetry of trapping block to make specific predictions about the single channel correlates of ATB. It is interesting that their peak value of P_open, ∼0.15-0.2, measured in patches containing only a single channel, corresponds very well with the prediction of the ATB model for very depolarized potentials when magnesium block is essentially zero.

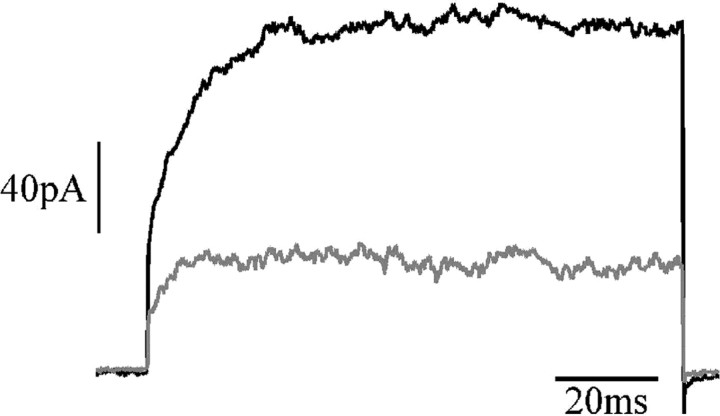
This study has used native extrasynaptic receptors, which may differ somewhat from synaptic receptors. There may be differences in subunit composition, with synaptic receptors preferentially containing NR2A subunits (Stocca and Vicini, 1998). The NR2 subunit type, predominantly A or B in this preparation (Monyer et al., 1994), could affect the time course of magnesium block. However, we found that ifenprodil, at a concentration (10 μm) that binds to and blocks the function of NR2B receptors but not NR2A receptors (Williams, 1993), blocked approximately two-thirds of the NMDAR current, but the slow fraction still accounted for just under half of the residual current (Fig. 12) (n = 3), strongly suggesting that slow unblock also takes place at the synapse. However, even extracellular NMDA receptors could make a significant physiological contribution, activated by spill-over or even by tonic extracellular levels of glutamate.

Figure 12.

Slow unblock persists after blockade of NR2B-containing receptors. A, NMDAR current responses to voltage steps from -70 to +40 mV. Black trace indicates control response, and the gray trace indicates the response after addition of 10 μm ifenprodil; 60 μm NMDA.

Possible structural mechanism

A faster channel closing conformational change when magnesium is lodged in the channel requires a molecular explanation. With the present state of knowledge of NMDAR channel structure, however, it is only possible to speculate about this. However, the substituted cysteine accessibility method data of Sobolevsky et al. (2002) suggest that the site for a trapping blocker lies deep in an outer vestibule, with the activation gate even further toward the cytoplasmic side. This suggests that, in order for occupation by magnesium to increase the rate of closure of the permeation gate, there should be an allosteric communication between the outer vestibule and the permeation gate. This could, for example, be transmitted by the long M3 segments, which appear to line the channel pore. Permeating calcium, if it binds at a similar site to the blocking magnesium, might have a similar effect on increasing closure rate, which would be potentially detectable in single-channel recordings as a reduced burst length in high calcium solutions.

Functional consequences of asymmetric trapping block

The asymmetric trapping block mechanism accounts for the behavior of NMDARs during the kind of voltage dynamics that are important for synaptic integration. There is evidence for nonlinear NMDAR-driven spike events in the basal dendrites of pyramidal neurons, even when sodium and calcium channels are blocked (Schiller et al., 2000), which could boost the input from these dendrites in a nonlinear, threshold manner. The rate of positive feedback in such events between voltage and NMDAR activation will be partly shaped by the process of slow unblock.

The slow unblock described by the ATB mechanism is expected to produce some complex effects during spatiotemporal activity patterns in the dendrite when NMDARs are activated, because the time scale of slow unblock-block is comparable with that of membrane potential trajectories during dendritic action potentials, affecting their conduction velocity, shape, and failure point. As shown in Figure 11, there is a strong contribution of NMDARs during repolarization, which results from slow unblock. This should assist the reciprocal excitation of apical dendrite and soma involved in backpropagating action potential-activated calcium spikes (Larkum et al., 2001). Also, NMDAR-mediated calcium influx will be strongest during repolarization or during fairly slow depolarizations; this will affect the timing and location of spike timing-dependent plasticity (Markram et al., 1997; Bi and Poo, 2001).

Computational modeling of NMDA receptor function

Many computational studies have attributed important roles to the voltage dependence of NMDAR function by assuming that the steady-state current-voltage relationship of NMDARs applies instantaneously (for review, see Koch, 1999). However, during electrical activity, the slow unblock-block processes result in a current that is radically different in time course from that predicted by the steady-state relationship. The ATB model will allow much more realistic computational studies of how NMDARs interact with other voltage-dependent channels to initiate and boost spikes. It can be easily incorporated into conductance-based models. For each compartmental population of NMDARs (e.g., a synapse), a 10-element vector of state occupation probabilities, p (see Materials and Methods), is maintained, and both p and the voltage- and agonist concentration-dependent rate matrix Q, which specifies the derivatives of the elements of p, are updated with time. For example, for simple Euler integration, p is updated according to the following:

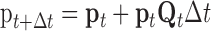2

or a more complicated integration method could be used. In the NEURON simulator (Hines, 1998), this can be incorporated with the NMODL KINETIC mechanism.

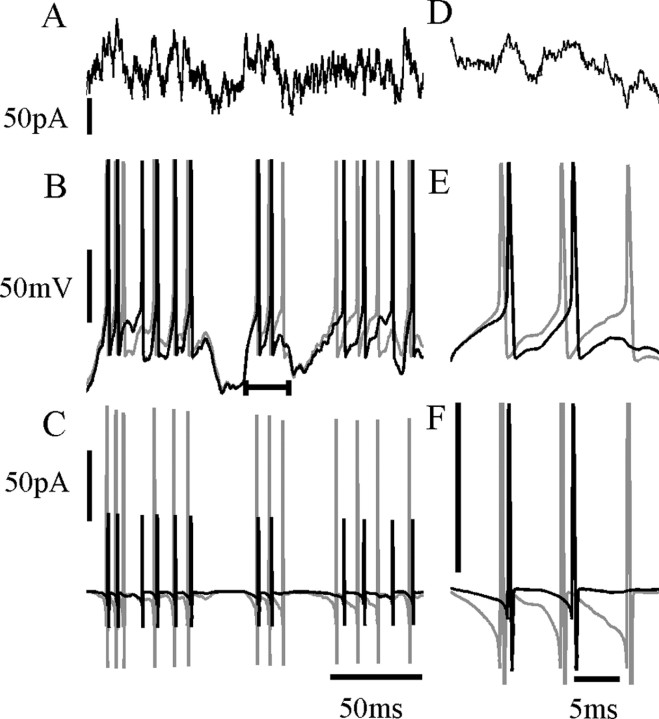
A complete set of rate constants only exists for room temperature, and additional study at physiological temperature will be required. We found that we obtained a reasonable fit to NMDAR current recorded during complex waveforms at a near-physiological temperature of 33°C by simply scaling Q up by a factor of ∼3 (data not shown). Although this approach may be a useful starting point, more accurate information is required about the temperature dependence of individual rate constants. Figure 13 shows a short example of model spike responses to a fluctuating current stimulus during NMDAR activation simulated at physiological temperature. When modeling an STB mechanism, which has effectively instantaneous unblock (gray traces), the cell fires earlier and more frequently than with the more sluggish ATB model (black), resulting in a spike train with very different timing in response to the same current stimulus. Average charge influx per NMDA receptor per spike was 0.183 fC (STB) versus 0.076 fC (ATB). Finally, it should be noted that this model is derived from data recorded in conditions of well buffered internal and external pH and calcium at presumably stationary levels of channel phosphorylation and in saturating extracellular glycine concentrations. The effects of these physiological variables on the slow voltage-dependent kinetics of the NMDAR need to be addressed in future studies.

Figure 13.

Comparison of STB and ATB mechanisms in a simple model of spike generation. A cell is modeled as a single compartment with the three-conductance model of Lytton and Sejnowski (1991). A, Fluctuating current stimulus (Ornstein-Uhlenbeck process). B, Voltage trajectory when open-channel probability is calculated using either the STB (gray) or ATB (black) models. Three hundred NMDAR channels are simulated in a constant concentration of 3 μm glutamate, with Q scaled up by three from room temperature values to simulate physiological temperature. C, Corresponding current through NMDA receptors. D-F, Amplified views of a segment of A-C (indicated by bar in B). Note the increased amplitude scale in F; current amplitude is truncated.