Environmental spatial and temporal variability and its role in non-favoured mutant dynamics

Abstract

Understanding how environmental variability (or randomness) affects evolution is of fundamental importance for biology. The presence of temporal or spatial variability significantly affects the competition dynamics in populations, and gives rise to some counterintuitive observations. In this paper, we consider both birth–death (BD) or death–birth (DB) Moran processes, which are set up on a circular or a complete graph. We investigate spatial and temporal variability affecting division and/or death parameters. Assuming that mutant and wild-type fitness parameters are drawn from an identical distribution, we study mutant fixation probability and timing. We demonstrate that temporal and spatial types of variability possess fundamentally different properties. Under temporal randomness, in a completely mixed system, minority mutants experience (i) higher than neutral fixation probability and a higher mean conditional fixation time, if the division rates are affected by randomness and (ii) lower fixation probability and lower mean conditional fixation time if the death rates are affected. Once spatial restrictions are imposed, however, these effects completely disappear, and mutants in a circular graph experience neutral dynamics, but only for the DB update rule in case (i) and for the BD rule in case (ii) above. In contrast to this, in the case of spatially variable environment, both for BD/DB processes, both for complete/circular graph and both for division/death rates affected, minority mutants experience a higher than neutral probability of fixation. Fixation time, however, is increased by randomness on a circle, while it decreases for complete graphs under random division rates. A basic difference between temporal and spatial kinds of variability is the types of correlations that occur in the system. Under temporal randomness, mutants are spatially correlated with each other (they simply have equal fitness values at a given moment of time; the same holds for wild-types). Under spatial randomness, there are subtler, temporal correlations among mutant and wild-type cells, which manifest themselves by cells of each type ‘claiming’ better spots for themselves. Applications of this theory include cancer generation and biofilm dynamics.

1. Introduction

One of the questions that has interested evolutionary theorists for almost 100 years is the generation and spread of mutants. Starting from early works of Haldane [1], Fisher [2] and Wright [3], researchers focused on the probability and timing of mutant fixation under various assumptions, see e.g. seminal work of Kimura on neutral evolution [4,5] and Patwa & Wahl [6] for a review on fixation probabilities of advantageous mutants. Around the 1950s, mutant evolution in random environments attracted attention of evolutionary biologists and mathematicians. Different aspects of this problem have been investigated, such as the evolution of mutation rates in random environments [7–10].

In [11], the role of a randomly fluctuating environment was studied by assuming that while the wild-types had constant numbers of offspring, mutants’ numbers of offspring were random (with the same mean), and changing every time step. It was shown that in this case the mutants were negatively selected. A more general setting of randomly fluctuating environments was studied by Frank & Slatkin [12] and Frank [13]. It was shown that even if the environmental changes affected the division rates of mutants and wild-types in a similar way, minority mutants had an intrinsic advantage due to frequency-dependence effects. A similar conclusion was reached in the study of Melbinger & Vergassola [14], who also obtained results on the timing of mutant fixation in randomly changing environments affecting the agents’ division rates. In [15], it was shown that a fluctuating environment changed the forces of selection and allowed mutants that were on average weaker to become fixated with a probability much larger than expected (based on their mean fitness). In ecology, a set of profound results have been obtained in the framework of the Modern Coexistence Theory, which is concerned with the instantaneous rate of increase of a rare species [16–18]. In particular, Chesson & Warner [19] have shown analytically, that temporal variability in division rates would lead to a positive rate of increase of the rare species (even if it is an inferior competitor), and that both species would (in the symmetric fitness scenarios) be attracted to a fixed point of equal abundance. This is known as the ‘storage effect’. Chesson & Warner [19] have further shown that variability in death rates would lead to the opposite effect, leading to a negative rate of increase of the rare species. Analytical results for extinction times have been derived by Kessler et al. [20], Hidalgo et al. [21] and Danino & Shnerb [22].

A different type of randomness is associated with the existence of ‘spots’ that may be characterized by different (random) conditions for the agents. For example, agents can be assumed to interact on a heterogeneous or random network, where not all vertices have the same number of connections and hence their fitness values are based on different numbers of interactions, making some vertices more advantageous than others. Several groups studied related problems, especially in the context of the game theory and cooperation (e.g. [23–28]). In a different style of modelling, fixation of mutants was studied in a spatially heterogeneous environment, represented by a multi-patch (finite island) model, where fitness values of mutants and wild-type agents were different depending on the patch. Both the high migration rate limit [29] and the low migration limit [30] have been studied. Gavrilets & Gibson [31] derived formulae for the probability of fixation for both beneficial and deleterious alleles in a symmetric two-deme system. These results were extended and generalized in the study of Whitlock & Gomulkiewicz [32], who reported that under symmetric migration, spatially non-homogeneous fitness in a metapopulation never decreased—and sometimes substantially increased—the probability of mutant fixation, compared to metapopulations experiencing homogeneous selection with the same mean selection intensity. The role of spatially variable environments in species coexistence has been also addressed by the Modern Coexistence Theory. In particular, the environmental influence on the growth rate of the rare invader has been studied analytically [33], finding a generally positive effect.

In [34], we studied the effect of spatial randomness on mutant fixation probability. Our setting was different from the finite island or the random graph models. We assumed that for wild-type and mutant cells, the division rates at different locations were drawn from identical probability distributions, and for a given realization they did not change in time. We showed that under the Moran or haploid Fisher–Wright processes on a complete graph or on a circle, as long as initially mutant cells were in a minority, their fixation probability was significantly higher than their initial frequency (which is the fixation probability under the neutrality assumption). We further demonstrated that the fixation time (conditioned on mutant fixation) was significantly affected by the randomness, and that randomness increased the mean conditional fixation time on a circle but decreased it on a complete graph [35].

In this paper, we explore aspects of mutant dynamics that have not been previously addressed in the literature. This includes systematic comparisons of (1) spatial versus temporal variation; (2) division rates versus death rates being affected by environmental randomness, (3) mass action versus spatially restricted systems and (4) birth–death (BD) versus death–birth (BD) Moran processes. To put our work in the context of the existing results, below we list some of the key novel findings reported in this paper.

(a) Classical results in non-spatial systems with temporal fluctuations can be destroyed by spatial interactions. It is well known that under temporal randomness in a completely mixed system, minority mutants experience (i) higher than neutral fixation probability and a higher mean conditional fixation time, if the division rates are affected by randomness and (ii) lower fixation probability and lower mean conditional fixation time if the death rates are affected. In this paper, we show that when spatial interactions among individuals are added, the above effect is weakened, and can be completely destroyed. Mutants in a circular graph experience neutral dynamics for the DB update rule in case (i) and for the BD rule in case (ii) above.

(b) The effect of spatial randomness is not the same as that of temporal randomness. We show that in the case of spatially variable environment, both for BD/DB processes, both for complete/circular graph, and both for division/death rates affected, minority mutants experience a higher than neutral probability of fixation. This is in contrast to the temporal fluctuation case, where, for example, when the death rates are affected by randomness, minority mutants experience a disadvantage. Fixation time results are also different under spatial compared to temporal randomness.

(c) Spatial and temporal correlations explain the observed differences. Finally, in this work, we discuss the nature of the two types of variability (temporal and spatial) and note a fundamental difference between the two, namely, spatial correlations of fitness values in the temporal case and temporal correlations of the fitness values in the spatial case.

This paper adds to the previous work on spatial and temporal environmental variability [14,16,17,19,21,22,36–51], and attempts to generalize and explain a large amount of results for the behaviour of mutants under spatial and temporal randomness.

2. Model description

We implement modifications of the classical, constant-population Moran process [52]. Let us denote the population size by N, the division and death rates of the wild-type cells as r_A and d_A, respectively, and division and death rates of the mutant cells as r_B and d_B, respectively. In the system with random environment, division and/or death rates of wild-type cells and mutants are subject to random change, see the electronic supplementary material, section S1 for complete details of the implementation.

In particular, to model temporal fluctuations, we assume that for each time-step, the division values r_A and r_B are chosen from a given probability distribution, see figure 1a for a schematic illustration. In this paper, we focus on the case where the probability distributions of r_A and r_B are the same. Similarly, the death rate values d_A and d_B are chosen from a single probability distribution. We are interested in mutant fixation probabilities and times, averaged over all realizations of the rate values.

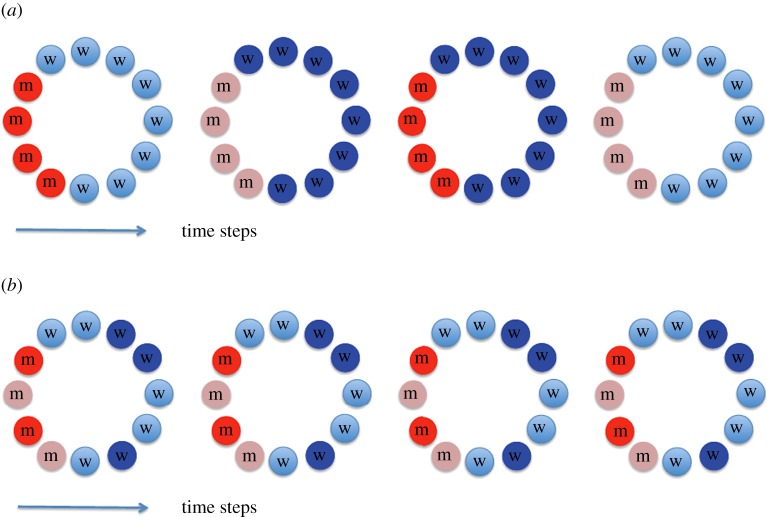
Figure 1.

A schematic illustrating temporal (a) and spatial (b) randomness. Cells (assumed to reside on a ring) are represented by circles. Mutants are coloured by reddish tones (marked by m) and wild-types by bluish tones (marked by w). Four consecutive time-steps are shown, and for simplicity it is assumed that the locations of the four mutant cells do not change (which is not the case in general). Saturation of the colour represents cells’ rate values, and the division rates and the death rates can each take two possible values. In (a), at each time step, all mutants and all wild-type cells have the same rate values, but they randomly change from step to step. In (b), both mutants and the wild-type cells have random fitness values determined by the cells’ locations, but they remain constant in time. (Online version in colour.)

To model spatial fluctuations, we assume that fitness values of each cell are defined by (a) its type and (b) its location. Each realization of the evolutionary process is characterized by a fixed set of wild-type fitness values, $r_A^1,\dots ,r_A^N$, and a fixed set of mutant fitness values, $r_B^1,\dots ,r_B^N$, where the superscript is referring to a specific location, and the values $r_A^i$ and $r_B^i$ are i.i.d. random variables for 1 ≤ i ≤ N. These values, once assigned, remain constant throughout the realization, see figure 1b for a schematic illustration of this model and a comparison with the setting with temporal randomness (panel (a)). Similarly, death rate values, $d_A^i$ and $d_B^i$ are assigned randomly for each realization.

3. Temporal randomness

3.1. Fixation probability and time in the case of temporal randomness

We start by studying the statistics of mutant fixation for the process on a complete graph, under temporal randomness. Assume that the division rates of wild-type and mutant cells are i.i.d. with standard deviation σ_r, and the death rates of wild-type and mutant cells are i.i.d. with standard deviation σ_d. In this paper, we are using a specific type of probability distribution, a two-valued, zero skewness distribution, where value 1 + σ occurs with probability 0.5 and value 1 − σ with probability 0.5 (here σ = σ_r for division rates and σ = σ_d for death rates). Other distributions were investigated in [34,53]; the results were found to be qualitatively similar.

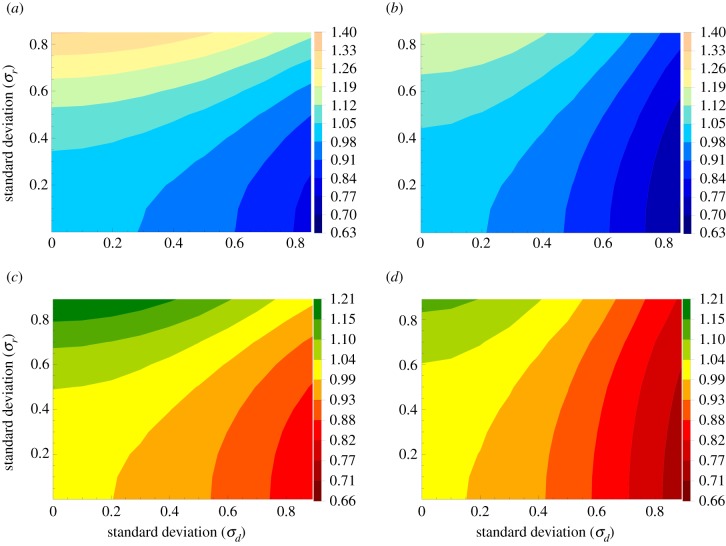
Results of numerical simulations are presented in figure 2. All simulations start with 1 mutant and N − 1 wild-type cells. In figure 2(a,b), the mean fixation probability is shown for both BD and DB processes, as a function of the standard deviations of the division rates (σ_d, horizontal axis) and the death rates (σ_r, vertical axes). Panels (c,d) show the corresponding mean conditional fixation times, also as functions of the two standard deviations.

Figure 2.

Temporal randomness, the case of a complete graph. Evolutionary properties of mutants with random birth/death are studied. Panels (a) and (b) give the results for the fixation probability for the BD and DB processes, respectively. Panels (c) and (d) give the result for the mean conditional fixation time for the BD and DB processes, respectively. We have used N = 5; 10⁶ realizations were run, and the quantities were divided by the corresponding values in the absence of any external randomness. (Online version in colour.)

We observe that, consistent with the findings of [12–14], the probability of fixation is an increasing function of σ_r. In other words, a minority mutant experiences a selective advantage in the presence of temporal randomness in the division rates. The mean conditional fixation time is also an increasing function of the randomness in the division rates, as reported in [14]. A very different result is observed as we increase the amount of randomness in death rates. Minority mutants experience a disadvantage in the presence of temporal randomness in death rates (we can see a decay in the probability of fixation in the horizontal direction). This result has been discussed in the context of the so-called storage effect (e.g. [19]). This effect has been used to explain the finding that the total number of species supported by the ecosystem increases due to the variability of the environment [51]; in order to obtain this mechanism, it is important that environmental stochasticity affects recruitment instead of mortality rates [19,54]. The negative selection acting on minority mutants under random death rates which we report here, is consistent with a decreased diversity of species under this type of randomness.

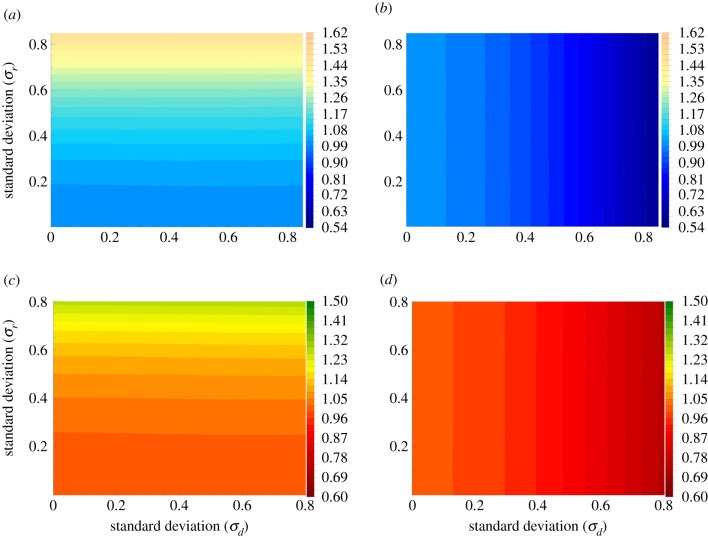
Results for the statistics of mutant fixation for temporal randomness on a circle are presented in figure 3, and they are strikingly different from the patterns observed in the case of the complete graph. Spatial restrictions imposed by the circular geometry eliminate any selective effects of temporal randomness in the case where the death rates are random for the BD process, and in the case where the division rates are random for the DB process. The dependence in the other direction retains the same tendency as was found for the complete graph.

Figure 3.

Temporal randomness, the case of a circular graph. Evolutionary properties of mutants with random birth/death are studied. Panels (a) and (b) give the results for the fixation probability for the BD and DB processes, respectively. Panels (c) and (d) give the result for the mean conditional fixation time for the BD and DB processes, respectively. We have used N = 6; 10⁶ realizations were run, and the quantities were divided by the corresponding values in the absence of any external randomness. (Online version in colour.)

A summary of results for the fixation probability for the model with temporal randomness is given in table 1. Results for the mean conditional fixation time for the model with temporal randomness are given in table 2.

Table 1.

Fixation probability under temporal randomness: summary of results. ‘Advantageous’ means that minority mutants are selected for (have higher than neutral probability of fixation). ‘Disadvantageous’ means that minority mutants are selected against (have lower than neutral probability of fixation). ‘Neural’ means that there is no selection for mutants.

	divisions random	deaths random
BD	advantageous	disadvantageous for complete graph neutral for circle
DB	advantageous for complete graph neutral for circle	disadvantageous

Table 2.

Mean conditional fixation time under temporal randomness: summary of results. ‘Increases/decreases/constant’ describe the change in the mean conditional fixation time as the randomness (in divisions or deaths) increases.

	divisions random	deaths random
BD	increases	decreases for complete graph constant for circle
DB	increases for complete graph constant for circle	decreases

3.2. When and why are mutants under positive (negative) selection?

In order to understand intuitively the behaviour of mutants in random conditions, we examine the expected increment of the number of mutants. Suppose that initially, there are m mutants in a population of N cells. Let us denote by P⁽¹⁾(+i) and P⁽¹⁾(−i) the probability that after one update, the number of mutants will increase (decrease) by i. The superscript in these notations refers to the number of steps considered. Then the expected increment of the number of mutants after one update is given by

$$Q^{(1)}=⟨P^{(1)}(+1)-P^{(1)}(-1)⟩,$$ 3.1

where averaging is performed over all realizations of the process. In general, the expected increment of the number of mutants after n updates is defined as

$$Q^{(n)}=⟨\sum _{i=-n}^{n}i{P}^{(n)}(i)⟩.$$ 3.2

How do we explain that in the case of temporal randomness, for random divisions, minority mutants are ‘selected for’ (that is, fixate with a probability greater than their initial proportion), and for random deaths, majority mutants are ‘selected for’ (this holds both for DB and BD on the complete graph)? Consider the process on the complete graph, and observe that the statistics of the probability of mutant increase in BD, equation (3.3), in the absence of randomness in death, are identical (up to the sign) to the statistics of the probability of mutant decrease in DB, equation (3.4), in the absence of randomness in divisions:

$$Q_{\mathrm{BD},{\sigma }_r,\mathrm{compl}.\hspace{0.17em}\hspace{0.17em}\mathrm{graph}}^{(1)}=⟨\frac{r_B-r_A}{m{r}_B+(N-m)r_A}\times \frac{m(N-m)}{N-1}⟩$$ 3.3

and

$$\begin{array}{r}-Q_{\mathrm{DB},{\sigma }_d,\mathrm{compl}.\hspace{0.17em}\hspace{0.17em}\mathrm{graph}}^{(1)}=⟨\frac{d_B-d_A}{m{d}_B+(N-m)d_A}\times \frac{m(N-m)}{N-1}⟩.\end{array}$$ 3.4

For the BD process, expression (3.3) contains the fraction of total fitness contributed by a mutant minus the fraction of the total fitness contributed by a wild-type cell. Assume that m < N/2. If in a particular situation, mutants have a smaller division rate than wild-types, the difference is measured against the total population fitness, which is relatively large, due to a majority of advantaged types. If mutants have a larger division rate than wild-types, this is measured against the total population fitness that is smaller due to a decreased contribution of the majority. This results in a larger contribution of terms corresponding to mutants dividing faster, and an overall positive mutant increment.

To show this more precisely, consider the case of the BD rule with random divisions. Suppose first that r_B = b, r_A = a and b > a, such that the contribution to $Q_{\mathrm{BD},{\sigma }_r}^{(1)}$ is positive. The opposite situation where r_B = a, r_A = b, happens with the same probability, and its contribution is negative. The absolute values of the two contributions are however different, and the sum of the two is given by

$$\frac{{(b-a)}^2(N-2m)}{ab(N+m(b/a-1))(N-m(1-a/b))}.$$ 3.5

Since b > a and m < N, both terms in the denominator are positive, and the total quantity is positive as long as m < N/2. Summing up over all possible values of a and b with b > a and the corresponding probabilities, we can see that the expected increment is positive for m < N/2. This argument shows that for any probability distribution of the division rates, mutants are effectively positively selected as long as they are in a minority. Exactly, the same argument shows that under the DB rule with random deaths, mutants are negatively selected as long as they are in a minority.

The other two cases on a complete graph (BD with random deaths and DB with random divisions) can be handled in a similar way.

This argument breaks down however once we consider a circular graph, in two out of four cases. Neutrality on the circle is expected when the random case corresponds to the second event: random deaths in BD and random divisions in DB. For the second event, there are only two cells that are competing, and there is no minority or majority in this case. This makes the mutant dynamics neutral for the BD process with random deaths and for the DB process with random divisions. To illustrate this, let us consider the case of random division rates on a circle. For the BD and DB processes, the expected increments are given by

$$Q_{\mathrm{BD},{\sigma }_r,\mathrm{circle}}^{(1)}=⟨\frac{r_B-r_A}{m{r}_B+(N-m)r_A}⟩$$ 3.6

and

$$Q_{\mathrm{DB},{\sigma }_r,\mathrm{circle}}^{(1)}=\{\begin{array}{cc}⟨\frac{2}{N}\frac{r_B-r_A}{r_B+r_A}⟩=0,& 1<m<N-1,\\ ⟨\frac{1}{N}\frac{r_B-r_A}{r_B+r_A}⟩=0,& \hspace{0.17em}m=1\text{ or }m=N-1.\end{array}$$ 3.7

We can see that in the former case, the expression is similar to the expression in (3.3), and results in a positive increment for minority mutants. The latter case averages out to zero, thus leading to neutral dynamics of mutants regardless of whether they are in a minority or a majority. The cases corresponding to random death rates are analysed similarly.

For completeness, we have also considered the case of a different update rule, the pair competition. In this model, two individuals are chosen randomly, and then one of them dies and the other one reproduces according to their relative fitnesses (which is subject to the influence of the variable environment). We have observed that the fixation probability remains constant (and equal 1/N) for the temporal randomness.

Results for mean conditional fixation time are summarized in table 2. We can see that the time to fixation exhibits exactly the same trends as the probability of fixation, see table 1: whenever the mutant behaves as if it is selected for (i.e. its probability of fixation increases), its mean conditional time also increases, and whenever the mutant’s fixation probability decreases, so does its mean conditional fixation time. For further details, see electronic supplementary material, section S2.

4. Spatial randomness

4.1. Fixation probability and time in the case of spatial randomness

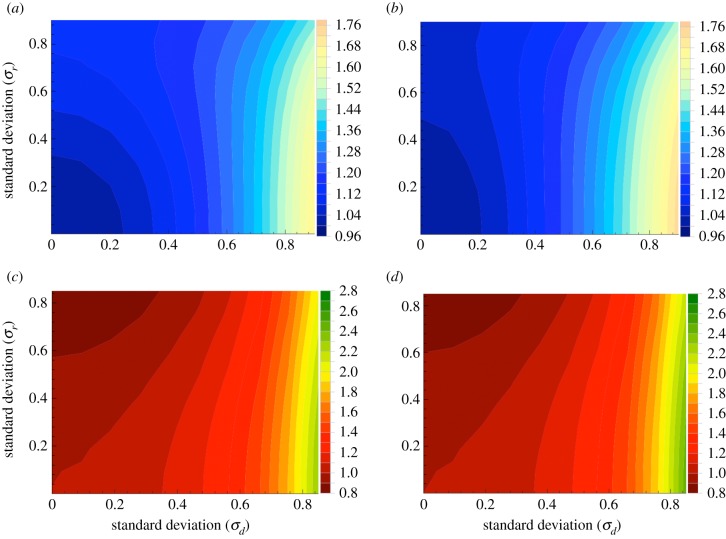
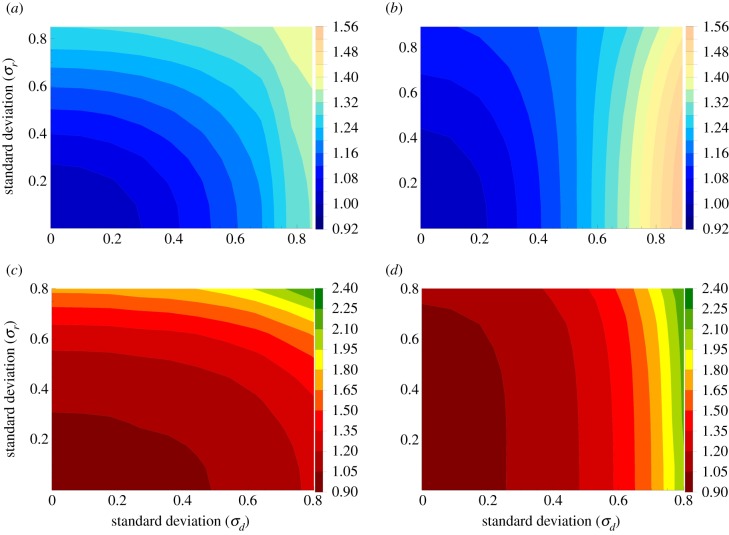
Next we turn to the case of spatial randomness. Results for evolutionary properties of mutant dynamics are presented in figure 4 for the complete graph, and in figure 5 for the circle. As before, for the numerical studies, we focus on the case where initially, there is one mutant in the system, and consider both the mean mutant fixation probabilities and the mean conditional fixation time. Again, both BD and DB processes are studied (BD in the left panels and DB in the right panels).

Figure 4.

Spatial randomness, the case of a complete graph. Evolutionary properties of mutants with random birth/death are studied. Panels (a) and (b) give the results for the fixation probability for the BD and DB processes, respectively. Panels (c) and (d) give the result for the mean conditional fixation time for the BD and DB processes, respectively. We have used N = 6; 10⁶ realizations were run, and the quantities were divided by the corresponding values in the absence of any external randomness. (Online version in colour.)

Figure 5.

Spatial randomness, the case of a circular graph. Evolutionary properties of mutants with random birth/death are studied. Panels (a) and (b) give the results for the fixation probability for the BD and DB processes, respectively. Panels (c) and (d) give the result for the mean conditional fixation time for the BD and DB processes, respectively. We have used N = 6; 10⁶ realizations were run, and the quantities were divided by the corresponding values in the absence of any external randomness. (Online version in colour.)

The dependence of the probability of mutant fixation on the standard deviation of the distribution of the division rates (σ_r, the vertical axes in all panels) are consistent with the results reported in [34,35]. We observe that for minority mutants, both for BD and DB processes, and for both complete and circular graphs

• —compared with zero environmental randomness, any amount of fluctuations in division and/or death rates results in an increase in fixation probability for minority mutants;
• —if σ_d = 0, the probability of mutant fixation is an increasing function of σ_r, that is, the positive selection acting upon minority mutant increases with randomness if it affects only division rates;
• —if σ_r = 0, the probability of mutant fixation is an increasing function of σ_d, that is, the positive selection acting upon minority mutant increases with randomness if it affects only death rates.

It can be seen that the dependence on σ_r is stronger for the BD process (figures 4a and 5a) compared to the DB process (panels (b) of the two figures). Compared to σ_r, σ_d appears to have a stronger effect on fixation probability. We also notice that while the probability of mutant fixation is a monotonically increasing function of σ_d, the dependence on σ_r is somewhat more complex: as a function σ_r, the probability increases for low σ_d, but this trend slows down and even reverses for higher σ_d.

For completeness, we have also performed simulations with the pair competition rule (when in a randomly chosen pair of connected individuals, the progeny of the one with the higher fitness replaces the one with the lower fitness). In this model, mutant fixation probability grows with the standard deviation, and the magnitude of the effect is stronger than that for the DB and BD processes (not shown).

We next turn our attention to the mean conditional fixation time, figures 4c,d and 5c,d. As the standard deviation, σ_d, increases, the fixation time grows for both processes (BD and DB), both for the circle and for the complete graph. This means that randomness in the death rates slows down mutant fixation in both mass action and the one-dimensional nearest neighbour scenarios.¹ Randomness in the division rates, however, affects the mean conditional fixation times differently, depending on the underlying graph [35]. For the complete graph, randomness in the division rates accelerates fixation (the fixation time decreases in the vertical direction in figure 4c,d). For the circle, the result is the opposite: randomness in the division rates decelerates mutant fixation (the fixation time increases in the vertical direction in figure 5c,d).

An important question is whether any of these effects become negligible with growing system size, N. Interestingly, the amount of advantage enjoyed by a minority species increases in large populations, allowing this ‘selection’ force to overcome random drift [34]. One way to measure the size of the effect as N increases is to compare the probability of mutant fixation (P_N) multiplied by N with unity. In a constant environment, we have P_N × N = 1 or neutral mutants. In a system under variable environment with N = 4 or N = 5, this quantity is less than 1% larger than 1. As the population size reaches N = 50, the value of P_N × N becomes 2.85 (i.e. 280% of that of a neutral mutant in a constant environment). For N = 600, the quantity P_N × N is about 15 (about a 1500% increase).

A summary of results for the fixation probability for the model with spatial randomness is presented in table 3. Results for the mean conditional fixation time for the model with spatial randomness are given in table 4.

Table 3.

Fixation probability under spatial randomness: summary of results. Terminology is consistent with that used in table 1.

	divisions random	deaths random
BD	advantageous	advantageous
DB	advantageous	advantageous

Table 4.

Fixation time under spatial randomness: summary of results. Terminology is consistent with that used in table 2.

	divisions random	deaths random
BD	decreases for complete graph increases for circle	increases
DB	decreases for complete graph increases for circle	increases

4.2. Symmetry breaking: the non-neutral behaviour of ‘neutral’ mutants

In order to explain the results of table 3 on an intuitive level, let us study the statistics of mutant cell dynamics. The mean increment of the number of mutants after n updates, Q⁽ⁿ⁾, is defined in equation (3.2). In the case of temporal randomness (§3.2), quantity Q⁽¹⁾ served as an indicator of the system’s behaviour. In particular, if minority mutants behaved as if they were selected for, we had Q⁽¹⁾ > 0 for m < N/2. Calculations change in the case of spatial randomness, as explained below.

For the BD process under spatial randomness, we can show that Q⁽¹⁾ = 0. This means that the expected increment in the number of mutants after 1 update is zero. Therefore, we check the expected increment after two steps. We obtain that Q⁽²⁾ > 0 if m < N/2 and Q⁽²⁾ < 0 if m > N/2, that is, minority mutants are selected for, but this manifests itself after two steps.

For the DB process under spatial randomness, the calculations are different depending on whether division rate or death rates are random. If only divisions are random and death rates are constant, we obtain that both Q⁽¹⁾ = 0 and Q⁽²⁾ = 0. Therefore, in this case we need to check the expected increment after three steps. We obtain that for N = 3, Q⁽³⁾ = 0 for all m, and for N > 3, Q⁽³⁾ > 0 if m < N/2 and Q⁽³⁾ < 0 if m > N/2, that is, a minority mutant is advantaged for N > 3, which is consistent with our findings reported in [34]. If deaths are also random, then for N ≥ 3 and m < N/2, we can show that Q⁽²⁾ is an increasing function of randomness.

To justify this approach, we focus on the correlations among division/death rates of cells. We will refer to these values simply as fitness values because they define reproductive success of cells. In the temporal randomness case, there is spatial correlation of mutant fitness values with each other (they are simply the same), and similarly, the wild-type fitness values at different spatial points are correlated (i.e. are the same), see figure 1a. Competition happens between two groups of individuals that experience this type of correlation, leading to the non-zero selection for (or against) one of the groups, see the arguments built around equations (3.3)–(3.5).

In the case of spatial randomness, there are no correlations among mutant or among wild-type fitness values at different locations, see figure 1b. So if we consider an individual snapshot, it is not clear what the ‘minority’ even means. All cells have random fitness values, and it appears that we have a number of different types (four types in the case of figure 1b, and possibly more types in the case of other distributions). Now, if we consider several temporal updates in a row, correlation patterns start to emerge. Unlike the temporal case, fitness values of individual spots remain the same, but of course this is only observed if we consider more than one update. That was the motivation to look at expected increments after more than one update.

As time goes by, mutant and wild-type cells redistribute in space, and this process (probabilistically) has a directionality. In order to explain this concept, let us consider a complete graph and assume for simplicity that fitness values of mutant and wild-type cells are anti-correlated, that is, each spot that is characterized by a high (low) mutant fitness will have a low (high) wild-type fitness. It was shown in [34] that such anti-correlated systems are characterized by stronger effects of randomness compared with uncorrelated systems. We claim that with each update, any change that happens in the configuration of wild-types and mutants is more likely to increase the fitness of cells than to decrease it. In general, cells of higher fitness are more likely to divide, and cells of lower fitness are less likely to divide and therefore are more likely to die (as division protects a cell from death). A death of a low fitness cell can either lead to no change (if the cell is replaced by a new cell of the same type), or it can lead to an increase of fitness at that spot in the cell is replaced by a new cell of the opposite type. Therefore, with each update, the expected fitness at each spot increases. What this means in practice is that mutant cells redistribute such that they tend to occupy spots with higher mutant fitness values, and similarly, wild-type cells redistribute trying to occupy spots with higher wild-type fitness values.

Now, it is clear that in the context of gaining higher fitness, a minority has an advantage compared to a majority. Indeed, the numbers of ‘good’ and ‘bad’ spots are equal on average for different configurations, and therefore it is much easier to find a configuration where a minority enjoys a large advantage than a configuration where a majority has a higher average fitness. In the case of the complete graph, this is illustrated schematically in figure 6, where we fix a fitness configuration with dark orange circles denoting mutant favourable spots and light blue circles denoting wild-type favourable spots. Starting from an initial state of two mutants, panel (a) shows a possible path where mutants grow and redistribute and occupy only favourable spots. This is not possible for the majority wild-type (panel (b)), because for any configuration some of them would be forced to occupy unfavourable spots. The same argument (with modifications) applies to systems with uncorrelated fitness values and to processes on a circle.

Figure 6.

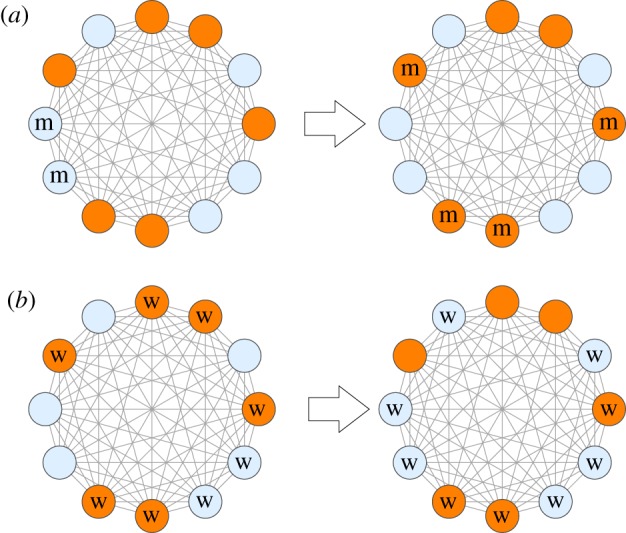
A schematic showing possible evolutionary paths where cells occupy spots that are favourable for them (the case of the complete graph). Here dark orange circles denote spots that are favourable for mutants and light blue circles—spots favourable for wild-type cells. (a) The locations of mutants are marked by ‘m’, the rest of the spots are assumed to be occupied by wild-type cells. Minority mutant cells expand and occupy favourable spots. (b) The majority wild-type cells are denoted by ‘w’. As they expand, it is impossible for them to redistribute in such a way that they only occupy favourable spots (because there are more wild-type cells than such spots). In general, it is easier for minority cells to explore fitness configurations in their favour compared to majority cells. (Online version in colour.)

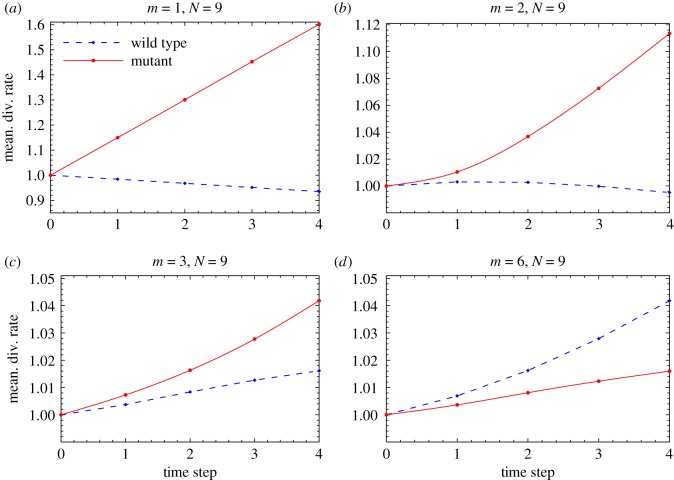
Figure 7 shows the mean division rates of mutant and wild-type populations (averaged over many runs) at several consecutive time steps. In panel (a), we start with one mutant in the system of nine cells, and we see that the mutants clerkly gain fitness advantage. The same trends holds for panels (b) and (c), where we start with two and three mutants out of N = 9, respectively; the fitness advantages gain by the mutants is smaller in panels (b) and (c) compared to panel (a), and also, in panel (c) we observe that the wild-type fitness is also experiencing an increase (but a smaller increase compared with the mutant minority). Finally, in panel (d) we start with six mutants out of nine cells (a majority). We can see that the mean division rates of the mutant majority grows slower than that of the wild-type minority.

Figure 7.

Spatial randomness: mean fitness of mutants and wild-type cells at several consecutive time steps, starting from (a) m = 1 mutant, (b) m = 2 mutants, (c) m = 3 mutants and (d) m = 6 mutants. The total number of cells is N = 9. Simulations with random division rates are performed under the BD update rule on a circle, with σ = 0.9 and mutant and wild-type division rates anti-correlated; 10 000 realizations were used. (Online version in colour.)

Results for fixation timing are summarized in table 4. We observe that the relationship between the probability of fixation and mean conditional fixation time is different under spatial randomness, compared to the case of temporal randomness (tables 1 and 2). We refer the reader to electronic supplementary material, §3 for further details.

5. Discussion

In this study, we present analysis of mutant evolutionary dynamics in random environments, and compare the cases of temporal and spatial randomness. We find that the two are quite different in the way they affect the mutant fixation probability and the mutant mean conditional fixation time.

The concept of temporal randomness is well established. There is large and growing literature on evolutionary dynamics in fluctuating environments [22,54–56], in addition to the papers already mentioned in the Introduction. The importance of temporal fluctuations of the environment has been emphasized in ecology for several decades, see e.g. [57] who introduced environmental fluctuations in the context of population extinctions. Others (e.g. [58]) used environmental fluctuations to explain observed population sizes and diversity.

Changing environments play a role in the evolution of bacterial colonies residing in a host [59,60], marine plankton dynamics [61], tropical island ecosystems [54] and many other ecological contexts. In microbial communities, organisms experience changes in chemical composition, local temperature or illumination of their surroundings [62]. For larger size species, fluctuations of temperature, light, precipitations, humidity, available nutrients, etc., can strongly influence the dynamics of the evolving community [21].

Here we focused on the dynamics of non-favoured mutants, that is, mutants whose (possibly random) division/death rates come from the same probability distributions as those of the wild-type cells. Consistent with previous findings, temporal randomness (random environmental fluctuations) can significantly affect the mutant fixation probability. In particular, if the environment directly affects division rates (making them random), then a non-favoured minority mutant experiences positive selection [12,14]; if the death rates are affected, then a non-favoured mutant experiences negative selection [19,51,54].

It turns out that once spatial considerations are taken into account, these results can be weakened or even completely suppressed. This happens if the process whose rates are affected by the environmental randomness does not involve competition of individuals in a group, where one species is a minority and the other a majority. In the case of circular geometry, for example, in a DB process, divisions that follow each death event are restricted to the two nearest neighbours of the removed individual, and thus if it is only division rates that are affected by temporal environmental fluctuations, no effects described for the non-spatial systems will manifest themselves, and a minority mutant will not enjoy a selective advantage. Similarly, in a BD process on a circle where divisions are random, a minority mutant will not experience negative selection, in contrast to the same case in mass action. While the phenomenon of selection suppressors has been described in [63,64] in the context of evolution on directed graphs, selection suppression reported here is of a different nature.

In terms of mean conditional fixation times (where averaging is performed both over all the realizations of the process and also over all the realizations of the rate values), we observe that under random division rates, the fixation times are longer and under random death rates, they are shorter, compared with the system in a constant environment. Longer fixation times indicate longer coexistence of the two species and also point at a possibly increased diversity under randomly fluctuating division rates. Similarly, short fixation times point towards a reduced diversity under randomly fluctuating death rates [19,21,51,54]. Again, these effects can be suppressed by spatial interactions.

We next turn to the phenomenon of spatial randomness. Spatial variability and its effect of local reproduction and death parameters have been studied in the past (e.g. [65,66]). An idea of ‘source’ and ‘sink’ habitats has been developed [65] where local regulation occurred through an outflow of organisms from sources (i.e. areas of enhanced reproduction) to sinks (locally insufficient reproduction). In some cases, heterogeneity of the environment manifests itself as a number of separate, discrete patches, such as separate islands containing populations of a plant species, or different hosts containing a type of parasite; then, metapopulation, or ‘deme’, models, have been used by ecologists successfully to describe the dynamics of such structured environment (e.g. [67]). In other contexts, however, one cannot assume that each uniform patch contains a large population of interacting individuals. One example of such an environment is a biofilm. Biofilms are characterized by microscale heterogeneities in physiologically important parameters, such as chemical gradients of nutrients, oxygen, waste products and signalling compounds, as well as heterogeneities in the flow of the interstitial fluid [68,69]. Localized zones that vary widely in their physiological conditions over microscope distances create a complex evolutionary environment for the bacteria [70,71]. Another example of a spatially heterogeneous environment is a tumour. Solid cancers are characterized by a highly complex microenvironment; there are e.g. regions of acidosis and hypoxia resulting from variable blood flow through leaky immature vessels [72,73]. Apart from active tumour cells, stroma, necrotic cells and blood vessels contribute to the complex ecology of tumours. The nutrients are distributed in a complex, non-uniform fashion. Inflammatory factors (such as cytokines, chemokines and growth factors) are constantly produced, which in turn attract tumour infiltrating cells, including macrophages, myeloid-derived suppressor cells, mesenchymal stromal cells and TIE2-expressing monocytes. All these non-malignant cell populations create the environment where the evolutionary tumour dynamics unfold [74]. Another relevant context where the microscale heterogeneity of organs’ environments is recognized is building the so-called organs-on-a-chip. One of the important aspects of building organs-on-a-chip is providing various cell types and extracellular matrix environments that approximate spatial heterogeneity of the real tissues [75,76].

It is situations like these, where the spatial scale of change of environmental factors is comparable with the scale of the patches occupied by a single individual, that are the focus of the present study. Unlike temporal randomness, spatial randomness always promotes (i.e. provides positive selection for) non-favoured mutants. This holds in the cases where division and/or death rates of individuals are affected by the random environment. Intuitively, this can be understood by envisaging the dynamics of birth and death in a spatially heterogeneous (but temporally constant) environment. Statistically speaking, rounds of deaths and divisions tend to increase the mean fitness of cells. Cells of each type are more likely to be removed from spots that are not favourable and to be gained (through reproduction) at spots that are favourable for them. The fundamental asymmetry between a minority and a majority type is the opportunity to colonize more and more such favourable spots. A small minority (on average) will have access to yet unexplored favourable spots. A large majority, as it expands even further, is actually likely to lose in average fitness, because typically there are not enough ‘good’ spots to accommodate all. This type of exploration gives rise to the evolutionary dynamics whereby minority mutants behave as if they were advantageous, no matter what processes (divisions or deaths or both) are affected by the randomness.

A different situation is observed when we study fixation times. It turns out that the geometry of the underlying network is the key. For the circular graph, spatial randomness in divisions and/or deaths delays fixation. For the stringent constraints imposed by the circular (one-dimensional) geometry, any disruption of the path to fixation presents an obstacle, with the overall effect of increasing the mean conditional fixation time. In contrast to this, randomness in division rates on the complete graph has the opposite effect of speeding up fixation. Since the complete graphs presents multiple paths to fixation, variation in division rates can actually open up opportunities for a faster colonization of the space, while the ‘dead zones’ that presented a serious problem in one-dimensional can now be overcome by going around them.

Finally, we note that it is partially the aim of this paper to emphasize the difference between the BD and DB processes. The most striking qualitative differences between BD and DB processes are observed for temporal randomness: (1) under temporal randomness (random divisions) on a circle, a minority mutant is advantageous for BD and neutral for DB. (2) Similarly, under temporal randomness (random deaths) on a circle, a minority mutant is neutral for BD and disadvantageous for DB. We have shown that the expected mutant increment after one time-step is zero, and steps are uncorrelated. In the case of spatial randomness, consecutive steps are correlated, and even if after one update the expected mutant increment is zero, it may not be after two or more updates. As a consequence, the two processes (BD and DB) are characterized by subtler, mostly quantitative differences under spatial randomness. These differences manifest themselves computationally in how many steps it takes to observe a non-zero expected mutant increment. For example, one has to go up to three steps to see a non-trivial effect for the DB process with random divisions, as opposed to only two steps for BD, accounting for an overall weaker effect of spatially random divisions under DB updates, compared to BD updates. For other interesting differences between DB and BD processes, see [77], where we showed that the isothermal theorem [63] broke down for the DB process with differing division rates of wild-types and mutants, and for the BD process with differing death rates.

Given how widely the Moran process is used, it is important to understand that in light of the above findings, the modelling choice (BD versus DB) may significantly affect the results. How does one interpret this difference? One may conclude that one of the formulations is wrong. More likely, different modelling choices may be suitable under different biological circumstances. For example, the DB process represents a death-driven system, where divisions only occur when death creates an empty space; on the other hand, the BD process assumes that cell divisions can happen regardless of space availability, but they lead to death of other cells (e.g. by crowding).

It appears, however, that reality is more complicated, and simplified models such as the (constant population) Moran process, or the Wright–Fisher process, or the contact process are but idealizations of the real biological process of cellular turnover. Therefore, when using such idealizations, one has to be aware of the consequences of the details of the modelling processes. In our previous papers, we have demonstrated that, for example, the Wright–Fisher model is characterized by a qualitatively similar behaviour when exposed to a random environment [35]; further, we argued (in a different context) that the contact process could be viewed as a hybrid between the DB and BD Markov models [78], but in other contexts, it exhibited qualitatively different trends compared to the Moran model [79].

There are a number of extensions of this study that are subject of current and future work. In this paper, we concentrated on the temporal randomness whose timescale is similar to that of divisions and deaths. It will be important to explore the influence of timescales on the results presented in this paper, see also [15] and references therein. Further, in the present study, we focus on two extreme cases: the nearest neighbours (circular) graph and the complete graph. The former model represents the case where cells are restricted to certain locations and the only movement occurs through cell renewal. The latter case (complete graph or mass action) represents the opposite end of the spectrum, where cells can divide and fill a space very far from their origin. This is an implicit way of incorporating migration in the system. By exploring both cases, we hope to get the range of phenomena to be expected in models that explicitly include migration. While we expect that such explicit migration models will not lead to qualitatively new phenomena, this is subject of our current work, which will build on our previous modelling of cell migration [80]. Finally, we note that in reality, the fitness of an individual may depend not only on the present state of the world, but also on its past states (for example, unfavourable conditions today may reduce an organism’s fitness tomorrow, even if the conditions change to favourable). We did not take these effects into account in this paper, but this will be an interesting future extension.

To conclude, this paper compares and contrasts temporal and spatial types of randomness and their role in the evolution of non-favoured mutants. Further work is required to introduce more realism in the system, by combining the two types of randomness and also introducing migration as a natural extension of the current models.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

No funding has been received for this article.