A primarily serial, foveal accumulator underlies approximate numerical estimation

Significance

The question of how people estimate numerical quantities is centrally important in cognitive psychology, neuroscience, and applied educational research. It is generally believed that estimation of numbers is rapid and occurs in parallel across a visual scene. Here, we show that people’s estimates are determined by a sequence of visual fixations, with both their mean estimates and their precision increasing as a function of how many points they foveate. This mechanism suggests that a considerable body of research which treats estimation as a purely numerical measure is likely to be missing an important part of the picture: Numerical estimation ability is closely tied to the mechanisms that control eye movements and attention.

Abstract

The approximate number system (ANS) has attracted broad interest due to its potential importance in early mathematical development and the fact that it is conserved across species. Models of the ANS and behavioral measures of ANS acuity both assume that quantity estimation is computed rapidly and in parallel across an entire view of the visual scene. We present evidence instead that ANS estimates are largely the product of a serial accumulation mechanism operating across visual fixations. We used an eye-tracker to collect data on participants’ visual fixations while they performed quantity-estimation and -discrimination tasks. We were able to predict participants’ numerical estimates using their visual fixation data: As the number of dots fixated increased, mean estimates also increased, and estimation error decreased. A detailed model-based analysis shows that fixated dots contribute twice as much as peripheral dots to estimated quantities; people do not “double count” multiply fixated dots; and they do not adjust for the proportion of area in the scene that they have fixated. The accumulation mechanism we propose explains reported effects of display time on estimation and earlier findings of a bias to underestimate quantities.

From infancy, humans are equipped with an approximate number system (ANS) that allows for inexact quantity estimation and comparison (e.g., refs. 1–4). This system is shared with our close and distant evolutionary relatives (e.g., refs. 5–7) and may be related to the development of exact numerical concepts and later mathematics in humans (4, 8–10). However, the defining feature of the ANS is that it is inexact, providing an approximate representation of quantity, which is likely useful in a variety of evolutionary contexts (e.g., refs. 6, 7, 11, and 12). The acuity of an individual’s ANS is often quantified in terms of their Weber fraction, $w$, which is a real number denoting how the noise in a representation scales with numerosity. Specifically, one popular psychophysical model of the ANS assumes that a number $n$ is represented by a Gaussian with mean $n$ and SD $w\cdot n$, so that a lower $w$ implies a higher-fidelity system.

The mechanisms supporting the ANS are often contrasted with other mechanisms for computing numerosity, such as counting and subitizing (13–15). Counting, for instance, is dependent on intentional, serial enumeration of a set; the ANS, in contrast, is often viewed as parallel, rapid, and automatic. This view is supported by response times, where counting takes around 300 ms per enumerated item, but approximate-number computations can take as little as 16 ms, independent of the number of objects (16). Additionally, researchers have identified populations of neurons that respond similarly for sequentially and simultaneously presented numerosities in monkeys (17), which has been taken as evidence that ANS representations are not the result of sequential processing.

However, recent evidence has muddied the simple picture of the ANS. Several studies have shown that individuals’ Weber fractions are highly task-dependent, differing between estimation and discrimination tasks (e.g., refs. 18 and 19). In fact, Weber fractions have poor retest reliability, even when measured by using the same task (20). Numerical estimates have also been found to be influenced by nonnumerical features of stimuli, such as the degree of clustering in a scene (21). Finally, the precision of numerical estimates is known to improve as stimuli are presented for a longer duration (16), suggesting that ANS estimation may involve some type of temporal process.

Despite this, prior computational models of the ANS have built speed and parallelism into their architecture. For instance, many of the dominant ANS models are feedforward neural network models, where input is processed in parallel and instantaneously (e.g., refs. 22–24). The objective of the present study is to critically evaluate the simple picture of the ANS as a rapid and entirely parallel process. In particular, we aim to capture the possible sequential mechanisms involved in numerical estimation using behavioral experiments and model-driven analysis. We present a model and behavioral data from two experiments that challenge the standard parallel perception theory. Our results lend support instead to an account of ANS estimation that involves sequential integration across visual fixations.

We ran estimation (Experiment 1) and discrimination (Experiment 2) tasks in which participants made nonsymbolic numerosity judgments at different exposure durations. Critically, we collected visual fixation data using an eye-tracker so that we could measure how participants’ ANS estimation was influenced by their path of visual fixations. We show that ANS estimates are the result of a serial accumulation process (25), such that estimates increase as a function of foveation. We present an analysis that quantifies the contribution of foveal, peripheral, and multiply fixated dots in an array which supports this interpretation. Our results suggest that individual differences in ANS acuity may reflect differences in cognitive processes that are not directly related to numerical estimation, including attention or visual-processing speed. This dependence on nonnumerical factors may explain why studies that train people’s ANS yield mixed results in transferring to mathematical knowledge (26–29).

Experiment 1

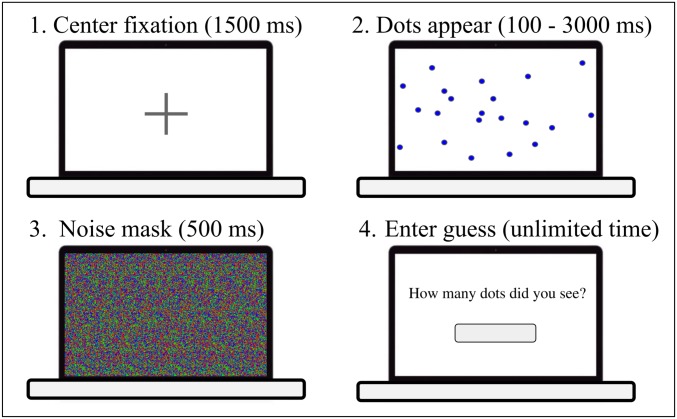
Since the visual mechanisms supporting the ANS have not been explored in detail, we first used the simplest paradigm possible to understand ANS estimation. Fig. 1 illustrates the sequence of displays shown on each trial. After viewing a fixation cross, participants were shown an array of randomly placed dots on a screen which were noise-masked after a short time. They were then prompted to enter an estimate in Arabic numerals. Subjects were not given feedback and thus had no push to recalibrate their response scale. We manipulated the amount of time that each display was visible to replicate and extend the previous work on the effect of timing on the ANS. Each participant completed 16 trials for each of four display-time conditions: 100; 333; 1,000; and 3,000 ms. We eye-tracked participants during this task to determine how their estimates were influenced by the number of dots in the path of their visual fixation. Importantly, the screen subtended a range of participants’ visual field that ensured that some of the dots could be seen foveally and others peripherally from the initial fixation.*

Fig. 1.

Each of the four images represents one stage of a trial in the estimation task, in their order. Stage 1: A fixation cross appears for 1,500 ms. Stage 2: The fixation cross is removed, and dots appear on the screen for between 100 ms and 3 s, depending on the condition. Stage 3: The display is masked by noise for 500 ms. Stage 4: A prompt appears asking for an estimate of the number of dots shown.

Results.

Replication of basic number psychophysics.

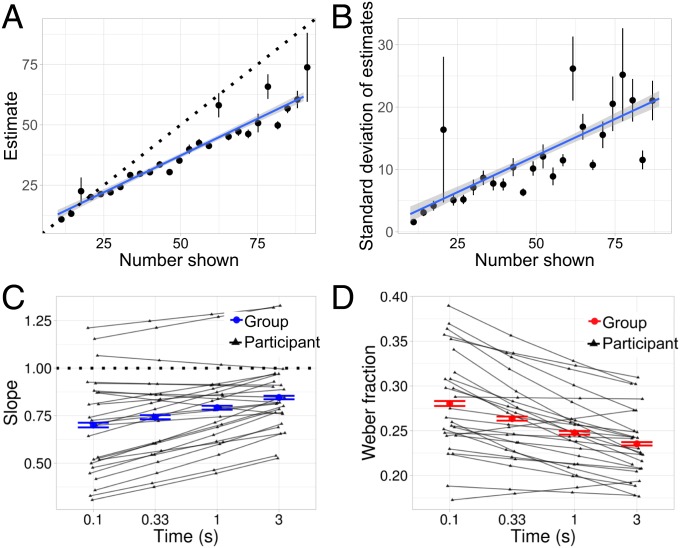
Fig. 2A shows how the mean estimate (y axis) varied as a function of the quantity displayed (x axis), collapsing over all time conditions. There are two aspects of this graph worth highlighting: First, mean estimates vary approximately linearly as a function of quantity, exactly as should be found in Weber models of the number system. Second, this shows a strong tendency to increasingly underestimate larger numbers,^† as shown by the fact that the slope of the line is less than 1, which would have corresponded to perfectly veridical estimation (assuming an intercept of 0). Both effects have been found robustly in the literature (e.g., ref. 31). Fig. 2B shows that Experiment 1 replicates the second traditional property of ANS estimation: scale variability, wherein the error in estimation increases linearly in magnitude.

Fig. 2.

(A) Estimates as a function of the number of dots presented, collapsing across time conditions. Points are binned means, with errors representing bootstrapped 95$\%$ CIs. (B) The SD of participants’ estimates as a function of the number of dots displayed, collapsing across time conditions. (C) Participant (black) and group-level (blue) slopes in each time condition of the estimation task are shown. Slopes represent the way the mean estimate scales as a function of quantity shown. (D) Participant (black) and group-level (red) Weber fractions in each time condition of the estimation task are shown.

More time improves estimation mean and variance.

To evaluate whether timing influenced participants’ ANS, we ran a hierarchical regression to estimate the effect of time on both the mean estimate and Weber fraction, including participant- and group-level regression effects fit jointly. The model assumed that means and SDs varied linearly as a function of quantity in accordance with Weber’s law. More specifically, on a trial that showed $n$ dots, each participant’s mean estimate was drawn from a Gaussian centered around $\mathrm{\beta }\cdot n$ and modeled with SD $w\cdot \mathrm{\beta }\cdot n$, where $\mathrm{\beta }$ and $w$ are hierarchically fit parameters (SI Appendix). The regression included logarithmic effects of time on mean estimates and Weber ratios, allowing us to extract each individual’s effective slope and Weber ratio as a function of time.

Fig. 2 shows the mean slope (Fig. 2C) and Weber fraction (Fig. 2D) in each time condition extracted from this model. The group-level means are shown in blue, and each participant is shown by a line in black. If participants’ estimates were unbiased (e.g., veridical estimation as opposed to underestimation), then the group mean slopes would be 1 (black dotted line), and if time did not have an effect, the group mean slopes and Weber fractions ($y$ axis) would remain constant across time ($x$ axis). In contrast, Fig. 2C shows that subjects consistently underestimate with slopes less than 1, but that this underestimation effect decreases with increasing time. Participants’ average slope increases by about $17\%$ (0.71–0.83) from the shortest to the longest time condition. This is what would be expected by quantity accumulation over time: More time increases reported quantities. Additionally, their average Weber fraction decreases by about $21\%$ (0.28–0.22) (SI Appendix, Table S1). Correspondingly, Fig. 2D shows that Weber fractions improve (decrease) with more time.

Foveation, not time, is what matters for estimation.

If ANS estimation is driven by accumulation of quantity across saccades, we should first expect that mean estimates increase with foveation. We should also expect that time has no effect when jointly considering foveation—i.e., that time simply allows for more saccades and nothing more. To evaluate this, we summed the number of dots that fell within $5^{○}$ (often called the “parafoveal region”) of the center of participants’ fixation paths for more than 50 ms on a trial.^‡ We denote the dots that are seen for at least this amount of time as “foveated.”

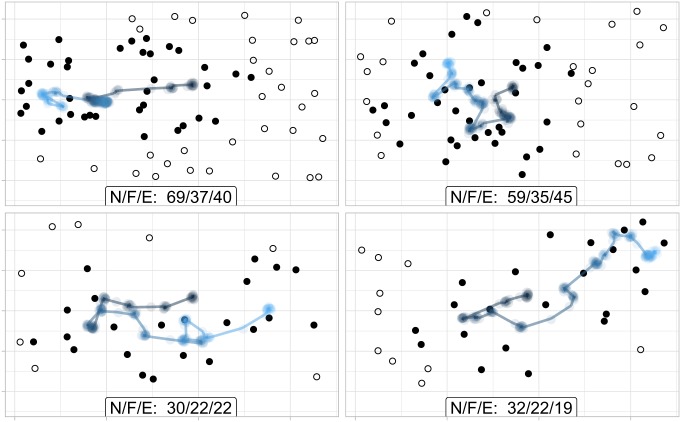
Fig. 3 provides four example trials, depicting a participant’s gaze path across the screen while the stimulus is being shown. The filled points represent “foveated” dots, and the unfilled points represent those that were not.^§ At the bottom of each display, the number of dots shown, foveated, and estimated are shown. We provide a more rigorous formalization and test of this idea in The Mechanics of ANS Estimation.

Fig. 3.

Example fixation paths of one subject in the 3-s time condition, with each panel representing a single trial. The points represent the dots displayed on their screen, where filled dots represent the ones that were foveated. At the bottom of each panel, a label N/F/E shows how many dots were shown $\left(N\right)$, how many were foveated $\left(F\right)$, and what quantity the participant actually estimated $\left(E\right)$.

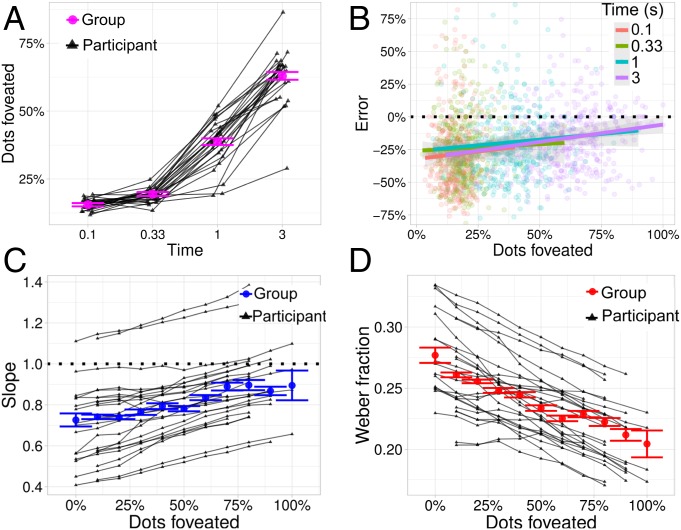
Fig. 4A shows the percent of dots that are foveated for each time condition. As should be expected, more dots are foveated with longer exposure duration. The average proportion of dots foveated more than tripled from the shortest to longest time condition (18–$64\%$). Consistent with the hypothesis that effects of time are due to accumulation of foveated dots, the effects of time on estimation disappeared when the effect proportion of dots foveated was jointly taken into account. Fig. 4B shows the percent deviation of estimates from the true quantity as a function of dots foveated, colored by time. That the lines overlap suggests that there is no effect of time when both foveation and time are taken into account.

Fig. 4.

(A) The proportion of dots foveated (y axis) as a function of time (x axis), at the group level (red) and for each participant (black). (B) The percent deviation of estimates from the true number of dots (y axis) as a function of the percent of dots foveated (x axis). Each time condition is grouped by color. (C) The slope of participants’ mean estimates (y axis) as a function of the percent of dots foveated (x axis). (D) Weber fractions (y axis) as a function of the percent of dots foveated.

To formally evaluate this, we ran a second hierarchical regression that was identical to the one reported above, except that it included a covariate for the effect of the proportion of dots foveated on the mean and variance of each participant’s estimate. This regression shows that the proportion of dots foveated significantly affected both the mean of participants’ estimates (Fig. 4C) and Weber ratios (Fig. 4D), and the effect of time disappeared when foveation was taken into account. Moreover, when $100\%$ of dots were foveated, participants were nearly unbiased (slope $\approx 1$ in Fig. 4C), suggesting that the underestimation bias previously observed was not miscalibration, but was, rather, due to participants not foveating all of the dots. In a separate analysis, we found that the observed effect of foveation on mean estimates held in each time condition separately (SI Appendix, Table 3).

Thus, these results provide an alternative account of prior findings of 1) underestimation and 2) effects of time. Indeed, both are unified into an account where serial accumulation of foveated dots drives numerical quantity estimates. This finding calls into question the construct validity of Weber ratios as a measure of numerical cognition, since numerical estimates depend on how many dots happen to be foveated, a capacity which is nonnumerical.

Experiment 2

Because there is evidence that Weber fractions may differ between estimation and discrimination tasks (19), it is important to replicate these patterns in a discrimination task. We ran a second experiment with the same participants as Experiment 1, again recording participants’ gaze. Participants saw two stimuli of dot arrays (as in Fig. 1) sequentially and were then asked to indicate which had a greater quantity. We manipulated timing in four conditions, which determined whether the first or second array of dots was visible for longer. Specifically, we crossed long and short durations to give presentation times of 100:100 ms, 1,000:100 ms, 100:1,000 ms, and 1,000:1,000 ms for the two displays. We predicted that, if ANS estimation relied on foveal accumulation in this task as well, timing would bias participants toward whichever display was presented for longer.

Results.

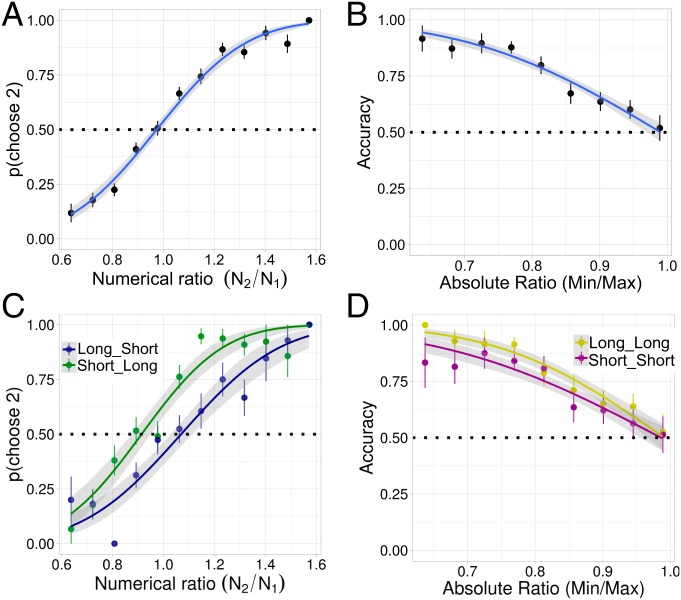
Participants’ responses as a function of ratio collapsed across time conditions can be seen in Fig. 5 A and B. Fig. 5A shows the proportion of participants who responded that the second display had more dots than the first as a function of the ratio of dots in the second display relative to the first. The proportion of participants who responded that the second display was more numerous increased monotonically with the ratio. Participants reported that the second display was more numerous on average ($56\%$ of the time), possibly suggesting an effect of memory. This is consistent with studies finding effects of recency in nonsymbolic magnitude comparison (32). Fig. 5B shows participants’ accuracy as a function of the absolute magnitude ratio, or the minimum magnitude over the maximum. Participants were able to discriminate ratios of $5:6$ with roughly $75\%$ accuracy.

Fig. 5.

(A) The probability that participants responded that the second display had more dots as a function of the ratio $N_1/N_2$, where $N_1$ and $N_2$ are the number of dots in the first and second display, respectively, collapsed across conditions. The fit curve (as well as all other fits in this display) is from a probit regression. (B) Accuracy as a function of the absolute ratio ($Min\left(N_1,N_2\right)/Max\left(N_1,N_2\right)$. (C) The probability participants responded that the second display had more dots in the long–short (blue) and short–long (green) conditions as a function of ratio. (D) Accuracy as a function of the absolute ratio in the long–long (yellow) and short–short (red) conditions.

Fig. 5C shows response curves for the critical conditions where the first and second displays were shown for different amounts of time, but the total presentation time was controlled (long–short versus short–long). The difference between the curves indicated a bias to choose the second display when it was long compared with when it was short, as predicted. Fig. 5D shows response curves for the conditions where the first and second displays are shown for the same amount of time, but overall presentation time differed (short–short versus long–long). The observed difference between the response curves in Fig. 5D indicates that responses in the long–long condition were more accurate than those in the short–short condition. Collapsing across ratios, participants chose the second display $62\%$ of the time in the short–long condition and $45\%$ of the time in the long–short condition, as predicted. Participants chose the second display at intermediate (though above-chance) rates in the short–short $\left(56\%\right)$ and long–long $\left(57\%\right)$ conditions (see SI Appendix for analysis).

Analogous to the analysis for Experiment 1, we used the eye-tracking data to determine whether participants’ visual samples mediated the observed effect of time. We found that the proportion of dots foveated had a significant effect on both the slope and Weber fraction, and, as with the estimation task, the effect of time on the slope disappeared. There was still an effect of time on Weber fraction, though it was heavily reduced (SI Appendix).

The Mechanics of ANS Estimation

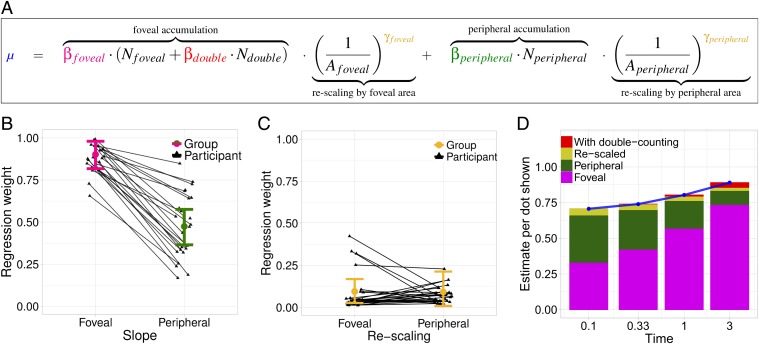
We next developed a statistical model that allowed us to use people’s behavioral data to quantify how different components of visual input contributed to numerical estimates. This model was parameterized in a way that allowed us to test a variety of a priori plausible hypotheses about how ANS accumulation might relate to visual behavior. Primarily, this allowed us to test separable contributions of several behaviorally measured factors to an estimated quantity $\mu$. The weight of each factor was inferred by the model. Fig. 6A shows all of these terms in the full equation for $\mu$, with the fit parameters in color and the behaviorally measured variables on each trial in black.

Fig. 6.

(A) The mean estimate, $\mu$, given as a function of the number of dots foveated, $N_{foveal}$; the number of dots not foveated, $N_{peripheral}$; the percent of screen area foveated, $A_{foveal}$; the percent of screen area not foveated, $A_{peripheral}$; and the number of dots foveated more than once, $N_{double}$. Each of these has a corresponding parameter quantifying its contribution to the estimate $\mu$. (B) Parameters ${\mathrm{\beta }}_{foveal}$ and ${\mathrm{\beta }}_{peripheral}$ capture the foveal and peripheral contribution to the accumulated count. (C) Parameters ${\gamma }_{foveal}$ and ${\gamma }_{peripheral}$ capture the degree to which the accumulated count is normalized by the percent of screen for area foveated ($A_{foveal}$) or peripheral ($A_{peripheral}$). (D) A visualization of how each factor contributes to $\mu$ over time. As exposure time increases, the average proportion of dots foveated increases, leading to differences in the expected contribution of each factor to the mean estimate.

The model assumed that there were five components that contributed to $\mu$. First were the number of dots foveated ($N_{foveal}$) and the number of dots not foveated ($N_{peripheral}$), which were each weighted by their corresponding regression parameters (${\mathrm{\beta }}_{foveal}$ and ${\mathrm{\beta }}_{peripheral}$). In addition, we tested the contribution of dots that were fixated more than once after first saccading away ($N_{double}$ weighted by the parameter ${\mathrm{\beta }}_{double}$). Finally, the proportion of area that has been foveated ($A_{foveated}$)—which we measured as percent of the screen within the $5^{○}$ window used above—and the area not foveated ($A_{peripheral}$) were allowed as scaling factors.

To fit this model to behavioral data, we again used a hierarchical Bayesian model which allowed partial pooling of parameters. Examination of the inferred parameters allowed us to characterize the mechanisms of ANS estimation in three critical ways: First, comparison of ${\mathrm{\beta }}_{peripheral}$ and ${\mathrm{\beta }}_{foveal}$ will show if the accumulation mechanism relies more, less, or equally on foveal and peripherally observed dots. This, in turn, tells us whether the ANS is primarily parallel or whether foveated dots contribute more to the observed estimates. Second, examination of ${\mathrm{\beta }}_{double}$ will tell us whether participants “double count” dots that are refoveated (${\mathrm{\beta }}_{double}\approx 1$) or not (${\mathrm{\beta }}_{double}\approx 0$). This will answer a basic question about ANS accumulation: Is it based on mere retinal input or on a spatially based picture of the world that is built up across saccades (e.g., ref. 33)? Third, do participants rescale their input by the area they have foveated (${\gamma }_{foveated}\approx 1$) to correct for their limited visual sample? Or, is estimation a more simple accumulator (${\gamma }_{foveated}\approx 0$) that does not take into account how much of the scene has been viewed? Note that our formalization does not test whether area, density, convex-hull, or some other continuous quantity is the basis of numerical estimation (10, 15, 34). Rather, this tests whether the ANS relies preferentially on foveated objects and whether it adjusts for the proportion of screen area that has been foveated. SI Appendix, however, presents results showing that convex-hull has little to no effect on mean estimates.

Fig. 6B shows the inferred group- and subject-level means for ${\mathrm{\beta }}_{foveal}$ (x axis) and ${\mathrm{\beta }}_{peripheral}$ (y axis). This shows that foveated dots contribute about twice as much as peripheral dots to estimates. Moreover, the value of ${\mathrm{\beta }}_{foveal}$ is ∼1, meaning that people veridically count one foveated dot as one more in their estimate.^¶ Interestingly, however, the peripheral dots do provide a nonzero contribution, explaining why ANS estimation is possible with very fast presentation times, albeit with a lower precision (16). Fig. 6C shows that both ${\gamma }_{foveal}$ and ${\gamma }_{peripheral}$ are near zero, indicating little area renormalization. This finding supports our primary claim that the estimation is based on accumulation, rather than inference using the density of dots observed in part of the scene. Finally, ${\mathrm{\beta }}_{double}$ was near 0 for all participants, indicating that there is almost no effect of seeing the same dot multiple times in the same display. This would happen, for instance, if people build up a mental image of the dot array that is fed to the accumulator.

Fig. 6D visualizes the relative contribution of each factor to mean estimates (y axis) across time conditions (x axis), as inferred by the model. At 0.1 s, peripheral and foveated dots contribute roughly equal amounts to estimates, accounting for the significant degree of underestimation given such a short exposure. However, as the exposure time increased, foveated dots contributed increasing amounts to the estimate, such that peripheral dots barely played a role in estimation at 3 s. Rescaling and double-counting played almost no role at any amount of time.

General Discussion

ANS estimation is typically thought to operate rapidly and in parallel. There is evidence to support this view. For instance, people can discriminate quantities at above-chance levels given only 16 ms of exposure (16). Studies have also demonstrated that reaction times are roughly constant across numerosities in humans and monkeys performing approximate numerical estimation and discrimination tasks (35, 36). The latency of number-sensitive neurons tends to be independent of numerosity in monkeys as well (17, 36). However, the results and analysis we present support an alternative theory: that ANS estimation relies on a serial accumulation mechanism that integrates information—either numerical quantity itself or lower-level visual content—across eye fixations.

Our experiments first replicate two prior behavioral findings: an underestimation bias (31) and a dependence of ANS acuity on time (16). We then showed that the underestimation bias decreases with time, such that participants estimated higher numbers as the stimulus’ duration increased. Such an influence of time is predicted by an accumulation model, but not by prior accounts that attribute underestimation to miscalibration of response scales (31). Finally, we showed that the effect of time is almost entirely mediated by visual fixations, suggesting that time matters, because with more time, subjects are able to fixate more of the display. Freely fit parameters from our model indicated that foveated points contribute twice as much to a numerical estimate as peripheral ones. This analysis also revealed that the accumulation likely does not adjust for area, nor does it double-count refixated dots. Together, these results suggest that a primarily foveal, serial accumulation mechanism is at the heart of ANS estimation, rather than the rapid, parallel mechanism previously proposed and commonly imagined.

A serial accumulator is similar to ANS models that perform temporal integration of, for instance, sequences of clicks (5), as well as an approximate version of counting logic observed in sequential presentation of quantities to primates (37). Thus, visual ANS estimation may share resources and processes with nonvisual quantity estimation, as experiments on cross-modal matching would suggest (38). Specifically, visual fixations may be a proxy for attention, which would be consistent with the finding that the numerosity of auditory and tactile stimuli are increasingly underestimated as their presentation rate increases (39, 40). Still, it is surprising to see such serial effects in visual displays since vision can in principle support parallel processes (41).

One limitation of the current work is that our results do not address the specificity of the accumulation mechanism. In particular, our results are consistent with at least two possibilities: Either numerical quantities themselves are being integrated across visual fixations, or people build up an increasingly precise image of the visual scene as they saccade, from which numerical information is later extracted. In either case, our results do show that performance in ANS tasks is largely determined by the serial component of this process.

Regardless of the ultimate mechanisms, our results raise an important methodological point for both basic cognitive research on the ANS and applied education research which relies on it. In light of our findings, it is difficult to interpret results from studies that compare participants’ performance across ANS tasks which use different display sizes or stimulus-exposure durations (e.g., refs. 13, 19, and 30). More broadly, our results suggest that the nearly universal use of ANS tasks to index a “pure” sense of number may be misguided. A full picture of ANS estimation will require integrating aspects of visual cognition such as attention and ocular-motor control to understand the cognitive mechanisms that translate visual scenes into abstract numerosities.

Materials and Methods

Experiment 1.

Participants were placed directly in front of a computer, with the eye-tracker mounted on top. The computer screen was 24 inches, with an aspect ratio of 16:10 and screen resolution of 1,920 × 1,200 pixels. The screen sat on an adjustable desk, which was vertically realigned for each participant to ensure that that the center of the screen was level with their eyes. The participants were fixed to a distance such that their eyes were 26 inches away from the screen, which was ensured by measurement with a yardstick. The screen subtended ∼$38^{○}$ of participants’ visual field left-to-right and $26^{○}$ top-to-bottom. The eye-tracker was a Tobii T60XL model, providing a readout of 60 samples per second. We used built-in Tobii software to calibrate participants to the eye-tracker.

Each dot had a radius of 10 pixels. The density of the dots in the images ranged from 0.01 to 0.07 dots/deg². Note that the constant dot size meant that it was not possible to directly test whether the ANS estimation uses number rather than another correlated dimension such as density. The number of dots displayed on each trial varied between 10 and 90 dots, inclusive. To determine the numerosities shown to a given subject, 16 numbers were chosen randomly from within that range. The same 16 numbers were shown to the participant in each of the 4 time conditions, with presentation order randomized across the conditions. The median range size across participants was 71 (minimum 54, maximum 79). The median lowest number shown was 14, and the median highest number shown was 86. The dots were placed on the screen at random locations, only constrained to be nonoverlapping. Participants entered their numerical estimates using a keyboard attached to the computer. The experiment was designed by using the Python library Kelpy (42); all of the code to run it can be found on the first author’s github page at https://github.com/samcheyette/accumulator_paper_files. All data and analysis used in the paper can be found there as well.

Participants.

A total of 27 adult subjects (15 female, 12 male) from the University of Rochester community were recruited to participate in the task. The participants’ ages ranged from 18 to 29 ($M=21.4$).

Procedure.

All study procedures were approved by the University of Rochester Institutional Review Board. After providing consent, participants were calibrated to the eye-tracker and subsequently began the experiment. The experiment consisted of 64 total trials, with 4 blocks of 16 trials each. Each 16-trial block contained one of the 4 different time conditions each subject underwent: 100; 333; 1,000; and 3,000 ms (together comprising all 64 trials); the order of the blocks was randomized across participants. On each trial, dots were displayed, followed by a noise mask. Subjects then typed their responses into a text box using a keyboard and pressed the enter key to move onto the next trial.

Experiment 2.

Experiment 2 was a sequential number-discrimination task with the same participants who completed Experiment 1. Likewise, the properties of the stimuli and materials used in Experiment 2 were the same as in Experiment 1 (e.g., dots in both had the same radius). Sixteen pairs of numbers were chosen randomly for each participant, with the ratio (the minimum over the maximum) of the number pairs constrained to be between 0.5 and 0.99. For a given subject, the same number pairs were used across the 4 time conditions, with their order randomized across conditions.

Procedure.

After completing Experiment 1, participants took a break (if needed), were recalibrated to the eye-tracker, and then began Experiment 2. In this task, participants saw 2 flashes of dots, one after the other, and were subsequently asked which stimulus they thought had a greater quantity of dots (pressing 1 or 2 on a keyboard). There were 4 conditions with 16 trials each (like Experiment 1), where each condition corresponded to a unique pair of stimulus durations for the first and second display. More specifically, the 4 conditions were (100; 100 ms), (100; 1,000 ms), (1,000; 100 ms), and (1,000; 1,000 ms).