Extreme Polygenicity of Complex Traits Is Explained by Negative Selection

Abstract

Complex traits and common diseases are extremely polygenic, their heritability spread across thousands of loci. One possible explanation is that thousands of genes and loci have similarly important biological effects when mutated. However, we hypothesize that for most complex traits, relatively few genes and loci are critical, and negative selection—purging large-effect mutations in these regions—leaves behind common-variant associations in thousands of less critical regions instead. We refer to this phenomenon as flattening. To quantify its effects, we introduce a mathematical definition of polygenicity, the effective number of independently associated SNPs (M_e), which describes how evenly the heritability of a trait is spread across the genome. We developed a method, stratified LD fourth moments regression (S-LD4M), to estimate M_e, validating that it produces robust estimates in simulations. Analyzing 33 complex traits (average N = 361k), we determined that heritability is spread ∼4× more evenly among common SNPs than among low-frequency SNPs. This difference, together with evolutionary modeling of new mutations, suggests that complex traits would be orders of magnitude less polygenic if not for the influence of negative selection. We also determined that heritability is spread more evenly within functionally important regions in proportion to their heritability enrichment; functionally important regions do not harbor common SNPs with greatly increased causal effect sizes, due to selective constraint. Our results suggest that for most complex traits, the genes and loci with the most critical biological effects often differ from those with the strongest common-variant associations.

Introduction

Genome-wide association studies (GWASs) have revealed that common diseases and complex traits are heritable and highly polygenic.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} There are usually no large-effect common SNPs, and heritability is evenly spread across thousands of small-effect SNPs. The polygenic distribution of heritability presents a challenge, as small-effect SNPs are difficult to detect (leading to “missing heritability”¹⁵) and are difficult to interpret.^{16, 17}

One factor contributing to the polygenic distribution of heritability is the complexity of the underlying biology: many genes and regions of the genome have a nonzero phenotypic effect if mutated. A plausible explanation for the large mutational target is that cellular networks are densely connected, such that nearly every gene expressed in a relevant cell type has a small phenotypic effect (the “omnigenic model”).¹⁷ A striking implication of this model is that disease genes with direct phenotypic effects would explain a minority of disease heritability.

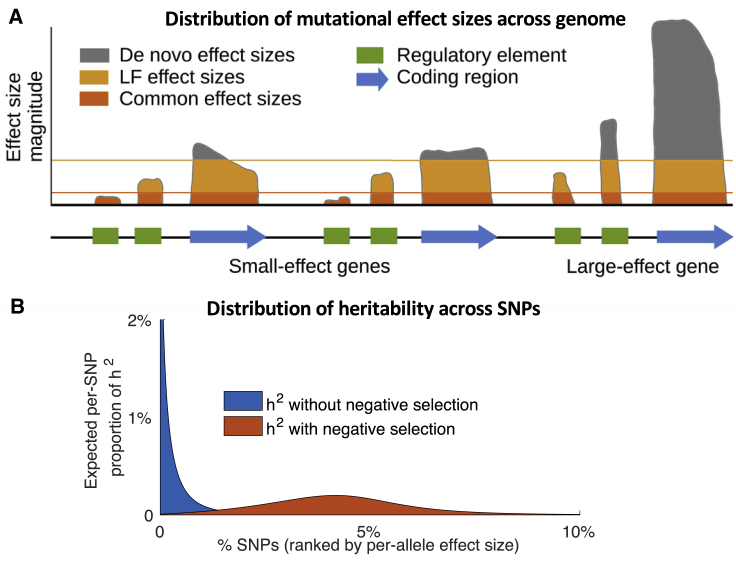
Although biological complexity clearly contributes to the polygenicity of complex traits, negative selection may also be a critical factor. Biological complexity determines the effect-size distribution of new mutations. We hypothesized that this distribution—in contrast to that of heritability—is dominated by a relatively small number of large-effect genes and loci (Figure 1A). In the absence of negative selection, the resulting distribution of heritability would be highly concentrated in these large-effect regions, and hence only moderately polygenic (Figure 1B). However, in the presence of negative selection, the heritability explained by any single SNP is limited, and mutations in these large-effect regions would not become common. As a result, heritability would be spread much more evenly across large- and small-effect regions alike (Figure 1B). We refer to this phenomenon—negative selection causing the distribution of heritability to be extremely polygenic—as flattening.

Figure 1.

Illustration of Flattening due to Negative Selection

(A) We illustrate the range of possible per-allele effect sizes for a SNP at each site for a toy example of three genes and nearby regulatory regions. Here, the distribution of de novo effects is not highly polygenic; it is dominated by coding mutations in a single large-effect gene (although other genes also harbor small effects). Negative selection imposes an upper effect size bound (possibly soft) on common variants (and, to a lesser extent, low-frequency variants), resulting in increased polygenicity. Within functionally important regions (e.g., coding), a larger proportion of variants have effect sizes near the bound, leading to especially large polygenicity. In practice, this bound may vary across the genome, but we hypothesize that it is much more even than the effect-size distribution of de novo variants.

(B) We illustrate the expected per-SNP proportion of heritability for SNPs ranked by per-allele effect size, for a hypothetical trait whose de novo effect-size distribution has a mixture of small- and large-effect mutations. In the absence of negative selection (blue), heritability is concentrated among a limited number of large-effect SNPs. In the presence of negative selection (orange), large-effect SNPs are prevented from becoming common, and thus explain little heritability; instead, heritability is spread across a large number of SNPs with small effects.

Negative selection has previously been shown to influence complex-trait genetic architectures. It limits the average per-allele effect sizes of common variants,^{12, 18, 19, 20, 21} especially in coding regions and brain regulatory elements.²⁰ It also causes average effect sizes to vary with linkage disequilibrium (LD) and allele age.¹⁹ Various models have been proposed for the mathematical relationship between phenotypic effect sizes and selection coefficients.^{22, 23, 24, 25, 26, 27, 28} However, it is currently unclear whether negative selection merely limits common-variant heritability on average without affecting how evenly it is spread across the genome—as in the model of Zeng et al.¹² and in one of the evolutionary models that we explore below—or whether it actually reshapes the genome-wide distribution of heritability.

Here, we investigate the hypothesis that negative selection flattens the distribution of heritability across the genome, explaining the extreme polygenicity of complex traits. We evaluate two specific predictions. First, heritability should be spread more evenly across common SNPs than across low-frequency SNPs. Ideally, we would compare the polygenicity of common SNPs and new mutations, but this comparison is not possible using GWAS data; instead, we compare common and low-frequency SNPs, reasoning that the polygenicity of low-frequency SNPs will lie in between the polygenicity of common SNPs and the polygenicity of new mutations (Figure 1A). Second, functionally important regions of the genome should not harbor common SNPs with greatly increased causal effect sizes, as the maximum effect size is determined by the strength of selection. Instead, their heritability enrichment should be predominantly explained by increased polygenicity: a larger proportion of SNPs in functionally important regions should have effect sizes close to the upper bound imposed by selection (Figure 1A). In order to evaluate these predictions, we introduce a mathematical definition of polygenicity, the effective number of independently associated SNPs (M_e). We develop a method, stratified LD fourth moments regression (S-LD4M), to estimate M_e from summary association statistics. We validate S-LD4M in simulations and apply it to summary statistics for 33 diseases and complex traits.

Material and Methods

Defining Polygenicity: The Effective Number of Independently Associated SNPs

In this manuscript, we use the term “polygenicity” to describe the phenomenon that heritability is spread evenly across many genes and loci, such that the strongest genetic associations explain a limited fraction of heritability (leading to “missing heritability”^{1, 2, 15}). According to this definition, schizophrenia, which is predominantly driven by thousands of small-effect common variants, is extremely polygenic.^{1, 4, 13} In contrast, severe neurodevelopmental disorders, which are predominantly driven by deleterious mutations in one or a few genes, are not highly polygenic—despite the fact that they are also influenced by many common variants (cumulatively explaining <10% of variance).²⁹ Previous studies defined polygenicity as the total number of SNPs with nonzero effects (i.e., the total number of independently associated SNPs) (M_t),^{1, 3, 6, 7, 8, 12, 13, 14} but this definition fails to describe how heritability is spread across causal SNPs; M_t could be similar for schizophrenia and a predominantly monogenic developmental disorder, despite their qualitatively different genetic architectures. Moreover, in practice, estimates of M_t implicitly rely on a detection threshold, causing them to vary with sample size and with the parametric model that is specified¹³ (see Simulations). Variability in sample size and power could bias comparisons among traits or between common and low-frequency SNPs.

We introduce a mathematical definition of polygenicity, the effective number of independently associated SNPs (M_e), which quantifies how evenly heritability is spread across loci. Roughly, if all associated SNPs have similar effect sizes, then M_e is equal to M_t. However, if a small number of SNPs explain a large proportion of heritability, then the number of independently associated SNPs can be literally large but effectively small—in terms of missing heritability, risk prediction, and biological implications—and M_e can be much smaller than M_t. Despite the widespread use of M_t to define polygenicity,^{1, 3, 6, 7, 8, 12, 13, 14} we use the term “polygenicity” to refer to M_e, as it is the even distribution of heritability—and not the number of SNPs with nonzero effects—that makes the genetic architecture of complex traits different from that of predominantly monogenic disorders.²⁹ We note that if several causal SNPs are in very strong linkage disequilibrium (LD) (see e.g., Hormozdiari et al.³⁰), then M_e counts them as a single associated SNP, hence our use of the term “independently associated” (see Appendix A).

If there is no LD between causal SNPs, the heritability of a trait is proportional to the second moment of its effect size distribution, $E\left[{\beta }^2\right]$, while M_e is inversely proportional to the fourth moment, $E\left[{\beta }^4\right]$. The fourth moment heavily weights SNPs with the largest effects, such that if m large-effect SNPs explain most heritability, then M_e will be close to m, irrespective of how many other SNPs may have small nonzero effects. We define:

$$\begin{array}{c}{M}_e=\frac{3M}{\kappa },\kappa =\frac{E\left[{\beta }^4\right]}{E{\left[{\beta }^2\right]}^2},\end{array}$$ (Equation 1)

where M is the number of SNPs, $\beta$ is the causal effect size of a SNP in standardized units (see below), and $\kappa$ is the kurtosis (normalized fourth moment) of $\beta$. We note that M_e is closely related to missing heritability and to polygenic prediction accuracy (see Appendix A, Properties of Me).

We define effect sizes $\beta$ in standardized units, i.e., the number of standard deviations increase in phenotype per 1 standard deviation increase in genotype. In these units, the squared effect size of a SNP is equal to the heritability it explains, and the kurtosis describes how evenly heritability is spread across SNPs. Thus, a rare SNP explaining little heritability will contribute little to M_e, even if its per-allele effect size is large.

We refer to h² divided by M_e as the average unit of heritability, denoted ${\text{E}}_{h^2}\left({\alpha }^2\right)$ (where $\alpha$ is the standardized marginal effect size of a SNP, inclusive of LD; see below); heritability is spread across loci in units of average size ${\text{E}}_{h^2}\left({\alpha }^2\right)$. $\text{This}\text{quantity }$can be visualized as the area under the curve in Figure 2A. For example, if 4 causal SNPs each contribute $1/6$ of heritability ($2/3$ of heritability in total) and 96 other causal SNPs have much smaller effects (standardized causal effects drawn from a mixture of two Gaussian distributions¹³), then the average unit of heritability is approximately $\left(1/6\times 2/3=1/9\right)$, and M_e ≈ 9 (Figure 2A bottom). More generally, adding a large-effect SNP increases ${\text{E}}_{h^2}\left({\alpha }^2\right)$ and decreases M_e (Figure 2B). In the case of a neurodevelopmental disorder predominantly caused by nearly penetrant mutations in one or a few genes, with thousands of common variants also having a small cumulative effect,²⁹ M_e will be small (e.g., ∼10), while M_t will be large (e.g., ∼10,000).

Figure 2.

Comparison of the Effective Number of Independently Associated SNPs (M_e) with the Total Number of SNPs with Nonzero Effects (M_t)

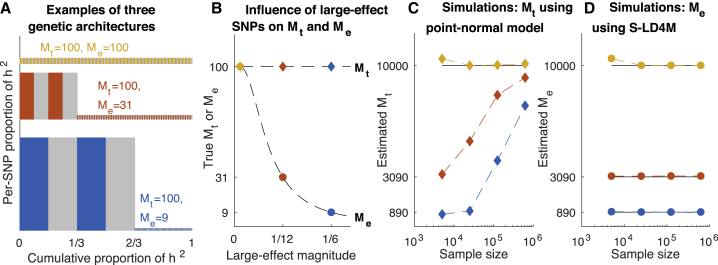
(A and B) Examples of three genetic architectures with M_t = 100.

(A) Each colored or gray block corresponds to one SNP; both height and width are proportional to the expected proportion of heritability explained by that SNP. The average unit of heritability, denoted ${\mathit{E}}_{{\mathit{h}}^2}\left({\mathit{\alpha }}^2\right)$, is the average height (equal to the total area) of the colored and gray regions. M_e is equal to ${\mathit{h}}^2/{\mathit{E}}_{{\mathit{h}}^2}\left({\mathit{\alpha }}^2\right)$.

(B) M_t and M_e as a function of the effect size magnitude of the four large-effect SNPs.

(C and D) Simulations of the same three genetic architectures with the number of SNPs (and causal SNPs) scaled up by 100×.

(C) Estimates of M_t under a point-normal model, at different sample sizes.

(D) Estimates of M_e using S-LD4M, at different sample sizes. Error bars denote 95% confidence intervals (based on 1,000 simulations) but are smaller than the data points.

M_e can be defined for categories of SNPs, such as low-frequency SNPs or coding SNPs. To compare categories of different size, we divide M_e by the number of SNPs in each category. We refer to differences in per-SNP M_e simply as differences in polygenicity. We define polygenicity enrichment as the per-SNP M_e of all SNPs in a category divided by the per-SNP M_e of all SNPs; analogously, we define heritability enrichment as the per-SNP heritability of all SNPs in a category divided by the per-SNP heritability of all SNPs (similar to previous work³¹). “All SNPs” refers to common (MAF ≥ 0.05) and low-frequency (0.005 ≤ MAF < 0.05) SNPs. Enrichment can be either >1 or <1 (i.e., depletion).

Estimating Polygenicity: Stratified LD Fourth Moments Regression

We developed a method, stratified LD fourth moments regression (S-LD4M), to estimate M_e from summary association statistics and LD from a reference panel. S-LD4M regresses squared ${\chi }^2$ statistics (i.e., fourth powers of signed Z scores) on LD fourth moments, defined as sums of r⁴ values to each category of SNPs. Intuitively, S-LD4M provides a bridge between the fourth moment of the marginal effect size distribution (i.e., squared ${\chi }^2$ statistics) and the fourth moment of the causal effect size distribution (which is related to M_e). S-LD4M relies on the following regression equation:

$$\begin{array}{c}E\left({\alpha }^4|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)\approx 3{\left({\ell }^{\left(2\right)}\tau \right)}^2+{\ell }^{\left(4\right)}K,\end{array}$$ (Equation 2)

where $\alpha$ is the marginal effect size of a SNP in per-normalized-genotype units; ${\ell }^{\left(2\right)}$ is the LD score (LD second moment) of a SNP; ${\ell }^{\left(4\right)}$ is the LD fourth moment, defined as the sum of r⁴ values over SNPs; $\tau$ is the S-LDSC regression coefficient;³¹ and K is the S-LD4M regression coefficient. K is proportional to the excess kurtosis of the effect-size distribution, compared with an infinitesimal model, and it is related to M_e:

$$\begin{array}{c}K=3\text{E}\left({\beta }^2\right)\left[{\text{E}}_{h^2}\left({\alpha }^2\right)-E\left({\alpha }^2\right)\right]=\frac{3h^2}{M}\left[\frac{h^2}{M_e}-\frac{h^2}{M_{indep}}\right],\end{array}$$ (Equation 3)

where h² is the heritability tagged by reference-panel SNPs, M is the number of SNPs, and M_indep is the effective number of independent SNPs.³² Under an infinitesimal genetic architecture, M_e = M_indep and K = 0. $E\left({\beta }^2\right)$and $E\left({\alpha }^2\right)$ are estimated using a slightly modified version of stratified LD score regression (S-LDSC).³¹ Thus, S-LD4M uses Equation 2 to estimate K and Equation 3 to estimate M_e from K. In the case of multiple annotations, ${\ell }^{\left(2\right)},{\ell }^{\left(4\right)},\tau$, and K are all vectors with one entry per annotation. Standard errors are computed by jackknifing on contiguous blocks of SNPs, similar to previous work.⁵ The runtime of S-LD4M scales linearly with the number of regression SNPs and quadratically with the number of annotations. Details are provided in Appendix A (Stratified LD Fourth Moments Regression). We note that previous studies have used fourth moments of the bivariate effect-size distribution (across two traits) to quantify pleiotropy³³ and causality.³⁴

We report results only for well-powered trait-annotation pairs, defined as having heritability Z-score greater than 2 and M_e Z-score greater than ½. Simulations suggested that log-scale estimates and estimated standard errors were approximately unbiased at these thresholds (see below). We report meta-analyzed results only for functional annotations for which at least 10 out of the 33 traits analyzed had well-powered estimates for that functional annotation.

In order to aggregate enrichment estimates across traits, we performed meta-analyses on a logarithmic scale, for both heritability enrichment and polygenicity enrichment. The meta-analyzed estimate was computed as the unweighted average of the log-enrichment estimates for well-powered traits. Standard errors were computed by jackknifing on the mean (i.e., without assuming that each trait has independent standard errors).

Our moment-based approach has some similarities with S-LDSC, which estimates heritability by regressing ${\chi }^2$ statistics on LD scores (LD second moments).³¹ We use a slightly modified version of S-LDSC to estimate heritability enrichment. We run S-LD4M and S-LDSC using the baseline-LD model,¹⁹ which includes 75 coding, conserved, regulatory, MAF-related, and LD-related annotations. When estimating the polygenicity and polygenicity enrichment of a category of SNPs, we restrict to well-powered traits. Further details are provided in Appendix A (Stratified LD Fourth Moments Regression). We have released open-source software implementing S-LD4M (see Web Resources).

Simulations

We simulated summary statistics directly using the asymptotic sampling distribution,³⁵ rather than by simulating individual-level data. Specifically, the distribution of the summary statistic vector, $\hat{\mathit{\alpha }}$, as a function of the true causal effect size vector $\mathit{\beta }$, was:

$$\begin{array}{c}\hat{\mathit{\alpha }}\sim N\left(\hat{R}\mathit{\beta },\frac{1}{N}\hat{R}\right).\end{array}$$ (Equation 4)

The estimated LD matrix $\hat{R}$ was equal to I in simulations with no LD. In simulations with LD, $\hat{R}$ was computed from UK Biobank data (N = 460k). Sample correlations were computed for all typed and imputed SNPs (M = 1.0M) within 0.1 M of each other on chromosome 1. Blocks of 5,000 SNPs were used, and R was set to zero for pairs of SNPs in different blocks. These choices were necessary for $\hat{R}$ to be stored in memory, due to the large number of SNPs. To ensure that $\hat{R}$ was positive semidefinite, negative eigenvalues were discarded, as previously described.³⁴

Simulations with No LD

We simulated 50,000 total SNPs, 9,600 small-effect SNPs, and 400 large-effect SNPs. For small- and large-effect SNPs, effect sizes were drawn from a normal distribution with mean zero and variance ${\sigma }_1^2$ and ${\sigma }_2^2$, respectively; in the three simulations (corresponding to the three example architectures in Figure 2A), ${\sigma }_1^2$ was equal to 1/10,000, 1/1,200, and 1/600, respectively. ${\sigma }_2^2$ was equal to $\left(1-400{\sigma }_1^2/9600\right)$, resulting in a heritability of 1. (We note that in all simulations, only $N{h}^2$ affects the results; for example, identical results are obtained at h² = 1 and N = 20k and at h² = 0.2 and N = 100k.) We performed simulations at N = 5,000, 25,000, 125,000, and 625,000.

Simulations with LD

We performed two sets of simulations with real LD patterns (see above). First, we performed simulations with no functional annotations. We specified that a certain percentage of common SNPs (MAF > 0.05) and a certain percentage of low-frequency SNPs (0.05 > MAF > 0.005) were causal. Conditional on being causal, effect sizes were drawn from a mixture of two normal distributions, with probability p₁ = 0.1 and p₂ = 0.9, and variance ${\sigma }_1^2=4{\sigma }_2^2$. The variance parameter was frequency dependent; it was proportional to [p(1 − p)]^0.25, where p is the allele frequency. We note that in simulations where we varied the polygenicity of low-frequency SNPs, we did not change the effect-size variance in order to fix the average per-SNP heritability. Thus, as we decreased the low-frequency polygenicity, low-frequency per-SNP heritability was decreased proportionally.

Second, we performed simulations with five real functional annotations (coding, enhancer, promoter, DHS, repressed). We specified a different probability of being causal for SNPs in each category: 1/2, 1/4, 3/20, 3/80, and 1/20, for SNPs in each annotation and SNPs in no annotation at all, respectively. When a SNP was in multiple annotations, the probability of being causal was the maximum of the respective values. Conditional on being causal, SNPs had independent and identically distributed effect sizes; their effects were drawn from a mixture of two normal distributions, with probability p₁ = 0.1 and p₂ = 0.9, and variance ${\sigma }_1^2=4{\sigma }_2^2\propto {\left[p\left(1-p\right)\right]}^{0.25}$. The variances were scaled so that the total (expected) heritability was 0.2.

Point-Normal Model Estimator

We implemented a maximum-likelihood estimator of the total number of SNPs with nonzero effects (M_t) under a point-normal model with known heritability and no LD. Because there was no LD, the likelihood was equal to the product over SNPs of the per-SNP likelihoods, as described in Vilhjálmsson et al.³⁶ We performed a grid search to estimate the proportion of causal SNPs, and the estimate of M_t was equal to the estimated proportion of causal SNPs times the total number of SNPs. We note that in the case of LD, the likelihood does not factor, and it is computationally difficult to compute the exact likelihood, motivating the use of sophisticated estimators and heuristics.^{12, 13} In the much easier case of no LD, these approaches are expected to have similar performance as the optimal maximum-likelihood estimator.

Evolutionary Modeling

We used evolutionary modeling to investigate the impact of flattening on the distribution of heritability across genes. In our evolutionary modeling, each SNP affected one gene and each gene affected both the trait and fitness. We specified a distribution of effect sizes for SNPs on genes (identical for every gene) and a joint distribution for the effect size and selection coefficient of each gene. The effect of a SNP on the trait was its effect on its gene times the gene effect size; its selection coefficient of a SNP was its effect on its gene times the gene selection coefficient. Using an analytical formula for the distribution of allele frequencies conditional on selection coefficients, we obtained the joint distribution of trait effects and allele frequencies for each gene. We chose to perform analytical calculations based on the stationary distribution of allele frequencies rather than forward simulations because none of the qualitative phenomena we sought to illustrate are dependent on linkage disequilibrium or background selection.

We considered two models. Under the first model, 5% of genes had large effect sizes $\left({\beta }_{gene}\right)$, and these genes had large selection coefficients (s_gene). We refer to this model as the “direct selection model” because it could arise from direct selection acting on the trait. Under the second model, there were no large-effect genes, and different genes had different selection coefficients. We refer to this model as the “pleiotropic selection” model because the amount of selection acting on a gene is independent of its phenotypic effect.

Under the direct selection model, s_gene was equal to ${\beta }_{gene}^2$, and ${\beta }_{gene}$ followed a mixture of normal distributions; 95% of genes had variance 10⁻³, and 5% of genes had variance 10⁻¹ (i.e., 10× larger effect sizes and 100× larger effect size magnitudes). As a result of this choice, the de novo effect size distribution is dominated by large-effect genes. In one secondary analysis, we also added a third mixture component, where 0.5% of genes had variance 10. In another secondary analysis, we increased the strength of selection; s_gene was equal to $5{\beta }_{gene}^2$.

Under the pleiotropic selection model, s_gene was independent of ${\beta }_{gene}$; ${\beta }_{gene}$ followed a normal distribution with variance 10⁻³ (so that there were no large-effect genes), and s_gene followed a gamma distribution with parameters $k=5/2$ and $\theta =1/\mathrm{1,250}$. As a result of this choice, the de novo effect-size distribution was polygenic.

Under each model, we specified a distribution of effect sizes for SNPs on each gene, denoted ${\beta }_{SNP\to gene}$. Each SNP affected one gene, and the distribution was identical for every gene. For the direct selection model, we specified an inverse-gamma distribution with parameters k = 100 and $\theta =1$. This is a heavy-tailed distribution; it causes the expected heritability explained by a gene to plateau as a function of the gene effect size, rather than decreasing after attaining a maximum. For the pleiotropic selection model, we specified a mixture of normal distributions; 75% of SNPs had variance 0.2, and 25% of SNPs had variance 0.02. This choice causes the effect size distribution to be highly polygenic, despite the lack of flattening in this model; it also leads to an appropriate relationship between allele frequency and per-SNP heritability.

The effect size of a SNP on the trait, denoted ${\beta }_{SNP}$, was equal to ${\beta }_{SNP\to gene}{\beta }_{gene}$. The selection coefficient of a SNP, denoted s_SNP, was equal to ${\beta }_{SNP\to gene}^2{s}_{gene}$. For each gene, we computed the joint distribution of ${\beta }_{SNP}$ and allele frequency p, using the formula for the probability density of p conditional on s_SNP:³⁷

$$\begin{array}{c}f\left(p|s_{SNP}\right)=\frac{1}{Z}{p}^{4N\mu -1}\left(1-p^{4N\mu -1}\right)\exp \left(-4N{s}_{SNP}p\right),\end{array}$$ (Equation 5)

where Z is a constant, N = 100, and $\mu =1/200$ (so that the exponent $4N\mu -1$ is equal to 1). We note that the model is overparameterized; for example, identical results would be obtained with 100× larger N and 100× smaller s_gene and $\mu$.

We simulated 20,000 genes. For each gene, we computed the second and fourth moments of ${\beta }_{SNP}$ for SNPs at allele frequencies p = 0.25, 0.05, 0.01, 0.002, 0.004, by multiplying the probability density function of ${\beta }_{SNP}$ by $f\left(p|s_{SNP}\right)$ and approximating the integral using a sum over ${\beta }_{SNP\to gene}^2=\left(1/5000\right),\left(2/5000\right),\dots ,8$. Averaging over genes, we computed the variance in per-allele effect sizes, the per-SNP heritability (variance times heterozygosity), and the relative polygenicity (inverse of kurtosis). We also computed the proportion of heritability explained by the 10% of genes with largest ${\beta }_{gene}^2$.

Distinct from the 20,000 simulated genes, we analytically computed the heritability explained by a gene as a function of ${\beta }_{gene}^2$. In the direct selection model, s_gene was equal to ${\beta }_{gene}^2$; in the pleiotropic selection model, for the purpose of this specific analysis, s_gene was fixed at 2 × 10⁻⁴. The heritability explained by a gene at a given allele frequency was defined as the variance of ${\beta }_{SNP}^2$ at that allele frequency, times the heterozygosity.

Results

Simulations

We performed simple simulations with no LD to evaluate the S-LD4M estimator of M_e (the effective number of independently associated SNPs) and a maximum-likelihood estimator of M_t (the total number of SNPs with nonzero effects) under a point-normal model (PN) (see Material and Methods). This estimator is expected to produce similar results as previous estimators of M_t under the same point-normal model.^{3, 8, 11, 12, 13, 14} We simulated 400 large-effect SNPs and 9,600 small-effect SNPs, with M = 50k total SNPs. The mixture of different causal effect sizes, violating the point-normal model, is consistent with evidence for real traits.^{12, 13} When there was a large difference between the causal effect sizes of large- and small-effect SNPs, PN produced biased and sample size-dependent estimates of M_t (Figure 2C and Table S1), consistent with recent work.¹³ In general, any method that estimates M_t will detect only SNPs with effect sizes greater than some threshold, where that threshold depends on modeling assumptions and power. In contrast, S-LD4M does not depend on parametric modeling assumptions, and it produces unbiased estimates of M_e (Figure 2D). Power-dependent bias would be especially problematic for comparing common vs. low-frequency polygenicity, due to lower power for low-frequency SNPs.

Next, we performed a series of simulations using real LD patterns to determine whether S-LD4M produces reliable estimates of polygenicity in realistic settings. We simulated summary association statistics from the asymptotic sampling distribution³⁵ for UK Biobank imputed SNPs on chromosome 1 ($M\approx 1.0\text{M}$ SNPs). We used $N=50\text{k}$ samples and h² = 0.2, to approximately match $N{h}^2/M$ (and hence the expected χ² statistic) for UK Biobank traits. We included MAF-dependent genetic architectures^{12, 21} and causal effect size heterogeneity. Details of each simulation are provided in the Material and Methods.

First, we assessed the ability of S-LD4M to estimate polygenicity for the set of all common and low-frequency SNPs. We determined that median estimates of M_e were approximately unbiased across a wide range of true values, although slight bias was observed for very low values of M_e (Figure 3A and Table S1). We report medians instead of means due to noise in the denominator of the estimator, which leads to instability in the mean. In general, S-LD4M is expected to produce approximately unbiased median estimates except when power is very low.

Figure 3.

Accuracy of S-LD4M Estimates in Simulations with LD

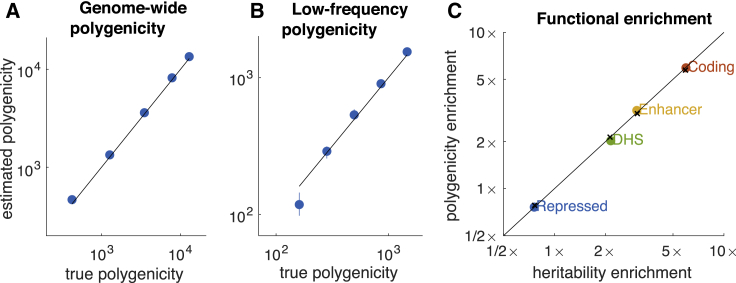
(A) Estimates of M_e for all SNPs (MAF = 0.5%–50%).

(B) Estimates of M_e for low-frequency SNPs (MAF = 0.5%–5%); common-SNP M_e is fixed at ∼1,000 in these simulations.

(C) Estimates of polygenicity enrichment and heritability enrichment in simulations with four functional categories. Black lines denotes y = x, and colored points denote estimates. In (C), $\times$denotes true values. Error bars denote 95% confidence intervals (based on 1,000 simulations) but are smaller than the data points in most cases. Numerical results are reported in Table S1.

Second, we fixed the polygenicity of common SNPs (MAF > 5%) at $M_e\approx \mathrm{1,000}$ and progressively reduced the polygenicity of low-frequency SNPs (MAF = 0.5%–5%), decreasing low-frequency heritability proportionally to fix the average effect size magnitude of causal low-frequency SNPs. Similar to Figure 3A, median estimates of low-frequency M_e were approximately unbiased for most values of M_e (Figure 3B). Some bias was observed at very low values of low-frequency M_e, owing to very low power (due to very low per-SNP heritability; see Material and Methods). We restrict our analyses of real traits to well-powered traits (see below). These estimates indicate that S-LD4M can be used to compare the polygenicity of common and low-frequency SNPs.

Third, we performed simulations with four real functional annotations, simulating equal heritability enrichment and polygenicity enrichment: coding (∼8× enriched), enhancer (∼5×), DNase I hypersensitivity sites (DHS, ∼2×), and repressed (∼0.75×), similar to our results on real traits (see below). We determined that S-LD4M produces approximately unbiased estimates of polygenicity enrichment (Figure 3C). We also considered an alternative model of heritability enrichment, under which polygenicity was approximately constant across functional categories. Estimates were approximately unbiased for enriched functional categories but biased for the repressed annotation (Figure S1). Despite the fact that this genetic architecture is less realistic (see below), we avoid reporting estimates of polygenicity for depleted functional annotations on real traits.

Fourth, we performed simulations to assess whether genetic architectures with non-random clustering of causal SNPs would bias our estimates of polygenicity enrichment for SNPs in functional categories. Such clustering is expected in real data (e.g., due to biologically important genes), and it could potentially lead to bias, as S-LD4M uses an LD approximation whose accuracy depends on LD between causal SNPs (however, we do not assume that linked SNPs have independent true causal effect sizes). We simulated clusters of either 5 or 50 causal SNPs (on average) across three genomic length scales (10, 100, 1,000 SNPs; roughly 3 kb, 30 kb, 300 kb on average). We determined that median enrichment estimates were approximately unbiased in each case, indicating that our LD approximation is robust to non-random clustering of causal SNPs (Figure S2).

Fifth, we performed simulations at different sample sizes and included a filtering step to exclude trait-annotation pairs with inadequate power (see Material and Methods). We performed simulations at N = 10k, N = 50k, and N = 250k, estimating both the genome-wide polygenicity and the polygenicity enrichment of five categories (four functional categories and low-frequency SNPs). At the default setting of N = 50k, genome-wide polygenicity estimates were unbiased (Table S2), and there was adequate power to estimate polygenicity enrichment: 61% of simulated traits were retained on average across categories, and polygenicity enrichment estimates were approximately unbiased (Figure S3 and Table S3). Similar results were obtained at N = 250k (Figure S3, Tables S2 and S3). At N = 10k, genome-wide polygenicity estimates remained unbiased (Table S2), but there was limited power to estimate polygenicity enrichment: only 8% of simulated traits were retained on average (including ∼0% of simulated traits for coding SNPs and for low-frequency SNPs), and polygenicity enrichment estimates were downward biased (Figure S3 and Table S3). Our analyses of real traits more closely correspond to N = 50k both in terms of average ${\chi }^2$ statistic and in terms of the proportion of traits retained (49% on average across categories). Nonetheless, we avoid reporting estimates of polygenicity enrichment for annotations having well-powered enrichment estimates for fewer than 10 out of the 33 traits that we analyzed.

Finally, we tested the calibration of our jackknife-based standard errors, once again considering different sample sizes and including a filtering step to exclude trait-annotation pairs with inadequate power. We assessed calibration using the normalized mean squared error, i.e., the actual squared error divided by the estimated squared error. We determined that our jackknife standard errors for both genome-wide polygenicity (Table S2) and polygenicity enrichment (Table S3) were approximately well calibrated or conservative. In particular, standard errors were moderately conservative when power was low to moderate (e.g., at N = 10k for genome-wide polygenicity), and well calibrated when power was high (e.g., at N = 50k for genome-wide polygenicity).

Polygenicity of Common SNPs across 33 Complex Traits

We applied S-LD4M to publicly available summary association statistics for 33 diseases and complex traits (average N = 361k; Table S4), including 29 UK Biobank traits^{38, 39, 40} (see Web Resources) and 4 additional common diseases. LD scores and LD fourth moments were computed using LD estimated from UK10K⁴¹ (M = 8.5 million SNPs after QC, MAF > 0.5%) and 75 baseline-LD model annotations.¹⁹ As in previous work,^{18, 19, 23, 31} we excluded the major histocompatibility complex, which has unusually large effect sizes and long-range LD due to balancing selection. (This choice increases M_e estimates for immune-related traits.) Details of our analyses are provided in the Material and Methods.

For most traits, M_e for common SNPs (MAF > 5%) ranged between 500 and 20,000 (10^2.7 and 10^4.3; Table 1). Fecundity- and brain-related traits were remarkably polygenic, with M_e estimates greater than 10,000. For number of children, the most polygenic trait, M_e was almost as large as effective number of independent SNPs, corresponding to an infinitesimal trait (log₁₀ M_e = 4.52 (0.13) vs. log₁₀ M_indep = 4.69). This estimate implies that most common SNPs are associated with this trait (though a much smaller fraction may be causal). Schizophrenia was also extremely polygenic (log₁₀ M_e = 4.14 (0.04)), consistent with previous work.^{1, 4, 13} Particularly high polygenicity for fecundity- and brain-related traits could result from particularly strong negative selection (see below), if these traits are strongly impacted by direct or pleiotropic selection; however, it is also possible that these traits have greater biological complexity. Red hair pigmentation and sunburn were the least polygenic traits, consistent with known large-effect common SNPs for pigmentation traits^{42, 43} (M_t may be much larger than M_e for these traits). We also estimated M_e without including annotations from the baseline-LD model, either using the 10 common MAF bins only or using no annotations (Table S5). Estimates using ten MAF bins were concordant with estimates using the baseline-LD model (log-scale r = 0.95; mean ${\text{log}}_{10}$ fold difference −0.03 (SD = 0.21)), and estimates using no annotations were approximately concordant but slightly smaller on average (log-scale r = 0.95; mean log₁₀ fold difference −0.13 (SD = 0.22)). This suggests that S-LD4M estimates are not contingent on accurately modeling LD-dependent architectures, which is critical in other contexts.

Table 1.

Estimates of Polygenicity for Common and Low-Frequency SNPs across 33 Complex Traits

Trait	${\mathbf{l}\mathbf{o}\mathbf{g}}_{\mathbf{10}}{\mathit{M}}_{\mathit{e}}$Common	${\mathbf{l}\mathbf{o}\mathbf{g}}_{\mathbf{10}}{\mathit{M}}_{\mathit{e}}$LF	Sample Size$\left(\mathit{N}\mathbf{or}{\mathit{N}}_{\mathit{e}\mathit{f}\mathit{f}}\right)$
Infinitesimal trait	4.69	4.98
Number of children	4.50 (0.13)	3.95 (0.23)	457k
Schizophrenia	4.14 (0.04)	3.10 (0.16)	111k
Smoking status	4.11 (0.02)	NA	458k
College	4.08 (0.05)	2.86 (0.20)	389k
Morning person	4.02 (0.02)	2.16 (0.25)	411k
Age at first birth – F	3.99 (0.04)	NA	169k
Neuroticism	3.99 (0.23)	NA	372k
FVC	3.87 (0.16)	NA	372k
CVD including HT	3.81 (0.03)	NA	400k
BP – systolic	3.81 (0.02)	2.31 (0.42)	423k
BMI	3.78 (0.12)	2.53 (0.21)	458k
IBD	3.60 (0.04)	3.19 (0.10)	86k
Height	3.56 (0.02)	2.91 (0.05)	458k
WHR	3.50 (0.04)	2.54 (0.09)	458k
Age at menarche	3.47 (0.09)	2.47 (0.26)	242k
FEV1/FVC	3.38 (0.05)	3.01 (0.16)	372k
WBC count	3.30 (0.10)	2.42 (0.18)	445k
Eczema	3.20 (0.05)	NA	324k
Asthma	3.12 (0.03)	NA	187k
Eosinophil count	3.05 (0.04)	NA	440k
RA	3.03 (0.10)	NA	85k
Platelet count	2.97 (0.04)	2.51 (0.10)	444k
AID	2.93 (0.05)	NA	197k
BMD – heel	2.90 (0.08)	NA	446k
Alzheimer’s	2.90 (0.11)	NA	47k
Type II diabetes	2.85 (0.14)	NA	74k
RBC distribution width	2.70 (0.05)	NA	443k
RBC count	2.67 (0.18)	NA	445k
Platelet distribution width	2.64 (0.08)	1.36 (0.54)	445k
Balding	2.59 (0.18)	2.16 (0.20)	180k
Age at menopause	2.55 (0.06)	NA	143k
Sunburn	1.99 (0.08)	NA	343k
Red hair	1.02 (0.22)	NA	81k

We report common variant estimates for all traits, and low-frequency estimates for well-powered traits (see Material and Methods). We also report the sample size; for binary traits we report the effective sample size, defined as N_eff = 4/(1/N_case + 1/N_control). The first row reports the effective number of independent SNPs.³²M_e is close to this value when marginal effect sizes approximately follow a normal distribution, which does not imply that every SNP is causal. Abbreviations: FVC, forced vital capacity; CVD including HT, cardiovascular diseases including hypertension (most cases have HT); BP, blood pressure; BMI, body mass index; IBD, inflammatory bowel disease; WHR, waist-hip ratio; FEV1, forced expiratory volume; WBC, white blood cell count; RA, rheumatoid arthritis; AID, autoimmune and inflammatory diseases; BMD, bone mineral density; RBC, red blood cell.

We compared our estimates of M_e with estimates of the total number of SNPs with nonzero effects (M_t) from Zeng et al.¹² and from Zhang et al.¹³ The estimates of Zeng et al.¹² were based on a point-normal mixture model, and the estimates of Zhang et al.¹³ were based on either a point-normal model or a 3-component (point-normal-normal) model, as determined via a model selection step. Our M_e estimates were correlated with both sets of M_t estimates (log-scale r = 0.90 and r = 0.63, respectively; Figures S4A and S4B and Table S6). The two sets of M_t estimates were only weakly correlated with each other (log-scale r = 0.20; Figure S4C and Table S6), largely due to discordant M_t estimates for intelligence and depression (neither of which was analyzed in this study). The M_t estimates of Zeng et al.¹² were ∼4× larger than both our M_e estimates and the M_t estimates of Zhang et al.,¹³ and the estimates of Zhang et al.¹³ had much larger standard errors. Consistent with our simulations and with the stated limitations of these studies, this discordance confirms that estimates of M_t will vary from study to study based on the parametric model that is assumed and the sample size of the study. We also compared our estimates of M_e to the values of M_e that would be implied under the model fit by Zhang et al.;¹³ these estimates were approximately concordant, both in relative value (log-scale r = 0.85 across 14 traits) and on average (mean log₁₀ fold difference 0.19 (SD = 0.38)) (Table S6). Finally, we compared the observed vs. expected distribution of ${\chi }^2$ statistics under a point-normal model (Figure S5 and Table S7), and we determined that a point-normal model does not fit the observed distribution of ${\chi }^2$ statistics.

We performed three secondary analyses. First, for 6 of the 33 traits, summary association statistics from independent cohorts were available. S-LD4M produced concordant M_e estimates for common SNPs on these data sets, despite the smaller sample size and much smaller number of regression SNPs (Table S8). (We did not estimate low-frequency M_e for these data sets, because summary statistics were not available for low-frequency SNPs.) Second, across all 33 traits, our estimates of M_e were not significantly correlated with effective sample size (Spearman r = −0.23, p = 0.19). Third, M_e provides an upper bound on the proportion of heritability explained by genome-wide significant loci for a trait (see Appendix, Properties of Me). We compared this bound with a direct estimate of this proportion (which may be upwardly biased by winner’s curse), and determined that the predicted bound corresponded fairly well with the estimate (Spearman r² = 0.61; Figure S6A). It also provided a conservative upper bound on the number of genome-wide significant SNPs (Figure S6B). Similar results were obtained when we used M_e estimates from an independent cohort (Figure S7).

Unequal Polygenicity of Common and Low-Frequency SNPs across 33 Complex Traits

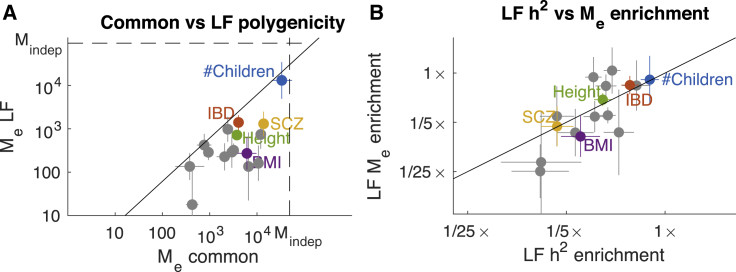
We compared per-SNP M_e estimates for common and low-frequency SNPs across 15 well-powered traits (Figure 4A and Table 1). Polygenicity was 3.9× (95% CI: 2.9–5.2×), smaller for low-frequency SNPs than for common SNPs on average, with substantial variation across traits. This difference represents a lower bound on the difference in polygenicity between common SNPs and de novo mutations. We are not currently aware of any possible explanation for this difference except for the influence of negative selection.

Figure 4.

Comparison of Common and Low-Frequency Polygenicity across 15 Complex Traits

(A) Estimates of M_e for common and low-frequency SNPs. Estimates are meta-analyzed across well-powered traits. Common-variant polygenicity was ∼4× greater on average than low-frequency polygenicity. Dotted lines denote the effective number of independent SNPs (M_indep) for common and low-frequency SNPs, respectively, corresponding to an infinitesimal (Gaussian) architecture. The solid line denotes equal per-SNP M_e.

(B) Estimates of polygenicity enrichment and heritability enrichment for low-frequency SNPs (compared to all common and low-frequency SNPs). The solid line denotes equal enrichment. Error bars denote 95% confidence intervals. Numerical results are reported in Tables 1 and S9.

The ∼4× difference in common vs. low-frequency polygenicity is the largest that we would expect to observe, as the per-SNP heritability of common SNPs is also 3.9× (95% CI: 3.5–4.4×) larger than that of low-frequency SNPs (consistent with previous estimates^{12, 21}). This concordance was consistent across traits (Figure 4B). The ratio h²/M_e (i.e., the average unit of heritability; see Material and Methods) is expected to either decrease or remain constant at decreasing allele frequencies; individual low-frequency SNPs are not expected to explain more heritability than individual common SNPs. Our estimates indicate that this ratio remains constant at allele frequencies above ∼0.005. This observation suggests three conclusions.

First, negative selection imposes a bound on per-SNP heritability that is approximately the same for common and low-frequency SNPs. (In units of per-allele effect size, the bound is higher for low-frequency SNPs.) This would occur under a model where selection coefficients scale with squared per-allele effect sizes, e.g., under the model of Simons et al.²⁸ and under the evolutionary models we consider below. We caution that the bound may vary across the genome, although it does not appear to vary across functional annotations (see below).

Second, the heritability of both common and low-frequency SNPs is predominantly explained by SNPs with standardized effect sizes near the effect-size bound, resulting in similar values of h²/M_e. This suggests that the de novo effect-size distribution is dominated by mutations with effect sizes at least as large as per-allele effect size bound for low-frequency SNPs. If mutations with effect sizes approaching the common-SNP effect-size bound explained an equal proportion of variance in the de novo effect-size distribution as mutations with effect sizes approaching the low-frequency effect size bound, then they would also explain an equal proportion of low-frequency heritability. However, these SNPs would contribute little to $E\left({\beta }^4\right)$, and h²/M_e would be ∼2× smaller for low-frequency SNPs than for common SNPs (note that h²/M_e = $E\left({\beta }^4\right)/3E\left({\beta }^2\right)$, ignoring LD; see Material and Methods).

Third, the difference in polygenicity between common SNPs and new mutations is likely to be much greater than 4× on average. The only way for this difference to be only ∼4× would be for the de novo effect-size distribution to be abruptly truncated near the per-allele effect-size bound for low-frequency SNPs; the variance of this distribution would need to be driven by mutations with effect sizes confined to a narrow range. Instead, it is more likely that this distribution is not abruptly truncated, and mutations with increasingly large effects explain increasing proportions of variance in the de novo effect-size distribution, up to some point well beyond the low-frequency effect-size bound. If so, then the de novo effect-size distribution would be much more sparse than the effect-size distribution of low-frequency SNPs, and the polygenicity of common SNPs would be $\gg 4\times$ the polygenicity of the de novo effect-size distribution. Indeed, we observed a ≥30× difference in our evolutionary models (see below).

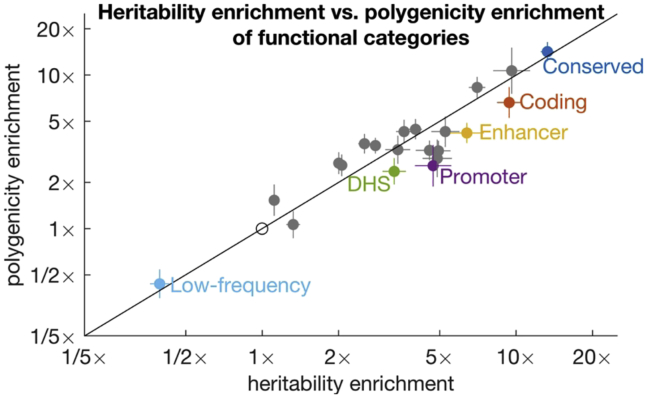
Polygenicity of Functional Categories across 33 Complex Traits

We compared estimates of polygenicity enrichment with estimates of heritability enrichment across 25 main functional categories from the baseline-LD model¹⁹ and meta-analyzed results across well-powered traits for 21 categories with at least 10 well-powered traits (Figure 5, Tables S9 and S10; 49% of trait-annotation pairs were well powered). For most annotations, polygenicity enrichment was approximately equal to heritability enrichment (regression slope = 0.93; r² = 0.88). For example, SNPs in conserved regions were 13× enriched for heritability and 14× enriched for polygenicity, and coding SNPs were 9.4× enriched for heritability and 6.6× enriched for polygenicity. (These functional enrichments for the union of common and low-frequency SNPs are larger than the corresponding enrichments for common SNPs, due to larger functional enrichment for low-frequency SNPs.²⁰) Thus, heritability enrichment in functional categories is predominantly driven by differences in polygenicity, rather than differences in effect-size magnitude. In particular, h²/M_e (i.e., the average unit of heritability) is constant across functional annotations, and the upper effect-size bound imposed by negative selection (Figure 1A) is approximately constant across annotations. In contrast, de novo mutations are expected to have much larger effect sizes in functionally important regions.⁴⁴ Thus, genetic signals of important functional regions are constrained by negative selection (Figure 1).

Figure 5.

Estimates of Polygenicity Enrichment and Heritability Enrichment of Functional Categories

We report estimates for 20 functional categories plus low-frequency SNPs. Estimates are meta-analyzed across well-powered traits. Error bars denote 95% confidence intervals. Complete results for each trait are reported in Table S9 and meta-analyzed results are reported in Table S10.

We compared functional enrichment between groups of related traits (8 brain-related, 6 blood-related, and 5 immune-related traits; Figure S8). Brain-related traits had smaller functional enrichments both for heritability and for polygenicity, consistent with previous findings.^{19, 20, 31} Smaller functional enrichment could be explained by stronger negative selection for these traits, which may strongly limit the enrichment of any functional category.²⁰ Stronger negative selection would also be consistent with greater genome-wide polygenicity for these traits (Table 1).

To investigate the relationship between functional enrichment and genome-wide polygenicity, we quantified the kurtosis explained by functional annotations (where kurtosis κ is inversely proportional to M_e; Equation 1). The proportion of kurtosis explained by functional annotations from the baseline-LD model ranged between 7% and 42% on the logarithmic scale (Figure S9A). Traits with smaller M_e (larger kurtosis) had larger kurtosis explained (r² = 0.78; Figure S9B).

GWAS Signals of Biologically Important Genes Are Constrained by Negative Selection

Flattening may lead to increased polygenicity not only at the level of SNPs, but also at the level of genes: as a consequence of negative selection, heritability is spread more evenly across genes, in comparison with the effect-size distribution of de novo mutations. GWAS effect sizes may be similar for SNPs near genes with small effects and for SNPs near genes with critical effects, and top GWAS SNPs may often implicate small-effect genes (Figure 1).

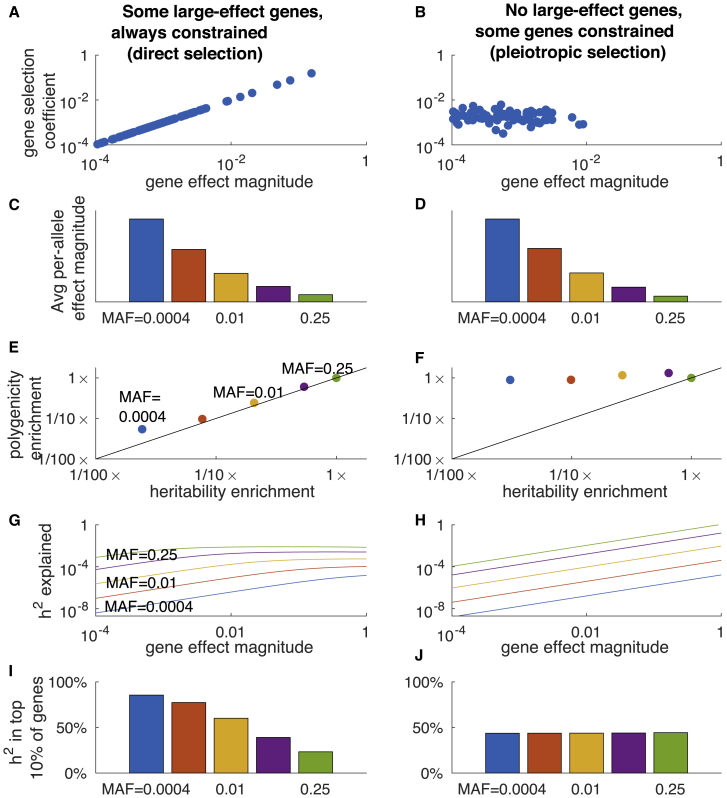
In order to investigate the impact of flattening on the distribution of heritability across genes, we explored two evolutionary fitness models: a model with both gene-level and SNP-level flattening, and a model with neither gene-level nor SNP-level flattening that is potentially realistic in other respects. Although these specific models depend on many unknown parameters, they provide examples of qualitative phenomena: the first model illustrates that flattening at the level of SNPs may result from flattening at the level of genes, and the second model illustrates that it is possible for negative selection to cause common variants and rare variants to have different average effect sizes but the same level of polygenicity (as in the model of Zeng et al.¹²). Under both models, SNPs affect genes and genes affect the trait. Each gene has a trait effect size and a selection coefficient. In the first model (Figure 6A and Table S11), 5% of genes had large effect sizes (10× larger than small-effect genes), and these genes are always strongly constrained. We refer to this model as the “direct selection” model because it could arise from direct selecting acting on the trait (but see below). In the second model (Figure 6B and Table S11), there are no large-effect genes and different genes have different levels of constraint. We refer to this model as the “pleiotropic selection” model. We did not consider a pleiotropic model with unconstrained large-effect genes, which would lead to an unrealistic non-polygenic architecture. Further details of the two models are provided in the Material and Methods.

Figure 6.

Gene-Level Flattening under an Evolutionary Model

In the left column (A, C, E, G, I), there are some large-effect genes, but direct stabilizing selection acting on the phenotype strongly constrains these genes. In the right column (B, D, F, H, J), there are no large-effect genes; pleiotropic stabilizing selection has varying effects on each gene, limiting common-SNP effect sizes on average.

(A and B) Joint distribution of gene effect size magnitudes and selection coefficients.

(C and D) Average squared per-allele effect sizes at different allele frequencies. The strength of selection was chosen to produce similar common-variant effect sizes in both columns.

(E and F) Heritability and polygenicity enrichment at different allele frequencies (relative to MAF = 0.25). Polygenicity at MAF = 0.25 is approximately equal for the two columns, due to the different distributions of gene effect sizes.

(G and H) Expected heritability explained by a single gene as a function of its effect size, for SNPs at different frequencies. In (G), the selection coefficient is proportional to the effect size. In (H), the selection coefficient is held constant.

(I and J) Proportion of heritability explained by the top 10% of largest-effect genes for SNPs at different allele frequencies. Numerical results are reported in Table S11.

We analytically inferred the genetic architecture that arises under each model (see Material and Methods). Under both models, common variants have smaller per-allele effect sizes than low-frequency variants (Figures 6C and 6D), concordant with real traits;^{12, 19, 21} moreover, both models produced a highly polygenic common-variant architecture (Table S11). However, polygenicity differed for the two models at lower allele frequencies (Figures 6E and 6F). SNP-level flattening (i.e., lower polygenicity at lower allele frequencies) was only observed under the direct selection model; polygenicity was ∼30× lower for de novo SNPs than for common SNPs (vs. ∼1.1× under the pleiotropic selection model). Similar our results on real traits (Figure 4), low-frequency polygenicity was ∼4× smaller, and low-frequency heritability was also ∼4× smaller (Figure 6E). Thus, a ∼4× difference between common and low-frequency polygenicity is consistent with a much greater difference between common and de novo polygenicity (moreover, see below).

The concordance between low-frequency polygenicity enrichment and heritability enrichment is expected: the selection coefficient of a SNP scales with its squared per-allele effect size, and as a result, the bound on per-SNP heritability is approximately a constant function of allele frequency. Most heritability is explained by SNPs with effect sizes near the bound, so h²/M_e is similar for common and low-frequency SNPs. However, in units of per-allele effect size, the bound is higher for low-frequency SNPs (Figure 1), so fewer variants approach the bound, leading to lower heritability and proportionally lower polygenicity. At allele frequencies smaller than 0.002, very few SNPs have effect sizes near the bound, so the heritability is predominantly explained by SNPs with effect sizes well below the bound, and h²/M_e decreases (Figure 6E).

For a real trait, the difference in polygenicity between common and de novo SNPs could be much larger than the ∼30× difference we observed under the direct-selection model. For example, when we added a few genes (0.25%) with extremely large effect sizes (100× larger than small-effect genes), the difference was ∼600×, while the difference between common and low-frequency SNPs was still ∼4× (Table S11). The difference in polygenicity between common and de novo SNPs could also be slightly smaller than ∼30× if the distribution of gene effect sizes is abruptly truncated, i.e., if there are no genes with effect sizes larger than the genes that explain most of the heritability of low-frequency SNPs. However, we observed that low-frequency SNPs have roughly equal heritability and polygenicity enrichment (Figure 4B). This concordance implies that at decreasing minor allele frequency, per-SNP heritability and polygenicity follow a linear relationship at allele frequencies greater than ∼0.005, similar to Figure 6E. While this trend is expected to plateau eventually, it is unlikely to plateau extremely abruptly, suggesting that the polygenicity of new mutations is even smaller than the polygenicity of variants at allele frequency ∼0.005, and much smaller than the polygenicity of low-frequency SNPs overall. Thus, we expect that the difference between the polygenicity of common and de novo SNPs is greater than one order of magnitude for most complex traits; complex traits would be far less polygenic if not for the influence of negative selection.

We caution that the difference between common vs. low-frequency polygenicity (and heritability) may be a poor proxy for the difference between common vs. de novo polygenicity when selection is sufficiently strong. When we increased the strength of selection in the direct selection model, we observed that the effects of flattening saturated at lower allele frequencies: despite stronger selection, the difference between common and low-frequency polygenicity decreased to ∼2×, owing to ∼2.5× increased polygenicity for low-frequency SNPs. In contrast, the difference between common and de novo polygenicity increased slightly to ∼40× (Table S11). Thus, the strength of selection affects both the total amount of flattening and the range of allele frequencies over which differential polygenicity is observed. This effect may explain why number of children, though extremely polygenic (perhaps due to particularly strong selection), has a small difference in polygenicity between common and low-frequency SNPs (Figure 4).

We analytically computed the heritability explained by a gene (gene-heritability) as a function of its effect size, for SNPs at different allele frequencies. Under the direct selection model, common variant gene-heritability was approximately constant as a function of gene effect size (except for genes with near-zero effect), illustrating that flattening can act at the level of genes (Figure 6G); the effect was weaker for rare SNPs. Under the pleiotropic selection model (which has no SNP-level flattening), there was also no gene-level flattening (Figure 6H). We computed the proportion of heritability explained by the top 10% of genes (ranked by effect size), at different MAF strata. This proportion was strongly frequency dependent under the direct selection model, but not under the pleiotropic selection model (Figures 6I–6J).

These results suggest that large-effect disease genes are always constrained, and that one way that this constraint could arise is direct selection acting on the disease itself. However, some forms of pleiotropic selection may produce similar effects as direct selection; for example, in the case of schizophrenia, pleiotropic selection on neurodevelopment broadly may mimic the effects of direct selection on schizophrenia specifically. Therefore, our results do not imply that direct selection is more important than pleiotropic selection and do not contradict models of selection that are primarily pleiotropic.^{24, 28}

If flattening occurs at the level of genes, then polygenicity should be increased near strongly constrained genes. We estimated the heritability and polygenicity of SNPs within 50 kb of 2,990 loss of function-intolerant genes from ExAC (“ExAC genic SNPs”).^{45, 46} These SNPs were more strongly enriched for polygenicity (∼2.9×) than for heritability (∼1.7×) (Table S12). Compared with all genic SNPs (±50 kb), ExAC genic SNPs had 1.9× (95% CI: 1.7–2.0×) larger polygenicity enrichment but only 1.3× (95% CI: 1.3–1.4×) larger heritability enrichment, implying 0.71× (95% CI: 0.66–0.76×) $\text{smaller}\text{average}\text{effect}\text{sizes}$ (Table S12). These estimates suggest that ExAC genes are more likely to be causal but also are more strongly constrained relative to their effect sizes when mutated. Moreover, they confirm that negative selection at the level of genes affects polygenicity at the level of SNPs.

If the GWAS signal of critical disease genes is constrained, then top GWAS loci should include a mixture of weak perturbations to critical, strongly constrained disease genes (like a “canary in a coal mine”⁴⁷) and strong perturbations to less critical, weakly constrained genes. In particular, common coding variants—usually representing strong perturbations—are more likely to harbor top associations for any gene, leading to increased polygenicity among coding variants (Figure 4); therefore, they may be less likely to implicate critical, strongly constrained disease genes. We tested this prediction for 37 fine-mapped IBD GWAS loci,⁴⁸ comparing the probability of loss-of-function intolerance (pLI)⁴⁵ between genes harboring coding or noncoding causal risk SNPs. Indeed, 0/8 candidate genes containing fine-mapped coding variants had high pLI (≥0.9), compared to 12/29 candidate genes near fine-mapped noncoding variants (rank-sum test p = 0.006 for difference; Figure S10 and Table S13). Although pLI is different from gene effect size, this difference suggests that critical disease genes can be detected by prioritizing SNPs with subtle, context-dependent regulatory effects on their target gene^{49, 50} over SNPs with overt coding effects.⁵¹

Discussion

Our flattening hypothesis makes directly testable predictions about complex trait polygenicity. Using a new mathematical definition of polygenicity, we compared the polygenicity of 33 complex traits across allele frequencies and functional categories. We determined that low-frequency variants have lower polygenicity than common variants and that biologically important functional categories have higher polygenicity in proportion to their higher heritability, consistent with the flattening hypothesis. Our results demonstrate that negative selection not only constrains common-variant effect sizes on average but flattens their distribution across the genome, explaining the extreme polygenicity of complex traits. The effect-size distribution of new mutations (not yet affected by negative selection) is far less polygenic, probably by orders of magnitude. Thus, the genes and loci with the most critical effects when mutated may not harbor the strongest common-variant associations.

Recent studies^{17, 52} proposed an “omnigenic model” of complex traits: a limited number of “core genes” have direct effects on a trait, but due to densely connected cellular networks, thousands of other “peripheral genes”—perhaps including every gene expressed in a relevant cell type—also contribute to heritability. Our results support the distinction between core and peripheral genes, suggesting that only a limited number of genes have critical phenotypic effects if mutated, and that these genes explain little heritability. (An alternative would be that many genes have direct phenotypic effects,⁵³ e.g., if a common disease is actually the union of multiple phenotypically similar but mechanistically distinct diseases or subtypes.⁵⁴) One might expect that core genes, even if they explain a minority of heritability due to the larger number of peripheral genes, would usually harbor the strongest common-variant associations; however, our results suggest that they may not, due to being strongly constrained by selection.

A key question is how many genes and loci have critical effects, and how this number varies among traits. Our evolutionary modeling indicated that for a trait whose low-frequency polygenicity is 4× smaller than its common-variant polygenicity, its de novo polygenicity may be 30–600× smaller, and the two extremes would have completely different biological implications. A difference of only 30× would imply that more than 100 genes (depending on common-variant polygenicity) have critical effects, possibly spanning many pathways, cell types, and stages of disease progression. On the other hand, a difference of 600× would suggest a much smaller number of critical genes and pathways, with many other genes and pathways having auxiliary effects. In autism, a study of parent-child trios⁵⁵ estimated that a few hundred genes harbor penetrant coding mutations, with considerable uncertainty. Other traits may have completely different de novo effect size distributions; for example, schizophrenia has much weaker total de novo enrichment, and de novo point mutations have unclear penetrance and polygenicity.^{56, 57} This question could be addressed by estimating polygenicity for increasingly rare variants. We only analyzed SNPs at allele frequencies greater than 0.005, due to poor imputation accuracy at lower frequencies. Given well-powered exome-sequencing data, it may be possible to apply S-LD4M to rare coding SNPs, probably aggregating association signals across genes.

Polygenicity has not precluded GWASs from producing biological insights,¹⁰ and our results suggest guidelines to accelerate their progress. First, GWAS follow-up studies should prioritize genes with evidence of constraint, as most critical disease genes are constrained. Loss-of-function variants provide a useful metric of constraint;⁴⁵ for GWASs, a maximally informative constraint metric might incorporate noncoding variation,⁵⁸ gene expression data,⁵⁹ and functional predictions.⁶⁰ Second, counter-intuitively, follow-up studies should prioritize associations that do not map to coding regions or large-effect regulatory elements—instead having weak or context-dependent regulatory effects—since SNPs with strongly deleterious effects on their target gene are less likely to implicate strongly pathogenic genes. As our ability to interrogate the gene-regulatory effects of GWAS SNPs improves,^{60, 61, 62} a potential pitfall would be to prioritize GWAS SNPs with the largest regulatory effects. Third, rare-variant based evidence from exome-sequencing studies, even if underpowered, can be used to prioritize GWAS genes. Indeed, exome-sequencing studies^{63, 64, 65} have been viewed as an attractive complement to GWASs,¹⁷ and our results support this perspective. However, moderately rare coding variants may suffer the same limitations as common regulatory variants.

Finally, this study has several limitations. First, the nonparametric approach that we used to define and estimate polygenicity may not be optimal for every application. A recent study¹³ fit a parametric model involving a mixture of normal distributions; this approach may provide more accurate estimates of missing heritability as a function of sample size, and it may more accurately predict the performance of risk prediction methods that make similar parametric assumptions.³⁶ Second, S-LD4M can produce biased estimates for depleted functional annotations, albeit in unrealistic settings (Figure S1). However, this bias does not affect enriched annotations or low-frequency variants, which are not in strong LD with common variants, and we have avoided reporting polygenicity estimates for depleted functional annotations. Third, S-LD4M produces noisy estimates for some annotations and traits, making it necessary to perform meta-analyses across well-powered traits, which may not be representative of all traits. Comparisons of heritability enrichment and polygenicity enrichment are not biased by this filtering process, as the same traits are used to estimate both types of enrichment. Fourth, S-LD4M can potentially be biased due to population stratification, and it should be applied only to data sets where stratification is well controlled. In particular, S-LD4M assumes that any stratification leads to approximately uniform inflation of χ² statistics; this assumption could be violated at loci under positive selection, such as at the LCT locus for height.⁶⁶ However, we have applied S-LD4M only to datasets that were corrected for population stratification (including UK Biobank, a relatively homogenous study). Fifth, although our evolutionary modeling supports the hypothesis that flattening affects the distribution of heritability across genes, an alternative is that SNP-level flattening results from increased allelic heterogeneity for common variants near large-effect genes. However, this explanation would require that there be many independent associations per gene. Despite evidence of allelic heterogeneity, it is not a common phenomenon that multiple independent, similarly strong associations implicate the same gene.³⁰ Sixth, we have not analyzed any rare diseases, which may differ from complex traits both in their biological complexity and in their relationship with fitness; our findings do not have implications for their genetic architectures.⁶⁷ Seventh, inferences about components of heritability can potentially be biased by failure to account for LD-dependent architectures.^{6, 19, 68, 69} All of our primary analyses used the baseline-LD model, which includes six LD-related annotations.¹⁹ The baseline-LD model is supported by formal model comparisons using likelihood and polygenic prediction methods, as well as analyses using a combined model incorporating alternative approaches.⁷¹ There can be no guarantee that the baseline-LD model perfectly captures LD-dependent architectures; however, our estimates of M_e were similar with or without including annotations from the baseline-LD model (Table S5), suggesting that our estimates are unlikely to be affected by imperfect modeling of LD-dependent architectures. Despite these limitations, this study advances our understanding of genetic architecture and the evolutionary processes that shape it.

Declaration of Interests

The authors declare no competing interests.

Published: August 8, 2019

Appendix A

The Effective Number of Independently Associated SNPs

Here, we provide three definitions of the effective number of independent causal SNPs (M_e). First, we define M_e in terms of the mixed fourth moments of the distribution of causal and marginal effect sizes. This generalizes the definition in Equation 1, which corresponds to the special case of no LD between causal SNPs. Second, we provide an alternative definition (under a random effects model) that formalizes the illustration in Figure 2A, involving the average unit of heritability explained by a causal SNP (see Material and Methods). Third, we provide a concise definition that provides less intuition. We show that these definitions are equivalent below (see Equivalence of Me Definitions).

First, let $\mathit{\beta }$ denote the random vector of causal effect sizes for common and low-frequency SNPs. Let R be the fixed LD matrix, and let $\mathit{\alpha }=R\mathit{\beta }$ denote the random vector of marginal effect sizes. We use the notation $\alpha ,\beta$ to denote randomly chosen entries of $\mathit{\alpha },\mathit{\beta }$. The heritability is $h^2=\text{E}\left({\mathit{\beta }}^{T}R\mathit{\beta }\right)=M\text{E}\left(\alpha \beta \right).$M_e is defined as:

$$\begin{array}{c}{M}_e=\frac{3M}{{\kappa }_e},{\kappa }_e=\frac{3\text{E}\left({\alpha }^2{\beta }^2\right)-2\text{E}\left({\beta }^4\right)}{\text{E}{\left(\alpha \beta \right)}^2}.\end{array}$$ (Equation A1)

Another possible definition of polygenicity is the effective number of causal SNPs, denoted M_e′:

$$\begin{array}{c}\begin{array}{c}{M}_e^{\text{'}}=\frac{3M}{{\kappa }_e\text{'}},{\kappa }_e^{\text{'}}=\frac{\text{E}\left({\beta }^4\right)}{\text{E}{\left({\beta }^2\right)}^2}.\end{array}\end{array}$$ (Equation A2)

The difference between M_e and M_e′ is analogous to the difference between the heritability $\text{E}\left({\mathit{\beta }}^{T}R\mathit{\beta }\right)$ and an alternative definition of heritability that does not account for LD between variants, $\text{E}\left({\mathit{\beta }}^T\mathit{\beta }\right)$. In the presence of perfect LD, M_e′ and $E\left({\mathit{\beta }}^T\mathit{\beta }\right)$ are unidentifiable without making a strong assumption (roughly, that linked SNPs have independent causal effect sizes; see below). The two definitions of polygenicity are equivalent in the special case of no LD between causal SNPs (because $\alpha =\beta$ whenever $\beta \ne 0$), as in Equation 1. M_e′ is different from the total number of causal SNPs, except when causal effect sizes follow a point-normal distribution. Because it is unlikely that causal effect sizes follow a normal distribution, we view the distinction between M_e and M_t as having greater importance than the distinction between M_e and M_e′.

Second, we consider a non-i.i.d. normal model:

$$\begin{array}{c}\beta \sim N\left(0,\Sigma \right)\end{array}$$ (Equation A3)

where $\Sigma$ is a diagonal matrix with diagonal entries ${\sigma }_1^2,\dots ,{\sigma }_M^2$. This flexible model generalizes the point-normal model. $h^2$ is equal to $\text{Tr}\left(\Sigma \right)$. Note that if $\Sigma \propto I$, then ${\kappa }_e^{\text{'}}$ is equal to 3 and M_e′ is equal to M. Above, we used the notation $\text{E}(.)$ to denote a uniform average across SNPs. We use the notation ${\text{E}}_{h^2}(.)$ to denote an average across components of heritability, i.e., a weighted average where the probability of choosing SNP i is equal to ${\sigma }_i^2/h^2$. Using this notation, we refer to ${\text{E}}_{h^2}\left({\alpha }^2\right)$ as the average unit of heritability, and M_e is equal to:

$$\begin{array}{c}{M}_e=\frac{h^2}{{\text{E}}_{h^2}\left({\alpha }^2\right)}.\end{array}$$ (Equation A4)

M_e′ can be defined in a similar manner:

$$\begin{array}{c}{M}_e^{\text{'}}=\frac{h^2}{{\text{E}}_{h^2}\left({\beta }^2\right)}.\end{array}$$ (Equation A5)

Third, M_e can also be defined without specifying that $\Sigma$ is a diagonal matrix. (The assumption that $\Sigma$ is diagonal is similar to the common assumption that $\text{E}\left({\mathit{\beta }}^{T}R\mathit{\beta }\right)=\text{E}\left({\mathit{\beta }}^T\mathit{\beta }\right)$.², ³¹) Let $S={\Sigma }^{1/2}R{\Sigma }^{1/2}$. In the diagonal case, $\text{S}$ is a weighted LD matrix, where the rows and columns are weighted by the expected effect size of each SNP. The heritability is equal to Tr(S) (in the diagonal case, $\text{Tr}\left(S\right)=\text{Tr}\left(\Sigma \right)$). M_e is equal to:

$$\begin{array}{c}{M}_e=\frac{\text{Tr}{\left(S\right)}^2}{\text{Tr}\left(S^2\right)}.\end{array}$$ (Equation A6)

This definition, though concise and natural, provides little intuition.

Properties of M_e

M_e has notable mathematical properties.

• •Identifiability. If there are two SNPs in perfect LD, there is no way to tell based on GWAS data whether one or both of them are causal. If a definition of polygenicity differs depending on whether one or both are causal, then it is unidentifiable. Indeed, M_e′ is larger if both SNPs are causal than if only one SNP is causal. However, because both SNPs have identical values of $E\left({\alpha }^2\right)$, the value of $E_{h^2}\left({\alpha }^2\right)$ (and therefore M_e$)$ is unaffected.
• •Missing Heritability. M_e gives an upper bound on the proportion of heritability explained by SNPs whose effect sizes exceed a specified threshold T, such as the genome-wide significance threshold. This proportion can be denoted $P_{h^2}\left({\alpha }^2>T\right)$. Because ${\alpha }^2$ is nonnegative,

$$\begin{array}{c}{\text{P}}_{h^2}\left({\alpha }^2>T\right)\le \frac{{\text{E}}_{h^2}\left({\alpha }^2\right)}{T}.\end{array}$$ (Equation A7)

This bound is relatively tight when $T\gg {\text{E}}_{h^2}\left({\alpha }^2\right)$. When T is a significance threshold (for example, $T=\left(30/N\right)$ corresponds to genome-wide significance), this bound is most relevant at low sample size.

• •Polygenic Prediction Accuracy. Intuitively, increased polygenicity makes prediction more difficult. If $\Sigma$ is given, there is a simple expression for the optimal risk prediction accuracy; this expression provides an upper bound on prediction accuracy in the case that Σ is not given:

$$\begin{array}{c}E\left(r^2\right)=h^2{\text{E}}_{h^2}\left(\frac{{\alpha }^2}{{\alpha }^2+\frac{1}{N}}\right).\end{array}$$ (Equation A8)

(see Polygenic Prediction Accuracy below for derivation). At large N, prediction accuracy converges to h². At small N, it is approximately a linear function of sample size with slope inversely proportional to M_e:

$$\begin{array}{c}E\left(r^2\right)\approx N{h}^2{\text{E}}_{h^2}\left({\alpha }^2\right)=N{h}^4/M_e.\end{array}$$ (Equation A9)

In practice, polygenic prediction is usually performed using large datasets for which this approximation is not appropriate.

• •Effective Number of Independent SNPs. Under an infinitesimal model, where every SNP is causal with a normally distributed causal effect size, M_e is equal to the effective number of independent SNPs³² (M_indep). M_indep is defined as the number of SNPs divided by the average LD score, or in notation similar to Equation A6, as

$$\begin{array}{c}{M}_{\mathit{indep}}=\frac{\text{Tr}{\left(R\right)}^2}{\text{Tr}\left(R^2\right)}.\end{array}$$ (Equation A10)

We note that M_e might be close to M_indep even when M_e′ is much smaller than M. For example, if the genome comprises perfect LD blocks of 100 SNPs each, then M_e can be equal to M_indep even if only 1 SNP per LD block is causal. We also note that the value of M_indep is strongly dependent on the range of allele frequencies that is specified, as rare SNPs (which have less LD) contribute strongly to M_indep. In contrast, M_e will not diverge if many rare SNPs are included, as these SNPs explain little heritability.

• •Symmetry. M_e is symmetric with respect to the two fixed parameters in the random effects model, R and Σ: M_e(R, Σ) = M_e(Σ,R). This property is shared by the LD-dependent definition of heritability, $\text{E}\left({\mathit{\beta }}^{T}R\mathit{\beta }\right)=\text{Tr}\left(\text{R}\Sigma \right)=\text{Tr}\left(\Sigma \text{R}\right)$. It is not shared by M_e′ or by the LD-independent definition of heritability, $E\left({\mathit{\beta }}^T\mathit{\beta }\right)=\text{Tr}\left(\Sigma \right)$.

Stratified LD Fourth Moments Regression

S-LD4M is justified by an approximate regression equation, which states that the expected value of ${\alpha }^4$ for SNP i is approximately proportional to the LD fourth moment of SNP i, with a proportionality constant that can be used to estimate M_e.

Let ${\ell }^{\left(2\right)},{\ell }^{\left(4\right)}$ denote the LD second moment (LD score⁵) and LD fourth moment, respectively, for a randomly chosen SNP:

$$\begin{array}{c}{\ell }_i^{\left(p\right)}=\sum _j{r}_{ij}^p\end{array}$$ (Equation A11)

The regression equation is:

$$\begin{array}{c}E\left({\alpha }^4|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)\approx 3E{\left({\alpha }^2|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)}^2+{\ell }^{\left(4\right)}K.\end{array}$$ (Equation A12)

In the first term, $\text{E}\left({\alpha }^2|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)={\ell }^{\left(2\right)}\tau$, where the coefficient $\tau$ is the variance of causal effect sizes.⁵, ³¹ In the second term, K is related to M_e:

$$\begin{array}{c}K=3\text{E}\left({\beta }^2\right)\left[{\text{E}}_{h^2}\left({\alpha }^2\right)-E\left({\alpha }^2\right)\right].\end{array}$$ (Equation A13)

Note that there are three kinds of expectations in Equations A12 and A13. First, $\text{E}\left({\alpha }^2|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)$ and $\text{E}\left({\alpha }^4|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)$ are conditioned on LD. Second, $E\left({\alpha }^2\right)$ and $E\left({\beta }^2\right)$ are not conditioned on LD; rather, they represent unweighted averages over all reference SNPs. Third, ${\text{E}}_{{\text{h}}^2}\left(a^2\right)$ is the average across components of heritability (not uniformly across SNPs).

In the case that there are $\text{P}$ functional annotations, ${\ell }_{\text{i}}^{\left(4\right)}$ and K are vectors of size 1 × P and P × 1, respectively (see below). Similar to S-LDSC, we make an additivity assumption for the fourth moments of SNPs in the intersection of annotations. Our simulations violate this assumption, but it does not appear to result in bias.

This regression equation relies on an LD approximation. Roughly, the LD approximation states that if SNP i is in LD with causal SNP j, then the expected marginal effect size of SNP i is proportional to the marginal effect size of SNP j. This approximation is exact in important special cases, suggesting that it will be robust in practice. First, we consider the stronger assumption that would be needed to estimate M_e′, which is roughly that linked SNPs have independent causal effect sizes. More precisely, we would need to assume that the contribution of causal SNP j to the marginal effect size of SNP i, not conditional on other SNPs, is proportional to the causal effect size of SNP j:

$$\begin{array}{c}cov\left({\alpha }_i^2,{\beta }_j^2\right)\approx r_{ij}^{2}var\left({\beta }_j^2\right).\end{array}$$ (Equation A14)

Note that the expectations are not conditioned on other SNPs; if causal SNPs tend to cluster together, then the approximation will be poor, because the presence of causal SNP j would suggest additional nearby causal SNPs, inflating the left side but not the right side. We weaken Equation A14 to obtain our LD approximation:

$$\begin{array}{c}cov\left({\alpha }_i^2,{\beta }_j^2\right)\approx r_{ij}^{2}cov\left({\alpha }_j^2,{\beta }_j^2\right).\end{array}$$ (Equation A15)

Now, we are assuming that the contribution of causal SNP j to the marginal effect size of SNP i is proportional to the marginal effect size of SNP j. Note that Equation A14 implies Equation A15 by applying Equation A14 to the case $i=j$. We show that Equation A15 implies Equation A12 below (Derivation of Regression Equation). Equation A15 is not violated when other causal SNPs k are in strong LD with SNP j $\left(r_{jk}^2\approx 1\right)$, since they would contribute to ${\alpha }_i^2$ in proportion to their contribution to ${\alpha }_j^2$ (because $r_{ik}^2\approx r_{ij}^2{r}_{jk}^2$). However, it could be violated if there were other causal SNPs in weak LD with SNPs i and j (violating $r_{ik}^2\approx r_{ij}^2{r}_{jk}^2$). Thus, Equation A15 is exact both in the case that there is no clustering of causal SNPs and in the case that there is very tight clustering; this type of approximation is expected to be robust in intermediate cases as well, and our simulations support this intuition (Figure S2).

Equations A14 and A15 have second-moment analogues that can be used to justify LD score regression.⁵, ³¹ LDSC has been justified by assuming that correlated SNPs have uncorrelated effect sizes; this assumption can be stated as:

$$\begin{array}{c}E\left({\alpha }_i{\beta }_j\right)=r_{ij}E\left({\beta }_j^2\right),\end{array}$$ (Equation A16)

which is analogous to Equation A14. This assumption allows LDSC to estimate a non-LD-dependent definition of heritability, $ME\left({\beta }^2\right)$. However, a weaker assumption is also possible, analogous to Equation A15:

$$\begin{array}{c}E\left({\alpha }_i{\beta }_j\right)\approx r_{ij}E\left({\alpha }_j{\beta }_j\right).\end{array}$$ (Equation A17)

This weaker assumption still holds when positively correlated SNPs tend to have positively (or negatively) correlated causal effect sizes. It allows LDSC to estimate $\text{E}\left(\alpha \beta \right)$, which is proportional to ${\mathit{\beta }}^{T}R\mathit{\beta }$, as follows:

$$\begin{array}{c}E\left({\alpha }_i^2\right)=\sum _j{r}_{ij}\text{E}\left({\alpha }_i{\beta }_j\right)\approx \sum _j{r}_{ij}^2\text{E}\left({\alpha }_j{\beta }_j\right)={\ell }_i^{\left(2\right)}E\left(\alpha \beta \right).\end{array}$$ (Equation A18)

Thus, although LDSC has previously been justified using the assumption that correlated SNPs have uncorrelated effect sizes, only this weaker assumption is strictly necessary in order to estimate the LD-dependent definition of heritability.

Equation A12 relates $E\left({\alpha }^4\right)$ with M_e. However, in practice, we do not observe $\alpha$, but rather a noisy estimate $\hat{\alpha }$. We can correct for sampling noise using:

$$\begin{array}{c}E\left({\hat{\alpha }}^2|\alpha \right)={\alpha }^2+\frac{1}{N},E\left({\hat{\alpha }}^4|\alpha \right)={\alpha }^4+6{\alpha }^2/N+3/N^2,\end{array}$$ (Equation A19)

where in practice we use the LD score regression intercept divided by N, denoted $1/\hat{N}$, instead of $1/N$. We caution that this equation assumes that sampling error follows a normal distribution, which may be false for rare SNPs. In the presence of population stratification, it may approximately hold if stratification is relatively even across the genome, but it would be violated if some regions of the genome have been under population-specific positive selection.

We perform a two-step inference procedure. First, we use a slightly modified version of S-LDSC³¹ (see below) to estimate $E\left({\alpha }_i^2\right)$ and $E\left({\beta }_i^2\right)$ for each SNP, conditional on their respective LD scores and annotation values. Second, we regress the $M\times 1$ vector

$$\begin{array}{c}{\hat{\mathit{\alpha }}}^4-\frac{6{\hat{\mathit{\alpha }}}^2}{N}+\frac{3}{N^2}-3{\left({\ell }^{\left(2\right)}\tau \right)}^2,\end{array}$$ (Equation A20)

whose expectation is ${\mathit{\alpha }}^4-3E{\left({\mathit{\alpha }}^2|{\ell }^{\left(2\right)}\right)}^2$, on the $M\times P$ matrix ${\mathit{l}}^{\left(4\right)}$ to obtain an estimate of the $1\times P$ vector K. (${\mathit{x}}^k$ denotes element-wise exponentiation.) The regression is weighted: the weight of SNP i is 1 divided by the LD fourth moment of SNP i (to all common and low-frequency SNPs). This choice prevents over-counting of high-LD regions (see below). For each annotation $A_p$, we add 3$E\left(E\left({\alpha }^2\right)E\left({\beta }^2\right)|A_p\right)$ to $K_p$ and estimate M_e for each category.

Our modified version of S-LDSC uses a slightly modified weighting scheme and does not exclude large-effect SNPs. The regression weight of each SNP is 1 divided by the LD score for that SNP to all common and low-frequency SNPs; this choice is similar to the original version of S-LDSC,³¹ but slightly modified for consistency with the weights used in S-LD4M. We do not exclude large-effect SNPs because these SNPs are important for estimating fourth moments; their exclusion would lead to upwardly biased estimates of M_e.

Equivalence of M_e Definitions

M_e can be defined in three equivalent ways. First, it can be defined in terms of fourth moments of the effect size distribution:

$$\begin{array}{c}{M}_e=\frac{3M}{{\kappa }_e},{\kappa }_e=\frac{3E\left({\alpha }^2{\beta }^2\right)-2E\left({\beta }^4\right)}{E{\left(\alpha \beta \right)}^2}.\end{array}$$ (Equation A21)

Second, it can be defined in terms of the average unit of heritability. Suppose that $\beta \sim N\left(0,\Sigma \right),$ where Ʃ is a diagonal matrix with entries ${\sigma }_1^2,\mathrm{...},{\sigma }_M^2$. The average unit of heritability is defined as:

$$\begin{array}{c}{E}_{h^2}\left({\alpha }^2\right)=\frac{1}{h^2}\sum _i{\sigma }_i^{2}E\left({\alpha }_i^2|R,\Sigma \right).\end{array}$$ (Equation A22)

$E_{h^2}\left({\alpha }^2\right)$ is proportional to ${\kappa }_e:$

$$3E\left({\alpha }^2{\beta }^2\right)=\frac{3}{M}\sum _{i}E\left({\beta }_i^2{\alpha }_i^2|\Sigma \right)=\frac{3}{M}\sum _{i,j}{r}_{ij}^{2}E\left({\beta }_i^2{\beta }_j^2|\Sigma \right)=\frac{3}{M}\sum _i\left[E\left({\beta }_i^4|\Sigma \right)+\sum _{j\ne i}{r}_{ij}^{2}E\left({\beta }_i^2\Sigma \right)E\left({\beta }_j^2|\Sigma \right)\right]$$

$$=\frac{3}{M}\sum _i\left[2{\sigma }_i^4+\sum _{i,j}{r}_{ij}^2{\sigma }_i^2{\sigma }_j^2\right]$$

$$\begin{array}{c}=2E\left({\beta }^4\right)+\frac{3}{M}\sum _i{\sigma }_i^{2}E\left({\alpha }_i^2|\text{Ó}\right),\end{array}$$ (Equation A23)

where we have used the fact that $E\left({\beta }_i^4|\Sigma \right)=3{\sigma }_i^4$. Rearranging,

$${\kappa }_e=\frac{3E\left({\alpha }^2{\beta }^2\right)-2E\left({\beta }^4\right)}{E{\left(\alpha \beta \right)}^2}=\frac{3}{M}\sum _i{\sigma }_i^{2}E\left({\alpha }_i^2|\Sigma \right)E{\left(\alpha \beta \right)}^2=\frac{3}{E\left(\alpha \beta \right)}{E}_{h^2}\left({\alpha }^2\right).$$ (Equation A24)

Substituting $h^2=ME\left(\alpha \beta \right),$ we have a second definition of M_e:

$$\begin{array}{c}{M}_e=h^2{E}_{h^2}\left({\alpha }^2\right).\end{array}$$ (Equation A25)

Third, define $S={\Sigma }^{1/2}R{\Sigma }^{1/2}$. Then:

$$Tr\left(S^2\right)=\sum _{i,j}{r}_{ij}^2{\sigma }_i^2{\sigma }_j^2=\sum _i{\sigma }_i^2\sum _j{r}_{ij}^2{\sigma }_j^2$$

$$\begin{array}{c}=h^2{E}_{h^2}\left({\alpha }^2\right).\end{array}$$ (Equation A26)

Thus, we obtain another equivalent definition:

$$\begin{array}{c}{M}_e=\frac{Tr{\left(S\right)}^2}{Tr\left(S^2\right)},\end{array}$$ (Equation A27)

where $Tr\left(S\right)=h^2$. This definition is slightly more general than Equation A25, since it does not require that Σ is a diagonal matrix. (Note that in the diagonal case, $Tr\left(S\right)=Tr\left(\Sigma \right)$; more generally, these definitions are different, corresponding to the difference between $E\left({\beta }^2\right)$ and $E\left(\alpha \beta \right)$.)

Polygenic Prediction Accuracy

If Σ is given, then it is clear what the optimal risk prediction scheme is. Given an estimate $\hat{\mathit{\alpha }}$ of the marginal effect-size vector $\mathit{\alpha }$, the expected phenotypic value of an individual with genotype $X$ is:

$$\begin{array}{c}E\left(X\mathit{\beta }|\hat{\mathit{\alpha }},\mathrm{\Sigma },X\right)=XE\left(\mathit{\beta }|\hat{\mathit{\alpha }},\mathrm{\Sigma }\right).\end{array}$$ (Equation A28)

The expected prediction $r^2$ is:

$$r^2=E\left(\left(X\mathit{\beta }\right)\left(XE\left(\mathit{\beta }|\hat{\mathit{\alpha }},\Sigma \right)\right)|\Sigma \right)$$

$$=E\left({\mathit{\beta }}^{T}RE\left(\mathit{\beta }|\hat{\mathit{\alpha }},\Sigma \right)\right)$$

$$\begin{array}{c}=E\left({\mathit{\beta }}^{T}E\left(\mathit{\alpha }|\hat{\mathit{\alpha }},\Sigma \right)\right).\end{array}$$ (Equation A29)

Conveniently, we have eliminated $E\left(\mathit{\beta }|\cdot \right)$ from the expression, so the optimal risk prediction accuracy does not depend on $R^{-1}$ (although the optimal risk predictor may). Now, $\hat{\mathit{\alpha }}\sim N\left(\mathit{\alpha },\left(1/N\right)R\right)$, so:

$$\begin{array}{c}E\left(\mathit{\alpha }|\hat{\mathit{\alpha }},\Sigma \right)=\frac{\hat{\mathit{\alpha }}E\left({\mathit{\alpha }}^2|\Sigma \right)}{\frac{1}{N}+E\left({\mathit{\alpha }}^2|\Sigma \right)}.\end{array}$$ (Equation A30)

Taking an expectation over SNPs,

$$r^2=ME\left(\alpha \beta \frac{E\left({\alpha }^2|\Sigma \right)}{\frac{1}{N}+E\left({\alpha }^2|\Sigma \right)}|\Sigma \right)$$

$$\begin{array}{c}=h^2{E}_{h^2}\left(\frac{{\alpha }^2}{\frac{1}{N}+{\alpha }^2}\right).\end{array}$$ (Equation 31)

When $N$ is large, $r^2$ converges to $h^2$; when $N$ is small, $r^2$ is approximately $N{h}^2{E}_{h^2}\left({\alpha }^2\right)=N{h}^4/M_e.$

Derivation of Regression Equation

We assume that:

$$\begin{array}{c}cov\left({\alpha }_i^2,{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\approx r_{ij}^{2}cov\left({\alpha }_j^2,{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\end{array}$$ (Equation A32)

We use this approximation as follows. First, we split up $E\left({\alpha }_i^4\right)$:

$$\begin{array}{c}E\left({\alpha }_i^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)=E\left({\alpha }_i^2\left[\sum _j{r}_{ij}^2{\beta }_j^2+\sum _{k\ne j}{r}_{ik}{r}_{ij}{\beta }_k{\beta }_j\right]|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right).\end{array}$$

Next, we use the fact that

$$E\left({\alpha }_i^2\left[\sum _j{r}_{ij}^2{\beta }_j^2\right]\right)=E\left({\left[\sum _j{r}_{ij}^2{\beta }_j^2\right]}^2\right)$$

and that

$$\begin{array}{c}E\left({\alpha }_i^2\left[\sum _{k\ne j}{r}_{ik}{r}_{ij}{\beta }_k{\beta }_j\right]\right)=E\left(2\sum _{k\ne j}{r}_{ik}^2{r}_{ij}^2{\beta }_k^2{\beta }_j^2\right)\end{array}$$

to obtain:

$$E\left({\alpha }_i^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)=E\left({\left[\sum _j{r}_{ij}^2{\beta }_j^2\right]}^2+2\sum _{j\ne k}{r}_{ij}^2{r}_{ik}^2{\beta }_j^2{\beta }_k^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)$$

$$\begin{array}{c}=3\sum _j{r}_{ij}^2\left[E\left({\alpha }_i^2{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-\frac{2}{3}{r}_{ij}^{2}E\left({\beta }_j^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\right].\end{array}$$ (Equation A33)

Now, we are ready to use Equation A32 to break down $E\left({\alpha }_i^2{\beta }_j^2\right)=cov\left({\alpha }_i^2,{\beta }_j^2\right)+E\left({\alpha }_i^2\right)E\left({\beta }_j^2\right)$:

$$E({\alpha }_i^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}=3\sum _j{r}_{ij}^2\left[cov\left({\alpha }_i^2,{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)+E\left({\alpha }_i^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)E\left({\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-\frac{2}{3}{r}_{ij}^{2}E\left({\beta }_j^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\right]$$

$$\approx 3\sum _{\mathit{j}}{r}_{ij}^2\left[r_{ij}^2(E\left({\alpha }_j^2{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-E\left({\alpha }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)E\left({\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)+E\left({\alpha }_i^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)E\left({\beta }_i^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-\frac{2}{3}{r}_{ij}^{2}E\left({\beta }_j^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\right]$$

$$=3E{\left({\alpha }_i^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)}^2+\sum _j{r}_{ij}^4\left[3E\left({\alpha }_j^2{\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-3E\left({\alpha }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)E\left({\beta }_j^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)-2E\left({\beta }_j^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)\right].$$ (Equation 34)

Similar to LD score regression, we assume that SNPs in LD with regression SNPs (i.e., SNPs j which are in LD with SNP i) are representative of a larger population of SNPs (e.g., all common SNPs), allowing us to replace $E\left({\cdot }_j|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)$ with $E\left({\cdot }_j\right)$:

$$E\left({\alpha }_i^4|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)=3E{\left({\alpha }_i^2|{\ell }_i^{\left(2\right)},{\ell }_i^{\left(4\right)}\right)}^2+\left(3E\left({\alpha }^2{\beta }^2\right)-2E\left({\beta }^4\right)-3E\left({\alpha }^2\right)E\left({\beta }^2\right)\right){\ell }_i^{\left(4\right)}.$$ (Equation A35)

We restate this equation for a randomly chosen SNP (rather than for a particular SNP i):

$$\begin{array}{c}E\left({\alpha }^4|{\ell }^{\left(2\right)},{\ell }^{\left(4\right)}\right)=3E{\left({\alpha }^2|{\ell }^{\left(2\right)}\right)}^2+{\ell }^{\left(4\right)}K,\end{array}$$ (Equation A36)

where

$$\begin{array}{c}K=3E\left({\beta }^2\right)\left[E_{h^2}\left({\alpha }^2\right)-E\left({\alpha }^2\right)\right].\end{array}$$ (Equation A37)

Web Resources

• SLD4M open-source software, https://github.com/lukejoconnor/SLD4M

• UK Biobank summary statistics, https://data.broadinstitute.org/alkesgroup/UKBB/