A simple convolutional neural network for prediction of enhancer–promoter interactions with DNA sequence data

Abstract

Motivation

Enhancer–promoter interactions (EPIs) in the genome play an important role in transcriptional regulation. EPIs can be useful in boosting statistical power and enhancing mechanistic interpretation for disease- or trait-associated genetic variants in genome-wide association studies. Instead of expensive and time-consuming biological experiments, computational prediction of EPIs with DNA sequence and other genomic data is a fast and viable alternative. In particular, deep learning and other machine learning methods have been demonstrated with promising performance.

Results

First, using a published human cell line dataset, we demonstrate that a simple convolutional neural network (CNN) performs as well as, if no better than, a more complicated and state-of-the-art architecture, a hybrid of a CNN and a recurrent neural network. More importantly, in spite of the well-known cell line-specific EPIs (and corresponding gene expression), in contrast to the standard practice of training and predicting for each cell line separately, we propose two transfer learning approaches to training a model using all cell lines to various extents, leading to substantially improved predictive performance.

Availability and implementation

Computer code is available at https://github.com/zzUMN/Combine-CNN-Enhancer-and-Promoters.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Through the three-dimensional structure of chromatin, distal DNA elements, such as enhancers and promoters, can be brought into close proximity and thus in contact/interactions with each other, achieving transcriptional regulation of the linked genes (Krivega and Dean, 2012). Recent biotechnologies, such as Hi-C (Rao et al., 2014), ChIAPET (Li et al., 2012), promoter capture Hi-C (Javierre et al., 2016), have made it feasible to experimentally measure nearby or distal enhancer–promoter interactions (EPIs). Such data have been used to link genome-wide association studies (GWAS) risk loci to their target genes, thus gaining insights into the genetic basis of complex diseases and traits (Dryden et al., 2014). It is now known that GWAS risk loci are enriched in enhancers, implicating their regulatory roles in disease etiology. Importantly, such data can be also used directly to boost statistical power in GWAS to identify risk loci (Wu and Pan, 2018).

As an alternative to experimental approaches to directly measuring EPIs, computational methods based on other genomic or epi-genomic data have been emerged to predict EPIs (Cao et al., 2017; Whalen et al., 2016). Yang et al. (2017) and Singh et al. (2016) further proposed machine learning methods with only DNA sequence data. In particular, given impressive performance of neural networks in image, video and language processing (LeCun et al., 2015) and increasing applications in computational biology (Angermueller et al., 2016; Liang et al., 2018), one would expect possibly promising performance by neural networks. Indeed, Singh et al. (2016) proposed a state-of-the-art neural network architecture called SPEID, a hybrid of a convolutional neural network (CNN) and a recurrent neural network (RNN) and demonstrated its highly competitive performance as compared to other computational methods using many types of epi-genomic data. An intuition of using a combination of a CNN and a RNN is to use the CNN for feature extraction while using the RNN to model sequential dependencies of DNA features. However, even in the domain of natural language processing, in which RNNs are most popular, it has recently been discussed that CNNs might perform as well as, or even better than, RNNs (Bai et al., 2018; Ying et al., 2017). Furthermore, we do not expect a long-range and strong dependency structure for DNA features such as motifs. Finally, due to only moderately large training data for EPIs, we hypothesized that a simpler model might perform as well as a more complex model like SPEID. Accordingly, we propose a much simpler CNN with only one-layer of convolution, one-layer of max-pooling and one-layer of fully-connected (FC) units, respectively, essentially the CNN component of SPEID without the RNN component. We demonstrate its slightly better predictive performance than SPEID. More importantly, in contrast to the current practice of training and testing for each cell line separately, we propose two transfer learning approaches to training a CNN with the data from all cell lines, leading to much improved performance. Although the current practice of training and testing for each cell line separately is well motivated by cell line-specific EPIs, as expected, there are also commonalities among the cell line-specific EPIs: based on their Hi-C data, Rao et al. (2014) reported that between 55% and 75% DNA interactions were shared among the cell lines. Accordingly, to take advantage of the commonalities among the EPIs across the cell lines, we propose training the CNNs using the training data from all cell lines to some extents, giving better predictions (with test data) for each cell line. However, we point out that it would not work with the naive way of simply training a CNN using all the data as if they were all from the same line, giving lower prediction accuracy rates than the current practice of training$/$testing each cell line separately.

2 Materials and methods

2.1 Data

We used the same EPI dataset packaged by Singh et al. (2016), available at $https ://genome.combio.cs.cmu.edu/\sim sss1/SPEID/all\_sequence\_data.h5.$ Each observation in the data contains an enhancer sequence, a promoter sequence and a binary class label indicating the presence or absence of their interaction for each of six cell lines (GM12878, HeLa-S3, IMR90, K562, HUVEC, NHEK); in the presence (or absence) of the interaction between a pair of an enhancer and a promoter, we call it a positive (or negative) pair. For each of the six cell lines, the total number of positive pairs ranges from 1254 (for IMR90) to 2113 (for GM12878) while that of negative pairs ranges from 25 000 (for IMR90) to 42 200 (for GM12878); the ratio of the two class sizes is about 1 to 20 for each cell line. Singh et al. (2016) applied a data augmentation procedure to balance the two classes: by adding some arbitrary subsequences to flank the original DNA sequences of the enhancer or promoter for each positive pair. For example, one can shift the first 20 bps to the end of the original sequence, or move the last 20 bps to the start of the original sequence to generate a new sequence for the enhancer or promoter for any positive pair. By data augmentation, we have an expanded subset of sequences with positive interactions, leading to balanced classes.

To examine the number of overlapping enhancers/promoters with positive EPIs between any two cell lines, we compared the genomic locations of enhancers and promoters in the data. Specifically, for any two cell lines, we first extracted the EPIs on the same chromosome, then compared the locations of enhancers and promoters. If the locations of the two enhancers overlap more than a threshold and the corresponding two promoters also overlap more than the threshold at the same time, we recorded the two EPI pairs overlapping. Table 1 shows the numbers of the overlapping EPIs between any two cell lines; the upper diagonal entries give the numbers with threshold = 100% while the lower diagonal with threshold = 20%. The results for other threshold values are shown in Supplementary Tables S6–S9. Some summary statistics for the percentages of the overlapping EPS between two cell lines with four different threshold values (at 100%, 80%, 50% and 20%) are the following: the maximum ranges from 4.88% to 10.30%, the minimum ranges from 0.88% to 1.67% and the mean ranges from 2.46% to 4.77%. Hence, there appear to be some, but not overwhelming, commonalities of the positive EPIs across the cell lines, which will have some implications to the performance of various training methods as discussed below.

Table 1.

The numbers of overlapping EPIs between any two cell lines with threshold at 100% (or 20%) shown in the upper (or lower) diagonal

Cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
# EPIs	2113	1740	1524	1254	1977	1291
GM12878	$•$	26	28	24	28	19
HeLa-S3	54	$•$	62	15	43	63
HUVEC	71	138	$•$	41	33	51
IMR90	43	28	65	$•$	11	42
K562	68	90	57	31	$•$	33
NHEK	38	133	91	52	70	$•$

2.2 Model structure

The architecture of our proposed CNN is displayed in Figure 1. It contains a single convolution layer and a max-pooling layer for each of the input enhancer and promoter sequences, respectively, followed with a FC layer and finally with a single neuron activated by the sigmoid function to output the probability of a positive interaction. Note that we followed the notation for Inception-v4 (Szegedy et al., 2016). For example, Letter ‘V’ in a max-pooling layer (MaxPool) means no paddings, while no letter in a convolution layer (Conv) means zero paddings to keep the output dimension the same as that of the input.

Fig. 1.

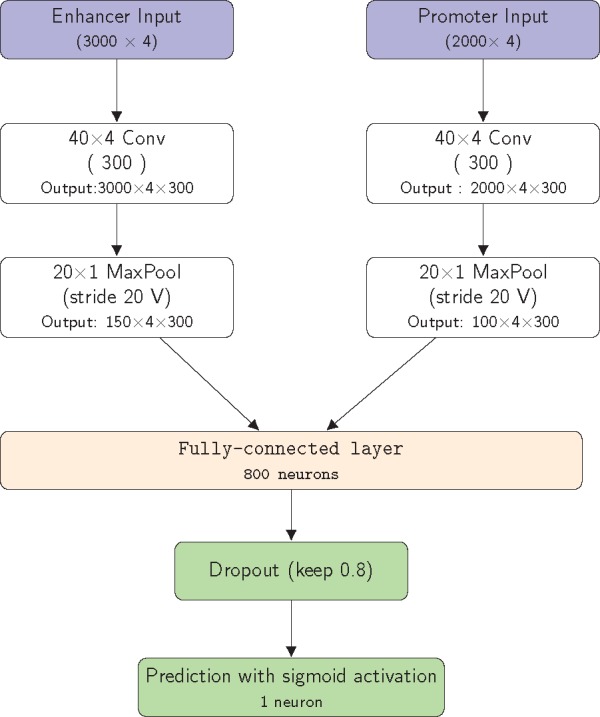
Diagram of our proposed CNN structure to predict EPIs based on only two DNA sequences covering an enhancer and a promoter, respectively. The output is a probability of interaction between the input enhancer and promoter sequences

This is essentially the CNN component in the hybrid CNN and RNN architecture of SPEID; the hyper-parameters in the CNN were set by default as that in SPEID. As mentioned before, with a only moderately large sample size, coupled with increasing evidence of sufficiently good performance of CNNs as compared to RNNs for sequence data (Bai et al., 2018; Ying et al., 2017), we conjectured a simpler CNN might suffice, which will be confirmed by our numerical study later.

As for a typical CNN, our proposed network structure can be decomposed into two parts for feature extraction and for prediction, respectively. The convolutional and pooling layers are used to extract some specific subsequences, presumably motifs for binding proteins [such as transcription factors, (TFs)] that facilitate EPIs. Since TF-binding motifs are known to be short, kernels of length 40 were hypothesized to be large enough and thus used in the convolution layer. Furthermore, because specific subsequence features or motifs may not be shared between two interacting enhancer and promoter (e.g. with different binding proteins), two separate convolutional/max-pooling layers are used for the two input sequences, respectively. The output of a convolutional layer is a set of 300 feature maps, each generated by one of 300 kernels. Then a max-pooling layer, by down-sampling, reduces its output dimension to 5% of its input (i.e. output of the convolutional layer). Finally, the feature maps from the two branches are concatenated to a flatten vector, which is input to the FC layer. We also note that, perhaps there is not much useful information beyond extracted motifs through one convolution and one pooling layers, even if we added one more convolution/pooling layer, we obtained similar results in our numerical studies (Supplementary Tables). In addition, perhaps there are no strong long-range dependences among the subsequence features or motifs in an enhancer or promoter sequence, we did not find the RNN component in SPEID useful either.

Finally, the FC layer consists of 800 neurons with ReLU as the activation function. Batch normalization (Ioffe and Szegedy, 2015) and dropout with a dropout rate of 0.2, i.e. keeping 80% of the connections (Srivastava et al., 2014) are applied to the output of the FC layer. Then the output of the fully connected layer is fed to a single neuron with the sigmoid activation function, giving the probability of having an interaction between an input enhancer sequence and an input promoter sequence.

2.3 Model training

We implemented our CNN models in Keras (available at $https ://github.com/fchollet/keras)$. Again the hyper-parameters were set as the same values as in SPEID unless specified otherwise. The models were trained in mini-batches of 50 or 100 samples by back-propagation with the binary cross-entropy loss, minimized by the Adam algorithm (Kingma and Ba, 2014) (with a learning rate of ${10}^{-5}$ as in SPEID). We also imposed an L2-norm penalty on the weight parameters in the FC layer (with a weight decay parameter of ${10}^{-6}$ as in SPEID). The starting values of the weights in each CNN model used the Glorot uniform initializer (Glorot and Bengio, 2010).

The current practice of training a model is to use cell-line specific data for cell line-specific prediction. For example, if we’d like to predict EPIs for cell line GM12878, then we would only use a training dataset for GM12878 only. While this is reasonable in light of well-accepted cell line-specific EPIs (and gene expression), there is possibility of gaining by using the data from all the cell lines. First, there are commonalities among the EPIs across the cell lines as shown earlier in our data. Second, using other cell lines will obviously increase the sample size, leading to perhaps more stable parameter estimates. Accordingly, we propose two transfer learning approaches to exploiting the use of the data from other cell lines to varying degrees. We note that, the naive way of combining all the data from all cell lines to train a CNN model did not work here: it gave lower accuracy rates for cell line-specific EPI prediction than that by cell line-specific training, though it improved for across-cell line predictions.

2.3.1 Basic training process: a benchmark

As in the current practice, we train and test a model on each cell line separately. For any given cell line, the training procedure is as follows:

1. Randomly partition the whole dataset (for the given cell line) into a training set (with 90% of the samples) and a test set (with 10% of the samples).

2. Apply the data augmentation procedure to create more interacting enhancer–promoter pairs, leading to an augmented training set with two balanced class sizes.

3. Train the model using the augmented/balanced training on set for 4 or 5 epochs to initialize the model.

4. Continue training the model using the original imbalanced training set for another 32 epochs.

5. Evaluate the performances of the trained model on the test data (for every cell line separately).

The above training process is the same as in SPEID except epoch numbers: SPEID used 32 epochs in Step 3 and 80 epochs in Step 4, while we used much smaller numbers of epochs due to our much simpler CNN structure. This training process representing the current standard is used as a benchmark. We tried to reduce the number of epochs (down to zero) in Step 3, since the data augmentation procedure was both time- and memory-consuming and found that the performance was not much affected.

We note that the above procedure can be also applied to the data combined over all the cell lines. But, due to cell line-specific EPIs, it did not yield predictive performance as good as the separate training/testing; that is, if we’d like to predict EPIs for a cell line, say GM12878, then using only the data from cell line GM12878 would give more accurate prediction of EPIs for GM12878 than using all the data combining over all the six cell lines to train the model before making predictions for only GM12878. However, we can modify the procedure in two ways to improve predictive performance for cell line-specific EPIs while taking advantage of the commonalities across the cell lines by using all the data from all the cell lines.

2.3.2 Using the data from other cell lines to pre-train a model

To take advantage of the data from other cell lines while maintaining cell line-specific EPIs, we propose a transfer learning in a weak form of using the data from other cell lines: for a given cell line to be predicted, we just use the data from all other cell lines to initialize the parameters in the CNN model before fully training the model using the cell line-specific data. For any given cell line of interest, the process is described below:

1. Pre-train a CNN model with the training data from other 5 cell lines for 6 to 8 epochs.

2. Train the model with the training data from the cell line of the interest for another 24 epochs.

3. Evaluate the model using cell line-specific test data.

Note that, for each cell line, the training data and test data were generated in the same way as described in Step 1 in Section 2.3.1. In addition, we did not apply the data augmentation procedure to expand the training data (to achieve the balanced classes) based on the results we found after comparing the performances between models with and without augmentation step; instead, in both the pre-training and training steps (Steps 1 and 2) we used the original training data with the imbalanced classes.

2.3.3 Transfer learning with the data from other cell lines

The second method we propose is in a stronger form of borrowing information from other cell lines, which is more like conventional transfer learning (Pan and Yang, 2010): we use the data from all cell lines to train the model for feature extraction, then use the cell line-specific data to update the FC layer for cell line-specific prediction. The training data and test data for each cell line were also generated in the same way as in Step 1 in Section 2.3.1. Again, we did not apply the data augmentation procedure and thus used only the original data with unbalanced classes. For any given cell line of interest, the training process is described below:

1. Pre-train a CNN model with the combined training data from all the 6 cell lines for 6 to 8 epochs.

2. Freeze the convolution and max-pooling layers (for both the enhancer and promoter branches).

3. Train the fully connected layer of the model with the training data from the cell line of interest for another 20 epochs.

4. Evaluate the model on the test data.

We used small numbers of epochs in the two new training procedures, partly to match with the 32 epochs used in the standard/benchmark training process for a fair comparison. We also trained the models for 40 epochs with the procedures in Sections 2.3.1 and 2.3.2 to see whether there would be any improvement with a larger number of epochs in training a CNN, but we did not see obvious improvement. The models were trained on a server with two GTX 1080 GPUs (devoted to the two input branches, respectively). For the training procedures in Sections 2.3.1 and 2.3.2, it took less than 1 h (for 40 epochs) and about 2.5 h (including 8 epochs for pre-training and 32 epochs for training), respectively.

3 Results

3.1 Model comparison

We first compare our proposed simple CNN architecture with SPEID, a hybrid of CNN and RNN; both are based on the current practice of cell line-specific training (i.e. the basic training process in Section 2.3.1). As done in the literature, we use the area under ROC curve (AUROC), area under precision-recall curve (AUPRC) and possibly F1 score as the evaluation criteria.

For fair comparison, in addition to our CNN models, we first ran the code of SPEID (downloaded from the authors’ website) using the same data and the same basic training process. As shown in Tables 2–5 and Figure 2, for cell line-specific training and testing (i.e. the diagonal elements in the tables), it is clear that our simpler CNN model performed as well as, or even slightly better than, the more complex SPEID, a hybrid of CNN and RNN: all of the AUROC and AUPRC values from our CNNs were either equal to or slightly larger than those from SPEID. On the other hand, for cross-cell line predictions (i.e. off-diagonal elements in each table), SPEID had a slight edge over our CNNs. The latter point might suggest slightly better feature extraction with the use of RNN in SPEID. Finally, although we only ran one round of training and testing for each model in our analyses, the results remained similar if we repeated the process multiple times as shown in the Supplementary Material.

Table 2.

AUROC for SPEID, in which cell line-specific CNNs were trained on cell line-specific training data as described in Section 2.3.1

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.91	0.53	0.60	0.55	0.57	0.54
HeLa-S3	0.55	0.94	0.56	0.52	0.61	0.53
HUVEC	0.58	0.55	0.92	0.51	0.59	0.52
IMR90	0.53	0.52	0.53	0.90	0.50	0.55
K562	0.57	0.54	0.55	0.58	0.94	0.56
NHEK	0.52	0.58	0.59	0.52	0.55	0.94

Fig. 2.

Prediction results of five methods under AUROC, AUPR and F₁ score

Table 3.

Area under PR curve for SPEID, in which cell line-specific CNNs were trained on cell line-specific training data as described in Section 2.3.1

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.78	0.07	0.07	0.09	0.08	0.06
HeLa-S3	0.06	0.82	0.08	0.05	0.07	0.08
HUVEC	0.07	0.08	0.77	0.07	0.08	0.07
IMR90	0.07	0.05	0.06	0.76	0.06	0.08
K562	0.07	0.08	0.08	0.07	0.80	0.06
NHEK	0.06	0.08	0.07	0.07	0.05	0.84

We note that, we also tried a deeper CNN with a second set of one convolution layer and one max-pooling layer added following the first set in our proposed CNN, but it gave similar results to that of our proposed CNN model (Supplementary Material). In addition, we also tried a CNN with an Inception-v4 module (Szegedy et al., 2016) added following the first set of convolution-pooling layers, but again it gave similar results (Supplementary Material).

We briefly comment on some comparisons of the performance between our simple CNN model and other existing methods for EPI prediction. First, as shown by Singh et al. (2016), SPEID performed similarly to TargetFinder (E/P/W) based on boosted trees with multiple types of (epi-)genomic data, such as DNase-seq, DNA methylation, TF ChIP-seq, histone marks, CAGE and gene expression (Whalen et al., 2016). Second, Mao et al. (2017) proposed an attention-based CNN, called EPIANN, for EPI prediction based on only DNA sequence data. Their numerical results demonstrate that EPIANN performed better than another DAN sequence-based method, PEP (Yang et al., 2017) and slightly worse than TargetFinder (E/P/W). Hence, given the above results, we conclude that our proposed simple CNN is competitive against other existing methods.

3.2 Advantages of transfer learning with other cell line data

For our CNN models, we first compare the results between using cell line-specific training data (Tables 4 and 5; Fig. 2) and using other cell line data to pre-train a model (Tables 6 and 7; Fig. 2). For cell line-specific predictions, there was a significant improvement for each cell line, more obviously shown by AUPRC. For example, using other cell line training to pre-train each CNN, we obtained the AUPRC values of 0.88, 0.90, 0.90, 0.90, 0.90 and 0.92 for the six cell lines, respectively (the diagonal elements in Table 7), compared to much smaller 0.79, 0.84, 0.79, 0.78, 0.82 and 0.86 (Table 5). Furthermore, even for cross-cell line predictions, the new method also clearly out-performed the standard/current practice of cell line-specific training. For example, as shown in the first rows of Tables 4 and 6, when we used the CNN model fitted for cell line GM12878 to predict EPIs for other five cell lines, the standard method yielded AUROC values of 0.51, 0.53, 0.53, 0.53 and 0.51, much smaller than 0.93, 0.92, 0.90, 0.86 and 0.97 obtained from the new method.

Table 4.

AUROC for our CNN models, in which cell line-specific CNNs were trained on cell line-specific training data as described in Section 2.3.1

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.94	0.51	0.53	0.53	0.53	0.51
HeLa-S3	0.53	0.96	0.51	0.58	0.54	0.50
HUVEC	0.56	0.59	0.93	0.54	0.49	0.47
IMR90	0.55	0.55	0.54	0.95	0.51	0.56
K562	0.55	0.53	0.52	0.52	0.96	0.51
NHEK	0.51	0.50	0.51	0.47	0.51	0.95

Table 5.

Area under PR curve for our models, in which cell line-specific CNNs were trained on cell line-specific training data as described in Section 2.3.1

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.79	0.05	0.06	0.07	0.06	0.05
HeLa-S3	0.05	0.84	0.06	0.06	0.05	0.05
HUVEC	0.06	0.06	0.79	0.05	0.08	0.05
IMR90	0.06	0.05	0.05	0.78	0.05	0.07
K562	0.05	0.05	0.05	0.05	0.82	0.05
NHEK	0.05	0.06	0.05	0.05	0.05	0.86

Table 6.

AUROC for our CNN models, in which the training data from other cell lines were used to pre-train each cell line-specific CNN as described in Section 2.3.2

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.96	0.93	0.92	0.90	0.86	0.97
HeLa-S3	0.91	0.96	0.92	0.87	0.87	0.94
HUVEC	0.91	0.94	0.97	0.90	0.82	0.97
IMR90	0.92	0.96	0.89	0.96	0.85	0.95
K562	0.85	0.94	0.90	0.86	0.96	0.97
NHEK	0.91	0.98	0.93	0.88	0.87	0.97

Table 7.

Area under PR curve for our CNN models, in which the training data from other cell lines were used to pre-train each cell line-specific CNN as described in Section 2.3.2

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.88	0.64	0.79	0.54	0.39	0.83
HeLa-S3	0.63	0.90	0.77	0.53	0.41	0.83
HUVEC	0.64	0.80	0.90	0.50	0.42	0.87
IMR90	0.64	0.83	0.71	0.90	0.42	0.59
K562	0.37	0.64	0.77	0.51	0.90	0.82
NHEK	0.66	0.81	0.81	0.38	0.44	0.92

Tables 8 and 9 and Figure 2 show the results of our CNN models based on transfer learning. First, transfer learning improved over the pre-training method for cell line-specific prediction: the former gave the AUROC values in the range of 0.98–0.99 and AUPRC values of 0.92–0.96, compared to that of the latter’s 0.96–0.97 and 0.88–0.92, respectively. Second, for cross-cell line predictions, however, neither method could dominate the other. For example, it is possible that transfer learning over-trained a CNN for some cell line-specific EPIs, thus losing its generalizability to other cell lines.

Table 8.

AUROC for our CNN models based on transfer learning (using the training data from all cell lines to train the feature extraction part of each cell line-specific CNN) as described in Section 2.3.3

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.98	0.94	0.92	0.89	0.92	0.96
HeLa-S3	0.84	0.98	0.96	0.90	0.95	0.96
HUVEC	0.84	0.91	0.99	0.88	0.92	0.95
IMR90	0.85	0.92	0.96	0.98	0.94	0.92
K562	0.83	0.94	0.93	0.93	0.99	0.97
NHEK	0.86	0.93	0.96	0.86	0.94	0.99

Table 9.

Area under PR curve for our CNN models based on transfer learning (using the training data from all cell lines to train the feature extraction part of each cell line-specific CNN) as described in Section 2.3.3

Training/test cell line	GM12878	HeLa-S3	HUVEC	IMR90	K562	NHEK
GM12878	0.92	0.70	0.80	0.54	0.75	0.84
HeLa-S3	0.42	0.95	0.80	0.56	0.78	0.85
HUVEC	0.37	0.62	0.95	0.50	0.78	0.85
IMR90	0.41	0.71	0.81	0.92	0.80	0.61
K562	0.39	0.67	0.80	0.57	0.95	0.86
NHEK	0.39	0.68	0.83	0.37	0.78	0.96

Figure 2 compares for each cell line the prediction performance of various methods, including SPEID, and our CNN models with the basic training (Section 2.3.1), with a weaker form of transfer learning (Section 2.3.2), with more conventional transfer learning (Section 2.3.3) and finally with the naive training of using all cell line data. The superior performance of our methods, especially the one with transfer learning, is clear.

4 Discussion and future work

In summary, we have proposed a simple CNN architecture for EPI prediction. First, based on the current practice of cell line-specific training, it performed as well as, if not slightly better, than the more complex hybrid of CNN and RNN in SPEID. This is perhaps related to only moderately large sample size of the EPI data, favoring not too complex models. In addition, currently there is a debate on the relative advantages of CNNs versus RNNs for sequential data; even for natural language data with strong long-range dependencies favoring RNNs, there is some empirical evidence showing that CNNs can perform equally well (Bai et al., 2018; Ying et al., 2017). Furthermore, we hypothesize that there is no strong long-range dependency in DNA sequence data, possibly too subtle to be detected and used with currently only moderately large sample sizes for EPIs; if true, it would suggest no need to use RNNs. Importantly, simpler or ‘lightweight’ CNN models are not only easier to train with faster convergence (as shown with smaller training epochs for our CNN structure), but have wider applicability, e.g. in mobile applications with limited computing and power resources (Howard et al., 2017; Iandola et al., 2016; Li et al., 2016).

Second, more importantly, we have proposed two transfer learning methods to train a CNN model by taking advantage of the data from other cell lines and their commonalities. Applied to the same simple CNN architecture, each method gave clearly better predictive results than the current practice, which, in general, should not be surprising given that there are known commonalities among cell line-specific EPIs. Nevertheless, the naive method of using all the training data from all cell lines to train a CNN did not perform well for cell line-specific predictions, because it lost the specificity for each cell line. On the other hand, between the two new methods we proposed, the second one based on transfer learning improved over the first method based on pre-training for cell line-specific predictions, but not necessarily for cross-cell line predictions, perhaps because they use the data from other cell lines to varying extents, striking different balances between sensitivity and specificity.

We also note that, based on the comparisons among SPEID, TargetFinder, EPIANN and PEP in the literature (Mao et al., 2017; Singh et al., 2016) and our comparison between our simple CNN and SPEID, we conclude that our simple CNN structure coupled with a new training method integrating data from other cell lines would perform competitively against other methods in predicting EPIs. Given the simplicity of our proposed CNN architecture, this is quite impressive because other methods are either based on more complex neural network architectures (such as SPEID and EPIANN) or using many more types of genomic and epi-genomic data (like TargetFinder).

Certainly we may further explore other CNN architectures and exploit the use of EPI data from other cell lines, which may yield better performance. For example, we chose the same input window size (i.e. sequences lengths for an input enhancer and a promoter) and the number of kernels as in SPEID; manual tuning might select better hyper-parameter values. Since we only used DNA sequence data, we may want to integrate sequence data with other genomic or epi-genomic data (Cao et al., 2017; Whalen et al., 2016) to improve performance. We could also integrate with other biological knowledge, such as gene networks (Kong and Yu, 2018). In this work, we have focused on predicting EPIs. As shown in other works (Mao et al., 2017; Singh et al., 2016; Yang et al., 2017), we can also analyze subsequence features selected by our CNN models to identify TF-binding motifs. These are also interesting topics worth to be investigated in the future.