A simple model for determining affinity from irreversible thermal shifts

Abstract

Thermal denaturation (Tm) data are easy to obtain; it is a technique that is used by both small labs and large‐scale industrial organizations. The link between ligand affinity (K _D) and ΔTm is understood for reversible denaturation; however, there is a gap in our understanding of how to quantitatively interpret ΔTm for the many proteins that irreversibly denature. To better understand the origin, and extent of applicability, of a K _D to ΔTm correlate, we define equations relating K _D and ΔTm for irreversible protein unfolding, which we test with computational models and experimental data. These results suggest a general relationship exists between K _D and ΔTm for irreversible denaturation.

1. INTRODUCTION

Thermal melt/thermal shift assays are common in biochemistry; they are experimentally simple, requiring no special protein tags nor immobilization, and the instrumentation is inexpensive. A typical format for this assay is to monitor protein unfolding as a function of temperature; the temperature at which half the protein has unfolded is the thermal melting point (Tm). A useful form of this assay is to compare the Tm of a protein between conditions; for example, an increase in Tm after the addition of a putative ligand is a positive indication for ligand binding. The shift between two conditions is called the ΔTm.

A thermodynamic (reversible) relationship for ΔTm as a function of ligand affinity (K _D) was described by Brandts and Lin.1 Unfortunately, temperature‐dependent unfolding is not readily reversible for many proteins,2 which means the Brandt equations cannot be used for many proteins. Thus, instead of a quantitative translation of ΔTm to K _D, it is instead common for ΔTm shifts to be interpreted qualitatively.

There have been several independent publications showing a strong correlate between ΔTm and K _D , 3, 4, 5, 6 including publications with hundreds of distinct proteins and ligands.7, 8, 9 These data sets contain irreversible unfolding, for which the Brandts equations cannot be applied, yet strangely these irreversible data seem to have the same correlate between ΔTm and K _D that is seen for reversible data. So, while it is clear a ΔTm to K _D correlate exists for some irreversible denaturation, it is unclear if this is a general feature of irreversible systems.

2. RESULTS

2.1. Equations to relate affinity to irreversible thermal denaturation

We will consider denaturation to be irreversible when unfolding is occurring, but the rate of folding is comparatively negligible over the timeframe and temperatures considered. Example of this could be an unfolded state with a high kinetic barrier for folding, or when aggregation outcompetes folding. To investigate the relationship between ΔTm and K _D during irreversible denaturation, we considered a protein and ligand system with four simplifying assumptions: (a) changes are two state; (b) the protein can unfold from the apo or the bound state; (c) ligand has a significant binding preference for folded protein; and (d) unfolding is not readily reversible (Figure 1a).

Figure 1.

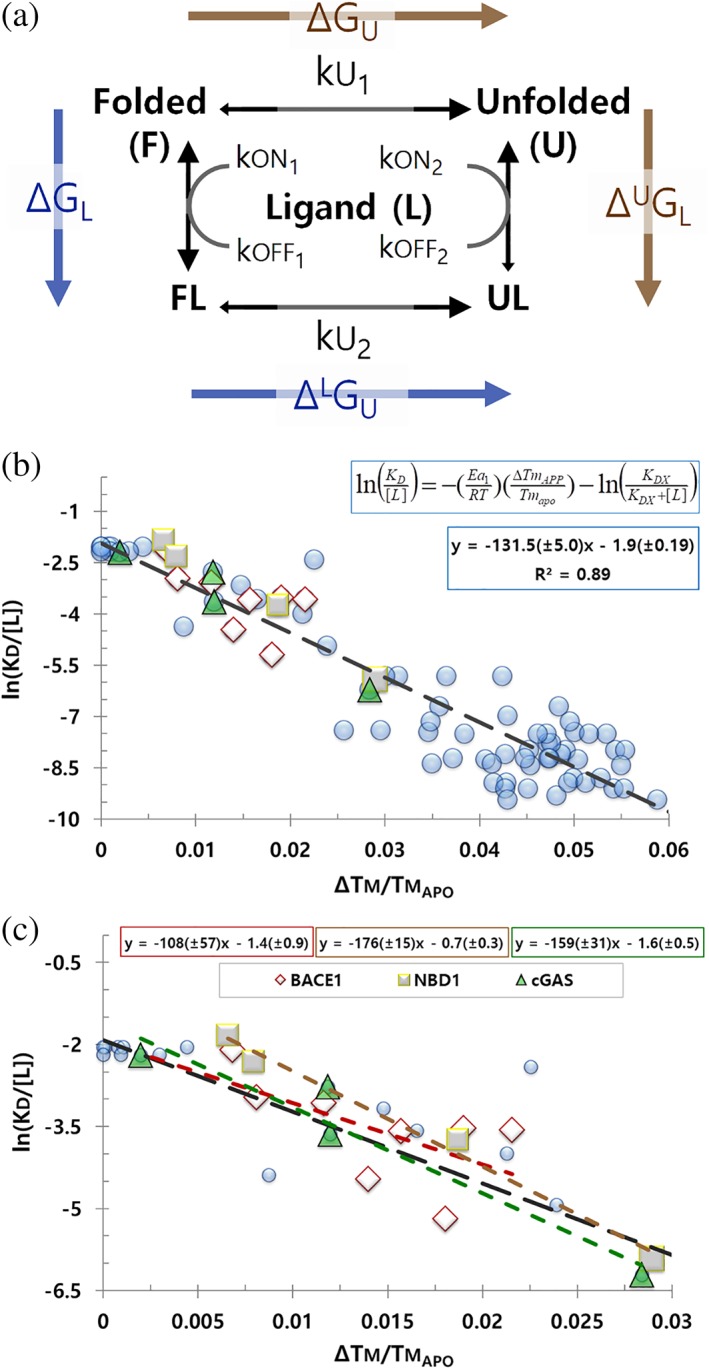
Model and ΔTm data for irreversible denaturation. (a) Irreversible unfolding model: apo folded (F), ligand‐bound folded (FL), apo unfolded (U), and ligand‐bound unfolded (UL). Ligand (L) has a significant preference for F over U; protein does not readily refold. Thermodynamic cycle in blue and gold. (b) $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ plot for irreversible unfolding. Proteins include the published values for BACE1 (diamonds),7 cGAS (squares),16 the NBD1 domain of CFTR (triangles),17 or other proteins available at Pfizer (circles). Fit and trendline for all proteins is shown; K _D span ca 10 to 0.05 μM. (c) Individual fits and trendlines for BACE1, cGAS, and NBD1 with their ligands; the black line is the global trendline for all proteins from panel b. Protein and ligands are not identified if they are part of an active therapeutic research program at Pfizer. All data in these figures are available to download

Experimental conditions begin with the protein and ligand in equilibrium, with negligible unfolding or folding, at standard pressure and temperature. Before heating, the free energy change for ligand binding (ΔG _L) is:

$$\mathrm{\Delta }{G}_L=\mathit{RT}\ln \left(1+\frac{\left[L\right]}{K_D}\right)$$ (1)

where R is the gas constant, T is the temperature in Kelvin, and [L] is the concentration of ligand. The thermodynamic transitions of this system are as follows: apo to unfolded (ΔG _u), apo to bound (ΔG _L), bound to unfolded‐bound (Δ^L G _u), and unfolded apo to unfolded‐bound (Δ^U G _L) (Figure 1a). The thermodynamic cycle is:

$$\mathrm{\Delta }{{}^{L}G}_U-\mathrm{\Delta }{G}_U=\mathrm{\Delta }{{}^{U}G}_L-\mathrm{\Delta }{G}_L$$ (2)

There are two unfolding rate constants for this system, ku ₁ for apo and ku ₂ for bound (folding is negligible in this model, thus the folding rate constants are not considered). We assume ku ₁ and ku ₂ are temperature‐dependent Arrhenius functions:

$$k=A_0{e}^{-\mathit{Ea}/\mathit{RT}}$$ (3)

where A ₀ is a constant relating the approach of the ground state to the transition state and Ea is the activation energy. Ea contains both the thermodynamic (ΔG) and kinetic energy barrier terms (ΔG^‡):

$$\mathit{Ea}=\mathrm{\Delta }G+\mathrm{\Delta }{G}^{‡}$$ (4)

For our system, the unfolded form of the protein accumulates as a function of ku ₁ and ku ₂ multiplied by the concentration of apo or bound protein. For simplicity, we will consider the conditions when the system has either 100% apo or 100% bound (i.e., no ligand, or saturating ligand). Since ku ₁ and ku ₂ are Arrhenius functions for the same protein, in the same buffer, at the same heating rates, and over a narrow temperature range relative to absolute, we assume the physical process governing their approach to transition states is the same10 and therefore their preexponential factors are closely approximate:

$$A_1\cong A_2$$ (5)

Given these conditions, it can be shown that the value of the apo unfolding rate constant, ku ₁, at Tm , _apo is closely approximate to the value of the bound unfolding rate constant, ku ₂, at Tm , _bound (Figures S1 and S2). Since ΔTm is related to these temperatures:

$$\mathrm{\Delta }\mathit{Tm}=\mathit{Tm}{,}_{\text{bound}}-\mathit{Tm}{,}_{\mathrm{apo}}$$ (6)

we now set the Arrhenius equations for these two conditions as equal:

$$A_1{e}^{-{\mathit{Ea}}_1/\mathit{RTm}{,}_{\mathrm{apo}}}=A_2{e}^{-{\mathit{Ea}}_2/R\left(\mathit{Tm}{,}_{\mathrm{apo}}+\mathrm{\Delta }\mathit{Tm}\right)}$$ (7)

After simplification of Equation (7) (see Supplemental Materials for detailed derivation), the activations energies can be expressed as:

$${\mathit{Ea}}_2={\mathit{Ea}}_1+{\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$$ (8)

The physical difference between ku ₁ and ku ₂, and therefore between Ea ₁ and Ea ₂, is the binding of ligand to the protein; thus, Equation (8) says ligand binding increases the activation energy of unfolding by a quantity ${\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{a}\mathrm{po}}}\right)$ compared to the apo unfolding activation energy. If ΔTm is positive, the total activation energy of Ea ₂ will be greater than Ea ₁, and ku ₂ will be a smaller rate constant than ku ₁.

For reversible unfolding, positive or negative ΔTm is dependent on the binding energy of the ligand for folded or unfolded protein.11, 12 To uncover the nature of this dependence for an irreversible system, we return to Equation (2), with the following substitutions:

$$\mathrm{\Delta }{G}_U={\mathit{Ea}}_1-\mathrm{\Delta }{G}_U^{‡}$$ (9)

and

$${\mathrm{\Delta }}^L{G}_U={\mathit{Ea}}_2-{\mathrm{\Delta }}^L{G}_U^{‡}$$ (10)

to find:

$$\left({\mathit{Ea}}_2-{\mathrm{\Delta }}^L{G}_U^{‡}\right)-\left({\mathit{Ea}}_1-\mathrm{\Delta }{G}_U^{‡}\right)=\mathrm{\Delta }{{}^{U}G}_L-\mathrm{\Delta }{G}_L$$ (11)

If we assume the energy barrier of unfolding for the apo state ($\mathrm{\Delta }{G}_U^{‡}$) and the bound state (${\mathrm{\Delta }}^L{G}_U^{‡}$) are closely approximate, then Equation (11) simplifies to:

$${\mathit{Ea}}_2-{\mathit{Ea}}_1=\mathrm{\Delta }{{}^{U}G}_L-\mathrm{\Delta }{G}_L$$ (12)

Substituting Equation (8) into Equation (12), followed by simplification gives:

$${\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{{\mathit{Tm}}_{\mathrm{apo}}}\right)=\mathrm{\Delta }{{}^{U}G}_L-\mathrm{\Delta }{G}_L$$ (13)

As with a reversible system, the change in stabilization, ${\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$, behaves as the difference of the ligand binding energy for folded and unfolded protein.11, 12

Since we have defined the system as having negligible ligand interaction with unfolded protein, Equation (13) simplifies to:

$${\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)=-\mathrm{\Delta }{G}_L$$ (14)

The observed ΔTm (ΔTm , _app) will be the sum of stabilization from ligand binding at the site of interest (ΔTm), plus any additional extrasite binding (ΔTmx):

$$\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}=\mathrm{\Delta }\mathit{Tm}+\mathrm{\Delta }\mathit{Tmx}$$ (15)

Substitution from Equations 1, 4, 15, followed by rearrangement gives:

$$\ln \left(\frac{K_D}{K_D+\left[L\right]}\right)=-\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)-\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$$ (16)

where K _DX is the affinity of extrasite binding. Under conditions of [L] ≫ K _D, Equation (16) behaves as:

$$\ln \left(\frac{K_D}{\left[L\right]}\right)=-\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)-\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$$ (17)

which describes the relationship of K _D and ΔTm for irreversible denaturation.

In deriving Equation (17), we assumed the ligand binding energy (ΔG _l) will not change with temperature. We also assume there is 100% bound protein when evaluating the expected ΔTm. We discuss these assumptions below.

Equation (17) is of the y = mx + b form; therefore, a linear relationship is expected for $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ for irreversible denaturation. To test this, we collected K _D and ΔTm for several proteins and ligands with affinities spanning approximately 1,000‐fold; these data are linear when plotted as $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ (Figure 1b). This relationship is consistent with the K _D to ΔTm correlate described by others.7, 8, 9

We were surprised to discover all the proteins and ligands we tested had similar slopes, $\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)$, and intercepts, $\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$ (Figure 1c). These proteins are not homologs, nor is there anything about them that would lead to the expectation they should have similar Ea ₁ values (77.9 ± 3.0 kcals/mol); likewise, the ligands are distinct, yet these data also support a similar $\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$ value (−1.9 ± 0.2; K _DX = 17.9 ± 1.9 μM under these conditions). The key similarities of this set of ligands may be that they are all noncovalent, single‐site binders, which do not require cobinders.

Given the similarity of the slope and intercept for these proteins, and the large amount of irreversible examples previously interpreted by the Brandts equations (>100 proteins, >700 ligands for a single protein),9 these data support a general likeness between proteins for irreversible thermal unfolding and binding. If correct, the relationship expressed in Equation (17), and the empirical fit of $\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)$ and $\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$, will serve others in prospectively estimating K _D from ΔTm. Consistent with this, we find that affinities calculated from ΔTm agree with affinities calculated by SPR or ITC (Table 1).

Table 1.

Comparison of K _D between ITC, SPR, or ΔTm

		a K D (μM)
Protein	Ligand	bITC or SPR	c Tm
dBASE1	Cmpd 3	14 ± 1.4	5.9 ± 0.59
	Cmpd 4	5.4 ± 0.54	5 ± 0.5
	Cmpd 5	4.8 ± 0.48	3.1 ± 0.31
	Cmpd 6	3 ± 0.3	1.2 ± 0.12
	Cmpd 7	2.9 ± 0.29	0.9 ± 0.09
	Cmpd 8	2.9 ± 0.29	1.8 ± 0.18
	Cmpd 9	1.2 ± 0.12	2.3 ± 0.23
	Cmpd 10	0.6 ± 0.06	1.4 ± 0.14
ecGAS	PF‐06928215	6.7 ± 0.67	3.2 ± 0.32
	Cmpd 17	0.2 ± 0.02	0.4 ± 0.04
	Cmpd 18	2.7 ± 0.27	3.1 ± 0.31
	Cmpd 19	13 ± 1.3	12 ± 1.2
fNBD1	ADP	19 ± 1.9	6 ± 0.6
	AMPPNP	11 ± 1.1	5 ± 0.5
	ATP	2.4 ± 0.24	1.2 ± 0.12
	PhET‐ATP	0.3 ± 0.03	0.3 ± 0.03

^aStandard error is estimated at 10% of values.

^bAffinities were determined by ITC for BASE1 and by SPR for cGAS and NBD1.

^cSlope and intercept values for ΔTm‐derived affinities were determined without data for the proteins they were to fit.

^dWithout BASE1, the global slope and intercept values are −130.3 (±5.4) and −1.9 (±0.21).

^eWithout cGAS, the global slope and intercept values are −131.2 (±5.3) and −1.9 (±0.20).

^fWithout NBD1, the global slope and intercept values are −129.7 (±5.2) and −2.0(±0.20).

2.2. Heating rate and ligand concentration effects

It is important to note that while the observed ΔTm is dependent on ligand concentration and K _D, it is also dependent on the heating rate. For irreversible unfolding, slow heating leads to low Tm values.13, 14 To test this effect, we collected experimental data at various heating rates, and calculated the expected ΔTm for these same heating rates through unfolding simulations based on the model depicted in Figure 1a. Our unfolding simulations look as expected for irreversible denaturation, with both the Tm and the ΔTm decreasing as a function of heating rate, which we also observe experimentally (Figure 2).

Figure 2.

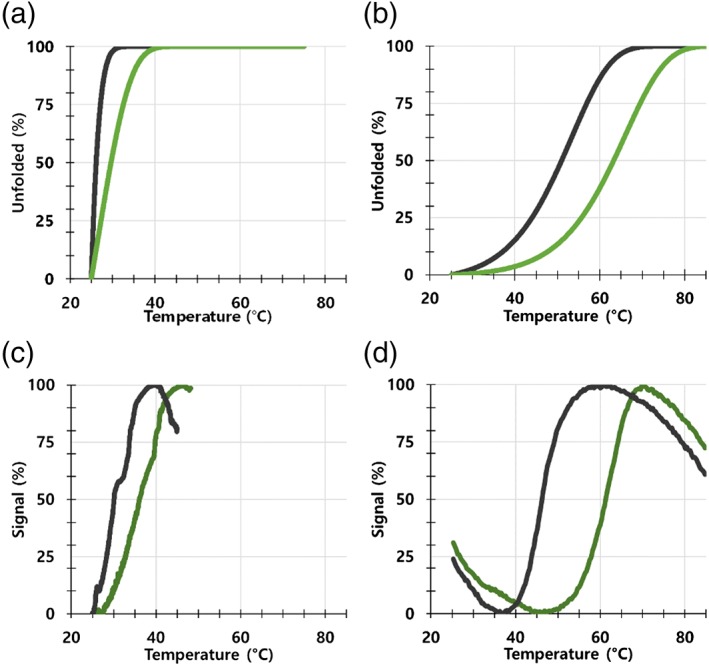
Experimental and simulated irreversible denaturation. Representative data showing the Tm calculated by simulations using a heating rate of (a) 0.03 or (b) 4°C/min, and experimental data using a heating rate of (c) 0.03 or (d) 4°C/min. Simulated and experimental data are for a K _D of 0.07 μM at 25°C. Apo (black) and bound (green) protein traces are shown. Protein and ligands are not identified because they are part of an active therapeutic research program at Pfizer. Protein and ligand are the same as used for Figure 3. All data in these figures are available to download

In simulations, we observe ΔTm is saturable as the limit of 100% protein occupancy (1:1 stoichiometry); however, when we collect ΔTm while varying ligand concentration, we find increasing the concentration of ligand past the saturation point still increases the ΔTm, even for high affinity ligands (ca 0.07 μM) (Figure 3a). The parsimonious interpretation of these data is extrasite binding (>1:1 stoichiometry) occurs as ligand concentration increases. An intriguing alternative explanation of these data is that ligand may be rescuing protein from the apo unfolding path by increasing the effective association rate (e.g., kon ×[L]) (Figure 1a). To test these hypotheses, we simulated fast and slow ligand association kinetics at variable protein occupancies. Changes in the kinetics of association and dissociation affect the simulated ΔTm; however, this effect is also saturable as the limit of 100% protein occupancy and does not explain an increasing ΔTm past saturating ligand concentrations (Figure S3).

Figure 3.

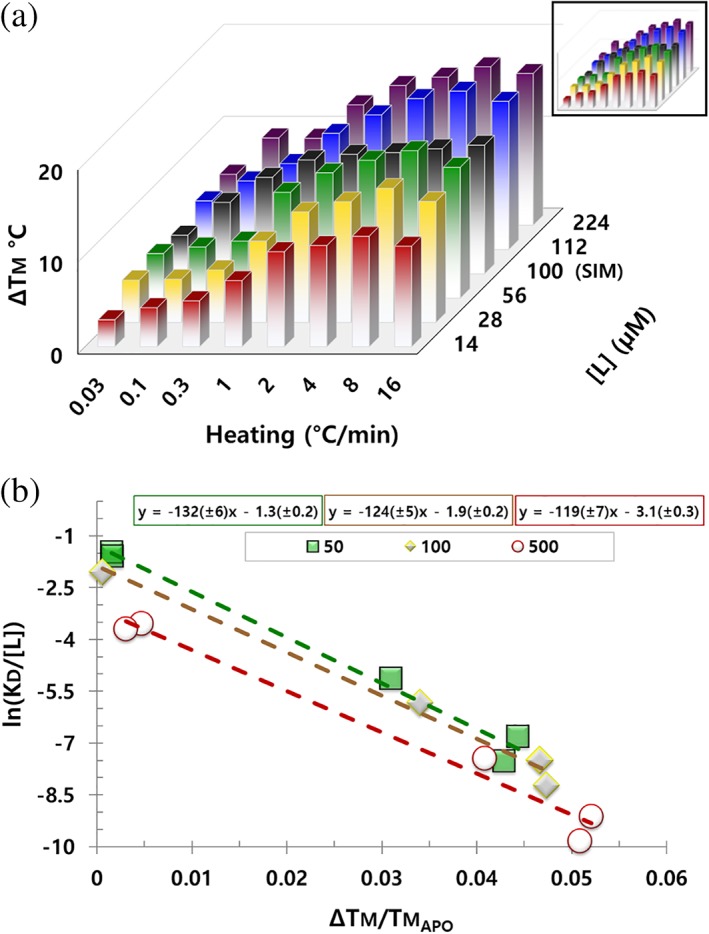
Heating and ligand effects on ΔTm. (a) ΔTm for a single protein, with a single ligand, while varying heating rate or ligand concentration. Ligand has a K _D of ca 0.07 μM at 25°C. Data in black are the ΔTm predicted by simulations at 100 μM ligand. These same data divided by Tm , _apo $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ are inset. (b) $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ plot for a single protein, with five distinct ligands, at three ligand concentrations. Ligands have K _D values of ca 20, 10, 0.7, 0.07, and 0.05 μM at 25°C. Ligand concentration was 50 (green), 100 (brown), or 500 μM (red); K _DX fit from these ligand concentrations is 19, 18, and 24 μM (intercepts of −1.3, −1.9, and −3.1). Protein and ligands are not identified because they are part of an active therapeutic research program at Pfizer. Protein is the same for both panels. All data in these figures are available to download

To further test ligand effects, we assayed compounds at various concentrations and then fit them to Equation (17). We find the slope, $\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)$, and the intercept, $\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$, change as ligand increases (Figure 3b). Since Ea ₁, the intrinsic unfolding energy of the apo protein, must be independent of ligand concentration, the apparent change in the fit value of Ea ₁ suggests further stabilization is occurring due to extrasite binding. Similarly, without extrasite binding (e.g., K _DX ≫ [L]), the intercept should reduce to zero, instead ligand causes a decrease in the intercept (a fit of the intercept for the 50, 100, and 500 μM data sets gives a K _DX of 19, 18, and 24 μM). Therefore, the direction of change in slope and intercept are consistent with this stabilization arising from weak extrasite binding at elevated ligand concentrations. Based on these data, it is not possible to say if this binding occurs at a cryptic site, or at the main site of a partially disrupted protein (either intrinsically or thermally disrupted). Since our model assumes two‐state transitions, Equation (17) does not account for intermediate folding effects such as partially disrupted protein populations.

3. DISCUSSION

We have expressed the expected relationship for K _D to ΔTm for an irreversible system, which helps explain the strong correlate between K _D and ΔTm seen in the literature. There is a dissonance in knowingly applying thermodynamic equations to nonequilibrium data; instead of using the Brandt equations, irreversible unfolding data should be interpreted using the $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ plots we describe here.

In deriving Equation (17), we have considered the temperature‐dependent changes in the activation energies of unfolding of apo (Ea ₁), bound (Ea ₂), or ligand binding energy (ΔG _L) to be negligible over this temperature range (please note the important difference in maintaining the value of ΔG _L at 25°C as constant, not the value of K _D at 25°C as constant (see Equation (1)). Since we are considering the unfolding of the same protein in apo or bound states, we expect similar temperature dependence to processes where purely protein–protein or protein–solvent interaction are concerned (i.e., all the interactions that do not involve ligand). This logic is manifest in Equation (8), where we find the statement: ${\mathit{Ea}}_2={\mathit{Ea}}_1+{\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$, which says the unfolding process is the same between the apo and bound proteins, but for the additional ${\mathit{Ea}}_1\left(\frac{\mathrm{\Delta }\mathit{Tm}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ term, which from Equation (14), we know to be the ligand binding energy (ΔG _L).

We can therefore conclude that, due to the subtraction of bound and apo data, the temperature‐dependent changes in the protein unfolding activation energy are not a concern since they are the same for both apo and bound protein. Due to the narrow temperature range considered, it is possible the temperature‐dependent change in ligand binding energy is small; however, this is not clear compared to the protein unfolding energy. Therefore, we suspect the temperature‐independent assumption for ligand binding energy to contribute the greatest uncertainty to Equation (17).

We have also assumed there is 100% bound protein when evaluating the expected ΔTm. If the system does not start with 100% bound, then the experimental ΔTm will be less than the true ΔTm according to the fraction that is apo (see Equation (19) in Methods). Kinetics of ligand association and dissociation may also affect the experimental ΔTm, particularly for large energy barriers of association or dissociation (Figure S3). We have attempted to address the occupancy and kinetics effects through unfolding simulations; from these models, we conclude the initial occupancy is the dominant concern compared to ligand binding kinetics. We expect this to be a durable result so long as the fold difference between ku ₁ and ku ₂ is small compared to the fold difference between the concentration of apo and bound protein (Figure S3 for further discussion).

To fit thermal denaturation to thermodynamic equations, it is necessary that the unfolding is reversible, and that the heating rate is slow enough that equilibrium is reached between each data point.12 Any system out of equilibrium cannot be fit by equations that assume complete reversibility has been achieved, and instead should be fit to an incomplete or irreversible model.

The literature suggests the majority of proteins irreversibly denature.2 Some of these proteins in this study were tested by both Tm and T agg assays (the latter of which demonstrates irreversible denaturation), and we tested a single protein for irreversible denaturation through heating‐rate‐dependent changes in Tm (see Figure 2), but we have not determined if all the proteins included in Figure 1b are irreversibly denatured, yet they still seem to conform to Equation (17). We expect this is due to the intrinsic irreversibility of many of these proteins, but should also result from the rapid heating rate we use. Rapid heating will favor the unfolding rate while limiting folding. In other words, even if a protein is normally reversible, measurements conducted at rates that preclude equilibrium from being reached should cause the system to conform to the framework of the model and derivations presented here.

Lastly, we found the values of Ea ₁ and K _DX are similar for many proteins (77.9 ± 3.0 kcals/mol and 17.9 ± 1.9 μM), suggesting there is a likeness between proteins for these terms sufficient for the prospective estimation of K _D from ΔTm for other proteins. Our values for Ea ₁ and K _DX are the consensus fit from several proteins and ligands; accuracy of K _D calculated from these terms will be limited by the error of the fit, deviation from the collection conditions used to estimate consensus Ea ₁ and K _DX values (100 μM ligand and a heating rate of 4°C/min, see Figure 3a for example effect), and the difference between these consensus values and the actual values of Ea ₁ and K _DX for a particular protein.

The similar values seen for proteins in $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ plots mean the K _D to ΔTm relationship is the same for these proteins. Three reasons occur to us for why there could be a robust K _D to ΔTm relationship: (a) most proteins have similar Tm , _apo values on the absolute scale, and ΔTm experiments compare two conditions over a very narrow temperature range, thus temperature‐dependent changes in energies and rates are minimized; (b) ΔTm is a comparison between the same protein in the same buffer at the same heating rate; this allows an estimation of ligand‐dependent effects while minimizing protein‐specific information; and (c) there is a fundamental likeness to all proteins; they are polymers of the same 20 amino acids, with generally similar‐sized hydrophobic packing spaces separated by hydrophilic secondary structure, this leads to similar protein–solvent interactions when averaged over the whole protein. Points (a) and (c) suggest it is reasonable that ΔTm data allow for an estimation of the similarities between proteins as they unfold, while points (b) and (c) suggest it is reasonable that ΔTm data allow for an estimation of the similarities between proteins due to ligand binding.

4. MATERIALS AND METHODS

4.1. Experiments

Proteins and ligands are not identified if they are part of an active therapeutic research program. Nucleotide‐binding domain 1 (NBD1) of Cystic Fibrosis Transmembrane Conductance Regulator, and the cyclic GMP‐AMP Synthase (cGAS) were expressed and purified as described.15, 16 Other proteins were purified at Pfizer using standard growth and purification techniques. All the proteins used in these experiments were shown to be greater than 95% pure by gel. Proteins were single domain or multidomain, with molecular weight spans of 20–80 kDa; proteins were either monomers or homodimers.

Ligand affinities for BASE1 are from the work reported by Lo et al.,7 SPR affinities for cGAS and NBD1 were determined as described.15, 16, 17 Other affinities shown here were determined at 25°C using SPR or estimated from Ki. Activity assays were performed using commercial kits following the manufacturer's protocol. SPR was performed using a Biacore T200 using CM3 or CM5 chips (GE Healthcare) with immobilized neutravidin to capture enzymatically biotinylated proteins (BirA ligase from Avidity).

Thermal shift assays were done in 20 mM HEPES pH 7.5, 150 mM KCl, and 1 mM TCEP. Assays were performed using a UNit375 (Unchained Labs) for T agg measurements monitoring static light scattering at 277 nm (SLS 277 nm), or a QuantStudio 6 Flex (Applied Biosystems, Thermo Fisher Scientific) for Tm measurements monitoring increased fluorescence of SYPRO orange (Sigma). We found the individual values of T agg and Tm were often several degrees distinct; however, this is typical of these different techniques as they are measures of different phenomena, and the values of ΔT agg and ΔTm were generally in close agreement. We chose to pursue SYPRO orange Tm data for subsequent experiments since the Tm signal‐to‐noise was always of a better quality than T agg.

For our standard experiments, the ligand concentration was 100 μM, heating rate was 4°C/min, and the SYPRO orange concentration was 1:1,000 the manufacturer's stock (the manufacturer does not provide an absolute concentration, but we used fivefold higher concentration than the recommended 1:5,000 dilution). Ligand concentration was chosen as a practical balance for a strong ΔTm signal against a concern for ligand solubility and extrasite binding. Similarly, our heating rate was chosen to balance a strong ΔTm signal against reductions in signal‐to‐noise arising from collecting data too rapidly.

Ligands stocks were in DMSO before dilution into protein assay buffer; apo and compound samples were made to contain the same final concentration of DMSO. Variation from our standard collection conditions, such as depicted in Figure 3a, included varying ligand concentration (e.g., between 14 and 448 μM) or heating rate (e.g., between 0.03 and 16°C/min); if not explicitly stated, collection conditions were 100 μM and 4°C/min.

Thermal shift data were imported into GraphPad Prism 7 and analyzed using Equation (18):

$$y\left(T\right)=\left(\frac{y_{\min }-y_{\max }}{1+e^{T-\mathit{Tx}}}\right)+y_{\max }$$ (18)

where y(T) is the temperature‐dependent signal, y _min and y _max are fits of the minimal and maximal signal, T is the temperature, and Tx is the T agg or Tm temperature.18 Affinity and ΔTm values were plotted for each protein if the affinity of the ligand was at least fivefold the ligand concentration, the fit of $\left(\frac{{\mathit{Ea}}_1}{\mathit{RT}}\right)$ and $\ln \left(\frac{K_{\mathit{DX}}}{K_{\mathit{DX}}+\left[L\right]}\right)$ was determined from a $\ln \left(\frac{K_D}{\left[L\right]}\right)$ v $\left(\frac{\mathrm{\Delta }\mathit{Tm}{,}_{\mathrm{APP}}}{\mathit{Tm}{,}_{\mathrm{apo}}}\right)$ plot. Best‐fit analysis was performed in GraphPad Prism 7, values and the standard error are reported. The best fit of Ea ₁ and K _DX for all proteins and ligands was 77.9 ± 3.0 kcals/mol and 17.9 ± 1.9 μM. All affinity and ΔTm data are available to download.

4.2. Simulations

In this system, folded protein (F) can be lost to the unfolded form (U), but the unfolded form was treated as effectively irreversible. Folded protein can bind to ligand (FL), and can then unfold (UL), but ligand binding to the unfolded form was unfavorable; thus, the UL complex was treated as immediately decomposing to U. Models were performed where the initial concentration of U was zero, the [L] is much greater than the protein concentration, which was fixed at 10 μM, and generally much greater than K _D.

Initial equilibrium occupancy (O _i) of FL was determined using Equation (19):

$$O_i=\left(\frac{1}{\frac{K_D}{\left[L\right]}+1}\right)$$ (19)

During simulations, the concentrations of each species can be calculated using these equations:

$${\left[U\right]}_t={\left[U\right]}_{t-1}+{\mathit{ku}}_1{\left[F\right]}_t\mathit{dt}+{\mathit{ku}}_2{\left[\mathit{FL}\right]}_t\mathit{dt}$$ (20)

$${\left[F\right]}_t={\left[F\right]}_{t-1}+\mathit{\text{koff}}{\left[\mathit{FL}\right]}_t\mathit{dt}-{\mathit{ku}}_1{\left[F\right]}_t\mathit{dt}-\mathit{kon}\left[L\right]{\left[F\right]}_t\mathit{dt}$$ (21)

$${\left[\mathit{FL}\right]}_t={\left[\mathit{FL}\right]}_{t-1}+\mathit{kon}\left[L\right]{\left[F\right]}_t\mathit{dt}-{\mathit{ku}}_2{\left[\mathit{FL}\right]}_t\mathit{dt}-\mathit{\text{koff}}{\left[\mathit{FL}\right]}_t\mathit{dt}$$ (22)

where species concentration at each time (e.g., [U]_t) is contributed from carryover from the prior time interval (e.g., [U]_t‐1), and an additional contribution from the convertible species (e.g., [F]_t) multiplied by its temperature‐dependent rate constant (e.g., ku ₁) over the time interval of integration (dt). Data were calculated using 0.1 s intervals, between 20 and 85°C with variable heating rates.

The value of unfolding rate constants for simulations was estimated based on early experimental data for a protein at 10 μM, with a Tm of ca 50°C, and a heating rate of 4°C/min. Based on this experiment, and a simple two‐state unfolding mechanism, we approximated the rate to be around 0.005 s⁻¹ at Tm. This rate gave good visual agreement between experimental and modeled data. Independent of our fit for the model to experimental data, we subsequently found prior work on irreversible unfolding using the same simplified Arrhenius‐based model we have used; in their work, these authors fit DSC curves for thermolysin to determine an average rate of 0.004 s⁻¹ at Tm , and an apo activation energy barrier (Ea) of 67.4 kcals/mol.14

Lacking initial estimates for the preexponential term (A ₀), or Ea, we used 0.005 s⁻¹ to calculate an apparent Ea of unfolding using the Eyring equation as an approximation for A ₀:

$$k=\frac{k_{B}T}{h}{e}^{\left(\frac{-\mathit{Ea}}{\mathit{RT}}\right)}$$ (23)

where k is the rate constant, k _B is the Boltzmann's constant, T is the temperature in Kelvin, and h is the Planck's constant.10 Using a rate constant approximation of 0.005 s⁻¹ at Tm, and k _B T/h as the preexponential factor, the activation energy barrier of apo unfolding is ca 22 kcals/mol.

The A ₀ and Ea values are lower than we ultimately observed experimentally (ca 1.9 × 10⁵¹ s⁻¹ and 77.9 ± 3.0 kcals/mol), but we chose to use these initial estimates for the remainder of these simulations as we reasoned it should not be necessary to have exact values for comparative analysis between heating rates for apo and bound protein, provided the logic leading to Equation (8) is valid. The values used here, though estimations based on initial data sets, were sufficient for our simulations to predict changes from heating rates or ligand binding. Our simulations, using a 4°C/min heating rate, are available to download.

Using the simulation as described, the heating rate can be changed, and the Tm expected is calculated using numerical integration over time from the initial equilibrium state (Equations 20, 21, 22). Using this simulation, we find good agreement between the predicted effect on Tm and ΔTm for an irreversible system, and experimental irreversible unfolding (Figure 2). These data demonstrate the protein is undergoing irreversible unfolding,13, 14 which is consistent with the simple unfolding model these simulations depict (Figure 1a).

CONFLICT OF INTEREST

The author declares no conflict of interest.

AUTHOR CONTRIBUTIONS

The work and writing was performed by J.H.

Supporting information

Appendix S1: Supporting Information

Appendix S2: Supporting Information

Hall J. A simple model for determining affinity from irreversible thermal shifts. Protein Science. 2019;28:1880–1887. 10.1002/pro.3701