Elucidation of near-resonance vibronic coherence lifetimes by nonadiabatic electronic-vibrational state character mixing

Significance

Excitation energy transfer (EET) remains one of the most highly discussed nonequilibrium transport phenomena in the fields of biophysics and physical chemistry because of the possible role of long-lived quantum coherences in enhancing transport efficiency. These coherences were first observed using 2D electronic spectroscopy, and their origin remains elusive. By modeling a vibronically coupled dimer with explicitly introduced dephasing mechanisms—such as electronic energy fluctuation and vibrational relaxation—we demonstrate that the coherence lifetime is highly correlated with the degree of electronic-vibrational mixing, implying that near the exciton-vibrational resonance, the vibronic system has an optimal balance between coherence lifetime and oscillator strength. The degree of vibronic coupling may thus be an optimizable parameter to enhance energy transfer.

Abstract

Recent work suggests that the long-lived coherences observed in both natural and artificial light-harvesting systems (such as the Fenna–Matthews–Olson complex) could be attributed to the mixing of the pigments’ electronic and vibrational degrees of freedom. To investigate the underlying mechanism of these long coherence lifetimes, a sophisticated description of interactions between the molecular aggregates and the nonequilibrium fluctuations in the surrounding environment is necessary. This is done by implementing the hierarchical equations of motion approach on model homodimers, a method used in the intermediate coupling regime for many molecular aggregates wherein the nonequilibrium environment phonons play nontrivial roles in exciton dynamics. Here we report a character change in the vibronic states—reflective of property mixing between the electronic and vibrational states—induced by an interplay between system coupling parameters within the exciton-vibrational near-resonance regime. This mixing dictates vital aspects of coherence lifetime; by tracking the degree of mixing, we are able to elucidate the relationship between coherence lifetime and both the electronic energy fluctuation and the vibrational relaxation dephasing pathways.

The role of quantum mechanics in biological systems has been a topic of extreme interest over the past decade. Quantum effects have been important in explaining many biological phenomena, including the avian magnetic compass, the vibrational theory of olfaction, and coherent excitation energy transfer (EET) in photosynthetic complexes (1–7). Photosynthesis ultimately enables life on Earth because most terrestrial and aquatic biomes initially draw their energy from solar photons. The photosynthetic process begins with solar light harvesting, whereby a collection of coupled pigments within an antenna complex catch photons and move the captured energy to a reaction center to separate charges. The protein scaffold of these pigment–protein complexes not only holds the pigments in place with defined orientations, it also perturbs the molecular eigenstates of individual pigment molecules and controls the coupling between pigments such that energy transfers efficiently to the reaction center, where charge separation occurs. This process has been optimized through natural selection with a quantum efficiency approaching unity (8, 9).

Although still under debate (10), a possible explanation for this efficiency came from the slow dephasing of coherences observed as long-lived oscillations in the 2D electronic spectra (2DES) of the Fenna–Matthews–Olson (FMO) complex (11). The FMO complex, functioning as a molecular wire that funnels excitation energy to the reaction center in the light-harvesting apparatus of green sulfur bacteria, has a homotrimer structure with $C_3$ symmetry, and each monomer contains eight bacteriochlorophyll a (BChl a) pigments (12). The coherent oscillations were found to persist in excess of 660 fs (11), with dephasing times of up to 1.5 ps (13, 14) at cryogenic temperature (77 K). Such long-lived oscillations in 2DES have been also observed in other photosynthetic complexes (15–17). These coherences were initially attributed to purely electronic origins (11, 13, 16). However, theoretical studies based on electronic states often underestimate the coherence lifetime observed in experiments (18, 19). Numerous proposed mechanisms, ranging from quantum transport (20, 21), vibrational coherence in the electronic ground state (22), correlated environment motion (23, 24), to quantum mechanically mixed electronic and vibrational states (vibronic excitons) (25–29) have failed to fully explain both the intensity and the lifetime of these coherences.

Among studies on vibronic excitons, the long-lived coherence is conditional to frequencies associated with Franck–Condon active vibrational modes that are nearly resonant with the electronic energy difference (exciton-vibrational resonance). For a detailed quantitative description of coherence lifetimes in a multichromophoric system, the introduction of interactions between the chromophores and environmental fluctuations must be performed with caution, to calculate correct exciton dynamics. While in most theoretical studies of vibronic excitons, the environmental interactions are either described solely by electronic energy fluctuations or by vibrational relaxation.

In the current work, we calculate exciton dynamics, linear absorption, and 2DES of systems comprised of model homodimers by implementing the hierarchical equations of motion (HEOM) approach (30), a nonperturbative method describing dissipative quantum dynamics under the intermediate coupling regime (where the electronic coupling strength is comparable to the reorganization energy).This allows us to build a more complete picture by investigating the effects of exciton-vibrational resonance on coherence lifetime considering the interplay between electronic energy fluctuations and vibrational relaxation concurrently. As such, we report how the character change of the state between electronic and vibrational degrees of freedom (DOFs) contribute to both coherence lifetime and intensity.

Model

Herein we consider simulations of the linear absorption and 2DES for several systems and modeling the underlying dynamics within a system of three homodimers with different interchromophore coupling schemes (electronic versus vibronic). The electronically coupled homodimer (ED) is modeled as Frenkel excitons (31), where each chromophore is modeled as a two-level system; this configuration forces us to only consider the zero-to-one exciton transition. The electronic ground ($|0$〉) and first excited ($|j$〉) states of the $j^{th}$ chromophore are connected via electronic excitation and deexcitation operators and are separated by the excitation energy, $E_j$. This coupling between chromophores $j$ and $l$ is managed through a Coulombic interaction parameter, $J_{jl}$. The corresponding system Hamiltonian of $N$-coupled chromophores thus reads as ${Ĥ}_{\mathrm{E}}={\sum }_j^N{E}_j|j\rangle \langle j|+{\sum }_{j\ne l}^N{J}_{jl}|j\rangle \langle l|$.

To model vibronically coupled homodimers (VDs), we consider a Holstein Hamiltonian model (32), coupled with a form similar to the Frenkel model, to describe the electronic states. The VD Hamiltonian will be written in a local vibronic basis, which explicitly couples electronic and vibrational DOFs. For simplicity, each chromophore is coupled to a single intramolecular vibrational mode with frequency ${\omega }_j$. At a basic level, the single chromophore Hamiltonian can be written as ${Ĥ}_j={\sum }_j^N{E}_j|j\rangle \langle j|+{Ĥ}_{vib}\left({\omega }_j\right)+{Ĥ}_{el-vib}\left({\omega }_j,S_j\right)$. Here, ${Ĥ}_{vib}\left({\omega }_j\right)$ is the vibrational Hamiltonian, described by a harmonic oscillator. $S_j$ is the dimensionless Huang–Rhys factor, representing the coupling strength between the electronic and nuclear DOF for chromophore $j$. We then complete the system Hamiltonian by including the $J_{jl}$ electronic coupling term as ${Ĥ}_{\mathrm{V}}={\sum }_j^N{E}_j|j\rangle \langle j|+{\sum }_{j\ne l}^N{J}_{jl}|j\rangle \langle l|+{\sum }_j^N{Ĥ}_{vib}\left({\omega }_j\right)+{\sum }_j^N{Ĥ}_{el-vib}\left({\omega }_j,S_j\right)$.

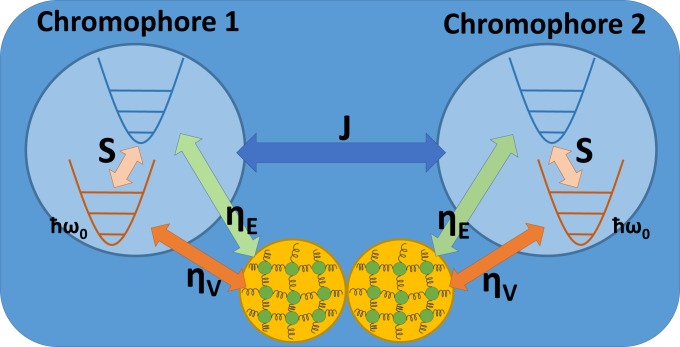
All other vibrational modes (from protein and/or solvent fluctuations) that couple to each chromophore are modeled by an independent phonon bath composed of $\xi$ harmonic oscillators; these baths are described by ${Ĥ}_{\mathrm{B}}$. We assume that the system is affected by the phonon bath through both electronic energy fluctuations and vibrational relaxation and thus arrive at a system-bath Hamiltonian organized as ${Ĥ}_{\mathrm{S}\mathrm{B}}={\sum }_{j=1}^N{\widehat{V}}_j{\widehat{B}}_j$, where ${\widehat{B}}_j$ is taken to be the collective bath operator and ${\widehat{V}}_j$ is the system operator that describes the effects of bath fluctuations on the states of chromophore $j$. ${\widehat{V}}_j$ is a function of both the dimensionless electronic energy fluctuation and the vibrational relaxation constants, ${\eta }_{\mathrm{E}}$ and ${\eta }_{\mathrm{V}}$, respectively. A schematic representation of the entire system and coupling scheme is provided in Fig. 1. For VD, these values are set to $\left({\eta }_{\mathrm{E}},{\eta }_{\mathrm{V}}\right)=\left(\mathrm{1,1}/3\right)$, while for ED, these coefficients are $\left({\eta }_{\mathrm{E}},{\eta }_{\mathrm{V}}\right)=\left(\mathrm{1,0}\right)$, as there are no system vibrational DOFs coupled to the bath oscillators in this case.

Fig. 1.

A schematic representation of both the vibrational states associated with the electronic ground state (red potential) and the first excited state (blue potential) within the local vibronic basis. The two Couloumbic-coupled chromophores are shown as blue circles, and each respectively couples to its individual phonon bath (orange circles).

Just as coupling the intramolecular vibrational modes to the electronic DOF shifts the equilibrium position of the system oscillator, the introduction of system–bath coupling shifts the equilibrium position of the bath oscillators. To maintain the translational symmetry of the Hamiltonian around the shifted equilibrium position, a counter term $H_{\mathrm{r}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{g}}$ is introduced in the total Hamiltonian (33), obtaining an effective system Hamiltonian. Detail of aforementioned Hamiltonians for exciton dynamics, linear spectra, and 2DES calculation are in SI Appendix.

Experimentally, rephasing 2D spectra are generated by sequential interaction of three broadband laser pulses with a sample to create a third-order polarization. This generates a 3D signal theoretically described by third-order nonlinear response functions, dependent on the waiting time between sequential pulses, $t_1$, $t_2$, and $t_3$ (34). The excitation and deexcitation of the system states by laser pulses are described by transition dipole operator, while the system dynamics during the waiting times are calculated by the HEOM method. For 2D spectral simulations of ED, we assume the total system is initially in a factorized state. For those simulations on VD—due to the possible thermal vibrational excitations—initial states are obtained by equilibrating the total system with the previously mentioned factorized states using HEOM (SI Appendix, Eq. S20); finally, the rephasing 2D spectra at waiting time $t_2$ is obtained after a double Fourier transform on the third-order nonlinear response function (SI Appendix, Eq. S25).

Results

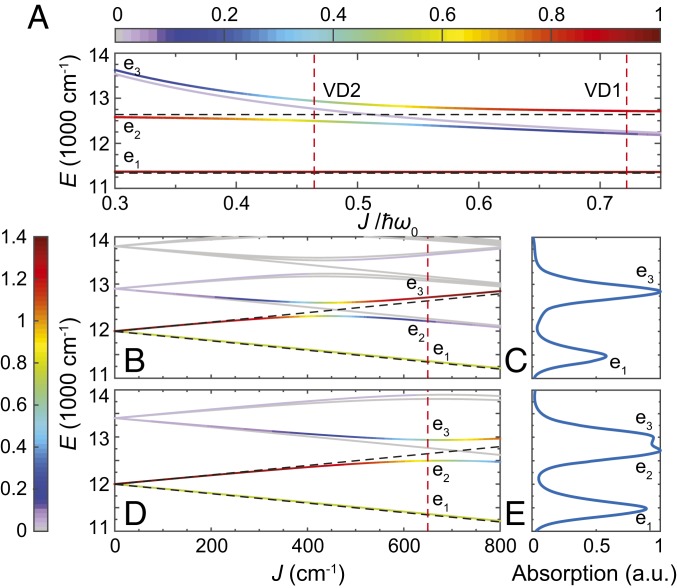
To demonstrate the effects of exciton-vibrational resonance on the distribution of oscillator strengths, both the transition energies from the zero–exciton-vibrational vacuum state to the one-exciton manifold and the oscillator strengths are calculated across the span of electronic coupling values by diagonalizing the system Hamiltonian, ${Ĥ}_{\mathrm{V}}$ (see Fig. 2). So as to avoid dark states capable of obscuring observations of coherence lifetime, we set the dihedral angle between transition dipole vectors equal to 2$\pi$/5, and both dipoles are set to be orthogonal to the vector connecting them. The parameter set selected to study the dimer was inspired by the J-aggregates of cyanine dyes C8O3 (29), in which exist a vibrational mode around 668 cm⁻¹ near-resonant to an exciton energy splitting with a very small Huang–Rhys factor $S=0.0006$. In the 2DES calculation, we consider two VDs, VD1 and VD2, at off- and near-resonant conditions, respectively. Without loss of generality, the site energy is set to 12,000 cm⁻¹, and the Huang–Rhys factor is set as $S=0.05$, typical for many pigment–protein complexes (25, 35).

Fig. 2.

The four lowest energy eigenstates in the one-exciton manifold of VD across $J/\hslash {\omega }_0$ and their corresponding electronic contribution ${\chi }_{el}$ are shown in color, with $J$ = 650 cm⁻¹ (A). The red dashes indicate the corresponding $J/\hslash {\omega }_0$ values for VD1 and VD2. The three eigenstates with largest oscillator strengths—$e_1$, $e_2$, and $e_3$—are specified in an increasing order of eigenenergies. Transition energies of (B) VD1 and (D) VD2 from the zero–exciton-vibrational ground state to the one-exciton manifold across the electronic coupling $J$, with the color representing the oscillator strength. The linear absorption spectra of (C) VD1 and (E) VD2 at $J$ = 650 cm⁻¹ are calculated via including a heat bath at 300 K. In B and D, the eigenstates of VD1 (VD2) at $J$ = 650 cm⁻¹ are indicated by the crossings between the solid lines and the red dashed line. The eigenenergies of ED are shown in black dashed lines with a splitting of $2J$. Except the degenerate case, the oscillator strengths of lower and higher electronic excited states (indicated by – and $+$) in ED are 1 – cos(2$\pi$/5) and 1 + cos(2$\pi$/5), respectively.

For all calculations described within this work, the electronic coupling $J=J_{12}$ is set to $650\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$, which is in the representative range of dimeric dyes and J-aggregates (36, 37). The vibrational energies ($\hslash {\omega }_0$) of VD1 and VD2 are set to 900 and 1,400 cm⁻¹, respectively. To better understand how the exciton-vibrational resonance ($J/\hslash {\omega }_0=0.5$) affects the properties of VD eigenstates, the electronic character of an eigenstate, ${\chi }_{el}$, is defined to be the sum of the probabilities of a vibronic eigenstate within the pure electronic states (SI Appendix, Eq. S5). When $J/\hslash {\omega }_0\lesssim 0.4$ or $J/\hslash {\omega }_0\gtrsim 0.6$, the VD eigenstates contain high electronic contributions (${\chi }_{el}=1$ features a pure electronic state) (Fig. 2A), and thus, the oscillator strengths are very similar to the ED case (Fig. 2B). The remaining region $0.4\lesssim J/\hslash {\omega }_0\lesssim 0.6$ represents avoided level crossings—although the lowest one-exciton band remains almost purely electronic—the higher bands now include vibronic and/or vibrational contributions, while the corresponding oscillator strengths are redistributed due to quantum mechanical mixing of vibrational and electronic DOFs (Fig. 2D). One important consequence attributed to this redistribution is the coherence amplitude enhancement in 2DES induced by transition dipole moment borrowing (from the electronic to the vibration transitions) (25, 26). This can be demonstrated by the enhancement of electronic character and the oscillator strength of the $e_2$ band as it moves from an off- to a near-resonance condition. The $e_2$ state in VD1 ($J/\hslash {\omega }_0=0.72$) is strongly vibrational/vibronic with a weak oscillator strength. However, under near-resonant conditions (such as VD2 with $J/\hslash {\omega }_0=0.46$), the $e_2$ state contains more electronic contributions, and this results in a significant increase of oscillator strength, which is apparent in the calculated linear absorption spectra at 300 K (Fig. 2 C and E).

To demonstrate the lifetime difference between electronic and vibronic coherence, we simulate the 2D coherent rephasing spectra of both the ED and VD models at 300 K with all-parallel pulse polarizations. The 2D spectra are calculated across the waiting time $t_2$ from 0 to 700 fs with an increment of 5 fs and are normalized (by the maximal magnitude occurring at $t_2=0$ and the corresponding 2DES shown in SI Appendix, Fig. S1). Fourier maps were generated to identify the origins associated with oscillating spectroscopic features at specific beating frequencies; these maps were built by fitting all of the $t_2$-evolving data points in the 2D spectra to exponentially decaying functions and subsequently performing a Fourier transform of the residual signal over $t_2$ (SI Appendix, Eq. S26). The technical details of the global fitting analysis behind obtaining the residual signal are introduced in ref. 37. After generating the Fourier maps, the largest amplitude of the map at each specific value of ${\omega }_2$ is collected to characterize important oscillation frequencies.

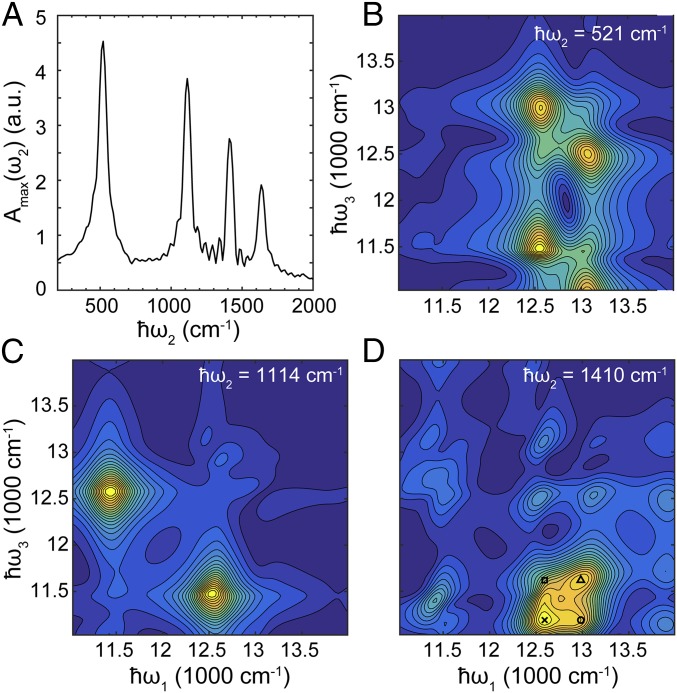
Within the ED model, there exists a single significant oscillation frequency persisting across the waiting time, which corresponds to the transition energy 2$J$ between the symmetric ($|+$〉) and the antisymmetric ($|-$〉) excitonic states (SI Appendix, Fig. S2). In VD2, four significant frequencies are found in the residual signal (Fig. 3A), including a purely vibrational frequency that originated from the ground state bleaching (GSB) pathway and the others attributed to the transitions between the $e_1$, $e_2$, and $e_3$ states. Fig. 3 B–D shows the Fourier maps corresponding to the leftmost three peaks in Fig. 3A. Fig. 3B shows the Fourier map of $\hslash {\omega }_2=521\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$, corresponding to the transition energy between states $e_2$ and $e_3$. Thus, the largest oscillatory contributions appear at the cross-peaks of $e_2$ and $e_3$. A similar situation occurs at the $e_1-e_2$ transition, shown in Fig. 3C. However, the Fourier map corresponding to the vibrational oscillations (Fig. 3D) shows that its largest oscillatory features have significant overlap with the cross-peaks of $e_1-e_2$ (${\mathrm{C}\mathrm{P}}_{21}$) and $e_1-e_3$ (${\mathrm{C}\mathrm{P}}_{31}$). For convenience we denote the cross-peaks in 2DES at $\left(\hslash {\omega }_1,\hslash {\omega }_3\right)=\left(E_m,E_n\right)$ as ${\mathrm{C}\mathrm{P}}_{mn}$.

Fig. 3.

(A) Maximum of the Fourier map indicating $t_2$ oscillations in the 2DES of VD2. Four major oscillation frequencies are found: From left to right they correspond to the $e_2-e_3$ transition, the $e_1-e_2$ transition, vibrational mode, and the $e_1-e_3$ transition, respectively. The corresponding Fourier maps are shown in B–D and in SI Appendix, Fig. S3. In D, we have found that at the lower diagonal cross-peaks of $e_1-e_2$ and $e_1-e_3$, there exist oscillations solely attributed to vibrations of electronic ground states. The markers specify the largest contributions, and their corresponding Feynman diagrams are shown in SI Appendix, Fig. S3.

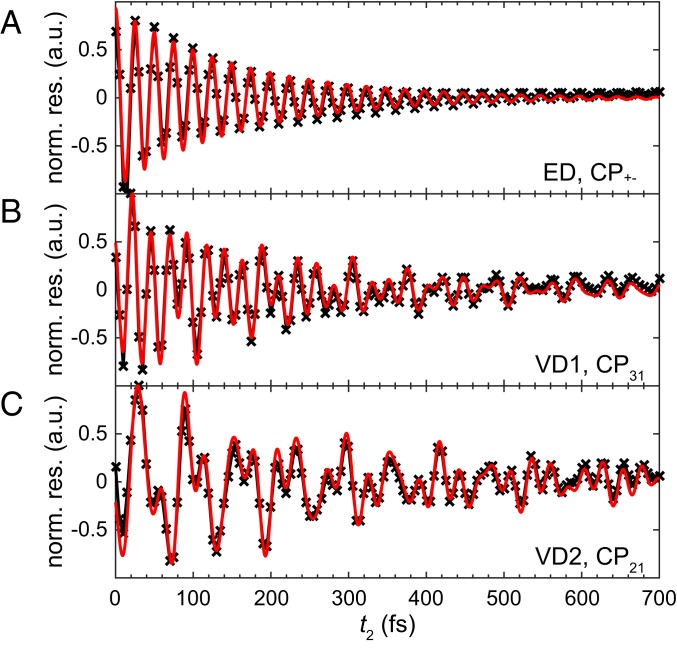
The coherence lifetime analysis of 2DES is performed by fitting the selected cross-peak signal in the residual spectra with exponentially decaying sinusoidal functions. In the ED case, there exists only one transition (between $|-\rangle$ and $|+\rangle$), and therefore, the cross-peak ${\mathrm{C}\mathrm{P}}_{+-}$ in the residual spectra is normalized and fit to a single exponentially decaying sinusoidal function. For ED, we obtain ${\tau }_{+-}=159.2$ fs and $\hslash {\omega }_2=1343\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 4A).

Fig. 4.

Normalized residual signals of the cross-peak amplitude oscillation of (A) ${\mathrm{C}\mathrm{P}}_{+-}$ in ED, (B) ${\mathrm{C}\mathrm{P}}_{31}$ in VD1, and (C) ${\mathrm{C}\mathrm{P}}_{21}$ in VD2 after subtracting the contribution of multiexponential decay from the original oscillations. The residual signal obtained from the simulated 2D spectra (black) are then fitted by exponentially decaying sinusoidal functions (red). The frequencies used for fitting are obtained from the overlap of Fourier maps at the selected cross-peak. The root-mean-square error (RMSE) of the fitting in B and C are $5.219\times 10^{-2}$ and $7.021\times 10^{-2}$, respectively.

For comparison, the same analysis has been performed on ${\mathrm{C}\mathrm{P}}_{21}$ of VD2 and ${\mathrm{C}\mathrm{P}}_{31}$ of VD1 in their respective residual 2D spectra. To minimize the discrepancies in dephasing caused by the differences in the overlap of transition frequencies and the bath spectral density, the cross-peaks from the VD models are chosen to match the transition frequencies of the ED model to the largest extent. In VD2, the ${\mathrm{C}\mathrm{P}}_{21}$ oscillation in the residual signal consists of three transition frequencies, which can be seen in Fig. 3 B–D, except the $e_1-e_3$ transition (the Fourier map of $\hslash {\omega }_2=1635\hspace{0.17em}{\mathrm{c}\mathrm{m}}^{-1}$ shows a signal at only ${\mathrm{C}\mathrm{P}}_{31}$ and ${\mathrm{C}\mathrm{P}}_{13}$; see SI Appendix, Fig. S3). After fitting the residual signal with three multi-exponentially decaying sinusoidal functions, we obtained an extralong lifetime oscillation (a coherence lifetime of 10.19 ps) possessing contributions from the vibrational mode (with an oscillation energy fit of 1,419 cm⁻¹). Furthermore, we obtained two other oscillations—attributed to the $e_1-e_2$ and $e_2-e_3$ transitions—with corresponding oscillation energies of 1,118 cm⁻¹ and 515 cm⁻¹, respectively. The fit values for coherence lifetimes at the above transitions are 331.7 fs and 272.2 fs, respectively (Fig. 4C). Similarly, in VD1, there are three oscillation frequencies involved in the ${\mathrm{C}\mathrm{P}}_{31}$ oscillation, noted by the Fourier maps (SI Appendix, Fig. S4). The coherence lifetimes extracted from the fitting are 193.1 fs, 229.1 fs, and 1.041 ps, corresponding to the $e_1-e_3$ transition, $e_2-e_3$ transition, and the vibrational mode of 924 cm⁻¹, respectively.

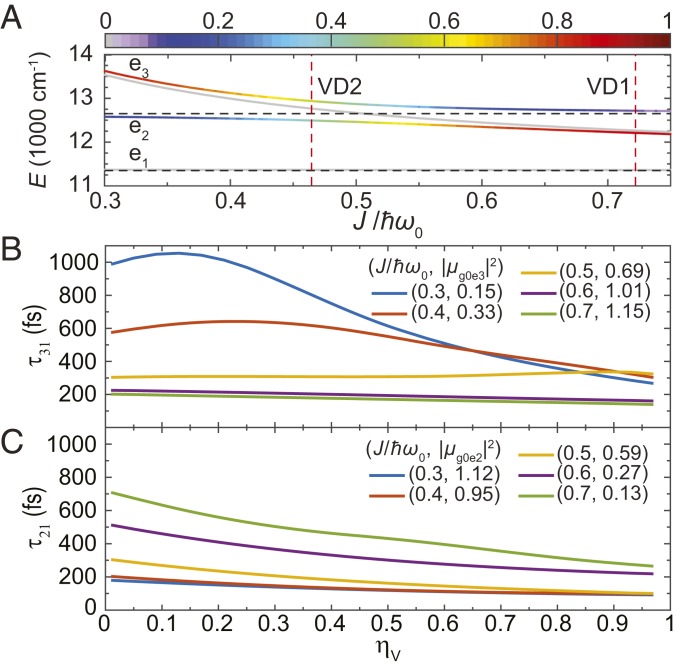
We further investigate how the coherence lifetimes in the VD models are affected by vibrational relaxation due to the coupling between the intramolecular vibration and the bath oscillators. This is done by simulating 1-ps evolutions of density matrices under different values of ${\eta }_V$, while keeping the electronic energy fluctuations constant (${\eta }_E=1$). An important characteristic indicating the amount of anticorrelated vibrational contribution in a particular state, ${\chi }_{v-}$, is introduced as $⟨g_{-}^1\left|\mathrm{T}{\mathrm{r}}_{\mathrm{E}}\rho \left(t\right)\right|g_{-}^1⟩$, where $\rho \left(t\right)$ is the system density matrix and $|g_{-}^1\equiv \left(|g^{\left(\mathrm{1,0}\right)\rangle }-|g^{\left(\mathrm{0,1}\right)\rangle }\right)/\sqrt{2}$ stands for the one-phonon state of the anticorrelated vibrational mode (Fig. 5A). Only the one-phonon state is considered, since the vibrational energies used in the VDs ($>$866.7 cm⁻¹) are much larger than the thermal energy ($\sim$208 cm⁻¹) at 300 K.

Fig. 5.

(A) Anticorrelated vibrational character ${\chi }_{v-}$ (color) of the four lowest energy eigenstates in the one-exciton manifold of VD. Coherence lifetime under the effect of vibrational relaxation for (B) ${\tau }_{31}$ and (C) ${\tau }_{21}$ comparison across different mixing parameters, $J/\hslash {\omega }_0$. The initial states are respectively set to $(|e_1⟩+⟨e_3|)/\sqrt{2}$ and $(|e_1⟩+⟨e_2|)/\sqrt{2}$ to resemble the signal generated by the first two laser pulses in 2DES, and the systems are then evolved under the effect of heat bath for 1 ps with different vibrational relaxation parameters ${\eta }_V$. The oscillator strengths of the (A) $g_0-e_3$ and (B) $g_0-e_2$ transitions are shown in 2-tuples with a corresponding value of $J/\hslash {\omega }_0$.

Here we use symmetric superposition states $(|e_1\rangle +|e_2\rangle )/\sqrt{2}$ and $(|e_1\rangle +|e_3\rangle )/\sqrt{2}$ as initial states to resemble the signal generated by the first two laser pulses in 2DES and fit the real-valued oscillations in ${\rho }_{e1e2}\left(t\right)\equiv \langle e_1\left|\rho \left(t\right)\right|e_2\rangle$ and ${\rho }_{e1e3}\left(t\right)$ with one or two exponentially decaying sinusoidal functions. The coherence lifetime of the $e_1-e_2$ transition, ${\tau }_{21}$, monotonically decreases with larger vibrational relaxation, irrespective of the $J/\hslash {\omega }_0$ value. However, increasing $J/\hslash {\omega }_0$ changes the fundamental properties of the $e_2$ state (from electronic and vibronic and to anticorrelated vibrational), and thus, we observe a decay of coherence lifetime insensitive to vibrational relaxation at $J/\hslash {\omega }_0\le 0.4$, which features electronic character with coherence lifetime ${\tau }_{21}$ in the range of 100$\sim$200 fs. When $J/\hslash {\omega }_0\ge 0.6$, the $e_2$ state contains large vibrational contributions, and ${\tau }_{21}$ exceeds 500 fs at low ${\eta }_V$. Consequently, ${\tau }_{21}$ becomes more responsive to vibrational relaxation, which can be observed as steeper slopes within Fig. 5C. A similar electronic-to-vibrational transition also occurs in ${\tau }_{31}$ when $J/\hslash {\omega }_0$ decreases from 0.7 to 0.3. However, we found that when the $e_3$ state acquires enough anticorrelated vibrational character, there appears a ${\eta }_V$ value that maximizes ${\tau }_{31}$. In the on-resonance condition ($J/\hslash {\omega }_0=0.5$), ${\tau }_{31}$ is almost immune to the vibrational relaxation even when the strength is comparable to that of the electronic energy fluctuations (${\eta }_V\simeq {\eta }_E=1$).

Discussion

We find that the coherence lifetimes in the VD cases (Fig. 4 B and C) have a significant contribution from the slowly dephasing vibrational coherence, evidenced by an amplitude $\sim$10% of the normalized residual cross-peak signal, which is absent in the ED case (Fig. 4A). This will generate an oscillatory signal that initially features fast-decaying vibronic coherence and turns into slowly decaying vibrational coherence within the picosecond scale, a phenomenon that has been observed experimentally (29). Taking VD2 as an example, this can be explained by the GSB pathways contributing to the 2DES (SI Appendix, Fig. S5), which are the major signal source of Fig. 3D. These pathways feature ground-state vibrational coherence $|g_0\rangle \langle g^{*}|$ [where $\langle g^{*}|=\langle g^{\left(\mathrm{0,1}\right)}|$ or $\langle g^{\left(\mathrm{1,0}\right)}|$] during waiting time $t_2$. From analyzing the GSB pathways, we have found that the largest two peaks are located at ($E_{e2},E_{e2}-\hslash {\omega }_0$) and ($E_{e3},E_{e3}-\hslash {\omega }_0$) (SI Appendix, Fig. S5 B and C) and the two other minor contributions at ($E_{e3},E_{e2}-\hslash {\omega }_0$) and ($E_{e2},E_{e3}-\hslash {\omega }_0$) (SI Appendix, Fig. S5 A and D) in Fig. 3D. Either ${\mathrm{C}\mathrm{P}}_{21}$ or ${\mathrm{C}\mathrm{P}}_{31}$ resides within the range of the aforementioned four peaks, and therefore, we observe vibrational coherence at both cross-peaks as long as the homogeneous broadening is not too small. Similar features appear in the VD1 case in the overlapping signal across Fourier maps at ${\mathrm{C}\mathrm{P}}_{31}$ (SI Appendix, Fig. S2 B and D).

When comparing the coherence lifetimes of the cross-peak amplitude oscillation across different homodimers, it was found that in VD2 the coherence lifetime ${\tau }_{21}$ (331.7 fs) is significantly longer than that of ED (${\tau }_{+-}=159.2$ fs). In contrast, the coherence lifetime ${\tau }_{31}$ of VD1 only shows a slight increase (193.1 fs) compared with that of the ED case. These results suggest that a longer coherence lifetime is associated with vicinity to an exciton-vibrational resonance. This result is in accordance with the theoretical work from Butkus et al. (38), who reported that the coherence lifetime extension occurs when the system is near the exciton-vibrational resonance, even with a small Huang–Rhys factor (S $<$ 0.1). A similar case using a heterodimer model with parameters inspired by the FMO complex is introduced in SI Appendix, Fig. S6. Recently, this phenomena has been observed experimentally in fluorescein heterodimers (39).

The coherence lifetime enhancement at near resonance can be better understood by tracking the fundamental character of states involved in the coherence, using the two indicators: electronic contribution ${\chi }_{el}$ (Fig. 2A) and anticorrelated vibrational character ${\chi }_{v-}$ (Fig. 5A). The $e_1$ state is almost always electronic in character (${\chi }_{el}\simeq 1$, ${\chi }_{v-}\simeq 0$) regardless of the mixing parameter $J/\hslash {\omega }_0$. The character of the $e_2$ and $e_3$ states change accordingly with $J/\hslash {\omega }_0$. When $J/\hslash {\omega }_0$ increases from 0.3 to 0.7, the $e_2$ state changes from electronic to vibronic and finally to anticorrelated vibrational, while the reverse transition occurs on the $e_3$ states simultaneously. Note that the state energetically resides between $e_2$ and $e_3$ and always possesses the smallest oscillator strength and contains a major contribution from correlated vibrations, regardless of $J/\hslash {\omega }_0$ (SI Appendix, Fig. S7). Although this state remains almost purely vibrational in the one-exciton manifold and is expected to have long coherence lifetime, the oscillator strength is too small to be identifiable by 2DES.

For coherence lifetime ${\tau }_{21}$, since the $e_2$ state possesses more anticorrelated vibrational character when $J/\hslash {\omega }_0$ increases, the coherence has more vibrational character, thus increasing the coherence lifetime. The increase of anticorrelated vibrational character can also be manifested through steeper slopes during an increase in the coupling between the intramolecular vibrational mode and the bath oscillators, ${\eta }_V$ (Fig. 5C). However, this coherence lifetime could not reach the level of ground-state vibrational coherence [about 2 ps with (${\eta }_E,{\eta }_V$) = (1, 1/3)] because the states in the one-exciton manifold are still subject to electronic energy fluctuations (${\eta }_E$). It is also worth mentioning that at $0.6<J/\hslash {\omega }_0<0.7$, the oscillator strength drops to less than 50% of the on-resonance case (20% of the pure electronic case), implying that the exciton-vibrational resonance provides a balanced optimum for both coherence lifetime and oscillator strength. The coherence lifetime ${\tau }_{31}$ can mostly be explained in the same fashion as above but with one exception: While the anticorrelated vibrational character of state $e_3$ increases, a maximum of coherence lifetime occurs at specific values of ${\eta }_V$ (Fig. 5B). The root cause of this unexpected behavior may also explain the observed insensitivity of ${\tau }_{31}$ to vibrational relaxation at $J/\hslash {\omega }_0=0.5$.

Finally, we propose experimental tests of our theoretical predictions mentioned earlier. Two-dimensional electronic spectra sensitive only to coherences can be measured by controlling the relative electric-field polarization of the four laser pulses used in a four-wave mixing experiment (40, 41). This allows us to suppress contributions to the measured third-order response from vibrational coherences and population dynamics in the zero- and one-exciton manifold, respectively. Analysis of both the amplitude and the phase of the Fourier maps can be used to identify vibronic coherences (38, 42, 43). Other experimental work has shown that the lifetimes of coherences between excited states in vibronically coupled dimers can be measured directly from the excited-state absorption signal in 2DES (28). As such, we can experimentally test if the lifetime of identified vibronic features corresponds to the lifetime range predicted in our model. One can also use synthetic approaches to tune the mixing parameter $J/\hslash {\omega }_0$ in a homodimer system by changing the linker length between the monomers (electronic coupling) or by introducing isotope substitutions (vibrational frequency). In addition, the degree of vibrational relaxation may be modified experimentally by changing the solvent (44). Finally, we note that 2DES is a powerful tool for measuring EET (45). As such, by tuning the electronic-vibrational character and thus the coherence lifetime synthetically, one can use 2DES to measure any changes in EET, thus experimentally testing the role of coherence lifetime in EET.

In conclusion, our model of vibronic dimers demonstrates the importance of the electronic and anticorrelated vibrational contribution to the mixing of electronic and vibrational DOFs, which dictates vital aspects of the coherence lifetime. From our calculated rephrasing of 2DES, we find a picosecond-long ground-state vibrational coherence as well as a resonantly enhanced coherence lifetime in the one-exciton manifold. By explicitly coupling our system to a phonon bath via the electronic energy fluctuations and vibrational relaxation, we both generate an excitation energy transport system displaying nonequilibrium dynamics and demonstrate a characteristic transition of coherence lifetime between electronic and vibrational character across the mixing parameter $J/\hslash {\omega }_0$. Importantly, in the near-resonance region, $J/\hslash {\omega }_0\approx 0.5$, the vibronic system has an optimal balance between coherence lifetime and oscillator strength. These results suggest that tuning the mixing between electronic and vibrational DOFs will likely be a useful experimental handle to control energy transport in quantum material engineering and synthetic light harvesting.