Lazy electrons in graphene

Significance

The Born–Oppenheimer approximation has had an ambiguous role in condensed matter theory for many years. Without it, solids would seem to be a “pea soup” of electrons and nuclei. On the other hand, using the adiabatic Born–Oppenheimer, one inevitably encounters multiple narrow avoided crossings of electronic energy levels as a function of nuclear positions. “Adiabatic” is key here: there exist “diabatic” Born–Oppenheimer approximations that the time-dependent tight-binding work reported here shows are much more robust. We find that the electrons are “lazy” in that they respond weakly and slowly to nuclear geometry changes. Our results suggest an electron–nuclear diabatic wave function that may have significant impact on analytical and numerical approaches to spectroscopy and dynamics of extended $\pi$-electronic systems.

Abstract

Within a tight-binding approximation, we numerically determine the time evolution of graphene electronic states in the presence of classically vibrating nuclei. There is no reliance on the Born–Oppenheimer approximation within the $p$-orbital tight-binding basis, although our approximation is “atomically adiabatic”: the basis $p$-orbitals are taken to follow nuclear positions. Our calculations show that the strict adiabatic Born–Oppenheimer approximation fails badly. We find that a diabatic (lazy electrons responding weakly to nuclear distortions) Born–Oppenheimer model provides a much more accurate picture and suggests a generalized many-body Bloch orbital-nuclear basis set for describing electron–phonon interactions in graphene.

In recent years, graphene has become perhaps the most popular 2D material studied for its optical, electronic, and mechanical properties. Electron–phonon interactions in graphene have become a focus because of their role in optical processes, thermalization of electrons, and superconductivity (1–6). Experimental measurements of electron coherence lengths as well as theoretical studies have suggested that electron–phonon interactions play a key role in relaxation of charge carriers following photoexcitation (7–9). Few theoretical studies investigate the time-dependent dynamics of electrons in the presence of phonons, and graphene electronic structure calculations typically assume static, unbroken perfect symmetry of the lattice. However, even at low temperatures, this symmetry exists only in an average sense if the vibrational modes of the nuclei are unfrozen.

The fixed nuclei Born–Oppenheimer (BO) approximation may of course be implemented for static, broken symmetry geometries. However, degenerate or nearly degenerate adiabatic electronic Bloch waves of high-symmetry nuclear configurations must very strongly mix among themselves, even for configurations within the zero point motion of the nuclei. Such extremely strong, spatially extended electronic mixing for tiny, even local, nuclear displacements cannot be physical. If it were, the relevance of Bloch band structure (10) for high-symmetry configurations would be called into question. Instead, something like the average nuclear positions holds sway, suggesting a diabatic wave function more attuned to the lazy or sluggish response of the electrons to instantaneous nuclear configurations and vindicating (to no one’s surprise) the textbook Bloch wave high symmetry treatments. Clearly, an intuitively diabatic mindset is already built into the canon of solid-state physics.

In this paper, we develop numerical evidence that a diabatic BO (DBO) approximation is much superior to the standard adiabatic one. As with the adiabatic BO (ABO) approximation, the electronic wave function in a diabatic formulation remains a function only of nuclear configuration. Electron–phonon inelastic scattering remains a clear breakdown or correction to the diabatic approximation, as it is in the adiabatic approximation. In molecular physics, electron–phonon inelastic scattering is called vibronic coupling.

Through numerical simulations, we study the explicit time evolution of electronic wave functions in the presence of lattice vibrations. Modeling the nuclei classically, we work within the single-particle picture for the electronic degrees of freedom to construct a time-dependent tight-binding electronic Hamiltonian whose matrix elements change with fluctuations in interatomic bond distances. We then directly solve the resulting time-dependent Schrödinger equation (TDSE) for the electronic states. In doing so, we are exactly solving for the electronic time evolution within the tight-binding approximation, without invoking any form of the BO approximation at all.

We do not include the back-action of the $\pi$-electronic states on the nuclear motions. This is justified by the infinitesimal importance of single electrons on the forces experienced by the carbon atoms in a large sample of graphene, and the relative unimportance of the $\pi$-electron cloud as against the in-plane orbitals responsible for most of the binding forces in graphene. However, back-action should be taken seriously in the future, especially when considering the full multielectron response to nuclear geometry fluctuations. It will also be clear from our results that the minor adjustments to the nuclear positions due to back-action as they jostle thermally will not qualitatively affect our central conclusion that $\pi$ electrons cannot and do not follow the details of nuclear motion in graphene.

Theory and Model

Vibrations break the symmetry of a periodic crystal, but for convenience and computations, symmetry may be partially restored at long range by using a supercell consisting of many primitive unit cells. The thermal motion is then taken to repeat at the supercell level. In this situation, within the ABO approximation, the motion preserves the band index $n$, where $n$ is an integer running from 1 to $N$, the number of atoms (with one basis orbital each) in the supercell. Projecting the true solution from the TDSE onto the ABO basis, we are able to understand whether the time evolution of the electron is described by the ABO approximation, which has been frequently used in condensed matter physics and quantum chemistry since its development in 1927 (11, 12). In fact, we will see a DBO approach is much closer to the truth.

We simulate a sheet of graphene with time-dependent nuclear vibrations by modeling the nuclei classically and the electronic degrees of freedom quantum mechanically (13, 14). Using a nearest-neighbor tight-binding model, we construct a time-dependent Hamiltonian for the electronic degrees of freedom. Using this Hamiltonian, we solve the TDSE and compare the true electronic states to ABO basis states.

The classical treatment of nuclear motion may be surprisingly close to reality. The “Schrödinger Correspondence Principle” (15, 16) linking the classical motion of harmonic oscillators (including infinite dimensional ones) to exact quantum evolution supports this statement. That is to say, as is discussed in ref. 16, Schrödinger showed that the mean position and momentum of quantum wave packets in a harmonic oscillator tend to obey the classical equations of motion. Thus, the treatment of nuclei as classical harmonic oscillators is a simplified yet justified approach to the investigating the quantum mechanical many-body problem.

Classical Nuclei.

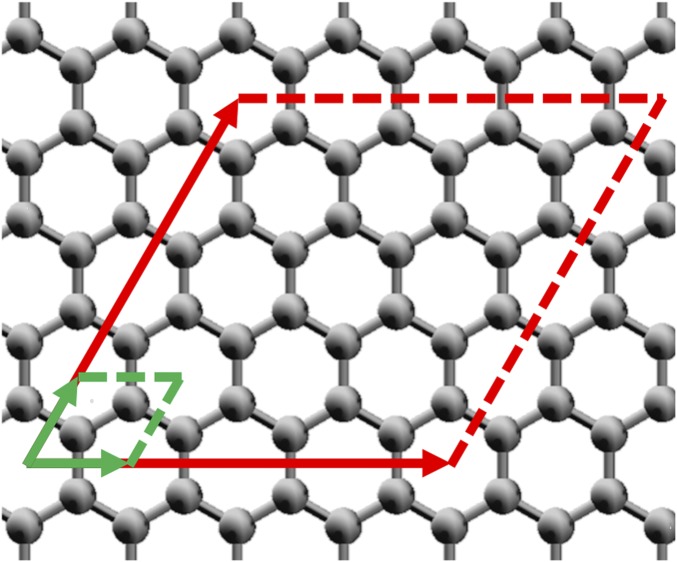
In order to consider a wide range of vibrational modes, we construct a supercell for graphene containing $N=32$ atoms, as shown in Fig. 1. The supercell lattice vectors are parallel to the standard hexagonal lattice vectors, with a scale factor of 4 such that ${\mathbf{a}}_1=\left(4a\sqrt{3},0\right)$ and ${\mathbf{a}}_2=\left(2a\sqrt{3},6a\right)$, where $a=0.142\hspace{0.17em}\text{nm}\approx 2.684a_0$ is the equilibrium bond distance, taking $a_0$ to be the Bohr radius.

Fig. 1.

Lattice vectors for the standard unit cell (green) and 32-atom supercell (red) used here for graphene’s honeycomb lattice.

We take the $i$th carbon nucleus to have position ${\mathbf{R}}_i\left(t\right)={\mathbf{R}}_{0,i}+{\tilde{\mathbf{R}}}_i\left(t\right)=\left(X_i\left(t\right),Y_i\left(t\right)\right)$, where ${\mathbf{R}}_{0,i}$ is the equilibrium position specified by the standard graphene lattice structure, and ${\tilde{\mathbf{R}}}_i\left(t\right)=\left({\tilde{X}}_i\left(t\right),{\tilde{Y}}_i\left(t\right)\right)$ is the time-dependent displacement from equilibrium. The in-plane interatomic forces that contribute to bond vibration are taken to be described by a nearest-neighbor harmonic potential

$$V\left(\left\{\mathbf{R}\left(t\right)\right\}\right)=\sum _{⟨i,j⟩}\frac{1}{2}M{\omega }_0^2{\left(\left|{\mathbf{R}}_i\left(t\right)-{\mathbf{R}}_j\left(t\right)\right|-a\right)}^2,$$ [1]

with $M=\mathrm{21,893.6}{m}_e$ as the carbon atomic mass, ${\omega }_0=0.0146\hspace{0.17em}\mathrm{r}\mathrm{a}\mathrm{d}\cdot \text{Ryd}/\hslash$ is the approximate C=C aromatic bond vibration frequency from infrared spectroscopy (17), and ${\sum }_{⟨i,j⟩}$ denotes a sum over all nearest-neighbor pairs of atoms. We acknowledge that out-of-plane vibrations could have an impact on electron–phonon coupling investigated in this paper, but we work within the 2D approximation with confidence that qualitatively our conclusions will remain unchanged. We assume toroidal boundary conditions for the supercell, allowing for atoms on one edge of the unit cell to have nearest-neighbor interactions with atoms on the opposite boundary without any acquisition of phase. This is the equivalent of considering the $\mathbf{k}=\left(\mathrm{0,0}\right)$—i.e., the phononic $\mathbf{\Gamma }$ point—solutions for the phononic band structure.

The classical eigenvalue problem for the normal modes becomes

$$M{\omega }^2{q}_i=\sum _j\frac{{\partial }^{2}V}{\partial q_i\partial q_j}{q}_j,$$ [2]

where $\mathbf{q}=\left(q_1,\dots ,q_{2N}\right)=\left({\tilde{X}}_1,{\tilde{Y}}_1,\dots ,{\tilde{X}}_N,{\tilde{Y}}_N\right)$ lists the components of each nucleus’s displacement from equilibrium. Let the $n$th eigenmode correspond to frequency $\omega ={\omega }_n$ and a normalized eigenvector $\mathbf{q}={\widehat{\mathbf{q}}}^{\left(n\right)}$. Any solution to the eigenmode problem can be expressed as a linear combination $\mathbf{q}\left(t\right)=\mathrm{R}\mathrm{e}\left[{\sum }_n{\rho }_n{e}^{\text{i}{\varphi }_n}{\widehat{\mathbf{q}}}^{\left(n\right)}{e}^{-\text{i}{\omega }_{n}t}\right]$, and the energy in the $n$th eigenmode is $U_n=\left(1/2\right)M{\omega }_n^2{\rho }_n^2$. We take each independent oscillator to have temperature $T$-dependent energy $U_n=k_{B}T$ such that ${\rho }_n=\sqrt{2k_{B}T/\left(M{\omega }_n^2\right)}$. Without loss of generality, we choose phase offsets as ${\varphi }_n=0$, and the nuclear coordinates $\left\{\mathbf{R}\left(t\right)\right\}$ are fully determined from

$$\mathbf{q}\left(t\right)=\mathrm{R}\mathrm{e}\left[\sum _n\sqrt{\frac{2k_{B}T}{M{\omega }_n^2}}{\widehat{\mathbf{q}}}^{\left(n\right)}{e}^{-\text{i}{\omega }_{n}t}\right].$$ [3]

Tight-Binding Hamiltonian.

Within the linear combination of atomic orbitals approximation, we write the single-particle electronic wave function

$${\psi }_{\mathbf{k}}\left(\mathbf{r},t\right)=\sum _i{a}_{\hspace{0.17em}\mathbf{k},i}\left(t\right){\xi }_{\mathbf{k},i}\left(\mathbf{r},t\right),$$ [4]

with Bloch wave basis state $\left|{\xi }_{\mathbf{k},i}\left(t\right)\right.⟩$ defined as

$${\xi }_{\mathbf{k},i}\left(\mathbf{r},t\right)=\frac{1}{\sqrt{\mathrm{\Omega }}}\sum _{\mathbf{s}}{e}^{\text{i}\mathbf{k}\cdot \mathbf{s}}\varphi \left(\mathbf{r}-{\mathbf{R}}_i\left(t\right)-\mathbf{s}\right),$$ [5]

where $\varphi \left(\mathbf{r}-{\mathbf{R}}_i\left(t\right)\right)\equiv {\varphi }_i\left(\mathbf{r},t\right)$ is the $2p_z$ atomic orbital centered on the $i$th nucleus, $\mathrm{\Omega }$ is the number of unit cells in the sample, and $\mathbf{s}$ is a lattice vector. Taking the onsite energies to vanish, the nearest-neighbor hopping integrals for the tight-binding Hamiltonian are

$$H_{ij}\left(t\right)=-h_0\exp \left[-b\left(\frac{R_{ij}\left(t\right)}{a}-1\right)\right],$$ [6]

where $R_{ij}\left(t\right)=\left|{\mathbf{R}}_i\left(t\right)-{\mathbf{R}}_j\left(t\right)\right|$, $h_0=2.7\hspace{0.17em}\text{eV}\approx 0.198\hspace{0.17em}\text{Ryd}$, and $b=3.37$ (18). The exponential parametrization tight-binding Hamiltonian is well-established in the literature, and the constants obtained from ref. 18 agree with the experimental result $\left|\partial H_{ij}/\partial R_{ij}\right|=6.4\hspace{0.17em}\text{eV}$. The overlap between any adjacent $2p_z$ orbitals vanishes: $⟨{\varphi }_i\left(t\right)\mid {\varphi }_j\left(t\right)⟩={\delta }_{ij}$.

Electronic Wave Function.

As an initial condition, we use a Bloch state with $\mathbf{k}$ such that ${\psi }_{\mathbf{k}}^{TD}\left(\mathbf{r},0\right)={\psi }_{n,\mathbf{k}}^{ABO}\left(\mathbf{r},0\right)$. This is an ABO fixed-nuclei electronic state for some initial nuclear configuration.

Solving the time-dependent tight-binding Hamiltonian numerically as the nuclei vibrate, we calculate the electronic wave function ${\psi }_{\mathbf{k}}^{TD}\left(\mathbf{r},t\right)$ without any reliance on the BO wave function ${\psi }_{n,\mathbf{k}}^{ABO}\left(\mathbf{r},t\right)$. The overlap of these 2 electronic states is used to assess how closely the electronic wave function adheres to the ABO approximation.

TDSE Solution.

The time-evolving electronic wave function is calculated using the TDSE $\text{i}\hslash \frac{\mathrm{d}}{\mathrm{d}t}\left|{\psi }_{\mathbf{k}}^{TD}\left(t\right)\right.⟩=Ĥ\left(t\right)\left|{\psi }_{\mathbf{k}}^{TD}\left(t\right)\right.⟩$. From Eq. 4, we have

$$\text{i}\hslash \frac{\mathrm{d}{a}_{\mathbf{k},i}}{\mathrm{d}t}=\sum _j{\left[H_{\mathbf{k}}\left(t_{\alpha }\right)\right]}_{ij}{a}_{\mathbf{k},j}\left(t\right),$$ [7]

where we have used the common tight-binding approximation $⟨{\varphi }_i\left(t\right)\mid {\varphi }_j\left(t\right)⟩={\delta }_{ij}$. Without the latter assumption of vanishing overlap between nearest-neighbor orbitals, in general one finds an additional term in the TDSE dependent upon $d\mathbf{R}/dt$ and $\partial S_{ij}/\partial R_{ij}$, where $S_{ij}=⟨{\varphi }_i\left(t\right)\mid {\varphi }_j\left(t\right)⟩$ (13). However, assuming vanishing nearest-neighbor overlap eliminates this term. As an initial condition, we may choose any arbitrary tight-binding state, but in our simulations, we will specifically select BO states—described in the following subsection—for the $t=0$ wave function such that ${\psi }_{\mathbf{k}}^{TD}\left(\mathbf{r},0\right)={\psi }_{n,\mathbf{k}}^{ABO}\left(\mathbf{r},0\right)$.

We also note that the supercell wave vector $\mathbf{k}$, which labels an eigenvalue of the operator that translates a Bloch state by a supercell lattice vector, is conserved in the time evolution due to translational symmetry. Thus, the wave function ${\psi }_{\mathbf{k}}^{TD}\left(\mathbf{r},t\right)$ retains the label $\mathbf{k}$ for all times $t$. The electronic character itself is expected to change over time, and retention of electronic character is measured by computing the squared modulus electronic autocorrelation $A_{\mathbf{k}}\left(t\right)={\left|⟨{\psi }_{\mathbf{k}}^{TD}\left(0\right)\left|{\psi }_{\mathbf{k}}^{TD}\left(t\right)\right.⟩\right|}^2$. This value indicates the probability of overlap of the true time-evolved wave function with the initial state, thus indicating the degree to which electronic character is preserved up to an overall phase.

ABO Approximation.

A discussion of the ABO approximation and its application to the time-dependent Hamiltonian $Ĥ\left(t\right)$ constructed previously is presented in SI Appendix, Supporting Information Text. For reference, we solve the TISE within the BO approximation $Ĥ\left(t_{\alpha }\right)\left|{\psi }_{n,\mathbf{k}}^{ABO}\left(t_{\alpha }\right)\right.⟩=E_{n,\mathbf{k}}\left(t_{\alpha }\right)\left|{\psi }_{n,\mathbf{k}}^{ABO}\left(t_{\alpha }\right)\right.⟩$ at various time points $\left\{t_{\alpha }\right\}$ for the coefficients $\left\{a_i^{\left(n\right)}\left(t_{\alpha }\right)\right\}$, resulting in a dispersion relation $E_{n,\mathbf{k}}\left(t_{\alpha }\right)$ with $N=32$ bands indexed by $n$.

Thus, the TISE results in the eigenvalue problem

$$\sum _j\left({\left[H_{\mathbf{k}}\left(t_{\alpha }\right)\right]}_{ij}-E_{\mathbf{k}}\left(t_{\alpha }\right){\delta }_{ij}\right)a_{\mathbf{k},j}^{\left(n\right)}\left(t_{\alpha }\right)=0,$$ [8]

where ${\left[H_{\mathbf{k}}\left(t_{\alpha }\right)\right]}_{ij}=⟨{\xi }_{\mathbf{k},i}\left(t_{\alpha }\right)\left|Ĥ\left(t_{\alpha }\right)\right|{\xi }_{\mathbf{k},j}\left(t_{\alpha }\right)⟩$. In the ABO approximation, an electronic state that begins in the $n$th band with supercell wave vector $\mathbf{k}$ will always remain on the same band by definition, and the character of the state at some time is fully dependent on the molecular geometry at that fixed instant. In other words, the ABO approximation (and BO states more generally) are memoryless. The supercell wave vector $\mathbf{k}$ is once again conserved in the time evolution, as was the case for the TDSE solution. Thus, the time-dependent fluctuations in the energy eigenvalues $\left\{E_{n,\mathbf{k}}\left(t\right)\right\}$ for a fixed supercell wave vector $\mathbf{k}$ correspond to tracing out time-dependent paths on the adiabatic potential energy surfaces $E_n\left(\left\{\mathbf{R}\left(t\right)\right\}\right)$, not on the reciprocal space bands. We emphasize that within ABO, both the quantum number $n$ and the supercell wave vector $\mathbf{k}$ are indeed preserved in the time evolution within ABO, while for the TDSE solution, the supercell wave vector $\mathbf{k}$ is preserved and band index $n$ is not a good quantum number. The supercell band structure $E_{n,\mathbf{k}}\left(t_{\alpha }\right)$ is shown for the 32-atom unit cell for an arbitrarily chosen time and nuclear displacement in Fig. 2. By linearly scaling the lattice vectors, the supercell’s Brillouin zone retains the symmetries of the standard graphene Brillouin zone. It can be easily shown that choosing an even scale factor of 4 maps the Dirac cones onto the $\mathbf{K}$ and $\mathbf{K}\prime$ points of the supercell Brillouin zone as well.

Fig. 2.

Band structure shown at an arbitrary time point using the graphene supercell. The symmetry of the standard Brillouin zone still exists, and the Dirac cones line up with the $\mathbf{K}$ points.

Numerical Methods.

In our simulation, we choose amplitudes for the vibrational eigenmodes corresponding approximately to room temperature, $T=300\hspace{0.17em}\text{K}$. In the time domain, our simulation runs from 0 to $\mathrm{30,000}\hspace{0.17em}\hslash /\text{Ryd}$, sampling such that $t_{\alpha +1}-t_{\alpha }=1\hspace{0.17em}\hslash /\text{Ryd}$.

$\mathbf{\Gamma }$ Point, Lowest Nondegenerate State.

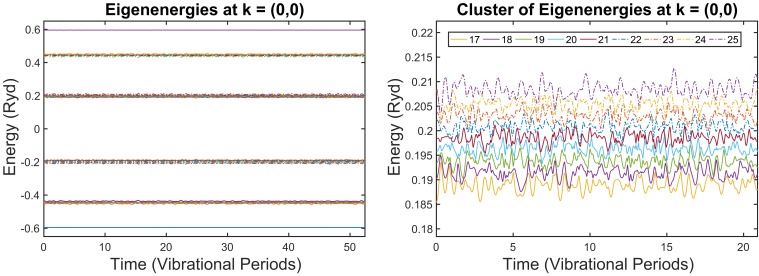
For reference we calculate the ABO band structure at every time $t_{\alpha }$ using $H_{{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t_{\alpha }\right)$ where ${\mathbf{k}}_{\mathbf{\Gamma }}=\left(\mathrm{0,0}\right)$. We first examine the time evolution of the ground electronic state (band index $n=1$) at ${\mathbf{k}}_{\mathbf{\Gamma }}$. From Fig. 3, we can clearly see that the lowest nondegenerate state is energetically separated from the $n=2$ band by $\approx 0.15\hspace{0.17em}\text{Ryd}$. Due to this energetic separation, there are few if any true avoided crossings in between the $n=1$ and $n=2$ potential energy surfaces. From the Landau–Zener formula, this would suggest that time evolving $\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩$ for initial condition $\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(0\right)\right.⟩=\left|{\psi }_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}^{ABO}\left(0\right)\right.⟩$ would allow overlap probability $P_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}^{ABO}\left(t\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$ to remain near 1 for all times. Moreover, we would expect that the squared modulus of the autocorrelation $A_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$ would also remain near 1, as electronic character should be preserved if 2 adiabatic potential energy surfaces are far from crossing. For electronic states on energetically isolated potential energy surfaces like these, we would expect the ABO approximation to provide a reasonable picture of the time evolution, at least for our small supercell, as the electronic wave function should closely match the Born-Oppenheimer state on the band in which it began. Thus, electronic character is preserved, and the BO basis predicts this reasonably due to a lack of avoided crossings. This situation changes radically for clusters of nearly degenerate states.

Fig. 3.

Time-dependent energy spectrum $E_n\left(t\right)$ at the $\mathbf{\Gamma }$ point, where $\mathbf{k}=\left(\mathrm{0,0}\right)$: the full spectrum (Left) and the cluster-containing band (Right) ($n=18$). On the abscissa, we have plotted time in terms the number of cycles of the shortest vibrational mode, which in our $N=32$ atom simulation is 190.679 $\hslash /\text{Ryd}$.

$\mathbf{\Gamma }$ Point, Nearly Degenerate State.

It is abundantly clear from Fig. 3 that, as a function of time, the band energies fluctuate significantly; nearly degenerate bands suffer avoided crossings in time. In particular, at the $\mathbf{\Gamma }$ point, we find 2 distinct clusters of 9 bands each—1 below and 1 above the Fermi energy—caused by the breaking of degeneracy due to nuclear displacements. The electronic states corresponding to the bands in these clusters are of particular interest; as suggested by time-dependent perturbation theory, we would expect these states to be highly coupled, making electronic time evolution unlikely to be adiabatic. Without loss of generality, we choose to investigate the behavior of the electronic state corresponding to band index $n=18$, marked by the purple band in Fig. 3.

Additionally, we measure the preservation of electronic character by calculating the squared modulus of the autocorrelation function $A_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$. A decay of this autocorrelation from 1 indicates that the electronic character of the initial state is not preserved in the time evolution.

Near $\mathbf{K}$ Point.

Experimental optical excitation of graphene electrons is commonly performed with photons of energy $\approx 1.5\hspace{0.17em}\text{eV}$ for electrons that are near the Dirac cones (19–21). We examine the behavior of electronic states with wave vector ${\mathbf{k}}_e=\left(k_{e,x},0\right)$ such that $E_{17,{\mathbf{k}}_e}\left(t\right)-E_{16,{\mathbf{k}}_e}\left(t\right)\approx 1.5\hspace{0.17em}\text{eV}$ for all $t$. As with the $\mathbf{\Gamma }$ point cases, we find that the bands tend to cluster where degeneracies of the bands within the supercell’s reduced Brillouin zone have been broken. Here, we select band $n=18$ to investigate electron time evolution (SI Appendix, Fig. S1); bands 18 and 19 exhibit numerous avoided crossings in the time domain.

As with the $\mathbf{\Gamma }$ point case, we solve Eq. 8 for $E_{18,{\mathbf{k}}_e}\left(t\right)$ and $\left|{\psi }_{18,{\mathbf{k}}_e}^{ABO}\left(t\right)\right.⟩$ and use $\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(0\right)\right.⟩=\left|{\psi }_{18,{\mathbf{k}}_e}^{ABO}\left(0\right)\right.⟩$ as the initial condition for the TDSE. The same measures of wave function overlap probability $P_{n,{\mathbf{k}}_e}\left(t\right)={\left|⟨{\psi }_{n,{\mathbf{k}}_e}^{ABO}\left(t\right)\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(t\right)\right.⟩\right|}^2$ and the squared modulus of the autocorrelation $A_{n,{\mathbf{k}}_e}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_e}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(t\right)\right.⟩\right|}^2$ are used to determine the validity of the ABO approximation and the preservation of electronic character, respectively.

Results

In the following sections, we present the results of our simulations, comparing the ABO and true electronic states.

$\mathbf{\Gamma }$ Point, Lowest Nondegenerate State.

While the results are not plotted here, the overlap probability $P_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}^{ABO}\left(t\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$ of the ABO and true electronic wave functions as well as the squared modulus of its autocorrelation $A_{1,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$ of the true wave function remain nearly 1 for all times, as expected for the lowest nondegenerate state. The energetic separation of the lowest nondegenerate state from the first excited state at the $\mathbf{\Gamma }$ point allows little to no diabatic transfer of the electronic to another ABO potential energy surface. As a result, we conclude that $\left|{\psi }_{{\mathbf{k}}_{\mathrm{\Gamma }}}^{TD}\left(t\right)\right.⟩$ remains approximately an instantaneous eigenstate of the time-dependent Hamiltonian at all times, and electronic character is well-preserved. This simulation confirms the idea that the ABO approximation is suitable for cases in which eigenstates are reasonably energetically separated.

$\mathbf{\Gamma }$ Point, Nearly Degenerate State.

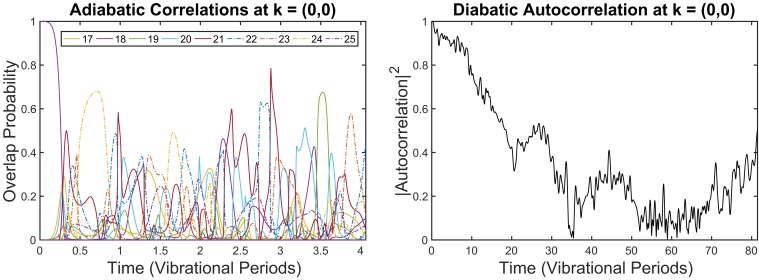
Fig. 4 shows the overlap probability $P_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}^{ABO}\left(t\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$ and $A_{18,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_{\mathbf{\Gamma }}}^{TD}\left(t\right)\right.⟩\right|}^2$. Examining Fig. 4, Left, given the initial conditions we set, the probability of overlap between the true state and the $n=18$ ABO state begins at 1. This probability drops essentially to 0 in less than $100\hspace{0.17em}\hslash /\text{Ryd}$; the periods of oscillation for the nuclear vibrational eigenmodes range from $190.7\hspace{0.17em}\hslash /\text{Ryd}$ to $657.3\hspace{0.17em}\hslash /\text{Ryd}$. Thus, we see that the ABO approximation breaks down within one vibrational period of the highest frequency eigenmode. It fails because at an avoided crossing the ABO approximation requires drastic changes in electronic character over very modest changes in nuclear configuration. The true time evolution is far more diabatic and electronic character-preserving, as we will see.

Fig. 4.

The probability of overlap $P_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)$ between each ABO state and the true time-evolved state beginning in ABO state $n=18$ at $t=0$ (Left) and the magnitude squared of the autocorrelation $A_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)$ for the same true state, showing the dramatically better persistence of a diabatic-like autocorrelation over an adiabatic one (Right). On the abscissa, time is plotted as number of cycles of the vibrational mode with the shortest period, which for $N=32$ atoms is 190.679 $\hslash /\text{Ryd}$.

Due to the incessant nuclear vibrations, the nearly degenerate manifolds of 9 ABO states are being constantly scrambled. Is there a diabatic (DBO) basis that approximates time evolution of the electronic wave function over much longer intervals, one that could be constructed in this case from the 9 ABO basis states?

From the squared modulus of the autocorrelation $A_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)$, we find that the electronic character of the actual time evolved quantum electronic state decays slowly, over a period of $\hspace{0.17em}10^4\hspace{0.17em}\hslash /\text{Ryd}$. This is 100 times slower that the period of nuclear vibrations. Since the nuclei are moving classically, yet the electronic state is remaining stable, we have unambiguous evidence of the prevalence of a diabatic evolution in favor of an adiabatic one.

Near $\mathbf{K}$ Point.

We present the overlap probabilities $P_{n,{\mathbf{k}}_e}\left(t\right)={\left|⟨{\psi }_{n,{\mathbf{k}}_e}^{ABO}\left(t\right)\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(t\right)\right.⟩\right|}^2$ and autocorrelation squared modulus $A_{18,{\mathbf{k}}_e}\left(t\right)={\left|⟨{\psi }_{{\mathbf{k}}_e}^{TD}\left(0\right)\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(t\right)\right.⟩\right|}^2$ for an electronic state near the $\mathbf{K}$ point in SI Appendix, Fig. S2. The scenario is similar to the $\mathbf{\Gamma }$ point case, where we see clustering of bands. Due to the folding of the Brillouin zone, $E_{n,{\mathbf{k}}_e}\left(t\right)$ has fewer bands per cluster than that of the $E_{n,{\mathbf{k}}_{\mathbf{\Gamma }}}\left(t\right)$. The time-dependent tight-binding electronic state $\left|{\psi }_{{\mathbf{k}}_e}^{TD}\left(t\right)\right.⟩$ overlaps substantially but erratically with ABO states 17, 18, and 19. As with the $\mathbf{\Gamma }$ point case, the ABO approximation breaks down within a timescale less than the highest nuclear oscillator period due to its prediction of rapid state change near an avoided crossing or conical intersection.

The autocorrelation function of the time-dependent tight-binding electronic state decays over time, although much less quickly than the ABO states at the $\mathbf{\Gamma }$ point. We can conclude that the electronic state loses its character at a timescale much larger than the vibrational period of the classical nuclear oscillations, in a manner highly suggestive of diabatic time evolution.

Extension to Larger Graphene Sample.

The eventual decay of the autocorrelation function is reminiscent of the initial sinusoidal behavior of a state that begins in a superposition of eigenstates in a 2-state system. When the eigenbasis is larger, the autocorrelation of any such initial state takes much longer to return to the original state. In a system whose adiabatic states are constantly changing due to the nuclear vibrations, an adiabatic state is no longer an eigenstate of the electronic Hamiltonian once the nuclei have shifted slightly. As a result, we see decay of the autocorrelation, which within any reasonable time, will likely not return to 1.

As described previously, the clustering of ABO bands tends to indicate whether or not an ABO state will mix with states with similar energies in a diabatic time evolution regime. We have confirmed that such clustering—and the avoided crossings that appear and disappear in the time domain—continues to appear with larger choices of supercells (SI Appendix, Fig. S3). At $N=50$ (a $5\times 10$ supercell), we have 50 bands, as expected, and the clustering of bands depends on the folding of the Brillouin zone.

Our representative simulation choosing an initial condition from an ABO state within one of these clusters similarly found that by $t=\mathrm{10,000}\hspace{0.17em}\hslash \text{/Ryd}$, the autocorrelation function slowly decayed to $\approx 0.6$ over the course of several vibrational periods (SI Appendix, Fig. S4). Our simulations, otherwise restricted by computational memory limits, demonstrate consistency of our conclusions regarding diabatic time evolution at various size scales of the graphene supercell.

Many-Body DBO Approximation.

We have said that the electrons in our simulations are lazy in some sense. However, they still evolve in time. Since the nuclear motion is taken to be classical here, with no back-reaction, we are also blind to electron–phonon inelastic scattering. However, we are not under the illusion that any simple guess for many-body wave functions can be essentially exact. What we strive for is something far better than the ABO Ansatz. We believe the numerical results strongly suggest such a guess, which we present now.

The present calculation took the $s$- and $p$-orbital backbone to give rise to a set of harmonic interactions, and the $p_z\hspace{0.17em}\pi$-orbital coefficients were treated exactly within tight binding and the time dependence induced by classically moving nuclei. The coupled equations of motion for the $\pi$-electron orbital coefficients owes nothing to the Born-Oppenheimer approximation, The exact time dependence turns out to be quite well approximated by the following hybrid of adiabatic and diabatic approximations: the atomic $\pi$ orbitals were taken to be bodily dragged anywhere the nuclei went; we can say the basis was “atomically adiabatic.” However, in setting free the coefficients of the orbital expansion of the molecular wave function, we found that the “molecularly diabatic” description based on the atomically adiabatic orbitals is very close to reality.

The division into coexisting adiabatic and diabatic worlds makes a great deal of sense when one considers relative timescales: the ability of a closely bound electron to follow a lone nucleus is given by a short timescale roughly on the order of $\hslash /e_{sp}$, where $e_{sp}$ the $s$-$p$ energy splitting. We can also expect the backbone in-plane molecular orbital system to behave adiabatically. It is too much to expect the extended $\pi$-electronic molecular wave function to follow adiabatically, making radical changes over many units cells for even very small and local nuclear displacements happening in a fraction of a vibrational period. Electronic states become sluggish or lazy compared to what would need to have been very fast adiabatic changes. This is a manifestation of the ubiquitous and unrelenting problem of close avoided crossings in the adiabatic picture. The electrons begin to track longer time and distance changes, content with something like average nuclear positions and not their faster fluctuations. If this were not the case, the relevance of the usual high symmetry, textbook Bloch wave analysis would be suspect.

How do we encode a diabatic nature into an appropriate many-body wave function? Starting with the Bloch wave function,

$${\psi }_{\mathbf{k}}\left(\mathbf{r}\right)=\frac{1}{\sqrt{N}}\sum _{\ell }{e}^{\text{i}\mathbf{k}\cdot {\mathbf{R}}_{\ell }}\varphi \left(\mathbf{r}-{\mathbf{R}}_{\ell }\right),$$ [9]

the key is to relax the idea that the nuclear sites ${\mathbf{R}}_n$ in the wave function above belong only to fixed high-symmetry positions and, instead, allow the nuclear coordinates within the familiar Bloch wave function to move, dragging their orbital $\varphi \left(\mathbf{r}-{\mathbf{R}}_n\right)$ with them. However, the nuclear positions cannot vary uninhibited: the nuclear excursions are taken to be moderated by a nuclear vibrational wave function: $\chi \left(\mathit{\eta },\mathbf{R}\right)$,

$${\psi }_{\mathbf{k}}\left(\mathbf{r},\mathbf{R}\right)=\frac{e^{\text{i}\mathbf{k}\cdot \mathbf{r}}}{\sqrt{N}}\sum _{\ell }\varphi \left(\mathbf{r}-{\mathbf{R}}_{\ell }\right)\chi \left(\mathit{\eta },\mathbf{R}\right),$$ [10]

where $\chi \left(\mathit{\eta },\mathbf{R}\right)$ is a normal mode eigenfunction, i.e.,

$$\left|\chi \right.⟩=\prod _n\left|{\eta }_n\right.⟩,$$ [11]

with

$$\begin{array}{ccc}\hfill ⟨{\xi }_n|{\eta }_n⟩=\frac{1}{\sqrt{2^{{\eta }_n}\hspace{0.17em}{\eta }_n!}}{\left(\frac{m{\omega }_n}{\pi \hslash }\right)}^{1/4}{e}^{-\frac{m{\omega }_n{\xi }_n^2}{2\hslash }}{H}_{{\eta }_n}\left(\sqrt{\frac{m{\omega }_n}{\hslash }}{\xi }_n\right),& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ [12]

and the normal modes ${\xi }_n$ are known linear combinations of the ${\mathbf{R}}_{\ell }$. Note that with the phase factor $e^{\text{i}\mathbf{k}\cdot \mathbf{r}}$, Eq. 10 extends Bloch Theorem to situations where it does not strictly apply. We call this the diabatic Bloch wave, or DBW, approach. It is a specification of diabatic, approximate many-body eigenfunctions, introduced here as far superior to traditional ABO states.

The DBW Ansatz is not yet a roadmap for a first principles many-body approach, because we are addressing only a single body electronic wave function, together with a many-body phonon basis. Here, only the Bloch orbitals are treated diabatically.

The DBW wave functions form a complete basis with which to expand more accurate eigenfunctions. Their simple analytical form makes them easy to work with. The real utility of this basis will become clear if it (and its extensions) perform well for spectroscopic matrix elements, bilayer systems, description of excitons, and beyond. These applications of the DBW remain for future work.

Summary

In this paper, we examined the time evolution of electronic states in graphene in the presence of classically modeled nuclear vibrations. Parameterizing the tight-binding Hamiltonian as a function of classically time-varying interatomic bond distances, we find that the electronic states generally tend to preserve their character over many typical vibrational periods in the presence of vibrations from many modes. This is diabatic, not adiabatic, behavior. The electrons may be described as “lazy,” in that they respond weakly and slowly compared to nuclear geometry changes. The ABO approximation predicts that near these avoided crossings, the electronic state would exhibit rapid changes in character which are not seen in the wave function calculated from the TDSE.

This is in stark contrast to many small molecules, but other molecules are sometimes best described by diabatic rather than adiabatic approximations; there is a substantial literature regarding this (see, for example, ref. 22 and references therein). By solving the TDSE, the true electronic wave function was projected onto the ABO basis. We find rapid decay of the adiabatic states, on the order of one vibrational period, and a few “revivals” over a short period. Not much insight is gained in the adiabatic picture; it is likely to become even less informative as the size of the supercell is taken to be larger. Within the ABO framework, we see that the inclusion of lattice vibrations leads to the appearance of numerous avoided crossings in the supercell band structure.

We have shown that, within one vibrational period, the ABO approximation breaks down because the actual time evolution of the electronic state is highly diabatic. A diabatic basis formed from a superposition of ABO states may provide a much better starting point spectroscopy, electron–phonon interactions and scattering, excitons, and more.