Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Aug 8;10(17):4914–4919. doi: 10.1021/acs.jpclett.9b01983

Accessing the Accuracy of Density Functional Theory through Structure and Dynamics of the Water–Air Interface

Tatsuhiko Ohto †, Mayank Dodia ‡, Jianhang Xu §, Sho Imoto ‡, Fujie Tang §, Frederik Zysk ∥, Thomas D Kühne ∥, Yasuteru Shigeta ⊥,∇, Mischa Bonn ‡, Xifan Wu §, Yuki Nagata ‡,*
PMCID: PMC6748669  PMID: 31393136

Abstract

graphic file with name jz9b01983_0004.jpg

Density functional theory-based molecular dynamics simulations are increasingly being used for simulating aqueous interfaces. Nonetheless, the choice of the appropriate density functional, critically affecting the outcome of the simulation, has remained arbitrary. Here, we assess the performance of various exchange–correlation (XC) functionals, based on the metrics relevant to sum-frequency generation spectroscopy. The structure and dynamics of water at the water–air interface are governed by heterogeneous intermolecular interactions, thereby providing a critical benchmark for XC functionals. We find that the XC functionals constrained by exact functional conditions (revPBE and revPBE0) with the dispersion correction show excellent performance. The poor performance of the empirically optimized density functional (M06-L) indicates the importance of satisfying the exact functional condition. Understanding the performance of different XC functionals can aid in resolving the controversial interpretation of the interfacial water structure and direct the design of novel, improved XC functionals better suited to describing the heterogeneous interactions in condensed phases.

Density functional theory-based molecular dynamics (DFT-MD) simulation is a technique for monitoring molecular motions based on the forces calculated using DFT exchange–correlation (XC) methods.1 While the majority of DFT-MD simulations have employed the generalized gradient approximation (GGA),2,3 the recent increase in computational resources and efficient algorithms have allowed for the use of higher-level DFT functionals such as meta-GGA4,5 and hybrid-GGA6,7 in DFT-MD simulations. Because DFT-MD can deal with complex liquid–solid and liquid–gas interfaces without any empirical force field modeling, it is increasingly being used for gaining molecular-level insight into the structure and dynamics of water at aqueous interfaces.8−14

Within the DFT framework, the accuracy of the predicted water properties is sensitive to the adopted XC approximations. Properties of bulk water as well as interfacial water predicted by DFT by applying low levels XC approximations such as GGA are sometimes unphysical. For example, GGA functionals tend to underestimate both the density of bulk water15,16 and its surface tension.17,18 These limitations arise from three significant drawbacks: (1) GGA methods fail to recover the nonlocal correlation necessary to account for van der Waals (vdW) interactions.16,19,20 (2) GGA methods, which depend only on electronic density n(r) and its gradient ∇n(r), provide inaccurate energetics, in particular, for strongly correlated systems.21 (3) GGA methods suffer from self-interaction error.22 These three drawbacks may be circumvented by the addition of van der Waals corrections, the extension of GGA to meta-GGA by adding a ∇2n(r)-dependency in the XC functional, and the extension of GGA to hybrid-GGA by mixing exact-exchange with GGA exchange energy, respectively. Although the accuracy of the GGA, meta-GGA, and hybrid-GGA functionals for water has been assessed in the gas phase or in the bulk, there is no rigorous and systematic assessment of the XC functionals for describing the structure and dynamics of interfacial water. Because a water molecule experiences heterogeneous intermolecular interaction at the interface unlike in the bulk, the systematic comparison of DFT-MD data at the different levels of theory can provide a unique and critical platform for examining DFT accuracy.

In this work, we explore the effect of meta-GGA and hybrid-GGA functionals on the structure and dynamics of the interfacial water together with the bulk water. The metrics for interfacial water are relevant to the sum-frequency generation (SFG) spectroscopy, allowing for direct comparison of the simulated data with the experimental results. We find that the revPBE0-D3(0) hybrid-GGA functional shows the best performance among the testified DFT methods, while the M06-L-D3(0) meta-GGA functional shows unexpected poor performance. Subsequently, we discuss the quality of the simulated SFG spectra of O–D stretch mode in isotopically diluted water, by linking with the ranking of the XC functionals, and provide insights into the controversial interpretation of the SFG spectra.8,23−26

To evaluate the different XC functionals, we consider the metrics for the interfacial water including the thickness of the interfacial region (δ), the fraction of the interfacial water molecules with a free O–D group, the lifetime of a free O–D group (τs), average angle of the free O–D group and the surface normal (⟨θ⟩), together with the bulk water density (ρ) and radial distribution function (RDF) of bulk water (see the details in the Supporting Information). The quantities related with the interface can be connected with various SFG measurements: The fraction of interfacial water with free O–H group was estimated to be 20–25% from the SFG measurements.27,28 Time-resolved SFG measurement identified the lifetime of a free O–H group as 1.1 ps.29 Furthermore, the information on the free O–H angle was obtained from the polarization-dependent SFG measurement, providing ⟨θ⟩ = 63°.30 Although the data can be essentially obtained for the free O–D group as well, it is currently not available. Thus, we used the POLI2VS data for the reference, because the POLI2VS reproduces the data for the free O–H group accurately.30,31 Note that the simulations did not include the nuclear quantum effects, whose effects were examined with force field-based classical MD and quantum mechanical partially adiabatic centroid MD (PA-CMD) simulations (see the Supporting Information).32,33 Here, characterizing the free O–D group of the interfacial water is the key for computing the quantities related to the interfacial water. We used the optimal free O–D group definition.31 More details of the calculations are provided in the Supporting Information.

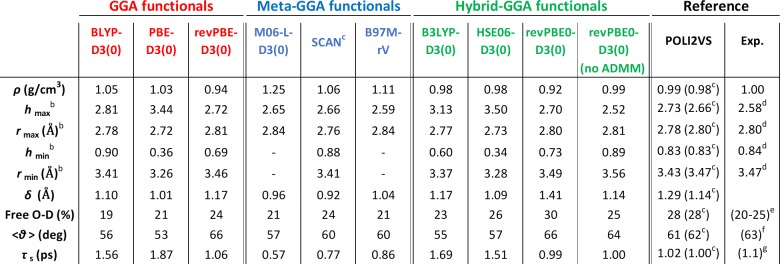
The data for selected XC functionals is summarized in Table 1. First, we focus on bulk data. The values of the bulk H2O density in our DFT-MD simulations for M06-L-D3(0), SCAN, B97M-rV, and revPBE0-D3(0) are in good agreement with previous reports,21,34−36 while 0.98 g/cm3 at both the B3LYP-D3(0) and HSE06-D3(0) have not been reported. Compared with the density of water predicted by the GGA functionals, the density predicted by hybrid-GGA functionals is relatively reduced, yet the density predicted by meta-GGA functionals is relatively elevated. Overestimation of the density of water with the meta-GGA functionals can be linked with the RDF data. As evident from the absence of the first minimum (hmin) in the RDF for B97M-rV and M06-L-D3(0) functionals, the hydration structure simulated with the meta-GGA functionals tends to be more disordered than that predicted by the hybrid-GGA. The improved density by the SCAN functional is attributed to the capture of dispersion forces beyond short-range. Under its influence, the water molecules at intermediate range on the H-bond network are attracted to each other by the nondirectional vdW interactions. As a result, the predicted water structure is softened by the increased population of interstitial water molecules.35

Table 1. Bulk and Interfacial Water Data Using Various DFT Methodsa.

graphic file with name jz9b01983_0003.jpg

Open in a new tab
a

The average error bars for ρ, hmax, rmax, hmin, rmin, δ, Free O–D %, ⟨θ⟩, and τs, are 0.01 g/cm3, 0.05, 0.01 Å, 0.03, 0.03 Å, 1.0%, 1.0°, and 0.1 ps, respectively.

b

hmax (rmax) and hmin (rmin) refer to the height (position) of the first maximum and first minimum of the RDF, respectively.

c

Simulations performed using 128 D2O molecules.

d

RDF data from ref (37).

e

O–H data from refs (27 and 28).

f

O–H data from ref (30).

g

O–H data from ref (29).

Subsequently, we focus on the structure of the interfacial water. Our data on the thickness of the interfacial water region (δ) indicates that the meta-GGA functionals predict smaller thickness than the GGA functionals, while the hybrid-GGA functionals predict larger thickness. The opposing predictions of the meta-GGA and hybrid-GGA functionals on the thickness δ are consistent with the predicted properties of the bulk water. The different trend is also reflected in the predicted fraction of the interfacial water molecules with free O–D groups; the fraction predicted using hybrid-GGA functionals is greater than that predicted using the GGA functionals, leading to an improved description by reducing the average deviation relative to the reference from 7% to 3%. On the other hand, the meta-GGA functionals predict free O–D angles very similar to those predicted using the GGA functionals. The free O–D angle also shows the different impact of the meta-GGA and hybrid-GGA. The hybrid-GGA functionals show a deviation of 5° from the reference value, similar to the deviation for the GGA functionals, while for the meta-GGA functionals the deviation is reduced significantly to 3°. As such, the meta-GGA and hybrid-GGA functionals have a different impact on the predicted structure of water at the water–air interface.

Now, we focus on the dynamics of interfacial water. Our data show that the GGA and hybrid-GGA functionals predict the free O–D lifetimes of 1.06–1.87 ps and 0.99–1.69 ps, respectively, while the meta-GGA XC functionals predict 0.57–0.86 ps. Compared with the reference value of ∼1 ps, the meta-GGA functionals predict quite fast free O–D dynamics, while the GGA and hybrid-GGA predict relatively slower dynamics. These different time scales of the dynamics further illustrate the different impact of the meta-GGA and hybrid-GGA functionals on the predicted behavior of the interfacial water and demonstrate that a smart combination of the meta-GGA and hybrid-GGA may substantially improve the description of the interfacial water.

By using the above-listed data, we rank the performance of various XC functionals. The score for the error is computed via

graphic file with name jz9b01983_m001.jpg 1

where κij is the score of the DFT method j for the calculated property i. χi denotes the value of the quantity i computed with the method j; χiref is the reference value of the quantity i, and σi is the standard deviation for an extensive set of DFT-MD trajectories.18,38 The smaller (larger) κi means that the prediction of the XC functional is better (worse). The details of the computation can be found in the Supporting Information. Figure 1a shows κ, the averaged κij value over i, for each of the different functionals j. This graph demonstrates that the revPBE-D3(0), SCAN, and revPBE0-D3(0) are the best XC functionals at the GGA, meta-GGA, and hybrid-GGA levels of theory, respectively. Among these, the calculation using the revPBE0-D3(0) hybrid-GGA functional shows the best performance, but at a substantially elevated computational cost (see Figure 1b). The revPBE-D3(0) GGA functional provides a reasonable description of the interfacial water, at a reduced computational cost. In contrast, the M06-L-D3(0) meta-GGA functional shows rather poor performance, which is somewhat surprising, given its excellent prediction of gas-phase energetics. It is however consistent with the claim of Medvedev et al.39,40 that the XC functionals like M06-L, which does not completely obey exact functional constraints, may produce inaccurate electronic densities. Our data indicate that an accurate description of the electronic density is more critical for bulk and interfacial water than for the gas phase.

Figure 1.

Figure 1

Open in a new tab

(a) Direct comparison of the ability of different functionals to accurately predict water properties. The smaller (larger) score κ corresponds to better (worse) predictive power of the functional. (b) Computational cost for different DFT-XC functionals. The data are normalized by the cost of the revPBE-D3(0) GGA functional.

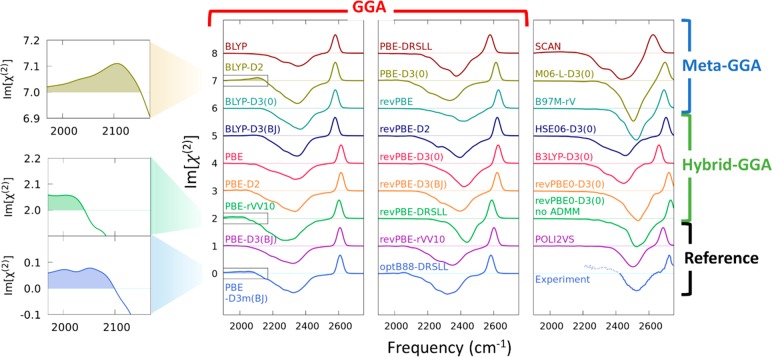
To connect the predicted structure of water with previously reported experimental SFG spectra,41 we computed the SFG response of the O–D stretch mode of interfacial HOD molecules in isotopically diluted water (O–D in H2O). The calculated spectra are displayed in Figure 2. All the simulated spectra show a sharp positive peak at 2550–2750 cm–1 and a broad negative peak centered at 2300–2500 cm–1. A positive (negative) peak corresponds to the free (hydrogen-bonded) O–D group of the interfacial water.28,42 Compared with POLI2VS data43 and experimental data obtained by the Tahara group,41 we conclude that revPBE0-D3(0) is the best for reproducing the SFG features at the isotopically diluted water–air interface. The excellent reproducibility of the vibrational spectra with the revPBE0-D3(0) functionals can also be found in the infrared spectra of the bulk water.44 Furthermore, the noticeable differences of the spectra exists with different XC functionals. For example, the spectra calculated at the PBE-D3m(BJ), BLYP-D2, and PBE-rVV10 functionals show a small, but non-negligible positive band below 2100 cm–1. This is in line with a claim of ref (24). However, Figure 1 clearly illustrates that all the XC functionals showing a positive 2100 cm–1 band do not reproduce the water properties accurately, implying that the presence of the positive 2100 cm–1 band may arise from the poor description of the interfacial water.

Figure 2.

Figure 2

Open in a new tab

Simulated SFG spectra of the O–D stretch mode in H2O for various XC functionals. The POLI2VS spectrum and experimental spectrum were obtained from refs (43) and (41), respectively. Because the experimental data was obtained for O–H in D2O, the frequency of the experimental data was scaled down by 0.73546 to convert the O–H stretch frequency to the O–D frequency. Note that a positive band below 2400 cm–1 (broken line region) in the experimental data has later been attributed to an experimental artifact of the measurement and should be absent.25,26 Each spectrum is offset by increments of 1 for clarity. The free O–D peak top of each spectrum was normalized to 2/3. The highlights of the low-frequency regions are displayed in the three panels in the left column.

We now discuss the SFG spectra simulated with the meta-GGA functionals. These show a variety of lineshapes, but all deviate somehow from the experimental data. When we focus on the data with the SCAN functional, one can notice that the negative feature is remarkably broad. In fact, the full width at half-maximum of the negative peak is 238 ± 32 cm–1, twice larger than the experimental data of 130 cm–1.41 Even compared with BLYP-D3(0) data of 189 ± 13 cm–1, the SCAN functional predicts a very broad feature elongated to the low-frequency region. These observations may explain the controversial assignment of the SFG spectra of H2O at the water–TiO2 interface,8,23 where BLYP-D3(0) does not show any positive SFG peaks in the low-frequency O–H stretch region, while the SCAN functional does indicate a positive peak in this frequency region. According to the current data, remodeling these SFG spectra with accurate XC functionals such as revPBE0-D3(0) or meta-hybrid GGA functionals such as SCAN045 is essential for resolving the controversy.

In conclusion, we have tested the quality of various GGA, meta-GGA, and hybrid-GGA functionals for a description of the structure and dynamics of water at the air–water interface. We established the significantly distinct impacts of the extension from GGA to meta-GGA and that to hybrid-GGA on the interfacial structure and dynamics. In particular, meta-GGA functionals tend to predict faster dynamics, while hybrid-GGA functionals tend to predict slower dynamics. This indicates that an appropriate combination of meta-GGA and hybrid-GGA may improve the description of interfacial water. Among the XC functionals considered here, revPBE0-D3(0) provides the best performance, while the unconstrained M06-L-D3(0) meta-GGA functional shows poor performance. Linking our results with the poor electron density prediction of the M06-L method indicates that the structure and dynamics of water at the water–air interface highlight the importance of the accurate electron density prediction.

By combining the information on the performance of the XC functional with the simulated SFG spectra of water, we found that the poor description of interfacial water tends to generate a positive low-frequency O–D stretch band. The SCAN functional tends to elongate the negative hydrogen-bonded O–D band to the low-frequency region excessively, which differs significantly from the experimental data. Again, the revPBE0-D3(0) predicts the SFG data most accurately. Our observations clearly guide the choice of the XC functional for simulating aqueous interfaces.

Computational Details

Born–Oppenheimer MD (BOMD) simulations were run using BLYP, PBE, and revPBE GGA functionals; M06-L and B97M-rV meta-GGA functionals; and B3LYP, revPBE0, and HSE06 hybrid-GGA functionals with the CP2K code,47 while Car–Parrinello48 MD (CPMD) simulation were run using the SCAN meta-GGA functional with the Quantum Espresso code.49 For hybrid-GGA functionals, we used the auxiliary density matrix method (ADMM).50 We also used various vdW correction schemes.51−56 For describing the core electrons, we used Goedecker–Teter–Hutter pseudopotentials57 and Hamann–Schlüter–Chiang–Vanderbilt norm-conserving pseudopotentials58 in BOMD and CPMD simulations, respectively. We simulated 160 D2O molecules in the simulation box (Lx, Ly, Lz) = (16.63 Å, 16.63 Å, 44.10 Å) for BOMD simulations, while 128 D2O molecules were simulated in the box (Lx, Ly, Lz) = (12.44 Å, 12.44 Å, 50.00 Å) for CPMD simulation. The water–air interface is parallel to the xy plane, and the surface normal forms the z-axis. We used the NVT ensemble with the target temperature of 300 K. Furthermore, we performed the MD simulation with the POLI2VS force field model59 for D2O.

For the SFG spectral calculations, we have used the surface-specific velocity–velocity correlation function formalism,60 which was developed for an efficient calculation of the SFG spectra with a limited length of the trajectories. The SFG spectra of isotopically diluted water can be computed from the DFT-MD trajectories of D2O by neglecting the intra/intermolecular couplings.60 The computed spectra are known to show higher frequency than the experimental data for the O–H (O–D) stretch mode, as the MD simulation with classical nuclei cannot account for nuclear quantum effects. To compensate the red-shift due to the nuclear quantum effects, we multiplied the computed frequency by a factor of 0.96.61 A similar red-shift was also confirmed through the comparison of classical and quantum simulation of the SFG spectra.62

Acknowledgments

We thank Prof. Shoichi Yamaguchi for fruitful discussions. We acknowledge the financial support from MaxWater project of Max Planck Society. X.W. was supported by National Science Foundation through Grant No. DMR-1552287. The computations were performed through the use of OCTOPUS at Cybermedia Center, Osaka University; local computing cluster at Max Planck Institute for Polymer Research, Max Planck Computing and Data Facility; and the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b01983.

  • Details of the MD and partially adiabatic centroid MD (PA-CMD) simulations, calculation protocols for target quantities, data set for MD simulations, ranking procedure, effect of ADMM, relative computational cost, simulation protocols for SFG spectra, and FWHM for the negative SFG feature (PDF)

Author Contributions

# T.O. and M.D. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

jz9b01983_si_001.pdf (1.1MB, pdf)

References

  1. Kühne T. D. Second Generation Car-Parrinello Molecular Dynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 391–406. 10.1002/wcms.1176. [DOI] [Google Scholar]
  2. Perdew J. P.; Chevary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
  3. Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  4. Becke A. D.; Roussel M. R. Exchange Holes in Inhomogeneous Systems: A Coordinate-Space Model. Phys. Rev. A 1989, 39, 3761–3767. 10.1103/PhysRevA.39.3761. [DOI] [PubMed] [Google Scholar]
  5. Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
  6. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  7. Perdew J. P.; Ernzerhof M.; Burke K. Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 1996, 105, 9982–9985. 10.1063/1.472933. [DOI] [Google Scholar]
  8. Calegari Andrade M. F.; Ko H.-Y.; Car R.; Selloni A. Structure, Polarization, and Sum Frequency Generation Spectrum of Interfacial Water on Anatase TiO2. J. Phys. Chem. Lett. 2018, 9, 6716–6721. 10.1021/acs.jpclett.8b03103. [DOI] [PubMed] [Google Scholar]
  9. Sulpizi M.; Gaigeot M. P.; Sprik M. The Silica-Water Interface: How the Silanols Determine the Surface Acidity and Modulate the Water Properties. J. Chem. Theory Comput. 2012, 8, 1037–1047. 10.1021/ct2007154. [DOI] [PubMed] [Google Scholar]
  10. Kuo I.-F. W.; Mundy C. J. An Ab Initio Molecular Dynamics Study of the Aqueous Liquid-Vapor Interface. Science 2004, 303, 658–660. 10.1126/science.1092787. [DOI] [PubMed] [Google Scholar]
  11. Ma M.; Tocci G.; Michaelides A.; Aeppli G. Fast Diffusion of Water Nanodroplets on Graphene. Nat. Mater. 2016, 15, 66–71. 10.1038/nmat4449. [DOI] [PubMed] [Google Scholar]
  12. Baer M. D.; Kuo I. F. W.; Tobias D. J.; Mundy C. J. Toward a Unified Picture of the Water Self-Ions at the Air-Water Interface: A Density Functional Theory Perspective. J. Phys. Chem. B 2014, 118, 8364–8372. 10.1021/jp501854h. [DOI] [PubMed] [Google Scholar]
  13. Kühne T. D.; Pascal T. A.; Kaxiras E.; Jung Y. New Insights into the Structure of the Vapor/Water Interface from Large-Scale First-Principles Simulations. J. Phys. Chem. Lett. 2011, 2, 105–113. 10.1021/jz101391r. [DOI] [PubMed] [Google Scholar]
  14. Kessler J.; Elgabarty H.; Spura T.; Karhan K.; Partovi-azar P.; Hassanali A. A.; Kühne T. D. Structure and Dynamics of the Instantaneous Water/Vapor Interface Revisited by Path-Integral and Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2015, 119, 10079–10086. 10.1021/acs.jpcb.5b04185. [DOI] [PubMed] [Google Scholar]
  15. Gillan M. J.; Alfè D.; Michaelides A. Perspective: How Good Is DFT for Water?. J. Chem. Phys. 2016, 144, 130901. 10.1063/1.4944633. [DOI] [PubMed] [Google Scholar]
  16. Lin I.-C.; Seitsonen A. P.; Coutinho-Neto M. D.; Tavernelli I.; Rothlisberger U. Importance of van Der Waals Interactions in Liquid Water. J. Phys. Chem. B 2009, 113, 1127–1131. 10.1021/jp806376e. [DOI] [PubMed] [Google Scholar]
  17. Nagata Y.; Ohto T.; Bonn M.; Kühne T. D. Surface Tension of Ab Initio Liquid Water at the Water-Air Interface. J. Chem. Phys. 2016, 144, 204705. 10.1063/1.4951710. [DOI] [PubMed] [Google Scholar]
  18. Ohto T.; Dodia M.; Imoto S.; Nagata Y. Structure and Dynamics of Water at the Water–Air Interface Using First-Principles Molecular Dynamics Simulations within Generalized Gradient Approximation. J. Chem. Theory Comput. 2019, 15, 595–602. 10.1021/acs.jctc.8b00567. [DOI] [PubMed] [Google Scholar]
  19. Grimme S.; Hansen A.; Brandenburg J. G.; Bannwarth C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. 10.1021/acs.chemrev.5b00533. [DOI] [PubMed] [Google Scholar]
  20. Klimeš J.; Michaelides A. Perspective: Advances and Challenges in Treating van Der Waals Dispersion Forces in Density Functional Theory. J. Chem. Phys. 2012, 137, 120901. 10.1063/1.4754130. [DOI] [PubMed] [Google Scholar]
  21. Ruiz Pestana L.; Mardirossian N.; Head-Gordon M.; Head-Gordon T. Ab Initio Molecular Dynamics Simulations of Liquid Water Using High Quality Meta-GGA Functionals. Chem. Sci. 2017, 8, 3554–3565. 10.1039/C6SC04711D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bao J. L.; Gagliardi L.; Truhlar D. G. Self-Interaction Error in Density Functional Theory: An Appraisal. J. Phys. Chem. Lett. 2018, 9, 2353–2358. 10.1021/acs.jpclett.8b00242. [DOI] [PubMed] [Google Scholar]
  23. Hosseinpour S.; Tang F.; Wang F.; Livingstone R. A.; Schlegel S. J.; Ohto T.; Bonn M.; Nagata Y.; Backus E. H. G. Chemisorbed and Physisorbed Water at the TiO2/Water Interface. J. Phys. Chem. Lett. 2017, 8, 2195–2199. 10.1021/acs.jpclett.7b00564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Liang C.; Jeon J.; Cho M. Ab Initio Modeling of the Vibrational Sum-Frequency Generation Spectrum of Interfacial Water. J. Phys. Chem. Lett. 2019, 10, 1153–1158. 10.1021/acs.jpclett.9b00291. [DOI] [PubMed] [Google Scholar]
  25. Nihonyanagi S.; Kusaka R.; Inoue K.; Adhikari A.; Yamaguchi S.; Tahara T. Accurate Determination of Complex χ(2) Spectrum of the Air/Water Interface. J. Chem. Phys. 2015, 143, 124707. 10.1063/1.4931485. [DOI] [PubMed] [Google Scholar]
  26. Yamaguchi S. Development of Single-Channel Heterodyne-Detected Sum Frequency Generation Spectroscopy and Its Application to the Water/Vapor Interface. J. Chem. Phys. 2015, 143, 034202 10.1063/1.4927067. [DOI] [PubMed] [Google Scholar]
  27. Du Q.; Freysz E.; Shen Y. R. Surface Vibrational Spectroscopic Studies of Hydrogen Bonding and Hydrophobicity. Science 1994, 264, 826–828. 10.1126/science.264.5160.826. [DOI] [PubMed] [Google Scholar]
  28. Du Q.; Superfine R.; Freysz E.; Shen Y. R. Vibrational Spectroscopy of Water at the Vapor/Water Interface. Phys. Rev. Lett. 1993, 70, 2313–2316. 10.1103/PhysRevLett.70.2313. [DOI] [PubMed] [Google Scholar]
  29. Hsieh C.-S.; Campen R. K.; Okuno M.; Backus E. H. G.; Nagata Y.; Bonn M. Mechanism of Vibrational Energy Dissipation of Free OH Groups at the Air–Water Interface. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 18780–18785. 10.1073/pnas.1314770110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sun S.; Tang F.; Imoto S.; Moberg D. R.; Ohto T.; Paesani F.; Bonn M.; Backus E. H. G.; Nagata Y. Orientational Distribution of Free O-H Groups of Interfacial Water Is Exponential. Phys. Rev. Lett. 2018, 121, 246101. 10.1103/PhysRevLett.121.246101. [DOI] [PubMed] [Google Scholar]
  31. Tang F.; Ohto T.; Hasegawa T.; Xie W. J.; Xu L.; Bonn M.; Nagata Y. Definition of Free O–H Groups of Water at the Air–Water Interface. J. Chem. Theory Comput. 2018, 14, 357–364. 10.1021/acs.jctc.7b00566. [DOI] [PubMed] [Google Scholar]
  32. Liu J.; Miller W. H.; Fanourgakis G. S.; Xantheas S. S.; Imoto S.; Saito S. Insights in Quantum Dynamical Effects in the Infrared Spectroscopy of Liquid Water from a Semiclassical Study with an Ab Initio-Based Flexible and Polarizable Force Field. J. Chem. Phys. 2011, 135, 244503. 10.1063/1.3670960. [DOI] [PubMed] [Google Scholar]
  33. Liu X.; Liu J. Critical Role of Quantum Dynamical Effects in the Raman Spectroscopy of Liquid Water. Mol. Phys. 2018, 116, 755–779. 10.1080/00268976.2018.1434907. [DOI] [Google Scholar]
  34. Del Ben M.; Hutter J.; Vandevondele J. Probing the Structural and Dynamical Properties of Liquid Water with Models Including Non-Local Electron Correlation. J. Chem. Phys. 2015, 143, 054506 10.1063/1.4927325. [DOI] [PubMed] [Google Scholar]
  35. Chen M.; Ko H.-Y.; Remsing R. C.; Calegari Andrade M. F.; Santra B.; Sun Z.; Selloni A.; Car R.; Klein M. L.; Perdew J. P.; et al. Ab Initio Theory and Modeling of Water. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 10846–10851. 10.1073/pnas.1712499114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Cheng B.; Engel E. A.; Behler J.; Dellago C.; Ceriotti M. Ab Initio Thermodynamics of Liquid and Solid Water. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 1110–1115. 10.1073/pnas.1815117116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Skinner L. B.; Huang C.; Schlesinger D.; Pettersson L. G. M.; Nilsson A.; Benmore C. J. Benchmark Oxygen-Oxygen Pair-Distribution Function of Ambient Water from X-Ray Diffraction Measurements with a Wide Q-Range. J. Chem. Phys. 2013, 138, 074506 10.1063/1.4790861. [DOI] [PubMed] [Google Scholar]
  38. Dodia M.; Ohto T.; Imoto S.; Nagata Y. Structure and Dynamics of Water at the Water–Air Interface Using First-Principles Molecular Dynamics Simulations. II. NonLocal vs Empirical van Der Waals Corrections. J. Chem. Theory Comput. 2019, 15, 3836–3843. 10.1021/acs.jctc.9b00253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Lyssenko K. A.; Bushmarinov I. S.; Medvedev M. G.; Perdew J. P.; Sun J. Density Functional Theory Is Straying from the Path toward the Exact Functional. Science 2017, 355, 49–52. 10.1126/science.aah5975. [DOI] [PubMed] [Google Scholar]
  40. Hammes-Schiffer S. A Conundrum for Density Functional Theory. Science 2017, 355, 28–29. 10.1126/science.aal3442. [DOI] [PubMed] [Google Scholar]
  41. Nihonyanagi S.; Ishiyama T.; Lee T.-K.; Yamaguchi S.; Bonn M.; Morita A.; Tahara T. Unified Molecular View of the Air/Water Interface Based on Experimental and Theoretical χ(2) Spectra of an Isotopically Diluted Water Surface. J. Am. Chem. Soc. 2011, 133, 16875–16880. 10.1021/ja2053754. [DOI] [PubMed] [Google Scholar]
  42. Bonn M.; Nagata Y.; Backus E. H. G. Molecular Structure and Dynamics of Water at the Water–Air Interface Studied with Surface-Specific Vibrational Spectroscopy. Angew. Chem., Int. Ed. 2015, 54, 5560–5576. 10.1002/anie.201411188. [DOI] [PubMed] [Google Scholar]
  43. Schaefer J.; Backus E. H. G.; Nagata Y.; Bonn M. Both Inter- and Intramolecular Coupling of O–H Groups Determine the Vibrational Response of the Water/Air Interface. J. Phys. Chem. Lett. 2016, 7, 4591–4595. 10.1021/acs.jpclett.6b02513. [DOI] [PubMed] [Google Scholar]
  44. Marsalek O.; Markland T. E. Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects. J. Phys. Chem. Lett. 2017, 8, 1545–1551. 10.1021/acs.jpclett.7b00391. [DOI] [PubMed] [Google Scholar]
  45. Hui K.; Chai J.-D. SCAN-Based Hybrid and Double-Hybrid Density Functionals from Models without Fitted Parameters. J. Chem. Phys. 2016, 144, 044114 10.1063/1.4940734. [DOI] [PubMed] [Google Scholar]
  46. Xu X.; Shen Y. R.; Tian C. Phase-Sensitive Sum Frequency Vibrational Spectroscopic Study of Air/Water Interfaces: H2O, D2O, and Diluted Isotopic Mixtures. J. Chem. Phys. 2019, 150, 144701. 10.1063/1.5081135. [DOI] [PubMed] [Google Scholar]
  47. Hutter J.; Iannuzzi M.; Schiffmann F.; Vandevondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  48. Car R.; Parrinello M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471–2474. 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
  49. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  50. Guidon M.; Hutter J.; Vandevondele J. Auxiliary Density Matrix Methods for Hartree-Fock Exchange Calculations. J. Chem. Theory Comput. 2010, 6, 2348–2364. 10.1021/ct1002225. [DOI] [PubMed] [Google Scholar]
  51. Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  52. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  53. Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  54. Smith D. G. A.; Burns L. A.; Patkowski K.; Sherrill C. D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. 10.1021/acs.jpclett.6b00780. [DOI] [PubMed] [Google Scholar]
  55. Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van Der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
  56. Vydrov O. A.; Van Voorhis T. Nonlocal van Der Waals Density Functional: The Simpler the Better. J. Chem. Phys. 2010, 133, 244103. 10.1063/1.3521275. [DOI] [PubMed] [Google Scholar]
  57. Goedecker S.; Teter M.; Hutter J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. 10.1103/PhysRevB.54.1703. [DOI] [PubMed] [Google Scholar]
  58. Hamann D. R.; Schlüter M.; Chiang C. Norm-Conserving Pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. 10.1103/PhysRevLett.43.1494. [DOI] [Google Scholar]
  59. Hasegawa T.; Tanimura Y. A Polarizable Water Model for Intramolecular and Intermolecular Vibrational Spectroscopies. J. Phys. Chem. B 2011, 115, 5545–5553. 10.1021/jp111308f. [DOI] [PubMed] [Google Scholar]
  60. Ohto T.; Usui K.; Hasegawa T.; Bonn M.; Nagata Y. Toward Ab Initio Molecular Dynamics Modeling for Sum-Frequency Generation Spectra; an Efficient Algorithm Based on Surface-Specific Velocity-Velocity Correlation Function. J. Chem. Phys. 2015, 143, 124702. 10.1063/1.4931106. [DOI] [PubMed] [Google Scholar]
  61. Smit W. J.; Tang F.; Sánchez M. A.; Backus E. H. G.; Xu L.; Hasegawa T.; Bonn M.; Bakker H. J.; Nagata Y. Excess Hydrogen Bond at the Ice-Vapor Interface around 200 K. Phys. Rev. Lett. 2017, 119, 133003. 10.1103/PhysRevLett.119.133003. [DOI] [PubMed] [Google Scholar]
  62. Medders G. R.; Paesani F. Dissecting the Molecular Structure of the Air/Water Interface from Quantum Simulations of the Sum-Frequency Generation Spectrum. J. Am. Chem. Soc. 2016, 138, 3912–3919. 10.1021/jacs.6b00893. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b01983_si_001.pdf (1.1MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES