Abstract
There are different views on which of the two forms of viral spread is more efficient in vivo between cell-free and cell-associated virus. In this study, discrete time human immunodeficiency virus models are formulated and analysed with the goal of determining the form of viral spread that is more efficient in vivo. It is shown that on its own, cell-free viral spread cannot sustain an infection owing to the low infectivity of cell-free virus and cell-associated virus can sustain an infection because of the high infectivity of cell-associated virus. When acting concurrently, cell-associated virus is more efficient in spreading the infection upon exposure to the virus. However, in the long term, the two forms of viral spread contribute almost equally. Both forms of viral spread are shown to be able to initiate an infection.
Introduction
Human immunodeficiency virus (HIV) is transmitted when infected blood, semen, vaginal fluids, or breast milk enter another person’s body. Once the virus enters the body, it can spread through target cells as a free viral particle or in cell-associated form [1, 2]. Cell-free virus, is the plasma virus, whereas cell-associated virus, is the intracellular progeny virion that has been produced but not yet budded off the manufacturing T-cell [3]. In cell-associated viral spread, the processes of budding, attachment and entry, proceed quickly at the sites of cell-to-cell contact. This partially protects the virus from the hostile extracellular environment and also concentrates the viral particles at the sites of infection [3]. In cell-free viral spread, the replicated viruses bud off from the producer cell, the virus has to diffuse and find a CD4 receptor on the CD4+ T cell, attach to the cell and finally enter the cell. Infected blood, semen, vaginal secretions, and breast milk contain both cell-free and cell-associated virus [3–5].
In vitro models have shown that cell-associated viral spread is more efficient than cell-free viral spread [2, 6–8]. However, there are different views on which of these forms of viral spread is efficient in vivo [9–12]. Understanding the mechanisms employed by the virus to spread within a host is of vital importance as this would provide useful information on treatment and vaccine development [13].
The majority of HIV transmissions occur through male-to-female transmission and the source of viral spread on this transmission route is not known (cell-free or cell-associated virus) [3, 4]. It has been shown that the levels of cell-free virus in blood and semen correlates with infectiousness [14, 15], a result that suggests that cell-free virus contributes significantly to transmission. However, transmission can also occur from individuals with undetectable cell-free virus [16], suggesting that cell-associated virus may have initiated the transmission.
Another common route of transmission is mother-to-child transmission. On this route of transmission, it was shown that the risk of HIV transmission was highly correlated with cell-associated viral load [17], a result that suggests that cell-associated virus contributes significantly to the spread of the infection. In male-to-male transmission, it has been observed that infectiousness correlates with cell-associated viral levels. There is a possibility that the form of virus efficient in transmitting the infection may vary among different routes of transmission. However, different views were obtained from sequence and phylogenetic studies [18–20], results that may lead to the conclusion that the form of transmission efficient, may not depend on the route of infection.
Even though there is growing evidence on the role of cell-associated virus in spreading the infection [10], this infection pathway has received little research attention [4] and thus its relative contributions remain elusive. Moreover, most experiments on protection from HIV acquisition are done using cell-free virus [3, 4] and thus there is need to find the contribution of cell-associated virus in spreading the infection and determine whether the outcomes of these experiments would change if cell-associated transmission pathway is also considered.
Mathematical modelling has been used as a basic tool in understanding the interplay between the HIV pathogen and the immune system and remains the mainstay in this field of research. The study [21] was one of the earliest work modelling the within host dynamics of the HIV infection. The work considered the free viral particles, susceptible and infected CD4+ T cells. Many pieces of work expanded this model to include the time delay in cell infection and viral spread and immune response, see for example [22–24] and the references therein. Several studies considered the two forms of HIV spread with the goal of determining the infection dynamics associated with the two forms of viral spread [25–28].
However, few studies have attempted to determine the relative contribution of each of the two forms of HIV spread within the host. The first study that aimed at finding the relative contribution of the different modes of viral spread is given in [29]. The study concluded that cell-to-cell viral spread was more efficient than cell-free viral spread. In 2007, another study [2] also came to the same conclusion. In the study [30], a model that considered susceptible and infected cells was formulated and fitted to the data of the study [2]. The study concluded that the two forms of viral spread contribute equally to viral spread thereby producing conflicting results to the previous results. A study that used an experimental-mathematical approach to elucidate the roles of the two forms of viral spread is given in the study [31]. The study concluded that cell-to-cell viral spread contributes over 60% of virus infection.
In this study, discrete time models which incorporate the life cycle of HIV are developed with the goal of determining the form of viral spread most efficient in vivo. Transmission of the infection maybe influenced by the presence of other sexually transmitted infections (STIs) that result in the inflammation or ulceration of the genital mucosa, type of sexual contact, genetic background of the recipient, circumcision status and the amount of infectious virus particles present in the inoculum [4, 32]. The models generalize across all transmission routes and do not include genetic background, STI infection status and any form of intervention. We model situations where the virus has been deposited into an uninfected individual either through sexual contact, breast milk or blood transfusion. This work is different from the previous work [30, 31] in that, models that consider the whole infection cycle of the virus are developed.
In vitro models have shown that cell-associated viral spread is more efficient than cell-free viral spread, in order to determine the form of virus more efficient in vivo, we formulated and analysed mathematical models that considered the two forms of viral spread. Separate models are developed for each mode of viral spread and the models are analyzed using dynamical systems theory to determine if any form of viral spread can sustain the infection on its own and also identify the infection cycle characteristics that determine the fate of each form of viral spread. A model that considers both forms of viral spread simultaneously is also formulated and analysed to compare these two forms of viral spread in vivo.
Results
Cell-free viral spread cannot sustain an infection
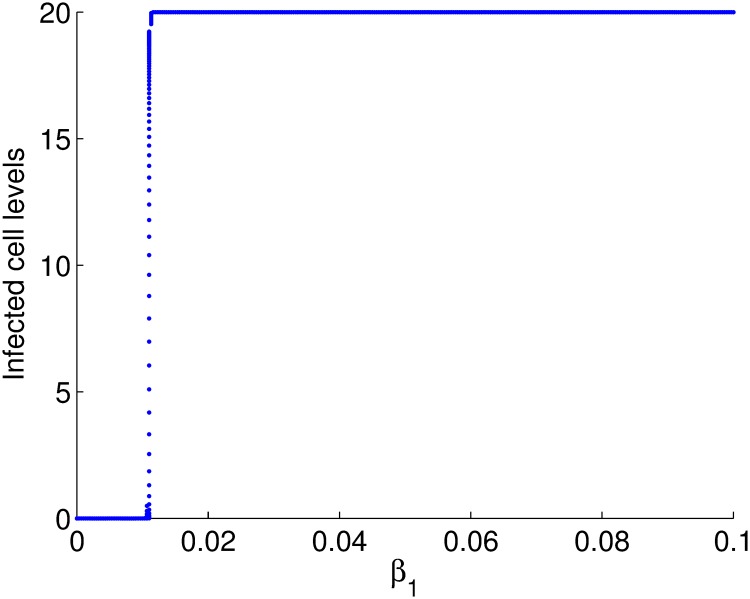
We set out to establish if cell-free viral spread can sustain an infection on its own. We developed a mathematical model that considered cell-free viral spread exclusively, Eqs (1)–(6). Using a bifurcation diagram and parameters obtained from literature on HIV infection, we observed that the disease free equilibrium exist and is unique for the cell-free transmission rate, β1 less than 0.01. The bifurcation diagram of the cell levels against the transmission parameter is given in Fig 1.
Fig 1. Bifurcation diagram of the cell levels against β1.
The infectivity of cell-free virus is in the order of 10−5 [33] and it can be seen from the bifurcation diagram that if β1 is within this range, the disease free equilibrium is stable. These results imply that for any biologically feasible parameter set, infection through cell-free virus dies out. We therefore conclude that cell-free viral spread can not sustain an infection on its own because of the low infectivity of cell-free virus.
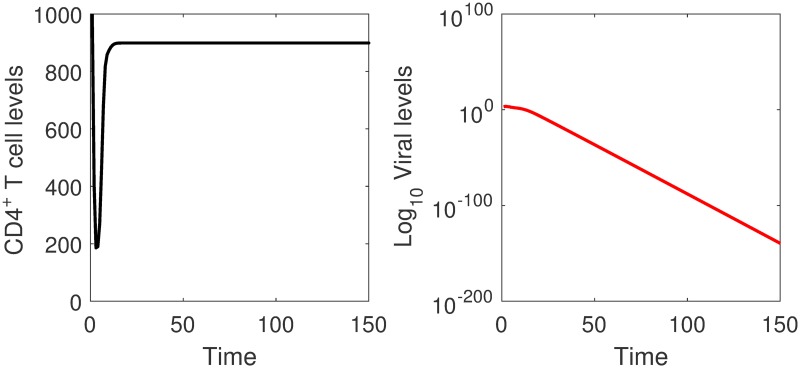
The result that cell-free viral spread does not spread efficiently is consistent with experimental observations in in vitro models [6–8]. It has been observed that the low infectivity to a particle ratio of the virus could not explain the efficient spreading in tissue cultures [8, 29, 34]. The virus is also able to spread in tissue cultures despite the presence of neutralizing antibodies that completely block cell-free viral spread [35], meaning that there is some form of transmission besides cell-free viral spread that will be spreading the infection. Numerical simulations for viral and uninfected cell levels are given in Fig 2.
Fig 2. Simulations of the cell-free viral spread model.
The viral levels approach zero and the CD4+ T cell populations converge to a non-zero steady state as time increases. The infection dies out on its own.
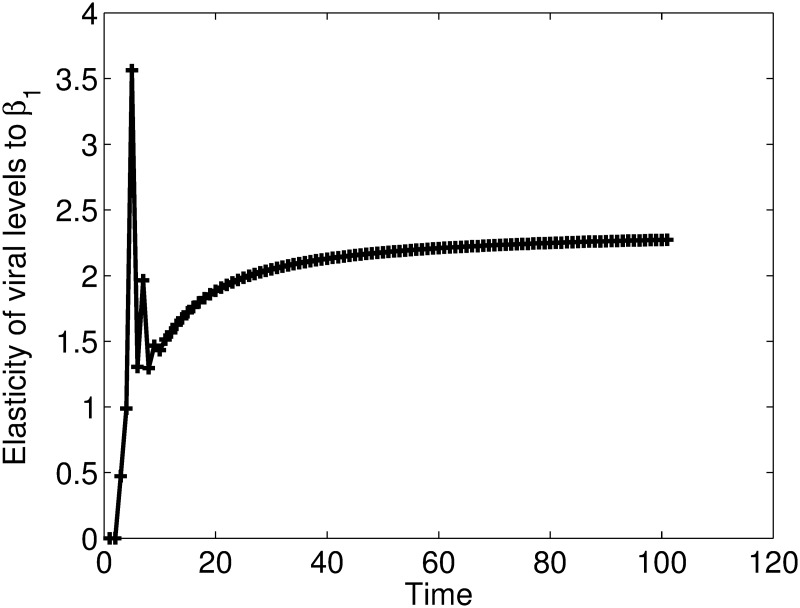
Results in Fig 2, suggest that cell-free virus does not spread efficiently since the viral levels are approaching zero with time. The CD4+ T cell levels decrease during the first few days of the infection but later stabilize at normal levels. The parameter ϕ, the number of virus particles produced per infected cell, seems to be important in determining the outcome of cell-free viral spread. Increasing this parameter to unrealistic values, changes the outcome of cell-free viral spread. A result that shows that the disease equilibrium will only exist for unrealistic parameter values. In Fig 3, we give the elasticity values of the viral levels to β1. The results show that the viral level is positively elastic to β1.
Fig 3. Elasticities of the viral levels to β1.
The results show that the viral level is significantly and positively elastic to β1. Increases in this parameter will result in increases in viral levels.
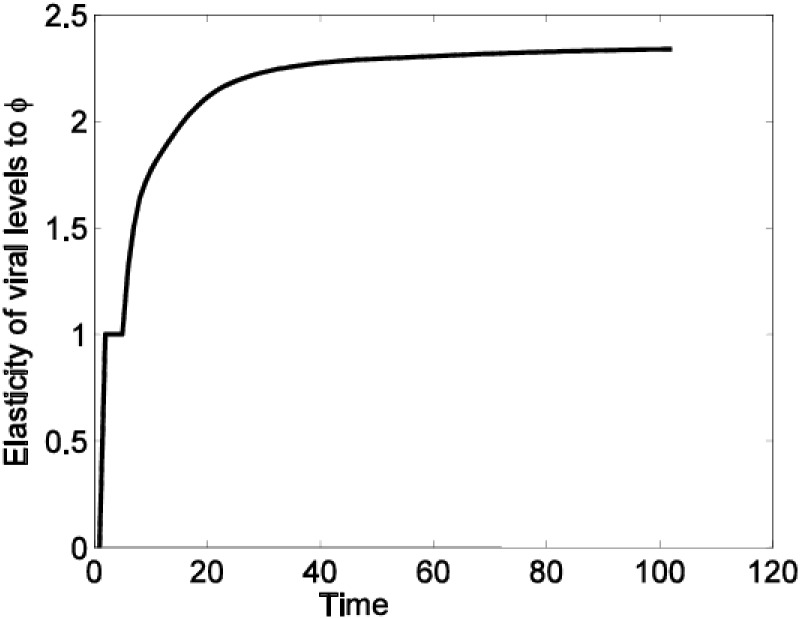
In Fig 4, we give elasticities of viral levels to the parameter ϕ.
Fig 4. Elasticities of the viral levels to ϕ.
The results show that the viral level is significantly and positively elastic to ϕ and thus increases in this parameter will result in increases in viral levels.
Results of Figs 3 and 4 show that increases in β1 and ϕ values will result in increases in the viral levels. Results from the above analysis indicate that cell-free viral spread can not sustain the infection on it’s own. However, the fact that cell-free virus could initiate an infection means that this form of viral spread should also be considered in the designing of prevention and intervention strategies. This is so because, even if the cell-free model indicates that the viral levels will approach zero with time, this may not be the case in vivo given the many mechanisms such mutations and the latent reservoir, which the virus employ in vivo and have not considered in this model.
Cell-to-cell viral spread cannot sustain an infection for small values of the transmission parameter
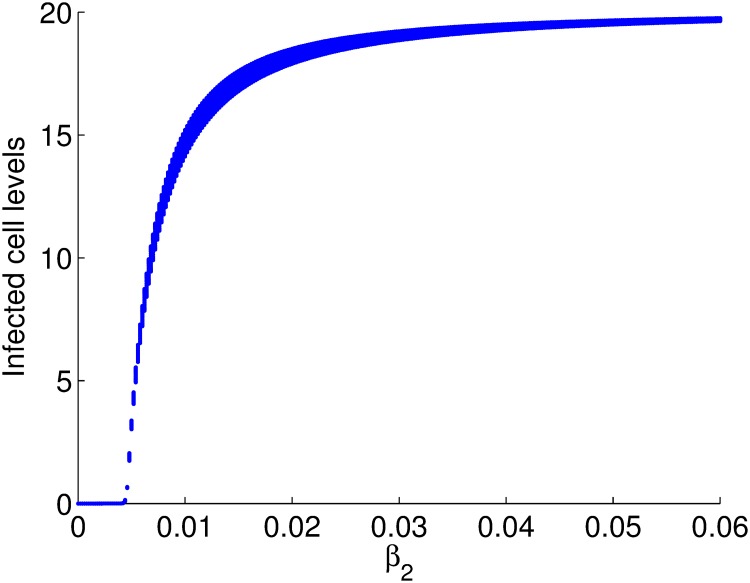
In order to check if cell-to-cell viral spread could sustain an infection on its own, we developed a mathematical model that considered cell-to-cell viral spread exclusively, Eqs (10)–(15). Using the parameters obtained from literature, we observed that existence of the disease equilibrium depends on β2, the infectivity (transmission rate) of cell-associated virus as shown in Fig 5.
Fig 5. Plots of f(T**) against T** where T** is the equilibrium value of infected cells.
The parameters used were β2 = 0.0000024 for Fig 5 a and β2 = 0.024 for Fig 5 b. The graph does not cross the zero line for small values of β2 and crosses the zero line for large values of β2 and thus there is no solution for small values of the transmission parameter. Existence of the disease equilibrium depends on the rate at which cells are infected. f(T**) is given in Eq 19.
We plot the bifurcation diagram of infected cells against the transmission parameter β2 and obtained the diagram in Fig 6, which confirms the results obtained in Fig 5.
Fig 6. Bifurcation diagram for cell levels against β2.
The disease free equilibrium is stable for β2 less than 0.005 and unstable for β2 ≥ 0.005 where the endemic equilibrium become stable. Time is measured in 0.5 days.
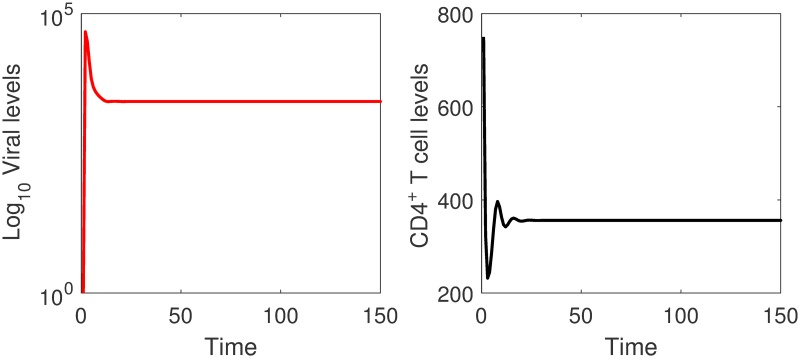
In Fig 7, simulations of the cell-associated viral spread model are given. It can be seen that cell-associated viral spread can spread the infection efficiently for large values of the transmission parameter.
Fig 7. Simulations of the cell-associated viral spread model.
The viral and the CD4+ T cell levels converge to non-zero steady states. Transmission through cell-associated virus will result in an endermic equilibrium state. β2 = 0.024.
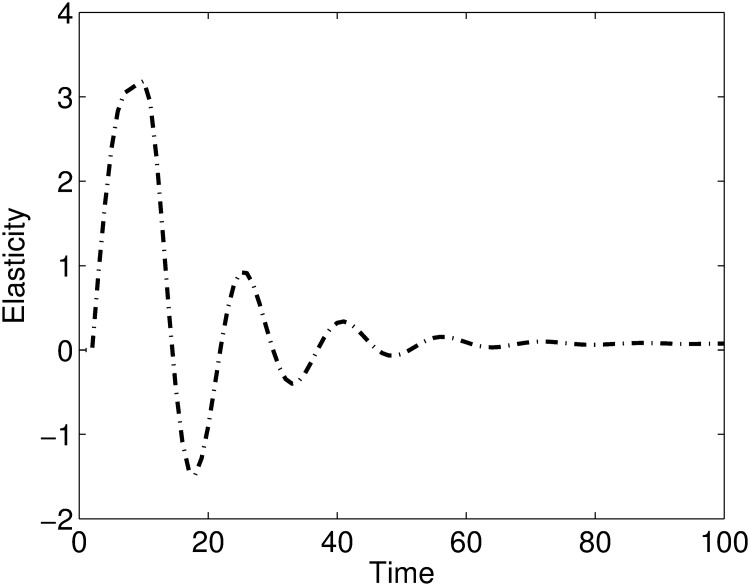
The elasticities of the viral levels to the transmission parameter β2 are given in Fig 8. The results show that the viral level is significantly elastic to β2 during the early days of the infection and weakly elastic to β2 as the infection progresses. Thus we can predict that cell-associated transmission parameter β2 is more important for infection transmission and is not that important in an established infection.
Fig 8. A plot of elasticities of the viral levels to β2.
The viral levels are sensitive to the transmission parameter β2 during the early days of the infection and as the infection progresses the viral levels become weakly sensitive to the transmission parameter.
Cell-to-cell viral spread is more efficient in spreading the virus
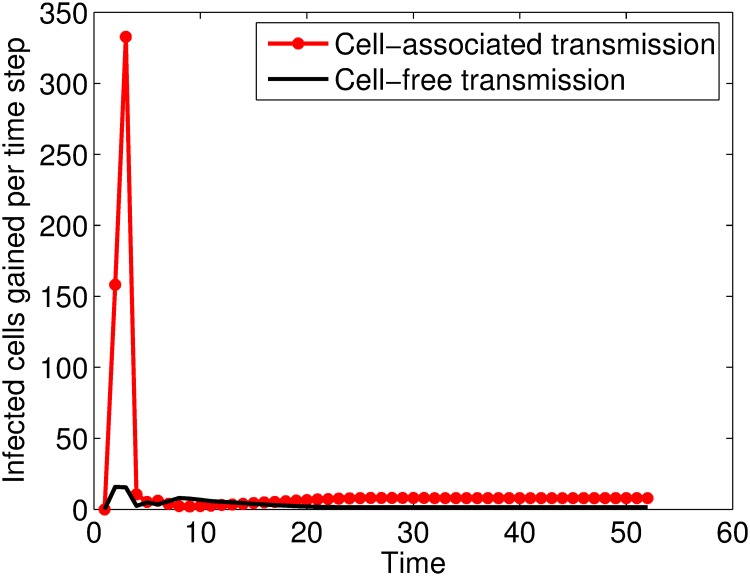
In an HIV infection, both forms of transmission occur concurrently [1, 2] such that the within-host HIV infection is best modelled by a model that considers both forms of transmission. In this scenario, a cell has to escape infection by cell-free virus and cell-associated virus for it to remain healthy. We group the infected cells according to the way they were infected and obtained the system of Eqs (26) and (27). Numerical simulation for the proportions of cells infected per time step grouped according to the mode of viral spread are given in Fig 9. It can be seen that both forms of viral spread result in new cells being infected, however, the relative contribution of cell-associated viral spread is higher than that of cell-free viral spread with a marked distinction in the first few days of the infection.
Fig 9. Plots of the infected cells gained per time step against time.
Time is measured in 0.5 days.
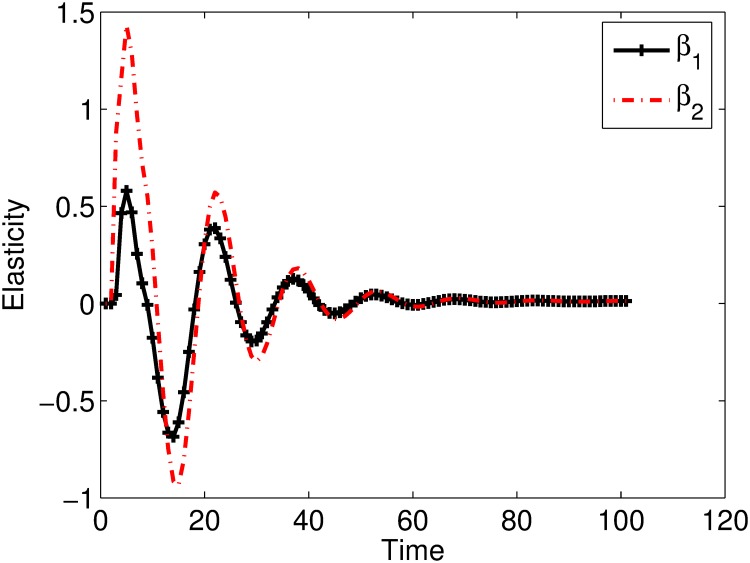
Elasticity analysis of the viral levels to transmission parameters β1 and β2 are given in Fig 10. It is shown that during the early days of the infection the viral level is more elastic to β2 than β1, a result similar to the above analysis that showed that cell-associated viral spread is more efficient in spreading the infection than cell-free viral spread.
Fig 10. Plot of the elasticities of the viral levels to the transmission parameters.
The viral level is more elastic to β2 than β1.
Elasticity analysis also predicts that viral levels are only sensitive to the transmission parameters during the early days of the infection. After infection establishment, strategies that target other stages of the viral life cycle can control viral levels better than those targeting the early stages of viral life cycle. These results are similar to the results obtained in [36–39].
Discussion
HIV infection is currently treated by highly active antiretroviral therapy (HAART), a therapy that only slows the development of AIDS in an infected individual and there is need to find a cure or a vaccine that prevents the occurrence of new infections. The development of a vaccine or a microbicide that prevents the occurence of new infection heavily relies on understanding the form of the virus that spreads efficiently. Even so, the form of HIV that spread efficiently is not yet clear [4, 40, 41]. Currently most of the vaccine research concentrate on cell-free viral spread [4, 40], though there are indications that cell-associated virus may play a significant role in the transmission of the HIV infection [16, 17, 20]. Discrete time models which consider the two forms of HIV spread across target cells were developed with the goal of determining the form of viral spread that is more efficient between cell-free and cell-associated viral spread.
The work started by developing a model that considered cell-free viral spread. The qualitative behavior of the model showed that the disease free equilibrium was the only stable equilibrium point for biologically feasible parameter sets. A result that implies that infection through cell-free viral spread will die out. A model that considered cell-associated viral spread was also developed. Existence of the disease equilibrium was shown to depend on the cell-associated transmission parameter. For small values of the cell-associated transmission parameter, the disease free equilibrium is stable and disease equilibrium is stable for parameter values greater than 0.005. From these results, we conclude that cell-free viral spread fails to thrive because of the low infectivity of cell-free virus and cell-associated viral spread thrives because of the high infectivity of cell-associated virus.
Since the infectious fluids contains both cell-free and cell-associated virus, a model that considers both forms of viral spread was also formulated. Plots of the proportions of cells infected by cell-free virus and cell-associated virus per time step showed that the proportion of cells infected by cell-associated virus was greater than that infected by cell-free virus with a marked difference during the early days of the infection. This result implies that the relative contribution of cell-associated virus in spreading the infection is greater than that of the cell-free virus. Elasticity analysis of the viral levels to the transmission parameters was performed. It was shown that the viral levels (and hence the infection) was more elastic to the infectivity of the cell-associated virus than the infectivity of free virus during the first few days of the infection. A result that also implies that the relative contribution of cell-associated virus in spreading HIV from primary sites of infection is greater than that of cell-free virus.
Our results coincide with the result in [19], where it was shown that a newly infected homosexual man was infected by the virus that was closely related to the transmitting partner’s seminal cells and not the seminal plasma virus and another study [17], where the cell-associated viral levels correlated with the risk of acquisition. In the study [10], the genotype of infecting virus matched that of HIV in semen cells of the transmitter in three (one heterosexual couple) out of five cases, a result that also suggested that cell-associated virus is a major contributor of new infections in humans. There are also ex vivo and in vivo model results that coincide with our result see for example [41].
Our models produces different results for different stages of the infection. We have shown that upon exposure to the virus, cell-associated viral spread is more efficient in spreading the virus, however with infection progression, two forms of viral spread contribute almost equally. Our results therefore agree with the results of the study [30] which concluded that the two modes of viral spread contribute equally to viral spread but with a difference that our models predict a marked difference in the early days of the infection. The difference maybe because of our use of matrix population models that can easily capture both the transient and asymptotic dynamics of the viral levels.
Our results also coincide with results of the study [31], which also used a mathematical model to quantify the contribution of the two forms of viral spread and concluded that cell-associated viral spread is more efficient than cell-free viral spread. We postulate that the differences in the results obtained in different studies could have been the timing of the experiments, some researchers could have been studying the transient dynamics hence obtaining a result that cell-associated virus is more efficient in spreading the infection than cell-free virus and others could have looked at the stage were the virus had established itself, where they would get the result that the two forms of viral spread contribute almost equally.
In this study, intervention strategies that target cell-associated viral spread are predicted to be more beneficial in controlling the spread of the HIV infection than those that target cell-free viral spread. Given the differences in which these two forms of transmission occur, vaccines and microbicides designed to prevent cell-free viral spread may not control cell-associated viral spread [13, 42]. This could explain why some vaccines and clinical trials designed to prevent HIV infection may have failed. Cell-to-cell viral spread can be controlled by microbicides of the surfactant class that disrupt membranes of infectious cells in genital secretions and semen, buffering agents that induce lower vaginal pH after intercourse and antibodies that target infected cells, just to mention a few [40].
There are gaps in knowledge on what transpires in continuously shaken cultures. Microscopic and micro-imaging techniques can improve our knowledge on what really transpires in continuously shaken cultures. Once the kinetics that occur in shaken cultures are clearly elucidated, the use of cell cultures in the estimation of parameters on models that consider the different forms of viral spread will help us correctly quantify the contribution of each form of viral spread.
Moreover, most active HIV replication occurs in lymph nodes [43, 44] where about 98% of lymphocytes reside [45, 46]. Understanding the mode of viral spread more efficient in these regions is of paramount importance in the control of the infection. However, cells are closely packed in lymphoid organs and are in the ranges of 106 cells per microliter and the dynamics of cells and the virus in lymphoid organs cannot be modelled with the models proposed in this study, where we assumed perfect mixing of cells and the virus. Cellular automata models can be used to model the dynamics in these regions and inform on the role of each form of viral spread in the HIV infection dynamics.
Models
The stages in the HIV replication cycle are; receptor binding, cell entry, uncoating, reverse transcription of viral RNA into DNA, nuclear entry, integration of the viral DNA into the host DNA and transcription and translation of viral RNA, assembly of progeny virus particles and budding [47]. The life cycle stages of the virus are divided into three stages: the mature virus (V), the HIV Deoxyribonucleic Acid (DNA) (D) and the Provirus (P) as illustrated in our previous study [48]. A Negative Binomial distribution method is used to estimate the duration of the provirus stage. This resulted in two pseudo-provirus stages as illustrated in [48]. We let P represent the pseudo-provirus stage 1 and Q represent the pseudo-provirus stage 2.
A discrete time cell-free viral spread model
This model considers cell-free viral spread whereby health cells are infected through contacts with free virus particles. We assume that a CD4+ T cell is infected by free virus particles through contacts of uninfected cells with the virus in a random fashion (contacts are assumed to be randomly distributed). Thus the model represent cell and virus interactions in the blood where perfect mixing of the cells and the virus is assumed. We let Dt, Pt, Qt, Vt, Tt and be the densities of the DNA, provirus stage 1, provirus stage 2, virus, the uninfected and infected CD4+ T cells per ml of blood at time t, respectively. Adopting the principles used in host-parasite interactions for the processes of attachment and entry of the virus into CD4+ T cells, we assume that the infection of CD4+ T cells is determined by the number of contacts/encounters of the virus with the CD4+ T cells. The number of contacts are assumed to be proportional to the product of the densities of the virus and the CD4+ T cells, that is N = β1VtTt, where β1 is the constant of proportionality representing the infectivity of the virus. The first contact is the only significant encounter. Since the encounters are assumed to be random, the encounters are described by a Poisson probability distribution and the average number of contacts per host (average number of virus attached to a CD4+ T cell) is given by β1Vt. Since the likelihood of escaping infection is the same as the probability of no encounters during the CD4+ T cell’s lifetime, the proportion of cells that survive infection per time step is given by the probability of zero encounters as P(0) = exp(−β1Vt). The HIV cell-free infection model takes the form:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where β1, θ1, θ2, θ3, ϕ, γ, K, μ and sT are positive parameters and D0, P0, Q0, V0, T0, * T0 ≥ 0. The time step for the model is 12 hours, which is equivalent to the amount of time spend in the D stage. Eq (1) models the amount of the DNA particles in a cell at time t + 1. Not all viruses that attach to a cell are successfully fused with the cell, uncoated and reverse transcribed [49, 50]. This means that β1, is a product of the probabilities of attachment, fusion, uncoating and reverse transcription.
It has been observed that all HIV unintegrated DNA are rapidly transported to the nucleus where they are either processed into the two types of DNA circles or integrated [51]. The DNA particles that circularise do not contribute to infection progression and are eventually degraded by the cell. This means that only those DNA particles that become integrated are involved in the infection dynamics and those that circularise though they maybe available in the next time step no longer participate in the infection dynamics. Thus if D does not integrate and become P at time t, it is assumed that it will not be available at time t + 1.
Provirus particles progress from provirus stage to the mature virus stage over a variable time. To calculate the proportion that goes to the virus stage and the proportion that remains in the provirus stage we used the Negative Binomial Distribution method as illustrated in [48]. The approach resulted in two identical pseudo provirus stages which we denote by P and Q. Eq (2) represents the amount of provirus in the pseudo provirus stage 1 and Eq (3) represents the amount of provirus in the pseudo provirus stage 2 at time t + 1 respectively. The parameter θ2, is the transition probability within these stages and between the provirus stage and the virus stage. The probability that a provirus survives and remain in the same pseudo provirus stage is given by θ3.
It has been assumed that the viral level at time t + 1, does not depend on the viral level at time t, because plasma virus have a mean life span of 0.3 days [21] and the time step for the model is 0.5 days, meaning that no plasma virus is able to survive to the next time step. The parameter ϕ represents the number of virus particles produced per replication cycle per infected cell. The expression θ2ϕQt gives virus production per cell. To get the virus production per ml of blood we multiply by the number of infected cells, T*, per ml of blood.
Eq (5) models the levels of CD4+ T cells at time t + 1. The parameter sT, represents the source of new CD4+ T cells from the thymus. It is assumed that addition from the thymus occurs at the beginning of the time step. We have assumed a density dependent growth function for these cells of the form . This was motivated by the fact that CD4+ T levels are regulated in vivo. Exponential functions are used when the rate of change of a substance depends on the current level, in this case the level of health cells at time t + 1 depends on the levels of both the infected and uninfected cells at time t and these cells have a carrying capacity of K cells per ml of blood. The exponential term therefore regulates the levels per each time step.
To proceed to the next time step, CD4+ T cells must survive infection by free virus. Since the likelihood of escaping infection is the same as the probability of no contacts during the CD4+ T cell’s lifetime, the probability of the CD4+ T surviving infection is given by exp(−β1Vt). Infection is assumed to occur at the end of the time step so that the expression, , gives the number of CD4+ T cells that survive infection per time step. The expression (1 − exp(−β1Vt)), gives the proportion of cells that become infected per time step, so that Tt(1 − exp(−β1Vt)) gives the gain term per time step. The parameter μ, gives the proportion of infected cells that die per time step, and 1 − μ, gives the proportion that survive per time step. Death is assumed to occur at the end of each time step.
Eqs (1)–(3), give the intracellular stages of the virus and the densities give the levels per infected cell. To get the levels per ml of blood we multiply by the total number of infected cell per ml of blood, . The distribution of the virus population at the different life cycle stages at time t + 1 can be represented in matrix form for easier manipulations as follows,
| (7) |
where and the equations for uninfected and infected cells remain as previously defined. The equilibrium value of infected cells, T* is given by
| (8) |
Solving Eq (8) is challenging and we resort to the graphical method. The equation is written as
| (9) |
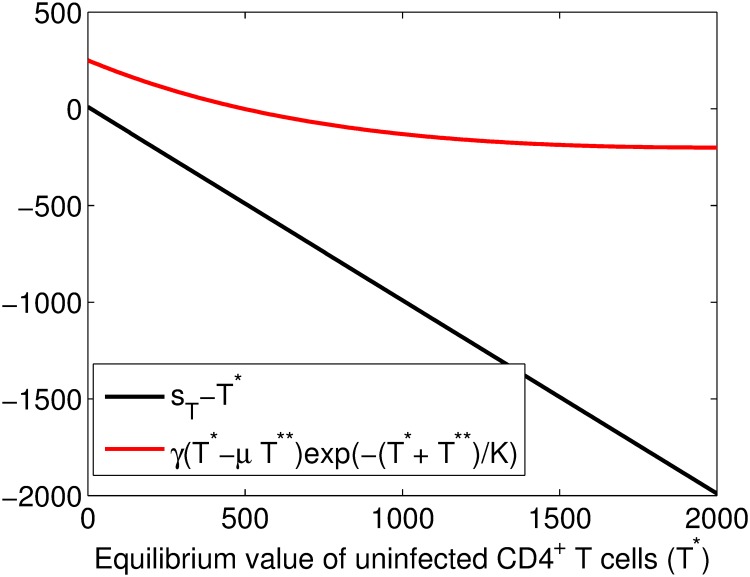
where . We plot the equation sT − T* on the same plot with , where their graphs intersect is the solution of Eq (8) and the plots are given in Fig 11. The graphs are not intersecting and thus there is no solution for the given parameter set.
Fig 11. Plots of sT − T* and against T*.
The graphs are not intersecting and thus there is no solution for the equation. The parameters used were , θ2 = 0.06315, θ3 = 0.43685, β1 = 0.000024, ϕ = 1000, sT = 10, μ = 0.5, K = 1500, γ = 2.7.
In order to determine if the transmission parameter β1, can contribute to the qualitative behavior of the model, we plot a bifurcation diagram of the cell levels against the transmission parameter Fig 1. Model analysis and the derivations of equilibrium values are given in the supporting information.
A discrete time cell-associated viral spread model
Immune cells communicate through short- and long-range connections. HIV takes advantage of these connections to disseminate through cell-to-cell viral spread. A review of how cell-to-cell viral spread occurs is given in [40]. Cell-to-cell spread of HIV depends on the formation of a virological synapse. We thus assume that infection of CD4+ T cells is determined by the number of contacts/encounters of infected cells and health CD4+ T cells. The model explains interactions of cells in the blood compartment where random mixing of cells can be assumed. The cell-associated viral spread model takes the form
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
The expression gives the average number of infected cell contacts per health CD4+ T cell (average number of infected cells attached to a health cell), where β2 represents the infectivity of cell-associated virus. We have assumed that all the virus that become attached to the cell will enter the cell as with the cell-free model. All the other parameters and variables are as previously defined in the cell-free viral spread model.
The system of Eqs (10)–(15) can be represented in matrix form for easier manipulation as,
| (16) |
| (17) |
where
and
The equilibrium value of infected cells is given by
| (18) |
Solving for T** is complex and we resort to graphical solutions. We let
| (19) |
The graphs of f(T**) against T** are given in Fig 5. Model analysis and the derivations of equilibrium values are given in the supporting information.
Cell-free and cell-associated viral spread model
The model that considers both forms transmission takes the form;
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
The definitions of parameters and variables remain as previously defined. In this model, it is assumed that a cell must survive infection by infected cells and cell free viral particles for it to remain healthy. Boundedness of the system of Eqs (20)–(25) follows from the boundedness of system of Eqs (1)–(6) and (10)–(15).
Contributions of the two forms of viral spread
We group the infected cells according to the way they were infected and the resulting equations for infected cells are
| (26) |
| (27) |
where , are cells infected by free virus and are cells infected by cell-associated virus at time t respectively. Numerical simulation for the proportions of cells infected per time step grouped according to the mode of transmission are given in Fig 9. Both forms of viral spread result in new cells being infected, however, the relative contribution of cell-associated viral spread is higher than that of cell-free viral spread.
The mathematical analysis of all the models are given in the supporting information.
Model parameters
In [51], the investigators revealed that all HIV unintegrated DNA are rapidly transported to the nucleus where they are either processed into the two types of DNA circles or integrated. It was observed that only a third will become integrated. We can thus approximate the proportion of DNA (D) that goes to the provirus stage as that is . The stage specific survival in the provirus stage is the proportion of replication competent provirus and was determined as [52]. The provirus stage take a variable duration, we used the Negative Binomial Distribution method to estimate its duration as illustrated in one of our studies [48]. This resulted in two pseudo-provirus stages with transition probability θ2 = 0.06315 and the probability of surviving and remaining in the same stage θ3 = 0.43685. The parameters of the model are given in Table 1.
Table 1. Parameter values.
| Parameter | Description | Value | Source |
|---|---|---|---|
| sT | Source terms of CD4+ T cells from thymus | 10cellsd−1 | [48] |
| K | Carrying capacity of CD4+ T cells | 1500 cells ml−1 | Est. |
| μ | Proportion of infected cells that die per time step | 0.5 to 1 | [33] |
| γ | Growth rate of CD4+ T cells | 2.7 cells d−1 | Est. |
| β1 | Virus infectivity | 2.4 × 10−5 ml−1 d−1 | [33] |
| β2 | Cell-associated virus infectivity | 100 − 1000 × β1 | [6, 8, 53] |
| ϕ | Virus production/provirus/cycle | 1000 virions | [29] |
| θ1 | Transition Probability | [33] | |
| θ2 | Transition Probability | 0.06315 | [48] |
| θ3 | Probability of surviving and remaining in provirus stages | 0.43685 | [48] |
Est. means that parameters were estimated/derived to simulate acceptable HIV dynamics.
Supporting information
Mathematical analysis of the models.
(PDF)
Acknowledgments
We acknowledge the useful comments from Gesham Magombedze.
Data Availability
All the relevant data are within the manuscript.
Funding Statement
The authors received no specific funding for this work.
References
- 1. Hübner W, McNerney GP, Chen P, Dale BM, Gordon RE, Chuang FYS, et al. Quantitative 3D video microscopy of HIV transfer across T cell virological synapses. Science. 2009;323: 1743–1747. 10.1126/science.1167525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Sourisseau M, Sol-Foulon N, Porrot F, Blanchet F, Schwartz O. Inefficient Human Immunodeficiency Virus replication in mobile lymphocytes. J. Virol. 2007;81(2): 1000–1012. 10.1128/JVI.01629-06 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Barreto-de-Souza V, Arakelyan A, Margolis L, Vanpouille C. HIV-1 vaginal transmission: cell-free or cell-associated virus? Am. J. Reprod. Immunol. 2014;71: 589–599. 10.1111/aji.12240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Sagar M. Origin of the transmitted virus in HIV infection: Infected cells versus cell-free virus. J. Infect. Dis.2014;210(3): S667–S673 10.1093/infdis/jiu369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Anderson DJ, Politch JA, Nadolski AM, Blaskewicz CD, Pudney J, Mayer KH. Targeting Trojan Horse leukocytes for HIV prevention. AIDS. 2010;24: 163–187. 10.1097/QAD.0b013e32833424c8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Sato H, Orestein J, Dimitrov D, Martin M. Cell to cell spread of HIV occurs within minutes and may not involve virus particles. Virology. 1992;186: 712–724. [DOI] [PubMed] [Google Scholar]
- 7. Mothes W, Sherer NM, Jin J, Zhong P. Virus cell-to-cell transmission. J. Virol. 2010;84(17): 8360–8368. 10.1128/JVI.00443-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Car JM, Hocking H, Li P, Burrel C. Rapid and efficient cell-to-cell transmission of human immunodeficiency virus infection from monocyte-derived macrophages to peripheral blood lymphocytes. Virology. 1999;265: 319–329. 10.1006/viro.1999.0047 [DOI] [PubMed] [Google Scholar]
- 9. Heath L, Frenkel LM, Foley BT, Mullins JI. Comment on “The origins of sexually transmitted HIV among men who have sex with men”. Sci. Transl. Med. 2010;2(5): 50le1 10.1126/scitranslmed.3001416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhu T, Wang N, Carr A, Nam DS, Moor-Jankowski R, Cooper DA, et al. Genetic characterization of human immunodeficiency virus type 1 in blood and genital secretions: evidence for viral compartmentalization and selection during sexual transmission. J. Virol. 1996;70: 3098–3107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Peters B, Whittall T, Babaahmady K, Gray K, Vaughan R, Lehner T. Effect of heterosexual intercourse on mucosal alloimmunisation and resistance to HIV-1 infection. Lancet. 2004;363: 518–524. 10.1016/S0140-6736(04)15538-4 [DOI] [PubMed] [Google Scholar]
- 12. Butler DM, Delport W, Kosakovsky SL, Pond M, Lakdawala K, Cheng PM, et al. The origins of sexually transmitted HIV among men who have sex with men. Sci. Transl. Med. 2010;2: 18re1 10.1126/scitranslmed.3000447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Virgin HW, Walker BD. Immunology and the elusive AIDS vaccine. Nature. 2010;434: 224–231. 10.1038/nature08898 [DOI] [PubMed] [Google Scholar]
- 14. Quinn TC, Wawer MJ, Sewankambo N, Serwadda D, Li C, Wabwire-Mangen F, et al. Viral load and heterosexual transmission of human immunodeficiency virus type 1. Rakai Project Study Group. N. Engl. J. Med. 2000;342: 921–929. 10.1056/NEJM200003303421303 [DOI] [PubMed] [Google Scholar]
- 15. Butler DM, Smith DM, Cachay ER, Hightower GK, Nugent C, Richman DD, et al. Herpes simplex virus 2 serostatus and viral loads of HIV-1 in blood and semen as risk factors for HIV transmission among men who have sex with men. AIDS. 2008;22: 1667–1671. 10.1097/QAD.0b013e32830bfed8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sturmer M, Doerr HW, Berger A, Gute P. Is transmission of HIV-1 in non-viraemic serodiscordant couples possible? Antivir. Ther. 2008;13: 729–732. [PubMed] [Google Scholar]
- 17. Rousseau CM, Nduati RW, Richardson BA, John-Stewart GC, Mbori-Ngacha DA, Kreiss JK, et al. Association of levels of HIV-1 infected breast milk cells and risk of mother-to-child transmission. J. Infect. Dis. 2004;190: 1880–1888. 10.1086/425076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Boeras DI, Hraber PT, Hurlston M, Evans-Strickfaden T, Bhattacharya T, Giorgi EE, et al. Role of donor genital tract HIV-1 diversity in the transmission bottleneck. Proc. Natl. Acad. Sci. U. S. A. 2011;108(46): E1156–E1163. 10.1073/pnas.1103764108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Gianella S, Mehta SR, Young JA, Vargas MV, Little SJ, Richman DD, et al. Sexual transmission of predicted CXCR4-tropic HIV-1 likely originating from the source partner’s seminal cells. Virology. 2012;434: 2–4. 10.1016/j.virol.2012.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Frange P, Meyer L, Jung M, Goujard C, Zucman D, Abel S, et al. Sexually-transmitted/founder HIV-1 cannot be directly predicted from plasma or PBMC-derived viral quasispecies in the transmitting partner. PLoS ONE. 2013;8: e69144 10.1371/journal.pone.0069144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: Virion clearance rate, infected cell life span and viral generation time. Science. 1996;271:1582–1586. 10.1126/science.271.5255.1582 [DOI] [PubMed] [Google Scholar]
- 22. Srivastava PK, Banerjee M, Chandra P. A primary infection model for HIV and immune response with two Discrete time delays. Differ. Equ. and Dyn. Syst. 2010;18(4): 385–399. 10.1007/s12591-010-0074-y [DOI] [Google Scholar]
- 23. Srivastava PK, Chandra P. Modelling the Dynamics of HIV and CD4+T Cells during primary infection. Nonlinear Anal. Real World Appl. 2010;11(2): 612–618. 10.1016/j.nonrwa.2008.10.037 [DOI] [Google Scholar]
- 24. Wang SF, Zou DY, Global stability of in-host viral models with humoral immunity and intracellular delays. Appl. Math. Model. 2012;36:1313–1322. 10.1016/j.apm.2011.07.086 [DOI] [Google Scholar]
- 25. Lai X, Zou X. Modeling HIV-1 virus dynamics with both virus-to-cell infection and cell-to-cell transmission. SIAM J. Appl. Math. 2014;74: 898–917. 10.1137/130930145 [DOI] [Google Scholar]
- 26. Wang J, Guo M, Liu X, Zhao Z. Threshold dynamics of HIV-1 virus model with cell-to-cell transmission, cell-mediated immune responses and distributed delay. Appl. Math. Comput. 2016;291: 49–161. [Google Scholar]
- 27. Elaiw AM, Raezah AA, Alofi AS. Effect of humoral immunity on HIV-1 dynamics with virus-to-target and infected-to-target infections. AIP Adv. 2016;6: 085204 10.1063/1.4960987 [DOI] [Google Scholar]
- 28. Lin J, Xu R, Tian X. Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Appl. Math. Comput. 2017;315: 516–530. [Google Scholar]
- 29. Dimitrov DS, Willey RL, Sato H, Chang LJ, Blumenthal R, Martin MA. Quantitation of human immunodeficiency virus type 1 infection kinetics. J. Virol. 1993;67(4): 2182–2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Komarova NL, Anghelina D, Voznesensky I, Trinitè B, Levy DN, Wodarz D. Relative contribution of free-virus and synaptic transmission to the spread of HIV-1 through target cell populations. Biol. Lett. 2013;9 10.1098/rsbl.2012.1049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Iwami S, Takeuchi JS, Nakaoka S, Nakaoka SM, Cell-to-cell infection by HIV contributes over half of virus infection. Elife. 2015;6(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Powers KA, Poole C, Pettifor AE, Cohen MS. Rethinking the heterosexual infectivity of HIV-1: a systematic review and meta-analysis. Lancet Infect. Dis. 2008;8: 553–563. 10.1016/S1473-3099(08)70156-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kirschner D. Using Mathematics to understand HIV immune dynamics. Not. Am. Math. Soc. 1996;43(2): 193–202. [Google Scholar]
- 34. Bangham CR. The immune control and cell-to-cell spread of human T-lymphotropic irus type 1. J. Gen. Virol. 2003;84: 3177–3189. 10.1099/vir.0.19334-0 [DOI] [PubMed] [Google Scholar]
- 35. Gupta P, Balachandran R, Ho M, Enrico A, Rinaldo C. Cell-to-cell transmission of human immmuno deficiency virus type 1 in the presence of azidothymidine and neutralizing antibodies. J. Virol. 1989;63: 2361–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Sedhagat AR, Dinoso JB, Shen L, Wilke CO, Siliciano RF. Decay dynamics of HIV-1 depend on the inhibited stages of the viral life cycle. Proc. Natl. Acad. Sci. U. S. A. 2008;105(12): 4832–4837. 10.1073/pnas.0711372105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Showa SP, Nyabadza F, Hove-Musekwa SD. A discrete HIV infection model with immunosenescence. Biol. Med. 2017;9: 420. [Google Scholar]
- 38. Sedhaghat AR, Siliciano RF, Wilke CO. Constraints on the dominant mechanism for HIV viral dynamics in patients on raltegraviar. Antivir. Ther. 2009;14: 263–261. [PMC free article] [PubMed] [Google Scholar]
- 39. von Kleist M, Menz S, Huisinga W. Drug-Class specific impact of antivirals on the reproductive capacity of HIV. PLoS Comput. Biol. 2010;6(3): e1000720 10.1371/journal.pcbi.1000720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Anderson JD. Finally, a Macaque Model for Cell-Associated SIV/HIV Vaginal Transmission. J. Infect. Dis. 2010;202(3): 333–336. 10.1086/653620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Kolodkin-Gal D, Hulot SL, Korioth-Schmitz B, Gombos RB, Zheng Y, Owuor J, et al. Efficiency of cell-free and cell-associated virus in mucosal transmission of human immunodeficiency virus type 1 and simian immunodeficiency virus. J. Virol. 2013;7(24): 13589–13597. 10.1128/JVI.03108-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Abela IA, Berlinger L, Schanz M, Reynell L, Gunthard H F, Rusert P, et al. Cell-cell transmission enables HIV-1 to evade inhibition by potent CD4bs directed antibodies. PLoS Pathog. 2012;8(4): e1002634 10.1371/journal.ppat.1002634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Pantaleo G, Graziosi C, Demarest JF, Butini L, Montroni M, Fox CH, et al. HIV infection is active and progressive in lymphoid tissue during clinically latent stage of disease Nature 1998. 362: 341–345. [DOI] [PubMed] [Google Scholar]
- 44. Embretson J, Zupancicl M, Ribas JL. Massive convert infection of helper T lymphocytes and macrophages by HIV during the incubation period of AIDS Nature 1992;362: 359–362. 10.1038/362359a0 [DOI] [PubMed] [Google Scholar]
- 45. Westermann J, Pabst R. Lymphocyte subsets in the blood, a diagonistic window on the lymphoid system. Immunol. Today 1990;11: 406–410. 10.1016/0167-5699(90)90160-B [DOI] [PubMed] [Google Scholar]
- 46. Rosenberg YJ, Janossy G. The importance of lymphocyte trafficking in regulating blood lymphocyte levels during HIV and SIV infections Sem. Immunol. 1999;11(2):139–54. [DOI] [PubMed] [Google Scholar]
- 47. Krämer A Kretzschmar M, Krickrberg K. (eds.) Modern infectious disease epidemiology: Concepts, methods, mathematical models and public health (Statistics for biology and health). Springer Science Business Media, LLC; 2010. [Google Scholar]
- 48. Showa SP, Nyabadza F, Hove-Musekwa SD, Magombedze G. A comparison of elasticities of viral levels to specific immune response mechanisms in human immunodeficiency virus infection. BMC Res. Notes 2014;7: 37 10.1186/1756-0500-7-737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Zack JA, Arrigo SJ, Weitsman SR, Go ASA, Haislip A, Chen ISY. HIV-1 entry into quiescent primary lymphocytes: Molecular analysis reveals a labile, latent viral structure. Cell 1990;61(2): 213–222. 10.1016/0092-8674(90)90802-l [DOI] [PubMed] [Google Scholar]
- 50. Zack JA, Haislip AM, Krogstand P, Chen ISY. Incompletely reverse-transcribed human immunodeficiency virus type I genomes function as intermediates in the retroviral life cycle. J. Virol. 1992;66: 1717–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Barbosa P, Charneau D, Durney N, Clavel F. Kinetic Analysis of HIV-1 early replicative steps in a coculture. AIDS Res. Hum. Retroviruses. 1994;10(1): 53–59. 10.1089/aid.1994.10.53 [DOI] [PubMed] [Google Scholar]
- 52. Brinchmann JE, Albert J, Vartal F. Few infected CD4+T cells but a high proportion of replication-competent provirus in the asymptomatic human immunodefiency virus type 1 infection. J. Virol. 1991;65(4): 2019–2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Dimitrov DS, Willey RL, Sato H, Chang LJ, Blumenthal R, Martin MA. Quantitation of human immunodeficiency virus type 1 infection kinetics. J. Virol. 1993;67(4): 2182–2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Mathematical analysis of the models.
(PDF)
Data Availability Statement
All the relevant data are within the manuscript.