Abstract
Aqueous electrolyte solutions containing multivalent ions exhibit various intriguing properties, including attraction between like-charged colloidal particles, which results from strong ion–ion correlations. In contrast, the classical Derjaguin–Landau–Verwey–Overbeek theory of colloidal stability, based on the Poisson–Boltzmann mean-field theory, always predicts a repulsive electrostatic contribution to the disjoining pressure. Here, we formulate a general theory of surface forces, which predicts that the contribution to the disjoining pressure resulting from ion–ion correlations is always attractive and can readily dominate over entropic-induced repulsions for solutions containing multivalent ions, leading to the phenomenon of like-charge attraction. Ion-specific short-range hydration interactions, as well as surface charge regulation, are shown to play an important role at smaller separation distances but do not fundamentally change these trends. The theory is able to predict the experimentally observed strong cohesive forces reported in cement pastes, which result from strong ion–ion correlations involving the divalent calcium ion.
Introduction
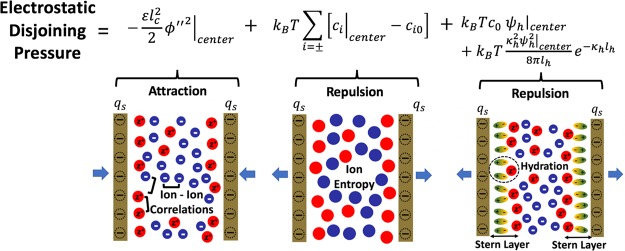
The accurate prediction of forces between charged surfaces in aqueous electrolytes is of paramount importance in diverse scientific disciplines, ranging from colloidal science to biophysics and polymer chemistry.1 Surface forces ultimately determine whether colloidal particles and macromolecules, such as DNA, proteins, and polymers, will aggregate or will remain stable in dispersions.2−6 Typically, two different types of forces operate between charged surfaces in electrolyte solutions: short-range van der Waals forces, which are predominantly attractive, and long-range electrostatic forces, which can be attractive or repulsive depending on the sign and magnitude of the charge on the interacting surfaces.7−9 The most widely used model of colloidal stability is the classical Derjaguin–Landau–Verwey–Overbeek (DLVO) theory,10,11 in which the electrostatic contribution to the disjoining pressure (force per unit area acting on the charged surfaces) is described using the Poisson–Boltzmann (PB) mean-field theory, which assumes that the ions residing in the electric double layer (EDL) at the charged surface feel a mean electrostatic potential from the smeared out (volume-averaged) charge density near the charged surface. The PB model also assumes that the dielectric permittivity of the solvent is constant and uniform, considers ions to be point-sized, and neglects any form of ion–ion correlations. The prediction of the disjoining pressure by the DLVO theory utilizing the PB model is in very good agreement1,12−25 with experimental data in the so called weak-coupling limit, that is, the limit corresponding to a low surface charge density, high solvent dielectric permittivity, low valency of counterions (those ions containing charge of sign opposite to that of the surface), or high temperature. In the case of multivalent electrolytes, ion–ion correlations become important due to the large valency of the counterions, and the PB model fails to describe the disjoining pressure acting between charged surfaces even qualitatively.26−30 In particular, the mean-field PB theory always predicts a repulsive EDL pressure contribution for like-charged surfaces, irrespective of the magnitude of the surface charge density, the ion concentration, or the valency of the counterions. This is in stark contrast to the experimental results31−34 and Monte-Carlo simulations,29,35−37 which have provided ample evidence of the phenomenon of like-charge attraction mediated by multivalent ions. This clear signature of electrostatic correlations is responsible for many important interfacial phenomena, including cement cohesion,34,38 biopolymer aggregation,39 and colloidal coagulation,30,40 and nevertheless, it still lacks a simple mathematical description.
Several theoretical approaches have been used in the past to explain like-charge attraction, including the theory by Perel and Shklovskii,41 the hypernetted-chain integral equation theory,35,42 and the dressed-ion theory.43,44 Although these theoretical approaches have certainly improved our understanding of ion–ion correlations, they lack the mathematical simplicity underlying the PB theory, which allows the disjoining pressure to be directly related to various system parameters, including the salt concentration, the ion valency, the solvent dielectric permittivity, the surface charge density, and the temperature. To this end, a simple and general theory of electrostatic correlations based on a Landau–Ginzburg-type continuum framework was recently developed by Bazant, Storey, and Kornyshev (BSK),45 and initially used to explain screening phenomena in solvent-free ionic liquids. Compared to the PB mean-field theory, the BSK free-energy functional adds an additional term containing the second derivative of the electrostatic potential to account for ion–ion correlations
| 1 |
where
ρ = e(z+c+ – z–c–) is the mean charge density, z± and c± are the valencies and concentrations,
respectively, of the cations and the anions, in the EDL of volume V, ϕ is the electrostatic potential, qs is the surface charge density, ϵ is the dielectric
permittivity of the solution, lc denotes
the electrostatic correlation length, and g(c+,c–) is
the entropic component of the total free energy and corresponds to
the entropy density arising from the translational entropy of the
ions. Note that 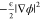 and ρϕ represent
the self-energy
of the electric field and the electrostatic potential energy of the
ions in this electric field, respectively. The potential gradient
term,
and ρϕ represent
the self-energy
of the electric field and the electrostatic potential energy of the
ions in this electric field, respectively. The potential gradient
term, 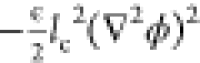 , is used to model an
additional contribution
to the self-energy resulting from electrostatic correlations between
the ions. The terms excluding the entropic contribution, g, arise via a charging process in which ions are added to a system
in which they interact with the electrostatic potential, ϕ.
Although the higher-order equation is still solved in the mean-field
of spatially averaged ϕ and ρ, the higher-order third
term implies the nonlocal nature of the free energy due to electrostatic
correlations. One can interpret this term as a phenomenological correction
to the mean-field PB framework that is solved for in the mean field.
This simple extension of the PB theory is a useful first approximation
of ion–ion correlation effects in ionic liquids46−50 and in so-called “water-in-salt” electrolytes.51
, is used to model an
additional contribution
to the self-energy resulting from electrostatic correlations between
the ions. The terms excluding the entropic contribution, g, arise via a charging process in which ions are added to a system
in which they interact with the electrostatic potential, ϕ.
Although the higher-order equation is still solved in the mean-field
of spatially averaged ϕ and ρ, the higher-order third
term implies the nonlocal nature of the free energy due to electrostatic
correlations. One can interpret this term as a phenomenological correction
to the mean-field PB framework that is solved for in the mean field.
This simple extension of the PB theory is a useful first approximation
of ion–ion correlation effects in ionic liquids46−50 and in so-called “water-in-salt” electrolytes.51
The BSK model has also been applied to electrolytic solutions52 and shown to capture various ion correlation effects, including electrophoretic mobility reversals of colloidal particles in multivalent electrolytes,53 micelle formation,54 and ion conduction through biological ion channels.55−58 The first challenge in applying the BSK theory to different systems is to find a suitable approximation of the electrostatic correlation length, lc. In the original article, Bazant et al.45 suggested using the Bjerrum length, lb, for dilute electrolytes and the ionic diameter for the opposite limit of room-temperature ionic liquids (where it is typically much larger than the Debye length). In the general case of a z:1 primitive-model electrolyte, where z is the valency of the counterion, the correlation length parameter was recently found to scale as59
| 2 |
where 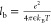 is the Bjerrum
length,1e is the unit
of elementary charge, and c0 is the bulk
salt concentration. Note that
the Bjerrum length corresponds to the length scale at which the electrostatic
interactions between two monovalent ions in the solution is comparable
to the thermal energy, kBT, where kB is the Boltzmann constant
and T is the absolute temperature. Physically, the
correlation length, lc, scales with the
diameter of a correlation hole in the electrolyte, beyond which the
mean-field equations are sufficient to describe the electrostatic
interactions between ions, as reflected in the PB model. In this article,
we describe ion–ion correlations using the BSK model for electrolytes
and study their influence on the disjoining pressure acting between
charged surfaces.
is the Bjerrum
length,1e is the unit
of elementary charge, and c0 is the bulk
salt concentration. Note that
the Bjerrum length corresponds to the length scale at which the electrostatic
interactions between two monovalent ions in the solution is comparable
to the thermal energy, kBT, where kB is the Boltzmann constant
and T is the absolute temperature. Physically, the
correlation length, lc, scales with the
diameter of a correlation hole in the electrolyte, beyond which the
mean-field equations are sufficient to describe the electrostatic
interactions between ions, as reflected in the PB model. In this article,
we describe ion–ion correlations using the BSK model for electrolytes
and study their influence on the disjoining pressure acting between
charged surfaces.
The second challenge in applying the BSK model is the choice of an additional boundary condition for the generalized Poisson equation, which is a fourth-order ordinary differential equation in our one-dimensional geometries. The second-order PB equation requires only one condition on each bounding surface, whereas the BSK equation requires two. Although mixed boundary conditions were first proposed,60 the standard choice, advocated by BSK for ionic liquids, has been to set the third derivative of the potential to zero, effectively cutting off ion–ion correlations at the distance of closest approach. Here, we take advantage of the recent development of more consistent and general boundary conditions, which are obtained by equating the normal Maxwell stress at the charged surface to its form in the absence of ion–ion correlations given by the contact theorem.59
We should stress here that the phenomenon of like-charge attraction can be modeled using solely the higher order term in the BSK functional eq 1 (see the Results section for details). However, for an accurate comparison of our theoretically predicted disjoining pressure with experimental data, we also incorporate some additional interactions, to arrive at a more complete generalization of the DLVO theory. In particular, the PB model assumes that ions are point-sized and are distributed throughout the electrolyte according to the Boltzmann distribution. This results in an exponential growth of counterions near the charged surface.60 In practice, however, the region closest to the charged surface is always hydrated by a condensed layer of water molecules. This layer is inaccessible to the counterions and is referred to as the Stern layer.11,61
Recently, Bohinc et al.62 formulated the Poisson–Helmholtz–Boltzmann model to describe solvent-mediated, nonelectrostatic interactions between ions based on a pair-wise Yukawa potential. In this model, in addition to electrostatic interactions, the ions experience a hydration (h) interaction given by, Uh/kBT = e–κh(r–lh)/r, where Uh is the hydration energy, r is the separation distance between the ions, κh is the inverse of the length scale corresponding to the decay of ordered water layers around an ion, and lh is the length scale at which Uh becomes comparable to the thermal energy, kBT. In this study, we follow the approach of Bohinc et al.62,63 to incorporate an additional solvent-mediated hydration interaction into the model in eq 1. Our approach serves two important purposes. First, we can self-consistently model both the Stern and the diffuse layer regions of the EDL using a single theory. Second, we can study the effect of the Stern layer region on the disjoining pressure acting between charged surfaces. Recall that in the Stern layer region, counterions are repelled from the charged surface due to the short-range hydration interactions, whereas coions, which carry charge of the same sign as that of the charged surface, are repelled due to the unfavorable repulsive electrostatic interactions with the charged surface. We later show that the short-range repulsive hydration forces reported by Israelachvilli and Pashley,64 as well as by LeNeveu and Rand,65 emerge naturally from the incorporation of hydration interactions into our model of the EDL.
After incorporating ion–ion correlations and hydration interactions into our EDL model, we implement a final modification by describing the phenomenon of surface charge regulation (CR). This is the electrochemical mechanism by which surfaces in contact with aqueous electrolytes acquire charge from the dissociation of surface species, such as the silanol groups that typically terminate glass or silica surfaces.66 In this case, the degree of dissociation depends strongly on the pH of the solution. To validate our theoretical predictions on like-charge attraction, we make use of the experimental data of Plassard et al.34 who measured the disjoining pressure acting between calcium silicate hydrate (CSH) layers in a calcium hydroxide electrolyte solution. We incorporate the mechanism of surface CR into our EDL model by assuming that the charge on the CSH layers results from the dissociation of silanol groups (SiO–) at the CSH surface,34 which allows us to relate the surface charge density on the CSH surface to the calcium hydroxide concentration in the solution.
The end result after incorporation of ion–ion correlations, hydration interactions, and surface CR—phenomena which are all currently neglected in the DLVO theory, is a complete, self-consistent theory of the disjoining pressure for multivalent electrolytes. Specifically, we demonstrate that our theory can be used to describe the phenomenon of like-charge attraction, including predicting the disjoining pressure, in reasonably good agreement with the experimental data of Plassard et al.34 for a broad range of salt concentrations.
Model and Methods
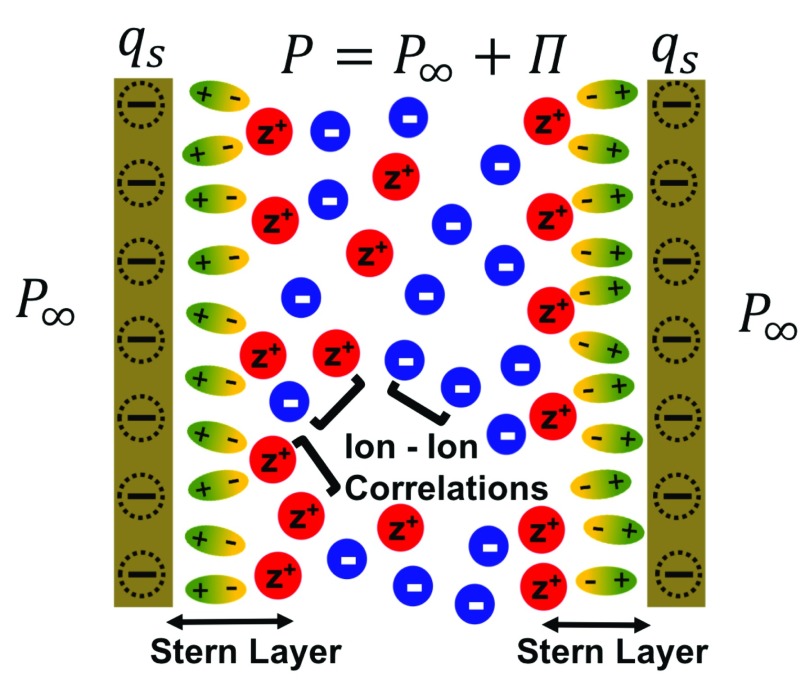
We begin our analysis by considering two similarly charged surfaces immersed in a z:1 electrolyte solution, where z denotes the valency of the counterion. For reference, we assume that both surfaces are negatively charged, which implies that cations are the positively charged counterions in this system. Because hydration interactions are short-ranged, we simplify our analysis by assuming that the hydration interactions are only relevant for the cations and negligible for the anions, which are anyway repelled because of the repulsive electrostatic interactions with the negatively charged surface. Therefore, in our model, the cations interact with the negatively charged surface through both electrostatic and hydration interactions, whereas the anions interact with the negatively charged surface only through electrostatic interactions. Furthermore, as shown in Figure 1, the region closest to the negatively charged surface is accessible only to the water molecules which serve as the source term for the boundary condition for the hydration potential (see below). As discussed by Brown et al.,63 this is similar in spirit to the surface charge density at the charged surface serving as the boundary condition for the electrostatic potential. The negatively charged surfaces electrostatically attract cations from the bulk reservoir, resulting in the formation of an EDL of ions in the region between the charged surfaces. As shown in Figure 1, the formation of the EDL results in the pressure felt by the charged surfaces, referred to as the disjoining pressure, being significantly different than the osmotic pressure in the bulk reservoir.
Figure 1.
Schematic of our model problem: a multivalent z:1 electrolyte is confined between two surfaces with surface charge density, qs. The disjoining pressure, Π, is defined as the difference in the pressure (P) felt between the plates due to the presence of the EDL and the pressure in the bulk reservoir (P∞). As shown here, the Stern layer which is the region closest to the charged surface is accessible only to the water molecules (depicted as ellipsoids) modeled using the hydration potential, whereas the concentration profiles of the cations (depicted as red spheres) and the anions (depicted as blue spheres) in the EDL are influenced by ion–ion correlations, described in our theory using the BSK model.
After incorporation of additional contributions from hydration interactions into eq 1, we arrive at the following general functional for the total Helmholtz free energy of the system
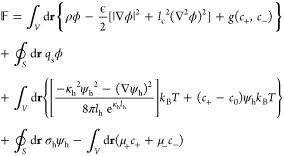 |
3 |
where ψh is the dimensionless hydration potential, σh is the surface density of water molecules at the charged surface which mediate the interaction of cations with the charged surface, and μ+ and μ– are the chemical potentials of the cations and anions, respectively. The terms in the 1st and 2nd rows in eq 3 are the same as those of eq 1 and correspond to the free energy of the system after incorporating ion–ion correlations into the PB model. Furthermore, the terms in the 3rd row and the 1st term in the 4th row in eq 3 result from the incorporation of hydration effects into our model. Finally, the last term in eq 3 couples the concentration of ions in the EDL confined by the charged surfaces to that in the bulk reservoir. Although the terms in eq 3 resulting from ion–ion correlations and hydration interactions have been reported in refs (45) and (62), respectively, for completeness, a detailed derivation of the Helmholtz free energy expression in eq 3 is provided in the Supporting Information document.
We note here that the incorporation of hydration interactions automatically accounts for the finite size of the ions. Therefore, there is no need to incorporate any additional excluded-volume interactions in our model, and we can retain the original expression for the entropy density, g(c+,c–), from the PB model given by
| 4 |
where c0i (i = ±) is the corresponding concentration of cations/anions in the bulk reservoir.
Next, we enforce the
conditions of thermodynamic equilibrium in
the system by setting 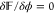 for the electrostatic
potential and
for the electrostatic
potential and 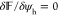 for the hydration potential
in eq 3, respectively.
For the
electrostatic potential, we obtain a fourth-order Poisson equation
and a boundary condition, respectively, given by
for the hydration potential
in eq 3, respectively.
For the
electrostatic potential, we obtain a fourth-order Poisson equation
and a boundary condition, respectively, given by
| 5 |
| 6 |
Similarly, the governing equations for the dimensionless hydration potential, ψh, and the corresponding boundary condition are given by
| 7 |
| 8 |
We note here that eq 7 does not contain any term which depends on
the concentration of
anions, c–, which is consistent
with our assumption that the hydration potential acts only between
cations. As discussed by Brown et al.,63eq 8 results from assuming
that each ordered water molecule near the negatively charged solid
surface acts like a source term for the hydration interaction of the
cations with the charged surface. At thermodynamic equilibrium, 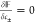 , which results in the following expressions
for the chemical potential of the counterions and the coions
, which results in the following expressions
for the chemical potential of the counterions and the coions
| 9 |
| 10 |
where c+0 and c–0 are the
bulk concentration of the
counterions and the coions, respectively. To satisfy the condition
of electroneutrality in the bulk, c+0 = c0 and c–0 = zc0 (c0 is the concentration of the undissociated z:1 salt).
Equating eq 10 at any
point in the EDL and in the bulk reservoir results in the following
expressions for the dimensionless counterion and the coion densities
in the EDL: c̃+ = e–zϕ̃+ψh, c̃– = eϕ̃, where, 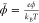 ,
, 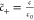 and
and  . For a numerical evaluation of the electrostatic
potential in the EDL, it is convenient to convert eq 5 into a dimensionless form, given
by
. For a numerical evaluation of the electrostatic
potential in the EDL, it is convenient to convert eq 5 into a dimensionless form, given
by
| 11 |
where x̃ = x/λD, λD is the Debye–Hückel
screening length, which for a z:1 electrolyte is
given by the expression: 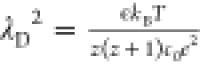 , ∇̃ = λD∇,
and δc = lc/λD is the dimensionless correlation length. The dimensionless
correlation length for a z:1 electrolyte is given
by the following expression in ref (59)
, ∇̃ = λD∇,
and δc = lc/λD is the dimensionless correlation length. The dimensionless
correlation length for a z:1 electrolyte is given
by the following expression in ref (59)
| 12 |
In eq 12, the quantity, lGC, denotes the Gouy–Chapman length, which is the length scale at which the interaction of a counterion with a uniformly charged surface becomes comparable to the thermal energy, kBT, and is given by
| 13 |
Similar to the electrostatic potential, the dimensionless governing equation for the hydration potential is given by
| 14 |
Note that the governing equation for the dimensionless electrostatic potential (eq 11) is fourth-order. Therefore, we need four boundary conditions to solve for the dimensionless electrostatic potential. Assuming that the negatively charged surfaces are located at −d/2 – lh and d/2 + lh, where d is the separation distance between the two negatively charged surfaces, corresponding to the region accessible to the ions, and lh is the hydration length parameter, eq 11 can be solved using the following four boundary conditions:
Note that boundary conditions (i) and (ii) result from equating the electric displacement field at the charged surface, which is similar to the approach used in the previous studies to derive the boundary conditions for the PB model. Furthermore, the boundary conditions (iii) and (iv) result from enforcing a force balance at contact, where ionic correlations must vanish.59 The boundary conditions to solve for the dimensionless hydration potential using eq 14 are given by:63
Note that for a given d, the actual domain over which the equations are being solved changes depending on whether the hydration potential is included in the model. If the hydration potential is included (i.e., lh ≠ 0), then the electrolyte domain lies between x = −d/2 – lh and x = d/2 + lh. If not (lh = 0), then the distance of closest approach must be subtracted, such that the electrolyte domain consists of the region between x = −d/2 and x = d/2. Such a distinction is important when the predicted disjoining pressure is compared using different models, as shown in the Results section, where the separation distance between the charged surfaces is denoted using d for all of the models considered.
Next, we present our derivation
of the disjoining pressure by expressing
the total free energy of the system as follows: 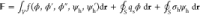 . At
thermodynamic equilibrium,
. At
thermodynamic equilibrium, 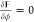 and
and 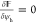 for the bulk variation, which together
with the mathematical identities of variational calculus can be used
to obtain the following relation (see the detailed derivation in the Supporting Information document)
for the bulk variation, which together
with the mathematical identities of variational calculus can be used
to obtain the following relation (see the detailed derivation in the Supporting Information document)
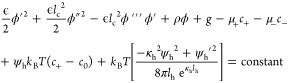 |
15 |
At thermodynamic equilibrium for a z:1 electrolyte, the following additional relations apply
| 16 |
| 17 |
Adding eqs 16 and 17 and then subtracting the resulting expression from eq 15 yields
| 18 |
We note here that eq 18 is valid for any arbitrary separation distance between the
two charged
surfaces. Furthermore, the left hand side (LHS) of eq 18 is a constant, which can be evaluated
at any point between two charged surfaces. Therefore, the constant
in eq 18 should be in
some way related to the pressure acting between the charged surfaces.
Indeed, in analogy to the constant in eq 18, the condition of thermodynamic equilibrium
ensures that the pressure is uniform throughout the region confined
between the two charged surfaces. The relationship between the constant
in eq 18 and pressure
becomes clearer when we consider the limit where the two charged surfaces
are placed very far apart, such that the electrostatic potential,
the hydration potential, and all higher-order derivatives of the electrostatic
and the hydration potentials reduce to zero at the mid plane between
the two charged surfaces. In this case, when evaluating the LHS of eq 18 at the mid plane between
the two charged surfaces, the first five terms involving the electrostatic
and the hydration potentials, as well as their higher-order derivatives
vanish and only the last two terms remain finite. Further, the free-energy
functional, f, becomes equal to the entropy density, g, and 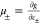 from eqs 16 and 17,
respectively. On the
other hand, the expression for the pressure in this case can be readily
obtained by using the thermodynamic relation: U/V = TS/V – P + ∑iμici,
where U denotes the total internal energy of the
system, S is the total entropy, and T, P, and V denote the temperature,
pressure, and total volume of the system, respectively. Because the
Helmholtz free energy, F, can be written as,
from eqs 16 and 17,
respectively. On the
other hand, the expression for the pressure in this case can be readily
obtained by using the thermodynamic relation: U/V = TS/V – P + ∑iμici,
where U denotes the total internal energy of the
system, S is the total entropy, and T, P, and V denote the temperature,
pressure, and total volume of the system, respectively. Because the
Helmholtz free energy, F, can be written as, 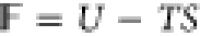 , and the free-energy functional, f, is equal to
the Helmholtz free energy per unit volume,
that is f = F/V, we obtain, −P =
, and the free-energy functional, f, is equal to
the Helmholtz free energy per unit volume,
that is f = F/V, we obtain, −P = 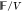 −
− 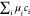 = f −
= f − 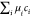 = g −
= g − 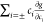 . Therefore,
the constant in eq 18 is equal to the negative of the
pressure, P, acting between the two charged surfaces,
which according to eq 18 is given by
. Therefore,
the constant in eq 18 is equal to the negative of the
pressure, P, acting between the two charged surfaces,
which according to eq 18 is given by
| 19 |
Using the expression for g from eq 4, and subtracting the pressure in the bulk reservoir obtained by setting the electrostatic potential, the hydration potential, and all higher-order derivatives of the electrostatic and the hydration potentials to zero in eq 19, the disjoining pressure, Π = P – P∞, is given by
| 20 |
It is noteworthy that the mathematical framework presented here to derive the disjoining pressure, as expressed in eq 20, is very general. In fact, in principle, this methodology can be used to derive a closed-form analytical expression of the disjoining pressure for any system given an expression for the free-energy functional, f, of the system. Indeed, a similar methodology was used previously by Misra et al.9 to derive an expression of the disjoining pressure for a different system where solvent polarization effects were included in the PB model.
Next, we analyze in more detail each of the terms contributing to the disjoining pressure predicted in eq 20. Specifically, the 1st term arises from the self-energy of the electrostatic field in the EDL, the 2nd and 3rd terms arise from ion–ion correlations, the 4th term is a contribution due to the translational entropy of the ions, and the 5th and 6th terms arise from the incorporation of hydration interactions into the EDL model. If hydration interactions are neglected, that is, ψh = 0 and ψh′ = 0, the 1st four terms in eq 20 yield the expression of the disjoining pressure in the context of the BSK model, given by
| 21 |
Furthermore, if ion–ion correlations are also neglected, that is if we set lc = 0 in eq 21, we recover the exact expression of the disjoining pressure for the PB model given by (see refs (11) and (67))
| 22 |
The disjoining pressure in eq 20 is uniform throughout the region confined by the two charged surfaces. However, one can obtain additional insights about the nature of the terms contributing to the disjoining pressure by evaluating eq 20 at the mid-plane between the two charged surfaces. For example, if the two surfaces carry charge of the same sign and magnitude (similarly charged), the 1st derivative of both the electrostatic and the hydration potentials are zero at the mid-plane between the two charged surfaces due to symmetry conditions. In this case, the predicted disjoining pressure is given by
| 23 |
Equation 23 clearly shows that the contribution from the water-mediated hydration interactions between the cations (last two terms in eq 23) to the disjoining pressure is always repulsive. The 2nd term in eq 23, which is the entropic contribution to the disjoining pressure, is also always repulsive. Note that the 2nd term in eq 23 corresponds to the disjoining pressure according to the PB model. This is the reason why the PB model always predicts a repulsive disjoining pressure between similarly charged surfaces, irrespective of the surface charge density, the salt concentration, and the valency of the counterions. In contrast, the 1st term in eq 23, which arises from the ion–ion correlations described by the BSK model, is always negative. Therefore, eq 23 predicts that there can be an attractive EDL contribution to the disjoining pressure even between similarly charged surfaces, as long as the attractive contribution due to ion–ion correlations dominates over the contributions due to the repulsive entropic and hydration interactions.
In addition to electrostatic interactions, van der Waals interactions between the two planar surfaces can contribute to the disjoining pressure, although their range is significantly short-ranged. The van der Waals contribution to the disjoining pressure can simply be added to eq 23, and is given by34
| 24 |
where Ah is the Hamaker constant and determines the magnitude of the van der Waals interaction between the two planar surfaces. It is noteworthy that the attractive disjoining pressure associated with the van der Waals interactions can also result in like-charge attraction, especially if the charged surface is neutralized by the multivalent counterions. However, the magnitude of the attraction resulting from the van der Waals interactions is highly system-specific. Indeed, the attractive contribution to the disjoining pressure resulting from the van der Waals interactions will depend on several factors: (i) the nature of the counterion neutralizing the charged surface, (ii) the thickness of the EDL of counterions neutralizing the charged surface, and (iii) the magnitude of the Hamaker constant of the interacting charged surfaces in air. All these effects can be captured in our model by defining an effective Hamaker constant to model the van der Waals interaction between charged surfaces in the presence of a confined electrolyte. Note that unless specifically stated, most of the results in this article will not include the contribution in eq 24 because our study is mainly focused on studying the EDL contribution to the disjoining pressure. However, we will include the van der Waals contribution to the disjoining pressure when comparing the theoretically predicted disjoining pressure to the experimentally measured one.
Finally, we also include the contribution due to the phenomenon of surface CR into our EDL model. Although there are several theoretical approaches to model surface CR,68,69 we have adopted the formulation by Behrens and Grier,66 which is useful to model surface CR in cases where the surface charge is related to the dissociation of silanol groups from the surface. Note that in the case of CSH layers, the surface dissociation of silanol groups is primarily responsible for the negative surface charge on the CSH layers, as reported in the study by Plassard et al.70 To model the variation of the surface charge density of CSH layers as a function of the solution pH,70 we consider reactions of hydroxide ions with silica sites, using the formulation of Behrens and Grier.66 In basic solutions involving hydroxide ions, the surface reaction proceeds as follows
| 25 |
The surface is composed of negative (dissociated) and neutral (undissociated) silica sites determined by the surface reaction equilibrium of the hydroxide ions interacting with the CSH layer. A total site balance on the Si atoms result in the following equation
| 26 |
where Γ is the total surface concentration of Si atoms, ΓSiO– and ΓSiOH are the surface concentrations of the negative and the neutral silica sites, respectively. Note that the surface charge density on the CSH layer can be expressed as the product of the number of negative silica sites times their charge, that is, qs = −eΓSiO–. Similar to the study by Behrens and Grier,66 we assume that the distribution of the hydroxide ions near the CSH layer satisfies the Boltzmann distribution given by, cOH–,s = cOH–,B exp(ϕ̃s), where ϕ̃s is the dimensionless electrostatic potential at the CSH layer, and cOH–,B and cOH–,s are the concentrations of hydroxide ions in the bulk and near the CSH layer, respectively. Furthermore, based on the surface chemical reaction in eq 25, the following relation is obtained
| 27 |
where Kb is the base dissociation equilibrium constant, and pKb is the logarithmic dissociation constant characteristic of the CSH–water interface. Because the Stern layer is already modeled self-consistently through the incorporation of water-mediated hydration interactions, the surface potential, ϕ̃s can be set equal to the potential at the surface located at (x = ±d/2 ± lh), without the need to account for the Stern capacitance, as done in ref (66). Using the relation, qs = −eΓSiO–, in conjunction with eqs 26 and 27, the expression for the surface charge density at the CSH layer is given by
| 28 |
Note that Γ and pKb are parameters characteristic of the CSH–water interface and can be obtained through fitting to experimental data. Because the correlation length is itself a function of the surface charge density through its dependence on lGC (see eqs 12 and 13), δc must be obtained in an iterative manner. Specifically, the dimensionless electrostatic potential (see eq 11) is solved using an initial guess for qs, and subsequently, the deduced value of ϕ̃s is used to adjust qs for subsequent iterations using eq 28. Finally, the converged value of qs is used to obtain the dimensionless electrostatic potential (see eq 11), and the disjoining pressure is obtained using eq 23 for various separation distances between the two similarly charged surfaces.
Results
Several key predictions of our theory are presented below. First, we consider the role of ion–ion correlations on the disjoining pressure acting between two similarly charged surfaces, including studying the dependence on the valency of the counterions and coions, the bulk salt concentration, and the surface charge density of the charged surfaces. Second, we study the effect of incorporating hydration interactions and surface CR on the disjoining pressure into our EDL model. Finally, after including the contribution of the van der Waals interactions to the disjoining pressure, we compare the predictions of the disjoining pressure made using our complete model with the experimental data of Plassard et al.34
Ion–Ion Correlations Cause Like-Charge Attraction
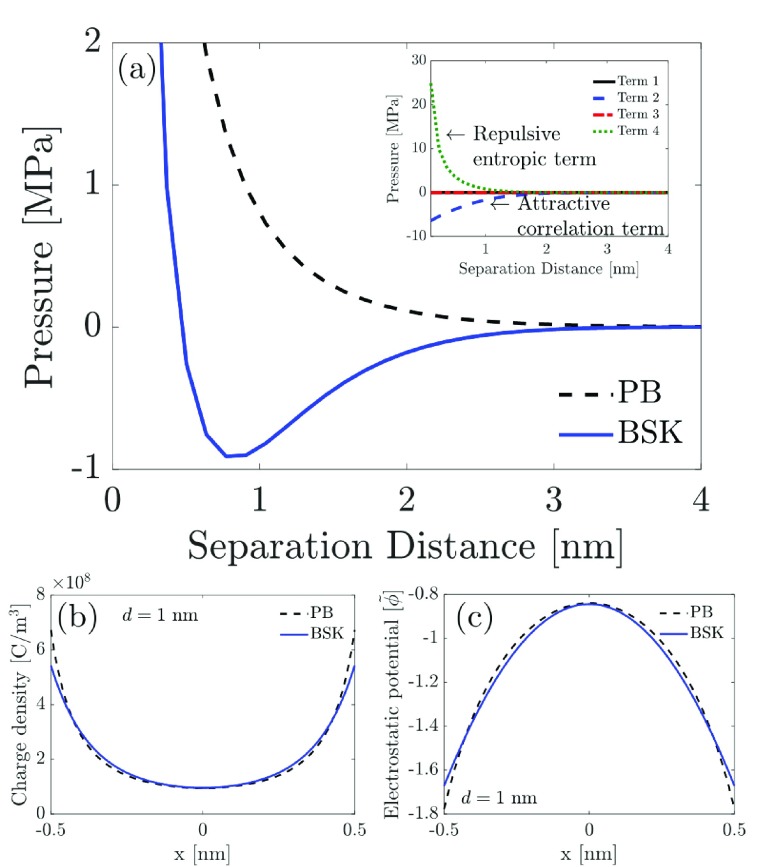
To isolate and properly quantify the effect of ion–ion correlations on the disjoining pressure, as described by the BSK theory, we initially neglect hydration interactions, surface CR, and van der Waals interactions in our EDL model. This is done by setting ψh = 0 in eq 20 (thereby neglecting hydration interactions), assuming that qs is an independent parameter irrespective of the bulk salt concentration (thereby neglecting surface CR), and setting Ah = 0 in eq 24 (thereby neglecting van der Waals contributions to the disjoining pressure). In Figure 2a, we utilize eq 21 to plot the disjoining pressure predicted using the BSK model as a function of the separation distance between the two charged surfaces for the case of a 2:1 electrolyte solution. Note that throughout the article, the water dielectric permittivity, ϵ, is expressed as ϵ = ϵrϵ0, where ϵ0 is the permittivity of vacuum (8.85 × 10–12 F m–1). In Figure 2a, the disjoining pressures predicted using the BSK model (see eq 21) and the PB model (see eq 22) are compared. Note that the governing equation for the dimensionless electrostatic potential in the PB model can be obtained simply by setting δc = 0 in eq 11, including using boundary conditions (i) and (ii) in the set of four boundary conditions used to solve eq 11 in the BSK model. As expected, the PB model always predicts a repulsive (positive) disjoining pressure irrespective of the separation distance between the two charged surfaces. Furthermore, the repulsive disjoining pressure predicted by the PB model decreases monotonically with an increase in the separation distance between the two charged surfaces. However, in stark contrast to the result predicted by the PB model, it is possible to obtain an attractive (negative) disjoining pressure using the BSK model. For example, as shown in Figure 2a, the disjoining pressure curve predicted by the BSK model displays an attractive well at a separation distance of ∼0.8 nm between the two charged surfaces. For separation distances greater than 1 nm, where the disjoining pressure predicted by the BSK model is negative and progressively goes to zero at larger separation distances, the attractive pressure resulting from ion–ion correlations dominates over the pressure arising from the entropic repulsion.
Figure 2.
Disjoining pressures operating between two similarly charged surfaces separated by a 2:1 electrolyte solution predicted using the BSK (eq 21) and the PB (eq 22) models for qs = −0.1 C/m2, c0 = 0.1 M, and ϵr = 80. (a) Variation of the disjoining pressure as a function of the separation distance between the two charged surfaces. The inset shows the contribution of the different terms in eq 21 based on the BSK model. (b,c) Comparison of the charge density and the dimensionless electrostatic potential profiles, respectively, predicted by the BSK model (eq 11) and the PB model (eq 11 with δc set to zero) when the separation distance between the two charged surfaces is 1 nm, and where x is the spatial coordinate perpendicular to the plane of the charged surface.
To better understand the above-mentioned competition, in the inset of Figure 2a, we plot the contributions to the disjoining pressure due to each of the four terms appearing in eq 21, all evaluated at the mid-plane between the two charged surfaces. Because we are considering similarly charged surfaces, the 1st derivative of the electrostatic potential is always zero at the mid-plane between the two charged surfaces. Therefore, the 1st and the 3rd terms in eq 21 do not contribute to the predicted disjoining pressure. Moreover, as shown in the inset of Figure 2a, the pressure resulting from ion–ion correlations (2nd term in eq 21) is always attractive (negative), whereas the entropic pressure (4th term in eq 21) is always repulsive (positive). For separation distances much smaller than 1 nm, the counterions get compressed between the two charged surfaces, thereby greatly enhancing the entropic contribution and making the overall disjoining pressure repulsive (positive). On the other hand, for separation distances larger than 1 nm, the disjoining pressure contribution from ion–ion correlations always dominates over the repulsive entropic contribution, which results in an overall attractive disjoining pressure as shown in Figure 2a. Interestingly, as Figure 2b shows, at a separation distance of 1 nm between the two charged surfaces, the mean charge density (ρ = zec+ – ec–) and the dimensionless electrostatic potential (ϕ̃) profiles obtained using the PB and the BSK models are very similar. The similarity in the two profiles suggests that the form of the Helmholtz free energy, F, and a self-consistent expression of the disjoining pressure, Π, derived from F, are essential in order to obtain a negative disjoining pressure in the context of the BSK model. For example, even if one utilizes eq 11 to solve for the electrostatic potential using the BSK model, use of eq 22 which corresponds to the disjoining pressure from the PB model would still result in a repulsive disjoining pressure for all separation distances between the similarly charged surfaces. Therefore, our study highlights the necessity to self-consistently incorporate terms in the predicted disjoining pressure (see eq 21) arising from ion–ion correlations to explain the phenomenon of like-charge attraction between similarly charged surfaces.
It is noteworthy that in the previous work, the BSK model was shown to describe overscreening, or charge-inversion, in the case of an EDL of solvent-free ionic liquids placed near a charged electrode.45 In this case, strong ion–ion correlations give rise to an oscillatory profile for the mean charge density, ρ, where the 1st layer of ions in the EDL overscreens the charge on the electrode, and subsequently, the net charge of the electrode together with the 1st layer of ions is progressively neutralized by additional layers of ions. In this study, we find that although both the phenomena of charge-inversion and like-charge attraction can result from strong ion–ion correlations, there is no direct correlation between them. In other words, it is not necessary for the phenomenon of like-charge attraction to occur concurrently with the phenomenon of charge-inversion.
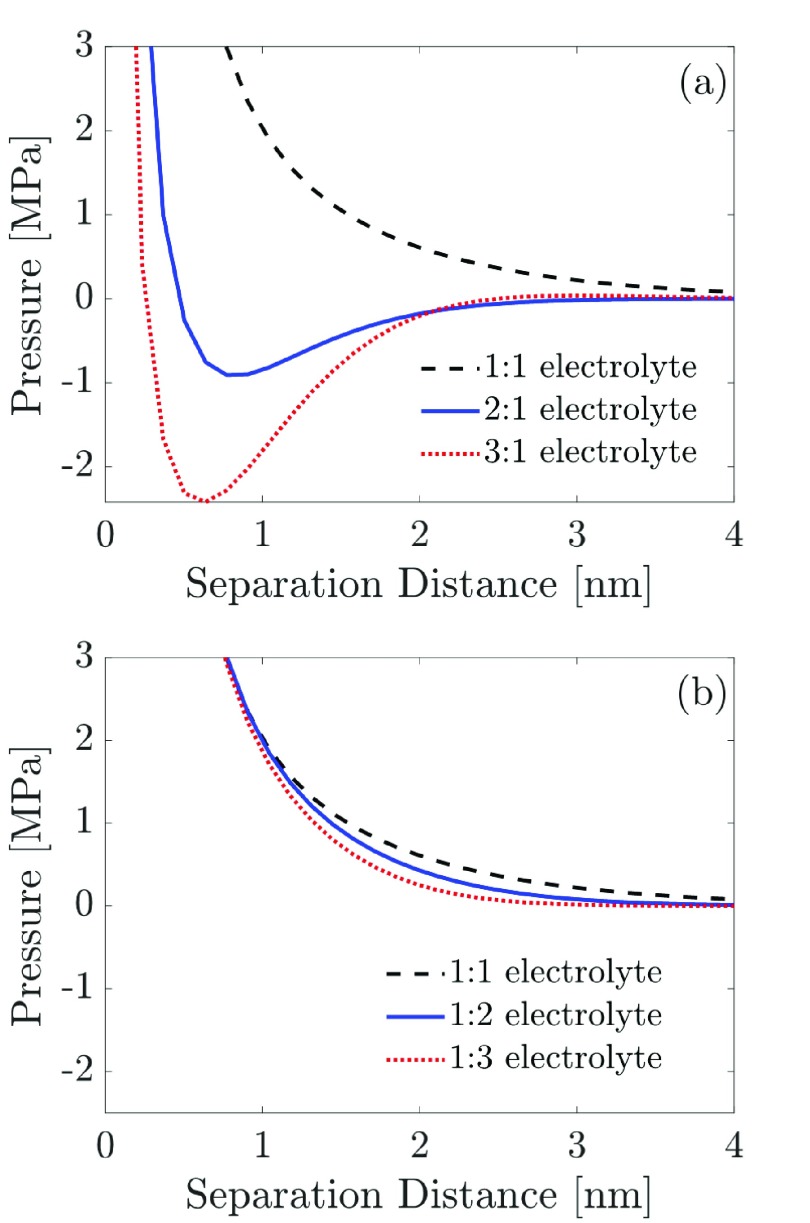
Next, we study how the counterion valency affects the disjoining pressure. As the counterion valency increases, the BSK theory predicts a stronger attractive contribution to the disjoining pressure, as shown in Figure 3a. The qualitative shape of the pressure profile also changes significantly as the counterion valency increases from 1 to 3, with a deep attractive well developing in the case of a 3:1 electrolyte. Moreover, the position of the minimum in the disjoining pressure shifts toward the left with an increase in the counterion valency, indicating an enhancement in the length scale over which an attractive disjoining pressure is observed due to ion–ion correlations. The predicted attraction is consistent with experimental observations of like-charge attraction and colloidal coagulation in the presence of multivalent salt ions.26−30 Physically, increasing the counterion valency, z, enhances ion–ion correlations, which is captured in our EDL model by a nonlinear dependence of the dimensionless correlation length on the counterion valency (see eq 12). Increasing the value of z increases the dimensionless correlation length parameter, which in turn enhances the attractive ion–ion correlation contribution to the disjoining pressure (see 1st term in eq 23).
Figure 3.
Effect of the ion valency on the predicted disjoining pressure acting between two similarly charged surfaces as a function of the separation distance between the two charged surfaces for z:1 and 1:z electrolytes (z = 1, 2, and 3) solutions using the BSK model (eq 21). To generate the various plots, we used the following parameter values: |qs| = 0.1 C/m2, c0 = 0.1 M, and ϵr = 80. (a) Predicted disjoining pressure of a z:1 electrolyte solution, corresponding to a negative charge on the two surfaces, qs = −0.1 C/m2. (b) Predicted disjoining pressure of a 1:z electrolyte solution, corresponding to a positive surface charge on the two surfaces, qs = +0.1 C/m2.
In addition to studying the variation of the predicted disjoining pressure with the counterion valency, it is also interesting to explore the dependence of the predicted disjoining pressure on the coion valency, that is, for a 1:z electrolyte solution. To this end, we utilize the same parameter values used to generate Figure 3a, except that we change the sign of the surface charge density, qs, on the two surfaces. This, in turn, is equivalent to studying a 1:z electrolyte solution instead of the z:1 electrolyte solution considered earlier. Furthermore, note that we also set z = 1 in eqs 12 and 13. In Figure 3b, we show plots of the predicted disjoining pressure for a 1:z electrolyte, where the sign of qs is positive. Interestingly, the predicted disjoining pressure is not sensitive to the coion valency, where the plots of the disjoining pressure predicted using different coion valencies, z = 1, 2, and 3, are all very similar to the predicted disjoining pressure plot for a 1:1 electrolyte solution. This indicates that the phenomenon of like-charge attraction is more strongly controlled by the valency of the counterion than by that of the coion. Our important finding that the coion valency plays an insignificant role in controlling the surface forces between two charged surfaces is well supported by the recent experimental data of Uzelac et al.71 These authors measured surface forces between charged silica particles mediated by multivalent coions and reported that the valency of the counterions, and not the valency of the coions, controls the surface forces operating between the charged silica particles that they considered.
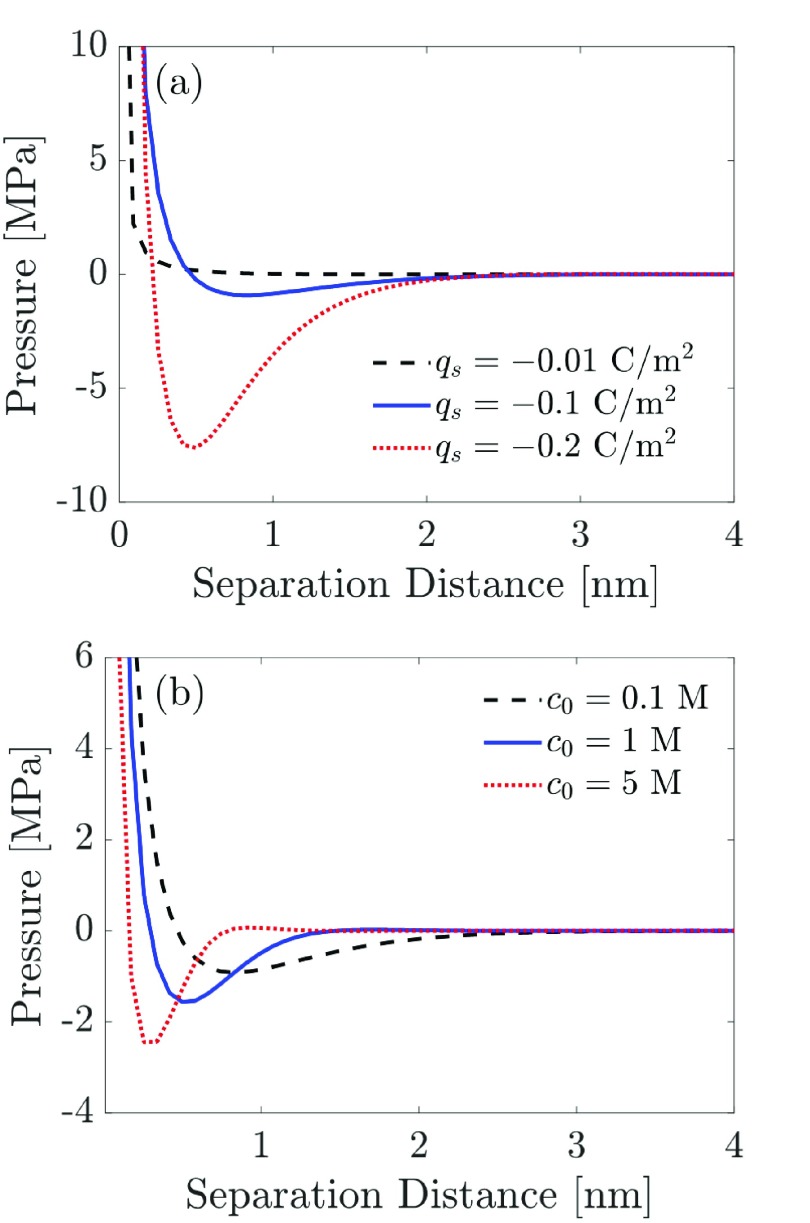
Next, we explore the dependence of the predicted disjoining pressure on the surface charge density and the salt concentration of the bulk reservoir. As shown in Figure 4a, increasing the surface charge density of the two charged surfaces for a 2:1 electrolyte solution results in an enhancement of the attractive well for the disjoining pressure as the magnitude of qs is increased from −0.01 to −0.2 C/m2. In the case of an electrolyte confined between two charged surfaces, increasing the surface charge density of the two surfaces results in an enhancement of the overlap of the EDLs produced by each surface because more counterions over an extended region are required to screen the increased charges on the surfaces. This results in an increase in the curvature, or the second derivative, of the electrostatic potential. As a result, the attractive ion–ion correlation contribution to the predicted disjoining pressure (2nd term in eq 21), which scales as the square of the 2nd derivative of the electrostatic potential, increases similarly. Consequently, increasing the surface charge density in the context of the BSK model results in a pronounced enhancement of the attractive well for the predicted disjoining pressure.
Figure 4.
Effect of the surface charge density and the salt concentration for a 2:1 electrolyte solution on the predicted disjoining pressure as a function of the separation distance between the two charged surfaces. (a) Predicted disjoining pressures for three surface charge densities, where the following parameter values were used to generate the three plots shown: c0 = 0.1 M and ϵr = 80. (b) Predicted disjoining pressures for three salt concentrations in the bulk reservoir, where the following parameter values were used to generate the three plots shown: qs = −0.1 C/m2 and ϵr = 80.
Our findings clearly show that the disjoining pressure predicted by the BSK model strongly disagrees with that predicted by the DLVO theory, which uses the PB model to predict the EDL contribution to the disjoining pressure acting between the two charged surfaces. Notably, increasing the surface charge density in the PB model enhances the overlap of the EDLs originating from the two similarly charged surfaces, which in turn results in an increased entropic repulsion and consequently, in an enhancement of the repulsive disjoining pressure acting between the two similarly charged surfaces. Although it is certainly true that like in the PB model, the magnitude of the repulsive entropic term (4th term in eq 21) also increases with an increase in the surface charge density in the BSK model, the attractive ion–ion correlation term completely dominates over the repulsive entropic term, leading to a deepening of the attractive well for the predicted disjoining pressure in the case of the BSK model. Our result is in good agreement with that obtained by Plassard et al.34 who experimentally measured the disjoining pressure operating between charged CSH layers in a calcium hydroxide salt solution. Indeed, Plassard et al.34 reported an enhancement of the attractive well for the experimental disjoining pressure upon increasing the surface charge density on the CSH layers. The fact that the DLVO theory fails to predict the experimentally observed trend, even at a qualitative level, demonstrates the importance and need for the availability of a theory such as the one presented here, which is capable of accurately modeling ion–ion correlations.
As shown in Figure 4b, the predicted disjoining pressure also depends strongly on the salt concentration of the bulk reservoir. Indeed, as the salt concentration increases, the depth of the attractive well increases, reflecting stronger ion–ion correlations. In addition, the position of the disjoining pressure minimum shifts toward the left, reflecting a decrease in the overlap of the EDLs originating from the two similarly charged surfaces. We have explored a wide parameter space for the dependence of the predicted disjoining pressure on salt concentration and surface charge density, as shown in the two contour plots in the Supporting Information document (see Figure S1).
We note that like-charge attraction can also be obtained in the limit of a counterion-only system (also referred to as the one-component plasma limit),29 where the surface charge is screened by a fixed number of counterions, with no coions present in the system. In this context, the BSK theory with the appropriate correlation length scale and boundary conditions has been shown to exactly match the strong and weak coupling limits for the counterion-only system.59 Furthermore, the BSK theory can also accurately reproduce the intermediate coupling limit, including describing correlation-induced like-charge attraction in the case of counterion-only systems.59
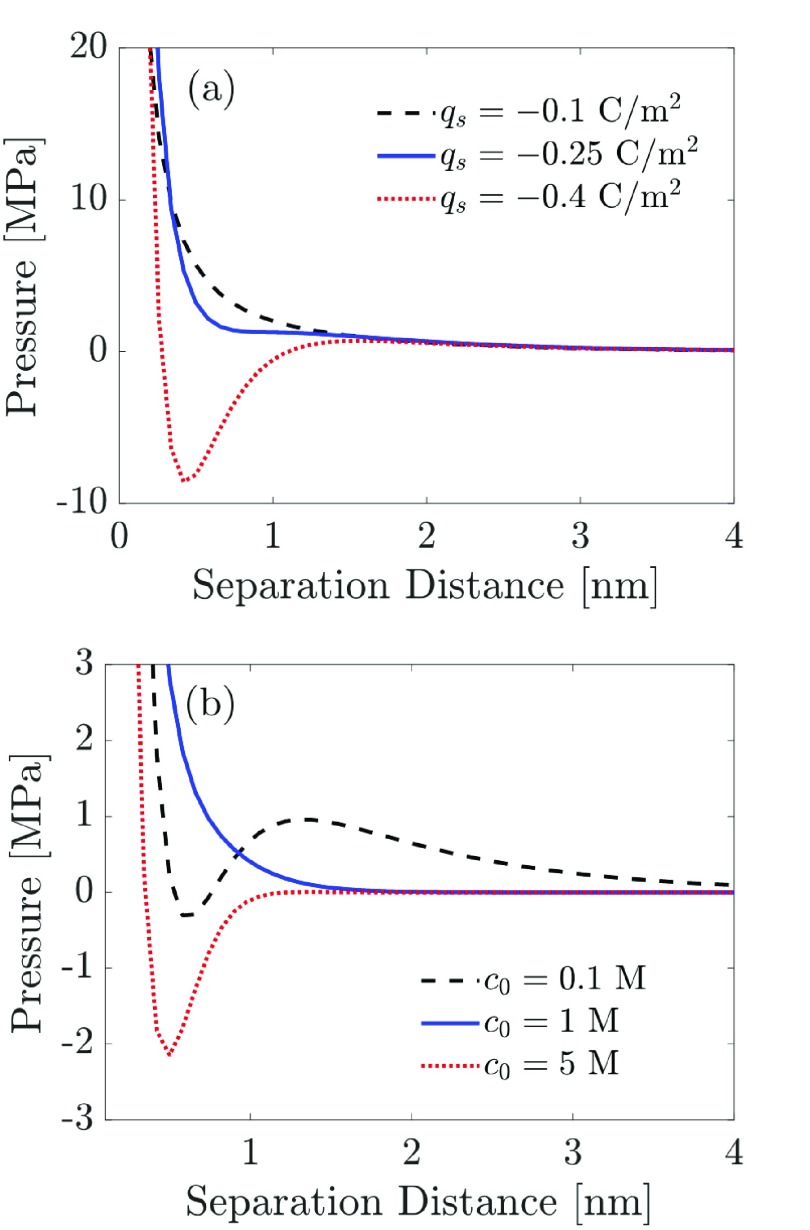
Another interesting question is whether the BSK theory can predict like-charge attraction in systems with monovalent counterions, as was shown recently in simulations of charged nanoparticles.72 In Figure 5, we show the predicted disjoining pressure curves for a 1:1 electrolyte solution with varying surface charge density and varying bulk salt concentration. Figure 5a clearly shows that, as the surface charge density increases from −0.1 to −0.4 C/m2, the disjoining pressure between two similarly charged surfaces predicted by the BSK theory can become strongly attractive (negative), even in the case of monovalent counterions.
Figure 5.
The disjoining pressure for a 1:1 electrolyte solution predicted by the BSK theory can be attractive depending on (a) surface charge density or (b) salt concentration. For (a), the bulk salt concentration is fixed at c0 = 0.1 M. For (b), the surface charge density is fixed at qs = −0.3 C/m2.
Furthermore, increasing the bulk salt concentration can result in the appearance of an attractive well in the disjoining pressure predicted by the BSK theory, similar to the ones predicted earlier in the case of a 2:1 electrolyte solution. However, very high bulk salt concentrations or moderate to high surface charge densities are needed to predict attractive disjoining pressures in the case of a 1:1 electrolyte solution. Our BSK model predictions for the disjoining pressure suggest that attractive interactions between two like-charged surfaces do not result exclusively from the presence of multivalent counterions. However, the presence of multivalent counterions can significantly augment the attractive disjoining pressure arising from ion–ion correlations, as shown earlier in Figure 3a.
Contributions to the Disjoining Pressure from Hydration Interactions and Surface CR
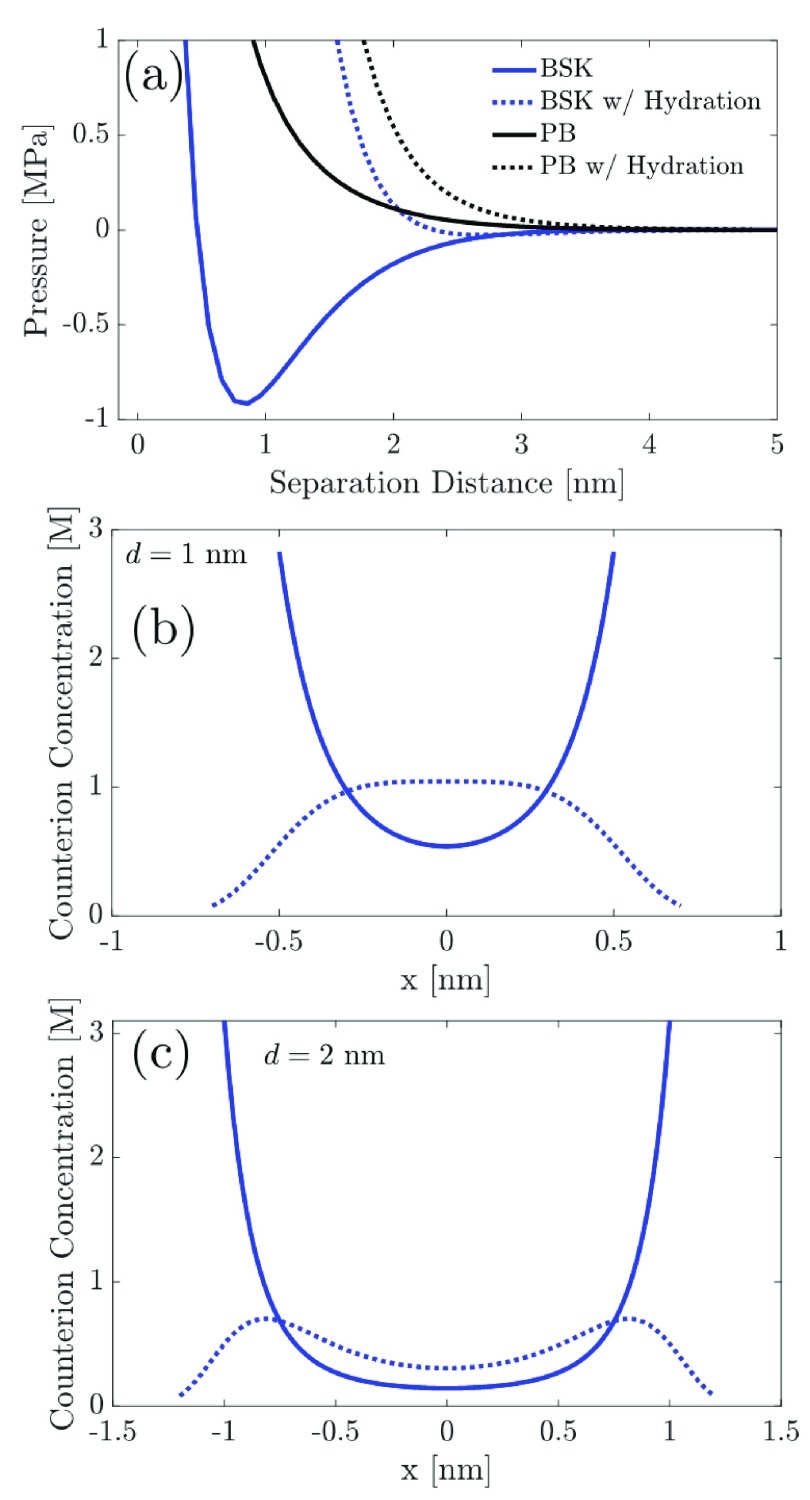
Along with the contributions from ion–ion correlations, it is also interesting to explore the role of short-range water-mediated hydration interactions between the cations on the predicted disjoining pressure. As expected, water-mediated hydration interactions prevent two cations from approaching each other too closely, where the distance of closest approach between any two interacting cations is controlled by the parameter, lh, which is the effective hydration size of the cation. In Figure 6, we plot the predicted disjoining pressure operating between two similarly charged surfaces for a 2:1 electrolyte solution, where we incorporated hydration interactions into both the PB model and the BSK model. As discussed earlier, incorporation of hydration interactions allows us to model the Stern layer self-consistently in both the BSK and PB models. However, for an appropriate comparison between the BSK model without hydration and the BSK model with hydration, we need to shift the plot obtained in the case of the BSK model with hydration toward the left by 2lh to be consistent with the distance of closest approach in the two models. Similarly, the plot for the PB model with hydration is also shifted leftward by 2lh.
Figure 6.
(a) Variation of the disjoining pressure with the separation distance between two similarly charged surfaces for a 2:1 electrolyte solution, predicted by the BSK and the PB models with inclusion/exclusion of the hydration potential. Note that the parameters used to generate these results include: qs = −0.1 C/m2, c0 = 0.1 M, ϵr = 80, σh = 5/nm2 (from ref (63)), κh–1 = 0.3 nm (from ref (63)), and lh = 0.2 nm. The parameters for the hydration potential (σh, κh–1, and lh) can be further fine-tuned to reproduce the experimental data. (b) Comparison of the counterion profiles predicted using the BSK model without hydration and the BSK model with hydration, for d = 1 nm, as a function of x, where x is the spatial coordinate perpendicular to the plane of the charged surface. (c) Same as (b), but for a separation distance of 2 nm between the two charged surfaces.
Figure 6a shows that incorporation of the hydration potential into both the PB and the BSK models results in a strong repulsive (positive) contribution to the predicted disjoining pressure. In the case of the PB model, addition of the hydration potential makes the predicted repulsive disjoining pressure even more repulsive. In the case of the BSK model, addition of the hydration potential results in a disappearance of the attractive (negative) well, with a very weak attractive (negative) disjoining pressure visible at ∼3 nm separation distance between the two charged surfaces. Note that the plots shown in Figure 6a were obtained using qs = −0.1 C/m2, corresponding to low to moderate surface charge densities, typically encountered on the two charged surfaces. However, as shown later in this section, surface charge densities reported in some experimental studies can exceed this value. In such cases, we will be able to recover the attractive well in the disjoining pressure predicted using the BSK model, where hydration interactions are included. Note that we selected qs = −0.1 C/m2 to carry out these calculations to demonstrate the key role of the hydration interactions in modulating the predicted disjoining pressure, especially at low to moderate surface charge densities on the two charged surfaces. Moreover, if the EDL is decomposed into Stern and diffuse layer regions, with the diffuse layer region modeled using an EDL theory such as the PB model, it follows that the contribution of the Stern layer to the predicted disjoining pressure cannot be modeled self-consistently. In this study, we use the hydration potential to model the Stern layer and self-consistently incorporate the repulsive contribution from the hydration potential to the predicted disjoining pressure (see 3rd and 4th terms in eq 23), which are currently neglected in the PB model. Furthermore, the predicted repulsive disjoining pressures resulting from the hydration potential can also qualitatively explain the repulsive pressures reported in the experimental data of Israelachvilli and Pashley64 and of LeNeveu and Rand.65
To further elucidate the role of hydration interactions in modulating the predicted disjoining pressure, in Figure 6b,c, we compare the counterion profiles predicted using the BSK model without hydration and the BSK model with hydration, when the two charged surfaces are separated by a distance of 1 and 2 nm, respectively. Note that the distances of minimum approach for the BSK model and BSK model with hydration are d and d + 2lh, respectively. This is the reason why the counterion profiles in the context of the BSK model with hydration extend beyond d in Figure 6b,c. An analysis of the counterion profiles in Figure 6b,c shows that in the case of the BSK model without hydration, the predicted counterion concentrations near the two charged surfaces (at x = ±0.5 nm and x = ±1 nm, where x is the spatial coordinate perpendicular to the charged surfaces) are unbounded and several folds higher than those predicted in the case of the BSK model with hydration. As discussed earlier, hydration interactions limit the counterion concentrations near the two charged surfaces to replicate a Stern layer region which is devoid of counterions. Consequently, to neutralize the charge on the two surfaces, the concentration of counterions at the mid-plane between the two charged surfaces (located at x = 0 in Figure 6b,c) is higher in the BSK model with hydration than in the BSK model without hydration. This results in an enhancement of the repulsive entropic contribution to the predicted disjoining pressure (2nd term in eq 23) in the BSK model with hydration, which together with the new repulsive terms arising from the incorporation of the hydration interactions (3rd and 4th terms in eq 23) contribute significantly toward making the overall predicted disjoining pressure repulsive, especially at smaller separation distances. As Figure 6b,c shows, increasing the separation distance between the two charged surfaces from 1 to 2 nm weakens the contribution from the hydration potential, such that the counterion concentration near the midplane (at x = 0) between the two charged surfaces, predicted using the BSK model with hydration (dotted blue curve), approaches that predicted using the BSK model without hydration (solid blue curve).
Finally, to complete our analysis, we consider the effect of surface CR on the predicted disjoining pressure and the predicted surface charge density, where qs is no longer an independent parameter but instead, depends on the bulk salt concentration. As a representative example, we consider two similarly charged CSH layers immersed in a calcium hydroxide salt solution. We consider this system because, in the next section, we will compare the disjoining pressure predicted by our theory for this system with the experimental data of Plassard et al.34 As discussed in the Model and Methods section, the value of qs in eq 28 depends on the bulk concentration of OH– ions as well as on the dimensionless surface potential. As a result, qs needs to be obtained in an iterative manner, such that eqs 11 and 7, together with the boundary conditions, and eq 28 are simultaneously satisfied.
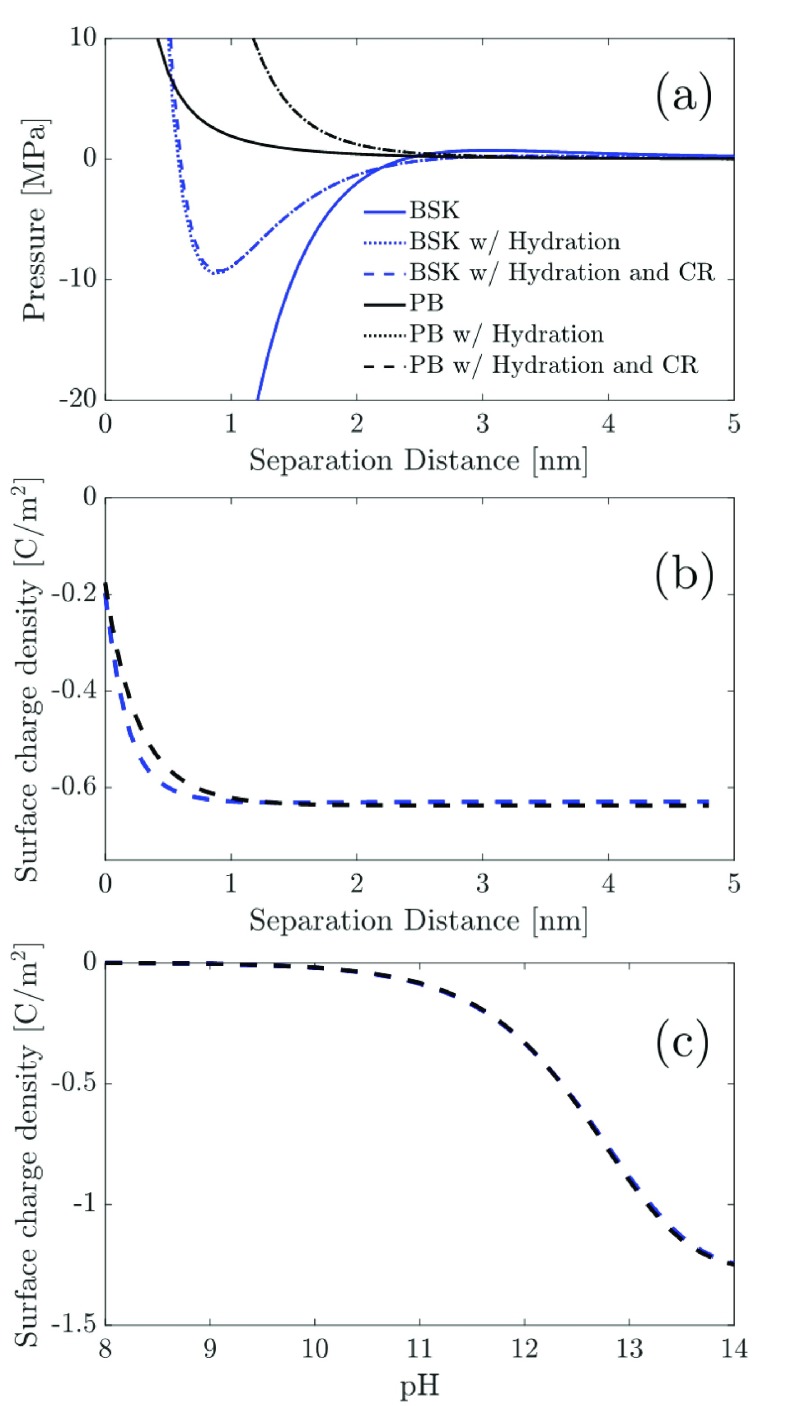
In Figure 7a, we plot the disjoining pressure as a function of the surface separation distance, d, predicted by first including hydration interactions into the PB and BSK models and, subsequently, by including surface CR in the BSK and PB models. The disjoining pressure versus the separation distance profiles were predicted for a bulk salt concentration of 19.1 mM, a typical concentration for which the experimental data of Plassard et al.34 is available. To predict the disjoining pressure when CR is neglected (e.g., BSK model and BSK model with hydration), we need to assign a value to the surface charge density, qs, which serves as an independent parameter. To this end, we choose qs = −0.63 C/m2, obtained by solving eq 28 using c0 = cOH–,B = 19.1 mM. Figure 7a shows that choosing a value of qs which is much larger than the qs value used to predict the results in Figure 6a, we predict large attractive (negative) disjoining pressures using the BSK model. Including hydration interactions in the BSK model results in a large repulsive (positive) pressure contribution to the disjoining pressure. However, for qs = −0.63 C/m2, the predicted attractive (negative) disjoining pressure contribution resulting from ion–ion correlations dominates over the repulsive (positive) contributions resulting from the entropy of the ions as well as from the hydration interactions (2nd, 3rd, and 4th terms in eq 23). This results in an attractive (negative) well at ∼1 nm separation distance between the two charged surfaces. For comparison, we also plotted the disjoining pressure profiles predicted using the PB model. It is clear that if ion–ion correlations are neglected, it will be impossible to predict an attractive (negative) well for the disjoining pressure using the PB model.
Figure 7.
(a) Disjoining pressure vs the surface separation distance profiles predicted by the BSK model without hydration, the BSK model with hydration, and the BSK model with hydration and with CR are compared with those predicted by the PB model without hydration, the PB model with hydration, and the PB model with hydration and with CR. The parameters used to generate the results shown here are: c0 = 19.1 mM, ϵr = 80, κh–1 = 0.3 nm, σh = 5/nm2, lh = 0.2 nm, Γ = 1 × 1018 m–2, and pKb = 4. Note that when CR is neglected, we used qs = −0.63 C/m2. (b) Surface charge density vs the surface separation distance profiles predicted using the BSK model with hydration and CR (blue dotted line) and the PB model with hydration and CR (black dotted line). Note that the parameters: c0, ϵr, κh–1, σh, lh, Γ, and pKb are the same as those used in (a), and that due to the incorporation of CR, qs varies with the separation distance between the two charged surfaces. (c) Surface charge density vs the solution pH profiles predicted using the BSK model with hydration and CR (blue dotted line) and the PB model with hydration and CR (black dotted line) for a separation distance of 4 nm between the two charged surfaces. Note that both surfaces are assumed to be negatively charged and to possess identical surface charge densities. Furthermore, the parameters used to generate the surface charge density profiles are the same as those used in (b).
Interestingly, after inclusion of the hydration interactions in the PB and BSK models, further inclusion of CR in the two models does not affect the predicted disjoining pressure profiles at all. This indicates that for both the BSK and PB models, the surface charge density is almost insensitive to the separation distance between the two charged surfaces. Indeed, as shown in Figure 7b, the surface charge density varies with the separation distance between the two charged surfaces only at very small separation distances and remains constant beyond a separation distance of 1 nm. In addition, there is not much difference between the predictions made using the PB and the BSK models, indicating that the dependence of the surface charge density on the separation distance between the two charged surfaces is insensitive to the modeling of ion–ion correlations. In fact, the surface charge density shows a very strong dependence on the pH of the solution. Recall that the concentration of OH– ions present in the calcium hydroxide salt solution in the bulk reservoir can be related to the pH of the solution using the relation, cOH–,B = 10pH-14. Therefore, increasing the pH of the solution results in a larger dissociation of silanol groups at the CSH layer (see eq 25), which in turn results in an increase in the surface charge density at the CSH layer. Once again, the striking similarity of the variation of qs with the pH of the solution, obtained using the PB and BSK models, indicates that the variation of the surface charge density with the pH of the solution is insensitive to the modeling of ion–ion correlations. Finally, we also note that the variation of qs with the solution pH, as predicted in Figure 7c, is in good qualitative agreement with that reported experimentally by Plassard et al.34 This finding is reassuring in terms of the values of the surface CR parameters, Γ and pKb, used to model the variation of qs with the solution pH in Figure 7c. For example, Plassard et al. have reported that increasing the solution pH from 10 to 12.5 results in a monotonic enhancement in the surface charge density, qs, at the CSH surface from −0.08 to −0.69 C/m2. Similarly, in Figure 7c, for a similar variation of the solution pH, we predict a monotonic enhancement of qs from −0.02 to −0.58 C/m2, for both the BSK and the PB models.
Comparison of the Disjoining Pressures Predicted from Our Complete Theory with the Experimental Data
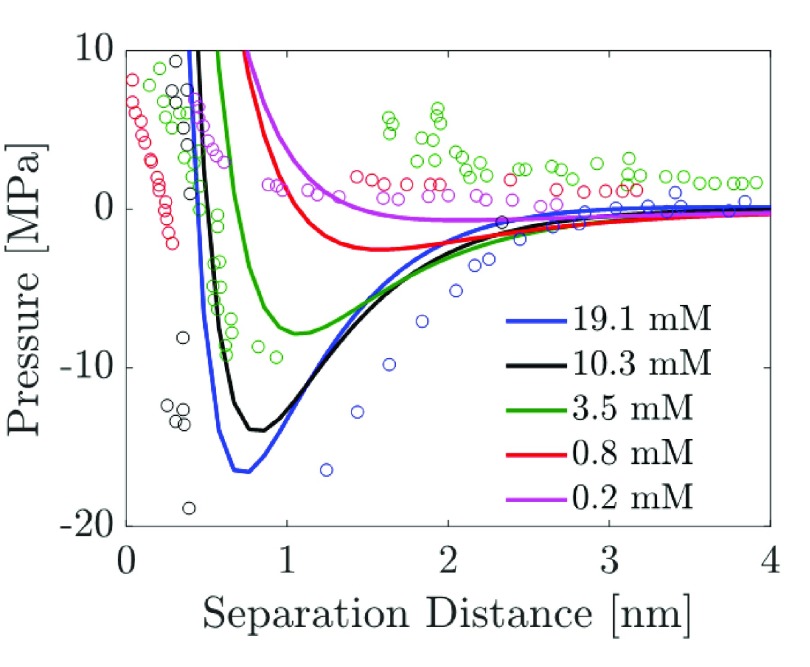
Plassard et al.34 used atomic force microscopy (AFM) to study the surface forces responsible for the strong cohesive strength of cement pastes. These authors observed strong attractive (negative) disjoining pressures operating between the CSH layers in the presence of a Ca(OH)2 electrolyte solution. They attributed the observed behavior to the strong ion–ion correlations between the divalent calcium ions. Plassard et al. noted that because the DLVO theory neglects ion–ion correlations, the disjoining pressure predicted by the DLVO theory is not consistent with their experimental findings even qualitatively. In Figure 8, we compare the disjoining pressure versus the surface separation distance profiles predicted by our complete theory (eqs 23 plus 24) to those measured by Plassard et al. (see Figure 5 in ref (34)) for five Ca(OH)2 salt concentrations. Plassard et al. measured the forces operating between the two CSH layers, and we converted their experimental surface force data into disjoining pressure data by dividing the reported surface forces by the surface area of the CSH layers, estimated to be 64 nm2 in their study.34
Figure 8.
Comparison of the disjoining pressure vs the surface separation distance predicted by our complete theory (eqs 23 and 24, solid lines) with the experimental data of Plassard et al.34 (circles) for the five Ca(OH)2 salt concentrations shown.
Note that in the study by Plassard et al., one of the CSH layers was coated over an AFM tip, whereas the other CSH layer was coated over a calcite crystal. A key assumption made by Plassard et al. (also implemented here) is that the interaction of the two CSH layers can be approximated as the interaction between two flat surfaces. Note that to solve for the disjoining pressure, we used the following parameters: lh = 0.1 nm, κh–1 = 0.3 nm, σh = 5/nm2, Γ = 1 × 1018 m–2, pKb = 4, and Ah = 14 × 10–20 J. The following parameters were used in our predictions: (i) the Hamaker constant, Ah, used in this study is the same as that determined by Plassard et al. by measuring the surface forces operating between two CSH layers in air, (ii) the values of the hydration parameters, σh and κh–1, used here are identical to those reported by Brown et al.,63 (iii) the value of the surface site density, Γ, is identical to that reported by Behrens and Grier,66 (iv) the pKb is the same as that used in Figure 7c, where we showed that the combination of the surface CR parameters, Γ and pKb, is able to predict the variation of qs with the solution pH in reasonably good agreement with the experimental data of Plassard et al., and (v) the lh parameter is obtained by fitting to the experimental disjoining pressure data. We note here that the choice of the parameters for the hydration potential, σh, κh–1, and lh, used to predict the disjoining pressure curves reported in Figure 8, is not unique. Although the values of σh and κh–1 are quite reasonable as noted in the study by Brown et al.,63 the value of lh (0.1 nm) used here is smaller than the hydration shell diameter of 0.48 nm reported for the Ca2+ ion (see the tabulated hydration shell radius in Table V of ref (73)). We note here that, in principle, one can choose a larger value of lh to be closer to the corresponding experimental value of the hydration shell diameter and still obtain similar disjoining pressure curves reported here by also concurrently changing the values of σh and κh–1. However, we found that following such an approach does not change any of the overall trends of the disjoining pressure curves reported here.
As shown in Figure 8, the disjoining pressures predicted by our complete theory are in good qualitative agreement with the experimental data of Plassard et al. for the five Ca(OH)2 concentrations considered. For the 0.2 mM Ca(OH)2 salt concentration, the predicted disjoining pressure is purely repulsive (positive) for all values of the surface separation distance (see the solid pink line) which agrees very well with the corresponding experimental data (see pink circles). However, as the Ca(OH)2 salt concentration increases, the experimental disjoining pressures become increasingly attractive (negative; see the red, green, black, and blue circles in Figure 8), a trend which is captured reasonably well by our theory (see the red, green, black, and blue solid lines in Figure 8). Note that the Hamaker constant for CSH reported by Plassard et al. is large when compared to the value for silica (Ah = 2 × 10–21 J) reported in the literature.74,75 However, in the Supporting Information document we show that, even if the Hamaker constant is reduced to Ah = 2 × 10–21 J, our theory can still capture the experimental trends with minor modification in the value of σh, as shown in Figure S2.
Finally, it is noteworthy that although our complete theory for the disjoining pressure (eqs 23 and 24) contains several parameters: σh, κh–1, lh, Γ, and pKb, these parameters are introduced in order to incorporate new physics into the EDL model, including hydration interactions and surface CR. However, most importantly, no fitting parameter is introduced in our theory to model ion–ion correlations because the dimensionless correlation length is determined directly based on eq 12. As Figure 8 clearly shows, accurate modeling of ion–ion correlations is essential to predict the attractive electrostatic contribution to disjoining pressures between similarly charged surfaces. This is, in fact, the main reason why the DLVO theory, which neglects ion–ion correlations, fails to model surface forces/disjoining pressures even qualitatively, especially in solutions containing multivalent salt ions.
Conclusions
In this article, we formulated a general theory of the disjoining pressure operating between two charged surfaces in a multivalent electrolyte solution. We used the BSK framework to model ion–ion correlations and derived a closed-form expression for the contribution resulting from ion–ion correlations to the disjoining pressure. In stark contrast to the predictions of the PB mean-field theory, which always predicts a repulsive (positive) disjoining pressure operating between two similarly charged surfaces, we showed here that the attractive (negative) disjoining pressure resulting from ion–ion correlations can dominate over an entropic repulsion, and thereby cause the overall disjoining pressure to be attractive (negative). Our theory predicts that both the magnitude as well as the sign of the disjoining pressure are strong functions of the counterion valency. Indeed, increasing the valency of the counterion significantly enhances the attractive pressure resulting from ion–ion correlations, thereby promoting attractions between similarly charged surfaces in aqueous solutions containing divalent and trivalent counterions. On the other hand, we found that the dependence of the disjoining pressure on the valency of the coion is insignificant. We also showed that the disjoining pressure in the case of monovalent ions can still be attractive, provided that the charge densities on the two charged surfaces are sufficiently high to induce significant ion–ion correlations.
Another important limitation of the DLVO theory of colloidal stability, and the PB model on which it is based, is that it predicts an enhancement of the repulsive disjoining pressure operating between two similarly charged surfaces when the surface charge densities of the two surfaces increase. This is in stark contrast with the available experimental data,34 which conclusively show that the disjoining pressure operating between two similarly charged surfaces becomes attractive upon increasing the surface charge densities of the two surfaces. Our new theory of the disjoining pressure can explain this experimental finding based on the existence of ion–ion correlations, which are neglected in the DLVO theory.
In addition to modeling ion–ion correlations, we also included water-mediated hydration interactions and surface CR in our theory to allow a direct comparison of the disjoining pressure predicted by our theory with the experimentally available disjoining pressure data. To this end, we showed that modeling the Stern layer self-consistently through water-mediated hydration interactions results in a significant repulsive contribution to the disjoining pressure, although the attractive pressure resulting from ion–ion correlations can still dominate over the repulsive pressures resulting from the entropy of the ions as well as from the hydration interactions. Furthermore, incorporation of surface CR into our model enabled us to relate the surface charge density at the charged surface directly to the salt concentration in the electrolyte solution. Finally, we demonstrated that the disjoining pressure operating between the CSH layers in a calcium hydroxide salt solution predicted by our theory is in reasonable qualitative agreement with the experimental data of Plassard et al.34 Therefore, we believe that the complete theory of surface forces presented here shows promise in overcoming the known limitations of the DLVO theory, especially for multivalent counterions.
In terms of future work, although the BSK model can describe electrostatic correlation effects at an interface, currently, it does not capture the Bjerrum pair formation, which can decrease the effective ion concentration in the bulk reservoir.76 Furthermore, the BSK model does not capture long-range oscillations in the charge density at high electrolyte concentrations.77 This can be corrected by considering weighted concentrations in the expression for the entropy of ions (i.e., the g(c+,c–) term in eq 3), as implemented in various theoretical approaches, including the classical density functional theory.77,78
Finally, at separation distances of ∼1 nm between the two charged surfaces, in addition to an attractive disjoining pressure resulting from ion–ion correlations, short-ranged attractive van der Waals interactions as well as repulsive hydration interactions can play important roles. A better estimation of the parameters used to model the van der Waals interactions, the hydration interactions, as well as of the scaling proposed for the correlation length may be carried out through a systematic comparison of the disjoining pressure predicted by our theory with that available experimentally, as well as that obtained using the Monte Carlo and molecular dynamics simulations.
Acknowledgments
R.P.M., J.P.d.S., D.B., and M.Z.B. acknowledge the financial support received as part of the Center for Enhanced Nanofluidic Transport (CENT), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under award # DE-SC0019112, for formulating the theory of surface forces and the accompanying analysis presented in this paper. J.P.d.S. and M.Z.B. also acknowledge the Amar G. Bose Research Grant for partial funding on the modeling of ion–ion correlations using the BSK model. J.P.d.S. also acknowledges support in the form of a National Science Foundation Graduate Research Fellowship under grant no. 1122374.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.9b01110.
Derivation of the expression for the Helmholtz free energy, derivation of eq 15 in the article describing the relation between the electrostatic potential, hydration potential, and their higher-order derivatives, contour plots showing the dependence of the disjoining pressure on the salt concentration and surface charge density, and comparison to experimental data for reduced Hamaker constant (PDF)
Author Contributions
§ R.P.M. and J.P.d.S. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Israelachvili J. N.Intermolecular and Surface Forces; Academic Press, 2015. [Google Scholar]
- de la Cruz M. O.; Belloni L.; Delsanti M.; Dalbiez J. P.; Spalla O.; Drifford M. Precipitation of highly charged polyelectrolyte solutions in the presence of multivalent salts. J. Chem. Phys. 1995, 103, 5781–5791. 10.1063/1.470459. [DOI] [Google Scholar]
- Raspaud E.; Olvera de la Cruz M.; Sikorav J.-L.; Livolant F. Precipitation of DNA by Polyamines: A Polyelectrolyte Behavior. Biophys. J. 1998, 74, 381–393. 10.1016/s0006-3495(98)77795-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solis F. J.; de la Cruz M. O. Collapse of flexible polyelectrolytes in multivalent salt solutions. J. Chem. Phys. 2000, 112, 2030–2035. 10.1063/1.480763. [DOI] [Google Scholar]
- Kornyshev A. A.; Lee D. J.; Leikin S.; Wynveen A. Structure and interactions of biological helices. Rev. Mod. Phys. 2007, 79, 943–996. 10.1103/revmodphys.79.943. [DOI] [Google Scholar]
- Dubin P.; Bock J.; Davis R.; Schulz D. N.; Thies C.. Macromolecular Complexes in Chemistry and Biology; Springer Science & Business Media, 2012. [Google Scholar]
- McCormack D.; Carnie S. L.; Chan D. Y. C. Calculations of Electric Double-Layer Force and Interaction Free Energy between Dissimilar Surfaces. J. Colloid Interface Sci. 1995, 169, 177–196. 10.1006/jcis.1995.1019. [DOI] [Google Scholar]
- Miklavic S. J.; Chan D. Y. C.; White L. R.; Healy T. W. Double Layer Forces between Heterogeneous Charged Surfaces. J. Phys. Chem. 1994, 98, 9022–9032. 10.1021/j100087a034. [DOI] [Google Scholar]
- Misra R. P.; Das S.; Mitra S. K. Electric double layer force between charged surfaces: Effect of solvent polarization. J. Chem. Phys. 2013, 138, 114703. 10.1063/1.4794784. [DOI] [PubMed] [Google Scholar]
- Derjaguin B. V. Theory of the stability of strongly charged lyophobic sols and the adhesion of strongly charged particles in solutions of electrolytes. Acta Physicochim. USSR 1941, 14, 633–662. [Google Scholar]
- Marshall C. E. “Theory of the stability of lyophobic colloids. The interaction of particles having an electric double layer.” E. J. W. Verwey and J. T. G. Overbeek, with the collaboration of K. van Ness. Elsevier, New York-Amsterdam, 1948, 216 pp., $4.50. J. Polym. Sci. 1949, 4, 413–414. 10.1002/pol.1949.120040321. [DOI] [Google Scholar]
- Derjaguin B. V.; Titijevskaia A. S.; Abricossova I. I.; Malkina A. D. Investigations of the forces of interaction of surfaces in different media and their application to the problem of colloid stability. Discuss. Faraday Soc. 1954, 18, 24. 10.1039/df9541800024. [DOI] [Google Scholar]
- Lyklema J.; Mysels K. J. A Study of Double Layer Repulsion and van der Waals Attraction in Soap Films. J. Am. Chem. Soc. 1965, 87, 2539–2546. 10.1021/ja01090a003. [DOI] [Google Scholar]
- Pashley R. M. Hydration forces between mica surfaces in aqueous electrolyte solutions. J. Colloid Interface Sci. 1981, 80, 153–162. 10.1016/0021-9797(81)90171-5. [DOI] [Google Scholar]
- Pashley R. M. DLVO and hydration forces between mica surfaces in Li+, Na+, K+, and Cs+ electrolyte solutions: A correlation of double-layer and hydration forces with surface cation exchange properties. J. Colloid Interface Sci. 1981, 83, 531–546. 10.1016/0021-9797(81)90348-9. [DOI] [Google Scholar]
- Pashley R. M.; McGuiggan P. M.; Ninham B. W.; Brady J.; Evans D. F. Direct measurements of surface forces between bilayers of double-chained quaternary ammonium acetate and bromide surfactants. J. Phys. Chem. 1986, 90, 1637–1642. 10.1021/j100399a037. [DOI] [Google Scholar]
- Smith C. P.; Maeda M.; Atanasoska L.; White H. S.; McClure D. J. Ultrathin platinum films on mica and the measurement of forces at the platinum/water interface. J. Phys. Chem. 1988, 92, 199–205. 10.1021/j100312a044. [DOI] [Google Scholar]
- Horn R. G.; Clarke D. R.; Clarkson M. T. Direct measurement of surface forces between sapphire crystals in aqueous solutions. J. Mater. Res. 1988, 3, 413–416. 10.1557/jmr.1988.0413. [DOI] [Google Scholar]
- Horn R. G.; Smith D. T.; Haller W. Surface forces and viscosity of water measured between silica sheets. Chem. Phys. Lett. 1989, 162, 404–408. 10.1016/0009-2614(89)87066-6. [DOI] [Google Scholar]
- Ducker W. A.; Senden T. J.; Pashley R. M. Direct measurement of colloidal forces using an atomic force microscope. Nature 1991, 353, 239–241. 10.1038/353239a0. [DOI] [Google Scholar]
- Ducker W. A.; Senden T. J.; Pashley R. M. Measurement of forces in liquids using a force microscope. Langmuir 1992, 8, 1831–1836. 10.1021/la00043a024. [DOI] [Google Scholar]
- Meagher L. Direct measurement of forces between silica surfaces in aqueous CaCl2 solutions using an atomic force microscope. J. Colloid Interface Sci. 1992, 152, 293–295. 10.1016/0021-9797(92)90030-p. [DOI] [Google Scholar]
- Vigil G.; Xu Z.; Steinberg S.; Israelachvili J. Interactions of Silica Surfaces. J. Colloid Interface Sci. 1994, 165, 367–385. 10.1006/jcis.1994.1242. [DOI] [Google Scholar]
- Larson I.; Drummond C. J.; Chan D. Y. C.; Grieser F. Direct force measurements between titanium dioxide surfaces. J. Am. Chem. Soc. 1993, 115, 11885–11890. 10.1021/ja00078a029. [DOI] [Google Scholar]
- Kampf N.; Ben-Yaakov D.; Andelman D.; Safran S. A.; Klein J. Direct Measurement of Sub-Debye-Length Attraction between Oppositely Charged Surfaces. Phys. Rev. Lett. 2009, 103, 118304. 10.1103/physrevlett.103.118304. [DOI] [PubMed] [Google Scholar]
- Jellander R.; Marčelja S.; Quirk J. P. Attractive double-layer interactions between calcium clay particles. J. Colloid Interface Sci. 1988, 126, 194–211. 10.1016/0021-9797(88)90113-0. [DOI] [Google Scholar]
- Kjellander R.; Marcelja S.; Pashley R. M.; Quirk J. P. Double-layer ion correlation forces restrict calcium-clay swelling. J. Phys. Chem. 1988, 92, 6489–6492. 10.1021/j100334a005. [DOI] [Google Scholar]
- Kjellander R.; Marčelja S.; Pashley R. M.; Quirk J. P. A theoretical and experimental study of forces between charged mica surfaces in aqueous CaCl 2 solutions. J. Chem. Phys. 1990, 92, 4399–4407. 10.1063/1.457750. [DOI] [Google Scholar]
- Moreira A. G.; Netz R. R. Simulations of counterions at charged plates. Eur. Phys. J. E: Soft Matter Biol. Phys. 2002, 8, 33–58. 10.1140/epje/i2001-10091-9. [DOI] [PubMed] [Google Scholar]
- Kékicheff P.; Marcelja S.; Senden T. J.; Shubin V. E. Charge reversal seen in electrical double layer interaction of surfaces immersed in 2:1 calcium electrolyte. J. Chem. Phys. 1993, 99, 6098–6113. 10.1063/1.465906. [DOI] [Google Scholar]
- Zohar O.; Leizerson I.; Sivan U. Short Range Attraction between Two Similarly Charged Silica Surfaces. Phys. Rev. Lett. 2006, 96, 177802. 10.1103/physrevlett.96.177802. [DOI] [PubMed] [Google Scholar]
- Besteman K.; Zevenbergen M. A. G.; Heering H. A.; Lemay S. G. Direct Observation of Charge Inversion by Multivalent Ions as a Universal Electrostatic Phenomenon. Phys. Rev. Lett. 2004, 93, 170802. 10.1103/physrevlett.93.170802. [DOI] [PubMed] [Google Scholar]
- Besteman K.; Zevenbergen M. A. G.; Lemay S. G. Charge inversion by multivalent ions: Dependence on dielectric constant and surface-charge density. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2005, 72, 061501. 10.1103/physreve.72.061501. [DOI] [PubMed] [Google Scholar]
- Plassard C.; Lesniewska E.; Pochard I.; Nonat A. Nanoscale experimental investigation of particle interactions at the origin of the cohesion of cement. Langmuir 2005, 21, 7263–7270. 10.1021/la050440+. [DOI] [PubMed] [Google Scholar]
- Kjellander R.; Åkesson T.; Jönsson B.; Marčelja S. Double layer interactions in mono- and divalent electrolytes: A comparison of the anisotropic HNC theory and Monte Carlo simulations. J. Chem. Phys. 1992, 97, 1424–1431. 10.1063/1.463218. [DOI] [Google Scholar]
- Guldbrand L.; Jönsson B.; Wennerström H.; Linse P. Electrical double layer forces. A Monte Carlo study. J. Chem. Phys. 1984, 80, 2221–2228. 10.1063/1.446912. [DOI] [Google Scholar]
- Abrikosov A. I.; Stenqvist B.; Lund M. Steering patchy particles using multivalent electrolytes. Soft Matter 2017, 13, 4591–4597. 10.1039/c7sm00470b. [DOI] [PubMed] [Google Scholar]
- Jönsson B.; Nonat A.; Labbez C.; Cabane B.; Wennerström H. Controlling the Cohesion of Cement Paste. Langmuir 2005, 21, 9211–9221. 10.1021/la051048z. [DOI] [PubMed] [Google Scholar]
- Bloomfield V. A. Condensation of DNA by multivalent cations: Considerations on mechanism. Biopolymers 1991, 31, 1471–1481. 10.1002/bip.360311305. [DOI] [PubMed] [Google Scholar]
- Kralchevsky P. A.; Paunov V. N. Contribution of ionic correlations to excess free energy and disjoining pressure of thin liquid films 1. Electric double layer inside the film. Colloids Surf. 1992, 64, 245–264. 10.1016/0166-6622(92)80105-b. [DOI] [Google Scholar]
- Perel V. I.; Shklovskii B. I. Screening of a macroion by multivalent ions: a new boundary condition for the Poisson-Boltzmann equation and charge inversion. Phys. A 1999, 274, 446–453. 10.1016/s0378-4371(99)00379-9. [DOI] [Google Scholar]
- Patey G. N. The interaction of two spherical colloidal particles in electrolyte solution. An application of the hypernetted-chain approximation. J. Chem. Phys. 1980, 72, 5763–5771. 10.1063/1.438997. [DOI] [Google Scholar]
- Kanduč M.; Moazzami-Gudarzi M.; Valmacco V.; Podgornik R.; Trefalt G. Interactions between charged particles with bathing multivalent counterions: experiments vs. dressed ion theory. Phys. Chem. Chem. Phys. 2017, 19, 10069–10080. 10.1039/c7cp00685c. [DOI] [PubMed] [Google Scholar]
- Kanduč M.; Naji A.; Forsman J.; Podgornik R. Dressed counterions: Strong electrostatic coupling in the presence of salt. J. Chem. Phys. 2010, 132, 124701. 10.1063/1.3361672. [DOI] [PubMed] [Google Scholar]
- Bazant M. Z.; Storey B. D.; Kornyshev A. a. Double Layer in Ionic Liquids: Overscreening versus Crowding. Phys. Rev. Lett. 2011, 106, 046102. 10.1103/physrevlett.106.046102. [DOI] [PubMed] [Google Scholar]
- Lee D. W.; Im D. J.; Kang I. S. Electric Double Layer at the Interface of Ionic Liquid - Dielectric Liquid under Electric Field. Langmuir 2013, 29, 1875–1884. 10.1021/la3040775. [DOI] [PubMed] [Google Scholar]
- Jiang X.; Huang J.; Zhao H.; Sumpter B. G.; Qiao R. Dynamics of electrical double layer formation in room-temperature ionic liquids under constant-current charging conditions. J. Phys.: Condens. Matter 2014, 26, 284109. 10.1088/0953-8984/26/28/284109. [DOI] [PubMed] [Google Scholar]
- Lee A. A.; Kondrat S.; Vella D.; Goriely A. Dynamics of Ion Transport in Ionic Liquids. Phys. Rev. Lett. 2015, 115, 106101. 10.1103/physrevlett.115.106101. [DOI] [PubMed] [Google Scholar]
- Jiang X.; Liu Y.; Qiao R. Current Rectification for Transport of Room-Temperature Ionic Liquids through Conical Nanopores. J. Phys. Chem. C 2016, 120, 4629–4637. 10.1021/acs.jpcc.5b11522. [DOI] [Google Scholar]
- Wang C.; Bao J.; Pan W.; Sun X. Modeling electrokinetics in ionic liquids. Electrophoresis 2017, 38, 1693–1705. 10.1002/elps.201600455. [DOI] [PubMed] [Google Scholar]
- McEldrew M.; Goodwin Z. A. H.; Kornyshev A. A.; Bazant M. Z. Theory of the Double Layer in Water-in-Salt Electrolytes. J. Phys. Chem. Lett. 2018, 9, 5840–5846. 10.1021/acs.jpclett.8b02543. [DOI] [PubMed] [Google Scholar]
- Storey B. D.; Bazant M. Z. Effects of electrostatic correlations on electrokinetic phenomena. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2012, 86, 056303. 10.1103/physreve.86.056303. [DOI] [PubMed] [Google Scholar]
- Stout R. F.; Khair A. S. A continuum approach to predicting electrophoretic mobility reversals. J. Fluid Mech. 2014, 752, R1. 10.1017/jfm.2014.354. [DOI] [Google Scholar]
- Santos M. S.; Biscaia E. C.; Tavares F. W. Effect of electrostatic correlations on micelle formation. Colloids Surf., A 2017, 533, 169–178. 10.1016/j.colsurfa.2017.07.079. [DOI] [Google Scholar]
- Liu J.-L.; Eisenberg B. Correlated Ions in a Calcium Channel Model: A Poisson-Fermi Theory. J. Phys. Chem. B 2013, 117, 12051–12058. 10.1021/jp408330f. [DOI] [PubMed] [Google Scholar]
- Liu J.-L.; Eisenberg B. Numerical methods for a Poisson-Nernst-Planck-Fermi model of biological ion channels. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2015, 92, 012711. 10.1103/physreve.92.012711. [DOI] [PubMed] [Google Scholar]
- Liu J.-L.; Eisenberg B. Analytical models of calcium binding in a calcium channel. J. Chem. Phys. 2014, 141, 075102. 10.1063/1.4892839. [DOI] [PubMed] [Google Scholar]
- Liu J.-L.; Eisenberg B. Poisson-Nernst-Planck-Fermi theory for modeling biological ion channels. J. Chem. Phys. 2014, 141, 22D532. 10.1063/1.4902973. [DOI] [PubMed] [Google Scholar]
- de Souza J. P.; Bazant M. Z.. Continuum theory of electrostatic correlations at charged surfaces. arXiv preprint arXiv:1902.05493, 2019. [Google Scholar]
- Bazant M. Z.; Kilic M. S.; Storey B. D.; Ajdari A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. 10.1016/j.cis.2009.10.001. [DOI] [PubMed] [Google Scholar]
- Stern O.The theory of the electrolytic double-layer. Z. Elektrochem. Angew. Phys. Chem. 1924. [Google Scholar]
- Bohinc K.; Shrestha A.; Brumen M.; May S. Poisson-Helmholtz-Boltzmann model of the electric double layer: Analysis of monovalent ionic mixtures. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2012, 85, 031130. 10.1103/physreve.85.031130. [DOI] [PubMed] [Google Scholar]
- Brown M. A.; Bossa G. V.; May S. Emergence of a Stern Layer from the Incorporation of Hydration Interactions into the Gouy-Chapman Model of the Electrical Double Layer. Langmuir 2015, 31, 11477–11483. 10.1021/acs.langmuir.5b02389. [DOI] [PubMed] [Google Scholar]
- Israelachvili J. N.; Pashley R. M. Molecular layering of water at surfaces and origin of repulsive hydration forces. Nature 1983, 306, 249–250. 10.1038/306249a0. [DOI] [Google Scholar]
- LeNeveu D. M.; Rand R. P. Measurement and modification of forces between lecithin bilayers. Biophys. J. 1977, 18, 209–230. 10.1016/s0006-3495(77)85608-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens S. H.; Grier D. G. The charge of glass and silica surfaces. J. Chem. Phys. 2001, 115, 6716–6721. 10.1063/1.1404988. [DOI] [Google Scholar]
- Chan D. Y. C.; Pashley R. M.; White L. R. A simple algorithm for the calculation of the electrostatic repulsion between identical charged surfaces in electrolyte. J. Colloid Interface Sci. 1980, 77, 283–285. 10.1016/0021-9797(80)90445-2. [DOI] [Google Scholar]
- Markovich T.; Andelman D.; Podgornik R. Charge regulation: A generalized boundary condition?. EPL 2016, 113, 26004. 10.1209/0295-5075/113/26004. [DOI] [Google Scholar]
- Trefalt G.; Behrens S. H.; Borkovec M. Charge Regulation in the Electrical Double Layer: Ion Adsorption and Surface Interactions. Langmuir 2016, 32, 380–400. 10.1021/acs.langmuir.5b03611. [DOI] [PubMed] [Google Scholar]
- Nonat A. The structure and stoichiometry of CSH. Cem. Concr. Res. 2004, 34, 1521–1528. 10.1016/j.cemconres.2004.04.035. [DOI] [Google Scholar]
- Uzelac B.; Valmacco V.; Trefalt G. Interactions between silica particles in the presence of multivalent coions. Soft Matter 2017, 13, 5741–5748. 10.1039/c7sm01168g. [DOI] [PubMed] [Google Scholar]
- Li Y.; Girard M.; Shen M.; Millan J. A.; Olvera de la Cruz M. Strong attractions and repulsions mediated by monovalent salts. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 11838–11843. 10.1073/pnas.1713168114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus Y. Ionic radii in aqueous solutions. J. Solution Chem. 1983, 12, 271–275. 10.1007/bf00646201. [DOI] [Google Scholar]
- Ackler H. D.; French R. H.; Chiang Y.-M. Comparisons of Hamaker constants for ceramic systems with intervening vacuum or water: From force laws and physical properties. J. Colloid Interface Sci. 1996, 179, 460–469. 10.1006/jcis.1996.0238. [DOI] [Google Scholar]
- Dishon M.; Zohar O.; Sivan U. From repulsion to attraction and back to repulsion: the effect of NaCl, KCl, and CsCl on the force between silica surfaces in aqueous solution. Langmuir 2009, 25, 2831–2836. 10.1021/la803022b. [DOI] [PubMed] [Google Scholar]
- Adar R. M.; Markovich T.; Andelman D. Bjerrum pairs in ionic solutions: A Poisson-Boltzmann approach. J. Chem. Phys. 2017, 146, 194904. 10.1063/1.4982885. [DOI] [PubMed] [Google Scholar]
- Martin-Jimenez D.; Chacon E.; Tarazona P.; Garcia R. Atomically resolved three-dimensional structures of electrolyte aqueous solutions near a solid surface. Nat. Commun. 2016, 7, 12164. 10.1038/ncomms12164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.; Jiang T.; Jiang D. E.; Jin Z.; Henderson D. A classical density functional theory for interfacial layering of ionic liquids. Soft Matter 2011, 7, 11222. 10.1039/c1sm06089a. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.