Modeling Protein Destiny in Developing Fruit^,

Proteomics and transcriptomics data for tomato fruit at nine developmental stages inform a mathematical model of the translation and degradation rate constants for over 1,000 proteins.

Abstract

Protein synthesis and degradation are essential processes that regulate cell status. Because labeling in bulky organs, such as fruits, is difficult, we developed a modeling approach to study protein turnover at the global scale in developing tomato (Solanum lycopersicum) fruit. Quantitative data were collected for transcripts and proteins during fruit development. Clustering analysis showed smaller changes in protein abundance compared to mRNA abundance. Furthermore, protein and transcript abundance were poorly correlated, and the coefficient of correlation decreased during fruit development and ripening, with transcript levels decreasing more than protein levels. A mathematical model with one ordinary differential equation was used to estimate translation (k_t) and degradation (k_d) rate constants for almost 2,400 detected transcript-protein pairs and was satisfactorily fitted for >1,000 pairs. The model predicted median values of ∼2 min for the translation of a protein, and a protein lifetime of ∼11 d. The constants were validated and inspected for biological relevance. Proteins involved in protein synthesis had higher k_t and k_d values, indicating that the protein machinery is particularly flexible. Our model also predicts that protein concentration is more strongly affected by the rate of translation than that of degradation.

Protein stability has been reported to play an important role in fine-tuning protein levels in cells (Hinkson and Elias, 2011; Vogel and Marcotte, 2012). The enormous complexity of the shape of protein expression profiles has motivated the search for regulatory factors at the level of transcription, translation, and degradation. One way to better understand time-dependent changes in protein abundance is to search for simple relationships between the contributing processes of protein synthesis and degradation. In other words, the first goal would be to find out how many and what protein abundances can be deduced directly from transcript profiles, without considering specific regulation mechanisms (e.g. posttranslational modifications such as phosphorylation and ubiquitination). A simple description of protein stability, especially when applied to enzymes, would help in understanding the contribution of the reprograming of metabolism to growth and developmental events in plants and fruits (Beauvoit et al., 2018). Establishing a full understanding of the processes that underpin changes in protein abundance under various physiological and developmental scenarios would increase our ability to model and rationally engineer plants (Nelson and Millar, 2015).

A systems-level understanding based on well-defined models is necessary to elucidate the mechanisms and functions that go beyond mRNA translation and protein synthesis. In the last 50 years, and particularly in recent years with the development of systems and synthetic biology, mathematical and computational models have been used to investigate translation and to shed light on the relationship between the various reactions in the translational system (von der Haar, 2012). One approach employs Totally Asymmetric Simple Exclusion Process-type models. These are largely based on statistical analyses of the behavior of ribosomes on mRNA. They have been developed to quantitatively understand the particle transport in a one-dimensional lattice and to evaluate the movement of ribosomes along the mRNA with a simplified transport problem. Totally Asymmetric Simple Exclusion Process-based models have been used to obtain steady-state information such as the average occupancy of each codon on the mRNA and translation rate, which are key in understanding mRNA translation. However, although this approach provides detailed prediction about translation, it does not directly address the issue of protein degradation.

An alternative approach uses ordinary differential equations (ODEs)-based models (Zhao and Krishnan, 2014). This approach tends to conceptualize reactions where the process of mRNA translation (equivalent to protein synthesis) is the outcome of several transitions that are described in a comprehensive fashion. It also addresses the issue of degradation. Changes in protein abundance may be described as a function of two main terms: (1) the rate of protein synthesis, which depends on mRNA abundance coupled to its translation efficiency; and (2) the disappearance of protein via both protein degradation and dilution of protein abundance by growth, when relevant. In the simplest form, the protein synthesis rate is proportional to the amount of mRNA, whereas the protein degradation rate is proportional to the amount of protein. Such an approach was used in a study targeting the ethylene biosynthesis pathway in tomato (Solanum lycopersicum) fruit (Van de Poel et al., 2014). However, to our knowledge, there has not yet been any study of this kind in plants at the genome level. On the other hand, protein turnover in the bacterium Lactococcus lactis (Dressaire et al., 2009) and in yeast (Saccharomyces cerevisiae; Tchourine et al., 2014) has been studied globally. Of note, the latter studies were performed under steady-state conditions but not during developmental sequences. However, modeling protein turnover would be particularly useful for studying developing plant organs such as fruits. Indeed, whereas degradation rate constants can be experimentally measured in plant tissues via isotope-labeling strategies (Nelson and Millar, 2015), estimating protein turnover by isotopic labeling is a tedious task, whether labeling, sampling, or data processing, and to date only few publications have reported such measurements in plants. In this work, quantitative transcriptomic and proteomic data collected during tomato fruit development and ripening were used to solve an ODE-based model for estimating the translation and degradation rate constants of >1,100 proteins. These constants, which could be validated with the literature data, provide new systems-level information about protein turnover in plants.

RESULTS AND DISCUSSION

Transcriptomic and Proteomic Profiles during Tomato Fruit Development

The tomato fruit used in this study were obtained from S. lycopersicum var Moneymaker plants grown under optimal production practices in a greenhouse located in the southwest of France (Sainte-Livrade sur Lot) during the summer of 2010 (see Biais et al., 2014 for details). Transcriptomics and proteomics analyses were performed on three replicates of pericarp samples collected at nine developmental stages, each replicate resulting from the pooling of at least 15 fruit of a given truss (trusses 5, 6, or 7). For the transcriptome analysis, Illumina-sequenced libraries were mapped on the ITAG 2.4 version of the tomato genome (S. lycopersicum var Heinz assembly v2.40, Sol Genomics Network; https://solgenomics.net/). To obtain absolute quantitative values, spikes were added at the beginning of the extraction procedure (see Supplemental Appendix S1). From 34,725 possible transcripts, 8,403 were not detected in any of the samples, probably because they were not expressed or their levels were too low. Subsequently, 3,445 transcripts were removed that were not detected in all three replicates of at least one developmental stage, leaving a total of 22,877 quantified transcripts. For the proteome analysis, label-free liquid chromatography tandem mass spectrometry (MS/MS) was used. Peptide ions, and subsequently the proteins from which they were derived, were quantified by integrating the signal intensities obtained from extracted ion currents with the MassChroQ software (http://pappso.inra.fr/bioinfo/masschroq/; Valot et al., 2011). Absolute quantification was achieved for 2,375 proteins using a mixed effects model from log₁₀-transformed intensities followed by a normalization using the “Total Protein Approach” developed by Wiśniewski et al. (2014). In this approach, the individual protein abundance, considered by its MS signal, is a fraction of the total protein content considered as the total of MS signals. To do this, it was assumed for a sample that the sum of protein abundances was equal to the total amount of proteins (Fig. 1). This normalization could, however, overestimate protein abundance, because all individual proteins were not quantified.

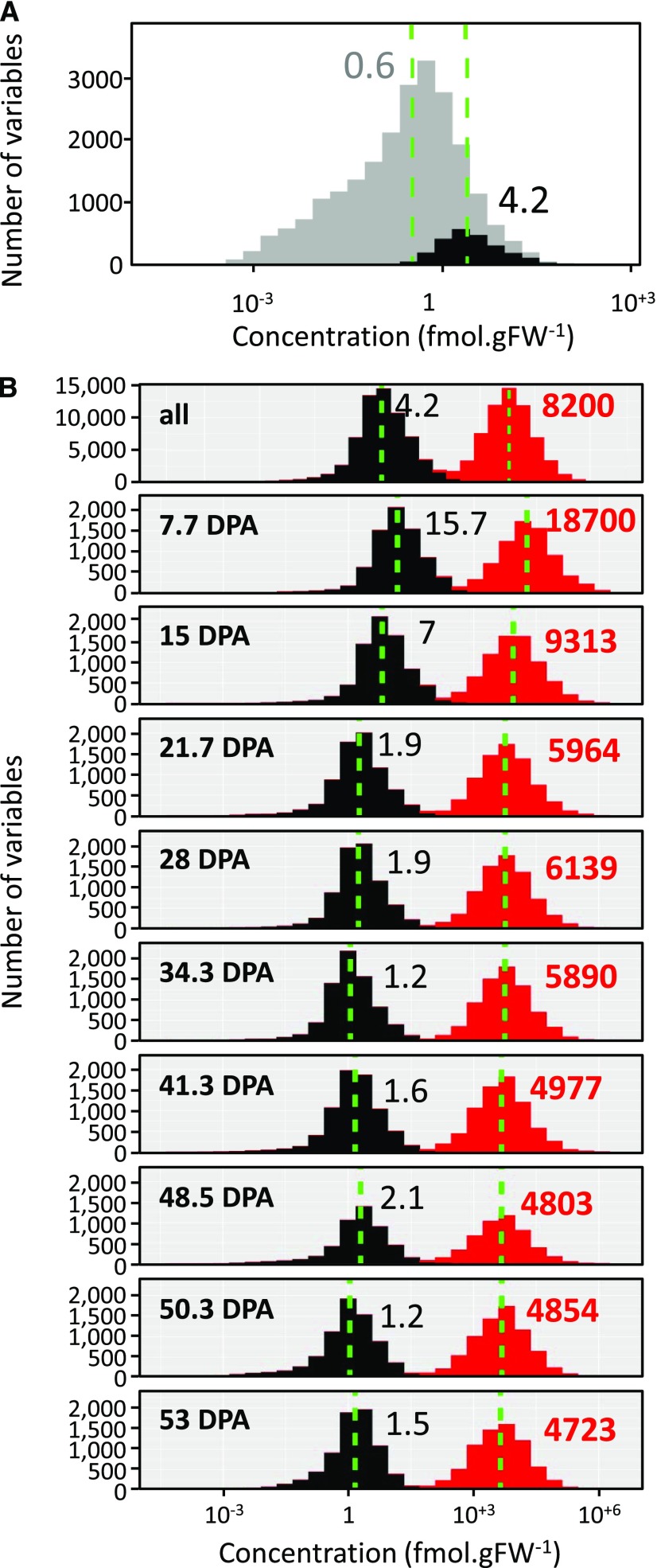
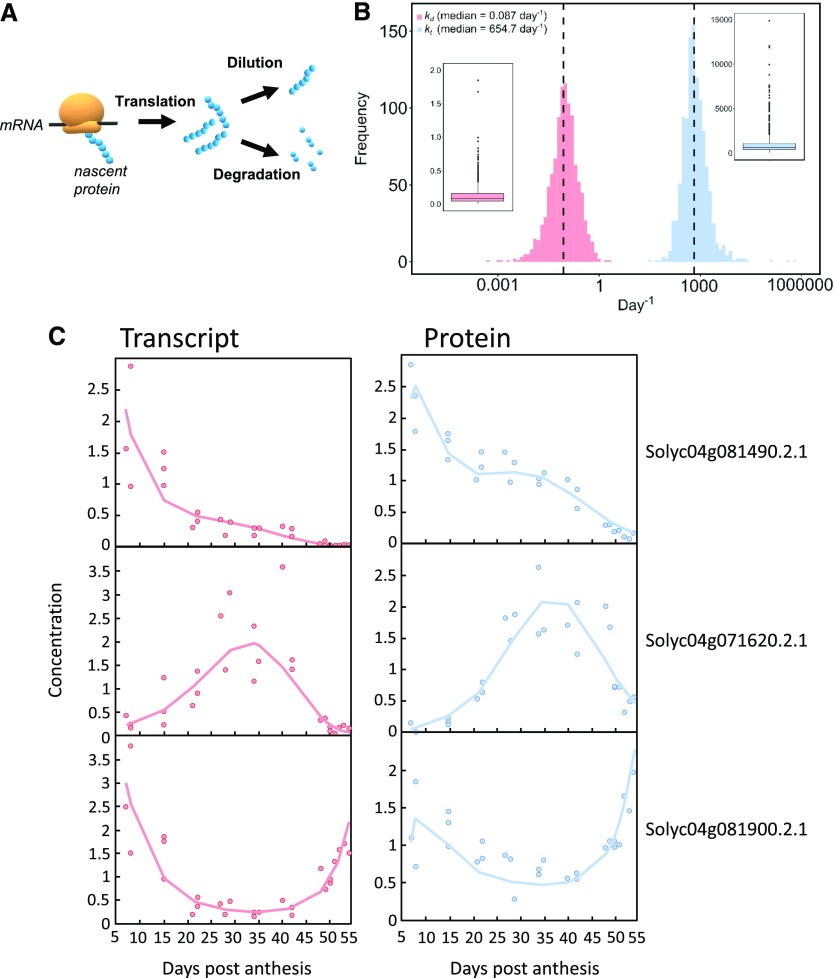
Figure 1.

Distribution of transcript and protein concentrations. A, Transcripts, all (22,877) in gray and the ones corresponding to the proteins (2,375) in black. B, Transcripts (gray) versus proteins (red) for all stages combined and at each of the nine stages of tomato fruit development identified by time (in days post anthesis [DPA]). Dashed green lines symbolize medians in all panels. Median values are shown in black for mRNA and in red for protein. FW, fresh weight.

The 2,375 quantified proteins represent 11% of the detected transcriptome. Taken individually, mRNAs corresponding to the detected proteins were among the most abundant transcripts, with a ratio of ∼7.5 between the respective medians of mRNA abundances (Fig. 1A). mRNA concentrations ranged from ∼0.001 to 3,500 fmol.gFW⁻¹ when considering the full dataset and from 0.01 to 440 fmol.gFW⁻¹ when considering the subset encoding the detected proteins (Supplemental File S1). Based on average values calculated during fruit development, the individual protein concentration ranged from 0.2 to 3,800 pmol.gFW⁻¹ with an average of 26.3 and a median of 4.21. This is in agreement with data previously obtained in Arabidopsis (Arabidopsis thaliana) leaves that had been cross-validated with enzyme activity data (Piques et al., 2009). It is likely that nondetected proteins were less abundant, poorly extracted, highly unstable, and/or difficult to detect due to the low ionization efficiency of their peptides (Schulze and Usadel, 2010).

The most abundant protein found in this dataset is encoded by the gene Solyc07g007750.2.1, which is annotated as a “defensin.” During fruit development, this protein represented more than 6% of the detected proteome and up to 8.6% at the initial stages of fruit development (Supplemental Fig. S1). Many plant defensins have been reported and they can harbor Cys-rich antimicrobial peptides that are classified into plant antifungal peptides (see Parisi et al., 2018 for review). Studies on this class of peptides presently concern its activity on microorganisms, in particular on the molecular features of the mechanism of action against bacteria and fungi (Lacerda et al., 2014). Among the other four most abundant proteins, two are annotated as “nonspecific (plant) lipid-transfer proteins.” On average, their respective concentrations were of 1,900 and 1,300 pmol.gFW⁻¹. The lipid-transfer proteins are known to be small but abundant and capable of exchanging lipids between membranes, with several other biological roles including antimicrobial defense, signaling, and cell wall loosening (see Yeats and Rose, 2008). Interestingly, each lipid-transfer protein displayed a unique profile with a higher abundance either at the beginning of fruit growth (Solyc10g075090.1.1) or at the end of development (Solyc10g075070.1.1). The third most abundant protein was annotated as “histone 3” (Solyc01g073970.2.1). Its average concentration was 1,800 pmol.gFW⁻¹. In eukaryotic cells, histone 3, together with other histone proteins (H2A, H2B, and H4), contributes to wrapping DNA before compaction of DNA strands in assemblies leading to nucleosomes (see Müller and Muir, 2015). Histone 3 represented 2.9% of the average total protein content, decreasing progressively to 1%. The fifth most abundant protein was a superoxide dismutase (Solyc01g067740.2.1), with 900 pmol.gFW⁻¹ (i.e. 1.4% of the detected proteome). In plants, superoxide dismutase catalyzes the production of O₂ and H₂O₂ from superoxide, thus protecting cellular components from oxidative stress. O₂^.− is known to denature enzymes, oxidize lipids, and fragment DNA (Smirnoff, 1993). Interestingly, the superoxide dismutase concentration remained constant during fruit development (ranging from 800 to 1,000 pmol.gFW⁻¹) whereas the total protein concentration decreased, thus leading to a higher abundance at ripening (>2.5% of the detected proteome; Supplemental Fig. S1). Furthermore, three ribosomal proteins (40S and 60S) were found among the 10 most abundant proteins in this dataset (Supplemental File S1).

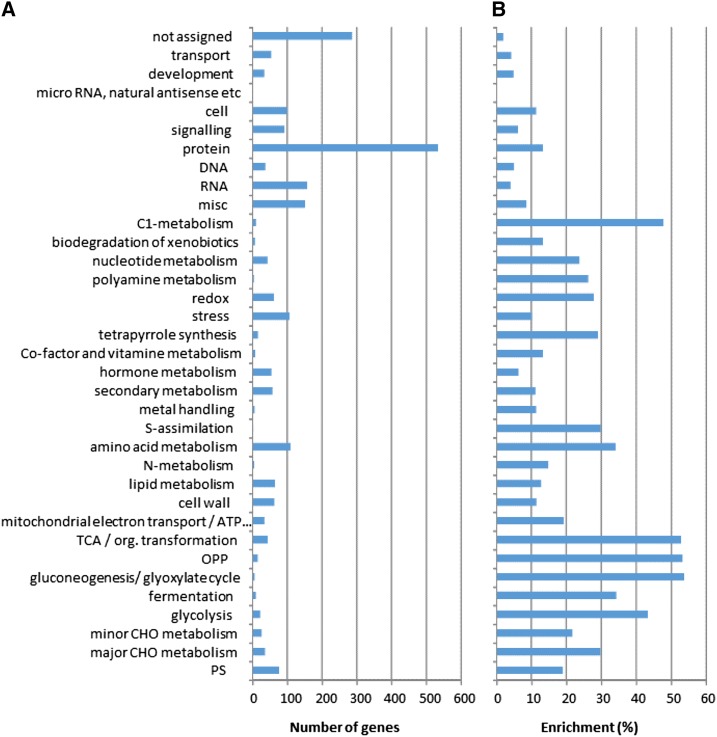
To assess whether some functional categories are overrepresented in the protein subset, we next analyzed the enrichment of the MapMan categories that were assigned using MapMan4 (Schwacke et al., 2019; Fig. 2). In line with previous results obtained in tomato fruit (Szymanski et al., 2017), the highest proportions were found for “gluconeogenesis/glyoxylate cycle” and “OPP,” and “TCA/org. transformation,” whose enrichments exceeded 50%. Relatively high proportions (>30%) were also found for “C1-metabolism,” “glycolysis,” “fermentation,” “amino acid metabolism,” “s-assimilation,” and “major CHO metabolism.” The lowest proportions were found for the bins “not assigned,” “RNA,” “transport,” and “development” (<5%). Although several enzymes involved in secondary metabolism were highly abundant, this category was underrepresented compared to primary metabolism with only 11% enrichment. However, the enrichment of the “protein” category (including protein synthesis, processing, transport, modification, and degradation) was only 13%, the highest number of detected proteins was found for this category (>500). In contrast, individual protein concentrations in this category were significantly lower than in the other categories (P value 4.3.10⁻¹⁰ according to Benjamini-Hochberg–corrected Wilcoxon sum rank test), with an average concentration of 18.3 pmol.g^-1FW versus 26.3 for all detected proteins. However, this category also represented >16% of the detected proteome (based on concentrations), indicating that protein synthesis, maturation, and degradation involve numerous genes and represent a massive investment in terms of energy and nitrogen (Li et al., 2014).

Figure 2.

Enrichment of MapMan categories. A, Number of genes corresponding to proteins detected within each functional category. B, Ratio between detected and nondetected proteins (enrichment expressed in %). TCA, tricarboxylic acid cycle; OPP, oxydative pentose phosphate; CHO, carbohydrate.

The median ratio between protein and mRNA abundance increased from ∼1,000 in the early stages to ∼3,000 at ripening. The analysis was further restricted to genes that were identified at both mRNA and protein levels, i.e. 2,375 mRNA-protein pairs. In this dataset, proteins were on average 2,636 times more abundant than the corresponding transcripts, as illustrated by the median of the protein/mRNA ratio (Fig. 1B). Considering the order of magnitude, this result is in agreement with previously reported ratios for eukaryotic cells like mouse fibroblasts (2,800; Schwanhäusser et al., 2011) and yeast (748; Lahtvee et al., 2017). This ratio also progressively increased during fruit development before stabilizing, with median values rising from ∼1,200 to 3,000. This is the result of a larger decrease in transcript concentration than in protein concentration.

Clustering Analysis Shows that Proteins Change More Gradually than Their Encoding mRNA

As reported previously, the large expansion of the vacuole at the expense of the cytoplasm during the initial stages of tomato fruit development has a strong effect on the data structure (Beauvoit et al., 2014; Biais et al., 2014). Thus, transcript and protein data were normalized before multivariate and univariate statistical analyses (median normalization, cube root transformation, and Pareto scaling).

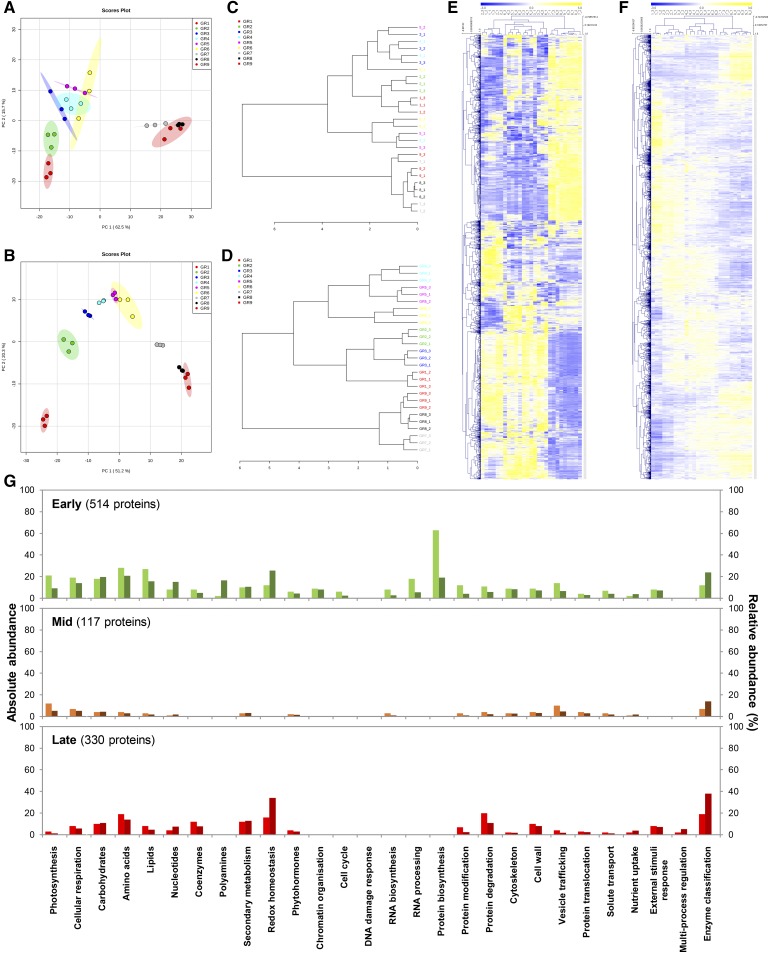
Global impacts of the growth stages on the transcriptome and the proteome were visualized by principal component analysis (PCA), and score plots were constructed using MetaboAnalyst (v4.0; Xia et al., 2015; median normalization, cube-root transformation, and Pareto scaling). Of the total variance, PC1 and PC2 captured 78.2% for transcripts (Fig. 3A) and 71.5% for proteins (Fig. 3B). For transcripts, stages 1–6 grouped quite closely but with a clear trajectory in PC1 and PC2 that recapitulated the developmental stage. Stages 7–9 also grouped together but were strongly separated in PC1 from stages 1 to 6 (Fig. 3A). This suggests two clear-cut phases of gene expression during tomato fruit development. Conversely, PC analysis of the proteomic data pointed rather to a stage-specific response with stages 1 and 2 distinctly separated, stages 3–6 substantially aligned across PC2, stage 7 separated, and stages 8 and 9 grouped (Fig. 3B). Thus, these data indicate that protein profiles fit better to fruit development than transcript abundances, with possibly three main phases. This was confirmed for both transcripts and proteins using dendrograms (distance shown as Pearson’s correlation after complete clustering in MetaboAnalyst) that showed relationships between samples (Fig. 3, C and D). Further analysis by bidimensional clustering (Pearson’s correlation after complete clustering using MeV v4.9.0; http://mev.tm4.org/#/welcome) also highlighted different patterns for transcripts and proteins (Fig. 3, E and F). Whereas the mRNA heatmap distinguished two main clusters (stages 1 to 6, and 7 to 9), the protein heatmap produced a gradual shift during fruit development. This suggests that fruit growth is accompanied by a strong shift in transcript accumulation but also by a harmonious change of protein profiles that follows the developmental stages over time.

Figure 3.

Multi- and univariate statistical analyses reveal differential induction patterns for transcript and protein abundances during fruit development. Abundance data of transcripts and proteins that paired together (2,375) were normalized before statistical analyses (median normalization, cube-root transformation, Pareto scaling). A and B, Global overview of unfiltered transcriptomic (A) and proteomic (B) profiles by PCA (n = 3; max variance explained is shown in brackets) indicates stage-specific responses during fruit growth. C and D, Dendrograms showing relationship between transcript (C) and protein (D) samples (Pearson’s correlation) confirmed multivariate outputs from PCA. E and F, Bidimensional clustering analysis of transcript (E) and protein (F) profiles (Pearson’s correlation) revealing distinct abundance patterns. G, Protein profiles were filtered by ANOVA (P < 0.01 with adjusted Bonferroni) yielding 1,363 proteins, then subsequently clustered by Pearson’s correlation (see Supplemental Fig. S2), which revealed three main clusters: “Early” (514 proteins), “Mid” (117), and “Late” (330). Proteins that paired with transcripts, or belonging to the different clusters, were mapped to metabolic function using Mercator4 (v1.0). For each metabolic function, absolute (left bars, light colors) and relative (right bars, dark colors) abundances are shown on the left and right axes, respectively.

We next wondered which metabolic functions might be linked to the changing protein profile during fruit development. We filtered the 2,375 proteomics features by stringent univariate statistics (analysis of variance [ANOVA] P < 0.01) with adjusted Bonferroni correction for false positive removal. Using the resulting significant markers (1,363), we performed bidimensional clustering (Pearson’s correlation) and identified three clusters that mapped to the “Early,” “Mid,” and “Late” phases of fruit development (see Supplemental Fig. S2; Supplemental File S1). Mercator4 v1.0 (https://plabipd.de/portal/mercator4) was used to map the metabolic functions that are presented as absolute and relative abundances in Figure 3G. Protein metabolism, especially protein synthesis, peaked in the “Early” phase at the beginning of fruit growth and was negligible in the later phases (Fig. 3G). This fits with the idea that production of the machinery for protein synthesis is a prerequisite to allow subsequent production of proteins of any metabolic function. Protein degradation and modification were high at ripening. Redox homeostasis was represented by an early peak and a second peak at ripening, in the “Early” and “Late” clusters, respectively (Fig. 3G). A very energy-consuming turbo metabolism underpins the development of young fruit (Beauvoit et al., 2014) and may ultimately lead to oxidative stress (Geigenberger and Fernie, 2014). To counter this, several cellular systems maintain the redox poise by detoxifying accumulating reactive oxygen species, as in pineapple (Ananas comosus) where catalase and ascorbate peroxidase mRNA accumulate in the early stages of fruit growth while the expressions of glutathione reductase and monodehydroascorbate reductase gene are upregulated in the later stages (Léchaudel et al., 2018). Abundant redox proteins included superoxide dismutase and ascorbate peroxidase in the “Early” phase, and monodehydroascorbate reductase and glutathione peroxidase in the “Late” phase (Supplemental Fig. S3). Further evidence was that alterations in the abundance of redox-associated proteins coincided coherently with high values for the primary metabolism, including photosynthesis, cellular respiration, carbohydrates, amino acids, lipids, polyamines, and coenzymes (Fig. 3G). This pattern was observed not only during the initial phases of fruit growth but also at ripening. This suggests that the primary metabolism is required to provide the initial building blocks for fruit growth and becomes damped during the expansion phase. At ripening, the central metabolism again increases. This is in agreement with the idea that the climacteric crisis is a characteristic of the phase between expansion and ripening (Colombié et al., 2017). In stark contrast, the expansion phase was associated with smaller proteomic changes, e.g. higher abundance in vesicle trafficking (Fig. 3G).

Correlation between Gene Expression and Proteins

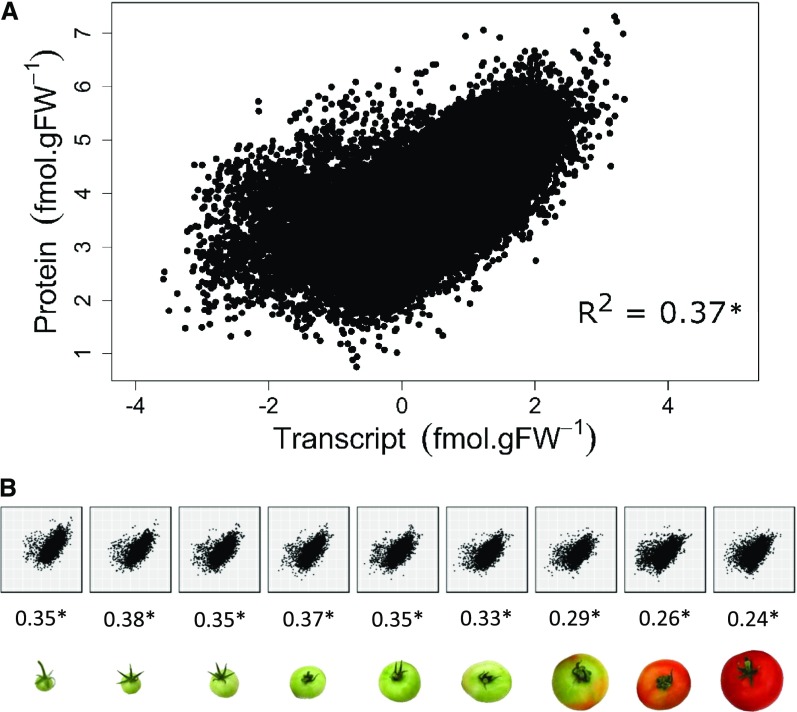
With data expressed on a gram basis and log-transformed to minimize the contribution of the most abundant proteins (extreme values), mRNA and protein datasets showed significant correlations between mRNAs and their encoded proteins (Futcher et al., 1999; Griffin et al., 2002; Maier et al., 2009; Schwanhäusser et al., 2011; Lahtvee et al., 2017) with a correlation coefficient of R² = 0.37 for all developmental stages (Fig. 4A). Note that the correlation coefficient decreased (R² = 0.20) when the regression was performed without log-transformed data. These values indicate only a moderate relationship between mRNA and protein concentrations. Interestingly, R² decreased during fruit development, indicating that the relation between mRNA and protein concentrations weakened over time (Fig. 4B). However, a significant correlation between log-transformed data indicates a power relation between mRNA and protein contents, as

Figure 4.

Correlation between 2,375 protein and transcript abundancies during fruit development. A, Correlation plot obtained for all stages. B, Correlation plots obtained at each of the nine stages identified by stage of fruit development. Correlation coefficients (R²) are given below each plot. Data were log-transformed before analysis.

where p is the protein content; r is the mRNA content; α is slope of the linear regression; and β is the intercept, which gives

Thus, according to Equation (2), there is no linear relation between p and r except when α = 1 (in this case, the relation would be strictly linear, so a logarithmic transformation of the data would not increase the correlation coefficient). According to Figure 4A, α was less than one in this study, which suggests that protein synthesis becomes less effective as the mRNA concentration increases. We conclude that this type of correlative model is not appropriate for studying time-series or for observations in which there are pre-existing proteins (e.g. a developed organ), probably because the protein stability exceeds the mRNA stability.

Another approach to evaluate the relation between mRNA and proteins is to perform a regression analysis during fruit development for each transcript–protein pair. When a linear regression analysis was performed with data expressed on a fresh weight basis, R² ranged between 0 and 1, with a median value of 0.52 (Supplemental Fig. S4). However, this somewhat tighter correlation was mostly due to dilution by growth, which affects protein and transcript abundance in parallel, leading to a secondary correlation that falsifies the actual relationship between transcript and protein abundance. Indeed, in most cases both mRNA and protein concentrations were much higher at the earliest developmental stage. Removing the first time point from the analysis had a relatively strong effect (the median value for R² dropped to 0.43), whereas removing any other time point had less effect.

Taken together, these observations led us to use a protein turnover model to estimate protein translation and degradation rates, taking into account protein translation, its stability and its dilution by growth.

Model Describing Protein Translation and Degradation

As mentioned in the introduction, protein and mRNA data can be linked using an ODE describing the time course of protein concentration, resulting from two terms—one for translation and the other for removal by degradation and/or dilution by growth. The processes and terms in the model are summarized in Figure 5A. Estimation of the rate of protein translation and degradation during development was based on the assumption that, on a fruit-basis, protein translation rate and protein degradation rate are proportional to transcript abundance and protein abundance, respectively. The calculation was performed according to Equation (3):

Figure 5.

Mathematical model of protein translation and degradation. A, Scheme of the main processes described in the mathematical model. B, Distribution and boxplot of both rate constants for translation (k_t) and degradation (k_d) that were satisfactorily fitted with the model for 1,103 proteins. C, Three satisfactorily fitted profiles of transcripts and proteins, for which protein peaks occurred at early, mid, and late stages of fruit development. Symbols correspond to transcript (red) and protein (blue) normalized experimental data. The red lines represent the fitting of the mRNA data and the blue line the fitting of the protein data.

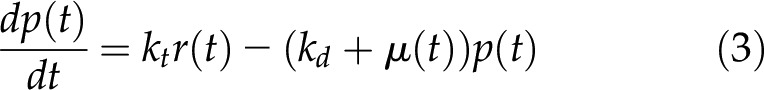where p(t) is the protein concentration in fmol.gFW⁻¹ at t; r(t) is the transcript concentration in fmol.gFW⁻¹ at t; k_t is the translation rate constant (day⁻¹); k_d is the degradation rate constant (day⁻¹); and μ(t) is the relative growth rate at t.

To solve the model, each of the 2,375 mRNA–protein pairs was described using a polynomial regression after log transformation for the mRNA concentrations and using Equation (3) for protein concentrations. Hence, fruit weight was fitted using a double sigmoid and a relative growth rate was deduced (Supplemental Fig. S5). To improve the numerical accuracy of the computations, mRNA and protein data were normalized on their respective averages calculated over the nine stages. Then, the values of the rate constants k_t and k_d were calculated using the least square method: For each protein concentration, the squared difference between the predicted value obtained by solving the ODE and the experimental value was minimized. Three criteria were used to evaluate the quality of the resolution automatically: (1) the score for each mRNA fit, (2) the score for each protein fit, and (3) a statistical evaluation of constant quality; simulations were also performed to test whether the time windows used in the study were adequate to describe protein turnover (see “Materials and Methods” and Supplemental Appendix S2). The model could be validated for 888 transcript-protein pairs using these criteria. Because criteria 2 and 3 appeared ambiguous for some pairs, a manual inspection was subsequently performed. This process allowed k_t and k_d to be satisfactorily solved for 1,103 mRNA–protein pairs, representing >46% of the total number of pairs (Supplemental File S1). For the remaining 1,272 pairs, (1) a high number of missing values could have penalized the resolution, especially for the protein dataset (clearly the case for 119 pairs); (2) mRNA and/or protein data were too noisy; (3) each individual parameter could not be estimated due to the high correlation between them (unclosed confidence region for criteria 3; and (4) proteins cannot comply to this mathematical model.

As already mentioned, the model assumes that k_t and k_d are constant during fruit development. It is therefore not possible to describe specific events such as the degradation of a given protein that might occur at a precise moment. Such events would likely lead to the model failing to provide a solution. Thus, for the transcript–protein pairs that could not be modeled satisfactorily, we manually inspected the protein data for time courses that pointed to time-dependent changes in degradation rate (i.e. a sharp decay at ripening). Fewer than 50 proteins were found that were strongly degraded at the beginning of ripening (Supplemental File S1). Within this group, a defensin and a small subunit of Rubisco were the two most abundant ones, based on concentration (respectively, the 69th and 102nd most abundant proteins found when averaging protein content over all developmental stages). However, these 50 proteins represented only a small fraction of the proteome, i.e. <1% based on concentrations, suggesting that ripening was not characterized by massive targeted proteolysis.

We next calculated the proportions of proteins for which the model could be satisfactorily solved within the three protein clusters shown in Figure 3B. The model performed well with clusters “Early” and “Mid,” but not so well for cluster “Late,” which corresponds to ripening (53%, 44%, and 34%, respectively, of the proteins could be solved; Table 1). This might be because the duration of the experiment does not cover the lifetime of a large proportion of the proteins that are synthesized at ripening.

Table 1. Protein clustering and turnover during fruit development.

The number of mRNA-protein pairs, for which protein translation and degradation rate constants (k_t and k_d, respectively) could be satisfactorily estimated from the model, was compared with the number of proteins found peaking within three clusters corresponding to early growth (cluster “Early”), fruit expansion (cluster “Mid”), and ripening (cluster “Late”).

Feature	Before Clustering	Cluster “Early”	Cluster “Mid”	Cluster “Late”
Number of mRNA–protein pairs	2,375	514	117	330
Number of mRNA–protein pairs solved satisfactorily	1,103	271	51	113
Median of kt (day−1) solved satisfactorily	772	766a	593	553a
Median of kd (day−1) solved satisfactorily	0.09	0.12a	0.09	0.04a

^aSignificance: Cluster 1 was significantly different for k_t (P value = 9.10⁻⁵) and k_d (1.10⁻¹⁴), and cluster 3 for k_t (2.10⁻³) and k_d (2.10⁻¹⁶); Wilcoxon rank sum test with Benjamini-Hochberg correction.

Together, these results indicate that for most of the abundant proteins (i.e. proteins quantified here), a specific regulation of protein synthesis or degradation cannot be postulated. It is striking that the changes in abundance of nearly one-half of the proteins that were quantified can be modeled on the assumption that k_t and k_d do not vary during fruit development and ripening. The proportion is likely to be higher because, under the above hypothesis, model resolution is more difficult when a substantial amount of protein synthesis and degradation occur outside the time interval of the experiment. Using an analogous approach with yeast, Tchourine et al. (2014) investigated which types of time-dependent expression profiles the cell could achieve without using regulatory factors, i.e. by assuming simple linear relationships between the contributing synthesis and degradation rates. Using the same linear differential equation to model time-dependent protein expression changes in yeast cells, they found that one-third of the genes were successfully modeled. As in our study, prediction quality was linked to low measurement noise and to the shape of expression profiles. A better predictability was obtained when both protein and mRNA levels increased, while sudden and singular shifts of expression led to low predictability.

Protein Translation Rate

The translation rate constant (k_t) gives the number of protein copies synthesized from a given mRNA template per day. It encompasses initiation, elongation, and termination rates (Gingold and Pilpel, 2011). Estimation of protein translation rate constants has been performed here at large-scale. It is worth mentioning that Li et al. (2017) have, for a large number of genes, calculated a so-called “synthesis rate constant” that encompasses mRNA concentrations and translation.

Validation

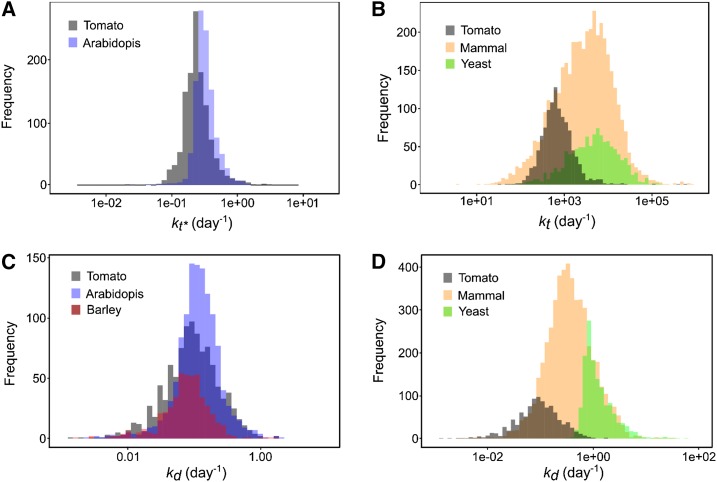
To validate this dataset, the literature was mined for protein translation rate constants obtained in eukaryotes, assuming that protein translation is a universal process that is highly conserved among eukaryotes. Unfortunately, to date only a few articles have reported protein translation rate constants on a comparable scale. There are two reports of translation efficiencies for ∼4,200 and 1,115 proteins, respectively, in mammalian fibroblast cultured cells (Schwanhäusser et al., 2011) and in yeast at steady state (Lahtvee et al., 2017). Superimposing the distributions of the k_t values indicates that the values found here were lower but within the same orders of magnitude (Fig. 6A). The median k_t value found for tomato fruit, 655 d⁻¹, which corresponds to ∼2 min to synthesize one protein copy, is lower than for yeast (4,930 d⁻¹) and for mammalian cells (2,981 d⁻¹). Although many species-dependent factors (e.g. temperature, substrate concentrations, etc.) and parameters (initiation efficiency, ribosome concentration, polysome density, codon usage, etc.) might explain these differences, it should be noted that the proteins under study may also differ considerably regarding their properties. It can nevertheless be concluded that the k_t values obtained here are plausible. To be able to compare these estimates with protein synthesis rate constants obtained in Arabidopsis (Li et al., 2017), we used the following equation with transcript and protein values averaged over the whole fruit development, as

Figure 6.

Comparison of rate constants between organisms. A, Distribution of 1,103 translation rate constants k_t* calculated for proteins of tomato fruit (gray, median 0.31 d⁻¹) superimposed with 1,228 values from Arabidopsis leaf (blue, median 0.23 d⁻¹; Li et al., 2017). B, Distribution of 1,103 translation rate constants k_t calculated for proteins of tomato fruit (gray, median 772 d⁻¹) superimposed with 1,115 values of yeast (green, median 4,930 d⁻¹; Lahtvee et al., 2017) and 4,247 values of mammal cells (yellow, median 2,981 d⁻¹; Schwanhäusser et al., 2011). C and D, Distribution of 1,103 degradation rate constants k_d calculated for proteins of tomato fruit (gray median 0.113 d⁻¹) superimposed with (C) 1,228 values from Arabidopsis leaf (blue, median 0.113 d⁻¹; Li et al., 2017) and 505 values from barley leaf (purple, median 0.076 d⁻¹; Nelson et al., 2014) and with (D) 1,384 values of yeast (green, median 1.03 d⁻¹; Lahtvee et al., 2017) and 5,028 values of mammal cells (fibroblast cells yellow, median 0.347 d⁻¹; Schwanhäusser et al., 2011). All rate constant values were log¹⁰-scaled.

As shown in Figure 6B, the distributions of the k_t* (in d⁻¹) found in tomato and Arabidopsis were largely superimposed, with similar profiles and closed median values, i.e. 0.23 d⁻¹ for Arabidopsis leaves and 0.31 d⁻¹ for tomato fruit.

Further important parameters for studies dealing with protein metabolism are polysome density, which results from the distance between ribosomes within polysomes, and elongation rate, which is expressed as the number of amino acids attached per second (Piques et al., 2009). Studies in yeast and mammalian cells have reported a distance of 200–300 nucleotides between two ribosomes within polysomes and a translation rate ranging from 3 to 10 amino acids per second (Iwasaki and Ingolia, 2016). To obtain an estimation of the elongation rate (V_elong), i.e. the overall rate of ribosome progression/elongation for the three major steps—initiation, elongation, and termination, and thus the number of amino acids added per second and per ribosome—we used a simplified version of the equation reported by Piques et al. (2009)

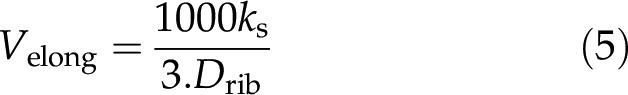where V_elong is expressed in (amino acids.ribosome^-1.s^-1); k_t is expressed in s⁻¹; D_rib is the ribosome density (ribosomes.kb^-1); and 3 is the ratio between mRNA and protein length (kb.amino acids⁻¹).

Assuming a ribosomal density of four or six ribosomes per kilobytes according to Iwasaki and Ingolia (2016), the elongation rate estimated from the median k_t (770 d⁻¹) ranged from 0.4 to 0.6 amino acids.ribosome⁻¹.s⁻¹. Although it is in the same order of magnitude, this estimation is lower than the elongation rates compiled by Iwasaki and Ingolia (2016), which ranged from 3 to 10 amino acids.ribosome⁻¹.s⁻¹ for eukaryotic cells. Note that the latter rates were obtained by directly monitoring nascent peptides via the use of tandem repeats of epitopes that bind fluorescent antibodies (Iwasaki and Ingolia, 2016 and references therein), whereas this estimation includes initiation, elongation, and termination rates. It is therefore possible that elongation rates are higher in tomato fruit. Indeed, although the identity of the rate-limiting step of translation remains controversial, the balance seems to be leaning more toward initiation as having the strongest influence (Gingold and Pilpel, 2011; Shah et al., 2013).

The Translation Rate Constant Is Highly Variable

There was no correlation between transcript concentration and k_t, confirming the results of Piques et al. (2009) who concluded that ribosomal occupancy depends more on individual features of transcripts than on transcript concentration. Indeed, the 1,103 k_t values that we found covered four orders of magnitude and the coefficient of variation (∼1,000%) was nine times higher than the coefficient of variation found for the corresponding k_d values. This is in line with the finding that initiation probabilities inferred for yeast genes vary by many orders of magnitude (Shah et al., 2013). Nevertheless, most values in our study lie in a narrower range. Almost 70% of the values for k_t were between 100 and 1,000, and 30% were between 1,000 and 10,000. Among the 10 proteins with the highest k_t values (>11,873 d⁻¹, corresponding to a protein being synthesized in <10 s per transcript), three are annotated for protein synthesis and two for protein degradation. Conversely, among the five proteins displaying the lowest k_t values (<117 d⁻¹, corresponding to a protein synthesized slowly in 20 min or more per transcript), three are annotated for DNA synthesis.

Can Gene Sequence Features Be Used to Predict Protein Synthesis Rates?

Codon usage is known to influence protein synthesis rates (Bulmer, 1991). We computed the number and proportion of each different codon in each sequence to check whether rare codons are overrepresented in proteins with slower synthesis rates, and vice versa. No such correlation was found, indicating that codon usage does not have a strong influence on k_t, using either Partial Least Square algorithms or generalized linear models. An in-depth analysis of 5′-UTR structures might give more insights into translation rates.

Protein Degradation Rate

We next investigated the estimated degradation rate constants (k_d) of the 1,103 mRNA–protein pairs for which the model resolution was considered as valid. The k_d median value obtained was 0.087 d⁻¹ (Fig. 5), which corresponds to a lifetime of ∼11 d and a half-life of ∼7.5 d.

Validation

To cross-validate the results, we compared the k_d calculated for tomato with degradation rate constants obtained by ¹⁵N labeling experiments for proteins of barley (Hordeum vulgare; 508 values; Nelson et al., 2014) and Arabidopsis (1,228 values; Li et al., 2017) leaves. The three distributions of k_d were in the same range (Fig. 6C). The median k_d value found here (0.087 d⁻¹) is also in accordance with a ³H₂0-labeling study performed in barley leaves, in which the k_d of the leaf proteome ranged from 0.065 to 0.154 d⁻¹ (Dungey and Davies, 1982), as well as with a ¹³CO₂-labeling study performed in rosettes of various Arabidopsis accessions, in which the degradation rate of the total protein pool ranged from ∼0 to 0.09 d⁻¹ (Ishihara et al., 2017).

The distributions of degradation rate constants of tomato fruit showed a larger deviation from those of other eukaryotes, i.e. mammal cells (fibroblasts, >4,200 values; Schwanhäusser et al., 2011) and yeast (1,384 values Lahtvee et al., 2017; Fig. 6B). The lower median values in yeast (1.03 d⁻¹) and mammal cells (0.35 d⁻¹) indicate that plant proteins are more stable. It is not known whether the turnover kinetics of individual proteins are highly conserved or if they have evolved to meet the physiological demands of individual species (Swovick et al., 2018). By conducting systematic analyses of proteome turnover kinetics in fibroblasts isolated from eight species, these authors found (1) a decrease in cross-species correlation of protein degradation rates as a function of evolutionary distance, and (2) a negative correlation between global protein turnover rates and maximum lifespan of the species. A comparable study including micro-organisms and plant cells could help to better understand the difference in turnover between organisms.

To further validate the results, the sd calculated for the k_d of subunits of protein complexes that are known or hypothesized to turnover in a coordinated manner was compared with the sd calculated for 100,000 randomly sampled same-sized groups of proteins, as in Li et al. (2017). The sd appeared significantly smaller for the proteasome (n = 29, P value = 0.04), plastidial ribosome (n = 9, P value = 0.03), and PSII (n = 3, P value = 0.04) but not for the mitochondrial electron transport chain (n = 14, P value = 0.4) and the cytosolic ribosomal proteins (Supplemental Fig. S6), the latter having also been found to be nonsignificant in Arabidopsis leaves (Li et al., 2017).

Additionally, k_d values calculated here were compared with those found in other species for various proteins or groups of proteins. Comparisons performed between tomato fruit and leaves of barley and Arabidopsis k_d (homologs with >60% homology) were inconclusive. No significant correlation was found for a hundred homologous barley and Arabidopsis proteins whose k_t had been previously found (Supplemental Fig. S7; Supplemental File S1). This result is not surprising because the correlation found between homologs of barley and Arabidopsis leaves was weak (0.38 when three outliers were removed; Li et al., 2017). More generally, conservation of the protein degradation rate constant between organisms is not especially expected because it can be different even for cells of two tissues of the same organism. For instance, Price et al. (2010) performed large-scale studies of protein dynamics to see if turnover kinetics of individual proteins are highly conserved or if they have evolved to meet the physiological demands of individual species. These turnover rates measured for ∼2,500 proteins in three mouse tissues (brain, liver, and blood) using organism-wide isotopic labeling were spanning four orders of magnitude and were significantly lower in the brain than in the liver and blood, with respectively 9, 3, and 3.5 d. In contrast, values found in human HeLa cells for 60S and 40S ribosomal proteins (Doherty et al., 2009) ranged from 0.11 to 0.74 d⁻¹ and from 0.02 to 2.64 d⁻¹, respectively. The ranges found for these two subgroups were very similar for 60S (0.04–0.58), and slightly less for 40S (0.04–0.44).

Finally, among the highest k_d corresponding to unstable proteins (k_d > 0.8 d⁻¹), four are not assigned, two are respectively annotated as “RNA, regulation transcription” and “nucleotide metabolism,” and one is the large subunit of ADP-Glc pyrophosphorylase (AGPase) involved in the starch pathway. Interestingly, AGPase has already been described as unstable in Arabidopsis leaves (Gibon et al., 2004) and in tomato fruit (Schaffer et al., 2000).

Proteins Involved in Protein Synthesis Are Less Stable

When considering genes with validated k_d, two “MapMan” functional categories were found with consistently higher k_d for “protein synthesis and RNA,” with Wilcoxon rank sum test P values of 4.2.10⁻² and 2.7.10⁻³, respectively (after Benjamini-Hochberg false discovery rate correction).

Can Protein Features Be Used to Predict Protein Stability?

It has been widely hypothesized that the protein degradation rate is directly linked to protein sequence. For example, it has been proposed that the N-terminal residue of proteins (Gibbs et al., 2016), hydrophobicity (Mann et al., 1984), enrichement in proline, glutamic acid, serine, and threonine domains (Rechsteiner and Rogers, 1996), or the presence of specific dipeptides (Ding et al., 2004) might have a direct effect on protein stability. To validate this assumption, we calculated instability indexes and aliphatic indexes, looked for proline, glutamic acid, serine, and threonine domains and generated 1,103 numerical features representing protein features such as physico-chemical information or amino acid composition. Using simple regression analyses, we found that some variables were significantly linked to k_d. For example, the P values found for the aliphatic and instability indexes were 6.10⁻¹⁰ and 7.10⁻⁴, respectively. However, the corresponding R² were <0.1. We then tried to build generalized linear models that would predict k_d based on combinations of descriptors. None of the combinations of predictors satisfactorily correlated with k_d values. From this analysis, it appears that the primary sequence is not enough to predict protein stability, at least on a global scale for this dataset. This result matches studies in yeast in which Tchourine et al. (2014) did not find any significant associations between any features for the rate constants of translation and degradation.

The Translation Rate has a Major Impact on Gene Expression

Strikingly, the translation rate constants were highly correlated with the protein–mRNA ratio calculated at the first stages of tomato fruit development, when protein degradation can be neglected (Supplemental Fig. S8). This result is in agreement with Li et al. (2014), who performed an absolute quantification of protein synthesis rates based on ribosome profiling in Escherichia coli. These authors showed that the synthesis rate, which is the product of mRNA and k_t, was proportional to protein abundance. Conversely, no correlation was found between the degradation rate constants and the protein–mRNA ratio. This result suggests that in growing organs the synthesis process controls protein abundancies much more efficiently than protein degradation, the former being much faster than the latter.

We then examined whether genes grouped in clusters “Early,” “Mid,” or “Late,” which encode proteins peaking during early growth, fruit expansion, and ripening stages, respectively (see Fig. 3), would differ regarding k_t and k_d values. As shown in Table 1, the cluster “Early” was significantly enriched with genes having higher k_t and k_d whereas the cluster “Late” was significantly enriched with genes having lower k_t and k_d. We next investigated whether very closely related isoforms would differ for k_t and k_d by selecting groups of putative paralogs (Supplemental File S1). Surprisingly, within most groups identified, there was a relatively strong variation for both constants, with a significant trend for both constants to be higher for paralogs belonging to the cluster “Early.” One interpretation is that genes with higher translation rates could have been selected for early fruit growth, which is a very fast phase of development. Alternatively, the trend to higher k_t during early growth could be because the protein synthesis machinery was more abundant and/or that metabolic activity was higher. As mentioned above, high metabolic activity is likely to result in higher reactive oxygen species production, which could in turn explain the higher k_d found for proteins peaking during early growth.

Concluding Remarks and Future Perspective

Quantitative transcriptomics and proteomics data can be used to model protein content as a function of mRNA content. This study suggests that such modeling is valid when performed over a developmental time course during which the modeled proteins are subject to both synthesis and degradation. In a simple model, we assumed that the rate of protein synthesis (amino acids added per time unit and transcript copy) is proportional to transcript abundance, and the rate of protein degradation (protein degraded per time unit and protein molecule) is proportional to protein abundance. For each transcript–protein pair, k_t and k_d can have different values, but these do not change during fruit development. Depending on when the transcripts and proteins peaked during fruit development, this simple model gave solutions for 34% to 53% of all transcript-protein pairs. The highest proportion of valid model resolutions was found for the proteins that accumulate during early growth, i.e. for the proteins that were essentially synthesized and degraded during the sampling period. The lower proportion of solutions for proteins that accumulate later in fruit ripening may be because the data set did not contain enough time points to estimate their degradation rates. Thus, it is likely that the proportion of proteins that obey this simple law is even higher.

It is striking that it was possible to estimate k_t and k_d constants for such a large proportion of proteins quantified, whereas high sophistication is often invoked in literature dealing with protein degradation (Hinkson and Elias, 2011). These results suggest that besides dilution by growth, transcription and translation are the most important points of control of protein concentration in developing tomato fruit. This view is reinforced by the fact that proteins involved in protein synthesis, and more generally those expressed in the early stages of growth, tend to have higher rate constants for both translation and degradation. On the other hand, ∼1,000 proteins were not successfully modeled, suggesting that the use of fixed-rate constants cannot be solved for any time course, for example because of the occurrence of more complex mechanisms such as delayed translation, regulation of translation, or regulation of protein degradation. A more detailed model describing regulations could estimate the rate constants with more experimental data to fit. Also, it will be important to design experiments with higher sampling frequency and seek for more sensitive proteomics to be able to catch less abundant proteins with higher turnover rates.

Whereas protein turnover has often been studied under steady-state conditions, for example in fully developed leaves (Dungey and Davies, 1982) or in rosettes, which are a mix of leaves at various developmental stages (Ishihara et al., 2017), this study emphasizes the importance of sampling during a developmental series. Indeed, many proteins in the developing tomato fruit can last for days or even weeks once synthesized, and there is no evidence of massive and targeted protein degradation that is specific to ripening (Sorrequieta et al., 2010; Ré et al., 2012). It seems rather that ripening coincides with the lifetime running out for a range of proteins that have been synthesized in the early stages of growth. Furthermore, ripening was also characterized by the de novo synthesis of many proteins (“Late” cluster), including those in primary metabolism. It is also likely that ethylene, the major orchestrator of ripening in climacteric fruits such as tomato (Liu et al., 2015), triggers protein synthesis rather than protein degradation. This view is supported by the observation that high CO₂, which inhibits ethylene-driven ripening, induces a substantial loss of protein in tomato fruit (Rothan et al., 1997). Thus, the question arises whether protein lifetime represents a major constraint in terms of the timing of shifts between developmental stages. It is indeed striking that tomato fruit need >50 d to grow and ripen. Furthermore, it seems obvious that protein stability represents a major issue for synthetic biology and that modeling of protein turnover will be of great help to support the engineering of cellular processes.

Future work must also focus on a deeper understanding of the rates of protein production and turnover and on the principles that govern their regulation. Especially, more work will be needed to understand the different processes governing protein synthesis in growing plant tissues. For instance, more detailed information about ribosome abundance will be needed to assess whether it influences k_t. Indeed, decreased ribosome abundance would probably lead to decreased k_t unless overall mRNA abundance falls in parallel with ribosome abundance. Then, ribosome footprinting with the identification of ribosomal binding sites on mRNA through ribosome stalling and sequencing the bound RNA fragments could improve the estimation of translation rates. It will certainly be useful to compare k_t values obtained with total mRNA and polysomal mRNA datasets to better apprehend the influence of initiation and elongation. It will also be important to extend the number of mRNA–protein pairs as only a relatively small fraction of the proteome could be quantified here.

Finally, no sequence-based features were found that could be used to predict k_t or k_d in this dataset. This may in part reflect the specificity of such mechanisms for small groups of proteins, which means they are difficult to detect in current datasets that contain only a small proportion of the total proteome. In addition, various physical and chemical factors (pH, temperature, etc.) that may potentially influence synthesis and degradation rates should be considered. Larger sets collected under various growth conditions, organs, and species would also make it possible to perform nontargeted machine-learning approaches and ultimately unravel novel features that impact protein synthesis and stability.

MATERIALS AND METHODS

Plant Material

The experimentation was conducted with Solanum lycopersicum var Moneymaker plants as described in Biais et al. (2014). Briefly, plants were grown under production conditions in a glasshouse in southwest France (44°23ʹ56ʹʹN, 0°35ʹ25ʹʹE) from June to October. The nutrient solutions used were adapted to plant growth and the water supply was adjusted to the climate using a drip irrigation system to maintain 20% to 30% drainage (pH adjusted to 5.9, electrical conductivity to 2.2 mS.cm⁻¹). On trusses 5, 6, and 7, flower anthesis was recorded and fruit were harvested at nine developmental stages, at ∼8, 15, 21, 28, 34, 42, 48, 50, and 53 days post anthesis. Samples were prepared by first removing seeds, jelly, and placenta, and then cutting the pericarp into small pieces, which were immediately frozen in liquid nitrogen. Samples were ground and stored at −80°C until analysis.

mRNA Extraction and Quantification

Total RNA was isolated from frozen tissue powder of tomato pericarp using Plant RNA Reagent (PureLink kit; Invitrogen) followed by DNase treatment (DNA-free kit, Invitrogen) and purification over RNeasy Mini Spin Columns (RNeasy Plant Mini kit; Qiagen), according to the manufacturer’s instructions. Total RNA concentration was determined by spectrophotometry. RNA integrity was assessed using the RNA 6000 Nano Kit with a Bioanalyzer 2100 System (Agilent Technologies). For each extract, a subsample of at least 5 μg of total RNA was used as the input material for RNA sample preparations. Transcripts were quantified absolutely using eight internal standards spiked in at the beginning of the total RNA extraction (in mole, 3.97.10⁻¹⁴ [spike 1], 4.01.10⁻¹⁵ [spike 2], 4.01.10⁻¹⁶ [spike 3], 4.02.10⁻¹⁷ [spike 4], 4.08.10⁻¹⁸ [spike 5], 4.04.10⁻¹⁹ [spike 6], 3.82.10⁻²⁰ [spike 7], and 3.82.10⁻²¹ [spike 8]). Spike sequences are given in Supplemental Appendix S1.

RNA sequencing (RNA-seq) was performed at the GeT-PlaGe core facility, INRA Toulouse. RNA-seq libraries were prepared according to Illumina’s protocols using the TruSeq Stranded mRNA Sample Prep Kit to analyze mRNA. Library quality was assessed using a Bioanalyzer (Agilent Technologies) and libraries were quantified by quantitative PCR using the Kapa Library Quantification Kit (Kapa Biosystems). RNA-seq experiments were performed on a HiSeq2000 or HiSeq2500 (2 × 100 bp; Illumina).

Genes were mapped to the S. lycopersicum var Heinz assembly v2.40, concatenated with the chloroplast (gi|544163592 ref|NC_007898.3) and mitochondrial genomes (gi|209887431|gb FJ374974.1), and an “artificial chromosome” containing the eight spike sequences. Genome data were from S. lycopersicum 2.5 and the corresponding ITAG2.4 gene models were downloaded from https://solgenomics.net/ (34,725 entries). The quality of libraries was checked with FastQC (Andrews, 2010). Quality and adapter trimming were performed with Trimmomatic v0.32 (Bolger et al., 2014). Trimmed reads were mapped to their respective genomes with Star v2.4.2a (Dobin et al., 2013) and the unique counts per locus were quantified with HTSeq (v0.6.1; Anders et al., 2015). Normalized fragments per kb per million (FPKM) mapped reads was calculated with the software Cufflinks v2.2.1 (http://cole-trapnell-lab.github.io/cufflinks/). Briefly, quantification based on FPKMs corresponds to the normalization of data by depth sequencing (summed fragment per sample) divided per one million, followed by normalization by gene length. FPKMs were then converted in transcripts per million quantification. For each sample, a standard curve performed with the spikes was used to estimate the concentration (fmol.gFW⁻¹) from the transcripts per million values. Nondefault parameters used for Trimmomatic (v0.32) and Star (v2.4.2a) are presented in Supplemental Appendix S1. All mRNA datasets are available via the GEO repository (Barrett et al., 2013) with the accession number GSE128739.

Protein Extraction and Quantification

Total tomato proteins were extracted as in Faurobert et al. (2007). Liquid chromatography MS/MS analyses were performed with a NanoLC-Ultra System (nano2DUltra; Eksigent) coupled with a Q-Exactive Mass Spectrometer (Thermo Electron) as in Havé et al. (2018). For each sample, 800 ng (4 μL from a 0.200-ng/μL solution) of protein digest were loaded onto a Biosphere C18 Precolumn (0.1 × 20 mm, 100 Å, 5 μm; Nanoseparation) at 7.5 μL min⁻¹ and desalted with 0.1% (v/v) formic acid and 2% (v/v) Acetonitrile. After 3 min, the precolumn was connected to a Biosphere C18 Nanocolumn (0.075 × 300 mm, 100 Å, 3 μm; Nanoseparation). The raw MS output files and identification data were deposited on-line using the PROTICdb database (http://moulon.inra.fr/protic/tomato_fruit_development). The MS proteomics data have also been deposited to the ProteomeXchange Consortium via the PRIDE (Perez-Riverol et al., 2019) partner repository with the dataset identifier PXD012877. Protein identification was performed using the protein sequence database of S. lycopersicum var Heinz assembly v2.40 (ITAG2.4) downloaded from https://solgenomics.net/ (34,725 entries). A contaminant database, which contains the sequences of standard contaminants, was also interrogated. Database search was performed with X!Tandem (v2015.04.01.1; http://www.thegpm.org/TANDEM/). Identified proteins were filtered and sorted by using X!TandemPipeline (v3.3.4; Langella et al., 2017). Criteria used for protein identification were (1) at least two different peptides identified with an E-value smaller than 0.01, and (2) a protein E-value (product of unique peptide E-values) smaller than 10⁻⁵. Using reversed sequences as a decoy database, the false discovery rate for peptide and protein identification were, respectively, 0.05% and 0%. Peptide ions were quantified based on extracted ion currents using the software MassChroQ (v2.2; Valot et al., 2011). Peptide intensities of each sample were normalized by using a method taking retention time into account, as described in Millan-Oropeza et al. (2017). Before protein quantification, peptides shared by several proteins were removed. In addition, peptides showing an unstable retention time across samples were considered as unreliable and removed. Protein abundancies were calculated with the “model” method based on peptide intensity modeling and described in Belouah et al. (2019). Briefly, this method is based on a linear model that takes into account the variable responses of peptide intensities to protein concentration.

Data Analysis

The mRNA–protein paired data (2,375) were preprocessed using the software MetaboAnalyst (v4.0; Xia et al., 2015; median normalization, cube-root transformation, and Pareto scaling; http://www.metaboanalyst.ca/) before multi- and univariate statistical analyses, thus providing normally distributed data. PCA and dendrograms (Pearson’s correlation, complete clustering) were constructed with MetaboAnalyst. MeV (v4.9.0) was used for bidimensional clustering (Pearson’s correlation, complete clustering; http://mev.tm4.org/), and subsequent filtering of mRNA-protein data (ANOVA P < 0.01 corrected for multiple testing by adjusted Bonferroni) to identify the Early, Mid, and Late clusters. Solycs belonging to each cluster were listed and converted to protein sequences (FASTA), which were subjected to Mercator4 (v1.0) for metabolic function annotation (Schwacke et al., 2019; http://www.plabipd.de/portal/web/guest/mercator4). Data were expressed as absolute abundance of proteins as well as relative abundance according to the bin size for each metabolic function.

A generalized linear model was built using the “glmnet” package (Friedman et al., 2010) under the “R” environment (R Core Team, 2017) to find correlations between k_d and protein features based on their sequence. A quantity of 1,926 were computed using the softwares protr (Xiao et al., 2015), ProtParam (Gasteiger et al., 2005), and biopython (Cock et al., 2009). The list of features and the values associated with each sequence are available in Supplemental File S2.

The software OrthoMCL (Li et al., 2003) was used to find groups of paralogous proteins in the list of well-modeled proteins. To minimize the risk of false positives, the following parameters were used: percentMatchCutoff = 75 and evalueExponentCutoff = −25. Annotation of proteins present in the clusters was performed using the software MapMan. Raw results are available in Supplemental File S1.

Accession Numbers

Sequence data from this article can be found in the GenBank/EMBL data libraries under accession numbers of the cited proteins, the five most abundant ones: Solyc07g007750.2.1 (defensin); Solyc10g075090.1.1 and Solyc10g075070.1.1 (lipid-transfer proteins); Solyc01g073970.2.1 (Histone 3); and Solyc01g067740.2.1 (superoxide dismutase). All mRNA datasets are available via the GEO repository (Barrett et al., 2013) with the accession number GSE128739. Proteomics data are available via ProteomeXchange with identifier PXD012877.

Supplemental Data

The following supplemental information is available.

• Supplemental Figure S1. Time course of protein and mRNA abundancies for the five most abundant proteins.

• Supplemental Figure S2. Clustering analysis reveals three waves of protein abundances during fruit development.

• Supplemental Figure S3. Profiles of selected redox protein markers during fruit development.

• Supplemental Figure S4. Correlation analysis performed with each mRNA–protein pair.

• Supplemental Figure S5. Growth of tomato fruit.

• Supplemental Figure S6. The protein degradation rates of the protein subunits of five major protein complexes.

• Supplemental Figure S7. Comparison of common degradation rate constants (k_d) annotated in plant tissues.

• Supplemental Figure S8. Translation rate constants (k_t) versus the protein–mRNA ratio.

• Supplemental Appendix S1. RNA-seq parameters and spikes.

• Supplemental Appendix S2. Modeling: Structural identifiability of the parameters, numerical simulation, and results analysis.

• Supplemental File S1. Abundance data for the 2,375 protein and mRNA pairs, calculated translation and degradation rate constants, clusters 1, 2, and 3 (early, mid, and late developmental stages, respectively), proteins specifically degraded at ripening, paralogs, Barley-versus-Tomato proteins, and Arabidopsis-versus-Tomato proteins.

• Supplemental File S2. List of features and values associated with each sequence for the 1,103 genes for which the model was solved satisfactorily.