Active wetting of epithelial tissues

Abstract

Development, regeneration and cancer involve drastic transitions in tissue morphology. In analogy with the behavior of inert fluids, some of these transitions have been interpreted as wetting transitions. The validity and scope of this analogy are unclear, however, because the active cellular forces that drive tissue wetting have been neither measured nor theoretically accounted for. Here we show that the transition between two-dimensional epithelial monolayers and three-dimensional spheroidal aggregates can be understood as an active wetting transition whose physics differs fundamentally from that of passive wetting phenomena. By combining an active polar fluid model with measurements of physical forces as a function of tissue size, contractility, cell-cell and cell-substrate adhesion, and substrate stiffness, we show that the wetting transition results from the competition between traction forces and contractile intercellular stresses. This competition defines a new intrinsic lengthscale that gives rise to a critical size for the wetting transition in tissues, a striking feature that has no counterpart in classical wetting. Finally, we show that active shape fluctuations are dynamically amplified during tissue dewetting. Overall, we conclude that tissue spreading constitutes a prominent example of active wetting — a novel physical scenario that may explain morphological transitions during tissue morphogenesis and tumor progression.

Living tissues are active materials with the ability to undergo drastic transitions in shape and dimensionality¹. When properly controlled, such morphological transitions enable development and regeneration. When regulation fails, however, aberrant morphological transitions underlie developmental defects and tumour formation^2,3. Transitions in tissue shape are regulated by a myriad of molecular processes that act upon a limited number of physical properties to ultimately determine tissue dynamics. To understand the nature of these physical properties and their impact on tissue shape, extensive research has focused on how a three-dimensional cell aggregate spreads on a substrate^4–8. Besides mimicking biological processes such as epiboly in zebrafish^9–12, the spreading of a cell aggregate is amenable to theoretical and experimental access, and has become a widespread model process.

Given the fluid behaviour of cell aggregates at long times, their spreading on a substrate has been studied as a wetting problem¹. In analogy with the case of a fluid drop, the extent to which the aggregate spreads on the substrate has been proposed to rely on a competition between cell-cell (W_cc) and cell-substrate (W_cs) adhesion energies^4,5 encoded in the so-called spreading parameter S = W_cs − W_cc. This parameter changes sign at the wetting transition that separates tissue spreading (S > 0) from retraction into a droplet-like aggregate (S < 0)^5,6,13,14. This analogy with the classical theory of wetting has successfully explained aspects of tissue wetting such as changes in contact angle as a function of cell-cell and cell-extracellular matrix (ECM) adhesion¹⁵. However, this conceptual framework overlooks the active nature of living tissues and, hence, it does not explicitly account for the ability of cells to polarize, generate traction forces, and couple such forces with adhesion dynamics. To a great extent, this limitation stems from the lack of direct measurements of cell-cell and cell-matrix forces during tissue wetting and dewetting.

To overcome these experimental and theoretical limitations, we performed a systematic quantitative study of the mechanics of tissue wetting as a function of cell-cell and cell-matrix adhesion, ECM ligand density, ECM stiffness, tissue size, and contractility. Our results cannot be explained solely in terms of the physics of passive fluids. Instead, we show that the tissue wetting transition and dewetting dynamics are well captured by a new framework for active wetting based on an active polar fluid model of tissue spreading.

E-cadherin expression induces dewetting of a cell monolayer

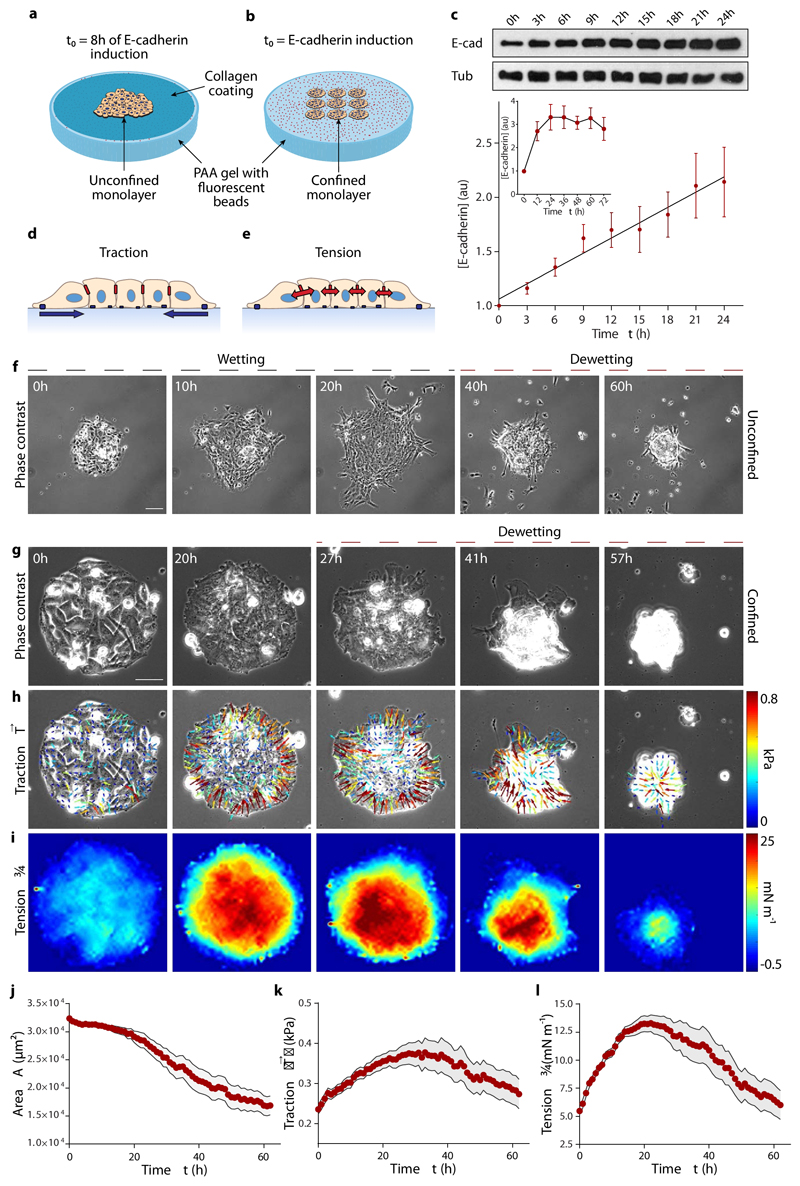
We designed an experimental assay to study wetting transitions of epithelial clusters induced by controlled changes in tissue mechanics. The idea behind the experimental approach is to progressively increase cell-cell adhesion in an epithelial monolayer while measuring its effect on cellular forces and tissue spreading. To this end, we use human breast adenocarcinoma cells (MDA-MB-231) transfected with a dexamethasone-inducible vector containing the human E-cadherin coding sequence¹⁶. In the absence of dexamethasone, these metastatic cells do not express significant levels of cell-cell adhesion proteins. On adding dexamethasone, the concentration of E-cadherin increases almost linearly in time for ~24h and plateaus thereafter (Fig. 1c, Supplementary Fig. 1). To study tissue wetting, MDA-MB-231 cells are seeded on a 12kPa polyacrylamide gel coated with collagen I (Fig. 1a). Initially, the cells form a monolayer within a circular opening of a polydimethylsiloxane (PDMS) membrane deposited on the gel. Eight hours after E-cadherin induction, the confining membrane is removed and the monolayer spreads. However, after ~20 hours, the monolayer often starts retracting, eventually becoming a spheroidal cell aggregate (Fig. 1f; Supplementary Fig. 2; Supplementary Movie 1, 2). Thus, the monolayer undergoes a transition from wetting to dewetting, which we refer to hereafter generically as wetting transition.

Fig. 1. E-cadherin expression causes an increase in traction forces and monolayer tension, and induces dewetting.

a,b, Scheme of the experimental setups. For spreading experiments, cells form a monolayer within the circular opening of a PDMS membrane. After 8 hours in the dexamethasone-containing medium, the PDMS membrane is removed and the monolayer spreads on the collagen-coated substrate (a). For confined monolayers, cells are seeded in circular islands of collagen on the substrate and allowed to cover them for 3 hours. Dexamethasone is then added to induce E-cadherin expression and time-lapse imaging starts (b). c, Quantification of E-cadherin upon addition of dexamethasone (inset, up to 3 days). Tub = tubulin. d,e, Illustration of traction forces (d) and monolayer tension (e). f, Spreading monolayer exhibiting a wetting transition at time t=25h. Scale bar = 100 μm. g-i, Phase contrast images (g), and maps of traction forces (h) and average normal monolayer tension (i) for a representative confined cell island of radius 100 μm. Monolayer dewetting starts at ~25 h. Scale bar = 40 μm. j-l, Evolution of monolayer area (j), mean traction magnitude (k) and mean average normal monolayer tension (l). Data are presented as mean ± s.e.m. n=18 cell islands.

To reproducibly study this transition, we seed cells on adherent (collagen I-coated) circular islands of controlled size (100 μm in radius) surrounded by an uncoated surface that cells cannot invade (Fig. 1b). We use Traction Force Microscopy to measure traction forces on the substrate (Fig. 1d)¹⁷, and Monolayer Stress Microscopy to measure tension within and between cells (Fig. 1e)^18,19. A few hours after E-cadherin induction, monolayers become cohesive (Fig. 1g). Cells at the edge polarize by extending lamellipodia towards the exterior of the island, generating radially-oriented inwards-pointing tractions (Fig. 1h; Supplementary Fig. 3)^20,21. Monolayer tension increases from the edge of the monolayer and reaches a maximum at the center (Fig. 1i). Note that monolayer tension is a bulk property and should not be confused with the interfacial surface tension that plays a central role in classical wetting phenomena. During the first ~25 hours of the experiment, tractions (Fig. 1k) and tension (Fig. 1l) rise in parallel with the increase in E-cadherin. As for unconfined spreading monolayers, the monolayer eventually retracts, decreasing its area (Fig. 1j) and dewetting the substrate to form a spheroidal aggregate, thus completing a transition from 2D to a 3D tissue geometry (Supplementary Fig. 4; Supplementary Movies 3, 4).

Formation of E-cadherin junctions activates myosin

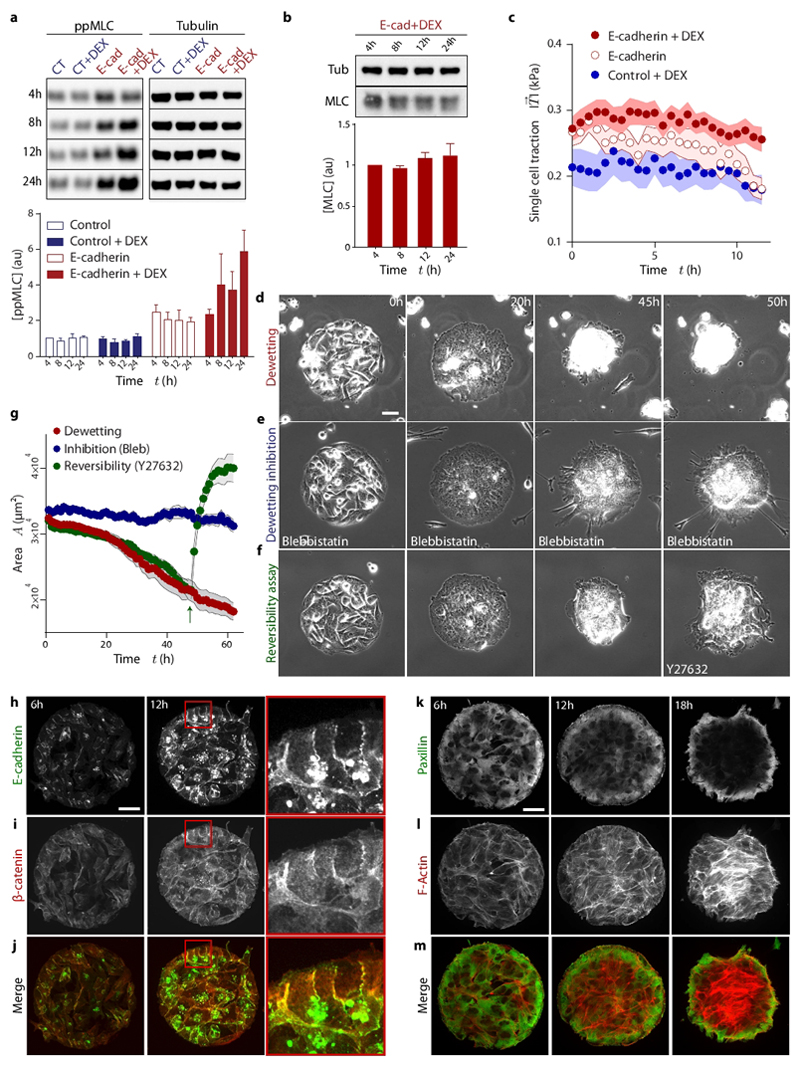
To study the mechanisms underlying the increase of tension we measure myosin levels and activity. During the first 24 hours of E-cadherin expression, myosin levels remain constant but di-phosphorylated myosin light chain (ppMLC) exhibits a ~3-fold increase (Fig. 2a, b). Untransfected cells (CT) or transfected cells lacking dexamethasone in their medium (labelled E-cad) show constant ppMLC levels (Fig. 2a), indicating that the observed response is not attributable to a secondary effect of dexamethasone addition or to transfection artifacts. Unlike in cohesive monolayers, expression of E-cadherin does not lead to an increase of tension in single cells (Fig. 2c). Consistently, monolayers show higher levels of ppMLC than single cells several hours after induction (Supplementary Fig. 5). Morever, abrogating cell-cell adhesions with EGTA (2 mM) prevents the builup of traction and tension, as well as the wetting transition (Supplementary Fig. 6, Supplementary Movie 5). Thus, we conclude that E-cadherin regulates myosin-generated contractility through a mechanism dependent on cell-cell junction formation. Notably, E-cadherin not only affects intercellular forces but also tractions, ultimately determining the global mechanics of the monolayer^22–25.

Fig. 2. Formation of E-cadherin junctions induces myosin phosphorylation, and hence the increase in tension that is responsible for monolayer dewetting.

a, Evolution of active myosin light chain (ppMLC) concentration. Control = Mock transfected cells; E-cad = cells transfected with E-cadherin under the dex-inducible promoter; DEX= treatment with dexamethasone. b, Evolution of total myosin light chain (MLC) concentration. c, Evolution of the average traction magnitude in single cells. d-f, Phase contrast images of a dewetting experiment (d), a cell island treated with blebbistatin (e) and a cell island treated with Y27632 once dewetting has started (t=46 h) (f). (g) Evolution of monolayer area for dewetting, dewetting inhibition and reversibility assays (green arrow indicates addition of Y27632). h-j, Immunostaining of E-cadherin (h), Beta-catenin (i) and merge images (j) at 6h and 12h after induction of E-cadherin expression (red square indicates the inset). k-m, Immunostaining of Paxillin (k), Actin (l) and merge images (m) at 6, 12 and 18 hours after induction of E-cadherin expression. Scale bars = 40 μm. Data are presented as mean ± s.e.m. Single cell tractions: n=24 cells. Dewetting inhibition: n=9 cell islands. Reversibility assay: n=16 cell islands.

Tissue tension induces the wetting transition

Next, we study the reorganization of adhesive and cytoskeletal structures in the monolayer. Upon induction of its expression, E-cadherin progressively accumulates at cell-cell contacts (Fig. 2h) and colocalizes with β-catenin (Fig. 2i, j), confirming the formation of adherens junctions. In parallel, the focal adhesion protein paxillin redistributes to the periphery of the monolayer (Fig. 2k), and supracellular stress fibers rich in active myosin massively form (Supplementary Fig. 7, Fig. 2l, m). These results suggest that dewetting is not directly caused by an increase in cell-cell adhesion, but rather by an increase in tension, which eventually causes the failure of cell-substrate adhesions. To test this hypothesis, we incubate the cells with blebbistatin (25 μM) to hinder the increase in contractility without impairing the over-expression of E-cadherin (Fig. 2d, e). This treatment reduces cellular forces (Supplementary Fig. 8) and delays dewetting (Fig. 2g; Supplementary Movie 6). Conversely, the addition of the ROCK inhibitor Y27632 (25 μM) during dewetting causes the monolayer to rewet the substrate (Fig. 2f, g; Supplementary Movie 6), thus demonstrating the active origin and reversibility of the transition. Together, these results show that the wetting transition results from a competition between active cellular forces, rather than simply between cell-cell and cell-substrate adhesion energies.

An active polar fluid model of tissue wetting

To understand how the wetting transition emerges from active cellular forces, we build upon a continuum mechanical model of epithelial spreading²⁶. Given the long time scales of the wetting/dewetting processes, we neglect the elastic response of the tissue^21,27–29, assuming that it has a purely viscous behaviour^26,30–35. Thus, taking a coarse-grained approach, the model describes the cell monolayer as a two-dimensional (2D) active polar fluid^36–39, namely in terms of a polarity field p(r,t) and a velocity field v(r,t) (Supplementary Note). Our 2D model does not aim at describing the out-of-plane flows and shape of the tissue, nor the dynamics of the contact angle. However, it allows us to predict the onset and initial dynamics of the wetting transition, which is the focus of our study.

The cell monolayer is unpolarized in the bulk and polarized at the edge (see Fig. 1g, h). Hence, we take a free energy for the polarity field that favours the unpolarized state p = 0 with a restoring coefficient a > 0, and that introduces a cost for polarity gradients, with K the Frank constant of nematic elasticity in the one-constant approximation⁴⁰:

$$F=\int \left[\frac{a}{2}{p}_{\alpha }{p}_{\alpha }+\frac{K}{2}\left({\partial }_{\alpha }{p}_{\beta }\right)\left({\partial }_{\alpha }{p}_{\beta }\right)\right]{\text{d}}^3\mathit{\text{r}}$$ (1)

We assume that the polarity field is set by flow-independent mechanisms, so that it follows a purely relaxational dynamics, and that it equilibrates fast compared to the spreading dynamics. Hence, δF/δp_α = 0, which yields

$${\text{L}}_c^2{\nabla }^2{p}_{\alpha }=p_{\alpha }$$ (2)

where $L_c=\sqrt{K/a}$ is the characteristic length with which the polarity decays from p_r(R) = 1 at the edge of the monolayer of radius R to p_r(0) = 0 at the center (red shade in Fig. 3a).

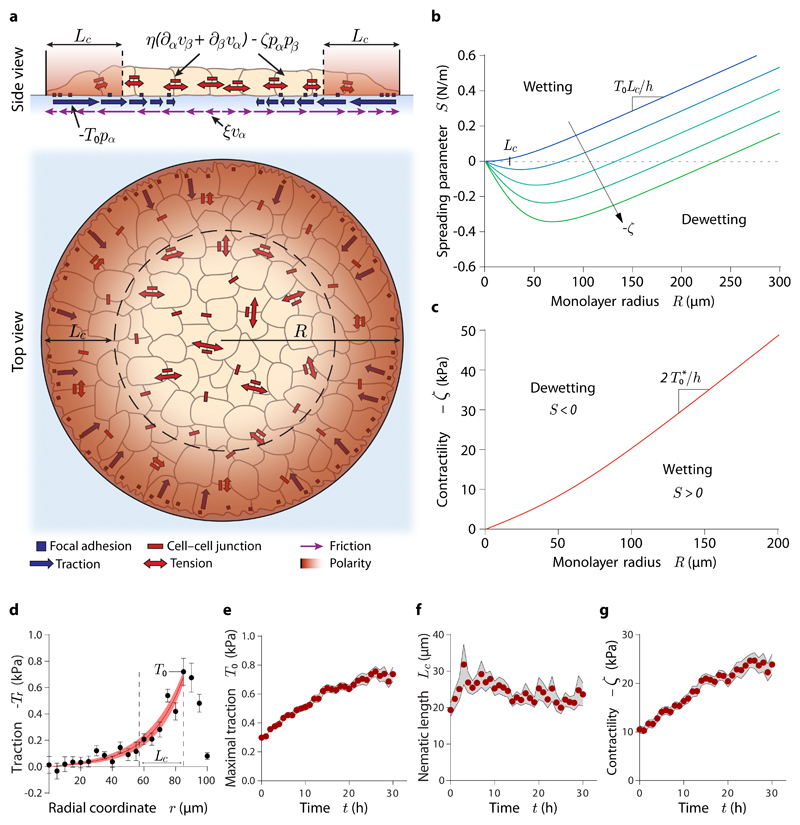
Fig. 3. Active polar fluid model of tissue wetting.

(a) Scheme of the model. (b) Spreading parameter of the monolayer as a function of its radius at increasing contractility (blue to green). The point at which S=0 indicates the critical radius for tissue wetting. (c) Predicted critical contractility for the wetting transition as a function of monolayer radius. (d) Representative example of a fit of the radial traction profile, from which we infer the evolution of the model parameters. (e-g) Evolution of the maximal traction (e), nematic length (f) and contractility (g) in islands of radius 100 μm. Data are presented as mean ± s.e.m. n=18 cell islands.

Then, force balance imposes

$${\partial }_{\beta }{\sigma }_{\alpha \beta }=T_{\alpha }$$ (3)

where σ_αβ and T_α are the components of the monolayer tension and traction stress fields, respectively. We relate these forces to the polarity and velocity fields via the following constitutive equations for a compressible active polar fluid⁴¹:

$${\sigma }_{\alpha \beta }^s=\frac{{\sigma }_{\alpha \beta }}{h}=\eta \left({\partial }_{\alpha }{\nu }_{\beta }+{\partial }_{\beta }{\nu }_{\alpha }\right)-\zeta p_{\alpha }{p}_{\beta }$$ (4)

$$f_{\alpha }=-\frac{T_{\alpha }}{h}=-\xi {\nu }_{\alpha }+{\zeta }_i{p}_{\alpha }$$ (5)

Here, h is the monolayer height, η is the monolayer viscosity, ζ is the active stress coefficient, ξ is the cell-substrate viscous friction coefficient, and ζ_i is the contact active force coefficient. These parameters are assumed to be time-dependent to account for the evolving mechanical properties of the monolayer. Note that ζ < 0 for contractile behaviour, and hence we call −ζ "contractility". In addition, we define the maximal traction stress exerted by polarized cells, T₀ = ζ_ih.

Assuming radial symmetry, neglecting cell-substrate viscous friction, and imposing stress-free boundary conditions, we analytically solve the model (Supplementary Note). Thus, we obtain the spreading velocity V = v_r(R) = dR/dt and, hence, the spreading parameter S = ηV⁸. In the experimentally relevant limit L_c ≪ R, it reads

$$S\approx \frac{T_0{L}_c}{h}R+\left(\zeta -\frac{3T_0{L}_c}{h}\right)\frac{L_c}{2}$$ (6)

Strikingly, the spreading parameter depends on the monolayer radius R, which entails the existence of a critical radius

$$R^{*}\approx \frac{1}{2}\left(3L_c-\frac{\zeta h}{T_0}\right)\sim \frac{1}{2}\frac{\zeta }{{\zeta }_i}$$ (7)

above which the tissue spreads (S > 0) driven by traction forces T₀ > 0 and below which it retracts (S < 0) driven by tissue contractility ζ < 0 (Fig. 3b). The competition between bulk and contact active forces defines a novel intrinsic lengthscale, L_p ≡ −ζ/ζ_i, of active polar fluids that naturally gives rise to the critical radius for the wetting transition, a striking property that has no counterpart in the classical wetting scenario.

Unlike for ordinary fluids, the wetting properties of tissues are not determined by local forces at the contact line but by the balance of forces across the entire monolayer, which results in the size-dependent wetting. Specifically, the internal, unpolarized region of the monolayer is subject to almost no external forces, and hence it is under a uniform tension set by traction forces at the polarized boundary layer. Because of the viscous rheology of the tissue, this uniform tension generates an outwards-directed flow with a linearly increasing velocity profile (Supplementary Fig. 9, 10; Supplementary Movie 7). Thus, larger monolayers exhibit a larger velocity right behind the boundary layer, which requires a higher contractility to induce monolayer dewetting (Fig. 3c; Supplementary Note). Finally, we suggest that the predicted non-monotonous flow profiles might induce the formation of 3D cell rims observed at the edge of epithelial monolayers^42,43.

Tissue wetting depends on tissue size and substrate properties

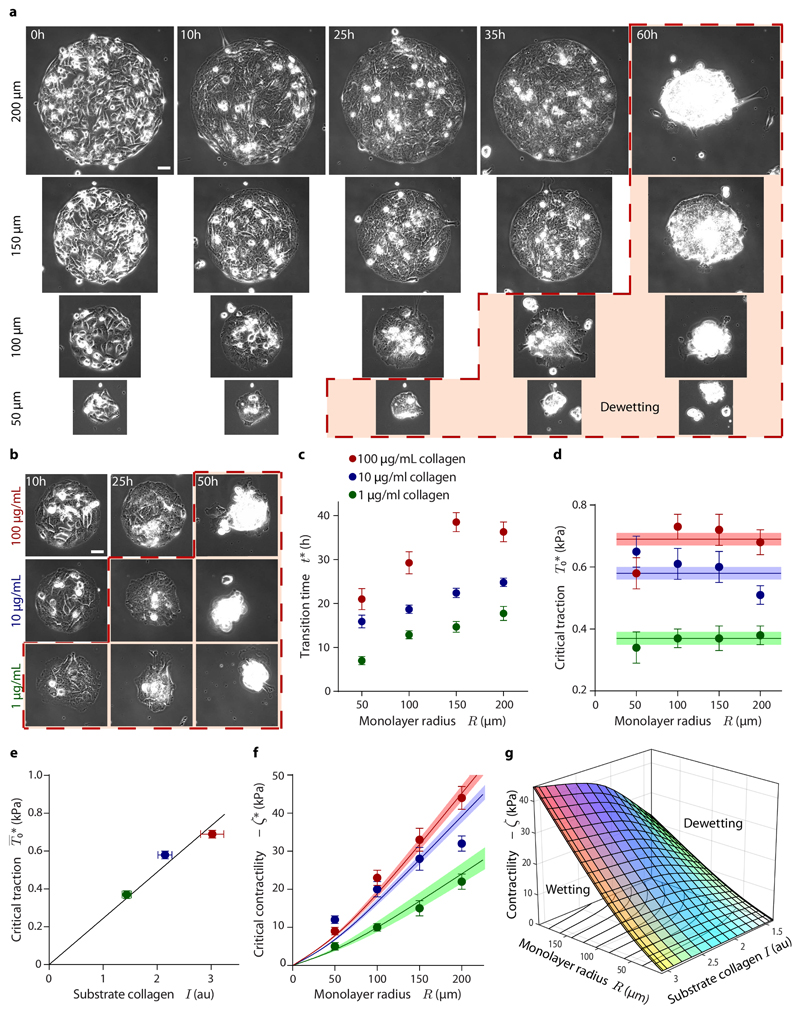
The model predicts that the wetting transition depends on monolayer size and tissue forces (Fig. 3b, c). To assess the role of these variables in the experiments, we generate circular islands of different radii (50, 100, 150 and 200 μm) on substrates of different ECM ligand densities (100, 10 or 1 μg/mL of collagen in the coating solution) (Fig. 4a, b). We also study cell monolayers on substrates of different rigidities (3, 12, and 30 kPa) (Supplementary Fig. 11). With the only exception of 30 kPa gels, on which dewetting does not occur in the time scale of the experiment, monolayers in all conditions feature a tension buildup phase and a dewetting phase (Supplementary Fig 11 b-d; Supplementary Fig. 12 a-k; Supplementary Movies 8, 9). However, the duration of each phase presents large quantitative differences (Fig. 4a, b; Supplementary Fig. 11a). To assess these differences, we implement a robust user-blind method to measure the time t* at which dewetting starts (Supplementary Fig. 13; see Materials and Methods). This analysis establishes that smaller monolayers dewet earlier than larger ones, and so do monolayers on softer and/or less densely coated substrates (Fig. 4c; Supplementary Fig. 11h). Therefore, tissue size as well as substrate adhesion and stiffness are key parameters in determining the wetting transition (Supplementary Movie 10). Of note, transition times span from 7 to 40h after E-cadherin induction and monolayers on stiff substrates do not dewet in the experimental time window (85h), which implies that changes in E-cadherin levels alone (Fig. 1c) cannot account for tissue dewetting.

Fig. 4. The wetting transition depends on substrate ligand density and monolayer radius.

a, Time evolution of epithelial monolayers of different initial radius. Larger monolayers dewet later. b, Time evolution of monolayers on substrates with different ligand density. Monolayers on substrates with higher ligand density dewet later. Islands are 100 μm in radius. The red dashed line and shade in (a) and (b) indicate dewetting. Scale bars = 40 μm. c, Wetting transition time as a function of monolayer radius and substrate ligand density. d, Critical traction as a function of monolayer radius and substrate ligand density. Horizontal lines show the average critical tractions at different collagen concentrations, with shadows indicating error margins. e, Average critical traction as a function of the relative amount of collagen on the substrate. f, Critical contractility as a function of monolayer radius and substrate ligand density. Lines show the critical contractility corresponding to the average critical traction for each collagen concentration, with shadows indicating error margins. g, Phase diagram of tissue wetting as a function of monolayer radius, contractility and substrate ligand density. The plotted surface corresponds to the observed wetting-dewetting transition. Data are presented as mean ± s.e.m. For islands on 100 μg/mL collagen: n=17 (200 μm radius), n=15 (150 μm radius), n=18 (100 μm radius), and n=11 (50 μm radius). For islands on 10 μg/mL collagen: n=17 (200 μm radius), n=15 (150 μm radius), n=17 (100 μm radius), and n=10 (50 μm radius). For islands on 1 μg/mL collagen: n=11 (200 μm radius), n=10 (150 μm radius), n=8 (100 μm radius), and n=8 (50 μm radius).

In our experiments, tissue forces increase with time until the wetting transition takes place. As a consequence, larger monolayers not only dewet later than smaller ones but also at higher tension (Supplementary Fig. 12a-c). This finding is consistent with our prediction (Fig. 3c) that larger monolayers require higher contractility to dewet or, equivalently, that for a given contractility only sufficiently large monolayers will wet. Thus, our experimental results do not directly establish but support the existence of a critical radius for tissue wetting. Future work should further assess the size dependence of the wetting transition using direct control of cell contractility.

To infer the values of model parameters, we fit the predicted traction profiles to the experimental data (Fig. 3a, see Materials and Methods). Hence, we obtain the time evolution of the model parameters T₀(t) and L_c(t). In addition, by imposing that the velocity of the tissue boundary vanishes during the wetting phase, we obtain the time evolution of the contractility −ζ(t) (Eq. 12, see Supplementary Note). The maximal traction T₀ and the contractility −ζ experience a ~3-fold increase, whereas the nematic length L_c remains constant (Fig. 3e-g). This analysis is performed for all experimental conditions (Supplementary Fig. 11e-g; Supplementary Fig. 14), from which we obtain the critical values of the parameters at the wetting transition, namely at time t*. The nematic length has a similar value of L_c ≈ 25 μm for all the experimental conditions (Supplementary Fig. 11f; Supplementary Fig. 14d-f), suggesting that, as considered in our model, it is an intrinsic property of the cell monolayer. Critical tractions $T_0^{*}=T_0\left(t^{*}\right)$ are largely independent of monolayer radius (Fig. 4d), but they increase with substrate rigidity (Supplementary Fig. 11i). Critical tractions also increase linearly with measured substrate ligand density (Fig. 4e; Supplementary Fig. 12l), suggesting that collagen is fully saturated with integrins at the wetting transition. The critical traction $T_0^{*}$ should thus be interpreted as the maximum force that cells can withstand before focal adhesions fail⁴⁴, and hence tissue spreading is not possible above it. Like critical tractions, the critical contractility −ζ* = −ζ(t*) increases with substrate rigidity (Supplementary Fig. 11j) and with ligand density (Fig. 4f). However, unlike critical tractions, the critical contractility also increases with monolayer radius (Fig. 4f). We summarize our results in a phase diagram for the tissue wetting transition as a function of contractility, substrate ligand density, and monolayer radius (Fig. 4g).

Active forces govern tissue morphology during dewetting

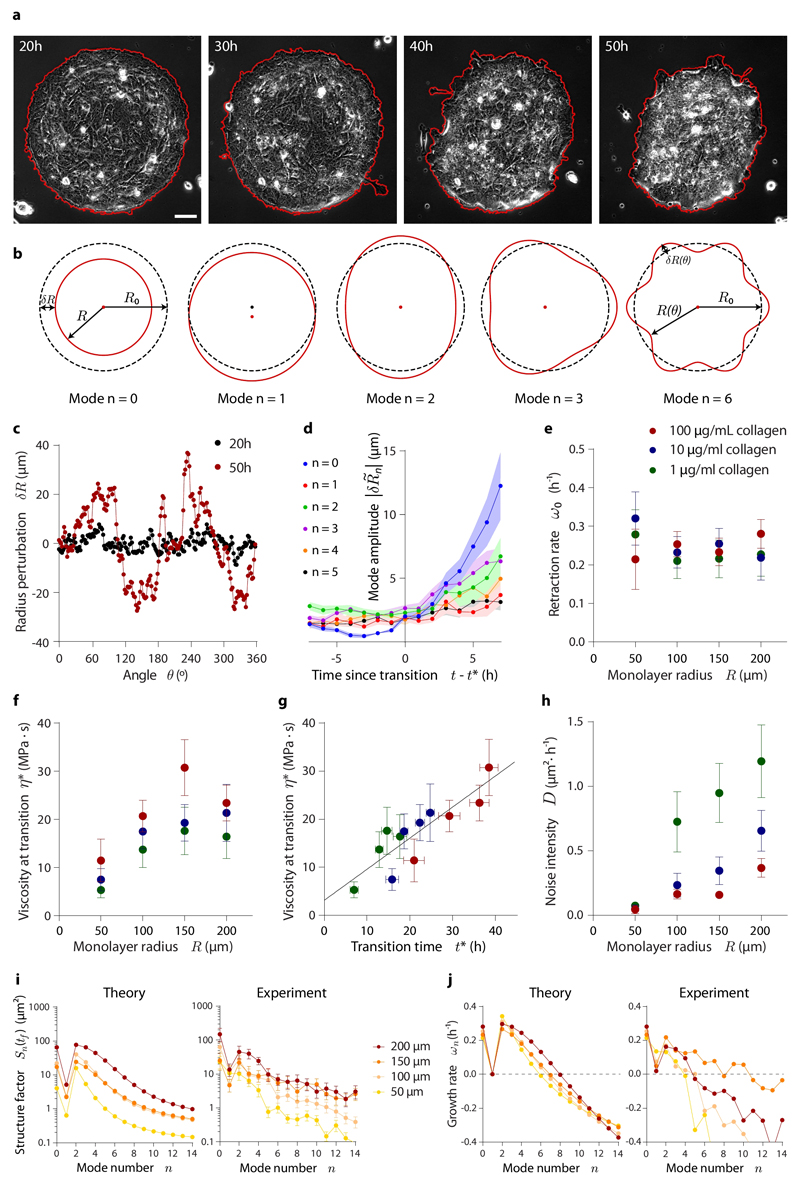
Our analysis thus far shows that an active polar fluid model captures the onset of dewetting as a function of the material properties and geometry of the tissue. Next, we focus on the early dynamics of tissue dewetting. Immediately after the onset of dewetting, the monolayer loses its circular symmetry, acquiring an elliptic-like shape before collapsing into a spheroidal cell aggregate (Fig. 5a; Supplementary Movie 11). This striking symmetry breaking is in stark contrast with the known isotropic dewetting of passive fluids^45–47. Although pinning of the contact line^46–48 may contribute to breaking the circular symmetry, the fact that monolayer retraction systematically tends to start at diametrically opposed points of the tissue boundary (Supplementary Movie 11) suggests the presence of a morphological instability of active origin. Indeed, from our active polar fluid model, we analytically predict a long-wavelength instability of monolayer shape during dewetting (Supplementary Note).

Fig. 5. Evolution of monolayer morphology during dewetting.

a, Phase contrast images of a 200 μm radius island that loses its circular symmetry during dewetting, as shown by its contour (red line). Scale bar = 30 μm. b, Illustration of the lowest shape perturbation modes of a circle. c, Initial and final radius perturbation profiles of the island shown in (a). Note that the final time point is well after the onset of dewetting, into the nonlinear regime of the instability not captured by our analysis. d, Evolution of the average amplitude of the lowest shape perturbation modes for 200 μm radius islands around the wetting-dewetting transition. e-h, Retraction rate, namely the growth rate of mode n=0 (e), monolayer viscosity at the wetting transition (f), and noise intensity of mode amplitudes (h) as a function of monolayer radius and substrate ligand density. Monolayer viscosity correlates with transition time (g). i-j, Structure factor of the monolayer boundary (i), and growth rate of shape perturbation modes (j) for islands of all different radii on substrates coated with 100 μg/mL of collagen. Theoretical predictions are shown along with average experimental data. Data are presented as mean ± s.e.m. Analyzed islands are the same as in Fig. 4, but some islands were discarded due to imperfections in the patterning introducing initial biases towards some perturbations modes (see Materials and Methods). For islands on 100 μg/mL collagen: n=12 (200 μm radius), n=9 (150 μm radius), n=16 (100 μm radius), and n=11 (50 μm radius). For islands on 10 μg/mL collagen: n=17 (200 μm radius), n=12 (150 μm radius), n=13 (100 μm radius), and n=6 (50 μm radius). For islands on 1 μg/mL collagen: n=9 (200 μm radius), n=10 (150 μm radius), n=8 (100 μm radius), and n=7 (50 μm radius).

To test the predictions, we characterize the evolution of tissue morphology by tracking the contour of the monolayer (Fig. 5a). The local radius perturbation δR(θ,t) = R(θ,t) − R₀ quantifies the loss of circular symmetry (Fig. 5c), and its Fourier transform dissects the contribution of each perturbation mode to the overall shape of the monolayer (Fig. 5b). Consistent with the predicted instability, the amplitudes $\left|\delta {\tilde{R}}_n\right|$ of the long-wavelength modes increase with time upon the onset of dewetting (Fig. 5d). Their predicted growth rates ω_n depend on a single yet-unmeasured parameter, the monolayer viscosity at the wetting transition, η*. Its value can be inferred from the retraction rate of the monolayer, ω₀, which we experimentally measure by fitting the exponential growth of the zeroth perturbation mode: $\delta {\tilde{R}}_0(t)=\delta {\tilde{R}}_0(t^{*})e^{{\omega }_0(t-t^{*})}$ (Fig. 5e; Supplementary Fig. 15). Comparing with the theoretical prediction (Supplementary Note)

$${\omega }_{\text{0}}\approx \frac{{{\rm T}}_{\text{0}}{L}_c}{\text{2}\eta h}$$ (8)

we obtain viscosities that increase with monolayer radius and substrate ligand density, spanning from 3 to 30 MPa·s (Fig. 5f). The tendency exhibited by the viscosity is similar to that of transition times (Fig. 4c). In fact, these two quantities linearly correlate (Fig. 5g), which suggests that monolayer viscosity increases with time in our experiment, likely due to a combination of cell-cell junction formation^26,49, increasing contractility⁵⁰, and increasing cell density⁴⁹.

Once the theoretical growth rates ω_n are known, we can predict the amplitudes of the different shape modes. Assuming that monolayer shape fluctuations are fast compared to the dewetting dynamics, we compute the structure factor of the monolayer boundary

$$S_n\left(t\right)=\langle {\left|\delta {\tilde{R}}_n\left(t\right)\right|}^2\rangle =\frac{D}{{\omega }_n}\left[e^{2{\omega }_n\left(t-t^{*}\right)}-1\right]$$ (9)

where D is the noise intensity of mode amplitudes (Supplementary Note). By fitting this prediction to the experimental data (Fig. 5i, Supplementary Fig. 16a), we infer the value of D, which increases with tissue size but decreases with substrate ligand density (Fig. 5h). This behavior is consistent with active shape fluctuations driven by the total traction force in the tissue, which scales linearly with monolayer radius (see Eq. 6), and damped by cell-substrate friction, which increases with substrate ligand density. Finally, we obtain experimental growth rates from the structure factors (Fig. 5j; Supplementary Fig. 16b; Supplementary Note). Despite their expected variability, our experimental results agree with the predictions, confirming that the growth of shape-changing perturbations, especially of mode n = 2, is responsible for the elliptic-like shape of the monolayer (Fig. 5i, j). Overall, these results show that active forces and shape fluctuations determine the morphological evolution during monolayer dewetting.

Discussion and outlook

Our results illustrate how E-cadherin adhesion regulates tissue mechanical properties and forces and, in turn, how these forces determine tissue shape, dynamics, fluctuations and dimensionality as a function of tissue size, contractility, substrate stiffness, and cell-cell and cell-substrate adhesion. In vivo, transitions in tissue morphology are characterized by changes in cell contractility^51,52, cell adhesion^53,54 and ECM composition^55,56. It is appealing to think that these changes translate into different wetting states. For example, this could explain increased tumor invasiveness when contractility decreases or critical traction increases due to an enhanced cell-substrate adhesion, ECM deposition or ECM stiffening. This scenario is supported by previous experiments associating E-cadherin-dependent epithelial retraction and suppression of tumor invasion in vivo⁵⁷. Furthermore, tumor growth per se implies an increase in tissue radius, possibly leading to a dewetting-wetting transition even if contractility and critical traction remain unaltered. In this line, the nucleation of a spreading monolayer from a growing cell aggregate has been previously reported⁴³.

Our analysis unveils fundamental features of tissue wetting that differ qualitatively from the classical wetting paradigm. We account for these differences by developing a theoretical framework for active wetting, which explicitly relates the wetting properties of tissues to active cellular forces. This framework, based on active gel theory, captures the mechanics of the wetting transition as well as the dynamics of monolayer morphology during the early stages of tissue dewetting. Furthermore, it allows the quantification of active stresses, viscosity, and active fluctuations in the tissue. In light of these results, we propose that tissue spreading can be understood as the wetting process of an active polar fluid, constituting the defining example of the general phenomenon of active wetting.

Methods

MDA-MB-231 cell culture

MDA-MB-231 cells were grown on Dulbecco Modified Eagle Medium (DMEM) media supplemented with 10% fetal bovine serum (FBS), 100 U mL^-1 penicillin and 100 μg mL^-1 streptomycin.

E-cadherin induction

Right before starting an experiment (t₀), normal cell media was replaced by media containing 10 nM of dexamethasone to induce the expression of E-cadherin.

Polyacrylamide gel substrate

Polyacrylamide (PAA) gels of 3, 12 and 30 kPa (Young modulus) were produced as described previously²³. Briefly, a solution containing 5.5 % acrylamide, 0.09 % bis-acrylamide (3 kPa); 7.5 % acrylamide, 0.16 % bis-acrylamide (12 kPa); or 12 % acrylamide, 0.15 % bis-acrylamide (30 kPa); plus 0.5% ammonium persulphate, 0.05% tetramethylethylenediamine and 0.64% of 200-nm-diameter red fluorescent carboxylate-modified beads was prepared and allowed to polymerize. PAA gel surface was then incubated with a solution of 2 mg/mL Sulpho-SANPAH under UV light for 5 minutes (wavelength of 365 nm at a distance of 5 cm). After that, 3 washes of 3 minutes each were performed to remove the excess of Sulfo-SANPAH. At this point, the gel was ready to add the ECM protein.

PDMS stencils

Polydimethylsiloxane (PDMS) membranes were fabricated as explained previously⁵⁸. Briefly, SU8-50 masters containing arrays of circles of different sizes (200 μm, 150 μm, 100 μm and 50 μm radius) were raised using conventional photolithography. Importantly, all the different sizes were included in the same array to allow having different conditions in the same gel, therefore decreasing experimental variability. Uncured PDMS was spin coated on top of the masters to a thickness lower than the SU8 features (35 μm) and cured at 80 °C for 2 hours. A thick border of PDMS was added for handling purposes. Finally, PDMS stencils were peeled off and stored in 96% ethanol at 4 °C until use.

Cell patterning on PAA gels

The PDMS stencils were incubated with a solution of pluronic acid F127 2% for one hour. After that, they were washed twice in Phosphate-Buffered Saline (PBS) and let dry for 20 minutes. For confined monolayers, the stencils were carefully placed on top of the PAA gels. Then a solution of rat tail type I collagen at the desired concentration was added on top of the PDMS openings and left at 4°C overnight. The day after, the collagen solution was washed and the PDMS stencils were removed. The PAA gels were washed twice with PBS. For cell seeding, the PBS was removed and a 75 μL drop containing ~500,000 cells was placed on top of the PAA gels. After 30 minutes, the unattached cells were washed away and more medium was added. Cells were allowed to spread for 3 hours before starting the experiment. In the case of unconfined monolayers, the PDMS stencil was placed on top of gels already coated with collagen. Cells fell in the openings and attached to the gel for 8h before releasing the confinement.

Time-lapse microscopy

Multidimensional acquisitions were performed on an automatic inverted microscope (Nikon Eclipse Ti) using a 20X objective (NA 0,75, air) for TFM experiments. MetaMorph (Universal Imaging) was used to image every hour during the duration of the experiment. Around 50 cell islands were imaged in parallel using a motorized stage. In the case of the 3D reconstruction (Supplementary Fig. 4, Supplementary Movie 4) and nuclei position analysis (Supplementary Fig. 10, Supplementary Movie 7), multidimensional acquisitions were performed on a Nikon microscope with a spinning disk confocal unit (CSU-W1, Yokogawa) using a 40X objective (NA 0.75, air) and a 20X (NA 0.75, air) respectively. IQ3 (Andor) software was used to image every 15 minutes with a Z-step of 1 μm. All microscopes were equipped with thermal, CO₂, and humidity control.

Traction force microscopy

Traction forces were computed using Fourier-transform traction microscopy with finite gel thickness from a gel displacements field¹⁷. Gel displacements were obtained using a custom-made particle image velocimetry (PIV). In brief, the fluorescent beads in any experimental timepoint were compared to a reference image obtained after cell trypsinization at the end of the experiment.

Monolayer stress microscopy

Monolayer tension was obtained using Monolayer Stress Microscopy as described previously^19,59. Force balance with tractions yields the tension field in the monolayer, as a second rank symmetric tensor. We computed the average normal stress as the mean of the xx and yy components. In this two dimensional approximation, tension has units of surface tension, namely N/m.

Western blot

~500,000 cells were seeded on 12 kPa (Young Modulus) PAA gels (for MLC and ppMLC) or plastic (for E-cadherin). After 3 hours, E-cadherin expression was induced and cells were sequentially lysed with Laemli 1x at the desired times post induction. Samples were then mechanically disaggregated using a syringe and centrifuged at 20000 x g for 15 minutes. Samples were heated at 95°C for 5 minutes and loaded on polyacrylamide gels (Any kd, Bio-rad) for electrophoresis. After that, proteins were transferred to a nitrocellulose membrane (Whatman, GE Healthcare Life Sciences) overnight. Membranes were blocked with 5% dry milk-Tris buffer saline-0.2% Tween, incubated with primary antibodies overnight at 4°C and, later, incubated with horseradish-peroxidase-coupled secondary antibodies for 1 hour at room temperature. Bands were revealed using LimiLight kit (Roche), imaged with ImageQuant LAS 4000 and quantified using ImageJ software. Tubulin was used as an endogenous control for normalization.

Immunostaining

MDA-MB-231 cells were washed with PBS, fixed with 4% paraformaldehyde (PFA) for 10 minutes and permeabilized in 0,1% Triton X-100 for 5 minutes. After washing, cells were blocked in 10% FBS for 1 hour and incubated with primary antibodies for 3 hours. Cells were then washed and incubated with the appropriate secondary antibody for 1 hour. After washing, cells were mounted in Mowiol reagent. Images were acquired using a Nikon microscope with a spinning disk confocal unit (CSU-W1, Yokogawa) using a 60X objective (NA 1.40, oil).

Antibodies

The primary antibodies used were: anti-E-cadherin monoclonal antibody (clone 36, BD Transduction Laboratories, no. 610181), anti-α-tubulin (clone B-5-1-2, Sigma-Aldrich, no. T5168), anti-β-catenin (clone 14, BD Transduction Laboratories, no. 610154), anti-paxillin (clone 349, BD Transduction Laboratories, no. 610051), anti-rat collagen type I (EMD Millipore, AB755P), anti-ppMLC (Cell Signaling Technology, #3674), and anti-MLC (Cell Signaling Technology, #3672). The secondary antibodies were: peroxidase-conjugated anti-mouse IgG (Jackson Immuno Research, no. 715-035-151) and peroxidase-conjugated anti-rabbit IgG (Jackson Immuno Research, no. 211-032-171) for western blot and Alexa Fluor 488 anti-rabbit (Invitrogen, Molecular Probes, no. A-21206), Alexa Fluor 488 anti-mouse (Invitrogen, Molecular Probes, no. A-11029), Alexa Fluor 555 anti-mouse (Invitrogen, Molecular Probes, no. A-28180), Alexa Fluor 640 anti-rabbit (Invitrogen, Molecular Probes, no. A-21245), Alexa Fluor 405 anti-mouse (Invitrogen, Molecular Probes, no. A-31553) for immunostaining. For western blot, anti-E-cadherin was diluted 1:2,000 and anti-α-Tubulin was diluted 1:5,000; anti-ppMLC was diluted 1:500; anti-MLC was diluted 1:200; secondary antibody was diluted 1:5,000. For immunofluorescence, primary antibodies were diluted 1:200 and secondary antibodies were diluted 1:400. F-actin was labelled with Phalloidin-TRITC (Sigma-Aldrich, no P1951) diluted 1:2,000.

Cell island segmentation

At every timepoint, cell islands were semi-automatically segmented using custom-made Matlab software. First, a preliminary mask of the island contour was performed automatically based on changes in contrast of phase contrast images. The errors in the automatic segmentation were manually corrected.

Immunostaining fluorescence intensity quantification

Both for ppMLC and collagen intensity quantifications, the region of interest (ROI) was segmented as explained above. The mean or median intensy in the ROI was calculated and the background intensity was substracted to every individual measurement.

Kymography

We obtained the radial coordinates of each pixel of the cell island masks by calculating its shortest distance to the edge. The radial direction of the edge was calculated and expanded to the inner pixels of the mask to decompose traction vectors in radial and tangential components. Finally, tractions or tensions were averaged according to their distance to the edge at every timepoint to build spatiotemporal kymographs.

Wetting transition definition

We defined an objective criterion to detect the wetting transition in different experimental conditions. First, cell islands are automatically segmented based on changes in contrast of the phase contrast images, followed by a manual correction of the errors in segmentation. Every cell island mask is divided in a specific number of circular sectors based on its initial radius (24 for 200 µm radius, 18 for 150 µm, 12 for 100 µm, and 6 for 50 µm). Using this each strategy sector has an approximately equal arc length at time 0 (~ 52 µm). The average radius of every sector is computed over time, obtaining a characteristic curve with a roughly constant value at the first time points that suddenly drops upon the onset of dewetting (Supplementary Fig. 13). This curve is fitted with a negative sigmoidal function

$$R\left(t\right)=a+\frac{b}{1+\text{exp}\left(\left(d+\text{ln}\left(2-\sqrt{3}\right)\right)t/c+d\right)}$$ (10)

using the non-linear least squares method. The transition time for every segment is defined as the time point at which the fitted function reaches the 95% of its initial value (open circles in Supplementary Fig. 13b to C). For the whole island, we define the onset of dewetting as the moment at which one sixth of the circular sectors are dewetting according to the criterion above.

Collagen amount quantification

Rat tail type I collagen immunostainings were performed on patterns made on polyacrylamide gels coated with three different collagen concentrations (100 μg/mL, 10 μg/mL and 1 μg/mL). The patterns were automatically segmented. Their mean intensity was calculated and corrected by subtracting the mean background intensity.

Model parameters fit

We fit the predicted radial traction force profile

$$T_r\left(r\right)=-T_{0}p\left(r\right)=-T_0\frac{I_1\left(r/L_c\right)}{I_1\left(R/L_c\right)}$$ (11)

where I₁ is the modified Bessel function of the first kind and first order (Supplementary Note), to the experimentally measured profiles at different times, as represented in kymographs as in Supplementary Fig. 3a. At each time point, the fitting algorithm searches for the radial position of the maximum of the experimental traction force profile, which sets the monolayer radius R(t). Then, the theoretical prediction is fit up to this point, discarding the outer region where the traction force progressively vanishes (Fig. 3d). Traction forces measured in this outer region may arise from poorly attached protrusions or be an artefact due to the long-range propagation of deformations in the elastic substrate used for traction force microscopy. These effects are not described by the model. From the fits, we obtain the time evolution of the maximal traction stress T₀(t) and the nematic length L_c(t). Finally, the contractility −ζ(t) during the wetting phase is given by (Supplementary Note)

$$-\zeta =-2T_0\frac{L_c}{h}\frac{I_2\left(R/L_c\right)}{I_1\left(R/L_c\right)-I_0\left(R/L_c\right)\left[\frac{I_0\left(R/L_c\right)}{I_1\left(R/L_c\right)}-\frac{2L_c}{R}\right]}$$ (12)

where I_n are the modified Bessel functions of the first kind and order n. To check the values of the contractility given by Eq. (12), we extracted the contractility via two other methods. First, this parameter can be obtained from fits of the radial tension profile in the monolayer (Supplementary Note):

$$\begin{array}{l}{\sigma }_{rr}\left(r\right)=T_0{L}_c\left[\frac{I_0^2\left(R/L_c\right)}{I_1^2\left(R/L_c\right)}-\frac{L_c}{R}\right]-T_0{L}_c\frac{I_0\left(r/L_c\right)}{I_1\left(R/L_c\right)}\\ \\ \\ +\frac{\zeta h}{2}\left[1+\frac{L_c}{R}\frac{I_0\left(R/L_c\right)}{I_1\left(R/L_c\right)}-\frac{I_0^2\left(R/L_c\right)}{I_1^2\left(R/L_c\right)}\right]\\ +\frac{\zeta h}{\text{2}}\frac{1}{I_1^2\left(R/L_c\right)}\left[\frac{1}{2}{I}_0\left(r/L_c\right)\left[I_0\left(r/L_c\right)+I_2\left(r/L_c\right)\right]-I_1^2\left(r/L_c\right)\right]\end{array}$$ (13)

In the fits of the tension kymographs, the monolayer radius R(t) is determined from the radial coordinate at which the stress vanishes, σ_rr(R) = 0. Second, the contractility can also be obtained from the average radial tension

$$\begin{array}{l}\sigma =\frac{1}{\pi R^2}{\displaystyle {\int }_0^{2\pi }d\theta {\displaystyle {\int }_0^R{\sigma }_{rr}r\psi dr}}\\ =T_0{L}_c\left[\frac{I_0\left(R/L_c\right)}{I_1\left(R/L_c\right)}-3\frac{L_c}{R}+2\frac{L_c^2}{R^2}\frac{I_0\left(R/L_c\right)I_1\left(R/L_c\right)-1}{I_1^2\left(R/L_c\right)}\right]\\ -\frac{\zeta h}{2}\left[1-\frac{I_0^2\left(R/L_c\right)}{I_1^2\left(R/L_c\right)}+\frac{L_c}{R}\frac{I_0\left(R/L_c\right)}{I_1\left(R/L_c\right)}+\frac{L_c^2}{R^2}\frac{I_0^2\left(R/L_c\right)-1}{I_1^2\left(R/L_c\right)}\right]\end{array}$$ (14)

All three methods yield fully compatible results. Note that, at the lowest order in the small dimensionless parameter L_c/R, the average tension is completely given by traction forces: σ = T₀L_c + 𝒪(L_c/R). Therefore, the contractility only contributes to the average stress at the first-order level in L_c/R, which explains the large values of this parameter compared to the stress in the monolayer.

Monolayer boundary Fourier transform

The local monolayer radius as function of the polar angle, R(θ), was computed via the same method than for wetting-dewetting transition definition. However, in this case, the number of segments was systematically multiplied by 8 to increase the spatial resolution. We obtained the radius perturbations as δR(θ) = R(θ) − R₀, where R₀ is the average initial radius. This function was Fourier-transformed to obtain the amplitude of every Fourier mode. Two Fourier modes were calculated in a different way. To obtain the evolution of mode n = 0, we systematically subtracted the mean radius of the island during the last 7 time points before wetting-dewetting transition from the current average radius. Respectively, mode n = 1 is the direct measure of the centroid motion. To average different replicates, we referred all times to the transition time of each island, namely that we used shifted times t − t*. Theoretical predictions for the growth rates are only valid in a linear regime of the instability, which is characterized by small amplitude perturbations with respect to the wavelength of the specific mode. We consider that a mode is in its linear regime when its amplitude does not exceed 10% of its wavelength. Once this threshold is reached, the mode is excluded from the analysis. Furthermore, islands with high mode amplitudes before dewetting (a specific mode whose amplitude exceeds 6 times the mean amplitude of all the other modes) were also excluded to avoid biases coming from irregularities in the patterning.

Retraction rate calculation

The growth rate of the perturbation mode n = 0 is obtained by fitting the exponential function $\delta {\tilde{R}}_0(t)=\delta {\tilde{R}}_0(t^{*})e^{{\omega }_0(t-t^{*})}$ to the evolution of its amplitude, from the last timepoint before the transition to 7 hours after the onset of dewetting. By choosing this time span, we ensured to have enough time points to perform reliable fits (Supplementary Fig. 16) while still having most of the perturbation modes in almost all monolayers within the linear regime of the instability. The error of ω₀ is defined as the 95% confidence interval.