Spatiotemporal dynamics of synthetic microbial consortia in microfluidic devices

Abstract

Synthetic microbial consortia consist of two or more engineered strains that grow together and share the same resources. When intercellular signaling pathways are included in the engineered strains, close proximity of the microbes can generate complex dynamic behaviors that are difficult to obtain using a single strain. However, when a consortium is not cultured in a well-mixed environment the constituent strains passively compete for space as they grow and divide, complicating cell-cell signaling. Here, we explore the temporal dynamics of the spatial distribution of consortia co-cultured in microfluidic devices. To do this, we grew two different strains of Escherichia coli in microfluidic devices with cell-trapping regions (traps) of several different designs. We found that the size of the traps is a critical determinant of spatiotemporal dynamics. In small traps, cells can easily signal one another but the relative proportion of each strain within the trap can fluctuate wildly. In large traps, the relative ratio of strains is stabilized, but intercellular signaling can be hindered by distances between cells. This presents a trade-off between the trap size and the effectiveness of intercellular signaling, which can be mitigated by increasing the initial seeding of cells in larger traps. We also built a mathematical model, which suggests that increasing the number of seed cells can also increase the strain ratio variability due to an increased number of strain interfaces in the trap. These results help elucidate the complex behaviors of synthetic microbial consortia in microfluidic traps and provide a means of analysis to help remedy the spatial heterogeneity inherent to different trap types.

Graphical Abstract

Synthetic gene circuits in bacteria have traditionally been constructed and characterized in single strains. ^1–4 In nature, however, microorganisms are commonly found in consortia of multiple interacting strains and species. This allows for population-level phenotypes that improve survival in environments that fluctuate across time and space. ^5–7 Synthetic biologists have begun designing gene circuits distributed across two or more communicating microorganisms to create synthetic microbial consortia that exhibit phenomena difficult to engineer into single strains. ^8–12 Synthetic microbial consortia allow complex pathways to be split among specialized strains, reducing the metabolic burden on each cell. ¹³ Optimizing each step of the divided pathway in separate strains is simpler than optimizing an entire pathway within a single cell. ¹⁴ In addition, synthetic consortia allow for the study of population-level phenotypes dependent upon intercellular and inter-strain communication. ⁵

Natural ecosystems of microorganisms depend significantly on their environment. This includes the effect of other organisms, abiotic factors, and the overall size of the ecosystem. Likewise, engineered ecosystems such as synthetic microbial consortia will also be impacted by these factors. We can control what other organisms and abiotic factors are included, but the overall size of a consortium will be determined by its growth environment. Here, we use microfluidic devices in order to systematically vary the environment of closely-packed microbial consortia in 2D experimental settings.

Microfluidic devices have long been used for assessing gene expression and growth of engineered bacteria as they allow for continuous growth and visualization over time. ^15–18 However, complications can arise when multiple strains are grown together within a microfluidic device. For instance, spatiotemporal strain ratio fluctuations can affect the relative amounts of intercellular signaling molecules and complicate the analysis of intercellular interactions. ^11,19 Another complication arises in microfluidic devices with large cell-trapping regions: Initial seeding and subsequent growth patterns can lead to large areas containing just a single strain. Because intercellular signaling molecules have a limited diffusion range in the trap and can be lost to open boundaries, cells in one portion of the trap may not communicate directly with cells in another. Therefore, if the strains within a consortium are not well mixed, signaling between the strains will occur only near their interfaces. However, in small traps, even well-mixed populations are subject to severe strain ratio instabilities, which can lead to the complete loss of one or more strains within a consortium.

In this study, we compared two common microfluidic devices (Fig. 1) by characterizing spatiotemporal population and signaling dynamics in consortia of two nearly identical engineered strains of E. coli. We found that temporal fluctuations of strain ratio in small trap experiments could become severe, whereas large traps stabilized the ratios. However, increased spatial separation of strains in large traps could limit intercellular signaling. We demonstrate how to address this problem by using a mathematical model that considers the expected spatial proximity of the two strains in one of the devices based on the number of cells that are initially seeded. On average, one can increase the number of cells seeded to ensure that cells of each type are close enough to exchange signaling molecules. However, our mathematical modeling suggests that increasing the number of seed cells may also increase strain ratio variability. Here, we find a balance of cell trapping area and number of seed cells to achieve the desired environment for strain stability and inter-strain signaling. Our results demonstrate the value of microfluidic devices as a tool for studying the dynamics of synthetic microbial consortia, despite the many intricacies they present.

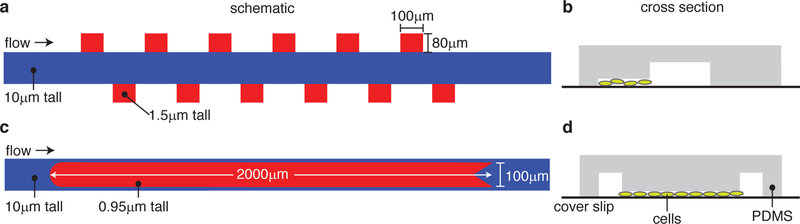
Figure 1: Designs of the microfluidic devices.

(a) Schematic of the “hallway” device. The blue region is the tall flow channel and the red regions are the shorter cell-trapping regions. (b) Cross section of the hallway trap device shown with cells in the trapping region. (cd) Same as (ab), but for the “open” device. See text for more details.

Results and Discussion

We examined synthetic microbial consortia in microfluidic devices with two distinct types of cell traps, as shown in Fig. 1 (also see Fig. S5). The “hallway” device ¹¹ contains several traps (80 µm × 100 µm) on either side of a media flow channel (Fig. 1a,b). Variations of the hallway device have been used in several studies to increase experimental replicates or to allow for multiple communicating populations. ^11,20,21 Because the traps in this device are small compared to the mean diffusion distance of HSL signaling molecules in one cell doubling period (a 20 min doubling time and HSL diffusion rate of 3 × 10⁴ µm²/ min sets a diffusion distance scale of ≈ 800 µm compared to the trap scale of 100 µm)^22,23 and because there are three closed walls (reflecting boundaries), cell-cell signaling molecules can quickly diffuse throughout the chamber with little to no spatial gradients (Fig. S4).

However, due to small effective trap area, each hallway trap can only contain a small population, ¹¹ which, as we will see, can amplify the severity of temporal strain ratio fluctuations. In contrast, the “open” device (no closed walls) has a single, longer trap ( 100 µm × 2000 µm) that is centered within the main flow channel (Fig. 1c,d). Similar trap configurations have been used to assess the spatiotemporal dynamics of large populations. ²⁰ Due to its larger trapping area, this trap can sustain a much larger population than an individual trap in the hallway device. However, the spatial degradation of cell-cell signaling becomes important: Diffusing molecules have a limited range compared to the spatial extent of the trap (see Fig. 6). Note that the two types of traps have different trap heights to allow for proper cell seeding in each design (see Methods). ²⁰

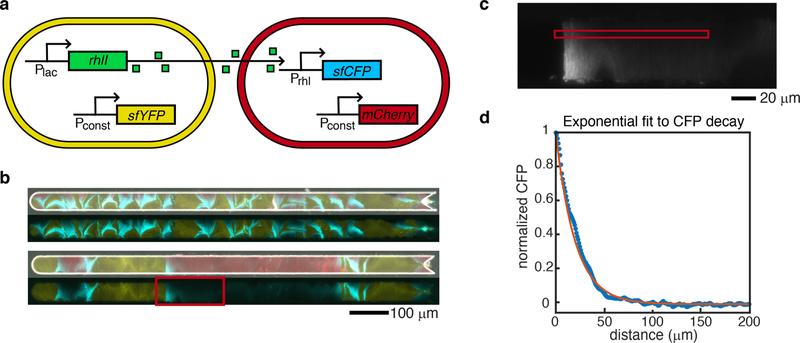
Figure 6: Sender-receiver consortium and signaling depth measurement.

(a) Schematic of the sender and receiver strain gene circuits. Genes shown are on plasmids. (b) In the top pair of images the larger number of thinner, interspersed bands results in sufficient intermingling of strains so that all receiver cells respond to QS molecules. The smaller number of thicker single-strain bands in the lower image pair leaves some receiver cells at a large distance from the sender strain. As a result, CFP signal decreases to background levels as the distance from a sender band increases. Top images of each pair are merged phase contrast, and yellow, red, and cyan fluorescent images from the microscope. Bottom images of each pair are only yellow and cyan fluorescent images merged to more clearly visualize CFP decay. (c) We selected a subset of the cells in the experimental image in (b) to determine the decay of CFP signal with distance from the sender strain. We averaged the signal in the red square over columns, and in a series of ten frames forward from the shown image, to generate the experimental CFP signal. Transition boundary from left (sender cells) to right (receiver cells) was automatically detected and set to the x-axis (distance) origin. (d) After threshold detection for receiver cells, response data was normalized and fit to an exponential decay with spatial decay parameter ξ. Experimental data shown as blue stars, fit curve in orange. Resulting fit: ξ =20 µm.

Strain Ratio Stability

We first studied how the growth of strains differs between the two trap designs. The open trap has a larger cell-trapping area that can hold approximately 70,000 cells, has all open wall boundaries, and is located within the media flow channel. The hallway traps can hold approximatley 3,000 cells each, contain three closed walls, and are located off to the side of the media ow channel.

To compare population growth in these two traps, we used two non-communicating strains of E. coli, each expressing a different fluorescent protein for identification; we refer to these as the “control” strains. These strains are the same BW25113 derivative transformed with a plasmid that constitutively expresses the gene encoding either yellow or cyan fluorescent protein (sfYFP or sfCFP). Because sfYFP and sfCFP differ by only a few point mutations, ^24,25 the growth rate, size, shape, and biofilm production of the two strains were identical (Fig. S6), and neither had a fitness advantage over the other in the microfluidic device. We mixed cultures of both strains and seeded many cells into the traps to increase the probability of simultaneously capturing both strains. We then mounted the microfluidic device onto an inverted microscope and monitored phase contrast, yellow fluorescence and cyan fluorescence channels every 6 minutes for up to 20 hours. To quantify the ratio of the strains as a function of time, we measured the total number of intracellular pixels containing either yellow or cyan fluorescence within a boolean mask computed for each frame for each image acquisition frame over time (see Methods).

As shown in Fig. 2a,b, strain ratios exhibited large temporal fluctuations when grown in the hallway trap. Boyer et al. ²⁶ demonstrated that a growing colony of bacterial cells in a three-walled trap is prone to a buckling instability when cells at the back of the trap become aligned with the back wall (due to the finite width of the back wall and the continuous axial growth of the rod-shaped bacterial cells, the cells buckle from the large axial stress that results). In our two-strain experiments, the buckling instability can translate directly to a strain ratio instability because cells at or near the closed back trap wall serve as progenitor cells for the entire trap population: Cells continuously grow and expand while pushing each other generally in random directions in bulk. However, only the open end of the trap is available for cells to exit the trap. Thus, the local strain ratio near the back of the trap effectively determines the strain ratio in the entire trap.

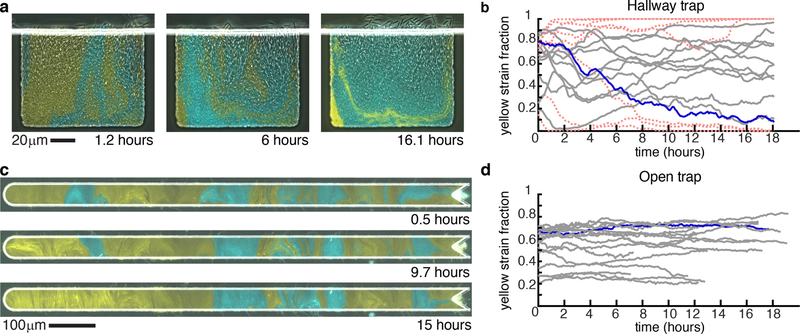
Figure 2: Strain fraction time series.

(a) Images of the two control strains grown in a hallway trap over time. (b) The fraction of the yellow strain in all experiments performed in the hallway trap with the experiment from (a) in blue. Red dotted lines signify traps that lose one strain completely. (c) Images of the two control strains grown in the open trap over time. (d) The fraction of the yellow strain in all experiments performed in the open trap with the experiment from (c) in blue. Time 0 was defined as the first image at which the entire trap was filled with cells.

We grew the same control consortium in the open trap and observed more stable strain ratio trajectories than in the hallway trap (Fig. 2c,d). We found that the range of fluctuations of the yellow strain fraction differed significantly between open and hallway trap experiments (Fig. 3a), (p < 0:01). In contrast to the hallway device, the open device has no closed walls and allows cells to grow in every direction, resulting in decreased axial growth pressure ²⁷ and an emergent alignment of the cells that is sustained in the bulk of the colony. ^27–29 When we consider the aspect ratio of the open device (see Fig. 1), cells will tend to form vertical columns, with the “mother” cells at or near the middle of a column establishing the strain column identity. ³⁰ The lateral movement of “mother” cells in the trap (i.e. those near the vertical center) has the highest impact on strain ratio: If a cell of one strain laterally displaces a cell of a second strain, the invading cell will become a “mother” cell and thereby change the population balance by eventually occupying the entire column. Such behavior is stochastic and may include lateral flux of varied intensity in both directions. We formulated a mathematical model to examine this mechanism with simulations of varied open-walled trap sizes, and we compare experimental and simulation results in the Supplementary Information.

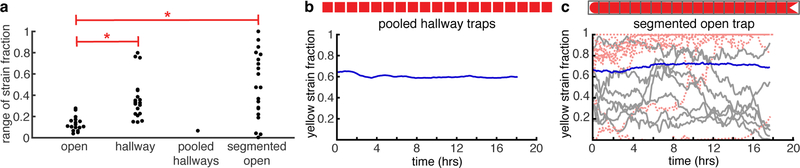
Figure 3: Strain ratio comparisons.

(a) The range of the yellow strain ratio fluctuations over time is significantly different in hallway traps (Fig. 2b) than in open traps (Fig. 2d, p < 0:01, student’s t-test). (b) When pooling data from all 20 hallway traps to mimic the population size in an open trap, the pooled yellow strain fraction is more stable. The range of this data is shown in panel (a) as “pooled hallways”. (c) Segmenting the data from the open trap experiment shown in Fig. 2c into hallway-sized segments and plotting the yellow strain fraction within each segment over time results in higher variability, compared to the overall ratio (blue line). Red dotted lines are lines that go to 0 or 1. The range of yellow strain fluctuationss within each segment are shown in panel (a) as “segmented open”. These fluctuations do not differ from those in hallway traps (p > 0:01), but do differ from fluctuations in the entire open trap ( p < 0:01).

Since the width of the open trapping region is 20:1 in ratio to its height, we expect the global strain ratio in this device to be less sensitive to random, lateral cell fluctuations when compared to the hallway device. Under an assumption that both strains are subject to similar stochastic lateral motion, the local fluctuations would be averaged over a larger area in a longer device. Thus, the increased strain stability in the open device may be attributed to an overall increase in population size (a large number effect).

Open traps can contain roughly 70,000 cells as compared to the roughly 3,000 cells in each hallway trap. We wanted to isolate the effect of population size on strain stability in order to better understand strain ratio fluctuations in the two devices. We began by pooling the data from all hallway traps to reach a population size close to that of the open trap and we then computed the strain ratio as a function of time. The pooled hallway data resembles that of the open trap in population stability (Fig. 3a,b). We also segmented the open trap data from Fig. 2c into sections of the same width as a single hallway trap. The strain ratio within each segment was less stable than that of the overall open trap. We obtained similar results when we segmented other open trap experiments (Fig. S7). The range of fluctuations of the yellow strain fraction in the segmented open trap were not different than in the hallway traps (p > 0:01, Fig. 3a,c), but differed from range fluctuations in the entire open trap (p < 0:01). These comparisons suggested that population size was a key factor in analyzing strain ratio fluctuations in these devices.

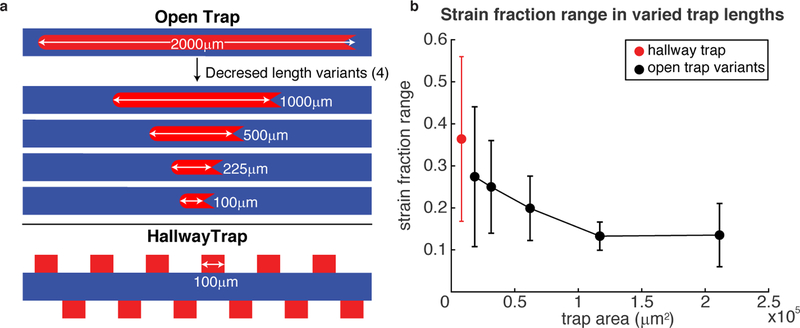
To gain an increased understanding of the spatiotemporal dynamics of strain ratio and the mechanisms of its stability in these types of microfluidic devices, we manufactured shorter versions of the open trap. We chose to alter the open trap rather than the hallway because of the reduced growth pressure in the open device as compared to the hallway device due to decreased buckling instability. ²⁷ To compare different population sizes, we fabricated open traps of four additional lengths: 100, 225, 500, and 1000 µm. We made the shortest open trap variant to be the same width of the hallway trap. We grew the same control strains in these additional devices and computed the range of the yellow strain fraction over time (each experiment required ≈ 18 hours, see Fig. S8). We computed the range by subtracting the maximum and minimum of the yellow strain fraction in each experiment (we found this measure to be a good indicator of variability of the strain ratio across experiments and devices; we also computed the variance of the yellow strain fraction and obtained similar results, see Fig. S9).

In Fig. 4b we show the average range of the yellow strain fraction versus the area of each cell-trapping region. This data shows that the mean strain fraction range rapidly decreases with increasing trap size, which is expected if local strain ratio fluctuations are averaged out over a larger trapping area. We noted, however, that the strain fraction range in the largest open trap (2 mm) was not significantly different than the that of the next smallest trap (1 mm). To determine if this was a limiting effect of increasing trap size, we noticed that whenever a larger number of cells were seeded into a trap the strain fraction range was slightly higher than if fewer cells were seeded. Further, we observed that whenever more cells were seeded the number of distinct “bands” once the trap was filled was greater (here a band is a region of the trap composed of almost entirely one strain). An increase in strain bands can increase strain ratio fluctuations by increasing the spatial density of random lateral invasions of “mother” cell positions by an adjacent band, as explained above. Although the mechanisms of the fluctuations are likely a combination of several stochastic factors, we wanted to see if any relationship existed between the number of strain bands (which increase with increased number of seed cells, see the following section) and the strain ratio variability. In Fig. S10 we reduced the data from the 2 mm open device to contain the same number of experiments (6) as for the smaller devices and also to contain a comparable number of bands (also see Fig. S11). The reduced data show a reduced measure of strain ratio instability, which suggests a causal connection.

Figure 4: Strain fraction stability for traps of varying size.

(a) Open traps with decreasing lengths were manufactured to determine how population strain ratio dynamics depend on the size of the population in each trap. (b) Filled circles show the empirical mean of the yellow strain fraction ranges ( max – min) for each trap size investigated; black circles: open-walled traps, red circle: hallway trap. The hallway trap and largest area open trap data points use the same data as in Fig. 2a,c. The other data points are averages of 6 experiments (Fig. S8). Starting with the smallest trap size, both the mean of the yellow strain fraction ranges and their standard deviations (error bars) generally decrease with increasing trap area for open traps. However, the largest open trap appears to level off, which we attribute to the larger average number of cells seeded for this data point (see Fig. 5 and Fig. S11, Supplementary Information).

In order to investigate the basis for strain ratio variability and the number of seed cells placed, we used a mathematical model to simulate strain-interface interactions and found that increasing the number of seed cells increased the variability, as observed in experiments (see the following section and Supplementary Information). Our data support a conclusion that a larger trap size favors increased strain stability in microfluidic experiments consisting of two (or more) strains. However, increasing the number of seeded cells can also affect strain stability, which can alter the spatial composition of strains critical to intercellular signaling.

Spatial patterning

Population composition needs to be stable to coherently sustain communication and distributed functionality across microbial consortia. ¹⁴ Additionally, spatial patterns and the physical separation of strains in a multi-strain experiment are important because intercellular signaling distance can be limited. For example, while the 2mm long open trap in our experiments described above increased strain ratio stability, it often produced spatial strain distributions that could hinder inter-strain signaling due to large separations of strain types. This is in contrast to the hallway device where signaling molecules from both strains appear to be homogeneously distributed in the trap (Fig. S4).

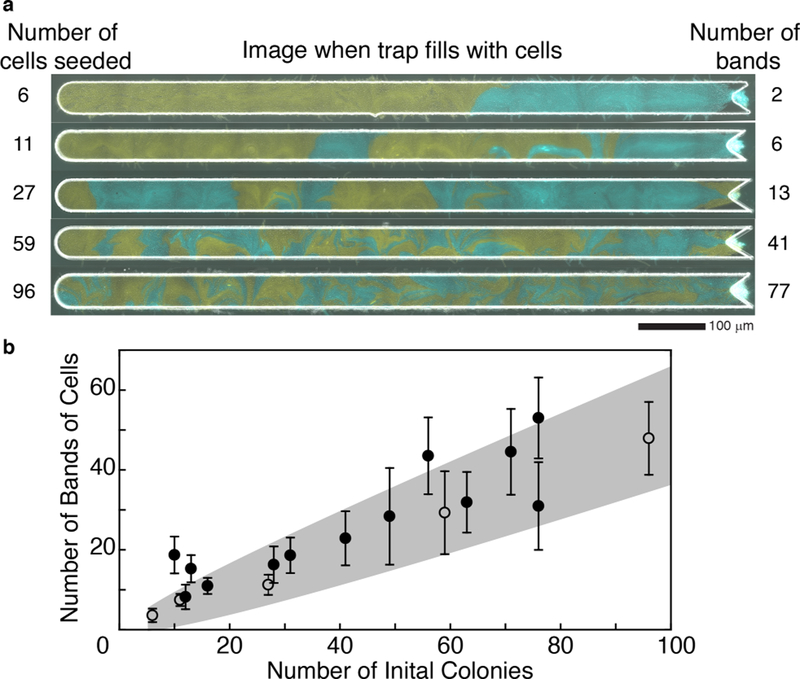
In our initial experiments with the longest (2 mm) open trap (Fig. 2d), we purposely seeded different amounts of cells into the trap of each experiment to determine the impact on spatial heterogeneity of the final population. We found that when fewer cells were initially seeded, larger bands of single strains formed in the trap (Fig. 5a). The average number of bands in a trap over time positively correlated with the number of initial “colonies” (Fig. 5b). We dene an initial “colony” as initial cells of the same strain that are touching because they will act the same as a single cell in forming bands (Fig. S12). To better understand the relationship between the number of initial cells seeded in the trap and the number of resulting bands in the full trap, we used a one-dimensional mathematical model to represent the initial seeding of the trap as a sequence of N flips of a fair coin, where N corresponds to the number of seed cells and H (heads) and T (tails) represent the two strains (see Supplementary Information). Single-strain bands in the trap correspond to runs of heads or tails, which have a geometric distribution in this model.

Figure 5: Emergent single-strain banding vs. number of cells seeded into trap.

(a) Images from five representative experiments with two strains grown in the largest open trap at the time the trap fills completely with cells. The number of cells seeded into each trap is given on the left, and the number of bands formed when the trap fills is given on the right. The greater the number of cells seeded into the trap, the more heterogeneous the population. (b) The number of bands (single-strain regions) increases approximately linearly with the number of seeded colonies. The points are from the same experiments shown in Fig. 2. Open dots correspond to the 5 examples shown in panel (a). The predicted range of bands (mean ± 3 s.d.) as a function of seeded cells is shaded in grey (see Supplementary Information).

Motivated by the large (20:1) aspect ratio of the 2 mm open device, we conjectured that this simple, one-dimensional model would capture the essential relationship between the number of seed cells and the resulting number of bands (see Supplementary Information for the band number distribution in the model), while remaining analytically and computationally tractable. Figure 5b illustrates the mean number of bands over time for each of 18 experiments. The shaded region depicts the model prediction (mean ± 3 s.d. - see Supplementary Information). As conjectured, the model is consistent with most of the experimental data. This consistency supports the intuitive conclusion that band formation depends on the amount of cells seeded into the trap.

Communication

To assess the effect of spatial population heterogeneity on communication in microbial consortia, we grew a “sender” and “receiver” consortium in the original (2 mm) open trap (Fig. 6a). The sender strain contained a plasmid coding for constitutive expression of sfYFP for strain identification and constitutive expression of the quorum sensing (QS) gene rhlI. The RhlI enzyme produces the QS molecule N-butyryl-L-homoserine lactone (C4-HSL). ³¹ This QS molecule diffuses out of the sender cells and into surrounding cells. The receiver strain contained a plasmid coding for constitutive expression of mCherry for identification and the C4-HSL regulated expression of sfCFP. Thus, varying C4-HSL capture by the receiver strain is experimentally quantified by varying measure of its CFP fluorescence.

When sender and receiver strains were co-cultured in the open trap, we observed regions of cyan fluorescence in receiver cells adjacent to bands of sender cells (Fig. 6b,c), but the signaling was of limited extent. This behavior is consistent with predictions of our mathematical model for diffusion-based signaling in this device where the concentration profile of the QS molecule along this domain is characterized by exponential decay from an idealized sender-cell boundary, (see Supplementary Information).The effective reach of QS molecules depends on the heterogeneity of the population and the bands of sender cells that form. A trap with a larger number of thin bands of each strain resulted in all receiver cells expressing significant amounts of CFP (Fig. 6b, and Fig. S13). However, in a trap with a few number of thick bands, the receiver cells reduced to background CFP expression with increased distance away from the sender-strain bands, as expected from our model. To estimate the limits on the signaling distance, we looked for an experimental image with adjacent “wide” bands of each strain in order to observe the isolated decay of CFP in the receiver strain as a function of distance from the sender-receiver strain boundary. We fit the decay of CFP in a narrow region near the middle of the trap to our model using an exponential decay with a single, spatial decay rate parameter ξ, and measured ξ = 20 µm (see example experimental receiver decay and exponential fit in Fig. 6d).

The average number of bands in the well mixed trap from Fig. 6b is 50. This is on the higher end of the experiments in Fig. 5b with an average strain fraction range of roughly 0.18 (Fig. S11). Comparing this value to the plot in Fig. 4b, the number of bands of strains (and therefore initial cells seeded) needed is in a range that results in a plateau of stability with increased cell trapping area. This suggests that one can still benefit from the strain stability of the larger trap size (and therefore greater amount of data) using the 2mm open trap while maintaining the well mixed culture needed for proper signaling.

Concluding remarks

Our results demonstrate that the population size within a microfluidic trap affects the spatiotemporal dynamics of microbial consortia. We have aimed in this study to characterize the ideal microfluidic trap environment for consortia by analyzing vital components such as strain ratio stability and quorum-sensing molecule signaling distance. Among the traps we tested, small traps allow for more spatially uniform signaling but suffer from strain ratio instability. By contrast, large traps exhibit more robust strain ratio stability. Our quantification of effective signaling distance implies that strains must be reasonably well-mixed in order for inter-strain communication to function properly. We have shown both experimentally and through modeling that such spatial heterogeneity can be achieved by altering the number of seed cells. Our experimental data also showed that increasing the number of seed cells in a large open trap can slightly increase strain ratio instability, suggesting competing objectives for our experiments. However, the 2mm open traps with large number of seed cells (resulting in thin bands of cells ideal for communication) still have more stable populations than the smaller traps and we have determined that the number of bands needed for proper signaling in the 2mm trap is whtin the range that aligns with stability in the 1mm trap but is not so large that the stability is less than the smaller trap sizes. Maintaining strain ratio stability and intercellular communication is vital for synthetic microbial consortia and our results suggest how to address this balance in the microfluidic environment.

Methods

Construction of non-communicating strains

The non-communicating strains contained plasmids built through PCR and restriction enzyme cloning. These plasmids contained ampicillin resistance and p15A origin. A constitutive P_Iq promoter ³² and modified bicistronic design ribosome binding site ³³ drove the expression of sfcfp or sfyfp mutants of sfgfp.^24,25 The fluorescent proteins were tagged with a mutagenized ssrA tag that ends with amino acids ASV. ³⁴ LAA, ASV, and untagged versions were constructed, sequence verified and then tested on a plate reader and microscope. ASV-tagged versions were selected because they had detectable expression on the plate reader and did not saturate the detector of the microscope camera. Downstream of the fluorescent protein gene is the iGEM registry B0014 terminator. The plasmids were individually transformed into BW25113 ∆araC ∆lacI³ E. coli cells using chemically competent cells and a heat shock transformation protocol.

The transformations were plated onto LB agar plates with 100 µg mL^–1 ampicillin and incubated 16–18 hours at 37 C. The next day a colony was picked from each to inoculate a 5 mL tube of LB broth with 100 µg mL^–1 ampicillin and in a shaking incubator at 37 C for 16–18 hours. The next day the cultures were diluted 1/1000 each into 50ml fresh LB with 100 µg mL^–1 ampicillin and grown about 2.5 hours until they reached an OD 600 nm of 0:15 – 0:2. While the cells grew, the microfluidic device was warmed to 37 C then flushed with 1% (v/v) Tween-20 to purge air. Then media and waste syringes were then prepped. A 20ml syringe with LB with 0.075% (v/v) Tween-20 and 100 µg mL^–1 ampicillin was attached to the media port of the microfluidic device. Two 10 mL syringes with sterile water were attached to the two waste ports of the microfluidic device. Once the cultures reached the proper OD, 15 mL of each culture was spun down at 2000 xg for 5 minutes at room temperature. The supernatant was removed, and the cells were resuspended in 10 mL total of LB with 100 µg mL^–1 ampicillin. This media was pre-warmed to 37 C. The 10 mL of mixed cells was seeded into a 10 mL syringe and attached to the microfluidic device.

The heights of the four syringes determine the flow of media through the device. The waste syringes were at the lowest height, the cell syringe began at a level higher than the waste but lower than the media to allow for cell loading, then it was lowered to around the waste syringe height to allow the media to reach the cells. When loading cells into the open trap, cells flew into the “V” on the right-hand side of the device and the line was flicked to apply enough pressure for the cells to go into the trap. They were then stuck in the trap whose height 0:95 µm was slightly less than the diameter of the cells 1 µm. Once the desired number of cells was trapped, the cell syringe was lowered to allow media flow to the cells. The device was then moved to a 60X oil objective and imaged immediately every 6 minutes at phase contrast, YFP, and CFP filter settings. They were imaged immediately to capture the initial number of cells.

For the hallway trap, the loading height of the cell syringe was adjusted to allow the cells to flow into the traps on their own. It was left at this loading height for 30 minutes to an hour to trap as many cells as possible. This was the best way to ensure both strains entered the traps. Afterwards the cell syringe was again lowered to allow media flow to the cells. The cells were allowed to grow prior to imaging for 2–4 hours before moving to a higher (100X) oil objective and imaged immediately every 6 minutes at phase contrast, YFP, and CFP filter settings.

Construction of sender and receiver strains

The sender strain used to test communication in the open trap had the same constitutive sfyfp plasmid used in the non-communicating strains above for identification. It also contained a plasmid encoding the rhlI (ATCC #47085) gene driven by a promoter under the control of LacI with the same bicistronic design ribosome binding site ³³ used previously. RhlI produces the C4-HSL QS molecule that can diffuse out the cell to nearby cells. ³¹ The rhlI gene was tagged with the original LAA ssrA degradation tag ³⁴ and had the iGEM registry B0014 terminator. This plasmid contained a kanamycin resistance gene for selection, pMB1 origin, and ROP element that reduces the copy number. ³⁵ This plasmid was transformed into a BW25113 ∆araC ∆lacI ∆sdiA strain with araC, cinR, and rhlR inserted at the attB site under constitutive promoter. ¹¹ There was no LacI in this strain, so rhlI was expressed constitutively. The receiver strain had a plasmid with the same backbone but contained an engineered promoter with an RhlR binding site driving the expression of sfcfp.^24,25 The sfcfp gene was not tagged for degradation but has the same iGEM registry B0014 terminator. This plasmid was transformed into the same BW25113 ∆araC ∆lacI ∆sdiA strain with araC, cinR and rhlR inserted at the attB site under constitutive promoter. ¹¹ The expression of sfcfp is dependent upon activation when RhlR binds C4-HSL ³¹ produced by the sender or exogenously added to the media. For identification, the receiver contained a plasmid identical to the constitutive sfyfp plasmid used in the sender and non-communicating strains, but with mCherry ³⁶ in place of sfyfp. These strains were transformed, cultured, and tested in the microfluidic devices using the same protocol as the non-communicating strains described previously.

Data analysis and microfluidic device construction

Individual fluorescent images obtained from the microscope Nikon Elements program were exported into tiff files for each time and channel – bit depth was conserved during export (12-bit). These images were analyzed using custom MATLAB code, and Ilastik machine learning software was used to identify cells for the strain ratio analyses. Images and videos were compiled in ImageJ. Wafer molds and the actual microfluidic devices were made using methods described in Ferry et al., 2011. ¹⁸ The device with original hallway trap is the same device used in Chen et al., 2015, ¹¹ and the open trap device is based off the device from Hussain et al., 2014 ³⁷ but with a rounded end and 2000 µm length. The varied length devices were constructed the same way as the original open and hallway traps, but with different length trap designs in the mask. For increased throughput, some open trap experiments were done using a parallel device we constructed which contains 4 of the original 2mm long open traps. This parallel device was designed off the biopixel device from Prindle et al., 2012. ²¹ We reduced the number of parallel channels to four, removed their traps, and inserted our narrow open traps. We also used this schematic for the 4 reduced length open traps in which one of the four length traps was inserted into each of the four parallel channels resulting in a device with four open traps with lengths of 1mm, 0.5mm, 0.225mm, and 0.1mm.