Holistic Approach to Partial Covalent Interactions in Protein Structure Prediction and Design with Rosetta

Abstract

Partial covalent interactions (PCIs) in proteins, which include hydrogen bonds, salt bridges, cation–π, and π–π interactions, contribute to thermodynamic stability and facilitate interactions with other biomolecules. Several score functions have been developed within the Rosetta protein modeling framework that identify and evaluate these PCIs through analyzing the geometry between participating atoms. However, we hypothesize that PCIs can be unified through a simplified electron orbital representation. To test this hypothesis, we have introduced orbital based chemical descriptors for PCIs into Rosetta, called the PCI score function. Optimal geometries for the PCIs are derived from a statistical analysis of high-quality protein structures obtained from the Protein Data Bank (PDB), and the relative orientation of electron deficient hydrogen atoms and electron-rich lone pair or π orbitals are evaluated. We demonstrate that nativelike geometries of hydrogen bonds, salt bridges, cation–π, and π–π interactions are recapitulated during minimization of protein conformation. The packing density of tested protein structures increased from the standard score function from 0.62 to 0.64, closer to the native value of 0.70. Overall, rotamer recovery improved when using the PCI score function (75%) as compared to the standard Rosetta score function (74%). The PCI score function represents an improvement over the standard Rosetta score function for protein model scoring; in addition, it provides a platform for future directions in the analysis of small molecule to protein interactions, which depend on partial covalent interactions.

Graphical abstract

1. INTRODUCTION

1.1. Partial Covalent Interactions.

Partial covalent interactions (PCIs) in proteins, defined here as hydrogen bonds,¹ salt bridges,² cation–π,³ and π–π interactions⁴ (Figure 1), are abundant in nature and contribute to both protein structure and protein-biomolecule interaction.⁵ These four PCIs are composed of a set of noncovalent interaction components.

Figure 1.

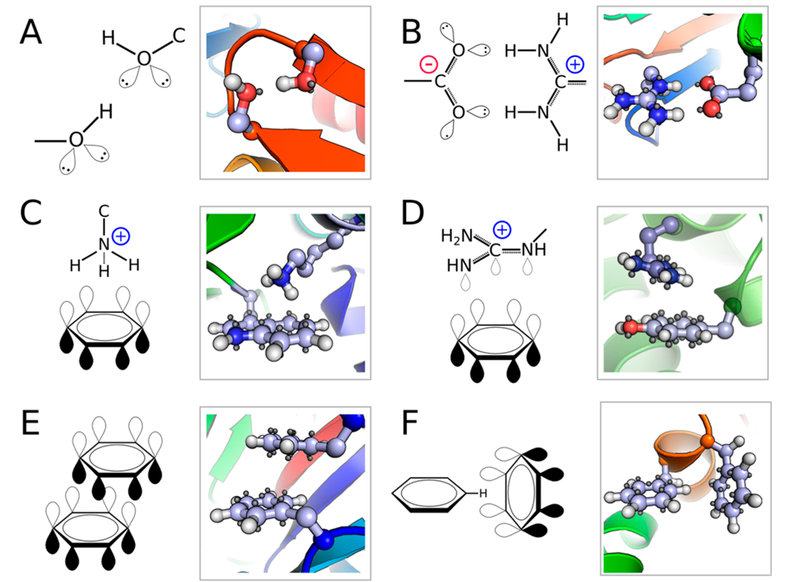
Representations of partial covalent interactions. Parts A–F each show a chemical schematic (left) along with a representative interaction from the Protein Data Bank (right). A) hydrogen bond, formed between S240 and S243 from 1daa. B) salt bridge, formed between R96 and E131 in 1wr8. C) T-stacked cation–π, formed between W361 and R370 in 2oiz. D) Offset parallel cation–π, formed between Y178 and R184 in 2bo4. E) Offset parallel π–π, formed between F285 and F348 in 1pam. F) T-stacked π–π, formed between F70 and F94 in 1vph.

Hydrogen bonds, a partially positive donor hydrogen atom that interacts with the lone pair orbital of an acceptor atom, combine an electrostatic effect with a semicovalent bond. Salt bridges, composed of two interacting charged amino acid side chains, are a combination of hydrogen bonding and additional electrostatic effects from the formal charges. Cation–π interactions are an electrostatic effect between a positively charged functional group in an amino acid side chain and a central negative charge, due to the delocalized orbital system, on the face of the aromatic ring.^6,7 π–π stacking, where two aromatic rings stack either off-face parallel or in a “T” arrangement are mostly dominated by the van der Waals effect with a quadrapole–quadrapole electrostatic effect hindering a fully eclipsed stacking configuration.^8,9 While these interactions are primarily electrostatic in nature, PCIs cannot be neatly explained by assigning a point charge on an atom and subsequently using a Coulombic score term. PCIs are defined by the interactions between orbitals and have unique, specific geometries that define an optimal interaction.

Quantum Mechanics (QM) methods are used to study the geometry and energetics of PCIs with fine-grained analysis of orbital shape and geometries; however, such calculations are computationally expensive, thereby limiting research to relatively small model systems and are prohibitive for large proteins.¹⁰ For example, hydrogen bonds are often analyzed in the context of small molecules such as formamide, acetamide, N-methylacetamide, or water dimers.^11—17 Other interactions, such as π–π and cation–π, are studied using benzene dimers and benzene cation pairings, respectively.¹⁸ Due to the simplicity of the small molecules used, the diverse nature of PCIs can be analyzed to determine optimal geometric arrangements. These detailed studies have yielded important insights into the driving forces of PCIs.

Hydrogen bonds can be decomposed into two main effects: charge transfer, or the lone pair orbital donating electron density to the unoccupied antibonding orbital of the donor (n → σ*), and the electrostatic interaction between the partially charged atoms.¹⁹ Hydrogen bonds have a specific, optimal geometry: the acceptor–hydrogen–donor atoms at an angle of ~120.0° and the acceptor base–acceptor–hydrogen–donor torsion angle, which implicitly measures the placement of the orbital, at ~180.0° (Figure 1A).

Salt bridges exist in proteins as the interaction between a negatively charged aspartate or glutamate and a positively charged arginine, lysine, or histidine. Energetically, the salt bridge is composed of two parts: hydrogen bonding between the hydrogen on the arginine, lysine, or histidine and the oxygen on the negatively charged residues and electrostatic effects between the charged residues²⁰ (Figure 1B).

Cation–π interactions are a predominantly electrostatic interaction.²¹ The aromatic side chains of phenylalanine, tyrosine, and tryptophan have a permanent quadrapole, which causes a concentration of partial negative charge above and below the face of the ring coupled with an increased ring of partial positive charge along the hydrogens on the edge of the ring. A positively charged side chain of arginine or lysine residues can then interact with this electronegative face.⁶ Primarily, these interactions take two geometric forms in proteins: a T-shaped form where a partial positively charged hydrogen atom of arginine or lysine approaches the aromatic ring (Figure 1C) or a parallel stacked interaction where the negatively charged π-electronical system of the arginine side chain interacts with the π-electronical system of the aromatic amino acid (Figure 1D).⁷ While quite different in nature, these interactions combine into a larger motif called the “aromatic box motif’ where a positively charged amino acid is surrounded in a box or cage of aromatic residues.⁷ An analysis of these interactions in the Protein Data Bank (PDB) found that there is, on average, one energetically significant cation–π interaction for every 77 residues in a protein.³

Similarly, two aromatic side chains can interact favorably in a π–π stacking or T-shaped arrangement. The precise nature of these interactions is still debated. Current theories posit that van der Waals interactions dominate the π–π stacking interaction energy, modulated by electrostatic effects from the aromatic quadrupole, which eliminates the centered parallel π–π stacking.^8,9 To avoid the energetically prohibitive centered π–π stacking, yet maximizing favorable dispersion effects, the interaction often exhibits an offset parallel arrangement in protein structures⁵ (Figure 1E). The T-shaped arrangement is an alternative conformation where partial positively charged hydrogens from the edge of one aromatic ring approach the partial negatively charged face of a second aromatic system (Figure 1F).

Here, we describe an approach to unify all protein-centric PCI bonding terms to better model these important and common interactions in the protein structure prediction algorithm Rosetta.²² We developed a pairwise decomposable knowledge based potential for PCIs, which is based on placing orbital proxies on atoms based on their type and hybridization. The orientation of these orbital proxies was determined by the Valence Shell Electron Pair Repulsion (VSEPR) theory,²³ which apply readily to the orbital distribution of the atoms types found in proteins (Figure 1). Using experimentally determined structures the relative geometry of these orbital–orbital interactions is analyzed to derive the potentials. We test if this holistic approach can replace the respective, diverse energy terms in the Rosetta score function without a loss in side-chain rotamer recovery or side-chain design. If successful, the PCI approach could facilitate not only a holistic approach to describing interactions within proteins, but in particular it could be expanded to enable a holistic scoring approach to protein interactions with the more diverse set of functional groups within small molecules, nucleic acids, or even inorganic surfaces.

1.2. The Rosetta Knowledge Based Potential Is Inconsistent in Scoring Partial Covalent Interactions.

Scoring of protein models in Rosetta is performed using a combination of Knowledge Based Potentials (KBPs) and physics-based terms. KBPs are based upon the assumption that the frequency of geometries observed in databases of protein structures, such as the PDB,²⁴ corresponds to their free energy according to the Boltzmann relation.²⁵ The advantage of this approach is that the complex rules that determine the geometry of PCIs in larger molecules are accurately represented. However, it is not trivial to decompose contributions into specific terms which can lead to the double-counting of interactions or oversimplification of the geometric parameters. After a set of geometric constraints has been determined to make the interaction, the probability density of the relative geometry X of two interacting partners is converted into an energy via the formula E(X) = – kT ln[P(X)] where E(X) is the energy associated from the measured quantity, k is Boltzmann’s constant, T is the absolute temperature, and P(X) is the probability density. Evaluation of the contribution during scoring is based upon the lookup of the geometrical measurements in a precalculated KBP.

The evaluation and scoring of partial covalent interactions in Rosetta, specifically hydrogen bonding, have been continuously modified and refined. The first introduction of a term in Rosetta to capture partial covalent interactions was by Simmons et al., who introduced a statistically driven pair potential, which captured the effects of both electrostatic interactions and hydrogen bonding interactions.²⁶ This method was used for low-resolution modeling and evaluated the likelihood of two residues being at a given distance from one another. The pair potential was then modified to work in full-atom modeling,²⁷ using this full-atom potential Kuhlman et al., successfully designed a novel protein de novo.²⁸

The initial inclusion of a specific hydrogen bond term was by Kortemme et al.,²⁹ who created a hydrogen bond KBP based upon frequently observed geometries in high resolution protein structures between a polar hydrogen and an acceptor atom.

Around the same time Misura et al.³⁰ developed and analyzed the use of an orientation dependent scoring function for side-chain pairs, specifically for π—π and cation–π interactions. However, the aromatic specific score terms had a negligible effect and were not included in the default score function.

A new default score function, Talaris2013 (and the incremental update Talaris2014),^31,32 addressed the non-native distribution of hydrogen bond geometry from the previous default Rosetta score function, score12’. The authors removed the pair term²⁷ and replaced it with an atom-centric Coulombic electrostatic model. They reparametrized the hydrogen bond function, creating a potential based on the distance and angles between donor and acceptor atoms. The function polynomials were fit to match native distribution. As electrostatic effects contribute to hydrogen bonding, care was taken to avoid double counting between the Coulombic term and the hydrogen bond term. The two terms, in conjunction with the other Talaris score terms, captured nativelike hydrogen bond geometric distributions.

Currently, cation–π and π—π interactions are not explicitly evaluated in the default Rosetta score function. While the score function includes standard electrostatic and van der Waals terms, they do not capture the aromatic quadrupole, which leads to the unique geometries of the cation–π and π—π interactions.

1.3. The Partial Covalent Interaction Score Function.

The present work seeks to develop a holistic approach to treating PCIs in Rosetta. We set out to develop a pairwise decomposable KBP for PCIs that 1) captures both covalent and electrostatic components of PCIs with 2) a detailed description of their geometry at a consistent level of detail and 3) is expandable to all PCIs. Our approach is chemistry-centered, placing orbital proxies on atoms based on their type and hybridization. The relative geometry of these orbital–orbital interactions is analyzed to derive the PCI. Our new score function replaces the hydrogen bond and pair KBPs in Rosetta (score12’ and Talaris2014), although the score terms can be mixed and matched with any Rosetta score terms. As we began working on this formidable challenge before Talaris updates to the Rosetta energy function were conceived, we included the previous standard Rosetta energy function score12’ as additional reference for comparison.

We find that the PCI KBP score function recapitulates accurate geometries of hydrogen bonds, salt bridges, cation–π, and π—π interactions in multiple Rosetta benchmarks (geometry, rotamer, and sequence recovery) and performs comparable if not superior to the established score functions. This is remarkable as many components of the Rosetta sampling and scoring framework have long been optimized for hydrogen bond and electrostatic score terms, and it would be unlikely that a novel KBP score function would match or exceed recovery results.

2. METHODS

2.1. New Atom Types Help Define Orbital Placement and Interactions.

Partial covalent interactions (PCIs) are mediated by interactions between bonding and nonbonding orbitals or two nonbonding orbitals. They are defined here as an antibonding (σ*) orbital from a hydrogen atom that engages a nonbonding, (lone pair) p-orbital (n), a σ* orbital interacting with a π-orbital of an aromatic system (π), or as two π-orbitals that interact with each other. The specific PCI types evaluated in this work being hydrogen bonds (n → σ*), salt bridges (n → σ*), cation–π (π → σ*), and π—π (π → π). Because the driving interactions are between participating orbitals, this led us to create a score function based on explicit orbital placement.

While molecular orbital theory provides a robust approach for modeling orbitals on atoms, the calculation of molecular orbitals is computationally expensive as each molecular orbital is influenced by the overall molecule and is therefore intractable in a protein system.¹⁰ Further, in order to develop a tractable, pairwise decomposable score function in Rosetta, geometric constraints are required to define the strength of the interaction. As molecular orbital theory gives only a probability of the location of an electron, a precise, computationally cheap, measurement cannot be performed.

Therefore, we propose a simpler method: the addition of orbitals on atoms with the geometry defined by the atom’s Gasteiger type.³³ Gasteiger typing classifies atoms based upon their geometrical arrangements and orbital occupancy. The generic form is [Chemical Symbol]_[Orbitals]. For example, a carbon atom in an aromatic ring system is designated as C_TrTrTrPi, where the first letter (C) represents the element, followed by the typing and geometrical arrangement of the orbitals (TrTrTrPi). In this case, there are three sigma orbitals geometrically arranged trigonally (Tr symbol), and one π-bond, designated by the symbol Pi. Since the explicit geometry and type of the orbital is given, orbitals that take part in PCIs can be easily assigned. Placement of the orbitals surrounding the atom is based upon the occupancy described by the Gasteiger atom types with geometric constraints defined by the VSEPR theory.²³ The VSEPR theory states that valence shell electron pairs around an atom repel each other and adopt a geometrical arrangement that minimizes this repulsion. The geometric angle for the orbitals was determined by the surrounding bonded atoms and modeled after VSEPR theory.

For the aromatic carbon in a ring system (C_TrTrTrPi), two single point orbitals are placed perpendicular, 90°, to the ring system with one above the ring system and one below. The distance at which the orbitals are placed is the covalent radius. An important aspect of hydrogen bonding is the interaction between the lone-pair orbital and the antibonding orbital on the hydrogen atom. However, the hydrogen atom covalent radius is small (~0.2 Å), so to simplify geometric representation and increase computational speed, the antibonding σ* orbital is placed at the atom coordinates. Since a precise definition of the atom type and the occupancy of the orbitals is defined, ligands, nucleotides, and noncanonical amino acids can readily be added to this score function.

2.2. Geometric Parameters for PCIs Include One Distance and Two Angles.

In the creation of a KBP score function specific geometries must be defined in order to measure their frequency in a database. For each of the PCIs measured, there are a total of three parameters, one distance and two angles. For hydrogen bonds and salt bridges (Figure 2A) the three geometric measurements are 1) the distance (δ_HOrb) between the orbital and hydrogen, 2) the angle (Ψ) between the Acceptor – Orbital – Hydrogen (AOH), and 3) the angle (Θ) between the Donor – Hydrogen – Orbital (DHO).

Figure 2.

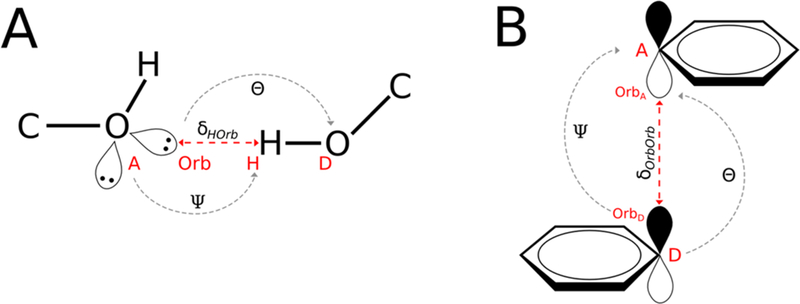
Schematic representation of the geometric definitions for the derivation of knowledge based potentials (KBP). A) δ_HOrb the distance between the acceptor lone pair orbital (Orb) and the donor hydrogen atom (H), Ψ the angle between the acceptor atom (A), the orbital (Orb), and the hydrogen atom (H), and Θ the angle between the orbital (Orb), hydrogen atom (H), and the donor atom (D). B) δ_orborb the distance between the donor orbital (Orb_D) and the acceptor orbital (Orb_A), Θ the angle between the donor atom (D), the donor orbital (Orb_d), and the acceptor orbital (Orb_A), and Ψ the angle between the donor orbital (Orb_d), the acceptor orbital (Orb_A), and the acceptor atom (A).

For interactions between π-orbitals, cation–π and π–π interactions (Figure 2B) the parameters are 1) the distance (δ_OrbOrb) between the two orbitals, 2) the angle (Ψ) between the Acceptor – Orbital – Orbital (AOO), and 3) the angle (Θ) between the Donor – Orbital – Orbital (DOO).

Inclusion of a direct measurement between angles involving the orbital removes the need to indirectly calculate the relationship between the acceptor, hydrogen, and donor using torsion angles between four atoms as has been previously done with the hydrogen bond potential.²⁹

2.3. Knowledge-Based Potential Derivation.

A KBP was created by observing the frequency and geometry of each pair of atom types that can form an interaction. For example, in the case of hydrogen bonds, the interaction can be defined as (n → σ*). In proteins, the nonbonding orbital, n, is found on atom types O_Tr2Tr2TrPi and O_Te2Te2TeTe, and the antibonding σ* orbital is found on atom types O_Te2Te2-TeTe, N_TrTrTrPi2, and N_Tr2Tr2TrPi. With the level of detail being modeled in the PCI method the antibonding orbital is represented by the hydrogen atom bound to the hydrogen bond donor (O_Te2Te2TeTe, N_TrTrTrPi2, and N_Tr2Tr2TrPi). This results in six total KBPs that describe both hydrogen bonds and salt bridges in proteins (Table 1). Overall a total of 16 PCI interactions are calculated.

Table 1.

16 Partial Covalent Interaction Types Measured

acceptor atom Gasteiger type (Rosetta type)a	donor atom Gasteiger type (Rosetta type)b	driving interactionc	protein centric termd	PCI score terme
C_TrTrTrPi (aroC)	N_TrTrTrPi2 (Narg/Nlysf)	π → σ*	cation-pi	pci_bonding_pi_h
	N_TrTrTrPi2 (Narg)	π → π	cation-pi	pci_bonding_pi_bonding_pi
	C_TrTrTrPi (aroC)	π → σ*	pi-pi	pci_bonding_pi_h
	C_TrTrTrPi (aroC)	π → π	pi-pi	pci_bonding_pi_bonding_pi
N_TrTrTrPi2 (Narg)	C_TrTrTrPi (aroC)	π → π	pi-pi	pci_bonding_pi_bonding_pi
	C_TrTrTrPi (aroC)	π → σ*	pi-pi	pci_bonding_pi_h
	N_TrTrTrPi2 (Narg)	π → π	cation-pi	pci_bonding_pi_bonding_pi
	N_TrTrTrPi2 (Narg)	π → σ*	cation-pi	pci_bonding_pi_h
	N_Tr2TrTrPi (Nhis)	π → σ*	cation-pi	pci_bonding_pi_h
	N_Tr2TrTrPi (Nhis)	π → σ*	cation-pi	pci_bonding_pi_h
O_Te2Te2TeTe (OOC)	N_TrTrTrPi2 (Narg)	π → σ*	salt bridge	pci_lone_pair_h
	N_Tr2TrTrPi (Nhis)	π → σ	salt bridge	pci_lone_pair_h
	O_Tr2Tr2TrPi (OH)	π → σ*	hydrogen bond	pci_lone_pair_h
O_Tr2Tr2TrPi (OH)	O_Tr2Tr2TrPi (OH)	π → σ*	hydrogen bond	pci_lone_pair_h
	N_Tr2TrTrPi (Nhis)	π → σ*	hydrogen bond	pci_lone_pair_h
	N_TrTrTrPi2 (Narg)	π → σ*	hydrogen bond	pci_lone_pair_h

^aGasteiger designation (and equivalent standard Rosetta designation) for the acceptor atom; the acceptor atom contains the orbital for the PCI bond.

^bGasteiger designation (and equivalent standard Rosetta designation) for the donor atom; the donor atom contains the hydrogen or orbital that interacts with the acceptor orbital.

^cOrbital-type designation for the acceptor atom (1) interaction with the donor atom (2).

^dProtein centric designation described by the driving interaction (3).

^eNew score term designation in Rosetta.

^fNarg and Nlys are equivalent and are denoted by Narg throughout the rest of the table.

For derivation of the PCI KBP, the RosettaFeatures reporter³¹ was used to obtain and store the geometric parameters using the top8000.³⁴ The top8000 data set contains monomeric proteins with at least 25% of side chains present, greater than 38 residues, and has a MolProbity score of <2.0.³⁵ Missing hydrogen atoms were added to all crystal structures using Reduce³⁶ and then converted to Rosetta hydrogen atom types via a Python script.

The probability distributions are initially computed by the shortest distance (δ_HOrb or δ_OrbOrb) between a hydrogen atom and an orbital or between any two orbitals. Once the shortest distance is calculated, the cosine of both Ψ and Θ is calculated (as defined in Figure 2). By taking the cosine of Ψ and Θ, a simple normalization is applied to each angle to account for a bias in observing a given angle by chance. Angles close to 90° are much more likely to occur in a protein environment than angles close to 0° or 180°. Therefore, the more likely angles, near 90°, are in the steepest part of the cosine function, whereas 0° and 180° are in the shallow part of the function. Use of the cosine avoids also computationally time-consuming calls to both the cosine and arccosine functions.

The observed frequencies were then binned by a two-dimensional table, by distance and angle. Two two-dimensional tables were created for each of the atom type pairs (see list in Table 1), one by distance and cos(Ψ) and the other by distance and cos(Θ). Bin sizes were set to 0.1 Å for distances δ_HOrb and δ_OrbOrb and 0.05 for both cos(Ψ) and cos(Θ). Pseudocounts were added to each bin fraction.

The inverse Boltzmann relation was then used to convert the propensity of the observed geometries into an energy: E(X) = –RT ln(P_observed(X)/P_background(X)) where E(X) is the energy X is the feature observed (distance and two angles), R is the gas constant, T is the temperature, P_observed(X) is the probability of the feature observed, and P_background(X) is the probability of the given observation seen by chance. The total energy for a given PCI is determined by the summation of E(PCI | X) where PCI is the partial covalent interaction being modeled, and X are the geometric measurements for the interaction. The expected background probabilities for the distances δ_HOrb and δ_OrbOrb were determined by dividing each bin fraction by the squared distance (r²), as short distances between features are less likely to occur than long distances by chance. The cosine function sets the expected background distribution probability function to 1 for both angle measurements. A bicubic interpolation of the energy for all distance/angle pairs for every PCI type was then performed. This has two effects: the energy function becomes a continuous, differentiable function, and it also ensures that δ_HOrb, cos(Ψ) and δ_HOrb, cos(Θ) remain tightly coupled and continuous during minimization.

2.4. Orbital Score Function Optimization.

The overall energy score, E, computed by Rosetta is a linear combination of weighted scoring terms. The base score function in Rosetta is composed of a decomposed Lennard-Jones potential (fa_atr, fa_rep, fa_intra_rep), a solvation term (fa_sol), a Coulombic electrostatic potential (fa_elec), proline ring closure energy (pro_close), a decomposed hydrogen bond potential for alpha helices, beta sheets, side chain to backbone, and side chain to side chain, respectively (hbond_sr_bb, hbond_lr_bb, hbond_bb_sc, hbond_sc), a disulfide bond potential (dslf_fa13), a phi/psi potential for each amino acid (rama), an omega backbone dihedral potential (omega), likelihood of rotamer (fa_dun), probability of an amino acid with a given phi/psi angle (p_aa_pp), a penalty for placing a tyrosine hydroxyl out of plane (yhh_planarity), and an amino acid reference penalty (ref):^37,38

$$E=W_{\text{atr}}{E}_{\text{atr}}+W_{\text{rep}}{E}_{\text{rep}}+W_{{\text{intra}}_{-}\text{rep}}{E}_{{\text{intra}}_{-}\text{rep}}+W_{\text{sol}}{E}_{\text{sol}}+W_{\text{hbond}}{}_{\text{\_sc}}{E}_{\text{hbond}}{}_{\text{\_sc}}+W_{{\text{hbond}}_{-}{\text{sr}}_{-}\text{bb}}{E}_{{\text{hbond}}_{-}{\text{sr}}_{-}\text{bb}}+W_{{\text{hbond}}_{-}\text{Ir\_bb}}{E}_{{\text{hbond}}_{-}\text{Ir\_bb}}+W_{{\text{hbond}}_{-}{\text{bb}}_{-}\text{sc}}{E}_{{\text{hbond}}_{-}{\text{bb}}_{-}\text{sc}}+W_{\text{dun}}{E}_{\text{dun}}+W_{p_{-}{\text{aa}}_{-}\text{pp}}{E}_{p_{-}{\text{aa}}_{-}\text{pp}}+W_{\text{pair}}{E}_{\text{pair}}+W_{\text{ref}}{E}_{\text{ref}}$$

The relative weights for all scoring terms were optimized by redesigning proteins in a data set of high resolution experimental structures to maximize the probability of recovering the native amino acid at each position in the protein.^27,29 Modification, addition, or removal of scoring terms therefore requires adjustment of the individual weights.

For simplification of score terms, the 16 total atom type interactions were divided into three classes: n → σ* orbitals are termed lone pair hydrogen interactions, orbital interactions involving π → σ* are termed bonding – π hydrogen interactions, and π → π interactions are termed bonding π – bonding π. Each PCI class is controlled by a separate weight and given the following names: pci_lone_pair_h (n → σ*), pci_bonding_pi_h (π → σ*), pci_bonding_pi_bonding_pi (π → π) (Table 1).

An advantage of KBPs is the ability to implicitly capture interactions that are difficult to model. However, care must be taken to avoid double-counting interactions. Consequently, with the introduction of the PCI score terms we removed all standard side-chain hydrogen bonding interactions, yielding the new total energy formula:

$$E=W_{\text{atr}}{E}_{\text{atr}}+W_{\text{rep}}{E}_{\text{rep}}+W_{\text{intra\_rep}}{E}_{\text{intra\_rep}}+W_{\text{sol}}{E}_{\text{sol}}+W_{\text{hbond\_sr\_bb}}{E}_{{\text{hbondsr}}_{-}\text{bb}}+W_{{\text{hbond}}_{-}\text{Ir}\_\text{bb}}{E}_{{\text{hbond}}_{-}\text{Ir}\_\text{bb}}+W_{\text{dun}}{E}_{\text{dun}}+W_{\text{p\_aa\_pp}}{E}_{\text{p\_aa\_pp}}+W_{{\text{fa}}_{-}\text{elec}}{E}_{{\text{fa}}_{-}\text{elec}}+W_{\text{ref}}{E}_{\text{ref}}+W_{\text{pci\_lone\_pair\_h}}{E}_{\text{pci\_lone\_pair\_h}}+W_{\text{pci\_bonding\_pi\_h}}{E}_{\text{pci\_bonding\_pi\_h}}+W_{\text{pci\_bonding\_pi\_bonding\_pi}}{E}_{\text{pci\_bonding\_pi\_bonding\_pi}}$$

With the addition, and removal, of score terms, the weights need to be reoptimized. An iterative approach was used to optimize weights for the new PCI score function. The following weights were changed iteratively by a factor of 0.05 and tested against a rotamer recovery benchmark: the new terms: pci_lone_pair_h, pci_bonding_pi_h, and pci_bonding_pi_bon-ding_pi, and the standard terms fa_atr (the attractive portion of the Lennard-Jones potential), fa_rep (the repulsive portion of the LJ potential), fa_sol (solvation term), and fa_elec (Coulombic term). Because PCIs counterbalance the cost of desolvating polar residues and are partially covalent, the weight for the solvation and the attractive and repulsive potential needed to be adjusted.

Once the highest possible rotamer recovery was achieved, the particle swarm optimization algorithm, OptE, was used to optimize the weight for all reference energies.³¹ After the reference energies have been optimized, a design benchmark was used to analyze the number and quality of PCIs recovered by Rosetta. Weights were then adjusted by 0.025 until the total number of PCIs designed matched the average number in native structures. A final round of OptE was used to adjust the reference energies to match the average amino acid composition seen in native proteins.

2.5. Benchmarks Used To Analyze Rotamer and Sequence Recovery.

The protein design data set benchmark was created through the protein sequence culling server PISCES.³⁹ X-ray structures with a sequence identity limit of 25%, resolutions better than 1.5 Å, and sequence lengths between 175 and 250 residues were identified. A total of 415 of crystal structures were obtained given these criteria. For the rotamer recovery benchmark all side-chain atoms must be present in the protein. This resulted in a set of 29 proteins with all side-chain atoms present and a resolution of 1.8 Å or better.⁴⁰ The data set is diverse, containing structures that are all α-helices, all β-sheets, and an α /β mix.

2.5.1. Rotamer Recovery.

Side-chain rotamer recovery was measured by systematically swapping out each amino acid side chain with rotamers from the Dunbrack rotamer library⁴¹ while keeping the conformations of all other side chains fixed. After the lowest energy rotamer is picked, the side chain is allowed to minimize. The χ angles of the lowest energy conformation are compared to original side-chain conformation. If all χ angles are equal with ±20°, then the residue is considered recovered. For the purposes of analysis, rotamer recovery was divided into two bins, surface residues and core residues. Residues with a neighbor count of 16 or less were considered surface residues, while residues with more than 16 neighbors were considered to be in the core of the protein. Neighbor counts are measured by the number of residues with a Cß (Cα for GLY) distance within 10 Å of the residue being repacked.

2.5.2. Sequence Recovery.

Protein design minimizes the total free energy of a tertiary structure through simultaneous optimization of the primary sequence and side-chain conformation. On a fixed backbone, amino acid side-chain identities and conformations are stochastically swapped and scored with the Rosetta all-atom score function. The sequence with the lowest total energy score is chosen as the optimal sequence for the given backbone. Sequence recovery is performed on the backbone coordinates after Rosetta energy minimization. If design is performed on a rigid backbone, small local clashes may exist in experimentally determined structures. During design these clashes may be relieved through replacing a large amino acid with a smaller one thereby producing an artificially low energy. Therefore, in order to relieve these small clashes, an all-atom refinement of experimental structures is done prior to design. The argument against design on an energy-minimized structure is that while local frustrations are removed, native interactions are optimized in the Rosetta energy function and thereby favor the native amino acid resulting in artificially high recovery rates. However, as comparisons are only being made between Rosetta score functions, and not to external methods, no single method will be biased over another.

3. RESULTS

3.1. Analysis of Orbitals in Experimentally Determined Crystal Structures.

Knowledge-based potentials (KBPs) were derived for each orbital class and driving interaction (see Methods) (Figure 3). For all PCIs, the most energetically favorable angle bin occurred at 180° forming a straight line between the Ψ angle (Acceptor – Orbital – Hydrogen or Orbital) and the Θ angle (Donor – Hydrogen or Orbital – Orbital), see Figure 3, cos(Ψ) and cos(Θ). However, the distance components, δ_HOrb and δ_OrbOrb, vary widely between the orbital classes. The rightmost panel of Figure 3A–E shows an experimentally determined example structure from the most energetically favorable angle/distance bin, the orbitals are displayed as a gray sphere, while hydrogen atoms are depicted as a white sphere.

Figure 3.

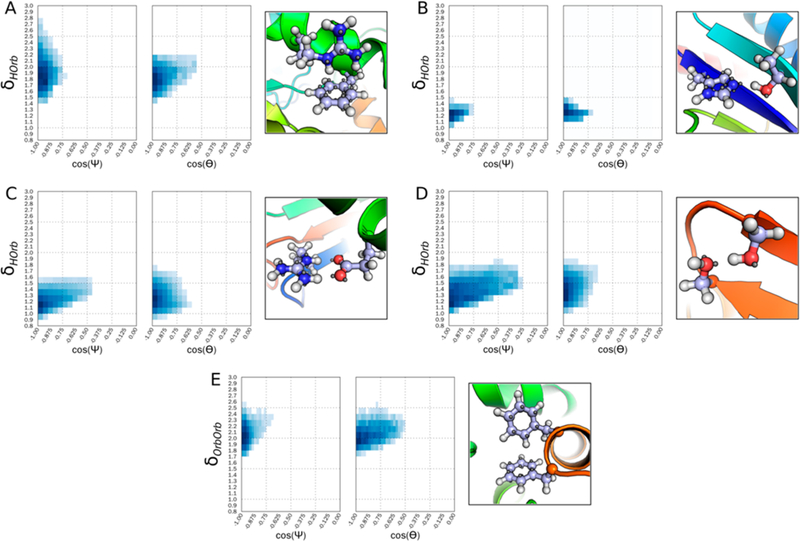
Energy potential for PCI between select side-chain interactions. Interactions are binned by hydrogen to orbital distance (A-D) or orbital to orbital distance (E), and both cos(Ψ) and cos(Θ), as defined in Figure 2. Additionally, a representation of the energetic minimum is shown for each interaction. A) Energy potential for a cation–π interaction between a C_TrTrTrPi atom interacting with a polar hydrogen on atom type N_TrTrTrPi2. B) Energy potential for a hydrogen bond between class N_Tr2TrTrPi interacting with a polar hydrogen on O_Tr2Tr2TrPi. C) Energy potential for a salt bridge between atom class O_Te2Te2TeTe interacting with a polar hydrogen on N_TrTrTrPi2. D) Energy potential for a hydrogen bond interaction between atom class O_Tr2Tr2TrPi interacting with a polar hydrogen on O_Tr2Tr2TrPi. E) Energy potential for a π–π interaction between the atom type C_TrTrTrPi interacting with another aromatic hydrogen (C_TrTrTrPi).

The PCI score function does not have distinct side-chain and backbone score functions based on atom hybridization; instead this effect is captured in the Gasteiger atom typing. For instance, the acceptor oxygen hybridization is different in a serine to serine hydrogen bond than in a serine to glutamate hydrogen bond. While they are both pci_lone_pair_h (n → σ*) interactions, the serine γ oxygen is typed as a O_Tr2Tr2TrPi (sp³), while the backbone carbonyl oxygen is typed as a O_Te2Te2TeTe (sp²). Thereby any difference in energy is captured by their frequency distributions and subsequent conversion into an energy score via the Boltzman distribution.

3.2. Testing the PCI Scoring Function.

An established test of the Rosetta score function involves the recapitulation of features observed in high-quality experimental crystal structures. We utilized a series of benchmarks that have been designed to test the new PCI score function against original crystal structure features, as well as the standard Rosetta score function, Talaris2014,³¹ and the previous standard, score!2’.²⁸

The first two tests examine recapitulation of crystal structure geometric parameters for hydrogen bonds, salt bridges, cation–π, and π–π interactions that were used to derive the KBP after perturbation of side chains and backbone atoms. The third test is based on the assumption that native protein sequences are close to optimal for their fold²⁷ and measure the ability of the score function to recover the amino acid identity of the native protein. The fourth test evaluates the packing density of designed structures versus the native structures, as native structures are often more densely packed than designed structures.⁴²

3.3. Relaxed Experimental Structures Recapitulate Nativelike Geometries.

The PCI score function was first tested to see if whether its use in the Rosetta relax protocol was able to recapitulate native geometries. To assess this ability, Lambert-azimuthal equal area projection plots were used,³² which show the distribution of hydrogen atoms around an acceptor orbital or atom. Plots were created for the native structures, the PCI score function, and the Talaris2014 score function, as well as each PCI: hydrogen bonds, salt bridges, cation–π, and π–π interactions. Distribution of atoms and orbitals should remain consistent between the relaxed models and the original crystal structures.

3.3.1. Hydrogen Bond Relax Comparison.

Figure 4 shows the comparison between the native distribution and Rosetta relaxed distribution of the hydrogen bond, specifically, a hydrogen bond between a hydroxyl donor (O_Tr2Tr2TrPi) with an sp² acceptor (O_Te2Te2TeTe). Two parameters compose the distribution: the BBase (BB) – Base (B) – Acceptor (A) – Hydrogen (H) torsional angle (Figure 4A, BAχ) and the Base – Acceptor – Hydrogen angle (Figure 4A, ∠BAH). Figure 4B displays the torsional angle BAχ as a Newman projection.

Figure 4.

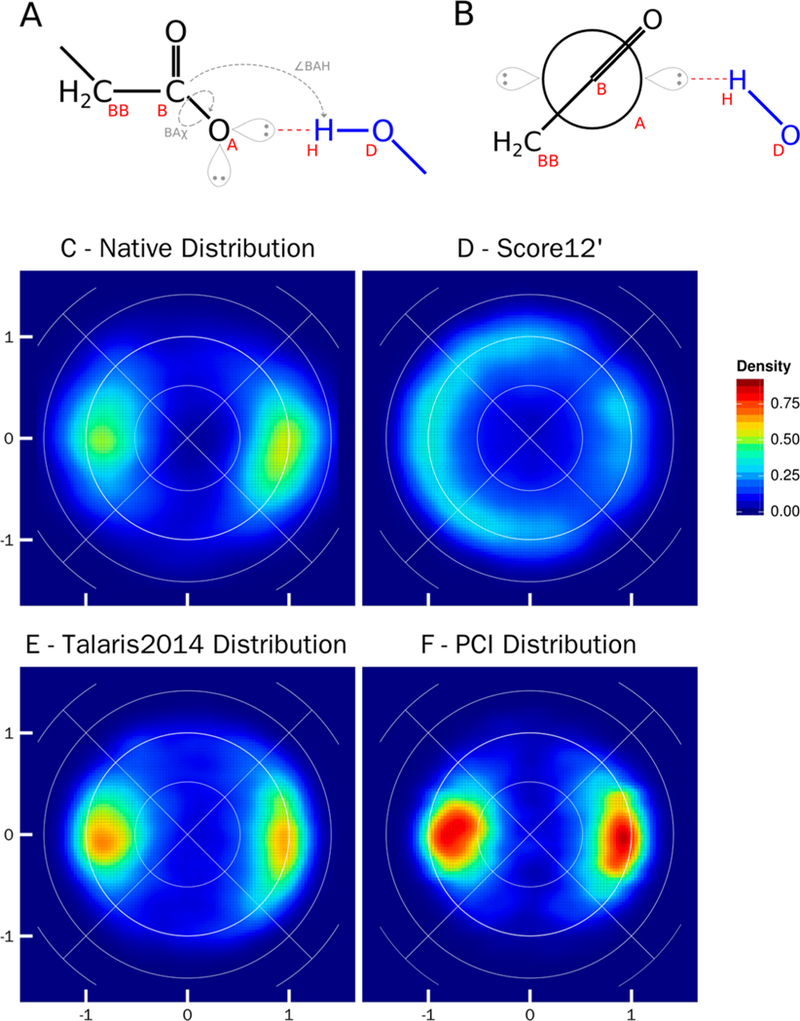
Lambert-azimuthal equal area plots for hydrogen bonds between an sp² acceptor (O_Te2Te2TeTe) and a hydroxyl donor (O_Tr2Tr2TrPi). A) Schematic representation of parameters used to create the equal area plots: ∠BAH the angle between the acceptor base (B), the acceptor (A), and donor hydrogen atom (H); BAχ the torsional angle between the acceptor Bbase (BB), acceptor base (B), acceptor (A), and the donor hydrogen atom (H). Orbitals are shown but are not included in the geometric calculations. B) Newman projection of the hydrogen bond, looking down the axis of the BAχ torsional angle. The acceptor fragment is in black, and the donor fragment is in blue. C) Lambert-azimuthal plot of the native crystal structure distribution, high density is located directly where the orbital of an sp² acceptor would be present. The y-axis plots 2*sin(∠BAH/2)*sin(BAχ), and the x-axis plots 2*sin(∠BAH/2)*cos(BAχ); the axes are the same for all graphs. D) Lambert-azimuthal plot of distribution post-Rosetta relax using score12’. E) Lambert-azimuthal plot of distribution post-Rosetta relax using Talaris2014. F) Lambert-azimuthal plot of distribution post-Rosetta relax using PCI.

The native hydrogen atom distribution with an sp² acceptor is a bimodal distribution around 0° and 180° for the BAχ torsional angle and 120° for the ∠BAH angle; this results in high density at (–1,0) and (1,0) in the Lambert-azimuthal plots (Figure 4C). As expected, these high-density regions correspond to the placement of the lone pairs on an sp² hybridized oxygen. The previous standard, score12’, showed a dispersed ring of density at a ∠BAH angle of 120° (Figure 4D), ignoring the sp² hybridized oxygen placement. Structures relaxed using the Talaris2014 score function have an equivalent distribution to native (Figure 4E), albeit with greater density. Structures relaxed using the PCI score function (Figure 4F) recapitulate the native distribution with the BAχ torsional angle having two high density regions at 0° and 180° and the ∠BAH angle centered at ~120°. The density of the PCI distribution is higher than native, but the geometry remains consistent. The plots are indicative that the geometric parameters used in the PCI score terms are correctly defined, resulting in nativelike conformations.

3.3.2. Salt Bridge Relax Comparison.

Figure 5 shows the comparison between the native distribution and Rosetta relaxed distribution of the salt bridge, specifically, a polar hydrogen donor to an sp² acceptor (O_Te2Te2TeTe). Salt bridge geometries specific to the PCI function were measured through definition of the Base (B) – Acceptor (A) – Orbital (Orb) – Hydrogen (H) torsional angle (Figure 5A, AOrbχ) and the Acceptor (A) – Orbital (Orb) – Hydrogen (H) angle (Figure 5A, ∠AOrbH).

Figure 5.

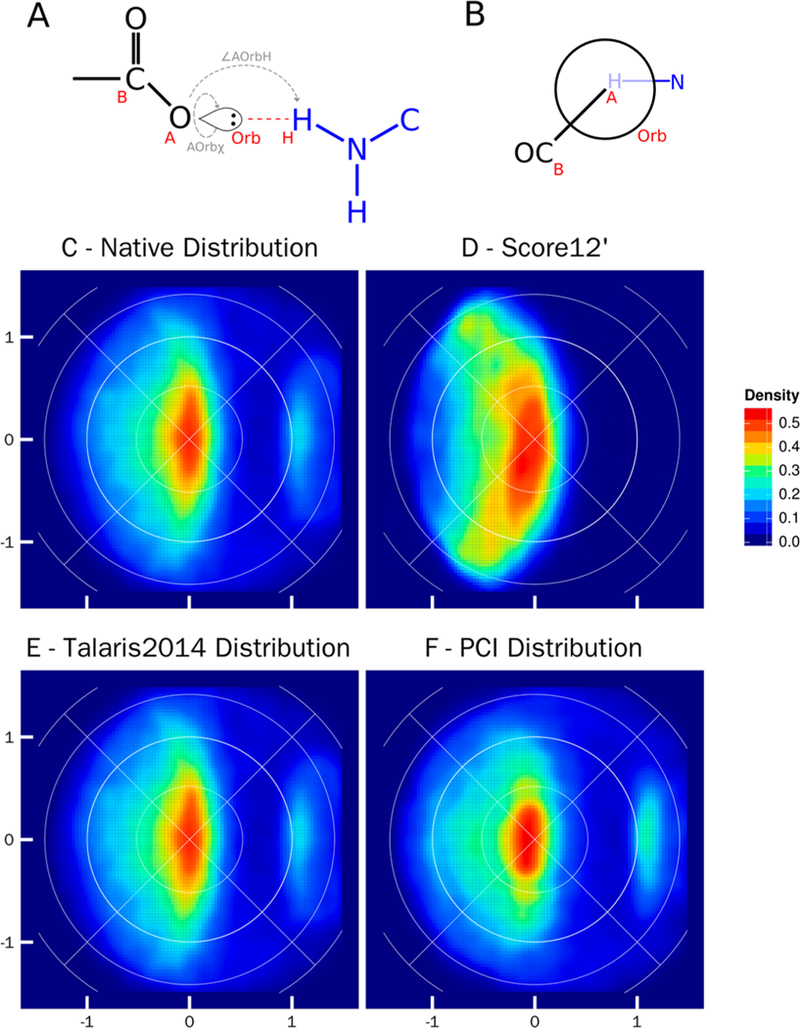
Lambert-azimuthal equal area plots for salt bridges between charged basic lysine and arginine (N_TrTrTrPi2) and aspartate and glutamate (O_Te2Te2TeTe). A) Schematic representation of parameters used to create the equal area plots: ∠AOrbH the angle between the acceptor (A), the orbital (Orb), and donor hydrogen atom (H); AOrbχ the torsional angle between the acceptor base (B), acceptor (A), the acceptor orbital (Orb), and the donor hydrogen atom (H). B) Newman projection of the salt bridge, looking down the axis of the AOrbχ torsional angle. The acceptor fragment is in black, and the donor fragment is in blue. In an ideal salt bridge the donor hydrogen atom will lie directly in line with the acceptor and orbital. C) Lambert-azimuthal plot of the native crystal structure distribution, the x-axis is computed as 2*sin(∠AOrbH/2) * cos(AOrbχ), and the y-axis is computed as 2*sin(∠AOrbH/2) * sin(AOrbχ); all four graphs have the same axes. D) Lambert-azimuthal plot of distribution post-Rosetta relax using score12’. E) Lambert-azimuthal plot of distribution post-Rosetta relax using Talaris2014. F) Lambert-azimuthal plot of distribution post-Rosetta relax using PCI.

In native crystal structures (Figure 5C), ideal salt bridges occur with an undefined AOrbχ torsional angle, as the Acceptor, Orbital, and Hydrogen points lie in a straight line. The ∠AOrbH angle has a maximum density at 180° (0,0 on the Lambert-azimuthal plots). The hydrogen atom density falls off as the ∠AOrbH angle decreases. Density also decreases rapidly as the AOrbχ torsional angle moves away from the line segment defined by (0, –1) to (0,1). Using relax with the old standard, score12’, results in a larger spread of the density along with a more pronounced curvature of the density around (0, –1) and (0,1) (Figure 5D). The relax protocol using Talaris2014 (Figure 5E) shows an almost equivalent geometry and density to the native distribution. The relax protocol using the PCI score function (Figure 5F) shows a clear preference for optimal salt bridge geometries with an undefined AOrbχ angle and an 180° ∠AOrbH angle (at 0,0 in Figure 5F). The distribution of hydrogen atoms around the orbitals is more focused when compared to the experimentally determined structures, indicating convergence in the relax protocol.

3.3.3. Cation–π Relax Comparison.

Figure 6 shows the comparison between the native distribution and the two Rosetta relaxed distributions of the cation–π interaction. Both T-stacked and offset parallel cation–π interactions are defined in equal area plots with a AOrbχ torsional angle as the Center of Mass (C) – Acceptor (A) – Orbital (Orb) – Hydrogen (H) and the ∠AOrbH angle as Acceptor (A) – Orbital (Orb) – Hydrogen (H) (Figure 6A). The orbital is the π-orbital belonging to the acceptor atom (Figure 6A–B).

Figure 6.

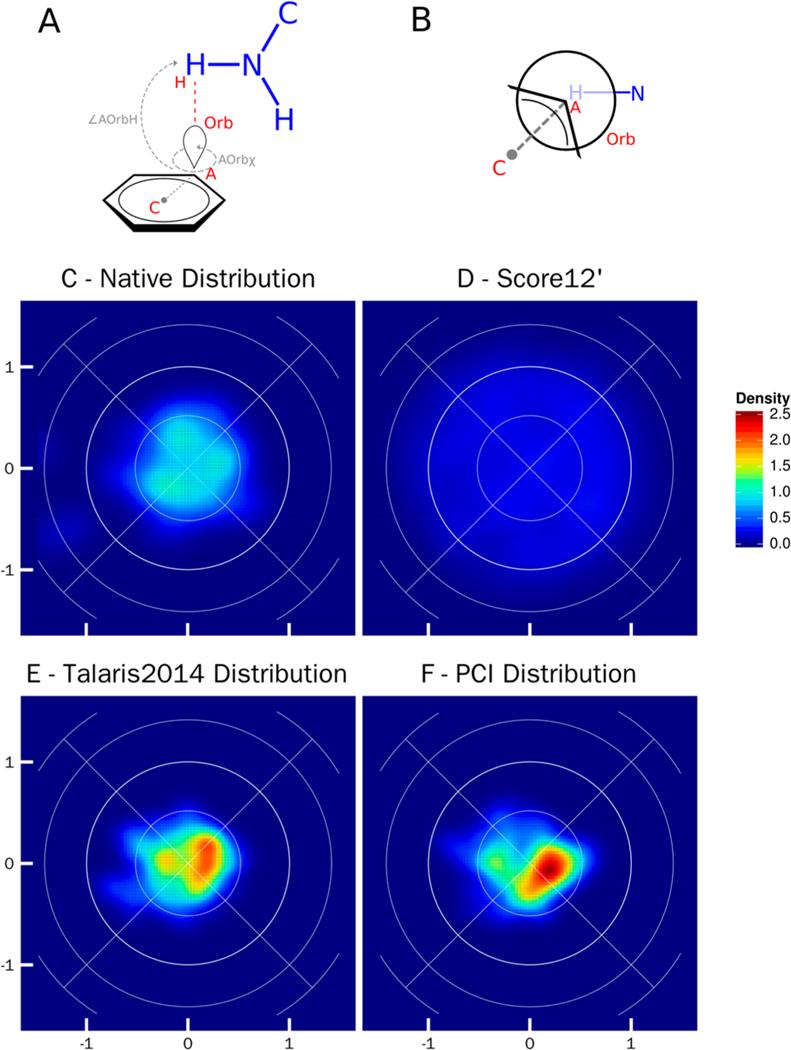
Lambert-azimuthal equal area plots for cation–π interaction between tryptophan, tyrosine, and phenylalanine (C_TrTrTrPi) and lysine and arginine (N_TrTrTrPi2). A) Schematic representation of parameters used to create the equal area plots: ∠AOrbH the angle between the acceptor (A), the orbital (Orb), and donor hydrogen atom (H); ∠Orbx the torsional angle between the ring center (C), acceptor (A), the acceptor orbital (Orb), and the donor hydrogen atom (H). B) Newman projection of the cation–π interaction, looking down the axis of the AOrbχ torsional angle. The acceptor fragment is in black, and the donor fragment is in blue. In an ideal cation–π interaction the donor hydrogen atom will lie directly in line with the acceptor and orbital. C) Lambert-azimuthal plot of the native crystal structure distribution, the x-axis is computed as 2*sin(∠AOrbH/2) * cos(AOrbχ), and the y-axis is computed as 2*sin(∠AOrbH/2) * sin(AOrbχ); all four graphs have the same axes. D) Lamber-azimuthal plot of distribution post-Rosetta relax using score12’. E) Lambert-azimuthal plot of distribution post-Rosetta relax using Talaris2014. F) Lambert-azimuthal plot of distribution post-Rosetta relax using PCI.

The native distribution for hydrogen atoms is centered at the π-orbital of the acceptor atom of the aromatic ring with an AOrbχ that is undefined (as was the case for the salt bridge) and an ∠AOrbH angle of 180° (Figure 6C). In a report on energetically favorable cation–π interactions, Gallivan et al.³ described the majority of favorable cation–π interactions occur with the N atom above the π-orbital. With the orientation of the N atom above the n-orbital, the acceptor–orbital–hydrogen angle is 180° as seen in the crystal structure Lambert-azimuthal plots. Score12’ (Figure 6D) shows a pronounced spread of density as compared to the focused, native distribution. The Talaris score function does not account for cation–π interactions; however, after relax with the Talaris2014 score function the hydrogen atom distributions are dispersed in a similar geometry to the crystal structure (Figure 6E). The PCI relax distribution shows a geometric distribution concurrent with Talaris2014 and native (Figure 6F). The regions of high density vary slightly between the Talaris and PCI distributions.

3.3.4. π–π Relax Comparison.

Figure 7 shows the comparison between the native distribution and Rosetta relaxed distribution of π–π interactions between Phe, Tyr, and Trp residues. There are two different types of π–π interactions modeled, parallel (Figure 7A) and T-stacked (Figure 7B). Parallel interactions are where two aromatic residues align where the plane of the rings lies parallel to one another. For scoring in PCI it is where an orbital of one sp² carbon of an aromatic ring interacts with the orbital of an sp² carbon on an adjacent aromatic ring. T-stacked interactions are where the plane of one ring lies perpendicular to the plane of the other interacting ring. For PCI scoring it is where the hydrogen atom of an sp² carbon interacts with the orbital of an sp² carbon on an adjacent aromatic ring–the hydrogen-to-orbital distance being closer than the orbital-to-orbital distance.

Figure 7.

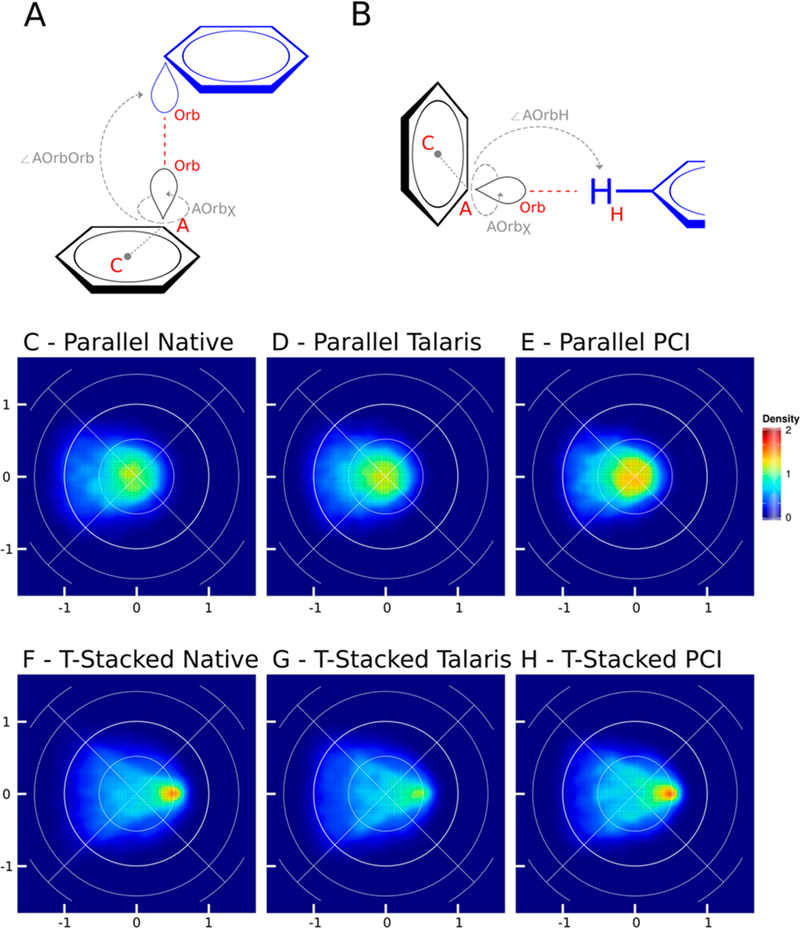
Lambert-azimuthal equal area plots for π–π interaction between two aromatic rings: tryptophan, tyrosine, and phenylalanine (C_TrTrTrPi). A) Schematic representation of parameters used to create the equal area plots for parallel stacked π–π interactions: ∠AOrbOrb the angle between the acceptor (A), the orbital (Orb), and the donor orbital (Orb); AOrbχ the torsional angle between the ring center (C), acceptor (A), the acceptor orbital (Orb), and the donor orbital (Orb). B) Parameters used to create equal area plots for T-stacked π–π interactions: ∠AOrbH the angle between the acceptor (A), the orbital (Orb), and donor hydrogen atom (H); AOrbχ the torsional angle between the ring center (C), acceptor (A), the acceptor orbital (Orb), and the donor hydrogen atom (H). C) Lambert-azimuthal plot of the parallel π–π interaction distribution in native crystal structures, the x-axis is computed as 2*sin(∠AOrbOrb/2) * cos(AOrbχ), and the y-axis is computed as 2*sin(∠AOrbOrb/2) * sin(AOrbχ); all three parallel interaction graphs (C–E) have the same axes. D) Lambert-azimuthal plot of parallel π–π distribution post-Rosetta relax using Talaris2014. E) Lambert-azimuthal plot of parallel π–π distribution post-Rosetta relax using PCI. F) Lambert-azimuthal plot of the T-stacked π–π interaction distribution in native crystal structures, the x-axis is computed as 2*sin(∠AOrbH/2) * cos(AOrbχ), and the jy-axis is computed as 2*sin(∠AOrbH/2) * sin(AOrbχ); all three T-stacked interaction graphs (F–H) have the same axes. G) Lambert-azimuthal plot of T-stacked π–π distribution post-Rosetta relax using Talaris2014. H) Lambert-azimuthal plot of T-stacked π–π distribution post-Rosetta relax using PCI.

The parallel π–π geometries were measured through definition of the Center of Mass (C) – Acceptor (A) – Orbital (Orb) – Hydrogen (H) torsional angle (AOrbχ) and the Acceptor (A) — Orbital (Orb) – Hydrogen (H) angle (∠AOrbH) (Figure 7A), whereas the T-stacked π–π geometries were measured through definition of the Center of Mass (C) – Acceptor (A) – Orbital (Orb) – Orbital (Orb) torsional angle (AOrbχ) and the Acceptor (A) – Orbital (Orb) – Orbital (Orb) angle (∠AOrbOrb) (Figure 7B).

Parallel π–π native density is shown in Figure 7C; the density is focused at the center of the plot in a roughly circular distribution with more diffuse density located on the left-hand side of the plot. This density is recapitulated in the Talaris (7D) and PCI (7E) relaxed distributions, with a slightly stronger central density in the PCI distribution compared to Talaris. T-stacked native density is shown in Figure 7F, and the density is tightly focused at the point (0.5,0), with a triangle shaped pattern of lesser density distributed to the left of the maximum density. The density is once again recapitulated in the Talaris (7G) and PCI (7H) relaxed distributions, with the PCI score function capturing the maximum tight density at (0.5,0). Figure S1 shows the distribution of both the parallel and T-stacked π–π interactions in a single plot, and the distribution shows negligible difference between the Talaris and PCI score functions.

3.3.5. Distribution of Partial Covalent Interactions between Score Terms.

Using the same data set, postrelax in Rosetta, as used in the Lambert-azimuthal plot analysis, the data was binned by the distance between orbitals, or hydrogen to orbital, and the angle formed by three atoms and/or orbitals (as defined in Figure 2). The data was analyzed using the same atom type distributions as in Table 1, although for brevity’s sake only five distributions are shown in Figure 8. Both the Talaris2014 and PCI score functions show similar distributions to the native data, although the bins are, as expected, smoother in comparison to native. Variations between Talaris2014 and PCI are minimal, as was reflected in the Lambert-azimuthal plots.

Figure 8.

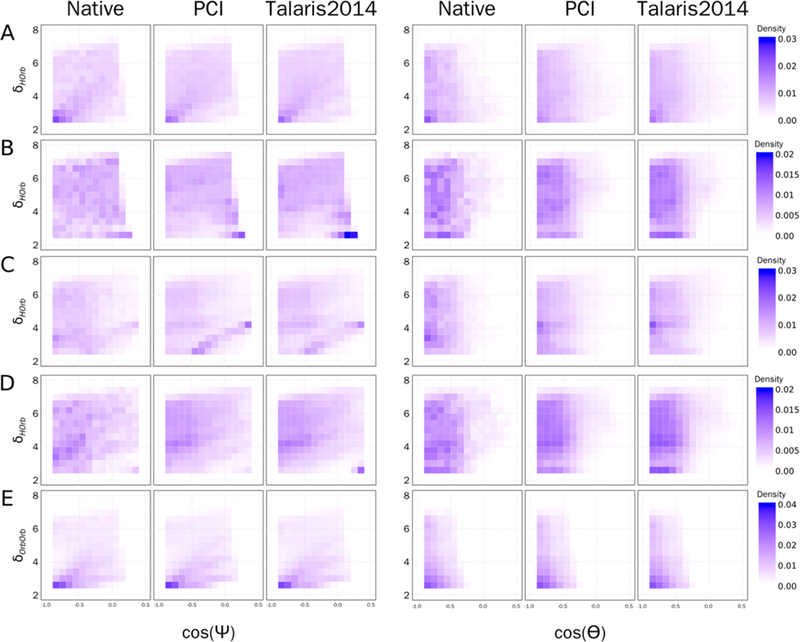
Distribution of partial covalent interaction frequency by hydrogen to orbital (δ_HOrb) or orbital to orbital (δ_OrbOrb) to the cos(Ψ) or cos(Θ) as defined in Figure 2. A) Frequency distribution for a cation–π interaction between a C_TrTrTrPi atom interacting with a polar hydrogen on atom type N_TrTrTrPi2. B) Frequency distribution for a hydrogen bond between class N_Tr2TrTrPi interacting with polar hydrogen on O_Tr2Tr2TrPi. C) Frequency distribution for a salt bridge between atom class O_Te2Te2TeTe interacting with a polar hydrogen on N_TrTrTrPi2. D) Frequency distribution for a hydrogen bond interaction between atom class O_Tr2Tr2TrPi interacting with polar hydrogen on O_Tr2Tr2TrPi. E) Frequency distribution for a π–π interaction between the atom type C_TrTrTrPi interacting with another aromatic hydrogen (C_TrTrTrPi).

3.4. Rotamer Recovery Demonstrates Energetic Minimum of PCI Score Function Is Close to Native Favorable Conformations.

Conformational sampling for proteins side chains is a combinatorial problem that produces a large search space. Experimentally determined structures contain side chains in an energetically favorable conformation. The “rotamer recovery” metric measures the recovery of the experimentally observed conformation of a protein side chain in the context of all other side chains in a protein. A stringent test for the score function is to see if the native position, or energetic minimum, of a side chain can be recovered through rotameric sampling. Rotamer recovery was evaluated on a data set of residues that contained all side-chain atoms. While partial covalent interactions only involve a subset of the 20 naturally occurring amino acids, all residues were considered during repacking (see Methods). Table 2 details the breakdown of rotamer recovery postrelaxed by amino acid type and location.

Table 2.

Rotamer Recovery for all Amino Acids^a

	score function	ARG	LYS	HIS	PHE	TRP	TYR	CYS	MET	ALA	ILE	LEU	VAL	GLY	PRO	SER	THR	ASN	GLN	ASP	GLU	Total Averaqe
	score 12’	45%	36%	65%	97%	91%	93%	97%	60%	100%	91%	83%	91%	100%	84%	86%	94%	60%	42%	68%	55%	82%
Core	Talaris2014	50%	38%	61%	96%	91%	93%	100%	63%	100%	90%	83%	91%	100%	83%	85%	94%	66%	49%	75%	59%	83%
	PCI	51%	40%	60%	95%	90%	93%	99%	66%	100%	90%	83%	91%	100%	85%	84%	94%	63%	52%	75%	55%	83%
	score 12’	15%	21%	35%	83%	84%	75%	88%	35%	100%	67%	71%	80%	100%	78%	64%	85%	39%	12%	59%	23%	58%
Surface	Talaris2014	15%	21%	35%	83%	84%	75%	88%	35%	100%	67%	71%	80%	100%	78%	64%	85%	39%	12%	59%	23%	58%
	PCI	23%	26%	38%	79%	84%	75%	88%	35%	100%	69%	71%	82%	100%	75%	66%	84%	45%	22%	61%	29%	61%
	score 12’	36%	31%	54%	94%	90%	90%	99%	57%	100%	86%	81%	89%	100%	78%	74%	89%	55%	33%	66%	38%	74%
Overall	Talaris2014	36%	31%	54%	94%	90%	90%	99%	57%	100%	86%	81%	89%	100%	78%	74%	89%	55%	33%	66%	38%	74%
	PCI	38%	32%	52%	93%	89%	90%	98%	59%	100%	86%	81%	90%	100%	80%	75%	89%	53%	36%	68%	39%	75%

^aRotamer recovery using score 12’, Talaris2014, or PCI, by iteratively trying each rotamer from the Dunbrack rotamer library at a given position. Recovery is broken out by core and surface residues, in addition to showing overall recovery. Surface residues are defined as residues with 16 or less neighbors; core residues have more than 16 neighbors.

Rotamer recovery improved when using the PCI score function (75.0%) as compared to the Talaris2014 score function (74.0%) and score12’ (74.0%). The overall improvement gained is from better rotamer recovery on the surface of the protein using the PCI score function (61% opposed to 58%) and similar performance within the core of the protein (both had 83% recovery). The two residues involved exclusively in hydrogen bond donation (Ser and Thr) showed no to slight improvement (1% and 0%, respectively) over Talaris2014. However, the Talaris2014 score function was the result of a concerted effort to reparametrize hydrogen bonding in Rosetta,³² although in terms of rotamer recovery there was little change in Talaris2014 over score12’. Residues involved in salt bridges (Arg, Lys, Asp, and Glu) showed an overall improvement of 1–2% recovery using the PCI score function over Talaris2014. These gains were most noticeable in surface residues with gains between 2 and 8%. Residues involved in cation–π or π—π interactions (Phe, Trp, Tyr) displayed no gain in rotamer recovery between Talaris2014 and PCI, even showing a slight decrease (1%). However, these residues are both at a high (~90%) recovery level using either score function, and many score terms (especially the terms related to van der Waals contacts) contribute to the overall score of these amino acids. Overall, using PCI, 9 residues improved rotamer recovery compared to Talaris2014, while only 5 declined in performance (none more than 2%); the rest were neutral. The largest gain in recovery was glutamine, which improved 3% between Talaris2014 and PCI. Rotamer recovery was further tested by analyzing if a native residue pair interaction was recovered postrelax. Talaris performs a few percentage points better than PCI in most residue pairs, and the complete table of pairs is in Table S1.

3.5. Side-Chain Design Identity Recovery Result in Nativelike Proteins.

In silico protein design is typically benchmarked on recovering side-chain identity in crystal structures, with the assumption that the native sequences of proteins are close to optimal for the protein fold.²⁷ Here we measured recovery to the native amino acid sequence using the standard and PCI score functions. A large data set of 414 monomeric proteins (see methods) was designed using an energy minimized, fixed backbone.

3.5.1. Sequence Recovery.

After a complete design of the protein, the recovery of the naturally occurring amino acid was measured (Table 3). Broadly speaking, for both PCI and Talaris2014, the core of the protein had significant sequence recovery over the surface residues. This is in part due to the restriction in the degrees of freedom in the core compared to the surface of the protein. The core of the protein has an increased chance for clashes between residues, whereas surface conformational sampling can result in little to no clashes between residues.

Table 3.

Sequence Design Identity Recovery and PSSM Recovery for All Amino Acids^a

	score function	ARG	LYS	HIS	PHE	TRP	TYR	CYS	MET	ALA	ILE	LEU	VAL	GLY	PRO	SER	THR	ASN	GLN	ASP	GLU	Total Averaqe	PSSM Recovery
	score 12’	43%	37%	49%	64%	58%	44%	45%	38%	64%	67%	68%	63%	79%	82%	47%	50%	28%	21%	52%	37%	57%	75%
Core	Talaris2014	39%	40%	43%	65%	52%	48%	60%	51%	63%	73%	82%	78%	92%	88%	59%	65%	54%	37%	57%	36%	64%	79%
	PCI	42%	42%	42%	64%	64%	54%	45%	38%	68%	69%	67%	65%	83%	87%	50%	59%	50%	36%	60%	44%	61%	75%
	score 12’	25%	24%	16%	32%	38%	37%	30%	10%	16%	33%	36%	34%	81%	73%	36%	40%	27%	20%	35%	24%	36%	70%
Surface	Talaris2014	35%	32%	20%	31%	42%	42%	31%	12%	13%	35%	44%	36%	81%	80%	36%	34%	36%	21%	46%	33%	40%	73%
	PCI	31%	36%	22%	33%	30%	41%	38%	13%	22%	37%	45%	34%	84%	81%	41%	43%	34%	19%	43%	26%	41%	69%
	score 12’	33%	29%	35%	58%	54%	43%	43%	30%	48%	61%	62%	57%	80%	77%	41%	45%	27%	20%	41%	28%	48%	72%
Overall	Talaris2014	40%	33%	34%	66%	63%	49%	43%	35%	53%	68%	74%	65%	82%	84%	39%	45%	40%	27%	48%	37%	54%	77%
	PCI	36%	38%	34%	58%	57%	51%	44%	30%	52%	64%	63%	59%	84%	83%	45%	52%	40%	27%	49%	32%	53%	72%

^aSequence design for all amino acids using score12’, Talaris2014, or PCI. Proteins were completely redesigned, and the recovery of the native amino acid at a given position was measured. For PSSM recovery, a position was labeled as “recovered” if the residue selected by design was sampled by evolution at the same position. Recovery is broken out by core and surface residues, in addition to showing overall recovery. Surface residues are defined as residues with 16 or less neighbors; core residues have more than 16 neighbors.

Design performance of PCI to Talaris2014 varied widely between residues, with an overall sequence recovery of 1% greater using Talaris2014 than PCI (Table 3 – “Total Average”). However, both Talaris2014 and PCI outperformed score12’ by 6 and 5 percentage points, respectively. Talaris2014 outperformed the PCI score function primarily in the design of hydrophobic residues (F, W, Y, M, A, I, L, V), where all but tyrosine was better recovered. The primarily hydrogen bond forming residues, serine and threonine, were better designed in the core by Talaris2014, and on the surface by PCI, for an overall gain of 6 and 7% recovery by PCI. Residues that can form salt bridges (Arg, Lys, Asp, and Glu) were all better recovered in the protein core by PCI versus Talaris2014 (2–8% improvement), while Talaris2014 outperformed 3 of the 4 residues on the surface. Residues involved in cation–π or π—π interactions (Phe, Trp, Tyr) displayed much better recovery in the core than on the surface, with an improvement of 12% greater in Trp recovery in the core. However, overall Phe, Trp, and Tyr recovery decreased slightly from Talaris2014 to PCI.

3.5.2. PSSM Recovery.

Sequence recovery, while an important metric for evaluating scoring functions, is limited by the assumption that the lowest free energy amino acid is the native residue. This is not necessarily true as multiple residues may have evolved for functionality and may be equally suitable for a given position. This limitation can be overcome by using a position specific scoring matrix (PSSM). PSSM recovery measures the fraction of amino acids that are converted to an identity that has been seen in evolution at a given position and accepts all amino acids sampled by evolution as acceptable. Both the Talaris2014 score function and the PCI score function were evaluated via PSSM recovery, using the same data set as the standard sequence recovery. Both the score12’ score function and the PCI score function performed similarly (Table 3 – “PSSM recovery”), with Talaris2014 outperforming both in the core and surface residues. The overall PSSM recovery for the structures was 72% and 77% for the PCI and Talaris2014 score function, respectively.

3.5.3. Partial Covalent Interaction Type Recovery.

One limitation of substitution analysis is the inability to identify the type of interactions created, and if, as is the focus of this work, the native partial covalent interactions are recovered. To this end, PCIs were measured between the native crystal structure data set and the designed models (Table 4).

Table 4.

Average Number of PCI Interactions by Score Type^a

	salt bridges	cation–π	π–π
native	12.6	4.5	7.8
score12’	21.6	3.6	7.6
Talaris2014	21.3	3.3	10.2
PCI	22.3	5.1	8.9

^aAverage number of interactions per protein in the data set; results are shown for native, score12’, Talaris2014, and the PCI score function.

For the PCI score function, the number of salt bridges stays consistent with Talaris, with both over-representing the average number due to Rosetta trying to satisfy charged residues on the surface of the protein. The number of cation–π bonds increases over Talaris bringing the average count closer to native. Talaris over-represents π–π bonds, whereas the PCI score function reduces the average closer to native.

3.6. Packing Metrics Calculations Show Better Packing with the Partial Covalent Interactions Score Function.

An aspect of highly stable proteins, proteins resistant to heat denaturation and enzymatic degradation, is how well the protein core excludes water. An indirect measurement of this feature is packing density, a measure of how well a protein is packed. Sheffler et al. demonstrated that packing metrics could be used to identify Rosetta designed models and native structures.⁴² Native structures are seen to be packed more densely when compared to the designed models. To this end, packing metrics were measured for the designed data set, both using Talaris2014 and the PCI score functions.

The overall packing density native structures was 0.70. Talaris2014 had a less-dense packing value of 0.62, and with the PCI score function the packing value increased slightly to 0.64 (Table 4). Although packing within the core of the protein is directly related to hydrophobic residues, the PCI score function after design packs the core tighter than the Talaris2014 score function. A possible explanation is that arrangement of outer core residues, which are typically amphipathic residues, is better geometrically arranged into PCI interactions which influences core packing.

4. CONCLUSIONS

In this work, we have introduced a new scoring function to Rosetta and illustrated that by the explicit modeling of orbitals on atoms better scoring and identification of PCIs occur. The standard Rosetta score function has been highly optimized for design and protein folding by many laboratories over the course of over a decade; this makes it difficult to improve upon. However, a litany of tests, including native geometry recovery, rotamer recovery, sequence recovery, and packing density, measured the performance of the new score function against the standard score function Talaris in Rosetta and showed modest improvement in rotamer recovery and packing density. While rotamer recovery using PCI improved compared to Talaris, sequence recovery or design performed slightly worse. This may be due to the reference energy, an estimation of the unfolded-state free energies, for each amino acid being less optimal than the reference energies in the Talaris score function. However, for all tests the PCI score function meets or exceeds the original benchmark, score12’.

After the manuscript was written, a new score function, REF15, became the new default score function in Rosetta.^38,43 The authors of the new score function optimized numerous parameters against a wide range of proteins, and other molecular systems, to achieve a score function that outperforms Talaris in a series of benchmarks. While the authors did introduce new score terms, there were no score terms specific to cation–π or π–π interactions. Future work will involve the testing of the PCI score function against the new standard.

Although the improvements shown are modest, introduction of orbitals on atoms allows for further optimization of the score function by through robust Gasteiger atom typing. Gasteiger atom typing, using the VSPER method, can be easily expanded to any atom type, especially for atom types that are found outside canonical amino acids. Further, the introduction of orbitals allows for the measurement of cation–π and π–π interactions, which have implications in correctly identifying nativelike ligand, DNA, and RNA models. This work will create a foundation to better handle noncovalent interactions between proteins and other noncanonical protein molecules. Future directions will focus on the application of the PCI score term to ligand-protein interactions, and the hypothesis that the assignment of partial point charges to the orbitals as well as atoms will allow for a more intricate view of atom-to-atom interactions.

ABBREVIATIONS

PCI

partial covalent interaction

KBP

knowledge based potentials

VSEPR

valence shell electron pair repulsion