The inherent multidimensionality of temporal variability: how common and rare species shape stability patterns

Abstract

Empirical knowledge of diversity–stability relationships is mostly based on the analysis of temporal variability. Variability, however, often depends on external factors that act as disturbances, which makes comparisons across systems difficult to interpret. Here, we show how variability can reveal inherent stability properties of ecological communities. This requires that we abandon one-dimensional representations, in which a single variability measurement is taken as a proxy for how stable a system is, and instead consider the whole set of variability values generated by all possible stochastic perturbations. Despite this complexity, in species-rich systems, a generic pattern emerges from community assembly, relating variability to the abundance of perturbed species. Strikingly, the contrasting contributions of different species abundance classes to variability, driven by different types of perturbations, can lead to opposite diversity–stability patterns. We conclude that a multidimensional perspective on variability helps reveal the dynamical richness of ecological systems and the underlying meaning of their stability patterns.

Introduction

Ecological stability is a notoriously elusive and multifaceted concept (Pimm 1984; Donohue et al. 2016). At the same time, understanding its drivers and relationship with biodiversity is a fundamental, pressing, yet enduring challenge for ecology (Elton 1946; MacArthur 1955; May 1973a; McCann 2000). The temporal variability of populations or ecosystem functions, where lower variability is interpreted as higher stability, is an attractive facet of ecological stability, for several reasons. First, variability is empirically accessible using simple time-series statistics (Tilman et al. 1996). Second, variability – or its inverse, invariability – is a flexible notion that can be applied across levels of biological organisation (Haegeman et al. 2016) and spatial scales (Wang & Loreau 2014; Wang et al. 2017). Third, variability can be indicative of the risk that an ecological system might go extinct, collapse or experience a regime shift (Scheffer et al. 2009). During the last decade, the relationship between biodiversity and ecological stability has thus been extensively studied empirically using invariability as a measure of stability (Tilman et al. 2006; Jiang & Pu 2009; Hector et al. 2010; Campbell et al. 2011; Gross et al. 2014; Pennekamp et al. 2018).

In a literal sense, stability is the property of what tends to remain unchanged (Pimm 1991). Variability denotes the tendency of a variable to change in time, so that its inverse fits this intuitive definition. However, variability is not necessarily an inherent property of the system that is observed (e.g. a community of interacting species), as it typically also depends on external factors that act as perturbations. Thus, the variability of a community is not a property of that community alone. It may be caused by a particular perturbation regime so that a different regime could lead to a different value of variability. All else being equal, stronger perturbations will generate larger fluctuations, and the way a perturbation’s intensity is distributed and correlated across species is also critical. In other words, a variability measurement reflects the response of a system to the specific environmental context in which it is embedded.

Despite this complexity, quantifying the fluctuations of an ecosystem property (e.g. primary production) can be of foremost practical interest as it provides a measure of predictability in a given environmental context (Griffin et al. 2009). However, to generalise results beyond the specific context in which variability is measured, use variability to compare the stability of different systems, establish links between different stability notions, or reconcile the conflicting diversity–stability patterns and predictions reported in the empirical and theoretical literature (Ives & Carpenter 2007), one needs to know how variability measurements can reflect a system’s inherent dynamical features.

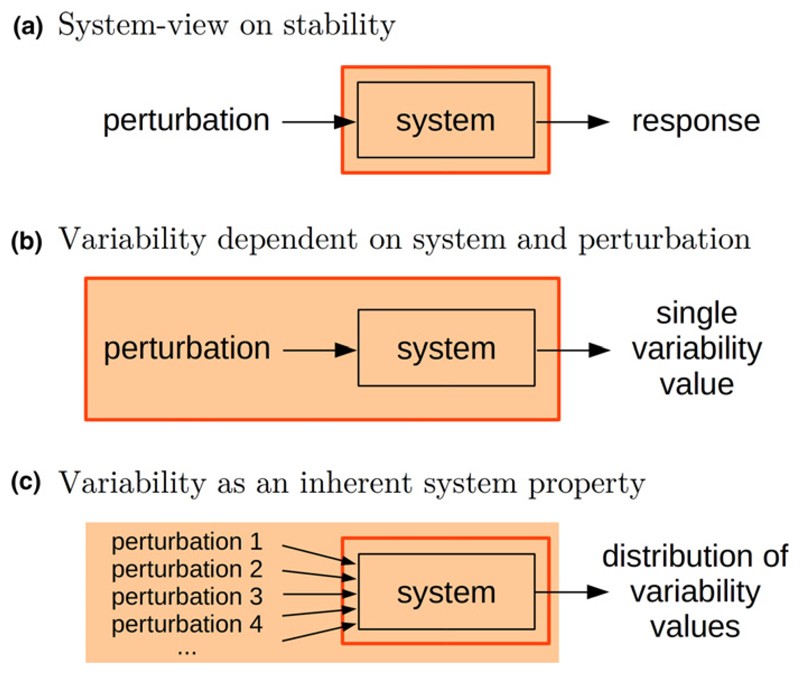
Here, we adopt an approach in which stability is viewed as the inherent ability of a dynamical system to endure perturbations (Fig. 1a). For simplicity, we will restrict to systems near equilibrium, by opposition to, for example limit cycles or chaotic attractors. We propose that a measure of stability should reflect, not a particular perturbation (as in Fig. 1b), but a system’s propensity to withstand a whole class of perturbations. We therefore consider a vast perturbation set, and study the corresponding range of community responses (Fig. 1c). Even from a theoretical perspective, considering all possible perturbations that an ecosystem can face is a daunting task. We will thus restrict our attention to weak stochastic perturbations, and derive analytical formulas for two complementary features of a community’s variability values: the average and maximum, corresponding to the mean- and worst-case perturbation scenarios respectively.

Figure 1.

Variability vs. stability. (a) Stability quantifies the way a system responds to perturbations, seen as an inherent property of the system (indicated by the red framed box). (b) By contrast, temporal variability is typically a feature of both the system studied and external factors that act as perturbations. (c) For variability to be an inherent property of the system, one can consider a whole set of perturbations, thus integrating out the dependence on specific external factors.

After having developed a general theory of variability that can be applied to any system near equilibrium, we turn our attention to species-rich communities assembled from random Lotka–Volterra models. We show that a simple variability–abundance pattern emerges from community assembly. We argue that this pattern is a generic expectation for diverse communities when interspecific interactions are strong enough, and will hold beyond random models (Barbier et al. 2018). This pattern, in conjunction with the type of perturbations considered (e.g. environmental or demographic stochasticity), determines the specific species abundance class that governs the variability distribution. In particular, we establish a fundamental link between species abundance, worst-case variability and asymptotic resilience – the long-term rate of return to equilibrium following a pulse perturbation. We finally illustrate that the contrasting contributions of various species abundance classes can be responsible for opposite diversity–invariability patterns.

Conceptual Framework

Perturbed communities

Let N_i(t) represent the abundance (or biomass) of species i at time t, and x_i(t) = N_i(t) – N_i its displacement from an equilibrium value N_i, with i running over S coexisting species that form an ecological community. We model variability as a response to stochastic forcing. We focus on stationary fluctuations caused by weak perturbations with zero mean, governed by the following dynamical system, written from the perspective of species i as

$$\frac{d}{\mathit{\text{dt}}}\underset{\text{fluctuations}}{\underbrace{x_i\left(t\right)}}={\displaystyle \sum _{j=1}^S\underset{\text{interactions}}{\underbrace{A_{ij}{x}_j\left(t\right)}}}+\underset{\text{perturbation}}{\underbrace{{\sigma }_i{\sqrt{N_i}}^{\alpha }{\xi }_i\left(t\right)}}.$$ (1)

The coefficients A_ij represent the effect that a small change in abundance of species j has on the abundance of species i. Organised in the community matrix A = (A_ij), they encode the linearisation of the nonlinear system of which (N_i) is an equilibrium. In the perturbation term, ξ_i(t) denotes a standard white-noise source (Arnold 1974; Van Kampen 1997). In discrete time, ξ_i(t) would be a normally distributed random variable with zero mean and unit variance, drawn independently at each time step (see Appendix S1 in Supporting Information).

Such models were studied by Ives et al. (2003) to analyse ecological time series. In their approach, stability properties are inferred from the system’s response to specific perturbations. Here, we build on a similar formalism, but explicitly explore a vast set of possible perturbations. Although environmental fluctuations often follow temporal patterns (Vasseur & Yodzis 2004; Ruokolainen et al. 2009; Fowler & Ruokolainen 2013), we will not consider autocorrelated perturbations. What we will explicitly consider, however, are temporal correlations between ξ_i(t) and ξ_j(t), a situation in which individuals of species i and j are similar in their perception of a given perturbation, a property known to have potentially strong, and unintuitive effects on species dynamics (Ripa & Ives 2003).

For the fluctuations of species abundance in eqn 1 to be stationary, the equilibrium state (N_i) must be stable. More technically, the eigenvalues of the community matrix A must have negative real part (May 1973a; Gurney & Nisbet 1998). The maximal real part determines the slowest long-term rate of return to equilibrium following a pulse perturbation. This rate is a commonly used stability measure in theoretical studies; we call it asymptotic resilience and denote it by ℛ_∞ (Arnoldi et al. 2016). To showcase links between stability concepts, we will compare asymptotic resilience to measures of community-wide variability.

Perturbation type

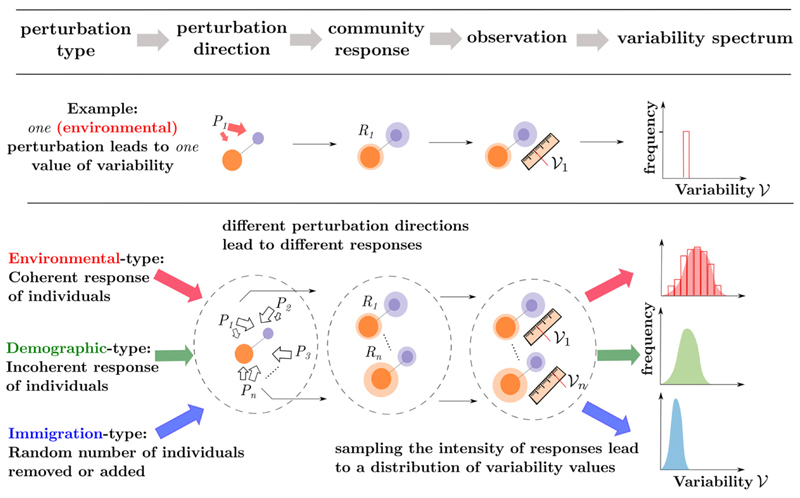
The perturbation term in eqn 1 represents the direct effect that a perturbation has on the abundance of species i. It consists of two terms: some power α of $\sqrt{N_i}$ and a species-specific term σ_iξ_i(t). The latter is a function of the perturbation itself, and of traits of species i that determine how individuals of that species perceive the perturbation. The former defines a statistical relationship between a perturbation’s direct effects and the mean abundance of perturbed species. It allows us to consider ecologically distinct sources of variability (Fig. 2).

Figure 2.

A theoretical framework for variability. Perturbations are characterised by their type, a statistical relationship between the direct effect of perturbations and the abundance of perturbed species. For a given type and fixed intensity, there remains a whole set of covariance structures of perturbations, that is various perturbation directions, that will be transformed by community dynamics into a whole set of community responses that is various covariance structures of species stationary time series. A sampling of those responses leads to a variability distribution, one for each perturbation type. Spanning all perturbation types leads to a family of variability distributions (in blue, green and red in the rightmost column).

When individuals of a given species respond in synchrony to a perturbation, the direct effect of the perturbation will be proportional to the abundance of the perturbed species, thus a value of α close to 2 (Lande et al. 2003). We call this type of perturbation environmental as fluctuations of environmental variables typically affect all individuals of a given species (Turelli 1981) leading, for example to changes in the population growth rate (May 1973b).

If individuals respond incoherently, for example some negatively and some positively, the direct effect of the perturbation will scale sublinearly with species abundance. For instance, demographic stochasticity can be seen as a perturbation resulting from the inherent stochasticity of birth and death events, which are typically assumed independent between individuals. In this case α = 1, and we thus call such type demographic (Lande et al. 2003).

Finally, setting α = 0 represents purely exogenous disturbances such as the random removal or addition of individuals. We call such perturbations immigration type. We stress, however, that actual immigration events could depend on population size, and that because we focus on zero-mean perturbations, perturbations of this type contain as much emigration than immigration. The reasoning behind this nomenclature is that, in an open system, fluctuations of an otherwise constant influx of individuals would correspond to an immigration-type perturbation.

More generally, varying α describes a continuum of perturbation types. Although not unrelated, the statistical relationship that defines perturbation type is not equivalent to Taylor’s law (Taylor 1961). The latter is an empirically observed power law relationship between the variance and mean of population fluctuations. In contrast to the perturbation type α, the exponent of Taylor’s law depends on community dynamics, for example on species interactions (Kilpatrick & Ives 2003). We will come back to this point below and in the Discussion.

Perturbation intensity

For a given community, and all else being equal, a more intense perturbation will lead to a more intense response. A disproportionate increase of the response with perturbation intensity would signal nonlinear dynamics (Zelnik et al. 2019). Near equilibrium, however, response intensity depends linearly on perturbation intensity (Ives et al. 2003). We now illustrate how to remove this trivial dependency, leading to our definition of community-wide variability.

Fluctuations induced by white-noise forcing are normally distributed, thus fully characterised by their variance and covariance. We thus construct a measure of community-wide variability based on the variance of species time series. To compare the variability of systems with different species richness, we use a community’s average variance:

$${\sigma }_{\text{out}}^2=\frac{1}{S}{\displaystyle \sum _i^{}\text{Var}}\left(N_i\left(t\right)\right).$$ (2)

Furthermore, in Appendix S2, we explain how this measure is related to the variance of ecosystem functions. In eqn 1, the perturbation intensity on species i is encoded in the term σ_i. We define perturbation intensity at the community level as the average intensity per species that is using the species-specific intensities ${\sigma }_i^2:$

$${\sigma }_{\text{in}}^2=\frac{1}{S}{\displaystyle \sum _i^{}{\sigma }_i^2}.$$ (3)

When increasing all species-specific perturbation intensities by a factor c, both ${\sigma }_{\text{in}}^2\text{and}{\sigma }_{\text{out}}^2$ increase by the same factor (see Appendix S2). To remove this linear dependence, we define variability 𝒱 as

$$𝒱=\frac{{\sigma }_{\text{out}}^2}{{\sigma }_{\text{in}}^2},$$ (4)

that is, the average species variance relative to perturbation intensity (see Ives et al. 2003 for a similar definition). Following previous work (Arnoldi et al. 2016; Arnoldi & Haegeman 2016; see Appendix S4), we construct invariability ℐ as

$$ℐ=\frac{1}{2𝒱}.$$ (5)

The factor 1/2 allows ℐ to coincide, for simple systems, with asymptotic resilience ℛ_∞ (Arnoldi et al. 2016, and Appendix S2).

Perturbation direction

At fixed intensity, perturbations can still differ in how their intensity is distributed and temporally correlated across species. Species with similar physiological traits will be affected in similar ways by, say, temperature fluctuations, whereas individuals from dissimilar species may react in unrelated, or even opposite, ways (Ripa & Ives 2003). We thus study the effect of the covariance structure of the perturbation terms that is the effect of the direction of perturbations.

Spanning the set of all perturbation directions defines a whole range of community responses. Assuming some probability distribution leads to a probability distribution over the set of responses that is a variability distribution (see Fig. 2). Spanning the set of perturbation types reveals a continuous family of variability distributions. In Fig. 2, we show three archetypal elements of this family, corresponding to α = 0 (blue distribution), α = 1 (green) and α = 2 (red).

For each distribution, we consider two complementary statistics: mean- and worst-case responses. In Appendices S3 and S4, we prove that the worst-case response is always achieved by perturbations with maximal interspecific correlations. We derive explicit formulas to compute the worst-case variability from the community matrix and species equilibrium abundances, given by eqns S18 and S24.

The mean-case scenario is defined as the average response over all perturbation directions. We prove in Appendices S3 and S4 that it is realised by a perturbation affecting all species independently and with equal intensity. This provides a simple way to compute this mean response from the community matrix and species abundances, given by eqns S19 and S25.

Results

Variability patterns for two-species community

We illustrate our variability framework on the following elementary example, in the form of a 2 × 2 community matrix

$$A=\left(\begin{array}{ll}-1\hfill & 0.1\hfill \\ -4\hfill & -1\hfill \end{array}\right).$$ (6)

This matrix defines a linear dynamical system that could represent a predator–prey community with the first species benefiting from the second at the latter’s expense. Its asymptotic resilience is ℛ_∞ = 1. Let us suppose that the prey, N₂ (second row/column of A) is 7.5 times more abundant than its predator, N₁ (first row/column of A) and consider stochastic perturbations of this community, as formalised in eqn 1.

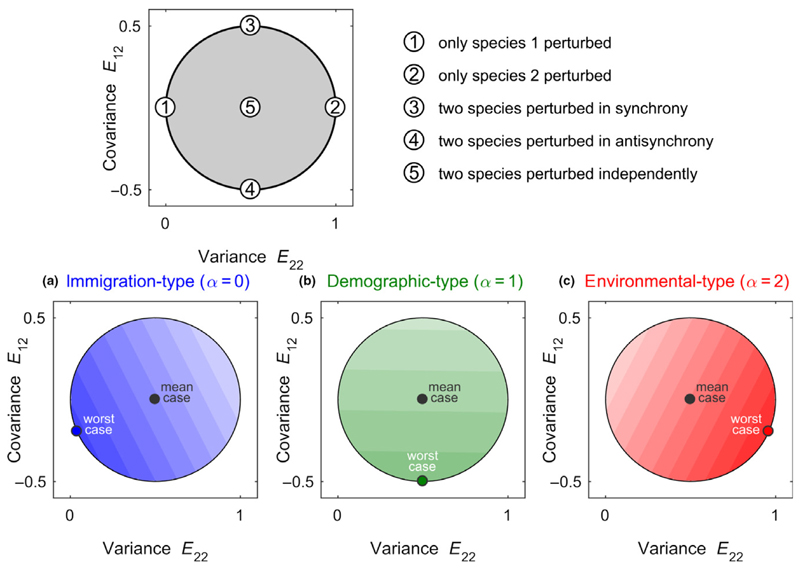
In Fig. 3, we represent the set of perturbation directions as a disc, in which every point is a unique perturbation direction (see Appendix S5 for details). The effect of a perturbation on a community is represented as a colour; darker tones imply larger responses, with the baseline colour (blue, green or red) recalling the perturbation type (α = 0, 1, 2 respectively). Points at the boundary of the disc correspond to perturbations with maximal interspecific correlations, which have the potential to generate the largest (and the smallest) variability. This is why the colour maps of Fig. 3 take their extreme values at the boundary. We see that variability strongly depends on the perturbation direction, and that this dependence is strongly affected by the perturbation type. For immigration-type perturbations (in blue), variability is largest when perturbing the predator species most strongly (the least abundant species in this example). For demographic-type perturbations (in green), perturbations that equally affect the two species but in opposite ways achieve the largest variability. For environmental-type perturbations (in red), variability is largest when perturbing the prey species (the most abundant species in this example). For all types, we see that positive correlations between the components of the perturbation (i.e. moving upwards on the disc) reduce variability (see Ripa & Ives 2003 for related results).

Figure 3.

Variability patterns for a two-species community. Top panel: For a two-species community, the set of all perturbation directions can be represented graphically as a disc (shaded in grey), with the variance of the perturbation term ξ₂(t) on the x-axis and the covariance between ξ₁(t) and ξ₂(t) on the y-axis. Some special perturbation directions are indicated (numbers 1–5, see also Appendix S5). Bottom panels: We consider a predator–prey system; the community matrix A is given by eqn 6 and the prey (species 2) is 7.5 more abundant than its predator (species 1). The induced variability depends on the perturbation directions (darker colours indicate larger variability), and this dependence in turn depends on the perturbation type α. For immigration-type perturbations (α = 0, in blue), variability is largest when perturbing species 1 most strongly. For demographic-type perturbations (α = 1, in green) perturbations that affect the two species equally strongly but in opposite ways achieve the largest variability. For environmental-type perturbations (α = 2, in red), variability is largest when perturbing species 2 most strongly. Notice that the worst case is always achieved by perturbations lying on the edge of the perturbation set. Such perturbations are perfectly correlated (see main text and Appendix S5).

Thus, in general, a given community cannot be associated to a single value of variability. Depending on the type of perturbations causing variability, different species can have completely different contributions. This stands in sharp contrast with asymptotic resilience ℛ_∞, which associates a single stability value to the community. We know from previous work (Arnoldi et al. 2016) that the smallest invariability value in response to immigration-type perturbations will always be smaller than ℛ_∞ (and larger than the slowest initial return rate, which determines a system’s reactivity (Neubert & Caswell 1997)). For any perturbation type and/or any perturbation direction there is, however, no reason to expect a relationship between invariability, asymptotic resilience, and reactivity.

Variability patterns in complex communities

The dimensionality of variability will be larger in communities comprised of many species, as their sheer number, S, increases the dimension of the perturbation set quadratically. Yet, when species interact, a generic structure can emerge from ecological assembly, revealing a simple relationship between variability and the abundance of perturbed species. To show this, we study communities assembled from Lotka–Volterra dynamics. We start from a large pool of species with randomly drawn dynamical parameters, and let the system settle to an equilibrium. During assembly species would go extinct, but by considering relatively small interspecific interaction strengths, we ensured that the dynamics were never cyclic nor chaotic. A complete description of the model is given in Appendix S6 and Matlab simulation code is available as supplementary material. We then applied our general variability framework to those communities. This enabled us to assess the community-wide impact of weak stochastic perturbations that do not cause extinctions.

In Fig. 4, we show the corresponding variability patterns for a single community, but the results hold more generally (see below). The species pool consists of S_pool = 50 species, with species interaction strengths one order of magnitude weaker than species self-regulation. After the assembly process, S = 40 species coexist in the community. In this species-rich context, the perturbation set cannot be represented exhaustively. We therefore plot the variability induced by weak species-specific perturbations (of various types) against the abundance of perturbed species. That is, we focus on the effect of a specific subset of perturbations, those affecting a single species. All perturbations without interspecific temporal correlations can be constructed by linear combination of species-specific perturbations. Linear combinations of species-specific perturbations will thus span all scenarios in which species are affected independently, but exclude scenarios in which they are perturbed in systematically correlated or anticorrelated way (in terms of the geometrical representation of Fig. 3, this amounts to restricting to the equator of the coloured discs).

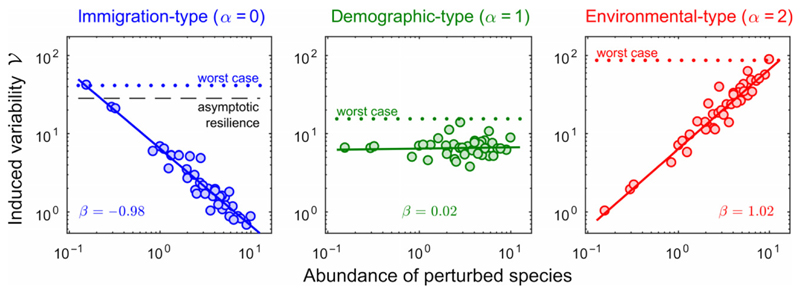
Figure 4.

Variability–abundance pattern in a complex community. We consider a community of S = 40 species, and look at the variability induced by perturbing a single species, whose abundance is reported on the x-axis. Left: When caused by immigration-type perturbations (α = 0), variability is inversely proportional to the abundance of the perturbed species (notice the log scales on both axis). The worst case is achieved by perturbing the rarest species, and is determined by asymptotic resilience (more precisely, it is close to 1=2ℛ_∞). Middle: For demographic-type perturbations (α = 1), variability is independent of the abundance of the perturbed species. The worst case is not necessarily achieved by focusing the perturbation on one particular species. Right: For environmental-type perturbations (α = 2), variability is directly proportional to the abundance of the perturbed species. The worst case is attained by perturbing the most abundant. The value β reported in each panel corresponds to the exponent of the fitted relationship $V_i\alpha N_i^{\beta }$ for each perturbation type α.

The leftmost panel shows a negative unit slope on log scales: when caused by immigration-type perturbations, variability is inversely proportional to the abundance of perturbed species. The worst-case scenario thus corresponds to a perturbation of the rarest species. Worst-case invariability is close to asymptotic resilience, which corroborates previous findings showing that the long-term rate of return to equilibrium is often associated with rare species (Haegeman et al. 2016; Arnoldi et al. 2018). In contrast, the middle panel of Fig. 4 shows that, for demographic-type perturbations, the induced community-wide variability does not depend on the abundance of the perturbed species. Finally, the rightmost panel shows a positive unit slope on log scales: when caused by environmental stochasticity, variability is proportional to the abundance of perturbed species. The worst case is thus attained by perturbing the most abundant one. Despite being intrinsically more stable than rare ones – in the sense that they buffer exogenous (immigration-type) perturbations more efficiently – common species are more strongly affected by environmental perturbations, and can thus generate the most variability.

Those patterns are not coincidental, but emerge from species interactions, as we illustrate in Fig. 5. In their absence, other patterns can be envisioned. Without interactions, the response to a species-specific perturbation involves the perturbed species only. The variability–abundance relationship is then 𝒱 = N^α/2r, with N = K. If r and K are statistically independent in the community (top-left panel in Fig. 5); this yields a different scaling than the one seen in Fig. 4. In the case of an r–K trade-off (i.e. species with larger carrying capacities have slower growth rate), abundant species would be the least stable species (bottom-left panel in Fig. 5, in blue) which is the opposite of what the leftmost panel of Fig. 4 shows. However, as interaction strength increases (from left to right in Fig. 5; the ratios of inter- to intraspecific interaction strength are 0, 0.02 and 0.1 approximately), we see emerging the relationship between abundance and variability of Fig. 4, regardless of the choice made for species growth rates and carrying capacities. The plotted results are generated assuming random interaction strengths, but we explain in Appendix S7 that those results reflects a generic limit-case behaviour that need not be specific to random interactions. The described variability–abundance patterns occur when species abundances are only faintly determined by their carrying capacities, but mostly by their many direct and indirect interactions with the rest of the community (see Appendix S7 for the precise statement).

Figure 5.

The emergence of the variability–abundance pattern (same procedure as in Fig. 4). Top row: intrinsic growth rates r and carrying capacities K are sampled independently. Bottom row: Species satisfy a r–K trade-off (r ~ 1/K). Colours correspond to the three perturbation types: α = 0 (blue), α = 1 (green) and α = 2 (red). The value β reported in each panel corresponds to the exponent of the fitted relationship $V_i\alpha N_i^{\beta }$ for each perturbation type. As interaction strength increases (left to right), we see emerging the relationship between abundance and variability described in Fig. 4 that is β = α – 1. Thus, when species interactions are sufficiently strong, variability always ends up being: inversely proportional (α = 0, blue), independent (α = 1, green) and directly proportional (α = 2, red) to the abundance of the perturbed species. Recall that the exponent α characterises the perturbation, while the exponent β describes the system response to the perturbation.

Although we considered a specific section of the perturbation set, the response to single-species perturbations can still span the whole variability distribution. In particular, for immigration-type and environmental perturbations, single-species perturbations realise the worst-case (perturbation of the rarest and most abundant species, respectively), the mean-case and the best-case scenarios (perturbation of the most abundant and rarest species respectively). For demographic-type perturbations, the situation is more subtle. Variability can be independent of species abundance, and, in general, extreme scenarios will be associated to temporally correlated perturbations affecting multiple species.

The variability–abundance patterns shown in Figs 4 and 5 should not be confused with Taylor’s law (Taylor 1961), a power law relationship between a species’ variance and its mean abundance. In fact, the variability–abundance pattern is dual to Taylor’s law: it represents the community response to single-species perturbations instead of that of individual species to a community-wide perturbation.

Diversity–invariability relationships

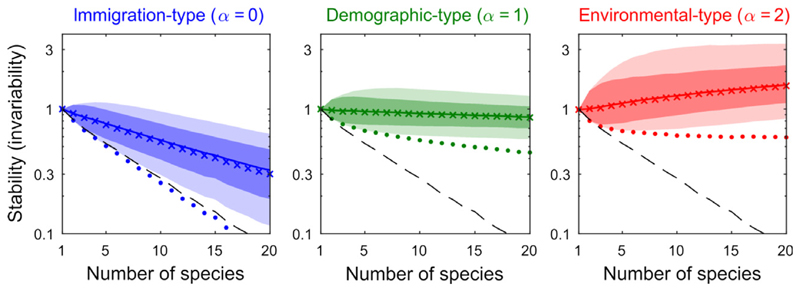
To illustrate implications of the generic variability–abundance pattern, we revisit the diversity–stability relationship, with stability quantified as invariability ℐ. We assembled communities of increasing species richness S, each associated with an invariability distribution generated from random perturbations, predictions for the mean- and worst-case scenarios, and a value of asymptotic resilience ℛ_∞.

The leftmost panel of Fig. 6 shows a negative relationship between invariability in the face of immigration-type perturbations, and species richness. Asymptotic resilience and worst-case invariability mostly coincide, with a decreasing rate roughly twice as large as that of the mean case. The middle panel suggests a different story. Mean-case demographic-type invariability stays more or less constant, whereas the worst case diminishes with species richness, although much more slowly than ℛ_∞. The relationship between diversity and stability is thus ambiguous. In the rightmost panel we see an increase in all realised environmental-type invariability values with species richness, showcasing a positive diversity–stability relationship.

Figure 6.

Different perturbation types yield contrasting diversity–stability relationships, with stability quantified as invariability ℐ. We generated random communities of increasing species richness S and computed their invariability distribution in response to random perturbations (1000 communities per species richness; 1000 perturbations per community). Full line: median invariability, dark-shaded region: 5–95th percentile, light-shaded region: minimum to maximum realised values. The ×-marks correspond to the analytical approximation for the median, the dots to the analytical formula for the worst-case. Dashed line is asymptotic resilience ℛ_∞. For immigration-type perturbations (α = 0, blue), diversity begets instability, with ℛ_∞ following worst-case invariability. For demographic-type perturbations (α = 1, green), the trend is ambiguous. For environmental-type perturbations (α = 2, red), all realised values of invariability increase with S.

The diversity stability relationships can be explained by the generic variability–abundance patterns of Figs 4 and 5 (see Appendix S8). In the case of immigration-type perturbations, species contributions to variability are proportional to the inverse of their abundance (first panel of Fig. 4). The worst-case scenario follows the abundance of the rarest species, which rapidly declines with species richness. As detailed in Appendix S8, mean-case invariability scales as the average species abundance, which also typically decreases with S.

The responses to demographic perturbations, in contrast, are not determined by any specific species abundance class (second panel of Fig. 4), so that no simple expectations based on typical trends of abundance distributions can be deduced.

We recover a simpler behaviour when looking at the response to environmental-type perturbation: abundant species now drive variability (rightmost panel of Fig. 4). As explained in Appendix S8, mean-case invariability now scales as the inverse of the average species abundance. The latter typically declines with S explaining the observed increase of mean-case invariability.

There is an analogy to be made between stability and diversity. As has been said about diversity metrics (e.g. species richness, Shannon entropy or Simpson index), different invariability measures ‘differ in their propensity to include or to exclude the relatively rarer species’ (Hill 1973). In this sense, different invariability measures can probe different dynamical aspects of a same community, with potentially opposite dependencies on a given ecological parameter of interest.

Discussion

Because it is empirically accessible using simple time-series statistics, temporal variability is an attractive facet of ecological stability. But there are many ways to define variability in models and empirical data, a proliferation of definitions reminiscent of the proliferation of definitions of stability itself (Grimm & Wissel 1997). Variability measurements often depend, not only on the system of interest, but also on external factors that act as disturbances, which makes it difficult to relate variability to other stability concepts. These caveats constitute important obstacles towards a synthetic understanding of ecological stability, and its potential drivers (Ives & Carpenter 2007).

We proposed to consider variability as a way to probe and measure an ecosystem’s response to perturbations, thus revealing inherent dynamical properties of the perturbed system. We did not seek for an optimal, single measure of variability but, on the contrary, we accounted for a vast set of perturbations, leading to a whole distribution of responses. We focused on the worst- and mean-case values of this distribution as functions of species abundance, their interactions and the type of perturbations that generates variability.

A perturbation-type characterises a statistical relationship between its direct effect on a population and the latter’s abundance. We distinguished between environmental perturbations, whose direct effects scale proportionally with population abundance; whose direct effects scale sublinearly with population abundance; and immigration-type perturbations, representing purely exogenous events such as the random addition and removal of individuals. Controlling for perturbation type and intensity, we considered all the ways this intensity can be distributed and correlated across species.

After having described a general (linear) theory for variability, which emphasises its highly multidimensional nature, we turned our attention towards species-rich communities assembled by random (nonlinear) Lotka–Volterra dynamics, seen as a generic limit of complex communities (Barbier & Arnoldi 2017). Because of the sheer number of species contained in such communities, we could have expected the dimensionality of perturbations and responses to be so large that variability distributions would be too complex to describe. However, the process of assembly allowed for a simple behaviour to emerge: a relationship between variability and the abundance of individually perturbed species. In essence, this pattern predicts that a species’ ability to buffer purely exogenous (immigration-type) perturbations is proportional to that species abundance. This pattern is not a universal feature of all communities, but will occur in diverse communities with relatively strong interactions and no community-wide structuring of the species interaction network (Appendix S7; see also Barbier et al. 2018). In conjunction to this simple pattern, the perturbation type determines species-specific contributions to the variability distribution, in a way that allows both common and rare species to drive community-wide variability patterns. This is reminiscent of diversity measures (Hill 1973), some of which (e.g. species richness) are sensitive to the presence of rare species, while others are mostly indicative of the distribution of abundant species (e.g. Simpson diversity index).

These connections with different diversity metrics can explain contrasting trends in stability (sensu invariability) as a function of species richness. That the response to immigration-type perturbations is driven by the least abundant species leads to a negative diversity–invariability relationship. Indeed, mean-case invariability is driven by the trend of species average abundance (cf. Appendix S8), which generally decreases with species richness. In contrast, in response to demographic perturbations, species contributions to variability can be independent of their abundance. In this case, variability is not expected to follow trends in abundance statistics, so that diversity–invariability patterns can be less predictable and harder to interpret. Finally, although common species buffer exogenous perturbations efficiently, they are also the most affected by environmental-type perturbations. This leads to a proportional relationship between average abundance and mean-case variability. Since mean abundance typically decreases with species richness, we get a positive diversity–invariability relationship.

Implications for empirical patterns

We showed that species abundances greatly affect variability distributions. This new insight has broad consequences. For example, it has been reported that ecosystem-level and population-level stability tend to increase and decrease, respectively, with increasing diversity (Jiang & Pu 2009; Campbell et al. 2011). Ecosystem-level stability is often quantified based on the variability of total biomass, which gives, by construction, a predominant weight to abundant species. In contrast, averages of single-species variabilities have been used to measure population-level stability (Tilman 1996). These averages are strongly affected, and can even be fully determined, by rare, highly variable species (Haegeman et al. 2016). Thus, here as well as in our theoretical results (Fig. 6), stability metrics governed by common, or rare, species tend to generate, respectively, positive and negative diversity–stability relationships. It would be interesting to test whether this observation holds more generally, for example if it can explain the results of Pennekamp et al. (2018), who found that a stability metric based on community-level variability increases with diversity, while a stability metric related to community-level resistance decreases.

The type of perturbations affects which species abundance class contributes most to variability. In turn, the physical size of the system considered affects which perturbation type dominates. This is well known in population dynamics (Engen et al. 2008), but it also transposes to the community level. At small spatial scales, implying small populations, we may expect variability to be driven by demographic stochasticity. At larger scales, implying larger populations, demographic stochasticity will be negligible compared with environmental perturbations. Just as changing the perturbation type transforms the respective roles of common and rare species, patterns of variability at different scales should reflect different aspects of a community (Chalcraft 2013), associated to different species abundance classes (abundant species at large spatial scales, rare/rarer species at small spatial scales).

In empirical systems for which different perturbation types can be applied experimentally, our theoretical predictions could be directly tested. In general, however, empirically determining the perturbation type might be a non-trivial task. To develop suitable methods, it might be helpful to first understand the link between the variability–abundance patterns (see Figs 4 and 5) and Taylor’s law (Taylor 1961). The latter is an empirically accessible pattern, relating the mean and variance of population sizes. We studied the behaviour of the community response to an individual species perturbation, while Taylor’s law focuses on the individual species response to a perturbation of the whole community. This duality also suggests that Taylor’s law is, at the community level, strongly affected by species interactions. This is known (Kilpatrick & Ives 2003), yet our approach could shed new light on the information regarding species interactions and other dynamical traits, actually contained in community-level Taylor’s laws.

On the dimensionality of stability

We noted a connection between variability and asymptotic resilience, the most popular notion in theoretical studies (Donohue et al. 2016). We showed that asymptotic resilience is comparable to the largest variability in response to a immigration-type perturbation, which is often a perturbation of the rarest species (first panel of Fig. 4). While asymptotic resilience is sometimes considered as a measure representative of collective recovery dynamics, we previously explained why that this is seldom the case (Arnoldi et al. 2018). The asymptotic rate of return to equilibrium generally reflects properties of rare ‘satellite’ species, pushed at the edge of local extinction by abundant ‘core’ species. In contrast, short-time return rates are typically controlled by abundant species and can exhibit qualitatively different properties.

The multiple dimensions of variability are related to the multiple dimensions of return times. Variability is an integral measure of the transient regime following pulse perturbations that is a superposition of responses to various pulses, some of which have just occurred and are thus hardly absorbed, while others occurred long ago and are largely resorbed. If abundant species are faster than rare ones (the case in complex communities, see Appendix S7), if they are also more strongly perturbed (e.g. by environmental perturbations), the bulk of the transient regime will be short: variability in response to environmental perturbations is associated with a short-term recovery. By contrast, if all species are, on average, equally displaced by perturbations (e.g. by immigration-type perturbations), rare species initially contribute to the overall community displacement as much as do abundant ones. Since their recovery is typically very slow, the transient regime will be long: variability in response to immigration-type perturbations is associated with a long-term recovery.

Ecologists have long acknowledged the multifaceted nature of ecological stability (Pimm 1984; Grimm & Wissel 1997; Ives & Carpenter 2007; Donohue et al. 2016); but here, we show that a single facet (variability) is in itself inherently multidimensional, thus suggesting that links across facets can be subtle. Short-term return rates may be linked with environmental variability, but environmental variability may have nothing to do with immigration-type variability, the latter possibly related with long-term return rates and driven by rare species. Because measures can be determined by different species abundance classes, we should not expect general and simple connections to hold between facets of ecological stability.

Conclusion

The multidimensional nature of variability can lead to conflicting predictions, but once this multidimensionality is acknowledged, it can be used to extensively probe the dynamical properties of a community. In particular, in species-rich systems, we revealed a generic pattern emerging from ecological assembly, relating species abundance to their variability contribution. This allowed connections to be drawn between variability and statistics of abundance distributions. We argued that similar patterns should underlie ecosystem responses to other families of perturbations (e.g. pulse perturbations). Therefore, we conclude that embracing the whole set of ecosystem responses can help provide a unifying view on ecological stability and shed new light on the meaning of empirical and theoretical stability patterns.