Multimodal Quantal Release at Individual Hippocampal Synapses: Evidence for No Lateral Inhibition

Abstract

Most CNS synapses investigated thus far contain a large number of vesicles docked at the active zone, possibly forming individual release sites. At the present time, it is unclear whether these vesicles can be discharged independently of one another. To investigate this problem, we recorded miniature excitatory currents by whole-cell and single-synapse recordings from CA3–CA1 hippocampal neurons and analyzed their stochastic properties. In addition, spontaneous release was investigated by ultrastructural analysis of quickly frozen synapses, revealing vesicle intermediates in docking and spontaneous fusion states. In these experiments, no signs of inhibitory interactions between quanta could be detected up to 1 msec from the previous discharge. This suggests that exocytosis at one site does not per se inhibit vesicular fusion at neighboring sites. At longer intervals, the output of quanta diverged from a random memoryless Poisson process because of the presence of a bursting component. The latter, which could not be accounted for by random coincidences, was independent of Ca²⁺ elevations in the cytosol, whether from Ca²⁺ flux through the plasma membrane or release from internal stores. Results of these experiments, together with the observation of spontaneous pairs of omega profiles at the active zone, suggest that multimodal release is produced by an enduring activation of an integrated cluster of release sites.

Neurons have evolved specific mechanisms to speed up exocytosis at synapses. These include the presence of vesicle intermediates in close contact with the plasma membrane, the active zone, and the precise colocalization of vesicles with Ca²⁺ channels (Augustine et al., 1987; Robitaille et al., 1990; Bezprozvanny et al., 1995; Zucker, 1996). Docked vesicles usually represent a significant fraction of the total vesicular pool, and a significant number of them might already be primed for release (Rosenmund and Stevens, 1996; Ryan et al., 1996). Because the morphological appearance of the presynaptic thickening shows complex intervesicular interactions (Harlow et al., 2001), a critical question is whether each one of these docked vesicles forms a bona fide release site and whether this can be engaged independently of its neighbors, an implicit assumption for standard quantal analysis (Redman, 1990; Jack et al., 1994). Most of what we know about this issue comes from work done at large peripheral synapses, such as the neuromuscular junction, with results either in favor of or against quantal independence (Rotshenker and Rahamimoff, 1970; Barrett and Stevens, 1972; Cohen et al., 1974; Bornstein, 1978). At central synapses, despite the presence of a large pool of docked or readily releasable vesicles (Harris and Sultan, 1995; Forti et al., 1997;Schikorski and Stevens, 1997), action potentials elicit synaptic responses that seem to arise from fusion of at most one vesicle (Perkel and Nicoll, 1993; Korn et al., 1994; Bolshakov and Siegelbaum, 1995;Stevens and Wang, 1995). Two hypotheses can be postulated: (1) no real impediment exists to prevent the simultaneous activation of multiple sites, but their release probability is so low as to make it very unlikely that they will work synchronously. This agrees well with reports on multivesicular release at inhibitory (Korn et al., 1994;Auger et al., 1998) but also excitatory (Tong and Jahr, 1994; Bolshakov et al., 1997; Ryan et al., 1997) synapses. Alternatively, (2) multivesicular release is prevented by a physical barrier raised by the initial exocytotic event. A negative interaction between sites, also known as “lateral inhibition” (Triller and Korn, 1985; Korn et al., 1994), has also arisen at hippocampal terminals, at which a decrease in release probability follows stimulation, fading away with a time constant of ∼6 msec (Stevens and Wang, 1995; Dobrunz et al., 1997). Unfortunately, evoked exocytosis does not allow an easy discrimination between effects mediated by vesicular release per se or by other downstream events, such as voltage-gated Ca²⁺ entry (Augustine et al., 1987;Zucker, 1996). In this respect, a careful analysis of the temporal pattern of occurrence of spontaneous release events, known to be independent from Ca²⁺ entry, might provide a straightforward answer.

By analyzing the stochastic properties of miniature excitatory currents (minis), we found no evidence for a physical barrier at intervals as short as 1 msec from the previous discharge, suggesting that in our experimental conditions, lateral inhibition is not present. At longer time intervals, a clear divergence from Poisson's law was present that was independent of Ca²⁺ elevations. The presence of pairs of omega figures fusing nearby and the lack of a clear dependency between bursting quanta suggest that functional release sites might be clustered.

MATERIALS AND METHODS

Hippocampal cell cultures. Postnatal CA3–CA1 hippocampal cultures were prepared from postnatal day 4 and 5 neonatal rats essentially as described previously (Malgaroli et al., 1995). Neurons were used for synaptic experiments 10–21 d after plating.

Whole-cell recordings. During whole-cell (WC) experiments, hippocampal neurons were continuously perfused with a bath solution containing 119 mm NaCl, 5 mm KCl, 2 mmCaCl₂, 2 mmMgCl₂, 25 mm HEPES, 30 mm glucose, 100 μmpicrotoxin (Sigma, St. Louis, MO), 25–100 μmd-2-amino-phosphonovalerate (APV) (Tocris Cookson, Bristol, UK), and 0.5 μm TTX (Latoxan, Rosans, France), adjusted to 305 mOsm and a pH of 7.4. Patch electrodes (2–5 MΩ) contained (in mm): 110 Cs-gluconate, 5 MgCl₂, 10 NaCl, 0.6–10 EGTA or BAPTA, 2 ATP, 0.2 GTP, and 49 HEPES, adjusted to a pH of 7.2 and 290 mOsm. Synaptic currents were recorded with an Axopatch 1D or an Axopatch 200A amplifier (Axon Instruments, Foster City, CA). Recordings were obtained at the soma of neurons using either the standard WC or the perforated WC configuration (0.25 μg/ml amphotericin B; Sigma) (V_hold = −50/−70 mV). Series resistance (5–20 MΩ) was constantly monitored by applying 1–5 mV depolarizing pulses. Current traces were filtered at 2–5 kHz and stored using a digital tape recorder. For evoked experiments, presynaptic neurons were stimulated using brief (100 μsec) constant-current injections delivered through small bipolar glass electrodes filled with physiological saline. Miniature and evoked currents were fully suppressed by application of CNQX (10 μm). In these experiments, drugs were applied primarily through the bath perfusion system and in a few cases via a motorized array of glass capillaries (diameter, 500 μm) positioned above the cells (gravity fed; complete exchange of solution in ∼20 msec). The Ca²⁺ channel blocker cadmium chloride (50–100 μm) was dissolved in control bath solution. BAPTA-AM (Molecular Probes, Eugene, OR) was first dissolved in DMSO and then added to control bath solution containing 0.05% BSA (final concentration, 25 μm; DMSO, 1:1000 final dilution). Salts and other chemicals were obtained from Sigma except as noted.

Synaptic loose-patch recordings. For loose-patch experiments, synapses were labeled withN-(3-triethylammoniumpropyl)-4-(4-(dibutylamino)styryl) pyridinium dibromide (FM1–43) as described previously (Forti et al., 1997). The pipette solution contained 119 mmNaCl, 5 mm KCl, 5 mmCaCl₂, 0 mmMgCl₂, 25 mm HEPES, 30 mm glucose, 100 μmpicrotoxin, 25–100 μm APV, and 0.5 μm TTX, adjusted to 305 mOsm and a pH of 7.4. The increased concentration of Ca²⁺ was balanced by removing Mg²⁺ to avoid changes in surface charge screening. The loose electrode (tip diameter, ∼2 μm; pipette resistance, 0.5–2 MΩ) was connected to an Axopatch 200A amplifier in voltage-clamp mode and held at the zero current potential. Pipettes were lowered to enclose selected fluorescent boutons, and loose seals were obtained spontaneously without applying any suction (seal resistance, 2–11 MΩ). During recordings, test potentials of 1 mV were continuously applied at 0.5 Hz to monitor seal-resistance stability. Current traces were filtered at 5 kHz and stored using a digital tape recorder. Experimental epochs accepted for analysis did not display seal-resistance variation in excess of 5% of mean value and had <1 mV drift in the voltage difference between the pipette (V_pipette) and the extracellular bath (V_bath) (V_pipette −V_bath). With seal resistance values two orders of magnitude larger than bath resistance, less than ∼1% of the synaptic current produced by synapses located outside the pipette would flow to ground through the loose electrode (in these conditions, signals up to a few hundred picoamperes would be below the threshold for detection).

Data analysis. Data were low-pass filtered at 3–5 kHz and digitized at 10–70 kHz off-line from a tape. Detection of miniature events was semiautomatic, as described previously (Malgaroli and Tsien, 1992). Briefly, minis were detected using two threshold-crossing criteria on the current signal and on its first derivative (thresholds: 3× background SD). Computer simulations estimated the undetected events to be <3% for signal-to-noise ratios of >4 and <20% for signal-to-noise ratios of between 3 and 4. For waveform analysis, minis were aligned with their starting point and cross-correlated over 8 msec. Cross-correlation coefficients (ρ) were compared using a FisherZ transform and independent t test; a value ofp < 0.05 was considered significant. All values throughout the text are mean ± SD.

Interval analysis. Before interval analysis, individual experiments were checked for stationarity by using the reverse arrangement test (RAT) (10 sec time window; accepted at the 5% level of significance; see below for details about the RAT). Intervals between successive minis, expressed as peak-to-peak distance, were log-binned and plotted on a log–log scale. The bin content was normalized for the bin width (McManus et al., 1987). This representation was best suited to handle the large variety of intervals encountered. The resulting histograms were fitted with nested exponentials (single and double exponentials nested in the triexponential model) using a Simplex algorithm and a maximum likelihood estimator (Sigworth and Sine, 1987). The minimum number of exponentials was chosen using the log-likelihood ratio test (Horn, 1987; Stricker et al., 1994). If minis represent streams of random events, the frequency distribution of intervals between consecutive events should display a monoexponential profile:

$$F(x)÷exp(-\lambda x),$$

where F(x) is the probability of having an interval greater than x, with λ being the mean number of events per unit of time. Log-binned frequency distribution indicated that for optimal fit of interval distributions, the sum of two decaying exponentials is required in three of seven single-bouton experiments and 14 of 24 WC experiments. In four of seven single-bouton experiments, the sum of three exponentials was needed. Regarding the analysis of WC mini-intervals, if we consider that each synapse generates spontaneous events according to a Poisson process, then the probability of finding k events in the time interval Δt is:

$$P(k)=\frac{exp(-{\mu }_i\times \mathrm{\Delta }t)\times {\mu }_i^k}{k!},$$

where μ_i is the mean Poisson rate at the ith synapse. With a population of independent synapses, the occurrence of minis at the soma is also a Poisson process, with a single parameter μ which is:

$$\mu =\sum _{i=1}^N{\mu }_i.$$

Bursts of minis were defined as groups of consecutive events with interevent intervals below a threshold,t_crit. The threshold was determined from the parameters of the best fit to interval histograms by requiring that t_crit minimized misclassifications of events belonging to each experimental component (Jackson et al., 1983). For analysis of waveform variability, pairs of consecutive minis, aligned to their starting point, were cross-correlated over an 8 msec time window. Distributions of correlation coefficients (ρ) were subdivided into two groups according to the instantaneous mini frequency [threshold at 3× (freq)], transformed with a Fisher Z transform, and compared using an independent t test (a value ofp < 0.05 was considered significant). To determine whether quanta belonging to a burst occurred independently, the run test (RT) and the nonparametric RAT were applied on bursts with n > 10 events (Bendat and Piersol, 1986). The RAT test, which is more sensitive in detecting monotonic trends, is calculated by converting the vector of sequential intervals into a matrix consisting of the digit 0 (for intervals followed by a longer interval) and 1 (for intervals followed by a shorter interval). After summing all entries, a score value A_N is obtained. If intervals do not display a monotonic trend, each interval is an independent observation of a random variable, andA_N will display a mean value:

$${\mu }_A=\frac{N(N-1)}{4}$$

with variance:

$${\varsigma }_{A_N}^2=\frac{N(2N+5)(N-1)}{72}.$$

The hypothesis of independence between successive intervals inside a burst was rejected or accepted at the α = 0.05 level of significance. Simulated distributions of minis were obtained using a Monte Carlo sampling method from monoexponential and biexponential cumulative distributions. These distributions were generated with a sample size ranging from 100 to 10,000 events. These sample sizes matched those encountered experimentally (range_WC= 450–2639 events, N = 978 ± 603, mean ± SD, n = 14 experiments; range_{single bouton} = 165–575 events, N = 398 ± 156, mean ± SD, n = 7 experiments). The time constants for monoexponential distributions were chosen near resting frequency (1 sec), whereas for biexponential cases, these ranged between 0.02 and 1 sec. Histograms were fitted and analyzed as described above. Averaged values are reported as mean ± SEM, and statistical comparisons were obtained using a Student's ttest if not otherwise indicated.

Quick freezing of hippocampal synapses. For these experiments, hippocampal neurons were grown in culture for 15 d on small plastic coverslips (0.25 cm²). Before fast freezing, coverslips were washed with a control Tyrode's solution (containing 0.5 μm TTX and 100 μm APV) and quickly positioned on the stage of a quick-freezing apparatus (Cryoblock mounted on a Cryofract 190; Reichert Jung S.A., Paris, France). Neurons were subsequently instantaneously frozen by impact against a copper block cooled to the temperature of liquid nitrogen. In these conditions, the freezing rate for a monolayer of cells a few micrometers thick is estimated to be ∼1.5 msec for a sample 40 μm thick (Heuser et al., 1979), an interval so short that ice crystals have insufficient time to grow and disrupt cellular structures. Neurons were subsequently fixed by freeze-substitution in 10% OsO₄ in acetone (from −90°C to 0°C in 60 hr), washed in acetone, rinsed in propylene oxide, and embedded in Epon. Ultrathin serial sections were obtained (70 nm; six or more sections per synapse), doubly stained with uranyl acetate and lead citrate, and examined with a Hitachi H-7000 microscope (Hitachi, Tokyo, Japan). Results are from the best two frozen preparations (n = 6 experiments, approximately five frozen coverslips per experiment, 20 mm²each), extensively serially sectioned. Omega figures were detected at the electron microscope: areas in which synapses with omega figures were present were photographed, and a full reconstruction was attempted on successive grids. The results presented are from a total ofn = 52 synapses that could be fully reconstructed plus an additional n = 1126 synaptic sections from other synapses. Docked vesicles were identified by morphometric analysis on 23 of these serially reconstructed synapses when a direct contact with the active-zone plasma membrane facing a clear postsynaptic area was present.

RESULTS

Analysis of interevent intervals: evidence for a bursting behavior

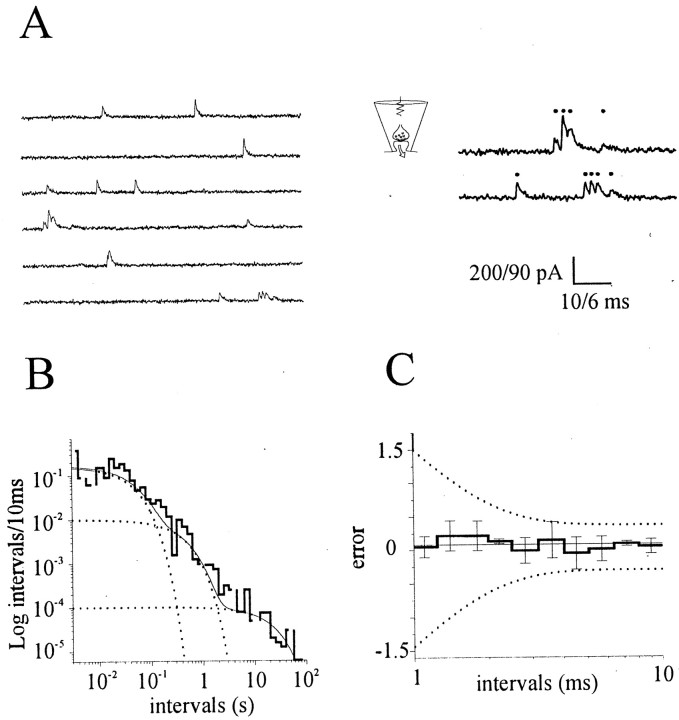
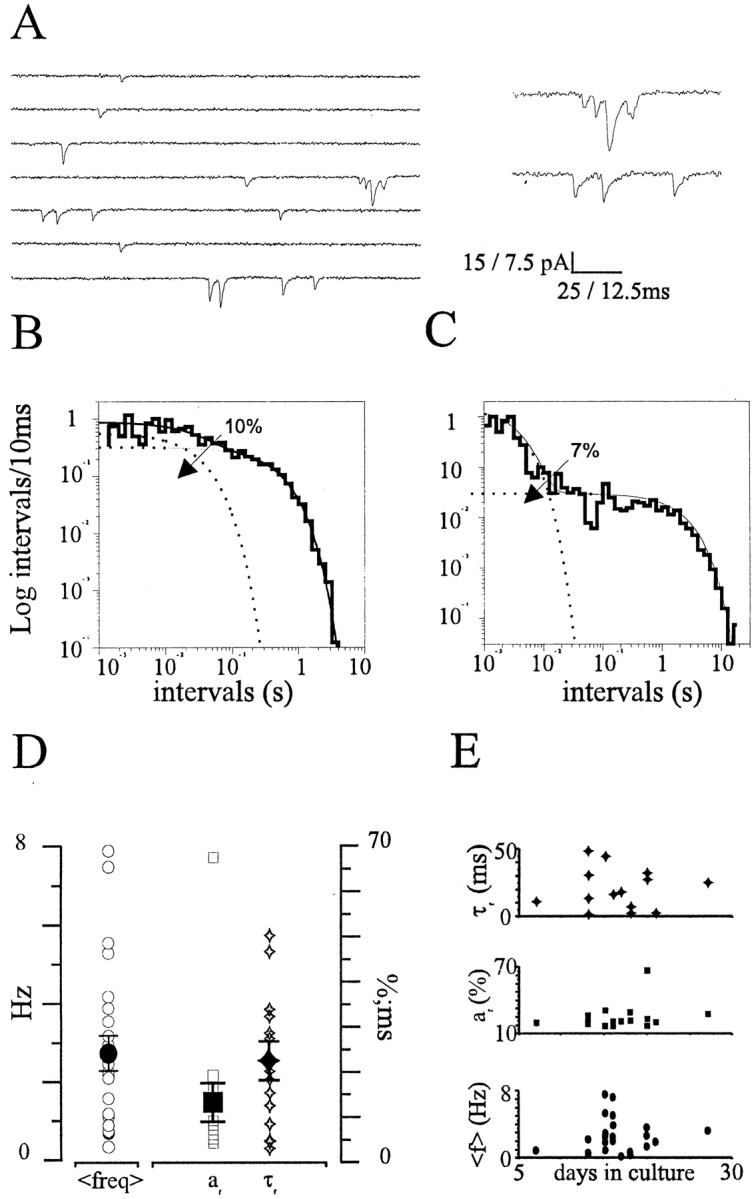
We recorded WC minis from CA3–CA1 hippocampal neurons in the presence of (in μm): 0.5 TTX, 100 picrotoxin, and 25 APV. In all neurons investigated (n = 24), current traces displayed frequent episodes, scattered throughout the recordings, in which multiple quanta were discharged along short intervals (burst), often with event superimpositions (Fig.1A). The statistical significance of this finding was tested by analyzing the distributions of interevent intervals from large data sets. According to predictions from Poisson's law, if these episodes represent random occurrences, the frequency distribution of intervals between consecutive events should display a monoexponential profile (Fatt and Katz, 1952; see also Materials and Methods). We therefore constructed frequency distributions of mini-intervals and searched for the best-fitting model. For this purpose, intervals were log-binned, with the bin content normalized for the bin width (McManus et al., 1987) and plotted on a log–log scale. This representation was chosen because it is better suited than linear binning when dealing with a large variety of time intervals. In the majority of experiments, contrary to Poisson predictions, multiple decaying exponentials were required for optimal fit of interval distributions (58% of the experiments;n = 14 of 24; p < 0.05; log-likelihood ratio test) (Fig. 1B,C). The relative area (a) and the time constants (τ) of bursting (or fast) and steady (or slow) components varied across different experiments, with the smallest detectable a_fast on the order of 3% (a_fast = 12 ± 4%;n = 14) (Fig. 1D). No significant correlation was found between the above parameters and the developmental stage of synapses in culture (p > 0.2) (Fig. 1E).

Fig. 1.

Occurrence of spontaneous minis in WC recordings and interval analysis. A, A WC current recording of minis from a hippocampal neuron. Short trains of minis can be seen consistently in these conditions (see also expanded traces on theright; holding potential = −60 mV). B, C, Log-binned mini-interval distributions from two representative WC experiments (B, τ_fast = 30.8 msec, τ_slow = 0.47 sec; C, τ_fast = 3.07 msec, τ_slow = 2.20 sec). D, Summary data for the mean mini frequency (freq), area (a_f), and time constant (τ_f) of the short-interval component (rangea_f = 3–66%, mean 12 ± 4%; range τ_f = 1.56–48.64 msec, mean 20.37 ± 4.07 msec). E, No correlation between τ_fast, a_f, and mean frequency (f) with the developmental stage of the hippocampal cultures (p > 0.1).

Monte Carlo sampling confirms the presence of a significant divergence from Poisson

To better address the statistical significance of this finding, we generated random intervals using Monte Carlo sampling methods from parental monoexponential and biexponential distributions. Random intervals were used to construct frequency histograms, and the best-fitting model was evaluated (Fig.2). Based on this analysis, the multiexponentiality encountered in ∼60% of probability distributions could not be accounted for by limited sampling. Parental monoexponential distributions were always properly identified, with precise estimates of their parameters, even for very small sample sizes (up to 100 random intervals) (Fig. 2A). Similar results were found when intervals were sampled from biexponential distributions (threshold for correct identification, n= 156) (Fig. 2B, dotted line, 5% confidence limit). In these conditions, asa_fast gets smaller (a_fast from 15 to 1%), the log-likelihood ratio score decreases, approaching the confidence limit of the analysis (Fig. 2C). For the smallesta_fast value encountered in our experiments (3%), the score was still above the 5% significance level (Fig. 2C, dotted line), and precise estimates of the original parameters could be recovered (e.g., witha_fast = 2%, the estimated value was 2.20 ± 0.17%, mean ± SD; n = 4). As illustrated in Figure 2D, when the relative values of the two time constants were varied, rejection of the monoexponential hypothesis could not be achieved for t ratios below ∼3 (Fig. 2D). On the basis of this analysis, we can conclude that the divergence from Poisson is highly significant.

Fig. 2.

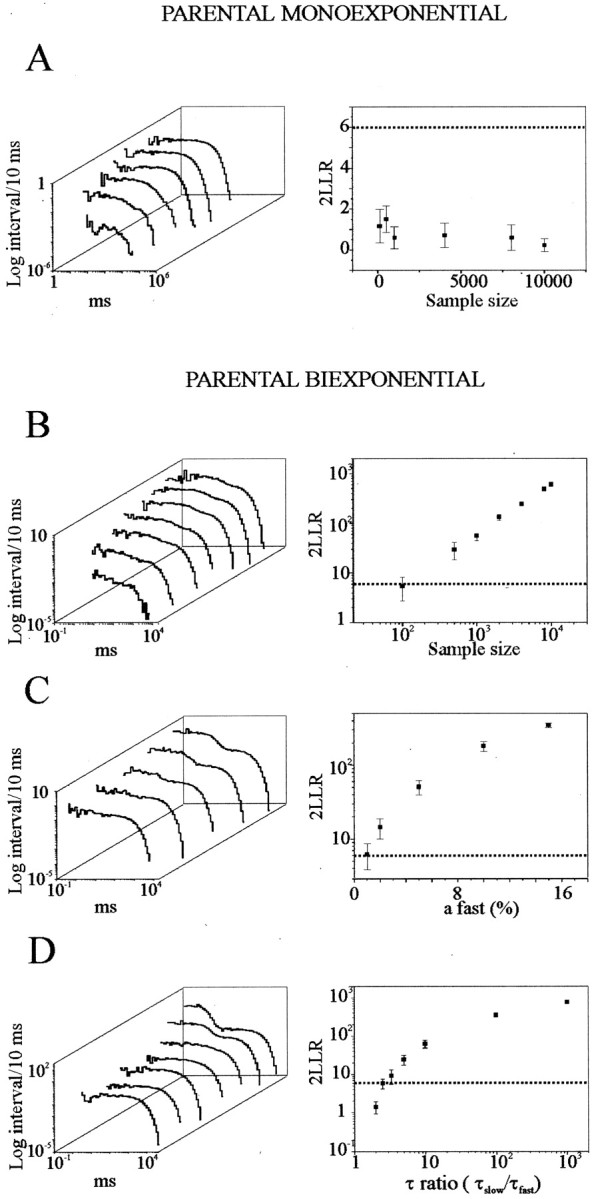
Resolution limits of interval analysis.A–D, Simulated log-binned distributions (left) and log-likelihood ratio (LLR) scores (right) obtained by Monte Carlo sampling from monoexponential and biexponential distributions while varying sample sizes (A, B), contribution from the short-interval component (C), and τ ratios (D).Right, Each point is the average of four different simulations (mean ± SD). Dotted lines represent the a = 0.05 level of significance to distinguish between the monoexponential versus the biexponential hypothesis. This resolution limit corresponds to: a sample size of n= 156 (B), area of the fast componenta_fast = 1.2% (C), and τ ratio = 2.98 (D). Parameters used in the above simulations are: A, t = 1 sec,n = 100, 500, 1000, 4000, 8000, and 10,000;B, τ_fast = 50 msec, τ_slow = 1 sec, a_fast= 15%, n = 100, 500, 1000, 2000, 4000, 8000, and 10,000; C, τ_fast = 50 msec, τ_slow = 1 sec, n = 2000,a_fast = 1, 2, 5, 10, and 15%;D, τ_slow = 1 sec,n = 2000, a_fast = 15%, τ_fast = 10, 50, 100, 200, 300, 400, and 500 msec.

Divergence from Poisson must arise at single boutons

One important consideration relates to the large number of sources of miniature events, a typical situation when recording from one hippocampal neuron and its multitude of synaptic connections. Therefore, a somatic recording electrode inescapably registers events produced by this mass of sources. On the basis of simple mathematical considerations, if N synaptic terminals are working independently of each other, releasing quanta in a random manner at different rates λ₁, … , λ_N, the sum of these releases would in the end be a Poisson process with parameters λ = λ₁ + … + λ_N (see Materials and Methods). Moreover, this conclusion would also be valid in the presence of a large variability in spontaneous quantal rates at different terminals, as reported previously in the same system (Murphy et al., 1994; Malgaroli et al., 1995). That is to say, even if multiple terminals are discharging quanta, the nonrandomness can only be either intrinsic to the release process at every terminal or produced by some form of very fast interaction between neighboring boutons, an unlikely possibility considering the rate of quanta discharge within a burst.

To further address this issue, we analyzed the amplitude and waveform of minis to see whether there was a significant change in these parameters during bursting episodes. If bursts of minis arise at individual sites, an increase in similarity would be expected, because both mini amplitude and waveform are much less variable when quanta are produced by one individual synapse (Forti et al., 1997). In addition, these events will suffer from an equal degree of cable filtering (Rall et al., 1992). Indeed, even by visual inspection, WC bursts consistently contained minis, which appeared much more homogeneous in size and waveform than quanta from resting periods. Also, when minis that belonged to different bursts were compared, their average waveforms were drastically different, suggesting that they were produced by different synapses. To get a quantitative estimate of this behavior, individual parameters from best fitting of interval distributions were used to determine an interval threshold (t_crit) subsequently used to isolate consecutive events belonging to the bursting or short-interval component. In this way, individual clusters of minis were isolated and compared inside individual experiments. Bursts were found to last, on average, 28.8 ± 3.8 msec, with an average of 2.8 ± 0.1 quanta per burst (mean ± SEM; n = 920 bursts;n = 14 experiments). When pairs of consecutive minis were compared, minis belonging to bursting episodes were much more similar in amplitude (n = 13 of 13 experiments;p < 0.05; paired t test; mean coefficient of variation_burst 0.40 ± 0.09 versus mean coefficient of variation_baseline 0.61 ± 0.12, mean ± SD) and waveform (cross-correlation coefficient, ρ: n = 6 of 9 experiments;p < 0.05). Regarding the generation of minis during bursts, using the RT and the nonparametric RAT (Bendat and Piersol, 1986), no sign of sequential correlation between minis could be found, and the hypothesis of independence was accepted in the vast majority of bursting episodes (n = 35 of 36, RT test;n = 34 of 36, RAT test). These results indicate that the occurrence of quanta during a burst does seem to diverge from a set of independent observations of a random variable (p < 0.05).

Multimodal release at single synapses: no evidence for lateral inhibition

To address this issue further, we used a technique that permits recording of quanta from individual small CNS synapses, chemically and electrically isolated from neighboring terminals (Forti et al., 1997). In this configuration, an individual bouton rendered fluorescent by FM1–43 (Betz and Bewick, 1992) can be enclosed inside a patch electrode (0.5 μm TTX, 25 μm APV, and 5 mm CaCl₂ in the recording pipette), and minis can be selectively recorded without any appreciable functional or morphological disruption (Forti et al., 1997). In all single-synapse experiments, brief episodic discharges of several quanta were consistently observed (n = 22 of 22) throughout the recordings (up to 25 min) (Fig.3A). As illustrated in Figure3B, interval distributions from single-synapse experiments consistently required multiple exponentials for best fitting, and this was independent of the experimental epoch analyzed (n = 7 of 7; p < 0.001; log-likelihood ratio test) (Horn, 1987; McManus et al., 1987). In these experiments, no significant correlation was found between the amplitude and either the rise time or instantaneous frequency of minis (n = 7;p = 0.4 and p = 0.14). On the basis of the interval threshold (t_crit), consecutive events belonging to the bursting or short-interval component (τ_fast = 168.8 ± 77.1 msec;a_fast = 48.5 ± 7.3%;n = 4 experiments) were isolated. According to this analysis, bursts were found to last, on average, 217 ± 206 msec (mean ± SEM; n = 4 experiments; range between 8 × 10⁻³ and 3.1 sec; 331 bursts), with 5.6 ± 1.4 quanta (mean ± SEM) discharged at a mean frequency of 26.4 ± 17.1 Hz (range, 8.9–43.5 Hz). Together, these episodes accounted for 26–58% of the total released quanta. Also in this recording configuration, no sign of sequential correlation was detected, and the occurrence of quanta during bursts did not diverge from a set of independent observations of a random variable (n = 20 of 22, RT test; n = 21 of 22, RAT test; p < 0.05).

Fig. 3.

Occurrence of spontaneous minis at individual synapses. A, Minis recorded from one hippocampal synapse with synaptic loose patch. Notice how trains of minis, each one marked by a dot, can occur in short intervals of time (right, expanded traces). B, Log-binned histogram of mini-intervals from the same single-bouton recording experiment as in A. Multiple exponentials were always required for best fit of interval distributions, indicating a divergence from simple Poisson statistics. The histogram presented was best fitted by the sum (solid line) of three decaying exponentials (dotted lines) (p < 10⁻⁴, τ_fast = 42.18 msec, τ_medium = 402.24 msec, τ_slow = 21.54 sec; relative areas, 51, 33, and 16%; n = 165 events). C, Ensemble plot from n = 6 single-synapse experiments illustrating the lack of inhibition at very short intervals. Each bin plots the mean ± SD of the difference between the bin entry and the fit value (error bars). The dotted lines plot the 5% confidence limits for a single-exponential distribution obtained with Monte Carlo random sampling methods (n = 11).

This large bursting contribution, larger than in WC recordings, might be explained by the loose-patch recording conditions, in which recording pipettes contain a higher Ca²⁺concentration than controls. We therefore tested the effects of the loose-patch pipette solution on WC minis. As expected, during this treatment, WC mini frequency increased significantly (f_control = 0.45 ± 0.12;f_calcium = 1.71 ± 0.43 Hz;n = 10; p < 0.05; paired ttest). In these conditions, frequency distributions of mini-intervals displayed a clear increase in the bursting component (a_{f control} = 8.3 ± 2.5%;a_{f calcium} = 38.5 ± 10.9%;n = 4 experiments; p < 0.05; pairedt test), with a slowdown of the mean bursting frequency [(τ_fast)_control = 13.3 ± 6.5 msec; (τ_fast)_calcium = 79.2 ± 36.9 msec; n = 4]. On the basis of burst analysis, this treatment did not change the occurrence of bursts (p = 0.1) but exerted a clear modulatory effect on burst duration (mean burst duration, 14.0 ± 0.8 msec in controls; 122.9 ± 13.0 msec in high Ca²⁺; p < 0.05). Hence, the significantly larger bursting contribution, with longer burst duration found with single-synapse recordings, can be explained by the higher Ca²⁺ concentration bathing the synapse.

Despite the presence of one or multiple facilitatory components, no evidence for a depressive interaction between successive quanta was found when recording from single synapses even at very short intervals. As shown in Figure 3C, between 1 and 10 msec, mini-interval distributions fell within the 5% confidence limits for a single-exponential distribution (Fig. 3C, dotted lines) (n = 6 experiments; p < 0.05). These results indicate that the probability of encountering a quantal event at very short intervals is not affected by the previous release history of the synapse. Hence, because the probability of exocytosis does not decrease after a release event, the presence of a use-dependent inhibitory interaction directly mediated by exocytosis per se [i.e., lateral inhibition (Stevens and Wang, 1995; Dobrunz et al., 1997)] can be ruled out. This inhibitory interaction between release sites has been postulated as the synaptic mechanism that prevents multivesicular exocytosis at many different CNS synapses.

Block of Ca²⁺ channels by cadmium does not suppress bursting

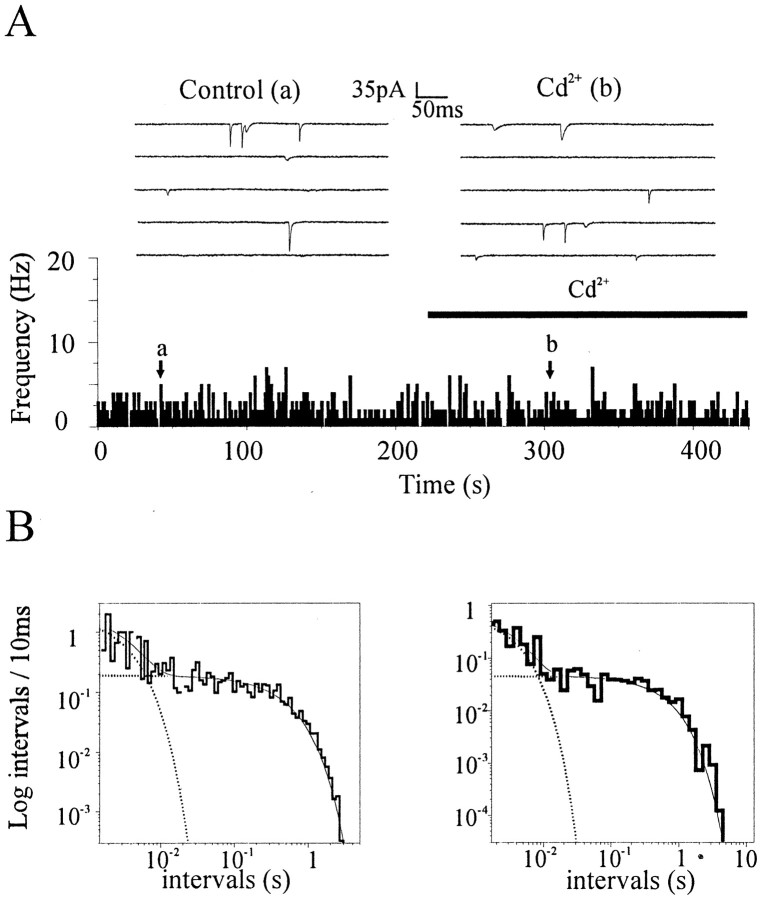
According to our results, the temporal occurrence of spontaneous quanta does not reflect simply the random release of vesicles but also some other superimposed process producing a transient increase in the probability of spontaneous release. The latter process, once initiated, seems to be modulated by Ca²⁺, because burst duration, but not burst occurrence, is more prominent in the presence of 5 mm extracellular Ca²⁺. Then a critical question is whether the low- and high-frequency components of spontaneous quantal discharge in physiological Ca²⁺ concentrations represent two steps of the same process or two diverging paths. Spontaneous release is usually considered as occurring independently from external Ca²⁺ (Dale and Kandel, 1990;Malgaroli and Tsien, 1992; Capogna et al., 1995). Despite this, a rise in cytosolic Ca²⁺ is known to produce an increase in the frequency of asynchronous or spontaneous quantal releases (Lev-Tov and Rahamimoff, 1980; Zucker and Lara-Estrella, 1983;Augustine et al., 1987; Zucker, 1996). For these reasons, the increase in quantal discharge during bursting episodes in 2 mmCa²⁺ might result from some sort of transient unbalance in presynaptic Ca²⁺levels. We have therefore tested the effects of Ca²⁺ channel blockers on spontaneous discharge. Because there is clear evidence that variable mixtures of different types of Ca²⁺ channels are present in hippocampal terminals and also contribute to transmitter release (Reuter, 1995), we used a broad-spectrum Ca²⁺ channel blocker, cadmium (50 mm). Cadmium applications fully suppressed Ca²⁺ currents and evoked postsynaptic responses (data not shown; 98 ± 9% reduction in EPSC amplitude;n = 5). Despite this clear action, no effects on mini frequency and mini amplitude were detected [f_control = 2.51 ± 0.75 Hz;f_Cd = 2.56 ± 0.74 Hz;n = 9; mini amplitude: control (I) = 39.43 ± 3.31 pA, Cd²⁺ (I) = 41.15 ± 2.97 pA; n = 5] (Fig.4A). When log-binned distributions of mini-intervals were constructed, if multiple decaying exponentials were required for optimal fit in control conditions, the same was found in the presence of Cd²⁺(n = 4 of 4; p < 0.01). In Figure4B, the two interval distributions obtained in control conditions (Fig. 4B, left) and in the presence of Cd²⁺ (Fig.4B, right) (same experiment as in Fig.4A) illustrate the biexponential nature of mini-interval distributions in both conditions.

Fig. 4.

Cadmium does not reduce mini frequency and the shape of interval distributions. A, Frequency plot of minis before and during the application of Cd²⁺ (100 mm). Notice how Cd²⁺ does not significantly reduce mini frequency. B, Log-binned histograms of mini-intervals from the same experiment as presented inA, before (left) and during (right) the application of Cd²⁺. In both conditions, histograms were better fitted by two exponential components (τ_control, 3.21 msec and 0.49 sec; τ_cadmium, 2.92 msec and 0.64 sec;a_fast-control = 4%,a_fast-cadmium = 8%;p < 0.05; n = 936 and 321 events).

Intraterminal Ca²⁺ buffering with BAPTA does not suppress bursting

Neurons are known to contain many different types of Ca²⁺ stores, including endoplasmic reticulum cisternas and mitochondria (Svoboda and Mainen, 1999). Release of Ca²⁺ from these organelles has been suggested to contribute to basal spontaneous quantal release (Frerking et al., 1997; Llano et al., 2000; Emptage et al., 2001) and also to slow oscillatory changes in mini frequency (Melamed et al., 1993). In theory, a transient release of Ca²⁺ from presynaptic Ca²⁺ stores would be capable of producing a change in spontaneous release, such as the one observed in the fast component of mini-intervals. As a test for this possibility, we examined the effect of BAPTA, a high-affinity, fast-binding kinetics Ca²⁺ chelator that has been shown to fully suppress synaptic responses evoked by action potentials (Adler et al., 1991). To introduce BAPTA into all synaptic terminals impinging on a postsynaptic neuron, we perfused neuronal cells with the membrane-permeable analog BAPTA-AM (incubation time ≥20 min). As indicated in Figure 5A, application of BAPTA-AM (in the presence of TTX) did not produce any significant effect on mini frequency (f_ctr = 2.14 ± 1.30 Hz,f_BAPTA = 1.74 ± 1.56, mean ± SD; n = 7; p > 0.1). To test for BAPTA entry inside nerve terminals, evoked responses were elicited by stimulating nearby presynaptic cells while BAPTA-AM was being perfused. As indicated in Figure 5B, a stable and almost complete suppression of evoked responses was always produced, occurring in just a few minutes, which remained unmodified after BAPTA-AM washout up to the end of recording (mean reduction = 94 ± 7%, mean ± SD; n = 4 of 4). This clear and long-lasting effect on evoked responses (up to 60 min) confirms not only that BAPTA accumulates in synapses but also that it does not leak out significantly at the end of the perfusion with BAPTA-AM during our experimental window. Despite this nearly complete suppression of evoked responses, both the frequency and amplitude of the miniature events acquired 30 min after the initiation of the perfusion with BAPTA (in the presence of TTX) were left unchanged [f_control = 1.69 ± 0.63 Hz; f_BAPTA = 1.43 ± 0.59 Hz; mini amplitude: control (I) = 22.34 ± 4.25 pA, BAPTA (I) = 26.03 ± 6.84 pA;n = 4 of 4; p > 0.05] (Fig.5B). Importantly, the frequency distributions of mini-intervals constructed from these experiments did not display any detectable change after perfusion with BAPTA (a_{f control} = 8 ± 3%; a_{f BAPTA} = 8 ± 3%; n = 3 of 3;p > 1) (Fig. 5C). The number of events per burst and the bursting frequency were also not significantly changed (events per burst, 2.5 ± 0.1 in controls and 2.6 ± 0.1 in BAPTA; burst duration, 16.7 ± 1.4 msec in controls and 19.7 ± 1.6 msec in BAPTA; p > 0.1). Together, these observations rule out the possibility that brief episodic elevations in presynaptic Ca²⁺, whether from influx through the plasma membrane or from release from internal stores, generate the divergence from Poisson described here.

Fig. 5.

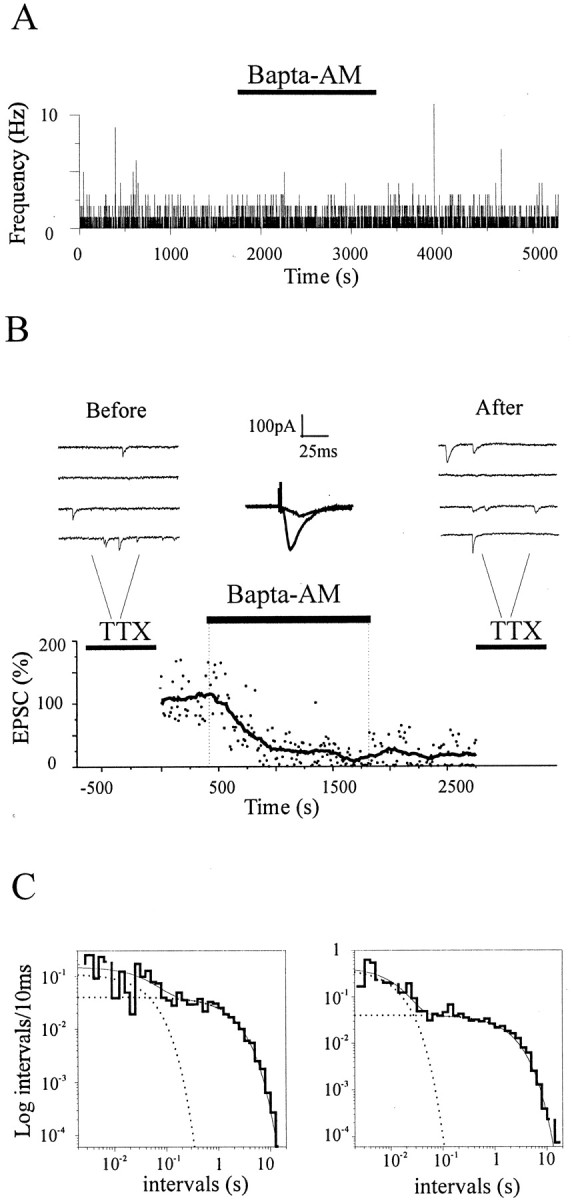
Loading nerve terminals with BAPTA does not affect mini frequency and interval distributions. A, Plot of mini frequency before, during, and after the application of BAPTA-AM (25 mm) to illustrate that BAPTA does not reduce mini frequency (0.48 ± 0.88 Hz before, 0.48 ± 0.76 Hz after; mean ± SD). B, Effects of BAPTA loading (BAPTA-AM, 25 mm) on evoked and spontaneous synaptic responses. Evoked responses were almost completely suppressed by BAPTA (t_1/2 ∼4 min), whereas mini frequency was left unaltered. Top, Consecutive traces with minis in the presence of TTX before (left) and after (right) BAPTA loading. Center, the superimposition of evoked responses 1 min before and 10 min after the beginning of BAPTA perfusion (averages of 5 consecutive traces).C, Log-binned histograms of mini-intervals before (left) and after (right) the application of BAPTA-AM. BAPTA did not abolish the fast component, and in both conditions, histograms were better fitted by the sum of two exponentials (p < 0.05; τ_fast-control = 48.64 msec, τ_slow-control = 2.18 sec,a_fast-control = 6%; τ_fast-BAPTA = 12.8 msec, τ_slow-BAPTA = 2.1 sec,a_fast-BAPTA = 5%;n = 877, 865 events).

Multiple figures of exocytosis–endocytosis visualized by quick freezing

To further extend these results, we used a nonelectrophysiological technique that permits study of exocytotic–endocytotic events at individual synapses. This is based on synapse vitrification by quick freezing (Heuser et al., 1979) in conditions in which only spontaneous events can occur (TTX and APV present, 2 mmCa²⁺). For a monolayer of hippocampal neurons in culture just a few tens of micrometers thick, freezing occurs after an estimated time well below 1 msec (Heuser et al., 1979). Therefore, this technique is particularly suited to the examination of structures that might undergo rapid changes after chemical fixation, such as vesicular intermediates of exocytosis–endocytosis (Smith and Reese, 1980). In these experiments, the cytoplasmic organization of vitrified hippocampal synapses showed the presence of a large pool of closely packed synaptic vesicles (the total recycling pool;n = 330 ± 27; n = 23 synapses), with clear accumulation of vesicles at the active zone (Fig.6A). A considerable number of these vesicles were juxtaposed to the plasma membrane, presumably docked at active sites (n = 18 ± 3) (Fig. 6A). These are the vesicles that presumably discharged during a bursting episode. Because a burst contains an average of approximately two to three quanta, it would correspond to the episodic discharge of ∼16% of the docked vesicular pool at an individual synapse. Interestingly, clear examples of vesicular fusions (omega figures) were sometimes revealed in these experiments (n = 23 omega figures from n = 52 fully reconstructed synapses and n = 1126 synaptic sections from other synapses that could not be reconstructed) (Fig.6B,C), a remarkable finding if one considers the rare occurrence of vesicles fusing spontaneously in the classic work done at the neuromuscular junction (Heuser et al., 1979). These fusions, supposedly the morphological counterpart of minis, were always localized at the center of the presynaptic area facing the postsynaptic density (i.e., the active zone of the synapse) (n = 23 of 23) (Fig. 6B,C). This is where evoked exocytosis is known to occur, suggesting that the same fusion complexes used for Ca²⁺-dependent exocytosis must be used during spontaneous discharge. In four cases, two adjacent fusing vesicles were clearly identified (n = 4 of 19 synapses) (Fig. 6D). Because the probability of a doublet occurring by chance, with two nearby vesicles spontaneously fusing or being retrieved, must be invisibly low, the latter finding strongly indicates that some clustering event took place. Additional supportive evidence arises from the analysis of coated vesicles (Fig.6E). Coated vesicles, slower intermediates of exocytosis–endocytosis, display a size that is consistent with an individual synaptic vesicle (Di Fiore and De Camilli, 2001). Numbers of coated vesicles should therefore correlate with the number of fusions occurring at each individual synapse before fast freezing. We counted the number of coated vesicles in those serially reconstructed synapses (n = 52) and compared the frequency of coated vesicles per synapse with Poisson prediction assuming random exocytosis–endocytosis at each synapse. The observed distribution strongly diverged from the Poisson expectation (reduced χ² = 1 × 10⁴¹), with an excess of synapses with multiple coated vesicles. Considering the speed of the freezing process (Heuser et al., 1979), the sharp temperature sensitivity of spontaneous exocytosis, and the slowness of synaptic endocytosis (t_1/2 ∼20 sec, from Heuser et al., 1979) and coat shedding (Di Fiore and De Camilli, 2001), these structures resulted from spontaneous exocytosis that occurred before synaptic freezing. Therefore, together these results strongly suggest that spontaneous release does not simply reflect random release of one vesicle at a time but rather involves periods of facilitated discharge, with multiple nearby vesicles undergoing exocytosis.

Fig. 6.

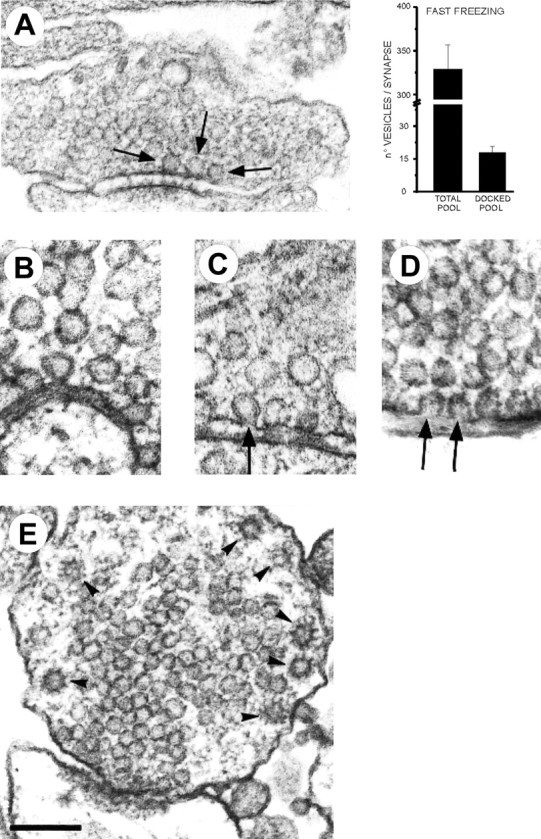
Spontaneous fusions seen with fast freezing of hippocampal synapses. A, A quick-freezing image of a hippocampal synapse. Arrows indicate the presence of three docked vesicles at the active zone. Right, Quantitative data from morphological analysis of the total recycling pool and docked pool (n = 23 serially reconstructed synapses). B, C, Spontaneous omega figures. Notice the occurrence of omega figures with narrow (B) or more widely open (C) fusion necks. Spontaneous fusions were always topographically restricted to the active zone.D, Examples of two omega figures simultaneously present at the same active zone. These always occurred in close spatial proximity. E, Example of a synapse with multiple coated vesicles. These vesicular structures were always localized at the periphery of presynaptic terminals. Scale bars: A, 0.2 μm;B–D, 0.1 μm; E, 0.15 μm.

DISCUSSION

Our experimental strategy was aimed at probing the dynamics of spontaneous quantal discharge at individual hippocampal synapses to reveal whether release sites behave independently. Since the pioneering work of Fatt and Katz (1952), spontaneous release of synaptic quanta has been considered a probabilistic process in which each quantum is randomly discharged from individual release sites. Release sites are assumed to behave independently and to discharge quanta at a very low and stable rate. These hypotheses have been confirmed by a large number of observations at the neuromuscular junction and at other peripheral terminals, although a few contrasting indications, with departures from the random Poisson hypothesis, have also been obtained (Rotshenker and Rahamimoff, 1970; Cohen et al., 1974; Bornstein, 1978). Regrettably, at the present time it is still unclear whether a similar description of the release process can be applied to small CNS synapses, in which only one active zone and a small number of release sites are present and where all components of the release machinery are confined in a fraction of a femtoliter.

Do release sites interact in a negative manner?

The assumption of statistical independence between release sites or vesicles is an important assumption when one needs to get estimates for the statistical parameters of transmitter release [i.e., the number of available vesicles or sites (N) and their release probability (p) by standard quantal analysis] (Redman, 1990; Jack et al., 1994). The ultrastructural analysis presented in Figure 6A shows that on average, 18 vesicles are docked at the active region of CA3–CA1 hippocampal synapses. On the basis of fluorescent measurements with FM1–43 (Ryan et al., 1996) and electrophysiological data (Rosenmund and Stevens, 1996), a significant fraction of these vesicles belong to the releasable pool, suggesting an equivalence between the number of docked vesicles and the number of release sites. But do sites release vesicles independently, or do they interact with each other? Each release site is presumably made by the interaction of a group of soluble N-ethylmaleimide-sensitive factor attachment protein receptor and SNARE proteins (Sutton et al., 1998; Bajjalieh, 1999) and hence is autonomous. However, there are reasons to believe that an independent behavior might not be so easily achieved (for example, the complex morphological appearance of the active region, with protein meshes spanning across long distances, thus bridging distant vesicles) (Harlow et al., 2001). These filamentous protein structures are presumably produced by the interaction of voltage-gated channels with t-SNARE proteins (Bezprozvanny et al., 1995; Seagar et al., 1999) but also by larger-molecular-weight proteins known to be present at synapses (tom Diek et al., 1998; Bajjalieh, 1999; Wang et al., 1999; Dawson-Scully et al., 2000; Betz et al., 2001). Moreover, although a large body of evidence seems to favor the SNARE hypothesis, it was suggested recently that a diffusible fusogenic protein(s) complex is the fundamental element of functional release sites (Peters et al., 2001). Along the same lines, in tiny hippocampal terminals in which hundreds of vesicles are packed together in little space, exocytosis of one vesicle might change the local activity or availability of some small diffusible components belonging to or associated with the SNARE complex, such asN-ethylmaleimide-sensitive factor, Munc 18, or even ATP molecules. Even the simple mechanical disarrangement of lipid bilayers that follows full fusion might influence the release of other vesicles (Triller and Korn, 1985). Such a spreading disruption of the active region would be severely attenuated during transient vesicular fusions (i.e., “kiss and run”) (Chow et al., 1992; Klingauf et al., 1998).

If exocytosis were to trigger some kind of negative signal spreading across the active zone, a refractory period in synaptic release would be expected (Stevens and Wang, 1995; Dobrunz et al., 1997; Matveev and Wang, 2000). The primary result of this study is that when the occurrence of spontaneous discharge is monitored from a single hippocampal synapse, no evidence for a depressive interaction between quanta is revealed. Lateral inhibition would be expected to reduce the probability of encountering quanta separated by very short intervals. The analysis of mini-intervals from WC recordings (Fig. 1), single-synapse recordings (Fig. 3), and the ultrastructural data (Fig.6) argue against this expectation. Hence, lateral inhibition of evoked responses (Stevens and Wang, 1995; Dobrunz et al., 1997; Matveev and Wang, 2000) might reflect either some processes upstream of vesicle fusion (i.e., inhibition of Ca²⁺ entry) or some intrinsic molecular difference with spontaneous release. Needless to say, a reduced synaptic output might also arise from a very low evoked release probability rather than from a physical barrier impeding multivesicular exocytosis. Regardless of the frequency of multivesicular exocytosis, because at CA3–CA1 hippocampal synapses AMPA receptors are not saturated by the content of a single vesicle (Forti et al., 1997; Liu et al., 1999), evoked multivesicular exocytosis would be capable of producing an impact on the synaptic input–output characteristics of these terminals.

Calcium and multimodal release

Our electrophysiological recordings of spontaneous quanta revealed that the dynamics of spontaneous quanta were more complex than previously thought and could not be predicted simply by applying the Poisson theorem (Fatt and Katz, 1952). This is because short epochs of multiple quantum releases were consistently found (Figs. 1-3) and were prominent enough to influence the ensemble WC behavior (Fig. 1). Ultrastructural data by quick-freezing of synapses agreed closely with this observation, revealing far too frequent pairs of spontaneous omega figures and multiple coated vesicles to be accounted for by random coincidences (Fig. 6B–E).

Both steady and transient increases in intraterminal cytosolic Ca²⁺ would be expected to produce a change in spontaneous release rates. Indeed, a correlated discharge of quanta, slower and longer lasting than described here, has been reported previously at the neuromuscular junction and has been found to depend on periodic fluctuations of intraterminal Ca²⁺ concentrations (Melamed et al., 1993). In analogy with this phenomenon, very brief Ca²⁺ transients from intracellular presynaptic stores have been suggested to drive spontaneous exocytosis in cultured hippocampal slices (Emptage et al., 2001) and multivesicular minis in cerebellar slices (Llano et al., 2000). In our experiments, when presynaptic Ca²⁺ influx through voltage-gated Ca²⁺ channels was suppressed or cytosolic Ca²⁺ was buffered, despite an almost complete suppression of evoked responses, no detectable effects on mini frequency and expression of the bursting component were found (Figs. 4 and 5). Because of the supralinear relationship between the presynaptic Ca²⁺concentration and transmitter release (Dodge and Rahamimoff, 1967), even a small reduction in such Ca²⁺transients should have produced large effects, but this was not the case. Therefore, brief and spontaneous changes in Ca²⁺ cannot account for either basal mini frequency or the brief bursting episodes observed at cultured hippocampal synapses. This does not exclude the possibility that under conditions in which the inositol triphosphate or other second messenger pathways are steadily activated, cyclic releases of Ca²⁺ from presynaptic stores could produce minis, as seen in brain slices (Llano et al., 2000; Emptage et al., 2001)

Interpretive models for synaptic bursting: the “macrosite” hypothesis

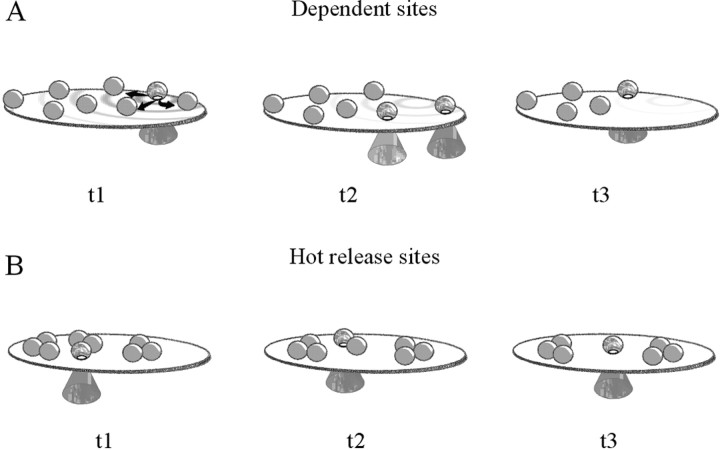
These results strongly indicate that the tendency for approximately two to three quanta to be released along a few milliseconds arises from small perturbation, intrinsic to the release machinery. After release, a site needs time before reuse (Rosenmund and Stevens, 1996; Rzyan et al., 1996); hence, the bursting mode must arise from vesicles that are already docked. Then, as depicted in Figure7, two plausible explanations for this behavior might be postulated. Release of one vesicle triggers additional exocytosis through some form of facilitation spreading across the active zone, linked to diffusion of a small messenger, protein, or lipid molecule (Fig. 7A). Because of the diffusive interaction between sites, such a mechanism should produce some degree of temporal correlation between releases. The alternative model is that a group of docking units is anatomically integrated (Harlow et al., 2001) with vesicles, together sensing some local perturbation (Fig. 7B). In the latter case, vesicles would still be released independently (i.e., Poisson releases), and bursts would be produced by a sudden increase in their Poisson rate.

Fig. 7.

Different scenarios for bursting of quanta at hippocampal synapses. A, Quanta are released at distant sites through diffusion of a small intracellular molecule. According to this scenario, releases would display some degree of dependency in their occurrence because they were triggered by this diffusing small signal. B, According to this model, a group of neighboring docked vesicles, tightly associated through some large molecular component (macrosite), gets absorbed in a hot or bursting mode and quickly discharges some or all of its vesicles.

When burst statistic was analyzed with RT and RAT tests, no clear sign of sequential correlation between minis could be found, suggesting that quanta during bursts are still released independently. Although the small sample and the short duration of bursts did not allow a more detailed analysis, the implication of these results is that the multimodal behavior is likely to reflect some structural or functional assembly features (macrosites) of the active zone rather than diffusional exchange of small molecules (Fig. 7B). When a macrosite becomes activated (“hot site”), its vesicles are released, and this is in agreement with findings of pairs of omega figures facing each other (Fig. 6). At this point, the lack of a better knowledge of the molecular organization of release sites precludes any deeper understanding of this synaptic behavior. Nonetheless, it is interesting to note that macroscopic bursting has been described previously at synapses after exposure to α-latrotoxin (Pumplin and Reese, 1977; Auger and Marty, 1997; Henkel and Sankaranarayanan, 1999), suggesting that the toxin might achieve its goal by stimulating one or more of these synaptic macrosites from outside.

Any possible functional role for bursting?

How do spontaneous release and bursting relate to the functional behavior of in situ CNS synapses? Up to now, most studies on the development of the nervous system and on processing of information by mature neuronal cells have failed to address the role of spontaneous release and concentrated only on correlated activity evoked by action potentials (Marder et al., 1996; Koch and Laurent, 1999). Clearly, a proper description of these processes should also take into consideration the large amounts of spontaneous activity to which neurons are subjected. Minis might be of particular importance for synaptic plasticity, because they occur in the absence of incoming electrical activity, and some evidence is beginning to accumulate in favor of their role (McKinney et al., 1999). In this context, the rapid discharge within a burst would certainly lead to a temporal summation in the postsynaptic spine, dramatically increasing the level of postsynaptic depolarization and the probability of Ca²⁺ influx through NMDA channels. Such a process would result in some sort of trophic support to resting synapses, thus circumventing the need for standard Hebbian mechanisms. Such modulation, possibly stronger at strong synapses, might have important implications for the development and/or maintenance of plastic changes (Bliss and Collingridge, 1993). Because Ca²⁺ modulates burst length, this phenomenon is worth a more detailed future investigation that would also consider regulation of release by activity-dependent processes, such as various short- and long-term plasticity phenomena (Lev-Tov and Rahamimoff, 1980; Zucker and Lara-Estrella, 1983; Malgaroli and Tsien, 1992; Lohof et al., 1993; Carroll et al., 1999; Antonova et al., 2001).