How to Build a Fast and Highly Sensitive Sound Detector That Remains Robust to Temperature Shifts

Abstract

Frogs must have sharp hearing abilities during the warm summer months to successfully find mating partners. This study aims to understand how frog hair cell ribbon-type synapses preserve both sensitivity and temporal precision during temperature changes. Under room (∼24°C) and high (∼32°C) temperature, we performed in vitro patch-clamp recordings of hair cells and their afferent fibers in amphibian papillae of either male or female bullfrogs. Afferent fibers exhibited a wide heterogeneity in membrane input resistance (R_in) from 100 mΩ to 1000 mΩ, which may contribute to variations in spike threshold and firing frequency. At higher temperatures, most fibers increased their frequency of spike firing due to an increase in spontaneous EPSC frequencies. Hair cell resting membrane potential (V_rest) remained surprisingly stable during temperature increases, because Ca²⁺ influx and K⁺ outflux increased simultaneously. This increase in Ca²⁺ current likely enhanced spontaneous EPSC frequencies. These larger “leak currents” at V_rest also lowered R_in and produced higher electrical resonant frequencies. Lowering R_in will reduce the hair cells receptor potential and presumably moderate the systems sensitivity. Using membrane capacitance measurements, we suggest that hair cells can partially compensate for this reduced sensitivity by increasing exocytosis efficiency and the size of the readily releasable pool of synaptic vesicles. Furthermore, paired recordings of hair cells and their afferent fibers showed that synaptic delays shortened and multivesicular release becomes more synchronous at higher temperatures, which should improve temporal precision. Together, our results explain many previous in vivo observations on the temperature dependence of spikes in auditory nerves.

SIGNIFICANCE STATEMENT The vertebrate inner ear detects and transmits auditory information over a broad dynamic range of sound frequency and intensity. It achieves remarkable sensitivity to soft sounds and precise frequency selectivity. How does the ear of cold-blooded vertebrates maintain its performance level as temperature changes? More specifically, how does the hair cell to afferent fiber synapse in bullfrog amphibian papilla adjust to a wide range of physiological temperatures without losing its sensitivity and temporal fidelity to sound signals? This study uses in vitro experiments to reveal the biophysical mechanisms that explain many observations made from in vivo auditory nerve fiber recordings. We find that higher temperature facilitates vesicle exocytosis and electrical tuning to higher sound frequencies, which benefits sensitivity and selectivity.

Introduction

Bullfrogs that jump into a cold pond must adapt quickly to a sudden temperature shift. Indeed, frogs adapt to a wide range of physiological body temperatures (Lillywhite, 1970). In summer, male frogs gather together and chorus to attract female frogs (Capranica, 1965). To successfully find mating partners, their hearing abilities must be sharp during the warm summer months. Bullfrog vocalization is composed of low- to mid-frequency sounds (200–2000 Hz) (Capranica, 1965; Smotherman and Narins, 2000; Simmons, 2004). In addition, hearing is also critical for hunting insects and for territorial behaviors (Emlen, 1968; Wiewandt, 1969). Insects flap their wings at frequencies ranging from 330 Hz (house flies) to 600 Hz (mosquitos), and can even reach 1040 Hz (small biting midges). All these sound frequencies are detected and transduced by one frog hearing organ, the amphibian papilla (van Dijk et al., 2011). Accordingly, recordings of spikes in bullfrog amphibian papilla auditory nerve fibers display tuning curves with greatest sensitivity and best frequencies (or lowest sound level thresholds) ∼500–650 Hz (Feng et al., 1975; Heffner and Heffner, 2007).

Hair cells transduce sound vibrations into graded electrical signals, which are then sent to the brain via all-or-none action potential (AP) spikes in the afferent fibers. At higher temperatures, in vivo single afferent fiber recordings have revealed an increase in spontaneous spike rates, a decrease in sound intensity threshold, a reduced latency of response to sound, and higher vector strength (or better phase-locking precision) (Stiebler and Narins, 1990; van Dijk et al., 1990). This indicates that the hearing organ of frogs transmit more sound information with higher sensitivity, shorter reaction times, and greater temporal precision at higher temperatures. What are the cellular and synaptic mechanisms that explain these in vivo observations?

Hair cells detect and transduce three aspects of sound: intensity, phase, and frequency. Information on the rapid onset and offset of sound transients must also be faithfully transmitted to the auditory nerves at ribbon-type synapses (Rutherford, 2015; Coate et al., 2019). Indeed, hair cells express ion channels with some of the fastest activation and deactivation kinetics (Engel, 2008; Heil and Peterson, 2017; Pangrsic et al., 2018). Sound signals are conveyed via transduction currents (I) mediated by K⁺ influx at the stereocilia bundles, resulting in graded receptor membrane potential (V_m) changes. The detection of low-level sounds is facilitated if hair cells have a large input resistance (R_in), given that V_m = R_in × I. However, phase-locking to higher frequency sounds with fine temporal precision requires shorter membrane time constants (τ_m = R_in × C_m, where C_m is the hair cell membrane capacitance), which requires a small R_in. How does the hair cell cope with these conflicting demands on its biophysical properties? Does hair cell R_in decrease when temperature increases, as observed in other bullfrog neurons (Santin et al., 2013)? If so, how do auditory hair cells and their synapses compensate for temperature-dependent changes in R_in to maintain both sound sensitivity and temporal fidelity?

To answer these questions, we performed in vitro voltage-clamp and current-clamp recordings from single hair cells and their afferent fibers in bullfrog amphibian papillae under both room (23°C–25°C) and high (30°C–33°C) temperature. Our results suggest that larger amplitudes and faster Ca²⁺ and K⁺ current kinetics lead to higher hair cell intrinsic electrical resonance frequencies, whereas shorter synaptic delays, more synchronous multivesicular release, and decreased R_in at high temperature contributes to more precise phase locking to sound signals. Moreover, we propose that hair cells compensate for lower R_in at high temperature by increasing the size of the readily releasable pool (RRP) of vesicles and the efficiency of exocytosis, resulting in an enhancement of sound sensitivity.

Materials and Methods

Animal care and tissue preparation.

Adult bullfrogs (Rana catesbeiana; Rana Ranch) of both sexes were used for experiments. Protocols for animal care and anesthesia were approved by the Institutional Animal Care and Use Committee of Oregon Health and Science University. Bullfrogs were sedated in 7°C–10°C water bath for ∼5–10 min, anesthetized by isoflurane (0.025 ml/g body weight) absorbed through the skin, and then double-pitched and decapitated. Amphibian papillae were carefully dissected, and the connection of hair cells and afferent fibers was exposed via a spit-open procedure as described previously (Keen and Hudspeth, 2006; Li et al., 2009).

Experimental design.

The acutely split-open tissue preparation was placed in a recording chamber perfused with artificial perilymph containing the following (in mm): 95 NaCl, 2 KCl, 2 CaCl₂, 1 MgCl₂, 25 NaHCO₃, 3 glucose, 1 creatine, and 1 sodium pyruvate, pH 7.30 (osmolarity 235 mOsm) at 1–2 ml/min, bubbling with 95% O₂ and 5% CO₂. Reagents and salts were obtained from Sigma-Aldrich, if not specified otherwise. Temperature was adjusted by heating the bath perfusion with a temperature controller (Warner Instruments), which changed bath temperature between room (23°C–25°C) and high (30°C–33°C) temperatures. Tissue temperature was measured continuously by a miniature thermistor placed close to the perfused amphibian papillae preparation during patch-clamp recordings.

The semi-intact preparation of hair cells and their connecting afferent fibers was placed on an upright microscope with a 60× water-immersion objective (Olympus, BX51WI) and digital CCD camera (QImaging). Whole-cell patch recordings were performed with an EPC-10/2 (HEKA) patch-clamp amplifier controlled by PatchMaster software (HEKA). Recording pipettes were pulled on a PP-830 vertical puller (Narishige) from borosilicate glass pipettes (1B150F-4, World Precision Instruments). Patch pipettes were pulled to resistances of 5–7 mΩ for hair cells. Pipettes were filled with the intracellular solution containing the following (in mm): 77 Cs-gluconate, 20 CsCl, 1 MgCl₂, 10 TEA-Cl, 10 HEPES, 2 EGTA, 3 Mg-ATP, 1 Na-GTP, and 5 Na₂-phosphocreatine, adjusted to pH 7.3 with CsOH. We used 2 mm EGTA as the mobile internal Ca²⁺ buffer of hair cells (Frank et al., 2009; Johnson et al., 2017). The pH-independent Ca²⁺ buffer BAPTA (2 mm) and another pH buffer MOPS (10 mm) were also used in some experiments (see Fig. 9). To measure resting membrane potential (see Fig. 5A), outward potassium current (see Fig. 5B,D), membrane input resistance (see Fig. 6), and resonant frequency (see Fig. 7), we used a more physiological K⁺-based internal solution containing the following (in mm): 77 K-gluconate, 30 KCl, 1 MgCl₂, 10 HEPES, 2 EGTA, 3 Mg-ATP, 1 Na-GTP, and 5 Na₂-phosphocreatine, adjusted to pH 7.3 with KOH. To preserve a more intact hair cell intracellular milieu, we also performed perforated-patch recordings using an internal solution with gramicidin (40–50 μg/ml; see Figs. 5A, 6) plus a fluorescent dye (AlexaFluor-488 Hydrazide; Thermo Fisher Scientific). Hair cells containing dye in their cytoplasm were excluded from analysis.

Figure 9.

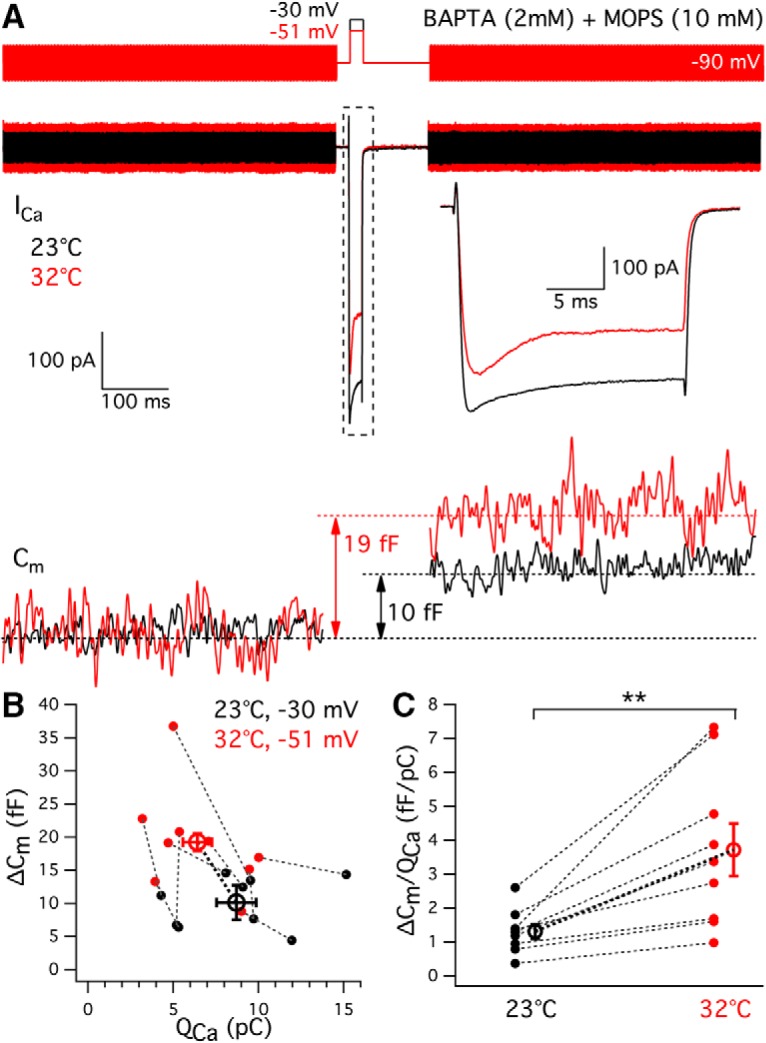
Exocytosis increases at high temperature, even when Ca²⁺ influx is reduced. A, The depolarization potential at high temperature was adjusted between −45 and −55 mV to elicit the same or less amount of Ca²⁺ influx to that at room temperature. To exclude temperature effects on pH or Ca²⁺ buffering, hair cells were patched with internal solution containing pH-insensitive Ca²⁺ buffer BAPTA (2 mm) and a different pH buffer MOPS (10 mm). Averages of Ca²⁺ currents (I_Ca) from nine hair cells triggered by depolarization to −30 mV at 23°C (black) and to −51 ± 2 mV at 32°C (red). The I_Ca was expanded in time scale from the one in a dashed line box. The membrane capacitance change (ΔC_m) was 10 fF at 23°C (black) and 19 fF at 32°C (red). B, ΔC_m versus Q_Ca from individual hair cells depolarized to −30 mV at 23°C (black) and to −51 mV at 32°C (red). Data points connected by a dashed line were recorded from the same hair cell. C, Exocytosis efficiency (ΔC_m/Q_Ca²⁺) increased from 23°C (black) to 32°C (red; p = 0.0042, n = 9). **p < 0.01.

Figure 5.

Hair cell resting membrane potential and ionic currents at high temperature. A, A K⁺-based internal pipette solution and current-clamp recordings with zero current injection were used to measure the V_rest of hair cells. Whole-cell recordings showed that V_rest hyperpolarized at high temperature (black circles, p = 0.006, n = 15). Gramicidin-mediated perforated patch recordings showed that V_rest remained the same at high temperature (blue dots, p = 0.88, n = 9). B, Whole-cell voltage-clamp recordings of hair cells with K⁺-based internal solution showed current changes in response of a step depolarization from −90 mV to −60 mV. The traces were averaged from five hair cells recorded at 22°C (black) and 32°C (red). Note the faster kinetics of the currents at 32°C. C, To reveal Ca²⁺ current, hair cells were patched with a Cs⁺-TEA-based internal solution. Hair cells were depolarized with a ramp depolarization from −90 mV to −50 mV for 400 ms at 22°C (black) and 31°C (red). The traces were averaged from five hair cells. D, Voltage-dependent K⁺ and Ca²⁺ currents were triggered by the same ramp stimulus with K⁺-based internal solution. The traces were averaged from 14 hair cells recorded at 22°C (black) and 32°C (red). Note how the larger outward K⁺ currents dominate the hair cell I–V curve. **p < 0.01.

Figure 6.

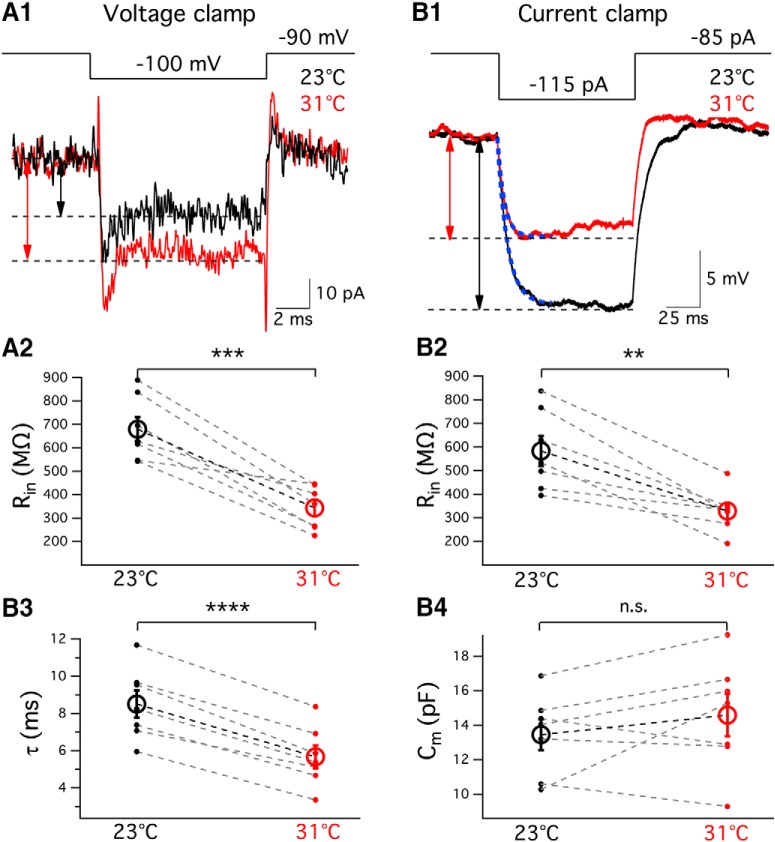
Temperature effects on hair cell passive membrane properties. A1, Inward currents were triggered by a small hyperpolarization from −90 to −100 mV at 23°C (black) and 31°C (red). The size of the current was the difference between baseline and the plateau inward current (dashed lines). B1, Hyperpolarized membrane potential in response to a −30 pA current injection under current clamp was recorded at 23°C (black) and 31°C (red). The change in membrane potential was calculated by subtracting baseline from plateau (dashed lines). A2, Using voltage-clamp measurements and R_in = ΔV/ΔI, the membrane input resistance (R_in) was lower at high temperature (p = 0.0006, n = 7). B2, Current-clamp measurements also showed that R_in decreased at high temperature (p = 0.0031, n = 7). B3, Membrane time constant (τ) was estimated by fitting a single exponential to a 40 ms time window of the voltage response following the initial current injection (B1, superimposed blue dashed lines). τ was faster at high temperature (p < 0.0001, n = 7). B4, C_m calculated using C_m = τ/R_in did not show significant change at high temperature (p = 0.2506, n = 7). A2, B2–B4, Dots represent individual values; open circles represent mean; bars represent SEM. **p < 0.01, ***p < 0.001, ****p < 0.0001.

Figure 7.

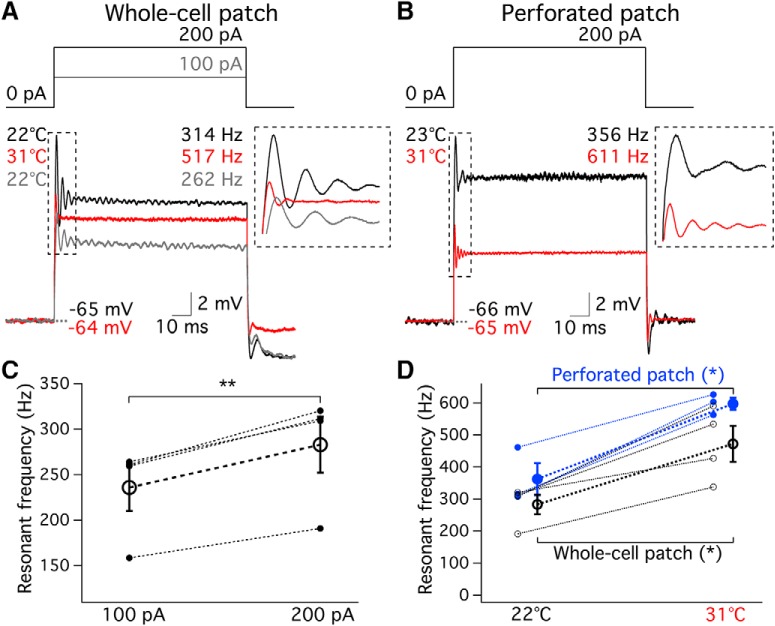
Hair cell resonant frequency increases at high temperature. A, Electrical resonance was elicited by stimulating hair cells with a current step in whole-cell patch. Black and red traces were evoked by a 200 pA current step at room and high temperature, respectively. Gray trace was evoked by a 100 pA current step at room temperature. Each of these three traces is the average response from three hair cells. Resonant frequencies were calculated by fitting the first 20 ms membrane voltage changes with a sine wave function (dashed line box inset). The resonant frequencies of black, red, and gray traces were 314, 517, and 262 Hz, respectively. B, Electrical resonance of hair cells was elicited by a 200 pA current step in gramicidine-mediated perforated patch. Black and red traces were averaged of 3 cells recorded at room and high temperature, respectively. The resonant frequencies of black and red traces were 356 and 611 Hz, respectively. C, Resonant frequencies of hair cells evoked by 100 pA current steps were lower than those evoked by 200 pA current steps (n = 4, p = 0.004). D, Results of both whole-cell (black, n = 4, p = 0.017) and perforated (blue, n = 3, p = 0.025) patch recordings showed that resonant frequency of hair cells increased significantly at high temperature. There was no statistical difference between resonant frequencies measured by whole-cell patch or perforated patch at either room (p = 0.80, unpaired t test) or high (p = 0.56, unpaired t test) temperature. *p < 0.05, **p < 0.01.

In voltage clamp, hair cells were held at a membrane potential of −90 mV. Membrane potentials were corrected for a liquid junction potential of 10 mV. In current clamp, hair cells were held at zero current. Whole-cell calcium currents (I_Ca) were leak-subtracted using a P/4 protocol. The uncompensated series resistances (R_s) in whole-cell recordings were 10.5 ± 0.4 mΩ for hair cells (n = 36). The uncompensated average R_s in perforated-patch recordings was 40.1 ± 1.3 mΩ (n = 9).

We used membrane capacitance (C_m) measurements to monitor exocytosis (vesicle fusion). Patch pipettes were coated with dental wax to minimize their stray capacitance. The C_m from hair cells was measured under whole-cell voltage-clamp conditions using the “Sine + DC” method (Lindau and Neher, 1988; Moser and Beutner, 2000). A 2 kHz sinusoidal command voltage of 50 mV peak-to-peak magnitude was superposed on the hair cell holding potential of −90 mV. The resulting current response was used to calculate C_m via a software emulator of a lock-in amplifier (Gillis, 2000). The increase of C_m (ΔC_m) evoked by membrane depolarization was measured as ΔC_m = C_m(response) − C_m(resting). Here C_m(resting) and C_m(response) were obtained by averaging capacitance data points before and after the depolarizing steps using Igor Pro 6.0 (WaveMetrics) software. We excluded recordings in which the uncompensated series resistance was >15 mΩ or the holding current was >100 pA. The thin steriocelia of hair cells may not be under full space clamp, so their contribution to resting C_m may be underestimated (Breneman et al., 2009).

Afferent fibers were patched with 8–10 mΩ patch pipette filled with the K⁺-based internal solution, as described above. Membrane potentials were corrected for a liquid junction potential of 10 mV. Spontaneous EPSCs were recorded from the voltage-clamped afferent fibers held at −90 mV. Spontaneous EPSPs were recorded in current-clamp mode from afferent fibers with zero current injection. The uncompensated R_s in whole-cell recordings of afferent fibers was 27.9 ± 3.2 mΩ (n = 8). An excessively high series resistance can reduce and filter large EPSC events because of significant voltage-clamp errors (Li et al., 2009). Therefore, we excluded afferent fibers with uncompensated series resistance >50 mΩ from analysis, and we electronically compensated afferent fiber whole-cell recordings up to 35% depending on the uncompensated series resistance to maintain a constant series resistance throughout the recordings.

Statistical analysis.

Statistical analysis was performed using Prism 6 (GraphPad Software) and Excel (Microsoft). Results are presented as mean ± SEM (n = number of cells). If not specified, statistical significance was determined using paired Student's t test. We chose p < 0.05 to be the criterion for statistical significance.

Data analyses and curve fitting were performed using Igor Pro 6.0. The threshold of an AP was defined as membrane potential (V_m) when the slope of V_m versus time started to increase compared with that of preceding EPSP. Our estimation was consistent with the threshold estimated by phase plots, which plot membrane potential slope (dV_m/dt) versus V_m (Yang et al., 2016). Biophysical properties of spontaneous EPSCs and EPSPs (i.e., amplitude, frequency, rise time, and τ_decay) were analyzed using a customized protocol written by Dr. Owen Gross. The rise time was calculated as the interval between 10% and 90% of the peak amplitude relative to baseline. The τ_decay of averaged EPSCs or EPSPs was estimated by a single exponential fit using the equation:

where I(t) is the current as a function of time, A is the amplitude at time 0, τ is the time constant, and I_ss is the steady-state current amplitude. The temperature coefficient (Q₁₀) is the coefficient by which a quantity increases after a change of 10°C. Q₁₀ values for amplitude, frequency, rise time, and time constant of decay as well as ΔC_m were calculated using the following equation:

where F_L and F_H are factors of interest measured at room (23°C–25°C) and high (30°C–33°C) temperature, respectively, and ΔT is the absolute value of the temperature difference.

Results

Most afferent fibers fire more spikes at higher temperature

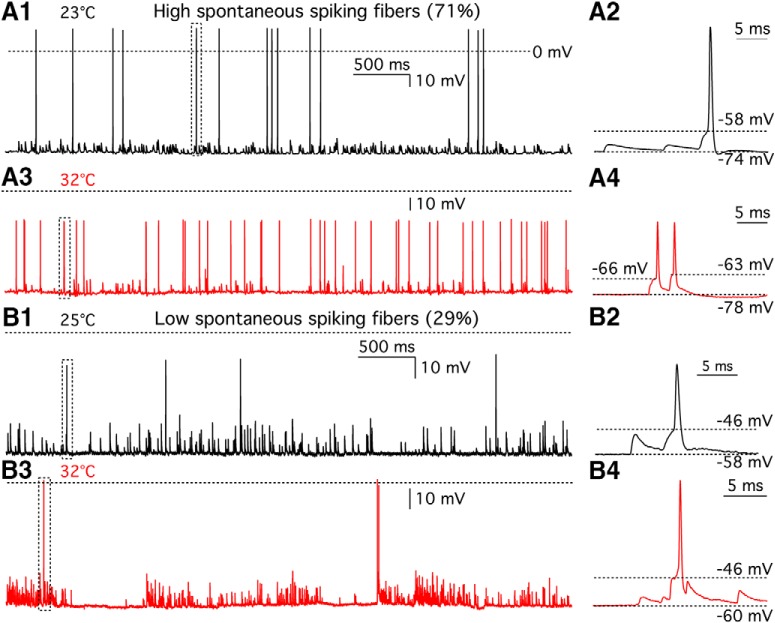
To determine the temperature dependence of spontaneous spikes at hair cell afferent fibers, we recorded spontaneous potential changes in afferent fibers using whole-cell current clamp with zero current injection. At 23.7 ± 0.2°C, the frequency of spikes was 2.0 ± 0.64 Hz, amplitude was 51.9 ± 6.8 mV, threshold was −51.0 ± 2.0 mV, and resting membrane potential (V_rest) of afferent fibers was −66.9 ± 2.1 mV (n = 18). Among these fibers, seven of them displayed big spikes that overshot 0 mV with higher threshold (Fig. 1A1). The amplitude of these big spikes was 85.7 ± 5.7 mV (n = 6), whereas the amplitude of spikes that did not overshoot was 35.0 ± 4.8 mV (n = 12, p < 0.0001). The threshold of the big spikes was −44.1 ± 2.4 mV (n = 6), whereas the threshold of small spikes was −54.8 ± 2.1 mV (n = 12, p = 0.0063, unpaired t test). There was no statistical difference between these two groups in frequency (overshooting: 2.02 ± 0.56 Hz vs nonovershooting: 1.99 ± 0.94 Hz, p = 0.98, unpaired t test) and V_rest (overshooting: −64.1 ± 4.6 mV vs nonovershooting: −68.3 ± 2.3 mV, p = 0.37).

Figure 1.

Heterogeneity in the temperature dependence of afferent fiber spikes. A1, Whole-cell current-clamp recordings of afferent fiber with zero current injection at 23°C. AP spikes and EPSPs can be clearly distinguished. Dashed line indicates 0 mV. A2, The spike shown in a dashed line box in A1 was expanded in time scale. Resting membrane potential (V_rest) was −74 mV, and AP threshold was −58 mV. A3, Spontaneous spikes from the same afferent fiber shown in A1 were recorded at 32°C. A4, Spikes shown in a dashed line box in A3 are expanded in time scale. V_rest was −78 mV. Thresholds of the first and the second AP were −66 and −63 mV, respectively. Five of seven afferent fibers (71%) fired more spikes at high temperature. B1, Spontaneous spikes were recorded from another afferent fiber at 25°C. Dashed line indicates 0 mV. B2, The spike shown in a dashed line box in B1 was expanded in time scale. V_rest was −58 mV, and AP threshold was −46 mV. B3, Spontaneous spikes from the same fiber shown in B1 were recorded at 32°C. B4, The spike shown in a dashed line box in B3 was expanded in time scale. V_rest was −60 mV, and AP threshold was −46 mV. Two of seven afferent fibers (29%) fired less spikes at high temperature.

For 7 of these 18 fibers, we successfully recorded spikes at both room and high temperature. Five of them fired more spikes at high temperature (Table 1; Fig. 1A1–A4). We called these fibers “thermal-positive fibers.” The temperature coefficient (Q₁₀) of spontaneous spiking rate was 4.0 ± 1.2 (n = 5), which was similar to that found in rat fibers (median Q₁₀ = 6.6) (Wu et al., 2016). Although threshold for firing an AP at high temperature (−58.6 mV) was lower than that at room temperature (−53.9 mV, n = 5, p = 0.0158), spike probability rates remain the same throughout temperature change: at room temperature, 25.8% of EPSPs evoked a spike; and at high temperature, 25.4% of EPSPs evoked a spike (n = 5, p = 0.97). A decrease in afferent fiber membrane input resistance at high temperature results in faster EPSP decay (see Fig. 4), making it more difficult for them to summate, which counteracts the potential increase in spike probability caused by lower thresholds. By contrast, in mammalian cochlear spiral ganglion neurons, 80%–97% of EPSPs evoke a spike under room temperature (Rutherford et al., 2012). The low spike failure rate of EPSPs in mammalian fibers may result from the smaller surface area and high input resistance of the mammalian postsynaptic bouton (Rutherford et al., 2012). In bullfrog amphibian papilla, each hair cell connects with 3–6 large claw-like afferent fiber endings and each fiber receives multiple ribbon synapses (Graydon et al., 2014), while each mammalian afferent fiber only connects with just one single synaptic ribbon (Liberman, 1980; Rutherford, 2015).

Table 1.

Temperature dependence of afferent fiber spikes

Thermal positive fiber (n = 5)	23.7 ± 0.5°C	31.1 ± 0.4°C	p	Q10
Frequency (Hz)	4.4 ± 1.9	9.4 ± 3.5	0.047	4.0 ± 1.2
Amplitude (mV)	75.7 ± 16.0	44.8 ± 11.1	0.075	0.6 ± 0.1
Threshold (mV)	−53.9 ± 4.3	−58.6 ± 4.0	0.016	1.1 ± 0.03
Resting potential (mV)	−70.1 ± 3.7	−70.7 ± 3.4	0.55	1.0 ± 0.02
Thermal negative fiber (n = 2)	24.2 ± 0.3°C	31.7 ± 0.4°C
Frequency (Hz)	0.7 ± 0.1	0.3 ± 0.2
Amplitude (mV)	46.8 ± 3.1	47.6 ± 8.4
Threshold (mV)	−48.6 ± 3.1	−43.4 ± 4.5
Resting potential (mV)	−66.1 ± 8.0	−65.1 ± 5.9

Values are mean ± SEM.

Figure 4.

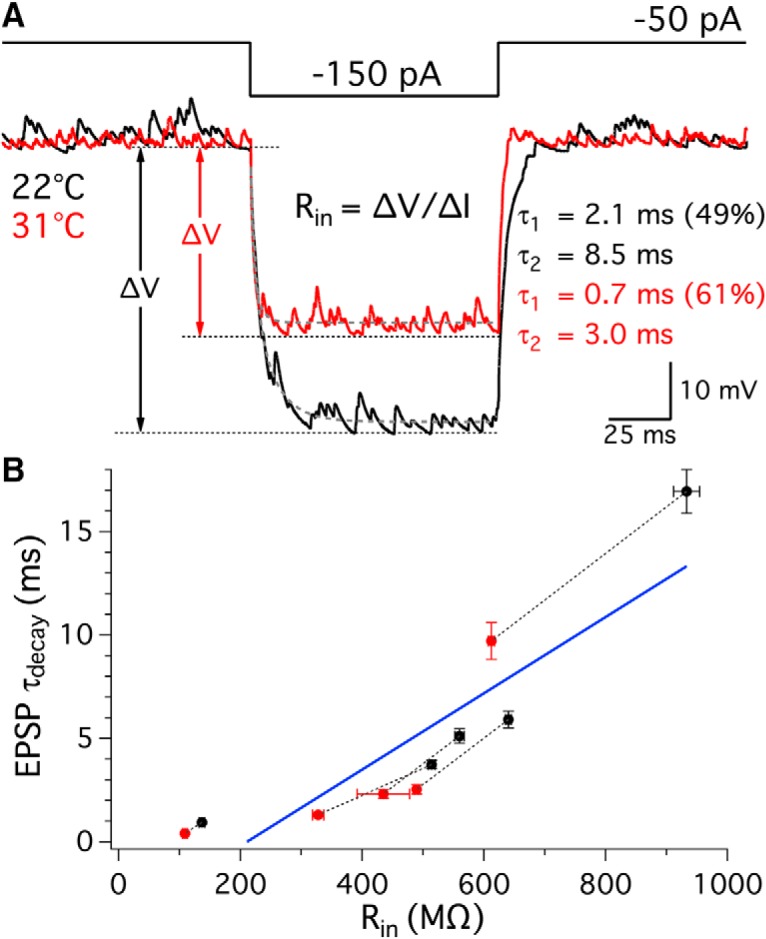
Afferent fiber membrane input resistance and EPSP decay kinetics. A, In current clamp, afferent fibers were hyperpolarized by injection of negative currents from −50 to −150 pA for 100 ms. Averages of membrane potential responses from one afferent fiber at 22°C and 31°C are shown in black and red, respectively. Red and black arrows indicate the absolute change in membrane potentials at 22°C and 31°C, respectively. Input resistance of an afferent fiber was calculated following Ohm's law, R_in = ΔV/ΔI. The decay phase of the membrane potential was fit by a double exponential function (gray dashed lines). B, τ_decay of EPSPs was plotted against R_in of the respective fibers. Each pair of data points recorded from the same afferent fiber is connected with a dashed line: room (black) and high (red) temperature (n = 5). A linear regression fit is shown in blue and indicates a positive correlation between EPSP τ_decay and R_in (slope = 0.018 ± 0.003, R² = 0.79, p = 0.0006).

The other two fibers fired less spikes at high temperature (Table 1; Fig. 1B1–B4), and we called these “thermal-negative fibers.” The thermal-negative fibers had low spontaneous spiking rate (<1 Hz; Table 1). In rat auditory nerve, spontaneous spiking rate increases during maturation of the cochlear from 3.87 Hz at P15–P17 to 12.85 Hz at P29–P32 (Wu et al., 2016). It is possible that some low-frequency spiking fibers in the frog may receive synaptic release from some immature hair cells at the edge of the amphibian papilla (Lewis and Li, 1975).

Frequencies of spontaneous EPSCs and EPSPs are enhanced at high temperature

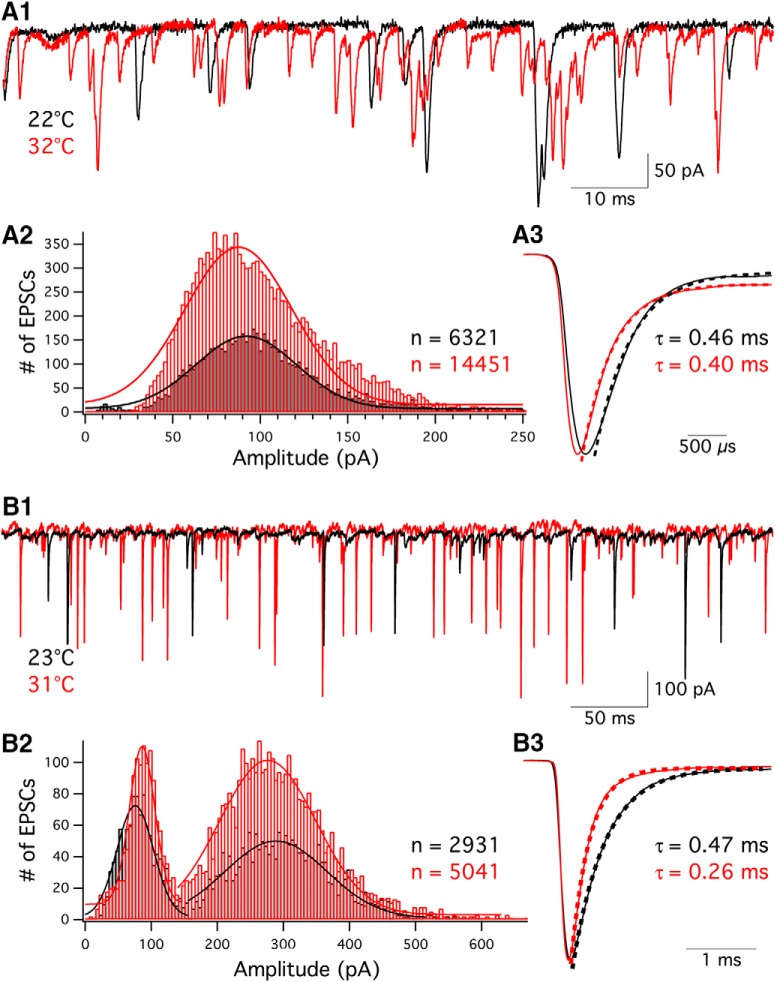
To examine how temperature affects hair cell spontaneous release, we recorded spontaneous EPSCs from afferent fibers without voltage-clamping their presynaptic hair cells under room (black traces) and high (red traces) temperature (Fig. 2A1,B1). The frequency of the EPSCs increased from 78.2 ± 9.5 Hz at room temperature to 115.2 ± 9.7 Hz at high temperature (n = 18, p = 0.0097; Table 2). The EPSC amplitude distribution of an afferent fiber in Figure 2A2 also shows that more EPSCs occurred under high temperature. The EPSC amplitude distribution was fit well with a Gaussian function (Fig. 2A2: R² = 0.96 at 22°C; R² = 0.93 at 32°C). The peaks of Gaussian fits fell at 93.5 pA at 22°C and at 89.7 pA at 32°C (Fig. 2A2), suggesting that the average EPSC amplitude did not increase at high temperature. Most afferent fibers (12 of 18) did not show an increase in EPSC amplitude at high temperature, and the average of EPSC amplitude remained the same as temperature changed (p = 0.61; Table 2). In Figure 2A3, average EPSCs were normalized to their peak values, and a single exponential function was used to fit the decay phase of EPSCs and determine the time constant of decay (τ_decay). The 10%–90% rise time and τ_decay of EPSCs were 223 ± 13 μs and 617 ± 36 μs (n = 18; Table 2) at room temperature, which are faster than that measured in immature rat afferent fibers (Yi et al., 2010) but similar to that measured in the afferent fibers of adult turtle (Schnee et al., 2013) and hearing rats (Grant et al., 2010). Elevating temperature decreased both 10%–90% rise time and τ_decay of EPSCs with Q₁₀ values of 1.7 and 1.8, respectively (Table 2). This is consistent with our previous findings showing that decreasing temperature from 25°C to 15°C slows down activation and decay of EPSCs in bullfrog afferent fibers (Li et al., 2009). Similarly, in rat AII amacrine cells, increasing temperature from 26°C to 34°C decreases both rise time and τ_decay of mEPSCs with Q₁₀ values of 1.3 and 1.5, respectively (Veruki et al., 2003). Calculating the integrals of EPSCs, we found that the postsynaptic charge transfer was decreased at high temperature (Table 2), which may be due to faster activation and deactivation (Fig. 2A3,B3) of postsynaptic AMPA receptors and faster glutamate transporter activity at high temperature (Auger and Attwell, 2000).

Figure 2.

Spontaneous EPSC frequency increases at high temperature. A1, EPSCs were recorded from an afferent fiber, which was voltage-clamped at −90 mV at 22°C (black) and 32°C (red). A2, A total of 6321 and 14451 EPSCs were obtained at 22°C (black) and 32°C (red), respectively. EPSC amplitude distributions were fit with a Gaussian function. A3, Average of EPSCs recorded at 22°C (black) and 32°C (red) were normalized to their peak value. Single-exponential fits to the decay phase of averaged EPSCs showed that τ_decay was 0.46 ms at 22°C (black dashed line) and 0.40 ms at 32°C (red dashed line), respectively. B1, EPSCs were recorded from another afferent fiber at 23°C (black) and 31°C (red). B2, A total of 2931 and 5041 EPSCs were obtained at 23°C (black) and 31°C (red), respectively. Two peaks are present on the amplitude distribution. EPSCs were divided into two groups according to their size: small EPSCs with amplitude <150 pA and large EPSCs with amplitude >150 pA. The EPSC amplitude distributions in each group were fit with a Gaussian function. B3, Average of EPSCs recorded at 23°C (black) and 31°C (red) were normalized to their peak value. Single-exponential fits to the decay phase of averaged EPSCs showed that τ_decay was 0.47 ms at 24°C (black dashed line) and 0.26 ms at 31°C (red dashed line), respectively.

Table 2.

Biophysical properties of afferent fiber EPSCs and EPSPs

EPSC (n = 18)	23.4 ± 0.1°C	31.1 ± 0.1°C	p	Q10
Amplitude (pA)	80.5 ± 6.8	77.7 ± 7.4	0.61	1.1 ± 0.2
Frequency (Hz)	78.2 ± 9.5	115.2 ± 9.7	0.0097	3.2 ± 1.1
Rise time (μs)	223 ± 13	150 ± 6	<0.0001	1.7 ± 0.1
τdecay (μs)	617 ± 36	400 ± 24	<0.0001	1.8 ± 0.1
Charge transfer (fC)	−71.3 ± 5.2	−47.9 ± 3.4	<0.0001
EPSP (n = 19)	23.4 ± 0.1°C	31.5 ± 0.1°C	p	Q10
Amplitude (mV)	3.9 ± 0.3	3.8 ± 0.4	0.8	1.1 ± 0.2
Frequency (Hz)	40.4 ± 6.1	56.9 ± 7.0	0.003	2.1 ± 0.5
τdecay (ms)	3.50 ± 0.69	1.67 ± 0.38	<0.0001	2.7 ± 0.4

Values are mean ± SEM.

Among all the afferent fibers recorded, 5 of 18 (28%) exhibited double peaks in the EPSC amplitude distribution at both room and high temperatures. Figure 2B1 shows EPSCs recorded from an afferent fiber that had a double-peak distribution (Fig. 2B2). Double- or triple-peak EPSC amplitude distributions have been observed previously in afferent fibers of mature rats (Grant et al., 2010) and turtle (Schnee et al., 2013). We divided EPSCs into two groups according to their amplitude: small EPSCs with amplitude <150 pA and large EPSCs with amplitude >150 pA. The frequency distributions of EPSC amplitude in each group were fit well with a Gaussian function (small events: R² = 0.94 at 23°C, R² = 0.93 at 31°C; large events: R² = 0.93 at 23°C, R² = 0.97 at 31°C). Under 23°C, the first and the second peak of the Gaussian fits were 78 and 292 pA, respectively. Under 31°C, the first and the second peak were 89 and 279 pA, respectively. Under 23°C, there were 65% of EPSCs >150 pA. The group of large EPSCs increased to 74% at 31°C.

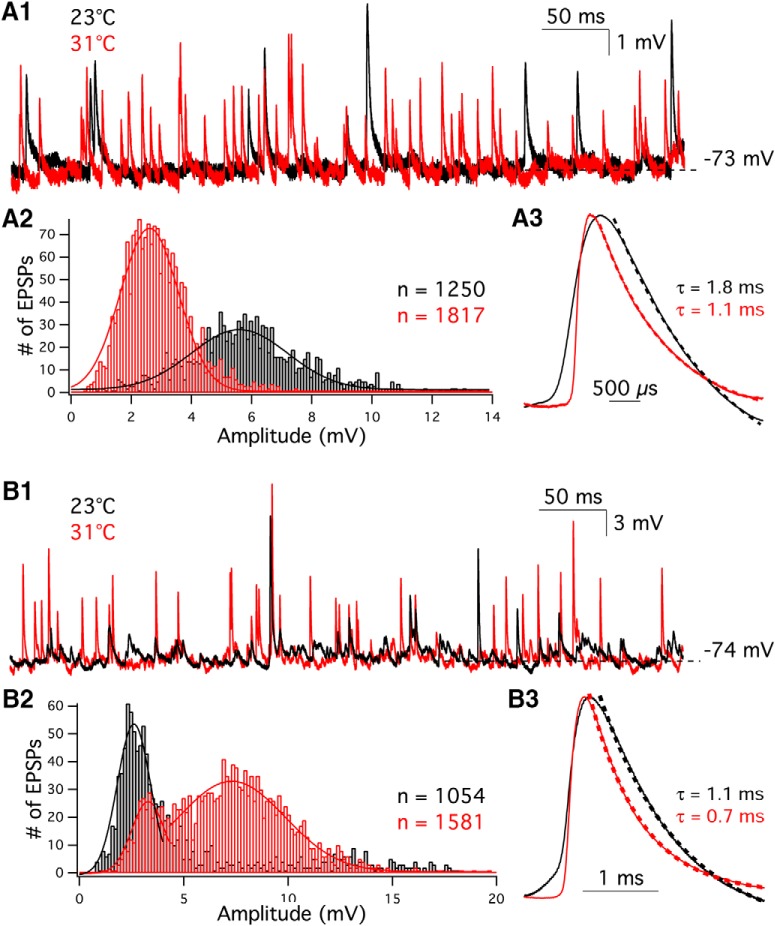
Spontaneous EPSPs were also recorded from afferent fibers using whole-cell current clamp with 0 pA holding current. Consistent with EPSCs, the frequency of EPSPs increased from 40.4 Hz at 23.4°C to 56.9 Hz at 31.5°C (n = 19, p = 0.003; Table 2). However, the response of EPSP amplitudes was variable: 58% (11 of 19) of the fibers showed a reduced average EPSP amplitude at high temperature. This could be caused by a strong activation of K⁺ currents in the afferents that blunts the EPSP amplitude at higher temperatures. However, averaging the entire dataset revealed no statistical difference in the amplitude of EPSPs between room and high temperature (3.9 ± 0.3 mV vs 3.8 ± 0.4 mV, respectively; n = 19, p = 0.8; Table 2).

Figure 3A shows one example with decreased EPSP amplitude at high temperature, and Figure 3B shows another example with increased EPSP amplitude at high temperatures. The EPSP amplitude distribution is shown in Figure 3A2, where 1250 and 1817 EPSPs events were counted from an afferent fiber at 23°C and 31°C, respectively. The amplitude distributions of EPSPs were fit well with a Gaussian function (Fig. 3A2: R² = 0.89 at 23°C; R² = 0.97 at 31°C). The peaks of the Gaussian fit are 5.7 mV at 23°C and 2.7 mV at 31°C. The single-exponential fit to the decay phase of averaged EPSPs (Fig. 3A3) showed that τ_decay was 2.7 ± 0.4 ms at room temperature (n = 19; Table 2). This is faster than that found in afferent fibers of immature rat (Yi et al., 2010). EPSPs shown in Figure 3B1 were recorded from the same afferent fiber with double-peak EPSC amplitude distribution as shown in Figure 2B2. During 30-s-long recordings, 1054 and 1581 EPSPs were recorded from another afferent fiber under room and high temperature, respectively (Fig. 3B2). The frequency distribution of EPSP amplitudes shown in Figure 3B2 also had double peaks at high temperature, but not under room temperature. Under 23°C, the peak of the Gaussian fit was 2.7 mV (R² = 0.87). Under 31°C, the first and the second peak were 3.4 mV (R² = 0.85) and 7.3 mV (R² = 0.81), respectively. In addition, the V_rest of the afferent fiber was slightly depolarized from −74.0 ± 0.7 mV at 23°C to −71.2 ± 0.8 mV at 32°C (p = 0.0012, n = 19).

Figure 3.

Spontaneous EPSPs are faster, and their frequency increases at high temperature. A1, EPSPs were recorded from an afferent fiber at 23°C (black) and 31°C (red). The membrane current of fiber was clamped at 0 pA. A2, A total of 1250 and 1817 EPSPs were recorded at 23°C (black) and 31°C (red), respectively. The EPSP amplitude distributions were fit with a Gaussian function. A3, Average EPSPs recorded at 23°C (black solid line) and 31°C (red solid line) were normalized to their peak values. Dashed lines are single-exponential fits to the decay phase of the average EPSPs. In this example, τ_decay was 1.8 ms at 23°C (black dashed line) and 1.1 ms at 31°C (red dashed line), respectively. B1, EPSPs were recorded from the same afferent fiber as shown in Figure 2B1–B3, at 23°C (black) and 31°C (red). B2, A total of 1054 and 1581 EPSPs were recorded under room and high temperature. B3, Average of EPSPs recorded at 23°C (black) and 31°C (red) were normalized to their peak values. Single-exponential fits to the decay phase of averaged EPSPs (dashed lines) revealed that τ_decay was 1.1 ms at 23°C and 0.7 ms at 31°C, respectively.

Afferent fiber membrane input resistance at high temperature

The τ_decay of EPSPs decreased at high temperature in all of the fibers recorded (Fig. 3B3; Table 2), which may due to lower membrane input resistance (R_in) at high temperature. We thus estimated R_in of the afferent fibers using current clamp: R_in = ΔV/ΔI, where ΔV was the change in membrane potential induced by a 100 pA current injection (Fig. 4A). The R_in of afferent fibers decreased from 557 ± 128 mΩ at 22.0 ± 0.1°C to 395 ± 85 mΩ at 32.0 ± 0.2°C (n = 5, p = 0.027). In this group of fibers, τ_decay of EPSPs was 6.5 ± 2.7 ms and 3.3 ± 1.7 ms at room and high temperature, respectively (n = 5, p = 0.041). The τ_decay was positively correlated with afferent fiber R_in (linear regression slope = 0.018 ± 0.003, R² = 0.79, p = 0.0006; Fig. 4B, blue line).

An afferent fiber is composed of two compartments: a calyx-type ending that contacted the hair cell and a long, thin fiber cable. We thus fit the decay phase of membrane potential change to a step current with a double exponential function (gray dashed lines superimposed over V_m trace; Fig. 4A, gray dashed lines superimposed over V_m trace) as follows:

We can then calculate a weighted mean time constant τ_mean using the following:

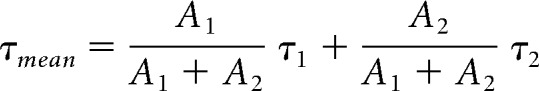The value of τ_mean was shorter at high temperature (4.8 ± 1.5 ms) than that at room temperature (7.8 ± 1.5 ms, n = 5, p = 0.0014). The τ₁ at room and high temperature was 3.2 ± 1.2 ms and 2.5 ± 1.5 ms, respectively, and the τ₂ at room and high temperature was 10.3 ± 1.3 ms and 6.0 ± 1.7 ms, respectively. The fact that a double exponential function with both fast (τ_f) and slow (τ_s) time constants is required to fit the voltage responses indicates that the afferent fiber is not isopotential (Golowasch et al., 2009), unlike the hair cell (see Fig. 6). Since the afferent axon has a cutoff end, due to the amphibian papilla isolation process, it can be modeled as a finite cable with an electrotonic length given by the following (Rall, 1969):

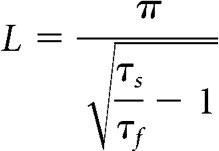We thus find that L = 2.1 for 22°C and L = 2.6 for 32°C for the afferent fibers. This is a relatively large value compared with hippocampal neurons where L = 0.9 (Brown et al., 1981), suggesting a strong attenuation of the voltage from the postsynaptic calyx terminal to the tip of the cutoff and sealed afferent axon. Therefore, the cluster of Na⁺ channels at the first axonal heminode must be fairly close to the calyx terminal to trigger a spike (Kim and Rutherford, 2016). By contrast, EPSP amplitude did not change significantly with temperature for this dataset (6.5 ± 0.7 mV vs 9.3 ± 2.2 mV at 22.1 ± 0.2°C and 32.0 ± 0.1°C, respectively; n = 5, p = 0.3). The linear regression of EPSP amplitude and R_in also did not show a significant difference (slope = −0.0016 ± 0.005, R² = 0.013, p = 0.76). In conclusion, the R_in of afferent fibers exhibits significant heterogeneity from 100 mΩ to 1000 mΩ, which could contribute to the in vivo variation in spontaneous spike rates and afferent fiber thresholds to sound stimulation (Stiebler and Narins, 1990; Shrestha et al., 2018).

Changes in R_in with temperature are also important because of membrane potential noise considerations (Fatt and Katz, 1952; Johnson, 1987). The mean square membrane voltage is given by the Nyquist theorem as follows:

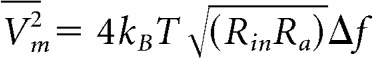here k_B is Boltzmann constant, T the temperature in degrees Kelvin (T = 273 + temperature in Celsius), R_in the membrane input resistance, R_a the axial cable resistance and Δf the noise frequency bandwidth. The frequency bandwidth is inversely proportional to the membrane time constant, which determines the cell cutoff frequency, and will thus increase at higher temperatures. The decrease in R_in with increasing temperature is thus important because it counteracts the increase in noise bandwidth with temperature. This helps to keep the membrane potential in a stable sub-threshold level.

Resting membrane potential of hair cells

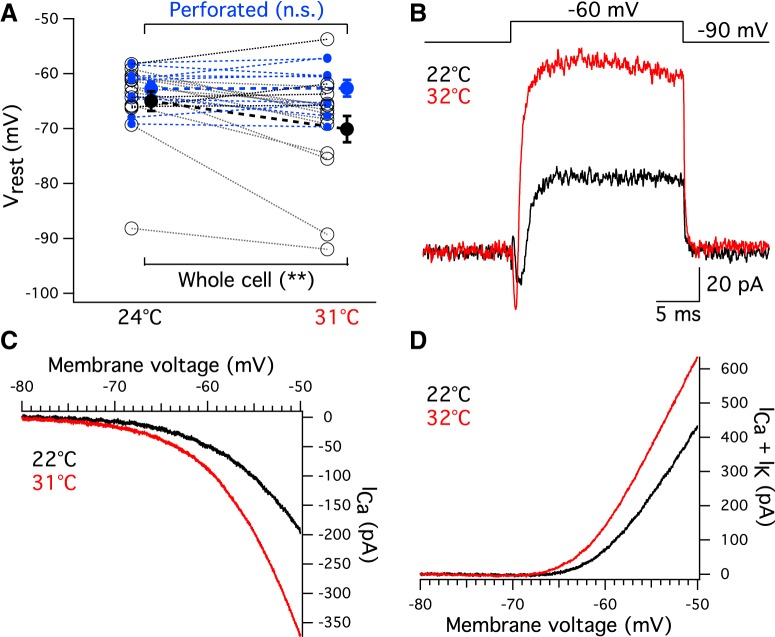
The increase in EPSC frequency at high temperature suggests more spontaneous vesicle release from hair cells, which may be due to a depolarization of V_rest at high temperature. We thus measured hair cell V_rest under whole-cell current clamp with a holding current at 0 pA. Unexpectedly, whole-cell recordings revealed that V_rest hyperpolarized from −65.0 ± 1.8 mV at 23.2 ± 0.3°C to −70.1 ± 2.3 mV at 31.2 ± 0.3°C (p = 0.006, n = 15; Fig. 5A, black circles). To prevent the dialysis of the hair cell constituents through the patch pipette, we also performed perforated-patch recordings using gramicidin (40–50 μg/ml). The perforated patch clamp showed that V_rest did not change at high temperatures (V_rest = −62.8 ± 1.3 mV at 23.4 ± 0.5°C and V_rest = −62.7 ± 1.5 mV at 31.6 ± 0.2°C, p = 0.88, n = 9; Fig. 5A, blue dots).

Hair cell potassium and calcium currents at high temperature

Under voltage clamp and with a K⁺-based internal pipette solution, we determined the voltage-dependent currents that are activated by a step-depolarization from −90 to −60 mV. A rapidly activating inward current was followed by a rapid and large outward current (Fig. 5B). The inward current was a Ca²⁺ current that is activated more quickly at higher temperatures in frog hair cells (Hudspeth and Lewis, 1988). Using Cs⁺-TEA-based or K⁺-based internal solutions, we recorded the I–V curves of Ca²⁺ currents (Fig. 5C) and the overall K⁺ + Ca²⁺ currents (Fig. 5D), respectively. Both types of currents increased in amplitude at high temperature. Importantly, the slope of voltage-dependent Ca²⁺ current was greater at high temperature, making Ca²⁺ influx more sensitive to small membrane potential changes. The increase in whole-cell outward K⁺ + Ca²⁺ current at high temperature explains the decrease in V_rest with temperature (Fig. 5A, black circles). In perforated patch recordings, a lack of change in V_rest could be due to a simultaneous and more compensatory increase in inward Ca²⁺ current and outward K⁺ current as temperature increases.

Hair cell membrane input resistance decreases at high temperature

At high temperature, an increase in Ca²⁺ and K⁺ currents around V_rest should result in a decrease in membrane input resistance (R_in). To check this, we performed whole-cell voltage and current-clamp recordings from hair cells. In voltage clamp, hyperpolarizing hair cells from −90 mV to −95 mV or −100 mV for 10 ms elicited small inward currents (Fig. 6A1). R_in was calculated from Ohm's law (R_in = ΔV/ΔI). R_in of hair cells decreased at high temperature (659.7 ± 54.3 mΩ at 23.2 ± 0.2°C and 343.7 ± 34.7 mΩ at 31.4 ± 0.2°C, p = 0.0006, n = 7; Fig. 6A2). Under current clamp, injection of −20 pA or −30 pA hyperpolarized the cells (Fig. 6B1). Current clamp also showed a decrease in R_in at high temperature (640.3 ± 56.4 mΩ at 23.2 ± 0.2°C and 389.3 ± 28.2 mΩ at 31.2 ± 0.2°C, p = 0.0023, n = 7; Fig. 6B2). Changes in current or membrane potential were determined by calculating the differences between baseline and plateau (Fig. 6A1, dashed lines, B1). There was no statistically significant difference in R_in measured with voltage clamp or current clamp at either room (p = 0.2598) or high (p = 0.7016) temperature (n = 7).

Some hair cells tend to be leakier toward the end of whole-cell recordings, and this may affect R_in (Ceballos et al., 2017). To control for this possibility, we first recorded R_in at room temperature and then heated the solution to high temperature. R_in decreased from 578.8 ± 49.8 mΩ at 24.0 ± 0.2°C to 315.8 ± 33.3 mΩ at 31.5 ± 0.2°C (p = 0.0001, n = 8). We then recorded from a distinct group of cells, first at high temperature and then at room temperature. R_in was also lower at high temperature (600.2 ± 38.2 mΩ at 24.1 ± 0.1°C and 277.6 ± 34.0 mΩ at 31.9 ± 0.1°C, p = 0.0146, n = 3). Thus, the order of recording did not affect R_in measured at either room (p = 0.81) or high (p = 0.53) temperature. This suggests that the decrease in R_in at high temperature was not due to hair cells becoming leakier toward the end of the recordings, but due to an increase in cell membrane conductance at high temperature (Fig. 5B).

Using current-clamp data, we also calculated the membrane time constant (τ). We fitted a single exponential to a 40 ms time window of the voltage response following the initial current injection (Fig. 6B1, superimposed blue dashed line). The time constant was 8.50 ± 0.73 ms at 23.2 ± 0.2°C and 5.67 ± 0.61 ms at 31.2 ± 0.2°C (p < 0.0001, n = 7; Fig. 6B3). We next determined the membrane capacitance (C_m) using the equation C_m = τ/R_in. The average value of C_m remained the same regardless of temperature changes (13.5 ± 0.9 pF at 23.2 ± 0.2°C and 14.6 ± 1.2 pF at 31.2 ± 0.2°C, p = 0.2506, n = 7; Fig. 6B4). This value of C_m is similar to previous whole-cell recordings in voltage clamp of C_m in bullfrog hair cells (Li et al., 2009). This agreement between voltage and current-clamp values for R_in and C_m is expected only for isopotential cells (Golowasch et al., 2009).

Electrical resonant frequency increases at high temperature

Unlike mechanical tuning in the mammalian cochlea, amphibian papilla hair cells in frogs are electrically tuned (Smotherman and Narins, 2000). Electrical resonance of amphibian papilla hair cells matches the characteristic (best) frequencies of the afferent fibers (Smotherman and Narins, 1999). The electrical resonance is a result of the interplay of voltage-gated ion channels and membrane capacitance (Crawford and Fettiplace, 1981; Art and Fettiplace, 1987; Hudspeth and Lewis, 1988). Since the conductance of voltage-gated calcium and potassium channels are temperature-dependent as shown in Figure 5, we expect electrical resonance to be temperature-sensitive. To elicit electrical ringing around resting membrane potentials, hair cells were injected a current step from zero current under whole-cell (Fig. 7A) or perforated patch clamp (Fig. 7B). Resonant frequency was estimated by fitting the first 20 ms of the damped oscillation in membrane voltage with a sine wave function (Li et al., 2014). In a previous study (Smotherman and Narins, 1999), it was shown that resonant frequency increases as larger depolarizing current steps are applied to the cell. Consistently, depolarizing hair cells with 100 pA current steps elicited a resonant frequency of 236 ± 26 Hz, while 200 pA current steps elicited a higher resonant frequency of 283 ± 31 Hz at room temperature (p = 0.0038, n = 4; Fig. 7A,C). To compare the resonant frequency measured with whole-cell recordings to perforated patch recordings, we chose the larger 200 pA current steps. The resonant frequency increased from 283 ± 31 Hz at 21.8 ± 0.4°C to 472 ± 56 Hz at 31.4 ± 0.6°C (p = 0.017, n = 4; Fig. 7D, black circle). Similarly, perforated patch recordings revealed that resonant frequency increased from 362 ± 50 Hz at 24.8 ± 2.1°C to 597 ± 19 Hz at 31.5 ± 0.3°C (p = 0.025, n = 3; Fig. 7D, blue dots). There was no statistical difference in resonant frequency measured by whole-cell recording and perforated patch at either room (p = 0.22, unpaired t test) or high (p = 0.13, unpaired t test) temperatures.

Hair cell resonant frequency also increases when resting membrane potential is depolarized (Hudspeth and Lewis, 1988; Smotherman and Narins, 1999). However, the resting membrane potential did not change for the whole-cell recordings of Figure 7A (−65.2 ± 0.5 mV at room temperature vs −63.8 ± 0.8 mV at high temperature, p = 0.23, n = 4). Similarly, resting membrane potential did not change with temperature for the perforated patch data (−66.0 ± 2.7 mV at room temperature vs −65.2 ± 2.6 mV at high temperature, p = 0.51, n = 3). Therefore, the increases of resonant frequency at high temperature are not due to changes in resting membrane potential. Instead, they are caused by faster activation and larger conductance of Ca²⁺ and K⁺ channels upon depolarization at high temperature (Hudspeth and Lewis, 1988; Smotherman and Narins, 1999). The resonant frequency measured at room temperature matches the results of in vitro whole-cell recordings of hair cells from amphibian papilla using a ZAP protocol (Frolov and Li, 2017). The Q₁₀ of resonant frequency of amphibian papilla hair cells (1.7 ± 0.1, n = 4 for whole cell; 1.9 ± 0.08, n = 3 for perforated patch) are similar to that recorded from frog saccular hair cells (Smotherman and Narins, 1998). This temperature-dependent shift in hair cell resonant frequency may be responsible for the temperature-induced shifts of best frequency observed at in vivo amphibian papilla auditory nerve fiber recordings (Stiebler and Narins, 1990).

Release efficiency increases at high temperature

A lower R_in at high temperature results in smaller membrane potential changes, which will decrease hair cell sensitivity to low-level sounds. To explore whether hair cells compensate for this putative loss in sensitivity, we studied the temperature dependence of vesicle exocytosis from hair cells using time-resolved membrane capacitance measurements (Lindau and Neher, 1988; Gillis, 2000). Changes in C_m (ΔC_m) were evoked by depolarizing voltage steps. We first used 20 ms depolarizing steps from a holding potential of −90 to −30 mV to evoke fast release that depletes the RRP consisting of vesicles docked near the clustered Ca²⁺ channels (Graydon et al., 2011) (Fig. 8A1). The depolarization triggered a larger Ca²⁺ current (Fig. 8A1) under high temperature than under room temperature (p < 0.0001, n = 7): Ca²⁺ charge transfer (Q_Ca) was 11.9 ± 1.3 pC at 23.3 ± 0.2°C and 15.9 ± 1.7 pC at 32.0 ± 0.3°C. The Q₁₀ of 20 ms pulse-evoked Q_Ca was 1.5 ± 0.05 (n = 7). Average resting membrane capacitance measured at high temperature (16.9 ± 0.7 pF) was similar to that measured at room temperature (15.7 ± 0.6 pF, p = 0.0841, n = 7). The ΔC_m increased from 27.2 ± 4.7 fF at room temperature to 51.6 ± 6.0 fF at high temperature (p = 0.0006, n = 7). The Q₁₀ of 20 ms pulse-evoked ΔC_m was 2.4 ± 0.4 (n = 7).

Figure 8.

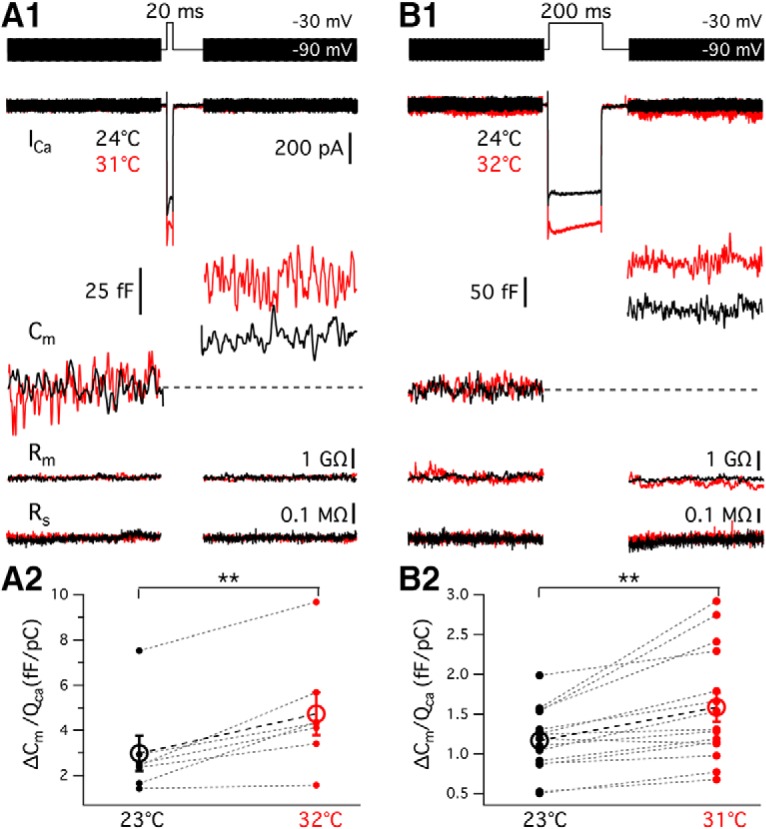
Hair cell exocytosis efficiency is enhanced at high temperature. A1, B1, The Ca²⁺ current (I_Ca), membrane capacitance (C_m), membrane resistance (R_m), and series resistance (R_s) traces obtained from a hair cell. A ΔC_m change was triggered by 20 ms (A1) and 200 ms (B1) depolarizing steps from −90 mV to −30 mV at room (black) and high (red) temperature. For the 20 ms depolarization: I_hold = −60 and −64 pA; C_m(resting) = 14.5 and 16.0 pF; R_m = 1.3 and 1.2 GΩ; R_s = 8.9 and 8.2 mΩ, at 24°C and 31°C, respectively. For recordings of 200 ms depolarization: I_hold = −69 and −43 pA; C_m(resting) = 11.3 and 12.8 pF; R_m = 1.2 and 1.5 GΩ; R_s = 14.0 and 11.3 mΩ at 24°C and 32°C, respectively. Exocytosis efficiency, calculated as the ratio of ΔC_m/Q_Ca²⁺, is shown for (A2) 20 ms (p = 0.0043, n = 7) and (B2) 200 ms (p = 0.0013, n = 15) depolarizations. The exocytosis efficiency is nearly threefold greater for the short 20 ms pulse than for the long 200 ms pulse. **p < 0.01.

Here, Q₁₀ is the ratio of the reaction rates for T_L = 296°K (23°C) and for T_H = T_L + 10°K = 306°K as follows:

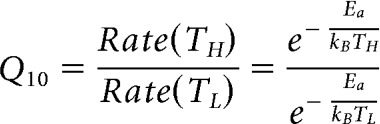where k_B ≈ 8.3 J/mol°K (Boltzmann constant) and E_a is the reaction activation energy barrier. From this equation, we obtain E_a = (lnQ₁₀)·75.2kJ/mol. The E_a for evoked exocytosis was thus 65.8 ± 10.0 kJ/mol ≈ 26.8 k_BT (n = 7), which was calculated from the Q₁₀ of 20 ms depolarizing pulses. This is within the E_a estimated for vesicle exocytosis mediated by SNAREpin and synaptotagmin molecules (20–140 k_BT) (Zhang and Jackson, 2008; Schotten et al., 2015; Mostafavi et al., 2017), although exocytosis in hair cells is mediated by otoferlin (Michalski et al., 2017).

Depolarizations from −90 to −30 mV for 200 ms (Fig. 8B1) not only depletes the RRP but also evokes sustained release of vesicles replenishing to the RRP (Graydon et al., 2011). Q_Ca evoked by the 200 ms depolarizing pulse was 99.7 ± 8.0 pC at 23.1 ± 0.2°C and 126.3 ± 9.7 pC at 31.3 ± 0.2°C (p < 0.0001, n = 15). ΔC_m evoked by 200 ms depolarizing steps increased from 109.8 ± 9.1 fF at room temperature to 192.1 ± 21.2 fF at high temperature (p < 0.0001, n = 15). The Q₁₀ of Q_Ca and ΔC_m evoked by a 200 ms pulse was 1.3 ± 0.04 and 2.0 ± 0.1 (n = 15), respectively. The Q₁₀ of exocytosis from bullfrog hair cells is close to that found in mouse inner hair cells using capacitance measurements (Q₁₀ = 2.1) (Nouvian, 2007) and in rat hippocampal neurons using FM1-43 destaining methods (Q₁₀ = 2.5) (Yang et al., 2005).

Plotting ΔC_m versus the corresponding Q_Ca²⁺, we obtained the efficiency of exocytosis as the ratio of ΔC_m/Q_Ca²⁺, which for 20 ms pulses increased from 3.0 ± 0.8 fF · pC⁻¹ at room temperature to 4.7 ± 1.0 fF · pC⁻¹ at high temperature (p = 0.0043, n = 7; Q₁₀ = 1.9 ± 0.3; Fig. 8A2). The ratio of ΔC_m/Q_Ca²⁺ for responses to 200 ms pulses increased from 1.2 ± 0.1 fF · pC⁻¹ at room temperature to 1.6 ± 0.2 fF · pC⁻¹ at high temperature (p = 0.0013, n = 15; Fig. 8B2). Recordings from mouse IHC also find that higher temperatures enhance Ca²⁺ influx and increase ΔC_m/Q_Ca²⁺ elicited by 20 ms depolarizing pulses, but not for sustained exocytosis (Nouvian, 2007). By contrast, our results with bullfrog hair cells indicate that the efficiency of both fast and sustained exocytosis increased under high temperature.

To further demonstrate that the increase in exocytosis is facilitated beyond a mere increase of Ca²⁺ influx under high temperature, we reduced Ca²⁺ influx using smaller depolarizing potentials at high temperature and measured ΔC_m jumps. We also used the pH-insensitive Ca²⁺ buffer BAPTA (Tsien, 1980) and a different pH buffer MOPS, which has similar temperature dependence with HEPES (Ellis and Morrison, 1982). A depolarization from −90 mV to a potential that varied from −46 to −56 mV (average: −50.6 ± 1.8 mV, n = 9) for 20 ms at 32°C elicited similar or less Ca²⁺ influx (6.4 ± 0.8 pC) to that triggered by 20 ms depolarization to −30 mV at 23°C (8.7 ± 1.2 pC, p = 0.0059, n = 9; Fig. 9A). However, even when Ca²⁺ influx was reduced, hair cells were still able to release more vesicles upon depolarization at high temperature (Fig. 9A). ΔC_m increased from 10.3 ± 1.3 fF at room temperature to 19.2 ± 2.6 fF at high temperature (p = 0.0028, n = 9; Fig. 9B). Consistent with previous results using internal EGTA and HEPES, exocytosis efficiency increased from 1.3 ± 0.2 at room temperature to 3.7 ± 0.8 at high temperature (p = 0.0042, n = 9; Fig. 9C). The results indicate that high temperature facilitates synaptic vesicle exocytosis, even when Ca²⁺ influx is reduced. Moreover, the effect is not due to temperature-dependent changes in cellular pH-dependent Ca²⁺ buffering.

RRP size is larger at high temperature

To compare the maximum size of hair cell RRP under room and high temperature, we used a dual-pulse protocol (Gillis et al., 1996). Two pulses of 100 ms duration are given with a 25 ms interval (Fig. 10A). The short 25 ms interval results in depression in the second release. Ca²⁺ current can also decline during the dual pulse due to inactivation. To avoid differences in Q_Ca during the first and second depolarization, the potentials of the first pulses are adjusted (Fig. 10A). The average of the first depolarizing potentials was −41.1 ± 0.7 mV (n = 11). The intervals between pulse pairs was 60–90 s to allow for full recovery. Under 23°C, the Ca²⁺ influx during the first and second depolarizing pulses was 31.8 ± 6.8 and 31.7 ± 6.8 pC, respectively (n = 4, p = 0.93; Fig. 10A,C). Under 31°C, the Ca²⁺ influx during the first and second depolarizing pulses was 62.8 ± 3.8 and 63.3 ± 3.1 pC, respectively (n = 7, p = 0.69; Fig. 10A,C). Consistently, both the first (p = 0.0019) and the second (p = 0.0009; Fig. 10C) pulses triggered more Ca²⁺ influx under high temperature. ΔC₁ and ΔC₂ were capacitance jumps triggered by the first and second depolarization. The maximum size of the RRP (B_max) was calculated according to the following:

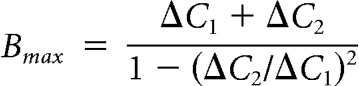This equation from Gillis et al. (1996) is derived based on the assumption that the same fraction of the pool is released with each pulse. If there is a larger fraction of release during the second pulse (e.g., due to residual Ca²⁺ from the first pulse) or significant numbers of vesicles have been refilled during the second pulse, then B_max will overestimate the actual initial pool size. Therefore, the actual pool size lies between ΔC₁ and B_max. In the example of Figure 10A, the B_max increased from 143 pF at 23°C to 175 pF at 31°C. On average, the B_max increased from 83 ± 20 fF (n = 4) at room temperature to 246 ± 47 fF at high temperature (n = 7, p = 0.0351, unpaired t test; Fig. 10B). These results showing an increase in RRP size with increasing temperature are similar to those reported for chromaffin cell exocytosis (Dinkelacker et al., 2000). In addition, the paired-pulse ratio ΔC₂/ΔC₁ did not change significantly upon temperature shift: 0.46 ± 0.19 at room temperature (n = 4) versus 0.69 ± 0.05 at high temperature (n = 7, p = 0.18; unpaired t test). This suggests that evoked release probability does not change with temperature shifts.

Figure 10.

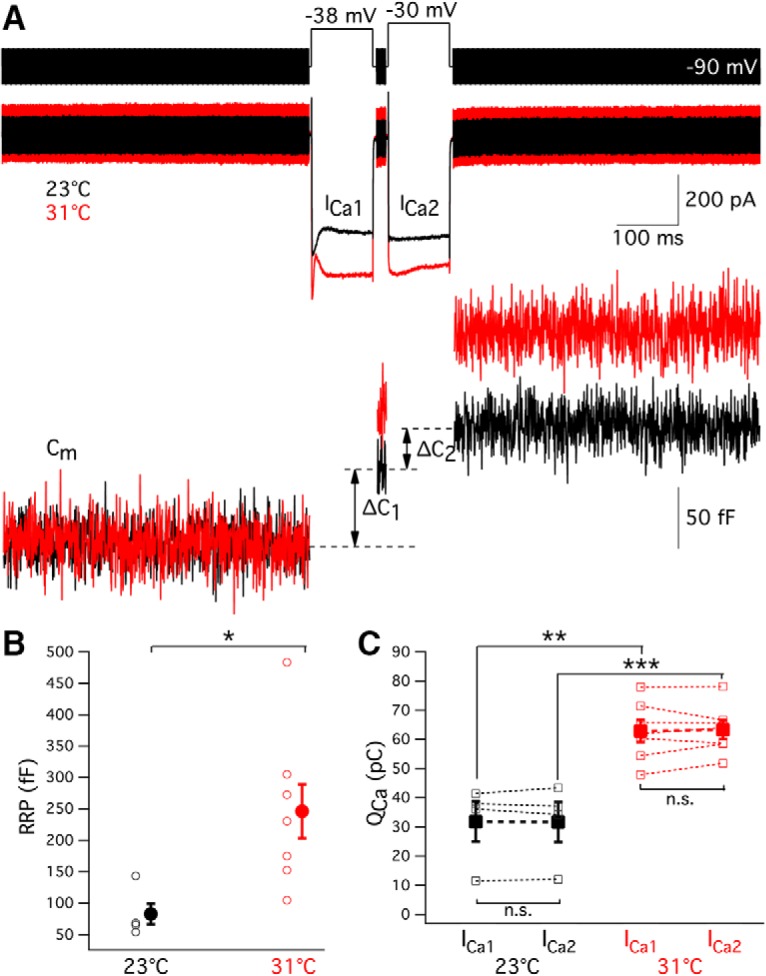
The RRP of vesicles is larger at high temperature. A, The paired pulse protocol used to calculate the maximum size of the RRP was composed of two 100 ms pulses with a 25 ms interval. The second pulse was depolarized to −30 mV. The first pulse was adjusted to give the same total amount of Ca²⁺ influx (Q_Ca) as the second pulse. It was different from cell to cell. In this example, the first depolarizing potential was −38 mV. The intervals between pulse pairs was 60–90 s to allow for full recovery. Ca²⁺ current recorded at 23°C and 31°C is shown in black and red, respectively. ΔC₁ and ΔC₂ are capacitance jumps triggered by the first and second depolarization, respectively. B, The maximum size of the RRP was calculated according to B_max = $\frac{\Delta C_1+\Delta C_2}{1-{\left(\Delta C_2/\Delta C_1\right)}^2}$. The value of B_max increased significantly from ∼83 fF (n = 4) at 23°C to 246 fF at 31°C (n = 7, p = 0.0351, unpaired t test). C, The Ca²⁺ influx during the first and second depolarizing pulses was 31.8 ± 6.8 pC and 31.7 ± 6.8 pC at room temperature (n = 4, p = 0.93), whereas the Ca²⁺ influx during the first and second pulses was 62.8 ± 3.8 pC and 63.3 ± 3.1 pC at high temperature (n = 7, p = 0.69). Both the first (p = 0.0005, unpaired t test) and the second (p = 0.0002, unpaired t test) pulses thus triggered more Ca²⁺ influx at high temperature. *p < 0.05, **p < 0.01, ***p < 0.001.

Ultrafast Ca²⁺ currents and short synaptic delays at high temperature

In vivo recordings of the auditory nerve fibers of two different species of frogs, Hyla regilla and Eleutherodactylus coqui, showed that the latencies of the first spike after the onset of a sound stimulus decreased when increasing temperature from 12°C to 25°C (Stiebler and Narins, 1990). To determine the temperature dependence of the synaptic delay at the hair cell afferent synapse, we performed paired recordings. We depolarized hair cells with two 20 ms depolarizing steps from −90 to −30 mV with 50 ms intervals (Fig. 11A) and recorded evoked EPSCs mediated by activation of AMPA receptors in the afferent fiber. After depolarization, Ca²⁺ ions entered into hair cells and triggered glutamate release (Fig. 11A). Due to EPSC rundown in some paired recordings, we only included the first trial from each pair in our analysis. Therefore, the data obtained at room and high temperatures were from two different groups of pairs. The average of EPSCs recorded at 22°C (n = 3) and 31°C (n = 6) is shown in black and red, respectively (Fig. 11A). Synaptic delay was measured from the onset of the pulse until the EPSC reached 10% of its maximum (Fig. 11C). The synaptic delay of the first EPSC (Fig. 11C) decreased from 2.03 ± 0.16 ms at room temperature (n = 3) to 1.28 ± 0.15 ms at high temperature (n = 6, p = 0.0183, unpaired t test; Fig. 11E). The synaptic delay of the second EPSC (Fig. 11C) shortened from 1.26 ± 0.10 ms at room temperature (n = 3) to 0.72 ± 0.05 ms at high temperature (n = 6, p = 0.001, unpaired t test; Fig. 11E). The first synaptic delay was longer than the second one under both room (n = 3, p = 0.008) and high (n = 6, p = 0.0206) temperature (Fig. 11D,E). The synaptic delay we measured from adult frog hair cell synapses is much shorter than that of the immature rat inner hair cell synapse (Goutman and Glowatzki, 2011).

Figure 11.

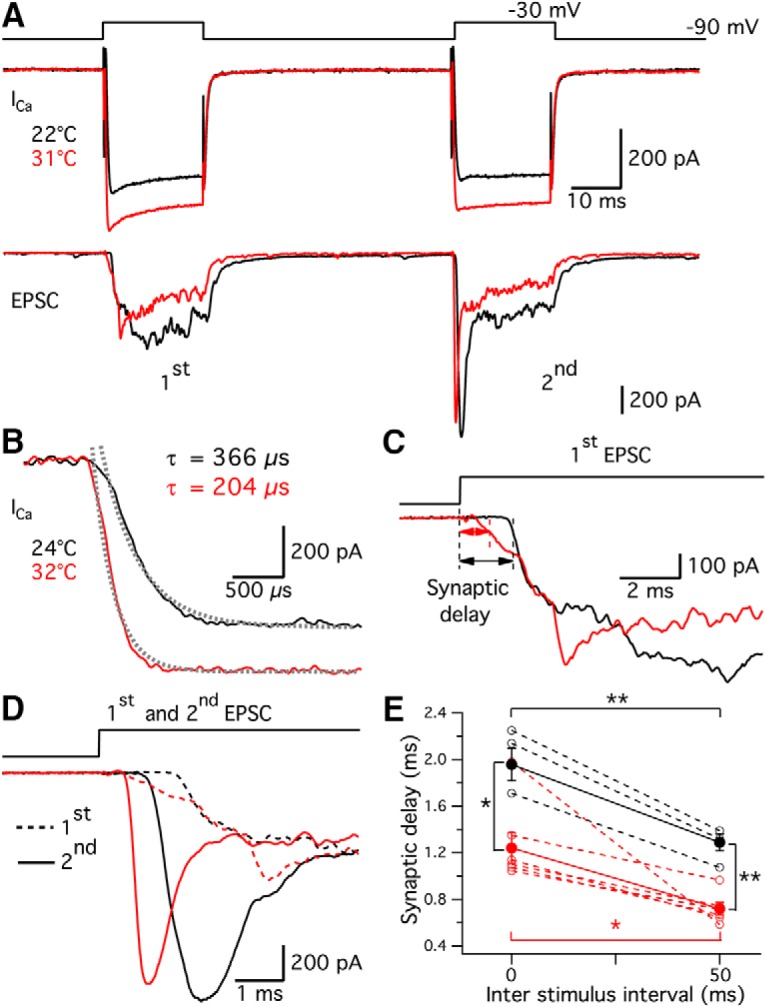
Shorter synaptic delays and faster EPSCs at high temperature. A, Two 20 ms depolarizing steps from −90 mV to −30 mV with 50 ms intervals were applied to a hair cell. Simultaneously, the postsynaptic afferent fiber was voltage-clamped at −90 mV. Average of calcium influx (I_Ca) elicited by the hair cell stimulus at 22°C (n = 3) and 31°C (n = 6) are shown in black and red, respectively. Synaptic vesicle glutamate release from the hair cell triggered a multiquantal EPSC in the afferent fiber. Black and red traces represent the averaged EPSCs at 22°C (n = 3) and 31°C (n = 6), respectively. Due to significant rundown, we only analyzed the first trial of each pair. Therefore, I_Ca and EPSC responses at room and high temperature were obtained from two different groups of pairs. B, Representative Ca²⁺ currents from another hair cell were triggered by a 20 ms depolarization from −90 mV to −30 mV at 24°C (black) and 32°C (red) using a P/4 protocol for leak subtraction. The activation time constant was derived from the single exponential fit after the capacitive transient (dashed lines). In this example, time constants of activation were 366 μs at 24°C (black) and 204 μs at 32°C (red). C, The rising phase of the first EPSC is shown on an expanded time scale. Synaptic delay was defined as the time between the start of stimulation and to when the EPSC reached 10% of the maximum. D, Overlay of the first (dashed lines) and the second (solid lines) EPSCs. Note the large synaptic facilitation of the second EPSCs. E, The synaptic delay of both the first (p = 0.0183, unpaired t test) and second EPSCs (p = 0.001, unpaired t test) decreased at 31°C. The first synaptic delay was longer than the second one under both 22°C (n = 3, p = 0.008) and 31°C (n = 6, p = 0.02). *p < 0.05, **p < 0.01.

Shorter synaptic delay is partially due to faster activation of Ca²⁺ current at high temperature. To determine the effect of temperature on the activation of I_Ca, we used P/4 leak subtraction to eliminate the capacitive transient. The Ca²⁺ current was evoked by a 20 ms depolarizing step from −90 to −30 mV (Fig. 11B). By fitting the activation phase of the Ca²⁺ current with a single exponential function (Fig. 11B, dashed lines), we calculated the time constant of activation: 377 ± 30 μs at 23.9 ± 0.1°C and 219 ± 19 μs at 31.5 ± 0.3°C (p < 0.0001, n = 8). The corresponding Q₁₀ was 2.2 ± 0.2 (n = 8), which is similar to the Q₁₀ of L-type Ca²⁺ channels activation in chick sensory neurons (Acerbo and Nobile, 1994), but higher than the Q₁₀ of gerbil inner hair cells (Johnson and Marcotti, 2008). The results indicate that high temperature speeds up the activation of Ca²⁺ channels and thus contributes to shortening the synaptic delay.

Paired-pulse ratio calculated from the charge transfer of EPSCs (EPSC₂/EPSC₁) was 1.00 ± 0.05 at room temperature (n = 3) and 0.92 ± 0.02 at high temperature (n = 6, p = 0.25, unpaired t test). Together with the paired-pulse ratio ΔC₂/ΔC₁, this suggests that high temperature does not affect overall release probability. However, high temperature improves temporal precision by shortening the synaptic delay; and under both temperatures, hair cell synapses exhibit pronounced short-term facilitation (Goutman and Glowatzki, 2011; see also Cho et al., 2011). Interestingly, these results differ greatly from those found in a conventional active zone synapse, the calyx of Held synapse, where synaptic delay of the second pulse was longer and EPSCs exhibit pronounced short-term depression (Wu and Borst, 1999).

Discussion

Temperature-dependent changes in EPSC, EPSP, and spike rates

Our in vitro whole-cell recordings of afferent fibers show that the frequencies of EPSCs and EPSPs increased at higher temperatures. This should produce an increase in AP spikes at higher temperatures. Indeed, afferent fiber spike rates mostly increased at higher temperatures (Fig. 1). In vivo single auditory nerve fiber recordings also show that spontaneous spike rates in the bullfrog amphibian papilla fibers increase at higher body temperatures (van Dijk et al., 1990). However, ∼30% of our recordings of afferent fibers decreased their spike rate at higher temperatures. We do not know the reasons for this heterogeneity. The underlying mechanisms that trigger spikes in the different afferent fibers require additional studies to explain the wide range of membrane input resistance (Fig. 4B). Interestingly, mammalian auditory nerve fibers also exhibit a heterogeneity in spike rates, gene expression, and membrane properties (Rutherford et al., 2012; Heil and Peterson, 2017; Shrestha et al., 2018).

What are the mechanisms that produce an increase in EPSC frequency? One obvious possibility we explored was a depolarization of the hair cell V_rest. Surprisingly, during whole-cell current-clamp recordings, the V_rest of hair cells hyperpolarized significantly (Fig. 5A). V_rest also hyperpolarizes in snail neurons at higher temperatures due to increased Na⁺/K⁺-ATPase activity (Gorman and Marmor, 1970). However, perforated patch recordings, which do not disturb the intracellular milieu, showed no significant change. The V_rest we observed in perforated patch mode was ∼−63 mV (Fig. 5A). Previous, sharp conventional electrode recordings of V_rest of turtle and frog hair cells reported values ∼−55 mV (Crawford and Fettiplace, 1980; Pitchford and Ashmore, 1987). At these membrane potentials, a small inward Ca²⁺ current is induced (Fig. 5C). This resting Ca²⁺ current increases at higher temperatures, which probably increases release probability and spike rates (Trapani and Nicolson, 2011). The frequency of spontaneous mEPSCs also increases at high temperature at the calyx of Held synapse (Kushmerick et al., 2006; Postlethwaite et al., 2007) and hippocampal synapses (Kim and Connors, 2012). However, unlike bullfrog hair cells, V_rest of the calyx of Held nerve terminal depolarizes when temperature increases from 24°C to 32°C (Kim and von Gersdorff, 2012). Finally, we note that our amphibian papilla hair cells are bathed in high external Ca²⁺, which blocks transduction channels; and recently, it was found that sudden heat rises can soften gating springs and open mechanotransduction channels on the stereocilia bundles of bullfrog sacculus hair cells (Azimzadeh et al., 2018). Therefore, we may be underestimating the physiological effects of temperature shifts on the hair cell, and V_rest may be more depolarized under in vivo conditions.

We found out that the average amplitude of the spontaneous EPSCs from bullfrog afferent fibers did not change at higher temperature (Fig. 2; Table 2). This differs from observations made in mammalian synapses where elevating temperature increases spontaneous mEPSC amplitude (Veruki et al., 2003; Kushmerick et al., 2006; Postlethwaite et al., 2007). Interestingly, we previously observed that a decrease in temperature from room temperature to 15°C resulted in a decrease in EPSC amplitude (Li et al., 2009). Spontaneous EPSC amplitudes may thus be saturated at room temperature. The average EPSP amplitude also did not change with temperature (Table 2). However, in 13 fibers where both EPSCs and EPSPs were recorded, EPSCs remained the same (p = 0.45), whereas EPSP amplitude decreased (p = 0.049, n = 13) at high temperature. This could result from a decrease in afferent fiber R_in at high temperature. Both EPSC and EPSP events increased in frequency at high temperature (Table 2). This can lead to greater summation of EPSPs, making them more likely to reach AP threshold. However, EPSP decay was also significantly faster at higher temperatures (Fig. 2A3,B3), which tends to reduce summation of noncoincident EPSPs. Therefore, it is possible that higher temperatures may reduce spike rates, as shown in Figure 1B. Both presynaptic and postsynaptic mechanisms may thus explain the heterogeneity in spike frequency changes with temperature seen in Figure 1.

Temperature-dependent changes in spike threshold may also explain the heterogeneity shown in Figure 1. Thermo-positive fibers fire more spikes spontaneously at high temperature with threshold decreasing by ∼5 mV, whereas thermo-negative fibers fire less spontaneous spikes at high temperature with threshold increasing by 5 mV (Table 1). Heterogeneity in the types and densities of voltage-gated Na⁺ and K⁺ channels among different fibers may explain these differences (Kim and Rutherford, 2016). Together, the temperature-dependent changes of spiking rates is due to presynaptic changes in hair cell exocytosis and postsynaptic changes in afferent fiber excitability.

Synaptic delay and phase locking at high temperature

Recordings of single frog auditory nerve fibers show that spike onset delay to sound stimulus decreased as temperature increased with Q₁₀ values of 1.6–2.5 (Stiebler and Narins, 1990; van Dijk et al., 1990). We performed paired recordings from hair cell to afferent fiber and revealed a shortening of synaptic delay at high temperature (Fig. 11E). This shorter synaptic delay was due in part to a faster activation kinetics of Ca²⁺ current at high temperature (Fig. 11B). In addition, the time constant of lipid membrane fusion is inversely correlated to temperature (Schotten et al., 2015), which may also contribute to the shorter synaptic delay at high temperature. A shorter synaptic delay will improve the spike phase-locking of the fibers because evoked EPSPs and spikes will be more phase-locked to the hair cell Ca²⁺ current activation. This may explain why in vivo recordings from single auditory nerve fibers indicate that vector strength increases at higher temperatures (Stiebler and Narins, 1990; van Dijk et al., 1990).

Higher temperatures and synaptic facilitation tend to synchronize depolarization-evoked multivesicular release (Fig. 11). Synaptic facilitation revealed by paired-pulse depolarization also reduced synaptic delays in both bullfrog hair cell synapses (Cho et al., 2011) and rat inner hair cell synapses (synaptic delay was 1.5 ms at room temperature) (Goutman and Glowatzki, 2011). Likewise, we measured here synaptic delays of 1.3 ms at 23°C and 0.7 ms at 31°C (Fig. 11E).

Electrical resonance at high temperature

The lowering of R_in at high temperature reduces the membrane time constant, allowing hair cells to better follow rapid membrane potential changes (Fig. 6). The intrinsic electrical resonant frequency of hair cells increased with temperature (Fig. 7), as expected from an increase in Ca²⁺ and K⁺ current amplitudes (Fig. 5B). We observed a large change in average resonant frequency from 320 to 530 Hz (Fig. 7D). These changes increase the dynamic range of frequency tuning of amphibian papilla hair cells and their connected afferent fibers. Indeed, in vivo recordings of frog auditory nerve fibers show higher characteristic frequencies (tuning curve tip or best frequency) at higher temperature (Stiebler and Narins, 1990).

Exocytosis efficiency and vesicle pool size at high temperature

Smaller R_in will inevitably result in smaller membrane potential changes (V_m = R_in × I) induced by the opening of mechanosensitive channels in the stereocilia. This predicted loss of sensitivity to sound signals is not observed in vivo. Indeed, the contrary is observed: the threshold for sound triggered spikes is reduced at high temperature (Stiebler and Narins, 1990). How can we explain this increase in fiber sensitivity?

First, we found that the steepness of the Ca²⁺ current I–V curve (Fig. 5C) increased at high temperature making Ca²⁺ influx more sensitive to membrane potential fluctuations around V_rest. The enlarged Ca²⁺ current could result from an increase in L-type Ca²⁺ channel open probability (P_o) and/or conductance (Lux and Brown, 1984; Klöckner et al., 1990; Acerbo and Nobile, 1994; Peloquin et al., 2008). The Q₁₀ of single L-type channel conductance in smooth muscle cells and retina is 1.6 and 3.0, respectively (Klöckner et al., 1990; Peloquin et al., 2008). Second, at hair cell synapses, a cluster of L-type Ca²⁺ channels is located within nanometers from docked vesicles under the synaptic ribbon (Brandt et al., 2005; Nouvian et al., 2006; Graydon et al., 2011; Kim et al., 2013). Fast activation of this cluster of Ca²⁺ channels produces a highly synchronous and fast multiquantal EPSC (Fig. 11D) (Grabner et al., 2016), which may help to explain the short latency and low jitter of the sound evoked first-spike in the auditory nerve (Wittig and Parsons, 2008).

We also observed an increase in exocytosis efficiency, which indicates the exocytosis increase is not proportional to the increase of Ca²⁺ current. A nonlinear power law dependence of exocytosis on free Ca²⁺ ion concentration could potentially explain our results of a high Q₁₀ = 2.4 for exocytosis elicited by 20 ms depolarizing pulses (Cho and von Gersdorff, 2012; Quiñones et al., 2012). However, a linear dependence of exocytosis on Ca²⁺ current charge has been found for mid-frequency tuned bullfrog hair cells (Keen and Hudspeth, 2006; Cho et al., 2011). Thus, vesicle fusion efficiency must be intrinsically higher at high temperature, as shown in Figure 9C. In addition to Ca²⁺ influx through L-type Ca²⁺ channels in the plasma membrane, Ca²⁺-induced Ca²⁺ release from intracellular stores can also be involved in nonlinear vesicle recruitment at auditory hair cells (Castellano-Muñoz et al., 2016).

Release probability increases at high temperature for some central synapses (Hardingham and Larkman, 1998; Volgushev et al., 2004), although we did not observe changes in release probability using a paired-pulse stimulation protocol (Figs. 10, 11). However, we did observe a significant increase in the RRP size at high temperature (Fig. 10). In addition to facilitating spontaneous vesicle fusion, temperature also facilitates sustained exocytosis by accelerating vesicle replenishment of the RRP (Pyott and Rosenmund, 2002; Kushmerick et al., 2006). Moreover, synaptic vesicle endocytosis is also highly temperature-sensitive (Fernández-Alfonso and Ryan, 2004; Micheva and Smith, 2005; Renden and von Gersdorff, 2007; Delvendahl et al., 2016). The kinetics of endocytosis may thus be rate limiting for prolonged exocytosis and requires further studies at hair cell synapses.