Adaptive Zone Model Predictive Control of Artificial Pancreas Based on Glucose- and Velocity-Dependent Control Penalties

Abstract

Objective:

Zone model predictive control (MPC) has been proven to be an efficient approach to closed-loop insulin delivery in clinical studies. In this work, we aim to safely reduce mean glucose levels by proposing control penalty adaptation in the cost function of zone MPC.

Methods:

A zone MPC method with a dynamic cost function that updates its control penalty parameters in real time according to the predicted glucose and its rate of change is developed. The proposed method is evaluated on the entire 100-adult cohort of the FDA-accepted UVA/Padova T1DM simulator and compared with the zone MPC tested in an extended outpatient study.

Results:

For unannounced meals, the proposed method leads to statistically significant improvements in terms of mean glucose (153.8 mg/dL vs. 159.0 mg/dL; p < 0.001) and percentage time in [70, 180] mg/dL (70.5% vs. 66.3%; p < 0.001) without increasing the risk of hypoglycemia. Performance for announced meals is similar to that obtained without adaptation. The proposed method also behaves properly and safely for scenarios of moderate meal-bolus and basal rate mismatches, as well as simulated unannounced exercise. Advisory-mode analysis based on clinical data indicates that the method can reduce glucose levels through suggesting additional safe amounts of insulin on top of those suggested by the zone MPC used in the study.

Conclusion:

The proposed method leads to improved glucose control without increasing hypoglycemia risks.

Significance:

The results validate the feasibility of improving glucose regulation through glucose- and velocity-dependent control penalty adaptation in MPC design.

I. Introduction

The development of continuous glucose monitoring (CGM) sensors and continuous subcutaneous insulin infusion pumps enables the design of artificial pancreas (AP) systems for patients with type 1 diabetes mellitus (T1DM). The overall goal is to achieve safe and satisfactory blood glucose regulation in terms of hyperglycemia and hypoglycemia prevention through designing closed-loop insulin delivery algorithms [1]–[3].

The authors’ group has been working on a zone model predictive control (MPC) approach to closed-loop insulin delivery [4]–[7], which has been evaluated in numerous clinical studies on more than 120 patients and 70,000 hours [8]–[12]. As euglycemia is defined as a range of blood glucose concentrations rather than a single value, a zone MPC penalizes the distance of glucose predictions from a carefully designed safe zone based on clinical requirements, which helps avoid unnecessary control moves and reduces glycemic variability and the risk of hypoglycemia. The original zone MPC for the AP was developed in Grosman et al. [4] utilizing an auto-regressive model with exogenous inputs, which was progressively extended to integrate a control-relevant state-space model [13] and a diurnal periodic target zone [5]. Asymmetric costs on insulin delivery above and below basal rate were further utilized in Gondhalekar et al. [6], to facilitate decoupled design for hyperglycemia and hypoglycemia. In a recent version of zone MPC [7], velocity-weighting and velocity-penalty were incorporated in the MPC cost function to reduce the likelihood of controller-induced hypoglycemia and achieve enhanced hyperglycemia correction. Although improved hemoglobin A1c was achieved in the corresponding clinical trial [12], improvements with average glucose were not obvious, which give rise to the need of developing further controller enhancements without weakening safety guarantees against hypoglycemia. In this work, we explore one promising approach by designing dynamic updating strategies for control penalty parameters.

The problem considered falls in the topic of adaptive AP design, for which a few different methods have been investigated in the literature. In earlier studies, basal rate and meal bolus adaptation were considered through run-to-run approaches utilizing sparse blood glucose (BG) measurements [14], [15]. The advent of CGM further enabled the utilization of advanced control approaches in adaptive AP design. For instance, a nonlinear adaptive MPC was proposed by Hovorka et al. [16] to maintain normoglycemia during fasting conditions using Bayesian model parameter estimation. El-Khatib et al. [17] employed a generalized predictive control (GPC) approach with a recursively updated subject model on a bi-hormone AP; a GPC approach was also explored in Turksoy et al. [18] to eliminate the need of meal or exercise announcements. A model predictive iterative learning control approach was proposed by Wang et al. [19] to adapt controller behavior on the basis of patient’s day-to-day lifestyle. Cameron et al. [20] developed a multiple model probabilistic predictive controller to obtain enhanced meal detection and prediction. In Toffanin et al. [21], a dynamic insulin-on-board approach was proposed to counteract the effect of insulin sensitivity circadian rhythm. Colmegna et al. [22] developed a switched linear parameter-varying approach to separately adjust controller behavior in hypoglycemia, hyperglycemia and euglycemia situations. Toffanin et al. [23] recently revisited the run-to-run approach to adapt the basal insulin delivery rate and carbohydrate-to-insulin ratio by taking into account the intraand inter-day insulin sensitivity variability. In Laguna Sanz et al. [24], a confidence index was incorporated in a zone MPC to allow controller parameter adaptation based on the accuracy of the prediction model in recent history. An MPC with event-triggered controller update strategies was proposed by Chakrabarty et al. [25] to reduce energy consumption of an embedded AP while maintaining satisfactory glucose regulation performance. A recent review of adaptive approaches to AP design can be found in Turksoy and Cinar [26].

The main difference of our work from existing adaptive MPC/GPC approaches in the literature is that a dynamic MPC cost function and a constant system model are utilized, instead of a constant cost function and a dynamically updated prediction model. Specifically, we propose an adaptive MPC cost function based on the values and change rates of glucose predictions, by exploiting the physiological properties of the insulin-glucose metabolic process. This approach is motivated by the multi-zone MPC design proposed in Grosman et al. [27]. However, the adapted controller parameters in Grosman et al. [27] were all kept piecewise constant according to the region in which the glucose level stayed, and more importantly, the effect of glucose trend on insulin dose calculation was not taken into account. To overcome these limitations, a continuous dependence of the control penalty parameters on both predicted values and trends of blood glucose is investigated in our work. A preliminary version of the design was reported in [28].

The performance of the proposed adaptive MPC is evaluated via extensive in silico tests on the 100-adult cohort of the US Food and Drug Administration (FDA) accepted Universities of Virginia (UVA)/Padova T1DM simulator [29] and comparative advisory-mode analysis based on the historical clinical data obtained in [12]. Compared with the zone MPC developed in [7], improved results are obtained by the proposed adaptive method in terms of mean glucose level and percentage time in the safe range without increasing the risk of hypoglycemia for both announced and unannounced meals. The robustness of the controller is evaluated utilizing a scenario-based approach [30] through considering different extreme situations; the proposed adaptive controller can behave properly in the scenarios of moderate meal-bolus mismatches, basal-rate mismatches and simulated unannounced exercise. In addition, through feeding the clinical data [12] obtained using the zone MPC in [7], we observe that the proposed method can help reduce glucose levels through suggesting additional but safe amounts of insulin.

II. Problem Description

The base controller for this work is the periodic zone MPC with velocity-weighting and velocity-penalty developed in [7]. Driven by the arrival of glucose measurements, the controller runs in discrete time and calculates a numeric control law every 5 minutes. Specifically, at discrete time instant i, the relative dose correction u_k of insulin infusion u_abs,k from the basal rate u_basal (namely, u_k ≔ u_abs,k − u_basal) is obtained by solving a constrained optimization problem of the form:

$${\text{u}}_{0:N_{\text{u}}-1}^{*}≔\text{arg}\underset{{\text{u}}_{0:N_{\text{u}}-1}}{\text{min}}J\left(x_i,{\text{u}}_{0:N_{\text{u}}-1}\right)$$ (1)

with cost function

$$J(\cdot ,\cdot )≔{\sum }_{k=1}^{N_{\text{p}}}\left({\check{\text{z}}}_k^2+Q\left({\text{v}}_k\right){\hat{\text{z}}}_k^2+\hat{D}{\hat{\text{v}}}_k^2\right)+{\sum }_{k=0}^{N_u-1}\left(\hat{R}{\hat{\text{u}}}_k^2+\check{R}{\check{\text{u}}}_k^2\right),$$ (2)

subject to system dynamics and safety constraints. In (2), ${\hat{\text{u}}}_k≔\text{max}\left({\text{u}}_k,0\right)$ and ${\check{\text{u}}}_k≔\text{min}\left({\text{u}}_k,0\right)$, which represent delivery rates above and below the basal rate u_basal, respectively; the separate weighting parameters $\hat{R}$ and $\check{R}$ on ${\hat{\text{u}}}_k$ and ${\check{\text{u}}}_k$ allow independent penalization of the costs of insulin delivery above and below basal rate. The detailed explanation of the other terms in (2) and the MPC algorithm can be found in the supplementary document of this paper and in [7].

In [6], [7], the control input penalties $\hat{R}$ and $\check{R}$) were fixed to constant values. A natural question to ask is whether improved glucose regulation performance can be obtained by further adapting these parameters, which have a clear and direct relationship with the controller behavior - smaller values of $\hat{R}$ and $\check{R}$ correspond to more aggressive controller activity and vice versa. In particular, we adjust the values of $\hat{R}$ and $\check{R}$ according to the glucose state prediction y_k (obtained via the prediction model of MPC) and glucose velocity

$${\mu }_k≔{\text{y}}_k-{\text{y}}_{k-1}.$$ (3)

We implement this idea by designing $\hat{R}$- and $\check{R}$-surfaces along continuum values of glucose prediction y_k and velocity μ_k. Consequently, the MPC cost function is modified from its original form in (2) to

$$J(\cdot ,\cdot )≔{\sum }_{k=1}^{N_{\text{p}}}\left({\check{\text{z}}}_k^2+Q\left({\text{v}}_k\right){\hat{\text{z}}}_k^2+\hat{D}{\hat{\text{v}}}_k^2\right)+{\sum }_{k=0}^{N_u-1}\left(\hat{R}\left({\mu }_k,{\text{y}}_k\right){\hat{\text{u}}}_k^2+\check{R}\left({\mu }_k,{\text{y}}_k\right){\check{\text{u}}}_k^2\right).$$ (4)

The objective of the design is to achieve enhanced control performance in terms of average blood glucose level and percent time in safe range [70, 180] mg/dL, without increasing risk of hypoglycemia. Note that $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ and $\check{R}\left({\mu }_k,{\text{y}}_k\right)$ are calculated from the predicted glucose y_k and velocity μ_k using the prediction model in the zone MPC.

III. Glucose and Velocity Dependent MPC Parameter Adaption

In this section, the proposed control penalty parameter adaptation approach is presented. We first present the detailed design and parameterization of $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ and $\check{R}\left({\mu }_k,{\text{y}}_k\right)$, and then provide discussions on the solution of the corresponding MPC optimization problem.

A. Design of $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$

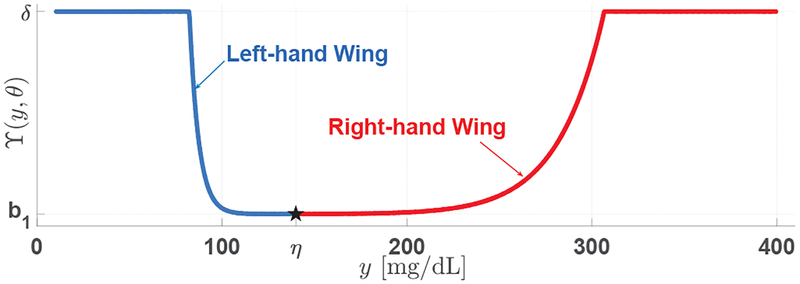
Before continuing, we introduce a basic function ϒ(y, θ) that is utilized to build $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$. Specifically, ϒ(y, θ) is designed by connecting two exponential functions with saturation:

$$\mathrm{\Upsilon }(y,\theta )≔\{\begin{array}{cc}\text{min}\left\{\delta ,\text{exp}\left[a_2(\eta -y+\mathcal{l})\right]+\left[b_1-\text{exp}\left(a_2\mathcal{l}\right)\right]\right\},\hfill & \hfill \text{if}y\le \eta ,\\ \text{min}\left\{\delta ,\text{exp}\left\{\left[a_1{(y-\eta )}^{\alpha }\right]\right\}+b_1\right\},\hfill & \hfill \text{otherwise},\end{array}$$ (5)

where θ ≔ [δ, a₁, a₂, b₁, α, η,ℓ] is a septuple that parameterizes this “bowl-shaped” function. In particular, δ and b₁ determine the maximum (saturation) and minimum values of the curve, respectively, a₁ and α control the “steepness” of the “right-hand wing” (namely, y > η) exponential function, a₂ decides the “steepness” of the “left-hand wing” (y ≤ η) exponential function, and η determines the connection point of the two exponential functions. An illustration of this function is provided in Fig. 1.

Fig. 1:

An illustration of the basic function defined in (5), composed of two exponential functions with saturation.

From (4), $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ penalizes insulin infusion above the basal rate and is usually in effect when y_k ≥ 80; because insulin delivery above basal rate is also the direct cause of low glucose values, $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ determines both glucose regulation performance and hypoglycemia risk and therefore is the major focus of parameter adaptation. To separately consider the scenarios of ascending and descending glucose sequences, we parameterize $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ according to the sign of predicted glucose velocity μ_k:

$$\hat{R}\left({\mu }_k,y_k\right)≔\{\begin{array}{cc}{\hat{R}}^{+}\left({\mu }_k,y_k,{\mathrm{\Theta }}^{+}\right)& \text{if}{\mu }_k\ge 0,\\ {\hat{R}}^{-}\left({\mu }_k,y_k,{\mathrm{\Theta }}^{-}\right)& \text{if}{\mu }_k<0,\end{array}$$ (6)

where Θ⁺ and Θ⁻ are two vector-valued parameters that determine the relationship of ${\hat{R}}^{+}$ and ${\hat{R}}^{-}$ with μ_k and y_k, respectively. In this work, ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ and ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$ are both designed based on the basic function ϒ(·, ·), but are parameterized with different parameters Θ⁺ and Θ·− due to their different roles in glucose regulation.

1). Designing ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$:

Specifically, we consider the following principles for the design of ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$, which is related to increasing glucose predictions:

• A1) given the same (non-negative) glucose velocity prediction μ_k, the aggressiveness of the controller (in terms of increasing insulin infusion above basal rate) should gradually decrease with the increase of y_k when y_k is above the normal range to avoid overdosing insulin (because a suitable amount of insulin may have been delivered during the period when the glucose is rising), and decrease with the decrease of y_k when it is below its normal value;

• A2) given the same glucose state prediction y_k, the controller’s activeness in terms of increasing insulin infusion should decrease with the decrease of |μ_k|, namely, the absolute value of glucose velocity.

These principles reflect the clinical safety requirements in blood glucose regulation, while still providing an opportunity to enhance control performance by exploiting glucose state and velocity dependent controller adaptation. To implement principle A1, we propose upper and lower bounds ${\overline{\Re }}^{+}\left({\text{y}}_k,{\theta }^{+}\right)$ and ${\underset{\_}{\Re }}^{+}\left({\text{y}}_k,{\theta }^{+}\right)$ for ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ as

$${\overline{\Re }}^{+}\left({\text{y}}_k,{\theta }_H^{+}\right)≔\mathrm{\Upsilon }\left({\text{y}}_k,{\theta }_H^{+}\right)$$ (7)

$${\underset{\_}{\Re }}^{+}\left({\text{y}}_k,{\theta }_L^{+}\right)≔\mathrm{\Upsilon }\left({\text{y}}_k,{\theta }_L^{+}\right)$$ (8)

by considering the two limiting cases μ_k = 0 and μ_k → ∞, respectively, where ${\theta }_H^{+}≔\left[{\delta }_H^{+},a_{1H}^{+},a_{2H}^{+},b_{1H}^{+},{\alpha }_H^{+},{\eta }_H^{+},{\mathcal{l}}_H^{+}\right]$ and ${\theta }_L^{+}≔\left[{\delta }_L^{+},a_{1L}^{+},a_{2L}^{+},b_{1L}^{+},{\alpha }_L^{+},{\eta }_L^{+},{\mathcal{l}}_L^{+}\right]$ are the parameter vectors. To address principle A2, we introduce an exponential decay function to allow the value of ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ to flow monotonically between the upper and lower bounds for μ_k ∈ [0,∞):

$${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)≔{\underset{\_}{\Re }}^{+}\left({\text{y}}_k,{\theta }_L^{+}\right)+\text{exp}\left(-{\tau }^{+}{\mu }_k\right)\times \left[{\overline{\Re }}^{+}\left({\text{y}}_k,{\theta }_H^{+}\right)-{\underset{\_}{\Re }}^{+}\left({\text{y}}_k,{\theta }_L^{+}\right)\right],$$ (9)

where τ⁺ is a parameter that determines the decay rate and

$${\mathrm{\Theta }}^{+}≔\left[{\theta }_L^{+},{\theta }_H^{+},{\tau }^{+}\right].$$ (10)

2). Designing ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$:

Following similar ideas, we consider the principles below to design ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$:

• B1) given a negative glucose velocity prediction μ_k < 0, the controller should decrease insulin infusion to avoid hypoglycemia, and should be even more cautious when the corresponding glucose prediction y_k is either low or extremely high;

• B2) given the same glucose prediction y_k, the aggressiveness of the controller should decrease with the increase of the absolute value of the glucose velocity |μ_k|.

To implement principle B1, we introduce upper and lower bounds ${\overline{\Re }}^{-}\left({\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$ and ${\Re }^{-}\left({\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$ for ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$, which are defined as

$${\overline{\Re }}^{-}\left({\text{y}}_k,{\theta }_H^{-}\right)≔\mathrm{\Upsilon }\left({\text{y}}_k,{\theta }_H^{-}\right)$$ (11)

$${\underset{\_}{\Re }}^{-}\left({\text{y}}_k,{\theta }_L^{-}\right)≔\mathrm{\Upsilon }\left({\text{y}}_k,{\theta }_L^{-}\right)$$ (12)

by considering the two limiting cases μ_k → −∞ and μ_k = 0, respectively, where ${\theta }_H^{-}≔\left[{\delta }_H^{-},a_{1H}^{-},a_{2H}^{-},b_{1H}^{-},{\alpha }_H^{-},{\eta }_H^{-},{\mathcal{l}}_H^{-}\right]$ and ${\theta }_L^{-}≔\left[{\delta }_L^{-},a_{1L}^{-},a_{2L}^{-},b_{1L}^{-},{\alpha }_L^{-},{\eta }_L^{-},{\mathcal{l}}_L^{-}\right]$ are parameter vectors. To address principle B2, we similarly introduce an exponential decay function to allow the value of ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ to flow monotonically between the upper and lower bounds for μ_k ∈ (−∞, 0):

$${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)≔{\overline{\Re }}^{-}\left({\text{y}}_k,{\theta }_H^{-}\right)-\text{exp}\left({\tau }^{-}{\mu }_k\right)\times \left[{\overline{\Re }}^{-}\left({\text{y}}_k,{\theta }_H^{-}\right)-{\underset{\_}{\Re }}^{-}\left({\text{y}}_k,{\theta }_L^{-}\right)\right],$$ (13)

where τ⁻ determines the decay rate and

$${\mathrm{\Theta }}^{-}≔\left[{\theta }_L^{-},{\theta }_H^{-},{\tau }^{-}\right].$$ (14)

3). Parameter design:

A two-step procedure is performed to determine the parameters in Θ⁺ and Θ⁻ for improved glucose regulation performance. In the first step, the parameters are iteratively tuned based on their roles using the 10-patient cohort of the UVA/Padova simulator [29] with the goal of achieving minimum average glucose values without increasing the risk of hypoglycemia, following a 24-hour in silico protocol with 3 unannounced meals of [50, 75, 75] g carbohydrate (CHO) at 08:00, 12:00 and 19:00, respectively. This step yields an optimal parameter pair $\left({\mathrm{\Theta }}_{*}^{+},{\mathrm{\Theta }}_{*}^{-}\right)$, the approximate optimality of which is also verified through Genetic Algorithm and Pattern Search Algorithm by solving a corresponding constrained optimization problem. As the zone MPC [7] achieved satisfactory performance for announced meals, the parameters design was done using unannounced meals and evaluated on both announced and unannounced cases to ensure safe and effective design.

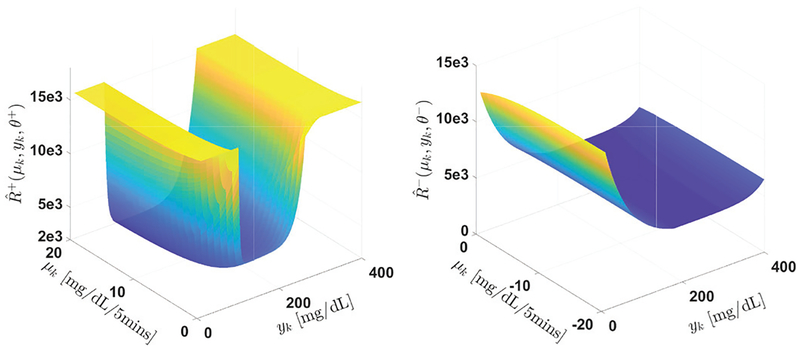
In the second step, the robustness of the controller is evaluated by considering scenarios of different measurement noises, basal rate mismatches, simulated exercise using undetected insulin delivery, and over/underestimated meal boluses. The effect of different meal sizes is also considered by testing a scenario of fasting (no meals), a snack scenario with [10, 30, 20] g CHO and a large meal scenario with [50, 100, 80] g CHO with/without meal announcements. The parameters (Θ⁺, Θ⁻) are then fine tuned on the basis of $\left({\mathrm{\Theta }}_{*}^{+},{\mathrm{\Theta }}_{*}^{-}\right)$ to ensure increased risk of hypoglycemia is caused by the obtained (Θ⁺, Θ⁻) compared with the original zone MPC and minimal performance degradation in terms of average glucose level is incurred compared with that of the pair $\left({\mathrm{\Theta }}_{*}^{+},{\mathrm{\Theta }}_{*}^{-}\right)$ The value of the obtained parameters are provided in TABLE I, and an illustration of the relationship of ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ and ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$ with glucose state y_k and glucose velocity μ_k is provided in Fig. 2. Considering the computation burden in this off-line parameter optimization procedure, the 10-patient cohort is used here as a “training dataset”. To ensure the performance of the designed parameters, the 100-patient cohort of the simulator is used as a “test dataset” to evaluate the performance of the design in Section IV.

TABLE I:

Parameters for Θ⁺ and Θ⁻

Parameters for Θ+	${\delta }_H^{+}$ 6,500	$a_{1H}^{+}$ 0.14	$a_{2H}^{+}$ 0.32	$b_{1H}^{+}$ 5,500	${\alpha }_H^{+}$ 0.75	${\eta }_H^{+}$ 130	τ+ 0.20
	${\delta }_L^{+}$ 15,500	$a_{1L}^{+}$ 0.11	$a_{2L}^{+}$ 0.20	$b_{1L}^{+}$ 2,000	${\alpha }_L^{+}$ 0.75	${\eta }_L^{+}$ 0.20
Parameters for Θ−	${\delta }_H^{-}$ 1,000,000	$a_{1H}^{-}$ 0.03	$a_{2H}^{-}$ 0.02	$b_{1H}^{-}$ 5,000	${\alpha }_H^{-}$ 1	${\eta }_H^{-}$ 180	τ− 0.20
	${\delta }_L^{-}$ 1,000,000	$a_{1L}^{-}$ 0.03	$a_{2L}^{-}$ 0.02	$b_{1L}^{-}$ 4,910	${\alpha }_L^{-}$ 1	${\eta }_L^{-}$ 180

Fig. 2:

Relationship of ${\hat{R}}^{+}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{+}\right)$ and ${\hat{R}}^{-}\left({\mu }_k,{\text{y}}_k,{\mathrm{\Theta }}^{-}\right)$ with μ_k and y_k.

B. Design of $\check{R}\left({\mu }_k,{\text{y}}_k\right)$

$\check{R}\left({\mu }_k,{\text{y}}_k\right)$ affects insulin infusion below the basal rate, which critically determines controller actions when the glucose concentration drifts toward or falls into the hypoglycemia region (y_k < 70 mg/dL). The proposed approach to designing $\hat{R}\left({\mu }_k,{\text{y}}_k\right)$ in Section III-A equally applies to $\check{R}\left({\mu }_k,{\text{y}}_k\right)$. To maintain minimal complexity of the controller, however, we resort to a simple and effective design here considering the different role of $\check{R}\left({\mu }_k,{\text{y}}_k\right)$. As mentioned in Section II, $\check{R}$ in (2) is usually set to a small value $(\check{R}=100)$ to ensure that proper pump suspensions are performed to avoid hypoglycemia events. To enhance this safety concern, it suffices to ignore the dependency of $\check{R}\left({\mu }_k,{\text{y}}_k\right)$ on μ_k and consider the following simple y_k-dependent multi-zone parameter adaptation formula:

$$\check{R}\left({\text{y}}_k\right)≔\{\begin{array}{cc}100,\hfill & \text{if}{\text{y}}_k>140,\hfill \\ 10,\hfill & \text{if}{\text{y}}_k\in [120,140],\hfill \\ 1,\hfill & \text{if}{\text{y}}_k<120,\hfill \end{array}$$ (15)

where a short-hand notation $\check{R}\left({\text{y}}_k\right)$ is used instead of $\check{R}\left({\mu }_k,{\text{y}}_k\right)$. The implication of this design is that when the glucose prediction y_k is conspicuously low, an active pump suspension strategy will be enforced, regardless of the glucose velocity μ_k.

IV. In Silico Performance Analysis

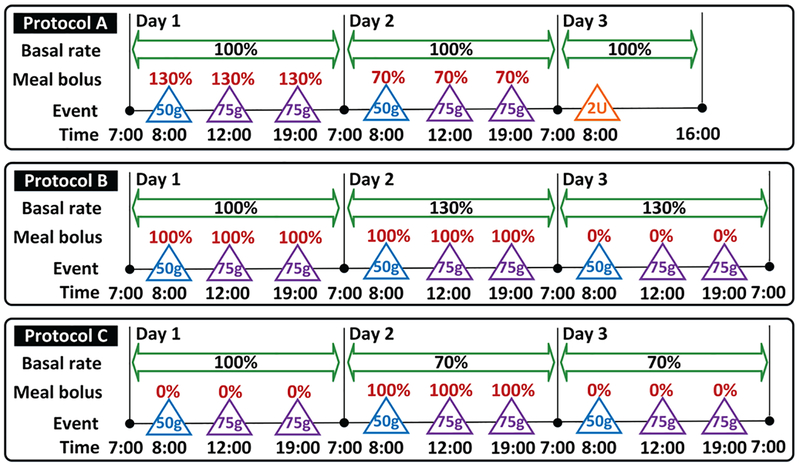
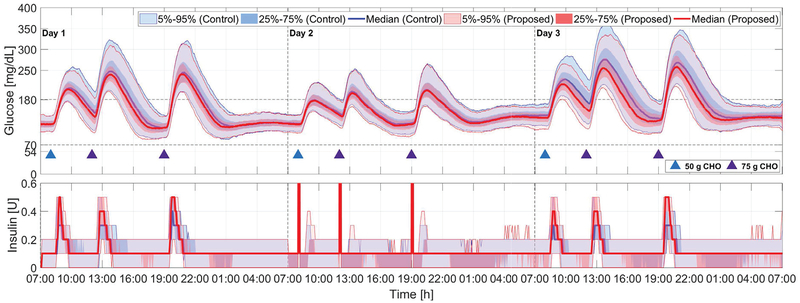
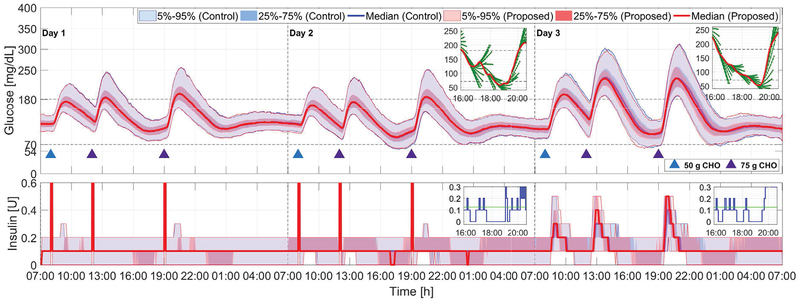
The proposed controller adaptation method is evaluated on the 100-adult cohort of the FDA accepted UVA/Padova T1DM simulator [29]. Three protocols (namely, Protocols A-C below) are designed to evaluate the performance of glucose regulation under various scenarios (see Fig. 3):

Fig. 3:

List of protocols used for performance evaluation of the proposed controller. The blue and purple triangles denote meals of 50 g and 75 g CHO, respectively. The orange triangle denotes unannounced insulin bolus of 2 units. Basal rate is provided in terms of percentages of the default value. Meal boluses are described in terms of the percentages of the actual meal sizes.

1. Protocol A is a 57-hour 6-meal protocol starting from 7:00 on Day 1. On Day 1 and Day 2, breakfast (50 g CHO), lunch (75 g CHO) and dinner (75 g CHO) are consumed at 8:00, 13:00 and 19:00, respectively. All the meals are announced but the meal boluses are calculated according to 130% and 70% of the actual meal sizes on Day 1 and Day 2, respectively, to evaluate the robustness of the controller with respect to over- and under-bolused meals. No meal is given on Day 3, but a 2-unit unannounced insulin bolus is applied at 8:00 AM to simulate the effect of exercise.

2. Protocol B is composed of 72 hours and 9-meals starting from 7:00 on Day 1. On Days 1–3, breakfast (50 g CHO), lunch (75 g CHO) and dinner (75 g CHO) are consumed at 08:00, 13:00 and 19:00, respectively. On Days 1–2, the meals are announced and 100% bolused, while meals are unannounced on Day 3. On Days 2–3, the basal rates of all subjects are increased by 30% of their normal values to evaluate controller’s behavior under overestimated basal rates for announced and unannounced meals.

3. Protocol C is also composed of 72 hours and 9-meals starting from 7:00 on Day 1. On Days 1–3, breakfast (50 g CHO), lunch (75 g CHO) and dinner (75 g CHO) are still consumed at 8:00, 13:00 and 19:00, respectively. Meals are unannounced on Day 1 and Day 3, but are 100% bolused on Day 2. On Days 2–3, the basal rates of all subjects are decreased by 30% of their normal values to evaluate controller’s behavior under underestimated basal rates given announced and unannounced meals.

Day 1 of Protocols B and C is used to evaluate the nominal scenarios of fully announced and unannounced meals, and Days 2–3 in these two protocols simulate the scenarios of over- and under-estimated meal boluses; Days 1–2 in Protocol A evaluate the effect of meal bolus mismatches, while Day 3 studies the effect of exercise. The proposed adaptive zone MPC with parameter setting in TABLE I is evaluated using these protocols, and the zone MPC with velocity-weighting and velocity-penalty [7] is used for the “control-group” comparisons, the results of which will be denoted as “control” in the tables and plots. The three protocols are simulated 10 times using all 100 virtual subjects and additive CGM noises with random seeds 1 through 10, which result in 1000 simulations for each protocol and each controller. The obtained results are summarized in Figs. 4–6, where the mean curves together with the 5%, 25%, 75% and 95% quartile curves are presented; a comparison of the statistics is provided in Tables II–IV, where the data for day & night and night time (24:00–06:00) are reported separately. The performance metrics are selected according to [31], [32], where details of the definitions can be found.

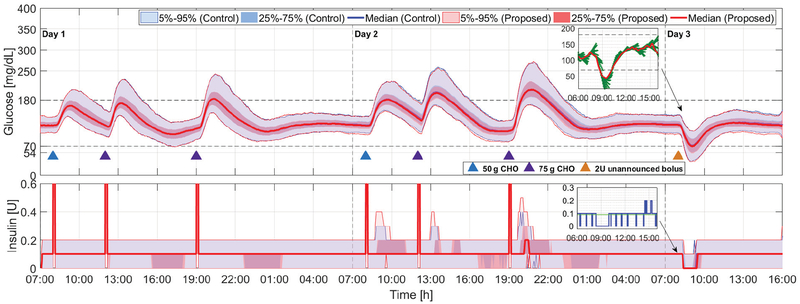
Fig. 4:

Comparison of the proposed method (red curves and light red areas) with the zone-MPC developed in [7] (blue curves and light blue areas) for Protocol A; see Section IV and Fig. 3. Blue and purple triangles denote meals of 50 g and 75 g CHO, respectively, and the orange triangle denotes a 2-unit unannounced insulin bolus. Snapshots of the glucose and insulin profile of a particular in silico subject on Day 3 obtained using the proposed adaptation method are also provided, where in the glucose panel the red curve denotes the CGM readings and the green curves denote the glucose predictions at each sampling instant, in the insulin panel the blue curve denotes insulin delivered at each time instant and the green line denotes basal rate.

Fig. 6:

Comparison of the proposed method (red curves and light red areas) with the zone-MPC developed in [7] (blue curves and light blue areas) for Protocol C; see Section IV and Fig. 3. Blue and purple triangles denote meals of 50 g and 75 g CHO, respectively.

TABLE II:

Glycemic metrics comparing the proposed method with the zone MPC developed in [7] (Protocol A)

Protocol A	Day 1			Day 2			Day 3
Metrics	Control	Proposed	p value	Control	Proposed	p value	Control	Proposed	p value
Day & night
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	0.047*	0.0 (0.0)	0.0 (0.0)	0.581	0.0 (2.0)	0.0 (3.7)	<0.001*
% time <70 mg/dL	0.0 (0.0)	0.0 (0.0)	0.037*	0.0 (0.0)	0.0 (0.0)	<0.001*	4.1 (11.1)	5.2 (11.7)	<0.001*
% time 70–180 mg/dL	95.5 (8.7)	95.4 (8.8)	0.679	81.7 (13.4)	83.1 (12.6)	<0.001*	95.8 (11.1)	94.8 (11.7)	<0.001*
% time >250 mg/dL	0.0 (0.0)	0.0 (0.0)	0.885	0.0 (0.0)	0.0 (0.0)	<0.001*	0.0 (0.0)	0.0 (0.0)	1.000
Mean BG (mg/dL)	129.3 (9.2)	129.2 (8.8)	<0.001*	143.6 (8.8)	141.8 (8.4)	<0.001*	114.6 (7.4)	113.7 (7.6)	<0.001*
SD BG (mg/dL)	26.4 (9.2)	26.4 (9.4)	0.635	33.9 (10.7)	33.8 (10.6)	0.005*	20.4 (11.5)	20.7 (11.6)	<0.001*
Night time (0–6 AM)
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000	-	-	-
% time < 70 mg/dL	0.0 (0.0)	0.0 (0.0)	0.090	0.0 (0.0)	0.0 (0.0)	0.014*	-	-	-
% time 70–180 mg/dL	100.0 (0.0)	100.0 (0.0)	0.341	100.0 (0.0)	100.0 (0.0)	0.024*	-	-	-
% time >250 mg/dL	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000	-	-	-
Mean BG (mg/dL)	118 (9.2)	118.2 (8.7)	0.004*	118.4 (8.4)	118.2 (8.4)	<0.001*	-	-	-
SD BG (mg/dL)	12.9 (6.8)	13.1 (7.0)	<0.001*	12.3 (6.3)	12.5 (6.6)	<0.001*	-	-	-
Mean BG at 7 AM (mg/dL)	122.0 (14.0)	121.0 (16.0)	<0.001*	122.0 (16.0)	121.0 (16.0)	<0.001*	-	-	-

Data in this table are shown as median (inter quartile range). Statistical significance is assessed by Wilcoxon signed-rank test. Statistically significant (p < 0.05) changes are highlighted in bold with asterisks.

TABLE IV:

Glycemic metrics comparing the proposed method with the zone MPC developed in [7] (Protocol C)

Protocol C	Day 1			Day 2			Day 3
Metrics	Control	Proposed	p value	Control	Proposed	p value	Control	Proposed	p value
Day & night
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	0.064	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	0.500
% time <70 mg/dL	0.0 (0.0)	0.0 (0.0)	0.397	0.0 (0.0)	0.0 (0.0)	0.096	0.0 (0.0)	0.0 (0.0)	0.001*
% time 70–180 mg/dL	66.3 (14.3)	70.5 (11.5)	<0.001*	84.7 (13.6)	85.8 (12.6)	<0.001*	56.1 (21.1)	64.8 (18.0)	<0.001*
% time >250 mg/dL	3.6 (10.8)	1.9 (7.1)	<0.001*	0.0 (0.0)	0.0 (0.0)	<0.001*	12.2 (17.2)	5.9 (13.4)	<0.001*
Mean BG (mg/dL)	159.0 (18.1)	153.8 (13.5)	<0.001*	148.9 (10.3)	146.1 (9.6)	<0.001*	180.6 (31.6)	166.4 (21.9)	<0.001*
SD BG (mg/dL)	47.7 (13.8)	45.6 (12.7)	<0.001*	27.7 (10.5)	28.4 (10.6)	<0.001*	49.6 (14.5)	45.3 (13.3)	<0.001*
Night time (0–6 AM)
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	0.219	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000
% time <70 mg/dL	0.0 (0.0)	0.0 (0.0)	0.010*	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	0.008*
% time 70–180 mg/dL	100.0 (0.0)	100.0 (0.0)	<0.001*	100.0 (0.0)	100.0 (0.0)	<0.001*	100.0 (7.5)	100.0 (0.0)	<0.001*
% time >250 mg/dL	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	0.143
Mean BG (mg/dL)	120.6 (9.0)	119.7 (8.2)	<0.001*	133.1 (10.8)	131.0 (9.8)	<0.001*	138.0 (17.8)	134.3 (12.6)	<0.001*
SD BG (mg/dL)	13.5 (7.3)	13.0 (7.3)	<0.001*	12.5 (5.7)	12.9 (6.2)	<0.001*	14.6 (8.3)	13.9 (6.9)	<0.001*
Mean BG at 7 AM (mg/dL)	122.0 (15.0)	121.0 (14.0)	<0.001*	140.5 (19.0)	136.0 (21.0)	<0.001*	140.5 (25.0)	135.0 (26.0)	<0.001*

Data in this table are shown as median (inter quartile range). Statistical significance is assessed by Wilcoxon signed-rank test. Statistically significant (p < 0.05) changes are highlighted in bold with asterisks.

A. Announced meals

The scenario of fully announced meals is considered on Day 1 of Protocol B for the original zone MPC and the proposed adaptive zone MPC (see Fig. 5 and TABLE III). Satisfactory performance for hypoglycemia prevention measured by percent time < 70 mg/dL and percent time < 54 mg/dL (severe hypoglycemia [32]) are observed for both controllers; in particular, a comparison of the values of these two performance metrics indicates that the proposed parameter adaptation approach does not introduce increased risk for hypoglycemia (percent time < 70 mg/dL, 0.0% vs. 0.0%, p < 0.001). As was indicated in [7], the glucose response is dominated by meal boluses for fully bolused meals and the effect of closed-loop control in terms of improvements in glucose regulation is concealed, given the fact that the original zone MPC is able to achieve good control performance for announced meals [6]. Consequently, the proposed adaptive approach only leads to a small performance improvement in terms of mean glucose (135.9 mg/dL vs. 136.5 mg/dL; p < 0.001) with very close percent time in the euglycemic range [70, 180] mg/dL (90.6% vs. 90.5%; p < 0.001). This discussion is consistent with the quartile curves in Fig. 5. Finally, we note that the controllers result in very close and satisfactory glycemic control performance for night time (24:00 – 06:00 h).

Fig. 5:

Comparison of the proposed method (red curves and light red areas) with the original zone-MPC developed in [7] (blue curves and light blue areas) for Protocol B; see Section IV and Fig. 3. Blue and purple triangles denote meals of 50 g and 75 g CHO, respectively. Snapshots of the glucose and insulin profile of a particular in silico subject obtained using the proposed adaptation method are also provided; keys are the same as the snapshots in Fig. 4.

TABLE III:

Glycemic metrics comparing the proposed method with the zone MPC developed in [7] (Protocol B)

Protocol B	Day 1			Day 2			Day 3
Metrics	Control	Proposed	p value	Control	Proposed	p value	Control	Proposed	p value
Day & night
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	0.012*	0.0 (0.0)	0.0 (0.0)	<0.001*	0.0 (0.0)	0.0 (0.0)	0.491
% time <70 mg/dL	0.0 (0.0)	0.0 (0.0)	<0.001*	0.2 (2.7)	0.0 (2.4)	<0.001*	0.0 (1.5)	0.0 (2.1)	0.024*
% time 70–180 mg/dL	90.5 (12.1)	90.6 (11.7)	<0.001*	93.3 (11.4)	93.3 (11.5)	1.000	71.8 (12.8)	73.6 (11.7)	<0.001*
% time >250 mg/dL	0.0 (0.0)	0.0 (0.0)	0.412	0.0 (0.0)	0.0 (0.0)	0.008*	0 (5.8)	0 (4.7)	<0.001*
Mean BG (mg/dL)	136.5 (8.4)	135.9 (8.0)	<0.001*	126.0 (9.2)	126.5 (9.3)	<0.001*	145.8 (13.8)	143.6 (12.7)	<0.001*
SD BG (mg/dL)	29.4 (9.6)	29.5 (9.7)	0.155	30.3 (10.2)	30.3 (10.4)	<0.001*	47.8 (14.0)	46.6 (12.6)	<0.001*
Night time (0–6 AM)
% time <54 mg/dL	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	0.152	0.0 (0.0)	0.0 (0.0)	0.011*
% time <70 mg/dL	0.0 (0.0)	0.0 (0.0)	0.007*	0.0 (0.0)	0.0 (0.0)	0.004*	0.0 (0.0)	0.0 (0.0)	0.627
% time 70–180 mg/dL	100.0 (0.0)	100.0 (0.0)	0.144	100.0 (0.0)	100.0 (0.0)	0.032*	100.0 (0.0)	100.0 (0.0)	0.292
% time >250 mg/dL	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000	0.0 (0.0)	0.0 (0.0)	1.000
Mean BG (mg/dL)	117.9 (8.3)	117.9 (8.0)	0.106	107.7 (8.1)	108.9 (7.9)	<0.001*	108.8 (8.0)	109.6 (8.0)	<0.001*
SD BG (mg/dL)	12.3 (6.6)	12.5 (6.7)	<0.001*	14.0 (7.1)	14.1 (7.6)	<0.001*	14.8 (7.9)	14.8 (8.1)	0.776
Mean BG at 7 AM (mg/dL)	122.0 (14.0)	121.0 (14.5)	<0.001*	107.0 (18.0)	108.0 (17.0)	<0.001*	107.0 (24.0)	108.0 (24.0)	<0.001*

Data in this table are shown as median (inter quartile range). Statistical significance is assessed by Wilcoxon signed-rank test. Statistically significant (p < 0.05) changes are highlighted in bold with asterisks.

B. Unannouced meals

Performance comparison for the scenario of unannounced meals is considered on Day 1 of Protocol C (see Fig. 6 and TABLE IV). In this scenario, the proposed adaptation approach is observed to achieve improved glucose regulation performance compared with the original zone MPC in terms of percent time in the safe range (70.5% vs. 66.3%; p < 0.001), percent time > 250 mg/dL (1.9% vs. 3.6%; p < 0.001), mean glucose (153.8 mg/dL vs. 159.0 mg/dL; p < 0.001). The performance improvement is achieved without increasing the risk of hyperglycemia, measured by percent time < 70 mg/dL (0.0% vs. 0.0%, p = 0.397) and percent time < 54 mg/dL (0.0% vs. 0.0%, p = 0.064). The underlying reason, as observed from Fig. 5, is that the proposed adaptation approach encourages reasonably more active insulin infusion when the glucose concentration is rapidly increasing and is able to safely turn off insulin infusion when the glucose stops to increase or decreases, due to the dynamic glucoseand velocity-dependent choice of $\hat{R}$ and $\check{R}$. Both controllers achieve satisfactory glycemic control performance for night time (24:00 – 06:00 h), as is also observed in the mean BG at 07:00 h (121.0 mg/dL vs. 122.0 mg/dL; p < 0.001). Combined with the observations in the previous subsection, the proposed method is able to achieve improved glucose control for unannounced meals while maintaining safety and performance for announced meals.

C. Moderate meal-bolus mismatch

Days 1–2 in Protocol A are utilized to evaluate the case that subjects provide modest over or under-estimates of meal sizes, which is less extreme but more realistic for meal announcements. The data are reported in Fig. 4 and TABLE II (Days 1–2). When meal boluses with sizes larger than required are provided, we observe in Fig. 4 (Day 1) that both controllers are able to maintain their outputs around basal rates and perform pump suspension if low glucose predictions occur (e.g., around 17:00 and 23:00 on Day 1 in Fig. 4). On the other hand, the proposed adaptation method compensates conservative meal boluses more actively (see Fig. 4 (Day 2)), and thus obtains slightly improved glucose regulation performance in terms of mean glucose (141.8 mg/dL vs. 143.6 mg/dL; p < 0.001) and percent time in the safe range (83.1% vs. 81.7%; p < 0.001). The improvements are small because of the small difference (70%) in the underestimated meal bolus from the exact bolus (100%). Clinically significant differences in hypoglycemia risk are not observed.

D. Simulated exercise response

Day 3 in Protocol A is utilized to evaluate the behavior of the controller under an unannounced insulin bolus (2 units), which emulates the effect of exercises that increase insulin sensitivity. As the subjects are fasting when the announced bolus is infused, hypoglycemia is inevitable in this scenario; but we observe that both controllers are vigilant in suspending insulin infusion when the risks of hypoglycemia are discerned from the glucose predictions (see the steep decrease in insulin delivery before the glucose readings drop below 70 mg/dL around 8:00–9:00 on Day 3 in Fig. 4), which indicates that the proposed adaptation approach is able to maintain appropriate controller behavior under unannounced exercise events and severe hypoglycemia episodes. This point can also be observed in the glucose and insulin example of an in silico subject on Day 3 obtained using the proposed adaptation method (see Fig. 4), where the controller is able to turn off insulin when the glucose predictions become low to ensure safety. Note that the proposed method yields slightly increased percent time < 70 mg/dL (5.2%, vs. 4.1%, p < 0.001); however, the increase is relatively small and expected with increased responsiveness of the controller.

E. Basal rate mismatch

Days 2–3 in Protocols B and C are utilized to analyze the sensitivity of the controller with respect to inaccurately estimated basal rates. Concretely, the basal rates are intentionally increased by 30% on Day 2–3 of Protocol B to simulate the effect of overestimated basal rates with announced and unannounced meals, which invariably increase the risk of hypoglycemia. From Table III and Fig. 5 (Days 2–3), we observe that the proposed method does not increase the risk of hypoglycemia compared with the original zone MPC. The snapshots of an in silico subject in Fig. 5 further confirm that the zone MPC behaves properly with the proposed parameter adaptation approach.

On Days 2–3 of Protocol C, the basal rates are reduced by 30% on Day 2–3 of Protocol B to simulate the effect of overestimated basal rates with announced and unannounced meals, which leads to lifted glucose profiles due to decreased “open-loop” insulin delivery. From Table IV and Fig. 6 (Days 2–3), we observe that the proposed approach compensates for the lack of basal insulin in a more active fashion, which leads to increased percentage time in the euglycemic range [70, 180] mg/dL (85.8% vs. 84.7%; p < 0.001) and mean glucose (146.1 mg/dL vs. 148.9 mg/dL; p < 0.001) for announced meals, and significant performance improvements in terms of percentage time in the euglycemic range (64.8% vs. 56.1%; p < 0.001) and mean glucose (166.4 mg/dL vs. 180.6 mg/dL; p < 0.001) for unannounced meals. This indicates the proposed approach is less sensitive to underestimated basal rates compared with the original zone MPC.

F. Comparison with existing results

We further compare the results obtained by the proposed method with existing in silico and experimental results in the literature, obtained using previous zone MPC controller schemes [8], [12], [24]. The results are summarized in Table V. For fully announced meals (100% meal bolus), the result obtained is close to that of a zone MPC with trust index proposed in [24], although the results in [24] were obtained using the 10-subject cohort of the T1DM simulator with a different size of dinner (100 g vs. 75 g). From Table V, we observe that patients usually have higher average glucose values and lower percentage time in range [70, 180] mg/dL with higher frequency of hypoglycemia in clinical studies, which justifies the need to reduce hyperglycemia while preventing the occurrence of hypoglycemia. By adjusting the control penalties adaptively according to the predicted glucose and rate of change, the proposed method provides one feasible and robust solution, as indicated by the in silico results in this section.

TABLE V:

Performance comparison with previous studies in the literature using zone MPC scheme.

	Mean BG (mg/dL)	% time 70–180 mg/dL	% time <70 mg/dL
Proposed (100% meal bolus)	135.9 (8.0)	90.6 (11.7)	0.0 (0.0)
Proposed (70% meal bolus)	141.8 (8.4)	83.1 (12.6)	0.0 (0.0)
Proposed (0% meal bolus)	153.8 (13.5)	70.5 (11.5)	0.0 (0.0)
Laguna Sanz et al. [24] in silico (100% meal bolus)	134.0 〈6.0〉	91 〈5.6〉	0.0 〈0.0〉
Dassau et al. [8] outpatient (overnight)	141 [130–158]	79.1 [60.4–86.1]	1.37 [0–2.84]
Dassau et al. [12] outpatient (week 12)	152.5 〈20.7〉	69.5 〈20.2〉	1.9 〈2.0〉

Data in this table are shown as median (inter quartile range) or mean standard deviation, or median [min-max], as per the original sources. Data in the first three rows are reproduced from the corresponding entries in Tables II–IV.

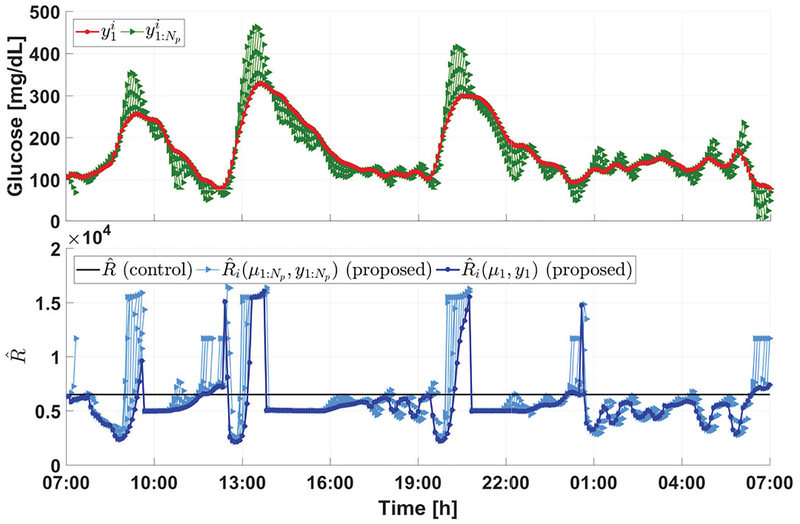
G. Control penalty adaptation

Finally, we note that the performance improvement of the proposed method is achieved through the adaptation of control penalty parameters. To illustrate this point, the relationship between $\hat{R}\left({\mu }_k^i,{\text{y}}_k^i\right)$ and ${\text{y}}_k^i$ for an in silico subject on Day 1 of Protocol C (which correspond to 288 controller update instants) is provided in Fig. 7. The superscript i here is used to represent the dependence of the variables on time. Compared with the constant choice of $\hat{R}$ in [7], we observe that the proposed parameter adaptation law turns off insulin infusion by choosing relatively larger values of $\hat{R}(\cdot ,\cdot )$ when the glucose predictions are relatively low, or extremely high, or decreasing, but allows active insulin infusion by choosing comparably small values only when the glucose predictions are steeply increasing above the nominal glucose range. This further explains the mechanism of the proposed adaptive approach to alleviate hyperglycemia without increasing hypoglycemia risks.

Fig. 7:

Illustration of control penalty adaptation. In the upper panel, the red curve shows the trend of first element ${\text{y}}_1^i$ in the glucose prediction sequence ${\text{y}}_{1:N_p}^i$ with respect to discrete time i, while the green curves denote the sequences of ${\text{y}}_{1:N_p}^i$. Note that the red and green curves denotes glucose predictions, which are different from actual CGM measurements. In the lower panel, the dark blue curve shows the trend of $\hat{R}\left({\mu }_1^i,{\text{y}}_1^i\right)$ with respect to discrete time i, the light blue curves denote the sequences of $\hat{R}\left({\mu }_{1:N_p}^i,{\text{y}}_{1:N_p}^i\right)$, and the black line indicates the constant $\hat{R}$ adopted in [7]. The superscript i used here indicates the dependence of a variable on time.

V. Advisory-mode comparisons using clinical data

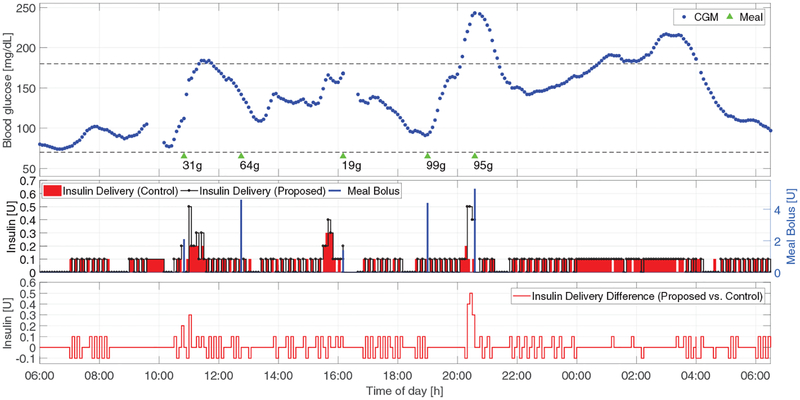
In this section, the historical clinical data obtained using the zone-MPC developed in [7] (the corresponding clinical results were published in [12]) are re-run using the proposed method to obtain the corresponding insulin command trajectory, assuming the controller received exactly the same input data. This is the so-called advisory-mode comparison [33] and allows dose-to-dose evaluation of the safety and effectiveness of the proposed method by feeding the identical glucose data obtained in the clinical trial to the controller.

The results are provided in Fig. 8. Compared with the approach in [7], the proposed controller is more active when the glucose level is escaping the safe euglycemic range from above, but is able to resemble almost-identical safe insulin commands when the glucose level is low or decreasing. As an example, we observe that driven by the rapidly increasing CGM values, the proposed controller would suggest (approximately) additional 1.2 units of insulin between 20:00 and 21:00, which would decrease the glucose levels after the 95 g meal to a safe but lower range, and thus further help reduce the hyperglycemia that happened between 01:00 and 04:00. This explains how the proposed method can obtain improved glucose regulation with lower average glucose levels in real-life scenarios, which fulfills our motivation of alleviating the high-average glucose effect introduced by the zone MPC [7] used in [12] (see Section I). Note that both the glucose response and the insulin command trajectory would be different had the proposed control law actually been employed.

Fig. 8:

Advisory-mode comparison of insulin command sequences of the proposed method (black curve in the second panel) with the zone-MPC developed in [7] (red bars in the second panel) based on clinical data from [12] (Clinical trial reg. no. NCT02705053, clinicaltrials.gov). Meals are denoted by green triangles with sizes below them. The difference of insulin delivery between the proposed method and that introduced in [7] is plotted in the third panel.

VI. Conclusions

In this work, a control penalty adaptation approach is developed for zone MPC of AP based on the predicted glucose and its rate of change. The obtained adaptive controller is able to actively perform insulin infusion when blood glucose is rapidly increasing above the nominal value, but cautiously reduces or suspends insulin infusion when glucose rate of change is positively small or negative, and when low glucose values are predicted. The effectiveness and robustness of the proposed method is evaluated on the 100-adult cohort of the FDA-approved UVA/Padova simulator through comparisons with the original zone MPC developed in [7]. Although the approach is developed for the zone MPC, it is rich enough to be generalized to other MPC formulations for AP (e.g., the enhanced set-point MPC with asymmetric exponential and quadratic costs [34]).