pldist: ecological dissimilarities for paired and longitudinal microbiome association analysis

Abstract

Motivation

The human microbiome is notoriously variable across individuals, with a wide range of ‘healthy’ microbiomes. Paired and longitudinal studies of the microbiome have become increasingly popular as a way to reduce unmeasured confounding and to increase statistical power by reducing large inter-subject variability. Statistical methods for analyzing such datasets are scarce.

Results

We introduce a paired UniFrac dissimilarity that summarizes within-individual (or within-pair) shifts in microbiome composition and then compares these compositional shifts across individuals (or pairs). This dissimilarity depends on a novel transformation of relative abundances, which we then extend to more than two time points and incorporate into several phylogenetic and non-phylogenetic dissimilarities. The data transformation and resulting dissimilarities may be used in a wide variety of downstream analyses, including ordination analysis and distance-based hypothesis testing. Simulations demonstrate that tests based on these dissimilarities retain appropriate type 1 error and high power. We apply the method in two real datasets.

Availability and implementation

The R package pldist is available on GitHub at https://github.com/aplantin/pldist.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Interest in the human microbiome has grown rapidly as its vital role in human health has become increasingly apparent. The microbiome, defined as the community of bacteria and other microorganisms living in and on a person, is associated with conditions such as obesity (Turnbaugh et al., 2009), graft-versus-host disease (Jenq et al., 2015), menopause symptoms (Mitchell et al., 2018) and type 2 diabetes (Qin et al., 2012). Its role also extends to mediating disease treatment responses. For example, the gut microbiome is associated with efficacy of dietary interventions in irritable bowel disease (Chumpitazi et al., 2015) and affects success of some cancer immunotherapies (Routy et al., 2018). Ongoing research continues to explore such associations.

Two approaches to characterizing the microbiome are 16s rRNA sequencing and shotgun metagenomics (Jovel et al., 2016). The former proceeds by amplifying and sequencing the 16S rRNA gene, then clustering reads into operational taxonomic units (OTUs) at a desired level of similarity. The 16S sequences may also be used to build a phylogenetic tree describing the evolutionary relationships between OTUs in the study. In shotgun metagenomics, all genetic material present is sequenced, resulting in more information about functional capability, but at substantially higher cost. Regardless of sequencing method, the sequencing data may be summarized as a set of taxon counts for each individual, potentially accompanied by a phylogenetic tree relating the taxa. This count matrix is frequently used for downstream analysis.

A common class of microbiome analyses evaluates each taxon independently for association with an outcome of interest using standard statistical methodology or microbiome-specific approaches. Due to the potentially large number of OTUs measured (hundreds to thousands), this type of analysis often requires severe multiple testing corrections. A popular alternative is distance-based multivariate analysis, which assesses the global association between the microbiome and many types of outcome measures (Koh et al., 2017; Plantinga et al., 2017; Tang et al., 2016; Zhan et al., 2017; Zhao et al., 2015). These methods use a relevant distance metric to quantify the dissimilarity between microbiomes, then compare the pairwise dissimilarities (often transformed to similarities) to similarity in outcome measures using a PERMANOVA-type test (Anderson, 2001).

The vast majority of distance-based methods cannot accommodate related samples. However, studies based on independent samples are easy to be confounded, since the human microbiome is highly variable and is subject to the influence of a large array of environmental factors. Longitudinal study of the microbiome, which uses each individual as his or her own control, has become increasingly popular due to its ability to reduce potential unmeasured confounding effects as well as to increase the statistical power by reducing large inter-subject variation (Faust et al., 2015). For example, Kong et al. (2012) compared children’s skin microbiome at baseline, during atopic dermatitis flares and post-treatment, finding substantially lower diversity during disease flares and restored diversity post-treatment. Lewis et al. (2015) studied the gut microbiome of children with Crohn’s disease across different 8-week treatment plans, tracking and comparing changes in the microbiome along with clinical response to treatment. Unfortunately, statistical methods for analyzing such longitudinal datasets are scarce.

Distance-based analysis can be modified to new settings, such as longitudinal studies, in two ways: by modifying the model used to relate pairwise distances to the outcome, or by modifying the distances themselves to accommodate additional information. Taking the former approach, a linear mixed model framework has allowed the extension of formal distance-based association tests to longitudinal study designs for quantitative phenotypes (Zhai et al., 2018; Zhan et al., 2018). Similar methods do not exist for more complex outcomes, such as time-to-event data, multivariate phenotypes or even dichotomous outcomes, and specialized extensions would be required for each of these models.

We instead consider modifying the distance metric. This approach has already proven valuable in the UniFrac family of distances: after the original proposal of (unweighted) UniFrac (Lozupone and Knight, 2005), differences in taxon abundance were incorporated into weighted UniFrac (Lozupone et al., 2007). Variance-adjusted weighted UniFrac improved power by weighting differences in branch proportions by the corresponding variance (Chang et al., 2011), and generalized UniFrac moderates the weight placed on abundant or rare lineages (Chen et al., 2012). Each of these adaptations allows greater flexibility and information content in the quantification of (dis)similarity.

In this spirit, we propose a UniFrac-type dissimilarity between two subjects that compares, instead of taxon abundances, a normalized measure of change between the two time points for each subject. We develop both an unweighted version of the dissimilarity, which considers only changes in taxon presence, and a generalized version, which incorporates changes in abundance. We then extend the measure of change for paired samples to more than two time points, and we incorporate this data transformation into non-phylogenetic dissimilarities. This paired and longitudinal distance-based approach, termed pldist, is independent of the choice of sequencing and quantification method, provided that the data may be summarized as a table of taxon counts and possibly a phylogenetic tree. pldist may be used in any existing distance-based testing framework or visualization procedure, allowing longitudinal analysis with a wide variety of outcome types. In contrast to a linear mixed model approach, pldist explicitly considers changes in the microbiome over time, permitting direct answers to the scientific questions often posed in longitudinal studies.

In the following sections, we introduce unweighted and generalized UniFrac dissimilarity metrics for paired data; generalize the underlying data transformation to more than two time points; incorporate the paired and longitudinal transformations into other dissimilarity metrics; perform simulation studies to verify proper type 1 error control and power to detect true longitudinal associations; and apply the methods to two real microbiome datasets.

2 Materials and methods

We begin by introducing two measures of dissimilarity for paired data that are analogous to the unweighted and generalized UniFrac distances (PUniFrac). Both utilize a two-stage approach. In the first stage, the changes in taxon presence (unweighted) or abundance (generalized) for each subject are summarized; in the second stage, these changes are compared across subjects, incorporating phylogenetic structure in much the same way as the other UniFrac distances. We then extend the transformations to more than two time points and incorporate the same Stage 1 data transformations into several non-phylogenetic metrics.

2.1 Paired UniFrac dissimilarities

The original unweighted UniFrac metric sums the lengths of branches on a phylogenetic tree that are unshared between two microbial communities (Lozupone and Knight, 2005). That is, if a taxon is present in one community but not the other, then the length of that taxon’s branch of the tree contributes to the distance between the communities.

To extend this to two time points, we define change between time points for subject i and taxon j based on taxon presence or absence. Suppose we have measured OTU abundance for p taxa on n subjects at two time points, t₁ and t₂. Let $p_k^{i,t_1}$ indicate the proportion of reads for subject i at time point t₁ that belong to taxon k. Then define

$$d_k^i(t_1,t_2)=I\left(p_k^{(i,t_1)}>0\right)-I\left(p_k^{(i,t_2)}>0\right)\in \{-1,0,1\}$$

for each subject $i=1,\dots ,n$ and taxon $k=1,\dots ,p$, where $I(·)$ is the indicator function. Hence $d_k^i(t_1,t_2)$ is nonzero if and only if the taxon was present at exactly one of the measured time points for subject i; $d_k^i=1$ if taxon k was present at time 2 but absent at time 1 (acquired between time points), and $d_k^i=-1$ if taxon k was present at time 1 but absent at time 2 (lost between time points). We will henceforth suppress the (t₁, t₂) notation and refer to these changes just as $d_k^i$.

The unweighted PUniFrac distance between subjects i and j is constructed based on $d_k^i$ and $d_k^{\mathit{j}}$ via

$$D_{\mathit{ij}}=\frac{\sum _{k=1}^p{b}_k\times \frac{1}{2}\left|d_k^i-d_k^{\mathit{j}}\right|}{\sum _{k=1}^p{b}_k}$$

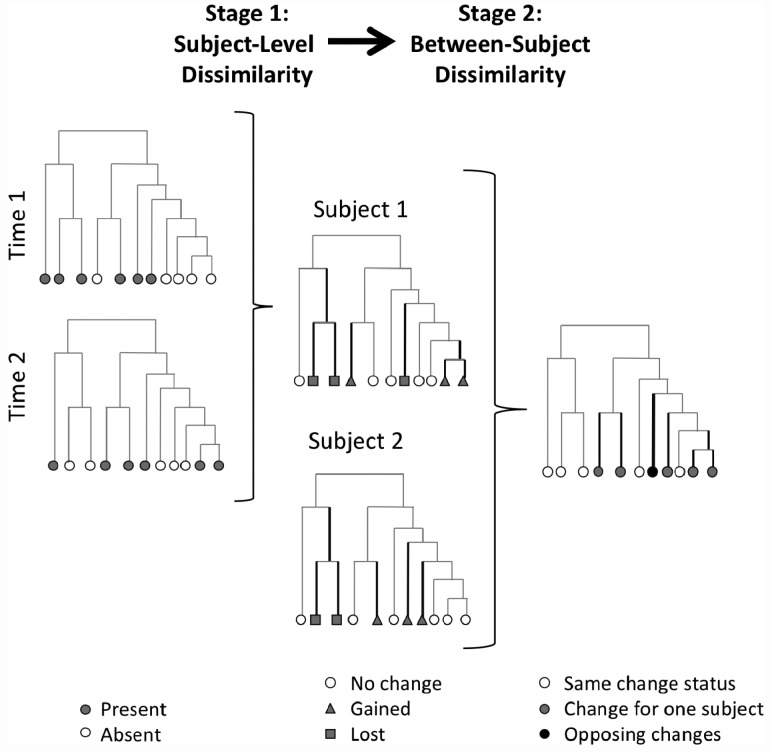
so that D_ij summarizes the difference between subjects i and j in changes in presence/absence, weighted by branch length and normalized to fall in [0, 1]. In Section 1 of the Appendix we prove that this metric is a proper distance. Figure 1 provides a visual representation of the approach.

Fig. 1.

Schematic for calculation of unweighted PUniFrac metric. Dark lines are phylogenetic distances that contribute to the PUniFrac dissimilarity, at half weight if the change was observed in one subject and full weight if opposing changes in presence or absence were observed

Weighted UniFrac at a single time point extends the unweighted UniFrac distance by defining differences between communities in terms of differences in taxon proportion rather than taxon presence. Generalized UniFrac then weights each branch by a term depending upon its overall abundance to avoid overweighting particularly rare or abundant lineages. The corresponding version for paired data is based upon similar adjustments.

For the generalized PUniFrac dissimilarity, we define change between times for subject i and taxon k based upon differences in abundance as

$$d_k^i(t_1,t_2)=\frac{p_k^{(i,t_2)}-p_k^{(i,t_1)}}{p_k^{(i,t_2)}+p_k^{(i,t_1)}}\in [-1,1].$$

The sign indicates whether the taxon was more (+) or less (−) abundant at time 2 than at time 1, and the difference in proportion is normalized by overall taxon abundance. Using this measure of change, we then construct the generalized paired UniFrac dissimilarity between subjects i and j via

$$D_{\mathit{ij}}=\frac{\sum _{k=1}^p{b}_k{({\overline{p}}_k^i+{\overline{p}}_k^j)}^{\gamma }\times \frac{1}{2}\left|d_k^i-d_k^j\right|}{\sum _{k=1}^p{b}_k{({\overline{p}}_k^i+{\overline{p}}_k^j)}^{\gamma }}$$

where ${\overline{p}}_k^i=(p_k^{(i,t_1)}+p_k^{(i,t_2)})/2$ is the average abundance of a particular taxon across times for subject i. The parameter $\gamma \in [0,1]$, which is constant for each matrix D, controls the weight on abundant branches. Larger γ places higher weight on the contribution of common taxa, whereas small γ places similar weight on common and rare taxa. Therefore D_ij summarizes the (normalized) difference in abundance of taxa between subjects, weighted by branch length and average taxon abundance.

To better understand this measure of dissimilarity, notice that the term involving magnitude of change in abundance is $\frac{1}{2}|d_k^i-d_k^j|$, corresponding to the ‘weighting’ term in weighted UniFrac. This is normalized to the absolute abundance of a taxon through the definition of $d_k^i$. For example, a change from a relative abundance of 0.2 to 0.1 results in exactly the same $d_k^i$ as a change from a relative abundance of 0.4 to 0.2. This takes its largest value of 1 if $d_k^i=1$ and $d_k^j=-1$, which happens if taxon k is gained in subject i and lost in subject j, or vice versa. It takes its smallest value of 0 if taxon k’s abundance changes equally in the two subjects. The ‘generalization’ (similar to generalized UniFrac) refers to the weighting of branch lengths by average abundance, ${({\overline{p}}_k^i+{\overline{p}}_k^j)}^{\gamma }$. This term does involve absolute proportions, so in the toy example above, it would weight a taxon with average abundance of 0.3 differently than a taxon with average abundance of 0.15.

The power of the test based on this D depends strongly on the choice of γ and the true association. We recommend trying a range of γ, such as (0.25, 0.5, 0.75, 1), and using a permutation test to assess overall significance. See Zhao et al. (2015) and Koh et al. (2017) for further descriptions of the permutation testing procedure for multiple kernels with continuous, binary and time-to-event outcomes.

In the Appendix we show by counterexample that this measure of dissimilarity is not guaranteed to satisfy the triangle inequality, so it is not a proper distance. Although proper distance metrics are preferable in some situations, for global analysis of the microbiome, this is often overlooked. Application of this dissimilarity is statistically valid despite potential failure of the triangle inequality, but it should be noted that these may not represent dissimilarities in Euclidean space without transformation.

2.2 Multiple time points

Longitudinal studies often include more than two time points. If the study has a balanced design, i.e. the same time points are observed for every individual, pairwise distances could be calculated between every pair of time points (or consecutive time points). The existing framework for omnibus tests of multiple kernels could then be used to see whether the outcome of interest is associated with changes in the microbiome between any pair of (consecutive) time points.

However, many longitudinal studies are not balanced, either by design or due to missing data. Previous studies have shown that variability of the microbiome, as well as composition, differs between healthy and diseased subjects. The gut microbiome of individuals with irritable bowel disease (IBD), for example, fluctuates more than that of healthy subjects (Halfvarson et al., 2017). Therefore, for studies with more than two observations per subject and potentially unbalanced designs, the paired transformations may be meaningfully extended to measures of compositional ‘volatility’ or variability of the microbial community.

The qualitative transformation for longitudinal data with q time points indicated by $\mathbf{t}=(t_1,\dots ,t_q)$ is defined as

$$d_k^i(\mathbf{t})=\frac{1}{q-1}\sum _{l=1}^{q-1}\left(\frac{1}{t_{l+1}-t_l}\right)· \left|I(p_k^{i,t_{l+1}}>0)-I(p_k^{i,t_l}>0)\right|$$

so that $d_k^i$ measures the average change in presence of taxon k for subject i in one unit of time. This is not equivalent to the paired transformation even when applied at two time points, since for the longitudinal transformation, only absolute magnitude of change is considered, not direction of change. That is, in the paired transformation, taxon gain is treated differently than taxon loss. In the longitudinal version, taxon gain and taxon loss are equivalent magnitudes of change in a single taxon.

Similarly, the quantitative transformation for longitudinal data with q time points is defined as

$$d_k^i(\mathbf{t})=\frac{1}{q-1}\sum _{l=1}^{q-1}\left(\frac{1}{t_{l+1}-t_l}\right)· \left|\frac{p_k^{(i,t_{l+1})}-p_k^{(i,t_l)}}{p_k^{(i,t_{l+1})}+p_k^{(i,t_l)}}\right|$$

so $d_k^i$ now measures the average change in abundance of taxon k for subject i in one unit of time (normalized to the average abundance across each pair of measured time points). The paired and longitudinal transformations are summarized in Supplementary Table S1.

Substituting these longitudinal $d_k^i$ for the paired $d_k^i$ in Section 2.1 yields longitudinal variants of the UniFrac metric that formally compare volatility, or average magnitude of fluctuations, in the microbiome across time for each subject. We refer to these as the LUniFrac dissimilarities. We caution that use of this transformation with highly unbalanced designs may be unreliable, since similar microbiome volatility may result in quite different $d_k^i$ values if there are substantially longer or shorter gaps between samples for different subjects.

Table 1 summarizes the scientific questions and analysis approaches that may be answered using these transformations and associated dissimilarity metrics.

Table 1.

Summary of study designs, associated scientific questions and recommendations for how to apply these methods to answer the specified questions

Question	Approach
Is change/difference between paired samples (e.g. two time points per subject or paired subjects) associated with a phenotype?	Paired transformations using any metric, or multiple metrics with omnibus test for overall significance
In a balanced design, is change/difference between any pair of time points associated with the phenotype?	Paired analysis for each pair of time points + omnibus test for overall significance
In a balanced or unbalanced design, is overall volatility (variability) of the microbiome over time associated with the phenotype?	Longitudinal transformations using any metric, or multiple metrics with omnibus test for overall significance

2.3 Non-phylogenetic distances and dissimilarities

The key difference between the PUniFrac or LUniFrac and standard UniFrac dissimilarities is the transformation applied to the paired or longitudinal data, as specified in the preceding sections and Supplementary Table S1. These transformations may also be incorporated into non-phylogenetic distances such as Gower’s distance (Gower, 1971), Bray-Curtis dissimilarity (Bray and Curtis, 1957), Jaccard distance (Jaccard, 1912) and Kulczynski distance (Kulczyński, 1928). For the quantitative longitudinal versions of non-phylogenetic dissimilarities, we do not normalize $d_k^i$ to the overall taxon proportion, since no weighting term exists to independently control the weight placed on abundant taxa. Thus the unnormalized quantitative transformation for paired data is defined as

$$d_k^i(t_1,t_2)=p_k^{(i,t_2)}-p_k^{(i,t_1)}$$

and in the longitudinal case as

$$\frac{1}{q-1}\sum _{i=1}^{q-1}\left(\frac{1}{t_{l+1}-t_l}\right) \left|p_k^{(i,t_{l+1})}-p_k^{(i,t_l)}\right|.$$

Using this definition, the quantitative versions of the non-phylogenetic dissimilarities place relatively high weight on higher-abundance taxa.

When using the paired or longitudinal transformations in a distance metric, some adjustments must be made to the definition of the dissimilarity due to differences in behavior between the $d_k^i$ and the original proportions $p_k^i$, namely, that $d_k^i$ need not sum to one for each individual and that paired $d_k^i$ may be either positive or negative. Supplementary Table S2 summarizes the single time point, paired and longitudinal variants of these four distances/dissimilarities as well as the unweighted and generalized UniFrac metrics.

2.4 Data compositionality and normalization

To account for compositionality, the data may be transformed to a space that is not compositionally constrained. Most commonly used is the centered log-ratio transformation (CLR), defined by $\text{clr}(p_j^i)=\text{log}(p_j^i/\text{gm}(p^i))$ where gm() indicates the geometric mean (Gloor and Reid, 2016). CLR-transformed data have a singular covariance matrix, which may be problematic for ordination or correlation-based analysis. This may be avoided by employing an isometric log-ratio transformation (ILR) instead, which uses a sequential binary partition to build an orthonormal basis that is interpretable in terms of subparts of the composition (Egozcue et al., 2003); the partition may also be based on phylogenetic information (Silverman et al., 2017). Although ILR may be mathematically superior to CLR for some ordination or correlation-based analyses (Filzmoser et al., 2009), CLR is more interpretable and more widely used, and features still correspond to biological taxa. We therefore use the CLR transformation.

Both CLR and ILR require no zero components, whereas microbiome data often has a high proportion of zeros. A variety of methods exist to eliminate zeros (Weiss et al., 2017); we take the simplest and most common approach, replacing zeros with a small pseudocount. We use the minimum rounding error of 0.5 to replace zero counts, or 1e−6 to replace zero proportions.

Following CLR transformation, within-subject changes $d_j^i$ represent the log of the ratio of fold-differences between the observed abundance of taxon j and the geometric mean abundance for subject i at each time. Similarly, differences between $d_j^i$, used in many of the distance metrics, is a ratio (between subjects) of ratios of fold-differences in taxon abundance.

2.5 Ordination analysis and testing

β-Diversity metrics have wide-ranging utility in microbiome data analysis. Four main uses for measures of β-diversity are data visualization, creation of low-dimensional representations of the microbiome for incorporation in downstream models, classification and clustering and global hypothesis testing. Distances or dissimilarities based on transformed paired or longitudinal data may be utilized in any analysis where a β-diversity matrix is required.

In ordination analysis, high-dimensional data are mapped into a low-dimensional space, often two or three dimensions, so that similar observations lie near each other in the low-dimensional space and dissimilar observations lie far from each other. Several well-known ordination methods are principal components analysis (PCA), non-metric multidimensional scaling (NMDS) and principal coordinates analysis (PCoA), also known as multidimensional scaling (MDS). Once the data are represented in low-dimensional space, observations may be plotted along these axes to visualize dissimilarity in the microbiome across several groups (Erb-Downward et al., 2011; Yatsunenko et al., 2012). The low-dimensional representation may also be included as a covariate or outcome measure in further analyses (Muegge et al., 2011; Qin et al., 2012).

For classification and clustering, the goal is again to explore relationships among samples, in this case by linking progressively more closely related samples. Clustering algorithms include hierarchical clustering, in which similarity between observations may be represented on a dendrogram, and discrete clustering methods such as K-means clustering or partitioning around medoids (PAM), which result in unstructured subgroups of samples. These types of methods have been used, for example, in relation to the idea of distinct ‘enterotypes’ in the gut microbiome (Arumugam et al., 2011; Koren et al., 2013). Although recently enterotypes have been increasingly viewed along a gradient rather than as discrete categories (Jeffery et al., 2012; Knights et al., 2014), discrete categorization remains a useful descriptive tool.

Finally, global hypothesis testing may be carried out by testing whether β-diversity differs across values of the outcome of interest. The category of distance-based multivariate analysis includes, among others, permutation-based methods such as PERMANOVA (Anderson, 2001) and kernel machine regression-based association tests (Chen and Li, 2013; Plantinga et al., 2017; Wu et al., 2016; Zhan et al., 2017; Zhao et al., 2015). All of these formally test whether individuals with more similar outcomes also tend to have more similar microbiomes (as measured by β-diversity).

Because all of these classes of analysis rely on a measure of β-diversity, distances based on paired and longitudinal transformations of microbiome profiles provide a straightforward means of extending each of these analyses to explore change in the microbiome across time.

3 Results

This section begins by presenting empirical size and power results. The pldist transformations and dissimilarities are then applied in a dataset examining the association between the gut microbiome and GVHD and one exploring the variability of the gut microbiome with antibiotic use.

3.1 Simulation studies

Simulations were performed to verify that use of paired and longitudinal dissimilarities preserves type 1 error control in existing kernel machine regression (KMR)-based global association tests and compare the power of tests based on phylogenetic or non-phylogenetic and quantitative or qualitative dissimilarities across association settings. All simulations were performed with both the normalized proportion-based $d_j^i$ and the normalized $d_j^i$ following CLR transformation.

3.1.1 Simulation methods

OTU counts for the first time point were simulated from a Dirichlet-multinomial distribution with parameters estimated from real respiratory-tract data (Charlson et al., 2010), as previously described (Plantinga et al., 2017; Zhao et al., 2015). The dataset includes 856 OTUs, for which we generated 1000 reads per sample. The subsequent time point(s) for each subject were generated by perturbation of the OTU counts from the previous time point. Specifically, the probability of an exact zero in each simulated dataset was generated as $1-\text{Beta}(3,30)$, yielding probability of exact zeros centered around about 8.2% with IQR of approximately 5% to 12%. Non-zero weights were generated as $\text{exp}(N(0,s\sqrt{2}))$ where $s\sim \text{Beta}(20,20)$ so that the nonzero weights ranged from 0 to approximately 40 with median 0.9 and IQR approximately 0.5 to 1.5. Zero counts can never change to nonzero counts based on this perturbation scheme; allowing taxon acquisition would improve power of the unweighted paired or longitudinal metrics, but it does not affect type 1 error and is unlikely to substantially impact the performance of the quantitative metrics. Two time points were generated for paired data and four for longitudinal data.

Quantitative, dichotomous and time-to-event outcomes were simulated using changes in OTU presence or abundance. OTUs were assigned to each of 20 clusters using the Partitioning Around Medoids (PAM) algorithm. A moderately common cluster (7.8% of reads) and a rare cluster (1.7% of reads) were selected to be associated with the outcome. In non-phylogenetic simulations, either the ten most common OTUs or 60 randomly selected OTUs were associated with the outcome.

Continuous outcomes were simulated as in Zhao et al. (2015) under the model

$$y=0.5X_{1i}+0.5X_{2i}+\beta \text{ scale}\left(\sum _{j\in \mathcal{A}}{d}_j^i\right)+{ϵ}_i$$

where ${ϵ}_i\sim N(0,1)$ and $d_j^i$ is the normalized change in taxon presence ($d_j^i$ defined as for unweighted LUniFrac) or proportion ($d_j^i$ defined as for generalized LUniFrac). The active set, $\mathcal{A}$, denotes the set of OTUs in the associated cluster. $X_{1i}\sim N(0,1)$ and $X_{2i}\sim \text{Bernoulli}(0.5)$ are time-invariant covariates, and the scale() function standardizes the total changes in OTU abundance in the associated cluster to have mean 0 and variance 1. Similarly, binary outcomes were simulated under the model

$$\text{logit}\left(E(y_i|X_i,Z_i)\right)=0.5X_{1i}+0.5X_{2i}+\beta \text{ scale}\left(\sum _{j\in \mathcal{A}}{d}_j^i\right)$$

Finally, as in Plantinga et al. (2017), survival times were simulated via

$$T_i=\frac{-\text{log}(U_i)}{\hspace{0.17em}\text{exp}\hspace{0.17em}\left(0.5X_{1i}+0.5X_{2i}+\beta \text{scale}\left(\sum _{j\in \mathcal{A}}{d}_j^i\right)\right)}$$

where $U_i\sim \text{Uniform}(0,1)$, and censoring times were generated independently from the microbiome to yield approximately 25% censoring. For type 1 error simulations, we set β = 0.

3.1.2 Size and power of KMR-Based tests

We first verify that the KMR-based tests for longitudinal, dichotomous and time-to-event outcomes have appropriate size using kernels computed from pldist dissimilarities (Koh et al., 2018; Plantinga et al., 2017; Zhao et al., 2015). Based on analysis using the R packages MiRKAT and OMiSA with pldist dissimilarities, when no true association exists, type 1 error is indeed controlled at or near the nominal level of $\alpha =0.05$ (Table 2 and Supplementary Tables S5 and S6).

Table 2.

Empirical size for each outcome type using PUniFrac dissimilarities (unweighted, K_U; generalized with $\gamma =0.5,\hspace{0.17em}{K}_{0.5}$; weighted, K_W), the quantitative (K_JQ) and qualitative (K_JB) paired Jaccard dissimilarities, and the omnibus test for all proposed dissimilarities ($K_{\text{omni}}$), based on 2000 simulations with n = 50, 100 or 200 and nominal level $\alpha =0.05$

Outcome type	n	KU	$K_{0.5}$	KW	KJQ	KJB	$K_{\text{omni}}$
Continuous	50	0.052	0.050	0.043	0.046	0.050	0.048
	100	0.052	0.054	0.051	0.046	0.042	0.050
	200	0.054	0.052	0.051	0.042	0.051	0.049
Binary	50	0.042	0.045	0.049	0.036	0.043	0.045
	100	0.050	0.043	0.046	0.042	0.044	0.045
	200	0.051	0.052	0.054	0.049	0.045	0.052
Time-to-Event	50	0.054	0.048	0.051	0.054	0.050	0.051
	100	0.047	0.052	0.047	0.050	0.044	0.047
	200	0.057	0.051	0.047	0.053	0.055	0.048

Power results for continuous outcomes are presented in Figure 2; results for binary and time-to-event outcomes are similar (Supplementary Figs S2–S7). The paired Jaccard index was chosen as a representative non-phylogenetic dissimilarity because the Jaccard index is fairly commonly used, but the results using other non-phylogenetic methods are generally similar to those using the Jaccard index. Supplementary Figures S8 and S9 compare the non-phylogenetic metrics in two simulation scenarios.

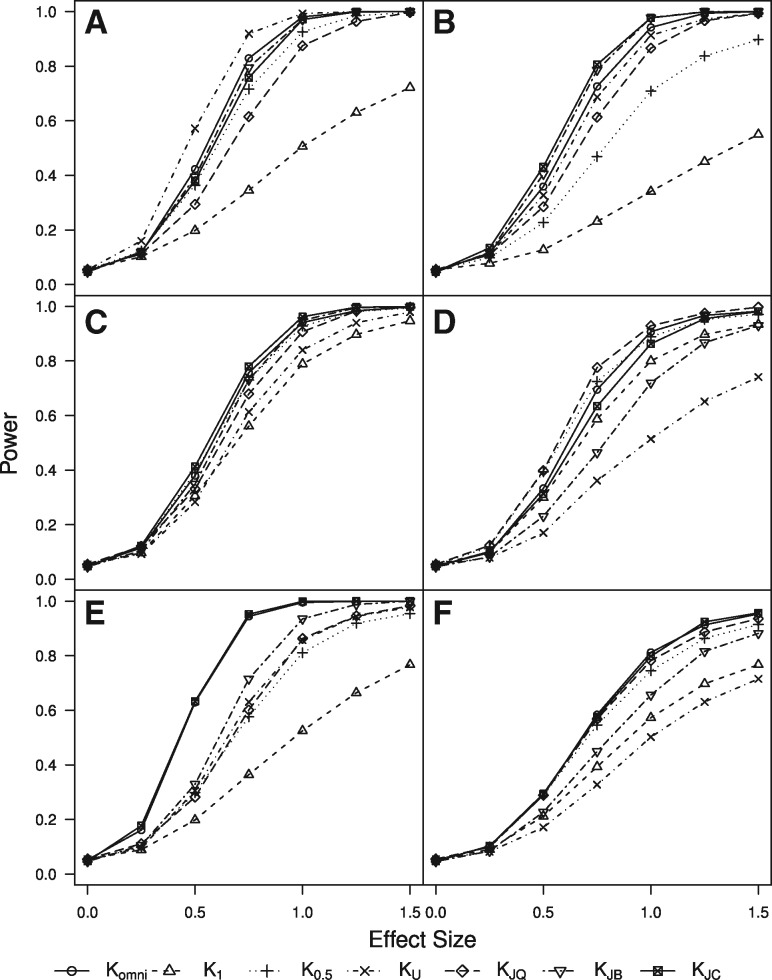
Fig. 2.

Empirical power based on 1000 simulated datasets with n = 100, two time points and continuous outcomes. K$\text{omni}\hspace{0.5em}$ is the omnibus test, K₁ and $K_{0.5}$ are generalized PUniFrac with γ  =  1 or 0.5, K_U is unweighted PUniFrac, K_JQ is the quantitative paired Jaccard kernel, K_JB is the qualitative paired Jaccard kernel, and K_JC is the Jaccard kernel using CLR-transformed proportions. The continuous outcome is associated with: (A) Change in presence of a rare cluster. (B) Change in presence of 60 randomly selected taxa. (C) Change in abundance of a moderately common cluster. (D) Change in abundance of the 10 most abundant taxa. (E) Change in CLR-transformed abundance of a moderately common cluster. (F) Change in CLR-transformed abundance of the 10 most abundant taxa

When the change in presence or absence of OTUs in a low-abundance phylogenetic cluster is associated with the outcome (Panel A), the unweighted PUniFrac kernel, which is based on changes in taxon presence or absence and incorporates phylogenetic information, has highest power. When 60 random OTUs are chosen to be associated with the outcome, many of them will be rare, since most OTUs are low-abundance. The binary paired Jaccard kernel, which is based on changes in taxon presence or absence, and CLR-transformed Jaccard kernel have highest power to detect associations between changes in presence of these randomly selected OTUs and the outcome (Panel B).

When the change in abundance of OTUs in a moderately common phylogenetic cluster is associated with the outcome (Panel C), the CLR-transformed Jaccard kernel interestingly has high power again, as does the generalized PUniFrac kernel ($\gamma =0.5$), which incorporates both phylogenetic structure and magnitude of abundnace changes. When changes in the abundance of the ten most common OTUs are associated with the outcome, phylogenetic structure does not improve power, since the associated taxa are not necessarily phylogenetically related. The quantitative paired Jaccard kernel, which has no phylogenetic component but is calculated using changes in taxon abundance, has highest power to detect associations in this case (Panel D).

For both CLR-transformed abundance of a common phylogenetic cluster (Panel E) and common but unclustered taxa (Panel F), the CLR-transformed Jaccard kernel again has highest power, demonstrating that it is a useful metric across a wide range of settings.

Therefore, as previously noted for each kernel machine regression-based test at single time points (Plantinga et al., 2017; Zhao et al., 2015), the power is generally highest when the selected kernel best matches the true form of the association between (changes in) the microbiome and the outcome, although the CLR-transformed Jaccard kernel performs well in most situations. In all settings, the omnibus test has power close to that of the best-performing kernel. The omnibus test therefore provides an attractive alternative to choosing a single kernel, since in most real-data settings, the true form of the association between the longitudinal microbiome and the outcome is not known in advance.

3.2 Gut microbiome and GVHD

Acute graft-versus-host disease (aGVHD) occurs in 30–70% of allogeneic blood or bone marrow transplant patients and is a leading cause of death following transplant. Current approaches to treatment and prevention are only moderately effective (Ferrara et al., 2009; Jagasia et al., 2015). There is evidence that the gut microbiome is involved in the immune response to transplant with or without concomitant antibiotic treatment regimens (Holler et al., 2014; Mathewson and Reddy, 2015; Vossen et al., 2014), but this relationship is not well understood. Therefore, Jenq et al. (2015) recently studied the association of diversity of the gut microbiome and abundance of the genus Blautia with time to severe aGVHD, aGVHD-related mortality and overall mortality.

The data were processed as described in Plantinga et al. (2017). We excluded any samples with fewer than 500 reads. To assess the sensitivity of this analysis to read depth variability, we also considered excluding samples with fewer than 1000 reads and rarefying to 500 or 1000 reads; results for all of the sensitivity analyses were similar to the primary results. We considered three analyses. For the first analysis, with paired data, we included the last sample taken pre-transplant as our first time point for each subject (range: 1–14 days pre-transplant) and the sample collected closest to day 12 post-transplant, but at most 4 days away, as our second time point (range: 8–16 days post-transplant). These time points represent points of scientific interest; in particular, we are interested in changes between the pre- and post-transplant microbiome, and aGVHD often occurs around 2–3 weeks post-transplant, so observations near Day 12 are close to when aGVHD may begin to occur. Subjects missing a pre-transplant sample were excluded, leaving 85 subjects total. For the second analysis, we included up to 6 observations per subject, randomly selecting 6 observations for subjects with more than 6 samples. Finally, for comparison, we analyzed the data at only the time point within four days of day 12 post-transplant (using the same set of subjects as in the first two analyses). All analyses were adjusted for age and sex by including them as covariates in the kernel machine regression (Plantinga et al., 2017). All quantitative kernels are based on CLR-transformed data to account for compositionality. For CLR-transformed single time point analysis, we calculated the Jaccard dissimilarity on CLR-transformed data with a constant added so that all values were positive, and the UniFrac distances using a method analagous to CLR-transformed LUniFrac.

Using MiRKAT-S along with the omnibus test to evaluate the association between the microbiome and adverse outcomes after allogeneic transplant, we find strong evidence for an association between changes in the gut microbiome and overall survival only in the post-transplant microbiome, although the association using the longitudinal distances without CLR transformation is also marginally significant (Table 3). The compositive adverse event (grade 2 aGVHD) is the only outcome significantly associated with the paired kernels using CLR-transformed data. For the longitudinal kernels, no significant associations were found using CLR-transformed data, but variability in relative abundances is associated with overall survival and the composite adverse event with grade 3 aGVHD. Based on these results, it appears that both changes in the microbiome (pre- versus post-transplant) and the post-transplant microbiome alone are associated with survival and grade 2 or grade 3 composite events (aGVHD, death or relapse), but the state of the post-transplant microbiome is most important for that association.

Table 3.

Omnibus P-values from MiRKAT-S based on P/LUniFrac kernels (unweighted and $\gamma =0.5$ or 1) and binary or quantitative Jaccard kernels

Analysis	CLR	OS	Adv (gr. 2)	Adv (gr. 3)
Post-transplant	No	0.007	0.018	0.012
	Yes	0.003	0.019	0.027
Paired	No	0.183	0.041	0.057
	Yes	0.061	0.004	0.091
Longitudinal	No	0.035	0.069	0.028
	Yes	0.226	0.326	0.538

Note: CLR indicates whether quantitative kernels used the CLR transformation. OS denotes overall survival. Adv (gr. X) denotes the composite outcome of relapse, aGVHD of the specified grade or death from any cause. Analyses were adjusted for age and sex.

3.3 Antibiotics and gut microbiome variability

To understand the temporal variability of the human microbiome, Flores et al. (2014) sampled microbial communities at several body sites weekly for three months in 85 college-age adults. The study population was predominantly Caucasian individuals in a healthy range of BMI values. We have between 7 and 10 samples for each of 75 individuals.

In this analysis, we consider the temporal variability of the gut (fecal) microbiome and its association with antibiotic usage. We consider variability in relative abundance and hence use non-CLR-transformed distances for this analysis. In the original study, although the largest shifts in the microbiome occurred soon after oral antibiotic usage at an individual level, no overall association between temporal variability (measured by median intra-individual UniFrac values) and antibiotic usage during the study period was found.

We examine the association between the non-phylogenetic longitudinal dissimilarities from pldist and an indicator that the individual ever used oral antibiotics during the study period using MiRKAT. To account for the effect of potentially different sampling intervals between subjects, we adjust for total number of samples along with sex as covariates in the kernel machine regression model. The longitudinal transformation essentially summarizes average change in each taxon (presence or abundance) per week, so that global tests assess whether variability in relative abundances (average weekly change) differs between subjects who did and did not take antibiotics.

We find borderline evidence of a global association between gut microbiome variability and antibiotic use during the study period (Table 4). The P-values are lower for each qualitative dissimilarity than the corresponding quantitative version, indicating that change in which taxa are present across the study period is driving this association. That is, we see different amounts of variability in community membership (taxon presence) among subjects who take antibiotics compared to those who do not, adjusting for sex and the number of samples per subject. Hence in this case, the longitudinal analysis can formalize suspected associations and clarify whether variability in presence or abundance is driving the association with antibiotic use.

Table 4.

Association between variability of microbiome and antibiotic use

	Bray-Curtis	Gower	Jaccard	Kulczynski	Omnibus
Qualitative	0.060	0.086	0.015	0.012	0.047
Quantitative	0.875	0.116	0.371	0.343

Note: P-values are from MiRKAT using quantitative and qualitative Bray-Curtis, Gower, Jaccard and Kulczynski kernels, adjusting for sex and number of observed time points.

4 Discussion

We have developed pldist, a family of data transformations and resulting ecological dissimilarities for paired or longitudinal microbiome data. Each of these dissimilarities compares changes in OTU presence, relative abundance or CLR-transformed relative abundance across time between different individuals. They may be used in any existing distance-based analyses, including testing in the kernel machine regression framework, PERMANOVA, ordination methods such as PCoA, and other distance-based global microbiome analyses. The family of transformations provides high power to detect associations between changes in the microbiome and clinical, biological or environmental outcomes.

Unequal sampling depth is a common concern for microbiome analysis. Rare taxa may be observed or missed in different communities due simply to the fact that one community had a higher overall read count than another. This matters especially for qualitative (i.e. dichotomized) transformations. If great variation in read counts exists, either rarefaction or an approach specifically targeted towards estimating sampling versus structural zeros is recommended prior to using qualitative transformations.

Compositionality, or the fact that relative abundances for each subject must sum to one, is an important consideration for microbiome analyses based upon relative abundances. In the context of longitudinal data, an important concern is that changes in the abundance of a single taxon can induce spurious changes in the relative abundance of many or all taxa. Therefore, changes in relative abundance are generally unable to provide evidence for association between one taxon and an outcome without specialized methods or transformations; absolute abundances from qPCR would be needed.

Because the goal of distance-based analysis is testing whether higher overall dissimilarity between microbiomes is associated with greater dissimilarity in outcomes, it matters somewhat less for distance-based analysis whether the observed changes in relative abundance are due to a large change in the absolute abundance of one taxon or smaller changes in many taxa. However, it remains important to account for data compositionality if results are to be understood on any scale except relative abundances Gloor et al. (2017). We use the CLR transformation for this purpose. Our simulation results and data analyses show that, although distance matrices are similar with and without CLR transformation, results may differ depending on whether or not the transformation is used. This choice should be based upon scientific interest in differences in relative abundances or log-ratios of abundances.

As in generalized UniFrac and other families of distances, the power of tests based on the proposed dissimilarities depends on the true form of the association between changes in the microbiome and the outcome. Omnibus tests, available for most microbiome kernel methods, allow multiple kernels to be considered simultaneously with minimal loss of power compared to the best individual kernel. Hence the use of multiple dissimilarities with an omnibus test is recommended for most applications of these methods. Because they can be used in existing testing frameworks, tests based on the pldist dissimilarities can be very fast, adjust for relevant covariates, and accommodate a variety of outcome types.

Funding

This work was supported by the National Institute of Allergy and Infectious Disease (NIAID) [grant number F31 AI131595 to AMP] and National Institute of General Medical Sciences [R01 GM129512 to MCW] of the National Institutes of Health.

Conflict of Interest: none declared.