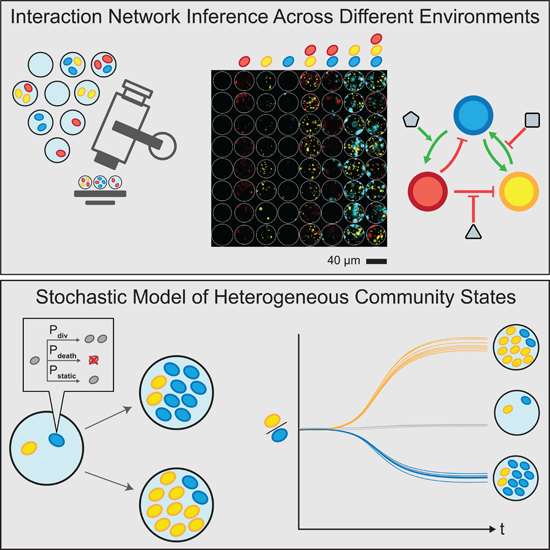
SUMMARY
Microbial interactions are major drivers of microbial community dynamics and functions but remain challenging to identify due to limitations in parallel culturing and absolute abundance quantification of community members across environments and replicates. To this end, we developed Microbial Interaction Network Inference in microdroplets (MINI-Drop). Fluorescence microscopy coupled to computer vision techniques were used to rapidly determine the absolute abundance of each strain in hundreds to thousands of droplets per condition. We showed that MINI-Drop could accurately infer pairwise and higher-order interactions in synthetic consortia. We developed a stochastic model of community assembly to provide insight into the heterogeneity in community states across droplets. Finally, we elucidated the complex web of interactions linking antibiotics and different species in a synthetic consortium. In sum, we demonstrated a robust and generalizable method to infer microbial interaction networks by random encapsulation of sub-communities into microfluidic droplets.
eTOC Blurb
Microorganisms often live in complex multi-species communities, where individual members interact with each other and the environment. These interactions are challenging to decipher and dictate the composition, functions, and dynamics of microbial ecosystems. We developed Microbial Interaction Network Inference in microdroplets (MINI-Drop) to identify the interactions within microbial communities across different environments with hundreds to thousands of droplet replicates. We showed that MINI-Drop can identify pairwise and higher-order interactions in a synthetic microbial community and developed a mathematical model to investigate heterogeneity in community assembly in small populations. Finally, we used MINI-Drop to elucidate a complex interaction network between combinations of antibiotics and species in a synthetic microbial community.
Graphical Abstract
INTRODUCTION
Microbial communities have a tremendous impact on diverse environments ranging from the human body to the plant rhizosphere (Berendsen et al., 2012; Clemente et al., 2012). Microbe-microbe and environment-microbe interactions are major determinants of microbial communities and microbiomes (Cao et al., 2019; Venturelli et al., 2016). Deciphering interaction networks in high-dimensional microbial communities is challenging due to the need to rapidly and accurately determine the absolute abundance of each community member across many sub-communities and environments (Cao et al., 2017; Harcombe et al., 2016).
The population sizes of microbial consortia can range from less than ten cells in mixed species biofilm aggregates to 1011 cells mL−1 in the human colon (Connell et al., 2014; Sender et al., 2016; Stoodley et al., 2001). Cellular growth history, the temporal order of strain colonization, or the initial phase of microbial competition can impact community assembly and lead to significant heterogeneity in community behaviors (von Bronk et al., 2017; Kong et al., 2018; Vega and Gore, 2017; Venturelli et al., 2018; Zhou et al., 2013). Our understanding of microbial consortia in small populations is limited due to technical challenges in the manipulation and analysis of small populations of cells (Connell et al., 2014). Therefore, high-throughput methods that can rapidly resolve microbial interaction networks across different initial community states, population sizes and environments would enable a better understanding of the key parameters shaping the structure and functions of microbial communities.
Microbial interaction network inference requires accurate measurements of the absolute abundance of each member of the community (Cao et al., 2017; Fisher and Mehta, 2014). Recent experimental efforts have used models trained on measurements of 1–3 member communities to predict community composition or function of up to 12 members to varying degrees of accuracy (Friedman et al., 2017; Guo and Boedicker, 2016; Kong et al., 2018; Mounier et al., 2008; Venturelli et al., 2018). Absolute abundance quantification of each member of a microbial community has ranged from low-throughput selective plating to count colony forming units (tens of samples per experiment) (Mounier et al., 2008) to optical density multiplied by relative abundance based on next-generation sequencing of samples generated through robotic high-throughput culturing (hundreds of samples per experiment) (Venturelli et al., 2018).
Encapsulation of microbial communities into microdroplets has been used to study ecological and evolutionary processes in microbial communities (Bachmann et al., 2013; Park et al., 2011). Water-in-oil droplets can be generated at kilohertz (kHz) rates using microfluidics, wherein cells from a mixed culture are randomly encapsulated into droplets yielding distinct sub-communities that can be studied in parallel (millions of samples per experiment). Each droplet is a miniaturized compartment that can be used to study interactions between community members in small populations. Microfluidic technologies enable the generation of well-controlled droplet environments of ~1% size variation (Guo et al., 2012). However, previous studies have not fully leveraged the capabilities of this technology to quantitatively investigate microbial communities. Further, we lack a systematic method to rapidly infer microbial interactions using droplet microfluidics in different environmental contexts.
To address this challenge, we developed Microbial Interaction Network Inference in microdroplets (MINI-Drop). To infer microbial interactions based on the absolute abundance of each strain across hundreds to thousands of samples, we developed an automated computational method coupled to fluorescence microscopy to rapidly segment droplet images and accurately count fluorescently labeled cells within each droplet. We tested the capability of MINI-Drop to accurately infer microbial interactions using a microbial interaction toolbox composed of positive and negative interactions mediated by distinct molecular mechanisms. Our results demonstrate that MINI-Drop can accurately decipher pairwise as well as higher-order interactions by analyzing droplets containing 1–3 strains. We investigated how the molecular composition of the environment shapes the ecological network of a three-member consortium. A probabilistic model of cell growth modified by microbial interactions described the compositional heterogeneity in community states across droplets, providing insight into the forces shaping community assembly in small populations. Finally, we investigated the complex interplay between combinations of antibiotics and temperature on the assembly and species interactions in a three-member consortium.
RESULTS
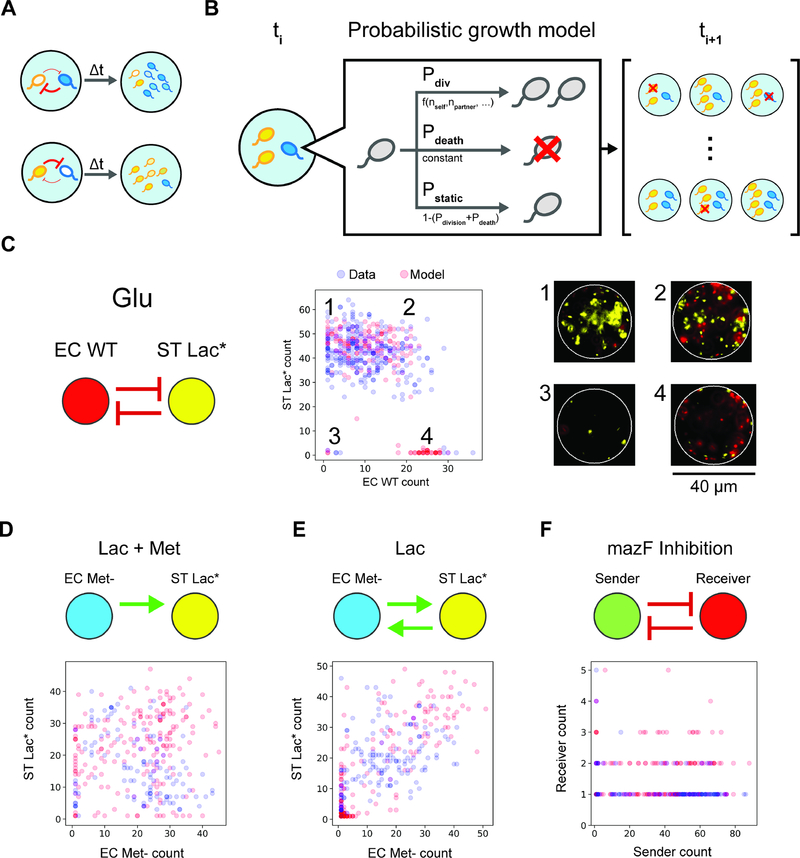
Microbial interactions represent the net impact (positive, negative or negligible) of an organism on the growth of another over a specified time interval (Cao et al., 2019). Microbial interactions can be quantified by evaluating the difference in phenotype (e.g. growth response or metabolic activity) of an organism in the absence and presence of another strain (partner strain). Encapsulation of cells in a microbial community into droplets using techniques from droplet-microfluidics enables parallel culturing of many sub-communities (Fig. 1a). To infer microbial interactions, we needed a scalable method to determine the absolute abundance of each strain within each droplet. The average fluorescence in each droplet may not be proportional to the number of cells due to variability in cellular growth rates, which dictates the rate of dilution of the fluorescent reporter (Fig. S1a). In addition, absolute abundance information is critical for accurate parameter estimation for computational models (Cao et al., 2017; Fisher and Mehta, 2014). Therefore, we developed an automated procedure using techniques from computer vision to rapidly identify droplets (Fig. S1b) and count the number of fluorescently labeled cells in each droplet (Fig. S1c). The droplets were binned according to strain composition (Fig. S1d) and the cell counts were used to infer the interaction type (positive, negative or negligible), strength and directionality (see STAR Methods).
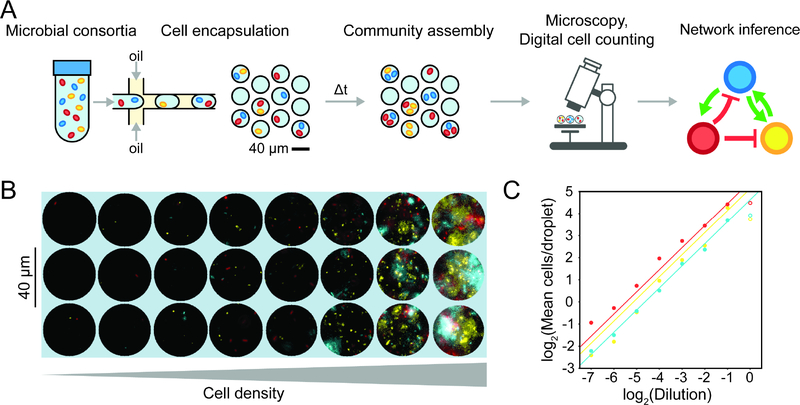
Figure 1. Overview and characterization of microbial interaction network inference in microdroplets (MINI-Drop).
(a) Overview schematic of the MINI-Drop method. A mixed microbial culture and oil are loaded into a droplet-forming microfluidic device. Cells are randomly encapsulated into droplets based on a Poisson distribution. The droplets are incubated for a period of time to allow cell growth and division and then imaged using fluorescent microscopy. A computer vision workflow rapidly identifies droplets and determines the number of each fluorescently labeled strain within each droplet (Fig. S1). A microbial interaction network is inferred based on the difference in the mean number of cells in the absence and presence of a partner strain. (b) Representative fluorescent microscopy images of droplets containing three bacterial strains labeled with YFP (ST Lac*), RFP (EC WT) or CFP (EC Met-) (see Tables S9–10). (c) Scatter plot of the dilution factor of the mixed culture vs. the log2 transform of the mean number of cells per drop (cell count distribution shown in Fig. S2a and analysis of mean fluorescence in Fig. S2b). Each data point represents the mean of 400–600 droplets and lines denote linear regression fits to the data excluding the highest dilution factor (indicated by empty circles to emphasize divergence from the linear trend). Red, yellow and blue data points correspond to EC WT, ST Lac* and EC Met-, respectively.
To evaluate the accuracy and dynamic range of the cell-counting method, CFP-labeled E. coli, RFP-labeled E. coli and YFP-labeled S. typhimurium were mixed in equal volumetric ratios and serially diluted to generate a broad range of cell densities (Fig. 1b). Each dilution of the mixed culture was encapsulated into 34 picoliter (pL) droplets (40 μm diameter), imaged using fluorescence microscopy, and analyzed using a computational workflow (see STAR methods). The number of cells of each fluorescently labeled strain decreased linearly with each dilution, with the exception of the highest density droplets (Fig. 1c) and the cell count distributions matched the expected Poisson distribution (Fig. S2a). These data demonstrate at least a 64-fold linear range of the cell counting method of each fluorescent reporter. In contrast, a similar analysis using the mean fluorescence across the droplet images was inaccurate in the dilution range below 2−4, which corresponds to the regime of cell counts for poorly growing strains (Fig. S2b). Accurate quantification of low cell counts is important for accurate estimation of the interaction strengths. In a separate experiment described below involving growth of fluorescently labeled strains in droplets (Table S1, E6), we analyzed the relationship between droplet diameter and the number of fluorescently labeled cells to determine if the experimental noise in this parameter contributed to the variability in cell growth across droplets. Our results showed that an ~8 mM variation in droplet diameter did not correlate with the number of cells labeled with CFP, YFP or RFP, demonstrating that this factor did not substantially contribute to differences in cell counts among droplets (Fig. S2c,d,e).
Investigating microbial interaction networks in two-member consortia
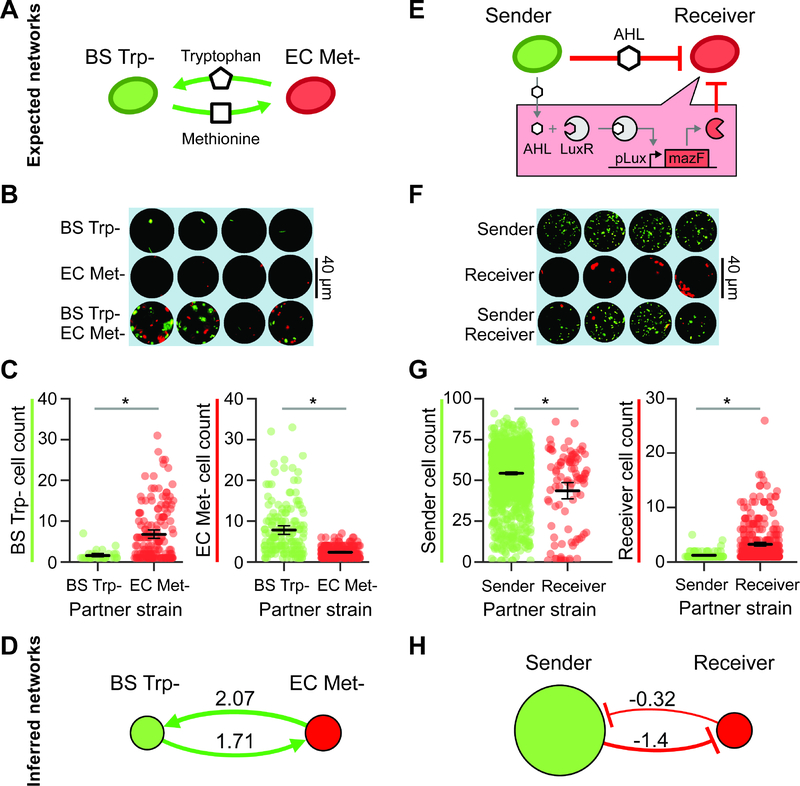
To determine whether MINI-Drop could illuminate microbial interactions in synthetic consortia, we investigated two-member consortia engineered to display defined interactions. A microbial interaction was defined as a statistically significant difference in the average number of cells of a given strain in the presence of a second strain (partner) compared to the absence of the partner at a specific time point. To investigate positive interaction networks with MINI-Drop, we constructed a consortium composed of an RFP-labeled E. coli methionine auxotroph (EC Met-) and a GFP-labeled B. subtilis tryptophan auxotroph (BS Trp-, Table S1, E1). In the absence of supplemented amino acids, the growth of B. subtilis requires secretion of tryptophan from E. coli and the growth of E. coli requires secretion of methionine from B. subtilis, which together generates a bidirectional positive interaction network (Fig. 2a). The two species were mixed in equal proportions based on OD600 measurements, encapsulated into droplets such that each droplet had 1–2 cells on average according to a Poisson distribution and the droplets were incubated at 37°C for 18 hours. The fluorescence microscopy images and cell count distributions demonstrated that single species droplets exhibited a low number of total cells, whereas droplets containing both species exhibited significantly higher number of cells of each strain (Fig. 2b,c). The inferred interaction network exhibited bidirectional positive interactions, mirroring the topology of the expected interaction network (Fig. 2a,d) and demonstrating that MINI-Drop could deduce positive interactions. In addition, both strains exhibited poor growth in absence of the partner strain (denoted by the size of the node in the network). The cell counts for BS Trp- and EC Met- were positively correlated, suggesting that the correlation structure in absolute abundance could be used to identify bidirectional positive interactions (Fig. S3a).
Figure 2. Investigating positive and negative microbial interaction networks using MINI-Drop.
(a) Schematic of the expected network for a synthetic consortium composed of an RFP-labeled E. coli methionine auxotroph (EC Met-) and a GFP-labeled B. subtilis tryptophan auxotroph (BS Trp-) (Table S1, E1). (b) Fluorescence microscopy image of representative single-species (EC Met- or BS Trp-) or two-member droplets. (c) Categorical scatter plot showing the number of BS Trp- or EC Met- cells in each droplet. The black horizontal line represents the mean and the error bars denote bootstrapped 95% confidence intervals for the mean. Gray lines denote statistically significant difference in means based on the Mann-Whitney U test (n=87, p=1.5e-6, left and n=372, p=3.8e–26, right). (d) The inferred interaction network for the EC Met-, BS Trp-consortium. The edge width is proportional to the log2 ratio of the average cell count in the presence of a partner to the average cell count in single strain droplets. Node size is proportional to the average cell count of each strain in single strain droplets. (e) Schematic of the expected network of an E. coli community that exhibits a strong unidirectional negative interaction. A GFP-labeled strain (sender) expresses LuxI, a synthetase for the quorum-sensing signal C6 acyl homoserine lactone (AHL). AHL binds to the receptor LuxR in an RFP-labeled strain (receiver) and activates the expression of a toxin MazF, generating a strong negative interaction (Table S1, E2). (f) Fluorescence microscopy image of representative droplets containing the sender strain, receiver strain or community. (g) Categorical scatter plot of the number of sender or receiver cells in each droplet in the presence or absence of a partner. The black line represents the mean and the error bars denote bootstrapped 95% confidence intervals for the mean. Gray lines denote statistically significant differences in the means (n=1512, p=2.2e–4, left, n=421, p=3.8e–14, right). (h) The inferred interaction network for the quorum sensing regulated toxin consortium.
We next investigated whether MINI-Drop could decipher negative interactions. A synthetic community was constructed wherein a GFP-labeled E. coli strain (sender strain) was engineered to express LuxI, a synthetase for the quorum-sensing signal C6 acyl homoserine lactone (AHL). AHL diffuses into the RFP-labeled E. coli strain (receiver strain), binds and activates the receptor LuxR, which regulates the expression of the MazF toxin (Fig. 2e, Table S1, E2). High expression levels of the endoribonuclease MazF inhibits cell growth by inducing mRNA decay (Venturelli et al., 2017), generating a strong negative interaction from the sender to the receiver strain. To characterize this community using MINI-Drop, the sender and receiver strains were mixed in equal proportions based on OD600, encapsulated into droplets and incubated at 37°C for 18 hr. The fluorescent microscopy images and cell count distributions showed that the number of receiver cells was significantly lower in droplets containing both the sender and receiver strains compared to the average number of receiver cells in single-strain droplets (Fig. 2f,g). The average number of sender cells in droplets containing the sender strain alone was 16.7-fold higher than the average number of receiver cells in droplets containing only the receiver strain, presumably due to leakiness of mazF from the pLux promoter in the absence of AHL. The inferred interaction network exhibited a strong negative interaction from the sender to the receiver and a weak negative interaction from the receiver to the sender (Fig. 2h). The node size of the receiver strain was significantly smaller than the sender strain, illustrating the substantial difference in single strain fitness in the absence of the partner. The cell counts of the sender and receiver were negatively correlated across droplets, suggesting that the absolute abundance correlation structure could be used to pinpoint bidirectional negative interactions (Fig. S3b).
The molecular composition of the environment shapes a microbial interaction network
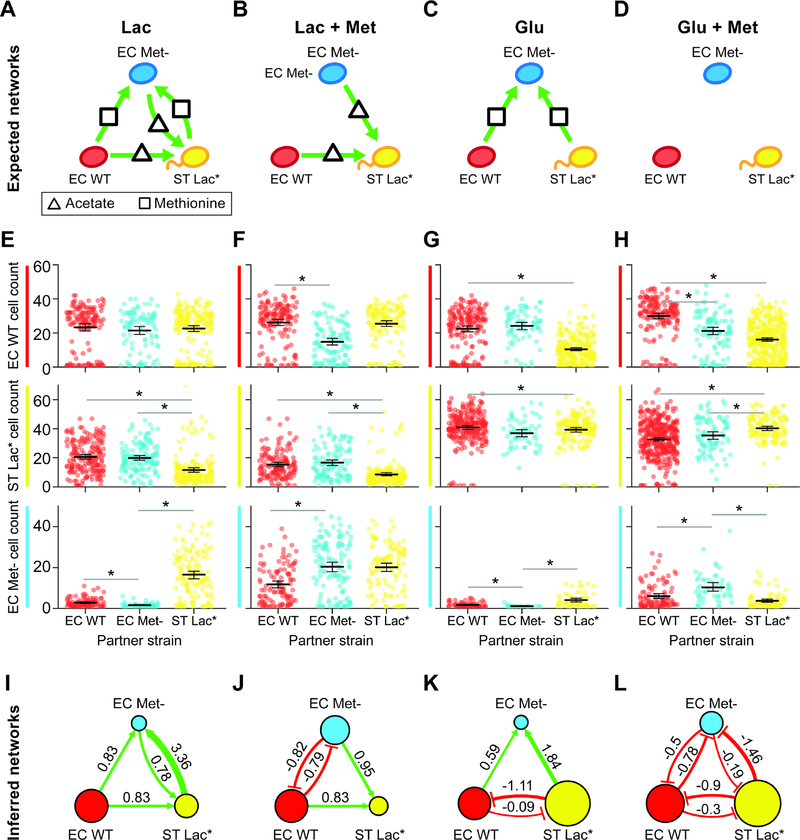
The molecular composition of the environment influences the energetic costs and benefits of microbial interactions in microbial communities (Cao et al., 2019; Harcombe et al., 2016; Liu et al., 2017). A key challenge is understanding how microbial interaction networks are modulated by environmental parameters. To investigate this question, we constructed a three-member community consisting of two strains that interact via bidirectional positive interactions and a third strain that promotes growth of constituent members of the community but does not receive a benefit from the community. Specifically, the strains included RFP-labeled E. coli (EC WT), CFP-labeled E. coli methionine auxotroph (EC Met-), and YFP-labeled S. typhimurium (ST Lac*) (Fig. 3a). This consortium was characterized in four conditions that varied the carbon source (lactose or glucose) and the presence or absence of supplemented methionine. In lactose minimal media, E. coli can consume lactose and secrete carbon byproducts that can be utilized as substrates by ST Lac* (Table S1, E3–6) (Harcombe, 2010). In the absence of supplemented methionine, the growth of EC Met- is dependent on methionine or intermediate(s) used to produce methionine that are secreted by constituent community members.
Figure 3. The molecular composition of the environment shapes the interaction network of a three-member consortium.
(a) Schematic of the expected microbial interaction network of a three-member consortium consisting of RFP-labeled E. coli (EC WT), CFP-labeled E. coli methionine auxotroph (EC Met-), and YFP-labeled S. Typhimurium deficient in lactose metabolism (ST Lac*) in lactose minimal media lacking supplemented methionine (Table S1, E3). Secreted carbon byproducts (acetate) and methionine are represented by a triangle and rectangle, respectively. Node colors and green arrows denote the type of fluorescent reporter and positive interactions, respectively. (b) Schematic of the expected microbial interaction network in lactose minimal media supplemented with methionine (Table S1, E4). (c) Schematic of the expected microbial interaction network in glucose minimal media lacking supplemented methionine (Table S1, E5). (d) Schematic of the expected microbial interaction network in glucose minimal media supplemented with methionine (Table S1, E6). (e) Cell count distributions in lactose minimal media for EC WT (top), ST Lac* (middle) or EC Met- (bottom). The black line represents the mean and the error bars denote the bootstrapped 95% confidence intervals for the mean. The gray horizontal bars indicate a statistically significant difference (p < 0.05, Table S2) based on the Mann-Whitney U test. (f) Cell count distributions in lactose minimal media supplemented with methionine for EC WT (top), ST Lac* (middle) or EC Met- (bottom). (g) Cell count distributions in glucose minimal media for EC WT (top), ST Lac* (middle) or EC Met- (bottom). (h) Cell count distributions of EC WT (top), ST Lac* (middle) or EC Met- (bottom) in glucose minimal media supplemented with methionine. (i) Inferred interaction network in lactose minimal media lacking supplemented methionine. The edge width is proportional to the log2 ratio of the average cell count in the presence of a partner to the average cell count in the absence of the partner. Node size is proportional to the average cell count of each strain grown in isolation. (j) Inferred network in lactose minimal media supplemented with methionine. (k) Inferred interaction network in glucose minimal media lacking supplemented methionine. (l) Inferred interaction network in glucose minimal media supplemented with methionine.
We used MINI-Drop to infer the pairwise microbial interaction network by analyzing the number of cells of each community member in single strain and two-member droplets. In lactose minimal media lacking supplemented methionine, the inferred network mirrored the expected network, exhibiting bidirectional positive interactions between ST Lac* and EC Met- and unidirectional positive interactions from EC WT to ST Lac* or to EC Met- (Fig. 3a,e,i, Table S1, E3, Table S2). In lactose minimal media supplemented with methionine, the positive outgoing interactions from EC WT or ST Lac* to EC Met- were absent in the network and bidirectional negative interactions linked EC Met- and EC WT (Fig. 3b,f,j, Table S1, E4). In glucose minimal media lacking supplemented methionine, the positive interactions from EC WT or EC Met- to ST Lac* were absent and instead EC WT and ST Lac* were coupled by bidirectional negative interactions (Fig. 3c,g,k, Table S1, E5). By contrast to the expected network, bidirectional negative interactions were inferred between all pairs of strains in glucose minimal media supplemented with methionine (Fig. 3d,h,l, Table S1, E6). The size of the EC WT node in the network did not vary significantly across conditions, indicating that the growth of EC WT was not sensitive to the environmental changes (Fig. 3i,j,k,l). By contrast, the size of the EC Met- or ST Lac* nodes were larger in the presence of methionine and glucose, respectively. Across all environments, the sign of the Pearson correlation coefficient clustered according to the pairwise network topology, wherein positive or negative correlation coefficients were associated with positive or negative interactions, respectively (Fig. S3, S4). These data show that correlations in the absolute abundance of strains across droplets can be used to classify two-member network topologies.
We next investigated the coexistence of all three strains across environmental conditions by examining three-member droplets. The cooperative network (lactose minimal media lacking methionine) displayed the highest strain coexistence, indicating that positive interactions were critical features of the network that promoted ecological stability (Fig. S5a). By contrast, the competitive network (glucose minimal media supplemented with methionine) exhibited the lowest strain coexistence across all conditions, suggesting that negative interactions can destabilize the community. Networks with combinations of positive and negative interactions displayed intermediate strain coexistence. The distributions of cell counts in three-member droplets exhibited a distinct clustering pattern in each condition, demonstrating that the environmental context is a major driver of community assembly (Fig. S5b). In sum, our results demonstrate that the microbial interaction network is highly context-dependent and the network topology changes from cooperative to competitive as a function of the molecular composition of the environment.
Investigating higher-order interactions using MINI-Drop
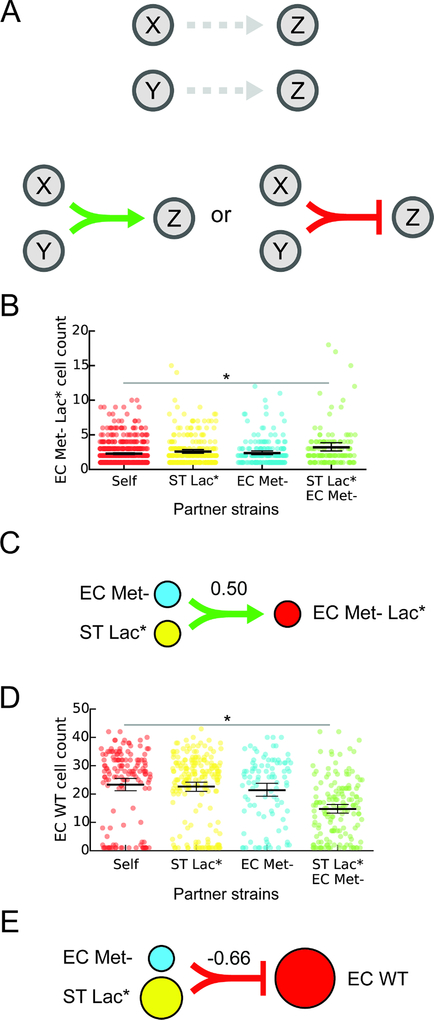
Higher-order interactions occur when a pairwise interaction is modified in the presence of a third community member (Bairey et al., 2016; Billick and Case, 1994) and these interactions are challenging to identify in microbial communities. We defined a higher-order interaction as a difference in the presence and sign (positive or negative) of an interaction in a three-member community compared to the presence and sign of the interaction in each two-member sub-community (Fig. 4a). We tested whether MINI-Drop could identify higher-order interactions by analyzing the cell count distributions of each strain in three-member droplets in addition to single-strain and two-member droplets. To do so, we studied a community consisting of RFP-labeled E. coli methionine auxotroph that is also deficient in lactose metabolism (EC Met- Lac*, Table S1, E7), EC Met- (CFP) and ST Lac*. In lactose minimal media lacking supplemented methionine, EC Met- and ST Lac* can secrete carbon byproducts and metabolites to rescue the methionine autotrophy and thus together enable the growth of EC Met- Lac*. Our results showed that the number of EC Met- Lac* cells was higher in the presence of both EC Met- and ST Lac* but not in the presence of either single strain, demonstrating that MINI-Drop could identify higher-order interactions (Fig. 4b, p=0.0012, Table S3). In the pairwise network, EC Met- (CFP) and ST Lac* displayed bidirectional positive interactions, recapitulating the expected network topology (Fig. 3a, Fig. S5c,d). In addition, the cell counts of EC Met- and ST Lac* displayed a strong positive correlation consistent with a bidirectional positive interaction topology (Fig. S3d).
Figure 4. Investigating higher-order interactions using MINI-Drop.
(a) Schematic showing an example of a higher-order interaction. Droplets containing two strains X and Z or Y and Z do not exhibit interactions. In three-member droplets, a negative or positive interaction from X and Y to Z is present and is defined as a higher-order interaction. (b) Categorical scatter plots of the number of EC Met- Lac* cells in droplets containing the single strain EC Met- Lac* (self), pairs of strains including EC Met- Lac* and EC Met- or ST Lac* or all three strains (EC Met- Lac*, EC Met- and ST Lac*). Black horizontal bars denote the mean number of cells per droplet and error bars represent the bootstrapped 95% confidence interval for the mean. The horizontal bar (gray) represents a statistically significant difference in means based on the Mann-Whitney U test (p = 1.2e–3, n = 703, Table S3). (c) Schematic showing the higher-order inferred network for the data shown in panel (b). The line width represents the inferred strength of the higher-order interaction. Node size is proportional to the average cell count of each strain grown in isolation. (d) Categorical scatter plots of the number of EC WT cells in droplets containing the single strain EC WT, two strains including EC WT and ST Lac* or EC Met- or all three strains (EC WT, ST Lac* and EC Met-) in lactose minimal media. The horizontal bar (gray) represents a statistically significant difference in means based on the Mann-Whitney U test (p = 2.9e–10, n = 296, Table S3). (e) Schematic showing a higher-order interaction inferred using the data shown in (d). The line width represents the strength of the inferred higher-order interaction. Node size is proportional to the average cell count of each strain grown in isolation.
To investigate other higher-order interactions that were present in our data, we analyzed droplets containing a three-member consortium (EC WT, EC Met- and ST Lac), two-member sub-communities and single strains across four different environments (Fig. 3, Table S1, E3–E6). Our results illuminated a higher-order interaction in lactose minimal media (Table S1, E3, Table S3), where EC WT was significantly inhibited in the presence of both EC Met- and ST Lac*, while no negative interaction was observed in the pairwise interaction networks of EC WT co-cultured with EC Met- or ST Lac* (Fig. 3a, Fig. 4d,e). This higher-order interaction could be explained by enhanced growth of the mutualistic pair EC Met- and ST Lac*, which in turn negatively impacted the growth of EC WT. Higher-order interactions occurred in one of twelve possible cases (3 community members in 4 environments) in the EC Met-, EC WT, ST Lac* consortium (Table S1, E3–6, Table S3). In sum, our results show that MINI-Drop can elucidate higher-order interactions in microbial consortia and that higher-order interactions in this consortium were infrequent across different environmental conditions.
The sensitivity of the MINI-Drop method was evaluated based on number of droplets (replicates) required to infer microbial interactions of different strengths in experiments E1–E7 (Table S1). Specifically, we analyzed the relationship between interaction strength magnitude, number of replicates, and interaction significance (p<0.05) (Fig. S6). Our results showed that the significance of each interaction increased exponentially as a function of the number of droplets (Fig. S6a). The strength of the interaction was inversely related to the number of droplets required for statistical significance of the interaction. For example, strong interactions required as few as 15 replicates whereas weak interactions required more than 50 replicates in order to be detected (Fig. S6b).
Discrete-time Markov model of community assembly
A stochastic population dynamic model was constructed to understand community assembly from a small number of cells and the heterogeneity in community composition across droplets. In small microbial populations, stochastic variation in intracellular molecular concentrations can impact community assembly and functions (Boedicker et al., 2009; Connell et al., 2014; Hansen et al., 2016). To model community assembly in small populations, microbial growth can be represented as a probabilistic event, such that two communities seeded with the same initial strain composition exhibit different steady-state community compositions (Fig. 5a) (Horowitz et al., 2010). We investigated whether the model could be parameterized to recapitulate the cell count distributions in two and three strain droplets.
Figure 5. Discrete-time Markov model of cell growth modified by microbial interactions can recapitulate cell count distributions in microfluidic droplets.
(a) Schematic of variability in community assembly in small populations. Stochasticity in intracellular molecular concentrations can alter the strength of microbial interactions, generating different community states (high blue cells, low yellow cells or the reciprocal). (b) Schematic of the discrete-time Markov model of cell growth modified by microbial interactions. At each time step, each cell can undergo cell division, cell death or remain static according to the probabilities Pdiv, Pdeath or Pstatic, respectively. (c) Inferred network topology using MINI-Drop (left) for the EC WT, ST Lac* consortium in glucose minimal media (Table S1, E5). Scatter plot of experimentally measured cell counts (blue circles, n=257) of EC WT and ST Lac* or model steady-states (red circles, n=200). This bidirectional negative interaction network generated qualitatively different community compositions corresponding to (1) low and high EC WT and ST Lac*, respectively, (2) high EC WT and ST Lac*, (3) low EC WT and ST Lac*, (4) high EC WT and low ST Lac*. Fluorescence microscopy images (right) of a representative droplet in each community state 1–4 are shown (right). (d) Inferred network for the EC Met-, ST Lac* consortium (top) in lactose minimal media supplemented with methionine (Table S1, E4). Scatter plot of experimentally measured cell counts (blue circles, n=118) of EC Met- and ST Lac* or model steady-states (red circles, n=200). (e) Inferred interaction network for the EC Met-, ST Lac* consortium in lactose minimal media (top, Table S1, E3). Scatter plot of experimentally measured cell counts (blue circles, n=141) of EC Met- and ST Lac* or model steady-states (red circles, n=200). (f) Inferred interaction network for the sender, receiver consortium (top, Table S1, E2). Scatter plot of experimentally measured cell counts (blue circles, n=93) of the sender and receiver strains or model steady-states (red circles, n=200).
In the model, communities are seeded according to a Poisson distribution with λ=1.5. Seeded communities that do not contain both strains were discarded and resampled. At each time step, strain i can undergo cell division, death or remain static according to the probabilities Pdiv,i, Pdeath,i, and Pstatic,i, respectively (Fig. 5b). The cell death state can also represent a non-growing or dormant state for the duration of the experiment. The probabilities Pdiv,i, and Pstatic,i, are a function of the number of cells of each strain with parameters specific to each strain and the probability Pdeath,i, is a fixed parameter. Negative interactions with self or non-self are represented by inverted sigmoidal logistic functions, such that the probability of cell division is inversely related to the cell number. Positive interactions are represented as sigmoidal logistic functions, such that the probability of cell division increases as a function of the number of partner cells (see STAR Methods).
We tested whether this modeling framework could recapitulate the experimental cell count distributions, based on the assumption that the measurement time points represent model steady-states. Models were constructed using the positive or negative interaction functions and model parameters were identified to recapitulate the cell count distributions of each strain. We constructed a model for the EC WT, ST Lac* community grown in glucose minimal media that exhibited a bidirectional negative interaction network (Fig. 5c, left). Our results showed three clusters representing distinct community states exhibiting high abundance of one strain (Fig. 5c, center, clusters 1 and 4), coexistence of both strains (Fig. 5c, center, cluster 2), or low cell counts of both strains (Fig. 5c, center, cluster 3). Representative images of droplets from each cluster showed significant differences in community composition (Fig. 5c, right). A model of a bidirectional negative interaction network displaying strong and weak negative interactions was able to recapitulate the cell count distribution (Fig. 5c, middle, Table S4).
We evaluated whether the model could recapitulate the cell count distributions of networks with positive interactions. Models constructed for the EC Met-, ST Lac* consortium in two different environments exhibiting unidirectional or bidirectional positive interactions (Table S1, E3–4) could recapitulate the cell count distributions (Fig. 5d,e). Next, a model was developed for the quorum sensing regulated toxin consortium (Table S1, E2) that displayed a bidirectional negative interaction network. A model of strong and weak bidirectional negative interactions recapitulated the negative correlation in the cell counts of the sender and receiver strains (Fig. 5f). Our results demonstrate that bidirectional negative interaction networks can realize distinct community state distributions (Fig. 5c,f). In the model, the number of partner cells required to impact the probability of cell division dictates the strength of an interaction (Fig. 5f, Fig. S7a). The toxin mediated negative interaction in the quorum sensing regulated toxin consortium (Table S1, E2) exhibited a higher sensitivity to partner cell number than the negative interaction from ST Lac* to EC WT in glucose minimal media (Table S1, E5, Fig. S7a). Therefore, the recipients of the strong negative interactions displayed different sensitivities to variations in donor cell number, providing insight into the differences in the cell count distributions.
We next tested whether the model could capture the experimental cell count distributions in two and three-member droplets using a single parameter set. A model parameterized to the cell count distributions of the EC WT, EC Met- and ST Lac* consortium in glucose minimal media lacking supplemented methionine (Table S1, E5) recapitulated the experimental distributions in two and three-member droplets (Fig. S8). In sum, the model was able to describe the cell count distributions for positive and negative interactions mediated by distinct molecular mechanisms, illustrating that a probabilistic growth model can explain the heterogeneity in community states in small populations.
Investigating pairwise and higher order drug interactions on community assembly
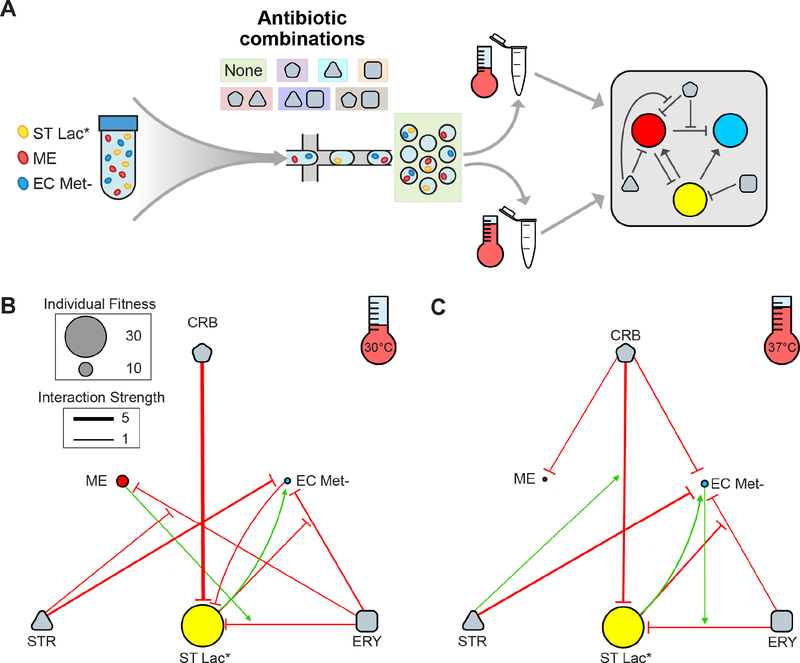
Antibiotic administration is a severe perturbation that alters community composition by reducing diversity in the human gut microbiome for a period of time before recovery (Palleja et al., 2018; Shaw et al., 2019). Synergistic or antagonistic interactions between different antibiotics can increase or reduce the effects of each single antibiotic on bacterial growth and viability. Previous work has investigated drug interactions on single bacterial strains but the effects of combinations of antibiotics on community assembly and interactions remains largely unknown (Kulesa et al., 2018; Tekin et al., 2018). Microbial interactions have been shown to be major variables shaping antibiotic tolerance in microbial communities (Adamowicz et al., 2018; Radlinski et al., 2017). We investigated whether MINI-Drop could elucidate the web of interactions linking antibiotic and species in a three-member microbial consortium consisting of EC Met-, ST Lac*, and RFP-labeled Methylobacterium extorquens (ME), a soil bacterium that can degrade methylamine to produce ammonia (Adamowicz et al., 2018). The effectiveness of antibiotics can vary with temperature (Cruz-Loya et al., 2019) and the growth of ME is inhibited by elevated temperatures (Attwood and Harder, 1972). Therefore, we sought to determine the effect of temperature on the interaction network.
The community was encapsulated in a modified Hypho medium (STAR Methods, Table S5) with all single and pairwise combinations of carbenicillin (CRB), streptomycin (STR), and erythromycin (ERY) at sub-lethal concentrations (Fig. S9a,b,c, Table S1, E8–21). The droplets in each condition were partitioned into two aliquots, incubated at 30°C or 37°C and then imaged following 36 or 18 hr, respectively, to account for slower growth kinetics at the lower incubation temperature (Fig. 6a). We inferred the interaction networks in each condition using the same analysis methods as the experiments described above (Fig. S10a,b). Due to the complexity of the system, we further analyzed the data to quantify various levels of interaction between combinations of antibiotics and species. Pairwise interactions between species (species-species) and each antibiotic and species (antibiotic-species) were determined by evaluating the ratio of the mean number of cells in the presence of a partner strain or antibiotic to the absence of these factors (Tables S6–8, Fig. 6b,c). Higher-order interactions were inferred by evaluating how antibiotic-species interactions changed in the presence of a second antibiotic or species (species-antibiotic-species or antibiotic-antibiotic-species) (Tables S6–8, Fig. 6b,c).
Figure 6. Combinatorial effects of antibiotics on community interactions and assembly.
(a) Overview schematic of the experimental design. A three-member community containing ST Lac*, ME, and EC Met- in modified Hypho medium was encapsulated with no antibiotics and with each individual and pairwise combination of carbenicillin (CRB), erythromycin (ERY), and streptomycin (STR). Droplets were incubated at 30°C or 37°C prior to imaging and inte raction network inference. (b) Inferred interaction network after incubation at 30°C for 36 hr. The edg e width is proportional to the log2 ratio of the average cell count between two conditions of interest (Tables S6–8). Only those edges with p<0.05 and log2 ratio magnitude greater than 0.5 are shown (all interactions are listed in Tables S7–8). Node size is proportional to the mean number of cells in single strain droplets in the absence of antibiotics. The arrows have a sign modifier based on the level of interaction as summarized in Table S6. For example, species-antibiotic-species interactions with a value greater than 1 are visualized as an inhibitory edge pointing to an inhibitory edge, with the net result being an increase in growth of the target species. This network representation was chosen such that each edge represents the ratio between two populations of droplets differing only by the presence of one variable (i.e. species or antibiotic) and is not meant to imply mechanisms of interaction. (c) Inferred interaction network after incubation at 37°C for 18 hr.
Our results showed that ST Lac* provided a substantial growth benefit to EC Met- at both temperatures, presumably due cross-feeding of methionine or missing intermediate(s) required to produce methionine. Notably, this positive interaction was preserved in the presence of ERY, eliminated with the addition of either STR or CRB and maintained in the presence of both ERY and CRB (Fig. S10a,b). Weak negative interactions were present in most cases where substantial growth of both species was detected, suggesting that growth correlated activities such as microbial competition or production of toxic compounds was a prevalent mode of interaction. At 30°C, the outgoing interaction from EC Met- to ME displayed a sign change from negative to positive with the addition of STR, demonstrating that the action of STR induced a growth benefit of ME in the presence of EC Met- (Fig. S10a).
For antibiotic-microbe interactions, STR primarily inhibited the growth of EC Met- without substantially suppressing the growth of ME or ST Lac* at both temperatures, mirroring the differences in susceptibility to STR in a larger population in microtiter plates (Fig. S9c). ERY weakly inhibited the growth of all three strains at 30°C, consistent with the microtiter plate experiment that showed reduced growth of all species in the presence of ERY (Fig. S9b). CRB strongly inhibited the growth of ST Lac* in both temperatures, but only substantially impacted the growth of EC Met- at 37°C, indicating that temp erature is a major variable influencing antibiotic susceptibility across different species (Fig. 6b,c).
We next examined how a second species impacted the interaction between an antibiotic and each community member (species-antibiotic-species interactions). The growth of EC Met- in the presence of ERY and ST Lac* was enhanced at both temperatures, suggesting that EC Met- was still able to benefit from the presence of ST Lac* despite inhibition of both strains by ERY (Fig. 6b,c, Fig. S10a,b). Notably, this positive interaction was not observed in the presence of CRB, but was observed in the presence of both ERY and CRB (Fig. S10a,b). The growth of ST Lac* in ERY was reduced in the presence of ME at 30°C or in the presence of EC Met- at 37°C, indicating that temperature is a critical parameter shaping microbial interaction networks (Fig. 6b,c). Notably, while inhibition of ST Lac* by ME at 30°C was maintained in the presence of ERY and was not detected in the presence of CRB, inhibition was detected in the presence of both CRB and ERY.
We examined how combinations of antibiotics influences the effects of single antibiotics on the growth of each species (antibiotic-antibiotic-species interactions). STR enhanced the growth of ME in the presence of ERY compared to ERY alone at 30°C, representing an antagonistic relationship between STR and ERY (Fig. 6b). By contrast, the growth inhibition of ST Lac* was further enhanced in the presence of both STR and CRB relative to CRB alone at 37°C, demonstrating a synergistic relationship between STR and CRB (Fig. 6c). Antagonism between STR and ERY and synergy between STR and ampicillin (same mechanism of action as CRB) have been previously reported for E. coli but here we observe similar antibiotic-antibiotic interactions in different bacterial species (Yeh et al., 2006).
The antibiotic-species and antibiotic-antibiotic-species interactions were inferred by comparing cell counts from different populations of droplets. As such, differences in environmental conditions could alter cell morphology or fluorescence and potentially contribute to variation in cell counts. For example, the cell morphology of ST Lac* and to a lesser extent EC Met- in droplets containing CRB were altered compared to the absence of CRB, which could impact the accuracy of the cell counting method (Fig. S9f) (Rolinson, 1980). Therefore, the magnitudes of these interactions should be considered as approximate. However, these data highlight a benefit of MINI-Drop, where a cell morphology change was detected in the presence of CRB that would have been overlooked by population-level measurements such as bulk fluorescence, selective plating, or sequencing-based methods.
To further understand how antibiotics impact community assembly, we evaluated the effects of antibiotics on species coexistence in three-member droplets (Fig. S9d,e). The presence of antibiotics globally reduced coexistence relative to the no antibiotic condition. In 30°C CRB conditions, coexistence was almost entirely eliminated due to its extreme impact on the growth of ST Lac* (Fig. 6b). Coexistence was lower in the presence of STR-CRB at 37°C relative to either STR or CRB alone, likely due to the synergistic impact of these antibiotics on growth inhibition of ST Lac* (Fig. 6c). Additionally, higher levels of coexistence were observed in all conditions containing CRB at 37°C compared to 30°C, potentially attributed to reduced inhibition of ST Lac* by CRB at 37°C.
DISCUSSION
We showed that MINI-Drop can rapidly infer pairwise as well as higher-order microbial interactions in two and three-member consortia in different environmental conditions compared to traditional methods to study microbial interaction networks (Friedman et al., 2017; Venturelli et al., 2018). While all of the examples in this work involved bacteria expressing fluorescent proteins, orthogonal fluorescent labeling of the bacterial outer membranes and proteins via click chemistry before encapsulation in droplets could be used to apply MINI-Drop to organisms that are not genetically tractable (Geva-Zatorsky et al., 2015; Hudak et al., 2017). In addition, droplets could be injected with fluorescent stains for metabolic activity, cell damage, nucleic acid content or reagents for biochemical assays to potentially distinguish different species and characterize single-cell phenotypes in a microbial community (Maurice and Turnbaugh, 2013). This method can be scaled to quantify interactions in higher-dimensional (>3 members) communities using compatible fluorescent labels or combinatorial fluorescent imaging of multiple reporters within the same cell. While the requirement for orthogonal fluorescent labels does limit the scalability of this approach, MINI-Drop provides the foundation for the development of imaging-independent techniques that could be applied to higher complexity communities.
In MINI-Drop, a single experiment generates hundreds to thousands of replicates of many sub-communities. The mean number of cells per drop following cell encapsulation can be manipulated to investigate the contribution of initial cell density to microbial interactions or increase the proportion of multi-strain droplets for interrogation of higher-order interactions. In the three-member consortia (Table S1, E3–6), strains with higher fitness in the absence of a partner tended to display outgoing negative interactions, whereas strains with lower fitness had the propensity for incoming positive interactions. Therefore, the competitive ability of the strain was an indicator of outgoing negative interactions, suggesting that the unexpected negative interactions (Fig. 3l) could be attributed to growth-coupled activities such as resource competition and/or metabolic waste by-product secretion. Future work could link MINI-Drop to fluorescent dye droplet barcoding to elucidate microbial interaction networks across a large number of environmental conditions in parallel (Hori et al., 2017; Kulesa et al., 2018; Miller et al., 2011). Using this droplet barcoding approach, interaction mechanisms could be inferred by screening candidate interaction-mediating molecules to identify conditions in which interactions are eliminated.
Previous methods of microbial interaction inference using modeling frameworks such as the generalized Lotka-Volterra (gLV) model are constrained by mathematical relationships (Momeni et al., 2017). For example, a gLV model of strong bidirectional positive interactions (mutualism) tends to be unstable, leading to potential underrepresentation of bidirectional positive interactions. Further, it is challenging to pinpoint if the failure of a pairwise gLV model to accurately fit experimental data is attributed to the presence of higher-order interactions or to unmodeled dynamics such as metabolites mediating the interactions. By contrast, MINI-Drop is not constrained to a defined mathematical framework and thus can readily identify higher-order interactions in the networks. We showed that MINI-Drop accurately inferred diverse interaction topologies including unidirectional positive, bidirectional positive or bidirectional negative networks. In addition to deciphering engineered interactions, MINI-Drop illuminated pairwise interactions as well as higher-order interactions that were not designed.
The throughput of the MINI-Drop method was enabled by coupling two automated and scalable technologies, droplet microfluidics and computational image analysis. The large number of sub-community replicates produced by MINI-Drop allows investigation of the contribution of initial conditions to the heterogeneity in community assembly in small populations. A probabilistic analysis of the distribution of community states provides insight into the stochastic forces shaping community behaviors. For example, we observed that bidirectional positive networks displayed frequent co-occurrence (Fig. 5e, Fig. S3, Fig. S4), whereas a bidirectional negative network can realize a set of distinct community states (Fig. 5c,e). The correlation structure between taxa in a microbial community is frequently used to identify potential interactions based on co-occurrence or co-exclusion patterns (Faust et al., 2012). Our results suggest that correlation structure may not illuminate negative interactions due to the potential for multiple community states. However, the mapping between correlation structure and interaction networks could differ at different population sizes and should be investigated.
Our stochastic growth model can recapitulate the heterogeneity in community states in two- and three-member consortia (Fig. 5, Fig. S8). This demonstrates that a simple probabilistic representation of cell growth, death and microbial interactions can give rise to multiple community steady-states from the same initial conditions. Our modeling framework could be used to predict the probability of strain growth as a function of the initial strain proportions and cell density. These parameters could be manipulated to maximize the likelihood of community member coexistence in multi-species consortia. Specific strains of bacteria have been shown to display positive density-dependent growth behavior referred to as an Allee effect wherein the per cell growth rate of the population is reduced in small populations (Kaul et al., 2016). We show that the model can exhibit an Allee effect and could be used to investigate key parameters influencing positive density-dependent growth behaviors in microbial populations (Fig. S7b–d). This phenomenon is unlikely to influence the heterogeneity in community states in our experiments due to the narrow range of initial cell counts and absence of cell adhesion. The Allee effect may play a larger role in community assembly for strains that display cell adhesion since the initial number of cells in each droplet could vary over a larger range.
We used MINI-Drop to elucidate a complex network of interactions between three bacterial species exposed to different combinations of antibiotics and varying temperature. This method demonstrated that antibiotics can significantly modify the species-species interaction network and species-species interactions in turn can modulate antibiotic tolerance (Fig. 6b,c). We identified cases of synergism and antagonism between antibiotics consistent with previous work (Yeh et al., 2006) and illuminated which combinations of antibiotic perturbations preserved or eliminated positive and negative interactions between species. In our experiments, the impact of temperature was particularly simple to assess because the population of droplets from each encapsulation could be partitioned and incubated at different temperatures. This further simplifies the application of MINI-Drop when considering environmental variables that are applied from a source external to the culture medium (e.g. gas composition, external radiation or light). The MINI-Drop method could be used to decipher significant interactions between strains and environmental parameters, which could inform the design of interventions to steer communities to desired states.
STAR METHODS
Lead Contact and Materials Availability
Further information and requests for reagents should be directed to and will be fulfilled by the lead contact, Ophelia S. Venturelli (venturelli@wisc.edu).
Materials Availability Statement
Plasmids and strains generated in this study (Table S9) are available upon request.
Experimental Model and Subject Details
General strain maintenance: Bacillus subtilis, Escherichia coli, Methylobacterium extorquens AM1, and Salmonella typhimurium LT2
All strains specified in Table S9 were maintained in 25% glycerol stocks prepared from cultures inoculated from single colonies and then stored at −80°C. Strains were recovered from glycerol stocks by inoculating liquid LB broth (Lennox, Sigma) or dilution streaking onto LB agar plates with appropriate antibiotics and culturing at 37°C, with the exception of Methylobacterium extorquens, which was streaked onto plates made with SOB Broth (Research Products International) and 15 g/L Bacteriological Agar (Bioworld) and cultured at 30°C. Precultures were inoculated either directly from glycerol stocks or from single colonies on dilution streaked plates.
Bacillus subtilis transformation
B. subtilis was inoculated into 1 mL MC medium (Loyo and Burton, 2018) and incubated for 4 hours at 37°C for transformation. Plasmid DNA was f irst linearized by treatment with ScaI restriction enzyme (New England Biolabs). Next, 200 ng of plasmid DNA was added to 200 ml cell culture and incubated for 2 hours at 37°C. Tr ansformed cells were selected by plating on LB plates containing 100 mg ml−1 spectinomycin (Gold Biotechnology). Plasmid pVP038 (Table S10) was transformed into B. subtilis 168, trpC2, cat to make B. subtilis 168, trpC2, cat, amyE::Pveg-gfp-spec (Table S9).
Escherichia coli cloning and transformation
PCR amplifications were performed using Phusion High-Fidelity DNA polymerase (New England Biolabs) and oligonucleotides for cloning were obtained from Integrated DNA Technologies. Standard cloning methods were used to construct plasmids. Plasmids were derived from a previously built construct library (Lee et al., 2011). Plasmids in Table S10 were transformed into strains as specified in Table S9.
Method Details
Bacterial cell culturing
For experiments E1–7 (Table S1), strains were grown for approximately 12 hours at 37°C in LB medium, diluted 1:50 into fresh LB medium, and then grown to an OD600 of 0.3–1 as measured on a 1 cm spectrophotometer (NanoDrop Thermo Fisher Scientific). Next, the culture (3 mL) was centrifuged for 2 min at 3,500 × g and supernatant was removed. The cells were washed 4X by resuspending the pellet in 0.5 mL of minimal media and centrifuged as described above. In experiment E1 (Table S1), cells were cultured in M9 supplemented with glucose (1X M9 salts, 2 mM MgSO4, 100 μM CaCl2, 0.4% glucose) and 25 g/mL chloramphenicol (Sigma). The cell cultures containing different strains were normalized to an OD600 of 0.15 and mixed in a 1:1 ratio. In experiment E2 (Table S1), B. subtilis and E. coli were mixed in a 2:1 volumetric ratio to account for differences in the cell number to OD ratios. Cells were cultured in LB media containing 50 ng/mL anhydrotetracycline (aTc, Cayman Chemicals), 0.1% arabinose (Sigma) and 25 g/mL chloramphenicol. In experiments E3–E7, cells were cultured in M9 media (1X M9 salts, 2 mM MgSO4, 100 μM CaCl2) supplemented with 0.4% glucose, 0.2% lactose and/or 200 μM methionine as indicated.
In experiments E8–21 (Table S1), a single colony of ME, ST Lac* and EC Met- (CFP) were each inoculated into modified Hypho media (Table S5) for 48 hr at 30°C with shaking. The OD600 was measured for each culture. Cultures were centrifuged for 2 minutes at 3,500 × g and resuspended in fresh modified Hypho medium to OD600 values of 0.20, 0.033, and 0.14 for ME, ST Lac* and EC Met-, respectively. These solutions were mixed in equal volume to form the community mixture. Immediately before cell encapsulation, antibiotic(s) (6 mg/mL carbenicillin disodium salt (Sigma), 10 mg/mL erythromycin (Sigma), and 2.5 mg/mL streptomycin sulfate salt (IBI Scientific)) were added to the community culture as specified and the culture was mixed by vortexing. All droplets for experiments E8–21 (Table S1) were encapsulated on the same day from the same community mixture to reduce variability across experiments.
Dynamic range of cell counting
The bacterial strains EC Met- (CFP), EC WT (RFP), and ST Lac* (YFP) were grown in LB medium to early stationary phase, centrifuged at 18,000×g for 1 min, decanted, and resuspended in M9 minimal medium without glucose. Next, the cells were centrifuged at 18,000 × g for 1 min, decanted and resuspended in a smaller volume of M9 minimal medium without glucose to concentrate the cells. The OD600 values of the concentrated EC Met-, EC WT and ST Lac* cultures were 14.4, 19.6, and 6.4, respectively. Equal volumes of each culture were combined to generate the mixed culture. The mixed culture was serially diluted by a factor of 2 until a dilution of 2−7 was reached. The diluted cultures were encapsulated separately using the droplet maker device and the resulting droplets were imaged and quantified using the computational image analysis pipeline.
Fabrication of microfluidic devices
Photoresist masters of 25 μm layer height were fabricated by spinning a layer of photoresist SU-8 3025 (Microchem) onto a silicon wafer (University Wafer), then baked at 95°C for 10 minutes. Following baking, photoresist master was patterned by UV photolithography over a photomask (Data S1, CADArt). The master was subjected to post-exposure bake at 95°C for 4 min and developed in fresh SU-8 developer (Microchem) for 6 min, prior to rinsing with isopropyl alcohol (Fischer Scientific) and baking at 150°C to remove the solvent. The microfluidic devices were fabricated by pouring poly(dimethylsiloxane) at a 11:1 polymer-to-crosslinker ratio (Dow Corning Sylgard 184) onto the master and curing at 65°C for 1 hr. The PDMS devices were excised with a scalpel and cored with a 0.75 mm biopsy core (World Precision Instruments) to create inlets and outlets. The device was then bonded to a microscope glass slide using an O2 plasma cleaner (Harrick Plasma), and channels were treated with Aquapel (PPG Industries) to render them hydrophobic. Finally, the devices were baked at 65°C for 20 min to evaporate excess Aquapel prior to use.
Encapsulation of cells into droplets and fluorescence microscopy
To encapsulate cells into droplets, 1 mL syringes (BD Luer Lok) were fitted with 27-gauge needles and PE/2 tubing. 500 μL of the culture was loaded into a 1 mL syringe. Fluorinated oil (3M Novec 7500) was prepared with 2% ionic Krytox 157 FSH surfactant (experiments E1–E6) (Dejournette et al., 2013) or 2% of a block copolymer of Jeffamine ED-900 and Krytox 157 FSH (experiments E7-E21) (Holtze et al., 2008) loaded into a 1 mL syringe. The free end of the tubing was primed and inserted into the droplet-making device. Droplets were generated using flow rates of 600 μL hr−1 oil and 300 μL hr−1 cell culture at a 30 μm × 25 μm junction, which generated ~40 μm diameter droplets at 4.8 kHz. After allowing at least 20 minutes for equilibration, droplets were collected into a 1.7 mL microfuge tube for at least 15 min and incubated as specified in each experiment. Droplets were loaded into chamber microscopy slides (Invitrogen C10228) and imaged with a 20X objective (Nikon, MRH10201) on a Ti-E Eclipse inverted microscope (Nikon). Fluorescence was imaged using the following filters (Chroma): (1) CFP: 436nm/20nm (ex), 480nm/40nm (em); (2) GFP: 470nm/40nm (ex), 525/50nm (em); (3) RFP: 560nm/40nm (ex), 630/70nm (em); and (4) YFP: 500nm/40nm (ex), 535nm/30nm (em).
Fluorescence microscopy image analysis
Custom code in Python was used for automated cell counting in droplets and microbial interaction network inference. Droplets were identified from the phase-contrast images using the Hough transformation algorithm (OpenCV 3, Pulli et al., 2012). Droplets with a diameter 10% larger or smaller than 40 μm were removed from the dataset. Fluorescent cells were segmented by identifying connected regions using the SimpleBlobDetector object (OpenCV 3, Pulli et al., 2012). Droplets were binned by the presence or absence of each fluorescently labeled strain. For experiments E1–7 (Table S1), interaction strength from strain j to strain i, where droplet d contains dk cells of strain k, was defined according to Equation 1.
| (1) |
For experiments E8–21, interaction strengths were calculated as described in the text and summarized in Tables S6–8. The impact of each species on each other species (species-species interaction) was inferred by comparing to the number of cells in single-species, no antibiotic droplets to two-species, no antibiotic droplets (6 possible interactions). The impact of each antibiotic on each species (antibiotic-species interaction) was inferred by comparing the number of cells in single-species, no antibiotic droplets to single-species, single-antibiotic droplets (9 possible interactions). The impact of each species on each antibiotic’s impact on each other species (species-antibiotic-species interaction) was inferred by comparing the number of cells in single-species, single-antibiotic droplets to two-species, single-antibiotic droplets (18 possible interactions). Finally, antibiotic-antibiotic-species interactions were inferred by comparing the number of cells in single-species, single antibiotic droplets to single-species, two-antibiotic droplets (9 possible interactions). Network schematics were drawn with Cytoscape 3.5 (Shannon et al., 2003).
Discrete-time Markov model of cell growth
A discrete-time Markov model was developed to recapitulate the experimentally measured cell count distributions. At each time step, the propagation of each strain is determined by computing the probability of cell division (Pdiv,i), cell death or cell growth dormancy for the duration of the experiment (Pdeath,i), and remaining unchanged (Pstatic,i) (Equations 2–4).
| (2) |
| (3) |
| (4) |
The parameter rdiv,io is the basal probability of cell division for strain i. The parameter rdeath,io represents the probability of cell death of strain i (constant). ni denotes the number of cells of strain I and sij defines whether the outgoing interaction of strain j (donor) to strain i is positive (sij = 1) or negative (sij = −1). The parameters kij and aij define the sigmoidal interaction function Iij, representing the incoming interaction for strain i produced by strain j (Equation 5)
| (5) |
The negative interaction function approaches zero as a function of nj whereas the positive interaction approaches (1 + aij)/aij as a function of nj. The values of aij and rdiv,i are constrained such that Pdiv,i ≤ 1 (Equation 6). The self-interaction function Iii(ni, sii, kii, aii) is less than one (sii = −1) and approaches zero as a function of ni leading to saturation of the number of cells of strain i. The interaction function Iij, is equal to 1 when nj = 0, representing the absence of an interaction between strain i and j. In the absence of an interaction between strain i and j, Pdiv,i is not dependent on strain j, (sij = −1,kij = 0, aij = 0). The outgoing interaction from the partner strain j, Iij(nj, sij, kij, aij), can be positive or negative depending on the value of the parameter sij. The parameters aij and kij determine the interaction sensitivity defined as the number of partner cells at the half-maximum of the interaction function, , (Equation 6), and the rate of change of the interaction as a function of the number of partner cells (Equation 7).
| (6) |
| (7) |
At each time step, the state transition of a cell is independent of all other cells and the cell’s prior history. The state transitions were simulated by sampling from a trinomial distribution determined by the probabilities Pdiv,I, Pdeath,I, and Pstatic,i. Communities were simulated for 100 time-steps wherein each time-step corresponded to 10.8 minutes of experimental time. Variables were constrained such that the cell populations reached a steady state within the simulation time. The initial conditions for the simulations were sampled from a Poisson distribution with λ=1.5. Communities that did not contain both strains were discarded and resampled. Model parameters are listed in Table S4.
Quantification and Statistical Analysis
All statistical analysis was performed using NumPy version 1.13.1 (van Der Walt, et al., 2011, Python 2 or 3 distributed through Anaconda). Statistical significance (p-value) between cell counts within droplets was computed using the two-sided Mann-Whitney U test. Error bars represent the 95% confidence interval of the mean.
Data and Code Availability
The droplet image analysis code and stochastic model are accessible on a GitHub repository at: https://github.com/ryanusahk/MINI-Drop-Supplementary-Code. The raw image files are available through Mendeley Data (doi10.17632/g5ch5r7d6m.1).
Supplementary Material
Data S1. Schematic of the Microfluidic Droplet Generation Device, Related to STAR Methods and Figure 1
Table S1. Strains and Media Conditions for Each Experiment, Related to Figures 2–4 and 6
Table S2. Interaction Magnitudes and Statistics for Experiments 1–7, Related to Figures 2 and 3
Table S3. Higher-order interaction calculations for Experiments 1–7, Related to Figure 4
Table S4. Stochastic model parameters, Related to STAR Methods and Figure 5
Table S4. Stochastic model parameters, Related to STAR Methods and Figure 5
Table S5. Modified Hypho Media Composition, Related to STAR Methods
Table S6. Types of Interactions in the Antibiotic Interaction Networks, Related to Figure 6
Table S7. Interactions from Antibiotics Experiments 8–14 (30°C), Related to Figure 6
Table S8. Interactions from Antibiotics Experiments 15–21 (37°C), Related to Figure 6
Table S9. Strains Used in this Work, Related to STAR Methods
Table S10. Plasmids Used to Generate Strains in Table S9, Related to STAR Methods
Table S11. Interaction Magnitudes and Statistics for Experiments 8–21, Related to Figures 6 and S10
Highlights.
Inference of microbial interaction networks in microfluidic droplets
Insight into synthetic microbial communities across different environments
Stochastic model of community assembly to study variability in community states
Elucidation of a complex web of interactions between antibiotics and a consortium
ACKNOWLEDGEMENTS
We would like to thank William Harcombe (University of Minnesota) for generously providing the E. coli Met- (CFP), S. typhimurium (YFP), and Methylobacterium extorquens (RFP) strains. We would like to thank Yu-Yu Cheng for assistance with construction of the engineered B. subtilis strain. We are grateful to Leland Hyman for assistance with droplet-microfluidics and Job Grant for synthesizing surfactants for droplet-microfluidics. This work was supported by the Army Research Office Young Investigator Award W911NF-17-1-0296. R.L.C. was supported in part by an NHGRI training grant to the Genomic Sciences Training Program (T32 HG002760).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Adamowicz EM, Flynn J, Hunter RC, and Harcombe WR (2018). Cross-feeding modulates antibiotic tolerance in bacterial communities. ISME J. 12, 2723–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwood MM, and Harder W (1972). A rapid and specific enrichment procedure for Hyphomicrobium spp. Antonie Van Leeuwenhoek 38, 369–377. [DOI] [PubMed] [Google Scholar]
- Bachmann H, Fischlechner M, Rabbers I, Barfa N, Branco dos Santos F, Molenaar D, and Teusink B (2013). Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci 110, 14302–14307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bairey E, Kelsic ED, and Kishony R (2016). High-order species interactions shape ecosystem diversity. Nat. Commun 7, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen RL, Pieterse CMJ, and Bakker PAHM (2012). The rhizosphere microbiome and plant health. Trends Plant Sci. 17, 478–486. [DOI] [PubMed] [Google Scholar]
- Billick I, and Case TJ (1994). Higher Order Interactions in Ecological Communities: What Are They and How Can They be Detected? Ecology 75, 1529–1543. [Google Scholar]
- Boedicker JQ, Vincent ME, and Ismagilov RF (2009). Microfluidic confinement of single cells of bacteria in small volumes initiates high-density behavior of quorum sensing and growth and reveals its variability. Angew. Chemie - Int. Ed 48, 5908–5911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Bronk B, Schaffer SA, Götz A, and Opitz M (2017). Effects of stochasticity and division of labor in toxin production on two-strain bacterial competition in Escherichia coli. PLoS Biol. 15, e2001457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao HT, Gibson TE, Bashan A, and Liu Y-Y (2017). Inferring human microbial dynamics from temporal metagenomics data: Pitfalls and lessons. BioEssays 39, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao X, Hamilton JJ, and Venturelli OS (2019). Understanding and Engineering Distributed Biochemical Pathways in Microbial Communities. Biochemistry 58, 94–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemente JC, Ursell LK, Parfrey LW, and Knight R (2012). The impact of the gut microbiota on human health: An integrative view. Cell 148, 1258–1270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connell JL, Kim J, Shear JB, Bard AJ, and Whiteley M (2014). Real-time monitoring of quorum sensing in 3D-printed bacterial aggregates using scanning electrochemical microscopy. Proc. Natl. Acad. Sci 111, 18255–18260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RS, Surette MG, and Elowitz MB (2007). Programming gene expression with combinatorial promoters. Mol. Syst. Biol 3, 145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cruz-Loya M, Kang TM, Lozano NA, Watanabe R, Tekin E, Damoiseaux R, Savage VM, and Yeh PJ (2019). Stressor interaction networks suggest antibiotic resistance co-opted from stress responses to temperature. ISME J. 13, 12–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dejournette CJ, Kim J, Medlen H, Li X, Vincent LJ, and Easley CJ (2013). Creating biocompatible oil-water interfaces without synthesis: Direct interactions between primary amines and carboxylated perfluorocarbon surfactants. Anal. Chem 85, 10556–10564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust K, Sathirapongsasuti JF, Izard J, Segata N, Gevers D, Raes J, and Huttenhower C (2012). Microbial co-occurrence relationships in the Human Microbiome. PLoS Comput. Biol 8, e1002606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher CK, and Mehta P (2014). Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. PLoS One 9, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Higgins LM, and Gore J (2017). Community structure follows simple assembly rules in microbial microcosms. Nat. Ecol. Evol 1, 0109. [DOI] [PubMed] [Google Scholar]
- Geva-Zatorsky N, Alvarez D, Hudak JE, Reading NC, Erturk-Hasdemir D, Dasgupta S, Von Andrian UH, and Kasper DL (2015). In vivo imaging and tracking of host-microbiota interactions via metabolic labeling of gut anaerobic bacteria. Nat. Med 21, 1091–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, and Boedicker JQ (2016). The Contribution of High-Order Metabolic Interactions to the Global Activity of a Four-Species Microbial Community. PLoS Comput. Biol 12, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo MT, Rotem A, Heyman JA, and Weitz DA (2012). Droplet microfluidics for high-throughput biological assays. Lab Chip 12, 2146–2155. [DOI] [PubMed] [Google Scholar]
- Hansen RH, Timm AC, Timm CM, Bible AN, Pelletier DA, Simpson ML, and Doktycz MJ (2016). Stochastic Assembly of Bacteria in Microwell Arrays Reveals the Importance of Confinement in Community Development. PLoS One 11, e0160135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harcombe W (2010). Novel cooperation experimentally evolved between species. Evolution (N. Y). 64, 2166–2172. [DOI] [PubMed] [Google Scholar]
- Harcombe WR, Betts A, Shapiro JW, and Marx CJ (2016). Adding biotic complexity alters the metabolic benefits of mutualism. Evolution 70, 1871–1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holtze C, Rowat AC, Agresti JJ, Hutchison JB, Angilè FE, Schmitz CHJ, Köster S, Duan H, Humphry KJ, Scanga RA, et al. (2008). Biocompatible surfactants for water-in-fluorocarbon emulsions. Lab Chip 8, 1632. [DOI] [PubMed] [Google Scholar]
- Hori Y, Kantak C, Murray RM, and Abate AR (2017). Cell-free extract based optimization of biomoleular circuits with droplet microfluidics. Lab Chip 17, 3037–3042. [DOI] [PubMed] [Google Scholar]
- Horowitz J, Normand MD, Corradini MG, and Peleg M (2010). Probabilistic model of microbial cell growth, division, and mortality. Appl. Environ. Microbiol 76, 230–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudak JE, Alvarez D, Skelly A, von Andrian UH, and Kasper DL (2017). Illuminating vital surface molecules of symbionts in health and disease. Nat. Microbiol 2, 17099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaul RB, Kramer AM, Dobbs FC, and Drake JM (2016). Experimental demonstration of an Allee effect in microbial populations. Biol. Lett 12, 20160070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khlebnikov A, Datsenko KA, Skaug T, Wanner BL, and Keasling JD (2001). Homogeneous expression of the PBADpromoter in Escherichia coli by constitutive expression of the low-affinity high-capacity araE transporter. Microbiology 147, 3241–3247. [DOI] [PubMed] [Google Scholar]
- Kong W, Meldgin DR, Collins JJ, and Lu T (2018). Designing microbial consortia with defined social interactions. Nat. Chem. Biol 14, 821–829. [DOI] [PubMed] [Google Scholar]
- Kulesa A, Kehe J, Hurtado JE, Tawde P, and Blainey PC (2018). Combinatorial drug discovery in nanoliter droplets. Proc. Natl. Acad. Sci 115, 6685–6690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T, Krupa R. a, Zhang F, Hajimorad M, Holtz WJ, Prasad N, Lee S, and Keasling JD (2011). BglBrick vectors and datasheets: A synthetic biology platform for gene expression. J. Biol. Eng 5, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu A, Archer AM, Biggs MB, and Papin JA (2017). Growth-altering microbial interactions are responsive to chemical context. PLoS One 12, e0164919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loyo CL, and Burton BM (2018). Quantitative Transformation Efficiency Assay for Bacillus subtilis. Bio-Protocol 8, e3109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurice CF, and Turnbaugh PJ (2013). Quantifying the metabolic activities of human-associated microbial communities across multiple ecological scales. FEMS Microbiol. Rev 37, 830–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller OJ, El A, Mangeat T, Baret J, Frenz L, El B, Mayot E, Samuels ML, Rooney EK, Dieu P, et al. (2011). High-resolution dose-response screening using droplet-based microfluidics. Proc. Natl. Acad. Sci 109, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Momeni B, Xie L, and Shou W (2017). Lotka-Volterra pairwise modeling fails to capture diverse pairwise microbial interactions. Elife 6, e25051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mounier J, Monnet C, Vallaeys T, Arditi R, Sarthou AS, Hélias A, and Irlinger F (2008). Microbial interactions within a cheese microbial community. Appl. Environ. Microbiol 74, 172–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palleja A, Mikkelsen KH, Forslund SK, Kashani A, Allin KH, Nielsen T, Hansen TH, Liang S, Feng Q, Zhang C, et al. (2018). Recovery of gut microbiota of healthy adults following antibiotic exposure. Nat. Microbiol 3, 1255–1265. [DOI] [PubMed] [Google Scholar]
- Park J, Kerner A, Burns MA, and Lin XN (2011). Microdroplet-enabled highly parallel co-cultivation of microbial communities. PLoS One 6, e17019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulli K, Baksheev A, Kornyakov K, and Eruhimov V (2012). Real-Time Computer Vision with OpenCV. Commun. ACM 55, 61–69. [Google Scholar]
- Radlinski L, Rowe SE, Kartchner LB, Maile R, Cairns A, Vitko NP, Gode CJ, Lachiewicz AM, Wolfgang C, and Conlon BP (2017). Pseudomonas aeruginosa exoproducts determine antibiotic efficacy against Staphylococcus aureus. PLOS Biol. 15, e2003981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolinson GN (1980). Effect of B-Lactam Antibiotics on Bacterial Cell Growth Rate. J. Gen. Microbiol 120, 317–323. [DOI] [PubMed] [Google Scholar]
- Sender R, Fuchs S, and Milo R (2016). Revised Estimates for the Number of Human and Bacteria Cells in the Body. PLoS Biol. 14, e1002533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon P, Markiel A, Ozier O, Baliga N, Wang J, Ramage D, Amin N, Schwikowki B, and Ideker T (2003). Cytoscape: A Software Environment for Integrated Models of Biomolecular Interaction Networks. Genome Res. 13, 2498–2504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw LP, Bassam H, Barnes CP, Walker AS, Klein N, Balloux F, and Shaw LP (2019). Modelling microbiome recovery after antibiotics using a stability landscape framework. ISME J Available Online March 15, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoodley P, Wilson S, Hall-Stoodley L, Boyle JD, Lappin-Scott HM, and Costerton JW (2001). Growth and Detachment of Cell Clusters from Mature Mixed-Species Biofilms. Appl. Environ. Microbiol 67, 5608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tekin E, White C, Kang TM, Singh N, Cruz-Loya M, Damoiseaux R, Savage VM, and Yeh PJ (2018). Prevalence and patterns of higher-order drug interactions in Escherichia coli. Npj Syst. Biol. Appl 4, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vega NM, and Gore J (2017). Stochastic assembly produces heterogeneous communities in the Caenorhabditis elegans intestine. PLoS Biol. 15, e2000633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venturelli OS, Egbert RG, and Arkin AP (2016). Towards Engineering Biological Systems in a Broader Context. J. Mol. Biol 428, 928–944. [DOI] [PubMed] [Google Scholar]
- Venturelli OS, Tei M, Bauer S, Chan LJG, Petzold CJ, and Arkin AP (2017). Programming mRNA decay to modulate synthetic circuit resource allocation. Nat. Commun 8, 15128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venturelli OS, Carr A, Fisher G, Hsu R, Lau R, Bowen BP, Hromada S, Northen T, and Arkin AP (2018). Deciphering microbial interactions in synthetic human gut microbiome communities. Mol. Syst. Biol 14, e8157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Walt S, Colbert SC, and Varoquaux G (2011). The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng 13, 22–30. [Google Scholar]
- Yeh P, Tschumi AI, and Kishony R (2006). Functional classification of drugs by properties of their pairwise interactions. Nat. Genet 38, 489–494. [DOI] [PubMed] [Google Scholar]
- Zhou J, Liu W, Deng Y, Jiang YH, Xue K, He Z, Van Nostrand JD, Wu L, Yang Y, and Wang A (2013). Stochastic assembly leads to alternative communities with distinct functions in a bioreactor microbial community. MBio 4, e00584–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Schematic of the Microfluidic Droplet Generation Device, Related to STAR Methods and Figure 1
Table S1. Strains and Media Conditions for Each Experiment, Related to Figures 2–4 and 6
Table S2. Interaction Magnitudes and Statistics for Experiments 1–7, Related to Figures 2 and 3
Table S3. Higher-order interaction calculations for Experiments 1–7, Related to Figure 4
Table S4. Stochastic model parameters, Related to STAR Methods and Figure 5
Table S4. Stochastic model parameters, Related to STAR Methods and Figure 5
Table S5. Modified Hypho Media Composition, Related to STAR Methods
Table S6. Types of Interactions in the Antibiotic Interaction Networks, Related to Figure 6
Table S7. Interactions from Antibiotics Experiments 8–14 (30°C), Related to Figure 6
Table S8. Interactions from Antibiotics Experiments 15–21 (37°C), Related to Figure 6
Table S9. Strains Used in this Work, Related to STAR Methods
Table S10. Plasmids Used to Generate Strains in Table S9, Related to STAR Methods
Table S11. Interaction Magnitudes and Statistics for Experiments 8–21, Related to Figures 6 and S10
Data Availability Statement
The droplet image analysis code and stochastic model are accessible on a GitHub repository at: https://github.com/ryanusahk/MINI-Drop-Supplementary-Code. The raw image files are available through Mendeley Data (doi10.17632/g5ch5r7d6m.1).