Significance
Networks provide useful models for many natural and manmade phenomena, such as transportation, financial, and social–ecological systems. This paper addresses network motifs as a mechanism for understanding resilience of such networks. The significance of this work can be viewed through an important example—namely, power-grid networks, constituting a core component of modern critical infrastructures. While most existing approaches focus on the analysis of global network characteristics, recent studies suggest that resilience of power grids may also be intrinsically connected to higher-order geometric features such as network motifs. Here, a systematic data-driven approach is developed that sheds light on the role of local topology and geometry in vulnerability of power grids and other complex networks.
Keywords: complex networks, network resilience, multivariate reliability, network motifs, data depth
Abstract
Network motifs are often called the building blocks of networks. Analysis of motifs has been found to be an indispensable tool for understanding local network structure, in contrast to measures based on node degree distribution and its functions that primarily address a global network topology. As a result, networks that are similar in terms of global topological properties may differ noticeably at a local level. This phenomenon of the impact of local structure has been recently documented in network fragility analysis and classification. At the same time, many studies of networks still tend to focus on global topological measures, often failing to unveil hidden mechanisms behind vulnerability of real networks and their dynamic response to malfunctions. In this paper, a study of motif-based analysis of network resilience and reliability under various types of intentional attacks is presented, with the goal of shedding light on local dynamics and vulnerability of networks. These methods are demonstrated on electricity transmission networks of 4 European countries, and the results are compared with commonly used resilience and reliability measures.
The past 2 decades have seen increasing interest in the application of tools developed in the interdisciplinary field of network analysis to improve our understanding of complex systems and critical infrastructures—e.g., transportation systems, power grids, food supplies, financial systems, and ecosystems.
Such complex systems are vulnerable to failure from various causes, including natural disasters, aging, and intentional attacks such as terrorism. Furthermore, these systems are intrinsically interdependent; as a result, failure of 1 system can lead to a catastrophic cascade of failures. Therefore, to minimize the risk of failure, the quantification of resilience and reliability is critically important and is of increasing concern in the analysis of a broad range of complex systems.
Most available approaches for assessing network resilience explore global topological characteristics—e.g., node degree distribution, mean degree, small-world properties, and, to a lesser extent, betweenness centrality (BC) measures—that is, primarily lower-order connectivity features that are investigated at the level of individual nodes and edges (1–5). However, many studies show that higher-order network features, or network motifs, play a fundamental role in understanding the organization, functionality, and hidden mechanisms behind many complex systems, from brain connections to protein–protein interactions to transportation congestion (6–10). Furthermore, recent studies of power system reliability indices and stability estimation suggest that robustness of the power grid is also intrinsically connected to network motifs (11, 12). The existence of motifs in a complex network are not by chance or random, and motifs tend to perform important functions (13). A recent study (14) shows how motifs throughout a complex network work together and coordinate their collective functions.
The existing methods for computing reliability of a network—e.g., reliability polynomials, network signatures, and survival signatures—assume that each network component (e.g., node or edge) works independently with a certain known reliability (15–18). Among them, some methods—e.g., network signatures—are based on the assumption that under random failures, component lifetimes are independent and identically distributed (i.i.d.) random variables (19–21). However, in real-world complex networks, the component lifetimes are not independent and, in most cases, are unknown. Another shortcoming of these methods is that they primarily consider random failures and do not address component failures from targeted attacks.
In this paper, we introduce a number of concepts to incorporate local higher-order structures into resilience and reliability analysis of complex networks that overcome some of the above-mentioned caveats of the existing methods. We start from emphasizing that the notion of network robustness is not uniquely defined, and an objective validation of vulnerability might require some ground-truth data on network behavior under attacks and failures, which are typically unavailable in many real-world scenarios due to, for example, data privacy and confidentiality. Nevertheless, we argue that a system’s resilience and robustness can be quantified in terms of its ability to maintain its original properties. In this paper, we assess how long a network can preserve its geometry; in turn, motifs offer an intrinsic description of network geometric properties. First, we present a motif-based analysis of network resilience under different intentional attack strategies. The previous methods in this area measure network resilience on the basis of some global network properties—e.g., the largest connected component, the average shortage path length (APL), diameter (D), etc.—and tend to ignore the local robustness of a network. We propose a motif-based performance measure, motif concentration, which represents local robustness of a network rather than measuring the global network characteristics. In particular, we analyze network motif dynamics under 2 intentional attack strategies—namely, attacked nodes are selected based on degree centrality and BC.
Second, to evaluate network reliability, we considered higher-order network features—i.e., motifs—as the components of a network. To illustrate these ideas, we considered power-grid networks as a case study, although the techniques described here can be applied to complex networks more generally. In the evaluated power-grid networks, we observed 6 types of 4-node connected motifs. We used these 6 types of 4-node connected motifs as the components of a network system, assuming that the reliability of the entire network depends on the lifetime of these 6 components. We evaluated the component (motif) lifetimes under failures from specific targeted attacks and combined them to obtain the reliability of the entire network. Here, we did not assume that the lifetimes of components are i.i.d., which overcomes limitations of the above-listed methods. Furthermore, the currently available approaches for assessing network robustness combine component reliability on the basis of either the minimal cut set, a minimal component set whose failure assures network failure, or the minimal path set (17, 21). However, these coefficients depend only on network design; therefore, finding them is computationally expensive for reasonable size networks.
Third, we introduce a nonparametric data depth approach to study characteristics of the multivariate motif concentrations and motif lifetimes distribution. We also compare multivariate concentration distributions of different networks using simple and easily interpretable 1- or 2-dimensional plots.
Finally, we present results of motif-based resilience and reliability analysis of 4 European power-grid networks. We also compare the results of our method with the results from existing techniques. We find that local motif-based properties as well as reliability of fragile and robust networks noticeably differ in terms of their sensitivity to the type of attack. These findings suggest that motifs can be useful metrics to characterize a level of network resilience to various types of attacks and that certain motifs can potentially serve as early warning indicators of system failure.
Graph Representation of Networks
We consider an undirected graph as a model of a complex network. Here, is a set of nodes, and is a set of edges. The order and size of are defined as the number of nodes and edges in —i.e., and , respectively. We assume that if an edge , then . A graph is connected if there exists a path from any node to any other node in . The distance is defined as the minimum path length from to in . The degree of a node is the number of edges incident to .
A graph is a subgraph of , if and . If is a subgraph of and contains all edges such that , then is called an induced subgraph of . Two graphs, and , are called isomorphic if there exists a bijection such that any 2 nodes and of are adjacent in if and only if and are adjacent in .
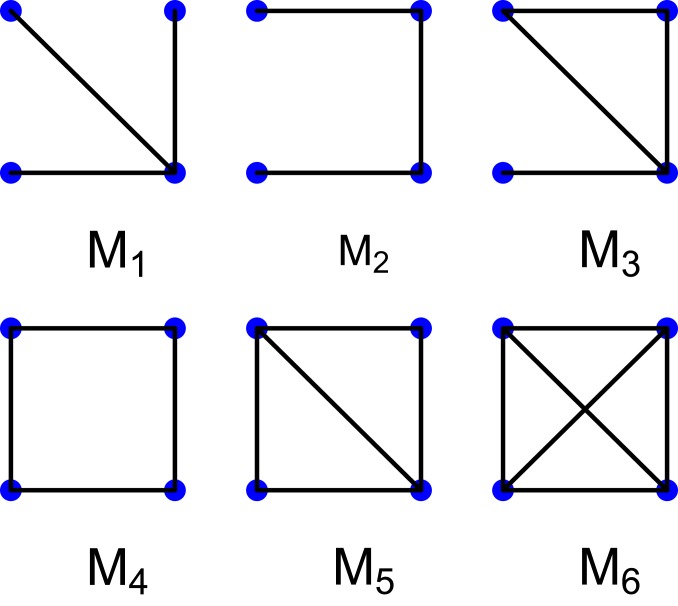
Analysis of higher-order structures of , or multiple-node subgraphs, provides invaluable insights into network functionality and organization beyond the trivial scale of individual nodes and edges. A motif here is broadly defined as a recurrent multinode subgraph pattern. Network motifs were introduced by ref. 6 in conjunction with the assessment of stability of biological networks and later have been studied in a variety of contexts (see the review in ref. 8). Formally, a motif is an -node subgraph of , where is .* If there exists an isomorphism between and , , we say that there exists an occurrence, or embedding of in . Fig. 1 shows all connected 4-node motifs. Throughout our study, we consider motifs which are induced subgraphs.
Fig. 1.
All connected 4-node network motifs.
Resilience and Reliability of Complex Networks
While there exists no unique definition, network resilience is broadly understood as the tolerance to errors or perturbations, which measures the ability of a network to maintain its functions under component failures from random errors or external causes. Resilience metrics of a network are typically topology-based measures—e.g., giant component, degree distribution, APL, D, clustering coefficient (CC), BC, etc. (4, 22, 23). Lower APL and higher CC are typically considered indicators of the small-world-ness property and are sometimes associated with higher resilience (3, 24). Networks with higher BC nodes tend to be more vulnerable to intentional attacks, but tend to exhibit higher robustness to random failures. This phenomenon is also typically valid for networks with high degree centrality (25, 26).
Furthermore, in the case of power-grid networks, refs. 27 and 28 propose an empirical robustness criterion, hypothesizing that a higher deviation of a degree distribution from the Poisson distribution tends to imply higher fragility of a power grid. In particular, the cumulative degree of a power-grid network is assumed to follow an exponential distribution , where is a normalization constant, is the node degree, and is a characteristic parameter. According to refs. 27 and 28, a power grid is considered to be robust if and fragile if .
In examining robustness to failures, the aim is to evaluate how a network behaves when a fraction of random or selective nodes are removed. In failure simulation, if the node to be removed at each step is selected at random, then the result is called a random failure. Random failures are considered to be errors, mainly due to component failures, errors in operations, storms, and other natural disasters. In the case of intentional attacks, the targeted node(s) to be removed at each iteration is selected based on its importance. For instance, if the nodes are selected in the decreasing order of their degree or BC, the resulting attack is called a degree-based attack or betweenness-based attack, respectively. In both random failures and targeted attacks, the nodes are removed until some stopping criterion is achieved—e.g., a predefined fraction of nodes removed. The current methods of measuring resilience and robustness under failures are predominantly based on global network properties. In these techniques, vulnerability under failure is commonly determined on the basis of the remaining connectivity, largest connected component, APL, etc., after a fraction of nodes have been removed (29). To investigate vulnerability properties at a local level, we present 3 motif-based methods: motif concentration, network reliability under a system-components framework, and nonparametric multivariate network lifetimes based on data depth.
Motif Concentration.
The typical resilience metrics described above are all global network characteristics and do not consider local higher-order structures. Analysis of higher-order network structures or motifs gives important insights into network functionality and organization beyond the global metrics. For instance, we can calculate the concentration () of an -node motif of type as the ratio of its number of occurrences () to the total number of -node motifs in the network—i.e., , where is the total number of -node motifs. Remarkably, in their studies of European power-grid networks, Rosas-Casals and Corominas-Murtra (28) find that power-system fragility seems to increase as the elements of the grid become more interconnected and the number of -node subgraph patterns such as stars begins to increase. More recently, ref. 30, which studies the impact of removing transmission lines with a high BC, suggests that fewer connections imply higher security. Therefore, we can say that there likely exists some functional nonlinear interaction among low connectivity, detour motifs (i.e., cycles) (12), and network resilience.
In this study, we introduce a motif-based performance measure, where we focus on remaining motif distributions, particularly, the decaying rate of a specific motif concentration, under targeted attacks and random failures. Algorithm 1 outlines how motif concentrations are calculated under a node-centrality-based attack. The method is the same for betweenness-based attacks, except that sorting of nodes is performed in terms of descending order of node BC.
Algorithm 1:
Attack Tolerance of Networks
| Input: Network . |
| Output: Motif concentrations under attacks. |
| 1: : the number of occurrences of -node motifs of type in , , where is the number of distinct -node motifs |
| 2: Concentration, |
| 3: -degree centrality of node . Calculate |
| 4: sorted by (descending) |
| 5: for to do |
| 6: |
| 7: |
| 8: Count for |
| 9: Calculate concentrations |
| 10: end for |
By considering motif concentration as a measure of resilience, we emphasize the response of a power grid to hazardous scenarios at a local level. Furthermore, commonly used performance measures—e.g., network connectivity and giant component—are affected by network order (31, 32), which obstructs direct comparison of multiple networks of different orders. One way to control for this confounding factor is to normalize the performance measures by their initial values. In contrast, the proposed measure, motif concentration, is a standardized metric which does not require extra normalization.
Network Reliability.
In many applications, from telecommunications to finance to power grids, it is often of interest to study a network’s resilience in terms of its lifetime distribution or reliability—i.e., how long the network system performs or operates effectively its intended functions. Most of the current methods for network reliability—e.g., reliability polynomials, and network signatures—assume that component (node/edge) lifetimes are known (16, 17, 20, 21). However, in real-world settings, especially under targeted attacks, node and edge lifetimes are not known. Here, we focus on 4-node motifs and their dynamics under failures and attacks as an alternative network-vulnerability indicator. In particular, we view each of the 4-node motifs—i.e., , , , , , and —as a component of a network since the lifetime of each 4-node motif affects the entire network reliability. [The proposed methodology is applicable to -node motifs; however, due to challenges in motif estimation (8), current studies are limited to at most 4-node motifs.) We evaluate the reliabilities of the motifs , , under a given attack strategy, and combine them to obtain a measure of the entire network’s reliability. Under a targeted attack, let be the event that a motif , , survives till time , where time refers to the number of attacks. Then, the survival/reliability function of can be written as , where is a nonnegative random variable representing the lifetimes—i.e., waiting time until the death of individual motifs in —and is the cumulative distribution function of , (33).
The reliability function can be modeled with various parametric and nonparametric methods (for an overview, see, e.g., refs. 34 and 35). For example, if the risks of failure for all motifs are equal and do not change with time, we can estimate the reliability function with the exponential model. That is, we assume that lifetimes follow an exponential distribution with parameter —i.e., Exponential (), . The reliability function of the motif can be written as . The mean lifetimes for motif under the exponential model is . In our study, to determine component (motif) lifetimes under different attack strategies, we employ a survival analysis technique in the epidemiological sense. Algorithm 1 counts the number of remaining motifs at each time in a degree-based attack. We can extend Algorithm 1 to count the number of motif deaths at time as . The lifetimes of motifs are then considered to be —i.e., . After determining lifetimes , we fit the reliability function and mean lifetimes of each motif using a suitable model as described above.
The rationale behind our approach is based on 2 interrelated hypotheses. First, we assume that the network fails if all -node motifs fail (i.e., disappear). Second, we say that the network is more robust if it tends to preserve longer its original geometric structure under random failures and attacks. In turn, network motifs can be used as 1 of the characterizations of a network geometry and hence as a characterization of network resilience. The next question is then how to integrate information from multiple -node motifs.
We can combine individual motif reliabilities under the system-components framework to obtain the reliability of the entire network, where the entire network is considered as a parallel system and motifs as its components (36). A parallel system continues to operate as long as at least 1 of its components continues to function. We can define the reliability function of the entire network as
| [1] |
where is the lifetime of the entire network. If the lifetimes of the 6 types of motifs are mutually independent, the network-reliability function becomes , where , . However, in practice, lifetimes of the 4-node network motifs may not necessarily be mutually independent, since motifs may share the same edges, and when a particular type of motif fails, it can affect the lifetimes of other motifs. Network components—i.e., 6 motif concentrations or 6 motif lifetimes—can be modeled with some appropriate multivariate distributions. In this paper, we introduce a nonparametric data-depth approach to study the characteristics of the multivariate distribution of the motif lives. Although nonparametric data depth-based tools are widely used in multivariate and functional data analysis—e.g., for visualization, clustering, and anomaly detection—data depth yet remains an unexplored concept in reliability analysis.
A data depth is a function with range that measures how deep or central an observed point , , is relative to a certain finite data cloud , or with respect to , a probability distribution in . For instance, in our case, can correspond to motif lifetimes . One commonly used data depth is a Mahalanobis (MhD) depth (37, 38). The MhD depth of with respect to a set is
where and are, respectively, the (sample) mean vector and covariance matrix of . There are a number of depth functions; for a comprehensive list, one may refer to refs. 37–39. Using a specific depth function, we can compute the depths of all sample points in the data cloud . A higher depth value implies a more central with respect to .
We can compare 2 multivariate distributions (e.g., and , in ) with their depth versus depth plot, which is commonly known as a DD plot. The 2-dimensional DD plot will be very close to a line if the 2 distributions are identical. Deviation from a line suggests that there are differences between the distributions either in location, skewness, scale, kurtosis, or other aspects. The -th central region is defined as the smallest region enclosed by the depth contours to accumulate probability . A sample estimate of is the convex hull that contains the deepest points. The volume of is a sample estimate of the volume of :
| [2] |
where if is an integer, and otherwise is rounded up to an integer. The plot of versus displays how the volume of the central region expands as increases and is referred to as the scale curve. If the scale curve of the multivariate distribution is constantly above that of the multivariate distribution , then is more dispersed and of larger scale than (37). The scale of 2 multivariate distributions can also be compared with a data-depth-based multivariate Wilcoxon rank sum test described in refs. 39 and 40.
We can compare multivariate motif concentration or lifetime distributions of networks, under a specific attack strategy, on the basis of data-depth techniques—i.e., the DD plot, scale curve, and data-depth-based scale test. Another technique for assessing network reliability for dependent components could be a square-root model (41) in a system-components framework, where in Eq. 1 is approximated by the geometric mean of its upper and lower bounds. The square-root model is a simple heuristic bounding technique that can be used to evaluate common-cause system failures when the components are dependent (36).
Case Study on Robustness of European Power-Grid Networks
We illustrate the utility of the proposed methodology in assessing the fragility of electricity transmission networks of 4 European countries—i.e., Germany, Italy, France, and Spain. The data were obtained from the Union for the Coordination of the Transmission of Electricity. Network nodes correspond to power stations/substations, and edges represent physical transmission lines connecting 2 nodes. Maps of the 4 power-grid networks, along with the information on numbers of nodes and edges, are shown in SI Appendix. SI Appendix, Table S2 presents global topological properties for the 4 power grids, and SI Appendix, Fig. S2 compares their degree distributions.
We studied the resilience of the 4 European networks under degree-based targeted attacks on the basis of 1 commonly used performance measure, the size of the giant component, and we compared the results with our proposed performance measures. SI Appendix, Fig. S3 shows the normalized giant component, after a fraction of nodes have failed. We found that the giant components in the French and Spanish networks disappeared more quickly as nodes were removed than did the giant components of the German and Italian networks. The Italian power grid exhibited the highest degree of robustness.
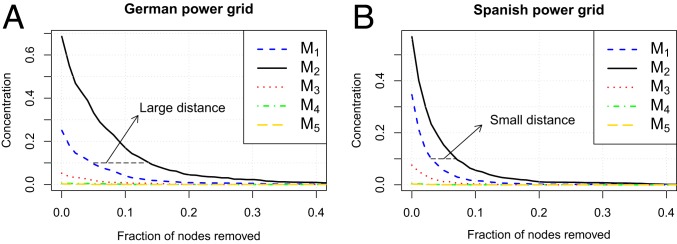
In the 4 European power-grid networks, we only observed 5 types of 4-node connected motifs: , , , , and . Thus, we considered these 5 types of 4-node connected motifs as the components of the power-grid networks. Fig. 2 and SI Appendix, Figs. S4 and S5 show the remaining motif concentrations of the 4 European power grids, after a fraction of nodes have been removed by degree- and betweenness-based attacks. We found that under both types of attacks, motif concentrations in the French and Spanish networks disappeared more quickly as the fraction of nodes were removed, than did the motifs of the German and Italian networks. Furthermore, there was a marked distance among motif concentration curves in the German and Italian networks, whereas the gap between the curves in the French and Spanish networks was narrower. This also suggests that the motif vanishing rates for the German and Italian power grids are slower than for the French and Spanish power grids.
Fig. 2.
Dynamics of 4-node motif concentrations under degree based attack. (A) German power grid. (B) Spanish power grid.
Instead of comparing their motif concentrations under attacks, we can more systematically compare networks in terms of their lifetime distributions. We estimate a reliability function for motif with the exponential model, where the lifetimes are assumed to follow an exponential distribution with constant hazard rate , . SI Appendix, Table S3 lists the estimated mean lifetimes of the 5 motifs. We found that under both degree- and betweenness-based targeted attacks, the mean motif lifetimes for the German and Italian networks were considerably greater than the mean motif lifetimes for the French and Spanish networks. Again, we assume that the motif lifetimes follow exponential distributions with parameters , . We assessed goodness of fit of exponential models for each motif in all 4 networks. We found that for all motifs in all 4 networks, the exponential model appropriately represented the motif lifetime data (see, e.g., SI Appendix, Fig. S6).
Since there are unknown and generally unstructured dependencies among the 5 motif lives, concentrations, or lifetimes, a more flexible data-driven approach to studying their lives is to use a 5-dimensional multivariate distribution. We computed different features of the multivariate concentration distribution of a power grid and compared them with multivariate concentration distributions of other power grids, on the basis of different data-depth techniques—e.g., the DD plot, scale curve, scale test, etc.—as described earlier.
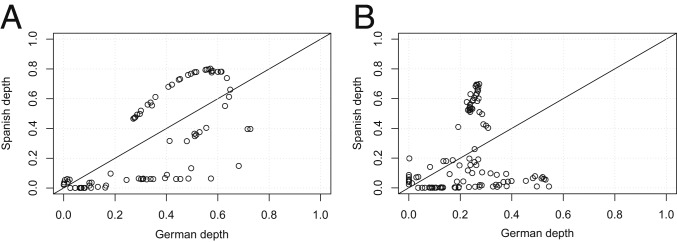
We first considered the pairwise DD plots, for both degree- and betweenness-based attacks, in Fig. 3 and in SI Appendix, Fig. S7, which clearly indicate a location difference in the German and Spanish power-grid concentration distributions, and also in the French and Italian distributions. The concentration distributions of the German and Italian power grids look similar, as do the French and Spanish power grids. Though in our study, we used the MhD depth function, other depth functions—e.g., projection depth, spatial depth, etc.—yield similar conclusions.
Fig. 3.
Comparisons of 2 European power-grid multivariate concentrations. (A) DD plot, degree-based attack. (B) DD plot, betweenness-based attack.
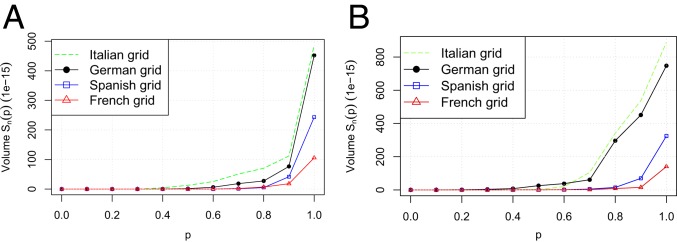
Second, we evaluated the scales of the 4 concentration distributions using Fig. 4. The scale curve of the Italian grid lies consistently above those of the other grids, and the Spanish and French grid scale curves are consistently below the Italian and German grid scale curves. This implies that the concentration distributions of the Italian and German power grids have larger scales than those of the Spanish and French power grids. For example, Table 1 lists the volume of the convex region, , amassing 80 central probability. We found that the volumes for the German and Italian grids were significantly larger than those of the Spanish and French grids. That is, the observations in the Spanish and French grid-concentration distributions are clustered tightly around their respective centers, while the observations in the Italian and German power grids’ concentration distributions are scattered at outlying positions.
Fig. 4.
Comparisons of the European power-grid multivariate concentrations. (A) Scale curve, degree-based attack. (B) Scale curve, betweenness-based attack.
Table 1.
Scale/dispersion (1e-15) of the 4 power-grid concentration distributions, under degree- and betweenness-based attacks
| Network | (degree-based) | (betweenness-based) |
| Italian grid | 70.31 | 341.19 |
| German grid | 27.45 | 296.32 |
| Spanish grid | 4.95 | 14.82 |
| French grid | 6.91 | 8.48 |
Finally, Table 2 summarizes the tests for scale differences of 4 power-grid concentration distributions. We see that the Italian and German power grids have higher scales than the Spanish and French grids. We also find that there is no scale difference between the Italian and German grids, or between the Spanish and French grids. From the test results and the scale curves in Fig. 4, we can conclude that under both degree- and betweenness-based targeted attacks, the Italian and German power grids survive longer than the Spanish and French grids. The data-depth-based results support our previous findings based on concentrations in Fig. 2. We also evaluated reliability of a network under the framework of a parallel system with dependent components (SI Appendix, Fig. S8). We found that under degree-based attacks, the Italian power grid exhibited the highest resilience, followed by the German grid. However, under betweenness-based attacks, the German power grid showed the highest resilience, followed by the Italian power grid. In both cases, the French and Spanish power grids showed the least resilience, since their survival probabilities rapidly decayed under attacks.
Table 2.
Multivariate Wilcoxon rank sum test for dispersion of 4 power-grid concentration distributions, under degree- and betweenness-based attacks
| Ho: Scale (grid i) = scale (grid j) | P (degree) | P (betweenness) |
| Ha: Scale (Italian grid) > scale (Spanish grid) | 0.01 | 0.01 |
| Ha: Scale (Italian grid) > scale (French grid) | 0.01 | 0.01 |
| Ha: Scale (German grid) > scale (Spanish grid) | 0.01 | 0.01 |
| Ha: Scale (German grid) > scale (French grid) | 0.01 | 0.01 |
| Ha: Scale (German grid) scale (Italian grid) | 0.15 | 0.62 |
| Ha: Scale (French grid) scale (Spanish grid) | 0.94 | 0.60 |
Note that the global performance measure—i.e., giant component (SI Appendix, Fig. S3) —categorized the Italian power grid as robust and tended to yield somewhat inconclusive results on the German power grid. In turn, all of the motif-based performance measures showed that both the Italian and German power grids are comparatively more robust than the French and Spanish power grids, which supports the results described in ref. 28. Analyses for other types of attack strategies were omitted for the sake of brevity, but they gave similar conclusions. (For a detailed study of all attack strategies, see ref. 42.)
Conclusion and Discussion
Assessing vulnerability of complex networks is a rapidly evolving research area, with applications ranging from brain connectome to the ecosystem of cryptocurrencies to power grids. Increasingly more studies in a broad range of disciplines involving complex networks indicate that network robustness appears to be intrinsically linked to network local geometrical properties. We have proposed a method to assess and classify fragility of complex networks based on the analysis of local network geometry—namely, network motifs. Motifs can be viewed as building blocks of a network and have received increasing attention in complex network analysis. Indeed, even basic -node motifs have been proven to unravel hidden mechanisms behind the functionality of various complex systems; however, to our knowledge, there are no previous studies assessing the relationship between motifs and system robustness. To integrate information from multiple motifs and their roles in network resilience, we have introduced a nonparametric data-depth approach to simultaneously evaluate different characteristics of the multivariate distributions of motif lives. As a case study, we have illustrated the utility of the method in application to resilience analysis of 4 European power-grid networks under targeted attacks. We have found that power systems exhibit different degrees of local sensitivity and degradation with respect to the type of attack and the type of motif. Hence, motif characteristics, such as motif concentrations, can be potentially used as alternative local metrics of network resilience, both in power grids and more generally in complex networks, as well as early warning indicators of system degradation and failure.
Supplementary Material
Acknowledgments
H.V.P. has been partially supported by NSF Grants DMS 1736417, CNS 1702808, and ECCS 1824710; and Y.R.G. has been partially supported by NSF Grants DMS 1736368, IIS 1633331, and ECCS 1824716. We thank Cuneyt Akcora, Murat Kantarcioglu, and Nozer Singpurwalla for motivating discussions on network reliability.
Footnotes
The authors declare no conflict of interest.
*Originally, motifs were defined as subgraphs that occur more or less frequently than expected by chance (6). However, nowadays motifs are typically defined more broadly as any -node subgraphs (8).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1819529116/-/DCSupplemental.
References
- 1.Albert R., Jeong H., Barabási A.-L., Error and attack tolerance of complex networks. Nature 406, 378–382 (2000). [DOI] [PubMed] [Google Scholar]
- 2.Schneider C. M., Moreira A. A., Andrade J. S., Havlin S., Herrmann H. J., Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. U.S.A. 108, 3838–3841 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pagani G. A., Aiello M., The power grid as a complex network: A survey. Physica A 392, 2688–2700 (2013). [Google Scholar]
- 4.Cuadra L., Salcedo-Sanz S., Del Ser J., Jiménez-Fernández S., Geem Z. W., A critical review of robustness in power grids using complex networks concepts. Energies 8, 9211–9265 (2015). [Google Scholar]
- 5.Rohden M., Jung D., Tamrakar S., Kettemann S., Cascading failures in AC electricity grids. Phys. Rev. E 93, 032209 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Milo R., et al. , Network motifs: Simple building blocks of complex networks. Science 298, 824–827 (2002). [DOI] [PubMed] [Google Scholar]
- 7.Pržulj N., Biological network comparison using graphlet degree distribution. Bioinformatics 23, e177–e183 (2007). [DOI] [PubMed] [Google Scholar]
- 8.Ahmed N. K., Neville J., Rossi R. A., Duffield N., Willke T. L., Graphlet decomposition: Framework, algorithms, and applications. Knowl. Inf. Syst. 50, 1–32 (2016). [Google Scholar]
- 9.Li P., Milenkovic O., “Inhomogeneous hypergraph clustering with applications” in Proceedings of the 31st International Conference on Neural Information Processing Systems, von Luxburg U., Guyon I., Bengio S., Wallach H., Fergus R., Eds. (Curran Associates, Red Hook, NY, 2017), pp. 2305–2315. [Google Scholar]
- 10.Akcora C. G., Dey A. K., Gel Y. R., Kantarcioglu M., “Forecasting Bitcoin price with graph chainlets” in PAKDD 2018 Pacific-Asia Conference on Knowledge Discovery and Data Mining, Phung D., Tseng V., Webb G., Ho B., Ganji M., Rashidi L., Eds. (Lecture Notes in Computer Science, Springer, Cham, Switzerland, 2018), vol. 10939, pp. 765–776. [Google Scholar]
- 11.Menck P. J., Heitzig J., Kurths J., Schellnhuber H. J., How dead ends undermine power grid stability. Nat. Commun. 5, 3969 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Schultz P., Heitzig J., Kurths J., Detours around basin stability in power networks. New J. Phys. 16, 125001 (2014). [Google Scholar]
- 13.Mangan S., Alon U., Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. U.S.A. 100, 11980–11985 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gorochowski T. E., Grierson C. S., di Bernardo M., Organization of feed-forward loop motifs reveals architectural principles in natural and engineered networks. Sci. Adv. 4, eaap9751 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown J. I., Colbourn C. J., Roots of the reliability polynomial. SIAM J. Discret. Math. 5, 571–585 (1992). [Google Scholar]
- 16.Satyanarayana A., Chang M.K., Network reliability and the factoring theorem. Networks 13, 107–120 (1983). [Google Scholar]
- 17.Boland P. J., Samaniego F. J., “The signature of a coherent system and its applications in reliability” in Mathematical Reliability: An Expository Perspective, Soyer R., Mazzuchi T. A., Singpurwalla N. D., Eds. (Springer US, New York, NY, 2004), pp.3–30. [Google Scholar]
- 18.Navarro J., Tony Ng H. K., Balakrishnan N., Parametric inference for component distributions from lifetimes of systems with dependent comp. Nav. Res. Logist. 59, 487–496 (2012). [Google Scholar]
- 19.Boland P., Samaniego F. J., Vestrup E M., “Linking dominations and signatures in network reliability” in Mathematical and Statistical Methods in Reliability, Lindqvist B. H., Doksum K. A., Eds. (Series on Quality, Reliability and Engineering Statistics, World Scientific, Singapore, 2002), vol. 7, pp. 89–103. [Google Scholar]
- 20.Kochar S., Mukerjee H., Samaniego F. J., The “signature” of a coherent system and its application to comparisons among systems. Nav. Res. Logist. 46, 507–523 (1999). [Google Scholar]
- 21.Coolen F. P. A., Coolen-Maturi T., Generalizing the Signature to Systems with Multiple Types of Components (Springer, Berlin, 2012). [Google Scholar]
- 22.Cohen R., Erez K., ben Avraham D., Havlin H., Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000). [DOI] [PubMed] [Google Scholar]
- 23.Piraveenan M., Uddin S., Chung K. S. K., “Measuring topological robustness of networks under sustained targeted attacks” in Proceedings of the 2012 International Conference on Advances in Social Networks Analysis and Mining (IEEE Computer Society, Washington, DC, 2012), pp. 38–45. [Google Scholar]
- 24.Kim C. J., Obah O. B., Vulnerability assessment of power grid using graph topological indices. Int. J. Emerg. Electr. Power Syst. 8, 1553-779X (2007). [Google Scholar]
- 25.Francisco Gutierrez F. U., Barocio E., Zuniga P., Vulnerability analysis of power grids using modified centrality measures. Discrete Dynam Nat. Soc. 2013, 135731 (2013). [Google Scholar]
- 26.Abedi A., Gaudard L., Romerio F., Review of major approaches to analyze vulnerability in power system. Reliab. Eng. Syst. Saf. 183, 153–172 (2019). [Google Scholar]
- 27.Sóle R. V., Rosas-Casals M., Corominas-Murtra B., Valverde S., Robustness of the European power grids under intentional attack. Phys. Rev. E 77, 026102 (2008). [DOI] [PubMed] [Google Scholar]
- 28.Rosas-Casals M., Corominas-Murtra B., Assessing European power grid reliability by means of topological measures. WIT Trans. Ecol. Environ. 121, 527–537 (2009). [Google Scholar]
- 29.LaRocca S., Johansson J., Hassel H., Guikema S., Topological performance measures as surrogates for physical flow models for risk and vulnerability analysis for electric power systems. Risk Anal. 35, 608–623 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Mureddu M., Caldarelli G., Damiano A., Scala A., Meyer-Ortmanns H., Islanding the power grid on the transmission level: Less connections for more security. Sci. Rep. 6, 34797 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nieto F. J., Coresh J., Adjusting survival curves for confounders: A review and a new method. Am. J. Epidemiol. 143, 1059–1068 (1996). [DOI] [PubMed] [Google Scholar]
- 32.Lindqvist B., Doksum K. A., Eds., Mathematical and Statistical Methods in Reliability (Series on Quality, Reliability & Engineering Statistics, World Scientific, Singapore, 2003), vol. 7. [Google Scholar]
- 33.Lawless J. F., Statistical Models and Methods for Lifetime Data (John Wiley & Sons, New York, NY, ed. 2, 2003). [Google Scholar]
- 34.Hosmer D. W., Lemeshow S., May S., Applied Survival Analysis: Regression Modeling of Time to Event Data (Wiley-Interscience, New York, NY, ed. 2, 2008). [Google Scholar]
- 35.Singpurwalla N. D., Reliability and Risk: A Bayesian Perspective (John Wiley & Sons, Ltd., Chichester, West Sussex, England, ed. 1, 2006). [Google Scholar]
- 36.Rausand M., Høyland A., System Reliability Theory: Models, Statistical Methods, and Applications (John Wiley & Sons, Ltd, New York, NY, ed. 2, 2004). [Google Scholar]
- 37.Liu R. Y., Parelius J. M., Singh K., Multivariate analysis by data depth: Descriptive statistics, graphics and inference. Ann. Stat. 27, 783–858 (1999). [Google Scholar]
- 38.Zuo Y., Serfling R., General notions of statistical depth function. Ann. Stat. 28, 461–482 (2000). [Google Scholar]
- 39.Li J., Liu R. Y., New nonparametric tests of multivariate locations and scales using data depth. Stat. Sci. 19, 686–696 (2004). [Google Scholar]
- 40.Liu R. Y., Singh K., A quality index based on data depth and multivariate rank tests. J. Am. Stat. Assoc. 88, 252–260 (1993). [Google Scholar]
- 41.Rasmussen N. C., Reactor safety study: An assessment of accident risks in U.S. commercial nuclear power plants(Wash-1400, U.S. Nuclear Regulatory Commission, Rockville, MD, 1975).
- 42.Dey A. K., Gel Y. R., Poor H. V., Motif-based analysis of power grid robustness under attacks. arXiv:1708.06738 (16 July 2017).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.