A computational framework for DNA sequencing microscopy

Significance

Traditional microscopy is based on the propagation of interactions between light and small-scale objects up to larger scales. Such information may be encoded in DNA and transmitted with next-gen sequencing to be later reconstructed and visualized computationally. We provide a mathematical framework and computational proof of concept for a form of DNA-sequencing–based microscopy that may be used to construct whole images without the use of optics. Such an approach can be automated in a parallel and multiplexable way that current optical and scanning-based techniques are unable to achieve.

Abstract

We describe a method whereby microscale spatial information such as the relative positions of biomolecules on a surface can be transferred to a sequence-based format and reconstructed into images without conventional optics. Barcoded DNA “polymerase colony” (polony) amplification techniques enable one to distinguish specific locations of a surface by their sequence. Image formation is based on pairwise fusion of uniquely tagged and spatially adjacent polonies. The network of polonies connected by shared borders forms a graph whose topology can be reconstructed from pairs of barcodes fused during a polony cross-linking phase, the sequences of which are determined by recovery from the surface and next-generation (next-gen) sequencing. We developed a mathematical and computational framework for this principle called polony adjacency reconstruction for spatial inference and topology and show that Euclidean spatial data may be stored and transmitted in the form of graph topology. Images are formed by transferring molecular information from a surface of interest, which we demonstrated in silico by reconstructing images formed from stochastic transfer of hypothetical molecular markers. The theory developed here could serve as a basis for an automated, multiplexable, and potentially superresolution imaging method based purely on molecular information.

Microscopic imaging has traditionally relied on optics to amplify signals derived from initially confined spatial regions. Exceptions include atomic force microscopy which images by using a probe to interact with the sample. DNA has a high information density, with storage levels of 5.5 petabits per cubic millimeter achieved (1), making it an attractive medium for encoding spatial information at microscales. In this paper, we present a theoretical foundation for a spatial information encoding approach that utilizes DNA sequencing and graph theory that could be used to generate whole images.

DNA-driven reactions can be coupled to optically acquired spatial information such as with proximity ligation assay (PLA) (2) and DNA-PAINT (3), where molecular interactions mediated by DNA are discovered using fluorescence. There is also a family of techniques for connecting spatial locations with single-cell RNA sequencing data: using a priori knowledge of spatial marker genes to associate unknown genes to approximate locations, the a priori data being in most cases obtained by microscopy such as with in situ hybridization or modeling of spatial expression patterns to retrieve locations of associated genes (4–9). Alternatively, direct microscopy-based in situ sequencing methods achieve precise context-sensitive spatial transcriptomic information without needing to scramble spatial data by dissociation prior to sequencing (10, 11).

Encoding spatial information in a way that is preserved in the scrambling during isolation and recovery from in situ contexts that can then be read and recovered with sequencing is a major challenge. A few techniques achieve this by encoding spatial information directly into a molecular format, e.g., in the form of DNA read during sequencing along with transcriptomic data. These methods are based on artificial generation of an addressable surface using printing or lithography (12–14).

Herein, we describe a computational framework for a method called polymerase colony (polony) adjacency reconstruction for spatial inference and topology (PARSIFT), for the purpose of encoding images, for example of the positions of specific molecules relative to others on a 2D plane, directly into a DNA-based format without transduction of information through any other medium without a priori surface addressing. PARSIFT utilizes the connectivity of vertices in a graph of paired DNA sequences to infer Euclidean spatial adjacency and next-generation (next-gen) sequencing to recover that information a posteriori.

Encoding of topological data in DNA sequence format is possible by using DNA barcodes (unique molecular identifiers), i.e., randomized stretches of bases within a sequence of synthetic DNA. Barcodes associated with spatial patches can establish an identity for those locations, each patch distinguishable from another by sequence. A DNA barcode with 10 bases has over 1 million possible sequences, and larger barcodes can be used to create effectively unique labels in a system. The basic unit of topological data is an edge or association between 2 adjacent patches by physically linking between their barcodes. Topological mapping with barcoding has been used to infer neural connectomes by building a network from cells sharing common barcodes left by cell-traversing viruses (15) as well as features of DNA origami (16).

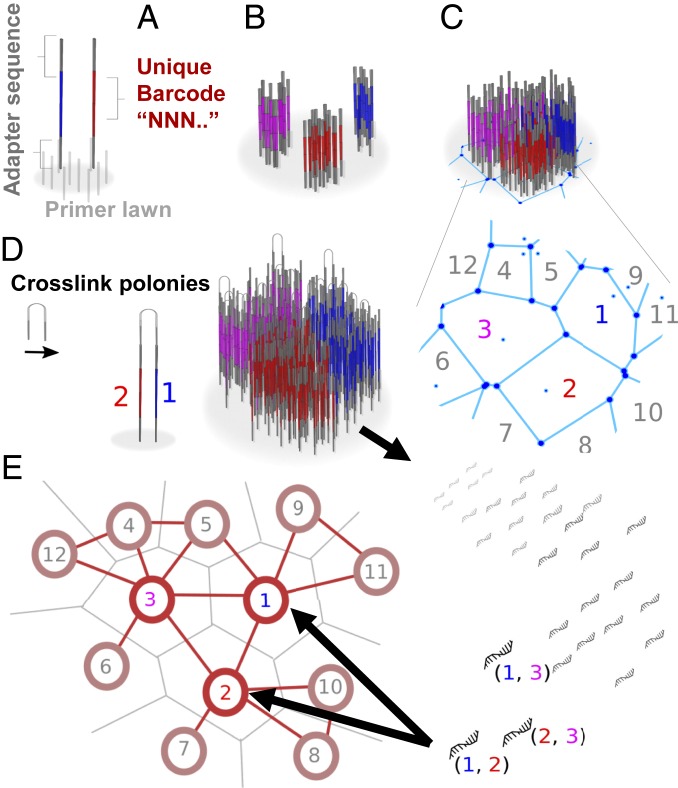
We can barcode surface patches using polony generation methods like bridge amplification (17), a 2-primer rolling-circle amplification (18), template walking amplification (19), or packing of barcoded beads (20). Unique “seed” strands are captured by primer strands on the surface (Fig. 1A) and locally amplified in the immediate vicinity where they landed. This generates numerous distinct patches, or “polonies,” of amplified DNA (Fig. 1B). Within each, all DNA is derived from a single seed molecule. Any of the above techniques could be applied to our method, although we focus herein on the polony-amplification by surface-primers approach.

Fig. 1.

Encoding and recovering metrics through polony adjacency. (A) Seed molecules with unique barcode sequences land randomly on a surface of primers. (B) Local amplification of seed molecules produces sequence-distinct polonies. (C) Saturation of polonies occurs when polonies are blocked from further growth by encountering adjacent polonies, forming a tessellated surface. (D) Random cross-linking of adjacent strands leads to pairwise association of nearby barcodes. (E) Recovery and sequencing of barcode pairs enable reconstruction of a network with similar relative positions of polonies to those on the original surface.

By growing polonies on a surface of primers to saturation (Fig. 1C), i.e., when growing polonies encounter the boundaries of other adjacent polonies, a tessellation of neighboring polonies forms. Each polony has a limited number of immediately adjacent neighboring polonies with their own respective barcodes. Although each patch is associated with a unique sequence according to its parent seed molecule, isolation of this DNA and subsequent sequencing would scramble information about the polony’s position and its neighboring polonies. Thus the critical step is to cross-link strands (SI Appendix, Fig. S1) from each polony to strands from adjacent polonies (Fig. 1D) in a way that enables both barcodes to be sequenced together in a single read. Recovery of the strands, i.e., stripping them from the surface followed by next-gen sequencing (by any means including nonoptical approaches such as Oxford Nanopore), thus preserves topological association between neighboring polonies as pairs of barcodes—a complete set of which constitutes the whole topological network of adjacent polonies (Fig. 1E). For random seed distributions we show that topological information alone, constrained by being a 2D planar network with known boundary geometry, retains significant spatial metrics of the original distribution. By generating such a mappable surface, we propose that localization of molecules bound to the surface can be done by covalent association with polonies, enabling inference of molecular spatial distributions and construction of images with polonies as pixels.

Results and Discussion

Voronoi Tessellation as a Model of Polony Saturation.

The spatial distribution of polonies on a surface, the a priori Euclidean information that is not explicitly accessible after isolation, can be preserved by associations between adjacent polony sequences and recovered with sequencing. Information that is available after sequencing and subsequent transformations of the data is then referred to as a posteriori.

Assume that seed molecule amplification on a bounded 2D surface, say in the shape of a disk, takes the form of a uniform circular growth. At the point of saturation, polonies have amplified to the extent that their expanding boundaries are restricted from further growth, having encountered neighboring polonies. The system of polonies then forms a planar Voronoi tessellation $T$ (SI Appendix, section A), appearing as a characteristic mosaic of polygons with the property that every point within a given cell is closer to its parent seed point than to any others. $T$ can also be represented by its plane dual Delaunay diagram $D=\left(P,L\right)$ whose vertices $P$ are the seed points of $T$ and edges $L$ are the line segments connecting the seed points of adjacent cells (polonies). By the geometric characteristics of $T$, all of the faces of $D$ are triangles (ref. 22, section 9).

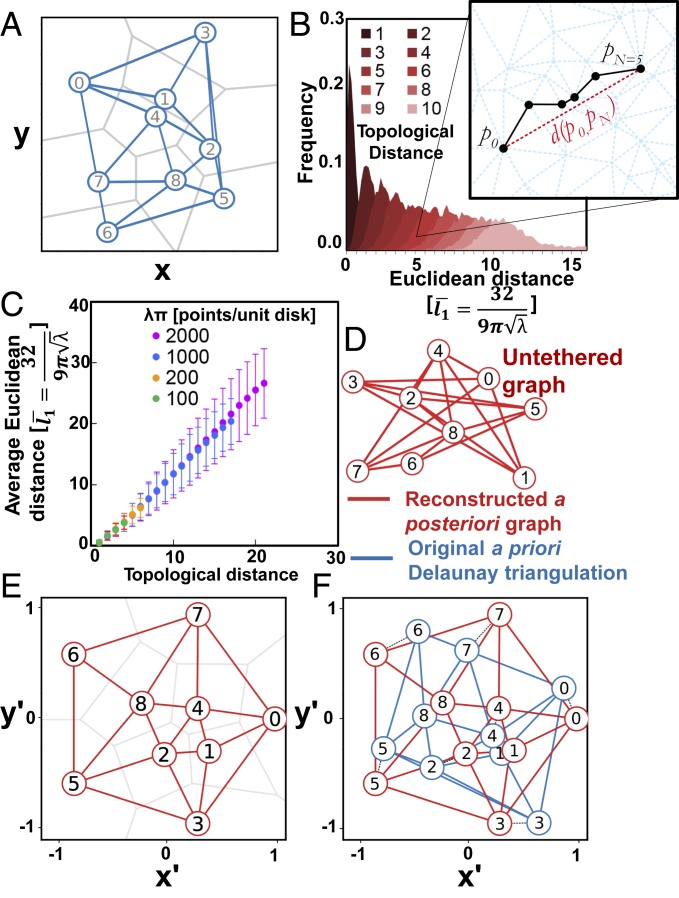
We refer to the graph defined purely by its vertices and edges without spatial considerations as the untethered graph. Fig. 2A presents a miniature Voronoi tessellation $T$ formed from 9 seed points within a square and its Delaunay diagram $D$. The untethered graph $G=\left(V,E\right)$ (Fig. 2D) is obtained from $D$ by omitting all geometric information, retaining only topological characteristics of the Delaunay diagram $D$. This includes a topological distance function $t\left(i,j\right)$ defined as the smallest number of edges that must be traversed to get from 1 vertex $i$ to another $j$, but no other information about the spatial origins of $G$ is explicitly stored (e.g., no Euclidean coordinates of the original points).

Fig. 2.

Encoding and recovering metrics via topology. (A) Nine seed molecule points distributed randomly on a plane, the induced Voronoi tessellation $T$ (gray lines), its Delaunay diagram $D$ (blue lines), and the untethered graph $G$. (B) The distribution of Euclidean distances associated with a given topological distance (path with the fewest edges between 2 points) sampled for random Poisson Delaunay triangulations (5,000 samples per topological distance value). (C) Euclidean distances normalized to the average length of a typical Poisson Delaunay edge (ref. 21, equation 9.9) plotted vs. topological distance for different Poisson intensities, exhibiting linearity between topological and Euclidean distance. (D) The untethered graph: a set of nodes (black) and edges (red) that constitutes the information preserved after dissociation from spatial context. (E) Reconstructed planar embedding of the initially untethered graph (red lines) using the Tutte embedding approach and corresponding Voronoi tessellation (gray lines). (F) Alignment of reconstructed embedding from E with the original Delaunay diagram from A.

Topological Metrics as a Proxy for Euclidean Metrics.

Let $P=\left\{p_k\mid k=1,\dots ,N\right\}$ be a planar placement of $N$ seed points, resulting from a Poisson-distributed seeding with intensity (i.e., polony density) $\lambda$ over an area $A$. Thus $N\approx \lambda A$, and an untethered graph representation $G=\left(V,E\right)$ of the true Delaunay diagram $D$ can be obtained by

$$\begin{array}{ll}\hfill V& =\left\{1,\dots ,N\right\},\hfill \\ \hfill E& =\left\{\left\{i,j\right\}\mid \text{barcodes}{w}_i\text{and}{w}_j\text{co}-\text{occur},\hspace{0.17em}i,j=1,\dots ,N\right\}.\hfill \end{array}$$

Since sufficiently long barcodes are with high probability unique (SI Appendix, section B), we treat pairs of barcodes as unique markers of polony adjacency. We postulate that with a sufficiently dense Poisson-distributed placement $P$, the topological metric on $G$ (with an appropriate linear scaling) approximates well the actual Euclidean metric of the points in $P$ (SI Appendix, sections D and E). Fig. 2B shows the Euclidean distance distributions for increasing topological distances from a reference vertex, for a large collection of Delaunay triangulations of Poisson random point sets. Fig. 2C then plots the scaled (ref. 21, equation 9.9) average Euclidean distances as a function of topological distances for Delaunay triangulations of random point sets generated by Poisson processes of increasing intensity $\lambda$, showing crucially that the 2 variables are proportional.

On this basis we propose that by finding a proper straight-line planar embedding of the untethered graph G we approximate also the metric properties of the underlying Delaunay diagram $D$ and the corresponding Voronoi tessellation $T$. A straight-line embedding of $G$ in a plane is determined by the placement $P\prime$ of its vertices, from which the line segments $L\prime$ corresponding to the edges can be deduced and thus denoted as $⟨G,P\prime ⟩$. Our hidden a priori embedding is the Delaunay diagram $D=⟨G,P⟩$, and the goal is to approximate this with a good a posteriori embedding $⟨G,P\prime ⟩$.

One constraint on our candidate $⟨G,P\prime ⟩$ is that it must be planar; i.e., no 2 edges may cross each other. This is due to the physical assumption that the barcode pairings correspond to polony adjacencies and thus cannot bridge nonneighboring polonies. There are several efficient algorithms for finding a plane embedding of a planar graph, 1 of which is the Tutte or barycentric embedding (23), applicable to Delaunay diagram-type graphs. Another quality constraint is that an average spatial density of the a posteriori vertex positions $\lambda \prime$ should be obtained from the final distribution with no systematic variation across the reconstructed area. Finally, if we were to generate a new Delaunay triangulation from the reconstructed points (as can be done from any arbitrary set of points), this should produce a similar set of edges to that in the original untethered graph that was the basis for reconstruction.

Our reconstruction approach (flow diagram in SI Appendix, Fig. S2) starts by determining the outer or boundary face of the Delaunay diagram $D$ underlying the untethered graph $G$. This can practically be done by finding, with an intermediate planar embedding, the plane face of $G$ that has the most vertices. Fixing the placement of the vertices on the boundary face, we then compute positions for the other vertices of $G$ by Tutte’s algorithm, which simply places each vertex at the average (barycenter) of its neighbors’ positions. In the case of a Delaunay diagram-type graph with the boundary face a convex polygon, this system is guaranteed to be nondegenerate (23), and the result will be a crossing-free straight-line embedding of $G$.

If spatial characteristics of the original Euclidean boundary are known—for instance if we specify that all boundary points must lie on a circle of known radius—then the embedding may also be scaled to match the original Euclidean metrics. Fig. 2E shows the Tutte embedding of the untethered graph (Fig. 2D) with boundary points arranged uniformly around the unit disk. For comparison, we have aligned the reconstructed graph with the original Delaunay diagram (Fig. 2F) by linearly transforming the planar graph to minimize the distance between corresponding vertices. We can see that relative positions are preserved albeit with local distortion that leads to slight displacement of each reconstructed vertex relative to its original seed counterpart. The algorithm thus returns approximate relative spatial positions of polonies from an input of paired polonies.

Simulation and Reconstruction by Embedding.

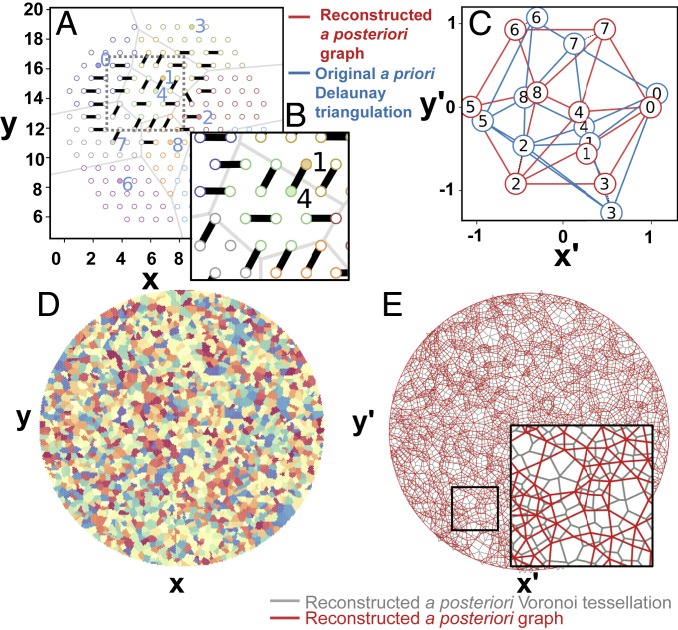
We simulate the primer lawn as a hexagonally packed disk of area $A$ with $M$ primer sites as the region of interest (ROI) (Fig. 3A). We simulate a random seeding at a polony density $\lambda$ by selecting $N=\lambda A$ random sites, followed by pairing of adjacent polony primer sites and scrambling of edge data prior to reconstruction. Fig. 3B shows how cross-linking leads to random pairing of adjacent sites, some of which are self-pairing events (providing no additional pairing information) and some of which are cross-polony sites that can be used to deduce the presence of a spatial boundary, with the fraction of information-bearing cross-pairs diminishing with the relative site density $\rho =M/\left(\lambda A\right)$, or average number of sites per polony (SI Appendix, Fig. S3). The probabilistic nature of the pairing opens up the possibility to miss an existing boundary, particularly when the boundary is small or when $\rho$ is low. A 2,000-polony simulated surface is shown in Fig. 3D, and SI Appendix, Fig. S4 shows site linking and the corresponding Delaunay triangulation of a 500-polony example.

Fig. 3.

Simulation of polony adjacency reconstruction. (A) Lattice diagram of primer lawn and polonies denoted with color and Voronoi cell boundaries. Solid circles indicate seed locations. (B) Illustration of random site pairing between adjacent primer sites. (C) Alignment between a priori and a posteriori points from A. (D) Larger simulated surface with a polony density $\lambda$ = 2,000 polonies per unit area and a relative site density $\rho$ = 50 sites per polony on average. (E) Reconstructed graph (red lines) and corresponding Voronoi tessellation (gray lines) computed using the Tutte embedding approach from scrambled edges derived from the simulated surface in D.

We reconstructed the topological network from the scrambled edges and performed intermediate embedding, boundary face determination, and Tutte embedding (Fig. 3C). For this larger reconstruction, spatial uniformity is more apparent, and we see that Voronoi cells take on the approximate size of polonies in the a priori surface, observe no obvious systematic changes in mesh density across the length of the ROI, and note the absence of crossed edges. Besides the Tutte embedding strategy, we developed 2 additional approaches for approximating Euclidean metrics from the untethered graph. One is a nondeterministic spring relaxation (24). This approach does not strictly require a crossing-free planar embedding and can thus lead to provably false positions involving nonplanar adjacency; however, this feature could also be advantageous if natural interpenetration of adjacent polonies leads to such topology. The last approach (SI Appendix, section F) is based on the notion of topological distance $t\left(i,j\right)$ and its role as a proxy for Euclidean distance. We extend the principle of geometric triangulation, whereby the set of distances of a point to other points in a plane can be converted to Cartesian coordinates, to incorporate $t\left(i,j\right)$ as a surrogate for Euclidean distance. In 1 variant of this method, a total topological distance matrix is reduced to 2 principal component vectors approximating the $x$ and $y$ coordinate vectors. In the alternative variant, $t\left(i,j\right)$ of each vertex are measured out only to peripheral vertices, reducing systematic distortions. A comparison of reconstructed meshes from the different approaches is shown in SI Appendix, Figs. S5 and S6.

Stamping and Image Formation.

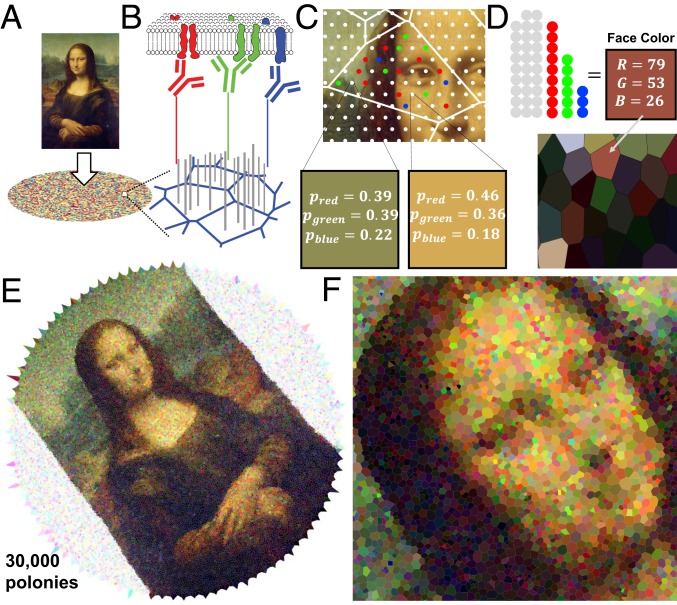
Knowledge of polony locations could be exploited to provide spatial information about objects of interest. We devised a basic model of image reconstruction from the principle of contact or diffusion-based transfer of molecules of interest to the mapped surface, i.e., a kind of molecular stamp. As proof of concept, we use an image (Fig. 4A) as a representation of a hypothetical probability distribution of 3 types of molecular markers labeled with identifying sequences called “red,” “green,” and “blue.” The image represents a surface of interest that we would like to sample from, for example a cell surface covered in oligo-tagged antibodies, each of which would be coupled enzymatically to a given polony upon contact (Fig. 4B) or diffusing RNA molecules like in ref. 14. The color of the image corresponds to the density of such markers and thus the probability that a marker of a particular color is placed on the polony surface. To simulate molecule transfer, the overlaid lattice of primer sites denotes points where a Monte Carlo sampling will occur in the corresponding position in the image. If the image pixel at a given primer site location has an RGB value dominated by red and green for example, then there is a higher probability of that site being occupied by either a green or a red marker (Fig. 4C). Realistically, molecular transfer introduces distortion, e.g., from curvature of cell membranes or lateral diffusion of mRNAs.

Fig. 4.

Voronoi image formation. (A) An image is overlaid on a surface of primer sites. (B) Molecular markers representing different targets (R, G, and B [red, green, and blue]) contact transferred to the polony surface and each covalently linked to a polony barcode. (C) Monte Carlo sampling to determine whether a marker is associated with a given site and if so which target by taking the probability from the RGB value normalized to 1 at the corresponding position in the image. (D) Tallying of markers and empty sites within a polony/Voronoi cell determines the color and brightness of that “pixel.” A subsequent image (D, Lower) is formed by coloring each cell accordingly. (E) Larger-scale reconstruction from scrambled edge data using the Tutte embedding approach with 30,000 polonies. (F) Close-up of E revealing individual Voronoi pixels. Adapted from Da Vinci, Leonardo. 1503–1506. Mona Lisa. Oil on wood. Paris: Musée du Louvre.

According to the reconstruction procedure, a Voronoi tessellation is produced from the final set of vertex positions—each cell of which constitutes a pixel that can be used to form an image. The final RGB value of the cell can be determined by tallying the markers that have associated with the primer sites in the polony as well as the number of unassociated sites (Fig. 4D). The Voronoi images shown in Fig. 4 E and F were generated with the scrambling step that removes any spatial information of the original image and reconstructed using our algorithm. Note that global rotation and chirality are not explicitly preserved from the original image. To place this 30,000-pixel image in experimentally relevant terms, we point to the work of Rodriques et al. (20), in which circular disks of barcoded 10-$\mathrm{\mu }$m beads (in their case sequenced optically in situ to obtain sequence addresses) are used to capture transcriptomic data from tissue slices. They report (20) a typical size of 70,000 10-$\mathrm{\mu }$m beads per 3-mm disk and obtain approximate single-cell resolution (SI Appendix, section H). Image reconstructions from the 4 approximation approaches are compared in SI Appendix, Figs. S5 and S6.

Assessment of Distortion and Precision.

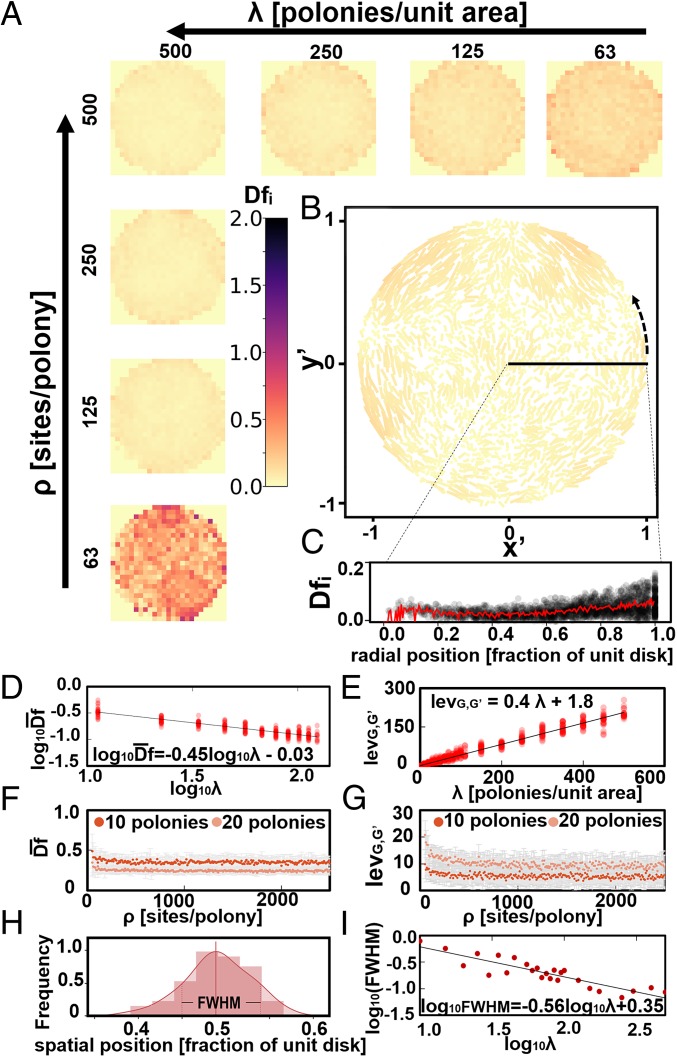
We may characterize reconstruction quality by defining a distortion metric. The a priori seed distribution points have a 1-to-1 correspondence with points in the a posteriori reconstruction, and since we generated the a priori points ourselves, we can directly compare corresponding original and inferred positions by applying a linear transform $Tx\left(P\right)$ (rotation, mirroring, scaling, and translation) to the set of reconstructed points that minimizes net displacement between the 2 distributions. Distortion is thus defined as the set of displacements $Df=\left(D{f}_i,\dots D{f}_N\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}d\left(P,Tx\left(P\prime \right)\right)\mid min\left({\sum }_{i=1}^{N}d\left(p_i,Tx\left(p_i^{\prime }\right)\right)\right)$. Averaged over multiple runs, we obtain 2D histograms (Fig. 5A and SI Appendix, Figs. S7 and S8) of distortion as a function of position in the ROI. Increasing the polony density ($\lambda$) reduces average distortion $\overline{Df}=\frac{1}{N}{\sum }_{i=1}^{N}D{f}_i$ (Fig. 5D and SI Appendix, Fig. S10) whereas changes in the site density $\rho$ (Fig. 5F and SI Appendix, Fig. S11) have a negligible effect on $\overline{Df}$ except at $\rho <100$ sites per polony near the point of network disconnection from absent edges. Examining a single simulation (Fig. 5B), we can visualize typical distortions, persistent over limited local scales and occurring with greater probability near the boundaries. Analysis of the radial distribution of this instance (Fig. 5C) reveals this as a mild systematic worsening near the boundary, an artifact introduced by the algorithm’s treatment of vertices on the boundary. SI Appendix, Fig. S9 compares single-instance distortions for the different reconstruction approaches.

Fig. 5.

Reconstruction quality. (A) Two-dimensional histograms of average displacement values binned by relative position in the unit disk ($n$ = 5,000/$\lambda$ simulations per histogram) for varied parameters ($\lambda$ and $\rho$). (B) Distortion in a single 2,000-polony Tutte embedding with lines connecting a priori and a posteriori vertex locations. Color map indicates line length (max = unit disk diameter 2.0). (C) Radial profile of distortion in B and 5-point moving average (red line). (D) Log-log plot of average displacement vs. $\lambda$ (points are single individual simulation reconstructions) and fixed $\rho =500$ sites per polony showing displacement ∼$\propto 1/\sqrt{\lambda }$. (E) Linear plot of Levenshtein distance ($le{v}_{G,G\prime }$) between untethered and a posteriori Delaunay graphs as function of polony. (D and E: $n$ = 25 simulations per $\lambda$ value). (F and G) Plot of average displacement (F) and plot of $le{v}_{G,G\prime }$ (G) each as a function of $\rho$ for 2 values of $\lambda$. Error bars represent SD (F and G: $n$ = 25 simulations per point). (H) Single instance of FWHM of a posteriori point spread function of a single site. (I) Log-log plot of FWHM vs. $\lambda$, scaling approximately according to the negative square root of polony density.

We also characterize reconstruction quality with Levenshtein distance ($le{v}_{G,G\prime }$), the number of edits needed to make 2 graphs identical, between the untethered graph and set of edges derived from a Delaunay triangulation $D\prime$ generated from the final reconstructed coordinates. Importantly, this metric is based only on a posteriori information, so it can be used in an experimental context where knowledge of the underlying distribution is unavailable. It weakly but positively correlates with distortion for a given $\lambda$ (SI Appendix, Fig. S13). $le{v}_{G,G\prime }$ grows linearly with $\lambda$ (Fig. 5E and SI Appendix, Fig. S10) and like distortion is relatively constant as a function of $\rho$ with a transient catastrophic breakdown at low $\rho$ (Fig. 5G and SI Appendix, Fig. S11). We also measured a classical resolution, the full width at half maximum (FWHM) of a point-spread function (Fig. 5H), by sampling the inferred position of a single site (taking its position to be the centroid of whatever Voronoi cell it lands in). Like distortion, FWHM is ∼$\propto 1/\sqrt{\lambda }$ (Fig. 5I), indicating that to halve the minimum size of distinguishable features, one should quadruple $\lambda$ (SI Appendix, Fig. S12). In experimental terms, polonies generated from techniques like template walking amplification, which forms polonies from sites that must be near the packing limit of oligo surface immobilization, can be on the order of nanometers (19) (SI Appendix, section G).

Conclusion

The 3 reconstruction methods (Tutte embedding, spring relaxation, and topological distance matrix) succeed in producing approximations of the original seed distributions that can be used to generate images. Tutte embedding exhibited the best estimated algorithmic complexity (based on run-time scaling with $\lambda$; SI Appendix, Fig. S14), making it the fastest technique which becomes significant for large reconstruction problems ($\lambda >\mathrm{10,000}$ polonies per unit area). Both Tutte embedding and spring relaxation had the lowest distortion levels, with Tutte embedding exhibiting slightly better $Df$ and $le{v}_{G,G\prime }$ scaling with $\lambda$. Tutte embedding was sensitive to catastrophic failure at low $\rho$, with singly connected edges crashing the reconstruction, and all 4 approaches were sensitive to disjoint subgraphs—making noisy and unconnected graph data a likely challenge for experimental scenarios. SI Appendix, Fig. S13 and section I discuss our attempts to move toward an algorithm that optimally exploits the available information, and future research should seek to establish a provably maximum-entropy reconstruction that is efficient and deterministic.

Along these lines, using information such as the number of self-pairing events could be useful to extract more information and weight edges according to estimated polony size and better control point placement. Alternatively, low-information content self-pairing events could be prohibited through a bipartite network approach whereby only pairings between A-type and B-type polonies would be allowed (SI Appendix, Fig. S15). The bridge amplification approach to polony generation leaves the possibility of doing this with 2 species of independent primers on the surface and 2 interpenetrating/overlapping and independently saturated polony surfaces. Another possible approach is series growth of polonies. In the basic concept presented in previous sections, a primer of uniform sequence is assumed; however, generation of a saturated layer of polonies that could then be used as primers for a subsequent polony generation step would then result in an overlapping of every second-layer polony with multiple first-layer polonies. This would result in efficient pairing of barcodes without the need for subsequent cross-linking steps.

At the time of publication, we are aware of concurrent works whose contributions are complementary to ours on development of DNA-sequencing–based microscopy (25, 26). The former work experimentally demonstrates DNA microscopy with images of mRNA in cells using locally confined cDNA amplifications and polymerase extension-based fusion of barcodes to connect spatial patches. Their approach differs from ours through the fact that fusion events are used as a direct distance metric, whereas our data instead rely on topology as a proxy for Euclidean metrics. The latter work uses series proximity ligation to associate planar spatial patches and form a network, using a spring relaxation approach for reconstruction.

PARSIFT is a concept for microscopic image reconstruction using spatial information encoding in DNA base format. We showed an in silico proof of concept by constructing a pipeline for taking decoupled edge data, generated from simulated polony distributions, that are then reassembled into a topological network and embedded in a Euclidean plane, resuming spatial characteristics of the original seed distribution. We saw that global distortions are low enough to resolve whole images. We hold that this framework and pipeline for reconstruction could be exploited for image acquisition of micro- and nanoscale surfaces with molecular libraries of potentially very high multiplicity and with throughput automated in a way that would not be possible with most optical approaches.

Supporting Information (SI Appendix)

The code is available at https://github.com/Intertangler/parsift.