Cell Receptor and Surface Ligand Density Effects on Dynamic States of Adhering Circulating Tumor Cells

Abstract

Dynamic states of cancer cells moving under shear flow in an antibody-functionalized microchannel are investigated experimentally and theoretically. The cell motion is analyzed with the aid of a simplified physical model featuring a receptor-coated rigid sphere moving above a solid surface with immobilized ligands. The motion of the sphere is described by the Langevin equation accounting for the hydrodynamic loadings, gravitational force, receptor-ligand bindings, and thermal fluctuations; the receptor-ligand bonds are modeled as linear springs. Depending on the applied shear flow rate, three dynamic states of cell motion have been identified: (i) free motion, (ii) rolling adhesion, and (iii) firm adhesion. Of particular interest is the fraction of captured circulating tumor cells, defined as the capture ratio, via specific receptor-ligand bonds. The cell capture ratio decreases with increasing shear flow rate with a characteristic rate. Based on both experimental and theoretical results, the characteristic flow rate increases monotonically with increasing either cell-receptor or surface-ligand density within certain ranges. Utilizing it as a scaling parameter, flow-rate dependent capture ratios for various cell-surface combinations collapse onto a single curve described by an exponential formula.

Graphical Abstract

The fraction of captured target cell decreases exponentially with increasing shear flow rate depending on cell-receptor and surface ligand density.

1. Introduction

Cancer progression is characterized by cells that invade locally and metastasize to nearby tissue or spread throughout the body [1]. During metastatic progression, cancer cells modulate their adhesive properties to allow for invasion from the primary tumors, transit into the circulatory system and establishment of secondary colonies in distant organs [2]. All these events occur through the specific interactions between cell receptors and their complementary ligands. In this biological process, free flowing cells first move in close proximity to the ligand-expressing substrate either by random motion or driven by the external forces. Initial receptor-ligand bindings are usually mediated by a group of cell receptors, which have fast association kinetics and high binding strength [3]. Once bond formations and rupture are balanced, cells undergo rolling adhesive motion where new bonds are continuously formed downstream compensating the rupture of old ones upstream. This transient and reversible adhesion slows down the cells and, thereby, enhances the efficiency of subsequent firm adhesion [3]. Afterwards, cells spread out and start the transendothelial migration into the surrounding tissue [4]. Considerable research effort has been devoted in recent years to the understanding of the dynamics and mechanisms involved in these steps.

Cell adhesion to a surface has long been a subject for intense research effort because of its immense physiological importance. Theoretical modeling of a fluid-borne cell adhesion presents significant challenges due to several aspects including cell membrane deformation, intermolecular bond mechanics and the fluidic environment around a rolling cell [5, 6]. Simplifying the cell structure as a rigid sphere, significant effort has been dedicated to develop theoretical models and numerical simulations describing the motion of such a sphere subjected to an imposed flow field near a surface [7, 8]. An analytical model, proposed to describe the binding rate between cell receptors and immobilized ligands under relative motion, suggests that the bond association rate could be enhanced due to the applied shear stress [9]. An external force exerted on a bond will alter its kinetic rate, typically shorten the bond lifetime, and an exponential model has been utilized to describe the relationship between rupture force and bond dissociation rate [10]. In an alternative approach, bonds are treated as stretched springs with the dissociation rate increasing as a function of the square of the rupture force [11]. Recently, a comprehensive theoretical model has been presented to study how cells move in linear shear flow above a wall to which they can adhere via specific receptor-ligand bindings [12]. Several dynamic states: firm adhesion, transient tethering, and rolling at reduced velocity have been observed in cell adhesive motion with diverse receptor-ligand combinations and varying bond kinetics [7, 13–16]. The extent of adhesion or rolling speed depends on both the cell receptor and surface ligand densities [17, 18]. Indeed, using a first-order dynamics model to study the cell adhesion process, the intrinsic rate constant for cell binding is found to increase with increasing density of either surface ligands or cell receptors [17]. Effects of ligand density on the jerky motion of cells have been studied using video microscopy to visualize the cell adhesion in shear flow. Tethering of cells becomes intermittent with decreasing surface ligand density, and the transient-tethering frequency is linearly proportional to the ligand density [18].

Microfluidic systems provide a unique opportunity for cell sorting and detection; they have been applied for continuous size-based separation, flow cytometry, and adhesion-based separation [19]. Requiring relatively simple equipment and providing superior observation capabilities, cell capture and adhesive rolling have been extensively studied using microfluidic devices [20, 21]. In particular, antibody-functionalized microchannels have been utilized for the isolation of cancer cells from either homogeneous or heterogeneous suspensions [22–24]. Epithelial cell adhesion molecule (EpCAM) is a trans-membrane protein highly expressed in the majority of human epithelial carcinomas, including colorectal, breast, prostate, head and neck, and hepatic carcinomas [25–30]. For this reason, EpCAM has been one of the most common target receptors for antibody based cancer cell isolation and detection from blood using microfluidic technology [22, 31]. In a landmark study, utilizing anti-EpCAM coated micro-posts, viable circulating tumor cells (CTCs) have selectively been separated from peripheral whole blood samples [22]. To determine the effect of cellular EpCAM expression on CTC capture efficiency, capture rates of several cancer cells lines have been compared. Interestingly, cells with relatively low EpCAM expression were captured as efficiently as high-level EpCAM-expressing cells. This could have been due to the augmented cell-substrate interactions inherent to the CTC-chip with microposts. In our previous work, the kinematics and dynamics of attachment and detachment of circulating tumor cells in antibody-functionalized microchannels have been investigated as a balance between the receptor-ligand association/dissociation rates and the applied hydrodynamic loads [32–34]. In this work, we experimentally explore the effects of cell receptor and surface ligand densities on tumor cell capture in antibody-functionalized microchannels under shear flow, and a previously reported theoretical model is employed to analyze the experimental data.

2. Experimental

2.1. Experimental arrangements

The microfluidic devices feature a single microchannel about 100μm in height, 1mm in width, and 30mm in length. The devices were fabricated using standard microfabrication technology. Polydimethylsiloxane (PDMS) mixture was poured on a silicon mold, de-gassed and cured. The cured PDMS substrates were peeled off the mold, and holes were drilled at both edges of each microchannel to serve as inlet/outlet. The PDMS grooves were then bonded onto oxidized silicon wafers to cap the microchannels. The fabricated microchannels were next functionalized following our standard protocol. The surface hydroxyl groups were silanated in 1% (vol/vol) 3-aminopropyltriethoxysilane (APTES from Sigma)-acetone solution, and activated with 2% (vol/vol) glutaraldehyde (Sigma) in 1×CMF-PBS. Recombinant protein G from E. coli (Zymed Lab Inc.) was incubated on the activated surface; this was followed by incubation of the microchannel surface with bovine serum albumin solution (BSA from Sigma, 2mg/ml in 1×CMF-PBS) to block the excessive silanol sites. Finally, EpCAM antibodies (MAB9601 Clone 158206, from R&D Systems) or anti-N-cadherin (C2542, Clone GC-4, from Sigma-Aldrich) were immobilized on the protein G layer.

Experiments were conducted by driving cell suspensions through the bio-functional microfluidic devices. The flow rate was adjusted using two syringe pumps (PhD 2000, Harvard Apparatus) to infuse buffer solution (1×CMF-PBS). The upstream pump at the inlet was operated at a forward motion, while the downstream pump was operated at a backward motion. Once cells enter the channel through a second inlet, they were carried away downstream by a steady flow allowing them to gradually sediment and interact with the functionalized channel bottom surface. The device fabrication process, surface functionalization with antibodies, and the experimental set-up are detailed elsewhere [35].

All experiments were carried out and monitored using a probe station (Signatone S-1160) equipped with a microscope (Motic Microscope PSM-1000), a CCD camera and a DVD recorder (Panasonic DMR-E85H). The time-dependent cell velocity can be determined directly from the video clips. The number of cells entering the microchannel N₀ was counted, typically in the range of 2000–2500. Once the cell sample had been fully loaded, the channel was flushed with the 1×CMF-PBS buffer solution to remove unbound cells. The washing flow rate was set to be sufficiently high for removal of unbound cells but sufficiently low for keeping captured cells unaffected. The flow was then stopped, and 22 images along the entire microchannel were recorded to determine the total number of captured cells N_A. A viability test for the captured cells was conducted using propidium iodide (PI) as a viability marker. Non-viable cells were labeled by red dye and detected under a fluorescent microscope. The results show that more than 80±5% of the stressed cells were still viable.

2.2. Cell culture

Two breast cancer cell lines MDA-MB-231 and BT-20, both expressing EpCAM receptors, were utilized in this study. MDA-MB-231 cells were grown in RPMI 1640 buffer containing L-glutamine (Cellgro) with 10% fetal bovine serum (FBS, Cellgro) and 1% penicillin-streptomycin (Invitrogen). BT-20 cells were grown in Eagle’s Minimum Essential Medium (EMEM from ATCC) with 10% FBS and 1% penicillin-streptomycin. The cell lines were maintained in humid environment at 37°C and 5% CO₂. Prior to each experiment, the cells were harvested using 4-mM Ethylenediaminetetraacetic acid (EDTA) and suspended in 1×CMF-PBS. The average diameter of suspended MDA-MB-231 and BT-20 cells is about the same, 20±2μm, as measured under a microscope. For practical applications, mixing CTCs with epithelia or blood cells is perhaps more desirable. However, for fundamental studies, two cell lines with very similar physical characteristics presents a more stringent selectivity test. Indeed, in a binary mixture of MDA-MB-231 and BT-20 cells, the cell type can be positively determined only by tagging each cell type with fluorescent labels of different color [35].

3. Theoretical

3.1. Physical and mathematical modeling

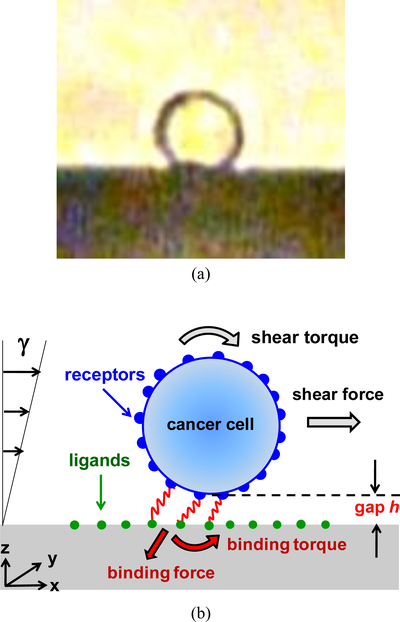
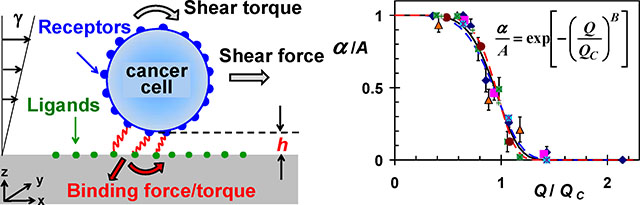
A side view of a typical CTC, with approximately a spherical shape, is shown in Figure 1a; a simplified physical model, illustrated in Figure 1b, was adopted to analyze the motion of such a CTC in a bio-functional microchannel [12]. The model features a rigid sphere of radius R in motion above a wall with distributed ligands. For flow rates under 3μl/min, the Reynolds number is much less than unity and inertial effects may be neglected. Hence, the flow around the cell is laminar and can be well described by Stokes flow. Cells are driven by both the shear flow and the direct forces which include a constant gravitational force due to a slight density difference between the cells and the surrounding medium, receptor-ligand binding forces, and thermal fluctuations for microscale objects experiencing diffusive motion. The motion of the sphere can be described by the following Langevin equation [12]:

$$d\mathbf{\text{X}}/dt={\mathbf{\text{U}}}^{\infty }+\mathbf{\text{M}}\left({\mathbf{\text{F}}}^S+{\mathbf{\text{F}}}^G+{\mathbf{\text{F}}}^B\right)+k_B{T}_a\nabla \mathbf{\text{M}}+w_t^I$$ (1)

where X is a six-dimensional state vector including three translational and three rotational degrees of freedom to describe the time-dependent configuration of the sphere with respect to a fixed Cartesian coordinate system as shown in Figure 1b. Similarly, U^∞ denotes the six-dimensional unperturbed velocity vector at the location corresponding to the center of the sphere. Both F^S and F^D are the combined force and torque vectors; F^S denotes the hydrodynamic loads due to the applied viscous shear flow, while F^G and F^B represent the direct forces/torques acting on the cell due to gravity and adhesion forces, respectively. M is a 6×6 mobility matrix, while k_B is the Boltzmann constant and T_a is the ambient temperature. The terms k_BT_a∇M and w_t^I describe the effects of thermal fluctuations, where w_t^I is Gaussian white noise. In a dimensionless form, the first-order discretized version of Equation 1 reads as follows:

$$\begin{gathered} \mathbf{\Delta }{\mathbf{\text{X}}}_t=\left[{\mathbf{\text{U}}}^{\infty }+\mathbf{\text{M}}\left({\mathbf{\text{F}}}^S+{\mathbf{\text{F}}}^G+{\mathbf{\text{F}}}^B\right)\right]\mathbf{\Delta }t+\frac{1}{Pe}\nabla \mathbf{\text{M}}\cdot \mathrm{\Delta }t \\ +\sqrt{\frac{1}{Pe}}w\left(\mathrm{\Delta }t\right)+O\left(\mathrm{\Delta }{t}^2\right) \end{gathered}$$ (2)

The cell radius R is used as the length scale, the inverse shear rate 1/γ as the time scale (γ=dU/dz), and 6πμR²γ as the force scale (μ is the viscosity). The dimensionless Péclet number, defined as Pe=(6πμR³γ)/(k_BT_a), describes the relative importance of convective versus diffusive motion of the sphere [8, 36, 37]. The mobility matrix M for a sphere above a wall depends on the gap between the sphere and wall [8]. Here, a numerical scheme described elsewhere [8, 37] is used to calculate each component of the mobility matrix, M, and the shear force vector, F^S.

Fig. 1.

(a) A side-view image of a typical CTC on a solid surface with approximately a spherical shape, and (b) An illustration of the physical model for the theoretical analysis; the cell is represented as a rigid sphere, with receptors on its surface, moving under linear shear flow above a surface immobilized with ligands; receptor-ligand bonds are modeled as linear springs.

The cell-surface adhesion force/torque due to receptor-ligand bindings is represented by the term F^B in Equation 2. The probabilistic nature of receptor-ligand bond formation and rupture follows the rules of adhesive dynamics [7, 12]. The receptors are modeled as reactive patches with a total number N_R randomly distributed on the cell surface, and the ligands are considered as dots on the channel bottom surface with uniform spacing D. An encounter complex is formed whenever the distance between a receptor and a ligand is smaller than a capture radius r₀ [38]. The complex can develop into the final receptor-ligand bond at an on-rate k_on during the time it exists, i.e., the probability for bond formation is [1–exp(–k_onΔt)] during a time step Δt. Bonds can rupture at a force-dependent off-rate k_off=k₀exp(F/F_d) [10, 18, 39], where k₀ is the dissociation rate at zero pulling force, F the force on the bond, and F_d=k_BT_a/x_c is the detachment force scale with reactive compliance x_c. Bond-rupture probability during the time step Δt is [1–exp(–k_offΔt)]. Multiple bonds may exist at every step and each existing bond is modeled as a spring with a spring constant K.

3.2. Modeling parameters

The theoretical model includes numerous dimensional parameters, which are estimated for the present experimental system. The cell radius R=10μm, with surface area of 1.26×10⁻⁵cm², was selected as the average radius of both MDA-MB-231 and BT-20 cells under rolling adhesion. The shear rate was determined based on numerical simulations of the flow fields in a microchannel corresponding to various flow rates. The shear rate γ=du/dz, where u is the flow streamwise velocity, was computed at z=10μm above the channel bottom surface; this location corresponds to the cell center when rolling on the surface. The flow shear rate ranges between γ=5.7 and 22.8 Hz for flow rates ranging from Q=0.75 to 3.0μl/min. All experiments were conducted at room temperature such that T_a=293K, and the dynamic viscosity of the buffer solution 1×CMF-PBS at room temperature is μ=1mPa·s. The gravitational force F^G is due to the density difference between the cells and the surrounding medium, Δρ, which can be deduced from the terminal sedimentation velocity of a spherical object as follows: V_t=2gR²Δρ/9μ; where g is the gravitational acceleration. To obtain the terminal velocity, the settling motion of several MDA-MB-231 cells in a glass capillary filled with 1×CMF-PBS buffer solution was recorded. The average terminal velocity of the cells, measured from the recorded video clips, was found to be about 7.4μm/s; hence, the estimated density difference is about Δρ=34kg/m³.

An unstressed off rate constant for EpCAM/anti-EpCAM binding has been reported to be k₀=0.0003 Hz [40], with a reactive compliance of x_c=2×10⁻¹¹m [39], while the on rate was estimated to be k_on=0.0137 Hz [33]. We assume the antibody ligands to be distributed on a square lattice with a lattice constant D; where D is obtained from D=N_L^−1/2, with N_L being the ligand surface density. Functionalizing the surface with an antibody solution at a concentration of 100μg/ml results in a ligand density of N_L=4×10¹⁰/cm², consistent with the value reported elsewhere [13, 18, 39]; thus, the lattice constant is assumed to be D=0.05μm. The reported number of EpCAM receptors per cell is 1,700 and 139,500 for MDA-MB-231 and BT-20 cells, with a corresponding cell receptor density of N_R=1.35×10⁸/cm² and 1.11×10¹⁰/cm², respectively [41]. Flow cytometry tests conducted on the cells used in this work were found to be in qualitative agreement with these reported data; the EpCAM expression level was found to be high in BT-20 cells and low in MDA-MB-231 cells.

Receptors and ligands have a finite spatial extent, and their binding sites diffuse within some region around their linkage. Hence, a capture volume with radius of r₀=h+50nm is introduced to account for the spatial distribution of the receptor-ligand binding sites [12]. Here, h is the cell-surface gap when the cell is rolling on the surface; it can be evaluated based on the cell rolling velocity on a surface due to applied shear flow. Similarly, the bond spring constant can be estimated based on the cell deceleration rate during capture as it comes to a stand still. Depending on the flow rate, the time step varies between Δt=0.004 and 0.2s for high and low shear rate, respectively. The values for the parameters used in this work are summarized in Table 1 in the Electronic Supplementary Information.

In the absence of receptor-ligand bindings between a cell and a surface, the cell moves at a reduced hydrodynamic velocity U_hydro compared to the unperturbed shear flow velocity U^∞ due to the wall effect. Therefore, omitting the binding force F^B, Equation 2 is rewritten as,

$$\begin{gathered} \mathrm{\Delta }{\mathbf{\text{X}}}_t=\left[{\mathbf{\text{U}}}^{\infty }+\mathbf{\text{M}}\left({\mathbf{\text{F}}}^S+{\mathbf{\text{F}}}^G\right)\right]\mathrm{\Delta }t+\frac{1}{Pe}\nabla \mathbf{\text{M}}\cdot \mathrm{\Delta }t \\ +\sqrt{\frac{1}{Pe}}w\left(\mathrm{\Delta }t\right)+O\left(\mathrm{\Delta }{t}^2\right) \end{gathered}$$ (3)

Equation 3 allows the calculation of U_hydro as a function of the cell-surface gap and the applied flow rate.

4. Resutls and Discussion

4.1. Cell dynamic states

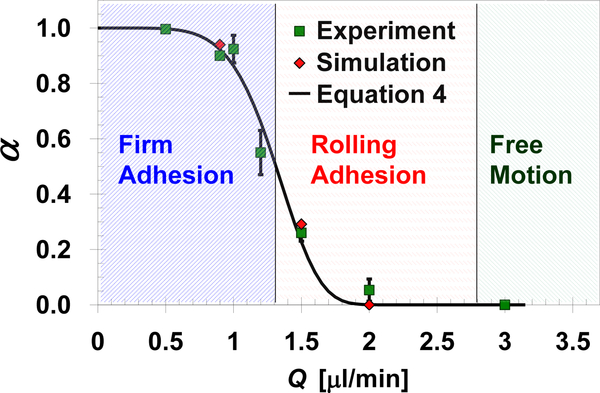
MDA-MB-231 cell suspensions were driven through microchannels functionalized with EpCAM antibodies at room temperature to characterize the cell capture efficiency under shear flow. The ratio between the number of attached cells N_A and the total number of loaded cells N₀ is defined as the capture ratio α≡N_A/N₀, which is plotted in Figure 2 as a function of the applied flow rate. This capture ratio diminishes under applied high flow rate and approaches unity as the flow rate decreases to zero. The continuous decrease in cell capture ratio with increasing flow rate is described by the following empirical formula [33]:

$$\alpha \equiv \frac{N_A}{N_0}=A\exp \left[-{\left(Q/Q_C\right)}^B\right]$$ (4)

where Q_C is a characteristic flow rate depending largely on the type and number of receptor-ligand bonds; B is the exponent controlling the functional slope; and A is the maximum capture ratio. The best fit of calculations based on Equation 4 to the experimental data yields Q_C=1.4μl/min and B=5.7.

Fig. 2.

Measured and calculated capture ratio of EpCAM-expressing MDA-MB-231 cells in anti-EpCAM functionalized microchannels as a function of the applied shear flow rate. The predicted capture ratio is calculated based on the velocity of 50 cells averaged over a 60s time period under each flow rate assuming: h=490nm, K=850nN/m, N_R=1.35×10⁸/cm², and D=0.05μm. The three characteristic dynamic states observed under certain flow rate ranges are marked by the shaded regions.

Depending on the applied flow rate, as marked in Figure 2, three distinct dynamic states have been observed: (i) firm adhesion, (ii) rolling adhesion, and (iii) free motion; a cell can be captured only under the firm adhesion state. Under low flow rate, Q<1.3μl/min, most of the cells experience the firm adhesion state resulting in the capture of more than 50% of the cells. Increasing of the flow rate up to 2.8μl/min, the receptor-ligand interaction forces are not strong enough to hold the cell firmly against the hydrodynamic loads; thus, most cells experience a rolling adhesion state characterized by a ‘stop-and-go’ jerky motion. When the flow rate is sufficiently high, Q>2.8μl/min, the receptor-ligand binding forces are negligible compared to the hydrodynamic loads; consequently, almost all cells move smoothly in a free motion state with a constant velocity close to the hydrodynamic velocity.

4.2. Gap-size and spring constant estimates

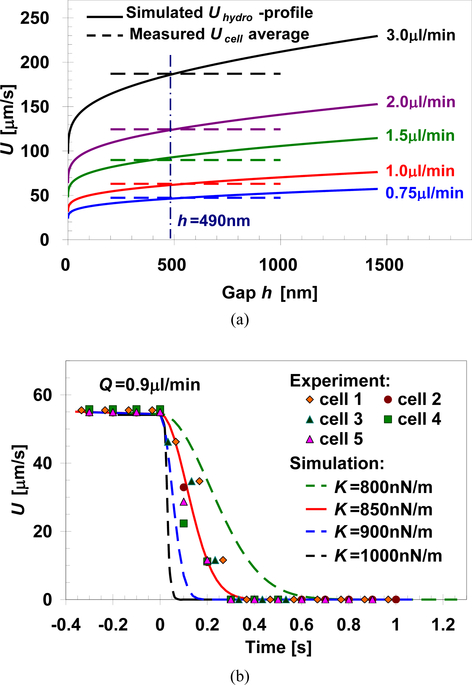
It is expected that when a cell is rolling on a functionalized surface, a certain gap h is maintained between the cell membrane and the antibody-functionalized surface as sketched in Figure 1b. The gap is an important parameter in determining its hydrodynamic velocity, in the absence receptor-ligand interactions, and in estimating the cell-surface adhesion force due to receptor-ligand bindings. The gap size is estimated by analyzing the free-motion dynamic state of MDA-MB-231 cells in antibody-functionalized microchannels. In the absence of receptor-ligand binding forces, a cell under shear flow rolls on a surface in a free motion state with a constant translational velocity termed hydrodynamic velocity U_hydro. Assuming the cell with a given diameter moves as a rigid sphere, analytical calculations of the hydrodynamic velocity as a function of the applied shear flow and the cell-surface gap size are available [12, 36]. Experimentally, it is important to measure the cell free motion velocity on an antibody-functionalized surface, to maintain similar boundary morphology, but without receptor-ligand bindings. Since MDA-MB-231 cells do not express N-cadherin receptors [42], cell suspensions were driven through microchannels functionalized with N-cadherin antibodies. The average velocity of the cells was measured from recorded video clips for 5 flow rate levels in the range of 0.75–3μl/min. The numerically computed family of five curves of the gap-size dependent hydrodynamic velocity (solid lines) is compared in Figure 3a with the cell velocities measured for the same flow rates (dash lines). The intersections between the measured cell velocities and the calculated hydrodynamic velocity curves, at the various flow rates, indicate a cell-surface gap of h=490nm independent of the flow rate. The same protocol was followed in functionalizing the tested microchannels with either EpCAM or N-cadherin antibody ligands; furthermore, these two antibodies are the same isotype of mouse IgG. Therefore, it is reasonable to assume that, aside from receptor-ligand interactions, the surface boundary conditions in both sets of microchannels are very similar. As a result, the gap size estimate of h=490nm is used for the analysis of MDA-MB-231 cell motion under shear flow on anti-EpCAM functionalized surfaces.

Fig. 3.

(a) Cell-surface gap estimate based on matching simulated gap-size dependent hydrodynamic velocity (solid lines) with average cell velocity measured under various flow rates (dash lines); the average free-motion velocity was measured for MDA-MB-231 cells passing through anti-N-cadherin functionalized microchannels with negligible receptor-ligand interaction, and (b) Spring constant estimate based on matching calculated spring-constant dependent cell velocity with measured cell velocity during capture; the firm-adhesion velocity was measured for MDA-MB-231 cells captured in anti-EpCAM functionalized microchannels under a flow rate of 0.9μl/min. The cell-surface gap is estimated to be about h=490nm, independent of the applied flow rate, while the spring constant is estimated to be about K=850nN/m assuming D=0.05μm and N_R=1.35×10⁸/cm² in the calculations.

The theoretical model accounts for receptor-ligand bonds as linear springs with a spring constant K. In order to estimate the value of K, the firm-adhesion dynamic state of MDA-MB-231 cells in antibody-functionalized microchannels is analyzed. Due to specific receptor-ligand bindings, under a limited flow rate range, the cell velocity decreases gradually until it comes to a complete stop. The time evolution of a cell velocity during this capture process can be measured from video recording. Using the mathematical model represented by Equation 3, the time-dependent cell velocity resulting in its firm adhesion can also be calculated for any given spring constant value. To facilitate the analytical calculations, several other parameters pertaining to the current system have to be prescribed; ligand spacing of D=0.05μm and cell receptor density of N_R=1.35×10⁸/cm² are selected following the discussion in Section 3.2; cell-surface gap of h=490nm is estimated in the last paragraph; and shear rate of γ=6.4Hz corresponds to the Q=0.9μl/min flow rate. Values of other required parameters are summarized in Table 1 in the Electronic Supplementary Information. A family of curves of time-dependent cell velocity, calculated for different spring constants, is compared in Figure 3b with measured velocity of MDA-MB-231 cells captured under shear flow rate of Q=0.9μl/min in an anti-EpCAM functionalized microchannel (symbols). The best agreement between the calculated and measured cell velocity prior to capture is obtained for a spring constant of K=850nN/m, and this value is used in modeling each EpCAM/anti-EpCAM bond as a linear spring.

4.3. Adhering cell dynamics

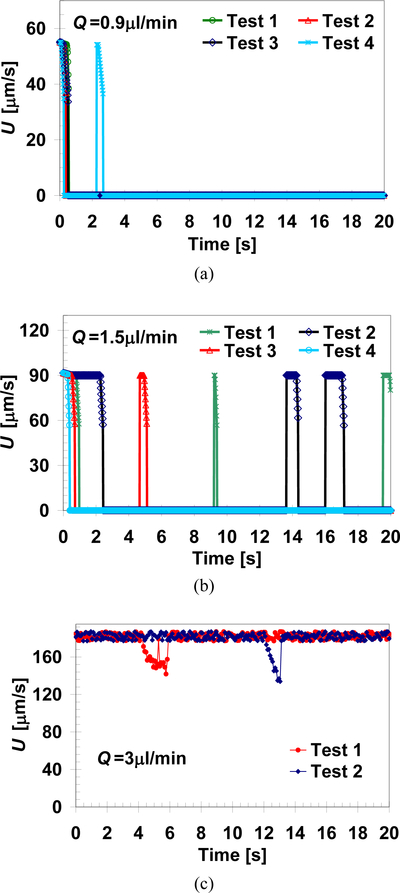
The motion of cells such as MDA-MB-231 on surfaces functionalized with proper counter-receptor ligands, e.g. EpCAM antibodies, can be described as the product of several independent and random variables. Consequently, the time-dependent velocity of cells rolling along a microchannel functionalized surface, due to an applied shear flow, varies significantly among individual cells even under seemingly identical experimental conditions. This is not only due to non-uniformities in cell and surface properties but also because of the probabilistic nature of the cell adhesion dynamics. Statistically, however, the cell population fraction under any particular dynamic state, for any given cell/surface combination, is determined by the applied flow rate; indeed, measured capture ratios are repeatable within experimental errors. To account for some of these effects in theoretical calculations, the cell receptors are randomly distributed on its surface; furthermore, the rules pertaining to the probabilistic adhesion dynamics are incorporated [12]. Consequently, although all the input parameters are deterministically prescribed, the mathematical model still yields a unique time-dependent velocity profile for each simulated cell. Examples of different time-dependent velocity profiles are depicted in Figure 4 for several cells subjected to three representative flow shear rates. Although each cell follows a different velocity profile over time, under a given shear rate, the time-averaged velocity of different cells is about the same, increasing with the applied shear rate. At Q=0.9μl/min, Figure 4a, the calculated velocity profiles indicate that the cells experience firm adhesion as all are captured in less than 3s. At Q=1.5μl/min, Figure 4b, the calculated cell velocity profiles feature ‘stop-and-go’ events typical to the rolling adhesion state. Free motion state is observed under higher flow rate of Q=3.0μl/min, Figure 4c, where most cells move with almost constant velocity with negligible instantaneous decelerations due to short-lived receptor-ligand bonds.

Fig. 4.

Simulated time evolution of the velocity of several cells under flow-rate dependent dynamic states of: (a) firm adhesion (Q=0.9 μl/min), (b) rolling adhesion (Q=1.5 μl/min), and (c) free motion (Q=3 μl/min). The numerical computations were carried out for: h = 490 nm, K = 850 nN/m, N_R = 1.35×10⁸/cm², and D = 0.05 μm (corresponding to the motion of MDA-MB-231 cells on an anti-EpCAM functionalized surface.)

Following experimental observations, the calculated cell motion can be classified into a particular dynamic state based on the ratio between the time-averaged cell velocity and its hydrodynamic velocity U_Ave/U_hydro as follows: (i) firm adhesion, U_Ave/U_hydro<0.01; (ii) rolling adhesion, 0.01<U_Ave/U_hydro<0.95; and (iii) free motion, U_Ave/U_hydro>0.95. The capture ratio, defined as the fraction of the total number of tested cells that undergo firm adhesion, can now be theoretically calculated for any given shear rate utilizing the U_Ave/U_hydro<0.01 criterion. The calculated cell capture ratios were obtained by simulating 50 different cells over a time period of 60 seconds at each flow rate; this period of time is sufficiently long to ensure convergence of the time-averaged randomly fluctuating velocity of the tested cells. Calculated capture ratios for various flow rates, shown in Figure 2, agree well with the corresponding measured values. This good agreement validates the theoretical approach justifying its application to explore effects of other parameters difficult to evaluate experimentally.

4.4. Surface-ligand density effect

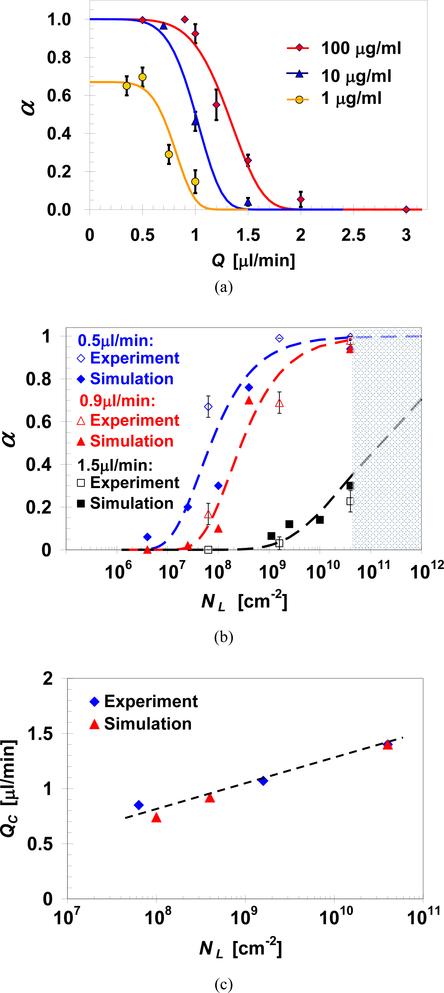
Experimentally, it is possible to manipulate the surface ligand density by controlling the concentration of the antibody solution used in immobilizing the surface ligands. Thus, to investigate the effect of ligand density on the cell capture ratio, microchannels were functionalized with EpCAM antibodies at concentrations of 1, 10, and 100 μg/ml. Capture ratios of MDA-MB-231 cells in these microchannels were measured as a function of the applied flow rate, and the results are summarized in Figure 5a. Clearly, if the applied flow rate is sufficiently high (Q>2μl/min), all loaded cells avoid capture resulting in zero capture ratio regardless of the ligand density. In general, under a given intermediate flow rate, the cell capture ratio increases with increasing antibody concentration. All loaded cells can still be captured, α=1, even after reducing the antibody solution concentration from 100 to 10μg/ml; although this requires a lower applied flow rate, Q<0.7μl/min. In contrast, upon further reduction of the antibody concentration to 1μg/ml, the maximum capture ratio obtained for the lowest flow rate tested is α=0.65. The best fit of Equation 4 to the experimental data yields values of Q_C=0.85, 1.05 and 1.4μl/min for microchannels functionalized with antibody solution concentration of 1, 10 and 100 μg/ml, respectively, and the same exponent constant B=5.7 for all three cases.

Fig. 5.

(a) Capture ratio measurements (symbols) and predictions based on Equation 4 (curves) of MDA-MB-231 cells as a function of the applied flow rate in microchannels functionalized with EpCAM antibodies at various concentrations; measured and predicted effect of surface-ligand density on: (b) MDA-MB-231 cell capture ratio under three selected flow rates, and (c) characteristic flow rate for the capture of MDA-MB-231 cells, with N_R=1.35×10⁸/cm², in anti-EpCAM functionalized microchannels.

The effect of ligand density is accounted in the present theoretical model. Cell capture ratio as a function of ligand surface density is calculated for N_R=1,700, corresponding to the MDA-MB-231 cell line, under 3 selected flow rates: 0.5, 0.9 and 1.5μl/min. To validate these calculations, the surface ligand densities used in the experiments are entered as the input parameters in the simulations. The surface ligand density is N_L=4.0×10¹⁰/cm² for an antibody concentration of C=100μg/ml.

Fitting the rest of the measured to the calculated capture ratios, for the same flow rate, yield estimates of N_L=1.6×10⁹ and 6.35×10⁷/cm² for C=10 and 1μg/ml, respectively. The predicted monotonic increase in capture ratio with increasing ligand density agrees reasonably well with the measured trend, as depicted in Figure 5b, under each of the tested flow rates. It should be noted that the surface ligand density has no theoretical upper bound, since each ligand is modeled as a point on the surface. However, in practice, the surface ligand density has an upper limit of 4×10¹⁰/cm² as marked in Figure 5b [13, 18, 39]. The characteristic flow rate increases monotonically with increasing surface ligand density as plotted in Figure 5c within the tested ligand density range.

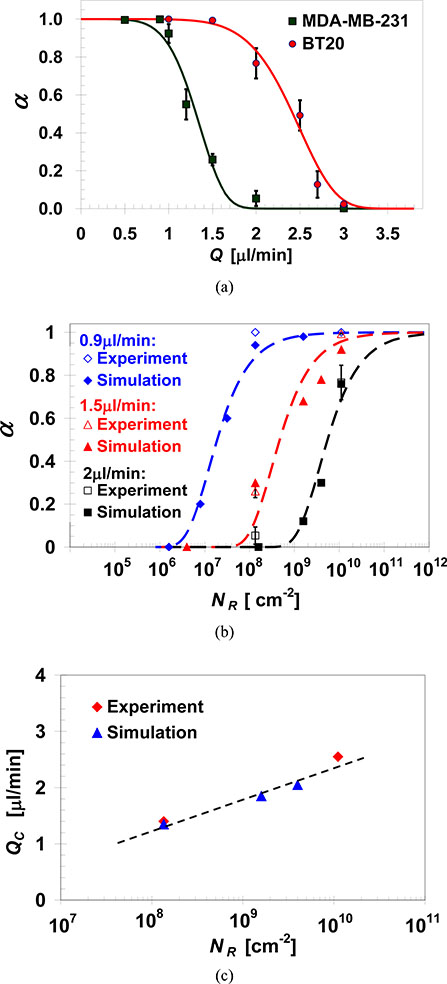
4.5. Cell-receptor density effect

Receptor density of a given cell line cannot be manipulated as easily as the surface ligand density; rather, in order to investigate the effect of receptor density, different cell lines expressing vastly different levels of the same receptor are utilized. Thus, suspensions of MDA-MB-231 and BT-20 cells with an EpCAM expression level of 1,700 and 139,500 per cell [41], respectively, were driven through microchannels functionalized with an EpCAM antibody solution at a 100μg/ml concentration. The measured capture ratios for both cell lines are summarized in Figure 6a as a function of the applied flow rate; capture ratio empirical predictions based on Equation 4 are also plotted yielding Q_C=1.4 and 2.55μl/min with and B=5.7 and 7.0 for MDA-MB-231 and BT-20 cells, respectively. As expected, for both cell lines, α→1 at the limit Q«Q_C and α→0 at the limit Q»Q_C. However, under the same intermediate flow rate, the capture ratio of BT-20 cells is much higher than that of MDA-MB-231 cells. Basically, MDA-MB-231 and BT-20 are two different types of cells, and one can attribute the different capture ratio to other biophysical differences between them. However, the two lines feature cells of very similar size, shape and compliance. The major difference between the two cells, with respect to the cell capture approach, is the cell receptors; therefore, most likely, the higher capture ratio of BT-20 cells is due to the higher expression level of EpCAM receptors.

Fig. 6.

(a) Capture ratio measurements (symbols) and predictions based on Equation 4 (curves) of MDA-MB-231 and BT-20 cells, varying in EpCAM receptor density, as a function of the flow rate in microchannels functionalized with EpCAM antibodies at a concentration of 100μg/ml; measured and predicted effect of cell-receptor density on: (b) MDA-MB-231 and BT-20 capture ratio under selected flow rates, and (c) characteristic flow rate for capturing MDA-MB-231 and BT-20 cells in anti-EpCAM functionalized microchannels with N_L=4.0×10¹⁰/cm².

Capture ratios calculated as a function of the receptor density for the highest ligand density of N_L=4.0×10¹⁰/cm² are compared in Figure 6b with measured rates available for only two receptor densities under 3 selected flow rates: 0.9, 1.5, and 2.0μl/min. The favorable agreement suggests that the theoretical model provides an acceptable estimation of the receptor number effect on cell capture ratio. Under any tested flow rate, the cell capture ratio increases with increasing receptor number; and, consistently, the characteristic flow rate increases monotonically with increasing cell receptor density as plotted in Figure 6c within the tested receptor density range.

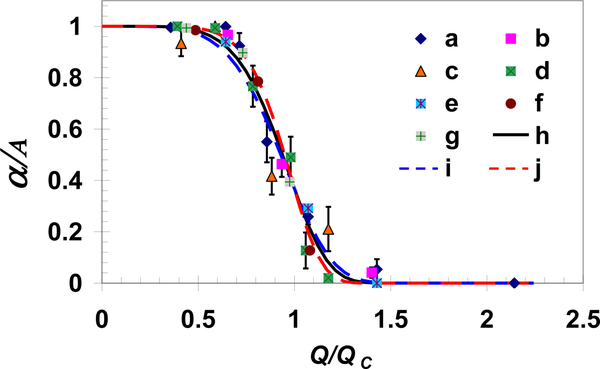
The cell capture ratio depends indirectly on both the cell-receptor and surface-ligand densities via the characteristic flow rate as expressed in Equation 4. The characteristic flow rate increases with increasing receptor or ligand density. Utilizing this characteristic flow rate to normalize the applied shear flow rate, all measured and calculated capture ratios collapse onto a single curve with B=6±1 as demonstrated in Figure 7. Hence, the reported cell attachment behavior may not be limited to a particular cell–surface combination but can be extended to other systems featuring cells in shear flow adhering to a surface via specific receptor-ligand bindings.

Fig. 7.

All measured and simulated normalized capture ratios as a function of the normalized flow rate collapse onto a single exponential function presented in Equation 4. Experimental data sets ‘a’, ‘b’, and ‘c’ are for MDA-MB-231 cells in a channel coated with EpCAM antibodies at concentrations of 100, 10, and 1μg/ml, respectively, while ‘d’ is for BT-20 cells in a channel coated with EpCAM antibodies at a concentration of 100μg/ml; data sets ‘e’, ‘f’ and ‘g’ are calculations for cell receptor densities of 5.4×10⁸, 6.4×10⁹ and 1.6×10¹⁰/cm², respectively, with ligand density of 4.0×10¹⁰/cm²; and curves ‘h’, ‘i’ and ‘j’ are exponential functions with exponents B=6±1.

5. Conclusions

The motion of circulating tumor cells under applied shear flow in antibody-functionalized microchannels has been investigated experimentally and analyzed theoretically. The cell motion is modeled as a rigid sphere, with receptors on its surface, moving under shear flow above a surface immobilized with ligands. The system is described mathematically by the Langevin equation, in which the receptor-ligand bonds are modeled as linear springs. Primarily depending on the applied flow rate, three distinct dynamic states of cell motion have been observed: free motion, rolling adhesion, and firm adhesion. The cell-surface gap and the spring constant were estimated by matching the predicted to measured cell velocity under free-motion and firm-adhesion dynamic states, respectively. The fraction of cells captured due to firm adhesion, defined as capture ratio, depends on the applied flow rate with a characteristic value that increases with increasing either cell-receptor or surface-ligand density. Utilizing this characteristic flow rate as a scaling parameter, all measured and calculated capture ratios for different receptor and ligand densities collapse onto a single exponential curve.