Abstract
Purpose
Intravoxel incoherent motion (IVIM) analysis gives information on tissue diffusion and perfusion and may thus have a potential for e.g. tumor tissue characterization. This work aims to study if clustering based on IVIM parameter maps can identify tumor subregions, and to assess the relevance of obtained subregions by histological analysis.
Methods
Fourteen mice with human neuroendocrine tumors were examined with diffusion‐weighted imaging to obtain IVIM parameter maps. Gaussian mixture models with IVIM maps from all tumors as input were used to partition voxels into k clusters, where k = 2 was chosen for further analysis based on goodness of fit. Clustering was performed with and without the perfusion‐related IVIM parameter , and with and without including spatial information. The validity of the clustering was assessed by comparison with corresponding histologically stained tumor sections. A Ki‐67‐based index quantifying the degree of tumor proliferation was considered appropriate for the comparison based on the obtained cluster characteristics.
Results
The clustering resulted in one class with low diffusion and high perfusion and another with slightly higher diffusion and low perfusion. Strong agreement was found between tumor subregions identified by clustering and subregions identified by histological analysis, both regarding size and spatial agreement. Neither nor spatial information had substantial effects on the clustering results.
Conclusions
The results of this study show that IVIM parameter maps can be used to identify tumor subregions using a data‐driven framework based on Gaussian mixture models. In the studied tumor model, the obtained subregions showed agreement with proliferative activity.
Keywords: clustering, diffusion, histology, IVIM, MRI, perfusion
1. INTRODUCTION
The vast number of available contrast mechanisms and capability to capture both anatomical and functional information in vivo make magnetic resonance imaging (MRI) an important tool for tumor characterization.1 Among the functional techniques, diffusion and perfusion MRI are frequently used for tumor diagnosis and response assessment due to their sensitivity to relevant tumor tissue characteristics.2 Diffusion MRI has the potential to probe microstructural tissue properties such as tumor cellularity and membrane integrity,3 whereas perfusion MRI can be used to evaluate the tumor vascularity.4 Therapy‐induced changes of these properties occur well before gross morphological changes, which make them highly interesting for e.g. early therapy response assessment.2, 5
It is increasingly recognized that clinically important tumor characteristics such as proliferative activity, cell death, and vascularization may vary substantially between different parts of the tumor.6 This intratumor heterogeneity can result in substantial differences in therapeutic effect across the tumor and it has been shown to be a strong indicator of clinical outcome.7, 8 Methods for assessment of the intratumor heterogeneity are thus becoming increasingly important for therapy response assessment and treatment planning.9
Quantitative in vivo imaging approaches, such as MRI, enable extraction of spatial information on tissue characteristics. Even so, most quantitative imaging studies of tumors resign to averaging parameter values over the entire tumor, with the potential loss of important information.9 Several methods have been suggested to account for tumor heterogeneity, such as 1D‐ or 2D‐histogram analysis and texture analysis, longitudinal voxelwise analysis or division of the tumor into subregions.9, 10, 11 Ideally, the method should capture the information on heterogeneity contained in the images in a compact way, but also provide a comprehensible interpretation. Histogram and texture analysis have shown promise as markers of tumor heterogeneity, but are completely based on mathematical descriptions of the distribution of data and often lack a clear biological meaning.12 Longitudinal voxelwise analysis is intuitive and has been proven useful for therapy response assessment, but is complicated by the need for high‐quality image co‐registration between time points. Partitioning of tumors into smaller regions for a subsequent, more localized analysis, provides interpretable results, but requires a proper way of defining the subregions if the results are to be relevant.
Several methods have been suggested for identification of tumor subregions based on MRI.9 The methods have been based on geometrical parameters, such as radial distance from the tumor center,13, 14 as well as functional characteristics based on different quantitative imaging‐derived parameters, either by predefined thresholds15 or by partitioning derived from the data itself.16 Among the data‐driven approaches, clustering methods such as k‐means clustering or Gaussian mixture models (GMM) have been proposed to enable partitioning of tumor voxels based on multiparametric data.16, 17 By including voxel data from multiple tumors and multiple time points, it is possible to produce clustering results with partitioning of voxels that is comparable across tumors and time.18
Since tumor subregions identified by clustering approaches are obtained in an unsupervised manner based on MR‐data only, they are not guaranteed to have a distinct biological meaning. However, such tumor subregions have shown agreement with histological analyses16, 19, 20 and have been used to monitor or predict treatment response.21, 22, 23
Most previous clustering studies have focused on identifying subregions based on properties of the tumor vascularity using various forms of dynamic contrast‐enhanced MRI.17, 18, 22, 23, 24, 25, 26, 27, 28, 29 But other MR techniques, such as mapping of the tissue relaxation and the apparent diffusion coefficient (ADC), have also been utilized successfully.16, 19, 20, 21, 22
Intravoxel incoherent motion (IVIM) imaging has been proposed as a way of acquiring both diffusion and perfusion information completely noninvasively with a single imaging sequence.30 Since both blood microcirculation and tissue water diffusion are motions that cause a reduced MR signal when diffusion weighting is applied, a model can be fit to the diffusion‐weighed imaging data to obtain model parameters describing the perfusion and diffusion within each voxel. The information attainable from IVIM parameter maps is thus interesting for tumor subregion identification by e.g. clustering.
The aim of this study was (1) to investigate if clustering of IVIM parameters can be used for identification of tumor subregions and (2) to evaluate the biological relevance of the obtained subregions by histological analysis.
2. METHODS
2.1. Tumor model
Samples from the human small intestine neuroendocrine GOT1 tumor cell line31 were subcutaneously transplanted into the neck region of 4 weeks old female BALB/c nude mice (n = 14, Charles River, Japan and Germany) under anesthesia.
The animals were fed with standard diet and water ad libitum, and when tumor diameters reached approximately 15 mm, they were injected intravenously with a non‐curative amount of 15 MBq Lu‐octreotate (specific activity: 26 MBq/mg octreotate, manufacturer: IDB Holland, the Netherlands) in a tail vein. Lu activity in syringes was measured before and after injection using a well‐type ionization chamber (CRC‐15R; Capintec, Iowa), and the estimated absorbed dose to tumor was 4.0 Gy, according to MIRD formalism.
MR experiments were conducted 13 days after Lu‐octreotate injection. At that time point, the tumor volume was either stable or increasing after the initial therapeutic response, which ranged from significant tumor volume reduction to reduced growth rate (data not shown).
The study was approved by the Ethical Committee on Animal Research in Gothenburg, Sweden. Data from the animals were also included in a previous study on therapy response assessment.14
2.2. MR imaging
MR imaging was performed on a horizontal bore 7T system (Bruker BioSpin 70/20AS MRI GmbH, Ettlingen, Germany; software: ParaVision 5.1), equipped with a maximum 400 mT/m gradient system, a 72 mm volume transmit coil, and an actively decoupled four‐channel array rat brain receiver coil (RAPID Biomedical GmbH, Rimpar, Germany). Magnetic field homogeneity within the tumor was optimized by field map‐based shimming (Bruker MAPSHIM). Diffusion‐weighted spin echo‐echo planar images (SE‐EPI) (Δ = 9 ms, δ = 4 ms) were acquired with three orthogonal gradient directions and b‐values 1.4, 14, 25, 36, 56, 82, 108, 421, and 751 s/ (5 animals) or 1.4, 5, 10, 20, 35, 50, 75, 100, 201, 401, 602 and 802 s/ (9 animals). Additional imaging parameters were: TE = 22 ms, TR = 1500 ms, number of signals averaged = 3, pixel size = 320 × 320 , slice thickness = 1000 μm, slice gap = 500 μm, partial Fourier acceleration = 1.5, and EPI echo spacing = 0.3 ms. The field of view (FOV) was approximately 14 × 26 (anterior‐posterior × left‐right directions) with phase encoding in the anterior‐posterior direction. The FOV was set to include the tumor and only very small amounts of other tissues. All animals were imaged in supine position, anesthesia was maintained using air and isoflurane (2‐3%, Isoba vet., Schering‐Plough Animal Health, Denmark), and body temperature was maintained by a heating pad and a circulating warm water system. The tumor was immobilized to reduce motion artifacts, by fitting it into a circular hole in the plastic cradle that supported the animal. Total scan time was approximately 3 minutes.
2.3. Model fitting
The IVIM effect was modeled using a biexponential model as follows:
| (1) |
where S(b) is the signal at the diffusion weighting characterized by the b‐value b, is the signal without diffusion weighting, f is the perfusion fraction, D is the tissue water diffusion coefficient and is the pseudo‐diffusion coefficient, describing the motion of water molecules in the capillaries.
The IVIM model (Equation 1) was fit voxel‐by‐voxel using a Bayesian method with prior distributions as shown in Table 1 and the mode used as central tendency measure, as described previously.32 Briefly, a Markov Chain Monte Carlo setup was used to sample the posterior distribution and parameter estimates were obtained by calculating the mode of the sampled marginal distributions of the posterior parameter distribution. The code is available at http://mathworks.com/matlabcentral/profile/authors/3680885‐oscar‐jalnefjord. A 3 × 3 in‐plane median filter was applied before model fitting to reduce noise level and residual effects of motion.
Table 1.
Prior distributions used for Bayesian IVIM model fitting
| Parameter | Distribution | Distribution parameters (other than limits) | Distribution limits (lower–upper) | |
|---|---|---|---|---|
| D | Lognormal | μ = −6, σ = 1 | 0‐5 /ms | |
| f | Uniform | — | 0‐1 | |
|
|
Lognormal | μ = −3.5, σ = 1 | 0‐1000 /ms | |
|
|
Uniform | — | 0‐2 |
and σ are given in numbers converting to /s.
is the maximum measured signal.
2.4. Clustering
The tumors were manually delineated in all slices using the image with the highest b‐value. The IVIM parameters D, f and from each voxel in every slice of all tumors were then included in a common set of data used as input to the clustering algorithms described below and outlined in Figure 1. All IVIM parameters were log‐transformed before clustering to better conform to being approximated by a sum of Gaussian distributions.
Figure 1.

Flowchart showing the MR analysis, including model fitting and clustering. IVIM parameter maps were calculated based on diffusion‐weighted images. The IVIM parameter maps from all tumors were used as input to the clustering algorithm, which produced both cluster maps, i.e. voxelwise class probabilities, and the cluster characteristics (class mean), (class covariance) and P(l) (prior class probability)
Soft clustering of data into k classes was performed by fitting a Gaussian mixture model (GMM) using the expectation maximization (EM) algorithm. Each iteration of the algorithm starts with calculation of the class probabilities given the current set of model parameters (E‐step) as:
| (2) |
where the superscript (t) shows the iteration index, is the class of voxel i, l is a given class label ranging from 1 to k, is a column vector containing D, f and , is the multivariate Gaussian probability density function with mean and covariance , and is prior class probability, also commonly denoted the mixing coefficient. The E‐step is followed by recalculation of the model parameters given the new class probabilities (M‐step) as:
| (3) |
| (4) |
| (5) |
where N is the total number of voxels and T indicates transpose. Fitting the GMM thus comprises estimation of k sets of prior class probabilities , mean vectors and covariance matrices .
Assuming that tumor subregions typically are larger than the voxel size, neighboring voxels are more likely to belong to the same cluster. Inclusion of this spatial information has previously been shown to enhance the clustering performance.20 Therefore, a Gaussian hidden Markov random field model (GHMRFM) was implemented as described by Zhang et al.33 The difference compared with the GMM is the prior class distribution, which is set to depend on the class of neighboring voxels. At each E‐step in the EM‐algorithm, the class probabilities are instead calculated as
| (6) |
where is given by the Gibbs distribution
| (7) |
where Z is a normalizing constant and denotes the classes of voxels in the neighborhood of voxel i, which was defined as the four voxels in the same image slice that shared a side with voxel i, i.e. the closest vertical and horizontal neighbors. Calculation of necessitates estimation of the class labels. This was achieved through maximization of the posterior class probability using iterative conditional modes.33, 34
The clustering was also performed based on only D and f to study the impact of exclusion of . This may be of interest since could be hampered by low precision or not be available at all depending on image quality and choice of Yuan et al35 and Lemke et al.36
The number of clusters, k, was chosen based on a heuristic method where the mixture model (GMM or GHMRFM) was fitted for k ∈ {1, …, 8}. For each k, the goodness of fit (GOF) was evaluated as:
| (8) |
where the term in the inner sum equals the numerator in Equation 2 or 6 depending on model. The optimal value of k was chosen by finding the knee in a GOF vs. k plot, i.e. by finding the maximum second derivative of GOF with respect to k. The rationale behind this method is that if the data originate from classes, the GOF will increase substantially when more classes are added to the model for . When additional classes are added for , the additional increase in GOF is associated with fitting random fluctuations in the data and the increase is therefore limited.37 For both the GMM's and GHMRFM's with or without included, the optimal k was determined to be 2 (Supporting Information Figure S1).
The GMM was fitted using the built‐in MATLAB function fitgmdist whereas the GHMRFM was fitted using an in‐house developed function in MATLAB. Twenty random initializations were used to avoid potential local optima. The fitting algorithms were initialized by assigning all data points randomly to the k classes. Convergence was considered when the relative change in GOF (Equation 8) between iterations was less than . The robustness of the results was assessed by ensuring that the results were consistent when the fitting was repeated. MATLAB code for generation of cluster maps is available at http://mathworks.com/matlabcentral/profile/authors/3680885‐oscar‐jalnefjord.
2.5. Histological analysis
Even if the clustering results in distinct partitioning of voxels, it cannot be guaranteed that the obtained clusters have a distinct biological meaning. Other potential sources of distinct variations in the parameter maps are image artifacts and system imperfections. To verify that the partitioning was due to biological variations, a histological analysis was performed in accordance with previous studies on identification of tumor subregions by clustering.16, 19, 20 Based on the characteristics of the clusters, i.e. the IVIM parameter combinations describing the mean vector of each class, it was hypothesized that the partitioning was related to proliferative activity and the histological analysis was chosen accordingly.
Immediately after the MR examination, the animals were killed by a lethal injection of sodium pentobarbitone (Pentobarbitalnatrium vet., Apotek Produktion & Laboratorier AB, Sweden, 60 mg/ml), followed by a heart incision. In order to achieve histological sections corresponding to the acquired images, the tumor was cut into two halves with the incision parallel to the MR imaging plane. The tumor was then embedded in paraffin (Thermo Scientific HM 355S Automatic, Fisher Scientific, Sweden) with the cut surface positioned to meet the sweep plane of the microtome knife and three μm thick sections were collected for histological analysis.
The staining procedure included pretreatment with EnVision FLEX Target Retrieval Solution (high pH; PT‐Link; Dako, Denmark) followed by incubations using Envision Flex (Dako, Denmark) and staining with a Ki‐67 antibody, against the Ki‐67 protein that is associated with cellular proliferation (AB9260; Merck Milipore). An autostainer Link (Dako, Denmark) was used for staining by following the manufacturer's instructions. Positive and negative controls were included in each run.
The stained tissue sections were digitally imaged using a Leica SCN400 Slide Scanner (40× magnification, Leica Microsystems, Germany), resulting in images of 0.25 × 0.25 resolution. To exclude background and adjacent tissue, the tumor tissue region was manually delineated. Segmentation of tumor tissue into proliferating or non‐proliferating regions was then performed on the digitized histological images in three steps as outlined in Figure 2. First, a 3‐dimensional color threshold was defined in the YCbCr color space in order to separate Ki‐67 positive pixels (light to dark brown) from Ki‐67 negative pixels. The color threshold outlined a rectangular block parallel with the coordinate axes of the color space. Second, an index defined as the proportion of Ki‐67 positive pixels in regions of 256 × 256 pixels (i.e. 64 × 64 ) was calculated. Finally, proliferating regions were identified by applying a 2% threshold to the index maps, where an index higher than 2% was considered consisting of proliferating cells. A board certified pathologist was shown histological regions indexed above and below 2%, and verified that the regions appeared as proliferating and non‐proliferating, respectively.
Figure 2.
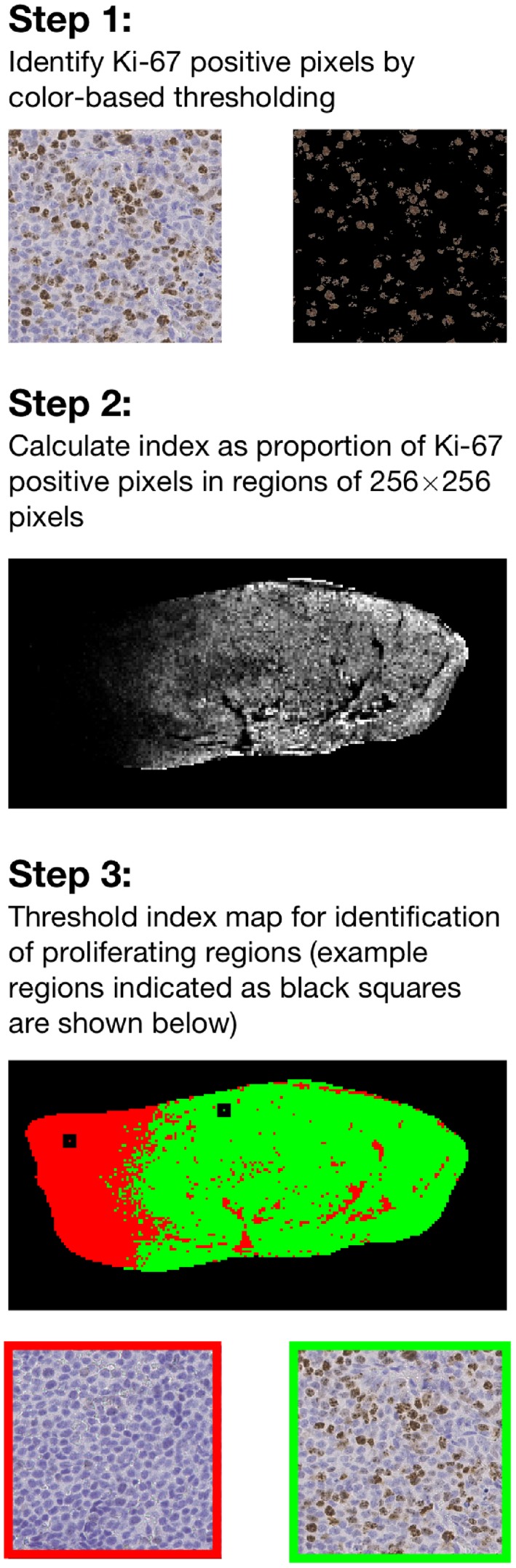
Flowchart showing the three steps in the histological analysis of Ki‐67 stained histological sections, which was used for identification of proliferating tumor regions. In the images shown in the first step, individual cells can be seen. Applying the color threshold identifies proliferating cells. The image in the second step is an index map of the entire tumor. The top image in the last step shows a thresholded index map where regions defined as proliferating are shown in green
2.6. Statistical analysis
The agreement between subregions obtained from clustering and histological analysis was quantified by calculating Lin's concordance correlation coefficient between areas of subregions belonging to the cluster with high perfusion and areas identified as proliferating by the histological analysis. To compensate for MR image distortions and for tissue shrinkage during the histological procedures, the tumor area in the histological index maps was set equal to the area of the tumor in the MR image.
3. RESULTS
3.1. IVIM parameter data and clustering results
The IVIM parameters displayed distributions on the log scale that appeared well suited for being described by a few Gaussian distributions as is assumed when fitting a GMM (1D histograms in Figure 3 and 2D histograms in Supporting Information Figure S2). The subsequent clustering resulted in one class with low diffusion and high perfusion and one with higher diffusion and lower perfusion (Table 2). The obtained cluster maps displayed distinct spatial patterns with large contiguous subregions in several tumors (Figure 4 and Supporting Information Figures S3‐S15).
Figure 3.
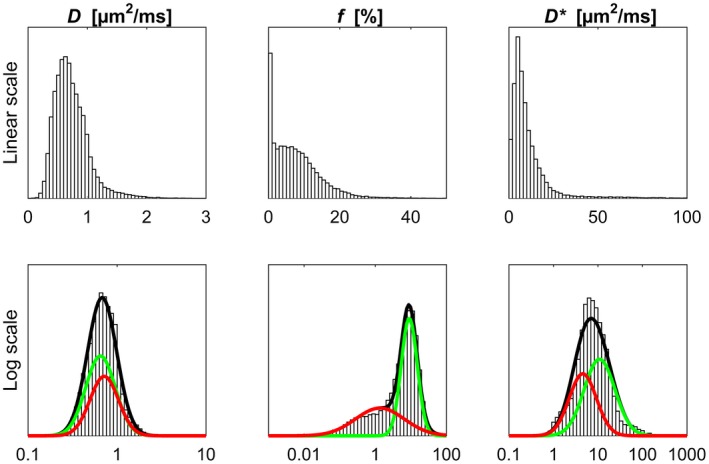
Distributions of IVIM parameter estimates on linear scale (top row) and log scale (bottom row) shown as histograms. The GMM fit based on log‐transformed data is superimposed on the histograms in black. The Gaussian distributions corresponding to the individual classes are shown in green and red (corresponds to class 1 and 2 in Table 2, respectively). The parameter data originate from all tumors in this study
Table 2.
Cluster characteristics for the different clustering approaches
| Without | With | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GMM | GHMRFM | GMM | GHMRFM | |||||||
| Class label l | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | ||
| P(l) (%) | 65 | 35 | 65 | 35 | 58 | 42 | 60 | 40 | ||
| D (/ms) | 0.65 | 0.73 | 0.62 | 0.78 | 0.65 | 0.72 | 0.61 | 0.80 | ||
|
|
f (%) | 8.8 | 1.0 | 9.2 | 1.0 | 9.0 | 1.4 | 9.5 | 1.3 | |
| (/ms) | — | — | — | — | 10.9 | 4.6 | 11.7 | 4.1 | ||
Note: P(l) is the prior class probability, i.e. the size of class l, and is the mean vector of class l contain values of D, f and .
Figure 4.
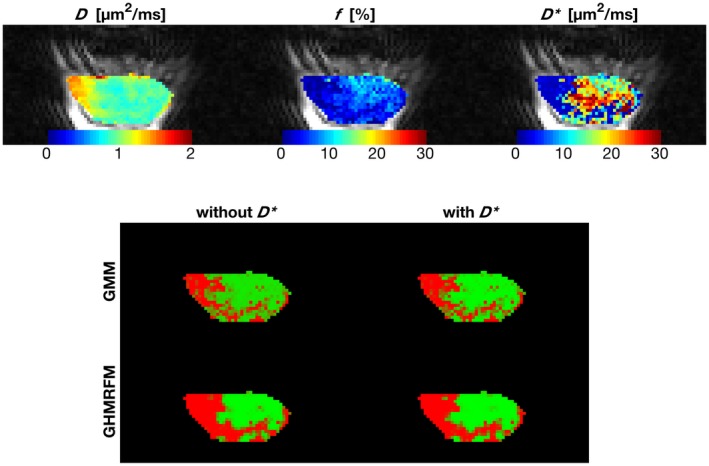
IVIM maps in color superimposed on the b = 1.4 s/ image (top) and cluster maps based on all clustering approaches (bottom) for an example tumor (same as in Figure 2). The cluster with high perfusion and low diffusion is shown in green in the cluster maps, while the cluster with low perfusion and somewhat higher diffusion is shown in red
Clustering with or without yielded similar results regarding cluster centers (Table 2) and spatial appearance (Figure 4 and Supporting Information Figures S3‐S15). Including spatial information in the clustering also had minor impact on the results (Table 2), although the cluster maps became somewhat more binary due to the support of information from neighboring voxels (Figure 4 and Supporting Information Figures S3‐S15).
3.2. Agreement with histological analysis
A strong agreement was found between the areas defined as proliferating by histological analysis and the cluster areas related to low diffusion and high perfusion, both regarding size (Figure 5) and spatial similarity (Figure 6 and Supporting Information Figures S16‐S18). The concordance coefficient was high for all the studied approaches, although slightly lower for results based on GMM with included, mainly due to underestimation (top right plot in Figure 5). Most of the non‐proliferating regions, as identified by histology, were also seen in the cluster maps (e.g. tumors 12 and 13 in Figure 6 and Supporting Information Figures S16‐S18). In a few cases, regions were marked as typically non‐proliferating by the clustering results although no such indication was supplied by the histological analysis (e.g. tumor 14 in Figure 6 and Supporting Information Figures S16‐S18).
Figure 5.
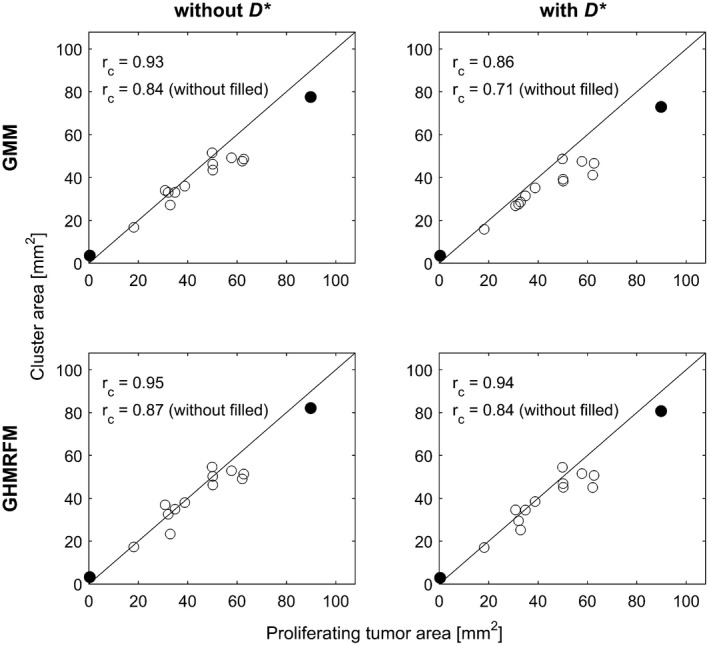
Scatter plots showing area of cluster with high perfusion and low diffusion identified by IVIM parameter clustering versus proliferating area derived from histological analysis. Lin's concordance correlation coefficient (), based on all data points, and when excluding the largest and smallest data point (filled circles), are shown in each plot along with the line of equality
Figure 6.
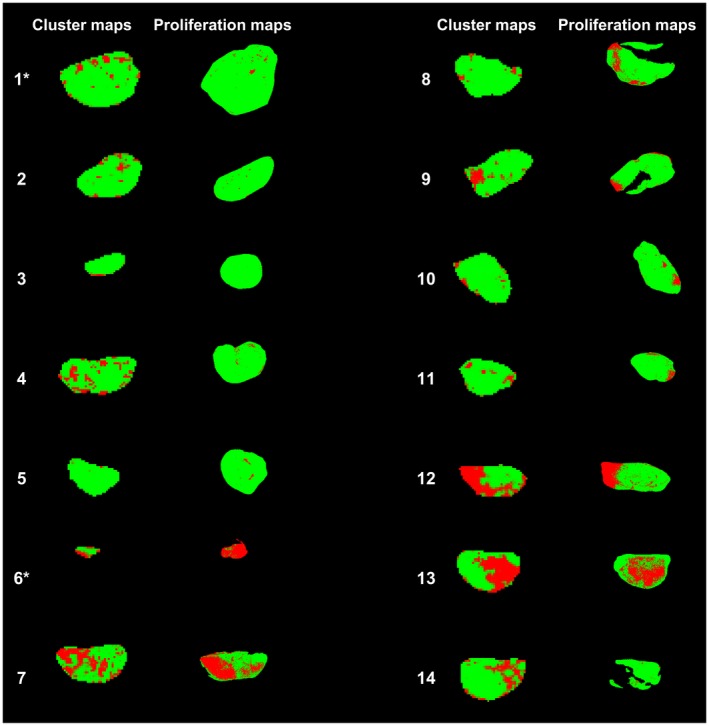
Cluster maps based on the GHMRFM without (approach with highest Lin's concordance correlation coefficient ()) and thresholded histology‐derived proliferation maps shown side‐by‐side for all tumors in this study. In the cluster maps, green indicates probability belonging to the cluster with high perfusion and low diffusion. In the thresholded proliferation maps, green pixels are above the threshold and are thereby considered to be proliferating. The tumors plotted as filled circles in Figure 5 are marked by an asterisk (*)
4. DISCUSSION
This study presents an IVIM‐based clustering framework that can be used to identify tumor subregions based on the functional information contained in the IVIM parameters. The results show that when applied to a mouse model of human neuroendocrine tumor, cluster maps displayed a strong agreement with proliferative activity derived from Ki‐67‐stained tumor sections. The presented framework enables spatially localized analysis of functionally specific tumor subregions and may prove useful in longitudinal studies where it can be used to follow the evolution of tumor subregions over time. Furthermore, unlike previous clustering approaches where perfusion‐related parameters have been included, the IVIM‐based approach used in the current study does not require an intravenous injection of a contrast agent and is completely noninvasive.
The cluster analysis resulted in one cluster that was described by relatively high perfusion and low diffusion, and another cluster that was described by a very low perfusion, but only marginally higher diffusion. Reduced diffusion is associated with growth in several types of solid tumors, where uncontrolled proliferation and evasion of cell death mechanisms lead to increased cell density and, consequently, hindered water diffusion. Furthermore, in order for cells to proliferate, adequate perfusion is required.2 This is in agreement with the results of this study, where the first cluster (high perfusion, low diffusion) corresponded spatially to the histological regions showing higher proliferative activity. Conversely, limited access to nutrients and oxygen due to inadequate perfusion will hamper proliferation. Moreover, tumor regions with low perfusion are more likely to be hypoxic or necrotic, and if tissue degradation is taking place, increased diffusion may be possible due to disintegration of membrane structures. The second cluster, described by very low perfusion and slightly higher diffusion may thus correspond to such tissue regions. This is supported by the fact that it corresponded spatially to low‐proliferation regions on the Ki‐67 index maps. While this reasoning applies to the studied tumor model, other tumor types may have other tissue characteristics. For example, some tumors thrive in hypoxic environments and would therefore likely be characterized by other combinations of IVIM parameters. It is therefore important to generate new clustering results for each specific setting, including tumor type and potential treatment.
Previous studies have shown that the diffusion coefficient was an important parameter for identification of necrotic regions.16, 19, 20 However, as is typical for the GOT1 tumor model, the tumors in this study did not display any obvious regions of necrosis, due to the slow tumor growth rate characteristics for these types of neuroendocrine tumors.31 In the current study, the perfusion parameter f was the parameter that showed a prominent split into multiple clusters. D could potentially play a more important role if IVIM‐based clustering is applied in tumors with more necrosis. In such case, it may be of interest to evaluate the proposed framework on a larger number of clusters.
Including as input to the clustering appeared to have very limited effects on the results. In low perfused tissue, estimates of are often associated with a high level of uncertainty due to the small signal fraction it is estimated from Lemke et al.36 In the present study, a Bayesian approach with lognormal prior distributions on D and was used to fit the model. The Gaussian shape of the distributions of those parameters, as seen in Figure 3, can thus partly be due to the prior distribution, especially for . Choosing a less informative prior distribution would be possible, but may then be even less useful because of high estimation uncertainty.32 However, if the data used as input to the clustering includes multiple highly perfused tissue regions where can be estimated with higher certainty, could potentially have an incremental value.
The clustering with GMM's gave cluster characteristics, including mean vectors, very similar to those with GHMRFM's, which indicates that a sufficient amount of information for clustering is contained in the IVIM parameter data. The difference between clustering based on GMM and GHMRFM was mainly a more distinct clustering into one or the other cluster, as would be expected due to the inclusion of information from neighboring voxels, especially in fairly homogeneous regions. Given the limited additional benefit in using GHMRFM, GMM appears preferable, especially based on computational cost since fitting a GHMRFM is associated with a computational time that is orders of magnitude longer than when fitting a GMM. For the data set used in this study, the computational time was on the order of seconds for GMM and minutes to hours for the GHMRFM on a modern laptop, with different computational time depending on the number of clusters. The difference between GMM's and GHMRFM's could potentially have been larger if no spatial filtering would have been applied prior to the model fit. However, the reason for filtering was not to obtain smoother parameter maps, but rather to get IVIM parameters of higher quality to enhance the subsequent clustering.
Previous studies have validated the clustering results by comparing the obtained tumor subregions with histological data16, 19, 20 or by relating them to treatment response.21, 22, 23 In the present study, the clustering results were compared with data from histological sections stained with a Ki‐67 antibody, which binds to actively proliferating cells. Proliferating tumor regions were identified as areas with a high proportion of Ki‐67 positive pixels, which was assumed to be equivalent to a high proportion of Ki‐67 positive cells. This histological validation method was chosen since it is related to a tissue property that is of interest for tumor tissue characterization, but is not directly related to any of the individual IVIM parameters. Studying the direct relationship between a single MR derived parameter and a histological counterpart e.g. D and cell density for hematoxylin and eosin staining,38 or f and microvessel density for CD‐31 staining39 has been done previously and was outside the scope of this study.
This study is associated with some limitations. The number of tumors is relatively small and only a single tumor model was studied. Still, the results clearly encourage future studies on the usefulness of IVIM in other tumor types, but future work should also address repeatability, by repeated MR measurements, and reproducibility, by scanning of additional subjects or animals, to assess the robustness of the clustering results. Also, the histological analysis was limited to a single staining. However, since the two identified classes were accurately described by differences in proliferative activity, use of additional stainings would mostly show correlations between stainings. In future studies, depending on the studied tumors it may be beneficial to include other types of stainings to enable assessment, e.g. the degree of hypoxia or necrosis in the tissue for a more thorough characterization of the obtained tumor subregions. Furthermore, no direct co‐registration between MR and histology was made. The spatial agreement between proliferating areas derived from histological analysis and cluster regions from MRI was therefore only qualitatively assessed in combination with a quantitative comparison of subregion areas. It is also unclear whether the differences in tumor size between MR images and Ki‐67 images can be compensated for by a simple scaling, as is assumed in the normalization used in this study. However, direct co‐registration between MR images and histological tumor sections remains difficult due to MR image distortions and tissue deformations during the histological preparation process, especially in homogeneous tumors where landmarks within the tumor are missing. Finally, the manual delineation of tumors in the image with highest b‐value may have biased the analysis toward excluding tumor tissue with high diffusion. However, this approach was chosen due to the limited contrast between tumor and surrounding tissue in images with a low b‐value. Alternatively, it would have been possible to, for example, use a co‐registered weighted reference image for delineation.40
5. CONCLUSIONS
The results of this study show that IVIM parameter maps can be used to identify tumor subregions using a data‐driven framework based on Gaussian mixture models. In the studied tumor model, the obtained subregions showed agreement with proliferative activity as derived from histological analysis.
Supporting information
FIGURE S1 Goodness of fit (GOF) and second derivative of GOF plotted versus the number of clusters k for all clustering approaches
FIGURE S2 Joint distributions of IVIM parameters before and after log transformation
FIGURES S3‐S15 IVIM parameter maps and cluster maps as seen in Figure 4 for all tumors except the one seen in Figure 4
FIGURES S16‐S18 Cluster maps and proliferation maps as seen in Figure 6 for clustering based on GHMRFM with or GMM with/without
ACKNOWLEDGMENTS
We are greatly thankful to Prof. Ola Nilsson for valuable contributions and discussions regarding the histological analysis and to Lilian Karlsson and Ann Wikström for their skillful technical assistance.
Jalnefjord O, Montelius M, Arvidsson J, Forssell‐Aronsson E, Starck G, Ljungberg M. Data‐driven identification of tumor subregions based on intravoxel incoherent motion reveals association with proliferative activity. Magn Reson Med. 2019;82:1480–1490. 10.1002/mrm.27820
REFERENCES
- 1. Marcus CD, Ladam‐Marcus V, Cucu C, Bouché O, Lucas L, Hoeffel C. Imaging techniques to evaluate the response to treatment in oncology: current standards and perspectives. Critical Rev Oncology/Hematol. 2009;72:217–238. [DOI] [PubMed] [Google Scholar]
- 2. Li SP, Padhani AR. Tumor response assessments with diffusion and perfusion MRI. J Magn Reson Imaging 2012;35:745–763. [DOI] [PubMed] [Google Scholar]
- 3. Padhani AR, Liu G, Mu‐Koh D, et al. Diffusion‐weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia 2009;11:102–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. O'Connor JPB, Jackson A, Parker GJM, Jayson GC. DCE‐MRI biomarkers in the clinical evaluation of antiangiogenic and vascular disrupting agents. Br J Cancer 2007;96:189–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer 2009;45:228–247. [DOI] [PubMed] [Google Scholar]
- 6. Hanahan D, Weinberg R. Hallmarks of cancer: the next generation. Cell 2011;144:646–674. [DOI] [PubMed] [Google Scholar]
- 7. Junttila MR, de Sauvage FJ. Influence of tumour micro‐environment heterogeneity on therapeutic response. Nature 2013;501:346–354. [DOI] [PubMed] [Google Scholar]
- 8. Shipitsin M, Campbell LL, Argani P, et al. Molecular definition of breast tumor heterogeneity. Cancer Cell 2007;11:259–273. [DOI] [PubMed] [Google Scholar]
- 9. O'Connor JPB, Rose CJ, Waterton JC, Carano RAD, Parker GJM, Jackson A. Imaging intratumor heterogeneity: role in therapy response, resistance, and clinical outcome. Clin Cancer Res. 2015;21:249–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Galbán CJ, Chenevert TL, Meyer CR, et al. The parametric response map is an imaging biomarker for early cancer treatment outcome. Nat Med. 2009;15:572–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Wiederer J, Pazahr S, Leo C, Nanz D, Boss A. Quantitative breast MRI: 2D histogram analysis of diffusion tensor parameters in normal tissue. Magn Reson Mater Phys Biol Med. 2014;27:185–193. [DOI] [PubMed] [Google Scholar]
- 12. Alic L, Niessen WJ, Veenland JF. Quantification of heterogeneity as a biomarker in tumor imaging: a systematic review. PLoS ONE 2014;9:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Gaustad JV, Benjaminsen IC, Graff BA, Brurberg KG, Ruud EBM, Rofstad EK. Intratumor heterogeneity in blood perfusion in orthotopic human melanoma xenografts assessed by dynamic contrast‐enhanced magnetic resonance imaging. J Magn Reson Imaging 2005;21:792–800. [DOI] [PubMed] [Google Scholar]
- 14. Montelius M, Spetz J, Jalnefjord O, et al. Identification of potential MR‐derived biomarkers for tumor tissue response to 177Lu‐Octreotate therapy in an animal model of small intestine neuroendocrine tumor. Trans Oncol. 2018;11:193–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Checkley D, Tessier J, Kendrew J, Waterton J, Wedge S. Use of dynamic contrast‐enhanced MRI to evaluate acute treatment with ZD6474, a VEGF signalling inhibitor, in PC‐3 prostate tumours. Br J Cancer 2003;89:1889–1895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Carano RAD, Ross AL, Ross J, et al. Quantification of tumor tissue populations by multispectral analysis. Magn Reson Med. 2004;51:542–551. [DOI] [PubMed] [Google Scholar]
- 17. Han SH, Ackerstaff E, Stoyanova R, et al. Gaussian mixture model‐based classification of dynamic contrast enhanced MRI data for identifying diverse tumor microenvironments: preliminary results. NMR Biomed. 2013;26:519–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Jacobs I, Hectors SJCG, Schabel MC, Grüll H, Strijkers GJ, Nicolay K. Cluster analysis of DCE‐MRI data identifies regional tracer‐kinetic changes after tumor treatment with high intensity focused ultrasound. NMR Biomed. 2015;28:1443–1454. [DOI] [PubMed] [Google Scholar]
- 19. Henning EC, Azuma C, Sotak CH, Helmer KG. Multispectral quantification of tissue types in a RIF‐1 tumor model with histological validation. Part I. Magn Reson Med. 2007;57:501–512. [DOI] [PubMed] [Google Scholar]
- 20. Katiyar P, Divine MR, Kohlhofer U, et al. A novel unsupervised segmentation approach quantifies tumor tissue populations using multiparametric MRI: first results with histological validation. Mol Imaging Biol. 2016;19:391–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Henning EC, Azuma C, Sotak CH, Helmer KG. Multispectral tissue characterization in a RIF‐1 tumor model: monitoring the ADC and T2 responses to single‐dose radiotherapy. Part II. Magn Reson Med. 2007;57:513–519. [DOI] [PubMed] [Google Scholar]
- 22. Berry LR, Barck KH, Go MA, et al. Quantification of viable tumor microvascular characteristics by multispectral analysis. Magn Reson Med. 2008;60:64–72. [DOI] [PubMed] [Google Scholar]
- 23. Wang P, Popovtzer A, Eisbruch A, Cao Y. An approach to identify, from DCE MRI, significant subvolumes of tumors related to outcomes in advanced head‐and‐neck cancer. Med Phys. 2012;39:5277–5285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Torheim T, Groendahl AR, Andersen EKF, et al. Cluster analysis of dynamic contrast enhanced MRI reveals tumor subregions related to locoregional relapse for cervical cancer patients. Acta Oncol. 2016;55:1294–1298. [DOI] [PubMed] [Google Scholar]
- 25. Andersen EKF, Kristensen GB, Lyng H, Malinen E. Pharmacokinetic analysis and k‐means clustering of DCEMR images for radiotherapy outcome prediction of advanced cervical cancers. Acta Oncol. 2011;50:859–865. [DOI] [PubMed] [Google Scholar]
- 26. Castellani U, Cristani M, Daducci A, et al. DCE‐MRI data analysis for cancer area classification. Methods Inf Med. 2009;48:248–253. [DOI] [PubMed] [Google Scholar]
- 27. Wu J, Gong G, Cui Y, Li R. Intratumor partitioning and texture analysis of dynamic contrast‐enhanced (DCE)‐MRI identifies relevant tumor subregions to predict pathological response of breast cancer to neoadjuvant chemotherapy. J Magn Reson Imaging 2016;44:1107–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Featherstone AK, O'Connor JPB, Little RA, et al. Data‐driven mapping of hypoxia‐related tumor heterogeneity using DCE‐MRI and OE‐MRI. Magn Reson Med. 2018;79:2236–2245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Longo DL, Dastrù W, Consolino L, et al. Cluster analysis of quantitative parametric maps from DCE‐MRI: application in evaluating heterogeneity of tumor response to antiangiogenic treatment. Magn Reson Imaging 2015;33:725–736. [DOI] [PubMed] [Google Scholar]
- 30. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval‐Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497–505. [DOI] [PubMed] [Google Scholar]
- 31. Kölby L, Bernhardt P, Ahlman H, et al. A transplantable human carcinoid as model for somatostatin receptor‐mediated and amine transporter‐mediated radionuclide uptake. Am J Pathol. 2001;158:745–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Gustafsson O, Montelius M, Starck G, Ljungberg M. Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting. Magn Reson Med. 2018;79:1674–1683. [DOI] [PubMed] [Google Scholar]
- 33. Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation‐maximization algorithm. IEEE Trans Med Imaging 2001;20:45–57. [DOI] [PubMed] [Google Scholar]
- 34. Besag J. On the statistical analysis of dirty pictures. J R Statis Soc Ser B (Methodological) 1986;48:259–302. [Google Scholar]
- 35. Yuan Q, Costa DN, Sénégas J, et al. Quantitative diffusion‐weighted imaging and dynamic contrast‐enhanced characterization of the index Lesion With multiparametric MRI in prostate cancer patients. J Magn Reson Imaging 2017;45:908–916. [DOI] [PubMed] [Google Scholar]
- 36. Lemke A, Stieltjes B, Schad LR, Laun FB. Toward an optimal distribution of b values for intravoxel incoherent motion imaging. Magn Reson Imaging 2011;29:766–776. [DOI] [PubMed] [Google Scholar]
- 37. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. 2nd ed. New York, NY: Springer; 2009. [Google Scholar]
- 38. Lyng H, Haraldseth O, Rofstad EK. Measurement of cell density and necrotic fraction in human melanoma xenografts by diffusion weighted magnetic resonance imaging. Magn Reson Med. 2000;430:828–836. [DOI] [PubMed] [Google Scholar]
- 39. Lee HJ, Rha SY, Chung YE, et al. Tumor perfusion‐related parameter of diffusion‐weighted magnetic resonance imaging: Correlation with histological microvessel density. Magn Reson Med. 2014;71:1554–1558. [DOI] [PubMed] [Google Scholar]
- 40. Montelius M, Ljungberg M, Horn M, Forssell‐Aronsson E. Tumour size measurement in a mouse model using high resolution MRI. BMC Med Imaging 2012;12:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 Goodness of fit (GOF) and second derivative of GOF plotted versus the number of clusters k for all clustering approaches
FIGURE S2 Joint distributions of IVIM parameters before and after log transformation
FIGURES S3‐S15 IVIM parameter maps and cluster maps as seen in Figure 4 for all tumors except the one seen in Figure 4
FIGURES S16‐S18 Cluster maps and proliferation maps as seen in Figure 6 for clustering based on GHMRFM with or GMM with/without


