Predicting Cell Populations in Single Cell Mass Cytometry Data

Abstract

Mass cytometry by time‐of‐flight (CyTOF) is a valuable technology for high‐dimensional analysis at the single cell level. Identification of different cell populations is an important task during the data analysis. Many clustering tools can perform this task, which is essential to identify “new” cell populations in explorative experiments. However, relying on clustering is laborious since it often involves manual annotation, which significantly limits the reproducibility of identifying cell‐populations across different samples. The latter is particularly important in studies comparing different conditions, for example in cohort studies. Learning cell populations from an annotated set of cells solves these problems. However, currently available methods for automatic cell population identification are either complex, dependent on prior biological knowledge about the populations during the learning process, or can only identify canonical cell populations. We propose to use a linear discriminant analysis (LDA) classifier to automatically identify cell populations in CyTOF data. LDA outperforms two state‐of‐the‐art algorithms on four benchmark datasets. Compared to more complex classifiers, LDA has substantial advantages with respect to the interpretable performance, reproducibility, and scalability to larger datasets with deeper annotations. We apply LDA to a dataset of ~3.5 million cells representing 57 cell populations in the Human Mucosal Immune System. LDA has high performance on abundant cell populations as well as the majority of rare cell populations, and provides accurate estimates of cell population frequencies. Further incorporating a rejection option, based on the estimated posterior probabilities, allows LDA to identify previously unknown (new) cell populations that were not encountered during training. Altogether, reproducible prediction of cell population compositions using LDA opens up possibilities to analyze large cohort studies based on CyTOF data. © 2019 The Authors. Cytometry Part A published by Wiley Periodicals, Inc. on behalf of International Society for Advancement of Cytometry.

Short abstract

Mass cytometry by time‐of‐flight (CyTOF) is a valuable tool for the field of immunology, as it allows high‐resolution dissection of the immune system composition at the cellular level 1. Advances in CyTOF technology provide the simultaneous measurement of multiple cellular protein markers (>40), producing complex datasets which consist of millions of cells 2. Many recent studies have shown the utility of CyTOF to identify either canonical or new cell populations while profiling the immune system. These include the characterization of cell population heterogeneity for a specific cancer 3, 4, 5, assigning signature cell populations when profiling a specific disease 6, and monitoring the immune system response to various infections 7, 8.

A key step in mass cytometry analysis is the accurate identification of cell populations in a given sample. The high number of dimensions in CyTOF data has forced researchers to depart from manual gating strategies based on two‐dimensional plots because it is very labor intensive and subjective 9. These limitations greatly impede the translational aspects of these technologies. Major efforts have been made to facilitate the analysis of CyTOF data by means of clustering (unsupervised learning) methods. These include SPADE 10, FlowSOM 11, Phenograph 4, and X‐shift 12, and they are often combined with dimensionality reduction methods like PCA 13, t‐SNE 14, 15, and HSNE 16, 17.

Clustering approaches are very instrumental in analyzing high‐dimensional data and identifying different cell populations in cytometry data. These populations are defined in a data‐driven manner, avoiding biases arising from manual gating 18. Thus, in explorative experiments, clustering approaches allow the identification of both canonical cell populations and (new) cell populations, which is particularly useful when looking for rare populations in case–control experiments. After clustering, manual input is required to annotate the discovered cell populations with biologically relevant labels. This can be done by visually exploring the data, either by gating the biaxial marker expression scatter plots in the case of Flow Cytometry (FC), by overlaying the marker expression profiles on a low‐dimension representation (e.g., tSNE), or by inspecting a heatmap of the markers' expression across clusters.

Generally, this annotation process works well, especially in small explorative experiments, in which all the samples are analyzed at once. However, in cohort studies with hundreds of biological samples, the clustering analysis is usually performed per sample, or small groups of samples, as samples are collected over long time periods, or due to computational limitation in the number of cells that can be analyzed at once. Consequently, the annotation process becomes time consuming, and, more importantly, limits the reproducibility of identifying cell populations across different (batches of) samples 19. The latter is especially pronounced when looking for deeper subtyping of cell populations rather than major populations.

These limitations are inherent to both FC and CyTOF, albeit more pronounced in the latter given the higher number of dimensions and the larger number of cells being measured. In the field of FC, several supervised approaches have been proposed to automatically identify cell populations. They have been shown to match the performance of centralized manual gating based on benchmark datasets from challenges organized by the FlowCAP (“Flow Cytometry: Critical Assessment of Population Identification Methods”) Consortium 20, 21. These approaches rely on learning the manual gating from a set of training samples, and transferring the learned thresholds for the gates to new test samples.

As gating is done based on two dimensional views of the data, this is not a feasible approach for CyTOF data, since the number of markers is generally around 40, resulting in ~2⁴⁰ of gates that need to be defined (one for every pair of markers). Moreover, manual gating generally assumes that cells of interest can be selected for by dichotomizing each marker, that is, splitting cells on the basis of a marker being positively or negatively expressed (identified by a threshold value, i.e., the gate). However, analyses of CyTOF data have repeatedly shown that cell population composition is much more complex, showing many clusters that are described by a combination of all marker expressions 17, requiring the need for a multitude of gates that increases the complexity of gating even further.

Consequently, for CyTOF data, alternative gating approaches need to be considered. Recently, two methods have been developed: Automated Cell‐type Discovery and Classification (ACDC) 22 and DeepCyTOF 23. ACDC integrates prior biological knowledge on markers of specific cell populations, using a cell‐type marker table in which each marker takes one of three states (1: positively expressed, −1: negatively expressed, 0: do not consider) for each cell population. This table is then used to guide a semi‐supervised random walk classifier of canonical cell populations (i.e., cell populations with defined marker expression patterns). DeepCyTOF applies deep neural networks to learn the clustering of one sample, and uses the trained network to classify cells from different samples. Both methods achieve accurate results on a variety of datasets. However, both methods rely on sophisticated classifiers. Interestingly, neither of these methods compared their performance to simpler classifiers. Further, both methods focused mainly on classifying canonical cell populations, which is not the main focus of CyTOF studies which usually relies on the large number of markers measured for deep interrogation of cell populations.

In this work, we show that a linear discriminant analysis (LDA) classifier can accurately classify cell populations in mass cytometry datasets. Compared to previous methods, LDA presents a simpler, faster and reliable method to assign labels to cells. Moreover, using LDA instead of more complex classifiers enables the analysis of large datasets comprised of millions of cells. To illustrate this, we tested the applicability of LDA in classifying not only canonical cell populations but also deeper subtyping of the human mucosal immune system across multiple individuals, where the classification task becomes harder as the differences between cell populations are much smaller.

Methods

We define a cell as the single measurement event in CyTOF data, $c\in {\mathcal{R}}^p$, where p is the number of markers on the CyTOF panel. Cells are being measured collectively from one sample, which is the biological specimen collected from an individual. A sample usually consists of thousands of cells, that is, $s\in {\mathcal{R}}^{n_{\mathrm{c}}\times p}$, where n _c is the number of cells in sample s. A CyTOF dataset consists of multiple samples, $d\in {\mathcal{R}}^{n_{\mathrm{s}}\times n_{\mathrm{c}}\times p}$, where n _s is the number of samples in the dataset that can comprise different groups of patients. Ultimately, we are interested in identifying cells that have a similar protein marker expression, that is, cells that belong to the same population of cells. Note that with this definition of cell population, similar cells can either represent cells with the same cell type and/or state, depending on which markers are considered 24. Usually the different cell populations are derived from clustering a large collection of cells collected from different samples using an unsupervised clustering approach.

Datasets Description

We used four public benchmark datasets to evaluate our classifier, for which manually gated populations were available and used as ground truth reference (Supplementary Table S1). First, the AML dataset is a healthy human bone marrow mass cytometry dataset 4, consisting of 104,184 cells analyzed using 32 markers resulting in 14 cell populations defined by manual gating. Second, the BMMC dataset is also a healthy human bone marrow dataset 4, 25, consisting of 81,747 cells analyzed with 13 markers, and 24 manually gated cell populations. Third, the PANORAMA dataset entails 10 replicates of mice bone marrow cells 12, analyzed using a mass cytometry panel of 39 markers and manually gated into 24 cell populations, with a total number of cells around 0.5 million. Finally, the Multi‐Center study dataset is a collection of 16 samples drawn from a single subject 23, where the first eight samples are collected at the same time and analyzed with the same instrument, and the last eight samples are collected 2 months later and analyzed with a different instrument. It contains ~930,000 cells, analyzed with 26 markers, where only eight markers were used for the manual gating process 23, resulting in four canonical cell populations in addition to a fifth class representing the unlabeled cells. In addition to the benchmark datasets, we used data that we collected from patients with gastrointestinal diseases as well as controls. This Human Mucosal Immune System mass cytometry (HMIS) dataset 6 consists of 102 samples: 47 peripheral blood mononuclear cells (PBMC) and 55 gut tissue samples. We focused on the PBMC samples only, which are further divided into 14 control samples, 14 samples with Crohn's disease (CD), 13 samples with celiac disease (CeD) and six samples with refractory celiac disease type II (RCDII). There are ~3.5 million cells in the 47 PBMC samples, which are measured with a panel of 28 markers. Prior to any further processing, dead cells, debris and non‐gated cells were removed. Measured expressions were transformed using hyperbolic arcsin with a cofactor of 5 for all datasets.

To annotate the HMIS dataset with cell population information, we clustered all cells across all PBMC samples simultaneously using Cytosplore^+HSNE 26. The motivation to choose Cytosplore^+HSNE is to reproduce similar cell populations to the ones defined in the original study of the HMIS dataset 6, 17. However, any other clustering method, such as FlowSOM or X‐shift, could be used for this task 18. We constructed three layers HSNE. For the top (overview) layer, we annotated the clusters into six major immune lineages on the basis of the expression of known lineage marker: (i) CD4+ T cells, (ii) CD8+ T cells, including TCRgd cells, (iii) B cells, (iv) CD3‐CD7+ innate lymphocytes (ILCs), (v) Myeloid cells, and (vi) Others, representing unknown cell types (Supplementary Fig. S1). This we denoted the HMIS‐1 dataset. Next, in order to find subtypes at a more detailed level, we explored one layer down for each of the six cell populations separately, producing six separate t‐SNE maps (Supplementary Fig. S1). For each map, we applied Gaussian mean shift (GMS) clustering 27, with a kernel size of 30 (default value). For each cluster, we calculated a cluster representation by taking the median expression of each marker for all individual cells annotated with that cluster. We automatically merged clusters when the correlation (Pearson's R) between cluster representatives is above 0.95. We discarded clusters containing less than 0.1% of the total number of cells (<3,500 cells). In total we ended up with 57 (clusters) cell populations (11 CD4+ T cells, 9 CD8+ T cells, 4 TCRgd cells, 11 B cells, 11 CD3‐CD7+ ILCs, 6 Myeloid cells, and 5 others) for the ~3.5 million PBMC cells, which we denoted the HMIS‐2 dataset. Cell counts per cell population and per sample are summarized in Supplementary Figure S2.

Cell Population Predictors

To determine cell populations in a newly measured sample, one would need to re‐cluster the new sample with all previous samples. Besides being a tedious task, cells from the new sample will influence the clustering and by that change the previously identified cell populations, affecting reproducibility. Therefore, we learn the different cell populations from a training set with annotated cells. The cell populations in the new sample can then simply be predicted by this learned cell‐populations predictor.

LDA. We propose to use a (simple) LDA classifier to predict cell populations in CyTOF data. To produce a cell population prediction for new cell x, LDA assign x to cell population class c_i for which the posterior probability of x being part of c_i is maximum, across all cell populations.

Assign x to $\arg \underset{\forall c_i}{\max }p\left(x|c_i\right)P\left(c_i\right).$

where $p\left(x|c_i\right)=\frac{1}{{\left(2\mathrm{\pi }\right)}^{k/2}{\left|{\Sigma }_i\right|}^{1/2}}{\mathrm{e}}^{-\frac{1}{2}{\left(x-{\mu }_i\right)}^T{{\Sigma }_i}^{-1}\left(x-{\mu }_i\right)}$, Σ_i = Σ ∀ c_i

P(c_i) is the prior probability of cell population class c_i, which is equal to the number of cells in cell population i divided by the total number of cells in the dataset, k is the number of features (protein markers in case of CyTOF), μ_i is the k‐dimensional mean vector of cell population class c_i, Σ_i is the k × k covariance matrix of cell population class c_i.

k‐NN. Further, to check whether the performance of a non‐linear classifier would outperform the linear LDA classifier, we tested the performance of a k‐NN classifier (with Euclidean distance and k = 50 neighbors). We adopted an editing approach when training the k‐NN classifier to reduce the training set size, and consequently keep testing times reasonable. The editing is done according to the following pseudo code. We start by creating a training set (Tr), by sampling 50,000 cells uniformly and without replacement from all samples in the original training data (OrgTr). Next, we create a test set (Te), by sampling another 50,000 cells uniformly and without replacement from OrgTr. The k‐NN classifier is then trained using Tr and used to make cell population predictions for Te. All correctly predicted cells from Te are ignored while the misclassified cells are added to Tr. We iterate these steps until there are no cells left within OrgTr, i.e. we have processed all cells. The final version of Tr contains much less cells than the original OrgTr, but will encompass the necessary representative cells from each cell population class to achieve a similar k‐NN performance.

 Input: Training_Data used to train the k‐NN classifier

 Output: reduced version of the Training_Data representative for the input data

 BEGIN

 Temp_Training ← random 50,000 cells from Training_Data

 while (not all Training_Data is covered)

  Temp_Testing ← another random 50,000 cells from Training_Data

  Apply prediction on Temp_Testing and add misclassified cells to Temp_Training

  Temp_Training ← Temp_Training + Misclassified from Temp_Testing

 end while

 Final_Training ← Temp_Training

 END

NMC. We also tested whether an even simpler classifier than LDA would be sufficient to accurately identify cell populations. We tested the nearest median classifier (NMC) which assigns each cell to the nearest median (median expression across all cells for a cell population) using (1 − R) as distance, with R being the Pearson correlation between the two expression vectors 28.

Performance Metrics

To evaluate the quality of the classification, we used four metrics:

1. The classification accuracy (fraction of correctly identified cell).

2. The F1‐score (harmonic mean of the precision and recall) for which we report the median value across all cell populations. When comparing to DeepCyTOF 23, we use the weighted average of F1‐scores per cell population size, to produce a fair comparison.

   $$\text{Weighted}\mathrm{F}1\text{score}=\sum _i\frac{n_i}{N}{F}_i$$

   where n_i is the number of cells in population i, N is the total number of cells in the dataset, and F_i is the F1‐score for cell population i.

3. The maximum difference in population frequencies, defined as $\mathrm{\Delta }f={\max }_i\left|f_i-{\widehat{f}}_i\right|$, where f_i and ${\widehat{f}}_i$ represents the true and the predicted percentage cell frequencies for the ith cell population, respectively.

4. The Root of Sum Squared Error (RSSE) per sample and per cell population, defined as $\text{RSSE}=\sqrt{\sum _{i=1}^n{\left(f_i-{\widehat{f}}_i\right)}^2}$. In case of measuring the error per sample, f_i and ${\widehat{f}}_i$ represents the true and the predicted percentage cell frequencies, respectively, for the ith cell population per sample, and n = n _t (total number of cell populations). In case of measuring the error per cell population, f_i and ${\widehat{f}}_i$ represents the true and the predicted percentage cell frequencies, respectively, for a certain cell population in the ith sample, and n = n _s (total number of samples).

Performance Estimation

The performance of a classifier is evaluated using three different cross‐validation setups:

1. CV‐Cells: Five‐fold cross validation applied over all the cells.

2. CV‐Samples: A leave‐sample‐out cross validation over all the samples, regardless of the number of cells within each sample. The classifier is trained using the cells of the samples in the training set, then the cell population prediction is done per left‐out sample.

3. Conservative CV‐Samples: Similar to CV‐Samples, but with the main difference that the ground‐truth reference labels, acquired by clustering, are not used for training. Instead, for each set of training samples the data is re‐clustered, resulting in new cell populations. These new cell populations are then used to train the classifier, which is subsequently used to predict the labels of the cells of the left‐out sample. Since the labels of the training set and the ground‐truth are now different, we matched the cluster labels by calculating their pairwise correlation (Pearson's R) using the median marker expression of each cluster. Each training cluster is matched to the ground‐truth cluster with which the correlation is maximum.

For the AML and the BMMC datasets, we evaluated the performance using the CV‐Cells setup only, since no sample information is provided. For the PANORAMA and Multi‐Center datasets, we used both the CV‐Cells and CV‐Samples setups, since we have the sample information. Considering the number of samples in each dataset, we used a five‐fold CV‐Samples for the PANORAMA dataset and a four‐fold CV‐Samples for the Multi‐Center dataset. For the HMIS‐1 and HMIS‐2 datasets, we used all three cross validation setups, using a three‐fold CV‐Samples and Conservative CV‐Samples.

Rejection Option

To be able to detect new cell populations, we decided to include a rejection option for LDA by defining a minimum threshold for the posterior probability of the assigned cell populations. Thus, a cell is labeled as “unknown” whenever the posterior probability is less than a predefined threshold set.

$$\text{Assign}x\text{to}\left\{\begin{array}{c}\arg \underset{\forall c_i}{\max }p\left(x|c_i\right)P\left(c_i\right),\underset{\forall c_i}{\max }\frac{p\left(x|c_i\right)P\left(c_i\right)}{p\left(x\right)}>\text{threshold}\\ \text{unknown},\text{otherwise}\end{array}\right.$$

Feature Selection

To avoid overfitting, we explored the need to reduce the number of markers (i.e., features) by applying feature selection on the training data. First, we applied a five‐fold CV‐Cells and used the classification performance for every individual marker on the training data to rank all markers in a descending order. Next, we applied another five‐fold CV‐Cells on the training data and trained as many classifiers as there are markers. The first classifier is based on the top marker only, the second one on the two top ranked markers, etc. Then we select the classifier which generates the best cross validation performance over the training set. This classifier is subsequently tested on the test set and the performance is reported.

Results

LDA Outperforms Complex Classification Approaches

To evaluate the performance of the LDA classifier, we compared LDA with two recent state‐of‐the‐art methods for classifying CyTOF data, ACDC 22 and DeepCyTOF 23. We used the AML, BMMC and PANORAMA datasets (used by ACDC) and the Multi‐Center dataset (the only available dataset used by DeepCyTOF). We compared the performance of LDA with our reproduced values, and the reported values in these two studies (Table 1). ACDC was applied only for the AML and BMMC datasets, for which the cell‐type marker table was provided.

Table 1.

Performance summary of LDA versus ACDC, DeepCyTOF, and NMC

	LDACV‐Cells	LDACV‐Samples	ACDCa	DeepCyTOFb	NMC
Accuracy
AML	98.13 ± 0.09	n.a.	98.33 ± 0.02	n.a.	97.34 ± 0.08
			98.30 ± 0.04c
BMMC	95.82 ± 0.10	n.a.	93.20 ± 0.70	n.a.	85.83 ± 0.21
	95.61 ± 0.16d		92.90 ± 0.50c
PANORAMA	97.16 ± 0.07	97.22 ± 0.31	n.r.	n.a.	94.72 ± 0.54
	97.70 ± 0.03d	97.67 ± 0.29d
Multi‐Center	98.51 ± 0.04	98.44 ± 1.66	n.a.	n.r.	98.24 ± 1.86
		98.82 ± 1.73e
Median F1‐score
AML	0.95	n.a.	0.94	n.a.	0.93
			0.93c
BMMC	0.85	n.a.	0.69	n.a.	0.62
	0.85d		0.60c
PANORAMA	0.93	0.93	0.88c	0.59 ± 0.01f	0.89
	0.95d	0.95d
Multi‐Centerb	0.99	0.99	n.a.	0.97 ± 0.01f 0.93c	0.98
		0.98e

n.a.: not available; n.r.: not reported.

^aThe ACDC performance values represent the training performance.

^bWeighted F1‐score.

^cReported values in the original study.

^dClasses considered unknown, similar to ACDC.

^eOnly one sample is training (Sample 2), similar to DeepCyTOF.

^fMean ± SD of 10 different runs.

Since there was no sample information available for the AML and BMMC datasets, we evaluated the performance of the LDA classifier on both datasets using the CV‐Cells setup only, and we are unable to run DeepCyTOF on those datasets. For the AML dataset, LDA achieved comparable performance in terms of accuracy and median F1‐score to ACDC. For the BMMC dataset, we applied the LDA classifier to classify all 24 cell populations, resulting in ~96% accuracy and 0.85 median F1‐score. To have a fair comparison with ACDC, we also considered four populations as unknown 22 then classified only 20 cell populations. In both cases, LDA outperformed ACDC, specially based on the median F1‐score. Similar conclusions can be observed when looking at the detailed performance per cell population, showing comparable performance for the AML dataset (Fig. 1A), and performance improvement for small populations in BMMC dataset (smallest 10 populations in Fig. 1B).

Figure 1.

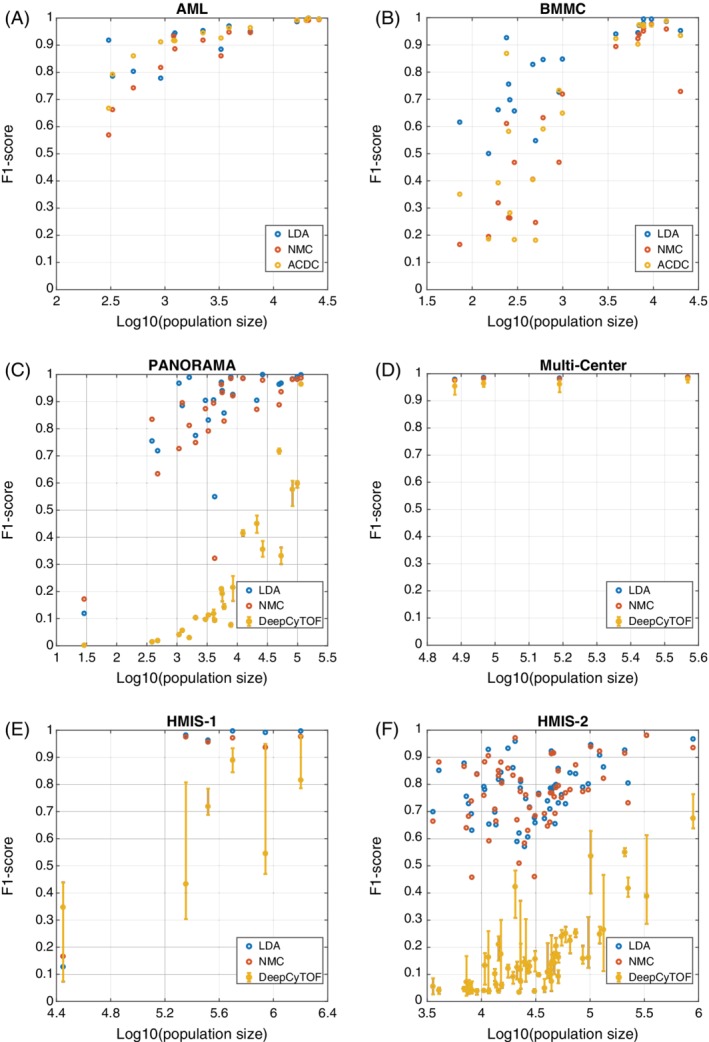
Classifiers performance comparison. Scatter plots of the F1‐score vs. the population size for (A) AML, and (B) BMMC, between LDA, NMC, and ACDC. Scatter plots of the F1‐score versus the population size for (C) PANORAMA, (D) Multi‐Center, (E) HMIS‐1, and (F) HMIS‐2, between LDA, NMC, and DeepCyTOF. Error bars for DeepCyTOF shows the maximum and the minimum performance across 10 different runs. [Color figure can be viewed at wileyonlinelibrary.com]

On the PANORAMA dataset, we tested the LDA classifier to classify all 24 populations using both the CV‐Cells and CV‐Samples setups. In addition, we tested the performance of LDA on 22 populations only to have a fair comparison with ACDC 22. In both cases LDA produces relatively high accuracy and median F1‐score, and outperformed ACDC and DeepCyTOF in terms of the median F1‐score (no accuracy reported by ACDC). Across all cell populations, LDA has a large F1‐score improvement compared to DeepCyTOF (Fig. 1C).

For the Multi‐Center dataset, we applied CV‐Cells and CV‐Samples yielding an accuracy of ~98% and weighted F1‐score of 0.99 for both setups. To have a fair comparison with DeepCyTOF, we only used sample no. 2 for training and tested the performance of LDA on the other 15 samples. Following DeepCyTOF, the “unlabeled” class was excluded from the training data and during testing any prediction with probability less than 0.4 was considered “unlabeled”. Next, the “unlabeled” class was excluded while calculating the cell population precisions. Overall, LDA achieved comparable performance to DeepCyTOF on the Multi‐Center dataset (Table 1, Fig. 1D), using a denoising encoder and excluding the additional calibration step 23. DeepCyTOF suffers from lack of reproducibility, producing different results in each run, which is not the case for LDA (Fig. 1C,D). Further, similar to DeepCyTOF, LDA has better performance on samples from the same batch as the training sample compared to samples from a different batch (Supplementary Fig. S3).

LDA Accurately Classifies Immune Cells in a Larger Dataset with Deeper Annotation of Cell Subtypes

To test our hypothesis that LDA can achieve acceptable performance on large datasets and with more detailed cell subtyping, we applied LDA to the HMIS dataset comprised of ~3.5 million cells. The HMIS data was clustered at two levels of detail (see Methods) resulting in two different annotations for the HMIS data set: HMIS‐1, representing six major lineages, and HMIS‐2 containing 57 cell populations. For both annotations, we applied all three cross validation setups, CV‐Cells, CV‐Samples and Conservative CV‐Samples (Table 2).

Table 2.

Performance summary of LDA, DeepCyTOF, NMC, and k‐NN on the HMIS dataset

	HMIS‐1		HMIS‐2
	Accuracy	Median F1‐score	Accuracy	Median F1‐score
LDA CV‐Cells	99.38 ± 0.01	0.99	87.19 ± 0.05	0.81
LDA CV‐Samples	99.02 ± 2.26	0.99 (0.98a)	86.11 ± 3.86	0.79 (0.87a)
LDA Conservative CV‐Samples	98.91 ± 1.87	0.99	78.69 ± 8.65	0.62
DeepCyTOFa	n.a.	0.72 ± 0.06b	n.a.	0.36 ± 0.02b
NMC	96.42 ± 3.19	0.96	83.34 ± 4.11	0.77
k‐NN CV‐Samples	n.a	n.a.	87.73 ± 4.09	0.81
k‐NN CV‐Samples with feature selection	n.a.	n.a.	86.33 ± 3.17	0.79

n.a.: not available.

^aWeighted F1‐score.

^bMean ± SD of 10 different runs.

We first tested the LDA performance on HMIS‐1, hence only classifying the canonical cell populations. LDA achieved an accuracy >99% and a median F1‐score > 0.98 for both CV‐Cells and CV‐Samples. Next, we applied LDA to HMIS‐2, which implied classifying cells into 57 different cell populations including abundant and rare cell populations. As expected, LDA had a lower performance on HMIS‐2 compared to HMIS‐1 using both CV‐Cells and CV‐Samples, with an accuracy ~86% and a median F1‐score ~0.80 (Table 2). The confusion matrix shows that the performance drop between HMIS‐1 and HMIS‐2 is mainly caused by misclassifications within the same major lineages (Supplementary Fig. S4A). We further investigated the LDA performance across different sample types (Control, CeD, RCDII, and CD) in the HMIS dataset. Figure 2A shows that LDA has the highest accuracy for the control samples, while the lowest accuracy is for the RCDII samples.

Figure 2.

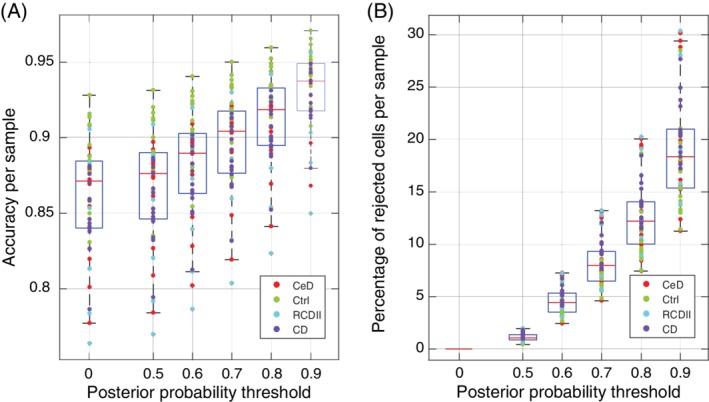
LDA accuracy and rejection size per sample. (A) boxplot of the LDA accuracy distribution per sample, while using a rejection threshold (0 = no rejection). (B) Boxplot of the rejection percentage per sample while using a rejection threshold (0 means no rejection). Each dot represents a sample colored according to the sample type (CeD: celiac disease; Ctrl: control; RCDII: refractory celiac disease type II; CD: Crohn's disease). [Color figure can be viewed at wileyonlinelibrary.com]

To better mimic a realistic scenario and avoid any leakage of information from the testing samples by considering all samples when pre‐clustering cells to determine the ground truth labels, we used a Conservative CV‐Samples setup to evaluate the LDA classifier (see Methods). For the HMIS‐1 dataset representing the major lineages, the performance of LDA in the Conservative CV‐Samples was comparable to the other setups (CV‐Cells and CV‐Samples), Table 2. The performance of the LDA classifier dropped when considering the Conservative CV‐Samples setup on HMIS‐2 that contains a multitude of cell populations. However, the lower performance can be explained by miss‐matching clusters between the training set and the ground‐truth, which introduces classification errors. For example, cluster “CD4 T 11” is never predicted by the classifier, which means all cells falling within this cluster will be misclassified (Supplementary Fig. S4B). This is because in all three folds, no training cluster matches to this ground‐truth cluster “CD4 T 11” (Supplementary Fig. S5). Whereas in case of HMIS‐1, with only six dissimilar clusters, the clusters map works perfectly, resulting in high performance (Supplementary Fig. S6).

We compared the performance of LDA on the HMIS dataset with DeepCyTOF (Table 2, Fig. 1E,F). For both HMIS‐1 and HMIS‐2 datasets, LDA outperforms DeepCyTOF, which particularly shows a poor performance for the deeply annotated HMIS‐2 dataset. These results show that LDA is robust and scalable to large datasets with deep subtyping of cell populations.

LDA Outperforms Simpler Classifiers

In order to explore to what extent a simple classifier can achieve high performance on identifying cell populations, we tested the NMC on all datasets. Our results show that the NMC has a comparable performance with the LDA on the Multi‐Center and HMIS‐1 datasets (Tables 1 and 2, Fig. 1D,E). However, LDA outperforms NMC on the AML, BMMC, and PANORAMA datasets (Table 1, Fig. 1A–C). Similar to ACDC, NMC suffers from large performance drop for the 10 smallest populations in the BMMC dataset (Fig. 1B). Also, LDA outperforms NMC on the deeply annotated HMIS‐2 dataset, showing performance improvement for the majority of the 57 cell populations (Table 2, Fig. 1F). These results show that a simpler classifier such as NMC can predict major lineages but are not sufficient to classify deeper annotated CyTOF datasets containing smaller (rare) cell populations.

LDA Accurately Estimates Cell Population Frequencies

One of the main aims of CyTOF studies is to estimate the frequencies of different cell populations in a given sample. We evaluated the LDA prediction performance in terms of predicted population frequencies, by calculating the maximum difference in population frequencies, Δf, for each dataset (see Methods). LDA produced comparable population frequencies to the manually gated populations, with Pearson R correlation >0.97, between the true and predicted population frequencies for all datasets (Fig. 3). We observed that some cell populations are harder to predict, including: (1) small populations, such as MPP in the BMMC dataset, and HSC and CLP in the PANORAMA dataset; and (2) populations that have similar cell populations in the dataset, such as “B‐cell Frac A–C (pro‐B cells)” in the PANORAMA dataset, where ~41% of the cells were misclassified into the similar B cell subtypes (IgD–IgMpos B cells, IgDpos IgMpos B cells, and IgM–IgD‐B cells), having a correlation of 0.86, 0.70 and 0.90 with “B‐cell Frac A–C (pro‐B cells)”, respectively. Overall, The maximum difference in population frequency (Δf) was 0.40%, 0.65%, 0.64%, and 0.83% for the AML, BMMC, PANORAMA, and the Multi‐Center datasets, respectively.

Figure 3.

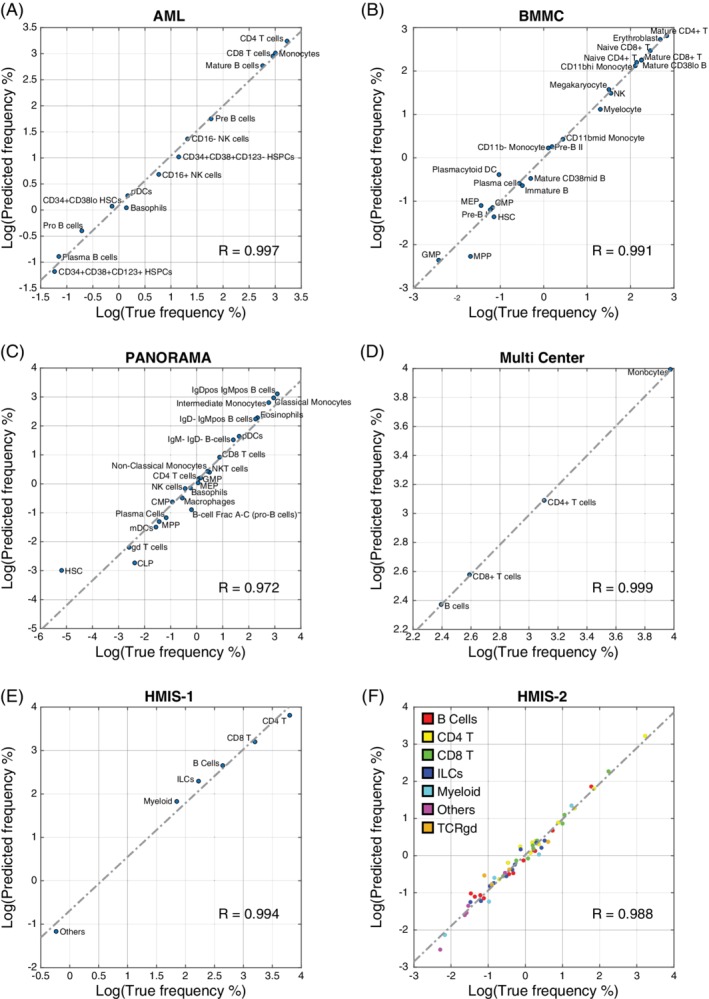
Scatter plots between true and predicted population frequencies. (A) AML, (B) BMMC, (C) PANORAMA, (D) Multi‐Center, (E) HMIS‐1, and (F) HMIS‐2. In each plot, the dashed line shows the leastsquares fit error line, and the R value represents Pearson correlation coefficient between true and predicted frequencies. [Color figure can be viewed at wileyonlinelibrary.com]

For the HMIS‐1 dataset, LDA has Δf of 0.59% across the six major cell populations. Interestingly, despite the drop in the accuracy of predicting cell labels on HMIS‐2 compared to HMIS‐1, the population frequencies are not significantly affected. The maximum difference of population frequencies in HMIS‐2 was 0.46% among all 57 cell populations (Fig. 3F). This small Δf shows that LDA produces accurate performance with respect to the ground‐truth reference, even at a detailed annotation level.

We investigated the population differences per sample and per cell population using the CV‐Samples setup in the HMIS‐2 dataset, by calculating the average squared differences between the estimated and true frequencies (RSSE, see Methods). We obtained small RSSE values with a maximum of 0.074 (sample no. 10) and 0.082 (“Myeloid 10” population) across different samples and different cell populations, respectively (Supplementary Fig. S7). For sample no. 10, the maximum absolute population difference was 5.17% for “Myeloid 3” cell population. For “Myeloid 10” cluster, the maximum absolute difference was 5.12% across all cells.

LDA Performs on Highly Abundant as Well as Rare Cell Populations

To evaluate the performance of LDA for abundant and rare cell populations, we investigated the F1‐score per cell population versus the population size. Figure 1F and Supplementary Figure S8A, show the F1‐score for all 57 cell populations in the HMIS‐2 dataset obtained using the CV‐Samples. Remarkably, LDA performs well for large cell populations, as well as the majority of the small cell populations, with a median F1‐score of 0.7915 for populations that contain less than 0.5% of the total cells.

For the Conservative CV‐Samples setup, the LDA performance is still high for large cell populations, but the F1‐score drops for small populations reinforcing that the drop in performance of the Conservative CV‐Samples is driven by the limitations with the cluster matching rather than the performance of the LDA (Supplementary Fig. S8B). For populations that contain less than 0.5% of the total cells, the median F1‐score is 0.4753. Similar patterns were observed for the other four datasets (Fig. 1A–D).

LDA as a Probabilistic Classifier Directly Allows the Detection of Unseen Cell Populations

A major advantage of clustering and visual analytics over classification approaches is the ability to identify novel unknown cell populations. Here, we show that LDA as a probabilistic classifier can be used to flag unknown cells that do not match any of the training cell populations. We incorporated a rejection option to allow the classification of a cell as “unknown” when the posterior probability of the classification of any cell is low. Figure 2A shows the classification accuracy across samples from the HMIS‐2 dataset, after excluding unknown cells for which the posterior probability is lower than a certain threshold. As expected, setting a threshold on the posterior probability resulted in more accurate predictions. For example, setting a threshold at 0.7 resulted in an accuracy of 89.54 ± 3.25% (compared to 86.11 ± 3.86% without any thresholds), while assigning ~8% of cells per sample as unknown. The performance improvement per population shows very little variation among all the 57 cell populations (Supplementary Fig. S9A). The difference in F1‐scores, between having no rejection and applying a threshold of 0.7, is 0.04 ± 0.02. This result shows that the rejection is not related to the overall population size, which can also be observed when calculating the rejected percentage of cells per cell population (Supplementary Fig. S9B).

Further, we observed a reverse pattern between the accuracy of cell classification and the percentage of cells classified as unknown per sample (Fig. 2A,B). For instance, LDA has the highest accuracy on classifying cells from the control samples and hence control samples are less likely to entail rejected (unknown) cells. On the other hand, the accuracy is the lowest on RCDII samples which also have the highest rejection percentages. Figure 2 further shows that both the accuracy and the rejection size increase with increasing the minimum threshold of the posterior probability.

Rejection Option Targets Rare Sample‐Specific Cell Populations

Next, we investigated the effect of the rejection option on rare and abundant cell populations. In the HMIS‐2 dataset, the population frequencies of the 57 cell populations varied from 25.2% to 0.1% of the total number of cells (Fig. 4A). Further, we observed a variable distribution of cell populations across different sample types (control, CeD, RCDII, and CD), Figure 4B. Although the majority of cell populations were evenly distributed over all samples, some were disease‐specific, especially the rare cell populations. Using a rejection threshold of 0.7, we calculated the rejection ratio per cell population per sample (Fig. 4D) as the number of cells assigned as “unknown” of one cell population in one sample, divided by the total number of cells of that cell population in all samples. We compared these rejection ratios with the cell population frequencies over the samples (Fig. 4C) where a value close to 100% means that the cell population is specific to only one sample. We observed a strong correlation between the cell population rejection ratios and the frequencies over the samples (Fig. 4E). For example, the majority of “Others 2” (83.87%) comes from one CeD sample, within which “Others 2” is prominently present (7.44% of the cells in this sample belong to “Others 2” Supplementary Fig. S2). The classifier rejects ~15% of these cells, representing a ~12% rejection ratio of the total number of “Others 2” cells. This is a relatively high rejection percentage compared to other cell populations (Fig. 4E). The main reason why there is a large rejection ratio for these cells, is because these cells are mainly present in one sample. When this sample is left out in the CV‐Samples procedure, during testing these cells are rejected because they are missing in the training data. These results support the validity of using the rejection option to label unknown cells, which are likely to be rare sample‐specific populations.

Figure 4.

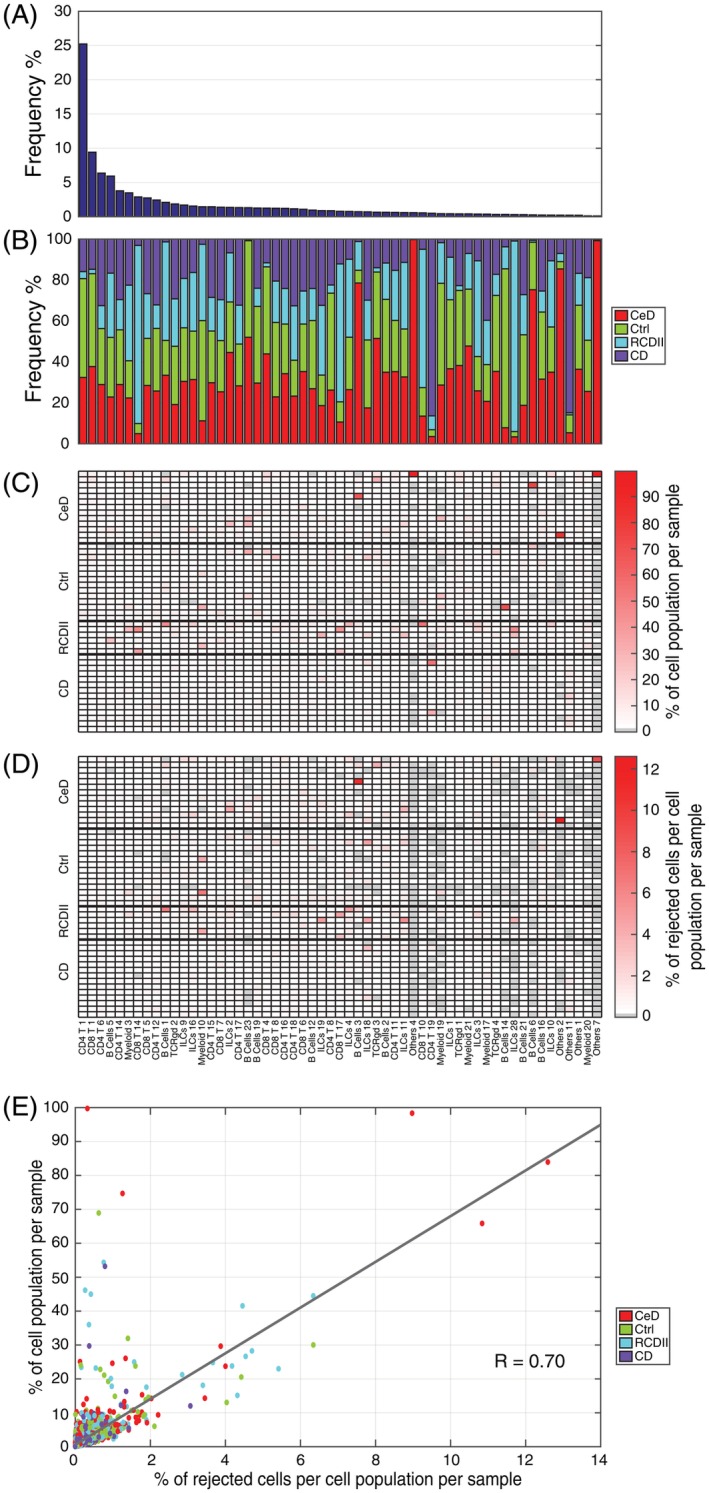
Rejection option effect on variable sized cell populations. (A) Cell population frequency across the HMIS‐2 dataset, in a descend order. (B) Cell population composition in terms of the different sample types (CeD, Ctrl, RCDII, and CD). (C) Cell population frequencies across samples, normalized by the cell population size across all samples, every column summation is 100%. (D) Percentage of rejected cells per cell population per sample, normalized by the cell population size across all samples, using a posterior probability threshold of 0.7. Cell populations follow the same order for (A–D). (E) Scatter plot between values in (C) and (D) showing a strong correlation of 0.70 between the rejection ratio and the cell population size, per sample. Each point represents a cell population in a particular sample, and points are colored according to the disease status of the sample annotation. [Color figure can be viewed at wileyonlinelibrary.com]

Linear Classification Is Sufficient for Accurate Classification of CyTOF Data

We have shown that a simple linear classifier such as LDA has a better performance compared to complex non‐linear classifiers such as ACDC and DeepCyTOF. To further illustrate that non‐linear classification does not perform better than linear classification, we compared the performance of LDA to a k‐NN classifier on the HMIS‐2 dataset. We found that LDA has a comparable performance to a k‐NN classifier with k = 50 (Table 2), suggesting that adding non‐linearity to the classification process does not improve performance.

Further, we checked the effect of having similar populations on the classification performance. For each cell population in the HMIS‐2 dataset, we compared the F1‐score with the correlation to the most similar population (Supplementary Fig. S10). For both, LDA and k‐NN classifiers, we observe a week negative relation, showing that the classifier performance is affected by the presence of similar cell populations in the dataset.

To reduce the computation time for the k‐NN classifier, we employed an editing scheme to reduce the size of the training data (see Methods). Using the proposed editing scheme, we reduced the training data size to an average of 300,000 per training fold (~12% of the original training set), resulting in a significant speedup of the training and testing times. However, the k‐NN classifier still takes on average 180x the time needed by LDA to make predictions for one sample.

Next, we investigated whether feature selection (using less markers during classification) would affect the performance of the classifiers. The k‐NN classifier selected only 20 (out of the 28) markers and retained a comparable performance to that obtained using all 28 markers. On the other hand, feature selection did not reduce the number of markers selected by LDA, indicating that LDA requires all the measured markers in order to achieve maximum performance.

Discussion

In this work, we showed that a linear classifier can be used to automatically assign labels to single cells in mass cytometry data. Using four different CyTOF datasets, we compared the performance of a LDA classifier to two recent methods: ACDC 22 and DeepCyTOF 23. Interestingly, LDA has better performance compared to ACDC and DeepCyTOF in all four datasets. Compared to ACDC, LDA does not require any additional biological knowledge or assumptions regarding the distribution patterns of markers. Additionally, ACDC requires a cell‐type marker table which has several limitations: (i) designing the table can be very challenging in the presence of many cell populations, (ii) it is not possible to specify the marker patterns for some cell populations (e.g., ACDC ignored 4 subtypes in the BMMC dataset because the table could not be constructed), and (iii) the table requires imposing assumptions on the marker distribution (currently binary) which can be challenging to model. Furthermore, results on the BMMC dataset show that LDA can detect rare cell populations having frequencies <0.5% of the total number of cells, like MPP, HSC, MEP and GMP, which were the main cause of the lower performance of ACDC 22. Compared to DeepCyTOF, in addition to having a better performance, LDA is a much simpler classifier which means it has substantial advantages with respect to the interpretability of the classifier prediction, reproducibility, and scalability to larger datasets with deep subtyping annotation.

We further evaluated LDA on a large CyTOF dataset with deep annotation of cell populations. We showed that LDA can accurately identify cell populations in a challenging dataset of 3.5 million cells comprised of 57 cell populations. Further, we showed that the errors made by LDA in assigning cell population labels to each cell has negligible influence on the estimates of cell population frequencies across different individuals. DeepCyTOF failed to scale, in terms of performance, to this large dataset with deep level of annotation. Its low performance is mainly due to the selection of one sample for training. Moreover, this approach is particularly not suitable when analyzing multiple samples from different cohorts (e.g., disease and controls). For instance, in the HMIS‐2 dataset, DeepCyTOF selected sample (number 27) as the training sample, which is a control sample containing only 55 of the 57 cell populations.

We also compared LDA to a simpler classifier such as the NMC, to test to which extend the classification task could be further simplified. We observed comparable performance in datasets containing large and major cell populations only, such as Multi‐Center and HMIS‐1, where the classification task is relatively easy. However, LDA produces better results for other datasets, having more detailed population subtyping, in which the classification task becomes more challenging, and NMC performance drops, especially for small populations as observed in the BMMC dataset.

To show that a linear classifier is sufficient to classify cells in mass cytometry data, we compared LDA to a non‐linear classifier (k‐NN). Indeed, the k‐NN classifier does not outperform LDA on the HMIS dataset, indicating that there is no added value in using non‐linear relationships between the markers. However, when we ran both classifiers with feature selection, LDA required the full set of markers to achieve the best performance. On the other hand, the k‐NN classifier was able to achieve the same performance as LDA but using less markers (20 instead of 28). This result suggests that a non‐linear classifier might be beneficial to reduce the number of required markers and free valuable slots on the CyTOF panel for additional markers. Alternatively, using the reduced marker set lowers costs when analyzing new samples, using a smaller CyTOF panel or even flow cytometry while retaining the ability to identify all cell populations of interest.

Further, the comparable performance of LDA and k‐NN indicate that in the full marker space, the cell population classes in the CyTOF datasets that we explored are well separable. Consequently, different clustering algorithms will perform similarly well on these datasets. We would like to note that more complex data might need more complex classifiers or clustering algorithms, for example when cell populations are less separable like continuous or smeary populations. We have shown that for the current datasets this is not necessary. In general, it will be difficult to predict beforehand which complexity is necessary, so that in practice multiple classifiers need to be evaluated.

Our results also show that the performance of LDA is not largely affected by either technical or biological variability. Technical variability is part of the Multi‐Center dataset which contains batch effects. The performances on the different batch samples remain relatively high (weighted F1‐score > 0.95, Supplementary Fig. S3), although, applying batch correction methods might still improve the overall LDA prediction performance 29, 30, 31. Biological variability is presented in the HMIS dataset, which includes samples from patients with different diseases, collected over time. The high performance on the deeply annotated HMIS‐2 dataset, shows LDA's robustness against these biological variations.

For the HMIS dataset, we relied on an initial clustering step to assign ground‐truth labels. To avoid any possible leakage of information from the test set of cells by including them into the clustering, we designed a conservative learning scheme. In the conservative scheme, we do not use the labels obtained by clustering the entire dataset (i.e., ground‐truth) for training, but rather re‐cluster the training data inside each fold. In addition, this scheme better resembles a realistic scenario in which the new unseen data is never included in the initial assignment of class labels for training. The performance of LDA in this conservative experiment is lower than the initial performance obtained by classical cross validation. However, the lower performance does not stem from the lack of generalization, as the results show high performance on the overview‐level, but rather from the difficulty in matching cluster labels between the ground truth and the training set.

Clustering approaches in general have an advantage over classification methods in that they can be employed to discover new cell populations. However, an additional advantage of using a probabilistic classifier such as LDA is that we can directly gain information regarding the accuracy of each decision made by inspecting the posterior probability. We showed that we can allow for a rejection option when the posterior probability of the classification of a particular cell is low. This rejection option can be used to identify “unknown” cells which might require additional investigation to determine their biological relevance. Additionally, we showed that these “unknown” cells are likely to be rare and sample‐specific. There is however a trade‐off between how confident we are on the correctness of the predictions and the size of the “unknown” class. A stringent threshold (i.e., high posterior probability) means that many cells will be classified as “unknown” which will further require manual investigation.

Taken together, we demonstrated the feasibility of using a simple linear classifier to automatically label cells in mass cytometry data which is a promising step forward to use mass cytometry data in cohort studies.

Availability

Data is available from Flow Repository (FR‐FCM‐ZYTT) and implementation is available on GitHub (https://github.com/tabdelaal/CyTOF-Linear-Classifier)

Competing Interests

The authors declare no competing interests.

Supporting information

MIFlowCyt‐Item‐Checklist

Supplementary Figure 1 Annotation of cells in the HMIS dataset. The middle image shows the embedding of the overview (top) HSNE layer, clustered into six major cell populations. Next, a separate tSNE map is obtained per cell population by exploring one layer down.

Supplementary Figure 2 Cell counts per cell population per sample for the HMIS‐2 dataset. Cell populations are ordered in descending order of the frequencies across all samples, and grouped according to the sample types (CeD = Celiac Disease, Ctrl = Control, RCDII = Refractory Celiac Disease Type II, CD = Crohn's Disease). All counts were log10 transformed.

Supplementary Figure 3 LDA performance for the Multi‐Center dataset, using only sample 2 as training and calculating the weighted F1‐score for the 15 remaining samples. Batch 1 is sample 1–8, and batch 2 is sample 9–16.

Supplementary Figure 4 LDA performance on the HMIS‐2 dataset. (A) Classification confusion matrix when using CV‐Samples setup, showing high percentages along the matrix diagonal, as well as that most of the misclassification (off‐diagonal values) falls within the major cell populations. (B) Classification confusion matrix when using Conservative CV‐Samples setup, showing lower percentages along the matrix diagonal compared to the CV‐Samples setup. Each cell (square) in the confusion matrix represents the percentage of overlapping cells between true and predicted class.

Supplementary Figure 5 Mapping of training clusters to ground‐truth clusters during the Conservative CVSamples setup of HMIS‐2 dataset. (A‐C) correlation maps for all three folds, highlighting the maximum correlation with a “+” sign.

Supplementary Figure 6 Mapping of training clusters to ground‐truth clusters during the Conservative CVSamples setup of HMIS‐1 dataset, highlighting the maximum correlation with a “+” sign.

Supplementary Figure 7 Bar plot of the Root of Sum Squared Error (RSSE) (A) per sample, and (B) per cell population.

Supplementary Figure 8 Relationship between performance and population size. Scatter plot of the F1‐score vs. the population size for the HMIS‐2 dataset evaluated using (A) CV‐Samples, and (B) Conservative CVSamples. Each dot represents one cell population and colored according to the major cell population annotation.

Supplementary Figure 9 (A) Cell populations F1‐score with and without rejection, using a rejection threshold of 0.7, (B) Scatter plot between the population size and the percentage of rejected cells per population, showing no correlation ≈ 0.

Supplementary Figure 10 Scatter plots showing the F1‐score per population vs the correlation of the most similar population in the HMIS‐2 dataset, for (A) LDA classifier, and (B) k‐NN classifier. In both classifier, we observed a week negative correlation.

Supplementary Table 1 Summary of the datasets used in this study.