Abstract
The unfolded protein response (UPR) is a collection of cellular feedback mechanisms that seek to maintain protein folding homeostasis in the endoplasmic reticulum (ER). When the ER is ‘stressed’, through either high protein folding demand or undersupply of chaperones and foldases, stress sensing proteins in the ER membrane initiate the UPR. Recently, experiments have indicated that these signalling molecules detect stress by being both sequestered by free chaperones and activated by free unfolded proteins. However, it remains unclear what advantage this bidirectional sensor control offers stressed cells. Here, we show that combining positive regulation of sensor activity by unfolded proteins with negative regulation by chaperones allows the sensor to make a more informative measurement of ER stress. The increase in the information capacity of the combined sensing mechanism stems from stretching of the active range of the sensor, at the cost of increased uncertainty due to the integration of multiple signals. These results provide a possible rationale for the evolution of the observed stress-sensing mechanism.
Keywords: unfolded protein response, endoplasmic reticulum stress, chemical sensing, mutual information, signal integration
1. Background
The unfolded protein response (UPR) is a cellular stress response resulting from excessive accumulation of unfolded and misfolded protein in the endoplasmic reticulum (ER). Detection of heightened protein concentration within the ER lumen triggers accelerated protein folding and degradation within the ER along with decreased protein synthesis. If efforts to restore protein homeostasis are unsuccessful, the cell begins the process of apoptosis. Malfunction of the UPR has been implicated in numerous protein misfolding diseases [1], including type II diabetes mellitus [2–4] and neurodegenerative diseases [5]. In yeast, the UPR is activated through a single pathway that depends on the transmembrane protein inositol-requiring enzyme 1 (Ire1) transmitting information about the activity of unfolded proteins within the ER lumen across the ER membrane. Oligomerization of Ire1 molecules activates the RNase domain, leading to the non-conventional spicing of HAC1 (or XBP1 in metazoan cells) mRNA [6]. Spliced HAC1/XBP1 is translated to produce a bZIP transcription factor, which upregulates many genes related to protein homeostasis [7,8]. In higher eukaryotes, two additional branches of the UPR are regulated by the ER-membrane proteins: protein-kinase-RNA-like endoplasmic reticulum kinase (Perk) and activating transcription factor 6 (Atf6). While Atf6 signalling involves transport of Atf6 out of the ER, Perk stress-sensing functions analogously to Ire1 signalling, with the lumenal domain of Perk closely resembling that of Ire1 [9–12]. In this work, we focus on the stress-sensing mechanisms of Ire1 and Perk.
Although significant progress has been made towards understanding the downstream cascade regulating chaperone production and ER-associated degradation [13], the actual mechanism through which protein concentration in the ER is detected by the Ire1 and Perk luminal domains has remained controversial. Observations that the overexpression of the ER chaperone BiP reduced the induction of the UPR led many to believe that BiP sequestration by unfolded proteins triggered the stress response [14,15]. This idea was further bolstered by observations that a mutant partially folded glycoprotein that could not bind BiP was also incapable of inducing the UPR [16], and that BiP constitutively binds Ire1, but shows a marked decrease in binding upon UPR activation [9,17].
By contrast, there is growing evidence to support the notion of unfolded proteins acting as ligands through direct binding with Ire1 and Perk. For one, an Ire1 mutant lacking subregion V, which is thought to contain the BiP-binding domain, did not bind BiP, but had negligible effect on UPR activation compared to the wild-type [18]. Furthermore, a ‘core’ mutant of Ire1, consisting of subregions II–IV, oligomerizes under physiological conditions but does not activate the UPR unless ER stress is present [19]. Ire1 dimers also display a shared groove similar to the peptide-binding domain of major histocompatibility complexes [11], and mutations at the floor of this domain prevent binding of the model UPR-inducing misfolded protein CPY* in yeast [20,21] and human cells [22]. Similarly, the Perk lumenal domain selectively binds misfolded proteins through an analogous groove, which may then induce conformational changes that promote oligomerization and kinase activity [23].
To integrate these observations, a hybrid model was proposed [24,25], in which direct binding of unfolded proteins is necessary for full activation of the UPR, perhaps through the stabilization of Ire1 (and Perk) dimers, but the activation is buffered by competitive BiP binding to Ire1 and client unfolded proteins. Recent mathematical modelling of the UPR [26] has shown that controlling the activity of the response through the BiP-titration mechanism allows for a more efficient use of chaperone in mitigating unfolded protein stress in the ER, providing a rationale for the evolution of BiP-modulated stress sensors. However, the same analysis demonstrated that including direct interactions between the sensors and unfolded proteins yielded no added benefit with regard to chaperone frugality. Hence, it remains unclear why the hybrid sensing mechanism that integrates signals of both chaperone and unfolded protein copy numbers has evolved.
In this work, we hypothesize that combining both signals provides more information about the state of stress in the ER. To test this hypothesis, we construct a minimal mathematical model of the hybrid signalling network that contains the BiP-titration and direct-unfolded-protein signalling mechanisms as special cases. Using numerical and analytical techniques, we show that a BiP-mediated sensor can make a more informative measurement of available chaperone in the ER lumen by incorporating a measurement of the unfolded protein concentration directly. This advantage comes from extending the active range of the sensor response, at the cost of greater uncertainty due to integration of the unfolded protein–sensor interaction with the chaperone–sensor interaction.
2. Model description
To develop a model of stress signalling in the ER, we employ a modular approach and take advantage of the separation in timescales between the protein–protein interactions within the ER that determine the sensor activity and the response time of the UPR. A schematic of the modular model is shown in figure 1, which consists of model for chaperone-assisted folding in the ER lumen (folding module), and a stochastic model of the stress-sensing proteins (stochastic sensor module).
Figure 1.

ER stress-sensing model schematic. In the lumen of the ER, unfolded proteins are bound by the chaperone BiP, which aids folding. Eventually, the stable folded proteins are released from the folding complex, and exported from the ER. The folding process is monitored by the transmembrane stress-sensing proteins Ire1 and Perk. In our model, ER stress is measured through one of the three mechanisms depicted in the bottom panel, and transmitted as stochastic time series of the transmembrane sensor activation. (Online version in colour.)
2.1. Folding module
The first module describes the folding of unfolded proteins with the assistance of chaperones within the ER lumen. The chaperone-assisted folding is modelled as an enzymatic reaction
| 2.1 |
and
| 2.2 |
where U is an unfolded protein, C is a chaperone (e.g. BiP in metazoa) and U · C is a complex of chaperone and unfolded protein undergoing folding. Reaction (2.1) captures the binding of unfolded proteins by chaperones, and the subsequent folding and export of the folded protein from the ER. Reactions (2.2) represent influx of nascent proteins and chaperones into the ER, and their subsequent degradation or dilution. In general, binding of nascent proteins by chaperones occurs rapidly upon translocation into the ER [27], whereas folding of a nascent protein requires substantially more time () [28]. The separation of these timescales allows for the approximation that the U and C are in a quasi-steady state with the folding complex U · C on timescales shorter than the folding time. Furthermore, we assume that significant changes in influx rate occur on a longer timescale than U · C complex formation time so that, on the timescales of interest, the total copy number of unfolded protein in the ER, U0, and chaperone in the ER, C0, are conserved quantities. This assumption can be justified by the fact that the important timescale for signalling results from protein–protein interactions and is of the order of seconds, while significant changes in the influx rate require changes in gene transcription and protein translation, both of which vary more slowly. Hence, on the timescale of protein–protein interactions within the ER, the folding module reduces to a simple bimolecular reaction mechanism with conserved protein and chaperone copy numbers. This leads to (quasi) steady-state populations of unfolded proteins, chaperones and folding complexes given by
| 2.3 |
| 2.4 |
| 2.5 |
where Kd is the dissociation constant between unfolded proteins and chaperones, and u, c and u · c are the steady-state copy numbers of unfolded proteins, unbound chaperones, and unfolded-protein–chaperone complexes in the ER, respectively. Without loss of generality, we set Kd = 1 and let all concentrations be measured relative to Kd. Throughout our analysis, we will treat the populations of u, c and u · c as deterministic, and focus on the fluctuations of sensor activity.
2.2. Stochastic sensor module
The second module in our description of the ER stress-sensing network is the transmembrane sensor. While metazoa have three distinct signalling pathways, we will focus here on the activation mechanisms of Ire1 and Perk, as they are thought to detect stress through the same mechanism and Ire1 is the most conserved of the three pathways. Early experiments of the UPR transciptional activation show BiP copy number is inversely proportional to activity of the UPR (see [15] for an example). Additionally, more recent experiments using mutant Ire1 that lacks the regions of BiP binding show that mutant cells deactivate more slowly than wild-type in dithiothreitol (DTT) washout experiments [25], indicating that BiP binding to Ire1 is relevant for deactivation kinetics. This evidence leads to the proposal of a minimal model, which assumes sensor activity decreases as BiP copy number increases. Our minimal model for the hybrid sensor mechanism consists of a two-state sensor with an activation rate that depends on the copy number of unfolded proteins and a deactivation rate that depends on the chaperone copy number:
| 2.6 |
where II is the inactive state of the sensor and IA is the active state. Since the inputs u and c are assumed to change much more slowly than the time required for the sensors to probe the state of the ER, we are interested in the equilibrium fluctuations of the sensors. To this end, the equilibrium activation constant for the two-state sensor is defined to be
| 2.7 |
where γ controls the baseline scale of sensor activity, α dictates the sensitivity of the response to changes in unfolded protein copy number and β sets the sensitivity of the response to changes in unbound chaperone copy number. In the limit as α → 0, u no longer directly influences the activity of the sensor, reducing to the mechanism in which sensor activity is regulated through chaperone titration only. On the other hand, in the limit as β → 0, the sensor activity is regulated only by direct interactions with unfolded proteins, with the chaperone providing no additional regulation of the sensor. From the biophysical chemistry point of view, dephosphorylation of the cytosolic domains of Ire1 and Perk is an essential step in their deactivation. However, once dephosphorylated and monomerized, BiP binding will prevent reactivation and an increase in BiP concentration will drive the equilibrium activation of Ire1 and Perk towards inactivity. It is sequestering of dephosphorylated monomers to prevent them from oligomerizing that our coarse-grained model captures through BiP-modulated inactivation (at a quasi-steady state). Hence, this simple push–pull model for sensor activity encompasses the core regulatory mechanisms involved in Ire1 and Perk activity.
To account for the stochasticity of the sensor’s activity, we model the probability of having nA active sensors as a function of time using a chemical master equation approach. Taking nA to be a random variable that represents the number of active sensor molecules (i.e. IA), and the total number of sensors in the system to be NI, the corresponding chemical master equations for reaction (2.6) is
| 2.8 |
where nA runs from 1 to NI − 1. At steady state, equation (2.8) can be solved exactly [29], giving the probability of active sensors conditioned on the inputs (u, c):
| 2.9 |
where the first term is a normalization constant that does not depend on nA, but does depend on u and c through KIA.
2.3. Quantifying information capacity of endoplasmic reticulum stress sensors
In our model of ER stress signalling, there are two inputs to the system: (U0, C0). We refer to this set of variables as the ‘state’ of the ER. Hence, the input (or prior) to our model is a joint distribution defining the state of the ER, q(U0, C0). However, the stress-sensing network is not necessarily seeking to measure either U0 or C0, but instead to measure the stress. While somewhat nebulously defined in the literature, ER stress should be a function of the state of the ER and quantify the potential for protein misfolding and aggregation. The simplest choice for a quantitative definition of ER stress would then be the number of unbound unfolded proteins, u(U0, C0), which we use here as our stress measure. Later, we will extend our analysis to consider the case in which the concentration of free chaperone, c(U0, C0), serves as the measure of ER stress.
We are interested in quantifying how well the sensor output nA characterizes our ER stress measure. A common metric for quantifying the signal transduction quality in a sensory network is the mutual information between the input stimulus and the sensory response [30–32]. Specifically, the mutual information quantifies the number of distinguishable input states that can be resolved by observations of the signal transduction network’s output. For two distributions X and Y (e.g. input and output distributions), the mutual information between X and Y is given by
| 2.10 |
where p(x, y) is the joint probability distribution of x and y and p(x) and p(y) are the respective marginal probability distributions. Hence, our metric for sensor mechanism quality is I(u; nA), the mutual information between ER stress (which we initially take to be free unfolded protein concentration) and the output of the stress sensor.
To calculate the mutual information, it is necessary to assume a prior distribution for the input q(U0, C0). A common choice is to assume a uniform distribution over the input variables. However, in the case of ER stress, this leads to an unrealistically large range of possible values for free unfolded protein. Were the prior to be a uniform distribution in U0 and C0, the range of u would be from to . Yet, ER stress sensors are sensitive to departures of the system from homeostasis and will not necessarily need to measure the level of stress when the chaperone content is maximal and total protein load is minimal as this state is both unlikely to occur and clearly not a state that requires a stress response. Similarly, should the protein client load be exceptionally high and the chaperone copy number be at its baseline expression level, a response should have already been initiated. Hence, we must construct a more informed prior to draw more definitive conclusions about the quality of different stress-sensing mechanisms. In particular, for the stress-sensing mechanism to be responsive to stress at different processing capacities, it should retain a sensitivity to a given range of unfolded protein copy number as the copy number of chaperone changes. This ensures the homeostatic control mechanism is effective as the protein production capacity of the ER changes. The simplest prior distribution with this property is a uniform distribution in the copy number of unbound unfolded proteins, u, and in total chaperone copy number, C0:
| 2.11 |
where Δu = umax − umin and ΔC = C0,max − C0,min. Note that since u and C0 are typically quite large, we treat them as continuous random variables and q(u, C0) is a continuous distribution. q(u, C0) can readily be transformed into a distribution in terms of U0 and C0 by inverting equation (2.3), or into a distribution in terms of unbound unfolded proteins and chaperones, u and c, using equation (2.4). With the prior distribution in this form, q(u, c), the probability distributions needed to calculate the mutual information in equation (2.10) can be readily calculated with the aid of the transfer function (2.9). Specifically, the marginal distribution of the input, p(u), is given by
| 2.12 |
The joint distribution between unfolded protein and active sensors is given by
| 2.13 |
Lastly, the marginal distribution of the output is
| 2.14 |
2.4. Numerical calculation and optimization of mutual information
An exact, closed-form expression for the mutual information is challenging to obtain due to the difficulty in marginalizing the joint distribution of u and nA. Hence, we calculate the mutual information numerically. While the number of active sensors is already a discrete quantity, it is necessary to discretize the prior distribution to determine a numerical value for the mutual information. This is done by dividing the range of inputs into discrete bins such that there are Nu equally spaced bins of u values between umin and umax, and NC values of C0 between C0,min and C0,max. The initial distribution is then transformed into a discrete distribution in the variables u and c with Nc bins between cmin and cmax. The mutual information can then be computed by numerically calculating the necessary (discrete) probability distributions p(u), p(nA) and p(u, nA), and applying equation (2.10) directly.
In order the compare the information for different sensor mechanisms, it is pertinent to compare the maximal amounts of information each mechanism can transmit, i.e. the channel capacity, across all sets of kinetic parameters. To calculate the channel capacity of each mechanism, the mutual information is numerically maximized over the kinetic parameters in each model: {α, γ} in the unfolded protein-mediated mechanism, {β, γ} in the chaperone-mediated mechanism, and {α, β, γ} in the hybrid mechanism. Details of the maximization procedure are provided in the electronic supplementary material.
3. Results
Using mutual information as a metric, we seek to quantify the effectiveness of different sensing mechanisms at monitoring protein homeostasis in the ER. In particular, we initially assume that the quantity of interest of the UPR regulatory network is the concentration of unfolded protein in the ER lumen and ask which sensing mechanism provides the most information about this quantity. Furthermore, once we have determined which sensing mechanism is most informative, we would like to then understand how this mechanism is able to better measure the level of stress in the ER. We do this with a combination of computational and asymptotic techniques to discern how integrating the signals measuring unfolded protein and free chaperone can be most effectively achieved. Lastly, we ask how the optimal sensing mechanism changes if the quantity of interest (i.e. the measure of ER stress) is the concentration of free chaperone, as opposed to unfolded proteins.
3.1. Direct sensing of unfolded proteins is more informative than chaperone-mediated sensing
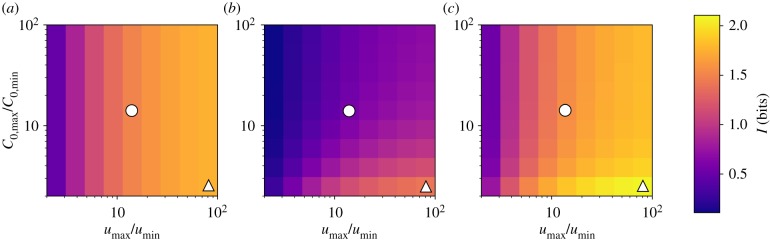
Following optimization of the mechanism-specific rate parameters, the only unconstrained parameters in our model are the ranges of the input distributions, C0,min, C0,max, umin, umax and the total number of sensors, NI. To show that the channel capacity of the direct sensing mechanism exceeds that of the indirect mechanism, we perform numerical calculations of the maximal mutual information for each mechanism across a broad range of prior distributions and for several values of NI (see electronic supplementary material). In figure 2, the maximal values of mutual information of each mechanism are displayed as heat maps for a range of prior distributions. In each case, C0,min and umin are fixed, and the upper bounds, C0,max and umax, are varied over several orders of magnitude. Comparing the mutual information of the unfolded protein-mediated and chaperone-mediated mechanisms for any particular set of input parameters shows that the unfolded protein-mediated mechanism will always provide more information about the unfolded protein concentration in the ER than the chaperone-mediated mechanism. Quantitatively, the difference between the information between the unfolded protein- and chaperone-mediated mechanisms, ΔIu−c, ranges between 0.19 and 1.08 bits for the chosen set of prior distributions. Additionally, figure 2c shows the channel capacity for the hybrid mechanism. Since this mechanism has an additional free parameter compared to the unfolded protein- and chaperone-mediated mechanisms, it clearly can provide at least as much information as the better of the two special cases. Figure 2c shows that, in general, the hybrid mechanism provides more information than either of the other two mechanisms (ΔIh−u ranges from 0.03 to 0.37 bits for chosen priors), and that this difference in greatest when the range of u is large and the range of C0 is small. Observing figure 2a shows the channel capacity for the direct mechanism is independent of the range of total chaperone in the input distribution. Intuitively, this makes sense as the direct mechanism only measures free unfolded protein concentration, and hence is decoupled from the chaperone concentration. This decoupling depends on our choice of input distributions: the probability distributions of free unfolded protein concentration between the chosen bounds are independent of chaperone concentration. This would not necessarily be the case for another choice of priors—for example, a uniform distribution of total unfolded protein (chaperone-bound and unbound)—in which case the free unfolded protein distribution would be coupled to the concentration of chaperone.
Figure 2.
Heat maps of channel capacity for unfolded protein-mediated (a), chaperone-mediated (b) and hybrid (c) mechanisms. The maximal information for each mechanism is computed for different ranges of the uniform prior distribution. The colour denotes the channel capacity in bits. In all cases, C0,min = 1000 and umin = 1000. The upper limits of the input distributions are then varied from 2 to 100 times the minimum values. In all cases, the unfolded protein-mediated mechanism provides a more informative measurement of unfolded protein concentration than does the chaperone-mediated mechanism. This result is qualitatively insensitive to the minimum values of C0 and u, as well as the number of sensors, NI (see electronic supplementary material). The white circles and triangles mark the input parameters for which the response probability distributions are shown explicitly in figure 3. (Online version in colour.)
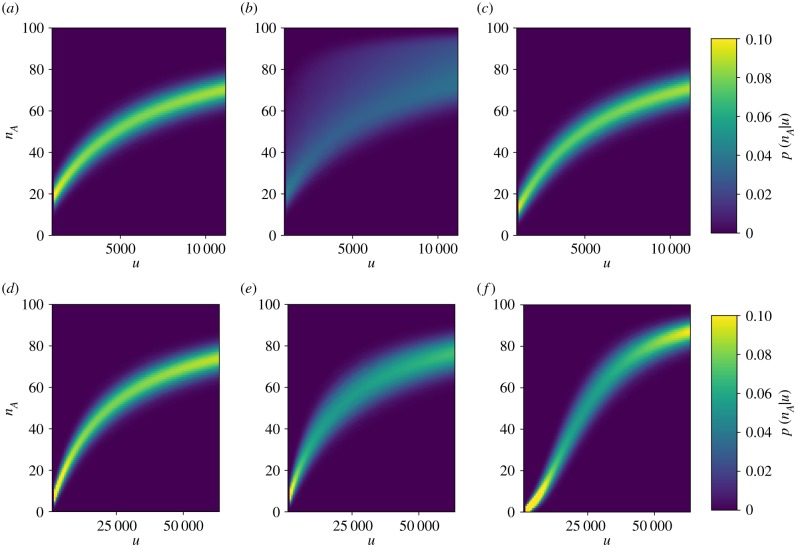
To better understand the difference in channel capacity between the unfolded protein-mediated and chaperone-mediated sensing mechanisms, we consider the optimized transfer functions (i.e. conditional probability distributions) for a specific prior distribution (figure 3). By comparing the conditional probability of activation for the unfolded protein-mediated mechanism (figure 3a) with that of the chaperone-mediated mechanism (figure 3b), we find that the chaperone-mediated mechanism provides a much more broadly distributed response for a given stimulus. Although the mean responses of the mechanisms are approximately the same, the chaperone-mediated mechanism lacks the specificity provided by the unfolded protein-mediated mechanism, making it far less informative about the number of unfolded proteins in the ER. In particular, the conditional probability of activation for the chaperone-mediated mechanism is skewed towards higher levels of activity. In the following section, we demonstrate that this is due to interference from indirectly measuring the concentration of unfolded protein through the concentration of chaperone.
Figure 3.
Conditional probabilities of activation as a function of free unfolded protein for the unfolded protein-mediated (a,d), chaperone-mediated (b,e) and hybrid (c,f ) mechanisms. The unfolded protein-mediated and hybrid mechanisms provide well-defined levels of activation for a given amount of unfolded protein, while the activation of the chaperone-mediated mechanism is much more dispersed. This dispersion greatly limits the information transmission of the chaperone-mediated mechanism. Prior distributions for the top row of panels correspond to those marked by white circles in figure 2, and for the bottom row of panels correspond to the prior distributions marked by white triangles. (Online version in colour.)
3.2. Indirect signalling interferes with the measurement of unfolded protein concentration
To better understand why the chaperone-mediated sensing mechanism provides significantly less information about the unfolded protein concentration than the unfolded protein-mediated or hybrid mechanisms, we consider the low-noise limit of the sensor signal transduction. In this limit, the intrinsic noise of the sensor is assumed to be negligibly small so that the sensor makes an exact measurement of the mean output for the noisy sensor. With this approximation, the only variance in the measurement will come from interference due to indirectly measuring the unfolded protein concentration, as opposed to the stochasticity of sensor activating and deactivating. We begin by approximating the transfer function p(nA|u, c) as Gaussian with mean, μ(u, C0), equal to the mean of the exact transfer function given in equation (2.9):
| 3.1 |
and
| 3.2 |
where σ is the standard deviation of the Gaussian approximation. Next, we derive an analytical expression for the conditional probability p(nA|u) for the hybrid mechanism in the limit as σ → 0. The conditional probabilities of activation for the unfolded protein- and chaperone-mediated models are then found by taking the limits as β → 0 and α → 0, respectively.
In general, the conditional probability of activation explicitly depends on the amount of chaperone present in the ER and is then given by
| 3.3 |
where q(C0) is given by marginalizing the prior distribution over u. In the case of the uniform priors used here, this simply results in a uniform distribution between C0,min and C0,max. To approximate the integral on the right-hand side of equation (3.3) we employ a saddle point approximation [33] (see electronic supplementary material for details), valid for small σ. This results in an explicit formula for the low-noise approximation to the conditional activation probability:
| 3.4 |
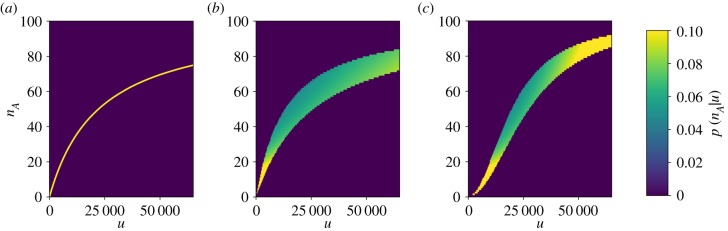
where μmin(u) = μ(u, C0,max) and μmax(u) = μ(u, C0,min). Hence the width of the conditional probability distribution depends directly on the range of chaperone concentrations, (C0,min, C0,max). In the limit as μmax → μmin, which corresponds to the unfolded protein-mediated mechanism (i.e. β → 0), equation (3.4) reduces to a Dirac delta function centred at the mean value, i.e. δ(nA − μ(u)). In this case, there is no uncertainty about the unfolded protein concentration given a reading of the sensor in the zero-noise limit. However, for both the chaperone-mediated and hybrid mechanisms, the dependence of activation on c leads to uncertainty even as σ → 0. Figure 4 shows the conditional activation probability distributions for each mechanism as a function of u in the zero-noise limit. For the chaperone-mediated and hybrid mechanisms, a degree of uncertainty persists even when the sensor makes a theoretically noise-free measurement due to multiple (u, C0) pairs producing the same sensor output. From equation (3.4), it is clear that this uncertainty is related to the range of values for C0 in the prior distribution. When the range set by ΔC0 shrinks, the precision of the measurement increases, as can be seen by comparing vertically aligned points in figure 2b,c. Hence, indirectly measuring u through a mechanism that involves chaperone titration introduces a source of noise that is independent of the stochastic nature of the protein–protein interactions that activate the sensor.
Figure 4.
Zero-noise limit of conditional probabilities of activation as a function of free unfolded protein for the unfolded protein-mediated mechanism (a), chaperone-mediated mechanism (b) and the hybrid mechanism (c). Prior distributions and parameters correspond to those marked by white triangles in figure 2. (Online version in colour.)
3.3. A hybrid sensing mechanism enhances information transmission by ‘stretching’ the dose–response curve at the expense of increased noise
The information capacity of the hybrid model, shown in figure 2c, is always greater than that of the unfolded protein-mediated mechanism. Since the unfolded protein-mediated mechanism is a special case of the hybrid sensing mechanism in which β = 0, the hybrid mechanism will always provide at least as much information, but it is not guaranteed that it should outperform the unfolded protein-mediated mechanism. In particular, it is not clear how introducing dependence on an additional random variable, C0, should increase the sensor's ability to measure u. The low-noise approximation showed that introducing C0 into the sensor activation function necessarily obscured the measurement of u since multiple values of u were then able to produce the same expected output of the sensor. One might expect this to imply that the direct measurement of u is the most effective way of measuring u.
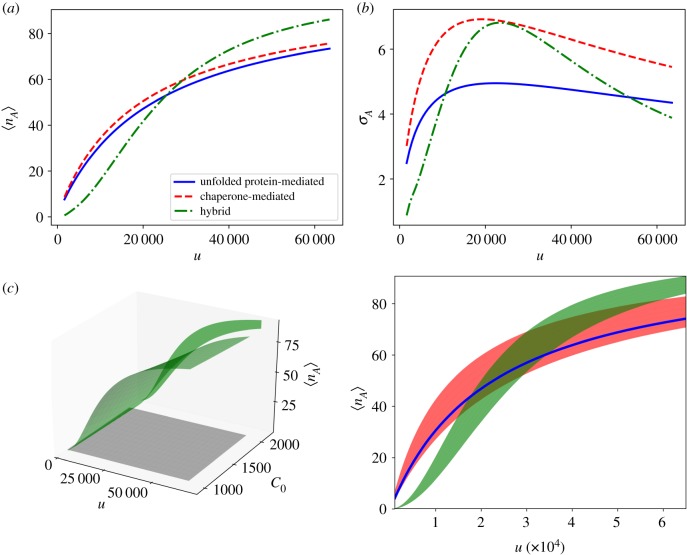
However, the hybrid mechanism improves the channel capacity beyond the maximal value for the unfolded protein-mediated mechanism. The asymptotic activation probability shown in figure 4c offers insight into how this occurs. The hybrid mechanism stretches the range of the sensor compared to the unfolded protein-mediated mechanism, but at the cost of increasing the noise. This is further evidenced by the numerically calculated mean values and standard deviations of the optimal activation functions for each mechanism, shown in figure 5a,b, respectively. The balance of these two competing effects determines the optimal parametrization of the hybrid sensor.
Figure 5.
Panels (a,b) show the mean activation and standard deviation for each mechanism as a function of unfolded protein. Panel (c) shows the surface of mean activation for the hybrid mechanism (green surface, left panel), over the uniform prior distribution (grey square), along with the projection of the hybrid mean activation surface onto the u–nA plane. On the right, the projections of surfaces of mean activation onto the u–nA plane are plotted for each mechanism. The hybrid mechanism (green shaded region), which provides the most informative signal, increases the range of activation at the expense of greater noise compared to the unfolded protein-mediated sensor (blue line). The chaperone-mediated mechanism (red shaded region) projects onto a broad area of the input–output space, making it a poor sensor of unfolded protein. Parameters and input distributions correspond to those marked by the white triangles in figure 2. (Online version in colour.)
The zero-noise limit sheds additional light on the trade-off between the range of the sensor and the interference due to measuring stress indirectly. Figure 5c shows the projection of the surfaces of mean activation onto the u–nA plane. These projections correspond to the same regions for which equation (3.4) is non-zero. The unfolded protein-mediated mechanism projects onto a single line in the u–nA plane since there is a one-to-one correspondence between u and mean sensor activation for this mechanism. The chaperone-mediated and hybrid mechanisms on the other hand, lack this one-to-one correspondence and a single mean output value corresponds to a range of values of u. The hybrid mechanism, however, effectively overcomes this added uncertainty by increasing the range of mean activation. In summary, the hybrid mechanism increases uncertainty due to indirectly measuring u through the chaperone concentration in order to extend the sensor operating range. This trade-off allows the hybrid mechanism to transmit maximal information about u.
3.4. A hybrid sensing mechanism also increases information about free chaperone concentration
Thus far, we have considered u to be the measure of stress that the cell aims to monitor. However, this need not be the case. For example, an ER with very few unbound chaperones indicates that the folding capacity is nearly exceeded by client unfolded protein demand and action must be taken to maintain proteostasis. Furthermore, it has been shown that a UPR that responds to the concentration of free chaperone, as opposed to free unfolded protein, can provide a more efficient response to acute stress [26]. In this section, we demonstrate that the hybrid mechanism can provide a more precise reading of free chaperone concentration in the same way it was able to provide a more precise measurement of unfolded protein concentration.
Figure 6 shows optimized conditional activation probabilities for each mechanism as a function of free chaperone. When the aim of the sensor is to measure free chaperone concentration, the unfolded protein-mediated sensor suffers from the same interference effect that the chaperone-mediated sensor suffered when the quantity of interest was unfolded protein. Both the chaperone-mediated sensor and the hybrid sensor provide relatively reliable measurements of the chaperone concentration. Again, it is possible to construct a low-noise approximation for the conditional activation probability (see electronic supplementary material):
| 3.5 |
where now μmin(c) = μ(c, U0,min) and μmax(c) = μ(c, U0,max).
Figure 6.
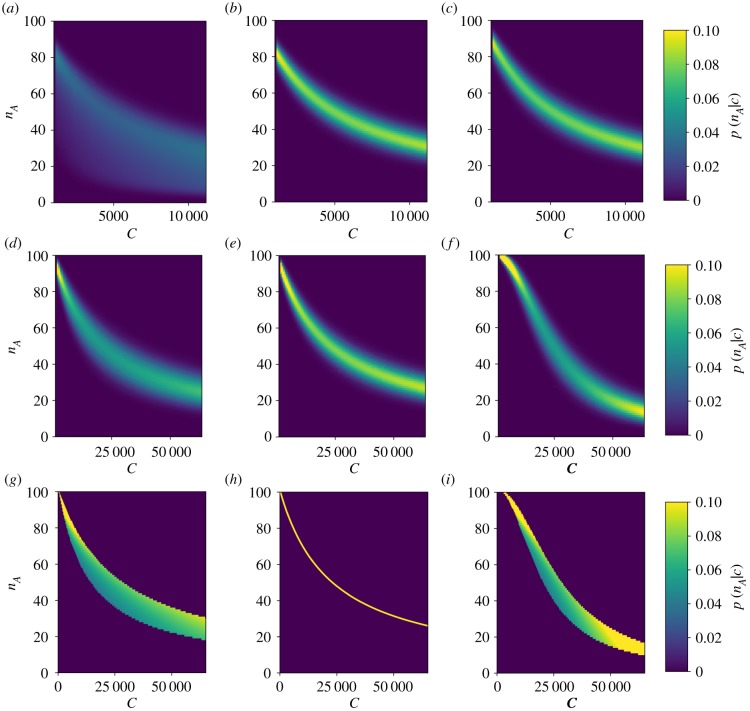
Conditional probabilities of activation as a function of free chaperone for the unfolded protein-mediated (a,d,g), chaperone-mediated (b,e,h) and hybrid (c,f,i) mechanisms. The top two rows show numerically calculated conditional probabilities of optimized parameter sets for two different prior distributions. The bottom row shows the low-noise approximation given in equation (3.5) for the same prior and parameters used in the middle row. The chaperone-mediated and hybrid mechanisms provide well-defined levels of activation for a given amount of free chaperone, while the activation of the unfolded protein-mediated mechanism is much more dispersed. This dispersion greatly limits the information transmission of the unfolded protein-mediated mechanism. The plotted results are for uniform prior distributions with ranges U0,min = 103, U0,max = 11.4 × 103, cmin = 103 and cmax = 11.4 × 103 for the top row, and U0,min = 103, U0,max = 2 × 103, cmin = 103 and cmax = 64.7 × 103 for the bottom two rows. The mutual information for priors with other ranges is provided in the electronic supplementary material. (Online version in colour.)
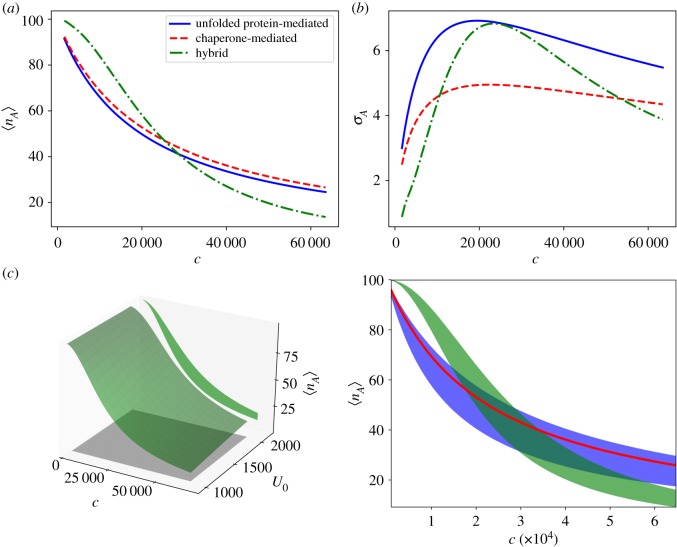
Equation (3.5), evaluated at optimized parameters for each mechanism, is shown in figure 6g,h,i. Analogously to the case where u was the quantity of interest, the hybrid mechanism is able to provide more information about the concentration of free chaperone than the chaperone-sensing mechanism by stretching the range of activation of the sensor for the same input range of c. As shown in figure 7a,b, this is again the result of allowing some additional uncertainty in the output for specific inputs in exchange for a greater range of outputs. Figure 7c provides a geometrical interpretation: identical values of c can produce different outputs, nA, for the unfolded protein-mediated and hybrid mechanisms. Geometrically, this corresponds to the surface of mean activation projecting onto a region in the c–nA plane with a finite area. Mitigating this uncertainty by increasing the range of the sensor’s response, the hybrid sensing mechanism allows for more informative measurements of the free chaperone concentration than a mechanism that only responds directly to free chaperones. This result, together with the similar result for measuring unfolded protein concentration, demonstrates that directly measuring the quantity of interest does not necessarily provide the most information about that quantity.
Figure 7.
Panels (a,b) show the mean responses and standard deviations of each mechanism as a function of free chaperone. Panel (c) shows the surface of mean activation for the hybrid mechanism (green surface, left panel), over the uniform prior distribution (grey square), along with the projection of the hybrid mean activation surface onto the c–nA plane. On the right, the projections of surfaces of mean activation onto the c–nA plane are plotted for each mechanism. The hybrid mechanism (green shaded region) increases the range of activation at the expense of greater noise as compared to the chaperone-mediated sensor (red line). The unfolded protein-mediated mechanism (blue shaded region) projects onto a broad area of the input–output space, making it a poor sensor of available chaperone. (Online version in colour.)
4. Discussion
ER stress is monitored by stress-sensing proteins in the ER membrane that are both activated by unfolded protein ligands and suppressed by unbound chaperones. However, it has not been established why such a mechanism evolved. We hypothesized that this hybrid mechanism of stress sensing could provide more information about the state of the ER than measuring only unfolded proteins or chaperones, while still allowing the UPR to take advantage of the added efficiency and buffering of sensors that respond to depleted chaperone.
Our results indicate that a sensor that is suppressed by chaperone provides less information about unfolded protein concentration in the ER than a sensor that is activated by unfolded proteins. In particular, this is because multiple input pairs (u, C0) can produce the same output of the chaperone-mediated sensor even when the signal is free of noise. This introduces inherent ambiguity into the sensor output with regards to the concentration of free unfolded proteins within the ER, i.e. ER stress. A mechanism that combines both direct unfolded protein sensing and chaperone sequestration of sensors is capable of providing more information than the unfolded protein-mediated mechanism alone. To do so, the hybrid sensor allows for a small increase in ambiguity of the mean sensor output for a given concentration of unfolded protein in order to extend the range of outputs.
Analogously, if the sensor evolved to measure the concentration of free chaperone in the ER, which is an alternative measure of ER stress, the chaperone-mediated sensor provides substantially more information than the unfolded protein sensor. The hybrid sensor then further increases the channel capacity of the chaperone-mediated sensor. Previous studies [25,26] have shown that the chaperone-mediated sensing mechanism provides a benefit in terms of the efficiency of the UPR when responding to acute stress events. However, the precision with which the sensor determines the level of stress in the ER was not considered. The present analysis illustrates that combining chaperone-mediated suppression with unfolded protein activation can increase the amount of information about ER stress transmitted out of the ER lumen.
By providing a more informative measurement of the stress level within the ER, the hybrid mechanism would allow for a more finely tuned UPR. Precise control over the UPR is important to organism fitness due to the substantial metabolic cost of maintaining proteostasis. For example, the chaperone BiP is present at one of the highest copy numbers of any protein in eukaryotic cells, ≈3 × 105 in yeast [34] and ≈2 × 107 in unstressed HeLa cells [35]. Upon stress, the copy number can increase more than 10-fold [35]. Decreasing the amount of chaperone required to mitigate an acute stress event can therefore make a substantial contribution to cellular energy expenditure. This is particularly true for secretory cells, such as pancreatic β-cells, where proinsulin mRNA translation rates reach approximately 106 molecules per minute in response to glucose stimulation [36–38], all of which must be processed in the ER. Overall, up to 20% of known genes go through transcriptional changes when the UPR is activated [39]. Additionally, for large stresses, the UPR induces apoptosis, further increasing the importance of reliable and precise ER stress measurements. Hence, the importance of precise UPR control provides a rationalization of the ER stress-sensing mechanism. A sensor that is repressed by available chaperones provides a relatively simple mechanism for monitoring and responding to chaperone abundance in the ER, and is able to capitalize on the advantages of using free chaperone as a measure of stress. However, the precision of this mechanism can then be further enhanced by incorporating a direct interaction with unfolded proteins into the activation mechanism.
This reasoning depends on the implicit assumption that the information capacity of the stress sensing network and the metabolic efficiency with which the network responds to stress are the main drivers of stress sensor evolution. While we acknowledge this to be an assumption, we believe it to be valid for two reasons. First, the metabolic costs of mitigating protein stress and maintaining protein homeostasis are substantial, especially for secretory cells. Hence, a more frugal use of chaperone upregulation in response to stress can significantly reduce cellular energy expenditure. Second, for the cell to take advantage of the more efficient stress response, the signal must be informative regarding the level of stress. In particular, it is essential for the first step in the signal transduction pathway—the measurement of stress in the ER—to transmit maximal information since the information processing inequality ensures that information will only be further degraded as it passes along the signalling pathway.
While incorporating the direct activation of the sensor by unfolded proteins enhances the information about ER stress beyond the capacity of the chaperone-mediated sensor alone, this may be only one of several benefits provided by direct unfolded protein–sensor interactions. For example, the binding of the unfolded protein could stabilize clusters of signalling molecules into long-lived signalling foci, changing the dynamics of the response [25]. Analysis of the binding groove formed by Ire1 dimers suggests that the peptide sequences that are recognized by the signalling complex are only partially overlapping with those which act as substrates for the chaperone BiP [20]. This could indicate that direct protein binding provides supplementary material about unfolded proteins in the ER that is not incorporated in the concentration of available BiP. Furthermore, it is possible that sensor oligomerization, which is important for sustained kinase activity of Ire1 and Perk, could change leading to more cooperative responses. In this case, we expect that combining multiple inputs would still allow for greater information transfer since the underlying trade-off between intrinsic sensor noise and sensor gain can still be manipulated by combining measurements of unfolded protein and chaperone concentrations. Explicit modelling of more complex mechanisms involving sensor oligomerization will be the topic of future studies. However, regardless of how these effects alter the response, our analysis indicates that incorporating the unfolded protein directly into the signalling mechanism can enhance the measurement of the free chaperone in the ER.
Our main finding in this work is that bidirectional control of ER stress sensor activity allows the cell to distinguish between a greater number of degrees of stress. It should be possible to test this result experimentally by using fluorescence resonance energy transfer-based assays of Ire1 activity along with a probe of BiP concentration within the ER. The ER could then be pharmacologically stressed (e.g. with DTT) to different degrees, allowing for the experimental construction of the probability of activation conditioned on BiP concentration and DTT dose. In this case, DTT dose would serve as the quantity that the stress sensor is attempting to measure. By showing that different DTT doses can produce the same mean sensor output when the BiP concentration varies, the experiments can recapitulate the lack of a one-to-one correspondence between input and output shown by the model in the low-noise regime. Furthermore, by using an Ire1 mutant lacking the BiP-binding region [25], it could be possible to compare the information capacity of the hybrid and direct unfolded protein mechanisms experimentally by reconstructing the probability of activation for Ire1 at a range of BiP and DTT concentrations. Our analysis suggests that the mutant which lacks chaperone binding capacity might show less noise for a specific DTT dose, but will have a greater range of non-saturating DTT concentrations.
The additional information capacity of the hybrid sensing mechanism represents a specific instance of a more general feature of signal integration in biochemical networks. Namely, it is possible to increase the precision with which one component of a multi-component system can be sensed by incorporating the signal from another coupled component. This will be the case for any instance in which the aim is to monitor the components of a bimolecular reaction, including enzyme catalysed reactions. Given the prevalence of such reactions in cellular biochemistry, we expect the results presented here to extend beyond the case of ER stress sensing.
5. Conclusion
This work provides two main results regarding stress sensing in the ER. First, on its own, the chaperone-mediated sensing mechanism provides a poor estimate of the concentration of unfolded proteins in the ER, but a rather precise measurement of the concentration of available chaperone. Hence, it appears that cells might have evolved to respond primarily to the depletion of available chaperone as opposed to unfolded protein copy number. Second, integrating the signal from free chaperones with direct sensor activation by unfolded proteins can improve the information about chaperone availability within the ER. Together, these results further our understanding of how cells monitor and maintain protein folding homeostasis within the ER.
Supplementary Material
Data accessibility
All codes used to generate and analyse results are available at https://github.com/santiago-schnell/Information-Processing-ER-Stress-Sensors.
Authors' contributions
W.S. and S.S. conceived the study. W.S. generated numerical results. W.S. and J.E. analysed the model. W.S., J.E. and S.S. interpreted the results and wrote the manuscript. All authors gave approval of the final version of the manuscript.
Competing interests
The authors declare no competing interests.
Funding
This work is partially supported by the University of Michigan Protein Folding Diseases Initiative. W.S. is funded through the Michigan IRACDA Program (NIH/NIGMS, grant no. K12 GM111725). J.E. is partially funded through the Postdoctoral Pediatric Endocrinology and Diabetes Training Program at the University of Michigan (NIH/NIDDK, grant no. T32 DK071212).
References
- 1.Oakes SA, Papa FR. 2015. The role of endoplasmic reticulum stress in human pathology. Annu. Rev. Pathol.: Mech. Dis. 10, 173–194. ( 10.1146/annurev-pathol-012513-104649) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cnop M, Foufelle F, Velloso LA. 2012. Endoplasmic reticulum stress, obesity and diabetes. Trends Mol. Med. 18, 59–68. ( 10.1016/j.molmed.2011.07.010) [DOI] [PubMed] [Google Scholar]
- 3.Eizirik DL, Cnop M. 2010. ER stress in pancreatic β cells: the thin red line between adaptation and failure. Sci. Signal. 3, pe7 ( 10.1126/scisignal.3110pe7) [DOI] [PubMed] [Google Scholar]
- 4.Volchuk A, Ron D. 2010. The endoplasmic reticulum stress response in the pancreatic β-cell. Diab. Obes. Metab. 12, 48–57. ( 10.1111/j.1463-1326.2010.01271.x) [DOI] [PubMed] [Google Scholar]
- 5.Hetz C, Saxena S. 2017. ER stress and the unfolded protein response in neurodegeneration. Nat. Rev. Neurol. 13, 477–491. ( 10.1038/nrneurol.2017.99) [DOI] [PubMed] [Google Scholar]
- 6.Korennykh AV, Egea PF, Korostelev AA, Finer-Moore J, Zhang C, Shokat KM, Stroud RM, Walter P. 2009. The unfolded protein response signals through high-order assembly of Ire1. Nature 457, 687–693. ( 10.1038/nature07661) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Travers KJ, Patil CK, Wodicka L, Lockhart DJ, Weissman JS, Walter P. 2000. Functional and genomic analyses reveal an essential coordination between the unfolded protein response and ER-associated degradation. Cell 101, 249–258. ( 10.1016/S0092-8674(00)80835-1) [DOI] [PubMed] [Google Scholar]
- 8.Yoshida H, Matsui T, Yamamoto A, Okada T, Mori K. 2001. XBP1 mRNA is induced by ATF6 and spliced by IRE1 in response to ER stress to produce a highly active transcription factor. Cell 107, 881–891. ( 10.1016/S0092-8674(01)00611-0) [DOI] [PubMed] [Google Scholar]
- 9.Bertolotti A, Zhang Y, Hendershot LM, Harding HP, Ron D. 2000. Dynamic interaction of BiP and ER stress transducers in the unfolded-protein response. Nat. Cell Biol. 2, 326–332. ( 10.1038/35014014) [DOI] [PubMed] [Google Scholar]
- 10.Chuan YL, Schroder M, Kaufman RJ. 2000. Ligand-independent dimerization activates the stress response kinases IRE1 and PERK in the lumen of the endoplasmic reticulum. J. Biol. Chem. 275, 24 881–24 885. ( 10.1074/jbc.M004454200) [DOI] [PubMed] [Google Scholar]
- 11.Credle JJ, Finer-Moore JS, Papa FR, Stroud RM, Walter P. 2005. On the mechanism of sensing unfolded protein in the endoplasmic reticulum. Proc. Natl Acad. Sci. USA 102, 18 773–18 784. ( 10.1073/pnas.0509487102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou J, Liu CY, Back SH, Clark RL, Peisach D, Xu Z, Kaufman RJ. 2006. The crystal structure of human IRE1 luminal domain reveals a conserved dimerization interface required for activation of the unfolded protein response. Proc. Natl Acad. Sci. USA 103, 14 343–14 348. ( 10.1073/pnas.0606480103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schnell S. 2009. A model of the unfolded protein response: pancreatic beta-cell as a case study. Cell. Physiol. Biochem. 23, 233–244. ( 10.1159/000218170) [DOI] [PubMed] [Google Scholar]
- 14.Dorner AJ, Wasley LC, Kaufman RJ. 1992. Overexpression of GRP78 mitigates stress induction of glucose regulated proteins and blocks secretion of selective proteins in Chinese hamster ovary cells. EMBO J. 11, 1563–1571. ( 10.1002/j.1460-2075.1992.tb05201.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kohno K, Normington K, Sambrook J, Gething MJ, Mori K. 1993. The promoter region of the yeast KAR2 (BiP) gene contains a regulatory domain that responds to the presence of unfolded proteins in the endoplasmic reticulum. Mol. Cell. Biol. 13, 877–890. ( 10.1128/MCB.13.2.877) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ng DT, Watowich SS, Lamb RA. 1992. Analysis in vivo of GRP78-BiP/substrate interactions and their role in induction of the GRP78-BiP gene. Mol. Biol. Cell 3, 143–155. ( 10.1091/mbc.3.2.143) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Okamura K, Kimata Y, Higashio H, Tsuru A, Kohno K. 2000. Dissociation of Kar2p/BiP from an ER sensory molecule, Ire1p, triggers the unfolded protein response in yeast. Biochem. Biophys. Res. Commun. 279, 445–450. ( 10.1006/bbrc.2000.3987) [DOI] [PubMed] [Google Scholar]
- 18.Kimata Y, Oikawa D, Shimizu Y, Ishiwata-Kimata Y, Kohno K. 2004. A role for BiP as an adjustor for the endoplasmic reticulum stress-sensing protein Ire1. J. Cell Biol. 167, 445–456. ( 10.1083/jcb.200405153) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oikawa D, Kimata Y, Kohno K. 2007. Self-association and BiP dissociation are not sufficient for activation of the ER stress sensor Ire1. J. Cell Sci. 120, 1681–1688. ( 10.1242/jcs.002808) [DOI] [PubMed] [Google Scholar]
- 20.Gardner BM, Walter P. 2011. Unfolded proteins are Ire1-activating ligands that directly induce the unfolded protein response. Science 333, 1891–1894. ( 10.1126/science.1209126) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Promlek T, Ishiwata-Kimata Y, Shido M, Sakuramoto M, Kohno K, Kimata Y. 2011. Membrane aberrancy and unfolded proteins activate the endoplasmic reticulum stress sensor Ire1 in different ways. Mol. Biol. Cell 22, 3520–3532. ( 10.1091/mbc.e11-04-0295) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Karagöz GE, Acosta-Alvear D, Nguyen HT, Lee CP, Chu F, Walter P. 2017. An unfolded protein-induced conformational switch activates mammalian IRE1. eLife 6, e30700 ( 10.7554/eLife.30700) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang P, Li J, Tao J, Sha B. 2018. The luminal domain of the ER stress sensor protein PERK binds misfolded proteins and thereby triggers PERK oligomerization. J. Biol. Chem. 293, 4110–4121. ( 10.1074/jbc.RA117.001294) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kimata Y, Ishiwata-Kimata Y, Ito T, Hirata A, Suzuki T, Oikawa D, Takeuchi M, Kohno K. 2007. Two regulatory steps of ER-stress sensor Ire1 involving its cluster formation and interaction with unfolded proteins. J. Cell Biol. 179, 75–86. ( 10.1083/jcb.200704166) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pincus D, Chevalier MW, Aragón T, van Anken E, Vidal SE, El-Samad H, Walter P. 2010. BiP binding to the ER-stress sensor Ire1 tunes the homeostatic behavior of the unfolded protein response. PLoS Biol. 8, e1000415 ( 10.1371/journal.pbio.1000415) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stroberg W, Aktin H, Savir Y, Schnell S. 2018. How to design an optimal sensor network for the unfolded protein response. Mol. Biol. Cell 29, 3052–3062. ( 10.1091/mbc.E18-01-0060) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Braakman I, Hebert DN. 2013. Protein folding in the endoplasmic reticulum. Cold Spring Harbor Perspect. Biol. 5, a013201 ( 10.1101/cshperspect.a013201) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hebert DN, Molinari M. 2007. In and out of the ER: protein folding, quality control, degradation, and related human diseases. Physiol. Rev. 87, 1377–1408. ( 10.1152/physrev.00050.2006) [DOI] [PubMed] [Google Scholar]
- 29.VanKampen N. 1976. The equilibrium distribution of a chemical mixture. Phys. Lett. A 59, 333–334. ( 10.1016/0375-9601(76)90398-4) [DOI] [Google Scholar]
- 30.Ziv E, Nemenman I, Wiggins CH. 2007. Optimal signal processing in small stochastic biochemical networks. PLoS ONE 2, e1077 ( 10.1371/journal.pone.0001077) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tkacik G, Callan CG, Bialek W. 2007. Information flow and optimization in transcriptional control. Proc. Natl Acad. Sci. USA 105, 12 265–12 270. ( 10.1073/pnas.0806077105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cheong R, Rhee A, Wang CJ, Nemenman I, Levchenko A. 2011. Information transduction capacity of noisy biochemical signaling networks. Science 334, 354–358. ( 10.1126/science.1204553) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mehta P, Goyal S, Long T, Bassler BL, Wingreen NS. 2009. Information processing and signal integration in bacterial quorum sensing. Mol. Syst. Biol. 5, 325 ( 10.1038/msb.2009.79) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ghaemmaghami S, Huh WK, Bower K, Howson RW, Belle A, Dephoure N, O’Shea EK, Weissman JS. 2003. Global analysis of protein expression in yeast. Nature 425, 737–741. ( 10.1038/nature02046) [DOI] [PubMed] [Google Scholar]
- 35.Bakunts A, Orsi A, Vitale M, Cattaneo A, Lari F, Tadè L, Sitia R, Raimondi A, Bachi A, vanAnken E. 2017. Ratiometric sensing of BiP-client versus BiP levels by the unfolded protein response determines its signaling amplitude. eLife 6, e30700 ( 10.7554/elife.30700) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schuit FC, In’t Veld PA, Pipeleers DG. 1988. Glucose stimulates proinsulin biosynthesis by a dose-dependent recruitment of pancreatic beta cells. Proc. Natl Acad. Sci. USA 85, 3865–3869. ( 10.1073/pnas.85.11.3865) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schuit FC, Kiekens R, Pipeleers DG. 1991. Measuring the balance between insulin synthesis and insulin release. Biochem. Biophys. Res. Commun. 178, 1182–1187. ( 10.1016/0006-291X(91)91017-7) [DOI] [PubMed] [Google Scholar]
- 38.Van Lommel L. et al. 2006. Probe-independent and direct quantification of insulin mRNA and growth hormone mRNA in enriched cell preparations. Diabetes 55, 3214–3220. ( 10.2337/db06-0774) [DOI] [PubMed] [Google Scholar]
- 39.Scheuner D, Kaufman RJ. 2008. The unfolded protein response: a pathway that links insulin demand with beta-cell failure and diabetes. Endocr. Rev. 29, 317–333. ( 10.1210/er.2007-0039) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All codes used to generate and analyse results are available at https://github.com/santiago-schnell/Information-Processing-ER-Stress-Sensors.