Abstract
The environment changes constantly at various time scales and, in order to survive, species need to keep adapting. Whether these species succeed in avoiding extinction is a major evolutionary question. Using a multilocus evolutionary model of a mutation‐limited population adapting under strong selection, we investigate the effects of the frequency of environmental fluctuations on adaptation. Our results rely on an “adaptive‐walk” approximation and use mathematical methods from evolutionary computation theory to investigate the interplay between fluctuation frequency, the similarity of environments, and the number of loci contributing to adaptation. First, we assume a linear additive fitness function, but later generalize our results to include several types of epistasis. We show that frequent environmental changes prevent populations from reaching a fitness peak, but they may also prevent the large fitness loss that occurs after a single environmental change. Thus, the population can survive, although not thrive, in a wide range of conditions. Furthermore, we show that in a frequently changing environment, the similarity of threats that a population faces affects the level of adaptation that it is able to achieve. We check and supplement our analytical results with simulations.
Keywords: adaptation, adaptive walk, changing environment, drift analysis, fitness landscape, strong selection weak mutation
Biological evolution has produced an extraordinary diversity of living organisms, highly adapted to their environment. However, the process of evolution is never‐ending—the environment changes constantly, and environmental change is often so widespread and severe that individuals cannot migrate to more suitable places nor physiologically accommodate to it (Bell and Gonzalez 2009). Populations must keep adapting in order to survive.
Environmental changes are inherent to nature, ubiquitous, and occurring over various time scales, from seasonal changes during the year to climatic changes over geological eras (Messer et al. 2016). The environment may be biotic; for instance, parasites and their hosts are tied in a never‐ending battle, with parasites fighting against the improving defense mechanisms of their hosts (Vermeij 1982; Gilman et al. 2012). In many social species, a significant part of the environment that individuals experience is given by their social partners, resulting in an environment that is itself evolving (Moore et al. 1997; Wolf et al. 1999). The dynamic nature of fitness landscapes has been pointed out already by Fisher (i.e., in a series of letters to Sewal Wright (Provine 1989) and in Fisher 1930). However, the analysis of adaptations in a changing environment has recently started to receive more attention, sparked by growing interest in conservation biology as well as in the evolution of drug resistance by various pathogens (Gallagher et al. 2015). Understanding the effect of a changing environment on the rate of adaptation is important from many different perspectives and has many potential applications.
Three main scenarios of environmental change have been studied from a theoretical perspective: (1) an abrupt change (e.g., addition of an antibiotic), (2) a gradually changing environment (e.g., progressive climate change), and (3) random fluctuations in selection. The ability of organisms to survive a single drastic environmental change, adapt rapidly, and avoid extinction has been investigated by the theory of evolutionary rescue. For instance, the evolution of drug resistance by bacteria, or heavy metal tolerance among plant populations growing on old mine tailings are classic examples of rapid evolution (Gonzalez et al. 2013). A series of theoretical studies have assessed the importance of genetic and environmental factors for population survival, including available genetic variation, recombination rates, population structure, and the severity and rate of environmental change (Pease et al. 1989; Lynch and Lande 1993; Bürger and Lynch 1995; Lande and Shannon 1996; Bell and Collins 2008; Orr and Unckless 2008; Polechová et al. 2009; Duputié et al. 2012; Schiffers et al. 2013; Carlson et al. 2014; Uecker et al. 2014; Uecker and Hermisson 2016). However, studies of evolutionary rescue usually investigate an effect of a single drastic environmental change and focus only on a single adaptive trait (but see Gomulkiewicz and Shaw 2012; Uecker and Hermisson 2016 for two traits).
From a different perspective, several theoretical and experimental studies have investigated adaptation across fitness landscapes with a moving optimum (Kopp and Hermisson 2009a, b; Matuszewski et al. 2014, 2015). For instance, Chevin et al. (2010) present an evolutionary model for the critical rate of environmental change beyond which a population must decline and go extinct. The authors highlight the major determinants of extinction risk in a changing environment but also identify additional research needed for improved predictions based on environmental change. This problem has also been investigated by several recent experimental studies that explored the evolutionary potential of marine organisms to adapt to rising levels of in the environment (Bell and Collins 2008; Fussmann et al. 2014).
Another insight into adaptation to variable environments comes from the studies of co‐evolution of host–parasite systems. These studies by definition assume that selection on a trait (e.g., a defense mechanism) changes with the adaptation of the corresponding trait of the adversary. It has been shown that the number of traits involved in adaptation seems to play a major role in co‐evolution of predator‐and‐prey systems, where often multiple traits are affected by the predator–prey (or parasite–host) interaction (Vermeij 1982; Gilman et al. 2012). Gilman et al. (2012) developed a model of a victim–exploiter system, in which the probability of a successful attack by an exploiter on a victim depends on several traits in each species. The authors investigated the influence of the number of traits on co‐evolutionary trajectories, assuming that each trait is functionally paired with a trait in the opposite species, and found out that multidimensionality of trait space promotes escape from the parasites and predators (Gilman et al. 2012). Furthermore, Doebeli and Ispolatov (2010) have shown that the number of traits under selection can have qualitative effects on the outcome of evolution even in single‐species systems.
The last group of studies focuses on random fluctuations in selection gradient, and the establishment of beneficial alleles subject to variable selection pressures (Uecker and Hermisson 2011; Waxman 2011; Peischl and Kirkpatrick 2012; Cvijovic et al. 2015a). For instance, Chevin (2013) derived the expected rate of adaptation and investigated limits to adaptation in this context. Cvijovic et al. (2015b) investigated the fate of a mutation in a fluctuating environment and discovered that environmental variability reduces the efficiency of selection. Moreover, the authors found that temporal fluctuations can dramatically increase fixation probabilities of deleterious mutations (Cvijovic et al. 2015b). It has been further suggested that a changing environment can change effects of new mutations from positive or negative to neutral (Mustonen and Lässig 2009). Simulations carried out by Kashtan et al. (2007) have shown that a varying environment can speed up adaptation by removing the local optima in which populations can get temporarily stuck. In another simulation study, Vincenzi (2014) investigated an impact of climate change causing increased frequency of gradually more extreme events in the context of anthropogenic environmental change. Vincenzi (2014) showed that survival chances decrease strongly and linearly with increasing strength of selection as well as with increasing climate trend and variability but are unaffected by the amplitude of mutations.
Even though the interest in adaptation to a changing environment is rapidly growing, a rigorous analysis of dynamic fitness landscapes—seascapes—has been hindered by technical difficulties. Most of the recent studies rely on simulations (Kopp and Hermisson 2007; Kashtan et al. 2007; Büchi and Vuilleumier 2014; Vincenzi 2014), offering only very limited analytical understanding of the problem. Furthermore, most of these studies investigate either a single drastic environmental change, adaptations with slowly moving optima, or in the randomly changing environment. Most importantly, these studies usually focus on a small number of adaptive loci. On the other hand, studies of gradual adaptation involving multiple loci investigate adaptation in the stable environment, assuming that the fitness landscape is fixed (Orr 2000; Chatterjee et al. 2014; Paixão, Pérez Heredia, et al. 2015). These studies have investigated the rate of adaptation and the time required for populations to adapt. This time has been shown to grow from polynomially to exponentially with the length of the genome, according to the complexity of the fitness landscape, as measured by both the number of loci and epistasis (Orr 2000; Chatterjee et al. 2014; Paixão, Pérez Heredia, et al. 2015; Pérez Heredia et al. 2016). However, as this time grows, it is likely that the environment changes; thus, it is necessary to replace the metaphor of a fixed, rigid fitness landscape by an idea of a dynamic “seascape” (Mustonen and Lässig 2009). Rigorous studies considering multiple adaptive loci in a changing environment are still missing.
Here, we build on static landscape studies to develop a multilocus evolutionary model of evolving populations and investigate adaptation in a changing environment in a strong‐selection–weak‐mutation (SSWM) regime. The population is assumed to be monomorphic, and in the absence of standing genetic variance for fitness, the outcome of adaptive processes crucially depends on new mutations. The environment changes between a defined set of conditions (threats). For instance, the population may experience selection pressure from a type of predator or parasite for a number of generations and evolve a defense mechanism. However, in time, selection pressure from the exploiter ceases, but a different exploiter appears, threatening the population.
We start with a single multilocus trait experiencing periods of strong selection alternating with periods of its absence and derive the expected level of adaptation the population can achieve, its minimum and maximum, as a function of the lengths of these periods. We then use the same approach to derive results for multitrait scenarios. Selection is directional, and the environments are determined extrinsically, unaffected by the organisms (as opposed to studies of co‐evolution). We focus on three different multitrait scenarios, according to the similarity of the fitness landscape at different time points. For each of these scenarios, we investigate the implication of the frequency of environmental fluctuations and the number of adaptive loci for adaptability. We first analyze simple additive fitness landscapes where all adaptive mutations contribute with the same fitness effect, then generalize our analysis (to some extent) for monotonic fitness functions. We focus on a saturating fitness function in detail and compare the results with the linear fitness function.
We show that frequent change between environmental conditions may prevent populations from adapting to a current threat but also from a large fitness loss upon environmental change and potential extinction. Thus, the population may survive, though not thrive, in a wide range of conditions. Furthermore, we show the effects of the number of loci on the time to adapt, and that in the frequently changing environment, the similarity of threats that a population faces affects the level of adaptation that it can achieve. Analytic results are checked and supplemented with simulations.
Methods
VARIABLE ENVIRONMENT: SEASCAPES
In the analysis of a single trait scenario, we assume periods of strong selection alternating with periods of no selection. In the analysis of multitrait models, we assume that the population evolves in an environment that changes every τ iterations (note that we do not consider biological generations, but mutation events). At each time point, the population is exposed to a set of conditions (e.g., parasites, predators, prey defense mechanisms, or abiotic conditions), described throughout as a “threat,” defining the fitness landscape. Threats are defined by the optimal response they require. We focus on three fitness seascapes that differ in the similarity of threats (Fig. 1):
Scenario 1: There is a single optimal response to any threat; adaptation to any given threat is independent of adaptation to any other threat (Fig. S1A).
Scenario 2: Threats have different optimal responses, but adaptations to any two threats overlap in all except two traits (Fig. S1B).
Scenario 3: Threats have conflicting optimal responses; better adaptation to one threat implies worse adaptation to “all” other threats.
All scenarios are described in detail in respective sections and in Supporting Information S1.3.
Figure 1.
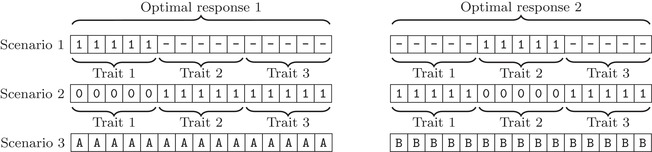
Optimal genotypes in different environments for all three scenarios. In the first scenario, only one trait is under selection at each time, other traits do not contribute to fitness. In the second scenario, all traits are under selection at all times, but optimal responses to all threats are similar to each other. In the third scenario, all loci are under selection at all times, but optimal responses are incompatible.
GENOTYPE
We assume that our population is haploid and monomorphic, thus, we do not consider linkage in this model. In the first two scenarios, the phenotype consists of k traits controlled by k sets of non‐overlapping genes, each with ℓ biallelic loci. The genotype is represented by a bit string (i.e., a vector of zeros and ones) of length . There are as many different threats (see below) as traits. In the last multitrait scenario, each threat requires a specific response; adaptations required in different environments are completely orthogonal, which is modeled by k possible alleles at each locus. Thus, this can be viewed as a single trait controlled by a single gene encoded by loci, but there are k alleles possible at each locus. The genotype is represented by a string of length n consisting of k (different) characters. Note that while the meaning of k is slightly different in each scenario, the main underlying variable is “the number of different environments,” or threats, affecting the population.
In the recent years, Fisher's geometric model (FGM) has been a popular choice for investigating adaptation in changing environments (Matuszewski et al. 2014; Martin and Lenormand 2015; Harmand et al. 2017). Our model assumes that we have k independent traits. Thus, similar to FGM, the phenotype can be described as a vector in a k dimensional space, with de novo mutations affecting the genotype. However, unlike in FGM, in which continuity of traits is assumed, our traits are encoded by ℓ biallelic loci, and thus the phenotypic space is discrete. Furthermore, the selection is not stabilizing but directional, so the phenotypes with the maximum fitness always lie at the borders of the phenotypic space. Finally, new mutations always affect only one trait and are thus non‐pleiotropic.
STRONG‐SELECTION–WEAK‐MUTATION
We further assume that the population is monomorphic most of the time, and that if a new mutation appears, it quickly fixes or is lost entirely, i.e., we assume a strong‐selection–weak‐mutation (SSWM) regime. The SSWM model applies when mutations are rare enough, and selection is sufficiently strong that the time between occurrences of new mutations is long compared to the time it takes a new genotype to replace the parent genotype (Gillespie 1984). Upon occurrence, a new mutation represents relatively high fitness advantage or fitness loss, and strong selection ensures that it either promptly replaces the original genotype or is entirely lost from the population (Fig. 2). Evolution thus occurs through “jumps” between different genotypes.
Figure 2.
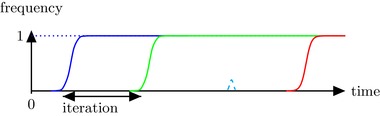
Illustration of the strong selection weak mutation regime. The ordinate represents the frequency of genotypes that carry a specific mutation. Most of the time, the population is composed of a single genotype, as new mutations (represented by different colors) are quickly either fixed (green, blue, red, solid) or lost (cyan, dashed). Adapted from Paixão et al. (2017).
FITNESS AND THE LEVEL OF ADAPTATION
In the main analysis, we assume fitness to be linearly dependent on the number of loci adapted to the current environment. Then we generalize our approach to any monotone fitness function. We analyze a saturating fitness function in detail and compare the results to those obtained for the linear fitness function. See Supporting Information S1.1 and S3.2 for details.
In order to compare scenarios, we derive the minimum and the maximum expected level of adaptation as a fraction of loci adapted to the threat out of all loci that could be adapted (the total number of loci under selection). In the linear‐fitness scenario, this fraction of adapted loci, denoted by f, is the same as the fraction of achieved fitness (assuming the maximum possible fitness is 1), thus, we occasionally use the terms “fitness” and “fraction” interchangeably. However, in a more general scenario, when fitness does not depend linearly on the number of adapted alleles, these terms are no longer interchangeable, and we always clearly specify which one we are discussing.
TRANSITION PROBABILITIES
Note that in our model, one “iteration” does not correspond to a biological generation. Rather, it represents one mutation event that takes on the order of generations to occur, where U is the genomic mutation rate (kept constant), N is the size of the population (kept constant), and P is a probability of fixation of a new mutation. In SSWM regime, we assume that . This assumption sets the timescale for our model. Iteration time can be converted to time in generations, if the parameters above are known for a given population.
All loci are equally likely to mutate, with the probability of a specific locus mutating is . Therefore, in expectation only one mutation occurs in the whole haploid genome per iteration, independent of the length of the genome. A new mutation is fixed or lost with the probability of fixation given by the fitness difference of the candidate mutation and the resident genotype. In our analysis, we do not discuss selection strength s, but focus on probability of fixation instead. We assume that selection is strong and positive mutations are fixed with probability , negative mutations cannot be fixed, while neutral mutations are fixed with probability .
DRIFT ANALYSIS
To analyze the time necessary to climb the fitness peak or to lose unused adaptation, we cast the SSWM regime described above as an evolutionary algorithm (see Appendix A.1) and employ so‐called “drift analysis” (He and Yao 2001; Lehre and Witt 2013). Drift analysis is traditionally used in the theory of evolutionary computation (EC) to analyze the time required for an algorithm to find the optimum (i.e., the time of adaptation), and the scaling of this time with the length of the input (i.e., the number of loci). Note that “drift” here is terminus technicus of the field of EC, representing a progress of the system in some particular direction, not “genetic drift,” as traditionally used by evolutionary biologists. Genetic drift (in biological sense) is partly subsumed in the fact, that neutral mutations may be fixed in the population (e.g., in traits that are not under selection in Scenario 1, or between various maladaptive alleles in Scenario 3).
Drift analysis is based on the estimation of the expected progress of a population toward the fitness peak in one time step , called “drift” in EC, where x is the current state of the system (e.g., the number of adapted loci). Drift theorems use upper or lower bounds on the net expectation of a progress to obtain bounds on the time to reach particular genotypes. The tightness of the upper bound on the time required to find the optimum depends on how tight the expression for the drift is. If the estimate of the drift is accurate, the drift theorem gives very accurate estimate of the time, or a very tight upper bound. A detailed description of the methods used, together with the complete derivations of the results, is provided in Appendix A.2.
ADDITIONAL INFORMATION
All supporting simulations were programmed in Python. The code is available on GitHub under https://goo.gl/k7eqzX. See Supporting Information S3.8 for details. A summary of the model assumptions is provided in Supporting Information S3.7.
Results
First, we analyze single‐trait and multitrait scenarios assuming that fitness is proportional to the fraction of adapted loci, all positive mutations are of the same size and have the same probability of fixation P. Then we generalize our results by relaxing assumptions on the fitness function and define fitness as an arbitrary monotone function growing with the number of loci adapted to the current environment. Thus, several cases of epistasis can be incorporated into the model.
SINGLE TRAIT UNDER PERIODIC SELECTION
We begin our analysis with a simple scenario of a single trait encoded by ℓ loci, in a genome of length n. Each iteration, a single mutation occurs in the whole genome, which may or may not fix in the population. We assume that a trait sometimes experiences strong selection pressure when alleles 1 are adaptive, while alleles 0 are not. During the strong selection phase, any mutation occurring in the trait is either positive and fixes in the population within a short time (one iteration) with probability P, or negative and does not fix. Therefore, the number of adapted loci in the trait, denoted x, is slowly increasing during this time. However, during periods without selection, all mutations within the trait are effectively neutral and fix with the probability , which may lead to a loss of potentially adaptive alleles.
We estimate the expected increase in the number of adapted loci by the probability of a positive mutation occurring and fixing in the population during the selection phase:
| (1) |
where is the probability that a beneficial mutation occurs in a given trait, and P is the probability that it fixes in the population. The expected gain of adaptive alleles after t iterations is
| (2) |
where x 0 is the initial number of loci adapted to the current threat. We used the fact that and replaced the discrete (iteration) model by a continuous time approximation.
If no selection is present, the expected change in the number of adapted loci within one iteration is
| (3) |
where is the probability that the neutral mutation fixes, is the probability that 0 allele mutates into 1, while is the probability that 1 mutates into 0. We can estimate the expected change in the number of adapted loci in the trait in the absence of selection after time t:
| (4) |
where x 0 is the number of adapted alleles at the beginning. Note that if , this expression is negative, meaning that the trait loses adapted loci.
If periods of strong selection () alternate with periods of no selection pressure (), after a long enough time, the population reaches a state when the adaptation gained during the period of selection is lost during absence of selection. A population adapting from an arbitrary state ends up fluctuating between the maximum and the minimum fraction of adapted loci, and , independent of the initial state
| (5) |
| (6) |
with the magnitude of oscillations
| (7) |
where and . Note that , , and are expectations of the maximum (minimum) fractions of the adapted loci from all adaptive loci at the given time.
COMPLETE ADAPTATION AND ITS LOSS
If the environment changes very rarely or periods of selection pressure are very long, the population can climb the temporary fitness peak by optimizing all loci in a trait under selection (, ). On the other hand, if the selection is absent for a long enough time, all mutations are effectively neutral, and the number of potentially adapted loci converges to ().
To get an idea of what “long enough time” means, we estimate the time necessary for adaptation of all loci in a trait under selection. We analyze this process as an adaptive walk in a static fitness landscape. Following the approach by Pérez Heredia et al. (2016), we apply the variable drift theorem to the decreasing number of non‐adapted alleles (thus ) and estimate an upper bound on the expected time the population requires to reach the fitness peak:
| (8) |
where we assumed that at the beginning, half of the alleles were already adapted (, and log refers to the natural logarithm. As the estimate of the expected change in one step is very accurate, this upper bound gives a very accurate estimate of the time required to climb the fitness peak.
It is also possible to use the generalized version of the variable drift theorem to estimate the time needed to achieve any level of adaptation, in any distance from the optimum, by using Equation (A2). Often, the population does not need to be fully adapted in order to survive. If, for instance, only 90% of loci need to be adapted for the population to do well in a given environment, the expected time is (see Supporting Information S1.2).
Using the same approach, we can also estimate how long it takes to lose the adaptation in the absence of selection (assuming that adaptation is lost if half of the alleles are non‐adaptive):
| (9) |
Note the similarity between Equations (8) and (9): the time to climb the fitness peak or to lose adaptation grows with the length of the genome n, as the total mutation rate is kept constant at 1 and the probability of mutation of any particular locus decreases with n. Furthermore, both times increase with , as the number of available loci for mutations decreases with the population approaching the optimum. Both times are dominated by waiting for the last few mutations to appear and fix in the population. The main difference between gaining and losing adaptation is caused by the different probabilities of fixation of adaptive and neutral mutations.
VARIABLE ENVIRONMENTS AND MULTIPLE TRAITS UNDER SELECTION
While the single trait model under periodic selection acts as a useful basic building block for more complicated scenarios, it is more realistic to assume that multiple traits contribute to fitness under different conditions. In such a case, the similarity of environmental conditions (defined by the similarity between optimal genotypes in different conditions) plays a major role in adaptation.
Here, we compare three scenarios with a variable similarity of environments. In all scenarios, we have k different environments that alternate in a regular manner. In the first two scenarios, different environments are matched with different traits, in the last scenario, with different alleles. In the first scenario, only one of k different, non‐overlapping traits come under selection in each environment. Adaptation against a pathogen is completely independent on adaptation to a different threat, such as drought. In the second scenario, all k traits are under selection at all times, but one trait characteristic of the environment requires a specific response in the opposite direction. For instance, zero alleles in a given trait bring resistance to a particular virus, but are costly in its absence. Thus, selection mostly favors one type of alleles (ones) at all loci, except in the trait that brings the resistance to the current virus, in which zero alleles are preferred. In the last scenario, all traits are under selection at all times, but there are k different alleles available for each locus and each type of environment requires a unique response. This happens if selection acts in different directions in different environments: for instance, adaptation to cold climate may be harmful in hot climates. Thus, this last scenario is somewhat similar to single traits scenario (with one trait controlled by loci) but with multiple (k) alleles. See Figures 1 and S1.
In each scenario, we analyze the rate of adaptation and the time required to reach the fitness peak as well as the magnitude of oscillations as a function of the frequency of environmental change. Furthermore, we analyze frequent environmental change and the dependence of the achieved level of adaptation (expected fraction of adapted alleles) as a function of the number of different environments k. Finally, we focus on a rarely changing environment and find timescales at which populations are expected to climb the temporary fitness peak.
Scenario 1: Selection acting at different traits in different environments
First, we investigate adaptation in a variable environment when selection acts on different traits at different times. For instance, a population is experiencing a long period of drought, then a long period of cold weather followed by parasite infestation. While only one trait is under selection at each time point, mutations in other traits may occur and fix. Such cryptic mutations do not affect an organism when they appear and are initially exempt from selection pressure. However, upon environmental change, they may act as a substrate upon which selection may operate (Masel 2006; Draghi and Plotkin 2011; Rajon and Masel 2013; Paaby and Rockman 2014).
As before, each trait is encoded by ℓ biallelic loci, where the adapted allele is represented by 1 and the maladapted allele is represented by 0 (see Fig. S2). As we assume k different environments, each trait experiences a period of selection pressure lasting τ iterations, during which it adapts to the given environment, and a times longer period with no selection pressure. Thus, this scenario is similar to the previous one when only a single trait was considered. We can use Equations (5), (6), and (7) to estimate oscillations in the fraction of adapted alleles by substituting and (see Table 1 and Fig. 3A).
Table 1.
Summary of the fraction of adapted alleles as a function of τ. Summary of our results for the minimum and the maximum fraction of adapted alleles as well as the magnitude of oscillations as a function of τ in all three scenarios with the linear fitness function. Comparison of these analytical results and simulations are shown in Figure 3
| Scenario 1 | Scenario 2 | Scenario 3 | |||||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
| Note |
|
|
|
||||
|
|
|
Figure 3.
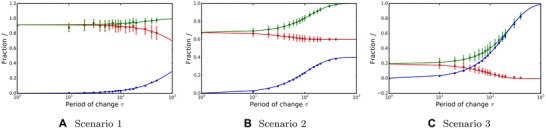
The dependence of the level of adaptation on the period of environmental change. Green denotes the expected maximum, red the expected minimum, and blue the size of oscillations. The lines depict analytical results, the dots simulation results. Mean and standard deviation of 200 periods were taken after stable oscillations were achieved. , , , . For larger τ in scenario 1, see Figure S4.
Frequent and rare environmental change
If the environment changes every iteration, i.e., at the same time scale as new mutations appear in the population (), after reaching some level of adaptation, potential beneficial mutations become rare and there is not enough time for a trait to adapt further between environmental changes. As the environment changes every iteration, all traits are likely to be approximately equally adapted. While it is likely that traits that have been recently under selection have more loci adapted than those that were neutral for a long time, in a frequently changing environment these differences are small and we can assume that all adapted loci are uniformly distributed across all traits. To simplify the analysis, we can focus on all traits at the same time.
We estimate the expected change in the number of adapted alleles in the whole genome X. We find the equilibrium between the rate at which new positive mutations are gained and the rate at which they are lost, by finding the threshold value of X allowing for positive drift. We can determine the number X of adapted loci in the whole genome in every type of environment:
and from that, the fraction of adapted alleles
| (10) |
Note that this expression is an approximation and can also be obtained from Equation (6) by replacing exponentials by the first two terms of their Taylor expansions.
Equation (10) shows that the expected level of adaptation that the population achieves in a frequently changing environment depends on the relative magnitude of and P. In large populations, neutral mutations have low probability of fixation and the fraction of adapted loci is close to 1. On the other hand, when P is small or the population is small, the fraction of adapted loci is close to 1/2. Note that τ is relative to the timescale defined by the mutation rate. To derive these results, we assumed that the mutation rate per locus () is very small. In biological terms, these results are relevant when the environment changes frequently compared to the expected time needed to mutate a particular locus.
The level of adaptation that the population achieves is independent of its initial adaptation level. Using the multiplicative drift theorem, we can also estimate the level of adaptation as a function of time, taking into account that adaptation slows down as the population reaches the optimum (see Supporting Information, Theorem 5 for the derivation and proofs). Furthermore, Equations (8) and (9) can be used to find the time necessary for a trait to climb the fitness peak, or to lose the adaptation completely (see Table 3 and Fig. 5A).
Table 3.
Summary of rare environmental change with linear fitness function. In all three scenarios, the time to reach the optimum (its upper bound) depends on the probability of fixation of positive mutations P, the mutation rate , and the logarithm of the number of loci encoding each trait. The logarithmic function comes from the fact that the adaptation is faster at the beginning, when many loci still need to be adapted, but slows down as the population approaches the fitness peak, as positive mutations become rarer
| Scenario 1 | Scenario 2 | Scenario 3 | ||||
|---|---|---|---|---|---|---|
| Time to find the fitness peak |
|
|
|
Figure 5.
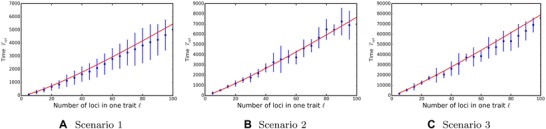
Time to climb the fitness peak as a function of the number of loci ℓ encoding each trait. The red lines depict analytical results, blue dots the simulation results. Mean and standard deviation of 100 independent trials. For dependencies on other parameters, see Figures S5, S7, and S9.
Scenario 2: Selection acting at all traits, with partial overlap between different environments
In the previous scenario, we assumed that threats were completely independent and adaptation to one threat did not hinder adaptations to different threats. However, in many biological situations, it is more realistic to assume that adaptations are not entirely compatible but partly antagonistic. For instance, while several (mainly loss of function) mutations can cause antibiotic resistance to multiple types of drugs, in the absence of antibiotics, these mutations are harmful, reducing the population growth (Breeze and Obaseiki‐Ebor 1983; Girgis et al. 2009).
To investigate such scenarios, we assume that while all traits are under selection at all times, one trait is characteristic for every environment and requires a specific response in the opposite direction. The direction of selection that is common for all the other traits is denoted as “principal direction.”
As all traits are independent, we begin by looking at a single trait. Similarly to the previous scenario, we estimate the expected increase in number of ones x if this trait experiences selection in the principal direction
| (11) |
and their decrease when the trait is experiencing selection pressure in the opposite direction
| (12) |
Following the same approach as in the single trait scenario, we can find the minimum and the maximum number (and fraction) of adapted loci that each trait is expected to reach. However, as all traits are under selection, we are more interested in the minimum and maximum fraction of all alleles that are contributing to the fitness. To find these, we cannot simply compare the gain and the loss of alleles in a single trait, as all the other traits experienced a different number of iterations under selection in the current direction. Furthermore, one trait is always under selection in the opposite direction, and alleles 0 count as adaptive. Thus, for the total fraction of the loci that are adapted, we have to sum them up over the number of periods that passed since the change in the selection direction, resulting in
| (13) |
and
| (14) |
and the resulting oscillations in fitness are
| (15) |
where . See Figure 3B for analytical results and simulations, and Supporting Information S1.5 for a detailed derivation.
Frequent and rare environmental change
Similarly to the previous case, if the environment changes frequently (i.e., every iteration), the population does not experience regular fluctuations in the fraction of adapted loci and stabilizes at approximately
| (16) |
To analyze the time required to find the fitness peak in a rarely changing environment, we denote with X the number of alleles that are adapted to the current threat, regardless whether it is 0 or 1 that is required at a given locus. The expected change in X is
| (17) |
If the population is allowed to climb the fitness peak, all traits are adapted to the given threat and thus, upon environmental change, change in the selection direction for two traits occurs. Therefore, the population loses a fraction of of adaptive alleles.
Using the multiplicative drift theorem, we find the (tight) upper bound on the expected time T necessary to find the current fitness peak:
| (18) |
where we assumed that two traits were completely maladapted. See Figures 5B and 4B for analytical results and simulations, and Supporting Information S1.5 for a detailed derivation.
Figure 4.
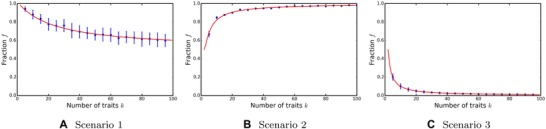
The dependence of the level of adaptation on the number of environments/traits k, when the environment changes every iteration. The red lines depict the analytical results, the blue dots the simulation results. Mean and standard deviation of 100 independent trials, taken after a stable level of adaptation was achieved.
Scenario 3: Adaptations in different environments are completely antagonistic
In this last scenario, we assumed that all traits (and loci) are under selection at all times but every environment requires a specific response (allele) at each locus. There are as many alleles per locus as there are threats (k), and threats are completely antagonistic, which means that adaptation to one threat inherently leads to maladaptation to different threats. Thus, there is no overlap between adaptations, and selection can point in any of k directions. For instance, while in some environments alleles for larger body size can be selected for, in other environments smaller body size can be beneficial.
As said before, this scenario can also be described as a single trait scenario with multiple available alleles per locus, and we will use similar approach as in the single trait scenario. The probability of a positive mutation occurring is , where X is the total number of alleles across the whole genome adapted to the current threat, and the factor comes from the fact that only one in possible mutations at each locus is positive at a given time. Thus, the expected gain of adaptive alleles of a particular type in each time step when this type is selected for is
| (19) |
while their loss during time periods when different alleles are adaptive is
| (20) |
The first part of Equation (20) describes a loss due to positive mutations occurring and fixing, while the second part of the equation captures the loss of alleles due to neutral mutations to other possible alleles.
Following the same approach as before, we find the maximum and the minimum expected fraction of adapted loci in the whole genome:
and the magnitude of oscillations is
where and . See Figure 3C for analytical results and simulations.
Frequent and rare environmental change
If the environment changes every iteration, all loci are expected to be equally adapted and, in expectation, of them will always be adapted to the current environment.
If the environment changes rarely, we use the variable drift theorem to find the maximum expected time to adapt all n loci:
where we assumed the worst case scenario with no adapted loci at the beginning. After this time, it is expected that all loci are adapted to the current threat, and if the environment changes, the population is completely maladapted to the new environment. See Supporting Information S1.6 for a derivation and Figures 4C and 5C for analytical results and simulations. As our simulations suggest (see Supporting Information S3.9), if the population is too small and unable to adapt fast enough, the pronounced fitness loss can lead to its extinction.
INTRODUCING STOCHASTICITY INTO ENVIRONMENTAL CHANGE
To simplify the calculations above, we have assumed that various environments change periodically and follow a defined order that does not change. However, as our theoretical calculations deal with expectations, our results apply to more general scenarios as well, where different threats occur in random order (assuming that they are all equally likely and of the same length).
Simulations of the environment changing between a set of threats in a random order support our results (Fig. S10). However, we observe that the variance in the minimum and the maximum number (or fraction) of adapted loci is increased, arising from the variance in time spent adapting to one type of threat. Furthermore, the expected minimum fraction of adapted loci is increased, especially in the last scenario. This arises due to two reasons: first, because the minimum level of adaptation is already close to 0 and cannot go lower, and second, because traits lose adaptation at an uneven rate, which is fast at first but then slows down. Thus, shortening the time when a trait is losing adaptation for environment i below the expected makes a larger difference than extending this time.
GENERALIZING THE FITNESS FUNCTION
All scenarios investigated above assumed that the fitness is proportional to the fraction of adapted loci, and all positive mutations are of the same size and thus have the same probability of fixation. We generalize our results by relaxing these assumptions on the fitness function and define fitness as an arbitrary monotone function growing with the number of loci adapted to the current environment. Thus, several cases of epistasis can be incorporated into the model. In Supporting Information S3, we provide a general approach to analyze such arbitrary monotone fitness functions.
Here, to investigate differences that may occur in contrast to linear fitness analyzed above, we consider adaptation in an epistatic fitness landscape where new adaptive mutations contribute less to the trait value than the previous ones. This results in fitness gain diminishing with the number of adapted loci in each trait as the trait is approaching its optimum. This means that positive mutations that occur earlier have a larger effect and are more likely to fix in the population. Note that in scenarios where the fitness is given by multiple traits (Scenarios 2 and 3), the fitness contributions across traits are additive. The formal definition of the fitness contributed by each trait is
| (21) |
where is the number of loci adapted to the current threat in a given trait i. The total fitness is then given as , where is the total number of loci adapted to the current environment and represents a fitness of an individual with all loci adapted to the current environment. Thus, an individual's fitness is expressed relative to a perfectly adapted individual.
We further assume that the probability of fixation for a positive mutation depends on the fitness contribution as (Kimura 1962). The probability of fixation of the first positive mutation is the largest, denoted , and the probability of the fixation of the last positive mutation is the smallest, denoted P 1. Neutral mutations fix with probability , where . We derive the expected fitness for the frequently changing environment () as a function of k. While analytical calculations only deal with this particular case, numerical simulations provide insight into scenarios with an arbitrary frequency of environmental change (Fig. 7).
Figure 7.
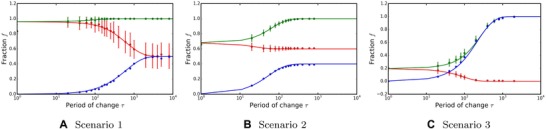
Dependence of the level of adaptation (fraction of adapted alleles) on the period of environmental change. Green depicts the expected maximum, red the expected minimum, and blue the size of oscillations. Dots depict simulation results. Mean and standard deviation of 200 periods, taken after stable oscillations were achieved. ; ; . Lines depict analytical results for the linear scenario assuming .
The main difference between these and the linear fitness scenarios is in the rate of adaptation. As large mutations are more likely to be fixed than the small ones, the saturating fitness function can lead to faster or slower adaptation compared to the linear scenario where all loci contribute equally. This depends on the fixation probability of such equal‐sized mutations compared to the fixation probabilities when a saturating fitness function is assumed.
Figure 7 shows results of simulations for saturating fitness in all three scenarios. Analytical results shown in this figure for comparison were calculated using the formula for linear fitness with the probability of fixation (see Fig. 6A). The close match between the simulated results of saturating fitness and the analytical results of linear fitness is caused by the fact that, for the parameters used (), even the last mutation brings significant advantage and thus fixes with a probability larger than 0.9.
Figure 6.
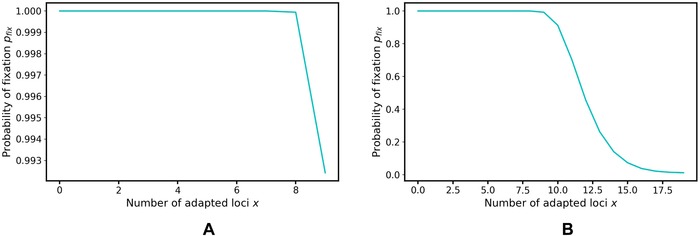
Probability of fixation of a new mutation depends on the number of loci that are already adapted.
Figure S12 illustrates results for more traits encoded by more loci (), where the last mutation brings only a small fitness advantage and thus fixes with probability close to (see Figure 6B). The difference between the saturating and linear fitness is more obvious: in the first scenario, the minimum expected fraction of adapted alleles is the same as in the linear scenario, while the maximum expected fraction is slightly lower than would be expected in the linear‐fitness case (analytical results calculated for linear fitness assumed ). This is caused by the very low probability of fixation of the last few alleles in the trait, so there is simply not enough time for them to fix (Fig. 6B). In the second scenario, this difference is even more extreme: despite the similarity between the environments, only a relatively low level of adaptation is achieved, not necessarily above as in the linear case. This is caused by the higher probability of some alleles to mutate and get fixed from 1 to 0 in one period than from 0 to 1 in periods, due to the higher fitness contribution that such a mutation can bring (i.e., ). With longer periods, both the minimum and the maximum fraction of adapted alleles increase. In the third scenario, we did not observe any difference between this and the linear scenario for , because only a small fraction of loci was adapted and thus new mutations fixed with high probability. However, for , when the fraction of adapted alleles reached at the end of the period should be larger than 0.6, we observed that the fraction of adapted loci that was actually reached was much lower than it would be in the linear case, as the probability of fixation is very low and thus more time is required for new beneficial mutations to fix.
Frequent and rare environmental change
In the saturating‐fitness scenario, not only the fraction but also the distribution of adapted loci among traits at any given time plays an important role. Therefore, in Table 4, we provide results for both the expected fraction of adapted loci and the expected fitness. We derive analytical expressions for both the lower and upper bounds for the expected fraction of adapted loci as a function of k, for the frequently changing environment ().
Table 4.
Summary of frequent environmental change, saturating fitness. For the saturating fitness function, we were unable to derive a general dependence of the fraction of adapted alleles, nor fitness on arbitrary τ. However, figures provided in Supporting Information S3.6 show simulation results for the saturating fitness for arbitrary τ in all three scenarios. For the fraction of adapted alleles, we were able to derive the upper and the lower bound, however, those are relatively loose. This table shows the summary of the results for all three scenarios with saturating fitness in a frequently changing environment
| Fraction | Fitness | |||
|---|---|---|---|---|
| Scenario 1 |
|
|
||
| Scenario 2 |
|
|
||
| Scenario 3 |
|
|
Figure S13 shows results of simulations as well as the derived bounds, assuming , . The bounds are very loose and do not provide much information in this case. However, for smaller ℓ, when , these bounds are tighter. Furthermore, a nice fit (green solid line) of the expected fraction of adapted alleles could be obtained by using the lower bound expression but substituting P 1 by ‘the lowest effective probability of fixation’ P 1eff. The lowest effective probability of fixation is the probability of fixation of the smallest mutation that actually gets fixed in the given conditions. In Scenarios 1 and 2 shown in Figure S13, the maximum fraction of adapted alleles is around 0.6, corresponding to 12 loci being adapted. Thus, the smallest mutation fixes with a probability of around 0.7 (see Fig. 6). Substituting this value into the lower bound, we obtained a close fit to the observed values. In the third scenario, the fraction of adapted alleles is much lower, leading to .
When considering a rarely changing environment, the minimum and the maximum fraction of adapted loci is not affected by the fitness function. Note here that we assume that “changing rarely” means that all loci have time to adapt/lose adaptation. This time depends heavily on the shape of the fitness function and the probability of fixation of the smallest mutation (see Supporting Information S3). In all cases, the maximum fraction of adapted loci is , while the minimum is in the first scenario, in the second, and in the third scenario. The minimum expected fitness also remains the same in the second scenario (), because exactly two traits are maladapted upon environmental change, and the third scenario (), because all traits are completely maladapted. However, the minimum expected fitness changes in the first scenario to . The maximum fitness is 1 in all scenarios (all loci adapted).
Discussion
Environmental fluctuations are expected to increase in frequency and severity within the near future. If these environmental changes are too widespread and severe for individuals to be able to migrate to more suitable areas or acclimatize physiologically, they can prove fatal.
We used multilocus models of evolving populations to investigate the role that the frequency of change and the similarity of fitness landscapes play in evolution. We showed that even though frequent environmental changes are in general considered to be harmful to the organisms, under some circumstances, a frequent environmental change can prevent the population from climbing a temporary fitness peak and losing fitness when an environmental change occurs. Thus, by staying maladapted, populations may survive, although not thrive, in a wide range of conditions.
BUILDING UP THE MODEL
Despite the fact that evolutionary algorithms were originally inspired by natural evolution, the theory of evolutionary computations developed in complete isolation from the theory of population genetics and natural evolution. However, it has been recently shown that many evolutionary models could be translated into a common framework with the theory of evolutionary computations, allowing methods from the field of computer science to be easily used in biological context (Paixão, Badkobeh, et al. 2015; Paixão, Pérez Heredia, et al. 2015). For instance, “drift analysis” employed here has been successfully used to study the length of adaptive walks in various classes of fitness landscapes, especially focusing on the scaling of these landscapes with the length of the genome (Pérez Heredia et al. 2016). Building on this approach, we extend this framework to variable fitness seascapes.
To define and analyze our models, we had to employ several strict assumptions and simplifications (summarized in Supporting Information S3.7). For instance, we assumed monomorphic populations, a regime of strong selection and weak mutation, and environmental changes occurring at the timescale comparable with the fixation of a new mutation within the population, or slower. While this is an unlikely timescale for most organisms with long generation times, we believe that our model is applicable to microbial settings and can be used to study the evolution of adaptation of microorganisms to diverse conditions, and provide insight into their evolution. Furthermore, it could be used in the analysis of other populations with large size and short generation times, for instance, phytoplankton. While phytoplankton populations are not monomorphic, our model could be used to provide some estimates for timescales necessary for adaptation, for instance in the study of adaptation to increasing acidification of the oceans and increasing temperature. To compare our results to those gained by observing natural populations, for instance by Bergland et al. (2014) investigating seasonal selection in Drosophila, it would be necessary to extend the model to polymorphic populations and allow for adaptation from the standing genetic variation. Furthermore, when discussing the probability of extinction, it is necessary to allow for a variable population size, as a decreasing population size may lead to a higher probability of mutation acceptance. We addressed this issue only briefly in simulations; more extensive analysis and simulations are still needed.
While matching different environments/threats with corresponding traits in our model may also seem rather artificial (and certainly is to a degree), similar scenarios have been documented in real organisms. For instance, the flowering phenology of Heuchera grossulariifolia and the emergence time of its seed‐parasitic moth Greya politella represent such a matching trait pair (Nuismer and Ridenhour 2008). A similar approach was also used in a study by Gilman et al. (2012). The authors investigated a scenario of a victim–exploiter system with multiple traits, where the exploiter has to overcome all defence mechanisms developed by the victim in order to succeed. The authors showed the importance of the correlation between the traits and demonstrated the advantage of the victim in this evolutionary race. While our models are somewhat similar (for instance, by assuming traits functionally paired with threats), in our study, environments were given extrinsically (were unaffected by the evolving population).
In the third multitrait scenario, we assumed that adaptations to different threats are contradicting each other, with adaptation gain in one environment implying the loss of adaptive alleles to a different threat. This situation is similar to a recent study by Toor and Best (2016). The authors examined theoretically the evolutionary behavior of a host population that must allocate defenses between two enemy populations, parasites and predators, with defense against one enemy constraining defense against the other. Our study presented here dealt with a similar scenario but assumed that the threats were changing in time.
ADAPTATION GAIN AND ITS LOSS
In the single trait scenario and the first multitrait scenario, a trait experiences alternating periods of selection pressure and periods of its absence. In both scenarios, mutations that are neutral in some conditions may have a selective advantage or disadvantage in a different environment. Such cryptic mutations have been shown to play an important role in evolution, by creating cryptic variation hidden from selective forces at some point, but serving as a substrate of substantial phenotypic (and fitness) variation later (Draghi and Plotkin 2011).
Both theoretical (Hermisson and Wagner 2004; Masel 2006; Rajon and Masel 2013) and empirical (Hayden et al. 2011) studies have shown the importance of cryptic genetic mutations for adaptation after environmental change. For instance, Rajon and Masel (2013) found that cryptic sequences may accelerate adaptation and facilitate large phenotypic changes, even in the absence of genetic diversity. Hayden et al. (2011) experimented with two evolving populations of a ribozyme (RNA enzyme) under selection for activity with its native substrate in different conditions (weak and strong selection). Both populations accumulated cryptic genetic variation that was revealed upon environmental change when the populations were tested on a different substrate. The authors found cryptic genetic variation that had accumulated in one environment facilitated adaptation to a new environment.
While we did not focus on genetic variation in our study (as we assumed monomorphic populations), we investigated and compared the time necessary to climb the fitness peak during the selection period, and time to lose the adaptation due to cryptic mutations when selection is absent. Our results show that both times grow as logarithms of the number of loci ℓ encoding each trait, as well as with the number of loci that control all traits that come under selection in the fluctuating environment, in our model defined as the size of the genome n. The total number of loci n plays a role mainly because we defined the mutation rate as , so mutations at each locus are less likely as the length of the genome increases. The main difference arises due to the different probabilities of mutation fixation, as neutral mutations (causing loss of adaptation) are fixed with probability , while positive mutations are fixed with higher probability. The logarithmic function comes from the fact that the adaptation is faster at the beginning, when many loci still need to be adapted, but slows down as the population approaches the fitness peak, as the positive mutations become rarer. Especially in the process of climbing the fitness peak, the time is dominated by waiting for the last maladapted locus to mutate and this mutation to fix in the population.
However, populations often do not need to be fully adapted in order to survive, or even thrive in the given environment; often, it is enough to be in the proximity of the fitness peak. This brings us to another interesting result: if the full adaptation is not required, but only some fraction of loci needs to be adapted in order for population to survive, the logarithmic function of ℓ disappears from the results. The expected time that population needs to get to the proximity of the fitness peak scales indirectly with the mutation rate and the probability of fixation of a new mutation as .
In our model, we assume that the selection is always strong enough that negative mutations cannot fix. However, in the more general scenario investigated by Pérez Heredia et al. (2016), the authors derived a condition on the selection strength enabling full adaptation. The authors showed that if the selection is not strong enough, the population reaches a mutation–selection balance when negative mutations fix at the same rate as positive mutations (the fixation probability is less, but the mutations are much more frequent), and it is unlikely for the population to adapt fully.
During the absence of selection we assumed that all mutations were truly neutral, leading to the loss of adaptation by cryptic mutations. However, the loss of function in the absence of selection is often driven by the advantage that such loss can bring. For instance, Moran et al. (2015) investigated the loss of vision in Mexican cavefish Astyanax mexicanus and found that eyesight represents a significant energetic cost. The authors showed that the loss of the visual system in the cave phenotype substantially lowered the amount of energy expended on expensive neural tissue, in particular for juvenile fish. Thus, mutations leading to the loss of function were actually positive in the cave environment, more reminiscent of the second scenario we investigated, with adaptations partially antagonistic in different environments, discussed below.
Optimal frequency of environmental change depends on the similarity of environments
We investigated three multitrait scenarios that differ in the similarity of environments, or, rather, adaptations that they require. In each case, we derived the minimum and the maximum fraction of loci that is expected to be adapted as a function of the frequency of the environmental change.
In the first case, different traits are under selection at different times. There is no direct cost of adaptation to one type of environment; however, deleterious mutations occur in neutral traits and get fixed by drift. Thus, the population experiences fitness loss when the environment changes, suddenly requiring the lost adaptation. As explained above, in such a case, the difference in the rate of adaptation and the rate of its loss is given mainly by the different probabilities of accepting adaptive and neutral mutations. As adaptation gain is faster, frequent environmental change will lead to all traits being well adapted (though not completely). Decreasing the frequency of environmental change will increase the maximum achieved fraction of adapted alleles only slightly, but it will significantly decrease the minimum, leading to large fitness loss upon environmental change.
In the second scenario, all traits are permanently under selection, with partial overlap and partial conflict in the direction of selection. Biological scenarios where a specific trait is adaptive in one but maladaptive in another environment have been observed in nature multiple times (Hottes et al. 2013; Moran et al. 2015). For instance, Hottes et al. (2013) discussed adaptations in bacteria occurring through the loss of function, when a loss of functional protein can lead to “rewiring” of a metabolic or signaling pathway more suitable in new conditions. Here, we observed that the overlap between different environments leads to most traits being highly adapted at all times, regardless the frequency of the environmental change. High frequency of environmental change leads to adaptation that is slightly higher than the minimum, but much lower then the maximum of the expected level of adaptation at lower frequencies of environmental change. In the other words, contrary to the previous case, with decreasing frequency (increasing time spent in one type of environment), the expected maximum is quickly increasing, while the minimum is decreasing only slightly.
Similar results of significant increase of the expected maximum and only a slight decrease of the minimum were observed in the third scenario. However, it is important to note that the minimum is quickly approaching 0 with the increasing time period, meaning that environmental change after a long time leads to complete maladaptation.
Comparing these three scenarios, we observed that if there is no overlap between the adaptations required in a different environment (no similarity of threats, Scenarios 1 and 3), frequent changes alternating between a given set of environments are better for the evolving population than rare changes, which may lead to significant fitness loss, and, under certain circumstances, threaten the persistence of the population. On the other hand, if the adaptation to one type of environment carries over if the environment changes due to the similarity between the threats, longer periods of a stable environment are more beneficial for the populations. Furthermore, there is a qualitative difference between the three scenarios: while in the first scenario, adaptation is lost only due to neutral mutations in the absence of selection, in the other two scenarios, there is a selection in different directions. Thus, in the first scenario population size N plays a role in the rate of degeneration, while in the second scenario it disappears from the results (see Table 1). The third scenario is a mix of the first two: adaptation is lost due to a selection in different direction, however, there is a possibility of neutral mutations.
A recent study by Matuszewski et al. (2014) also considered dynamics of a changing environment. The authors investigated adaptive walks using Fisher's geometric model with a moving optimum and found that in the environmentally limited regime (slow environmental change), the population followed the optimum closely, adaptive steps were small, and their multivariate distribution mirrored the shape of the fitness landscape. On the other hand, in the genetically limited regime, the population followed the optimum with a large gap, adaptive steps were large, and their distribution was determined primarily by the distribution of new mutations. This means that populations were better adapted in an environment that was changing slowly. However, the geometric model the authors used is somewhat similar (i.e., assumptions of an SSWM regime), it differs in some crucial assumptions. For instance, the authors assumed universal pleiotropy, while in our model, each locus contributed strictly to one trait. Furthermore, in our model, the optimum “jumps” repeatedly between a set of conditions, while in the study of Matuszewski et al. (2014), the optimum was moving linearly at a steady pace. This suggests that the nature of the environmental changes plays an important role in determining the importance of the environmental change.
Rare environmental changes lead to higher fitness loss
Our results suggest that in some situations, rare environmental changes may lead to overspecialization of the population, that is unable to cope with the environmental change. In all scenarios, extending the period of a constant threat lead to a higher expected maximum fraction of adapted alleles and a lower minimum. Thus, longer periods result in higher fitness loss upon environmental change. This effect is the largest in the third scenario, when adaptation to one threat contradicts adaptation to all the other threats, leading to the complete maladaptation if the environmental change occurs after a long time. Note that the definition of the “long time” depends on the number of loci encoding each trait, the number of traits, and several other parameters, for instance, mutation rate, as discussed above.
An extensive fitness loss can lead to shrinking of the population, or, if the individuals of a particular generation are unable to cope with the new conditions (), even to the population's extinction. These populations could, however, survive in a frequently changing environment. While in our analytical model we assumed constant population size, we ran several simulations explicitly considering demography and population growth rates in different environment. These simulations prove that under some conditions, increasing the frequency of the environmental change indeed prevented the population from extinction (see Supporting Information S3.9). However, to properly investigate the parameter space and the conditions upon which extinction is likely or inevitable, extensions of the model considering standing genetic variation and more extensive simulations are necessary.
Our results are in agreement with predictions by Lynch and Gabriel (1987) and Kassen (2002), stating that frequent environmental fluctuations lead to generalism, selecting for genotypes that perform well across a range of different environments. These predictions have been already supported by experimental observations in microbes. For instance, Ketola et al. (2013) observed that strains of bacterial pathogen Serratia marcescens that evolved in fluctuating temperature outperformed in novel environment the strains that evolved in constant temperature. In a recent study of multiple species of bacteria, Saarinen et al. (2018) found that the clones evolved in the fluctuating environment were more tolerant to environmental fluctuations than the clones evolved in the constant environment. Studies of antibiotic resistance also suggest that less frequent, but stronger antibiotic treatments are more likely to cause the local extinction of the bacterial population (Wu et al. 2014)
In a frequently changing environment, similarity of threats affects the level of adaptation
When the environment changes frequently relative to the time scale defined by the mutation rate (comparably to the expected time needed to get mutation at a particular locus), there is no time for populations to adapt to the current threat. However, populations also experience (almost) no fitness loss when the environment changes. The achieved fitness of the population is given as a mean fitness across all environments and depends on the variability of the environments modulated by the number of traits k in our model. In the first scenario, there is no similarity between threats, and the expected fitness (fraction of adapted alleles) that the population achieves decreases as more threats can affect the population, and individual traits are under selection less often. The expected level of adaptation depends on the relative magnitude of and P. The larger populations tend to be more adapted then small ones: in large populations, neutral mutations have lower probability of fixation and the fraction of adapted loci is close to 1. On the other hand, when P is small or the population is small, the fraction of adapted loci is close to 1/2 due to random genetic drift (see Table 2).
Table 2.
Summary of frequent environmental change with linear fitness function. The table shows the dependence of the level of adaptation in a frequently changing environment in all three scenarios with the linear fitness function. While in the first and the third scenario the expected level of adaptation decreases with k, in the second scenario the level of adaptation increases. This is due to the overlap in adaptation in the second scenario: all except two traits are always under selection in the same direction, resulting in a diminishing difference between the threats as k increases
| Scenario 1 | Scenario 2 | Scenario 3 | ||||
|---|---|---|---|---|---|---|
| Fraction of adapted alleles |
|
|
|
Similarly, in the third scenario the expected fitness that the population achieves decreases with k even steeper. On the other hand, in the second scenario, we assumed that adaptations of all traits except two are always shared between the threats, so that the fraction of loci in conflict is decreasing with increasing k. The expected fitness therefore increases with the number of threats. It would be interesting to fix the fraction of traits in conflict, rather than their absolute number. However, we leave this for future studies.
GENERALIZATIONS
We generalized our models in two ways: by adding stochasticity to the order of threats affecting the population, and by generalizing the fitness function. Both generalizations did not drastically affect the results. The results were qualitatively similar to those obtained for the linear fitness and deterministic environmental change, suggesting their generality and robustness. However, there are several other useful possibilities to extend our study. For instance, adaptation by new mutation is only one way that population can survive, mostly applicable at long timescales. In shorter timescales, the role of standing genetic variation, ignored in our model, is more pronounced. Releasing the assumption of monomorphic populations would loosen the assumption on long timescales of environmental change and short generation times. Such an extension would enable to apply the model to many more species and come up with more concrete predictions. Furthermore, in order to answer the crucial questions about the persistence or extinction of the populations, it is necessary to consider demography explicitly. Modeling variably sized populations that are expanding if adapted to the environment, but shrinking if maladapted, would shed more light onto the complex problem of population extinction. We only briefly addressed this issue in our simulations, but our results suggest that although the frequency of environmental change undoubtedly plays a vital role in preventing population extinction, several other aspects are crucial as well (see Supporting Information S3.9 for preliminary results and further discussion). More studies are needed to investigate the parameter space and the important factors leading to the extinction of populations.
Our study is just one of the first steps toward the analysis of the complex problem of adaptation in a changing environment. However, this topic is becoming central to many areas of biology. We hope that extensions of our study will lead to practical outcomes, for instance, in the field of conservation biology, or evolution of antibiotic or herbicide resistance.
Associate Editor: S. M. Flaxman
Handling Editor: Mohamed A. F. Noor
Supporting information
Fig S1. Scheme of the first two scenarios.
Fig. S2. In this scenario, only one trait is under selection at each time.
Fig. S3. The number of adapted loci and fitness varies in time.
Fig. S4. The dependence of the level of adaptation on the period of environmental change.
Fig. S5. Time to find the temporal optimum in scenario 1, and its dependence on various parameters.
Fig. S6. In this scenario, all traits are under selection at all times.
Fig. S7. Time to find the temporal optimum in scenario 2, and its dependence on various parameters.
Fig. S8. All traits are under selection at all times.
Fig. S9. Time to find the temporal optimum in scenario 3, and its dependence on various parameters.
Fig. S10. Minimum (red), maximum (green) and magnitude of the fitness oscilations (blue) in all three models, when environments change in random order.
Fig. S11. Markov chain with two states, representing the value of any bit.
Fig. S12. Dependence of the level of adaptation (fraction of adapted alleles) on the period of environmental change.
Fig. S13. Dependence of the level of adaptation (fraction of adapted alleles) on the number of traits.
Fig. S14. Examples of simulation of evolving population.
Fig. S15. Extinction rate depends on the length of the period τ, as well as growth rate function.
AUTHOR CONTRIBUTIONS
Barbora Trubenová analyzed the model and wrote the article.
Martin S. Krejca analyzed the model and wrote the article.
Per Kristian Lehre analyzed the model and wrote the article.
Timo Kötzing analyzed the model and wrote the article.
ACKNOWLEDGMENTS
The authors would like to thank to Tiago Paixao and Nick Barton for useful comments and advice. This project has received funding from the European Union's Seventh Framework Programme for research, technological development, and demonstration under Grant Agreement 618091 Speed of Adaptation in Population Genetics and Evolutionary Computation (SAGE). Furthermore, this project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska‐Curie grant agreement no 704172 (RACE).
Appendix A. Definitions
In the following sections of the Appendix and mainly in the Supporting Information, we provide detailed definitions and derivations of the results. As many of the methods used were borrowed from the theory of evolutionary computations, the language is more technical than biological. The main concept is based on casting the SSWM regime as an evolutionary algorithm, applied to specific optimization problems (fitness landscapes). Many results are shown in the form of theorems and proofs, which were then translated into biological terminology and interpretation, shown in the main manuscript.
SSWM as an algorithm
Algorithm 1.

“Mutate one bit” means that a bit is flipped from 1 to 0 or the other way round in scenarios 1 and 2, while in scenario 3 it means that the bit value is changed to any other .
“Termination criterion” is either reaching a complete adaptation (fitness peak) or other defined state, e.g., some distance from the optimum.
Drift theorems
In our analysis, we use the so‐called “variable drift theorem” (Johannsen 2010), which can be applied when for any state of the system x the expected change between two consecutive states () is at least some positive function of the current state:
| (A1) |
In such a case, the (modified) variable drift theorem (Johannsen 2010; Pérez Heredia et al. 2016) states that the expected time to reach some distance a from the optimum, starting at an initial distance of X 0, is bounded by
| (A2) |
By defining , we can calculate the upper limit on the expected time to reach the optimum (fitness peak).
Special cases of the variable drift theorem that we also occasionally used in our analysis are the “Multiplicative drift theorem” (Doerr et al. 2012) and the Additive drift theorem (Lehre and Witt 2013).
Theorem A1
( (Generalized variable drift theorem (Pérez Heredia et al. 2016))) Consider a stochastic process on . Suppose there is a monotonic increasing function such that the function is integrable on [1, m], and with expected progress towards the optimum such that
for all . Then the expected first hitting time of any state from for is at most
The proof of the theorem is provided in (Pérez Heredia et al. 2016).
Theorem A2
( (Additive drift theorem (Lehre and Witt 2013))) Let be a stochastic process over some bounded state space , and the first hitting time of state 0. Assume that . Then:
- (i)
If , then .
- (ii)
If , then .
Both results are conditioned on a starting point X 0, but by applying the law of total expectation, we can avoid the starting condition obtaining and for the first and second result respectively. The proof can be found in (Lehre and Witt 2013).
Theorem A3
( (Multiplicative drift theorem (Doerr et al. 2012))) Let be nonnegative random variables over , each with finite expectation, and let .
Suppose there exists an such that, for all t,
Then
Theorem A4
( (Tail bounds for multiplicative drift (Doerr and Goldberg 2013; Lehre and Witt 2014))) Let be nonnegative random variables over , each with finite expectation, and let .
Suppose there exists an such that, for all t,
Then, for all ,
LITERATURE CITED
- Bell, G. , and Collins S.. 2008. Adaptation, extinction and global change. Evol. Appl. 1:3–16. http://doi.wiley.com/10.1111/j.1752‐4571.2007.00011.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell, G. , and Gonzalez A.. 2009. Evolutionary rescue can prevent extinction following environmental change. Ecol. Lett. 12:942–948. [DOI] [PubMed] [Google Scholar]
- Bergland, A. O. , Behrman E. L., O'Brien K. R., Schmidt P. S., and Petrov D. A.. 2014. Genomic evidence of rapid and stable adaptive oscillations over seasonal time scales in Drosophila . PLoS Genet. 10:e1004775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breeze, A. S. , and Obaseiki‐Ebor E. E.. 1983. Mutations to nitrofurantoin and nitrofurazone resistance in escherichia coli k12. Microbiology 129:99–103. [DOI] [PubMed] [Google Scholar]
- Büchi, L. , and Vuilleumier S.. 2014. Coexistence of specialist and generalist species is shaped by dispersal and environmental factors. Am. Nat. 183:612–624. [DOI] [PubMed] [Google Scholar]
- Bürger, R. , and Lynch M.. 1995. Evolution and extinction in a changing environment: a quantitative‐genetic analysis. Evolution 49:151–163. [DOI] [PubMed] [Google Scholar]
- Carlson, S. , Cunningham C., and Westley P.. 2014. Evolutionary rescue in a changing world. Trends Ecol. Evol. 29:521–530. [DOI] [PubMed] [Google Scholar]
- Chatterjee, K. , Pavlogiannis A., Adlam B., and Nowak M. A.. 2014. The time scale of evolutionary innovation. PLoS Comput. Biol. 10:e1003818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin, L.‐M . 2013. Genetic constraints on adaptation to a changing environment. Evolution 67:708–721. [DOI] [PubMed] [Google Scholar]
- Chevin, L.‐M. , Lande R., and Mace G.. 2010. Adaptation, plasticity, and extinction in a changing environment: towards a predictive theory. PLoS Biol. 8:e1000357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cvijovic, I. , Good B., Jerison E., and Desai M., 2015a. The fate of a mutation in a fluctuating environment. Proc. Natl. Acad. Sci. USA 112:E5021–E5028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cvijovic, I. , Good B., Jerison E., and Desai M. 2015b. The fate of a mutation in a fluctuating environment. bioRxiv 07. [DOI] [PMC free article] [PubMed]
- Doebeli, M. , and Ispolatov I.. 2010. Complexity and diversity. Science 328:494–497. [DOI] [PubMed] [Google Scholar]
- Doerr, B. , and Goldberg L. A.. 2013. Adaptive drift analysis. Algorithmica 65:224–250. [Google Scholar]
- Doerr, B. , Johannsen D., and Winzen C.. 2012. Multiplicative drift analysis. Algorithmica 64:673–697. [Google Scholar]
- Draghi, J. A. , and Plotkin J. B.. 2011. Molecular evolution: Hidden diversity sparks adaptation. Nature 474:45–46. [DOI] [PubMed] [Google Scholar]
- Duputié, A. , Massol F., Chuine I., Kirkpatrick M., and Ronce O.. 2012. How do genetic correlations affect species range shifts in a changing environment? Ecol. Lett. 15:251–259. [DOI] [PubMed] [Google Scholar]
- Fisher, R. 1930. The genetical theory of natural selection. Vol. 154 Oliver and Boyd, Edinburgh, U.K. [Google Scholar]
- Fussmann, G. , Bell G., and Low‐Décarie E.. 2014. Aquatic primary production in a high‐ world. Trends Ecol. Evol. 29:223–232. [DOI] [PubMed] [Google Scholar]
- Gallagher, A. J. , Hammerschlag N., Cooke S. J., Costa D. P., and Irschick D. J.. 2015. Evolutionary theory as a tool for predicting extinction risk. Trends Ecol. Evol. 30:61–65. [DOI] [PubMed] [Google Scholar]
- H Gillespie, J . 1984. Molecular evolution over the mutational landscape. Evolution 38:1116–1129. [DOI] [PubMed] [Google Scholar]
- Gilman, R. , Nuismer S., and Jhwueng D.‐c.. 2012. Coevolution in multidimensional trait space favours escape from parasites and pathogens. Nature 483:328–330. [DOI] [PubMed] [Google Scholar]
- Girgis, H. S. , Hottes A. K., and Tavazoie S.. 2009. Genetic architecture of intrinsic antibiotic susceptibility. PLoS One 4:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomulkiewicz, R. , and Shaw R.. 2012. Evolutionary rescue beyond the models. Philos. Trans. R. Soc. Lond. B Biol. Sci. 368:20120093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez, A. , Ronce O., Ferriere R., and Hochberg M. E.. 2013. Evolutionary rescue: an emerging focus at the intersection between ecology and evolution. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 368:20120404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmand, N. , Gallet R., Jabbour‐Zahab R., Martin G., and Lenormand T.. 2017. Fisher's geometrical model and the mutational patterns of antibiotic resistance across dose gradients. Evolution 71:23–37. [DOI] [PubMed] [Google Scholar]
- Hayden, E. J. , Ferrada E., and Wagner A.. 2011. Cryptic genetic variation promotes rapid evolutionary adaptation in an RNA enzyme. Nature 474:92–95. [DOI] [PubMed] [Google Scholar]
- He, J. , and Yao X.. 2001. Drift analysis and average time complexity of evolutionary algorithms. Artif. Intell. 127:57–85. [Google Scholar]
- Hermisson, J. , and Wagner G. P.. 2004. The population genetic theory of hidden variation and genetic robustness. Genetics 168:2271–2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hottes, A. K. , Freddolino P. L., Khare A., Donnell Z. N., Liu J. C., and Tavazoie S.. 2013. Bacterial adaptation through loss of function. PLoS Genet. 9:e1003617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johannsen, D. 2010. Random Combinatorial Structures and Randomized Search Heuristics. Ph.D. thesis, Universität des Saarlandes, Saarbrücken, Germany and the Max‐Planck‐Institut für Informatik.
- Kashtan, N. , Noor E., and Alon U.. 2007. Varying environments can speed up evolution. Proc. Nat. Acad. Sci. USA 104:13711–13716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kassen, R . 2002. The experimental evolution of specialists, generalists, and the maintenance of diversity. J. Evol. Biol. 15:173–190. [Google Scholar]
- Ketola, T. , Mikonranta L., Zhang J., Saarinen K., Örmälä A. M., Friman V. P., Mappes J., and Laakso J.. 2013. Fluctuating temperature leads to evolution of thermal generalism and preadaptation to novel environments. Evolution 67:2936–2944. [DOI] [PubMed] [Google Scholar]
- Kimura, M . 1962. On the probability of fixation of mutant genes in a population. Genetics 47:713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp, M. , and Hermisson J.. 2007. Adaptation of a quantitative trait to a moving optimum. Genetics 176:715–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp, M. , and Hermisson J. 2009a. The genetic basis of phenotypic adaptation i: Fixation of beneficial mutations in the moving optimum model. Genetics 182:233–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp, M. , and Hermisson J. 2009b. The genetic basis of phenotypic adaptation ii: The distribution of adaptive substitutions in the moving optimum model. Genetics 183:1453–1476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande, R. , and Shannon S.. 1996. The role of genetic variation in adaptation and population persistence in a changing environment. Evolution 50:434–437. [DOI] [PubMed] [Google Scholar]
- Lehre, P. K. , and Witt C.. 2013. General drift analysis with tail bounds. ArXiv e‐ prints.
- Lehre, P. K. , and Witt C. 2014. Concentrated hitting times of randomized search heuristics with variable drift. in Proc. of ISAAC'14, Pp. 686–697.
- Lynch, M. , and Gabriel W.. 1987. Environmental tolerance. Am. Nat. 129:283–303. [Google Scholar]
- Lynch, M. , and Lande R.. 1993. Evolution and extinction in response to environmental change Pp. 234–250, in Kareiva P., Kingsolver J., and Huey R., eds. Biotic interactions and global change. Sinauer Associates, Sunderlands, MA. [Google Scholar]
- Martin, G. , and Lenormand T.. 2015. The fitness effect of mutations across environments: Fisher's geometrical model with multiple optima. Evolution 69:1433–1447. [DOI] [PubMed] [Google Scholar]
- Masel, J . 2006. Cryptic genetic variation is enriched for potential adaptations. Genetics 172:1985–1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matuszewski, S. , Hermisson J., and Kopp M.. 2014. Fisher's geometric model with a moving optimum. Evolution 68:2571–2588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matuszewski, S. , Hermisson J., and Kopp M. 2015. Catch me if you can: adaptation from standing genetic variation to a moving phenotypic optimum. Genetics 200:1255–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer, P. W. , Ellner S. P., and Hairston N. G.. 2016. Can population genetics adapt to rapid evolution? 32:408–418. [DOI] [PubMed] [Google Scholar]
- Moore, A. J. , Brodie E. D. I., and Wolf J. B.. 1997. Interacting phenotypes and the evolutionary process: I. Direct and indirect genetic effects of social interactions. Evolution 51:1352–1362. [DOI] [PubMed] [Google Scholar]
- Moran, D. , Softley R., and Warrant E. J.. 2015. The energetic cost of vision and the evolution of eyeless Mexican cavefish. Sci. Adv. 1:e1500363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustonen, V. , and Lässig M.. 2009. From fitness landscapes to seascapes: non‐equilibrium dynamics of selection and adaptation. Trends Genet. 25:111–119. [DOI] [PubMed] [Google Scholar]
- Nuismer, S. L. , and Ridenhour B. J.. 2008. The contribution of parasitism to selection on floral traits in Heuchera grossulariifolia . J. Evol. Biol. 21:958–965. [DOI] [PubMed] [Google Scholar]
- Orr, H. 2000. Adaptation and the cost of complexity. Evolution 54:13–20. [DOI] [PubMed] [Google Scholar]
- Orr, H. , and Unckless R.. 2008. Population extinction and the genetics of adaptation. Am. Nat. 172:160–169. [DOI] [PubMed] [Google Scholar]
- Paaby, A. B. , and Rockman M. V.. 2014. Cryptic genetic variation: evolution's hidden substrate. Nat. Rev. Genet. 15:247–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paixão, T. , Badkobeh G., Barton N., Çörüş D., Dang D.‐C., Friedrich T., Lehre P., Sudholt D., Sutton A., and Trubenová B.. 2015. Toward a unifying framework for evolutionary processes. J. Theor. Biol. 383:28–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paixão, T. , Pérez Heredia J., Sudholt D., and Trubenová B.. 2015. First steps towards a runtime comparison of natural and artificial evolution Pp. 1455–1462, in Proceedings of the 2015 Genetic and Evolutionary Computation Conference (GECCO 2015). ACM, New York, NY. [Google Scholar]
- Paixão, T. , Pérez Heredia J., Sudholt D., and Trubenová B.. 2017. Towards a runtime comparison of natural and artificial evolution. Algorithmica 78:681–713. [Google Scholar]
- Pease, C. , Lande R., and Bull J.. 1989. A model of population growth, dispersal and evolution in a changing environment. Ecology 70:1657–1664. [Google Scholar]
- Peischl, S. , and Kirkpatrick M.. 2012. Establishment of new mutations in changing environments. Genetics 191:895–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez, Heredia, J. , Trubenová B., Sudholt D., and Paixão T.. 2016. Selection limits to adaptive walks on correlated landscapes. Genetics 2015:803–825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polechová, J. , Barton N., and Marion G.. 2009. Species' range: adaptation in space and time. Am. Nat. 174:E186–E204. [DOI] [PubMed] [Google Scholar]
- Provine, W. B. 1989. Sewall Wright and evolutionary biology. Univ. of Chicago Press, Chicago, IL. [Google Scholar]
- Rajon, E. , and Masel J.. 2013. Compensatory evolution and the origins of innovations. Genetics 193:1209–1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saarinen, K. , Laakso J., Lindström L., and Ketola T.. 2018. Adaptation to fluctuations in temperature by nine species of bacteria. Ecol. Evol. 8:2901–2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiffers, K. , Bourne E., Lavergne S., Thuiller W., and Travis J.. 2013. Limited evolutionary rescue of locally adapted populations facing climate change. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 368:20120083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toor, J. , and Best A.. 2016. Evolution of host defense against multiple enemy populations. Am. Nat. 187:308–319. [DOI] [PubMed] [Google Scholar]
- Uecker, H. , and Hermisson J.. 2011. On the fixation process of a beneficial mutation in a variable environment. Genetics 188:915–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker, H. , and Hermisson J. 2016. The role of recombination in evolutionary rescue. Genetics 202:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker, H. , Otto S., and Hermisson J.. 2014. Evolutionary rescue in structured populations. Am. Nat. 183:E17–E35. [DOI] [PubMed] [Google Scholar]
- Vermeij, G . 1982. Unsuccessful predation and evolution. Am. Nat. 120:701–720. [Google Scholar]
- Vincenzi, S . 2014. Extinction risk and eco‐evolutionary dynamics in a variable environment with increasing frequency of extreme events. J. R. Soc. Interf. 11:20140441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waxman, D . 2011. A unified treatment of the probability of fixation when population size and the strength of selection change over time. Genetics 188:907–913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, J. B. , Brodie E. D. I., and Moore A. J.. 1999. Interacting phenotypes and the evolutionary process. II. Social evolution. Am. Nat. 153:254–266. [DOI] [PubMed] [Google Scholar]
- Wu, Y. , Saddler C. A., Valckenborgh F., and Tanaka M. M.. 2014. Dynamics of evolutionary rescue in changing environments and the emergence of antibiotic resistance. J. Theor. Biol. 340:222–231. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1. Scheme of the first two scenarios.
Fig. S2. In this scenario, only one trait is under selection at each time.
Fig. S3. The number of adapted loci and fitness varies in time.
Fig. S4. The dependence of the level of adaptation on the period of environmental change.
Fig. S5. Time to find the temporal optimum in scenario 1, and its dependence on various parameters.
Fig. S6. In this scenario, all traits are under selection at all times.
Fig. S7. Time to find the temporal optimum in scenario 2, and its dependence on various parameters.
Fig. S8. All traits are under selection at all times.
Fig. S9. Time to find the temporal optimum in scenario 3, and its dependence on various parameters.
Fig. S10. Minimum (red), maximum (green) and magnitude of the fitness oscilations (blue) in all three models, when environments change in random order.
Fig. S11. Markov chain with two states, representing the value of any bit.
Fig. S12. Dependence of the level of adaptation (fraction of adapted alleles) on the period of environmental change.
Fig. S13. Dependence of the level of adaptation (fraction of adapted alleles) on the number of traits.
Fig. S14. Examples of simulation of evolving population.
Fig. S15. Extinction rate depends on the length of the period τ, as well as growth rate function.


