Bayesian Confidence Intervals for Multiplexed Proteomics Integrate Ion-statistics with Peptide Quantification Concordance

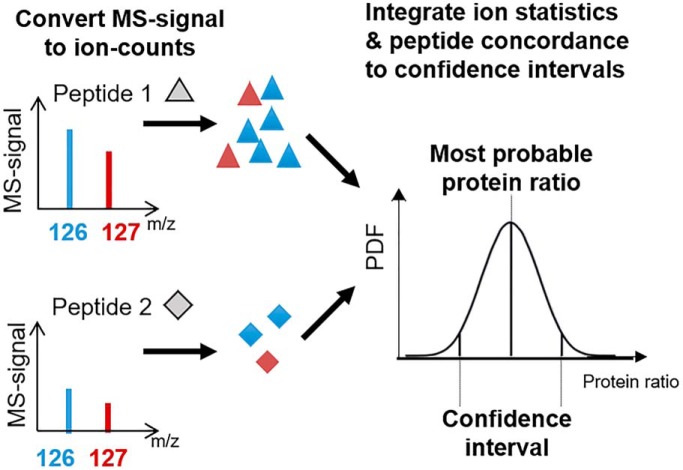
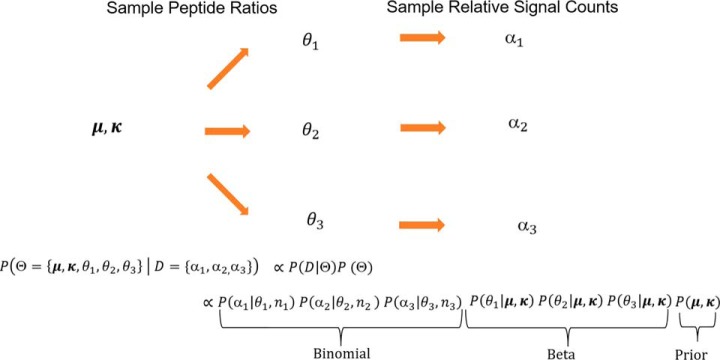
Multiplexed proteomics has become a powerful tool to assay biological systems. So far, the data is typically interpreted via naive peptide averaging. Here, we present a Bayesian approach that integrates peptide quantification concordance and ion statistics into the most probable answer with confidence intervals. Our approach considers low signal peptides, does not require replicates, and detects smaller significant changes than alternative approaches. Thus, our method increases the value of proteomics experiments, helping researchers to interpret data and prioritize resources.

Graphical Abstract

Highlights

• Bayesian Beta-Binomial model integrates ion statistics with peptide ratio agreement.

• Model appropriately interprets information from low signal peptides.

• Confidence can be assigned even without replicates.

• Model adds sensitivity to detection of small changes.

Abstract

Multiplexed proteomics has emerged as a powerful tool to measure relative protein expression levels across multiple conditions. The relative protein abundances are inferred by comparing the signals generated by isobaric tags, which encode the samples' origins. Intuitively, the trust associated with a protein measurement depends on the similarity of ratios from the protein's peptides and the signal-strength of these measurements. However, typically the average peptide ratio is reported as the estimate of relative protein abundance, which is only the most likely ratio with a very naive model. Moreover, there is no sense on the confidence in these measurements. Here, we present a mathematically rigorous approach that integrates peptide signal strengths and peptide-measurement agreement into an estimation of the true protein ratio and the associated confidence (BACIQ). The main advantages of BACIQ are: (1) It removes the need to threshold reported peptide signal based on an arbitrary cut-off, thereby reporting more measurements from a given experiment; (2) Confidence can be assigned without replicates; (3) For repeated experiments BACIQ provides confidence intervals for the union, not the intersection, of quantified proteins; (4) For repeated experiments, BACIQ confidence intervals are more predictive than confidence intervals based on protein measurement agreement. To demonstrate the power of BACIQ we reanalyzed previously published data on subcellular protein movement on treatment with an Exportin-1 inhibiting drug. We detect ∼2× more highly significant movers, down to subcellular localization changes of ∼1%. Thus, our method drastically increases the value obtainable from quantitative proteomics experiments, helping researchers to interpret their data and prioritize resources. To make our approach easily accessible we distribute it via a Python/Stan package.

Mass spectrometry-based proteomics has undergone a remarkable revolution and is now able to identify ∼10,000 proteins in a single experiment (1–3). However, because of the difficulty in predicting ionization efficiency of peptides during electrospray, the signal measured in the mass spectrometer is not a direct readout for the peptide concentration in a sample. Proteomics is well suited for comparing the abundance change of the same peptides/proteins among multiple conditions (e.g., replicates, perturbations, or time-points). In so-called label-free proteomics, the peptide signal is compared between multiple different runs and changes of ∼2-fold can be detected as significant (4). Even smaller relative protein abundance changes can be detected by encoding multiple conditions with heavy isotopes and analyzing the samples simultaneously. In MS1 based approaches like SILAC the different conditions contain different numbers of heavy isotopes and conditions are encoded by differing peptide masses. However, because of the increase in complexity of the MS1 spectrum with more conditions, this approach is only feasible for analyzing up to three conditions at a time (5). A breakthrough for proteomics was the introduction of isobaric tags (6). These tags, which are chemically attached to the peptides, act as barcodes for the different conditions. Each tag has the same mass and only on fragmentation are the distinct reporter ions released. Because of the identical masses, the MS1 spectrum does not increase in its complexity with more conditions and currently up to 11 conditions (channels) can be compared in a single experiment (7). Initially, the co-isolation and co-fragmentation of other peptides led to major artifacts. However, more recently these artifacts have been overcome with the introduction of MultiNotch MS3 (TMT-MS3), QuantMode, and the complement reporter ion approach (TMTc+) (8–12). With these methods, data of superb quality can be generated and changes of ∼10% can be detected as significant (13).

Despite these impressive capabilities of quantitative multiplexed proteomics, a remarkable shortcoming is the lack of confidence assigned to these measurements. Typically, the average peptide ratio is reported as the estimate of protein relative abundance, which is only the most likely ratio with a very naive model. Various factors can distort the measurements: peptide-to-spectra matching uncertainty, enzymatic digestion efficiency, post-translational modifications, and interference (11). Generally, there is no sense of how much we can trust the data (14). Noise models have been presented to handle peptide-to-protein aggregation in label-free settings. However, these approaches are not easily transferable to multiplexed proteomics, where the data is of a very different nature (15–17). Using multiplexed data, previous studies considered measurement agreement among peptides assigned to a protein, but the underlying ion-statistics were ignored (18, 19). Because multiplexed proteomics data is compositional in nature, the peptide signal in each channel is usually converted into proportions. However, conversion to proportions comes with a drawback of losing the information on the signal strength with which that proportion was measured. Hence, the integration of errors because of poor signal strength and the peptide ratio concordance has been a challenge. With replicate experiments, confidence can be calculated with standard approaches like the t test or ANOVA (9, 20, 21). For these approaches, protein level measurements typically weigh peptides by ion-signal but ignore the underlying agreement among peptide measurements. For approaches based on replicate protein-level measurements, the confidence of the measurement can obviously only be expressed for the intersection of protein sets measured in all repeated experiments. Moreover, these approaches may lead to unwarranted high confidence when multiple experiments have wrong but concordant measurements and each experiment ignores the disagreement at the peptide level. Also, peptides which are measured with the signal below an arbitrary level are ignored (9, 22).

Most proteins are measured via multiple peptide quantification events. Intuitively, for a protein-level measurement, one should be able to use both the agreement between measurements from all assigned peptides, and the signal strength for each of those measurements, to assign both a quantification value and an associated confidence. However, to our knowledge there is currently no way to integrate all this information to express the confidence of protein level quantification. Supplemental Fig. S1 summarizes the challenge to express confidence for multiplexed proteomics measurements. Assigning confidence is important because it allows one to assess the significance of changes and enables researchers to prioritize valuable time and resources in follow-up experiments.

In this paper, we propose a novel, mathematically rigorous method for computing and representing the uncertainty of quantitative multiplexed proteomics measurements. Our method is based on a generative hierarchical Bayesian model of a two condition Beta-Binomial method (or the Dirichlet-Multinomial for the multiple-condition scenario). We call our method BACIQ¹ (Bayesian Approach to Confidence Intervals for protein Quantitation - pronounced BASIC).

Beta-Binomial models have been previously used in the context of proteomics for the scenarios involving multiple levels of noise, for example accounting for within and between sample variation of the spectral count data (23) or to deconvolute the isotopic incorporation of N15 into natural abundance, partially and fully labeled distributions (24). A challenge in applying a beta-binomial model to multiplexed proteomics data is that the peptide signal is not the direct readout of the number of ions. We demonstrate a calibration approach that converts the peptide signal to the number of ions.

Our approach allows us to represent uncertainty for both individual peptides as well as multi-peptide proteins and considers peptides regardless of the signal strength, thereby increasing the sensitivity of proteomics measurements. Our method does not require multiple repeated experiments, but if such repeats are available, it integrates the results providing the output and confidence for the union (not intersection) of all separately measured proteins. If the repeats are available, BACIQ is more predictive than the standard approach using a t test. Further, we demonstrate the power of our method by re-analyzing a previously published proteomics dataset that studies the change of subcellular protein localization on addition of an Exportin-1 inhibitor Leptomycin B (13). With BACIQ, we can identify ∼2x more Leptomycin B responders compared with our previously published naive analysis and detect subcellular localization changes of as low as 1% to be significant at 5% FDR.

EXPERIMENTAL PROCEDURES

Sample Preparation

The single proteome standard and the two-proteome interference sample was prepared mostly as previously described (10, 13, 25). HeLa S3 cells were grown in suspension to 1 × 10⁶ cells/ml. Cells were harvested by spinning at 160 RCF for 5 mins at room temperature. After two washes with PBS, the pellet was flash frozen in liquid nitrogen. The pellet containing about 600 μg of total protein was resuspended in 1 ml of lysis buffer containing 25 mm HEPES pH 7.2, 2% SDS and protease inhibitors (complete mini., EDTA-free; Roche). Cells were lysed by sonication: 6 pulses, 10 s each, at 75% amplitude.

E. coli cell culture was harvested at 0.5 OD and spun down at 4,000 RCF for 20 min at 4 °C. The pellet containing about of 650 μg of total protein was resuspended in 1 ml of lysis buffer containing 8 m Urea, 2 m Thiourea, 50 mm HEPES pH 7.2, 2% SDS, 5 mm DTT. Cells were lysed by sonication: 10 pulses, 30 s each, at 75% amplitude.

Two hundred microliters of HeLa lysate was reduced with 5 mm DTT for 20 min at 60 °C. Further, both samples - 200 μl of HeLa lysate and 200 μl of E. coli lysate were alkylated with 15 mm N- Ethylmaleimide (NEM) for 30 min at room temperature. The excess of NEM was quenched with 5 mm DTT for 10 min at room temperature in both samples. Next, 200 μl of lysate were methanol-chloroform precipitated as previously described (26). Protein concentration was determined using the bicinchoninic acid (BCA) protein assay (Thermo Fisher). The samples were resuspended in 6 m guanidinium chloride in 10 mm EPPS pH 8.5 with a subsequent dilution to 2 m guanidine chloride in 10 mm EPPS pH 8.5 for digestion with Lys-C 20 ng/μl (Wako, Japan) at room temperature overnight. Further the samples were diluted to 0.5 mm Guanidine Chloride in 10 mm EPPS pH 8.5 and digested with Lys-C 20 ng/μl, and TMT 10 ng/μl at 37 °C overnight. The digested samples were dried using a vacuum evaporator at room temperature and taken up in 200 mm EPPS pH 8.0. 10 μl of total E. coli or human peptides were labeled with 3 μl of TMT 20 μg/μl. TMT reagents were dissolved in anhydrous Acetonitrile. TMT samples were labeled for 2 h at room temperature. Further, labeled samples were quenched with 0.5% Hydroxylamine solution (Sigma, St. Louis, MO) and acidified with 5% phosphoric acid (pH<2) with subsequent spin at 16,000 RCF for 10 min at 4 °C. The samples were dried using a vacuum evaporator at room temperature. Dry samples were taken up in HPLC grade water and stage tipped for desalting (27). The samples were resuspended in 1% formic acid to 1 μg/μl and 1 μg of each sample was analyzed with the MultiNotch MS3 approach (9).

The samples were labeled with the desired mixing ratios: 1.0:1.0:1.0:1.2:1.2:1.2 for E. coli, and 1.0:1.0:1.0:1.0:1.0:1.0 for HeLa (Fig. 6A).

Fig. 6.

Validating our method with a differential expression experiment. A, Six samples were prepared by mixing material from two species as follows. Six identical human samples (i.e. proportions across 6 channels were 1.0: 1.0: 1.0: 1.0: 1.0: 1.0) were mixed with an E. coli sample in two sets of three as shown (i.e. proportions across 6 channels were 1.0: 1.0: 1.0: 1.2: 1.2: 1.2). A mixture of peptides from the two proteomes was analyzed by LC-MS. B, Comparison of our method with a one tailed t test to detect significantly changing proteins. BACIQ can detect statistically significant changes without replicates, whereas the t test requires replicates. ROC plot indicates that our method is superior to the t test when the same number of replicates are used. Even without replicates, our method (red) nearly outperforms the t test with two replicates (dashed yellow). We achieve close to perfect detection of the significantly changing proteins by using the BACIQ analysis with three replicates (blue). C, A comparison of our method (with pooled variance across proteins) with the compMS. BACIQ outperforms compMS, the method that ignores ion statistics in assigning confidence.

LC/MS Analysis

1 μl per sample were analyzed by LC-MS. LC-MS experiments were performed on Orbitrap Fusion Lumos (Thermo Fischer Scientific). The instrument was equipped with Easy-nLC 1200 high pressure liquid chromatography (HPLC) pump (Thermo Fischer Scientific). For each run, peptides were separated on a 100 μm inner diameter microcapillary column, packed first with ∼0.5 cm of 5 μm BEH C18 packing material (Waters) followed by 30 cm of 1.7 μm BEH C18 (Waters). Separation was achieved by applying 4.8–24% acetonitrile gradient in 0.125% formic acid and 2% dimethyl sulfoxide over 120 min at 350 nL/min at 60 °C. Electrospray ionization was enabled by applying a voltage of 2.6 kV through a microtee at the inlet of the microcapillary column. The Orbitrap Fusion Lumos was using a MultiNotch-MS3 method (9).The survey scan was performed at resolution of 120k (200 m/z) from 350 Thomson (Th) to 1350 Th, followed by the selection of the 10 most intense ions for CID MS2 fragmentation using the quadrupole and a 0.5 Th isolation window. Indeterminate and singly charged, and ions carrying more than six charges were not subjected to MS2 analysis. Ions for MS2 were excluded from further selection for fragmentation for 90 s. MS3 spectra were acquired in the Orbitrap with 120 k resolution (200 m/z) and simultaneous precursor selection of the five most abundant fragment ions from the MS2 spectrum. The TMTc+ experiments were performed as previously described with 0.4 Th isolation window on an Orbitrap Fusion Lumos (8).

MS Data Analysis

A suite of software tools developed in the Gygi Lab was used to convert mass spectrometric data from the Thermo RAW file to the mzXML format, as well as to correct erroneous assignments of peptide ion charge state and monoisotopic m/z (28). We used RawFileReader libraries from Thermo, version 4.0.26 to convert the raw files into mzXML file format. Assignment of MS2 spectra was performed using the SEQUEST algorithm v.28 (rev. 12) (29) by searching the data against the appropriate proteome reference dataset acquired from UniProt (Escherichia coli (strain K12) with Proteome ID UP000000625, Organism ID 83333, Protein count 4267 and downloaded on Nov 26, 2017; Homo Sapiens (human) with Proteome ID UP000005640, Organism ID 9606, Protein count 71599 and downloaded on April 29, 2018) (30) including 114 common contaminants like human Keratins and Trypsin (uploaded on PRIDE with the identifier PXD012285). This forward database component was followed by a decoy component which included all listed protein sequences in reversed order (31). Searches were performed using a 20-ppm precursor ion tolerance, where both peptide termini were required to be consistent with Trypsin or Lys-C specificity, while allowing one missed cleavage. Fragment ion tolerance in the MS2- spectrum was set at 0.02 Th (TMTc+) or 1 Th for MutliNotch-MS3. NEM was set as a static modification of cysteine residues (+125.047679 Da), TMT as a static modification of lysine residues and peptides' N termini (+229.162932 Da), oxidation of methionine residues (+ 15.99492 Da) as a variable modification. An MS2 spectral assignment false discovery rate of 0.5% was achieved by applying the target decoy database search strategy (31). Filtering was performed using a Linear Discriminant analysis with the following features: SEQUEST parameters XCorr and unique Δ XCorr, absolute peptide ion mass accuracy, peptide length, and charge state. Forward peptides within three standard deviation of the theoretical m/z of the precursor were used as positive training set. All reverse peptides were used as negative training set (28). Linear Discriminant scores were used to sort peptides with at least seven residues and to filter with the desired cutoff. Furthermore, we performed a filtering step on the protein level by the “picked” protein FDR approach (32). Protein redundancy was removed by assigning peptides to the minimal number of proteins which can explain all observed peptides, with above described filtering criteria (33, 34). For the MS3 method, we only included the peptides that were observed with the isolation specificity of at least 75%. Isolation specificity is defined as the fraction of target ion intensity compared with the total ion intensity in the precursor ion isolation window visible in the MS1 spectrum (9, 11, 19). We did not use isolation specificity filtering for the TMTc+ method, as co-isolation of other peptides does not perturb the measurement results for this method (8). TMTc+ data were analyzed as previously described (8). To correct for pipetting errors in the synthetic experiments, we normalized the signal such that the median peptide ratio between two channels corresponds to the desired mixing ratios.

Implementation of BACIQ

We developed a hierarchical Beta-Binomial model to assign confidence to the estimate of protein ratio in different conditions. The model and the inference was implemented using Stan (36), specifically the Python flavor. Stan's sampling functionality was used to execute Monte-Carlo Markov Chain to obtain a sample from the posterior distribution over parameters of the model.

The source code for BACIQ in the Python flavor is available via GitHub: https://github.com/wuhrlab/BACIQ.

RESULTS

Peptide Measurements Map to Coin-flips

Let us begin by discussing the measurement of peptides that are labeled with isobaric tags encoding two different conditions (e.g. case and control) (Fig. 1A). With multiplexed proteomics we can measure the relative abundance of peptides among multiple conditions. For the sake of simplicity, we will discuss the two-condition case for most of the paper, but all our approaches and the provided code can be generalized to the multi-condition case. Once peptides from different conditions are labeled with isobaric tags, they are combined into one test tube, in which we have a “true ratio” of peptide abundances across conditions. The aim of the proteomic experiment then is to recover this “true peptide ratio” and assign confidence to the measurement. During MS analysis, the peptides get ionized and fragmented. On fragmentation, respective fragments of the isobaric tag are released, encoding the different conditions. The relative abundance of the ions encoding the different conditions is used to quantify the relative abundance of the peptides in the two conditions (Fig. 1B). However, the limited number of ions by which measurements are performed introduce measurement errors because of ion-statistics.

Fig. 1.

Peptide measurements are analogous to coin-flips: A, Peptides are labeled with isobaric tags encoding the different conditions case and control (red and blue). Shown are examples for two peptides with the identical relative abundance (true ratio) between case and control. B, After ionization and fragmentation, the relative signal of fragments produced by the isobaric tag can be used to quantify relative peptide abundance. These quantification spectra not only contain information about the peptide relative abundance but also the MS-signal. This signal is proportional to the number of ions. C, The problem of estimating the posterior probability of the “true peptide fraction” θ becomes identical to the estimation of a coin's fairness, given a certain number of head and tail measurements. The probability of “true peptide fraction” θ is a beta distribution with α, β as the shape parameters, where α, β represent the number of ions in the two channels. D, Intuitively, the fewer ions we measure the more the measured peptide ratio tends to divert from the true ratio between case and control. A higher ion-count (top row) results in a tighter probability distribution than a low ion-count (bottom row). For more than two cases this approach can be generalized with a Dirichlet distribution.

We will be describing model parameters in terms of “true peptide fraction”, instead of “true peptide ratio”. Because the relationship between “fraction” and “ratio” is invertible, we can easily transfer the estimates and confidence intervals obtained for the “true peptide fraction” into “true peptide ratio” using the change of variables (37). The process of estimating the “true peptide fraction” and assigning confidence to the estimate is analogous to evaluating the coin's fairness θ - the underlying probability of getting say Heads, on observing (α, β) number of Heads and Tails respectively in n = α + β coin tosses. For an individual peptide this translates to estimating the probability distribution of “true peptide fraction” θ, on observing (α, β) number of ions for two channels out of n total ions with which this peptide is measured. Using the Bayesian approach, the probability of true peptide fraction θ, given the observed data (D = {α, β}) can be written as follows:

$$P\left(\theta |D=\left\{\alpha ,\beta \right\}\right)\propto P\left(D=\left\{\alpha ,\beta \right\}|\theta \right)P\left(\theta \right)$$

With binomial likelihood and a conjugate prior of Beta (0, 0) (see Supporting Information for the justification on choice of likelihood and prior), the posterior probability is,

$$\begin{array}{c}\propto Bin\left(D=\left\{\alpha ,\beta \right\}|n,\theta \right)Beta\left(\theta |0,0\right)\\ \propto {\theta }^{\alpha }{\left(1-\theta \right)}^{\beta }{\theta }^{0-1}{\left(1-\theta \right)}^{0-1}\\ \propto {\theta }^{\left(\alpha -1\right)}{\left(1-\theta \right)}^{\left(\beta -1\right)}\end{array}$$

With appropriate normalizing constant, this posterior has an analytical form of Beta, where (α, β) are the shape parameters (Fig. 1C) (38). As expected, confidence intervals tend to be wider for measurements with lower ion count (Fig. 1D).

Isobaric tags are most commonly read out in the Orbitrap mass analyzer, where the raw signal divided by the Fourier transform-noise is proportional to the ion-count (39). Throughout the paper we will refer to this read out as “MS-signal.” To be able to apply the Binomial distribution to the proteomics data, the challenge is to find the proportionality constant for converting MS-signal into the number of ions.

Conversion of Mass Spectrometer Signal to Ions

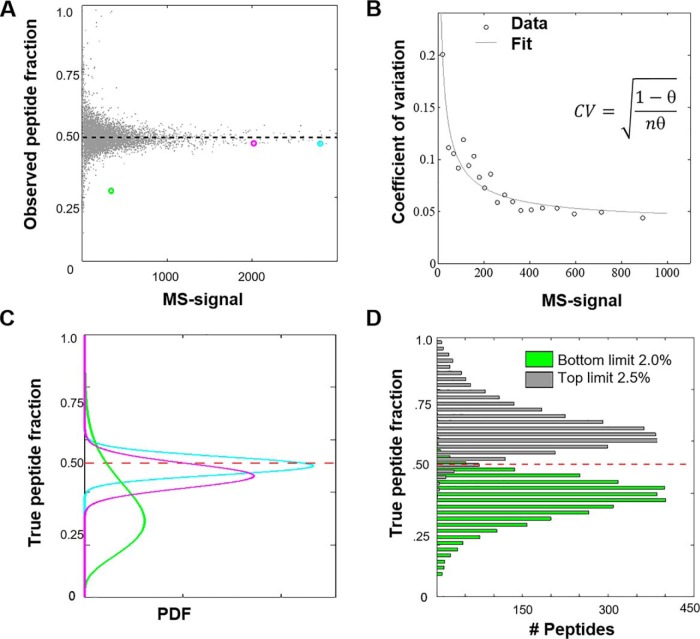
The peptide ratio measurement converges to a true ratio when measured with high MS-signal. To deduce how MS-signal relates to confidence, we generated and analyzed a proteomics sample in which all peptides are labeled with the identical 1:1 ratio. To this end, we mixed the TMT-NHS ester solutions with the desired ratio before adding peptides for labeling. In this experiment, measurement distortions are predominantly because of ion statistics. The peptides were analyzed with TMT-MS3 or via the complement reporter ion approach (TMTc+) on an Orbitrap Lumos (8, 9). Fig. 2A presents a scatter plot in which each point represents a single peptide from a TMT-MS3 dataset of a total of ∼10k quantified spectra. The observed peptide fraction of the signal converges to an asymptotic value, just like the observed fraction of Heads in a sequence of coin-tosses converges to a true fraction with the increasing number of tosses. The functional form of the convergence of the true fraction of Heads (fairness) with n coin tosses is represented with coefficient of variation of a Binomial distribution ($\sqrt{1-\theta /n\theta }$, where θ is the underlying fairness of the coin ('probability of getting Heads') (see Supporting Information). To treat the continuous MS-signal as a proxy for the number of coin flips, we fit a single parameter m, as a multiplier to an MS-signal s where n = ms to the data binned on the MS-signal (Fig. 2B). When we perform this analysis on an Orbitrap Lumos for a TMT-MS3 experiment with 50K mass resolution, we observe a conversion factor of 2.0. Interestingly, the conversion factor differs when we repeat the equivalent experiment on a different instrument (Orbitrap Elite), with different resolutions, or methods for data acquisition (Table I). Makarov et al. previously reported that this conversion factor should scale inversely with the square-root of the Orbitrap resolution (39). Our measurements are in rough agreement with this prediction. When we increase resolution from 15K to 120K on the Lumos we expect the conversion factor to reduce by 2.8-fold, we observe a 3.5-fold decrease. We suspect that the different conversion factors on different instruments is because of differences in Orbitrap electronics and data processing. For a limited number of cases, we have repeated these measurements for various instruments of the same model and obtained very similar results suggesting that for a given instrument model and resolution the conversion factors are invariant. We observe slightly smaller conversion factors for TMTc+ data into apparent counts compared with TMT-MS3 data. This is most likely because of some additional noise that is introduced during the deconvolution process of the complement reporter ion clusters (8, 10). Based on previous reports (39), we likely underestimate the number of actual ions by a small factor. Nevertheless, the good fit to the data (Fig. 2B) indicates that the conversion into pseudo-counts allows us to model the relationship between mass spectrometer signal and measurement noise because of ion-statistics. Importantly, this calibration step only must be performed once for any type of instrument and is conveniently supplied here for two commonly used mass spectrometers at various resolutions (Table I).

Fig. 2.

Conversion of MS-signal into counts and assigning confidence to the measurement of a single peptide. A, We generated a sample in which all peptides are labeled with two different TMT-tags and mixed with identical ∼1:1 ratio. When we plot the observed peptide ratio in one channel versus the summed MS-signal in both channels, measurement with higher MS-signal asymptotes to true underlying fraction (dashed line). B, Assuming ion-statistics is the dominant noise source, we can fit the coefficients of variation (CVs) and obtain the conversion factor of MS-signal to the number of ions or pseudo-counts. The data shown was obtained on an Orbitrap Lumos with 50K mass resolution. Our best estimate for the conversion factor is 2.0. C, Plot of the probability distributions of the “true peptide fraction” for the three examples color-coded to correspond to three peptide data points in sub-figure (A) D, Histogram of the upper and lower bound values for the 95% confidence intervals. The observed percentage of peptides for which the true answer is outside of the 95% confidence interval is 2.0% and 2.5% respectively for over- and under-estimation, which are symmetric and in good agreement with the expected total 5%.

Table 1. Multiplier for the MS-signal to be converted into Binomial event counts. Shown are the multiplier values for the Orbitrap Lumos or Orbitrap Elite for TMT-MS3 or TMTc+ experiments and various Orbitrap resolutions.

Instrument	Resolution	Multiplier low m/z TMT	Multiplier TMTc+ (0.4 Th)
Orbitrap Elite	15K	4.5	N/A
Orbitrap Elite	30K	3.3	N/A
Orbitrap Elite	60K	2.5	N/A
Fusion/Lumos	15K	3.4	2.7*
Fusion/Lumos	30K	2.6	2.1
Fusion/Lumos	50K	2.0	1.9
Fusion/Lumos	60K	1.8	1.7
Fusion/Lumos	120K	1.3	1.3

*Extrapolated.

Assigning Confidence Intervals for Individual Peptides

With the conversion factor at hand, we can convert the MS-signal into the number of ions and calculate the confidence associated with the “true peptide fraction” with Beta distribution as derived above. Fig. 2C illustrates the posterior probability of true-peptide fraction for three peptides at the various levels of total MS-signal as color-coded in Fig. 2A. A higher signal gives a tighter distribution.

We next verify that the confidence intervals obtained agree with observations. Computing the 95% confidence intervals we expect that the true answer will lie outside of the confidence interval ∼5% of the time and will be symmetrically split between over and under estimation. Indeed, Fig. 2D shows that we overestimate 2.0% of the time and underestimate 2.5% of the time. We repeated this demonstration for peptides labeled in different ratio and obtained consistent results, showing that beta distribution indeed is a good general model for expressing confidence for single peptide measurements (supplemental Fig. S2).

Only Considering Ion Statistics Produces Inadequate Confidence Intervals on the Protein Level

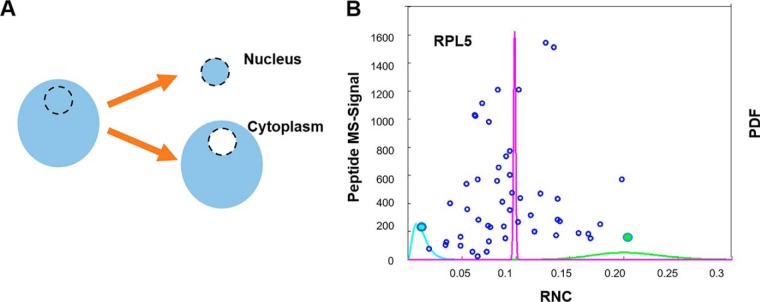
So far, we have shown that we can adequately express the confidence intervals for peptide measurements. If ion statistics was the only source of noise, we could sum up all counts from peptides mapped to a protein and express confidence intervals at the protein level. This approach works well for the above designed synthetic experiment, where all peptides in a mixture were labeled together and show the exact same ratio (supplemental Fig. S3). However, in real experiments, other factors like differences in digestion efficiency, labeling problems, erroneous peptide-to-protein assignment, post-translational modifications, chemical interference, and so forth might produce significant additional noise. To test whether only considering ion-statistics is valid for multiplexed proteomics measurements, we revisited our previous publication of nucleocytoplasmic partitioning in the frog oocyte (13) (Fig. 3A). We observe that the relative nuclear concentration (RNC) [Nuc]/([Nuc]+[Cyto]) measurements for peptides for one protein disagree with each other. This is shown by the mutual exclusiveness of the confidence interval for the two extreme peptides of one protein (Fig. 3B). Moreover, when we evaluate the confidence based on the sum of all the peptides mapped to a protein, we observe that the probability distribution is unjustifiably narrow (Fig. 3B). This suggests that besides ion-statistics, other significant sources of error contribute to the errors in proteomics measurements and we must take these sources into account to adequately express confidence intervals at the protein level.

Fig. 3.

Only considering ion-statistics does not produce accurate confidence intervals at the protein level: A, To evaluate the confidence intervals of peptides from the same protein, we revisited our previously published experiment, where we measured the localization of proteins between nucleus and cytoplasm in the frog oocyte. B, Blue discs show 50 measured peptides (RNC and MS-signal) assigned to the Ribosomal Protein L5 (RPL5). We show the beta posterior probabilities for two extreme peptides (leftmost in blue and rightmost in green). Note that these peptides' probability distributions are basically mutually exclusive, i.e. the most generous confidence intervals would exclude each other. Additionally, we show the distribution based on summing up all the peptides together (magenta) which corresponds to unjustifiably tight confidence. This example illustrates that for the expression of confidence intervals on the protein level, we cannot assume that ion-statistics is the only source of measurement error in proteomics experiments. Rather, we have to integrate other sources of errors e.g. because of differences in sample handling.

Confidence Intervals at the Protein Level That Integrate Ion Statistics and Agreement Among Peptides Mapped to the Same Protein

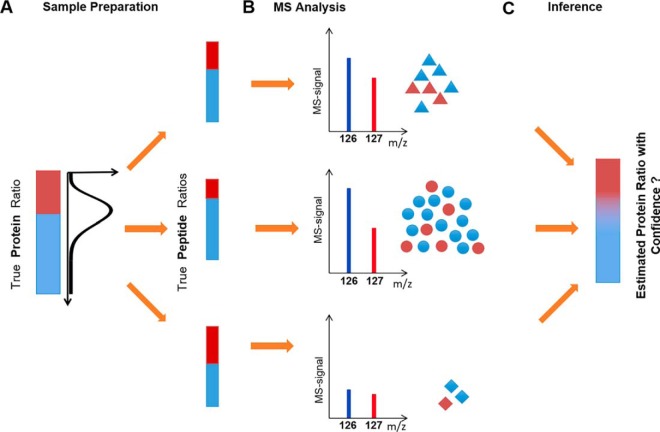
The goal is to develop a model that gives out a probabilistic distribution for the “true protein ratio” for every protein. Mathematically, achieving the above objective involves calculating the conditional probability of a true protein ratio given the observed corresponding peptide data—called the posterior distribution. Bayes theorem lets us model this distribution by asking the same question in a converse, more tractable manner that is, what is the likelihood of observing the peptide measurement data for a given protein ratio? This likelihood function can be approximated by reviewing the entire proteomics experiment as a data generating process, starting with a true protein ratio (Fig. 4). The protein is digested into peptides, which are labeled with isobaric tags. This process can introduce disagreement among “true peptide ratios” because of the differences in sample handling. We represent this first step as an equivalent of sampling peptide ratios for the constituent peptides of a given protein from the probability distribution parameterized according to the “true protein ratio” (Fig. 4A). In the second step the peptide is ionized and fragmented and its ratio is measured on the mass spectrometer. Because of the limited number of ions measured for each peptide, the observed ratio deviates from the true peptide ratio. This step can be represented as sampling the number of ions in one channel from a probability distribution parameterized over true peptide ratio, for each peptide separately. Importantly, different peptides are measured with different MS-signal and therefore with different confidence on the underlying “true peptide ratio” (Fig. 4B). We have adequately modeled this second step in previous sections. However, we aim for an approach that integrates ion statistics and agreement among peptide measurements to estimate the true protein ratio and the confidence associated with it (Fig. 4C).

Fig. 4.

Schematic of the data generating process for modeling confidence for proteins with multiple peptide measurements. A, The “true protein ratio” can be distorted because of differences in sample handling (e.g. digestion and isobaric-labeling) and give rise to multiple peptides with differing “true peptide ratios”. The peptide ratios for the constituent peptides of a given protein are sampled from the probability distribution parameterized according to the “true protein ratio” B, Each peptide is measured via the mass spectrometer. Based on the number of ions used to measure each peptide, the confidence in quantification varies. The observed data is sampled from a probability distribution given a true peptide ratio, for each peptide separately C, The goal is to infer the underlying true protein ratio between the conditions and generate confidence using the agreement between multiple peptide measurements and their respective MS-signals.

For each protein in a two-condition case, the above description of the entire process can be mathematically represented as a generative two-level Beta-Binomial model (38):

• The unobserved true peptide fractions θ_i, where i = 1,2,3, …, I indexes the number of peptides for the protein, are sampled from a beta distribution with a, b as the shape parameters. The shape parameters of a beta distribution represent pseudo counts. In order to make the true protein fraction a parameter of the model, we used a reparameterization of the Beta distribution in terms of mean μ = a/(a + b) and precision κ = a + b. We assume the target of our estimation (true protein fraction) to be the mean of the beta distribution as represented by the parameter (μ)

• Given true underlying peptide fraction θ_i, the number of ions in one channel α_i can be modeled using a Binomial distribution, with n_i representing the sum of counts in the two channels. Here, α_i and n_i represent the observed peptide data.

All the unobserved parameters (μ, κ, θ₁, θ₂, … θ_I) are modeled by a joint probability distribution conditioned on the observed data. Because each of the peptide measurements are independent from each other, the probability distributions for every peptide can be modeled separately and multiplied together. Fig. 5 represents the graphical model.

Fig. 5.

Mathematical model for estimating the protein fraction and its confidence: The entire data generation process can be adequately described with the Beta-Binomial process (or Dirichlet -Multinomial process for more than two cases). To draw the parallel with figure 4, we consider the two condition three peptide case. We assume an underlying beta-distribution with mean μ and precision κ representing the probability distribution of true protein fraction, from which peptide fractions θ_i for the constituent peptides of a given protein are sampled. Given a true underlying peptide fraction θ_i, we can sample the number of ions in a channel α_i from Binomial distribution. Each peptide is independently sampled from its respective binomial distribution with the true peptide fraction of θ_i and total number of ions n_i.

Based on the graphical model, for a single protein, the Beta-Binomial model is implemented as follows

$$P\left(\mu ,\kappa ,{\theta }_1,{\theta }_2\dots {\theta }_I|{\alpha }_1,{\alpha }_2\dots {\alpha }_I\right)\propto P\left(\mu \right)P\left(\kappa \right){\displaystyle \prod _{i=1}^{I}P\left({\theta }_i|\mu ,\kappa \right)P\left({\alpha }_i|n_i,{\theta }_i\right)}$$

Where we set the priors (Please see the Supporting Information for the justification of priors used) and likelihood distributions as follows: -

$$\begin{array}{c}P\left(\mu \right)=Uniform\left(0,1\right)\\ P\left(\kappa \right)=Exponential\left(0.05\right)\\ P\left({\theta }_i|\mu ,\kappa \right)=Beta\left({\theta }_i|\mu ,\kappa \right)\\ P\left({\alpha }_i|n_i,{\theta }_i\right)=Bin\left({\alpha }_i|n_i,{\theta }_i\right)\end{array}$$

We marginalize the latent variables to get the posterior distribution of μ conditioned on observed data D, P(μ|D). The estimated value of the true protein fraction μ is given by the median of the posterior distribution P(μ|D) and the uncertainty associated with this estimate is given by the confidence intervals derived from P(μ|D).

The maximum-likelihood estimate (MLE) of these distributions is not available in a closed form, thereby making the problem analytically intractable (40). One approach would be to numerically search for an MLE and estimate the curvature of the likelihood function from the Hessian at the MLE using the asymptotic normality (41). Unfortunately, however, this approach did not turn out to be numerically robust (not shown). A robust alternative approach is accomplished using Monte-Carlo Markov Chain (MCMC) methods implemented in statistical inference language Stan (see Supporting Information) (36). Essentially, it consists of exploring the space of possible protein ratios, computing the likelihood of observed peptide data given a guess at the protein ratio and assembling a large set of plausible ratio samples to use its histogram as posterior probability representation. Please refer to Materials and Methods section for the download link to the software.

Validation of BACIQ by Comparing to Existing Approaches

We produced a standard containing peptides with different labeling ratios. We asked how reliable our approach was in distinguishing proteins, which show different expression levels (increase by 20%) and proteins that are unchanged. We mixed equal amounts of human proteins across six samples with E. coli proteins in different mixing ratios in triplicates (Fig. 6A). Thus, ideally all E. coli proteins should be identified as “differentially expressed” on a background of uniformly expressed human proteins. This synthetic experiment simulates an essential application of having the complete probability distribution, where confidence intervals can be used to prioritize the follow-up targets of a proteomic experiment.

We first compared BACIQ to the widely used t-tests on replicate measurements. Crucially, although the t test requires at least one repeat, our method can be applied to a single experiment, as well as two and three repeats by merely combining measurements. As shown in Fig. 6B, even using no replicates our method outperforms the t test-based classification with two repeats for the most relevant false positive (FP) rates. For the same number of replicates, BACIQ outperforms the t test for all FP-rates. Using three replicates, BACIQ achieves a close to perfect distinction. Similar outperformance of BACIQ over the t test can also be observed for 1.1-fold and 1.4-fold changes (supplemental Fig. S5A and S5B).

We then compared our model to a recent Bayesian model (compMS) that assigns confidence to the multiplexed proteomics measurements by accounting for agreement among peptides but ignoring ion statistics (19). The compMS model shares variance across all the proteins. For a fair comparison, we modified BACIQ to also pool the variance across proteins (Please see the Supporting Information for partially pooled Beta-Binomial model). ROC curves indicate that BACIQ outperforms the compMS model (Fig. 6C). We are currently not convinced that sharing peptide variance across proteins can be rigorously justified outside the synthetic case of ratio standards. We therefore have conservatively chosen to use the BACIQ without pooling variance across proteins for the rest of this paper. As a control in supplemental Fig. S6 we show that BACIQ does not show any significant improvement in point-measurement accuracy and is comparable to other approaches in the detection of trivial large fold changes (supplemental Fig. S5C). In conclusion, BACIQ is a powerful tool to detect comparatively small expression differences even in the absence of replicates.

Re-analyzing Subcellular Relocalization Data With BACIQ Increases Detection of Significant Responders to Leptomycin B by ∼2-fold

To assess BACIQ under real-world scenarios, we reanalyzed a previously published proteomic dataset that investigated the change of subcellular localization on Leptomycin B (LMB) addition (13). Leptomycin B is a highly potent and specific inhibitor of Exportin-1 (42), which is responsible for the transport of proteins out of the nucleus into the cytoplasm. On treatment, we expect substrates of Exportin-1 to move toward the nucleus (Fig. 7A) because of competing transport with importins or because of passive diffusion through the nuclear pore. Importantly, in this data set, we can use hundreds of proteins small enough to diffuse through the nuclear pore to normalize for equivalent amounts of nuclear and cytoplasmic material (supplemental Fig. S7).

Fig. 7.

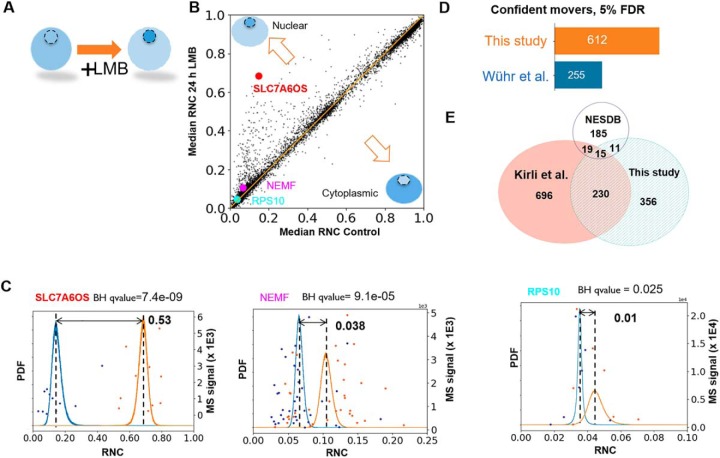
Re-analysis of subcellular movement on Exportin-1 inhibition with BACIQ. A, On inhibition of Exportin-1 with Leptomycin B (LMB) we expect Exportin-1 substrates to move toward the nucleus. We compared the RNC in control and drug treated samples to identify the proteins that confidently shift toward the nucleus regardless of initial nucleocytoplasmic distribution. B, A scatterplot indicating the shift in RNC post LMB treatment. Most proteins seem unaffected by the treatment. The proteins above the diagonal indicate movement toward the nucleus and those below the diagonal indicate movement toward the cytoplasm. C, The raw peptide data and probability distributions of RNC for three different proteins (shown as discs in B). The blue curve represents the probability distribution of RNC before adding the drug and the orange curve represents the probability distribution of RNC after adding the drug. With our approach, we can detect the movement toward the nucleus of as little as 1%. D, Applied to the entire dataset BACIQ detects 750 putative Exportin-1 substrates (612 unique gene symbols) at 5% false discovery rate. With identical FDR, BACIQ extracts ∼2× more proteins as significantly moving compared with our previously published naive analysis. E, Venn diagram shows the overlap in unique gene symbols of the LMB responders at 5% FDR from this study with Cargo database based on Exportin-1 affinity experiments (Kirli et al.), and a database curated from literature (NESDB). The overlap with both databases is highly significant with p values of 5.5 e-29 (Kirli et al.) and 3.1e-6 (NESDB) based on hypergeometric test.

On comparing the median relative nuclear concentration (RNC) of control and drug treated samples, we observe that most of the proteins do not show any obvious shift. Proteins off the diagonal show apparent movement toward the nucleus or cytoplasm (Fig. 7B). Fig. 7C shows RNC distributions from the Beta-Binomial model of the control (blue) and drug treated (orange) samples for three different proteins. Naively, as we did in our previous publication, one could rank proteins by the magnitude of their movement toward the nucleus as likely Exportin-1 substrates. BACIQ, however, not only allows us to consider the magnitude of movement but assign probability to the movement using the RNC distributions of control and drug treated samples.

In large scale datasets the probability assigned to a single discovery is not particularly meaningful as thousands of hypotheses are tested. We must therefore apply a multiple hypotheses correction procedure. In the discussed experiment, we can use movement toward the cytoplasm on LMB treatment as a conservative noise model. Indeed, we observe that the p values of the probabilities of the cytoplasmic movers follow a uniform distribution, which is expected under the assumption of true null (supplemental Fig. S8) (43). We used the standard Benjamini Hochberg multiple hypothesis correction procedure to assign q-values to the probability of movement (44). The Probable RNA polymerase II nuclear localization protein, SLC7A6OS, is one of our topmost hits with a median RNC shift of 0.53 and a q-value of 7.0 e-9 (supplemental Table S1).

But BACIQ can detect much more subtle changes. Among the newly assigned movers, BACIQ assigns highly significant q-values of 1.0 e-4 to Nuclear export mediator factor, (NEMF) with 3.8% movement toward the nucleus. Even a change of subcellular localization as small as 1% results in a q-value of 0.025 for the 40S ribosomal protein S10, (RPS10) (Fig. 7C).

With an estimated false discovery rate (FDR) of 5%, we detect ∼750 putative Exportin-1 substrates, accounting for 612 unique gene symbols. Importantly, by reanalyzing previously published data with our newly developed statistical tool we discover ∼2x more significant LMB responders (Exportin-1 substrates) as compared with our previous naïve analysis at an identical FDR (Fig. 7D). The Görlich and Chook groups identified Exportin-1 substrates in orthogonal approaches using either an affinity assay (45) or by curating a list from the literature (46). Our list of putative Exportin-1 substrates above the 5% FDR threshold exhibits a highly significant overlap with both these resources (p values 5.5 e-29 and 3.1 e-6 respectively, hypergeometric test) (Fig. 7E). Although there is still substantial disagreement among the three compared studies the overlap seems encouraging and might point toward an emerging consensus of Exportin-1 substrates. We believe the overlap is particularly meaningful because of the drastically different approaches by which these data sets were created.

DISCUSSION

We have shown how a hierarchical Beta-Binomial model can be used to adequately reflect uncertainty in quantitative multiplexed proteomics measurements. We presented the method and the implementation of a modeling pipeline which can assign confidence for both an individual peptide and multiple peptide proteomic measurements. We demonstrated how to estimate a calibration multiplier for a given instrument and mass resolution and then use that multiplier to convert a continuous MS-signal value into event counts suitable for Beta-Binomial modeling. Although we demonstrate our approach in this paper for two condition scenarios, the entire framework can also be applied to multicondition cases using Dirichlet-Multinomial distribution. We validated our approach on the peptide and protein levels in synthetic samples for which we knew the true answer (Fig. 2, 6). To evaluate BACIQ in a real-world scenario we re-analyzed a previously published dataset of subcellular localization movement on inhibition of Exportin-1 with Leptomycin B. Without having to perform any additional experiments we increased the number of highly confident Exportin-1 substrates by ∼2×. The mathematically rigorous integration of ion-statistics with concordance among different peptide measurements mapped to the same protein allowed us to confidently identify movement of some proteins by ∼1% toward the nucleus as significant at 5% FDR. The comparison with resources from other groups allowed us to independently validate this approach (45, 46) and points toward an emerging consensus on Exportin-1 substrates.

So far, we have only tested the BACIQ approach for data acquired with TMT-MS3 and TMTc+. We expect that with some adaptations BACIQ might be adequate for MS1-based labeled quantitative proteomics methods like SILAC or reductive methylation (47, 48). The systematic error associated with MS2-based multiplexed measurements will lead to inadequate confidence intervals for the underlying true protein ratios (11). Nevertheless, despite these erroneous measurements, we suspect that BACIQ could still be useful for the prioritization of systematic changes in an experiment. Although TMT-MS3 methods mitigate these systematic errors to some extent, the measurements still are distorted toward a 1:1 ratio. Additionally, the proteomics data suffers from errors in peptide identifications, which directly impacts the quantification. There have been various attempts to model these errors (49, 50). Bayesian methods provide a natural framework to integrate the above sources of errors and expand the model. In summary, we anticipate that our new statistical tool, BACIQ will be highly valuable for researchers wanting to identify significant changes in proteomics studies and help to optimize the allocation of valuable resources for follow up studies.

Data Availability

The mass spectrometry proteomics data have been deposited to the Proteome-Xchange Consortium via the PRIDE (35) partner repository with the dataset identifier PXD012285. It can be accessed using: https://www.ebi.ac.uk/pride/archive/.