Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Sep 16;4(14):15956–15965. doi: 10.1021/acsomega.9b01997

OnionNet: a Multiple-Layer Intermolecular-Contact-Based Convolutional Neural Network for Protein–Ligand Binding Affinity Prediction

Liangzhen Zheng 1, Jingrong Fan 1, Yuguang Mu 1,*
PMCID: PMC6776976  PMID: 31592466

Abstract

graphic file with name ao9b01997_0006.jpg

Computational drug discovery provides an efficient tool for helping large-scale lead molecule screening. One of the major tasks of lead discovery is identifying molecules with promising binding affinities toward a target, a protein in general. The accuracies of current scoring functions that are used to predict the binding affinity are not satisfactory enough. Thus, machine learning or deep learning based methods have been developed recently to improve the scoring functions. In this study, a deep convolutional neural network model (called OnionNet) is introduced; its features are based on rotation-free element-pair-specific contacts between ligands and protein atoms, and the contacts are further grouped into different distance ranges to cover both the local and nonlocal interaction information between the ligand and the protein. The prediction power of the model is evaluated and compared with other scoring functions using the comparative assessment of scoring functions (CASF-2013) benchmark and the v2016 core set of the PDBbind database. The robustness of the model is further explored by predicting the binding affinities of the complexes generated from docking simulations instead of experimentally determined PDB structures.

1. Introduction

High binding affinity between a small molecule or a short peptide and a receptor protein is one of the major selecting criteria in drug discovery.1 Although the binding affinity could be measured directly through experimental methods, the time cost and financial expenses are extremely high. Therefore, there is an urgent need to develop accurate computational binding affinity prediction models. Several computational methods have been developed to estimate the protein–ligand binding affinity.2,3 Given the three-dimensional (3D) structure of a protein–ligand complex, the binding free energy could be approximated through scoring functions or using the molecular mechanics Poisson–Boltzmann and surface area continuum solvation (MMPBSA) method and alchemy binding free energy estimation. It is well known that the scoring functions used for binding affinity estimation after a docking pose search are not accurate enough and result in a high false-positive rate.4 While the MMPBSA method5 could provide binding free energies, but not the absolute values, it outperforms the docking scoring functions in general, but it is more time-consuming. Finally, the alchemy binding free energy estimation6 is very accurate; however, it consumes extremely high computational resources, and thus, it is not suitable for large-scale binding energy estimation during virtual screening.

Generally, the negative logarithms (pKa) of the dissociation constants (Kd), half inhibition concentrations (IC50), and inhibition constants (Ki) were used to represent the experimentally determined binding affinities. Therefore, the performance of “scoring power” was evaluated majorly using two metrics: the Pearson correlation coefficients (R) between the experimental pKa and the predicted pKa, and the standard deviations (SD) of the regression.7 The performance of scoring functions has been thoroughly evaluated.7−9 Based on one of the most popular benchmarks, the comparative assessment of scoring functions v.2013 (CASF-2013, or PDBbind database v2013 core set), the accuracies of the most commonly used scoring functions7,8 were compared and evaluated. In addition, the prediction powers of the scoring functions implemented in two open-source docking packages (AutoDock and AutoDock Vina, respectively)9 were also assessed using the CASF-2103 benchmark. Among the scoring functions, X-Score, ChemScore, and ChemPLP show the best scoring power and “ranking power”, whereas the scoring function implemented in AutoDock Vina shows moderately good “ranking” power. The best scoring function, X-score, could achieve a SD = 1.78 and R = 0.61 with the CASF-2013 benchmark.7

In recent years, another category of predictors, machine learning (ML) based scoring functions or prediction models, has emerged as a type of fast and accurate binding affinity prediction method.10−18 The early examples such as RF-scores16 and NNScore15 generated ML models for binding affinity predictions. RF-score is a random-forest regression model constructed using the intermolecular interaction features. These two methods have been applied further to re-score the docking results in virtual screening for lead discovery.19,20

Different from traditional ML methods, deep convolutional neural networks (CNNs) are more powerful in the sense that they do not rely on experts for feature selections, which is very tricky.21−24 The nonlinear transformations of the raw dataset (the three-dimensional coordinates of the protein–ligand complex in this case) could uncover the hidden patterns in the data.21,22 It thus makes CNNs very suitable not only for image classifications, voice processing, and natural language processing but also for drug discovery.1,10−12,21,25 CNN models have been applied for assessing whether a specific molecule is a potential binder of a target.26−28 The performance of such classification models was quite sensitive to the selections of the negative samples (receptor–decoy complexes).29,30

Later, CNN models were adopted for binding affinity predictions,10−12,31 and have also been applied for virtual screening.20,32,33 For example, AtomNet26 and KDEEP17 both applied the deep convolutional neural network (CNN) model and took the vectorized grids within a cubic box centered at the ligand as the features for the protein–ligand complex, showing good performance for protein–ligand binding affinity predictions. Other features, such as the protein–ligand topological fingerprints, were also adopted for ML or CNN models.31,34

Taking CASF-2013 as the benchmark, one of the most accurate binding affinity prediction tools so far has been Pafnucy,12 which outperformed other methods in predicting binding affinity, given the three-dimensional protein–ligand complex structures. For the Pafnucy predictor, the chemical information within a box of size 20 Å × 20 Å × 20 Å centered on all ligand atoms was extracted at every 1 Å grid, resulting in a 21 × 21 × 21 × 19 high-dimensional dataset. Then the dataset was fed to a CNN model,35 and it achieved the best prediction performance (R = 0.7 and SD = 1.61) so far.

However, we realize that the interactions collected within the 20 × 20 × 20 grid box are rather localized around the ligand. It is well known that the electrostatic interactions, very important in protein–ligand and protein–peptide interactions, are long-range interactions36,37 and may not be fully accounted for in the cubic box of size 20 Å. Meanwhile, the features included in the grid box, such as the atomic partial charges, were calculated using empirical methods, such as AM1-BCC calculations.38,39 These features may not be very accurate and may give rise to noises in the model.

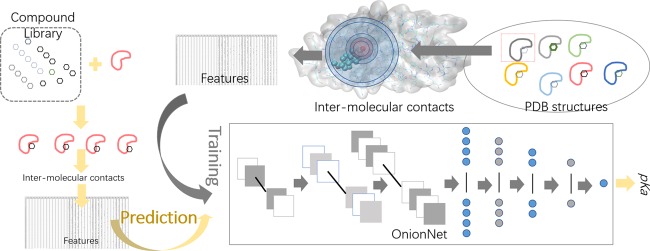
In this study, a different philosophy is applied: nonlocal protein–ligand interactions are included with minimum bias and noises. To further reduce the orientation biases induced by using features of direct 3D coordinates, element-specific contacts between proteins and ligands, which are internal coordinates and invariant under rotational operations, are considered in our model. Such element-specific intermolecular interaction features in a linear summation form have previously been adopted in the RF-score model.16 To account for both the local and nonlocal interactions, the contacts between the proteins and the ligands are grouped into different distance ranges. Such protein–ligand interaction features are named multiple-layer intermolecular features. We trained a CNN model (named “OnionNet” hereafter) with the PDBbind v2016 dataset40 as our benchmark and compared our results with the predictions of different scoring functions (described in the CASF-20137,8) and Pafnucy12 using the same stand-alone CASF-2013 dataset and PDBbind v2016 core set.7 Our OnionNet model achieves a root-mean-squared error (RMSE) of 1.278 and 1.503 for the 290 complexes from the PDBbind v2016 core set and 108 complexes from CASF-2013, respectively, and outperforms the RMSE of 1.42 and 1.69 obtained by Pafnucy. Consistently, the coefficients R of 0.812 and 0.786, higher than those of Pafnucy and another model reported by Indra Kundu et al.,13 are achieved by our model on these two benchmark datasets.

The robustness of our OnionNet model is tested by inputting predicted protein–ligand complex structures/poses using docking simulations. The outcoming predicted binding affinities are comparable to those fed with the experimentally determined PDB complex structures. The datasets, the OnionNet model file, and necessary preprocessing scripts could be found in the git repository at http://github.com/zhenglz/onionnet/. The codes could be freely modified according to GNU General Public License v3.

2. Results

The customized loss, RSME, and R were monitored during the training process of the OnionNet model. The best model was obtained with a minimal loss for the validating set at epoch = 89 (Supporting Information Figure S1). The prediction accuracy of the model was determined based on the following evaluation metrics: RMSE, SD, MAE, and R.

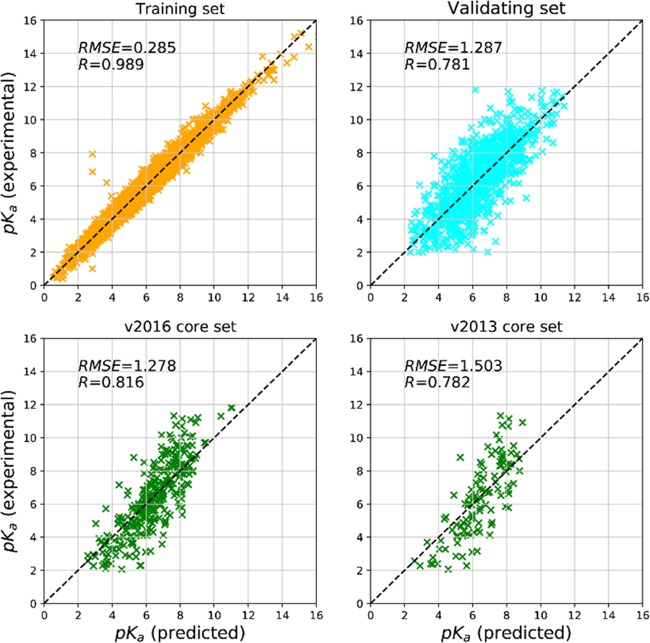
Our model achieves correlation coefficients higher than 0.7 and a relatively small RMSE (1.287, 1.278, and 1.503) on the validating set and two testing sets (Table 1). The predicted pKa and measured pKa are highly correlated for the two testing sets and validating set (Figure 1). The accumulated absolute error curves of the validating and testing sets suggest that ∼60 and ∼50% of the samples have a small deviation (∼1.0) of pKa from the measured pKa. The peak of the ΔRMSE distribution is around 0.4 and 0.7 for the validating and testing sets, respectively (Figure S2 in the Supporting Information).

Table 1. Performance of the OnionNet Model on Different Datasets.

dataset R RMSE MAE SD
training set 0.989 0.285 0.219 0.274
validating set 0.781 1.287 0.983 1.282
v2016 core set 0.816 1.278 0.984 1.257
v2013 core set 0.782 1.503 1.208 1.445
Open in a new tab

Figure 1.

Figure 1

Open in a new tab

Scatter plots of the OnionNet-predicted pKa against the experimentally measured pKa.

3. Discussion

3.1. Performance Comparison with Different Scoring Functions

Traditional ML models for protein–ligand binding classifications and binding affinity predictions heavily relied on the feature design and selections.41 The often-adopted protein–ligand binding fingerprints include 3D raw structural models and/or the amino acid sequences and ligand cheminformatics data, such as the atomic orbitals, hybridization states, atomic charges, and molecular topological information.11,12 Taking the atomic charge as an example, hybrid empirical methods, such as AM1-BCC charges, are usually adopted to calculate the “partial charge” of each atom without considering the solvent environment and dipole moments.12 In this study, we employed simple features without many hypothesis and estimations. The distance-based contacts and chemical element type of each atom (from both the protein and the ligand) are the only information considered. There are a few main advantages of using the distance-based contacts: (1) fewer features would be generated; (2) minimum bias or noise would be introduced; (3) large space around the ligand and both the local and nonlocal protein–ligand interactions would be taken into consideration; (4) they are internal coordinates and invariant under rotational operations.

The intuitive “simple” features, however, achieve similar performance to those of other complicated feature-based ML or CNN models (such as KDEEP, Pafnucy, RF-Score, and kNN-Score).10−13,17 Taking the PDBBind v2016 core set database as the testing set, our OnionNet model obtained very similar performance to KDEEP,17 a latest 3D-convolutional neural network model. The comparisons between the performances of the OnionNet model and other scoring functions are provided in Table 2. The ML- and CNN-based scoring functions (OnionNet, KDEEP, Pafnucy, RF-Score,42 and kNN-Score) achieve higher accuracies than the popular classic scoring functions (X-Score, ChemScore, ChemPLP, AutoDock Vina score, and AutoDock score). The OnionNet model obtained good correlations between the predicted pKa and the experimentally measured pKa. A very recent DNN-based AGL43 model applied multiscale weighted labeled algebraic subgraphs to describe the interaction between proteins and ligands. Thus, it may provide a more complete local environmental description than what we used in the current model that only pairwise contacts are counted. Not surprisingly, it shows better performance, with an RMSE of 1.271 and a Pearson’s correlation coefficient of 0.833, which indicates that adding novel features related to the essential physical and biological information really helps in improving the prediction power of the score functions. Meanwhile, our current model utilizes shell-like descriptors to catch the nonlocal interactions as well as the local interactions between proteins and ligands.

Table 2. Comparison of the Prediction Power of Scoring Functions with the Core Sets of PDBbind v2016 and v2013 Benchmarksa.

scoring functions RMSE R v201644
OnionNet 1.278 0.816  
KDeep17 1.27 0.82  
RF-Score-v317 1.39 0.80  
Pafnucy12 1.42 0.78  
AGL43 1.271 0.833  
scoring functions SD R v20137
OnionNet 1.45 0.78  
AGL43 1.45 0.792  
Pafnucy12 1.61 0.70  
RF-Score-v312 1.51 0.74  
kNN-Score14 1.65 0.672  
X-Score14 1.78 0.614  
ChemScore14 1.82 0.592  
ChemPLP14 1.84 0.579  
AutoDock Vina9 1.90 0.54  
AutoDock9 1.91 0.54  
Open in a new tab
a

Detailed training and test sets used are reported in Supporting Information Table S1.

To demonstrate the statistical reliability, our model has been independently trained for many times. The standard deviations of the R and RMSE values of our model are relatively small (Supporting Information Table S2). A t-test was performed by comparing the R values of our repeated runs with 0.7 (the R value of Pafnucy), assuming the null hypothesis: the average R value of our OnionNet model repeated runs is not higher than R = 0.7. The one-tail p-value of the t-test is around 9.8 × 10–25, meaning the null hypothesis can be rejected confidently. Thus, the reliability of the performance of our OnionNet model is statistically approved.

3.2. Feature Importance of the Element-type Combinations and “Shell” Location

An understanding of the influence of features on model performance is very important for further model optimization. However, neural networks have a reputation of being used as “black boxes”,45 i.e., the importance of the feature is “hidden” and not easy to dig out. Here, we tackle the problem by removing a set of specific features, re-training the model with the missing features in the original training and validating sets, and evaluating the performance loss due to the lack of that set of features (see the Supporting Information). A ΔLoss is defined as the difference between the loss of a model with missing features and the loss of the best model without missing features. The larger the ΔLoss, the higher the loss of the model with the missing features, and the more important those features.

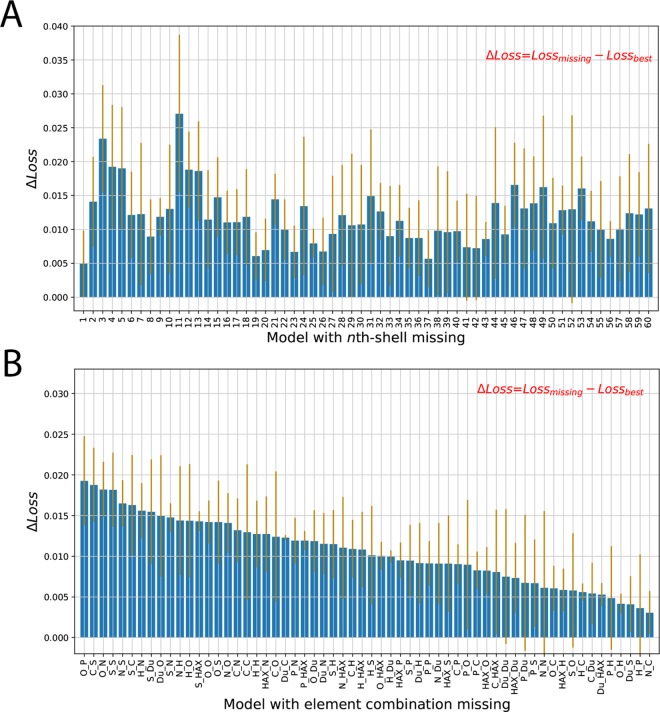
We first explored the stability of the model upon missing features in a specific layer of shells, as well as the importance of the features in this shell. From Figure 2A, the ligand proximal shells (with smaller shell indices, from 1 to 15) have relatively higher ΔLoss than the ligand distal shells (with larger shell indices, from 15 to 60). The larger ΔLoss, thus, suggests that the contributions from the ligand proximal shells are more important than the ligand distal shells. This finding is quite consistent with our intuition that local interactions, such as van der Waals interactions, are important. It is worth mentioning that the first shell is not the most important for the performance of the model, partially due to the fact that there are very few contacts in the first shell and some close steric crashes between the protein and the ligand will harm the interaction. The highest peak is around shell 11 (5.5–6 Å), indicating that the medium-range interactions contribute to the performance of the model significantly. Interestingly, some distal shells, such as 46, 49, and 53 (23–27 Å), also have large contributions, which demonstrates the importance of the nonlocal interactions.

Figure 2.

Figure 2

Open in a new tab

Performance change (ΔLoss) due to missing features: (A) missing 64 features in a specific shell around the ligand; (B) missing a set of 60 features, with the same element-type combination missed in each one of the 60 “shells”. The performance change is defined as the difference between the loss of the model with missing features and the loss of the best model. The orange bars indicate the standard deviations of the ΔLoss for five independent runs.

Furthermore, we explore the feature importance of different element-pair combinations. We iteratively removed 1 type of element-pair combination (out of 64) and then quantified the performance change due to the missing of a set of 60 features (1 feature per shell). The most important element-pair combination is “O_P”, which is mostly involved in strong electrostatic interactions (Figure 2B). Next, “C_S” is another important element-pair combination, which is involved in hydrophobic interactions. And the contacts of protein oxygen and sulfur atoms with ligand nitrogen, sulfur, or phosphorus atoms also play important roles, whereas the interactions between protein carbon atoms and ligand hydrogen have minor contributions. The enrichment of sulfur- and phosphate-related element combinations possibly emphasizes the importance of the less common elements as the “signposts” for input information extraction. On the other hand, the missing of one element-pair combination or one shell of contact interactions does not cause great decreases in the performance of the model, which indicates the stability of this model.

3.3. Robustness of the Binding Affinity Prediction Model

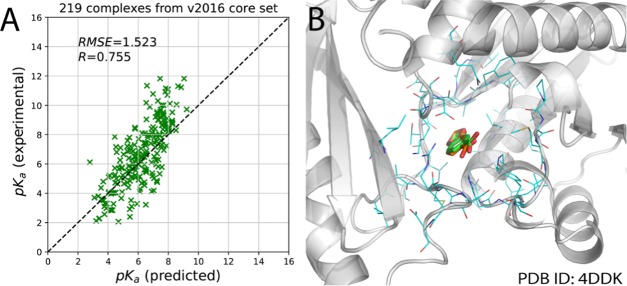
It is well known that some classifiers (such as decision tree and deep neural networks) are quite sensitive to the input training data, and small changes in the training samples would cause great accuracy loss.46−48 Thus, there is a risk that training only with the experimental structures may render the model less able to achieve accurate binding affinity prediction when the protein–ligand complex structures are generated from docking simulations; in other words, the robustness of the model may be questionable. To further explore the robustness of the OnionNet model, we directly applied our model to predict the binding affinity of the docking poses for a small set of protein–ligand complexes (Supporting Information). Docking packages (such as AutoDock Vina) could produce some binding poses with small RMSDs. If the RMSD between the docking pose and the native conformation is less than 2 Å, the docking pose is called the native-like binding pose (Figure 3). In total, 219 out of 290 docked complexes in the PDBbind v2016 core set benchmark were selected for pKa prediction, and the R and SD values of the predicted pKa against the true pKa of this set of complexes are 0.755 and 1.523, respectively (Figure 3A). The performance of the OnionNet model with the inputs from the native-like docking poses is slightly worse than the results obtained directly from the crystal or NMR structures. Taking pantothenate synthetase (PDB ID: 4DDK)49 as an example, its ligand 1,3-benzodioxole-5-carboxylic acid (0HN) was extracted from the protein pocket and re-docked back into the pocket using AutoDock Vina, and a small RMSD of 0.569 Å was achieved between the best pose and the native pose of the ligand (Figure 3B). And the binding affinity (pKa) of the native pose is 2.29, whereas with OnionNet, the predicted binding affinity based on the crystal structure and the “native-like” pose is 3.436 and 3.421, respectively. Thus, the OnionNet model is found to be robust and insensitive to the small variations of the ligand binding poses. Our finding here also supports a previous study in which it is reported that using docking-generated structures in the training of a machine learning model could even enhance the prediction power of that model.50

Figure 3.

Figure 3

Open in a new tab

Scatter plots of the predicted pKa against the experimentally determined pKa for the selected complexes from the v2016 core set (A) and an alignment of a re-docked native-like pose with its native pose (B). The carbon atoms in the native and native-like “good” poses for the ligand are in orange and green, respectively, whereas the oxygen and nitrogen atoms are in red and blue.

4. Conclusions

To accurately predict the binding affinity between the molecule and the target is one of the most important steps in structure-based drug design. To improve ligand binding affinity prediction, we came up with an OnionNet model, which is based on simple but powerful multiple-layer intermolecular contact features. The OnionNet model achieves very good performance (R = 0.78 and RMSE =1.503) in comparison with the current deep learning (DL)-based and classic scoring functions using the CASF-2013 dataset as the benchmark. The stability and robustness of the model were verified through re-training with missing features and predicting the binding affinity on the docking poses. Further improvement of the model would make it suitable for general lead discovery tasks.

5. Computational Methods

5.1. Featurization of Protein–Ligand Complexes

The intermolecular interaction information was extracted from the 3D structures of protein–ligand complexes (Figure 4). First, we defined a series of boundaries around each atom of the ligand, and the space between boundary k – 1 and boundary k, thus, forms a shell with a thickness of δ. If k = 1, the distance between the atom in the ligand and the nearest point of the boundary is d0, and for boundary k (when 2 ≤ k ≤ N), the minimal distance between the ligand atom and the boundary is (k – 1)δ + d0.

Figure 4.

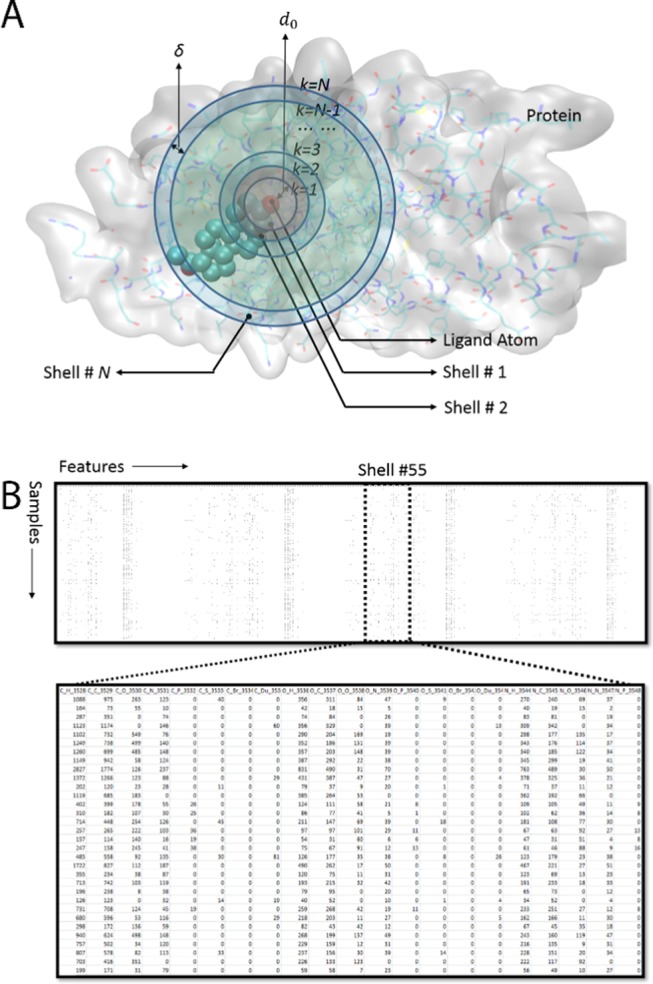
Figure 4

Open in a new tab

Featurization of the protein–ligand complexes based on contact numbers in protein–ligand interaction shells. (A) Definition of the “shell-like” partitioning of the protein around the ligand in the three-dimensional space; PDB ID 1A28 is used as an example here. (B) Glimpse of the features of the contact numbers. The features are presented column-wise, whereas the samples are presented row-wise; each row is the information we extracted from one protein–ligand complex, and one column contains a specific feature calculated from all samples.

Second, the element-pair-specific contact numbers are calculated for the ligand atoms and the protein atoms in each of the N shells. In the original RF-score paper,16 9 different elements were considered, and 1 single distance cutoff (1.2 nm) was used, thus it resulted in totally 81 features. The rationale behind this research seemed quite straightforward and simple, but the RF-score still achieved the state-of-the-art performance at that time. However, we further considered the possibility of choosing different distance cutoffs to include both the short-range and long-range element-specific interactions.

Here, in this study, we select eight element types (EL), C, N, O, H, P, S, HAX, and Du (Dummy, representing all remaining elements) to quantify the contact types between atoms in ligands and proteins. Here, HAX represents any one of the four halogen elements F, Cl, Br, and I. Although P, HAX, and Du may not exist in normal proteins, we keep the elements to maintain the generalization ability of the model. For example, in future, we may incorporate the scoring function to guide the molecular simulations of the ligand binding to the protein with phosphorylation or other types of modifications.

For shell n (between boundaries k = n – 1 and k = n, 1 ≤ n ≤ N), 64 features (considering all possible combinations of elements in a ligand and its target) are used to present the intermolecular interaction information between the ligand and the protein atoms.

5.1.
5.1.

For any element-pair combination ECTs,Tt, the contact number is the summation of contacts between atom r in shell k of the protein (with element type Ts) and atom l in the ligand (with element type Tt), whereas Rn,Ts is the total number of atoms whose element type is Ts, and LTt is the total ligand atom number for type Tt. The contact number between atom r and l is 1 if the distance dr,l between them is within the range (k – 2)δ + d0 ≤ dr,l < (k – 1)δ + d0, otherwise 0.

For example, in shell n (between boundary k and k – 1), the value of the element pair “C_C” (ECTs,Tt, Ts = “C”, Tt = “C”) is the contact number of protein–ligand carbon atom pairs within the distance cutoff ranging from d = (k – 2) δ + d0 to d = (k – 1)δ + d0.

In this study, we define N = 60 shells with d0 = 1.0 Å and δ = 0.5 Å. The distance from the farthest boundary (k = 60) to the atoms in the ligand is 30.5 Å. It, thus, results in 3840 features, considering both local and nonlocal interactions between the protein and the ligand. If converted to a grid box as in Pafnucy,12 the size will be more than 61 Å × 61 Å × 61 Å, 27 times larger than the one used in Pafnucy.

5.2. Dataset Preparation

The OnionNet model was trained and tested with the protein–ligand three-dimensional structures and binding affinities from the updated PDBbind database v201644 (http://www.pdbbind.org.cn/) (Figure 5), which was also used by the Pafnucy model. We adopted the same procedure as in the Pafnucy model. The model was trained with the training set and the validating set, while two testing sets were generated for performance evaluation of the model.

Figure 5.

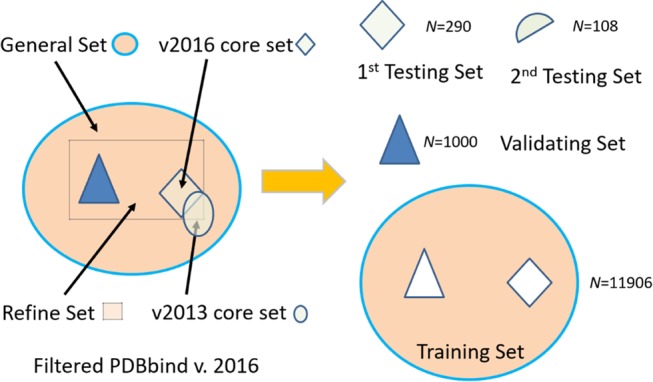
Figure 5

Open in a new tab

Datasets used in the model. The original PDBbind v.2016 dataset was filtered to keep only the protein–ligand complexes, with measured Ki or Kd binding affinities. The remaining filtered dataset was thus divided into three disjoint datasets for training, testing, and validation. However, two overlapping testing sets were used to compare the performance of our model with other scoring functions. The numbers of protein–ligand complexes are labeled in each set in the figure.

There are three overlapping subsets in the original PDBbind v2016 dataset: the core set, the refined set, and the general set. The refined set contains the refined protein–ligand complexes with high-quality binding affinity measurements. The general set contains all protein–ligand complexes of the PDBbind dataset v2016. First, we extracted all 290 complexes in the v2016 core set and assigned them into the first test set. Then for the remaining complexes in the v2016 refined set, 1000 complexes were randomly selected and used as the validating set. Finally, the remaining 11 906 complexes in the v2016 general set (by removing all complexes in the first test set and the validating set) were adopted for the training set.

The core set (v2013), or the CASF-2013 benchmark, a subset of the PDBbind database v2013, which was selected by Li et al.,7 selects PDB complexes after clustering and is primarily used for validating docking scoring function and the CADD benchmark. To compare the performance of our model with other scoring functions conveniently, we prepared a second test set containing 108 complexes from the v2013 core set by removing the overlapping complexes adopted in the validating and training sets. The second test set (called the v2013 core set hereafter) is found to be the subset of the v2016 core set (first test set).

Before protein–ligand complex featurization, we ignored all water molecules and ions. The ligand structures (in mol2 format) were converted to PDB format and combined with the receptor PDB file. To be consistent with previous studies, no further modifications were made to the protein–ligand complexes. A protein–ligand complex structure was first treated by mdtraj51 and the element types of each atoms were thus determined, and the contact numbers were calculated, as described in the previous section.

To predict the binding affinity, it is a general practice to transform Ki and Kd into the negative log form to train the ML models.12 In the PDBbind v2016 dataset, the binding affinities of protein–ligand complexes were provided in Ki, Kd, and IC50. We transformed the binding affinities into pKa using the following equation:

5.2.

where Kx represents IC50, Ki, or Kd.

Besides using PDB structures, 219 poses with a native-like structure (RMSD with respect to the native PDB structure was less than 2 Å), generated using vina docking software, were prepared for model robustness evaluation. The detailed procedures for the docking and pose selections are described in the Supporting Information (Part 4).

5.3. Deep Neural Network Model

A modified deep convolutional neural network (CNN) was constructed. The architecture of the network is summarized in Figure 6.

Figure 6.

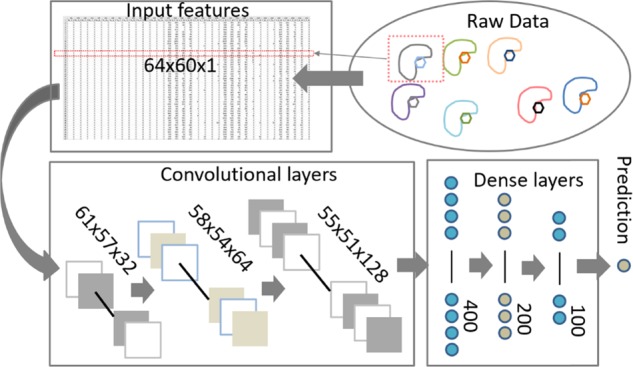
Figure 6

Open in a new tab

Workflow of the protein–ligand binding affinity prediction with the OnionNet model.

For each protein–ligand complex, the 3D interaction information is converted into a two-dimensional (2D) tensor to mimic a picture with only one color channel. The input features are thus fed into the three-layer convolutional layers, the results are thus flattened and passed to four dense layers, and outputs of the last dense layer are transferred to the last layer, the output layer, for pKa prediction.

The input numerical dataset has 3840 features, which were reshaped to a (64, 60, 1) matrix to mimic an image dataset with only one channel. A sequential model was initialized and followed by 3 two-dimensional convolutional layers. We tried one-dimensional convolutional networks, and the performance is worse than the 2D convolutional models. Regarding the reasons for the best performance of the CNN model, we believed that the Y-axis (the different distance-range-based shells) has an intrinsic relationship with the X-axis (atom pairs); for example, favorable interactions, such as hydrogen bonds and salt bridges, always require a certain atom pair within a certain distance range. CNN may be able to capture such local connections. See more discussions in the Supporting Information Table S2.

For the OnionNet model (mCNN-01 in the Supporting Information), there were 32, 64, and 128 filters in the three convolutional layers, and the kernel sizes were all set as 4, with strides as 1. No pooling layers were attached to the three convolutional layers. The results of the last convolutional layer were flattened and passed to the following four dense layers with 400, 200, and 100 units. Finally, an output layer was attached with only 1 neuron to generate the predicted pKa. Several different CNN models have been explored (Supporting Information), and the above-mentioned model achieves the best performance.

A customized loss function was defined to train the model better. During the training of our CNN models, instead of using the default mean-squared error (MSE) as the loss function, we designed a new customized loss function to optimize

5.3.

where R and RMSE are the correlation coefficient and root-mean-squared error, respectively, and α is a tunable parameter with positive and less than 1 value. In this study, α = 0.8 is used. The rationale is that both high correlation and low root-mean-squared error are the training target. We found that when α = 1.0, the loss function being only determined by R, the model has a high R value but with a high RMSE value as well. The detailed selection of α is described in the Supporting Information.

The kernel sizes were 4, and the stride was 1, and no padding was applied in the convolutional layers. For both the convolutional layers and dense layers, a rectified linear units (ReLU) activation function was adopted.52 This ReLU function is a fast yet powerful activation function, which has been used in a lot of other deep learning models.53 ReLU was also applied after the convolutional layers and the dense layers (not including the output layer). A stochastic gradient descent (SGD) optimizer was chosen to search for optimal weights in the model.22,23 The learning rate was set as 0.01 with a decay constant 10e–6 and a momentum of 0.9. Another optimizer, Adam, an extension of the SGD optimizer, was also tested, but it made the loss decay very slowly. The batch size (=128) for training was carefully selected (Supporting Information Table S2). Training with small batch sizes rendered the decay of the model’s loss faster but induced overfitting issues.54 Batch normalization was added to each layer except for the last output layer.55 L2 regularization was added to the convolutional layers and dense layers to handle the overfitting problem. The λ parameter was 0.001, a commonly used value to have a reasonable level of regularization. We screened the optimal dropout probabilities and found that a 0.0 probability in our model achieved the highest prediction accuracy and quick convergence using the validating set, probably because of the use of batch normalization. Therefore, we did not apply the dropout to the model (with dropout rate = 0.0). An early stopping strategy was adopted to avoid overfitting issues by holding the training when the change in the validating set loss was smaller than 0.01 after a certain number of epochs (Nunchange = 40) (Supporting Information). The training of the models was based on Keras56 with Tensorflow57 as backend.

5.4. Evaluation Metrics

Several evaluation metrics were used to assess the model accuracy including RMSE, which quantifies the relative deviations of the predicted values from the experimentally determined values by summing up all squared residuals for each of the samples and dividing by the number of samples and then computing the square root to have the same physical unit as the original variable (pKa in this study).

5.4.

We also calculated another metric, standard deviation (SD) of the regression, which was also adopted in the CASF-2013 benchmark7 and Pafnucy.12

5.4.

where a and b are the slope and interception of the linear regression line of the predicted and measured pKa data points.

Mean absolute error (MAE) is another useful evaluation measurement. Different from RMSE, MAE is the average of the summed absolute differences of the prediction values to the real values.

5.4.

And finally, R was another evaluation metric. It is generally introduced to estimate the correlation relationship between two variables; therefore, the predicted pKa and the real pKa in this research.

5.4.

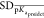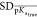where Inline graphic and Inline graphic are the standard deviations of the predicted pKa and the real pKa. The bar notation indicates the mean value of pKa.

Acknowledgments

This research was supported by MOE Tier 1 Grant RG146/17. The computing facility was supported by the National Supercomputing Centre, Singapore (https://www.nscc.sg).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01997.

  • Model training; customized loss function; model training with missing features; predicting pKa of the native-like docking poses; HIV protease docking and re-scoring; training sets of the score functions in the main text (Table 2; Table S1) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b01997_si_001.pdf (311.1KB, pdf)

References

  1. Wang C.; Zhang Y. Improving scoring-docking-screening powers of protein–ligand scoring functions using random forest. J. Comput. Chem. 2017, 38, 169–177. 10.1002/jcc.24667. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Sliwoski G.; Kothiwale S.; Meiler J.; Lowe E. W. Computational methods in drug discovery. Pharmacol. Rev. 2014, 66, 334–395. 10.1124/pr.112.007336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ou-Yang S.-s.; Lu J.-y.; Kong X.-q.; Liang Z.-j.; Luo C.; Jiang H. Computational drug discovery. Acta Pharmacol. Sin. 2012, 33, 1131–1140. 10.1038/aps.2012.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jain A. N. Bias, reporting, and sharing: computational evaluations of docking methods. J. Comput.-Aided Mol. Des. 2008, 22, 201–212. 10.1007/s10822-007-9151-x. [DOI] [PubMed] [Google Scholar]
  5. Genheden S.; Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Helms V.; Wade R. C. Computational alchemy to calculate absolute protein–ligand binding free energy. J. Am. Chem. Soc. 1998, 120, 2710–2713. 10.1021/ja9738539. [DOI] [Google Scholar]
  7. Li Y.; Han L.; Liu Z.; Wang R. Comparative assessment of scoring functions on an updated benchmark: 2. Evaluation methods and general results. J. Chem. Inf. Model. 2014, 54, 1717–1736. 10.1021/ci500081m. [DOI] [PubMed] [Google Scholar]
  8. Li Y.; Su M.; Liu Z.; Li J.; Liu J.; Han L.; Wang R. Assessing protein–ligand interaction scoring functions with the CASF-2013 benchmark. Nat. Protoc. 2018, 13, 666–680. 10.1038/nprot.2017.114. [DOI] [PubMed] [Google Scholar]
  9. Gaillard T. Evaluation of AutoDock and AutoDock Vina on the CASF-2013 benchmark. J. Chem. Inf. Model. 2018, 58, 1697–1706. 10.1021/acs.jcim.8b00312. [DOI] [PubMed] [Google Scholar]
  10. Gomes J.; Ramsundar B.; Feinberg E. N.; Pande V. S.. Atomic convolutional networks for predicting protein-ligand binding affinity, arXiv preprint arXiv:1703.10603. arXiv.org e-Print archive. https://arxiv.org/abs/1703.10603 (submitted March 30, 2017).
  11. Öztürk H.; Ozkirimli E.; Özgür A.. DeepDTA: Deep Drug-Target Binding Affinity Prediction, arXiv preprint arXiv:1801.10193. arXiv.org e-Print archive. https://arxiv.org/pdf/1801.10193.pdf (submitted July 5, 2018). [DOI] [PMC free article] [PubMed]
  12. Stepniewska-Dziubinska M. M.; Zielenkiewicz P.; Siedlecki P. Development and evaluation of a deep learning model for protein-ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. 10.1093/bioinformatics/bty374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kundu I.; Paul G.; Banerjee R. A machine learning approach towards the prediction of protein–ligand binding affinity based on fundamental molecular properties. RSC Adv. 2018, 8, 12127–12137. 10.1039/C8RA00003D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Khamis M. A.; Gomaa W. Comparative assessment of machine-learning scoring functions on PDBbind 2013. Eng. Appl. Artif. Intell. 2015, 45, 136–151. 10.1016/j.engappai.2015.06.021. [DOI] [Google Scholar]
  15. Durrant J. D.; McCammon J. A. NNScore: a neural-network-based scoring function for the characterization of protein–ligand complexes. J. Chem. Inf. Model. 2010, 50, 1865–1871. 10.1021/ci100244v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Ballester P. J.; Mitchell J. B. A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. 10.1093/bioinformatics/btq112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Jiménez J.; Skalic M.; Martínez-Rosell G.; De Fabritiis G. KDEEP: Protein–Ligand Absolute Binding Affinity Prediction via 3D-Convolutional Neural Networks. J. Chem. Inf. Model. 2018, 58, 287–296. 10.1021/acs.jcim.7b00650. [DOI] [PubMed] [Google Scholar]
  18. Feinberg E. N.; Sur D.; Wu Z.; Husic B. E.; Mai H.; Li Y.; Sun S.; Yang J.; Ramsundar B.; Pande V. S.. PotentialNet for Molecular Property Prediction, arXiv preprintarXiv:1803.04465. arXiv.org e-Print archive. https://arxiv.org/abs/1803.04465 (submitted March 12, 2018). [DOI] [PMC free article] [PubMed]
  19. Ballester P. J.; Mangold M.; Howard N. I.; Robinson R. L. M.; Abell C.; Blumberger J.; Mitchell J. B. Hierarchical virtual screening for the discovery of new molecular scaffolds in antibacterial hit identification. J. R. Soc., Interface 2012, 9, 3196–3207. 10.1098/rsif.2012.0569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Wójcikowski M.; Zielenkiewicz P.; Siedlecki P. Open Drug Discovery Toolkit (ODDT): a new open-source player in the drug discovery field. J. Cheminf. 2015, 7, 26 10.1186/s13321-015-0078-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Angermueller C.; Pärnamaa T.; Parts L.; Stegle O. Deep Learning for Computational Biology. Mol. Syst. Biol. 2016, 12, 878. 10.15252/msb.20156651. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. LeCun Y.; Bengio Y.; Hinton G. Deep learning. Nature 2015, 521, 436–444. 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
  23. Goodfellow I.; Bengio Y.; Courville A.. Deep Learning; MIT Press, 2016. [Google Scholar]
  24. Schmidhuber J. Deep learning in neural networks: An overview. Neural Networks 2015, 61, 85–117. 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
  25. Gawehn E.; Hiss J. A.; Schneider G. Deep learning in drug discovery. Mol. Inf. 2016, 35, 3–14. 10.1002/minf.201501008. [DOI] [PubMed] [Google Scholar]
  26. Wallach I.; Dzamba M.; Heifets A.. AtomNet: a Deep Convolutional Neural Network for Bioactivity Prediction in Structure-based Drug Discovery, arXiv preprint arXiv:1510.02855. arXiv.org e-Print archive. https://arxiv.org/abs/1510.02855 (submitted Oct 10, 2015).
  27. Wen M.; Zhang Z.; Niu S.; Sha H.; Yang R.; Yun Y.; Lu H. Deep-learning-based drug–target interaction prediction. J. Proteome Res. 2017, 16, 1401–1409. 10.1021/acs.jproteome.6b00618. [DOI] [PubMed] [Google Scholar]
  28. Zhang H.; Liao L.; Cai Y.; Hu Y.; Wang H. IVS2vec: A tool of Inverse Virtual Screening based on word2vec and deep learning techniques. Methods 2019, 166, 57–65. 10.1016/j.ymeth.2019.03.012. [DOI] [PubMed] [Google Scholar]
  29. Lim J.; Ryu S.; Park K.; Choe Y. J.; Ham J.; Kim W. Y.. Predicting Drug-target Interaction using 3D Structure-embedded Graph Representations from Graph Neural Networks, arXiv preprint arXiv:1904.08144. arXiv.org e-Print archive. https://arxiv.org/pdf/1904.08144.pdf (submitted April 17, 2019). [DOI] [PubMed]
  30. Ryu S.; Kwon Y.; Kim W. Y.. Uncertainty Quantification of Molecular Property Prediction with Bayesian Neural networks, arXiv preprint arXiv:1903.08375. arXiv.org e-Print archive. https://arxiv.org/abs/1903.08375 (submitted March 20, 2019). [Google Scholar]
  31. Cang Z.; Wei G.-W. TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. PLoS Comput. Biol. 2017, 13, e1005690 10.1371/journal.pcbi.1005690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Imrie F.; Bradley A. R.; van der Schaar M.; Deane C. M. Protein Family-Specific Models Using Deep Neural Networks and Transfer Learning Improve Virtual Screening and Highlight the Need for More Data. J. Chem. Inf. Model. 2018, 58, 2319–2330. 10.1021/acs.jcim.8b00350. [DOI] [PubMed] [Google Scholar]
  33. Tsubaki M.; Tomii K.; Sese J. Compound–protein interaction prediction with end-to-end learning of neural networks for graphs and sequences. Bioinformatics 2019, 35, 309–318. 10.1093/bioinformatics/bty535. [DOI] [PubMed] [Google Scholar]
  34. Cang Z.; Wei G. W. Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction. Int. J. Numer. Meth. Biomed. Eng. 2018, 34, e2914 10.1002/cnm.2914. [DOI] [PubMed] [Google Scholar]
  35. LeCun Y.; Bengio Y.. Convolutional Networks for Images, Speech, and Time Series. The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, 1995; Vol. 3361, pp 255–258. [Google Scholar]
  36. Dagliyan O.; Proctor E. A.; D’Auria K. M.; Ding F.; Dokholyan N. V. Structural and dynamic determinants of protein-peptide recognition. Structure 2011, 19, 1837–1845. 10.1016/j.str.2011.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Leckband D.; Israelachvili J.; Schmitt F.; Knoll W. Long-range attraction and molecular rearrangements in receptor-ligand interactions. Science 1992, 255, 1419–1421. 10.1126/science.1542789. [DOI] [PubMed] [Google Scholar]
  38. Mukherjee G.; Patra N.; Barua P.; Jayaram B. A fast empirical GAFF compatible partial atomic charge assignment scheme for modeling interactions of small molecules with biomolecular targets. J. Comput. Chem. 2011, 32, 893–907. 10.1002/jcc.21671. [DOI] [PubMed] [Google Scholar]
  39. Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
  40. Wang R.; Fang X.; Lu Y.; Wang S. The PDBbind database: Collection of binding affinities for protein–ligand complexes with known three-dimensional structures. J. Med. Chem. 2004, 47, 2977–2980. 10.1021/jm030580l. [DOI] [PubMed] [Google Scholar]
  41. Deng W.; Breneman C.; Embrechts M. J. Predicting protein–ligand binding affinities using novel geometrical descriptors and machine-learning methods. J. Chem. Inf. Comput. Sci. 2004, 44, 699–703. 10.1021/ci034246+. [DOI] [PubMed] [Google Scholar]
  42. Li H.; Leung K.-S.; Wong M.-H.; Ballester P. J. Improving AutoDock Vina Using Random Forest: The Growing Accuracy of Binding Affinity Prediction by the Effective Exploitation of Larger Data Sets. Mol. Inf. 2015, 34, 115–126. 10.1002/minf.201400132. [DOI] [PubMed] [Google Scholar]
  43. Nguyen D. D.; Wei G.-W. AGL-Score: Algebraic Graph Learning Score for Protein–Ligand Binding Scoring, Ranking, Docking, and Screening. J. Chem. Inf. Model. 2019, 59, 3291–3304. 10.1021/acs.jcim.9b00334. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Liu Z.; Su M.; Han L.; Liu J.; Yang Q.; Li Y.; Wang R. Forging the Basis for Developing Protein–Ligand Interaction Scoring Functions. Acc. Chem. Res. 2017, 50, 302–309. 10.1021/acs.accounts.6b00491. [DOI] [PubMed] [Google Scholar]
  45. Alain G.; Bengio Y., Understanding Intermediate Layers using Linear Classifier Probes, arXiv preprint arXiv:1610.01644. arXiv.org e-Print archive. https://arxiv.org/abs/1610.01644 (submitted Oct 5, 2016).
  46. Dietterich T. G.Ensemble Methods in Machine Learning, International Workshop on Multiple Classifier Systems, 2000, Part of the Lecture Notes in Computer Science Book Series. Springer, 2000; pp 1–15.
  47. Lavecchia A. Machine-learning approaches in drug discovery: methods and applications. Drug Discovery Today 2015, 20, 318–331. 10.1016/j.drudis.2014.10.012. [DOI] [PubMed] [Google Scholar]
  48. McCann M. T.; Jin K. H.; Unser M.. A Review of Convolutional Neural Networks for Inverse Problems in Imaging, arXiv preprint arXiv:1710.04011. arXiv.org e-Print archive. https://arxiv.org/abs/1710.04011 (submitted Oct 11, 2017).
  49. Newman J.; Seabrook S.; Surjadi R.; Williams C. C.; Lucent D.; Wilding M.; Scott C.; Peat T. S. Determination of the structure of the catabolic N-succinylornithine transaminase (AstC) from Escherichia coli. PLoS One 2013, 8, e58298 10.1371/journal.pone.0058298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Li H.; Leung K.-S.; Wong M.-H.; Ballester P. J. Correcting the impact of docking pose generation error on binding affinity prediction. BMC Bioinf. 2016, 17, 308 10.1186/s12859-016-1169-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. McGibbon R. T.; Beauchamp K. A.; Harrigan M. P.; Klein C.; Swails J. M.; Hernández C. X.; Schwantes C. R.; Wang L.-P.; Lane T. J.; Pande V. S. MDTraj: a modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 2015, 109, 1528–1532. 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Nair V.; Hinton G. E. In Rectified Linear Units Improve Restricted Boltzmann Machines, Proceedings of the 27th International Conference on Machine Learning (ICML-10), 2010; pp 807–814.
  53. Ramachandran P.; Zoph B.; Le Q. V.. Searching for Activation Functions, arXiv preprint arXiv:1710.05941. arXiv.org e-Print archive. https://arxiv.org/abs/1710.05941 (submitted Oct 16, 2017).
  54. Keskar N. S.; Mudigere D.; Nocedal J.; Smelyanskiy M.; Tang P. T. P., On large-batch training for deep learning: Generalization gap and sharp minima, arXiv preprint arXiv:1609.04836. arXiv.org e-Print archive. https://arxiv.org/abs/1609.04836 (submitted Sept 15, 2016).
  55. Ioffe S.; Szegedy C.. Batch normalization: Accelerating deep network training by reducing internal covariate shift, arXiv preprint arXiv:1502.03167. arXiv.org e-Print archive. https://arxiv.org/abs/1609.04836 (submitted Sept 15, 2016).
  56. Chollet F. Keras. https://keras.io
  57. Abadi M.; Barham P.; Chen J.; Chen Z.; Davis A.; Dean J.; Devin M.; Ghemawat S.; Irving G.; Isard M. In Tensorflow: A system for large-scale machine learning. OSDI’16 Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation,Keeton K.USENIX Association: Berkeley, CA; 2016; pp 265–283.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b01997_si_001.pdf (311.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES