Abstract
The present study aims to compare the robustness under various conditions of latent class analysis mixture modeling approaches that deal with auxiliary distal outcomes. Monte Carlo simulations were employed to test the performance of four approaches recommended by previous simulation studies: maximum likelihood (ML) assuming homoskedasticity (ML_E), ML assuming heteroskedasticity (ML_U), BCH, and LTB. For all investigated simulation conditions, the BCH approach yielded the most unbiased estimates of class-specific distal outcome means. This study has implications for researchers looking to apply recommended latent class analysis mixture modeling approaches in that nonnormality, which has been not fully considered in previous studies, was taken into account to address the distributional form of distal outcomes.
Keywords: latent class analysis, Monte Carlo simulation, distal outcome
Finite mixture modeling (McLachlan & Peel, 2004), in particular latent class analysis (LCA; Collins & Lanza 2010; Goodman, 1974; Lazarsfeld & Henry, 1968), has been employed by applied researchers from a diverse range of fields to analyze populations containing unobservable or underlying latent subgroups defined by multifaceted individual-specific observed characteristics. Investigating unobserved heterogeneity by identifying unknown subgroups based on observed indicators or variables (i.e., latent classes) is a major research topic in many fields, including psychology (De Cuyper, Rigotti, Witte, & Mohr, 2008; McCutcheon, 1985; Ulbricht, Rothschild, & Lapane, 2015), education (Darney, Reinke, Herman, Stormont, & Ialongo, 2013; Ing & Nylund-Gibson, 2013; Pastor, Barron, Miller, & Davis, 2007), criminology (Cavanaugh et al., 2012; Mulder, Vermunt, Brand, Bullens, & Van Merle, 2012), sociology (Anderson, Ramo, Cummins, & Brown, 2010; Komro, Tobler, Maldonado-Molina, & Perry, 2010; Oxford et al., 2003), and medical science (Anderson et al., 2010; Lanza, Tan, & Bray, 2013; Mathur, Stigler, Lust, & Laska, 2014; Roberts & Ward, 2011).
Recently, the prediction of distal outcomes using latent class membership has been a focal point for not only applied researchers but also methodology researchers interested in analysis (Bakk, Oberski, & Vermunt, 2016; Bakk & Vermunt, 2016; Bray, Lanza, & Tan, 2015). LCA estimates the class-specific means of a distal outcome by including an auxiliary indicator as the outcome. When the distal outcome is incorporated into LCA, however, it may appear to define the latent distal outcome variable as one of the indicators, which can distort the class membership classification results. To explain the differences in class-specific means across classes without distorting the classification of the original latent class model, two strong assumptions regarding the distal outcome need to be met: homoskedasticity across classes and a normal distribution of the outcome within each latent class (Bakk et al., 2016; Bakk, Tekle, & Vermunt, 2013; Bakk & Vermunt, 2016; Lanza et al., 2013). However, it is more reasonable to hypothesize that the distribution of distal outcomes within each class is nonnormal. For example, the floor or ceiling effect can skew outcome responses, especially in education. For example, the distribution of ability test scores may exhibit a high degree of kurtosis if the test is either too difficult or easy for a specific latent class.
Several approaches for dealing with distal outcomes have been suggested and tested using simulations, including one-step and stepwise models. The use of one-step approaches, in which LCA is conducted with the distal outcome included as an additional response indicator, has not been supported by the results of previous simulations because of the strong possibility of distorted classification in the original latent class model (Asparouhov & Muthén, 2014a, 2014b; Bakk et al., 2013; Bakk et al., 2016; Bakk & Vermunt, 2016; Bray et al., 2015; Lanza et al., 2013; No & Hong, 2018). In contrast, the use of stepwise approaches, including three-step maximum likelihood (ML; Vermunt, 2010), three-step BCH (Bolck–Croon–Hagenaars; Bolck, Croon, & Hagenaars, 2004; Vermunt, 2010), and LTB (Lanza–Tan–Bray; Lanza et al., 2013), has been recommended based on the results of multiple simulation studies under various modeling conditions, including variation in sample size, classification quality, heteroskedasticity, and the nonnormality of the distal outcome across classes. However, although the recently developed stepwise ML, BCH, and LTB approaches have been shown to yield unbiased estimates of class-specific distal outcome means in previous simulation studies, it is still unknown which approach is the most stable or robust for more realistic underlying conditions, particularly, the nonnormality of distal outcomes. This is because the distribution of distal outcome variables has been treated as normal in previous simulation research, with the exception of a few studies (Asparouhov & Muthén, 2014b; Bakk & Kuha, 2018; Bakk & Vermunt, 2016; Dziak, Bray, Zhang, Zhang, & Lanza, 2016) that employed bimodal or skewed distributions for the distal outcome.
Table 1 summarizes the performance of mixture modeling approaches from previous simulation studies in terms of their robustness or stability under various conditions. As can be observed, the three-step approaches and the LTB approach are particularly stable under a variety of simulation conditions. This research thus examines the stability or robustness of these recommended stepwise mixture modeling approaches (i.e., the three-step ML approach, the three-step BCH approach, and the LTB approach) when the assumption of normality for the distal outcome within the classes is violated, and investigates the effects of changes in heteroskedasticity, sample size, and entropy. The two-step approach recently proposed by Bakk and Kuha (2018) is not considered for this study because it is not widely supported by software and it remains unfamiliar to researchers.
Table 1.
Previous Simulation Studies.
| Simulation study | Simulated approaches | Recommendation | Distal outcome distribution |
|---|---|---|---|
| Bakk, Tekle, and Vermunt (2013) | 1-step 3-step |
1-step 3-step |
Normal |
| Lanza, Tan, and Bray (2013) | 3-step LTB |
LTB | Normal |
| Asparouhov and Muthén (2014a) | 1-step 3-step LTB |
1-step 3-step LTB |
Normal |
| Asparouhov and Muthén (2014b) | 1-step 1-step PC 3-step ML 3-step BCH LTB |
3-step BCH | Normal |
| 1-step 1-step PC 3-step ML 3-step BCH LTB |
3-step BCH | Normal Bimodal |
|
| Bray, Lanza, and Tan (2015) | Non-inclusive LTB Inclusive LTB |
Inclusive LTB | Normal |
| Bennik and Vermunt (2015) | Mode 1-step 3-step 3-step ML 3-step BCH |
1-step Any 3-steps |
Normal (multilevel) |
| Bakk and Vermunt (2016) | 3-step ML 3-step BCH LTB |
3-step BCH | Normal |
| 3-step ML 3-step BCH LTB |
3-step BCH | Bimodal | |
| Bakk, Oberski, and Vermunt (2016) | 3-step BCH 3-step LTB LTB |
3-step BCH LTB |
Normal |
| Dziak, Bray, Zhang, Zhang, and Lanza (2016) | 3-step 3-step ML 3-step BCH Inclusive 3-step Quadratic 3-step |
3-step BCH | Normal Binary Skewed |
| No and Hong (2018) | 1-step 3-step ML 3-step BCH LTB |
3-step ML 3-step BCH |
Normal |
| Bakk and Kuha (2018) | 1-step 2-step 3-step 3-step ML 3-step BCH |
2-step | Normal Skewed Bimodal |
Note. Distal outcome distribution = within-class distribution of distal outcomes; PC = pseudo-class draws approach (Bandeen-Roche, Miglioretti, Zeger, & Rathouz, 1997); Mode = the use of mode between levels in multilevel latent class analysis; ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bolck, Croon, and Hagennarrs (Vermunt, 2010; Bolck et al., 2004); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); 3-step = stepwise mixture modeling approach (Bolck et al., 2004); 3-step ML = stepwise maximum likelihood approach (Vermunt, 2010); 3-step BCH = stepwise BCH approach (Vermunt, 2010); 3-step LTB = stepwise LTB approach (Bakk, Oberski, & Vermunt, 2016); Inclusive 3-step = 3-step approach based on an inclusive model (Dziak et al., 2016); Quadratic 3-step = 3-step approach based on a quadratic model (Dziak et al., 2016); 2-step = alternative stepwise mixture modeling approach (Bakk & Kuha, 2018).
By expanding the range of mixture modeling applications and utilizing more realistic distribution assumptions for distal outcomes, this research will contribute to a better understanding of bias-corrected mixture modeling approaches, thus providing more robust and realistic guidelines for applied researchers. In particular, this study answers the following questions:
What is the optimal stepwise mixture modeling approach when the distribution of the distal outcome is assumed to be nonnormal?
How is the performance of the different mixture modeling approaches affected by changes in the homoskedasticity of the distal outcome, the sample size, and the classification quality?
Theoretical Background
Basic Latent Class Analysis
In LCA, population heterogeneity is explained by identifying unobserved subgroups that are mutually exclusive and exhaustive. An LC model for particular latent class can be formulated as
| (1) |
where represents the full response vector for the individual subject . Suppose there is a set of categorical response items in an LC model; the response of subject to item is denoted by . represents the discrete latent class variable, with the total number of classes denoted by .
The full response vector can be divided into two parts: for the unconditional probability of membership in latent class and for the conditional class-specific distribution of the response vector . The second part of the LC model equation can be converted into Equation (2) under the assumption of the local independence of the response variables within each class:
| (2) |
An extended LC model that contains the continuous distal outcome variable can be expressed as
| (3) |
where represents the class-specific distribution of the distal outcome, which is defined as a univariate normal distribution within each class. As shown in Equation (3), the inclusion of the distal outcome variable may distort classification results by altering the latent class information due to the distal outcome serving as an additional response variable (Bakk & Vermunt, 2016; Petras & Masyn, 2010). Furthermore, when the assumption of normality within each class is violated for the distal outcome, more classes are likely to be extracted (Bauer & Curran, 2003). To overcome the disadvantages of simultaneous modeling using a one-step approach, stepwise mixture modeling (i.e., three-step approaches) and other stepwise approaches can be employed.
Approaches for Continuous Distal Outcomes
The mean of the distal outcome within each class can be estimated using one-step or three-step approaches, but it has been shown in previous research that the one-step approach can distort the LC solution and requires the strong assumption of normality for the distal outcome within each class. To overcome these limitations, a three-step approach (Vermunt, 2010) was developed in which the relationship between class membership and the distal outcome is investigated using the class membership that is assigned in the absence of the distal outcome in the first step of LCA.
The first step of the three-step approach is the construction of a measurement LC model that contains categorical response variables to identify latent classes. In the second step, subjects or individuals are assigned to each latent class based on their responses, using either modal or proportional assignment. Posterior class membership probability is calculated by applying the parameters obtained in the first step to Bayes’s theorem, as shown in Equation (4):
| (4) |
Information on the distribution of each latent class with a certain response pattern can be derived from the posterior class membership probability , establishing a classification mechanism in which subjects or individuals who show similar response patterns are classified into the same latent class.
The overall quality of the classification, which is expressed as the classification error, is obtained in the second step of the three-step approach by averaging the probabilities of assigned class membership conditional on true class membership as shown in Equation (5):
| (5) |
The association between class membership and the distal outcome is analyzed in the final step of the three-step approach. The posterior class membership probability is used in conjunction with the classification error introduced in Equation (5) to obtain
| (6) |
However, the estimates of the class-specific distal outcome means produced by the three-step approach have been shown to exhibit bias in the direction of attenuation, which has led to the development of alternative stepwise approaches that incorporate attenuation correction (Bolck et al., 2004), such as the ML approach (Vermunt, 2010), the BCH approach (Bolck et al., 2004; Vermunt, 2010), and the LTB approach (Lanza et al., 2013).
The ML Approach
The ML approach estimates from Equation (6) freely using maximum likelihood estimation while is fixed in the second step. The parameter is estimated by maximizing the log-likelihood function:
| (7) |
The distributional form of the distal outcome within each class needs to be specified for the estimation of class-specific distal outcome means, with a normal distribution typically selected. The variance of distal outcome can be either homoskedastic or heteroskedastic; this is modeled using ML_E for equal variance across classes and ML_U for unequal variance across classes.
The ML approach yields unbiased estimates for class-specific means only when the assumption of normality is satisfied within each class (Bakk et al., 2013). If this assumption is violated, the ML approach provides inaccurate information on class membership due to the substantial distortion in the classification in the third step due to the nonnormal distribution of the distal outcome (Asparouhov & Muthén, 2014b).
The BCH Approach
The BCH approach weighs the relationship between class membership and the distal outcome using the elements of the inverse of the matrix of classification error probabilities as shown in Equation (8):
| (8) |
From Equation (8), can be decomposed as follows because it can be obtained by considering all response patterns of all latent classes :
| (9) |
The classification error serves as a regression weight in the relationship between and (Vermunt, 2010). In order to identify the association between class membership and the distal outcome , the BCH approach uses the inverse elements of the matrix of classification error (Bakk & Vermunt, 2016).
The pseudo-weighted log-likelihood function is maximized in the BCH approach as in Equation (9), which was modified by Vermunt (2010). The pseudo-log-likelihood function is expressed using the modified BCH approach as
| (10) |
where denotes the class assignment weight, which is transformed into , which puts weight on records per individual or subject. In the BCH approach, the robust or sandwich standard error estimator is employed to account for multiple records.
In the BCH approach, the classification definition remains stable even when the distal outcome distribution is misspecified. The robustness of a misspecified distribution can be attributed to weighted multiple group analysis, in which it is less likely that a class shift will arise because of the groups corresponding to the latent classes defined in advance (Asparouhov & Muthén, 2014b; Bakk et al., 2016).
Although the BCH approach outperforms other stepwise mixture modeling approaches in the presence of heteroskedasticity across classes, it is possible that the observations will have negative weights if the entropy is low, thus generating inadmissible estimates for the distal outcome (Asparouhov & Muthén, 2014b).
The LTB Approach
The main difference between the LTB approach and the ML and BCH approaches is whether the distributional assumptions of the distal outcome have a strong effect on the estimation of the association between latent class membership and the distal outcome. In the LTB approach, estimation is conducted using two steps.
In the first step of the LTB approach, the distal outcome serves as a covariate or predictor in the latent class model. Inclusion of the distal outcome as a covariate produces the basic latent class model below:
| (11) |
The probability of class membership given the covariate is denoted by , which is summarized by a multinomial logistic regression model with intercepts and slopes for class as shown in Equation (12):
| (12) |
Subsequently, the distal outcome means within each class are estimated based on Bayes’s theorem, which is applied to obtain the class-specific distribution of the distal outcome :
| (13) |
The LTB approach performs well in situations where the relationship between the latent classes and distal outcome is a linear logistic one (Asparouhov & Muthén, 2014b; Bakk & Vermunt, 2016). Furthermore, it is known that the degree of bias is likely to increase in the presence of heteroskedasticity using the LTB approach (Asparouhov & Muthén, 2014b).
Method
Monte Carlo Simulation
This study aims to compare the robustness of previously recommended stepwise approaches in dealing with distal outcomes in LCA under realistic conditions, that is, assuming the heteroskedasticity and nonnormality of the class-specific means within each class. To achieve this, Monte Carlo simulations were conducted under various conditions.
Simulation Design and Population Values
Study 1
Data sets for Study 1 were generated from a four-class model with eight observed indicators or response variables (Figure 1). To preserve consistency and continuity, the model was designed to be similar to those of previous simulation studies (Asparouhov & Muthén, 2014b; Bakk et al., 2013; Bakk et al., 2016; Bakk & Vermunt, 2016; Lanza et al., 2013). All of the indicators in the present study were binary, while a continuous nonnormal distal outcome was used in the analysis model for Study 1 to assess the simulation performance of the target approaches.
Figure 1.
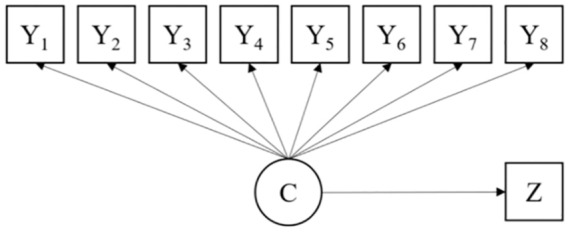
Research model for Study 1.
The model population values for Study 1 are summarized in Table 2. Class proportion was equal across the four classes (i.e., 0.25 for each class) as in previous simulation studies. The skewness and kurtosis of distal outcomes within each class were varied so that there was a transition from low nonnormality in Class 2 to high nonnormality in Class 4. Variance among classes was set at 1 when determining performance under equal variance, while a variance of 1, 4, 9, and 25 was set for each of the four classes, respectively, to simulate unequal variance. Entropy, which is a measure of classification quality, was derived by varying the class-specific probabilities of each observed indicator, as shown in Table 2.
Table 2.
Population Values for Studies 1 and 2.
| Class 1 | Class 2 | Class 3 | Class 4 | ||
|---|---|---|---|---|---|
| Class proportion | .25 | .25 | .25 | .25 | |
| Skewness (Z) | 0 | −2 | −2 | −3 | |
| Kurtosis (Z) | 0 | 7 | 15 | 21 | |
| Mean (Z) | −1 | −0.5 | 0.5 | 1 | |
| Threshold (X), Threshold (Z) | 0.5 | 0.3 | 0.2 | — | |
| Variance (Z) | Equal | 1 | 1 | 1 | 1 |
| Unequal | 1 | 4 | 9 | 25 | |
| Entropy | .5, .6, .7, .8 |
Note. Threshold (X) is for Study 1 and Threshold (Z) is for Study 2. The reference class for predictor (X) is Class 4.
Study 2
Study 2 investigated the situation where a predictor is introduced to mixture modeling with the distal outcome. The analysis model for Study 2 is presented in Figure 2.
Figure 2.
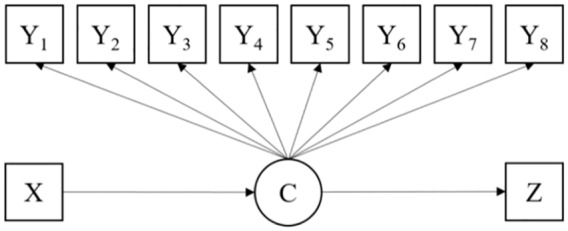
Research model for Study 2.
All simulation conditions were the same as those in Study 1. The inclusion of a predictor requires thresholds for that predictor to be assigned in order for multinominal logistic regression to run. A normal auxiliary variable was generated as a predictor of the latent class, with Class 4 used as a reference group for multinominal logistic regression.
Manipulated Simulation Conditions
To compare the robustness of stepwise mixture modeling with distal outcomes in LCA under conditions that are realistic for many types of applied research, four components of the simulation shown to be strongly associated with modeling performance in previous simulation studies were manipulated: mixture modeling approach (ML_E, ML_U, BCH, and LTB), variance (homoskedasticity and heteroskedasticity), total sample size (100, 200, 500, and 1,000), and entropy (.5, .6, .7, and .8). Except for sample size, these conditions were all set to be similar to those in previous studies in order to reflect realistic research conditions.
Data Generation and Analysis
Data Generation
Data generation was conducted using two steps: generating data with a normally distributed distal outcome in Step 1 and transforming the distal outcome into a nonnormal distribution in Step 2 by increasing the skewness and kurtosis. The 500 sample data sets for each simulation condition were all created with the distal outcome distributed normally within each class for the first phase of data generation. In total, 64,000 data sets for each study were generated in Step 1 of the data generation process.
Data Transformation
To investigate and compare the performance of the mixture modeling approaches when the distal outcome is characterized by heteroskedasticity and nonnormality, a situation which is considered standard in applied research, the distal outcomes from each data set generated in Step 1 of data generation were transformed into a nonnormal distribution that followed the skewness and kurtosis values defined in the population values and that was either homoskedastic to test the effect of equal variance or heteroskedastic to test the effect of unequal variance.
Fleishman’s cubic transformation (Fleishman, 1978; Vale & Maurelli, 1983; Wicklin, 2013) was applied to give the distal outcome a nonnormal distribution. In Fleishman’s method, a cubic transformation is applied to a univariate standard normal distribution so that a nonnormal distribution with a given skewness and kurtosis can be obtained, as defined by the polynomial below:
| (14) |
where denotes a nonnormal distribution, with the expected skewness and kurtosis attained by transforming normal distribution with the cubic coefficients , , and . Table 3 shows the cubic coefficients for Fleishman’s transformation employed in this research.
Table 3.
Fleishman’s Transformation Cubic Coefficients.
| Class | Skewness | Kurtosis | |||
|---|---|---|---|---|---|
| 1 | 0 | 0 | — | — | — |
| 2 | −2 | 7 | 0.761585275 | −0.260022598 | 0.053072274 |
| 3 | −2 | 15 | −1.202197410 | −0.456105414 | 0.220734564 |
| 4 | −3 | 21 | −0.681632225 | −0.637118193 | 0.148741042 |
Note. In SAS, a univariate normal distribution has a skewness of 0 and kurtosis of 0; c1, c2, and c3: cubic coefficients for Fleishman’s transformation.
To test the effect of heteroskedasticity, a linear transformation of the distal outcome was carried out to produce the desired variances for the distal outcome within each class, as shown in Table 3. Fleishman’s transformation and linear transformation were applied simultaneously in Step 2 of the data generation process. The transformation was conducted with SAS 9.4 for Windows (SAS Institute, Cary NC) using SAS/IML functions that implement Fleishman’s cubic transformation and linear transformation.
External Monte Carlo Simulation
Monte Carlo simulations can be conducted internally or externally with Mplus (Muthén & Muthén, 1998-2015). In this research, external Monte Carlo simulations in which the transformed data sets were analyzed individually and the results were summarized were implemented in R 3.2.4 (R Core Team, 2016) with the MplusAutomation package (Hallquist & Wiley, 2016).
Evaluation Criteria
The bias in within-class mean estimation, the mean squared error (MSE) of the estimated means, and the nonconvergence rate (NCR) were examined in order to compare the robustness of the target stepwise approaches in testing the association between class membership and distal outcomes.
Bias in Within-Class Mean Estimation
The bias in within-class mean estimation provides information on the degree to which the estimated class-specific means differ from the true population values. How accurately the approaches of interest examined the association between latent class membership and the distal outcome could thus be inferred from their bias values.
Let denote the estimated within-class mean for a certain class for one of the target approaches, and represents the number of replications. For a particular latent class under a certain simulation condition, class-specific mean bias can be modeled using
| (15) |
In the present research, this formula represents the averaged differences between the estimated within-class mean for a distal outcome and the true population value across 500 replications. The value calculated using this formula is referred to as the proportional bias.
A cutoff point for the absolute bias of 0.10, which is lower than what is generally considered a tolerable degree of bias, was applied in this research. (Bandalos, 2006; Muthén & Muthén, 2002).
Mean Squared Error
Both the accuracy and consistency of estimated values can be investigated by comparing the MSE under the same conditions because the MSE simultaneously reflects the biasedness and the variance of the estimates across replications based on the following equation:
| (16) |
where represents the estimated class-specific means and denotes the number of replications. In this research, the MSE was compared between the simulation conditions. It was expected that less biased estimates would have lower MSE values.
Nonconvergence Rate
The stability of the target approaches was measured using the NCR. When predicting a distal outcome based on latent class membership information, the higher the NCR, the lower the stability of the modeling approach. The NCR is expressed as the ratio of the number of nonconverging simulations to the number of total simulations:
| (17) |
where denotes the number of total simulations for modeling approach , and represents the number of converging simulations.
Results
Study 1
Bias in Within-Class Mean Estimation
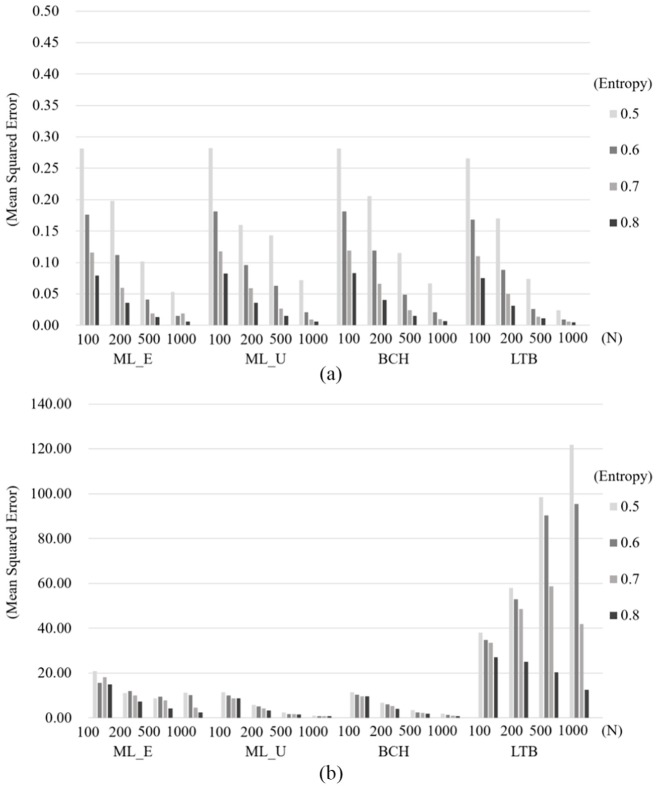
Table 4 shows the bias in within-class mean estimation and the MSE across different simulation conditions averaged over 500 replications. A general change in bias with changes in simulation conditions, including sample size and classification quality, can be observed in Figure 3a for homoskedastic variance and Figure 3b for heteroskedastic variance.
Table 4.
Bias in Within-Class Mean Estimation and Mean Squared Error in Study 1.
| Bias |
Mean squared error |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variance | Sample size | Entropy | ML_E | ML_U | BCH | LTB | ML_E | ML_U | BCH | LTB |
| Equal | 100 | .5 | −0.399 | −0.391 | −0.396 | −0.308 | 0.281 | 0.282 | 0.281 | 0.266 |
| .6 | −0.252 | −0.245 | −0.246 | −0.168 | 0.176 | 0.181 | 0.181 | 0.168 | ||
| .7 | −0.176 | −0.172 | −0.175 | −0.123 | 0.116 | 0.118 | 0.119 | 0.110 | ||
| .8 | −0.120 | −0.123 | −0.120 | −0.085 | 0.079 | 0.082 | 0.083 | 0.075 | ||
| 200 | .5 | −0.311 | −0.197 | −0.309 | −0.171 | 0.198 | 0.160 | 0.206 | 0.170 | |
| .6 | −0.202 | −0.112 | −0.203 | −0.114 | 0.112 | 0.096 | 0.119 | 0.088 | ||
| .7 | −0.103 | −0.053 | −0.105 | −0.047 | 0.060 | 0.059 | 0.066 | 0.050 | ||
| .8 | −0.053 | −0.027 | −0.054 | −0.020 | 0.036 | 0.036 | 0.040 | 0.031 | ||
| 500 | .5 | −0.181 | −0.237 | −0.174 | −0.061 | 0.102 | 0.143 | 0.115 | 0.074 | |
| .6 | −0.078 | −0.135 | −0.075 | −0.018 | 0.041 | 0.063 | 0.049 | 0.026 | ||
| .7 | −0.017 | −0.062 | −0.016 | 0.011 | 0.019 | 0.027 | 0.024 | 0.014 | ||
| .8 | −0.011 | −0.036 | −0.008 | 0.001 | 0.013 | 0.015 | 0.015 | 0.011 | ||
| 1,000 | .5 | −0.099 | −0.125 | −0.092 | −0.009 | 0.053 | 0.072 | 0.067 | 0.024 | |
| .6 | −0.025 | −0.051 | −0.022 | 0.003 | 0.015 | 0.021 | 0.021 | 0.009 | ||
| .7 | −0.017 | −0.007 | 0.005 | 0.009 | 0.019 | 0.009 | 0.010 | 0.006 | ||
| .8 | −0.002 | −0.004 | 0.002 | 0.001 | 0.006 | 0.006 | 0.007 | 0.005 | ||
| Unequal | 100 | .5 | −0.496 | −0.404 | −0.446 | −0.381 | 20.946 | 11.490 | 11.381 | 38.014 |
| .6 | −0.130 | −0.062 | −0.097 | 0.115 | 15.545 | 10.021 | 10.330 | 34.829 | ||
| .7 | −0.037 | −0.087 | −0.115 | 0.275 | 18.140 | 8.775 | 9.634 | 33.488 | ||
| .8 | −0.142 | −0.095 | −0.146 | 0.130 | 14.963 | 8.735 | 9.669 | 27.081 | ||
| 200 | .5 | −0.293 | −0.127 | −0.326 | 0.230 | 11.167 | 5.873 | 6.760 | 57.891 | |
| .6 | −0.235 | −0.033 | −0.184 | 0.386 | 11.980 | 5.136 | 6.064 | 52.841 | ||
| .7 | 0.038 | 0.004 | −0.023 | 0.315 | 9.931 | 4.303 | 5.396 | 48.596 | ||
| .8 | 0.047 | −0.003 | 0.011 | 0.586 | 7.233 | 3.414 | 4.113 | 25.067 | ||
| 500 | .5 | −0.076 | −0.033 | −0.144 | 1.062 | 8.826 | 2.394 | 3.433 | 98.486 | |
| .6 | 0.179 | −0.029 | −0.041 | 1.341 | 9.434 | 1.675 | 2.450 | 90.287 | ||
| .7 | 0.228 | 0.062 | 0.080 | 1.402 | 7.770 | 1.704 | 2.218 | 58.601 | ||
| .8 | 0.122 | 0.040 | −0.015 | 0.655 | 4.202 | 1.529 | 1.796 | 20.262 | ||
| 1,000 | .5 | 0.251 | 0.009 | −0.067 | 2.049 | 11.219 | 0.930 | 1.818 | 121.753 | |
| .6 | 0.428 | 0.023 | −0.021 | 2.708 | 10.169 | 0.838 | 1.284 | 95.383 | ||
| .7 | 0.347 | 0.073 | 0.045 | 1.805 | 4.660 | 0.788 | 0.980 | 41.859 | ||
| .8 | 0.183 | 0.008 | 0.021 | 0.618 | 2.472 | 0.727 | 0.836 | 12.591 | ||
Note. ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bolck, Croon, and Hagennarrs (Bolck et al., 2004; Vermunt, 2010); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); ML_E = ML approach assuming equal variance among classes; ML_U = ML approach assuming unequal variance among classes.
Figure 3.
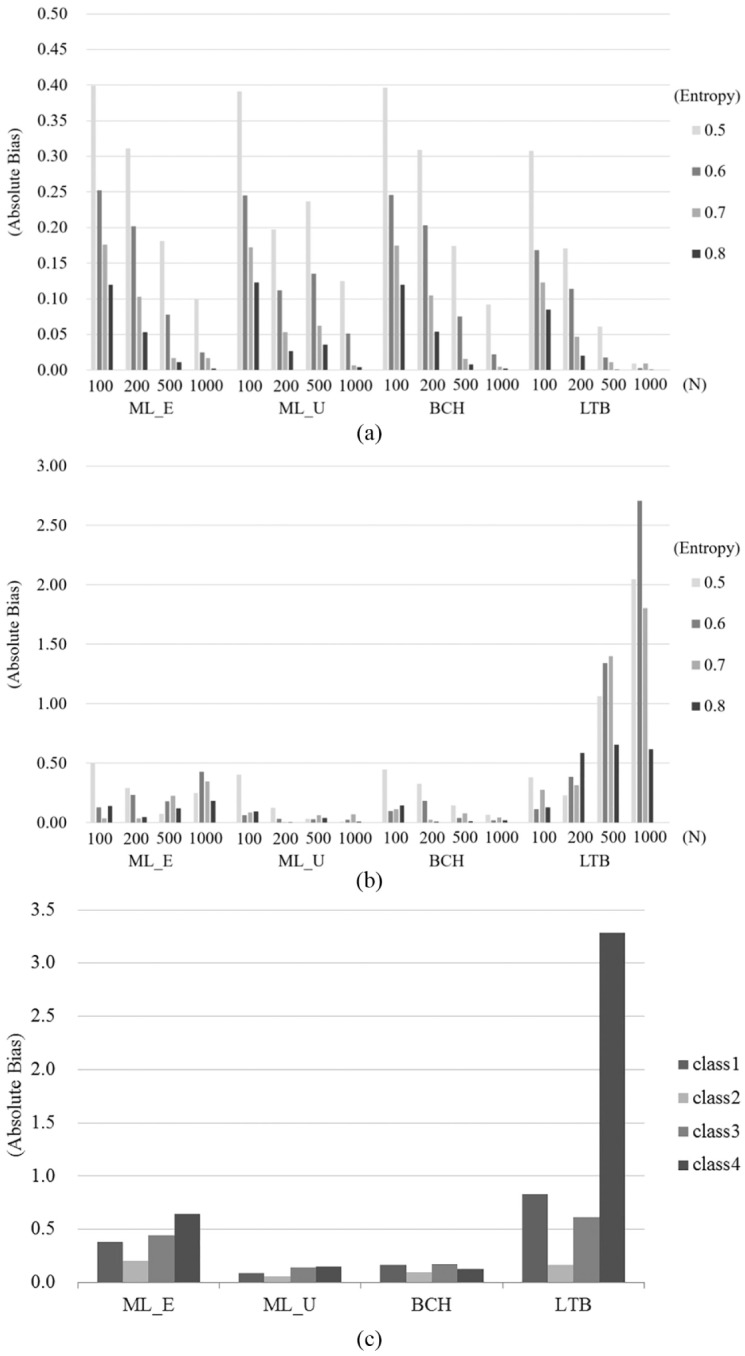
(a) Absolute bias in Study 1 (under equal variance). (b) Absolute bias in Study 1 (under unequal variance). (c) Absolute bias across classes in Study 1 (under unequal variance).
Under homoskedasticity, it can be seen that the bias in class-specific mean estimation generally decreased with larger sample size and higher entropy. While the estimates obtained using the LTB approach were less biased than those obtained using the other approaches under almost all conditions, the level of bias in within-class mean estimation among the ML_E, ML_U, and BCH approaches was similar.
Unlike the case with homoskedasticity, the LTB estimates were increasingly biased as the sample size increased under heteroskedasticity, as were the estimates for the ML_E approach. At the same time, the degree of bias fell as classification quality increased. On the other hand, lower levels of bias were identified in the estimates from the ML_U and BCH approaches under unequal variance. In fact, under heteroskedasticity, the bias in the estimation of within-class means using ML_U and BCH was the lowest of the approaches.
Little difference in bias among the approaches was detected under equal variance. However, as Figure 3c indicates, the bias in class-specific mean estimation increased in relation to nonnormality of the distal outcome. The LTB approach produced the highest levels of bias, while the ML_U and BCH yielded relatively lower levels under heteroskedasticity. It can be seen that the violation of the normality assumption for the distal outcome distorted the estimated within-class means, which interacted with heteroskedasticity across the latent classes.
Mean Squared Error
Under homoskedasticity (Figure 4a), the MSE decreased with an increase in sample size and entropy increasing for all conditions. The estimates using the LTB approach were less biased than those of other approaches, though the differences between approaches were not substantial. Under heteroskedasticity (Figure 4b), the estimates using the ML_E, ML_U, and BCH approaches also had a lower MSE with an increase in sample size and entropy. The LTB approach was also sensitive to the sample size, but in the opposite direction (i.e., MSE increased with increasing sample size). However, as with the other approaches, LTB estimates had a lower MSE when entropy was higher. Of the approaches simulated under unequal variance, the ML_U and BCH approaches had the lowest MSE.
Figure 4.
(a) Mean squared error in Study 1 (under equal variance). (b) Mean squared error in Study 1 (under unequal variance).
Similar to the results of the bias, the MSE was higher when the distal outcome was nonnormal and the variance was unequal. The MSE values from the LTB under unequal variance were the highest of the four approaches, while the other three approaches were similar in their MSE values under heteroskedasticity. In contrast, MSE values under homoskedasticity were not discernibly different between the approaches when the distal outcome had a nonnormal distribution.
Nonconvergence Rate
The NCRs for Study 1 under both equal and unequal variance are presented in Table 5. Under both forms of variance, BCH and LTB converged in 100% of simulations, which illustrates that the two approaches are highly stable when examining the association between class membership and a continuous nonnormal distal outcome.
Table 5.
Nonconvergence Rate in Study 1.
| Estimation approach | ||||||
|---|---|---|---|---|---|---|
| Variance | Sample size | Entropy | ML_E | ML_U | BCH | LTB |
| Equal | 100 | .5 | 0.0 | 0.0 | 0.0 | 0.0 |
| .6 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .7 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 200 | .5 | 0.0 | 0.2 | 0.0 | 0.0 | |
| .6 | 0.0 | 0.2 | 0.0 | 0.0 | ||
| .7 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 500 | .5 | 0.0 | 0.0 | 0.0 | 0.0 | |
| .6 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .7 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 1,000 | .5 | 0.0 | 0.0 | 0.0 | 0.0 | |
| .6 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .7 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| Unequal | 100 | .5 | 2.2 | 11.6 | 0.0 | 0.0 |
| .6 | 4.0 | 8.4 | 0.0 | 0.0 | ||
| .7 | 6.2 | 2.8 | 0.0 | 0.0 | ||
| .8 | 6.2 | 0.8 | 0.0 | 0.0 | ||
| 200 | .5 | 9.8 | 23.6 | 0.0 | 0.0 | |
| .6 | 9.8 | 13.4 | 0.0 | 0.0 | ||
| .7 | 8.2 | 2.8 | 0.0 | 0.0 | ||
| .8 | 5.4 | 1.2 | 0.0 | 0.0 | ||
| 500 | .5 | 19.6 | 24.2 | 0.0 | 0.0 | |
| .6 | 12.8 | 8.0 | 0.0 | 0.0 | ||
| .7 | 7.6 | 1.6 | 0.0 | 0.0 | ||
| .8 | 3.2 | 0.0 | 0.0 | 0.0 | ||
| 1,000 | .5 | 15.8 | 18.4 | 0.0 | 0.0 | |
| .6 | 9.2 | 1.6 | 0.0 | 0.0 | ||
| .7 | 3.6 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.8 | 0.0 | 0.0 | 0.0 | ||
Note. ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bolck, Croon, and Hagennarrs (Bolck et al., 2004; Vermunt, 2010); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); ML_E = ML approach assuming equal variance among classes; ML_U = ML approach assuming unequal variance among classes.
Under homoskedasticity, 0.2% of the simulations using the ML_U approach were nonconverging when the sample size was 200 and the entropy was .5 or .6. Under heteroskedasticity, simulations with smaller sample sizes and lower entropy exhibited a higher nonconvergence rate across the simulation conditions when ML_E and ML_U were used, except for a sample size of 100 with ML_E. For all conditions under unequal variance, the nonconvergence rate of ML_U was higher than that of ML_E. In summary, the robustness of ML_E when analyzing the association between class membership and the distal outcome cannot be guaranteed with small samples and low classification quality.
Study 2
Bias in Within-Class Mean Estimation
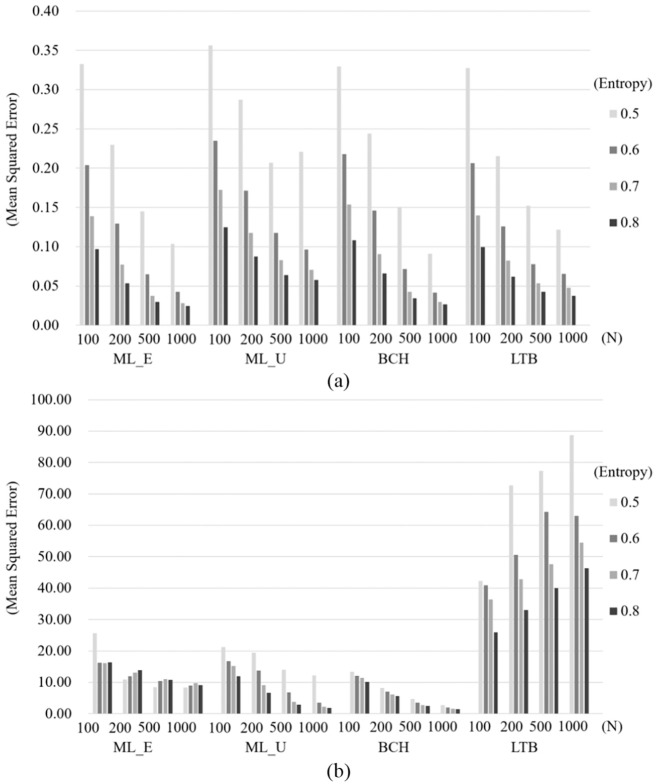
The bias in within-class mean estimation and MSE for the simulation conditions for Study 2 exhibited a similar pattern to that found in Study 1 (Table 6).
Table 6.
Bias in Within-Class Mean Estimation and Mean Squared Error in Study 2.
| Bias | Mean squared error | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variance | Sample size | Entropy | ML_E | ML_U | BCH | LTB | ML_E | ML_U | BCH | LTB |
| Equal | 100 | .5 | −0.427 | −0.433 | −0.436 | −0.331 | 0.333 | 0.356 | 0.329 | 0.328 |
| .6 | −0.295 | −0.299 | −0.317 | −0.224 | 0.204 | 0.235 | 0.218 | 0.206 | ||
| .7 | −0.212 | −0.221 | −0.236 | −0.157 | 0.139 | 0.172 | 0.154 | 0.140 | ||
| .8 | −0.138 | −0.155 | −0.172 | −0.107 | 0.097 | 0.125 | 0.108 | 0.100 | ||
| 200 | .5 | −0.341 | −0.371 | −0.361 | −0.191 | 0.230 | 0.287 | 0.244 | 0.215 | |
| .6 | −0.207 | −0.218 | −0.235 | −0.098 | 0.130 | 0.171 | 0.146 | 0.126 | ||
| .7 | −0.115 | −0.133 | −0.154 | −0.037 | 0.077 | 0.117 | 0.091 | 0.082 | ||
| .8 | −0.061 | −0.086 | −0.110 | −0.019 | 0.054 | 0.088 | 0.066 | 0.062 | ||
| 500 | .5 | −0.217 | −0.236 | −0.237 | −0.018 | 0.145 | 0.207 | 0.150 | 0.152 | |
| .6 | −0.106 | −0.105 | −0.136 | 0.029 | 0.065 | 0.118 | 0.072 | 0.078 | ||
| .7 | −0.040 | −0.061 | −0.080 | 0.032 | 0.037 | 0.083 | 0.042 | 0.054 | ||
| .8 | −0.016 | −0.026 | −0.063 | 0.020 | 0.030 | 0.064 | 0.034 | 0.042 | ||
| 1,000 | .5 | −0.142 | −0.143 | −0.153 | 0.051 | 0.104 | 0.221 | 0.091 | 0.122 | |
| .6 | −0.056 | −0.074 | −0.081 | 0.047 | 0.043 | 0.096 | 0.042 | 0.065 | ||
| .7 | −0.021 | −0.032 | −0.059 | 0.030 | 0.028 | 0.070 | 0.029 | 0.048 | ||
| .8 | −0.009 | −0.008 | −0.055 | 0.018 | 0.024 | 0.058 | 0.027 | 0.037 | ||
| Unequal | 100 | .5 | −0.027 | −0.407 | −0.269 | 0.009 | 25.634 | 21.224 | 13.298 | 42.274 |
| .6 | −0.102 | −0.425 | −0.251 | 0.221 | 16.216 | 16.737 | 12.057 | 40.826 | ||
| .7 | 0.266 | −0.240 | −0.052 | 0.347 | 16.047 | 15.133 | 11.417 | 36.397 | ||
| .8 | 0.434 | −0.196 | 0.024 | 0.623 | 16.269 | 11.923 | 10.166 | 25.876 | ||
| 200 | .5 | −0.020 | −0.727 | −0.193 | 0.462 | 10.916 | 19.402 | 8.209 | 72.673 | |
| .6 | 0.340 | −0.512 | −0.011 | 0.940 | 11.895 | 13.762 | 6.988 | 50.538 | ||
| .7 | 0.704 | −0.261 | 0.129 | 1.492 | 13.141 | 9.115 | 6.092 | 42.862 | ||
| .8 | 0.925 | −0.178 | 0.179 | 1.687 | 13.834 | 6.639 | 5.628 | 33.028 | ||
| 500 | .5 | 0.436 | −0.816 | 0.037 | 1.662 | 8.472 | 13.953 | 4.709 | 77.265 | |
| .6 | 0.770 | −0.491 | 0.160 | 2.721 | 10.388 | 6.816 | 3.570 | 64.227 | ||
| .7 | 1.174 | −0.329 | 0.219 | 3.293 | 10.987 | 3.813 | 2.805 | 47.579 | ||
| .8 | 1.253 | −0.275 | 0.255 | 2.898 | 10.773 | 2.869 | 2.528 | 39.944 | ||
| 1,000 | .5 | 0.758 | −0.916 | 0.205 | 2.841 | 8.341 | 12.149 | 2.728 | 88.742 | |
| .6 | 1.233 | −0.389 | 0.279 | 4.411 | 9.001 | 3.559 | 1.938 | 63.036 | ||
| .7 | 1.447 | −0.305 | 0.284 | 4.146 | 9.774 | 2.279 | 1.655 | 54.450 | ||
| .8 | 1.416 | −0.248 | 0.284 | 3.480 | 9.131 | 1.813 | 1.489 | 46.292 | ||
Note. ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bock, Croon, and Hagennarrs (Bolck et al., 2004; Vermunt, 2010); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); ML_E = ML approach assuming equal variance among classes; ML_U = ML approach assuming unequal variance among classes.
Under homoskedasticity, the degree of bias in the class-specific distal outcome means was similar for all four approaches examined in Study 2 (Figure 5a). As the sample size and entropy increased, the estimates became less biased for all approaches. The BCH approach exhibited a slightly higher estimate bias than did ML_E and ML_U, while the LTB approach had the lowest bias. However, the difference in bias among the approaches was minor overall.
Figure 5.
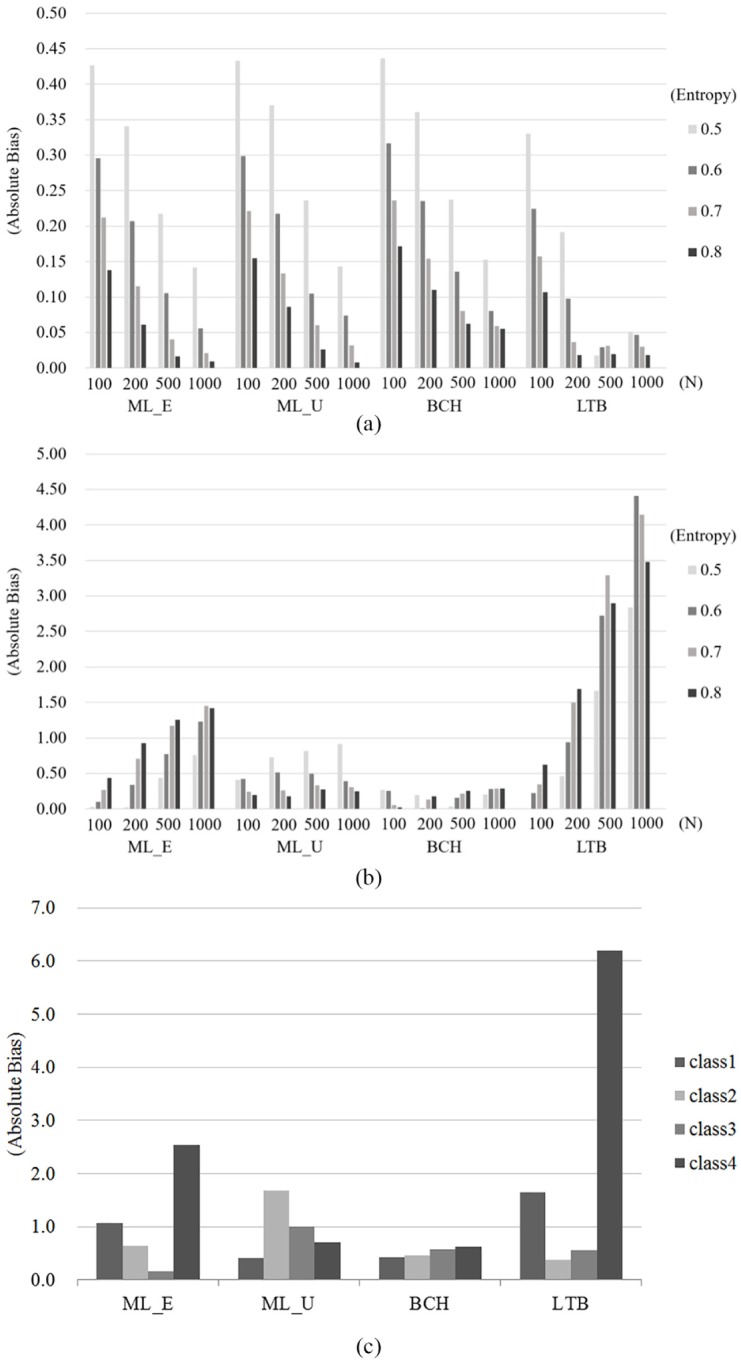
(a) Absolute bias in Study 2 (under equal variance). (b) Absolute bias in Study 2 (under unequal variance). (c) Absolute bias across classes in Study 2 (under unequal variance).
Under heteroskedasticity (Figure 5b), the mean estimation bias for ML_U decreased as the sample size and entropy increased, as in Study 1. In contrast, the estimates with the ML_E, BCH, and LTB approaches under unequal variance were generally more biased with larger samples and higher entropy. Overall, bias under heteroskedasticity was lowest for BCH estimates and highest for LTB estimates.
The results for bias when the distal outcome had a nonnormal distribution were similar to those in Study 1, though the overall degree of bias was higher in Study 2. It is assumed that the introduction of the predictor variable affected the estimation of the distal outcome. Nonnormality appeared to have little influence on bias under equal variance while, as shown in Figure 5c, the degree of bias in class-specific mean estimation rose as the degree of nonnormality of the distal outcome increased under unequal variance. In addition, bias using LTB was higher than for the other approaches under heteroskedasticity, indicating that LTB was the least robust approach under the most realistic conditions.
Mean Squared Error
Under homoskedasticity (Figure 6a), the MSE for all approaches decreased with an increase in both sample size and classification quality, while the difference in MSE between the approaches was not large. However, under heteroskedasticity (Figure 6b), MSE patterns varied between the approaches. LTB estimates tended to have a higher MSE with larger sample sizes, while ML_U and BCH estimates exhibited a similar pattern to those generated under equal variance (i.e., a smaller MSE with larger sample sizes and entropy). Overall, BCH estimates had the lowest MSE under heteroskedasticity.
Figure 6.
(a) Mean squared error in Study 2 (under equal variance). (b) Mean squared error in Study 2 (under unequal variance).
The overall MSE values in Study 2 were higher than those in Study 1. It could be because the inclusion of the predictor variable affected the estimation process for the latent class model. However, MSE patterns were similar between the two studies, with little difference observed between the approaches in their MSE values under equal variance and distal outcome nonnormality leading to considerable differences between the models under unequal variance. Overall, the higher the degree of nonnormality, the higher the MSE for the approaches. LTB produced the highest MSE, thus exhibiting weak stability in terms of LCA modeling with distal outcomes.
Nonconvergence Rate
Table 7 illustrates the NCR for Study 2 under both homoskedasticity and heteroskedasticity. BCH and LTB led to convergence in 100% of the simulations, but the ML approach often failed to converge when the distribution of the distal outcome was nonnormal.
Table 7.
Nonconvergence Rate in Study 2.
| Estimation approach | ||||||
|---|---|---|---|---|---|---|
| Variance | Sample size | Entropy | ML_E | ML_U | BCH | LTB |
| Equal | 100 | .5 | 0.4 | 8.4 | 0.0 | 0.0 |
| .6 | 0.6 | 6.0 | 0.0 | 0.0 | ||
| .7 | 0.0 | 7.2 | 0.0 | 0.0 | ||
| .8 | 0.0 | 4.6 | 0.0 | 0.0 | ||
| 200 | .5 | 1.4 | 30.8 | 0.0 | 0.0 | |
| .6 | 0.0 | 27.6 | 0.0 | 0.0 | ||
| .7 | 0.0 | 22.2 | 0.0 | 0.0 | ||
| .8 | 0.0 | 14.4 | 0.0 | 0.0 | ||
| 500 | .5 | 1.0 | 65.2 | 0.0 | 0.0 | |
| .6 | 0.2 | 53.8 | 0.0 | 0.0 | ||
| .7 | 0.0 | 32.4 | 0.0 | 0.0 | ||
| .8 | 0.0 | 10.6 | 0.0 | 0.0 | ||
| 1,000 | .5 | 0.0 | 83.4 | 0.0 | 0.0 | |
| .6 | 0.0 | 74.2 | 0.0 | 0.0 | ||
| .7 | 0.0 | 38.2 | 0.0 | 0.0 | ||
| .8 | 0.0 | 9.8 | 0.0 | 0.0 | ||
| Unequal | 100 | .5 | 3.2 | 4.8 | 0.0 | 0.0 |
| .6 | 3.0 | 3.4 | 0.0 | 0.0 | ||
| .7 | 2.4 | 1.4 | 0.0 | 0.0 | ||
| .8 | 1.8 | 1.0 | 0.0 | 0.0 | ||
| 200 | .5 | 6.4 | 19.2 | 0.0 | 0.0 | |
| .6 | 2.8 | 7.6 | 0.0 | 0.0 | ||
| .7 | 1.2 | 2.6 | 0.0 | 0.0 | ||
| .8 | 1.4 | 0.6 | 0.0 | 0.0 | ||
| 500 | .5 | 6.8 | 24.2 | 0.0 | 0.0 | |
| .6 | 0.6 | 16.4 | 0.0 | 0.0 | ||
| .7 | 0.2 | 3.6 | 0.0 | 0.0 | ||
| .8 | 0.2 | 0.4 | 0.0 | 0.0 | ||
| 1,000 | .5 | 3.6 | 7.6 | 0.0 | 0.0 | |
| .6 | 0.0 | 1.4 | 0.0 | 0.0 | ||
| .7 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| .8 | 0.0 | 0.0 | 0.0 | 0.0 | ||
Note. ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bolck, Croon, and Hagennarrs (Bolck et al., 2004; Vermunt, 2010); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); ML_E = ML approach assuming equal variance among classes; ML_U = ML approach assuming unequal variance among classes.
Under equal variance, few ML_E simulations led to nonconvergence for sample sizes below 500 with low entropy, especially below .6. On the other hand, the majority of ML_U simulations exhibited nonconvergence with a decrease in sample size and entropy.
Under unequal variance, the total NCR with the ML_E approach was higher than under equal variance. However, ML_U still exhibited a higher rate of nonconvergence than did ML_E under heteroskedasticity. Overall, it can be seen that nonconvergence becomes more of an issue as the sample size and entropy decreases. In summary, nonconvergence was more likely using the ML_U approach under unequal variance.
Conclusion and Discussion
LCA is a form of mixture modeling that accounts for unobserved population heterogeneity in observed response variables using latent classes and that has been widely employed in applied research in a diverse range of fields. By establishing typological classification based on a set of observed indicators and exploring relational associations between latent class membership and distal outcomes, which can be considered an external or auxiliary variable, LCA modeling can be employed to investigate a great variety of research questions.
When incorporating distal outcomes as external variables in LCA modeling, stepwise mixture modeling approaches, such as the three-step ML approach, the three-step BCH approach, and the LTB approach, have been generally recommended because their performances have been reported to be robust and stable in several previous simulation studies. However, most previous simulation research has been conducted under relatively ideal situations in which the factors that strongly influence the performance of mixture modeling approaches when a distal outcome is incorporated were set at optimal levels.
In the present study, the robustness of four LCA approaches (ML_E, ML_U, BCH, and LTB) in examining the association between latent class membership and a continuous distal outcome was investigated under more realistic conditions, including relatively smaller sample sizes and increasing levels of skewness and kurtosis within each latent class for the distal outcome variable. A total of 500 sample data sets consisting of a combination of two class-specific variance types (homoskedasticity and heteroskedasticity), four sample sizes (100, 200, 500, and 1,000), and four entropy levels (.5, .6, .7, and .8) were generated and tested using the four LCA modeling approaches to estimate the distal outcome in two studies.
The BCH approach exhibited the most robust and stable performance of the four approaches analyzed. The BCH approach generally produced less bias than the ML_E, ML_U, and LTB approaches under all investigated conditions. The robustness of the BCH approach can be attributed to the weighting method it employs in the estimation of class-specific means, with classification errors on an individual level taken into account. Its robustness was proven when it exhibited the lowest overall MSE values, a measure which quantifies the degree to which the estimated class-specific means and those of the true population differ. The stability of the BCH approach was confirmed when all of the simulations using this approach completely converged, while the ML_E and ML_U approaches led to cases of nonconvergence.
Although the BCH approach yielded unbiased estimates under most of the simulation conditions, careful application should be considered in problematic situations where the total sample size is below 200 and the expected classification quality is below .6 in terms of entropy. This is because, in these situations, even the BCH approach can produce biased estimates of class-specific means. Nevertheless, the BCH approach is superior to the other approaches in that it is able to estimate the association between class membership and distal outcomes with the most stability.
On the other hand, the bias in the estimates of the class-specific means using ML_E and ML_U differed with the type of class-specific variance. While both ML_E and ML_U performed similarly to the BCH approach under homoskedasticity, the ML_E approach under heteroskedasticity produced increasingly biased estimates as the sample size and classification quality increased, which directly contrasted with the general pattern of bias in this research. It is assumed that the low robustness of ML_E stems from its assumption of equal variance within each latent class, which conflicts with the heteroskedastic variance in the data set. This inferior performance by ML_E is supported by the MSE results. The overall MSE for ML_E was higher than that of ML_U, indicating that the variance in the estimated class-specific means was significant. The NCR was also generally high for the ML_E approach.
In contrast, the ML_U approach exhibited a robustness and stability that was comparable to BCH in all simulation conditions, even under heteroskedasticity, in terms of both bias and MSE. However, the analysis of NCRs in both Study 1 and Study 2 found that ML_U could not handle heteroskedasticity or the nonnormal distribution of distal outcomes. Thus, it is generally recommended that the ML_E and ML_U approaches be used with caution for small sample sizes and cases of low entropy.
Of the four LCA mixture modeling approaches investigated in this research, overall bias and MSE were highest for LTB, particularly, under heteroskedasticity. However, the LTB approach performed well when the variance in the distal outcome within each latent class was equal, generating a relatively low bias and MSE. The fact that the LTB approach was more biased under heteroskedasticity than the other three-step approaches is consistent with previous research (Asparouhov & Muthén, 2014b; Bakk & Vermunt, 2016; No & Hong, 2018). Even though LTB has an advantage in that no strong distributional assumptions have to be postulated, applied researchers should be cautious with its use. In particular, the LTB approach should be considered strictly nonapplicable when there are multiple distal outcomes.
Table 8 summarizes the performance of the four mixture modeling approaches investigated in this research. It shows that the BCH was the most robust and stable approach in that its biasedness and MSE were within a satisfactory range and all simulations converged without any problems.
Table 8.
Comparison of Mixture Modeling Approach Performance.
| Criteria | Variance condition | ML_E | ML_U | BCH | LTB | ||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | ||
| Bias | Equal | g | g | g | g | g | g | g | g |
| Unequal | g | g | g | g | g | g | ng | ng | |
| MSE | Equal | g | g | g | g | g | g | g | g |
| Unequal | g | g | g | g | g | g | ng | ng | |
| Convergence | Equal | g | g | ng | ng | g | g | g | g |
| Unequal | ng | ng | ng | ng | g | g | g | g | |
Note. ML = maximum likelihood–based approach (Vermunt, 2010); BCH = BCH approach, named after the developers Bolck, Croon, and Hagennarrs (Bolck et al., 2004; Vermunt, 2010); LTB = LTB approach, named after the developers Lanza, Tan, and Bray (Lanza et al., 2013); MSE = mean squared error; S1 = Study 1; S2 = Study 2; g = “good,” indicating that the performance of the approach was good; ng = “not good,” indicating that the performance of the approach was not good.
Future research should investigate the robustness and stability of the ML and BCH approaches with multiple distal outcomes and/or categorical distal outcomes, which may lead to different results to those presented in the present research. Furthermore, the effect of negative weighting (Asparouhov & Muthén, 2014b) and the underestimation of the standard error in small samples with low entropy on the performance of the approaches are also interesting research directions for the future. Recently improved LTB approaches that expand the logistic component of the model with quadratic and higher order terms (Bakk et al., 2016) or which correct standard error underestimation using bootstrap or jackknife standard error should also be explored with Monte Carlo simulation. In terms of simulation research models, longitudinal mixture modeling, growth mixture modeling, and latent transition analysis, which are employed to reveal population heterogeneity over time, could also be further examined. In addition, the performance of multilevel class-analysis models (Bennink, Croon, & Vermunt, 2013, 2015) could be investigated under the detailed simulation conditions outlined in this research.
With its diverse and more realistic simulation conditions, it is expected that this study will offer researchers useful guidance in terms of selecting LCA mixture modeling approaches for the analysis of distal outcomes. The main contribution of this study is that the nonnormality of the distal outcome was manipulated according to the degree of skewness and kurtosis, something that few studies have addressed. By taking skewness and kurtosis into account, researchers can conduct analysis that reflects realistic research situations, in which it is more likely for the distal outcome to have a skewed nonnormal distribution and a certain degree of kurtosis. This study thus offers clear guidelines for selecting the most robust approach for mixture modeling with distal outcomes in terms of outcome distribution, classification quality, and total sample size. In particular, the BCH approach is the most strongly recommended of the four tested models for the analysis of the association between latent class and distal outcomes, except for situations in which none of the approaches performed well (i.e., a total sample size less than 200 and an entropy less than .6).
LCA modeling with distal outcomes offers a greater range of research opportunities for many applied researchers, especially in the educational field, which is primarily interested in the underlying characteristics of learners. By classifying and predicting results using LCA, educational researchers can broaden their research on unobserved learner characteristics. This study thus provides useful guidelines for the use of LCA with distal outcomes.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Unkyung No  https://orcid.org/0000-0003-3358-3700
https://orcid.org/0000-0003-3358-3700
References
- Anderson K. G., Ramo D. E., Cummins K. M., Brown S. A. (2010). Alcohol and drug involvement after adolescent treatment and functioning during emerging adulthood. Drug and Alcohol Dependence, 107, 171-181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asparouhov T., Muthén B. (2014. a). Auxiliary variables in mixture modeling: Three-step approaches using M plus. Structural Equation Modeling, 21, 329-341. [Google Scholar]
- Asparouhov T., Muthén B. (2014. b). Auxiliary variables in mixture modeling: Using the BCH method in Mplus to estimate a distal outcome model and an arbitrary secondary model. Mplus Web Notes, 21(2), 1-22. [Google Scholar]
- Bakk Z., Kuha J. (2018). Two-step estimation of models between latent classes and external variables. Psychometrika, 83, 871-892. [DOI] [PubMed] [Google Scholar]
- Bakk Z., Oberski D. L., Vermunt J. K. (2016). Relating latent class membership to continuous distal outcomes: Improving the LTB approach and a modified three-step implementation. Structural Equation Modeling, 23, 278-289. [Google Scholar]
- Bakk Z., Tekle F. B., Vermunt J. K. (2013). Estimating the association between latent class membership and external variables using bias-adjusted three-step approaches. Sociological Methodology, 43, 272-311. [Google Scholar]
- Bakk Z., Vermunt J. K. (2016). Robustness of stepwise latent class modeling with continuous distal outcomes. Structural Equation Modeling, 23, 20-31. [Google Scholar]
- Bandalos D. L. (2006). The use of Monte Carlo studies in structural equation modeling research. In Hancock G. R., Mueller R. O. (Eds.), Structural equation modeling: A second course (2nd ed., pp. 385-426). Greenwich, CT: Information Age. [Google Scholar]
- Bandeen-Roche K., Miglioretti D. L., Zeger S. L., Rathouz P. J. (1997). Latent variable regression for multiple discrete outcomes. Journal of the American Statistical Association, 92, 1375-1386. [Google Scholar]
- Bauer D. J., Curran P. J. (2003). Distributional assumptions of growth mixture models: Implications for overextraction of latent trajectory classes. Psychological Methods, 8, 338-363. [DOI] [PubMed] [Google Scholar]
- Bennink M., Croon M. A., Vermunt J. K. (2013). Micro–macro multilevel analysis for discrete data a latent variable approach and an application on personal network data. Sociological Methods & Research, 42, 431-457. [Google Scholar]
- Bennink M., Croon M. A., Vermunt J. K. (2015). Stepwise latent class models for explaining group-level outcomes using discrete individual-level predictors. Multivariate Behavioral Research, 50, 662-675. [DOI] [PubMed] [Google Scholar]
- Bolck A., Croon M., Hagenaars J. (2004). Estimating latent structure models with categorical variables: One-step versus three-step estimators. Political Analysis, 12, 3-27. [Google Scholar]
- Bray B. C., Lanza S. T., Tan X. (2015). Eliminating bias in classify-analyze approaches for latent class analysis. Structural Equation Modeling, 22, 1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanaugh C. E., Messing J. T., Petras H., Fowler B., La Flair L., Kub J., . . . Campbell J. C. (2012). Patterns of violence against women: A latent class analysis. Psychological trauma: Theory, Research, Practice, and Policy, 4, 169-176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins L. M., Lanza S. T. (2010). Latent class and latent transition analysis. Hoboken, NJ: Wiley. [Google Scholar]
- Darney D., Reinke W. M., Herman K. C., Stormont M., Ialongo N. S. (2013). Children with co-occurring academic and behavior problems in first grade: Distal outcomes in twelfth grade. Journal of School Psychology, 51, 117-128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Cuyper N., Rigotti T., Witte H. D., Mohr G. (2008). Balancing psychological contracts: Validation of a typology. International Journal of Human Resource Management, 19, 543-561. [Google Scholar]
- Dziak J. J., Bray B. C., Zhang J., Zhang M., Lanza S. T. (2016). Comparing the performance of improved classify-analyze approaches in latent profile analysis. Methodology, 12, 107-116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleishman A. (1978). A method for simulating non-normal distributions. Psychometrika, 43, 521-532. [Google Scholar]
- Goodman L. A. (1974). Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika, 61, 215-231. [Google Scholar]
- Hallquist M., Wiley J. (2016). MplusAutomation: Automating Mplus model estimation and interpretation (R package version 0.6-3.9000). Retrieved from https://github.com/michaelhallquist/MplusAutomation
- Ing M., Nylund-Gibson K. (2013). Linking early science and mathematics attitudes to long-term science, technology, engineering, and mathematics career attainment: Latent class analysis with proximal and distal outcomes. Educational Research and Evaluation, 19, 510-524. [Google Scholar]
- Komro K. A., Tobler A. L., Maldonado-Molina M. M., Perry C. L. (2010). Effects of alcohol use initiation patterns on high-risk behaviors among urban, low-income, young adolescents. Prevention Science, 11, 14-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanza S. T., Tan X., Bray B. C. (2013). Latent class analysis with distal outcomes: A flexible model-based approach. Structural Equation Modeling, 20, 1-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarsfeld P. F., Henry N. W. (1968). Latent structure analysis. Boston, MA: Houghton Mifflin. [Google Scholar]
- Mathur C., Stigler M., Lust K., Laska M. (2014). A latent class analysis of weight-related health behaviors among 2-and 4-year college students and associated risk of obesity. Health Education & Behavior, 41, 663-672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCutcheon A. L. (1985). A latent class analysis of tolerance for nonconformity in the American public. Public Opinion Quarterly, 49, 474-488. [Google Scholar]
- McLachlan G., Peel D. (2004). Finite mixture models. New York, NY: Wiley. [Google Scholar]
- Mulder E., Vermunt J., Brand E., Bullens R., Van Merle H. (2012). Recidivism in subgroups of serious juvenile offenders: Different profiles, different risks? Criminal Behaviour and Mental Health, 22, 122-135. [DOI] [PubMed] [Google Scholar]
- Muthén L. K., Muthén B. O. (1998-2015). Mplus user’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Muthén L. K., Muthén B. O. (2002). How to use a Monte Carlo study to decide on sample size and determine power. Structural Equation Modeling, 9, 599-620. [Google Scholar]
- No U., Hong S. (2018). Comparison of mixture modeling approaches in latent class models with external variables under small samples. Educational and Psychological Measurement, 78, 925-951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxford M. L., Gilchrist L. D., Morrison D. M., Gillmore M. R., Lohr M. J., Lewis S. M. (2003). Alcohol use among adolescent mothers: Heterogeneity in growth curves, predictors, and outcomes of alcohol use over time. Prevention Science, 4, 15-26. [DOI] [PubMed] [Google Scholar]
- Pastor D. A., Barron K. E., Miller B. J., Davis S. L. (2007). A latent profile analysis of college students’ achievement goal orientation. Contemporary Educational Psychology, 32, 8-47. [Google Scholar]
- Petras H., Masyn K. (2010). General growth mixture analysis with antecedents and consequences of change. In Piquero A. R., Weisburd D. (Eds.), Handbook of quantitative criminology (pp. 69-100). New York, NY: Springer. [Google Scholar]
- R Core Team. (2016). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; Retrieved from https://www.R-project.org/ [Google Scholar]
- Roberts T. J., Ward S. E. (2011). Using latent transition analysis in nursing research to explore change over time. Nursing Research, 60, 73-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulbricht C. M., Rothschild A. J., Lapane K. L. (2015). The association between latent depression subtypes and remission after treatment with citalopram: A latent class analysis with distal outcome. Journal of Affective Disorders, 188, 270-277. [DOI] [PubMed] [Google Scholar]
- Vale C., Maurelli V. (1983). Simulating multivariate nonnormal distributions. Psychometrika, 48, 465-471. [Google Scholar]
- Vermunt J. K. (2010). Latent class modeling with covariates: Two improved three-step approaches. Political Analysis, 18, 450-469. [Google Scholar]
- Wicklin R. (2013), Simulating data with SAS, Cary, NC: SAS Institute. [Google Scholar]