High-efficiency single-photon generation via large-scale active time multiplexing

Time multiplexing with a low-loss adjustable optical delay line enables largely enhanced emissions of heralded single photons.

Abstract

Deterministic generation of single- and multiphoton states is a key requirement for large-scale optical quantum information and communication applications. While heralded single-photon sources (HSPSs) using nonlinear optical processes have enabled proof-of-principle demonstrations in this area of research, they are not scalable as their probabilistic nature severely limits their generation efficiency. We overcome this limitation by demonstrating a substantial improvement in HSPS efficiency via large-scale time multiplexing. Using an ultra-low loss, adjustable optical delay to multiplex 40 conventional HSPS photon generation processes into each operation cycle, we have observed a factor of 9.7(5) enhancement in efficiency, yielding a 66.7(24)% probability of collecting a single photon with high indistinguishability (90%) into a single-mode fiber per cycle. We also experimentally investigate the trade-off between a high single-photon probability and unwanted multiphoton emission. Upgrading our time-multiplexed source with state-of-the-art HSPS and single-photon detector technologies will enable the generation of >30 coincident photons with unprecedented efficiency.

INTRODUCTION

In the past two decades, photon pair sources based on spontaneous parametric downconversion (SPDC) and spontaneous four-wave mixing have been used for many groundbreaking quantum information experiments (1). However, it is very difficult to further scale up quantum information and communication applications by simply using multiple photon pair sources, since photon pairs cannot be generated deterministically; for a mean number of photon pairs per pump pulse μ, the generation probability of k photon pairs is given by μ^k/(μ + 1)^k+1. Therefore, the single pair generation probability peaks at only 25% due to the non-negligible likelihood (∼μ^k) of unwanted zero and multiple pair generations. For example, a recent 12-photon experiment (2) using six SPDC sources needed to keep μ < 0.05 to suppress the multipair emissions, resulting in a 12-photon coincidence generation rate of only <0.01/s and a final detection rate of only a small event per hour.

In 2002, Pitmann and co-workers (3) and Migdall and co-workers (4) independently proposed “multiplexing” as a technique to overcome the probabilistic nature of SPDC sources. In general multiplexing methods (see Fig. 1A), a twin photon (signal photon) generated by multimode, probabilistic SPDC processes is rerouted to a single mode by adaptive optical switches controlled in accordance with a mode analysis of the other twin photon (idler photon), whose mode is correlated (or entangled) to that of the “heralded” signal photon. In this case, the single-photon generation probability for such a multiplexed heralded single-photon source (HSPS) is no longer constrained by the 25% limit and can reach as high as a multiplexed heralding probability

$$P_H=1-{(1-p)}^N$$ (1)

where N is the number of multiplexed modes and p is the probability of a trigger detector signal per mode, i.e., approximately the product of μ and the trigger system detection efficiency η_t for one SPDC mode. Thus, for a sufficiently large number of multiplexed modes, one can achieve pseudo-deterministic generation of heralding signals and thereby heralded single photons. Since the proposals in 2002, this promising method has been theoretically analyzed and extended (5–12).

Fig. 1. Multiplexed HSPSs and our implementation.

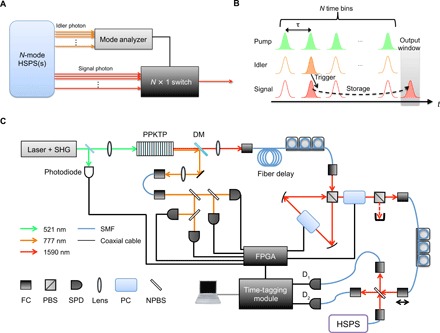
(A) Simplified diagram of a general multiplexed HSPS. Multimode SPDC source(s) probabilistically generate photon pairs in which a signal-photon state is correlated to its twin idler-photon state. According to a mode analysis of an idler photon, an adaptive N × 1 optical switch converts a signal-photon state to a predetermined output mode, e.g., time bin. (B) Timing diagram of our time-multiplexed scheme. Our HSPS pumped with a period τ (probabilistically) generates photons in N different time bins. An adjustable delay line can delay signal photons for an arbitrary integer multiple of τ so that any initial time bin state of a heralded photon is converted to a fixed output time bin. (C) Schematic diagram of our experimental setup. See Materials and Methods for experimental details. SHG, second harmonic generation; PPKTP, periodically poled potassium titanyl phosphate; DM, dichroic mirror; FC, fiber coupler; SMF, single-mode fiber; FPGA, field-programmable gate array.

For practical implementations of multiplexed HSPSs, there are two challenges in addition to large-scale multiplexing: First, losses in both HSPS and optical switches should be very low because lost single-photon states, unlike classical states of light, cannot be restored. The other challenge is to generate indistinguishable photons necessary to achieve high-visibility multiphoton interference central to most photonic quantum-gate operations (13, 14). Therefore, HSPSs and optical switches also need to generate and maintain pure single-photon states in each multiplexed mode and then convert those to an identical pure state. Some experimental attempts have demonstrated large-scale multiplexing (15, 16), low-loss photon generation/rerouting (15, 17), or indistinguishable single-photon generation (17–19), but none of previous experiments simultaneously achieves all three key requirements.

RESULTS

Experimental method

Here, we demonstrate the first large-scale and low-loss multiplexing to produce heralded single photons with very high probability and indistinguishability. To achieve such a high-quality single-photon source, we implemented a time-multiplexing system, extending the method proposed by Pittman and co-workers (3) as shown in Fig. 1 (B and C). With our method, one can implement a large-scale multiplexing with only one HSPS and adjustable delay line [which in general works as a quantum memory (20)], while other demonstrated methods, such as spatial-multiplexing (4) and frequency-multiplexing (21, 22) methods, require a number of HSPSs, and/or optical switches, and/or conversion lasers. In our time-multiplexing scheme, a HSPS pumped by N sequential pump pulses with a period τ (= 10 ns) probabilistically generates photon pairs. An adjustable delay line triggered by a heralding signal stores a heralded photon for an arbitrary integer multiple of τ. A stored photon is released at a certain predetermined output time bin regardless of its birth time bin, and thereby N time bin modes of heralded single photons are multiplexed into the single output time bin. We implemented this scheme with high-quality components: Our heralded photons at 1590 nm have 88% coupling efficiency into a first collection single-mode fiber and 91% spectral indistinguishability (23). An adjustable delay line consisting of a very low-loss optical switch [a Pockels cell (PC)] and polarizing beam splitter (PBS) and built with careful spatial-mode management has only 1.2% loss per cycle. Moreover, to maintain the temporal indistinguishability of multiplexed single photons, the cycle length is matched to τ within 0.01 ps, much less than the 6.1-ps pulse duration of heralded single photons. The delay line’s group velocity dispersion, which can also make single photons distinguishable in terms of storage cycles, is negligible for the 0.8-nm bandwidth of our single photons.

Time-multiplexed single-photon generation

We characterized our time-multiplexed photons using a setup with a nonpolarizing beam splitter (NPBS) and two single-photon detectors (SPDs) to measure single-photon counts and unwanted multiphoton contributions simultaneously. The multiplexed heralding probability shown in Fig. 2A is estimated as P_H = H/R, where H is the heralding signal rate and R = 500 kHz is the repetition rate of the multiplexing process (currently limited by our PC electric driver). Figure 2B shows the multiplexed single-photon probability estimated by

$$P_1=\frac{1}{R\mathrm{\eta }}\{S_1+S_2-C(\frac{4}{\mathrm{\eta }}-1\left)\right\}$$ (2)

where S_i is a single count rate of detector i, C is a coincidence count rate between detectors 1 and 2, and η = 0.426 is the net transmission of the optics from the second collection fiber (after the delay line) to SPDs. In Eq. 2, C is included to correct for multiphoton contributions in S₁ and S₂ (see Materials and Methods for details). Our source was tested for three different mean photon numbers per pulse: For μ = 0.18, we observed nearly saturated P_H (= 0.977) with N = 40 time bins. With this condition, we observed P₁ = 0.667(24), corresponding to E = 9.7(5) times enhancement over the nonmultiplexed case (for N = 1). To our knowledge, this is the highest single-photon probability after single-mode fiber coupling [some semiconductor single-photon sources (24–26) have demonstrated higher single-photon extraction probabilities after a first collection lens but poor coupling into a single-mode fiber, and therefore substantially poorer potential performance in any applications that requires photons in a single spatial mode; see Table 1]. With μ = 0.05 and 0.004 and N = 40, we observed (P_H, P₁) = [0.639, 0.412(13)] and [0.082, 0.051(2)], respectively. Although the heralding probabilities did not reach saturation for these lower mean photon numbers, the enhancement factors are much higher than for μ = 0.18: E = 18.7(9) and 27.9(20) for μ = 0.05 and 0.004, respectively.

Fig. 2. Experimental results.

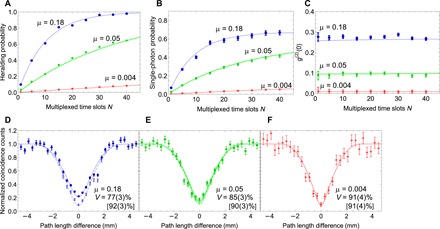
(A) heralding signal probability P_H, (B) single-photon probability P₁, and (C) second-order autocorrelation function g⁽²⁾(t = 0) versus the number of multiplexed time bins N. P_H and P₁ are significantly enhanced as N, while g⁽²⁾(0) is approximately unchanged for all different mean photon numbers μ. (D to F) Observed Hong-Ou-Mandel interference for synchronized photons with N = 40. Empty circles, squares, and diamonds in (D) to (F) show data points after subtracting accidental coincidences. Solid and dashed lines are the best-fit theoretical curves (23) for raw coincidences and those after subtracting accidental coincidences, respectively. V denotes the interference visibility without (with) subtracting accidental coincidences. Error bars are estimated by Poissonian photon counting statistics.

Table 1. Comparison of performances of single-photon sources.

MUX, multiplexed HSPS; E, single-photon enhancement factor in MUX; I, indistinguishability; C_M = P₁^MR, predicted M-fold coincidence generation rate, assuming that M-independent sources can be prepared and synchronously operated. Note that P₁ is the probability of preparing a single photon that is coupled into a single-mode fiber. For sources reported for different experimental parameters, results with conditions demonstrating the highest P₁ are shown.

References	Type of source	R (MHz)	PH	P1	E	g(2)(t = 0)	I
(32)	SPDC	~170	—	~0.02	—	~0.1	0.91
(2)	SPDC	~80	—	~0.03	—	~0.1	0.962(11)
(17)	MUX	80	~0.01	~0.001	~4	~0.5	0.887(38)
(15)	MUX	0.05	0.99	0.386(4)	5.6	0.48(3)	~0.05
(18)	MUX	10	~0.01	~0.002	2	~0.2	0.91(16)
(24)	QD	82	—	~0.001	—	0.0028(12)	0.996
(25)	QD	80	—	0.14	—	0.013	0.603(6)
(26)	QD	76	—	0.337	—	0.027	0.93
This work (MUX)	μ = 0.18	0.5	0.98	0.667(24)	9.7(5)	0.269(7)	0.92(3)
	μ = 0.05	0.5	0.64	0.412(13)	18.7(9)	0.088(7)	0.90(3)
	μ = 0.004	0.5	0.08	0.051(2)	27.9(20)	0.007(7)	0.91(4)
Possible improvement	μ = 0.1	5	0.99	0.75	12.5	0.05	0.99

Unwanted multiphoton contributions can be quantified by the second-order autocorrelation function g⁽²⁾(t = 0), which can be estimated by

$$g^{(2)}(t=0)=\frac{\mathit{CR}}{S_1{S}_2}$$ (3)

For μ = 0.18, 0.05, and 0.004, we observed g⁽²⁾(t = 0) ~0.27, ~0.09, and ~0.007, respectively, all of which were approximately constant versus N (see Fig. 2C and Table 1). This indicates that the time-multiplexing technique successfully enhances the single-photon generation probability without increasing the multiphoton noise relative to the single-photon fraction. The g⁽²⁾(t = 0) increases with μ due to higher multiphoton noise, and therefore, there is a trade-off between g⁽²⁾(t = 0) and P₁. However, as we discuss below, our observed g⁽²⁾(t = 0) can be further suppressed without reducing P₁ by introducing high-efficiency photon number–resolving (PNR) heralding detectors.

We directly measured the indistinguishability of the time-multiplexed photons by Hong-Ou-Mandel interference (HOMI) (27). For this measurement, we prepared an additional nonmultiplexed HSPS, whose heralded single photons were coupled to the second input port of the NPBS so they could be interfered with the time-multiplexed photons (see Fig. 1C). Our observed HOMI dips with N = 40 are shown in Fig. 2 (D to F) . The respective estimated visibilities with the best-fit theoretical curves (23) for μ = 0.18, 0.05, and 0.004 were V = 77(3)%, 85(3)%, and 91(4)%, respectively, with raw coincidence count rates, i.e., without accidental subtraction. Our observed visibility is lower for higher μ because of higher multiphoton noise as shown in Fig. 2B. However, for all mean photon numbers, those visibilities after subtracting background counts are ~90%, similar to that for two nonmultiplexed photons from our HSPS (23). Thus, we conclude that the spectral and temporal indistinguishability of our heralded photons is well maintained even after the multiplexing system. Moreover, the uncorrected visibility should be similarly improved by incorporating PNR detector.

DISCUSSION

Possible improvements

We expect that our demonstrated source can be made even more efficient by following feasible improvements with currently available technologies: First, for precisely and efficiently heralding only single-photon states and excluding multiphoton contributions, high-efficiency PNR detectors can be introduced. Higher efficiency detectors lower the mean photon number of the HSPS needed to achieve saturated heralding signal rates; therefore, multiphoton contributions and g⁽²⁾ can be significantly reduced while maintaining or even increasing P₁. High-efficiency superconducting nanowire detectors (28), either with a cascade configuration or with intrinsic PNR capability (29), are preferable for this improvement. Our setup for these measurements had four cascaded silicon detectors, but their ∼62% detector efficiencies enable only partial PNR capability and did not well suppress the g⁽²⁾ of our source. The spectral indistinguishability of our HSPS can also be improved by using an optimized pump laser wavelength (23). Incorporating group velocity matching conditions with custom poling of nonlinear optical crystals (30, 31) can eliminate peripheral lobes of the ordinary phase-matching function and can achieve >99% spectral indistinguishability. The system repetition rate of our demonstrated source is presently limited by the 1-MHz switching rate of available bulk PCs. However, we expect that faster devices will be available in the near future. With the feasible improvements (>95% trigger detection efficiency, multiplexing N = 100 time bins, >99% spectral indistinguishability, and R = 5 MHz, see details in the Supplementary Materials) P₁, g⁽²⁾, and indistinguishability can be enhanced to ~ 75%, ~0.05, and ~99%, respectively.

Comparison with other single-photon sources

A comparison of our source with other representative single-photon sources including nonmultiplexed SPDC sources (2, 32), multiplexed HSPSs (15, 17, 18), and semiconductor quantum dot (QD) sources (24–26) is shown in Table 1. Our source for μ = 0.18 significantly outperforms all other state-of-the-art sources in P₁ and has a single-photon indistinguishability I comparable to the best indistinguishable photon sources. The g⁽²⁾(t = 0) for μ = 0.18 is worse than semiconductor sources and is not directly applicable for multiphoton applications requiring high-visibility HOMI (as shown in Fig. 2D); however, the aforementioned improvement of trigger detectors can make it comparable, rendering our source useful for these applications. In addition, our source for μ = 0.05 still has a higher P₁ than all of the previously demonstrated single-photon sources, while its g⁽²⁾(t = 0) is lower than nonmultiplexed SPDC sources that are successfully used for 10- and 12-photon generations (2, 32). This indicates that our demonstrated source is readily applicable for demonstrations of >10-photon applications with orders of magnitude higher coincidence rates than in previous demonstrations.

We can also consider how well our methods would perform at producing multiple individual photons. Figure 3 shows predicted multiphoton generation rates C_M for our time-multiplexed HSPS, together with those of the most efficient nonmultiplexed SPDC source (2) and QD single-photon source (26). C_M = P₁^MR denotes an M-photon coincidence generation rate with the assumption that M identical sources are prepared and operated synchronously. For lower photon numbers, P₁ has less influence on C_M, and R is the relatively important factor. Our source with its lower repetition rate (R = 500 kHz) is less efficient compared to other sources. However, P₁ is very critical for higher photon numbers, and our source with very high P₁ is orders of magnitude brighter than the other sources for M > 15, while the best nonmultiplexed SPDC and QD sources are limited to create up to 10 and 17 photons with reasonably high event rates (C_M > 1/s), our source is capable of >30-photon event generation. Moreover, with the feasible improvements outlined above, even >50-photon event generation is possible; such a highly scalable resource would be critical for future photonic quantum information processing.

Fig. 3. Predicted M-photon coincidence production rate C_M for different single-photon sources.

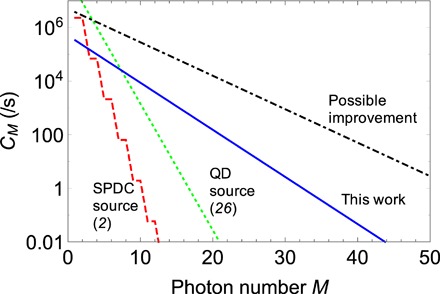
While our time-multiplexed source is less efficient for lower M due to its lower repetition rate, orders of magnitudes better success rates are expected for M > 15.

Scalability is also important for multiphoton generation. Our time-multiplexing approach can be compatible with integrated optics, which are obviously quite scalable in terms of fabrication and robustness, but mitigating loss in such a scheme remains a major challenge. Instead, scalable implementation (with a tabletop size at largest) is possible with bulk optics by efficiently extracting multiple individual photons from one source. For example, as demonstrated in (33), sequentially produced photons from one source can be efficiently stored into a large optical storage ring that can hold photons in multiple time bins. In the same experiment, photons in a storage ring have been successfully used for time bin–encoded quantum computing. One can also use a photon router (26, 34) that can distribute sequential photons from one source to different input ports of an optical circuit. Note that both schemes can be further improved by applying our time-multiplexing and low-loss optical switching techniques. Conversely, combining these photon storing and/or routing techniques with our time-multiplexed source would enable a tabletop implementation for large-scale multiphoton generation.

In summary, we have demonstrated large-scale time multiplexing for efficient and indistinguishable single-photon generation. Our HSPS and adjustable delay line developments allow multiplexing up to 40 time bin modes of heralded single photons, with very low loss and high indistinguishability. Consequently, our time-multiplexed HSPS has a significantly better single-photon emission probability than those in previous demonstrations and has expected orders of magnitude higher multiphoton event rates. Incorporating currently available technologies with our source can further improve multiphoton noise and indistinguishability, enabling the first resource for quantum applications using >50 individual photons. We anticipate that this time-multiplexed source with these unprecedented efficiencies will be an optimal resource for large-scale photonic quantum computation systems, particularly for quantum walk (35) and boson sampling (36) investigations, to demonstrate “quantum computational supremacy” over classical computation systems.

MATERIALS AND METHODS

Heralded single-photon source

A 20-mm-long periodically poled potassium titanyl phosphate crystal pumped by a frequency-doubled Yb laser (λ = 521 nm, τ = 10.0 ns) generated collinear photon pairs via SPDC. Idler photons at 777 nm were detected by a cascade of four Si avalanche photodiode detectors, each of which has a ∼62% detection efficiency. The detector cascade allowed us to reduce the effect of each SPD’s saturation and to resolve the approximate photon number in a time bin. Signal photons at 1590 nm were sent to an adjustable delay line via a (fixed) fiber delay line. With a group velocity matching condition in the SPDC process, 91% spectral indistinguishability of heralded single photons were achieved without spectral filtering (23). Transmission probabilities for idler and signal photons after a first collection fiber were 84 and 88%, respectively. Similar performance was observed in another nonmultiplexed HSPS used for HOMI measurements. For this latter nonmultiplexed HSPS, we used μ = 0.008 so that unwanted multiphoton states degrade the HOMI visibilities only ~1%.

Fixed predelay line

The heralded photons were first directed into a 100-m fiber delay line, which holds the photons for ~500 ns. This compensates for the electronic latencies (~100 ns from a trigger photon to firing the PC); the rest of the delay (~400 ns) allowed us to select the latest heralded time bin for up to N = 40. Storing only the “latest-born” heralded photon minimizes the number of storage cycles and the associated loss (15). Lengthening a delay fiber makes it possible to extend the number of multiplexed time bins N, enabling a saturated P_H with lower μ. However, this may require more careful group velocity dispersion management and fiber length stabilization. Our current 100-m-long dispersion-shifted fiber in our temperature-stabilized laboratory is sufficiently stable without these additional efforts. After the fixed fiber delay, the photons were directed into the adjustable delay.

Adjustable delay line

Our adjustable delay line consisted of a 10-ns delay loop, custom Brewster-angled PBS, and a PC comprising a pair of rubidium titanyl phosphate crystals. The spatial modes of the loop were stabilized by two concave mirrors, each of which has radius of curvature of 1.00 m. A field-programmable gate array module processes input signals from four trigger SPDs, triggering the PC. When a heralded photon enters into the delay line through the PBS, the PC was activated, rotating that photon’s polarization by 90° to store and delay it in the loop. After delaying for the necessary integer multiples of τ = 10 ns, the stored photon was released by a second switching of the PC. The single-pass cavity loss is 1.2%, corresponding to a photon 1/e lifetime of ~830 ns (= 83 cycles). The slight loss is due to the loss in the PC (0.8%) and two concave mirrors (0.2% for each). The group velocity dispersion of the adjustable delay line is ~1.2 × 10⁻³ ps² per cycle, negligibly small compared to the photon coherence time (6.1 ps). Thus, the cycle-dependent chromatic dispersion, which could degrade spectral indistinguishability of the synchronized photons, is negligible for up to N = 40. Our delay line was built with high mechanical stability optics mounts in a temperature-stabilized laboratory and has a small long-term cycle length drift (∼0.01 ps/hour), much less than the 6.1-ps single-photon pulse duration. A PC and PBS after the delay line comprise an optical shutter that only transmits photons heralded in an allowed output time bin.

Estimation of P₁

We estimated a single-photon probability P₁, assuming that the probability of more than two photons is negligibly small; a multiplexed k-photon probability P_k for k ≥ 3 is expected <1.5% of P₁ for μ = 0.18 in our experiment. We modeled our SPDs as bucket detectors that discriminate between zero and one or more photons. The NPBS’s transmission/reflection ratio is also assumed to be 1. With those assumptions, single and coincidence count rates are given by

$$S_i=\frac{P_{1}R\mathrm{\eta }}{2}+P_{2}R\{\frac{\mathrm{\eta }}{2}+\frac{\mathrm{\eta }(2-\mathrm{\eta })}{4}\}$$ (4)

$$C=\frac{P_{2}R{\mathrm{\eta }}^2}{2}$$ (5)

where P₂ is the probability of a two-photon state after multiplexing. The second and third terms in Eq. 4 are the respective detector click probabilities that one and two of two photons arrive at detector i. Equation 2 is obtained by substituting Eq. 5 into Eq. 4.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/10/eaaw8586/DC1

Table S1. Experimental parameters.

Reference (37)