Microwheels on Microroads: Enhanced Translation on Topographic Surfaces

Abstract

Microbot locomotion is challenging because of the reversible nature of microscale fluid flow, a limitation that can be overcome by breaking flowfield symmetry with a nearby surface. We have used this strategy with rotating wheel-shaped microbots, μwheels, that roll on surfaces leading to enhanced propulsion and fast translation speeds. Despite this, studies to date on flat surfaces show that μwheels roll inefficiently with significant slip. Taking inspiration from the mathematics of roads and wheels, here we demonstrate that μwheel velocities can be significantly enhanced by changing microroad topography. In this, we observe that periodic bumps in the road can be used to enhance the traction between μwheels and nearby walls. While continuous μwheel rotation with slip is observed on flat surfaces, a combination of rotation with slip and non-slip flip occurs when μwheels roll upon surfaces with periodic features, resulting in up to four-fold enhancement in translation velocity. The surprisingly fast rolling speed of μwheels on bumpy roads can be attributed to the hydrodynamic coupling between μwheels and road surface features, allowing non-slip rotation of entire wheels along one of their stationary edges. This road/wheel coupling can also be used to enhance μwheel sorting and separation where the gravitational potential energy barrier induced by topographic surfaces can lead to motion in only one direction and to different rolling speeds between isomeric wheels, allowing one to separate them not based on size but on symmetry.

Introduction

Microscale propulsion has attracted significant interest in recent years because of the desire for self-directing in vivo devices (1, 2) and the challenging nature of low Reynolds number flows (3). External field-based approaches, especially those employing magnetic fields, are among the most promising because they are inherently non-contact and require no chemical fuel. To enable propulsion induced by magnetic torque (4, 5) and without addition of external forces or field gradients, microbot symmetry must be broken with either appropriately designed shape (6–9) or with proximity to walls (10–20). Fabricating asymmetric microdevices of suitable geometry can be challenging however, motivating wall-based methods such as microwalkers (10), artificial cilia (11), microworms (12), microcarpets (13), microwheels (μwheels) (14, 17), microlassos (18) and microswimmer swarms (15, 16, 19, 20).

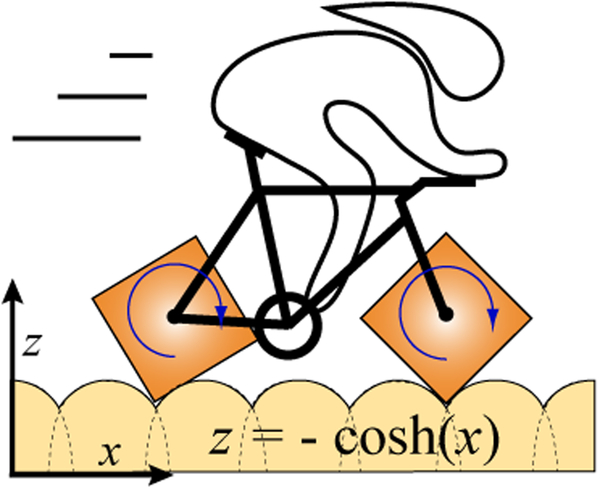
Smooth surfaces however are associated with significant slip, with inefficiencies that set the upper limit on translation velocity. Here, we identify surface topographies that register with μwheel structure, taking inspiration from the mathematics of roads and wheels where it can be shown that, for any given wheel shape, there is a complementary road for optimal translation (21, 22). For example, smooth-riding bicycles can be made with square-shaped wheels on roads constructed from a series of truncated catenaries (Fig. 1). In this manuscript, we investigate the translation of μwheels of varying size and shape on surfaces designed to mimic their corresponding ideal roads with the goal of enhancing translation velocity. In doing so, we develop methods where wheels of different structure interact differently with different roads, providing opportunities for not only faster devices but also for μwheel separations and sorting, paving the path towards designing micro- and nano-devices capable of enhanced translation, control and movement within real topographically-complex environments.

Figure 1.

Square-wheeled bicycles can translate smoothly on roads constructed from truncated catenaries.

Discussion

μWheel translation on flat surfaces

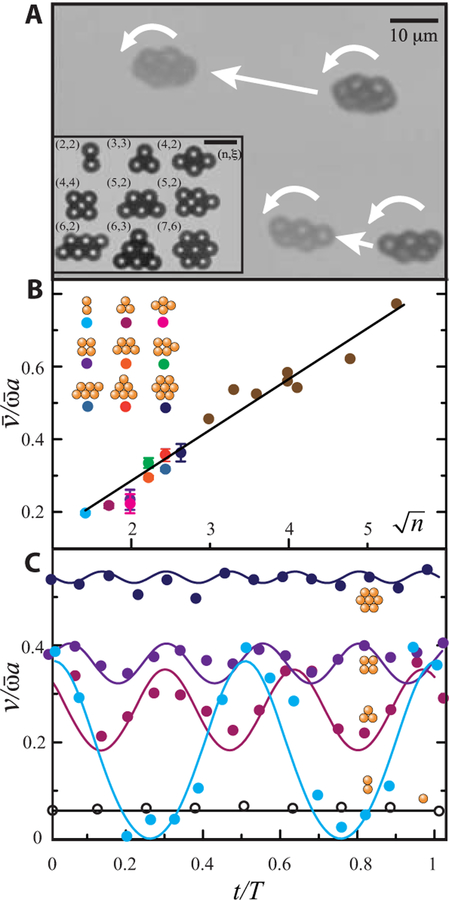
Building upon previous work where we have demonstrated that colloidal devices such as pumps and valves can be assembled in 2D with external fields (23, 24), we have recently demonstrated that uniform 3D magnetic fields can create colloid-based μwheels capable of rapid translation on flat surfaces (14, 17). In this, negatively charged superparamagnetic particles of radius a, denser than their surrounding solvent, assemble into close-packed μwheels via isotropic interactions induced by an in-plane rotating magnetic field, $B_{xy}\text{cos}\left({\omega }_{M}t\right)\widehat{x}+B_{xy}\text{sin}\left({\omega }_{M}t\right)\widehat{y}$, where B_xy is the field strength, ω_M/2π is the applied field frequency, and $\widehat{x}$ and $\widehat{y}$ are directional unit vectors (Fig. S1). In studies here, we irreversibly bind μwheel constituent particles together with the addition of positively-charged polyelectrolytes (poly(diallyldimethylammonium chloride)) during assembly, yielding a mixture of μwheels of varying size and morphology (Fig. 2A inset). We characterize these μwheels with the number of constituent particles n and the degree of rotational symmetry ξ.

Figure 2.

μWheel translation on flat surfaces. A) A 5-mer (5,2) and a 7-mer (7,6) translate at different velocities in the same applied field. Inset: μwheels of different size (1 < n < 7) and symmetry (2 < ξ < 6). Scale bars: 10 μm. B) Time-averaged velocity (normalized by the frequency and particle radius) of μwheels of different size (2 < n < 29). Brown dots correspond to μwheels with n>7. C) Instantaneous velocity profiles for singlet (1,1), dimer (2,2), trimer (3,3), square (4,4), and 7-mer (7,6) μwheels. Symbols are experimental measurements and solid lines are calculations based on Eqn. 2 and S6, where T is one full rotational period.

In the presence of an in-plane rotating magnetic field, fabricated μwheels lie flat and spin on a surface without net translation; however, upon application of an additional AC field along the z-direction, $B_z\text{cos}\left({\omega }_{M}t+\phi \right)\widehat{z}$, where φ is the phase lag between the z- and xy-component, μwheels stand up and roll (Fig. 2A and Movie S1). Specifically, they incline relative to the surface and spin in the same plane as the field at a camber angle θ_c = tan⁻¹(B_xy/B_z). The angular rotational frequency ω of a μwheel is related to the applied angular field frequency ω_M as

$$\begin{gathered} \omega ={\omega }_M,{\omega }_M\le {\omega }_c \\ \omega ={\omega }_M-\sqrt{{\omega }_M^2-{\omega }_c^2},{\omega }_M>{\omega }_c \end{gathered}$$ (1)

where ω_c is the critical frequency related to the overall applied field strength (25). In this work, we typically run experiments with 0.628 ≤ ω_M ≤ 314 rad/s. For two-dimensional disc-like μwheels, the time-averaged translation velocity $\overline{\nu }\propto \omega R_n$ with radius $R_n\propto \sqrt{n}a$, leading to $\stackrel{-}{\nu }/\omega a\propto \sqrt{n}$. Supporting this scaling, experiments show that larger μwheels roll faster on flat substrates (Fig 2B) and μwheels of similar size, such as diamond and square-shaped tetramers, roll with similar velocity. We note that the slope of the line in Fig. 2B, $\stackrel{-}{\nu }/\omega R_n$ is far from unity (~ 0.1), indicating significant slip during rolling, consistent with earlier studies (14, 17).

Since μwheels are assembled from individual spherical colloidal building blocks, their perimeter is not strictly circular. As a result, μwheel translation on flat surfaces is influenced by geometry and the specific manner in which μwheels interact with the surface. This is seen in Fig. 2C, where the instantaneous velocities of μwheels over one period of rotation demonstrate oscillations inversely proportional with their degree of rotational symmetry. To describe this observation, we model the rolling of μwheels of different size and symmetry on flat surfaces by extending the analysis of Tierno, et al. (26, 27). While greater detail can be found in the Supplementary Information, here we focus on dimers (n=2, ξ=2), whose motion is shown in Movie S2 and Fig S2B. In this case, the instantaneous velocities parallel v(t) and perpendicular v_z(t) to the substrate can be written as

$$\frac{\nu \left(t\right)}{V_0}=\frac{dx}{dt}=-\frac{1}{2}\left({\beta }_2-{\beta }_1\right)\text{cos}\left(\omega t\right)\frac{{\nu }_z\left(t\right)}{V_0}=\frac{dh}{dt}=\frac{1}{2}\left({\alpha }_2-{\alpha }_1\right)\text{sin}\left(\omega t\right)$$ (2)

where x and h are the displacements of a dimer parallel and perpendicular to the substrate based on the center-of-mass. V₀ = 4ωaf/3 is a characteristic velocity, where f(a/h) is a correction factor that accounts for the rotation of a sphere near a wall (28–30)(see SI Section 2). β_i and α_i are the hydrodynamic mobilities of lobe i moving parallel and perpendicular to the substrate and are functions of the lobe-wall separation h_i. In our work, since μwheels are very close to the substrate, we use expressions (Eqn. S3) based on asymptotic lubrication theory (31), which provides the correct limits that α_i, β_i → 0 when the contact distance a/h_i → 1.

We solve Eqn. 2 for dimers and plot the instantaneous velocities in Figs. S2B and S2C. In our calculations, we set the initial separation between the μwheel edge and the substrate to 0.2a = 450 nm, determined by balancing the buoyancy force on the μwheel and the electrostatic repulsion between the μwheel and the substrate. We see that v(t) varies with the dimer orientation during rolling and reaches a maximum when the dimer stands up and a minimum when it is parallel to the surface. This behavior arises from the difference in the hydrodynamic mobilities (β₁ − β₂) between lobes which depends on lobe-wall separations h₁ and h₂ (Eqn. S3). When a dimer is suspended in bulk fluid far away from the substrate, no net translation is expected because their mobilities are equal, β₁ = β₂ = 1; similarly, when a dimer is very close to the substrate but lies parallel with both lobes equally separated from the substrate, v = 0 since, once again, the mobilities equal and β₁ = β₂ = 0. When the dimer stands up however, the difference in mobilities β_i is largest and the dimer has the greatest speed. Matching μwheel symmetry, the dimer orientation changes twice per rotation as does the velocity. We note that during rotation the μwheel center of mass does not remain a constant distance from the substrate (Fig. S2C), rather it oscillates with the same period as its lateral velocity because of differences in mobilities α_i between lobes. Indeed, only perfectly circular wheels such as monomers roll with their center of mass constant elevation above a flat substrate. Note that over the course of rotation our modeling predicts only ~0.1a oscillation from the average center-of-mass to substrate separation, a short distance that explains relatively smooth rolling during dimer translation. This can also be observed by tracking the displacement of the centers of mass of both lobes, which exhibit a charactristic 180° phase difference (Fig. S2D). By solving Eqn. S6 for μwheels with different degrees of symmetry (2 ≤ ξ ≤ 6), we observe similar features in v and v_z. As shown in Fig. 2C, predictions for the lateral velocities v correspond to our experimental data.

μWheel translation on periodic topographic surfaces

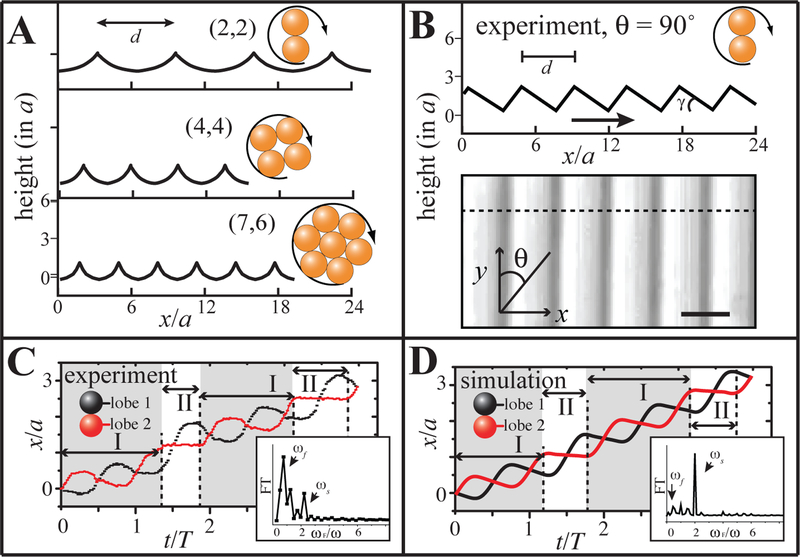
On flat surfaces, μwheels demonstrate significant slip (~90%) because the μwheel-wall hydrodynamic interaction contributes weakly to net translation. We improve coupling and increase translation velocities by introducing periodic features on the substrate. In our case, as wheel shape varies, substrate structure can be modified to accommodate, most simply by changing road periodicity and spacing to match wheel features. Ideal substrates for rolling without slip for μwheels of different symmetry can be predicted numerically (Fig. 3A and see SI for details).

Figure 3.

μWheel translation on topographic surfaces. (A) The calculated commensurate “roads” for μwheels of size n = 2, 4, and 7 where optimal spacings d are 6.3a, 3.8a, and 3.1a. (B) Experimental geometry (measured by AFM along θ = 90°) with minimum spacing of d = 4.4a and blaze angle γ = 26°; spacing can be readily increased by lowering translation angle θ. Maximum height = 1.7a and arrow indicates blaze direction. Scale bar: 4 μm. (C) Experimental measurement of displacement of the centers of mass of two dimer lobes with time rolling along θ ~ 90° against the blaze direction. Mode I: rotation with slip; Mode II: non-slip flipping. (insets: Fourier transform of the instantaneous velocity). (D) Calculated displacement of the centers of mass of two lobes of a dimer rolling along a textured surface with trapezoidal bumps (Fig. S3B) Insets show the Fourier transforms of the instantaneous velocity.

To mimic continuous surfaces with repeating catenary features we fabricate topographic surfaces using polydimethylsiloxane (PDMS) replicas of linear diffraction gratings (Fig. 3B). Experimental measurement by atomic force microscopy (AFM) shows the spacing between ridges = 9.9 μm, maximum height of 3.83 μm, and blaze angle of γ = 26°. One of the advantages of this surface is that effective spacings between ridges can be varied by simply changing μwheel rolling angle θ (Fig. 3B). We begin with dimers where, by tracking the center of mass of each lobe, we identify two distinct translation modes during rolling (Fig. 3C and Movie S3). Mode I occurs when dimers translate between two peaks, during which they rotate along their center of mass, evidenced by the characteristic 180° phase difference between lobes. This mode is the same as observed on flat substrates (Fig. S2D) and is associated with weak wheel-surface interaction, significant slip, and a relatively low net translation velocity. With addition of surface features however, a second mode, Mode II, appears where μwheels approach and flip over peaks. In Mode II, the lobe adjacent to the peak remains almost motionless while the other rotates approximately a full dimer length; essentially the dimer flips without slip. This is reflected by the almost constant lateral position for the red lobe during Mode II in Fig. 3C. As dimers roll on these periodic surfaces, these two modes alternate, effectively via “slip and flip”, leading to a faster net translation velocity on patterned surfaces than on flat ones.

To better understand the slip and flip translation of μwheels on textured surfaces, we again use Eqn. 2 but now incorporate surface topography h_s(x) into the mobilities α_i and β_i in Eqn. S3 via h₁ = h + a cos ωt − h_s(x + a sin ωt) and h₂ = h − a cos ωt − h_s(x + a sin ωt), where h₁ (h₂) is the separation between the center of lobe 1 (lobe 2) and the patterned substrate (Fig. S3A). We note that this method is an approximation, as the calculation of exact sphere mobilities near non-flat surfaces is nontrivial and only the influence of walls with small-amplitude, sinusoidal deformations have, to date, been reported (32). As a result and instead of modelling the rolling of dimers along surfaces that exactly match our experiments, we use small trapezoidal bumps to represent microroad surface features. As shown by h_s(x) in Fig. S3B, the spacing between bumps d is 4.4a, the same as that between gratings in our experiments. The height and length of the bumps are then tuned to be 0.38a and 0.2a, so that the dimer rolls at the same time-averaged speed as observed in our experiments. The instantaneous velocities parallel (v^p) and perpendicular $\left({\nu }_z^p\right)$ to the topographic substrate can then be solved numerically (Eqns. 2, S3, and S8) and their motion shown (Movie S4). In Fig. 3D, we plot the lateral displacement of the center-of-mass of each dimer lobe. Interestingly, we also observe the appearance of the translation Mode I slip characterized by a 180° phase difference and Mode II flip with almost zero displacement of one lobe (the red line in Fig. 3D). By further examining Movie S4, we find that the existence of bumps on the road makes lobe 2 (red) contact the bump closely. As a result, its parallel and perpendicular hydrodynamic mobilities are almost zero following lubrication theory (11, 30). Therefore, lobe 2 remains stationary while lobe 1 (black) rotates along lobe 2’s center of mass, leading to a flip. Since α₂, β₂ ~ 0, the difference in mobilities between the two lobes, and hence the translation velocity, is at a maximum during flip. This model reveals that non-circular μwheels can roll faster on appropriate bumpy microroads due to the hydrodynamic coupling and the resulting non-slip flip. Although the sawtooth-like surface topography in our experiments is more complicated, the simplified trapezoidal bumps in our modeling captures the underlying physics. In fact, when we set a very small initial separation of 0.05a between the dimer edge and flat substrate in simulations, we observe sequential lobe flips instead of normal rolling (Movie S5). This again is due to the dramatic mobility drop of one lobe that is very close to the substrate while the other lobe simply rotates around it.

The slip and flip modes are also apparent via Fourier transform of the instantaneous μwheel translation velocity v^p (Figs. 3C–3D insets), where two frequency peaks arise. The first frequency, the slip frequency ω_s, is related to the angular rotational frequency and μwheel symmetry, ω_s = ξω. The second frequency, the flip frequency ω_f, is related to how often a μwheel encounters a surface peak, governed by the surface feature spacing d and μwheel rolling angle θ : ${\omega }_f=2\pi {\overline{\nu }}^p\text{sin}\theta /d$, where ${\stackrel{-}{\nu }}^p$ is the average μwheel lateral translation velocity on a topographic surface.

With a combination of slip and flip, ${\stackrel{-}{\nu }}^p$ can be expressed as ${\overline{\nu }}^p=\frac{{\int }_0^{{\tau }_s}{\nu }_{s}dt+{\int }_0^{{\tau }_f}{\nu }_{f}dt}{{\int }_0^{\tau }dt}=\frac{{\tau }_s}{\tau }{\overline{\nu }}_s+\frac{{\tau }_f}{\tau }{\overline{\nu }}_f$, where v_s and v_f as well as τ_s and τ_f are the instantaneous translation velocities and periods for the slip and flip motion with τ = τ_s + τ_f. Note that τ_f and τ are related to ω_s and ω_f by τ_f = 2π/ζω = 2π/ω_s and τ = 2π/ω_f. If we define C_s and C_f as the propulsion coefficients for slip and flip, then ${\stackrel{-}{\nu }}_s=C_s\omega R_n$, ${\stackrel{-}{\nu }}_f=C_f\omega R_n$, and ${\stackrel{-}{\nu }}^p=\omega R_n\left[\left(1-\frac{{\omega }_f}{{\omega }_s}\right)C_s+\frac{{\omega }_f}{{\omega }_s}{C}_f\right]$. Recalling that the average μwheel translation velocity on flat surfaces $\stackrel{-}{\nu }=C\omega R_n$ (Fig. 2B), the ratio of average translation velocities becomes proportional to ω_f/ω_s as

$$\frac{{\overline{\nu }}^p}{\overline{\nu }}=\left(\frac{C_f}{C}-\frac{C_S}{C}\right)\frac{{\omega }_f}{{\omega }_S}+\frac{C_f}{C}.$$ (3)

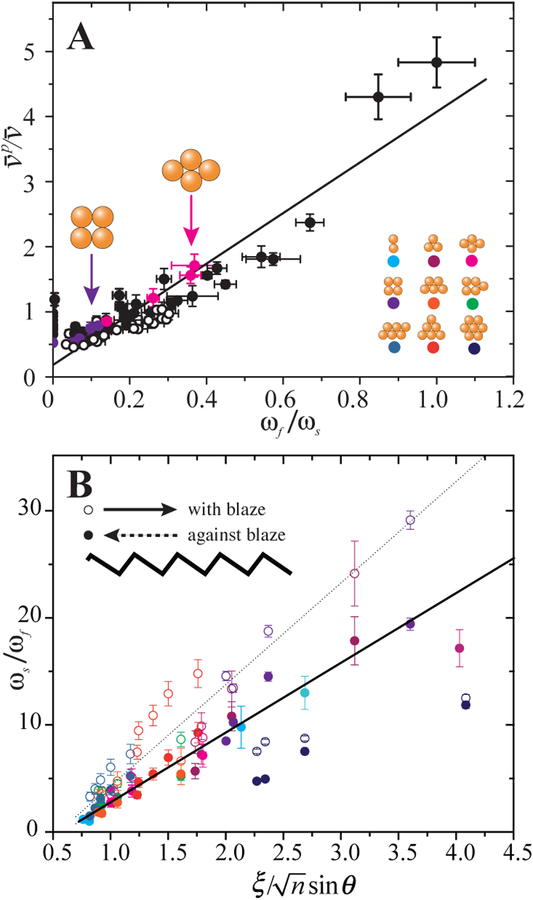
Following Eqn. 3, we measure ${\overline{\nu }}^p$, ω_s and ω_f for rolling μwheels of different size and symmetry at different rolling angles θ, both along and against the blaze direction (Fig. 4A). We fit experimental data with Eqn. 3 to find C_f/C = 4.07, C_s/C = 0.22. The ratio C_s/C < 1 indicates some slowing down in the flip mode along θ = 0° due to channel edges. The ratio C_f/C > 1 indicates that efficient flipping leads to roughly four-fold faster net translation velocity on topographic surfaces. Indeed, by adjusting the spacing between bumps on the microroad, we can completely eliminate the slip mode, allowing the dimer to flip continously as shown in Movie S6. Via substitution of Eq. 3, the ratio of ω_s/ω_f becomes

$$\frac{{\omega }_s}{{\omega }_f}=\frac{\xi \omega d}{2\pi {\overline{\nu }}^p\text{sin}\theta }=\left(\frac{d}{2\pi a{C}_s}\right)\cdot \frac{\xi }{\sqrt{n}\text{sin}\theta }+\left(\frac{C_f}{C_s}-1\right)$$ (4)

suggesting a linear relationship between ω_s/ω_f and $\xi /\sqrt{n}\text{sin}\theta$. This is observed experimentally (Fig 4b) where deviations for 7-mers can be attributed to effectively smaller symmetry degrees. In addition, the bigger slope associated with rolling along the blaze indicates a longer time required to climb inclined surfaces between peaks, a feature not included in our simple model.

Figure 4.

(A) The ratio of topographic to flat surface μwheel average translation velocities ${\stackrel{-}{\nu }}^p/\stackrel{-}{\nu }$ with the ratio of spatial/rotational frequency ω_f/ω_s. Open and closed symbols represent with and against the blaze direction. The line is a fit from Eqn. 3. (B) The dashed line is a fit with the blaze, the solid line against the blaze direction. Symbols identical to those of Fig. 2B.

A μwheel “rectifier”

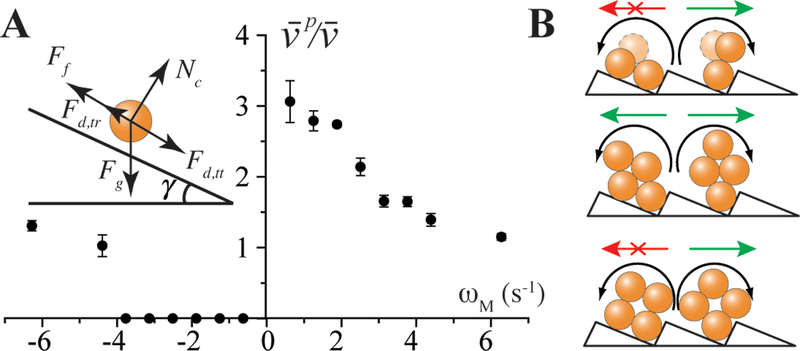
One advantage of constructing surfaces from diffraction gratings is that the surface feature slope is steeper in one direction of travel, the blaze direction, than the other (Fig. 3B) allowing us to investigate the impact of energy barrier on rolling. If the magnetic field frequency is below a critical value, dimers will be trapped between surface features when rolling against the blaze direction (Fig. 5 and Movie S7). If the direction is switched however, dimers translate readily at all field rotation frequencies, a rectifying effect that can be understood by considering the relevant forces (33, 34). For a μwheel rolling along a surface slope with angle γ (Fig. 5A inset), μwheels experience (i) a translation-rotation coupling hydrodynamic force $F_{d,tr}~6\pi \eta \omega R_n^2$ where η is the solvent viscosity, (ii) a gravitational force F_g = mgsinγ where $m=n\mathrm{\Delta }\rho \left(\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi a^3\right)$ is the effective μwheel mass, and (iii) a wet friction force F_f = μ_kmg cos γ here μ_k is the kinetic friction coefficient. The balance between these three forces determines whether a μwheel can overcome the geometric barrier to reach the next surface peak or, if F_f + F_d,tr < F_g, be trapped. Since F_d,tr is proportional to the angular rotational frequency ω, there exists a critical frequency ω* below which the dimer does not translate. By letting F_f + F_d,tr ~ F_g, we estimate that ω* ~ 3.73 rad/s for dimers rolling along θ = 90° against the blaze direction, close to the experimentally determined value (ω*~3.77 rad/s). Also aiding translation here is that the slope length along the blaze direction is shorter than the dimer long axis allowing it to easily roll over surface peaks without having to overcome the larger gravitational energy barrier (Fig. 5B). For μwheels larger than the slope length in either direction, diamond-shaped tetramers for example, rectifying disappears as they can translate in either direction at all frequencies. On the other hand, the square-shaped tetramer can only move with the blaze direction at all frequencies.

Figure 5.

(A) The ratio of dimer translation velocities on topographic/flat surface ${\stackrel{-}{\nu }}^p/\stackrel{-}{\nu }$ with field frequency. Negative frequencies indicate propulsion direction again the blaze direction. The inset shows the force balance on the μwheel. (B) Illustration of the “rectifier” effect for dimer (2,2), diamond (4,2), and square (4,4) μwheels.

Separation of isomeric μwheels by symmetry

For a given rotation rate and on flat surfaces, μwheel size is the most important factor in determining velocity and isomeric μwheels roll at approximately the same speed; for example, diamond- and square-shaped tetramers translate at similar velocities (Fig. 2A and Fig. 6A) and they cannot be easily separated from each other. Topographic surfaces however can be exploited to separate isomeric μwheels. For example, diamond wheels interact more effectively with the textured surfaces than squares with (ω_f/ω_s)_diamond > (ω_f/ω_s)_square (Fig. 4A). With a larger velocity enhancement for diamond μwheels (Fig. 4B) one can separate them from square μwheels by rolling them simultaneously on the same textured surface (Fig. 6B and Movie S8). An alternative approach to separate isomers is to take advantage of the “rectifier” effect and manipulate the applied field frequency as there is a frequency range within which the difference in the change of gravitational energy during rolling between diamond and square wheels is large enough so that diamond wheels translate continuously while square wheels remain stationary (Fig. 6C and Movie S9). Our observations are reminiscent of physical methods that rely on geometric constraints such as arrays of posts or obstacles to bias the net transport direction of objects of different size including cells and colloids for separations (35–37). Instead of size, here we utilize the coupling between translation speed and symmetry of objects induced by patterned surfaces, offering a new way to separate microscopic objects.

Figure 6.

Composite images of diamond and square μwheels translating on an (A) flat surface vs. on a (B) textured surface (against the blaze direction) with the same time interval under identical field conditions (Movie S8). (C) A diamond and square translating against the blaze under low magnetic field frequency (Movie S9).

Conclusion

We have investigated the rolling of superparamagnetic μwheels of different size and symmetry driven by a rotating magnetic field on flat and textured surfaces. On flat surfaces, the overall translation speed of μwheels is governed by their size with significant slip during rotation. With addition of periodic features on the surface however, we observe two alternating translation modes, slip and flip, which are tied to surface topography. The flip mode arises because of the hydrodynamic coupling between the textured surface and the μwheel, which allows simple rotation of the whole wheel along one of its stationary edges. Since the flip motion shows no slip, the overall μwheel translation velocity is significantly enhanced. We further demonstrate that the unique propulsion behavior of μwheels on topographic surfaces can be utilized for separation of isomeric μwheels of different symmetry. The hydrodynamic coupling between textured surfaces and μwheels revealed in our study could lead to more efficient propulsion of microdevices in topographically complex environments.

Materials and Methods

Materials.

Dynabeads^® M-450 epoxy (4.5 μm in diameter) were obtained from Thermo Fisher Scientific Inc. Poly(diallyldimethylammonium chloride) (PDADMAC, M_w = 40–50k) was purchased from Sigma-Aldrich Co. LLC. and used as received. Polydimethylsiloxane (PDMS) (Sylgard 184 Kit) was purchased from Dow Corning.

μWheel fabrication.

To assemble and permanently link μwheel constituent particles, a mixture of 20 μL Dynabeads^® M-450 epoxy (10 mg/mL) and 200 μL 1% poly(diallyldimethylammonium chloride) (M_w = 40–50k) was placed under an x-y planar rotating magnetic field (B_xy = 5–6 mT) at room temperature for 20–30 min. In this process, μwheels of differing size and structure were formed, each irreversibly bound due to bridging of the positively-charged polyelectrolytes across negatively-charged Dynabeads^® composing each wheel.

Topographic surface fabrication.

We fabricated polydimethylsiloxane (PDMS) replicas of diffraction gratings (Thorlabs) of known spacing (100 lines/mm, #GR2550–10106). In this, a commercially available PDMS two-component kit was used where a mixture of elastomer and curing agent (10:1) was poured over the grating and cured under vacuum for 60 min. Once cured, PDMS replicas were peeled from the masters and placed on a cleaned glass slide for use.

Magnetic field control.

A 3D magnetic field was created with five air-cored copper solenoid coils (50 mm inner diameter, 51 mm length, and 400 turns with current capacity of 3.5 A) as shown in Fig. S1A. Current signals controlled by Matlab (Mathworks, Inc.) and an output card (National Instruments, NI-9263) were amplified (KEPCO, BOP-40–5m) and then passed through those coils to generate the magnetic field. In-time signal monitoring was performed via a data card (National Instruments, NI-USB-6009) and gaussmeter (VGM Gaussmeter, Alphalab, Inc.). μWheel propulsion was captured at a frame rate of 200 fps via CCD camera (Epix, Inc., SV643M) mounted on an inverted microscope (Olympus, IX 71).

Supplementary Material

main

Fig. S1 Experimental setup and the rolling of a μwheel under a 3D magnetic field.

Fig. S2 μWheels translating on flat surfaces.

Fig. S3 Schematics for modelling the rolling of a dimer on a textured surface and textured surface with trapezoidal bumps used in the simulations.

Fig. S4 Calculation of an ideal road for a square (4,4) μwheel translating without slip.

movie S9

Movie S9 Translation of a diamond and square against the blaze direction.

movie S1

Movie S1 Translation of a 7-mer and a 5-mer under a 3D magnetic field on a flat surface.

movie S2

Movie S2 Top: Simulation of a dimer translating on flat surface (by solving Eqn. 2) with same rotation frequency in experiments. Bottom: Translation of a dimer under a 3D magnetic field on a flat surface.

movie S3

Movie S3 Translation of a dimer under a 3D magnetic field on a topographic surface along the blaze direction.

movie S4

Movie S4 The simulated translation (slip and flip) of a dimer on a topographic surface with evenly spaced trapezoidal bumps.

movie S5

Movie S5 The simulated translation (sequential flip of two lobes) of a dimer on a flat substrate.

movie S6

Movie S6 The simulated translation (continuous flip) of dimer on a topographic surface with trapezoidal bumps spaced by d=1.39a.

movie S7

Movie S7 The rectifier effect for the translation of a dimer under a 3D magnetic field on a topographic surface.

movie S8

Movie S8 Comparison of a diamond and square μwheel translation on the flat (top) vs. topographic surface against the blaze direction (bottom).