A framework for measuring the time-varying shape and full-field deformation of residual limbs using 3D digital image correlation

Abstract

Effective prosthetic socket design following lower-limb amputation depends upon the accurate characterization of the shape of the residual limb as well as its volume and shape fluctuations.

Objective

This study proposes a novel framework for the measurement and analysis of residual limb shape and deformation, using a high-resolution and low-cost system.

Methods

A multi-camera system was designed to capture sets of simultaneous images of the entire residuum surface. The images were analyzed using a specially developed open-source three-dimensional digital image correlation (3D-DIC) toolbox, to obtain the accurate time-varying shapes as well as the full-field deformation and strain maps on the residuum skin surface. Measurements on a transtibial amputee residuum were obtained during knee flexions, muscle contractions, and swelling upon socket removal.

Results

It was demonstrated that 3D-DIC can be employed to quantify with high resolution the time-varying residuum shapes, deformations, and strains. Additionally, the enclosed volumes and cross-sectional areas were computed and analyzed.

Conclusion

This novel low-cost framework provides a promising solution for the in-vivo evaluation of residuum shapes and strains, as well as the potential for characterizing the mechanical properties of the underlying soft tissues.

Significance

These data may be used to inform data-driven computational algorithms for the design of prosthetic sockets, as well as of other wearable technologies mechanically interfacing with the skin.

I. Introduction

The residual limbs of people with lower-limb amputation undergo considerable changes in volume and shape. Sanders and Fatone [1] have published a comprehensive review of the sources, measurement techniques, values, and clinical management strategies of residual limb volume change. The most drastic changes occur in the post-operative period, i.e. the first 12–18 months post-amputation [1]. However, even mature residual limbs (>12–18 months post-amputation) undergo fluctuations in volume and shape [1], [2]. The short-term (within a day) changes typically occur due to pooling of blood in the venous compartment, arterial vasodilatation, and changes in the interstitial fluid volume [1]. Short-term volume loss usually occurs as a result of pressure and shear stresses applied on the soft tissues by the prosthetic socket. For example, Zachariah et al. [2] quantified the volume changes in six persons with unilateral transtibial amputation, and reported volume increase ranging from 2.4% to 10.9% upon socket-removal (post-doffing). The amount of daily volume fluctuation varies among amputees as a function of comorbidities, prosthesis fit, activity level, hydration, dietary habits, and more [1]. In addition, higher frequency (in the order of seconds) shape changes occur due to muscle activation and changes in the knee and hip joint angles.

A good prosthetic socket fit is critical for allowing a comfortable and stable transfer of loads between the residual limb and the distal components of the prosthesis. However, shape and volume changes lead to changes in limb-socket interface stress distributions, thereby causing problems in maintaining a well-fitting prosthetic socket. On the one hand, volume reduction might lead to: 1) increased pistoning of the residuum within the socket, 2) areas of high stress around the distal end and bony prominences, and 3) a compromised transfer of loads between the limb and the socket. On the other hand, volume increase might also lead to increased stresses at the skin interface. Regions of high stress are typically areas where patients report pain and discomfort, and where skin ulcerations occur. Poor socket fit can lead to dermatological problems [3] and deep tissue injury [4], [5], as well as to indirect musculoskeletal problems as a result of asymmetric loading of the limbs and compensatory movements due to discomfort and incorrect alignment [6].

Prosthetic sockets are almost always patient-specific, and their design and manufacturing process is presently still a largely artisanal procedure. Typically, the initial socket geometry is obtained by casting the residual limb of the patient and forming a positive plaster mold, which is then manually modified with an aim to optimize the load distribution over the surface of the residuum. The success of the socket design process highly depends on the experience and skill of the prosthetist, and typically requires manual and iterative design evaluation, demanding repeated patient feedback [7]. Moreover, the process is non-repeatable and largely non-data driven. Alternatively, a pressure-casting concept can be used, whereby the residuum is casted while it is loaded through the medium of a pressurized fluid (typically water or air). The premise behind this concept is that sockets designed using pressure-casted molds would distribute the pressures equally across the residuum surface, and require minimal adjustments by the prosthetist. However, a previous study has shown that these sockets do not produce hydrostatic pressure profiles during standing and gait [8]. Moreover, comparison of comfort levels of pressure-casting sockets versus traditional hands-on sockets have shown inconclusive results [9], [10].

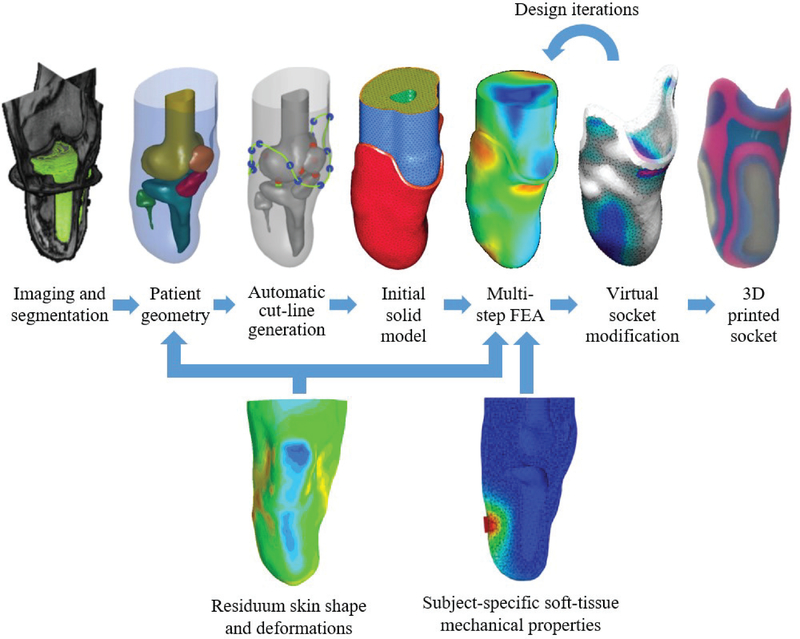
A clear necessity in the field is a design and manufacturing framework, which is still patient-specific, yet data-driven, accurate, repeatable, and based on clear scientific rationale. Considerable efforts have been made in recent decades to develop new methods for digitizing and automating socket design and manufacturing procedures. In particular, finite element analysis (FEA) has been utilized to investigate the soft tissue load distribution [11]–[13] and generate socket designs [14], [15]. An example of a recently published data-driven computational socket design framework [14] is illustrated in Fig. 1: Segmented MRI data are employed for creating a patient-specific geometry, which is then used to automatically generate the initial liner and socket geometries. Then, the model is meshed with volumetric elements to form a FEA model with the desired material properties and boundary conditions. Multi-step loading conditions are then applied to the model, which simulate the desired liner donning pressure, socket donning pressure, and body-weight loading. The FEA results are then utilized to drive socket design modifications in an iterative process, until a final design is exported and manufactured.

Fig. 1.

Schematic overview of a data-driven computational design framework [14]. Top row: MRI data is segmented to obtain patient-specific geometry. Anatomical landmarks are used to generate the socket cut-line, as well as the initial geometries of the liner and socket. Then, the model is meshed to form a FEA model, and the FEA results are utilized to drive socket design modifications in an iterative process, until a final design is exported and manufactured. Bottom row: additional measurements are required to improve the design process. Residuum time-varying shapes and deformations may be used to inform the source geometry, as well as the design iterations, and subject-specific soft-tissue mechanical properties obtained in-vivo are necessary to realize a more accurate mechanical FEA model.

In order to enhance and improve this framework, additional measurements are required. Specifically, residuum skin shapes acquired using MRI or CT suffer from drawbacks, such as: 1) low resolution, 2) motion artifacts, and 3) potential shape distortion caused by bed support. In addition, only a single shape is typically acquired, disregarding any volume and shape fluctuations. Hence, more accurate and time-varying shape measurements may be utilized to devise designs, which take into account residuum volume and shape changes. Moreover, subject-specific soft tissue mechanical properties obtained in-vivo are essential for realizing an accurate and realistic mechanical FEA model. Recently published reviews of studies using FEA to investigate the amputated lower limb [11] and of existing technologies and open challenges related to prosthetic sockets [16], both concluded that future work is required to investigate changes in soft tissue shape and mechanical properties of residual limbs.

Different techniques have been proposed for measuring residuum volume changes (e.g water displacement, anthropometric measurements, contact probes, optical and laser scanning, ultrasound, CT, MRI, and bioimpedance [1]). However, some of these techniques (e.g. water displacement and bioimpedance) are incapable of measuring shape changes, which are essential for translating these measurements into improved prosthetic socket design. Moreover, the majority of techniques which are capable of measuring shape to some extent (e.g., contact probes, ultrasound, CT, and MRI), require a long time (on the order of minutes) for a complete scan of the residuum, which makes them impractical for measuring short-term changes. Most of these methods also cannot measure the unloaded shape of the residuum, since they require that contact is made between the skin and either the measurement device or the exam bed. Other methods also suffer from limitations that hinder their usability. For example, optical silhouette scanning cannot pick up concavities of the residual limb, and both optical silhouette scanning and laser scanning require that the scanner is moved around the limb, and are thereby affected by errors induced by movements of the residuum during the scan, even if the scan is relatively fast (1–2 s) [1], [2]. Systems based on fringe projection/ structured light [17], [18] may provide instantaneous measurement of the limb shape if a sufficient number of scanners are used simultaneously. However, they do not track material points; therefore, measurement of surface deformations and strains cannot be achieved.

The aim of the work presented in this paper was to develop a system for providing high resolution, accurate, and simultaneous measurement of the time-varying shape, as well as full-field deformation and strain maps, of an unsupported residual limb. Other considerations for the system were its non-invasive nature, low cost and relatively small size. To this end, three-dimensional digital image correlation (3D-DIC) was selected as the fundamental method. 3D-DIC is a full-field noncontact optical-numerical technique to measure shapes and full-field displacements, deformations, and strains, on the surface of almost any material. The capabilities of 3D-DIC make it particularly suitable for a wide range of biomedical engineering applications, for measuring hard and soft tissues at different dimensional scales, from the microscopic level to the organ level [19].

Successful surface reconstruction and tracking using 3D-DIC requires that the surface is provided with a random speckle pattern, and that each surface point is viewed from at least two cameras. This allows the DIC algorithm to match sets of corresponding points in different images, by finding the maximum correlation of the local pixel intensity distribution in subset areas of the images [20]. Next, stereo triangulation is employed for obtaining the position of each point in 3D space based on its positions in two or more stereo-images [20]. Consequently, the temporal changes in the measured 3D positions of material points are used to quantify the displacement, deformation, and strain fields [20].

Existing 3D-DIC software packages are typically designed for systems with a small number of cameras (2–4), and do not provide a practical solution for multi-camera systems, which are necessary for imaging the entire residuum surface. To solve this problem, a recent work by the authors developed an open-source 3D-DIC software, named MultiDIC, which allows for the reconstruction of the dynamic behavior of surfaces from multiple cameras [21]. MultiDIC was specifically tailored for experimental setups consisting of a large number of cameras. It comprises unique features that enable surfaces obtained by different stereo-pairs to be reconstructed in the same global coordinate system and merged into a continuous mesh, and offers a fast calibration procedure, even when a large number of camera-pairs is used.

A further challenge with shape change analysis, which is common to all previously mentioned scanning techniques, is that different shapes are obtained independently, such that the surface points are not corresponded among the different scans. This requires an alignment/registration procedure to be applied in order to compute the difference between the shapes. Consequently, the results are dependent on the selected registration algorithm [22], [23], since there is no closed-form solution for this registration. Using our method, this problem is avoided entirely, since the correspondence between surface points is inherently tracked using 3D-DIC, thereby allowing a closed-form solution to be applied [24]. For the same reason, only 3D-DIC allows for local full-field deformation and strains measurement, while other scanning techniques can only evaluate out-of-plane displacements.

In the present study, the experimental setup developed in our previous study [21] was modified to incorporate a larger number of cameras, adequate for measuring transtibial residual limbs, and a new custom calibration object was designed and fabricated to accommodate the modified camera setup. This paper presents the new experimental setup and the data analysis methods, which were developed to evaluate not only the deformation and strain distributions, but also the volumes and cross-sectional areas of the residuum. In-vivo measurements on the residuum of one subject with unilateral transtibial amputation were acquired during three tests: 1) knee flexion and extension, 2) muscle contractions, and 3) post-doffing swelling. The capabilities of the new framework in collecting high-resolution time-varying measurements of the residuum are demonstrated, and the results are analyzed and discussed with respect to previous studies and future applications.

II. Materials and Methods

A. Experimental setup

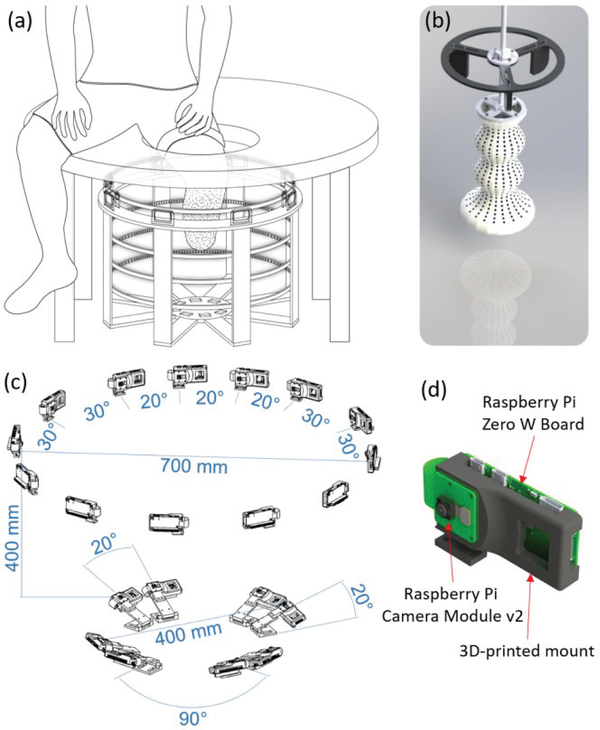
A stereo camera rig was designed and fabricated, to hold up to 40 camera units. Each unit contains a Raspberry Pi Camera Module V2, featuring a Sony IMX219 8-megapixel 3.674 × 2.760 mm² CMOS sensor, connected to a Raspberry Pi Zero-w (see also [21]). All cameras were connected and synchronously controlled using an Ethernet hub connected to a PC. Each set of simultaneous images from all cameras is referred to as a scan, and each instantaneous state of the residuum is referred to as a configuration. For the experiments described in this paper, a total of 21 cameras were used, arranged in 17 stereo-pairs, as follows: 13 cameras were placed radially in a 700 mm diameter circle, resulting in 10 stereo-pairs having 30° between them, and 3 stereo-pairs having 20° between them, as shown in Fig. 2(c). In addition, 8 cameras, arranged in 4 stereo-pairs, were placed on the bottom of the rig facing upwards, to image the distal end of the residuum, as shown in Fig. 2(c). Prior to human subject testing, the camera configuration was verified by conducting preliminary tests on residual limb replicas (plaster cast molds), in order to ensure sufficient coverage and reconstruction accuracy. In the previous study, only 12 cameras, all having 30° between them, were used radially [21]. However, it was found that a narrower angle between the cameras is necessary for successfully reconstructing the anterior surface of the limb, especially around the anterior part of the knee, since these regions are typically characterized by higher curvatures than the rest of the limb. The system configuration obtained a mean image spatial resolution of ~0.127 mm/pixel.

Fig. 2.

(a) Schematic of the experimental setup: the circular scanner features a circular rig holding multiple cameras and LED strips. The subject is seated on a table with a hole directly above the center of the scanner, through which the speckled residual limb is inserted. (b) The 3D-printed calibration object design. The additional features on top of the calibration object are used for positioning it through the hole in the table in the correct position inside the scanner. (c) The dimensions of the multi-camera stereo setup. 13 cameras were positioned on the top ring of the scanner, creating 13 stereo-pairs. 10 pairs had 30° and 3 pairs had 20° between the cameras. The relative positions and orientations of the bottom cameras are also indicated. (d) A custom 3D-printed mount was designed to hold a Raspberry Pi board and camera in each of the positions shown in sub-figure (c).

The rig was placed under a padded table featuring a hole through which a residual limb could be inserted while a subject was sitting comfortably, as illustrated in Fig. 2(a). The measured limb was illuminated using arrays of flexible LED strips to provide bright and uniform lighting conditions. The total materials-cost of the imaging system was approximately $2,000, including 21 Raspberry Pi boards and cameras, LEDs, Ethernet hub, power supplies, and all the necessary cables and connectors.

A custom 3D calibration object was designed and additively manufactured using a multi-color 3D-printer (Connex Objet500, Stratasys, Eden Prairie, MN, USA) which offers high-precision (build resolution 600 dpi, accuracy of up to 200 microns). The calibration object was designed to incorporate a total of 700 black square dots over a white background, arranged as follows: 20 columns with 28 rows each on the upper (semi-cylindrical) part of the calibration object which is visible by the top cameras, and 20 concentric columns with 7 rows each on the lower part of the calibration object which is visible by the bottom cameras, as shown in Fig. 2(b). The 3D coordinates of the centroids of black dots are known within the precision of the printer. By comparing the positions of identified image points with the known 3D coordinates, the direct linear transformation (DLT) parameters can be obtained for each camera [21], thereby allowing the 3D reconstruction of image points identified in images taken by two cameras. To ensure the quality of the stereo calibration, the calibration object was designed such that a highly redundant number of control points (at least 112) are visible by each stereo-pair, and that the dots are not co-planar, include a large range of depth, and are located in the capture volume in the same approximate positions where residual limbs are captured.

The accuracy of synchronization between the cameras was evaluated by simultaneously imaging an LED array controlled by an Arduino microcontroller, with a granularity of 1 ms. Analysis of the images revealed that the cameras were synchronized to within ±30 ms.

The accuracy of DIC measurements depends on the quality of the speckle pattern, which is influenced by the speckle size distribution, density, randomness, contrast, and edge sharpness [20]. To this end, a custom speckling stencil was made by laser-cutting a thin rubber sheet with a random speckle pattern designed to have a uniform 1.8 mm speckle size (~14 pixel) and 50% density. White and black temporary tattoo inks (ProAiir, USA) were used for applying the speckle pattern on the skin. First, a uniform layer of white ink was applied to the skin surface using an airbrush to create a homogenous background for enhancing contrast. Next, the speckle pattern was applied with black ink using the airbrush through the stencil. The temporary tattoo ink was selected for being safe for use on the skin, as well as durable enough to withstand donning and doffing of the liner and socket, which allows for the correlation of images taken before and after walking with the socket.

The errors associated with the experimental system and software were previously evaluated [21], and were found to be smaller than 0.01 mm for shape and displacement measurements, and in the order of 10⁻³ for strain measurement.

B. Data collection

One unilateral transtibial amputee (male, age: 47 years, height: 1.90 m, weight: 84 kg, activity level: K4, cause of amputation: trauma, time since amputation: 25 years) was recruited and tested following approval by the Committee on the Use of Humans as Experimental Subjects of the Massachusetts Institute of Technology. The following tests were sequentially performed:

1). Knee flexion and extension

The subject doffed the socket and liner in order to apply the speckle pattern using the stencil and airbrush, while the limb was in a horizontal position on the scanner table. The speckling procedure took approximately 20 minutes. Then, the subject inserted his residual limb into the scanner and seven scans were acquired in different knee angles: one in a relaxed natural angle, three in increasing levels of knee flexion, and three in increasing levels of knee extension. The natural knee angle was defined as a reference configuration for this test.

2). Post-doffing swelling

The subject donned his liner and socket, and walked at a self-selected speed for 10 minutes. Then, the subject returned to the scanner, and doffed the socket and liner while sitting on the scanner table. A subsequent set of measurements was initiated immediately (<10 s) post-doffing. Scans were captured every 20 seconds for 10 minutes (a total of 30 scans). The first scan (immediately post-doffing) was defined as a reference configuration for this test.

3). Muscle contractions

The subject was instructed to perform a series of 8 different muscle contractions, corresponding to two levels (maximum and approximately half-way) for each of the following movements of the phantom ankle joint: dorsiflexion, plantarflexion, eversion, and inversion. One scan was performed at each of these configurations. An additional scan was performed at a relaxed state (without muscle contraction) before the set of contracted scans. This scan was defined as the reference configuration for this test. Moreover, the subject was instructed to relax his muscles between each of the four phantom movements, in order to start from the same relaxed baseline.

In addition, simultaneous images of the calibration object were captured before and after each test, to ensure that the stereo calibration parameters did not change during the course of the trials.

C. Data analysis

For each set of scans, the images were analyzed using MultiDIC, an open-source 3D-DIC MATLAB toolbox developed by the authors [21]. The algorithms implemented in MultiDIC have been previously described in detail [21]. The four main steps comprising the 3D-DIC procedure are summarized below.

1). 2D-DIC of speckle images

The images of the speckled residuum were analyzed for each of the 17 stereo-pairs, to obtain the correlated 2D (pixel) positions of a dense set of points in a specified region of interest (ROI) for each stereo-pair, across all time-frames. All the 2D-DIC analyses were performed using a subset size of 30 pixels [25], in order to ensure that each subset contains at least three pattern features [26], and using a step size of 20 pixels (less than 50% overlap), which has been previously recommended for minimizing the potential for increasing strain variability [27].

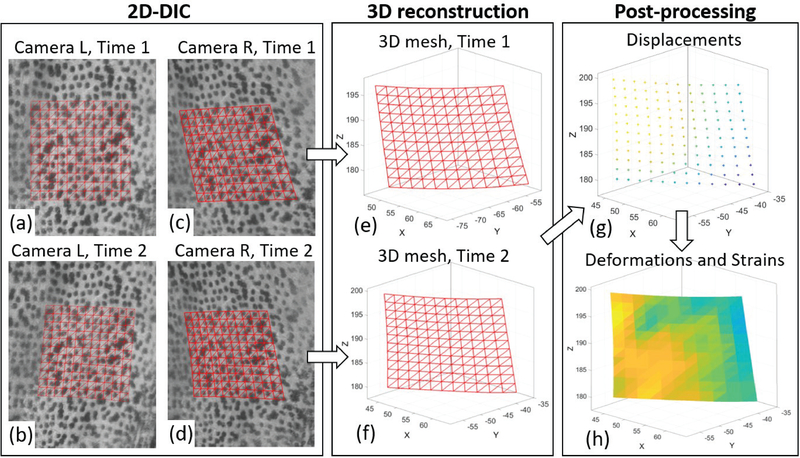
Fig. 3(a–d) illustrate an example of 2D-DIC results obtained on four images captured in two configurations (two from each camera). The set of correlated points is contained inside the ROI defined for this stereo-pair. Fig. 4 shows a zoomed-in view of the speckled surface, with a smaller ROI. A triangular mesh is defined on the reference image (a) by sub-dividing the square grid of measurement points, such that each measurement point corresponds to a vertex of a triangle, the set of triangles are connected by their common edges and vertices, and the same mesh is preserved for all the configurations [21]. Fig. 4(b–d) show the corresponding correlated points on the rest of the images, and demonstrate how corresponding triangles are deformed.

Fig. 3.

Workflow of residual limb surface reconstruction using 3D-DIC. Portions of the speckled residual limb imaged by camera 11 (a,b) and camera 12 (c,d) are shown in two configurations: extended knee (top row) and flexed knee (bottom row). The points correlated between all four images (a-d) are plotted with red crosses on top of the images. The resultant 3D point clouds (e,f) and triangular meshes (g,h) are plotted for the two configurations. All the axes in plots (e-h) are in millimeters.

Fig. 4.

Schematic workflow of 3D-DIC for one stereo-pair. Portions of the speckled surface imaged by the left (L) camera (a,b) and right (R) camera (c,d) are shown in two time steps corresponding to the reference configuration (Time 1) and a deformed configuration (Time 2). The reference square point grid is defined on the reference image (a), and the points are then identified on the images (b-d) using 2D-DIC. In addition, a triangular mesh is defined on the reference image by sub-dividing the squares, and the mesh connectivity is preserved in all the images. Then, the image points from each stereo pair are reconstructed in a 3D coordinate system using stereo triangulation (e,f). The displacements from Time 1 to Time 2 are calculated on the measurement points (g), and consequently the 3D deformations and strains are calculated on the triangular elements (h).

2). Stereo calibration

In this step, the mapping between 2D image points and 3D points was established, using the DLT method [21]. The images of the calibration object were analyzed to obtain the DLT calibration parameters for each camera. This was achieved by identifying the centroids of the black dots on the calibration images and matching them with their 3D positions, known from the calibration object design process [21]. Using this process, the reconstructed 3D coordinate system associated with each of the cameras is the same coordinate system in which the points on the calibration object were defined, such that no additional transformations are required. To evaluate the accuracy of the stereo calibration, the 3D reconstructed coordinates of the calibration object points were compared with their true coordinates, to obtain the reconstruction errors, which are then evaluated in terms of the mean error and the root mean square error [21].

3). 3D reconstruction

The correlated points on the speckle images and the DLT calibration parameters, were utilized to reconstruct the 3D point clouds for each scan, using stereo triangulation [21]. Previous tests have shown that for the low-cost Raspberry Pi cameras used in this study, a distortion correction routine improves the accuracy of the 3D-DIC measurements [21]. Therefore, distortion correction was applied for all the obtained image points (both speckle and calibration points) before 3D reconstruction. Fig. 3(e–f) illustrate how correlated image points from one stereo-pair are used to reconstruct the 3D point clouds in two different configurations (extended and flexed knee). Fig. 4(e–f) illustrates how the triangular mesh connectivity is transformed from the 2D images to the 3D point cloud, and Fig. 3(g–h) illustrate how the triangular mesh represents the skin surface.

4). Post-processing

Since all the points are corresponded between the different scans, the time-varying 3D positions can be analyzed to obtain the 3D displacement vector of each point. Fig. 4(g) illustrates the value of the displacement magnitude calculated on each measurement point. Next, the deformation gradient tensor F is calculated for each triangular element and for each configuration, with respect to the reference configuration [28], [29]. It should be noted that even though the reference configuration defines a zero-strain state in this analysis, it does not necessarily reflect a stress-free state of the skin.

Subsequently, the right and left Cauchy-Green deformation tensors (C and B, respectively), and the associated Green-Lagrangian and Eulerian-Almansi finite strain tensors (E and e, respectively), are defined by

$$\begin{gathered} \mathbf{C}={\mathbf{F}}^{\mathbf{T}}\mathbf{F};\mathbf{B}=\mathbf{F}{\mathbf{F}}^{\mathbf{T}} \\ \mathbf{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I});\mathbf{e}=\frac{1}{2}\left(\mathbf{I}-{\mathbf{B}}^{-1}\right), \end{gathered}$$ (1)

where I is the unity second order tensor. Moreover, the spectral decompositions of these tensors are given by

$$\begin{gathered} \mathbf{C}={\lambda }_1^2\left({\mathbf{N}}_1\otimes {\mathbf{N}}_1\right)+{\lambda }_2^2\left({\mathbf{N}}_2\otimes {\mathbf{N}}_2\right)+{\lambda }_3^2\left({\mathbf{N}}_3\otimes {\mathbf{N}}_3\right) \\ \mathbf{B}={\lambda }_1^2\left({\mathbf{n}}_1\otimes {\mathbf{n}}_1\right)+{\lambda }_2^2\left({\mathbf{n}}_2\otimes {\mathbf{n}}_2\right)+{\lambda }_3^2\left({\mathbf{n}}_3\otimes {\mathbf{n}}_3\right) \\ \mathbf{E}={\text{E}}_1\left({\mathbf{N}}_1\otimes {\mathbf{N}}_1\right)+{\text{E}}_2\left({\mathbf{N}}_2\otimes {\mathbf{N}}_2\right)+{\text{E}}_3\left({\mathbf{N}}_3\otimes {\mathbf{N}}_3\right) \\ \mathbf{e}={\text{e}}_1\left({\mathbf{n}}_1\otimes {\mathbf{n}}_1\right)+{\text{e}}_2\left({\mathbf{n}}_2\otimes {\mathbf{n}}_2\right)+{\text{e}}_3\left({\mathbf{n}}_3\otimes {\mathbf{n}}_3\right), \end{gathered}$$ (2)

where λ_i are the principal stretches, Ni and n_i are the principal directions in the reference and current configurations, and E_i and e_i are the principal Green-Lagrangian and Euler-Almansi strains, respectively. Since each triangular element is planar, one of the principal stretches must equal to one (e.g. λ₃ = 1), and one of the principal strains must equal to zero (e.g. E₃ = e₃ = 0). Furthermore, their associated directions (N₃ and n₃) are normal to the plane of the triangle in the reference and current configurations, respectively. Consequently, the maximum Green-Lagrangian and Euler-Almansi surface shear strains are given by ${\gamma }_E=\frac{1}{2}\left|{\text{E}}_1-{\text{E}}_2\right|$ and ${\gamma }_e=\frac{1}{2}\left|{\text{e}}_1-{\text{e}}_2\right|$, respectively.

Furthermore, the dilatation J, which corresponds to the relative surface area change of the triangular element, is given by

$$\text{J}=\det (\mathbf{F})={\lambda }_1{\lambda }_2=\frac{\text{A}(\text{t})}{\text{A}(0)}.$$ (3)

where A(t) is the area of the triangular element at time t, and t = 0 represents the reference configuration.

Assuming a homogenous deformation field within each triangular element, this method obtains the finite (nonlinear) deformation and strain field with the same spatial resolution as the DIC measurement, independently from adjacent data points and numerical derivatives, and does not comprise any filtering or smoothing of the strain within this resolution.

Furthermore, the 3D surface obtained for each scan was used to calculate the volume of the residual limb, by integrating over the surface using Gauss’ theorem, which is defined as

$$\underset{\text{S}}{\iint }\mathbf{X}\cdot \mathbf{n}\text{dS}=\underset{\mathbf{V}}{\iiint }\nabla \mathbf{X}\text{dV},$$ (4)

where S is the surface enclosing the volume V, X is an arbitrary vector, n is the unit vector normal to the surface S at each integration point, and ∇ is the divergence operator. If X is selected such that it satisfies ∇ X= 1, (4) becomes:

$$\underset{\text{S}}{\iint }\mathbf{X}\cdot \mathbf{n}\text{dS}=\underset{\mathbf{V}}{\iiint }\text{d}\text{V}=\text{V},$$ (5)

such that the total volume can be calculated by means of a surface integral. Then, (5) can be written in a discrete form, such that the total volume enclosed by the surface can be calculated by means of a simple summation over the triangular mesh:

$$\text{V}=\sum _{\text{i}=1}^{{\text{N}}_{\text{f}}}{\text{A}}_{\text{i}}{\mathbf{X}}_{\text{i}}\cdot {\mathbf{n}}_{\text{i}}$$ (6)

where N_f is the total number of triangular faces in the mesh, A_i is the area of the i^th triangle, and n_i is the unit vector normal to the i^th triangle.

Next, for interpretation of the volume change post-doffing, the volume data were analyzed by curve-fitting the volume change versus time using the one-term and the two-term exponential decay functions:

$$\begin{gathered} \mathrm{\Delta }\text{V}(\text{t})=\mathrm{\Delta }{\text{V}}_0\left(1-{\text{e}}^{-{\text{k}}_0\text{t}}\right) \\ \mathrm{\Delta }\text{V}(\text{t})=\mathrm{\Delta }{\text{V}}_1\left(1-{\text{e}}^{-{\text{k}}_1\text{t}}\right)+\mathrm{\Delta }{\text{V}}_2\left(1-{\text{e}}^{-{\text{k}}_2\text{t}}\right) \end{gathered}$$ (7)

where ΔV(t) is the volume change at time t (t = 0 represents the time of the first scan post-doffing), ΔV₀ and ΔV₁ + ΔV₂ represent the volume change which the residuum exponentially approaches in the one-term and two-term predictions, respectively, and k_i are the exponential decay constants.

In addition, cross-sectional areas in the coronal plane were computed along the length of the limb for each scan. The changes in the cross-sectional areas were compared between scans, to determine the distribution of the volume change in the proximal-distal direction.

Using the proposed method, shape changes, deformations, and strains, can be successfully calculated even if the residuum undergoes large motions between scans. However, to visualize local displacements, it is convenient to subtract the rigid body motion (RBM) from the overall motion, such that local displacements can be visualized without large movements of the entire body. Therefore, the optimal RBM was calculated for each deformed configuration, such that the residuum shapes are all aligned with the shape in the reference configuration. Since the points in all the configurations are corresponded, this registration can be performed using closed-form solutions, which minimize the root mean square deviations between the point clouds [30], [31]. Conversely, previously used scanning methods do not provide corresponded point clouds; therefore, a closed-form solution cannot be obtained, and their alignment is therefore susceptible to local minima [22], [23].

III. Results

A. 3D Reconstruction Errors

Table 1 reports the 3D reconstruction mean and root mean square errors for each camera-pair, associated with the stereo calibration process, after applying distortion correction. Using the mean image spatial resolution of the current setup, the mean values of ε_M and ε_R are 0.016 pixel and 0.386 pixel, respectively.

TABLE I.

3D Reconstruction Errors

Pair Index	Camera Indices	εM [mm]	εR [mm]
1	[1,2]	0.002	0.051
2	[2,3]	0.003	0.047
3	[3,4]	0.002	0.057
4	[4,5]	0.001	0.053
5	[5,6]	0.002	0.046
6	[6,7]	0.001	0.034
7	[7,8]	0.003	0.058
8	[8,9]	0.002	0.041
9	[9,10]	0.001	0.042
10	[10,11]	0.002	0.044
11	[11,12]	0.001	0.054
12	[12,13]	0.001	0.057
13	[13,1]	0.001	0.046
14	[14,15]	0.001	0.038
15	[16,17]	0.002	0.055
16	[18,19]	0.001	0.051
17	[20,21]	0.003	0.044
All pairs (mean)		0.002	0.049

ε_M = Mean Error, ε_R = Root Mean Square Error.

B. Residual limb measurements

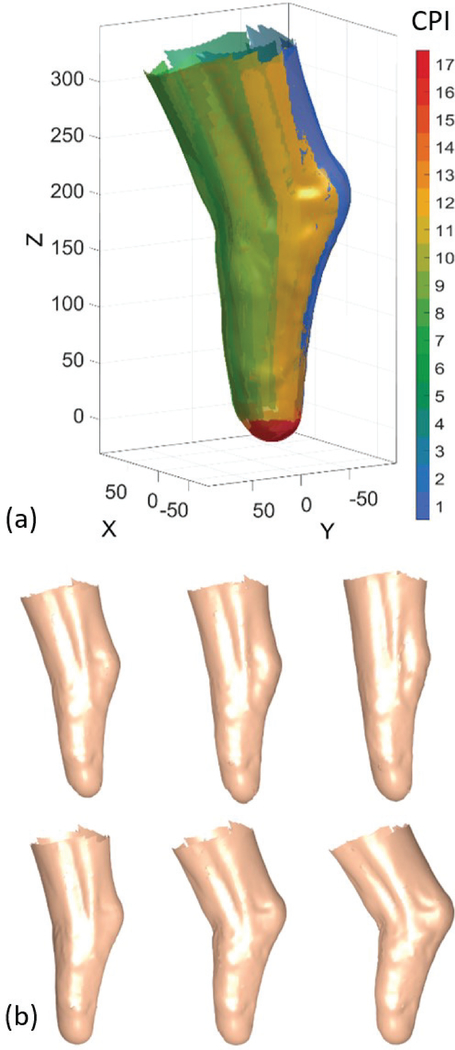
Fig. 3 shows an example of four images captured during the knee flexion series, from one stereo-pair (two adjacent cameras), in two different knee angles. The 3D surface reconstructed from this stereo-pair makes up one out of 17 surfaces, which together construct the full residuum shape, as shown in Fig. 5(a). Sufficient overlaps between surfaces reconstructed from adjacent stereo-pairs ensure a reliable reconstruction of the entire residuum surface across all scans. Fig. 5(b) shows the full residuum reconstructions and the temporal change in the residuum shape for the scans captured in test no. 1 (knee flexions). The complete triangular mesh representing the surface of the residuum reconstructed in the different steps contained approximately 68,000 triangular faces and 37,000 vertices. The (mean ± standard deviation) values of the triangles edge lengths (distance between adjacent vertices) and areas were 2.89 ± 0.69 mm, and 3.32 ± 0.88 mm², respectively.

Fig. 5.

3D reconstruction results. (a) Reconstruction of the residuum surface from 17 camera-pairs, represented as different surface colors. Pairs 1–13 and 14–17 are from the cameras on the top ring and on the bottom plate of the scanner, respectively. (CPI = camera-pair index). (b) Short-term temporal change in residuum shape during knee extension and flexion.

1). Knee flexion and extension

For the series of scans captured in step 1, the relaxed pose (natural knee angle ~15° flexion) was selected as the reference configuration. Three levels of knee extension and three levels of knee flexion were captured and analyzed as deformed configurations. Fig. 6 plots the minimum and maximum Eulerian principal surface strains (magnitude and direction) for the first and last deformed configuration: maximum extension (~0°), and maximum flexion (~30°). During flexion, peak tensile strains (~0.15) were measured mostly directly above the patella, and peak compressive strains (~−0.25) developed in the posterior part of the knee, both mainly in the proximal-distal direction. During extension, peak compressive strains (~−0.45) were measured over the medial-anterior part of the knee, and peak tensile strains (~0.1) were measured mostly over the posterior part of the knee.

Fig. 6.

Eulerian strain measurements during knee flexion test. Two deformed configurations out of seven are plotted: most flexed in the top row (a,b) and most extended in the bottom row (c,d). The strains were calculated with respect to the reference configuration, which is not necessarily a stress-free configuration. The minimum and maximum Eulerian principal strain e₁ and e₂ are plotted on the left (a,c) and right (b,d) plots, respectively. Strain magnitudes are plotted as colors and their directions are plotted as black lines, with length proportional to their magnitude. The anatomical view showing the largest absolute values are shown for each subplot. All the results represent raw data. No kind of filtering or smoothing procedures were applied. Holes in the mesh appear where vertices could not be correlated reliably, such that the surface color from the opposite side of the surface is visible through the holes.

2). Post-doffing swelling

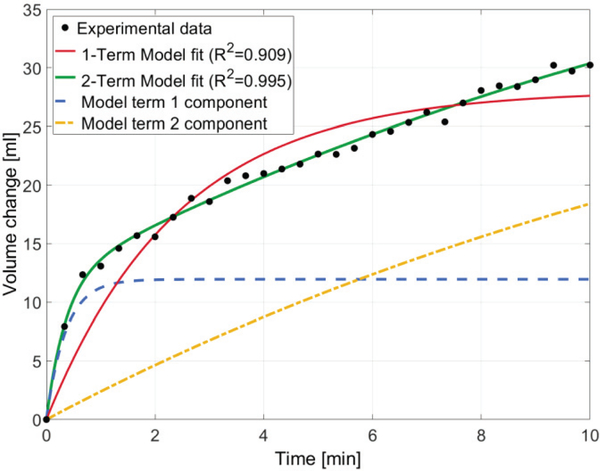
Removal of the socket resulted in an immediate and fast increase in the residuum volume, followed by a slower monotonic increase, as demonstrated in Fig. 7. Modeling the volume change with the one-term exponential function given in equation (7) revealed a good fit (R² = 0.909), and resulted in the following fitted parameters: ΔV₀ = 28.08 ml, k₀ = 0.41 min⁻¹. Modeling the volume change with the two-term exponential function revealed an excellent fit (R² = 0.995), and resulted in the following fitted parameters: ΔV₁ = 11.96 ml, k₁ = 2.80 min⁻¹, ΔV₂ = 40.03 ml, k₂ = 0.06 min⁻¹.

Fig. 7.

Residual limb volume change post-doffing plotted against time. The black data points represent experimental volume data computed directly from DIC data, the red and green solid lines represent the one and two-term exponential curve fits, respectively. The dashed blue and yellow lines represent the contribution of each model term to the overall two-term fit.

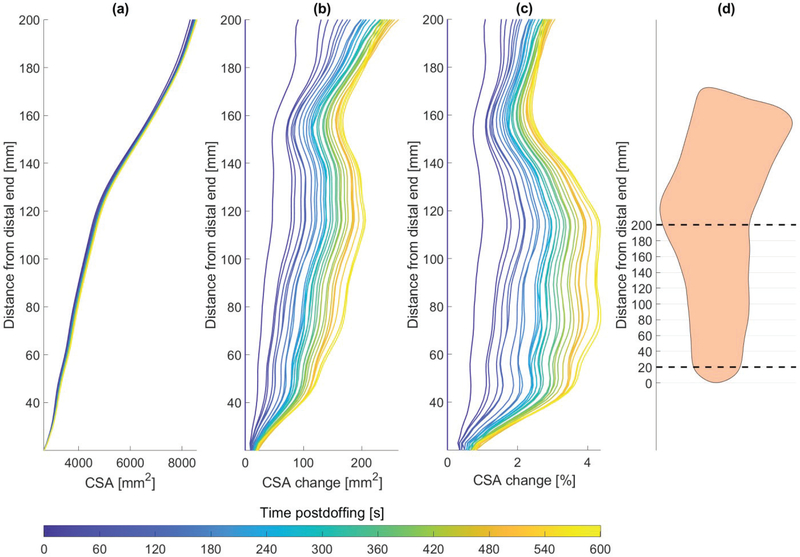
Fig. 8 plots the cross-sectional area change over time, for coronal slices between 20 mm above the distal end and the level of the knee joint. The results show an increase of up to 4.4% in the cross-sectional area, with the largest values being between 70–120 mm from the distal end.

Fig. 8.

Residual limb cross-sectional area (CSA) (a), area change (b), and percentage area change (c), over time post-doffing, as captured in 30 successive scans. (d) The cross-sectional areas were computed for coronal slices from 20 mm above the distal end up to the knee joint. The dashed lines represents the region for which cross-sectional areas are plotted in (a-c) over a lateral view contour of the residual limb shape.

Only surface deformation (and not internal volumetric deformation) can be measured using DIC. Nevertheless, the local area change represents a close measure to local volumetric change. During the post-doffing swelling measurement, the local relative area change increased consistently, reaching a maximum at the last measurement (t = 10 min), with values ranging between 0.98–1.1 across the limb (mean ± standard deviation: 1.027 ± 0.024). The region with the largest area change was the medial-posterior portion of the residuum, over the approximate location of the inner head of the gastrocnemius (1.039 ± 0.021). The anterior and distal parts of the residuum exhibited mostly low values of J (1.004 ± 0.005).

3). Muscle contractions

Activation of different muscles in the residuum was achieved by means of instructed movements of the phantom limb (ankle dorsiflexion, plantarflexion, eversion, and inversion). The measured total volume change was very small (<1%) for all the configurations. The cross-sectional area change ranged between −2% and 3%, with the largest absolute values obtained during maximum plantarflexion. Maximum shear strain results are plotted for this configuration in Fig. 9, overlaid with the image taken from one of the cameras, showing the medial-posterior aspect of the residuum, where the maximal shear strains were observed.

Fig. 9.

Maximum Green-Lagrangian shear strain map during muscle contraction. The image and strain results correspond to the maximum plantarflexion configuration. The largest strain values in this configuration were observed in the medial-posterior region of the residuum. 3D-DIC results from two adjacent camera-pairs which contain the same camera (pairs 5 and 6) are interlaid on the image captured by camera 6.

IV. Discussion

This paper describes a new framework for the measurement of residual limb time-varying 3D shape, and full-field deformation and strain, using 3D-DIC. The experimental system and analysis methods were developed to provide high-resolution, accurate and fast measurement, while overcoming some of the limitations of previous methods. Specifically, a challenge for successful in-vivo measurements is that subject motion during the measurements is inevitable. Therefore, imaging methods whereby the scanner has to be moved around the body segment are susceptible to errors which typically exceed other sources of measurement errors [1]. Our system allows for the instantaneous measurement of the entire surface of the residuum, by simultaneously imaging the entire surface of the residuum using multiple synchronized cameras. Moreover, the shape registration/ alignment problem, which is typically encountered when using other scanning techniques [22], [23], is avoided entirely when using 3D-DIC, since the correspondence between surface points is inherently tracked.

We demonstrated how time-varying shapes, as well as the enclosed volumes and cross-sectional areas, could be measured. In addition, the method allows for the measurement of the full-field surface deformation and strain distribution. To the best of our knowledge, this is the first work to reconstruct the residual limb skin surface using 3D-DIC, and to quantify temporal changes in the surface deformation and strain distributions. Temporal shape change of the transtibial residuum have been previously measured using other imaging methods, as reported in a recent review by Sanders et al. [1]. However, only few of the reported techniques were capable of performing instantaneous measurements of the entire limb, and none of them was capable of measuring full-field surface strains, because they could not track the displacements of material points.

Another previous work [32] has developed a low-cost method for measuring skin strain on a residual limb by capturing a large number of images and tracking the positions of markers painted on the skin. However, the spatial resolution and accuracy achieved using this technique is relatively low (limited by the number of markers), and a full scan of the limb is not instantaneous, which makes it impractical for in-vivo dynamic measurements.

Using the proposed framework, we measured in one transtibial amputee, the shape and volume changes post-doffing in intervals of 20 seconds. The volume change we measured reached 30.2 ml, or 3.3%, after 10 minutes. This value falls within the range of volume change (~1–10%) previously reported by Zachariah et al. using a silhouetting optical method on six patients [2]. However, due to the small number of subjects, no statistical comparison could be made. Moreover, the volume change is comparable to the fluid volume increase reported by Sanders et al. using bioimpedance [33], which was 2.8% ± 2.0% 10 minutes post-doffing, after 30 minutes of combined walking, sitting, and standing. It is noted, however, that bioimpedance is capable of measuring only fluid volume, and not the entire residuum volume.

The volume change over time post-doffing was well fitted with a single-term and a two-term exponential functions (R²=0.909 and R²=0.995, respectively). The fitted parameters suggest that the predicted maximum volume increase is 28 ml (3.1%) and 52 ml (5.7%), using the single-term and the two-term exponential functions, respectively. The second value is closer to the volume measured before donning, which was 49 ml larger than the volume measured immediately post-doffing, and both values are within the range reported by Zachariah et al. [2]. However, their study revealed large variability, both inter-subject and intra-subject, which suggests that a larger sample size is required for devising any generalized conclusion regarding this fitting.

The cross-sectional area increase reached a maximum of 263 mm², or 4.4%. The results shown in Fig. 7 indicate that the cross-sectional area increase was non-uniform along the length of the residuum. The largest percentage increase was observed in slices between 70 and 120 mm from the distal end. This same region also exhibited the largest surface area change, particularly in the medial-posterior aspects of this region, which is the region corresponding with the inner gastrocnemius muscle. This finding suggests that coping with volume change by means of adding or removing a uniform thickness sock/liner, might not provide an adequate solution for socket fit. Instead, regional adjustment of socket volume may be required to compensate for volume changes. The detailed local shape change map provided by our method can be employed in the future for devising improved solutions for local volume adjustments.

In the present study, we also evaluated the changes caused by the contraction of different muscles in the residual limb. The volume and cross-sectional area changes were found to be much smaller than those measured during post-doffing swelling (−1.1%−1% volume change and −1.8%−0.9% cross-sectional area change). To the best of our knowledge, only one study has previously assessed the effect of activated muscles on the residuum volume [34]. They measured a volume change between −4.2% and 14.2% as the subjects activated their gastrocnemius and tibialis anterior muscles simultaneously. The volume changes found in our study were much smaller. However, a direct comparison cannot be made due to the different nature of the muscle contractions performed. Moreover, in the previous study each scan was reported to last 10 seconds. This is a relatively long period, during which leg movement can greatly affect the measurement. Conversely to the small total volume change, relatively large strain values were observed locally. This finding suggests that despite the small effect that muscle contractions had on the total volume, local accommodations for muscle contraction might be required for devising optimal socket fit.

The present study suffers from four main limitations. Firstly, the proposed method requires that the limb is speckled with ink before the measurement, a process that can be time consuming (~20 minutes in our case). Secondly, since the method is optical in nature, measurements cannot be done while the residuum is inside a socket. Thirdly, the contribution of the synchronization latency between the cameras (~30 ms) to the 3D reconstruction error has not been assessed. In the future, the experimental setup can be improved by replacing the software-controlled synchronization with a hardware trigger. Fourthly, results were obtained on one subject only, and serves merely as a proof of principle for the proposed framework. Therefore, further research is needed for generalizing the conclusions reported here.

Furthermore, it is noted that the deformations and strains in this study were calculated with respect to a reference configuration, which is not necessarily stress-free. It is known that even in a “relaxed” or “unloaded” configuration, human skin typically exists in a stretched state, in directions and magnitudes which, among other factors, depend on the distribution and properties of the collagen fibers within the skin [35]. Thus, the strain values obtained using the method presented in this study should be considered with caution if used to evaluate the mechanics of the skin, as they do not necessarily directly relate to internal stress. For example, previous studies have estimated the pre-strain in the skin of the arm to be on the order of ~0.2, and in some cases even up to 0.55 [36], [37]. Therefore, the compressive strains measured in this study (up to ~−0.45) reflect deviation from a pre-tensioned state, such that the skin might still be under tension even when negative strains are measured. Despite this limitation, these values still provide useful information in the context of prosthetic socket design, because they can be used to inform the design of liners and sockets that can conform to the deformations experienced by the residuum.

It is noted that while the framework presented here was demonstrated only for the case of a transtibial residuum, the framework can be straightforwardly generalized to other body parts. Different camera specifications and setup might be necessary for smaller length-scales, higher frequencies, or smaller deformations; however, the entire analysis framework is not limited to the specific case investigated here.

The utilization of 3D-DIC for obtaining shape and deformations offers a unique advantage in the context of prosthetic socket design and biomechanical analysis, because it provides an opportunity to quantify several important measures using one measurement system. Firstly, it allows an accurate shape measurement, which is essential for any type of computational socket design, whether the socket is designed in a manual fashion using a CAD system [38], [39], or if the design is automatically informed by FEA [14], [40]. Secondly, the ability to evaluate time-varying deformations provides additional valuable data, which can be utilized to inform improved socket designs, which account for these variations. Thirdly, the use of optical image data and ink on the skin allows for marking of specific anatomical points and regions, which can then be accurately transferred into the computational model. For instance, scars and skin grafts can be marked with ink, such that they are automatically represented in the 3D geometrical model, and then be utilized to inform the socket design algorithm. Lastly, the full-field surface deformation measurements can be also employed for evaluating the subject-specific mechanical properties of the residuum soft tissues, which are crucial for creating an accurate FEA model of the limb [11], [14]. This may be done by combining 3D-DIC data with known loads, such as force/torque measurement during indentation tests [41], [42]. Then, using inverse FEA, the rich displacement and deformation data obtainable by 3D-DIC can be used to estimate the material parameters according to a selected material model [41], [43]. The residuum soft tissues are often characterized using hyperelastic and/or viscoelastic material models, which are typically nearly incompressible [11], [42]. Nevertheless, the framework presented in this paper can be used to inform inverse computational models for volume loss and recovery which characterize the soft tissues using multiphasic/poroelastic material models [44] to simulate the load-induced extracellular fluid transport which drives volume and shape change [33].

Future work will incorporate the methods demonstrated here in clinical studies, whereby the measured shapes and full-field deformations of the residual limbs of transtibial amputees will be utilized, together with MRI measurements, to inform the computational design of subject-specific optimized prosthetic sockets. Moreover, these methods will be used to evaluate the subject-specific soft tissue mechanical properties using inverse FEA simulations of in-vivo indentation tests and pressure-induced volume change.

V. Conclusion

This paper presents a new framework, based on multi-view 3D-DIC, for the measurement of the time-varying shapes, displacements, deformations, and strains of residual limbs. The framework allows for instantaneous scans of the entire surface of the limb to be captured by simultaneously imaging the residuum using 21 low-cost camera modules. A 3D-DIC MATLAB toolbox specially developed by the authors was employed for processing the image data, thereby obtaining 3D triangular meshes representing the skin surface, which are corresponded between the different scans. These data allow for the calculation of the full-field surface deformations and strains, as well as the time-varying volumes and cross-sectional areas. Measurements on one transtibial amputee were obtained during knee flexions, residuum muscle contractions, and post-doffing swelling. It was demonstrated that 3D-DIC can be utilized to quantify time-varying residuum shapes and deformations with high resolution in various configurations of the residuum. Results from this preliminary investigation provide a starting point for characterizing residual limb shape and volume change, as well as for implementing these measurements in a computational prosthetic socket design framework and soft tissue material characterization. Moreover, this framework may prove useful for various other wearable technologies, exoskeletons, and prosthetic and orthotic devices, which mechanically interface with the human skin.