Allometry of mitochondrial efficiency is set by metabolic intensity

Abstract

Metabolic activity sets the rates of individual resource uptake from the environment and resource allocations. For this reason, the relationship with body size has been heavily documented from ecosystems to cells. Until now, most of the studies used the fluxes of oxygen as a proxy of energy output without knowledge of the efficiency of biological systems to convert oxygen into ATP. The aim of this study was to examine the allometry of coupling efficiency (ATP/O) of skeletal muscle mitochondria isolated from 12 mammal species ranging from 6 g to 550 kg. Mitochondrial efficiencies were measured at different steady states of phosphorylation. The efficiencies increased sharply at higher metabolic rates. We have shown that body mass dependence of mitochondrial efficiency depends on metabolic intensity in skeletal muscles of mammals. Mitochondrial efficiency positively depends on body mass when mitochondria are close to the basal metabolic rate; however, the efficiency is independent of body mass at the maximum metabolic rate. As a result, it follows that large mammals exhibit a faster dynamic increase in ATP/O than small species when mitochondria shift from basal to maximal activities. Finally, the invariant value of maximal coupling efficiency across mammal species could partly explain why scaling exponent values are very close to 1 at maximal metabolic rates.

Significance statement

Until now, most of the studies used the fluxes of oxygen as a proxy of energy output without knowledge of the efficiency of mitochondrial oxidative phosphorylation system to convert oxygen into ATP. Here we found a positive correlation between mitochondrial efficiency and body mass at a basal metabolic rate only. At a maximum metabolic rate, we did not observe this relationship. Allometry of mitochondrial efficiency is thus dependent on metabolic intensity. These observations reveal that smaller mammals are less efficient for producing ATP, thereby producing more heat at rest, but are as efficient as larger species when muscle energy demands reach maximum intensity.

1. Background

Body mass dependence of individual metabolic rate has been heavily documented for a long time [1] because it is linked to biological processes at all levels of the organization, ranging from cells to ecosystems [2–6]. Empirical and theoretical studies describe the body mass dependence of individual metabolic rate in the form P = aM^b, where P is the metabolic rate and M the body mass [3]. The proportionality constant ‘a’ varies within and between species and the scaling exponent ‘b’ ranges from approximately 0.60 to 0.94 depending on clades and metabolic activity [7–9]. Several hypotheses have been suggested to explain the mechanistic basis of this power law for interspecific metabolic scaling. One hypothesis deals with the rates of resource supply to cells via branching or fractal-like structures [10,11]. Another hypothesis examines the sum of various cellular and mitochondrial properties involved in energy demand and supply pathways, i.e. in ATP turnover [8,12–16]. Mitochondria significantly contribute to metabolism in aerobic eukaryotic organisms by providing most of the cellular energy needs in the form of ATP [17]. The coupling efficiency (ATP/O ratio) is an important parameter of this energy transduction process, as it affects how much oxygen is needed to yield ATP in sufficient quantities to sustain animal performance.

However, not all of the mitochondrial oxygen consumption is coupled to ATP synthesis. A significant proportion of the electrochemical gradient of protons built up by the respiratory chain is consumed through proton conductance pathways in the inner membrane [18]. These proton leak reactions account for a significant proportion of cellular resting metabolic rates, 20% in hepatocytes, 50% in resting skeletal muscle and up to 20–25% of whole-body basal metabolic rate [18]. It follows that a significant part of mitochondrial oxygen consumption is not directly linked to ATP synthesis but rather is dissipated as heat. Because proton leak and ATP synthesis compete for the same driving force (the proton motive force), the activity of proton leakage across the inner membrane greatly alters the amount of ATP molecules synthetized by mitochondria for each oxygen atom consumed, i.e. the mitochondrial coupling efficiency [18,19]. Proton leak has been found to correlate negatively with increasing body mass in species from different taxa [20–23]. Given that proton leak is a major determinant of coupling efficiency [19], we hypothesized an increase in the coupling efficiency of mitochondria with body mass.

Nevertheless, oxygen consumed to counteract proton leakage decreases sharply as more ATP is synthesized, indicating that coupling efficiency will also increase steeply as mitochondrial ATP synthesis increases [24,25]. This relationship would indicate that proton leak would have less impact on coupling efficiency when mitochondrial metabolism shifts from basal non-phosphorylating to maximal phosphorylating activities. Accordingly, the global impact of proton leak upon coupling efficiency would decrease during the dynamic transition of mitochondrial activities from basal to maximal oxidative phosphorylation states. Whether such a dynamic functioning of mitochondrial bioenergetics depends upon body mass has not been tested and quantified yet. Therefore, the aim of the present study is to evaluate (i) how mitochondrial oxidative phosphorylation fluxes (oxygen consumption and ATP synthesis) and resulting coupling efficiency (ATP/O ratio) evolves during the transition from basal non-phosphorylating to maximal phosphorylating states, and (ii) whether these parameters correlate with body mass in mammals.

2. Material and methods

(a) Animals and tissue sampling

We selected 12 species of mammals ranging from 6 g (pygmy mouse) to 550 kg (bovine), representing a 92 000-fold difference in body mass and approximately 35-fold difference in mass-specific metabolic rate (electronic supplementary material, table S1). Muscle tissue from every mammal studied (all males) was acquired fresh and used for mitochondrial extraction. Pygmy mice (Mus minutoïdes) and feral mice (Mus musculus) were obtained from laboratories (ISEM, Montpellier, France for M. minutoides; LBBE, Lyon, France for M. musculus) and killed by cervical dislocation. Striped mice (Rhabdomys pumilio), European hamsters (Cricetus cricetus), golden hamsters (Mesocricetus auratus) and black rats (Rattus rattus), were obtained from laboratories (IPHC, Strasbourg, France for R. pumilio and C. cricetus; Chronobiotron, Strasbourg, France for M. auratus; Jardin Zoologique de la Citadelle, Besançon, France for R. rattus) and were killed under isoflurane-induced general anaesthesia. Fresh tissue for bovines (Bos taurus), horses (Equus caballus) and sheep (Ovis aries) were obtained from a local slaughterhouse (Cibevial, Corbas, France). Fresh tissues for all other mammals were obtained from pest control (Nutria, Myocastor coypus), local farmers (rabbits, Oryctolagus cuniculus) or Fondation Pierre Vérot at Saint-André-de-Corcy, France (boar, Sus scrofa). All experiments were conducted in accordance with the animal care guidelines of the Ministère de la Recherche et de l'Enseignement Supérieur.

(b) Mitochondrial isolation

For pygmy mice, skeletal muscle samples from three or four individuals were used for each mitochondrial preparation. Muscle mitochondria were isolated in an ice-cold isolation buffer (100 mM sucrose, 50 mM KCl, 5 mM EDTA, 50 mM Tris-base, pH 7.4) according to a standard extraction protocol, involving Potter homogenization, protease digestion and differential centrifugations, all steps at 4°C [26]. Briefly, hind-limb skeletal muscles from pygmy mice and feral mice were cut up finely, homogenized with a Potter–Elvehjem homogenizer (five passages) and thereafter treated with protease Subtilisin A (1 mg g⁻¹ muscle wet mass) for 5 min in an ice-bath. The muscle mixture was diluted 1 : 2 in an isolation buffer and centrifuged at 1000g for 10 min and the resulting supernatant centrifuged at 8700g for 10 min. The resulting pellet was resuspended in isolation buffer and centrifuged at 1000g for 10 min to remove any cellular debris contaminating mitochondrial suspensions. The resulting supernatant was filtered through cheesecloth and centrifuged at 8700g for 10 min to pellet mitochondria. This procedure was applied to small samples of tissue in order to minimize the loss of mitochondrial material [27]. For all other mammals, mitochondria were isolated as described previously [26]. Protein concentrations were determined in mitochondrial suspension using the Biuret method with bovine serum albumin as standard. To take into account any contamination with haemoglobin, the absorbance of the same volume of mitochondria assayed in Biuret solution without copper sulfate was subtracted.

(c) Mitochondrial oxidative phosphorylation efficiency

Mitochondrial oxidative phosphorylation efficiency was determined at 37°C by measuring oxygen consumption and associated ATP synthesis in 500 µl respiratory buffer (120 mM KCl, 5 mM KH₂PO₄, 1 mM EGTA, 2 mM MgCl₂, 20 mM glucose, 1.6 U ml⁻¹ hexokinase, 0.3% essentially free-fatty acid bovine serum albumin (w/v) and 3 mM Hepes, pH 7.4) as described previously [28]. Respiration was measured in a glass cell fitted with a Clark oxygen electrode (Rank Brothers Ltd, UK) and calibrated with air-saturated respiratory buffer. Mitochondria were energized with a mixture of respiratory substrates (5 mM pyruvate/2.5 mM malate/5 mM succinate). Thereafter, different steady states of phosphorylation were obtained by adding different concentrations of ADP (10, 20, 100 and 500 µM). The phosphorylating respiration rates were recorded for 3 min, then four 100 µl aliquots of mitochondrial suspension were withdrawn every 30 s and immediately quenched in ice-cold 100 µl perchloric acid solution (10% HClO₄, 25 mM EDTA). Samples were kept on ice less than 2 h until being assayed at the end of the day time experiment. Then, denatured proteins were centrifuged at 20 000g for 5 min (4°C), and 180 µl of the resulting supernatants were neutralized with KOH solution (2 M KOH, 0.3 M MOPS). Neutralized samples were centrifuged at 20 000g for 5 min (4°C) and the mitochondrial ATP production was determined from the glucose-6-phosphate content of the resulting supernatants [28]. Glucose-6-phosphate content was determined by spectrophotometry at 340 nm in an assay medium consisting 7.5 mM MgCl₂, 3.75 mM EDTA, 50 mM triethanolamine–HCl, pH 7.4 at room temperature) supplemented with 0.5 mM NAD and 0.5 U glucose-6-phosphate dehydrogenase from Leuconostoc mesenteroides [29]. Note also that we determined oxygen consumption and ATP synthesis rates in the presence of oligomycin (2 µg ml⁻¹) in order to make sure that ATP synthesis rates were specific of the mitochondrial ATP synthase activity. Oligomycin-insensitive ATP synthesis activity was measurable only at 100 and 500 µM ADP. In our mitochondrial preparations, these oligomycin-insensitive ATP synthesis rates did not correlate with a body mass of mammals, averaging 21 ± 1 nmol ATP min⁻¹ mg⁻¹ of protein and 73 ± 4 nmol ATP min⁻¹ mg⁻¹ of protein in the presence of 100 µM and 500 µM ADP, respectively. These values were taken into account to calculate the rate of mitochondrial ATP synthesis.

Respiratory control ratio was calculated as the ratio between the rates of ADP (500 µM)-induced maximal phosphorylating respiration and oligomycin (2 µg ml⁻¹)-induced basal non-phosphorylating respiration [25]. Mitochondrial respiratory control ratios ranged from 4.2 to 8.1, with a mean of 5.5 ± 0.3, and did not depend on body mass (electronic supplementary material, table S1). Accordingly, mitochondria from larger mammals functioned as well as those from smaller species.

(d) Statistical analyses

All statistical analyses were conducted on data corrected by the phylogenetic independent contrast model [30] in order to get the data phylogenetically independent using R software 3.5.0 (R Foundation for Statistical Computing, Vienna, Austria, 2018). Briefly, a phylogenic tree has been created from the mammal phylogenetic super-tree proposed by Fritz et al. [31] using the ‘phytools’ package (electronic supplementary material, figure S1). Then, data were log10-transformed and corrected by the PIC function found in the ‘ape’ package that uses the phylogenetic independent contrast method described by Felsenstein [30], which assumes a Brownian motion as an evolution model for life-history traits [30]. Finally, allometric relationships between body mass and mitochondrial bioenergetics parameters (oxygen consumption rate, ATP synthesis rate and efficiency) were analysed by the linear model (LM) with body mass as a fixed term. Normality and homoscedasticity criteria for the model's residues were checked by a Shapiro–Wilk normality test coupled to the plot diagnostics for an LM object. Means are given ±s.d. and p-values less than 0.05 were considered as significant.

3. Results and discussion

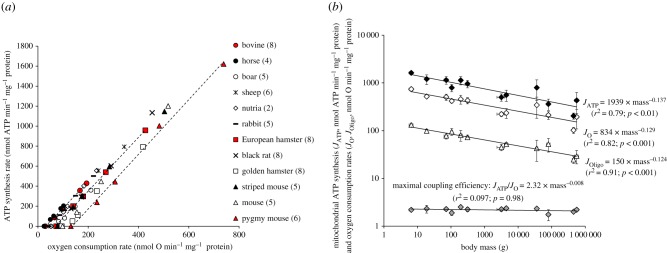
The relation between the rates of ATP synthesis and oxygen consumption is linear and differs for each mammal species (figure 1a). The maximal rates of ATP synthesis and oxygen consumption (the highest points to the right of the linear relationships in figure 1a) decreased with an increasing body mass of mammals according to the same scaling exponents (figure 1b). Consequently, the maximal coupling efficiency of mitochondria, calculated as the ratio between the maximal fluxes of oxygen consumed and corresponding ATP synthetized, was independent of body mass (figure 1b). The slopes of linear relationships shown in figure 1a were also independent of body mass (slope_ATP/O = 2.84 × mass^−0.006; r² = 0.096, F_1,10 = 0.00; p = 0.885), but the intercepts with the x-axis, i.e. the basal non-phosphorylating respiration measured in the presence of oligomycin (J_Oligo), decreased with increasing body mass of mammals (figure 1b). In the basal non-phosphorylating respiration, there is no ATP synthesis, the proton motive force is high, the proton leak-dependent respiration is maximal and controlled mostly by the activity of the proton leak pathway [25]. Thus, the data suggest that mitochondrial proton conductance in skeletal muscle mitochondria would depend negatively on body mass in mammals, as reported previously for liver mitochondria in species from different taxa [20–23].

Figure 1.

Body mass dependence of mitochondrial oxidative phosphorylation activity and efficiency. (a) Relationships between the rates of ATP synthesis and oxygen consumption in muscle mitochondria isolated from mammals of different body mass. Red symbols illustrate the linearity of the relationships for three mammal species taken to cover the whole range of body mass (bovine with the highest mass, pygmy mice with the lowest mass and European hamster with an intermediate mass). Values are means from (n) independent mitochondrial preparations; (n) is given alongside the name of the species. Error bars (s.d.) are omitted for clarity but were on average 19% for maximal oxygen consumption (ranging from 7% in mice to 47% in sheep) and 25% for maximal ATP synthesis rate (ranging from 9% in pygmy mice to 46% in sheep). (b) Relationships between body mass and maximal ATP synthesis rate (J_ATP, black diamonds; F_1,10 = 20.54; p < 0.01), maximal phosphorylating oxygen consumption (J_O, white diamonds; F_1,10 = 32.17; p < 0.001), oligomycin-induced basal non-phosphorylating oxygen consumption (J_Oligo, white triangles; F_1,10 = 49.49; p < 0.001) and maximal coupling efficiency (J_ATP/J_O, grey diamonds; not significant) of muscle mitochondria from mammals. Values are means ± s.d. (Online version in colour.)

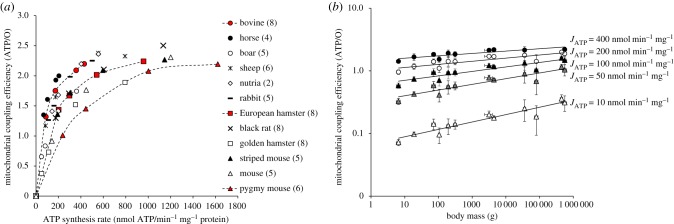
The data further indicate that the linear relationships were parallel and significantly shifted to the left in larger mammals. In other words, larger mammals consume less oxygen to produce a given amount of ATP and thus are more efficient than smaller species. This is better shown in figure 2a where mitochondrial efficiency (ATP/O ratio) is plotted against the rate of ATP synthesis. The effective ATP/O ratio rose steeply as the ATP synthesis rate increased, reaching the same maximum but at the different maximal phosphorylating activity (figure 2a). Calculation of the effective ATP/O ratio of mitochondria working at fixed ATP synthesis rates shows that mitochondrial coupling efficiencies had a positive dependence on body mass (figure 2b). This positive dependence on body mass was even stronger as mitochondria were closer to a non-phosphorylating state (figure 2b). Hence, when the rate of ATP synthesis is reduced 40-fold, the mitochondrial efficiency dropped by 20-fold in the smallest mammal and only by 7-fold in the largest one. Smaller mammals thus exhibited a more flexible coupling efficiency, being able to reduce their effective ATP/O ratio to lower values than larger species. Alternatively, mitochondria from larger mammals reach their maximal coupling efficiency faster than those from smaller species when mitochondrial metabolism shifts from a basal non-phosphorylating to a maximal phosphorylating state (figure 2). With all data taken into consideration, it appears that divergences in coupling efficiency values and flexibilities among species can be explained mostly by one trait of mitochondrial function: the basal non-phosphorylating respiration (i.e. the intercept on the abscissa axis in figure 1a). Because proton leaking and ATP synthesis compete for the same driving force, i.e. the proton motive force, when ATP synthesis decreases, the proton current via leak pathway increases, leading to an increase in oxygen consumption and associated drop in ATP/O ratio. In this context, the drop in coupling efficiency should be more pronounced in mitochondria with higher proton conductance. Hence, the higher drop in the ATP/O ratio of smaller mammals shown in figure 2b at low levels of ATP synthesis could be explained mostly by a higher proton leak activity compared with larger mammals.

Figure 2.

Body mass dependence of mitochondrial coupling efficiency varies with ATP synthesis levels. (a) Relationships between mitochondrial efficiency (ATP/O ratios) and the rates of ATP synthesis in muscle mitochondria from mammals of different body mass. Red symbols illustrate the nonlinearity of the relationships. Values are means from n independent mitochondrial preparations; (n) is given alongside the name of the species. Error bars (s.d.) are omitted for clarity but were on average 10% for maximal ATP/O ratio (ranging from 4% in pygmy mice to 30% in boar) and 25% for maximal ATP synthesis rate (ranging from 9% in pygmy mice to 46% in sheep). (b) Relationships between ATP/O ratio calculated for a given ATP synthesis rate and body mass are: at 400 nmol ATP min⁻¹ mg⁻¹ ATP/O = 1.46 × mass^0.038 (black circles; r² = 0.73; F_1,8 = 9.91; p < 0.05); at 200 nmol ATP min⁻¹ mg⁻¹, ATP/O = 1.01 × mass^0.050 (white circles; r² = 0.67; F_1,10 = 10.41; p < 0.01); at 100 nmol ATP min⁻¹ mg⁻¹, ATP/O = 0.60 × mass^0.071 (dark triangles; r² = 0.78; F_1,10 = 15.58; p < 0.01); at 50 nmol ATP min⁻¹ mg⁻¹, ATP/O = 0.32 × mass^0.091 (grey triangles; r² = 0.84; F_1,10 = 20.57; p < 0.01); at 10 nmol ATP min⁻¹ mg⁻¹, ATP/O = 0.07 × mass^0.118 (white triangles; r² = 0.88; F_1,10 = 27.99; p < 0.001). Values are means ± s.d. (Online version in colour.)

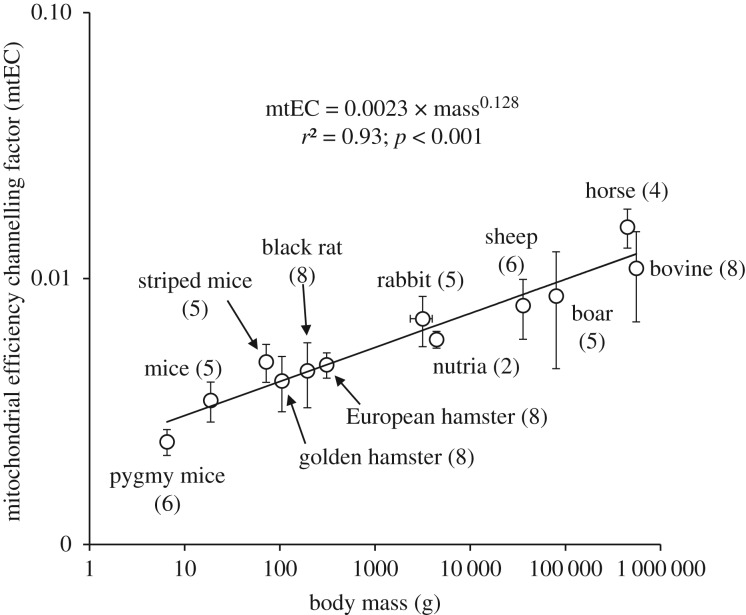
Nevertheless, mitochondrial coupling efficiency (ATP/O ratio) is not only controlled by proton leak but also by ATP synthesis reactions, which involve properties of the F₁F₀-ATP synthase, the adenine nucleotide translocase and the phosphate carrier [32,33]. Given that half to two-thirds of the basal proton conductance could also be catalysed by the adenine nucleotide carrier [33], this highlights the complex interplay between reactions that control mitochondrial efficiency during the transition from resting to maximal mitochondrial activities. Therefore, we cannot completely rule out that both proton leak and phosphorylation reactions may interact to mechanistically explain why ATP/O ratios reached their maximum faster in large mammals than in small species during the dynamic transition from basal to maximal oxidative phosphorylation state (figure 2). Notwithstanding the underlying mechanisms and in order to find a single parameter that could integrate these two sides of the mitochondrial efficiency control, we propose to use the gradient of the nonlinear curve seen in figure 2a as an integrative coupling factor. To do so, we fitted the relationships between ATP/O ratios and the rates of ATP synthesis with a mono-exponential function $[\mathrm{ATP}/\mathrm{O}=\mathrm{P}/{\mathrm{O}}_{\max }\times (1-{\mathrm{e}}^{-\mathrm{mtEC}\times J_{\mathrm{ATP}}})],$ where J_ATP is the ATP synthesis rate and ‘mtEC’ is the gradient of the nonlinear curve which we named the mitochondrial efficiency channelling (mtEC) factor, because it describes how fast coupling efficiencies seen in figure 2a reach their maximum. Figure 3 indicates that there was a strong and significant positive dependence of this mtEC factor on body mass in mammals, with an exponent of 0.13. Accordingly, skeletal muscle mitochondria would reach their maximal efficiency 3.25-fold faster with an increase in body mass of 10 000-fold.

Figure 3.

Relationship between body mass and mitochondrial efficiency channelling factor. Values are means ± s.d. from (n) independent mitochondrial preparations. The efficiency channelling factor significantly and positively depended on body mass (F_1,10 = 48.40; p < 0.001).

4. Conclusion

All the results show that smaller mammals have a more flexible coupling efficiency, being able to reduce their mitochondrial coupling efficiency to lower values than larger species. Such flexibility of coupling efficiency may explain the higher mass-specific heat generation of small mammals imposed by their high surface-area-to-volume ratio, and more generally, differences in mass-specific basal metabolic rate between endotherms of different masses. In addition, with skeletal muscles being the major tissue contributing to the maximal metabolic rate [8], the invariant value of maximal coupling efficiency across mammal species reported here could give a mechanistic explanation for why scaling exponent values are very close to 1 at maximal metabolic rates, i.e. at maximum ATP turnover.

Ethics

All experiments were conducted in accordance with the animal care guidelines of the Ministère de la Recherche et de l'Enseignement Supérieur.

Data accessibility

Mean datasets of mitochondrial bioenergetics parameters for all of the species shown in the manuscript are accessible from Dryad Digital Repository system: https://dx.doi.org/10.5061/dryad.fh4vb2c [34].

Authors' contributions

Conception of the study and design of the work: D.R., Y.V.; acquisition and analysis: M.B., C.R., D.R.; interpretation of data and validation: M.B., D.R., Y.V.

Competing interests

The authors declare that they have no competing financial interests.

Funding

The project was financially supported by the Centre National de la Recherche Scienfique (CNRS) and the University of Lyon. M.B. was in receipt of a fellowship from the Ministère de l'Enseignement Supérieur et de la Recherche.