Probing of NMDA Channels with Fast Blockers

Abstract

Using whole-cell patch-clamp techniques, we studied the interaction of open NMDA channels with tetraalkylammonium compounds: tetraethylammonium (TEA), tetrapropylammonium (TPA), tetrabutylammonium (TBA), and tetrapentylammonium (TPentA). Analysis of the blocking kinetics, concentration, and agonist dependencies using a set of kinetic models allowed us to create the criteria distinguishing the effects of these blockers on the channel closure, desensitization, and agonist dissociation. Thus, it was found that TPentA prohibited, TBA partly prevented, and TPA and TEA did not prevent either the channel closure or the agonist dissociation. TPentA and TBA prohibited, TPA slightly prevented, and TEA did not affect the channel desensitization. These data along with the voltage dependence of the stationary current inhibition led us to hypothesize that: (1) there are activation and desensitization gates in the NMDA channel; (2) these gates are distinct structures located in the external channel vestibule, the desensitization gate being located deeper than the activation gate. The size of the blocker plays a key role in its interaction with the NMDA channel gating machinery: small blockers (TEA and TPA) bind in the depth of the channel pore and permit the closure of both gates, whereas larger blockers (TBA) allow the closure of the activation gate but prohibit the closure of the desensitization gate; finally, the largest blockers (TPentA) prohibit the closure of both activation and desensitization gates. The mean diameter of the NMDA channel pore in the region of the activation gate localization was estimated to be ∼11 Å.

Considerable progress has been achieved over the last few years in studies of the molecular structure of the NMDA subtype of glutamate receptors (for review, see McBain and Mayer, 1994; Dingledine et al., 1999) (Kuryatov et al., 1994;Kuner et al., 1996; Krupp et al., 1996, 1998; Laube et al., 1997, 1998;Villarroel et al., 1998; Anson et al., 1998; Beck et al., 1999). However, some fundamental questions concerning their gross architecture and gating have not yet been finally settled. Present-day views on the functional architecture of voltage-sensitive Na⁺ and K⁺channels are primarily based on the data obtained in studies of the mechanism of their direct blockade by various quaternary ammonium cations (for review, see Hille, 1992; Armstrong and Hille, 1998).

Probing with blocking compounds has also been used in studies of the functional architecture of some ligand-gated channels, in particular nicotinic acetylcholine channels and NMDA receptor channels. The use of this method clearly demonstrated that the activation gate of these channels is located in the external vestibule (Neher and Steinbach, 1978). Then, by analogy with voltage-sensitive channels (Armstrong, 1971; Strichartz, 1973; Yeh and Narahashi, 1977; Cahalan, 1978;Armstrong and Croop, 1982), it was found that, depending on the type of interaction with the gating machinery, most of the blockers of open receptor-operated channels can be subdivided into at least two groups, namely, those that do not prevent the channel closure, yielding the so-called trapping block (Neely and Lingle, 1986; Huetter and Bean, 1988; MacDonald et al., 1991; Johnson et al., 1995; Blanpied et al., 1997; Chen and Lipton, 1997; Sobolevsky et al., 1998) and those that prohibit the channel closure (Koshelev and Khodorov, 1992, 1995; Costa and Albuquerque, 1994; Vorobjev and Sharonova, 1994; Benveniste and Mayer, 1995; Johnson et al., 1995; Antonov and Johnson, 1996).

A comparative analysis of blocking effects of a series of organic cations on NMDA channels led Koshelev and Khodorov (1992, 1995) to suggest that, along with the activation gate, the NMDA channel, like the voltage-sensitive Na⁺ channel, is equipped with a desensitization gate; the closure of the latter was assumed to underlie the channel desensitization.

In the present study we investigated the interaction of tetraalkylammonium compounds (TAA) with open NMDA channels using a set of kinetic models. We found the criteria for distinguishing the blockers with a kinetics faster than the channel closure (fast blockers), which prohibited or did not prohibit the channel closure, desensitization, and agonist dissociation. According to these criteria, we analyzed the action of tetraethylammonium (TEA), tetrapropylammonium (TPA), tetrabutylammonium (TBA), and tetrapentylammonium (TPentA). The results of this analysis provide new evidence in favor of the hypothesis on the existence of functionally and spatially distinct activation and desensitization gates in the NMDA channel and offer a radically new approach to the study of their reciprocal position. Thus, TAA proved to be useful tools to study NMDA channel gating.

MATERIALS AND METHODS

Pyramidal neurons were acutely isolated from the CA-1 region of rat hippocampus using “vibrodissociation techniques” (Vorobjev, 1991). The experiments were begun after 3 hr of incubation of the hippocampal slices in a solution containing (in mm): NaCl, 124; KCl, 3; CaCl₂, 1.4; MgCl₂, 2; glucose, 10; and NaHCO₃, 26. The solution was bubbled with carbogen at 32°C. During the whole period of isolation and current recording, nerve cells were washed with an Mg²⁺-free 3 μmglycine-containing solution (in mm: NaCl, 140; KCl, 5; CaCl₂, 2; glucose, 15; and HEPES, 10, pH 7.3). Fast replacement of superfusion solutions was achieved by using the concentration jump technique (Benveniste et al., 1990a; Vorobjev, 1991) with one application tube. This technique allows substitution of the tubular for the flowing solution with a time constant <30 msec but backward with the time constant of 30–100 msec (Sobolevsky, 1999). Therefore, except where noted, the rate of the solution exchange was fast at the beginning of any application and slightly slower at its termination. The currents were recorded at 18°C in the whole-cell configuration using micropipettes made from Pyrex tubes and filled with an “intracellular” solution (in mm: CsF, 140; NaCl, 4; and HEPES, 10; pH 7.2). Electric resistance of the filled micropipettes was 3–7 MΩ. Analog current signals were digitized at 1 kHz frequency.

Statistical analysis was performed using the scientific and technical graphics computer program Microcal Origin (version 4.1 for Windows). The data presented are mean ± SE; comparison of the means was done by ANOVA, with p < 0.05 taken as significant.

The kinetic models used to simulate the action of the blockers (Fig.1) were based on the conventional rate theory and used independent forward and reverse rate constants to simultaneously solve first-order differential equations representing the transitions between all possible states of the channel. These models were obtained from a completely symmetric model for the open-channel blockade (model 5) by means of consecutive reduction of the blocked states. The processes of NMDA channel activation, opening, and desensitization were described in accordance with a kinetic model proposed by Lester and Jahr (1992). The choice of values of the kinetic constants was made as described previously (Sobolevsky and Koshelev, 1998). Thus, the values of the kinetic constants for the agonist binding and unbinding were l₁ = 2 μm⁻¹ · sec⁻¹ andl₂ = 25 sec⁻¹, respectively; the entrance and recovery from desensitization were γ = 1.2 and ε = 0.8 sec⁻¹, respectively, and the kinetic constant of the channel closure was α = 200 sec⁻¹. The value of the rate constant of the channel opening,β, was chosen according to the value of the open probability, P₀ =β/(α + β), which was previously defined in a wide range of 0.04–0.5 (Jahr, 1992; Lester et al., 1993;Lin and Stevens, 1994; Benveniste and Mayer, 1995; Colquhoun and Hawkes, 1995; Rosenmund et al., 1995; Lu et al., 1998). In the majority of computer experiments, except where noted, the value ofP₀ was taken to be rather low (0.09) by the reason clarified in Results. The values of the blocking and unblocking kinetic constants, k₁ andk₂, respectively, were too fast to be estimated. The value of the unblocking kinetic constant was taken to be sufficiently high, k₂ = 1000 sec⁻¹. The value of k₁ was taken arbitrarily (3.5 μm⁻¹ · sec⁻¹, as for TBA in the previous study by Sobolevsky, 1999) but the blocker concentration was measured in the values of the microscopicK_d =k₂/k₁. As it will be shown below from variation of the values ofk₂ andk₁, their arbitrary choice does not affect the major conclusions of this paper.

Fig. 1.

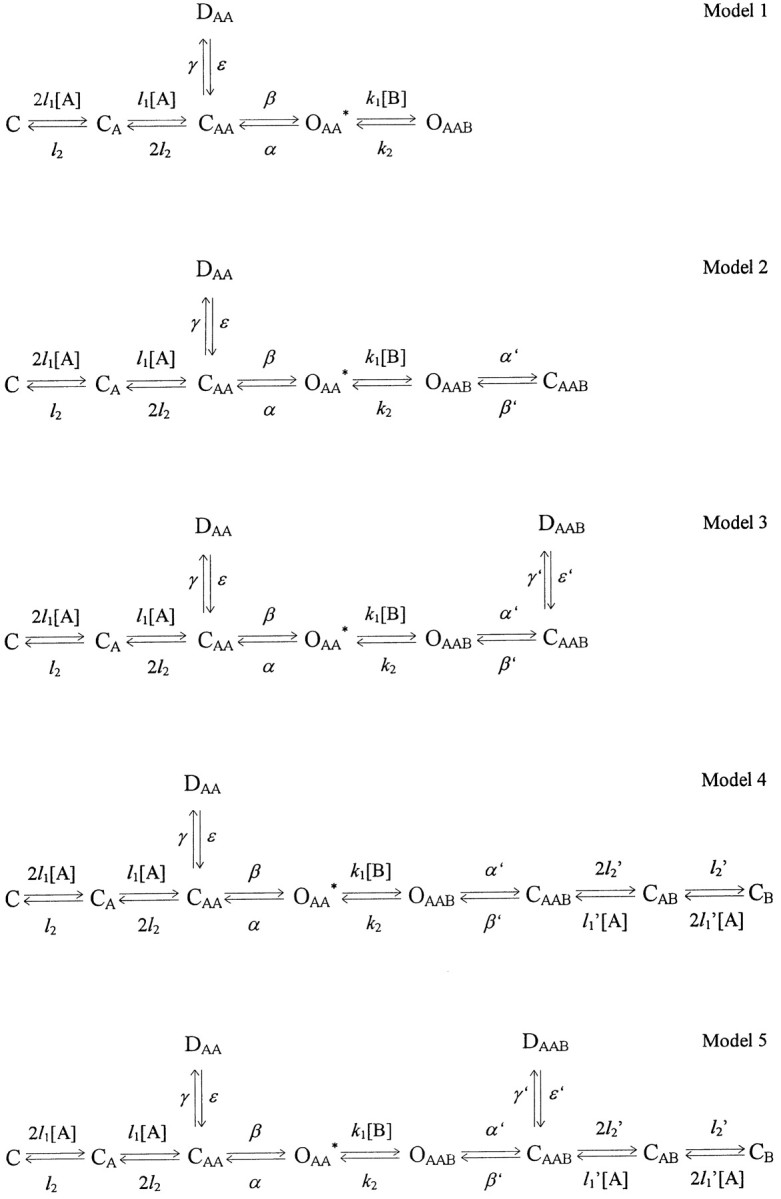
Kinetic models used to simulate the open-channel blocker action. C, D, O, Channel in closed, desensitized, and open states, respectively; subscripts A, AA, B, binding of one agonist and two and one blocker molecules to the channel, respectively; asterisk, conducting state,[A], [B], agonist and blocker concentrations, respectively.

Differential equations were solved numerically using the algorithm analogous to that described previously (Benveniste et al., 1990b).

Tetraalkylammonium compounds were purchased from Aldrich (Milwaukee, WI). The three-dimensional structures of the blockers were obtained with the help of Molecular Modeling System HyperChem (release 3 for Windows).

RESULTS

Concentration and voltage dependence of the TAA-induced blockade

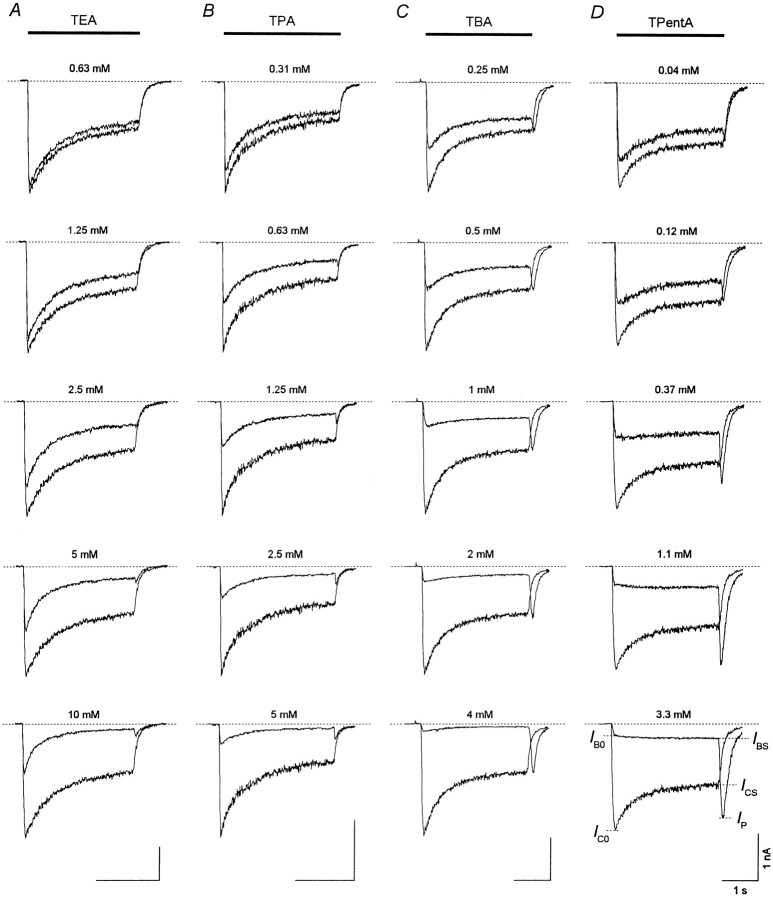
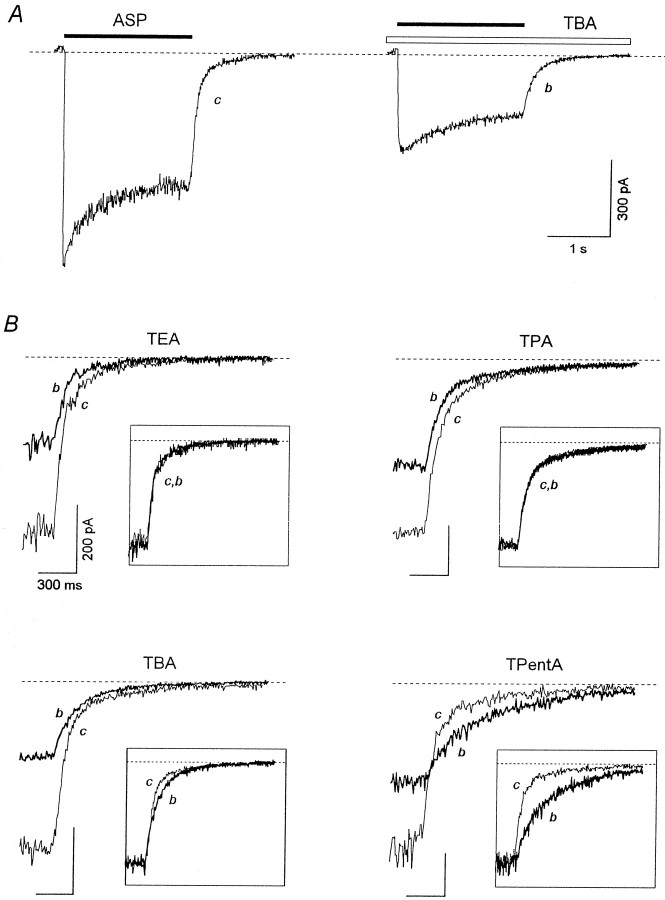
At the holding potential of −100 mV, aspartate (ASP) (100 μm) elicited an inward current through the NMDA channels, which after the initial fast rise (τ < 30 msec) up to the value, I_C0, decreased gradually (τ = 250–750 msec) to the stationary level,I_CS. This current decay under the continuing action of the agonist is interpreted as a result of NMDA receptor channel desensitization. When coapplied with ASP, TAA suppressed both initial, I_B0 (measured at the termination of the initial fast current increase), and stationary, I_BS, currents. Representative superpositions of the currents elicited by ASP alone (control) or by ASP coapplied with TEA, TPA, TBA, and TPentA used at different concentrations are shown in Figure2. Termination of ASP coapplication with each of these blockers was followed by a transient increase in the inward current (“hooked” tail current), which was absent in the control. In all the experiments with TEA and TPA, the maximal value of the hooked current, I_P, was smaller than I_CS at any blocker concentration. In contrast, for TBA at high concentrationsI_P was greater thanI_CS in 60% of the cells (n = 32 of 53), and even greater thanI_C0 in three cells (n= 3 of 53). The maximal value of the hooked current for TPentA used at high concentrations was always greater thanI_CS (n = 22), and in six cells (n = 6 of 22) it was larger thanI_C0. The amplitude of the hooked tail current, I_P −I_BS, increased with the blocker concentration for all TAA. However, this increase was considerably greater for TBA and TPentA than for TEA and TPA. Another important difference between the hooked tail currents concerns their time course. In the case of ASP coapplication with TEA or TPA, the hooked tail current always lay below the control tail current. In contrast, for TBA and TPentA the hooked tail current and the control tail current intersected.

Fig. 2.

Coapplications of TAA with ASP. The control current elicited by ASP (100 μm) application is superimposed with the current induced by ASP coapplication with TEA, TPA, TBA, or TPentA at different concentrations. A transient increase in the inward current (the hooked-tail current) appears after termination of the agonist and the blocker coapplication and is more pronounced at high TAA concentrations. The same labels apply to all calibrations.

The blockade of NMDA channels by TAA was voltage-dependent. The current responses to ASP application and to ASP coapplication with TBA (2 mm) at the holding potential,E_h, which varied from −100 to 40 mV (with the step of 20 mV), are shown in Figure3A. The control and blocked stationary I–V curves are shown in theinset. The degree of the stationary block, 1 −I_BS/I_CS, (as well as the amplitude of the hooked tail current; Fig.3A) diminished with membrane depolarization (Fig.3B). According to the model of Woodhull (1973), the voltage dependence can be fitted with the following equation:

$$1-I_{BS}/I_{CS}=1-1/(1+[B]/K_{0.5}(0)\times exp(\delta {FE}_{\text{h}}/RT)),$$ Equation 1

where K_0.5(0) = 5.34 ± 0.27 mm is the equilibrium dissociation constant at E_h = 0, and δ = 0.60 ± 0.02 (n = 7) is the fraction of the electric field that contributed to the energy of the blocker at the blocking site. F, R, and T have their usual meanings. The values of δ andK_0.5(0) estimated for other compounds are presented in Table 1. The value ofδ increased for TAA with a decrease in the alkyl chain length from 0.29 ± 0.03 (TPentA) to 0.90 ± 0.04 (TEA). This means that according to the Woodhull model the smaller TAA penetrate deeper into the membrane electric field. All the experiments described below were performed at the holding potential of −100 mV.

Fig. 3.

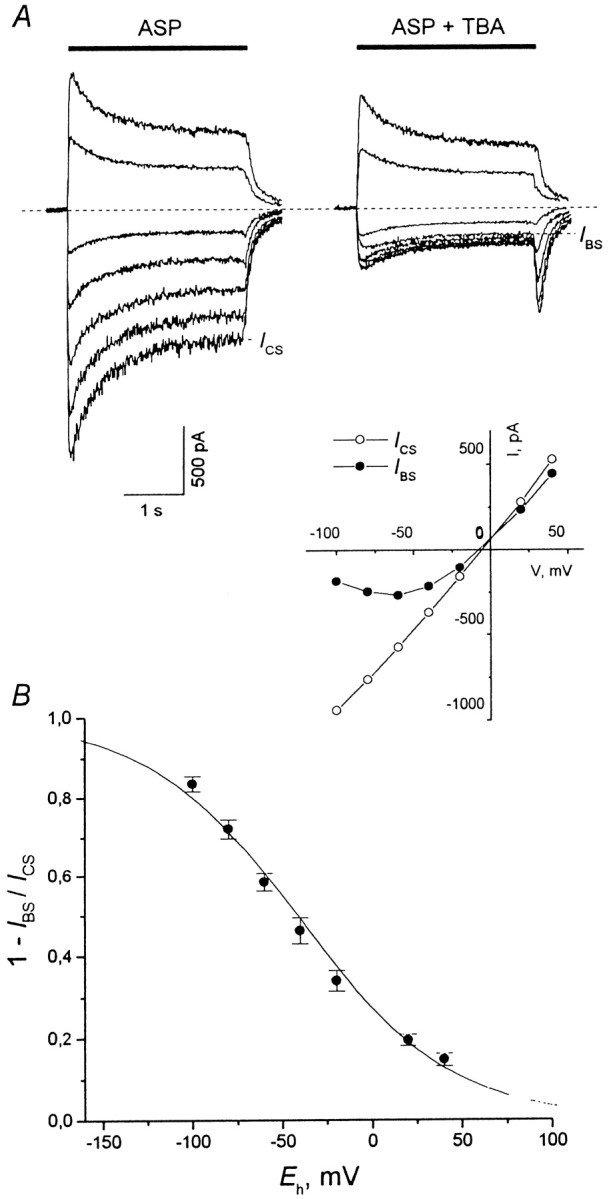
Voltage dependence of the stationary current inhibition. The voltage dependence is illustrated with 2 mmTBA as an example. A, Experimental curves. ASP (100 μm) was applied alone (left traces) or was coapplied with 2 mm TBA (right traces) for 3 sec at different holding membrane potentials,E_h = −100, −80, −60, −40, −20, 20, and 40 mV. The degree of the stationary current inhibition, 1 −I_BS/I_CS, diminished with membrane depolarization. Inset, Control and blocked stationary I–V curves.B, The mean 1 −I_BS/I_CSvalues were plotted against E_h. The fitting with Equation 1 (solid line) gave the following values of parameters: K_0.5(0) = 5.34 ± 0.27 mm and δ = 0.60 ± 0.02 (n = 7).

Table 1.

Voltage dependence parameters

Compound	δ	K0.5(0) (mm)	n
TEA	0.90  ± 0.04	62.2  ± 6.0	6
TPA	0.72  ± 0.05	10.0  ± 1.5	4
TBA	0.60  ± 0.02	5.34  ± 0.27	7
TPentA	0.29  ± 0.03	1.84  ± 0.11	5

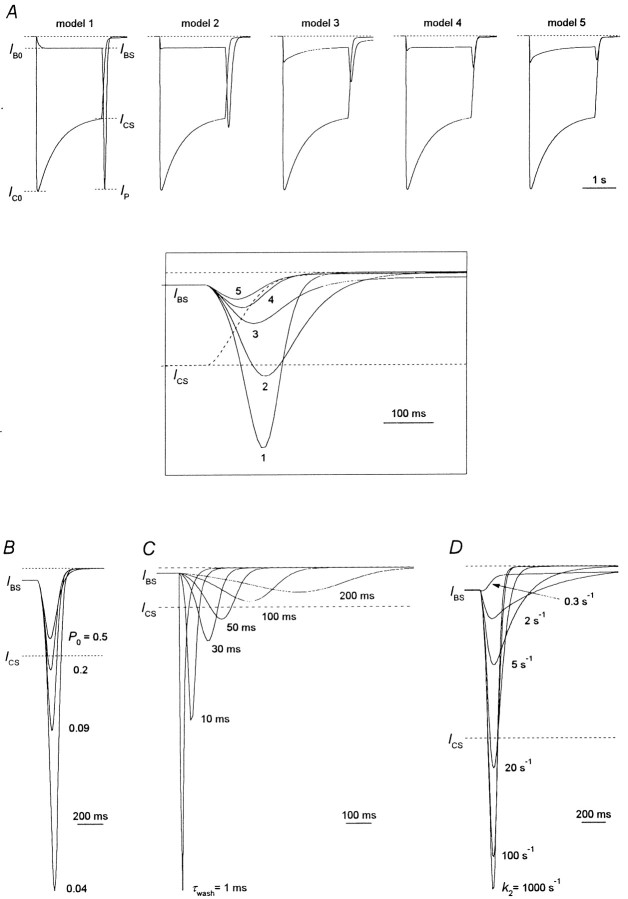
To study the effect of the TAA on NMDA channel closure, desensitization, and agonist dissociation, we considered five kinetic models (Fig. 1; see Materials and Methods). The first model implies that the blocker prohibits both the channel closure and desensitization. In the second model, the blocker can be trapped in the closed channel but does not allow the channel to desensitize and the agonist to dissociate from the channel. The third model implies that the blocker only prohibits the agonist dissociation from the blocked channel. Model 4 describes the situation when the blocker prohibits the channel desensitization but does not prohibit the channel closure and the agonist dissociation from the blocked channel. The fifth model is completely symmetric and implies that the blocker prohibits neither the channel closure and desensitization nor the agonist dissociation.

We tried to classify the action of the fast NMDA channel blockers according to models 1–5 assuming, for simplicity sake, that the rate constants for the transitions between the blocked states of the channel (α′, β′, γ′, ε′, l₂′, and l₁′) are equal to the corresponding rate constants for the nonblocked channels (α, β, γ, ε,l₂, andl₁). Multiple experimental and modeling protocols will be used to associate each blocker with a model.

On the condition that the blocking kinetics is rather fast, all five models predict the appearance of the hooked tail current immediately after the termination of the agonist and the blocker coapplication (Fig.4A). The kinetic analysis showed that the ascending phase of the hooked current reflects the blocker dissociation from the channel (transition from O_AAB to O_AA* state), whereas the falling phase reflects the processes of the channel closure, desensitization and the agonist dissociation. In Figure4A the degree of the stationary current inhibition, 1 −I_BS/I_CS, is the same for all models (0.86). To achieve this degree of stationary current inhibition, the blocker concentration was taken equal to 175, 16, 7, 13, and 6.5 K_d for models 1, 2, 3, 4, and 5, respectively. The significant difference in blocker concentration ([B]) for different models clearly demonstrates that the apparent affinity of the blocker (1/IC₅₀) is defined not only by its association–dissociation kinetics (the association and dissociation rate constants for different models were the same) but, to a considerable extent, by the blocker effect on the channel closure, desensitization, and agonist dissociation.

Fig. 4.

Simulated hooked tail currents. A, The simulated currents in response to the agonist application are superimposed with simulated currents in response to the agonist coapplication with the blocker. All models 1–5 predict the appearance of the hooked current after termination of the agonist and the blocker coapplication. To obtain the same degree of the stationary current inhibition,I_BS/I_CS, we used the blocker concentrations [B] = 175, 16, 7, 13, and 6.5K_d for models 1, 2, 3, 4, and 5, respectively. Hereafter (except as noted) the time constant of the solution exchange, τ_wash, = 30 msec, the open probability, P₀, = 0.09, and the kinetic constant of the blocker dissociation,k₂, = 1000 sec⁻¹.Inset, The control tail current (dashed line) and the hooked tail currents predicted by models 1–5 (solid lines) are superimposed. All the models except for model 5 predict the intersection of the control and hooked tail currents. B, Hooked tail currents predicted by model 1 at different P₀ values. The hooked currents at P₀ = 0.04, 0.09, 0.2, and 0.5 were plotted after the stationary levels of the control simulated current at different P₀ values were normalized. The value of P₀ was varied by means of change in the value of the rate constant of the channel opening, β. The degree of the stationary block is the same at differentP₀ values. β = 8.33, 20, 50, and 200 sec⁻¹; [B] = 413, 175, 77, and 23.5K_d for P₀ = 0.04, 0.09, 0.2, and 0.5, respectively. C, Hooked tail currents predicted by model 1 at differentτ_wash values. The hooked currents atτ_wash = 1, 10, 30, 50, 100, and 200 msec are presented. [B] = 175 K_d.D, Hooked tail currents predicted by model 1 at different k₂ values. The hooked currents atk₂ = 0.3, 2, 5, 20, 100, and 1000 sec⁻¹ (k₁ = 1.05, 7, 17.5, 70, 350, and 3500 mm⁻¹ · sec⁻¹, respectively) are presented. [B] = 175K_d.

The amplitude of the hooked current,I_P −I_BS, is different for different models (Fig. 4A, inset). It would be tempting to choose this amplitude as a criterion by which the action of the blocker can be attributed to one of models 1–5. However, we found that a number of factors affect the amplitude of the hooked current. We illustrated this with the simplest model (model 1) as an example.

The first factor is the value of the open probability,P₀. A rise inP₀ increases the magnitude of the simulated control current and enhances the simulated current stationary inhibition at a given blocker concentration. Thus, to achieve the same degree of the stationary current inhibition, we took smaller [B] at higher P₀; the relative amplitude of the hooked current, (I_P −I_BS)/I_CS, decreased with increasing P₀. This can be clearly seen in Figure 4B, where the stationary levels of the control simulated current at differentP₀ were normalized.

The time constant of the solution exchange (assuming that the solution exchange is a single-exponential process; Benveniste et al., 1990b),τ_wash, is the next factor that crucially affects the amplitude of the hooked current (Fig. 4C). The hooked current becomes higher and thinner with diminishingτ_wash.

A qualitatively inverse dependence of the amplitude of the hooked current on the value of the unblocking rate constant,k₂, is observed (Fig.4D). The hooked current becomes smaller and wider with the slowing of the blocking kinetics, and atk₂ = 0.3–0.5 sec⁻¹ it disappears completely.

The next factor is the blocker concentration, [B] (Fig.5A). The higher the [B], the deeper is the block and the greater is the amplitude of the hooked current. Such an experimental dependence is clearly seen in Figure2.

Fig. 5.

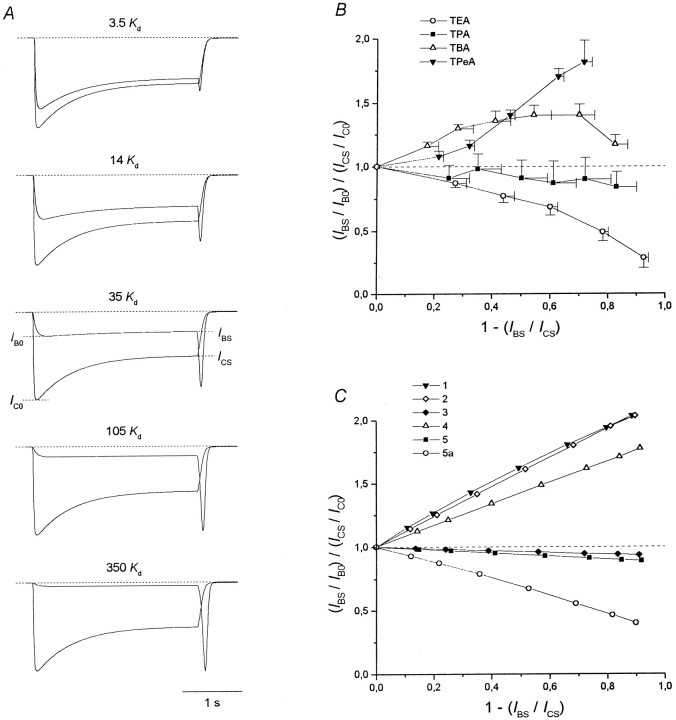
Plateau/peak ratio. A, The current responses to the agonist application and its coapplication with the blocker at different concentrations ([B] = 3.5, 14, 35, 105, and 350K_d) predicted by model 1 are superimposed. B, The experimental values of the plateau/peak ratio normalized to the control, (I_BS/I_B0)/(I_CS/I_C0), are plotted against the degree of the stationary current inhibition, 1 −I_BS/I_CS, for different TAA. C, (I_BS/I_B0)/(I_CS/I_C0) curves predicted by models 1–5 and 5a. Values of parameters forA and C:P₀ = 0.09,τ_wash = 30 msec, andk₂ = 1000 sec⁻¹.

The nature of the dependencies of the hooked current amplitude onP₀,τ_wash,k₂, and [B] will be considered elsewhere. However, the variety of parameters that affect the amplitude of the hooked current (as well as its latency) makes it doubtful to consider this value as a criterion of choice among models 1–5. Apparently, it would be much better to find a qualitative criterion. For example, the intersection of the hooked tail current and the control tail current (Fig. 4A, inset) is predicted by models 1–4 (but not by model 5) at anyP₀,τ_wash,k₂, and [B] values considered. Thus, we have obtained the first criterion, which allows us to select a model for describing the action of a blocker. This criterion permits one to distinguish the blockers whose action can be described by model 5 from those whose action can be described by models 1–4. According to this criterion, the TEA and TPA action can be described by model 5, whereas the TBA and TPentA action can be described by one of models 1–4. Other qualitative criteria should be found to make a choice between models 1–4. The first of these criteria is the plateau/peak ratio.

Plateau/peak ratio

As can be seen from Figure 2, the plateau/peak ratio for the block,I_BS/I_B0, may differ significantly from that for the control,I_CS/I_C0. To compare the plateau/peak ratio for the block and the control, we calculated it at different blocker concentrations. The mean values of the normalized plateau/peak ratio, (I_BS/I_B0)/(I_CS/I_C0), for different NMDA open-channel blockers were plotted against the degree of the stationary current inhibition, 1 −I_BS/I_CS(Fig. 5B), which increased monotonically with [B] (Fig.2). The mean (I_BS/I_B0)/(I_CS/I_C0) values for TPentA (n = 7) and TBA (n = 10) were greater than unity; those for TPA (n = 5) were slightly lower than unity. However, individual measurements for TPA revealed three cells in which the normalized plateau/peak ratio was lower than unity and two cells in which the normalized plateau/peak ratio was slightly higher than unity. The (I_BS/I_B0)/(I_CS/I_C0) values for TEA (n = 5) were considerably lower than unity.

Models 1–5 also demonstrate different plateau/peak ratios for the block with respect to the control (Fig. 4A). For example, the simulated currents at different blocker concentrations (Fig. 5A) indicate that for model 1 the gradual current decay during the agonist application diminishes with an increase in [B]. The values of the normalized plateau/peak ratio calculated for all models are plotted in Figure 5C. Evidently, these values are higher than unity for the models that imply that the blocker prohibits the channel desensitization (models 1, 2, and 4) and slightly lower than unity for the models that predict that the blocker does not prohibit this process (models 3 and 5). Therefore, the reason, whyI_BS/I_B0>I_CS/I_C0for models 1, 2, and 4, is the absence of the D_AAB state in which the blocked channels can be gradually accumulated during the agonist and the blocker coapplication. Thus, the greater the gradual decrease in the simulated currents during the agonist and the blocker coapplication for models 3 and 5 in comparison with that of models 1, 2, and 4 (Fig. 4A) indicates that in the first case both blocked and nonblocked channels desensitize, whereas in the second case it is only the nonblocked channels that desensitize.

According to the plateau/peak ratio criterion, TPentA and TBA prohibited channel desensitization, whereas TPA did not. In the case of TBA, the reason by which the (I_BS/I_B0)/(I_CS/I_C0) curve is bent down at high values of 1 −I_BS/I_CS(Fig. 5B) is not clear. Presumably, it can be explained by nonspecific TBA-induced inhibition of NMDA receptors or a comparatively slow TBA-induced blockade of the residual nonselective cation current (Xiong et al., 1997). The fact that in some cells the normalized plateau/peak ratio for TPA is slightly higher than unity indicates that under certain conditions TPA can decrease the probability of NMDA channel desensitization. The plateau/peak ratio criterion is valid at any P₀ (from 0.04 to 0.5) andτ_wash (from 0 to 300 msec) but only for fast blockers (k₂ > 10 sec⁻¹), because a high value ofI_B0/I_BScan be a consequence of the noncomplete initial blockade of the channels because of a slow development of the block.

The (I_BS/I_B0)/(I_CS/I_C0) curve for TEA proved to be much lower than even those predicted by models 3 and 5 (Fig. 5B). This fact can imply (Sobolevsky, 1999) either (1) the existence of a slow blocking kinetics component, or (2) that TEA promotes the channel desensitization by increasing the number of desensitized states or because of a shift of the C_AAB − D_AAB equilibrium toward the D_AAB state. To examine the first possibility, model 5 was modified by addition of a new blocking site, site 2 (Model 5a)

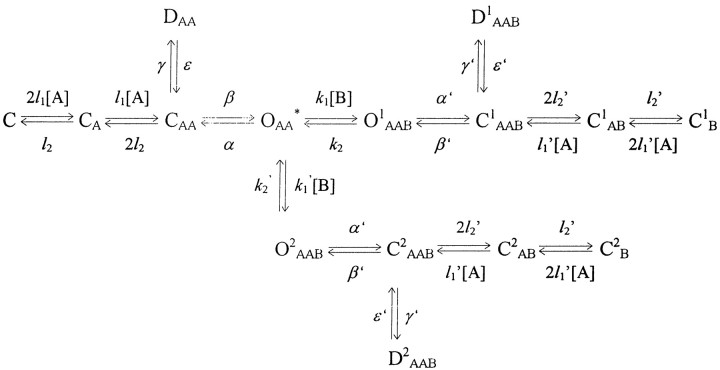
Model 5a.

Model 5a does not contain any additional assumptions. In this sense, this model is the simplest one. Thus, the properties of site 2 are qualitatively similar to those of site 1. The blocker can bind to site 2 during the channel opening and does not prohibit the subsequent channel closure, desensitization, and agonist dissociation. Sites 1 and 2 cannot be occupied simultaneously, because the amplitude of the fast component in the recovery kinetics for TEA in the continuous presence of ASP does not depend on the blocker concentration (Sobolevsky, 1999, his Fig. 5). The main difference between these two sites is in their respective rates of blocker association and dissociation. Thus, the value of the dissociation rate constant from the new site 2 was taken to be 250 times lower than k₂:k₂′ = 4 sec⁻¹. The value of the association rate constant was lowered proportionally (k₁′ =k₁/250 = 0.014 μm⁻¹ · sec⁻¹), so that the value of the microscopic K_d =k₂/k₁ remained the same (0.29 mm). The (I_BS/I_B0)/(I_CS/I_C0) curve predicted by model 5a is shown in Figure 5C. At high blocker concentrations, the plateau/peak value becomes much lower than unity in compliance with that observed in the TEA experiment (Fig.5B). The modifications of model 5 implying that the blocker favored channel desensitization predicted a similar change in (I_BS/I_B0)/(I_CS/I_C0) curve (data not shown). The criterion that allows one to distinguish these modifications of model 5 from model 5a will be considered below.

Blocking kinetics in the continuous presence of the agonist

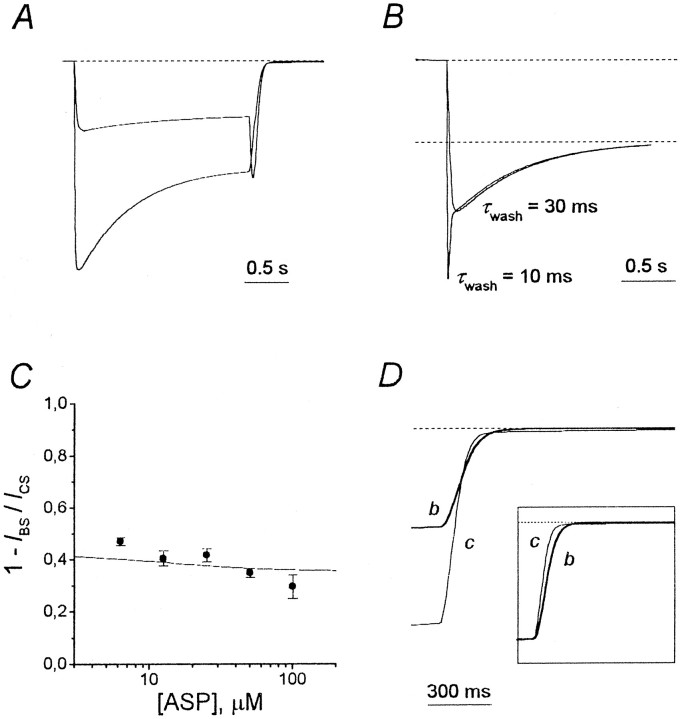
Investigation of the blocking kinetics in the continuous presence of the agonist provides valuable information about the mechanism of the blocker–channel interaction (Sobolevsky and Koshelev, 1998;Sobolevsky, 1999). The experimental protocol is shown in Figure6A with TPentA as an example. The blocker was applied when the ASP-induced current already reached its stationary level, I_CS. Examples of the recovery kinetics are shown in Figure6B. The recovery kinetics for all TAA contained a fast ascending component, which reflected the rapid dissociation of the blocker from the channel (the transition from O_AAB to O_AA*); the time constant of this component is mainly determined by the process of the solution exchange (Sobolevsky, 1999).

Fig. 6.

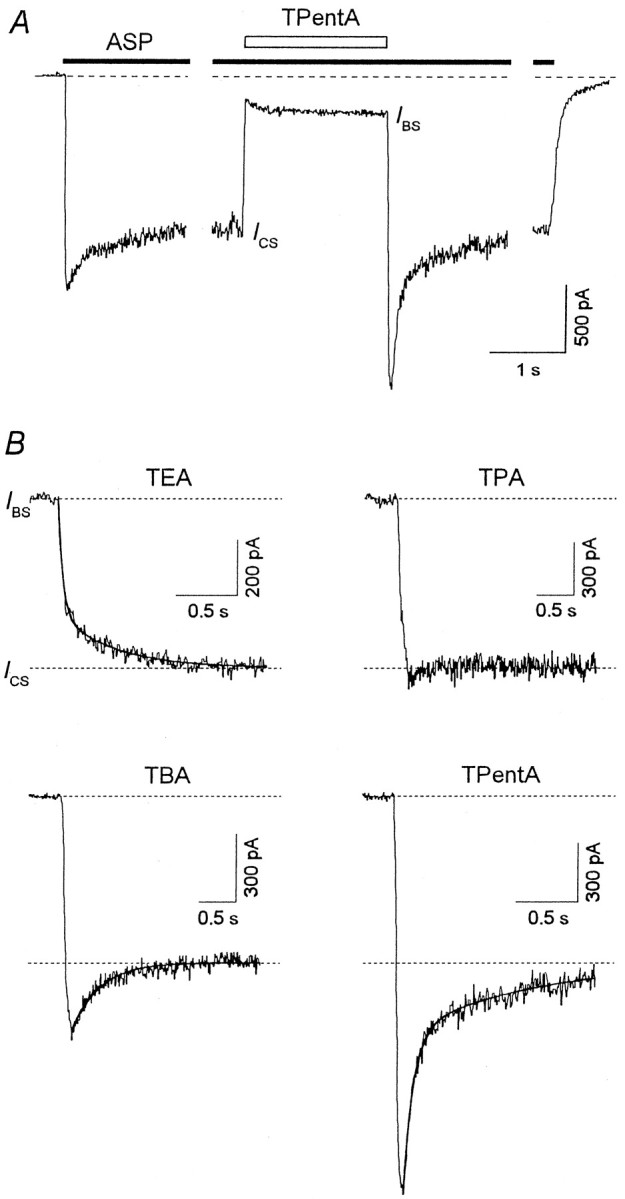
The TAA recovery kinetics in the continuous presence of ASP. A, The experimental protocol. TPentA (2 mm) was applied for 2 sec in the continuous presence of ASP (100 μm) when the inward current gained its stationary level, I_CS. The solution exchange at the termination of TPentA application was fast. B, Representative examples of the current recovery after termination of TEA (5 mm), TPA (2 mm), TBA (2 mm), and TPentA (2 mm) application in the continuous presence of ASP. The solid lines are double-exponential fittings of the recovery kinetics in the cases of TEA and TPentA (τ_fast = 40 msec,τ_slow = 440 msec, andA_fast = 0.68 for TEA;τ_fast = 74 msec,τ_slow = 987 msec, andA_fast = 0.68 for TPentA) and a single-exponential fitting in the case of TBA (τ = 368 msec).

Along with a fast component (τ_fast = 155 ± 27 msec; n = 8), the recovery kinetics for TEA also contained a slow component with the time constantτ_slow = 2.04 ± 0.34 sec (n = 8). The amplitude of the fast component,A_fast, measured as a relative weight of the fast exponent in the sum of the fast and slow components, was 0.69 ± 0.04 (n = 8).

In the case of TPA, the slow component, if existed, was small. The value of A_fast for TPA was either slightly lower (n = 4) or slightly higher (n = 4; see the example in Fig. 6B) but, on the average, was equal to unity.

In the case of TBA, the fast component was so large that after a rapid increase the current reached a value exceeding considerably the stationary current level. As in the previous study (Koshelev and Khodorov, 1995), the recovery current exceeding the stationary level,I_CS, will be referred to as an “overshoot.” In the majority of experiments with TBA, the fast ascending phase of the overshoot was followed by a slow (τ_slow = 389 ± 38 msec;n = 10) current decrease back toI_CS. However, in three cells for which the solution exchange was comparatively fast (τ_wash ≤ 10 msec), the descending phase of the current contained, along with the slow component, also a fast component.

Such a fast component was present in the recovery kinetics for TPentA, which also exhibited an overshoot. Double-exponential fitting of the overshoot descending phase allowed us to determine the time constants of the fast and slow components, τ_fast = 54 ± 7 msec and τ_slow = 596 ± 85 msec (n = 7), respectively; the amplitude of the fast component, A_fast, is 0.63 ± 0.04 (n = 7).

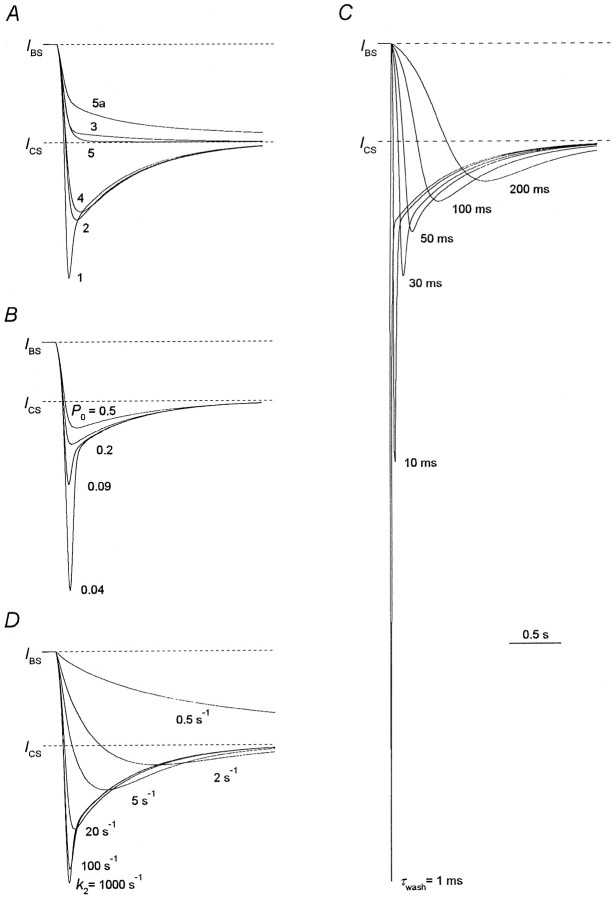
Computer simulation showed (Fig.7A) that the overshoot in the recovery kinetics is predicted by models 1, 2, and 4 but is not predicted by models 3 and 5. Thus, the recovery kinetics predicted by model 5 contains only a fast component (the involvement of the second component is not justified statistically, Fischer's test; Korn and Korn, 1974). There is a small slow component in the recovery kinetics predicted by model 3. The fitting of the recovery curve predicted by model 3 gave the values of the time constants,τ_fast = 80 msec andτ_slow = 1.2 sec, and the amplitude of the fast component, A_fast = 0.93. Therefore, the existence of an overshoot is the criterion distinguishing fast NMDA channel blockers that prohibit channel desensitization from those that do not. This criterion is valid at any blocker concentration in the range of theP₀,τ_wash, andk₂ values identified in the legend to Figure 4. According to this criterion, TEA and TPA do not prohibit channel desensitization, whereas TBA and TPentA do. The above-mentioned cases for TPA, when A_fast was somewhat larger than unity can be interpreted as cases when TPA slightly hinders channel desensitization.

Fig. 7.

Modeling of the recovery kinetics in the continuous presence of the agonist. The values of parameters are the same as listed in the legend to Figure 4. A, Recovery kinetics predicted by models 1–5 and 5a. B, Recovery kinetics predicted by model 1 at different open probabilities,P₀. The simulated currents atP₀ = 0.04, 0.09, 0.2, and 0.5 are presented. C, Recovery kinetics predicted by model 1 at different time constants of the solution exchange,τ_wash. The simulated currents atτ_wash = 1, 10, 30, 50, 100, and 200 msec are presented. D, Recovery kinetics predicted by model 1 at different kinetic constants of the blocker dissociation,k₂. The simulated currents atk₂ = 0.3, 2, 5, 20, 100, and 1000 sec⁻¹ are presented.

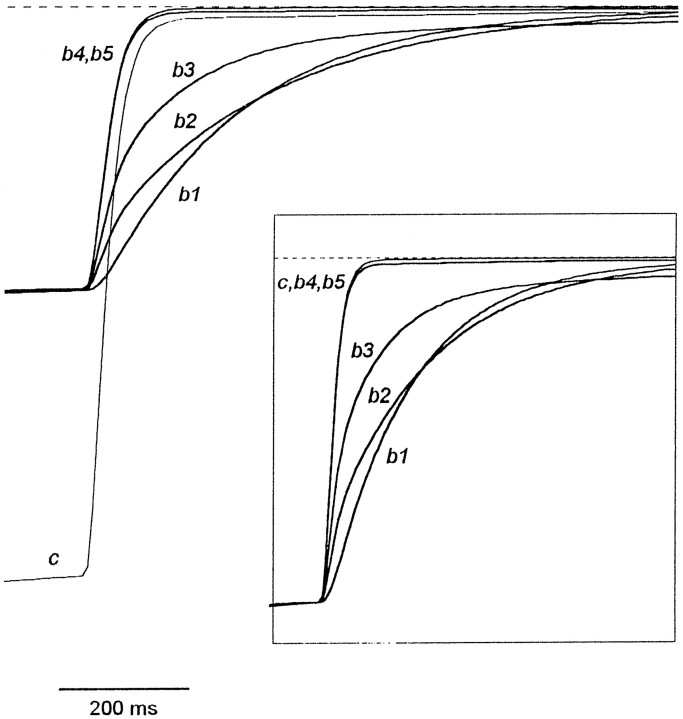
Another important conclusion, which clearly follows from the consideration of the recovery kinetics, concerns the effect of the blocker on the NMDA channel closure. Model 1, which is the only one implying that the blocker prohibits the channel closure, predicts the existence of a fast component in the falling phase of an overshoot. Thus, the falling phase of the overshoot predicted by models 2 and 4 contains only a slow component with the time constant,τ_slow = 600 msec. In contrast, the falling phase of the recovery kinetics for model 1, along with a slow component, contains also a fast component. The double-exponential fit of the recovery kinetics illustrated in Figure 7A revealed the time constant and the amplitude of this component:τ_fast = 35 msec;A_fast = 0.4. Our simulations showed that the slow component of the falling phase reflects channel desensitization (the slow transition from C_AA to D_AA) and does not depend on the agonist association–dissociation kinetics. The latter conclusion was confirmed by the observation that the time constant of the slow component for the falling phase of the overshoot did not depend on the agonist type. Thus, this time constant was 394 ± 65 msec for ASP and 377 ± 32 msec for NMDA (these values were not significantly different (p > 0.7; n = 6). The fast component of the falling phase of the overshoot reflects the closure of the unblocked channels (the transition from O_AA* to C_AA). The fast component for model 1 appears if the channel closure is slower than the blocker dissociation and is not masked by a more slow solution exchange, i.e., β <k₂ and β < 1/τ_wash, respectively. These conditions are fulfilled at any blocker concentrations if the channel has a low open probability (P₀ < 0.1; Fig.7B), the solution exchange is not very slow (τ_wash < 50 msec; Fig. 7C), and the blocker dissociation constant is fast enough (k₂ > 20 sec⁻¹; Fig.7D) (for models 2 and 4 the fast component in the falling phase of an overshoot does not appear at any values ofP₀,τ_wash, andk₂).

Therefore, we have considered TPentA as a blocker that prohibits the NMDA channel closure. Our experiments with TBA, in which the value of τ_wash was comparatively low (≤10 msec), and the falling phase of the recovery kinetics contained the fast component may imply that TBA at least hampers the channel closure if not prohibits it. The appearance of the fast component in the falling phase of the recovery kinetics for TPentA and TBA was that reason, which forced us to adopt the value of the open probability,P₀, to be rather low (0.09).

The experimental value of A_fast for TEA (0.69 ± 0.04) was noticeably lower than the values predicted by models 3 (0.93) and 5 (1.00). The recovery kinetics predicted by model 5a is shown in Figure 7A. The value ofA_fast (0.67) is close to that observed in the experiment with TEA. As in the case of the plateau/peak criterion, we also examined the modifications of model 5, implying that the blocker promotes channel desensitization (see above). These modifications provide similar changes in the recovery kinetics as those predicted by model 5a (data not shown). Only the following criterion allows one to restrict the choice of model 5 modification, satisfactorily describing the blocking effect of TEA.

Dependence of the stationary current inhibition on the agonist concentration

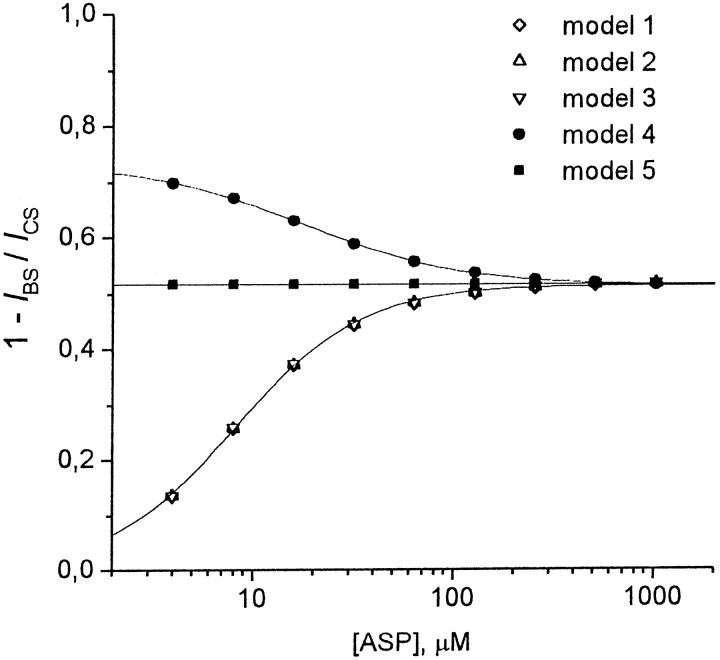
Tetraalkylammonium compounds demonstrated different dependencies for the degree of the stationary current inhibition, 1 −I_BS/I_CS, on the agonist concentration. The superposition of the currents elicited by ASP application and its coapplication with TPentA (1 mm) at different ASP concentrations is shown in Figure 8A. As seen, the degree of TPentA-induced stationary current inhibition increases with ASP concentration. The mean values of 1 −I_BS/I_CSfor TEA (2 mm), TPA (1 mm), TBA (0.15 mm), and TPentA (1 mm) depending on ASP concentration are shown in Figure 8B. The degree of the stationary current inhibition did not depend on the agonist concentration for TEA (the mean values were not significantly different, p > 0.9;n = 7) and TPA (the mean values were not significantly different, p > 0.3; n = 6). In the case of TBA, 1 −I_BS/I_CSdecreased (the mean 1 −I_BS/I_CSvalues were significantly different, p < 0.003;n = 5), whereas in the case of TPentA it rose with the agonist concentration (the mean 1 −I_BS/I_CSvalues were significantly different, p < 10⁻⁶; n = 6).

Fig. 8.

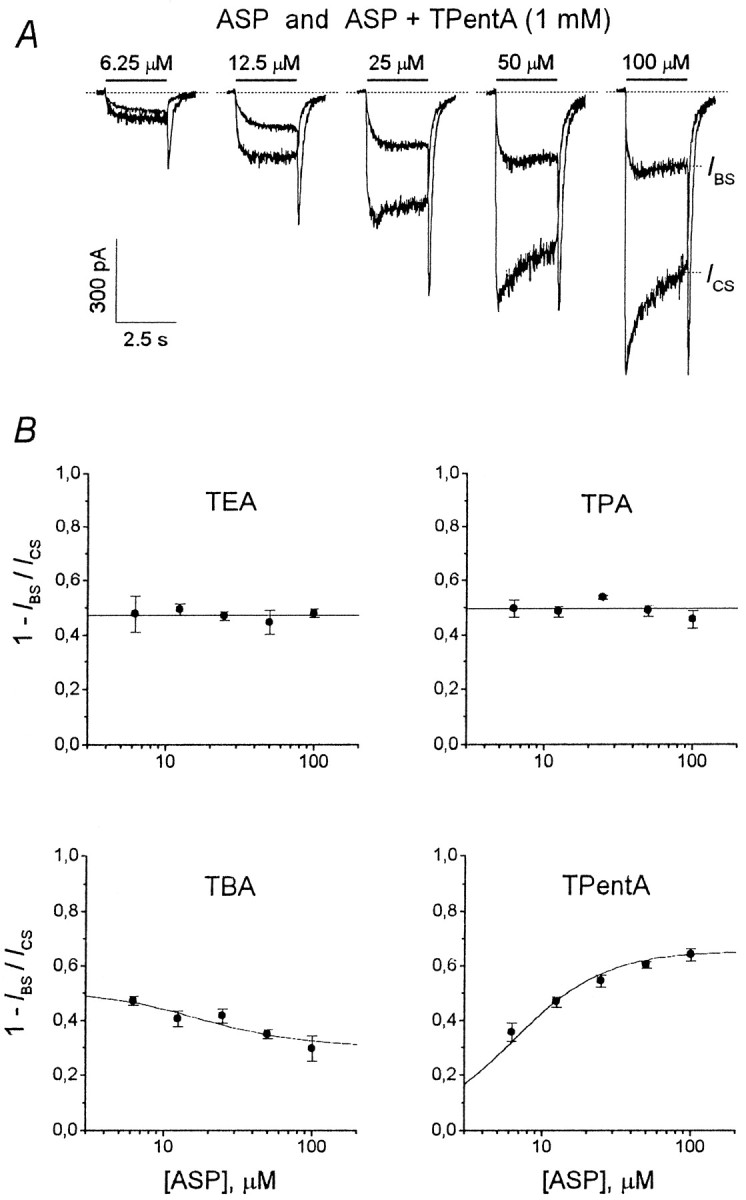
Experimental dependence of the stationary current inhibition on the agonist concentration. A, Example of experimental curves. ASP alone and together with 1 mmTPentA was applied for 2.5 sec at concentrations of 6.25, 12.5, 25, 50, and 100 μm. The superposition of the control and blocked currents at each ASP concentration is shown. B, The mean values of the degree of the stationary current inhibition, 1 −I_BS/I_CS, for tetraalkylammonium compounds were plotted against the ASP concentration. The 1 −I_BS/I_CSvalues for TEA (2 mm) and TPA (1 mm) were not significantly different at different ASP concentrations. The mean 1 −I_BS/I_CSvalues for TEA (0.47 ± 0.02; n = 7) and TPA (0.50 ± 0.01; n = 4) are represented byhorizontal lines and correspond to the agonist dependence predicted by model 5 at [B] = 0.91 and 0.98K_d, respectively. The 1 −I_BS/I_CSvalues for TBA (0.15 mm) and TPentA (1 mm) were significantly different at different ASP concentrations. The degree of the stationary current inhibition decreased with the ASP concentration for TBA (n = 8) and increased for TPentA (n = 6). The solid lines are the predictions of model 4 at [B] = 1.02 K_dfor TBA and model 1 at [B] = 51 K_d for TPentA (see Results).

Models 1–5 also predicted qualitatively different agonist dependencies (Fig. 9). 1 −I_BS/I_CSfor models 1–3 increased with the agonist concentration. The corresponding agonist dependencies coincided at the blocker concentration, [B] = 28, 2.6, and 1.1K_d for models 1, 2, and 3, respectively, and were well fitted with the following logistic equation:

$$1-\frac{I_{BS}}{I_{CS}}=\frac{A_1-A_2}{1+([A]/[A{]}_0{)}^{\wedge }{n}_{\text{Hill}}}+A_2.$$ Equation 2

The values of parameters were as follows:A₁ = 0,A₂ = 0.515 ± 0.002, [A]₀ = 8.18 ± 0.15 μm, and n_Hill= 1.39 ± 0.04. On the contrary, the 1 −I_BS/I_CSvalue for model 4 decreased with the agonist concentration. The corresponding agonist dependence at [B] = 2.5K_d was well fitted with Equation 2 atA₁ = 0.733 ± 0.003,A₂ = 0.515 ± 0.001, [A]₀ = 17.9 ± 0.6 μm, and n_Hill= 1.13 ± 0.03. The degree of the stationary current inhibition for model 5 did not depend on the agonist concentration and was equal to 0.515 at [B] = 1.1 K_d. Therefore, the models that imply that the agonist cannot dissociate from the blocked channel (models 1–3) predict an increasing degree of block with increasing agonist concentration, whereas the models that imply that the blocker does not prevent the agonist dissociation predict a decreasing degree of block with increasing agonist concentration (model 4) or no dependence of the degree of block on agonist concentration at all (model 5). The agonist dependence criterion is valid at any values of [B] in the range of the P₀,τ_wash, andk₂ values identified in the Figure 4legend. By this criterion, the action of TAA must be described by one of models 1–3 in the case of TPentA, by model 4 in the case of TBA, and by model 5 in the cases of TPA and TEA. The corresponding simulated agonist dependencies for TEA, TPA, TBA, and TPentA are shown in Figure8B by solid lines at [B] = 0.91K_d (model 5), 0.98K_d (model 5), 1.02K_d (model 4), and 51K_d (model 1), respectively. The fitting parameters for TBA (model 4) and TPentA (model 1) were as follows: A₁ = 0.518 ± 0.002,A₂ = 0.304 ± 0.001, [A]₀ = 15.9 ± 0.3 μm, and n_Hill= 1.18 ± 0.02 for TBA and A₁ = 0, A₂ = 0.655 ± 0.003, [A]₀ = 6.46 ± 0.10 μm, and n_Hill= 1.42 ± 0.04 for TPentA. The agonist dependence criterion is sensitive to the blocker effect on desensitization. Thus, model 5, implying that the blocker does not affect channel desensitization, demonstrates the absence of the agonist dependence, although the same model without a desensitized blocked state (model 4), implying that the blocker prohibits the channel desensitization, predicts that the degree of the stationary current inhibition diminishes with the agonist concentration. Correspondingly, all the modifications of model 5, implying that the blocker promotes channel desensitization predict an increasing agonist dependence (data not shown). In contrast, model 5a, implying the existence of two blocking sites, demonstrates the absence of the agonist dependence as in the case of the nonmodified symmetric model 5. Therefore, modifications of model 5, implying that the blocker promotes channel desensitization, cannot describe the TEA action, for which the fraction of the stationary current inhibition did not depend on ASP concentration (Fig. 8B). However, it can be well described by model 5a with two binding sites that cannot be occupied simultaneously by two different TEA molecules and differing by the rates of the blocker binding to and dissociation from them. A variety of two-site model modifications could be also offered to describe the effects of TEA. Thus, the consequence of occupation of the sites could be different (Sobolevsky, 1999): (1) any site can be available from the external media, but the blocking molecule bound to one of them cannot “jump” to the other; (2) only one site can be available from the external medium, and the second site can be occupied via a sequential jump of the blocker molecule from the first site; and (3) both sites are available from the external medium, and the blocker bound to one of them can jump to the other. A much greater number of two binding site models could be obtained by possible variations of the kinetic constants. Analysis of such a huge variety of two binding site models was not the aim of the present study, and here we will not develop this topic any more. The only clear conclusion that can be made from the consideration of model 5a is the existence of a fast-occupied TEA blocking site in the NMDA channel, the blocker molecule binding to which does not prevent the channel closure, desensitization, and agonist dissociation.

Fig. 9.

Agonist dependencies of the stationary current inhibition predicted by models 1–5. The degree of the stationary current inhibition, 1 −I_BS/I_CS, rises with the agonist concentration for models 1–3, decreases for model 4, and is constant for model 5. The agonist dependencies predicted by models 1, 2, and 3 coincided at [B] = 28, 2.6, and 1.1K_d, respectively, and were well fitted with Equation 2 (solid line). The values of the fitting parameters were as follows: A₁= 0, A₂ = 0.515 ± 0.002, [A]₀ = 8.18 ± 0.15 μm, andn_Hill = 1.39 ± 0.04. The fitting of the agonist dependence predicted by model 4 at [B] = 2.5K_d (solid line) gave the following values of the fitting parameters:A₁ = 0.733 ± 0.003,A₂ = 0.515 ± 0.001, [A]₀ = 17.9 ± 0.6 μm, andn_Hill = 1.13 ± 0.03. The degree of the stationary current inhibition for model 5 did not depend on the agonist concentration and was equal to 0.515 at [B] = 1.1K_d. The values of parameters were as follows: P₀ = 0.09,τ_wash = 30 msec, andk₂ = 1000 sec⁻¹.

Another important criterion for the effect of the blocker on agonist dissociation is the kinetics of tail currents after termination of the agonist application in the continuous presence of the blocker. This criterion is not sensitive to the effect of the blocker on channel desensitization.

Tail currents in the continuous presence of the blocker

In contrast to the agonist and the blocker coapplication (Fig. 2), the application of ASP in the continuous presence of the blocker was not followed by the hooked current, as illustrated in Figure10A with TBA (1 mm). The kinetics of the tail current after ASP application in the continuous presence of the blocker (b) was different in comparison with that of the control (c) for different blockers (Fig. 10B). Such blockers as TEA and TPA did not affect the tail current kinetics: the bdecay was practically identical to the c decay. This fact is clearly illustrated in the insets, where the normalizedc and b curves are superimposed. In contrast, TPentA caused a pronounced delay in the current recovery kinetics, which is manifested in the intersection of curves c andb. Such an intersection was never observed in the case of TBA: curves c and b were tangent, or curveb was clearly below curve c (Fig.10B). However, there was a small delay in the recovery kinetics, which can be revealed only after superposition of the normalized tail currents (Fig. 10B, inset). In the majority of cells (n = 14 of 16), the normalized curve c was below the normalized curve b, but in 2 of 16 cells these curves coincided.

Fig. 10.

Effects of the continuous presence of the blocker on tail currents. A, Experimental protocol with TBA as an example. ASP (100 μm) was applied for 2 sec in the control external solution or in the continuous presence of 1 mm TBA. B, The control tail currents (c) are superimposed with the tail currents in the continuous presence of TEA (2 mm), TPA (0.6 mm), TBA (1 mm), and TPentA (0.5 mm) (b). The same labels apply to all calibrations. Insets, Superposition of the normalized curves c and b.

Computer simulation clarified the origin of all these effects. Figure11 shows that the time course of the tail current in the continuous presence of the blocker predicted by models 4 and 5 is very similar to the control tail current: the nonnormalized curves b4 and b5 do not intersect with the control curve c, whereas the normalized curvesb4 and b5 coincide with curve c (seeinset). In contrast, intersection of curves b1,b2, and b3 with curve c points to a considerable blocker-induced delay in the tail current kinetics predicted by models 1, 2, and 3, respectively. The common feature of these three different models (1–3) is that they exclude the agonist dissociation from the blocked channel. Thus, it is just the trapping of the agonist in the blocked channel that is responsible for the delay in the final channel closure in the presence of the blocker in the washout solution. The criterion of the tail currents in the continuous presence of the blocker is valid at any values ofP₀ (from 0.04 to 0.5),τ_wash (from 0 to 300 msec), and [B] andk₂ > 0.3 μm/sec. According to this criterion, TEA, TPA, and TBA,do not prohibit the agonist dissociation, whereas TPentA does.

Fig. 11.

Tail currents in the continuous presence of the blocker predicted by models 1–5. The experimental protocol is the same as shown in Figure 10A. The control tail current (c) is superimposed with the tail currents in the continuous presence of the blocker for models 1–5 (curvesb1–b5, respectively). Curvesb1–b3 intersect with curvec, whereas curves b4 andb5 do not. To achieve the same degree of the stationary current inhibition, the blocker concentration was different for different models: [B] = 28, 2.55, 1.09, 2.07, and 0.98K_d for models 1, 2, 3, 4, and 5, respectively. The values of the parameters are as follows:P₀ = 0.09,τ_wash = 30 msec, andk₂ = 1000 sec⁻¹.Inset, Normalized curves c andb1-b5. The control tail current (curve c) and the normalized tail currents in the continuous presence of the blocker predicted by models 4 and 5 (curves b4 andb5) practically coincide.

The criterion under consideration can also be named as a criterion of the blocker-induced prolongation of NMDA channel activation. Thus, the blocker prohibiting the agonist dissociation induces prolongation of NMDA channel activation. If during such prolongation we accelerate the channel transition from the blocked state, O_AAB, to the nonblocked state, O_AA* (models 1–3), a large-amplitude tail current will be generated. Such acceleration was achieved in the experiments with 9-aminoacridine by termination of the blocker application (Benveniste and Mayer, 1995; Koshelev, 1995) or membrane depolarization (Benveniste and Mayer, 1995). In the latter case, the large-amplitude tail current had an outward direction. Our computer experiments showed that the amplitude of such tail currents increases with the blocker concentration (when the occupation of the blocked states increases) and a decrease in the time between the termination of the agonist application and the accelerating stimulus, whereas their kinetics is mainly defined by the rate constant of the blocker dissociation, k₂ (data not shown).

Consideration of TAA action according to a set of criteria

Based on consideration of models 1–5, the present study reveals a set of criteria that allow one to determine the effect of fast blockers on the channel closure, desensitization, and agonist binding (dissociation). These criteria are listed in Table2.

Table 2.

Criteria attributing the blocker effect to one of the kinetic models

Model	Intersection of the control tail current and the tail current after the agonist and the blocker coapplication (Fig.4A, inset)	Channel desensitization criteria		Channel closure criterion, fast component in the falling phase of the overshoot (Fig. 7A)	Agonist dissociation criteria		Examples of the blockers
		The normalized plateau/peak ratio (IBS/IB0)/(ICS/IC0) > 1 (Fig. 5C)	The recovery current overshoot in the continuous presence of the agonist (Fig. 7A)		Agonist dependence (Fig. 9)	Intersection of the control tail current with the tail current in the continuous presence of the blocker (Fig. 11)
1	+	+	+	+	Increasing	+	TPentA
2	+	+	+	−	Increasing	+	−
3	+	−	−	−	Increasing	+	−
4	+	+	+	−	Decreasing	−	TBA
5	−	−	−	−	Constant	−	TPA
5a	−	−	−	−	Constant	−	TEA

According to criteria listed in Table 2 and taking into account everything mentioned above, TEA action can be described by model 5a with two blocking sites, to which two blocker molecules cannot bind simultaneously. To explain the inability of the simultaneous occupancy, these sites can be supposed to overlap or to be located so close that electrostatic repulsion does not allow two TEA molecules to bind to them simultaneously (Sobolevsky, 1999). The binding of the TEA molecule to the fast occupied site (the main site, becauseA_fast = 0.67) does not prohibit the channel closure, desensitization, and agonist dissociation from the blocked channel. Elucidation of the properties of the second, slowly occupied TEA blocking site requires further experiment.

The effect of TPA can be best described by model 5. Therefore, we may conclude that TPA does not prohibit the channel closure, desensitization, and agonist dissociation from the blocked channel. The cases when the A_fast and (I_BS/I_B0)/(I_CS/I_C0) values were slightly higher than unity gave us the reason to suppose that TPA can slightly prevent NMDA channel desensitization.

TPentA action can be well described by model 1. According to this model, TPentA prohibits both the channel closure and desensitization and the agonist dissociation from the blocked channel.

According to the set of criteria listed in Table 2, TBA action should rather be described by model 4. However, some observations point to the necessity of its modification. These observations are as follows: (1) in contrast with the prediction of model 4 with α′ = α, β′ = β,l₂′ =l₂, andl₁′ =l₁ (see Fig. 4A), in the majority of experiments the hooked current exceeded the value of the stationary control current, I_CS(see Fig. 2); (2) at low values of the time constant of the solution exchange, τ_wash ≤ 10 msec, the fast component appeared in the falling phase of the recovery kinetics of TBA in the continuous presence of ASP; (3) in accordance with modeling prediction (Fig. 11), the control tail current and the nonnormalized blocked tail current in the continuous presence of TBA did not intersect (Fig. 10B). However, in the majority of experiments the normalized blocked tail current lay above the control tail current (Fig. 10B, inset); this circumstance is in obvious contradiction with model 4, which predicted their coincidence (Fig. 11, inset).

In principle, modification of model 4 can be fulfilled by means of changes in the closure–opening transition (O_AAB–C_AAB) or the agonist binding–dissociation transitions (C_AAB–C_AB–C_B). When we modified model 4 via changes in the agonist binding–dissociation transitions, in compliance with the three facts listed above, we were forced to predict that the blocker hampered the agonist dissociation from the closed blocked channel. Such a modification did not predict the fast component in the falling phase of the recovery kinetics in the continuous presence of the agonist (similar to model 2) and considerably changed the agonist dependence of the stationary block by transforming it from the “descending type” predicted by the nonmodified model 4 (Fig. 9) to the “ascending” one similar to the agonist dependencies predicted by models 1–3. However, in the cases when the solution exchange was comparatively fast, the descending phase of the TBA recovery kinetics contained the fast component (see above), and the agonist dependence observed experimentally was descending (Fig. 8B). Therefore, the only possibility to modify model 4 to simulate the experimental observations was to correct the O_AAB–C_AAB transition, implying that the blocker increased the open probability of the blocked channel. There are two ways to increase the open probability. The first one is to increase the kinetic constant of the channel opening, β′. In this case, the blocker promotes the channel opening. The second one consists in reducing the rate constant of the channel closure, α′. In this case, the blocker slows the channel closure. This case is especially natural because the larger tetraalkylammonium compound, TPentA, was found to prohibit the channel closure. Both cases stipulate similar changes in the modeling kinetics. An example of predictions of model 4, implying that the blocker slows the channel closure, is shown in Figure 12. The kinetic constant of the channel opening, β, was assumed to be the same (20 sec⁻¹) for a blocked and a nonblocked channel. In contrast, the value of the closure rate constant for the blocked channel was assumed to be 10 times lower (α′ = 20 sec⁻¹) than that for the nonblocked channel (α = 200 sec⁻¹). Thus, the open probability of the blocked channel (0.5) proved to be greater than the open probability of the nonblocked channel (0.09). Such a modified model 4 predicts the appearance of the hooked current exceeding the stationary level of the control current (Fig. 12A), as well as the appearance of the fast component in the falling phase of the recovery kinetics in the continuous presence of the agonist at high values of τ_wash and in its absence at low values of τ_wash (Fig.12B). The agonist dependence of this modified model 4 remained descending as for the nonmodified model 4 (Fig.12C). Such a descending agonist dependence is the main reason why TBA action cannot be described, for example, by modified model 5, because any modification of model 5 assuming that the blocker increases the open probability for the blocked channel predicts the ascending agonist dependence (which is intermediate between those predicted by models 1 and 5). The tail current in the continuous presence of the blocker was delayed so that it even slightly intersected the control tail current (Fig. 12D). The fact that the normalized tail current in the continuous presence of the blocker for the modified model 4 lies below the control tail current is obvious from Figure 12D, inset. Therefore, the modified model 4 is able to simulate all the major features of the TBA-induced kinetics and the stationary parameter behavior. From this we may conclude that TBA allows the agonist dissociation from the blocked channel but prohibits the channel desensitization and partly inhibits the channel closure.

Fig. 12.

Predictions of model 4, implying that the blocker slows the channel closure. The open probability for the nonblocked channel (the C_AA–O_AA* transition),P₀,= β/(α + β) = 0.09, whereas the open probability for the blocked channel (the C_AAB–O_AAB transition),P₀′, = β/(α′ + β) = 0.5. The blocker concentration for A, B, andD, [B], = 12.3 K_d. The values of parameters, except as noted specially, are as follows:P₀ = 0.09,τ_wash = 30 msec, andk₂ = 1000 sec⁻¹.A, The hooked current exceeds the level of the stationary control current, I_CS.B, The falling phase of the recovery kinetics in the continuous presence of the agonist contains only one visible component when τ_wash = 30 msec and two components when τ_wash = 10 msec.C, Agonist dependence. The value of the stationary current inhibition, 1 −I_BS/I_CS(solid line), decreased with the agonist concentration. This curve is the fitting of the modeling data ([B] = 7.18K_d) with Equation 2. The values of the fitting parameters are as follows:A₁ = 0.423 ± 0.001,A₂ = 0.357 ± 0.001, [A]₀ = 13.0 ± 0.6 μm, andn_Hill = 1.19 ± 0.04. Thesolid circles are the experimental data for TBA.D, The tail current in the continuous presence of the blocker (b) does not lie below the control tail current (c), as was the case with the nonmodified model 4 (see Fig. 11), but slightly intersects it. The blocker-induced delay in the tail current kinetics becomes clear when curvesc and b are normalized (inset).

Therefore, the blocking action of TAA can be described by models 1, 4, and 5 (modified when necessary). This finding raises the question, are models 2 and 3 realistic, or can the blocker permit channel closure but not the agonist dissociation? Thus, Benveniste and Mayer (1995)supposed that the open state should manifest increased affinity for agonist. The best answer to this question would be to give an example of the blocker that would satisfy the criteria for models 2 and 3. However, we did not find such an example. The positive answer to this question would mean the existence of additional allosteric interaction between the blocker binding site and the agonist receptor. In our opinion, the existence of such a complex additional mechanism in the NMDA channel is doubtful.

DISCUSSION

Summarizing the results of the comparative analysis of interaction of different TAA with open NMDA channels, we may conclude that (1) there are blockers that prohibit (TPentA), partly prevent (TBA), or do not prevent (TPA and TEA) either the channel closure or the agonist dissociation; and (2) there are blockers that prohibit (TPentA and TBA), slightly prevent (TPA), or do not prevent (TEA) the channel desensitization. The first conclusion confirms the existence of an NMDA channel activation gate postulated previously. The second conclusion speaks well for the earlier hypothesis about the existence of a desensitization gate in the NMDA channel (Koshelev and Khodorov, 1992). The existence of a blocker that prohibits channel desensitization but does not prohibit the channel closure (TBA) provides clear evidence that there are two functionally and spatially different NMDA channel structures responsible for the activation and desensitization processes.

The mechanism of the blocker action affects its apparent affinity to NMDA channels. The apparent affinity can be measured by the values of 1/IC₅₀ or 1/K_0.5(0) at 0 mV (Table 1). A decrease in K_0.5(0) with the lengthening of the alkyl chains can be explained by a gain in the energy of hydrophobic interactions of TAA with the NMDA channel, which affects the microscopic K_d =k₂/k₁. However, the difference between the K_dvalues for some blockers is considerably greater than that between the corresponding IC₅₀[K_0.5(0)] values, because the latter depends on the mechanism of the blocker action, and IC₅₀/K_dincreases from TEA to TPentA. Thus, although models 5a for TEA and 5 for TPA predict IC₅₀/K_d = 1, the modified model 4 for TBA predicts IC₅₀/K_d = 12.7, and model 1 for TPentA predicts IC₅₀/K_d = 29.1.

The size of the blocking molecules that prohibit the closure or desensitization is larger than the size of the blockers that only partly prevent these processes and considerably larger than the size of the blockers that do not prevent the closure or desensitization. This fact supports the earlier proposed hypothesis (Koshelev and Khodorov, 1994) that the size of the blocker plays a critical role in its interaction with the gating machinery of the NMDA channel and provides evidence that the gating is local and cannot be, for example, the whole pore pinch or a twist (Hille, 1992). Based on the present notion that NMDA channel is a pore with a small cytoplasmic vestibule and a large extracellular vestibule that contains a narrow region extending ∼6 Å outward from the selectivity filter with a cross-sectional area of 22–26 Ų (Villarroel et al., 1995; Zarei and Dani, 1995), we tried to represent schematically the pore region with two blocking sites (Sobolevsky and Koshelev, 1998; Sobolevsky, 1999) and binding sites for permeant ions (Antonov et al., 1998) (Fig.13).

Fig. 13.

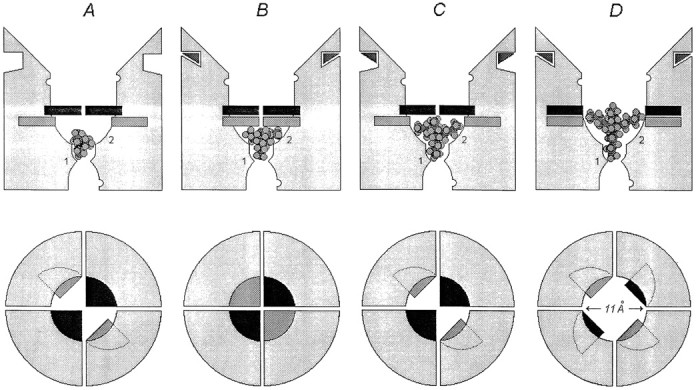
Hypothetical schematic representation of the NMDA channel pore region illustrating the interaction of TAA with the gating machinery. First line, Side view. The narrowest part of the pore is the selectivity filter. The blocking sites are indicated by1 and 2. The binding sites for permeant ions (one in the intracellular vestibule and two in the extracellular vestibule) are indicated by open semicircles. The activation gate is black, whereas the desensitization gate is gray. TEA and TPA permit the closure of both activation and desensitization gates; TBA prohibits the closure of the desensitization gate but permits the closure of the activation gate; and TPentA prohibits the closure of both activation and desensitization gates. Different blocked states of the NMDA channel are illustrated with different TAA. A, TEA is bound to the channel in the closed, agonist-unbound state (C_B).B, TPA is bound to the channel in the desensitized state (D_AAB). C, TBA is bound to the channel in the closed, agonist-bound state (C_AAB).D, TPentA is bound to the channel in the open state (O_AAB). Second line, The above view illustrates the positions of the activation (black) and desensitization (gray) gates in different states of the channel. The four segments symbolize the four NMDA receptor channel-forming subunits.

In Figure 13 the positively charged nitrogens of TAA at the blocking positions are shown to be located slightly deeper for small TAA than for large ones. Nevertheless, the difference in the measured δ for TAA is great (0.90 for TEA and 0.29 for TPentA; see Table 1). Although the Woodhull model can be too rough for the description of the NMDA open-channel block because of possible excessive “ionic pressure” in the narrow part of the pore (Ruppersberg et al., 1994), the effect of permeant cations (Antonov et al., 1998), or possible surface charge effects of TAA on the local electric field (Zarei and Dani, 1994), such a great difference in δ not only supports the notion represented in Figure 13 when the smaller blocker can penetrate deeper into the NMDA channel pore than the larger blocker but also confirms the suggestion that the electric field in NMDA channel is far from being uniform and is concentrated near the blocking sites and the selectivity filter (Subramaniam et al., 1994; Antonov et al., 1998).

In Figure 13 the two different structures responsible for channel activation and desensitization are represented as activation and desensitization gates located in the external vestibule of the NMDA channel pore. This representation is in obvious contradiction with the conclusion made by Beck et al. (1999), who stated that the extracellular vestibule does not contain any channel gate. However, these authors stated that their experimental paradigm cannot resolve possible subtle conformational changes of pre-M1, M3_C, and M4_N segments that may be associated with channel gating. Additionally, two of the mutants studied (S535C and Y629C) failed to generate detectable glutamate-activated currents, thus indicating that the corresponding residues may participate in the formation of the channel gate.

Taking into account that only one TAA blocking molecule can bind to the open NMDA channel (Zarei and Dani, 1995; Sobolevsky, 1999), the representation in Figure 13 provides a clear illustration of the results of the present study: TEA and TPA permit the closure of both activation and desensitization gates; TBA prohibits the closure of the desensitization gate but does not exclude the closure of the activation gate; and TPentA prohibits the closure of both activation and desensitization gates. According to models 1–5, the agonist can bind to or dissociate from the channel only when the activation gate is closed but the desensitization gate is open. Additionally, the desensitization gate can close only when the activation gate is already closed.

There are several types of NMDA channel desensitization (McBain and Mayer, 1994). Under our experimental conditions (3 μmglycine), glycine-dependent desensitization (Mayer et al., 1989) was hardly probable. Calcium-dependent inactivation manifested at low agonist concentrations (Legendre et al., 1993) was not observed in our experiments either (see Fig. 8A). Thus, practically we dealt only with glycine-independent desensitization (Sather et al., 1990).

The small difference in the sizes of TBA and TPentA molecules requires close location of the activation and desensitization gates deep in the channel pore. It is doubtful that both gates consist of consecutive segments of the same pore-forming amino acid chain but, rather, of fragments of different transmembrane domains, most probably belonging to different NMDA subunits (Fig. 13). The latter observation is in good agreement with the recent findings on the molecular determinants of the NMDA channel structure and function. Thus, the NR1 (but not NR2) subunit proved to be necessary and enough to form functional NMDA receptors (Moriyoshi et al., 1991; Yamazaki et al., 1992; Nakanishi et al., 1992). On the other hand, the fragments of the NR2 subunit are responsible for NMDA receptor glycine-independent desensitization (Krupp et al., 1998; Villarroel et al., 1998).

One could suppose alternative structures of the NMDA channel gating machinery. For example, the structure responsible for channel desensitization may not be obviously the gate within the channel pore but some entity within the pore-forming walls that is able to fix the completely closed activation gate (thus transposing the channel into the nonconducting desensitized state). Within the frame of this hypothesis, TPentA holds the activation gate fully open, prohibiting both desensitization and the agonist dissociation. TBA does not allow the activation gate to close completely, as TEA and TPA do, but only partly, and in this “half-open” state desensitization does not occur either, but the agonist can dissociate. However, this alternative hypothesis demands the involvement of new half-open states of the channel into the kinetic models, whereas the hypothesis illustrated in Figure 13 is in good agreement with a simple activation kinetic model used in the present study (Lester and Jahr, 1992).

Irrespective of the structure of the desensitization mechanism, the diameter of the open NMDA channel pore at the level of the activation gates is approximately equal to the size of TPentA (11.1 Å), calculated as the mean of the two smallest dimensions of the smallest size box containing space-filling models of the TPentA molecule (HyperChem). The distance from the activation gate to the deep blocking site 1 should not be larger than the length of 1-ammonio-5-(1-adamantanemethylammonio)pentane dibzomide (16.7 Å), the stretched molecule that at holding potentials more positive than −90 mV is thought to bind to site 1 by its ammonium end group and that prevents the closure of the activation gate by its adamantane head (Antonov et al., 1995; Johnson et al., 1995; Antonov and Johnson, 1996).

In experiments with 9-aminoacridine (Costa and Albuquerque, 1994;Koshelev and Khodorov, 1994, 1995; Benveniste and Mayer, 1995) it was hypothesized that this blocker prohibits NMDA channel closure. Our study of 9-aminoacridine-induced kinetics (Sobolevsky, 1999) revealed the existence of two nonoverlapping 9-aminoacridine blocking sites in the open NMDA channel, which can be occupied by two 9-aminoacridine molecules simultaneously. It was suggested that 9-aminoacridine binding to the shallow site (Fig. 13, site 2) in the orientation across the channel pore prevented the closure of the activation and/or desensitization gates. Taking into account the cross-cut size of the 9-aminoacridine molecule (11.1 Å), we may conclude that this suggestion is in good coincidence with the hypothesis represented in Figure 13.

In conclusion, TAA have proved to be useful tools in studies of the gross architecture of the NMDA channel, and one could thus expect that a combination of this experimental approach with molecular biology methods may ensure considerable progress in the deciphering of molecular mechanisms of channel gating.