Significance
Electric polarization due to polar structural distortion is a central characteristic of an ferroelectric (FE) material, which is normally unattainable in a metallic system because itinerant electrons screen the internal electric field. A possible exception for a polar metal is if the itinerant electrons are decoupled with FE distortion, as proposed by Anderson and Blount. Here, we reveal an unusual FE phase transition in recently discovered polar metal LiOsO3, different from the typical transition in insulating FEs, with dramatic temperature-dependent electron−phonon coupling. Our results provide a look at models for FE transitions with the interplay between FE dipoles and itinerant electrons, suggesting that an improvement of the Anderson and Blount model is needed.
Keywords: Raman, ferroelectric phase transition, itinerant electrons, polar metal
Abstract
Ferroelectric (FE) distortions in a metallic material were believed to be experimentally inaccessible because itinerant electrons would screen the long-range Coulomb interactions that favor a polar structure. It has been suggested by Anderson and Blount [P. W. Anderson, E. I. Blount, Phys. Rev. Lett. 14, 217−219 (1965)] that a transition from paraelectric phase to FE phase is possible for a metal if, in the paraelectric phase, the electrons at the Fermi level are decoupled from the soft transverse optical phonons, which lead to ferroelectricity. Here, using Raman spectroscopy combined with magnetotransport measurements on a recently discovered FE metal LiOsO3, we demonstrate active interplay of itinerant electrons and the FE order: Itinerant electrons cause strong renormalization of the FE order parameter, leading to a more gradual transition in LiOsO3 than typical insulating FEs. In return, the FE order enhances the anisotropy of charge transport between parallel and perpendicular to the polarization direction. The temperature-dependent evolution of Raman active in-plane 3Eg phonon, which strongly couples to the polar-active out-of-the-plane A2u phonon mode in the high-temperature paraelectric state, exhibits a deviation in Raman shift from the expectation of the pseudospin−phonon model that is widely used to model many insulating FEs. The Curie−Weiss temperature (θ ≈ 97 K) obtained from the optical susceptibility is substantially lower than Ts, suggesting a strong suppression of FE fluctuations. Both line width and Fano line shape of 3Eg Raman mode exhibit a strong electron−phonon coupling in the high-temperature paraelectric phase, which disappears in the FE phase, challenging Anderson/Blount’s proposal for the formation of FE metals.
Ferroelectric (FE) materials typically exhibit a spontaneous electric polarization that can be reoriented by an applied electric field. This spontaneous polarization is a consequence of a structural transition from a high-temperature (T) paraelectric state to a low-T FE state. Such FE structural transitions traditionally occur in insulators, not in metals, since free electrons will screen the long-range Coulomb interactions that favor off-center displacements (1, 2). The understanding of the order−disorder FE transitions in many insulating FEs is mainly based on so called “pseudospin−phonon model” (3–8). In this phenomenological model, the up and down spin is used to represent the 2 polarization states related to unstable phonons, and then the model Hamiltonian describes the pseudospin−phonon coupling for the FE transitions.
The concept of FE metals was first proposed theoretically by Anderson and Blount in 1965 (9). Applying Landau theory to a continuous structural phase transition, they hypothesized that a transition from paraelectric phase to FE phase may occur in metals if, in the paraelectric phase, the itinerant electrons are decoupled from the unstable phonon responsible for polar order. To be considered as an FE metal, 3 criteria have to be met: 1) a second-order structural transition, 2) the removal of an inversion center, and 3) the emergence of a unique polar axis. In reality, such materials are rare. Cd2Re2O7 was once considered to be the most promising candidate, but it was eventually identified as a piezoelectric metal because of its lack of a unique polar axis (10, 11). A breakthrough has been achieved with the recent discovery of LiOsO3, which has been identified as a clear example of an FE metal (12). At room temperature, the crystal structure (Fig. 1A, with space group ) of LiOsO3 consists of corner-sharing distorted OsO6 octahedra, in which Os atoms are located at the centers and Li atoms are located at the central points between pairs of Os atoms. Neutron and convergent beam electron diffraction experiments (12) have demonstrated that, at temperatures below 140 K, the Li and Os atoms deviate from the central symmetric points along the c axis, and the crystal structure transforms into a noncentrosymmetric phase (R3c). Intriguingly, both the electrical resistivity and first-principles calculations (12–16) indicate that the metallic nature of the material is preserved over the entire temperature range studied. This FE-like structural transition in the metallic state, which is contrary to common intuition, has attracted considerable theoretical interest. Several mechanisms, including soft modes (13), order−disorder transition (14–16), hybridization between the eg orbitals of Os and the p orbitals of oxygen (17), and the screening of the intrinsic dipoles due to the ion displacement by the itinerant electrons of Li ions (18), have been proposed. Furthermore, it has been suggested that the centrosymmetric-to-noncentrosymmetric transition can induce a topological phase transition and provide a unique example of such a hybrid “Weyl FE semimetal” (19). However, many fundamental questions remain to be addressed: 1) Is the “pseudospin−phonon model” suitable for the understanding of FE transition in such metallic system? 2) How do FE order and itinerant electrons influence each other when they coexist in the same system? 3) Is this system described by Anderson/Blount theory?
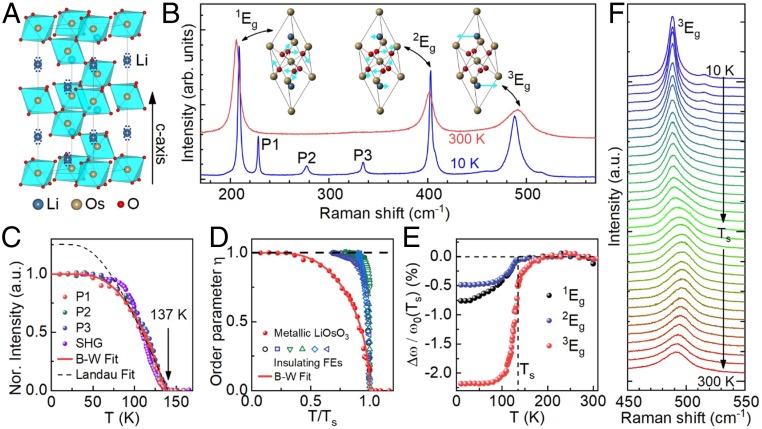
Fig. 1.
(A) The centrosymmetric crystal structure of LiOsO3 with possible polar deviation from central symmetric position of Li atoms along the c axis (dashed circles). (B) Raman spectra of LiOsO3 at 10 K and 300 K. The vibrational patterns of 3 Eg modes are shown in Insets. (C) T dependence of the normalized Raman intensities of P1, P2, and P3 modes compared with the absolute SHG signal (16). (D) The order parameter of the phase transition in LiOsO3 compared with that of other typical insulating FEs (see main text). (E) Relative Raman shift of 1Eg, 2Eg, and 3Eg after subtracting the ordinary T-dependent phonon frequency. The red solid curves in (C) and (D) represent the fitting result to the Bragg−Williams formula. The black dashed curve in (C) shows the fitting result to the Landau formula, while the black dashed lines in (D) and (E) are guides for the eye. (F) T dependence of Raman spectra for the 3Eg mode.
In this study, we report a study of the interplay between FE order and itinerant electrons in LiOsO3 and demonstrate that the “pseudospin−phonon model” is not adequate to explain the FE transition. The Raman experiment gives the order parameter of the structural phase transition and the divergent behavior of the dielectric susceptibility near Ts, which confirms a second-order order−disorder FE transition (14–16). The order parameter and the dielectric susceptibility display 2 unusual behaviors indicative of an FE transition in polar metals compared to typical FE insulators: a more gradual increase of the polarization near the critical temperature, which results from the screening and excitations of the itinerant electrons. Equally important is the observation that the T dependence of Raman-active 3Eg mode, which strongly couples to the polar-active out-of-the-plane A2u phonon, exhibits appreciable electron−phonon coupling in high-T paraelectric phase, but very weak coupling in the low-T FE state. This observation raises question about the applicability of Anderson and Blount theory (9). Specifically, what is missing is a prediction of how small the electron−phonon coupling needs to be in the paraelectric metal phase in order to have an FE transition. Finally, transport measurements reveal that this FE ordering substantially enhances the anisotropy of charge transport, presumably because of the changes of the band structure and the noncentrosymmetric distribution of electron density due to the FE ordering.
Results and Discussions
Unusual Order−Disorder Transition.
Fig. 1B displays the Raman spectra taken at T = 10 and 300 K. The observed phonon modes are consistent with the theoretical results for Raman-active modes in both paraelectric and FE phases (13, 15). There are 3 modes appearing in all data as a function of temperature, appearing at 205.9 (1Eg), 401.9 (2Eg), and 491.7 (3Eg) cm−1, which have been assigned as the rotational mode of OsO6, bending mode of OsO6, and the in-plane vibration mode of Li atoms (15), respectively. All 3 modes exhibit a similar behavior in the T dependence of energy across the centrosymmetric −noncentrosymmetric (R3c) structural phase transition. But 3Eg, which we will focus on, is unique, with the largest change near the critical temperature. The Raman spectrum exhibits 3 new peaks (labeled as P1, P2, and P3) at 10 K compared to 300 K. These modes are mainly due to the vibration of Os and O atoms and are Raman activity with E/A1 symmetry in the low-T phase (15). Thus, by tracking the T dependence of the intensities of these modes, one can accurately determine the transition temperature Ts where the inversion symmetry breaks. Since the Raman intensities of these new modes are proportional to the square of the order parameter (20, 21), T-dependent Raman spectra can be used as the order parameter.
The T-dependent intensities of the P1, P2, and P3 modes indicate that a second-order order−disorder phase transition occurs at Ts 137 K. As shown in Fig. 1C, the normalized intensities of 3 phonon modes produce a single T-dependent curve, smoothly decreasing with increasing temperatures, and eventually disappear at Ts (more-detailed T dependence of Raman spectra is given in SI Appendix, Section S1). The shape of the Raman order parameter suggests a second-order structural phase transition, which can be fitted perfectly with the single-parameter Bragg−Williams model ( where η = tanh(Tsη/T) is the order parameter) (22), a standard model describing for the order−disorder transition with short-range interactions. This fit yields the transition temperature Ts 137 K. In contrast, the modified 3-parameter Landau solution for a displacement transition (16, 23, 24) will not successfully fit our data throughout the entire temperature range (see the dashed curve in Fig. 1C). These findings allow us to conclude the observed structural transition is a second-order−type order−disorder transition, consistent with the earlier report of the order parameter determined by second harmonic generation (SHG) measurements (16), as well as the heat capacity and resistivity measurements which show no sign of thermal hysteresis (12). However, as shown in Fig. 1D, the behavior of order parameter for metallic LiOsO3 is significantly different from that of typical insulating FE compounds [(NH2CH2COOH)3·H2SO4 (25), NaNO2 (26), KH2PO4, KH2AsO4, RbH2PO4, and RbH2AsO4 (27)]. The order parameter of metallic LiOsO3 exhibits much more gradual evolution as T approaches Ts. Such a distinct T-dependent behavior of the order parameter in LiOsO3 must be related to its metallic character, which will be discussed later.
To explore this order−disorder transition, one needs to gain more insight into the static/dynamic behavior of Li atoms across the transition. According to the neutron scattering results, the structural transition across Ts is directly associated with the polar deviation from central symmetric position of Li atoms along the c axis (Fig. 1A) (12). Dynamically, this should be reflected in the energy of the A2u phonon mode associated with the vibration of Li along the c axis. Neutron scattering experiment has not yet provided the necessary information on the change of the position and dynamics of Li atoms simply due to the small size of Li and possible disorder nature near the transition. Theoretically, the A2u mode is unstable in the high-T phase (imaginary energy) (13). The remover of the A2u mode in the low-T phase is responsible for the noncentrosymmetric transition and also the importance of spontaneous symmetry breaking in LiOsO3. If the A2u mode does not exist in the low-T phase, it is hard to test the Anderson and Blount theory (9). But, as we will demonstrate, the Raman-active 3Eg mode couples to the Raman-inactive A2u mode in the high-T paraelectric state, providing a way of testing Anderson and Blount model.
As illustrated in Fig. 1E, the relative Raman shift of the 3 Eg phonon modes exhibits anomalous behavior across Ts. After subtracting the normal T-dependent phonon frequency [denoted as ω0(T), obtained by fitting the measured frequency data ωph(T) for T > 180 K to function (28)], the relative Raman shift , which reflects the change intrinsically (due to the FE phase transition) across Ts is 2.2% for 3Eg, 0.5% for 2Eg, and 0.8% for 1Eg mode. Evidently, 3Eg is particularly sensitive, with the largest anomaly. The T-dependent Raman spectra for 3Eg mode are presented in Fig. 1F, exhibiting systemic evolution from symmetric to asymmetric line shape with increasing temperatures. As we have discussed above, the phase transition is second-order, thus excluding the possibility that this 3Eg spectral feature involves 2 peaks in the vicinity of Ts. The existence of asymmetry should be intrinsic and be characterized by Fano line shape (29), due to the interaction of the phonon modes with the electron−hole pair continuum in the metallic LiOsO3.
The polar-active A2u mode associated with the Li vibration along the c axis couples to the Raman-active 3Eg in-plane mode associated with the in-plane vibration of Li atoms in the high-T paraelectric phase (Fig. 1 B, Inset). The A2u mode does not exist in the low-T FE phase (15). Such a coupling is illustrated in Fig. 2 A and B. The 3Eg mode is highly sensitive to the subtle change of Li positions because of its direct connection to Li, although the vibration direction of 3Eg is perpendicular to that of the A2u mode. Li ions, on average, are located at the center of double wells as the equilibrium position above the transition (T > Ts) (Fig. 2A) (13–15, 30, 31), while the broken centrosymmetry below Ts results in an asymmetric potential well by freezing Li to 1 side of the potential well (Fig. 2B). The A2u mode is not a normal mode of the low-T phase, since it has imaginary frequency (13). As discussed later, this is reflected by the significant change of 3Eg frequency and line width across the order−disorder transition compared to other observed 3Eg modes.
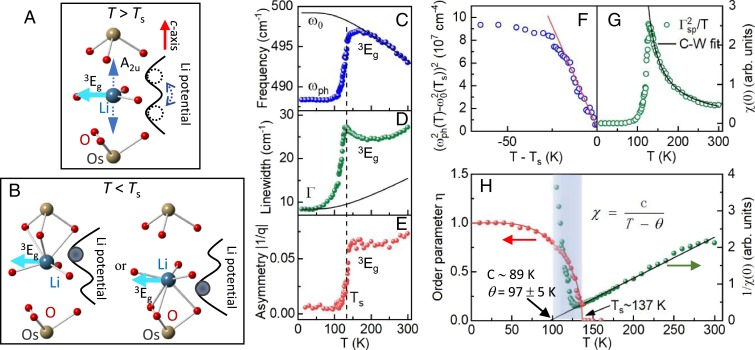
Fig. 2.
(A and B) The coordination environment of Li atoms with a schematic Li potential well diagram at (A) high-T and (B) low-T phases. (C−E) T dependence of the (C) frequency, (D) line width, and (E) asymmetry factor |1/q| of the 3Eg mode. The solid curves in C and D are the ordinary T-dependent phonon frequency and width without phase transition, and the dashed horizontal lines in (C−E) represent the transition temperature Ts. (F) T dependence of the second power of the squared 3Eg phonon shift below Ts. The solid curve is a linear fit to the data between 0 K and 18 K with an intercept of ∼0.36*107 cm−4. (G) T dependence of the dielectric susceptibility χ(0) calculated according to χ(0) ∝ Γ2sp/T. (H) Comparison of 1/χ(0) and the order parameter of LiOsO3. The black solid lines in (G) and (H) represent Curie−Weiss fits with Curie−Weiss temperature θ = 97 ± 5 K. The temperature range θ ≤ T ≤ Ts is highlighted in gray.
Fig. 2 C–E displays the evolution of the 3Eg mode frequency, line width, and asymmetry factor |1/q|, respectively, extracted with Fano line shape fitting to the Raman spectra measured at different temperatures (see SI Appendix, Section S2 for more details). As shown in Fig. 2C, the 3Eg mode shows a gradual increase in energy with lowering temperature in the paraelectric phase, reflecting the ordinary T-dependent behavior of phonon frequency ω0(T) (the solid curve in Fig. 2C), but then drops by ∼11 cm−1 for T below Ts. After eliminating the ordinary T dependence of phonon frequency, the abrupt softening of 3Eg mode below Ts mirrors the FE transition, consistent with theory (9). As T approaches Ts, the line width tends to diverge, forming a cusp-like behavior, shown in Fig. 2D. The 3Eg mode is damped in the high-T paraelectric phase. Consistent with the increase in width is the Fano asymmetry, given by the asymmetry factor |1/q| shown in Fig. 2E, which exhibits an enhancement starting at ∼100 K, indicating strong electron−phonon coupling for this mode in the paraelectric phase, but not in the polar metal FE phase (29, 32). The origin of this behavior will be discussed.
We utilize the pseudospin−phonon model (3) to analyze the uncharacteristic T-dependent behavior of the A2u-couplied 3Eg mode. The pseudospin−phonon model is a phenomenological model widely used to describe the conventional insulating systems with an order−disorder FE phase transition (3–8). In our case, the configuration of double wells for Li (Fig. 2 A and B) can be mapped to a pseudospin (1 well for “spin up” and another 1 for “spin down”), which strongly couples to Li vibrations (3Eg and A2u modes). The coupling results in a renormalization of 3Eg mode where the renormalized frequency is given by (3)
| [1] |
where C is a constant, and is the thermal average of the pseudospin S and corresponds to the order parameter or polarization (see SI Appendix, Section S3 for details). The formula establishes the relationship between phonon energy and polarization because Li−O bonds are intrinsically related to the positions of Li. The critical exponent for the order parameter is ½, since the order parameter can be described by the Bragg−Williams model (see above), that is, Ps ≈ (Ts – T)1/2. It means that the second power of the squared phonon shift should be proportional to (Ts – T). As shown in Fig. 2F, such linear dependence fits to our data as T → Ts. However, there is significant nonzero intercept (∼0.36*107 cm−4), indicating that an additional term has to be added to Eq. 1, or additional contribution must be considered to the Raman shift. In other words, the pseudospin−phonon model alone is not adequate to describe the FE transition in this polar metal.
The fluctuations of polarization near Ts are accompanied by the fluctuations of phonon energy, that is, the line width broadening (Fig. 2D). The line width contributed by the pseudospin−phonon coupling is given by the difference between the frequency and its thermal average . Eq. 1 gives
| [2] |
where is the dielectric susceptibility, k is the Boltzmann constant, and V is the volume of the crystal (3, 8). The line width Γsp is obtained by subtracting the ordinary thermal broadening (28) from experimental line widths (Fig. 2D, where the thermal broadening contribution is given by the solid curve; see also SI Appendix, Section S1 for details). Therefore, the dielectric susceptibility χ(0) can be determined through , and the result is presented in Fig. 2G. It should be noted that obtained from the optical method represents the local rather than global dielectric susceptibility. As shown in Fig. 2 G and H, the dielectric susceptibility above the transition is well described by the Curie−Weiss behavior with the Curie constant C = 89 K and Curie−Weiss temperature θ = 97 ± 5 K. The Curie constant obtained here is a typical value for the order−disorder transition (1) but almost 3 orders of magnitude smaller than that of a typical displacement transition (∼105 K). However, the obtained value of Curie−Weiss temperature is 30% smaller than Ts, which is unusual compared with the case in conventional insulating FE materials where θ ≈ Ts and also unexpected from the pseudospin−phonon model (3–8). In insulating FE compounds, θ obtained from the T dependence of susceptibility that reflects the fluctuations of FE dipoles is approximately identical to Ts. In metallic LiOsO3, a smaller θ value than Ts suggests a suppression of FE fluctuations. Such a renormalized dielectric response behavior is consistent with the gradual evolution of order parameter (Fig. 1D) and the deviation in Raman shift of 3Eg mode from the pseudospin−phonon model (Fig. 2F) observed in the temperature window θ ≤ T ≤ Ts as highlighted in Fig. 2H. The Fano asymmetry factor |1/q| (Fig. 2E), which is a measure of the electron−phonon coupling strength, increase dramatically at the temperature coinciding with θ rather than Ts. All of the results indicate that itinerant electrons existing in this system strongly affect the FE phase transition through the screening of lattice.
Interplay between FE Ordering and Itinerant Electrons.
To reveal the influence of FE ordering on electronic properties, that is, the other side of the interplay between FE ordering and itinerant electrons, we conducted transport measurements. The magnetic field dependence of the Hall resistivity (ρxy) (Fig. 3A), measured with the standard setup schematically shown in Fig. 3B, exhibits excellent linearity which allows us to extract the Hall coefficient RH = ρxy/µ0H (Fig. 3C). RH remains negative in a wide temperature range up to 300 K, indicating that the dominant carriers are electrons. Moreover, RH exhibits pronounced T-linear behaviors with different slopes in both phases, resulting in a clear kink at Ts. The slope is steeper in the FE phase (Fig. 3C).
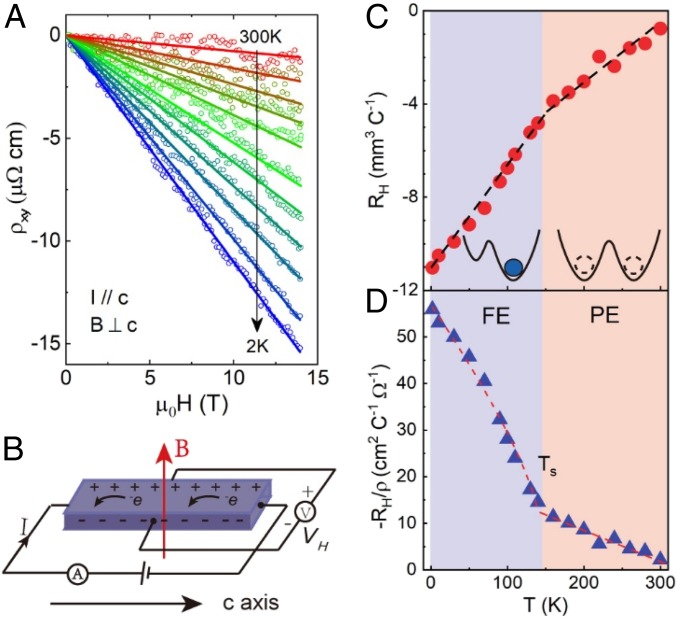
Fig. 3.
Effects of FE ordering on the electronic properties of LiOsO3. (A) Hall resistivity ρxy vs. magnetic field at several representative temperatures measured with (B) a standard 4-probe ac apparatus. The solid lines are guides for the eye. (C) T dependence of the Hall coefficient RH. (Inset) Illustration of the Li potential well in the paraelectric and FE phase, respectively. (D) T dependence of −RH/ρ, which reflects the anisotropic scattering along the Fermi surface. The dashed line is a guide to the eye.
In a simple metal with an isotropic relaxation time, the expected Hall coefficient RH = 1/ne is independent of temperature (33). The pronounced T-dependent behavior of RH may arise from either a strong multiband effect or a T-dependent anisotropic scattering. In fact, the negative value and linear field dependence of ρxy (Fig. 3A) companied with small magnetoresistance (SI Appendix, section S4) in all measured temperature ranges strongly indicate that all carriers are electrons with similar mobility. This is inconsistent with the multiband scenario (33, 34). Alternatively, the pronounced T dependence of RH may come from anisotropic scattering of electrons over the Fermi surface, which is evidenced by the T-dependent magnetoresistance data (see SI Appendix, Section S4 for detailed discussion about the magnetoresistance data). In this scenario, RH is given by (33)
| [3] |
where denotes an average over the Fermi surface and denotes the momentum-dependent relaxation time of the itinerant electrons. According to the above equation, the pronounced T-dependent RH suggests a strong T-dependent anisotropic scattering in LiOsO3.
To view the T dependence of anisotropic scattering along the Fermi surface, we plot as a function of temperature in Fig. 3D, which eliminates the influence of the T dependence of carrier concentration n. The result shows that the anisotropic scattering increases linearly with decreasing temperature, with an obvious upturn below Ts. The rhombohedral symmetry permits a T-dependent and anisotropic τ along the c and a/b axes, which determines the linear T dependence of -RH/ρ above Ts. The surprising upturn of –RH/ρ below Ts suggests an additional electronic anisotropy in the FE phase. As we demonstrate in our theoretical model analysis below, the FE ordering modifies the band structure and affects the electron scattering, which influence the electron transport along the c axis compared with that in ab plane.
All of the experimental data point to the important role that electrons play in the FE transition in LiOsO3. The gradual increase of the order parameter, the modulation of electron−phonon coupling, the suppression of FE fluctuations, and the modified transport properties consistently point to the conclusion that the interplay between the FE ordering and itinerant electrons is essential to understand polar/metal transitions. Much of our data, such as the electron−phonon coupling, and the magneto transport raise questions about the validity of the Anderson and Blount model, suggesting a more realistic model with better predictive capabilities is needed.
Theoretical Modeling.
In an attempt to understand the intriguing interplay of the FE order and the itinerant electrons and to reveal more of the underlying physics in this unique system, we consider an effective pseudospin−fermion model, expanded from the pseudospin model discussed earlier. The Hamiltonian is written as
| [4] |
where creates an itinerant electron at Os site i in orbital a (here, we have dropped the spin index of the c operator for simplicity) and is the pseudospin operator describing the local electric dipole formed by the displacement of a Li ion. refers to the Hamiltonian in pseudospin−phonon model; its explicit form can be found in SI Appendix, Section S3 or ref. 3. The first term of the above Hamiltonian includes the electron hopping contribution, where denotes summation up to a certain number of neighboring pairs and the hopping integral could be determined through fitting to density functional theory (DFT) results. The third term of the Hamiltonian represents the Coulomb interaction among the electric dipoles induced by the Li ion distortion. The second term of the Hamiltonian describes the interaction between the itinerant electrons and the local electric dipoles. The FE distortion of the Li ions imposes an electric field on the itinerant electrons, which acts as a Stark effect that hybridizes electrons in orbitals with different parities. Here, we consider the hybridization of the Os 5d and O 2p orbitals (a; b = d; p). Such a hybridization leads to a noncentrosymmetric distribution of the electron density near each Os−O octahedron (Fig. 4A), which partially screens the electric dipole generated by the displacement of the Li ion (Fig. 4B).
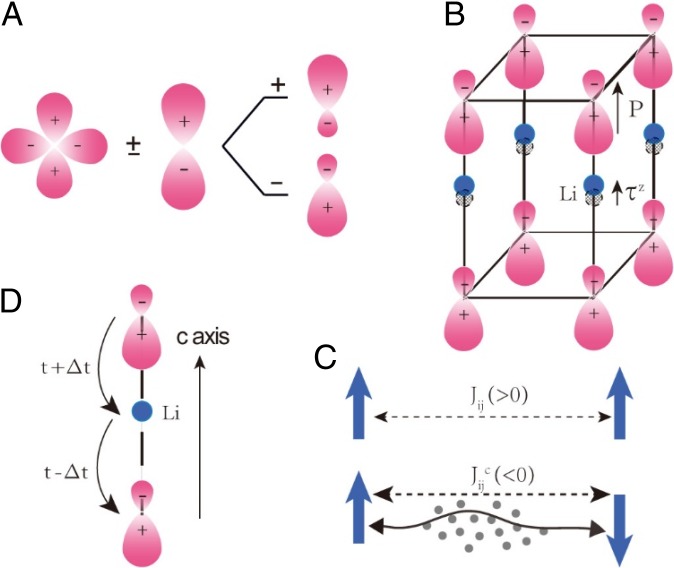
Fig. 4.
Illustration of the theoretical model. (A) Hybridization between the d and p orbitals of the itinerant electrons that is induced by the Li ion distortion. (B) Noncentrosymmetric electron density distribution induced by the local electric dipole associated with the Li ion distortion. (C) (Upper) FE coupling (>0) without itinerant electrons and (Lower) anti-FE coupling (<0) mediated by itinerant electrons (black dots) with a small Fermi momentum. See SI Appendix, Section S5 for more details. (D) Schematic of the change in the electron transport along the c axis caused by the FE ordering of the Li ions.
By integrating out the itinerant electrons from Eq. 4, the long-range interactions among the pseudospins Jij are renormalized. Especially, for a small Fermi momentum kF, < 0 up to a certain number of neighboring pairs, which introduces a frustration between dipoles and suppresses the ordered moment (Fig. 4C and SI Appendix, Section S5). Meanwhile, the excitation of the itinerant electrons introduces an additional damping of the electric dipoles. Such a damping effect is like the 1 in the Hertz−Millis theory of spin density waves (35, 36), and is also known to suppress the ordered moment. Because of both effects, the order parameter η = in LiOsO3 is significantly renormalized as compared to those in insulating FE materials (Fig. 1D). In addition, the excitations of itinerant electrons produce an imaginary part to the dynamical dielectric susceptibility and suppress the value of the dielectric susceptibility. As a result, the fitted Curie−Weiss temperature θ, which is proportional to, is reduced, smaller than Ts (Fig. 2H).
The FE ordering also influences the properties of the itinerant electrons. As Li ions become ordered, the process of an electron hopping over a Li ion along the c axis changes (Fig. 4C). This not only gives rise to additional anisotropy in the electronic structure but also modifies the relaxation time for scattering in this direction (see SI Appendix, Section S5 for more detail). These phenomena create electronic anisotropy that accounts for the change in the slope of the Hall coefficient in the FE ordered phase.
By adding a Coulomb interaction term in Eq. 4, we are able to study the effect of electron correlation in the system. This effect is of great interest for the LiOsO3 system because it should reveal how this metallic FE system is related to its insulating counterpart. However, there are few studies of this topic so far, as most theoretical studies on LiOsO3 are based on first-principles calculations. Our phenomenological model study provides an opportunity to answer several important questions, such as how the FE order evolves across the metal−insulator transition as the electron correlation increases and whether there might be a magnetic order or even other exotic types of orders that could coexist with the FE order.
Conclusion
In summary, we report a study of the FE transition in LiOsO3, exploring the interplay between FE ordering and electron itinerancy. Through Raman measurements, we confirm that the phase transition at Ts = 137 K is the second-order order−disorder type with more gradual evolution of order parameter as T approaches Ts than that in typical insulating FEs. Characterization the T-dependent evolution of 3Eg phonon, which strongly couples to the polar-active A2u phonon, reveals a deviation in Raman shift from the pseudospin−phonon model, indicating that the pseudospin−phonon model alone is not adequate to describe the phase transition. The Curie−Weiss temperature (θ ≈ 97 K) is substantially lower than Ts, suggesting a strong suppression of FE fluctuations. The line width and Fano line shape asymmetry of 3Eg mode show an anomalous enhancement slightly below and above Ts, indicating a strong electron−phonon coupling in the paraelectric phase, extending into the FE phase. All of these results demonstrate that the FE ordering is renormalized by the interactions of itinerant electrons to lattice in this metallic system. It is observed that FE order significantly enhances the anisotropy of charge transport between parallel and perpendicular to the polarization direction. The strong interplay between FE ordering and itinerant electrons suggests that the weak coupling between the electrons at the Fermi level and the (soft) phonon(s) seems not a strict prerequisite for the formation of polar metals. Our findings pave the way toward the fundamental physics of this FE metal and developing applications thereof.
Methods
High-quality LiOsO3 crystals were grown via solid-state reaction under high pressure. The details of the crystal growth can be found in ref. 6. After cleaving the LiOsO3 single crystals, we obtained glossy sample pieces with flat surfaces and then quickly transferred 1 piece into a UHV cryostat with a vacuum of better than 10−8 mbar. Raman experiments were performed using a Jobin Yvon LabRam HR800 spectrometer equipped with a volume Bragg grating low-wavenumber suite, a liquid-nitrogen−cooled back-illuminated charge-coupled device detector and a 632.8-nm He−Ne laser (Melles Griot). The laser was focused to a spot with a diameter of ∼5 µm on the sample surface. The laser power was limited to less than 1 mW to avoid overheating. All Raman measurements were performed on the same surface, and the results were confirmed with a high-resolution Raman system based on a Jobin Yvon T64000 spectrometer. Electrical transport measurements were performed using a Quantum Design physical property measurement system (QD PPMS-14) over the temperature range from 2 K to 300 K and under magnetic fields of up to 14 T. The transverse magnetoresistance and Hall resistance were measured with a standard 4-probe ac apparatus in which the current was parallel to the c axis and the magnetic field was perpendicular to the c axis. The Hall resistivity was obtained from the resistance difference measured under positive and negative magnetic fields to effectively eliminate the effect of any misalignment of the voltage wires; that is, ρxy(H) = (ρ(H) - ρ(-H))/2. A detailed description of our effective pseudospin-fermion model can be found in SI Appendix.
Supplementary Material
Acknowledgments
This work was supported by the Ministry of Science and Technology of China (Grants 2016YFA0300504 and 2017YFA0302904) and the National Science Foundation of China (Grants 11474357, 11774419, and 11774399). Y.S. was supported by the Chinese Academy of Sciences (Grants XDB07020100 and QYZDB-SSWSLH043). J.Z. was supported by the National Science Foundation under Grant DMR 1608865. E.W.P. was supported by the National Science Foundation under Grant DMR-1504226. Computational resources were provided by the Physical Laboratory of High Performance Computing at Renmin University of China.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1908956116/-/DCSupplemental.
References
- 1.Lines M. E., Glass A. M., Principles and Applications of Ferroelectrics and Related Materials (Oxford University Press, New York, 2001). [Google Scholar]
- 2.Keppens V., Structural transitions: ‘Ferroelectricity’ in a metal. Nat. Mater. 12, 952–953 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Schaack G., Winterfeldt V., Temperature behavior of optical phonons near Tc in triglycine sulphate and triglycine selenate. Ferroelectrics 15, 35–41 (1977). [Google Scholar]
- 4.Kumar P., Ramesh K. P., Muthu D. V. S., Evidence for phase transitions and pseudospin phonon coupling in K0.9(NH4)0.1H2AsO4. AIP Adv. 5, 037135 (2015). [Google Scholar]
- 5.Moreira J. A., et al. , Coupling between proton pseudo-spins and normal modes in ferroelectric glycinium phosphite. Phys. Rev. B Condens. Matter Mater. Phys. 72, 094111 (2005). [Google Scholar]
- 6.Matsushita M., Anomalous temperature dependence of the frequency and damping constant of phonons near Tλ in ammonium halides. J. Chem. Phys. 65, 23–28 (1976). [Google Scholar]
- 7.Laulicht I., Luknar N., Internal-mode line broadening by proton jumps in KH2PO4. Chem. Phys. Lett. 47, 237–240 (1977). [Google Scholar]
- 8.Laulicht I., On the drastic temperature broadening of hard mode Raman lines of ferroelectric KDP type crystals near Tc. J. Phys. Chem. Solids 39, 901–906 (1978). [Google Scholar]
- 9.Anderson P. W., Blount E. I., Symmetry considerations on martensitic transformations: “Ferroelectric” metals? Phys. Rev. Lett. 14, 217–219 (1965). [Google Scholar]
- 10.Sergienko I. A., et al. , Metallic “ferroelectricity” in the pyrochlore Cd2Re2O7. Phys. Rev. Lett. 92, 065501 (2004). [DOI] [PubMed] [Google Scholar]
- 11.Tachibana M., Taira N., Kawaji H., Takayama-Muromachi E., Thermal properties of Cd2Re2O7 and Cd2Nb2O7 at the structural phase transitions. Phys. Rev. B Condens. Matter Mater. Phys. 82, 054108 (2010). [Google Scholar]
- 12.Shi Y., et al. , A ferroelectric-like structural transition in a metal. Nat. Mater. 12, 1024–1027 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Sim H., Kim B. G., First-principles study of octahedral tilting and ferroelectric-like transition in metallic LiOsO3. Phys. Rev. B Condens. Matter Mater. Phys. 89, 201107 (2014). [Google Scholar]
- 14.Liu H. M., et al. , Metallic ferroelectricity induced by anisotropic unscreened Coulomb interaction in LiOsO3. Phys. Rev. B Condens. Matter Mater. Phys. 91, 064104 (2015). [Google Scholar]
- 15.Jin F., et al. , Raman phonons in the ferroelectric like metal LiOsO3. Phys. Rev. B 93, 064303 (2016). [Google Scholar]
- 16.Padmanabhan H., et al. , Linear and nonlinear optical probe of the ferroelectric-like phase transition in a polar metal, LiOsO3. Appl. Phys. Lett. 113, 122906 (2018). [Google Scholar]
- 17.Giovannetti G., Capone M., Dual nature of the ferroelectric and metallic state in LiOsO3. Phys. Rev. B Condens. Matter Mater. Phys. 90, 195113 (2014). [Google Scholar]
- 18.Yao Q., Wu H., Deng K., Kan E., Ferroelectric-like structural transition in metallic LiOsO3. RSC Adv. 4, 26843 (2014). [Google Scholar]
- 19.Yu W. C., et al. , Nonsymmorphic cubic Dirac point and crossed nodel rings across the ferroelectric phase transition in LiOsO3. Phys. Rev. Mater. 2, 051201 (2018). [Google Scholar]
- 20.Tenne D. A., et al. , Probing nanoscale ferroelectricity by ultraviolet Raman spectroscopy. Science 313, 1614–1616 (2006). [DOI] [PubMed] [Google Scholar]
- 21.Xi X., et al. , Strongly enhanced charge-density-wave order in monolayer NbSe2. Nat. Nanotechnol. 10, 765–769 (2015). [DOI] [PubMed] [Google Scholar]
- 22.Bragg W. L., Williams E. J., The Effect of thermal agitation on atomic arrangement in alloys. Proc. R Soc. A Math. Phys. Eng. Sci. 145, 699–730 (1934). [Google Scholar]
- 23.Hayward S. A., Salje E. K. H., Low-temperature phase diagrams: Non-linearities due to quantum mechanical saturation of order parameters. J. Phys. Condens. Matter 10, 1421–1430 (1998). [Google Scholar]
- 24.Petzelt J., Dvořák V., Changes of infrared and Raman spectra induced by structural phase transitions: I. General considerations. J. Phys. C Solid State Phys. 9, 4355 (1976). [Google Scholar]
- 25.Zhang K. C., Song J. C., Wang M., Fang C. S., Lu M. K., Study of the growth and pyroelectric properties of TGS crystals doped with aniline-family dipolar molecules. J. Cryst. Growth 82, 639–642 (1987). [Google Scholar]
- 26.Wurfel P., Ruppel W., NaNO2 thin films for pyroelectric detector arrays. Ferroelectrics 91, 113–125 (1989). [Google Scholar]
- 27.Levitskii R. R., Lisnii B. M., Baran O. R., Thermodynamics and dielectric properties of KH2PO4, RbH2PO4, KH2AsO4, RbH2AsO4 ferroelectrics. Condens. Matter Phys. 4, 523–552 (2001). [Google Scholar]
- 28.Balkanski M., Wallis R. F., Haro E., Anharmonic effects in light scattering due to optical phonons in silicon. Phys. Rev. B Condens. Matter 28, 1928–1934 (1983). [Google Scholar]
- 29.Fano U., Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878 (1961). [Google Scholar]
- 30.Xiang H. J., Origin of polar distortion in LiNbO3-type “ferroelectric” metals: Role of A-site instability and short-range interactions. Phys. Rev. B Condens. Matter Mater. Phys. 90, 094108 (2014). [Google Scholar]
- 31.Benedek N. A., Birol T., ‘Ferroelectric’ metals reexamined: Fundamental mechanisms and design considerations for new materials. J. Mater. Chem. C Mater. Opt. Electron. Devices 4, 4000–4015 (2016). [Google Scholar]
- 32.Cerdeira F., Fjeldly T. A., Cardona M., Effect of free carriers on zone-center vibrational modes in heavily doped p-type Si. II. Optical modes. Phys. Rev. B 8, 4734–4745 (1973). [Google Scholar]
- 33.Hurd C. M., The Hall Effect in Metals and Alloys (Springer, New York, 1972). [Google Scholar]
- 34.Ziman J. M., Electrons and Phonons (Oxford University Press, New York, 2001). [Google Scholar]
- 35.Hertz J. A., Quantum critical phenomena. Phys. Rev. B 14, 1165–1184 (1976). [Google Scholar]
- 36.Millis A. J., Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B Condens. Matter 48, 7183–7196 (1993). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.