Abstract
Anxiety is characterized by altered responses under uncertain conditions, but the precise mechanism by which uncertainty changes the behaviour of anxious individuals is unclear. Here we probe the computational basis of learning under uncertainty in healthy individuals and individuals with a mix of mood and anxiety disorders. Participants chose between four competing slot machines with fluctuating, reward/punishment outcomes during safety and stress. We predicted that anxious individuals under stress would learn faster about punishments, and exhibit choices that were more affected by them, formalising our predictions as parameters in reinforcement-learning accounts of behaviour. Overall, data suggest that anxious individuals are quicker to update their behaviour in response to negative outcomes (i.e. increased punishment learning-rates). When treating anxiety, it may therefore be more fruitful to encourage anxious individuals to integrate information over longer horizons when bad things happen, rather than try to blunt responses to negative outcomes.
Introduction
Mood and anxiety disorders are the most common mental health problems in the developed world, accounting for 4% of all years lived with disability1. Despite this, we have very little understanding of the mechanisms driving pathological feelings of anxiety, and the associated alterations to cognitive processes, such as decision-making, when people are anxious. This hinders our ability to improve treatments2.
Altered psychological, behavioural and neural responses to uncertainty are thought to be key to the manifestation of anxiety3. Firstly, anxious individuals report finding uncertain situations distressing4. Secondly, anxious individuals have been shown to be averse to uncertain decisions – preferring less profitable but more predictable options over more profitable but uncertain ones5. Finally, in translational research, a well-established dissociation is made between the processing of predictable and unpredictable threats6, with unpredictable threats used as a pre-clinical model of anxiety, in which uncertainty is a central component, while predictable shocks are a model for fear/phobias. In humans, the neural signatures of unpredictable threat responding7 overlap with those engaged by pathological anxiety8 indicating that this model is relevant to understanding the pathological state.
Decision-making under uncertainty is nevertheless ubiquitous in daily life9. ‘Multi-armed bandit’ tasks can probe this decision making under uncertainty by asking individuals to select one of multiple slot machines (i.e. bandits) with slowly fluctuating payoffs. On any given trial, the best option might be one that you chose recently (and so have some knowledge about), or it might be one you haven’t chosen (and so do not have up-to-date information about). Computationally it has been demonstrated that the balance of decision-making about which bandit to choose can be captured through reinforcement-learning algorithms, which approximately optimise decisions based on the history of feedback from the bandits9,10. Specifically, decisions are made according to the relative weights afforded to rewards and punishments (i.e. sensitivity – how much one anticipates liking being rewarded or disliking being punished), and how quickly information is integrated over time (i.e. learning rates – how quickly one might switch bandits following a punishment, or how long one persists in choosing a previously rewarded bandit). If altered response to uncertainty were a core feature of anxiety symptoms, we would predict that the mechanisms parameterised by reinforcement-learning models should differ in individuals with high levels of anxiety symptomatology11. Specifically, given that anxiety is associated with a bias towards aversive processing – i.e., negative affective bias 12–14- we might predict that anxiety will selectively increase the weights of aversive-specific parameters in reinforcement-learning algorithms: i.e., punishment sensitivity and punishment learning rate.
In this study, we therefore sought to formalise the differences in decision-making under uncertainty between healthy individuals and those with high levels of anxiety in terms of differences in the parameters of reinforcement-learning models. Moreover, given that the diathesis-stress hypothesis15 predicts that some symptoms of mood and anxiety disorders are only revealed when an individual is under stress13, we also transiently induced stress in participants using threat of unpredictable shock (where shock probability was unrelated to the participant’s behaviour). We predicted, therefore, that anxiety symptoms would selectively increase punishment sensitivity and punishment learning rate in the reinforcement-learning algorithm, and that this would be exaggerated under acute stress.
Results
Healthy controls (M=88) and individuals with unmedicated mood and anxiety symptoms (N=44; see Table 1 for full demographics), completed a four armed bandit task under conditions of threat of shock (stress) and safety as illustrated in Figure 1. Data available online16 (see data availability statement).
Table 1. Demographics.
The counts or mean / standard deviation (s.d.) / max / min for demographic and mood measures are presented. Ravens refers to IQ estimate obtained from Raven’s progressive matrices. State and Trait refer to anxiety from the State-Trait Anxiety Inventory; BDI refers to depression (Beck Depression Inventory). The Higher Ed count represents those who are in undergraduate education or higher. * = this group were recruited from the institutional subject database, so are estimated to be ~90% in the Higher Ed group, but detailed information is unfortunately not available.
| Asymptomatic | Symptomatic | |||||||
|---|---|---|---|---|---|---|---|---|
| N | 88 | 44 | ||||||
| Female | 50 | 28 | ||||||
| Higher Ed | * | 37 | ||||||
| mean | (s.d) | min | max | mean | (s.d) | min | max | |
| Age | 23 | (5.1) | 18 | 41 | 29 | (8.7) | 20 | 64 |
| Ravens | -- | -- | -- | -- | 8 | (2.6) | 3 | 12 |
| STAI State | 38 | (9.8) | 18 | 53 | 47 | (10.7) | 21 | 68 |
| STAI Trait | 41 | (10.6) | 20 | 69 | 57 | (8.2) | 41 | 74 |
| BDI | 7 | (7.1) | 0 | 36 | 20 | (9.4) | 6 | 54 |
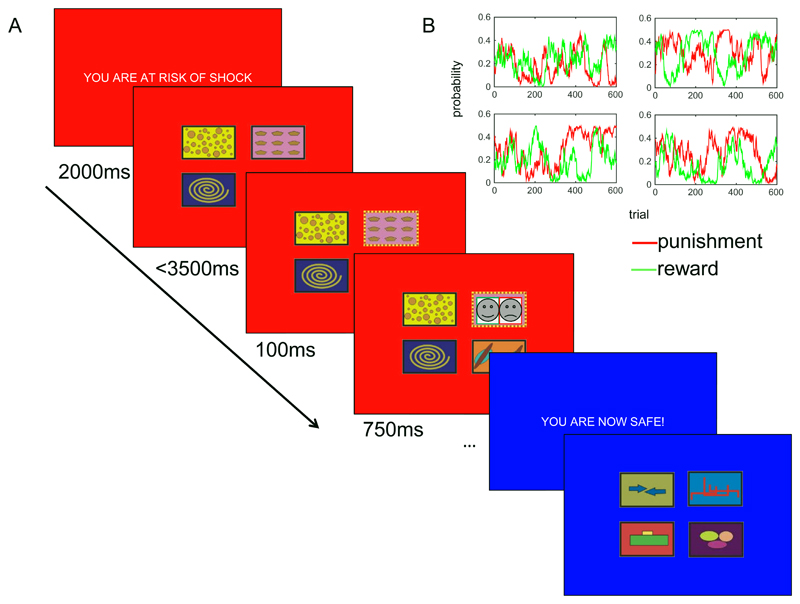
Figure 1. Task schematic.
A) Participants were asked to select one of four bandits on each trial. Following selection (here illustrated as top right under the threat condition, indicated in red), the bandit border changed colour (to blue, indicating safety), followed by the outcome (here illustrated as a combined reward and punishment; note that these were black and white photos of real human happy/fearful faces in the original experiment) overlaid on the selected bandit. The task proceeded in the same manner under the safe condition, but with a different set of bandits. B) Example of the independent fluctuation of reward and punishment probabilities across four bandits. At the start of a new condition, the bandits started with the probabilities they finished with at the end of the previous condition. I.e. the bandits at the end of one safe block paused during the subsequent threat block.
Self-report analysis
As expected the mood and anxiety group demonstrated higher levels of trait anxiety (data missing from 1 participant in each group; t(128)=8.7, p<0.001, d=1.6, [95%CI 1.2, 2.0]), and recent depression symptoms (data missing from 3 patients; 4 controls; t(124)=9.0, p<0.001, d=1.7, [95%CI 1.2, 2.01]), relative to healthy controls (Table 2). Moreover, participants reported feeling more anxious under the threat relative to the safe conditions (data missing for the second block for 1 patient; F(1,129)=319, p<0.001, η2=0.7, [95%CI 0.62, 0.77]) but this did not differ according to group (group*condition interaction: F(1,129)=0.04, p=0.8, η2<0.001, [95%CI 0, 0.03]).
Table 2. Model specification.
We fitted seven different models using the hBayesDM package. NP= number of parameters. Model = model names implemented in the hBayesDM package.
| Model | NP | Parameters | |||||
|---|---|---|---|---|---|---|---|
| bandit4arm_4par | 4 | Reward Sensitivity | Punishment Sensitivity | Reward Learning Rate | Punishment Learning Rate | ||
| bandit4arm_lapse | 5 | Reward Sensitivity | Punishment Sensitivity | Reward Learning Rate | Punishment Learning Rate | Lapse | |
| igt_pvl_decay | 4 | Decay Rate | Shape | Consistency | Loss Aversion | ||
| igt_pvl_delta | 4 | Learning Rate | Shape | Consistency | Loss Aversion | ||
| bandit4arm_2par_lapse | 3 | Reward Learning Rate | Punishment Learning Rate | Lapse | |||
| bandit4arm_singleA_lapse | 4 | Reward Sensitivity | Punishment Sensitivity | Learning Rate | Lapse | ||
| bandit4arm_lapse_decay | 6 | Reward Sensitivity | Punishment Sensitivity | Reward Learning Rate | Punishment Learning Rate | Lapse | Decay |
Model agnostic task analysis
As expected, participants were more likely to repeat a choice following a win than a loss (F(1,130)=78, p<0.001, η2=0.4, [95%CI 0.25, 0.48]). However this was not modulated by group (group x outcome interaction: F(1,130)=0.18,p=0.68, η2=0.001, [95%CI 0, 0.04]) or stress condition (stress condition x outcome interaction: F(1,130)=2.6,p=0.11, η2=0.019, [95%CI 0, 0.09]), and the three-way interaction was not significant (F(1,130)=3.6, p=0.061, η2=0.026, [95%CI 0, 0.1]).
A Bayesian version of the same analysis confirmed that the winning model included only outcome (logBF10=91), which scored 8 times better than the next best model (main effects of outcome and stress condition; logBF10=89.3). The full set of Bayes Factors from this analysis is presented in supplementary table 1.
Modelling results
We fit seven models to the data (Table 2). The winning model fit with a full prior specification was the six-parameter model that included a lapse and a decay parameter (Table 3a). We then fit the top two models with the different combinations of group/condition hierarchical priors and demonstrated that both models were actually best fit using only two priors; one for each group (Table 3b). Of note, however, uniquely for the decay model using a single prior, our model fitting procedure did not converge, likely because the single prior failed to capture the nature of the underlying distribution (which may be better represented by two distributions as seen in Table 3). Specifically, there are multiple Gelman-Rubin statistics17 (R^) greater than 1.1 (even if we increase the number of samples in the chains from 2k to 10K). As such, fit indices such as LOOIC are not meaningful and are not reported.
Table 3. Model and prior fits.
a) The winning model is that with the lowest Leave-One-Out Information Criterion (LOOIC). The lowest two numbers (for bandit4arm_lapse and bandit4arm_lapse_decay) are displayed in bold. b) The lowest LOOIC is then obtained when the top two models are fit with two priors: one for symptomatic and one for healthy individuals (Diagnosis priors). † Note that fitting the decay model with a single prior did not converge rendering the LOOIC value meaningless.
| a) Model | LOOIC |
|---|---|
| bandit4arm | 128456 |
| bandit4arm_lapse | 128198 |
| igt_pvl_decay | 132008 |
| igt_pvl_delta | 131774 |
| bandit4arm_2par_lapse | 140144 |
| bandit4arm_singleA_lapse | 129120 |
| bandit4arm_lapse_decay | 126289 |
| b) Prior | LOOIC | |
|---|---|---|
| bandit4arm_lapse | bandit4arm_lapse_decay | |
| Diagnosis and Condition Priors (4) | 128198 | 126289 |
| Diagnosis Priors (2) | 128166 | 126094 |
| Condition Priors (2) | 128225 | 126233 |
| Single Prior (1) | 128174 | † |
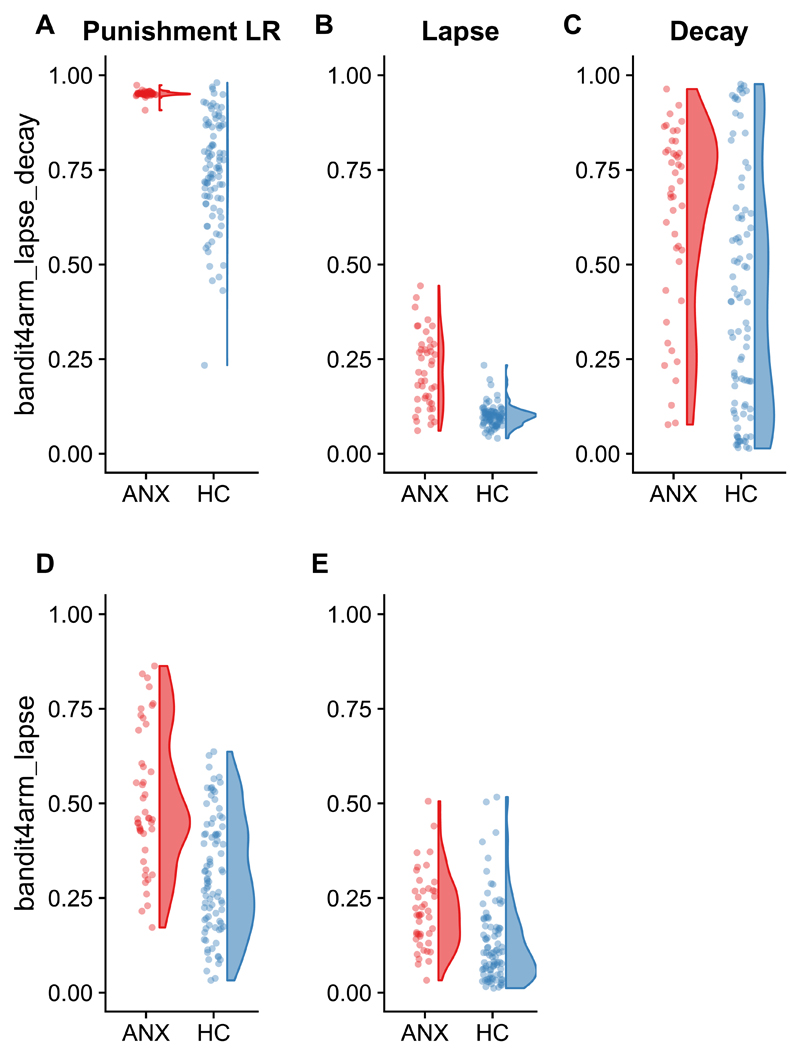
Extracting the parameters from the models fit using two priors (one for each group) demonstrated elevated (i.e., HDI for the comparison across groups does not overlap zero) punishment learning rate and lapse parameters in symptomatic relative to control individuals. In the model including a decay parameter, decay rate was also elevated in the symptomatic group (Table 4; Figure 2). Of note, this same pattern (main effect of group on punishment learning rate and lapse parameters only) was seen when parameters were extracted from the 4 prior model, and there was no effect of condition on any parameter (see supplementary results 1).
Table 4. Parameter estimates and group comparison on the winning model and prior combination.
Values represent the mean (standard deviation) of the final estimated posterior mean estimates for each individual. The ‘Group HDI’ column comprises the upper and lower bounds of the 95% highest density intervals (HDI) of the comparison between the symptomatic and control groups. If the HDI does not encompass zero, we consider there to be a meaningful difference between the groups. We find a main effect of group on the punishment learning rate, lapse, and decay (when included) parameters only (in bold).
| bandit4arm_lapse | Symptomatic | Control | Between group HDI |
| Reward Sensitivity | 7.47 (2.91) | 9.61 (4.87) | -4.55 0.65 |
| Punishment Sensitivity | 7.41 (7.21) | 6.67 (4.83) | -4.95 2.24 |
| Reward Learning Rate | 0.31 (0.30) | 0.25 (0.22) | -0.11 0.17 |
| Punishment Learning Rate | 0.51 (0.18) | 0.31 (0.15) | 0.08 0.38 |
| Lapse | 0.21 (0.10) | 0.13 (0.11) | 0.02 0.2 |
| bandit4arm_lapse_decay | Symptomatic | Control | Between group HDI |
| Reward Sensitivity | 11.41 (5.03) | 10.94 (7.20) | -4.77 6.35 |
| Punishment Sensitivity | 4.64 (5.02) | 3.00 (3.10) | -0.87 1.93 |
| Reward Learning Rate | 0.21 (0.23) | 0.23 (0.22) | -0.13 0.07 |
| Punishment Learning Rate | 0.95 (0.01) | 0.75 (0.14) | 0.04 0.26 |
| Lapse | 0.22 (0.10) | 0.10 (0.03) | 0.04 0.18 |
| Decay | 0.61 (0.25) | 0.41 (0.31) | 0.10 0.40 |
Figure 2. Group difference in parameters.
Higher point estimates of A) punishment learning rates (LR), B) lapse rates and C) decay rates in the symptomatic group (ANX; N=44) relative to the healthy controls (HC; N=88) in the bandit4arm_lapse_decay model The same pattern is seen in D) punishment learning rates and E) lapse rates in the bandit4arm_lapse model (which does not include a decay parameter). The final estimated posterior mean of each parameter for each individual is plotted in each panel.
Model check
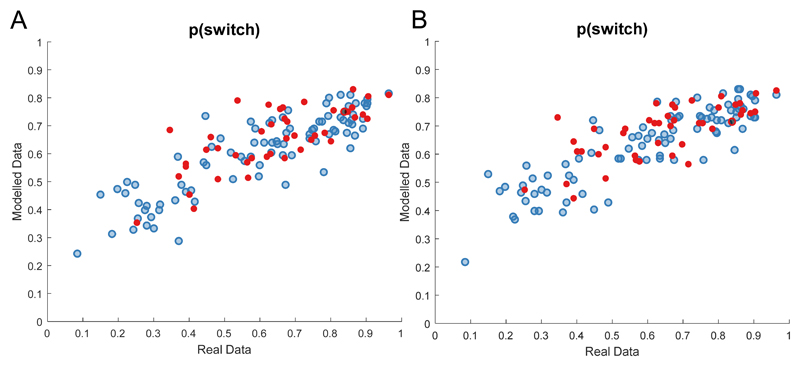
Finally, we simulated data for this model for each participant based on their parameter estimates. For both the simulated and real data we calculated the proportion of all trials on which participants switched bandits. Real and simulated data showed close correspondence (r(132)=0.84, p<0.001, [95%CI 0.78, 0.89] for both models; Figure 3).
Figure 3. Sensitivity plots.
Simulated data for each individual (N=132) shows close correspondence with real data on a simple metric ‘p(switch)’ – i.e. the proportion of trials in which the individual (or simulated agent) selected a different bandit from the previous trial. Healthy controls (N=88) plotted in blue, symptomatic in red (N=44); dashed line represents the identity. This is true for the A) bandit4arm_lapse_decay and B) bandit4arm_lapse models.
Moreover, simulated data recapitulated the model-agnostic analysis. There was a main effect of outcome (F(1,130)=434, p<0.001, η2=0.8, [95%CI 0.70, 0.81]) driven by greater stay probability following wins than losses, which did not interact with diagnosis (F(1,130)=0.003, p=0.95, η2<0.001, [95%CI 0, 0.008]).
Continuous symptom analyses
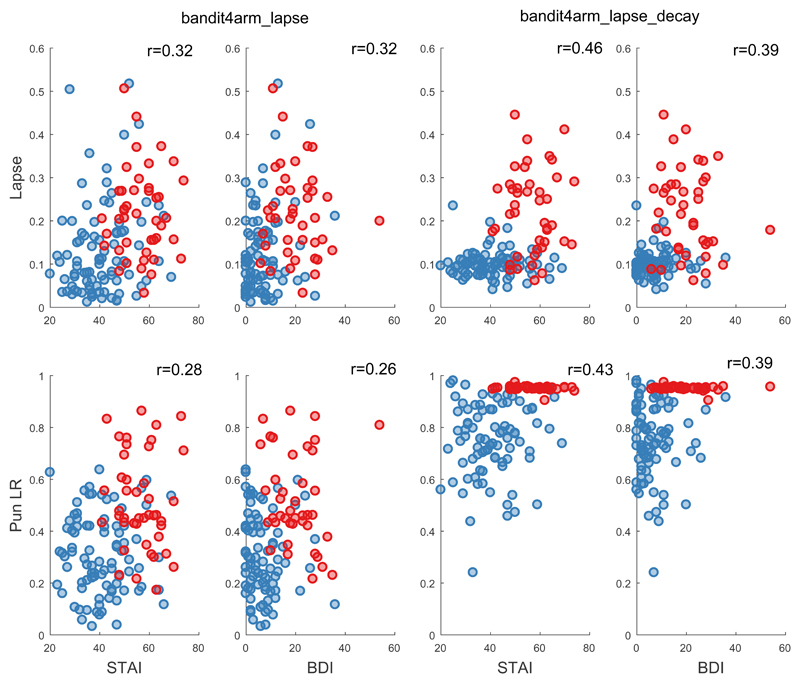
Extracting each individual’s posterior mean estimated parameters supported the existence of positive correlations between trait anxiety and the lapse (lapse: r(130)=0.32 [95%CI 0.16, 0.47], logBF10=4.5, p<0.001, lapse_decay: r(130)=0.42 [95%CI 0.27, 0.56], logBF10=10.44, p<0.001), and punishment learning rate (lapse r(130)=0.28 [95%CI 0.11, 0.43], logBF10=2.9, p=0.001, lapse_decay: r(130)=0.42 [95%CI 0.27, 0.56], logBF10=10.4, p<0.001), but no supported correlation for the decay parameter (lapse_decay: r(130)=0.19 [95%CI 0.02, 0.35], logBF10=0.074, p=0.032) or any other parameter (all logBF10<0.4). Trait anxiety was, as expected, strongly correlated with recent depression symptoms (BDI; r(126)=0.8, [95%CI 0.73, 0.85] logBF10=60,p<0.001), and so similar correlations were observed between BDI scores and model parameters (Figure 4). Of note, the interaction between trait anxiety and parameters of interest remained significant (all t=3.1-5.1, p<0.002) when age was additionally included as a predictor in the models, suggesting that the effects were not driven by age.
Figure 4. Continuous Symptom Analysis.
Individual parameter posteriors (Lapse on top row, Punishment learning rate on bottom row) for both models (bandit4arm_lapse left two columns, bandit4arm _lapse_decay right two columns) plotted against anxiety symptoms (STAI) in left column and depression symptoms (BDI) in the right column. Healthy controls (N=88) plotted in blue, symptomatic (N=44) in red. Note that the Punishment learning rate parameter is at the boundary for the symptomatic group in the decay model. The r value is the correlation co-efficient between the symptom and the parameter for the entire sample. Note that the lowest score on the STAI is 20 (score 1 for ‘almost never’ on all 20 questions).
Discussion
We found that higher mood and anxiety symptoms were associated with altered decision-making in the aversive domain; specifically greater punishment-learning rates. This finding was partially consistent with our hypotheses. Contrary to our hypotheses, however, we found no evidence that this was influenced by stress, and no evidence of a group difference in punishment sensitivity. Moreover, the higher learning rate for punishments occurred in combination with lower reliance on the modelled reinforcement-learning parameters in general (as evidenced by an increased influence of the lapse parameter in the symptomatic group) and increased propensity to ‘forget’ the previous values of unchosen options (i.e. increased reliance on a decay parameter).
A greater punishment learning rate means that individuals with mood and anxiety symptoms learn faster about punishments, and will therefore more readily update their behaviour on the basis of more recent negative outcomes instead of integrating over longer time scales. This is also reflected in the lower stay probabilities immediately following punishment in the model agnostic analysis (which was recapitulated in the model simulations). Importantly, this occurred in the absence of evidence for a group difference in punishment sensitivity, which suggests that anxious individuals do not over-weigh punishments per se. This lack of evidence for an effect of anxiety on punishment sensitivity is consistent with our prior work with reinforcement learning paradigms13, as well as work indicating similar loss aversion between anxious and healthy individuals (albeit in the context of higher risk aversion)5. Taken together these results indicate that it is not that anxious individuals weigh negative outcomes more heavily in themselves; rather they use that information differently. Specifically, a greater punishment learning rate implies that individuals with anxiety integrate information about threats over fewer trials, will over-estimate the probability of bad outcomes, and hence engage in avoidance behaviours18. Clinically this might result in overestimating negative events. For example, in the aftermath of a heavily reported plane crash an anxious individual might overestimate the risk of it re-occurring and therefore avoid flying14. In the long run, such avoidance behaviour will reduce an anxious individual’s ability to update learning and hence over-estimation persists, and avoidance behaviour is upheld.
The clarity that it is the learning rate, rather than sensitivity to punishment, which is elevated in mood and anxiety disorders12,19 may be important in relation to potential interventions that could mitigate such a negative bias. Specifically, we may not need to ‘blunt’ aversive responses through treatment – rather we should focus on treatments that seek to modify how negative information is used20. Indeed, changing the way individuals use the same information is one principle underpinning psychological interventions for mood and anxiety disorders, such as Cognitive Behavioural Therapy20. One specific recommendation that follows from our findings is in line with what is already practiced in exposure therapy20: Therapists expose patients to sources of anxiety (e.g. a spider) and encourage them to hold off on implementing decisions on the basis of predicted negative outcomes (i.e. running away) until they learn how infrequent (or frequent) the negative outcomes (i.e. the spider causing them harm) are20. The present work takes us a step towards formalising the behavioural effect as a defined parameter in a reinforcement learning model which we can directly measure and hence target to refine future treatments.
The altered punishment learning rates in the symptomatic group do, however, need to be considered in the context of an accompanying increased reliance on the lapse parameter and the decay parameter. In the model, the lapse parameter quantifies dependence on a form of ‘unexpected’ responding. This could occur from participants losing concentration on a trial and choosing at random, or possibly increasing their tendency towards undirected exploration in an attempt to avoid unpredictable punishments21. In other words, anxiety may shift the balance in explore-exploit trade-offs towards exploration, perhaps as a form of ‘exploration-driven avoidance’, in which individuals shift their behaviour to avoid bad outcomes. This should be considered alongside prior work demonstrating that high anxiety (in healthy individuals) is associated with impoverished ability to detect shifts from stable to unpredictable punishments – perhaps because their default assumption is that the environment Is unpredictable22. Increased exploration may therefore be due to an assumption of increased unpredictability. The effect on the decay parameter suggests that anxious individuals also ‘forget’ the previous values of unchosen bandits more rapidly, which could also contribute to their propensity towards increased exploration. Future experiments should test the different predictions made by these explanations. However, the lapse parameter also captures aspects of decision-making that are not encompassed by the model. In other words, what we have consigned to categories of irreducible uncertainty might actually be reduced by more sophisticated and proficient models. Our data are available online16 (see data availability statement) for future exploration of different models as the field and literature develop.
Finally, it is worth noting that we found no evidence that the modelled effects were affected by acute stress. We predicted that they would be because the diathesis-stress hypothesis predicts that symptoms of anxiety will be exacerbated in stressful circumstances15. Indeed, our prior work indicated that reliance on Pavlovian avoidance biases in anxiety disorders is exacerbated by the same stress manipulation adopted here13. Nevertheless it remains possible that such an effect exists, but that it is weak relative to the strong effects of diagnosis and outcome, and the current study was simply underpowered to detect it. Alternatively our threat of shock manipulation might not be sufficiently strong. Future work may consider measuring concurrent startle responding during the task to confirm efficacy of the manipulation beyond self-report. Another caveat is that the reinforcers we used (faces) may not have been as motivating as other outcomes, such as money. It is possible that ‘stronger’ outcomes may have driven changes in sensitivities and/or revealed a significant influence of stress. Alternatively, it may be that stronger feedback would actually remove the group effects we observe23. Either way, future work should explicitly test the impact of modulating feedback strength on task performance. Relatedly, it is possible that the within-subject nature of the safe/threat conditions meant that the overall context was anxiogenic and there was no true baseline. Note though, that self-report measures did vary across conditions, and also that many prior studies have shown within-subject differences using this manipulation12. However, a between subject design with separate groups, and critically a safe group with no electrode contact, would control for this. A final caveat is that we recruited a mixed sample of anxiety and depression. Our post-hoc analyses (see supplementary results 2) provide some evidence that there is no difference in parameters across the different diagnostic groupings. However, the study was not designed to disambiguate depression from anxiety, which are, in any case, highly co-morbid (and highly correlated at a symptom scale level) and may not represent true ‘natural kinds’. On a related note, although we have no a priori reason to suspect that IQ or socio-economic status differed between our groups (or that it drives group differences), we do not have full data on this and so cannot entirely rule it out.
These findings extend our prior work attempting to formalise the behavioural alterations seen in anxiety disorders in terms of computational models5,13. Such models aim to bridge the gap between observable symptoms (which form the basis of current diagnostic categories) and the underlying cognitive computations in the brain. Ultimately, the experience of debilitating anxiety emerges from interactions between an individual and their environment; and fully optimised treatments are unlikely to emerge without a clearer understanding of how these symptoms emerge mechanistically. Formally specifying some of the behavioural changes that occur in clinical anxiety takes us a step closer to this goal.
Methods
Participants
We recruited 132 participants, N=88 healthy controls (50 female; age=23±5) and N=44 with unmedicated mood and anxiety symptoms (28 female; age=28±9) from the local community (i.e. not through clinical services, but rather through advertisements on noticeboards and internet sites; this was to increase the probability of recruiting unmedicated participants). The two groups were recruited through separate advertising campaigns. The symptomatic group responded to an advert asking for people for whom anxiety/depression was impacting their lives, and then underwent a standardized clinical screen. The groups did not significantly differ in gender (X2=0.65, p=0.5) but the patient group was slightly older (mean ages: 29 vs 23; t(130)=4.4, p<0.001,d=0.8 [95% CI 0.4, 1.2]). We set an a priori minimum group size of N=40 in the original grant application (MR/K024280/1) based on a previously observed difference between groups of effect size d=1.0924, which was decreased to 0.7 for the purpose of a conservative power analysis. The final N=44 in the clinical group and N=88 in the healthy group, provides >95% power for a between-groups t-test with α = 0.05 (two-tailed). Ultimately we wanted to collect as much data as possible within our time and financial constraints, as parameter recovery in modelling is dependent upon sample size25. Critically, model comparison and inference was only completed after we stopped recruitment.
Although our focus was on anxiety symptoms, we recruited a mixed sample because mood and anxiety disorder symptoms show considerable overlap, and the disorders are strongly comorbid indicating that they may not be mechanistically dissociable. The majority of our pathological sample (N=28) had a mixed diagnosis of Generalised Anxiety Disorder (GAD) and Major Depressive Disorder (MDD); eight had GAD diagnosis alone; three had panic disorder with MDD; and five had MDD alone (These diagnoses were assigned according to the Mini International Neuropsychiatric Interview (MINI) and completed by a trained researcher under the guidance of a clinical psychologist or psychiatrist)26. The average number of depressive episodes was 5 (SD±7), with the average onset of first episode 20±8 years. All were currently unmedicated, but N=18 had tried psychiatric medication more than 6 months prior to the experiment, and N=21 had undergone some form of psychological treatment. Exclusion criteria were any form of psychiatric medication within the last 6 months, any current psychiatric diagnosis (other than major depression or anxiety disorder), neurological disorder, or pacemaker. Continuous measures of anxiety symptomatology were obtained using the State-Trait Anxiety Inventory (STAI) and recent depression symptoms using the Beck depression inventory (BDI). All participants provided written informed consent and were reimbursed £7.50/hour for participation. The study obtained ethical approval from the UCL Research Ethics Committee (Project ID Numbers: 1764/001 and 6198/001). Of note, all relevant data distributions are plotted. In some cases they are non-normal, but the inference (e.g. using Bayesian model comparison approaches) is not reliant on the same assumptions as classic frequentist statistics. Due to the nature of the recruitment, data collection and analysis were not performed blind to the conditions of the experiments and the participants were not randomised into groups. Task stimuli and threat condition were, however, randomised across participants.
Four-armed bandit task
The task was adapted from Seymour et al10 and presented using the Cogent toolbox for MATLAB on a laptop computer. Positive feedback was a single happy face, and negative feedback was a single fearful face (consistent with our prior work13,19). The task was completed under alternating conditions of safe and threat (see Stress manipulation section below), with a different set of four bandits in each condition leading to a total of 8 bandits (a set of 4 that was consistent throughout the safe condition; 4 throughout the threat condition).
On each trial, participants were asked to select one of the four bandits (within 3.5s) and were then provided (for just the selected bandit; Figure 1A) with one of: 1) no feedback, 2) positive feedback, 3) negative feedback, or 4) both positive and negative feedback. The probabilities of these outcomes fluctuated independently and slowly across bandits, such that the bandit that was most beneficial changed over time (Figure 1B) and participants had to keep track of reward and punishment separately. Note, however, that the outcomes themselves were binary (present or not). The participants were instructed to “try to get happy faces! avoid fearful!”. The bandits remained in the same spatial location on every trial. The face stimuli were chosen because our prior work using them showed that RL mechanisms (striatal prediction error signals) are sensitive to the same stress manipulation19 (and this study itself built on a line of studies27 that explored the impact of stress on the same stimuli in other contexts). There was no additional outcome (e.g. monetary loss/gain).
Stress manipulation
State anxiety was induced via threat of unpredictable electric shocks delivered with two electrodes attached to the non-dominant wrist using a Digitimer Constant Current Stimulator (Digitimer Ltd, Welwyn Garden City, UK). The appropriate shock level was established using a shock work-up procedure prior to testing. Specifically, up to five shocks of increasing intensity were administered, and participants rated each one on a scale from 1 (barely felt) to 5 (unbearable), with the final shock level set to 4. The experimental task was programmed using the Cogent toolbox for MATLAB 2014, presented on a laptop and administered under alternating safe and threat blocks. At the start of the safe block, the background colour changed to blue and proceeded by a 2000ms message stating: “YOU ARE NOW SAFE!” At the start of the threat block, the background colour changed to red and the message: “YOU ARE AT RISK OF SHOCK” was presented for 2000ms. The electrodes remained on the participant’s wrist throughout both types of condition. Participants were told that they might receive a shock only during the threat condition but that the shocks were not dependent on their performance. As a manipulation check, participants retrospectively rated how anxious they felt during the safe and threat conditions on a scale from 1 (“not at all”) to 10 (“very much so”). This well-established12 manipulation has been shown to have high reliability19 and replicability28. There were four threat and four safe conditions, each involving 50 trials and lasting ~5 minutes each. Thus, there were a total of 400 trials for a max duration of ~45 minutes depending upon participant response times. Participants received one shock per threat condition (four in total). They were given shocks on the 33rd trial of the 1st and 3rd threat conditions and the 15th trial of the 2nd and 4th threat conditions.
Manipulation check and model agnostic task analysis
The retrospective manipulation check was taken once in the middle and once at the end of the task (i.e. first half/second half) and analysed in a 2 (half) x 2 (condition) x 2 (diagnosis) repeated measures ANOVA. For model agnostic task analysis, we calculated stay probability following win only and loss only trials (excluding trials in which both wins and losses were given) and included them in a 2 (outcome) x 2 (condition) x 2 (diagnosis) repeated measures ANOVA. We implemented frequentist and Bayesian (adopting a default Cauchy prior) repeated measures ANOVAs using JASP29 (for data and associated JASP analyses see data and code availability statements). All t-test are 2 sided, and effect sizes calculated using the default settings in JASP. For frequentist tests we used an alpha level of .05.
Computational Modelling
We fitted seven different models10 using the HBayesDM package for R30 (for code see code availability statement). This toolbox simplifies the implementation of hierarchical Bayesian parameter estimation using STAN. We fit 3 chains for each model with 1000 burn in samples and 2000 samples. For more details please refer to30. Previous studies showed that hierarchical parameter estimation outperforms individual parameter estimation in parameter recovery31. We fit the models, shown in Table 2, to three pieces of information per trial: choice (1:4), gain (0,1) and loss (0,-1).
The bandit4arm models (where i refers to a given bandit, t refers to trial) were calculated by inputting reward and punishment values separately to the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
Choice probability was determined by passing the reward and punishment values through a softmax function in the ‘_4par’ model, where j represents all the bandits:
| (5) |
For the ‘_lapse’ model, the addition of an irreducible noise parameter (i.e. ‘lapse’) allowed for the possibility of decisions made at random, irrespective of the inferred values of the bandits (sometimes referred to as ‘trembling hand’ decisions)32. Of note, this lapse parameter serves a similar purpose as an (inverse) temperature parameter in the softmax, but it is less liable to trade off against the other parameters 33:
| (6) |
For the ‘_2par_lapse’ model, there were no sensitivity parameters in Equations 3 and 4. For the ‘_singleA_lapse’ model, there is a single learning rate across equations 1 and 2 (i.e. this parameter is not allowed to take on separate values depending on whether the outcome was rewarding or punishing. For the ‘_lapse_decay’ model we added a decay rate based on34 such that the weights of features that were not chosen gradually decayed to 0, according to the decay rate:
| (7) |
We implemented the two ‘IGT_pvl’ models, exactly following30,35. These models are substantially worse at describing the current data (Table 3a) but are detailed in supplementary methods 1. Briefly they are ‘prospect valence learning’ models which integrate aspects of reinforcement learning and prospect theory learning models.
Model selection
Parameters for all models were initially fit under four separate hierarchical priors: 1) anxious/depressed individuals under threat; 2) healthy controls under threat; 3) anxious/depressed individuals under safe; 4) healthy controls under safe. The winning model was defined as the model with the lowest Leave-One-Out Information Criterion (LOOIC) summed across these four priors.
We then followed up initial model selection with a subsequent exploration of all four combinations of group/condition priors (1: all four, 2: two representing each condition, 3: two representing each group and 4: one pooling everyone together) on the top two models. We then compared parameter estimates from the top two models across the two groups using 95% highest density intervals (HDI). Specifically, for each comparison, we calculated the difference in the hyper parameters and reported the 95% HDI of the difference. If this HDI did not overlap zero, we consider there to be a meaningful difference between the groups36,37. Note that 96% HDI are not testing if we can reject the null hypothesis (i.e., that two groups are the same on a given parameter), but instead whether the hyper parameters differ between the groups/conditions36,37. To illustrate group differences we plotted the individual mean posterior parameter estimates using raincloud plots38.
Finally, parameter estimates from the top two model/prior combinations were used to simulate choices for each individual and then compared to each individual’s real choices to confirm that models were not only the best of those tested, but also realistic models of the data (we required a correlation of greater than 0.7). Finally, we confirmed that simulated data recapitulated patterns observed in the model agnostic task analysis.
Continuous symptom analysis
Individual parameters (mean posterior estimates) for the overall winning model were extracted and correlated with individual trait anxiety and depression scores in Bayesian and Frequentist correlation matrices using JASP29.
Supplementary Material
Acknowledgements
This research was funded by a Medical Research Foundation Equipment Competition grant (C0497, Principal Investigator O.J. R.), and a Medical Research Council Career Development Award to O.J.R. (MR/K024280/1). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Footnotes
Data Availability
All data used in this analysis are available on OSF osf.io/2jx87 (DOI 10.17605/OSF.IO/UB6J7)16
Code Availability
Scripts for model fitting are available on OSF here osf.io/2jx87 (DOI 10.17605/OSF.IO/UB6J7)16 as Supplemental Software for this manuscript. For the HBayesDM package, please see https://github.com/CCS-Lab/hBayesDM
Competing interests
The authors declare no competing interests
Contributions
OJR, JA, RLB conceived and designed the work; OJR, JA and RLB acquired the data, OJR, JA, VV,JPR, PD and W-YA analysed and interpreted data; W-YA and OJR contributed to the creation of new software used in the work. All authors drafted the work or substantively revised it. All authors have approved the paper and are personally accountable for their own contributions.
ORCID: 0000-0002-3100-1132
References
- 1.(IHME), I. f. H. M. a. E. GBDCompareDataVisualization. [Accessed 17/11/16].
- 2.LeDoux JE, Pine DS. Using neuroscience to help understand fear and anxiety: a two-system framework. American journal of psychiatry. 2016;173:1083–1093. doi: 10.1176/appi.ajp.2016.16030353. [DOI] [PubMed] [Google Scholar]
- 3.Grupe DW, Nitschke JB. Uncertainty and anticipation in anxiety: an integrated neurobiological and psychological perspective. Nat Rev Neurosci. 2013;14:488–501. doi: 10.1038/nrn3524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Birrell J, Meares K, Wilkinson A, Freeston M. Toward a definition of intolerance of uncertainty: A review of factor analytical studies of the Intolerance of Uncertainty Scale. Clinical psychology review. 2011;31:1198–1208. doi: 10.1016/j.cpr.2011.07.009. [DOI] [PubMed] [Google Scholar]
- 5.Charpentier CJ, Aylward J, Roiser JP, Robinson OJ. Enhanced risk aversion, but not loss aversion, in unmedicated pathological anxiety. Biological Psychiatry. 2017;81:1014–1022. doi: 10.1016/j.biopsych.2016.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grillon C. Models and mechanisms of anxiety: evidence from startle studies. Psychopharmacology. 2008;199:421–437. doi: 10.1007/s00213-007-1019-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robinson OJ, Overstreet C, Allen PS, Pine DS, Grillon C. Acute tryptophan depletion increases translational indices of anxiety but not fear: serotonergic modulation of the bed nucleus of the stria terminalis? Neuropsychopharmacology. 2012;37:1963–1971. doi: 10.1038/npp.2012.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Robinson OJ, et al. The dorsal medial prefrontal (anterior cingulate) cortex–amygdala aversive amplification circuit in unmedicated generalised and social anxiety disorders: an observational study. The Lancet Psychiatry. 2014;1:294–302. doi: 10.1016/S2215-0366(14)70305-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Daw ND, O'Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;441:876–879. doi: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Seymour B, Daw ND, Roiser JP, Dayan P, Dolan R. Serotonin selectively modulates reward value in human decision-making. The Journal of Neuroscience. 2012;32:5833–5842. doi: 10.1523/JNEUROSCI.0053-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sharp PB, Eldar E. Computational Models of Anxiety: Nascent Efforts and Future Directions. Current Directions in Psychological Science. 2019 0963721418818441. [Google Scholar]
- 12.Robinson OJ, Vytal K, Cornwell BR, Grillon C. The impact of anxiety upon cognition: Perspectives from human threat of shock studies. Front Human Neurosci. 2013;7 doi: 10.3389/fnhum.2013.00203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mkrtchian A, Aylward J, Dayan P, Roiser JP, Robinson OJ. Modeling avoidance in mood and anxiety disorders using reinforcement learning. Biological psychiatry. 2017;82:532–539. doi: 10.1016/j.biopsych.2017.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gagne C, Dayan P, Bishop SJ. When planning to survive goes wrong: predicting the future and replaying the past in anxiety and PTSD. Current Opinion in Behavioral Sciences. 2018;24:89–95. doi: 10.1016/j.cobeha.2018.03.013. [DOI] [Google Scholar]
- 15.Monroe SM, Simons AD. Diathesis-stress theories in the context of life stress research: implications for the depressive disorders. Psychological bulletin. 1991;110:406. doi: 10.1037/0033-2909.110.3.406. [DOI] [PubMed] [Google Scholar]
- 16.Robinson OJ. Altered learning under uncertainty in unmedicated mood and anxiety disorders - EU storage. 2018 doi: 10.17605/OSF.IO/UB6J7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical science. 1992;7:457–472. [Google Scholar]
- 18.Bach DR. Anxiety-like behavioural inhibition is normative under environmental threat-reward correlations. PLoS computational biology. 2015;11:e1004646. doi: 10.1371/journal.pcbi.1004646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Robinson OJ, Overstreet C, Charney DS, Vytal K, Grillon C. Stress increases aversive prediction-error signal in the ventral striatum. Proc Natl Acad Sci U S A. 2013 doi: 10.1073/pnas.1213923110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Deacon BJ, Abramowitz JS. Cognitive and behavioral treatments for anxiety disorders: A review of meta-analytic findings. Journal of clinical psychology. 2004;60:429–441. doi: 10.1002/jclp.10255. [DOI] [PubMed] [Google Scholar]
- 21.Wilson A, Fern A, Ray S, Tadepalli P. Proceedings of the 24th international conference on Machine learning; ACM; pp. 1015–1022. [Google Scholar]
- 22.Browning M, Behrens TE, Jocham G, O'Reilly JX, Bishop SJ. Anxious individuals have difficulty learning the causal statistics of aversive environments. Nat Neurosci. 2015;18:590–596. doi: 10.1038/nn.3961. http://www.nature.com/neuro/journal/v18/n4/abs/nn.3961.html#supplementary-information. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lissek S, Pine DS, Grillon C. The strong situation: A potential impediment to studying the psychobiology and pharmacology of anxiety disorders. Biological psychology. 2006;72:265–270. doi: 10.1016/j.biopsycho.2005.11.004. [DOI] [PubMed] [Google Scholar]
- 24.Robinson OJ, Cools R, Carlisi CO, Sahakian BJ, Drevets WC. Ventral striatum response during reward and punishment reversal learning in unmedicated major depressive disorder. Am J Psychiatry. 2012;169:152–159. doi: 10.1176/appi.ajp.2011.11010137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maxwell SE, Kelley K, Rausch JR. Sample size planning for statistical power and accuracy in parameter estimation. Annu Rev Psychol. 2008;59:537–563. doi: 10.1146/annurev.psych.59.103006.093735. [DOI] [PubMed] [Google Scholar]
- 26.Sheehan D, et al. The validity of the Mini International Neuropsychiatric Interview (MINI) according to the SCID-P and its reliability. European Psychiatry. 1997;12:232–241. [Google Scholar]
- 27.Carlisi CO, Robinson OJ. The role of prefrontal–subcortical circuitry in negative bias in anxiety: Translational, developmental and treatment perspectives. Brain and Neuroscience Advances. 2018;2 doi: 10.1177/2398212818774223. 2398212818774223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mkrtchian A, Roiser JP, Robinson OJ. Threat of shock and aversive inhibition: Induced anxiety modulates Pavlovian-instrumental interactions. Journal of Experimental Psychology: General. 2017;146:1694. doi: 10.1037/xge0000363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Team, J. JASP (Version 0.7. 5.5)[Computer software] Google Scholar. 2016;765:766. [Google Scholar]
- 30.Ahn W-Y, Haines N, Zhang L. Revealing neurocomputational mechanisms of reinforcement learning and decision-making with the hBayesDM package. Computational Psychiatry. 2017;1:24–57. doi: 10.1162/CPSY_a_00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ahn W-Y, Krawitz A, Kim W, Busemeyer JR, Brown JW. A model-based fMRI analysis with hierarchical Bayesian parameter estimation. Journal of neuroscience, psychology, and economics. 2011;4:95. doi: 10.1037/a0020684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guitart-Masip M, et al. Go and no-go learning in reward and punishment: interactions between affect and effect. Neuroimage. 2012;62:154–166. doi: 10.1016/j.neuroimage.2012.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huys QJ, Pizzagalli DA, Bogdan R, Dayan P. Mapping anhedonia onto reinforcement learning: a behavioural meta-analysis. Biol Mood Anxiety Disord. 2013;3:12. doi: 10.1186/2045-5380-3-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Niv Y, et al. Reinforcement learning in multidimensional environments relies on attention mechanisms. Journal of Neuroscience. 2015;35:8145–8157. doi: 10.1523/JNEUROSCI.2978-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ahn WY, Busemeyer JR, Wagenmakers EJ, Stout JC. Comparison of decision learning models using the generalization criterion method. Cognitive Science. 2008;32:1376–1402. doi: 10.1080/03640210802352992. [DOI] [PubMed] [Google Scholar]
- 36.Ahn W-Y, et al. Decision-making in stimulant and opiate addicts in protracted abstinence: evidence from computational modeling with pure users. Frontiers in psychology. 2014;5:849. doi: 10.3389/fpsyg.2014.00849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kruschke J. Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press; 2014. [Google Scholar]
- 38.Allen M, Poggiali D, Whitaker K, Marshall TR, Kievit R. Raincloud plots: a multi-platform tool for robust data visualization. PeerJ Preprints. 2018;6 doi: 10.12688/wellcomeopenres.15191.1. e27137v27131. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.