The Processing of First- and Second-Order Motion in Human Visual Cortex Assessed by Functional Magnetic Resonance Imaging (fMRI)

Abstract

We have examined the activity levels produced in various areas of the human occipital cortex in response to various motion stimuli using functional magnetic resonance imaging (fMRI) methods. In addition to standard luminance-defined (first-order) motion, three types of second-order motion were used. The areas examined were the motion area V5 (MT) and the following areas that were delineated using retinotopic mapping procedures: V1, V2, V3, VP, V3A, and a new area that we refer to as V3B. Area V5 is strongly activated by second-order as well as by first-order motion. This activation is highly motion-specific. Areas V1 and V2 give good responses to all motion stimuli, but the activity seems to be related primarily to the local spatial and temporal structure in the image rather than to motion processing. Area V3 and its ventral counterpart VP also respond well to all our stimuli and show a slightly greater degree of motion specificity than do V1 and V2. Unlike V1 and V2, the response in V3 and VP is significantly greater for second-order motion than for first-order motion. This trend is evident, but less marked, in V3A and V3B and absent in V5. The results are consistent with the hypothesis that first-order motion sensitivity arises in V1, that second-order motion is first represented explicitly in V3 and VP, and that V5 (and perhaps also V3A and V3B) is involved in further processing of motion information, including the integration of motion signals of the two types.

The primate cerebral cortex contains multiple representations of visual space. One important visual area is MT or V5 (Allman and Kaas, 1971; Dubner and Zeki, 1971; Zeki, 1974), which seems to be involved in processing information about movement. A human homolog of V5 or MT has been identified, at the boundary of Brodmann’s areas 19 and 37, using positron emission tomography (PET) (Zeki et al., 1991; Watson et al., 1993), functional magnetic resonance imaging (fMRI) (Tootell et al., 1995), magnetoencephalography (MEG) (Anderson et al., 1996), and anatomical studies (Clarke and Miklossy, 1990; Tootell and Taylor, 1995). Some other studies [Cheng et al. (1995) using PET techniques; Greenlee et al. (1995) and Greenlee and Smith (1997) using neuropsychological procedures] have identified motion-sensitive areas at rather more anterior and dorsal locations, raising the possibility that there may be several areas in human cerebral cortex that are specialized for processing motion.

In parallel with these anatomical and physiological discoveries, advances in our understanding of human motion perception have been made using psychophysical and computational techniques. Most studies of motion perception have centered on first-order motion that is motion defined by spatiotemporal changes in luminance. However, there has been considerable recent interest in “second-order” motion stimuli, i.e., motion of structures defined not by luminance but by the second-order characteristics of the stimulus (Chubb and Sperling, 1988; Cavanagh, 1991; for review, see Smith, 1994). Various authors have suggested that there are two separate motion-detecting systems, one that can be modeled conventionally (Adelson and Bergen, 1985) and is insensitive to second-order motion and one that is sensitive to second-order motion (Chubb and Sperling, 1988; Wilson et al., 1992).

We have investigated whether the functional dissociation between first- and second-order motion is reflected in anatomical differences in the cortical regions that are used in the analysis of the two types of motion. In a previous paper (Greenlee and Smith, 1997), we used neuropsychological methods and concluded that there is substantial overlap between the substrates of the two systems. In this paper, we have used fMRI techniques in healthy human volunteers. Our experiments were conducted with two principal questions in mind. First, does the motion area V5 or MT respond well to second-order motion? Second, what is the site of detection of second-order motion? We report three principal findings. First, we confirm the existence of a number of visual areas described by others, and we have identified a new visual area that we call area V3B. Second, we show that human V5 or MT is indeed strongly activated by second-order motion. The activity is primarily motion-specific, in accord with previous studies of V5. Third, we show that area V3 and its ventral counterpart VP respond more strongly to second-order than to first-order motion. This result raises the possibility that V3 (lower hemifield) and VP (upper hemifield) are the first visual areas in which information about second-order motion is represented explicitly.

Parts of this paper have been published previously in abstract form (Greenlee et al., 1997; Singh et al., 1997; Smith et al., 1997).

MATERIALS AND METHODS

Subjects

The subjects were 13 healthy human volunteers (10 male and 3 female) who were paid for their time. Informed consent was obtained in writing. The data from four subjects were not used in the analysis because the functional images were distorted or showed generally low activation levels, leaving a database of nine subjects (18 hemispheres).

Visual stimulation

Visual stimuli were generated by an Apple 7600 computer and were projected onto a rear-projection screen covering one end of the bore of the scanner, using an LCD projector (resolution 640 × 480 at 66 Hz). The subject lay on his or her back in the scanner, looking upward at a mirror in which an image of the projection screen was reflected. The screen was at the end nearest to the head of the subject, and so the field of view was not restricted by the body. This arrangement gave a usable image that was approximately circular and had a diameter of 30° at the viewing distance of 1.2 m. The mean luminance of the image was 35 cd/m². Stimulus presentation was synchronized to the image acquisition procedure by means of a pulse generated by the computer controlling the scanner.

Motion stimuli

Various motion stimuli were used, including first-order motion, second-order motion, and several control stimuli that contained no motion. The motion stimuli all consisted of alternately expanding and contracting concentric rings (see Fig.1a,b). The direction of motion (expansion or contraction) reversed every 1.2 sec. The various motion stimuli differed in terms of how the concentric rings were defined. The use of radial motion ensured that all directions of motion were present in the image and also facilitated central fixation. Such an arrangement has been shown previously to generate good fMRI activation in the case of first-order motion (Tootell et al., 1995). Figure 2 shows space–time plots illustrating the main stimulus types.

Fig. 1.

Examples of the visual images used in the study.a, One frame from an animation sequence in which the contrast of a sample of 2-D noise is sinusoidally modulated along the radius. The phase of the sinusoid changes smoothly over time to produce expanding or contracting second-order motion. In the experiments, the mean luminance was the same in regions of high and low contrast (luminance distortions may have been introduced by the printing process). b, Similar to a but a case in which the noise is luminance-modulated and the amplitude of the noise remains constant to give first-order motion. c, Ahemifield checkerboard used for retinotopic mapping. The checks reverse polarity at a rate of 8 Hz to give a high-contrast stimulus that is broadband in both spatial and temporal frequency. The flickering hemifield rotates slowly about the central fixationpoint. d, A checkerboardwedge that flickers and rotates in the same way as thehemifield in c does.

Fig. 2.

Space–time plots illustrating the various types of motion stimuli used in the experiments. Each plot represents a section along the radius of the circular grating in the original image (shown horizontally) seen at successive points in time (represented vertically). a, Contrast-modulated, two-dimensional dynamic noise (2ndDyn). Eachframe consists of 2-D noise the contrast of which is sinusoidally modulated. On each update (every 30 msec), the noise sample is replaced by a new one, and the contrast modulation moves a short distance to the left, giving smoothleftward motion over time. b, Contrast-modulated, two-dimensional, high-pass-filtered static noise (2ndFilt). In this case, the carrier is again 2-D noise, but this time the noise is filtered to remove the lowest spatial frequencies, and the noise sample remains the same over time. Again, the contrast envelope drifts smoothly to the left. c, Flicker-frequency-modulated two-dimensional noise (2ndFlick). Eachframe consists of binary, two-dimensional noise of uniform contrast, and no spatial structure is visible within it. Over time, the noise sample is replaced in some areas but not in others to form a frequency-defined grating. The boundaries of the regions in which the noise is dynamic drift smoothly leftward over time. d, Luminance-modulated, two-dimensional dynamic noise (1stDynLow). Each frame consists of 2-D noise the luminance of which is sinusoidally modulated with an amplitude calculated to give similar visibility to the contrast modulation shown in a. On each update, the noise sample is replaced, and the luminance modulation moves to the left.e, Luminance-modulated, two-dimensional, high-pass-filtered static noise (1stFiltLow). The noise is the same as that in b, and the luminance is modulated to give similar visibility to the contrast modulation in b.f, Luminance-modulated, two-dimensional, high-pass-filtered static noise (1stFiltHigh). The noise is the same as that in e except that the amplitude of the luminance modulation is much greater.

Three classes of second-order motion stimuli were used. The type best understood and most commonly used in psychophysical experiments is contrast modulation. Accordingly, two of our images were of this type. Both had noise carriers, dynamic in one case and static in the other. In each case the image was gamma-corrected by displaying a contrast modulation of the type used in the experiment and by adjusting the correction for minimum luminance modulation between low- and high-contrast regions. However, it is inevitable that the correction was imperfect. This means that small distortion products may have arisen from residual luminance nonlinearities in the projection system. These distortion products are in the first-order (luminance) domain and are expected to activate the first-order motion system. In practice, any such distortion products would have very small amplitudes and would be unlikely to generate measurable fMRI signals. Nonetheless, a third type of second-order motion, namely a modulation of carrier flicker frequency rather than of carrier contrast, was included as a safeguard because it is immune to the problem of gamma-related brightness nonlinearities and therefore provides pure second-order motion.

More specifically, the three second-order motion stimuli used were as follows.

2ndDyn. This stimulus was dynamic two-dimensional (2-D) noise (pixel size, 8 min arc) the contrast of which was spatially modulated by a radially symmetrical sinusoidal profile to create a circular sine grating (see Figs. 1a, 2a). The mean contrast of the noise was 25%, the contrast modulation depth was 100%, and the spatial frequency of the modulation was 0.8 c/°, measured along the radius. Smooth motion was produced by continuously updating the phase of the modulating sinusoid to produce a speed of 4.4 °/sec (3.5 Hz) measured along the radius. The phase of the sinusoid was updated, and the noise sample was replaced simultaneously, at a rate of 33 Hz. For a detailed rationale for the use of dynamic noise carriers, see Smith and Ledgeway (1997). In essence, it overcomes the potential problem of local first-order artifacts associated with the use of static noise.

2ndFilt. High-pass filtered static 2-D noise the contrast of which was modulated as in 2ndDyn (see Fig. 2b) was used to produce a second-order motion stimulus that lacked the strong temporal luminance flicker that is contained in 2ndDyn and that is expected to generate cortical activity in its own right. High-pass spatial filtering provides an alternative solution to the problem of local first-order artifacts associated with the use of static noise, and again a detailed rationale for its use is given in Smith and Ledgeway (1997). The filter cut-off was 0.8 c/°, i.e., only the very lowest spatial frequencies were removed. Again, the mean contrast of the noise was 25%, the contrast modulation depth was 100%, the spatial frequency of the modulation was 0.8 c/°, and the drift speed was 4.4 °/sec.

2ndFlick. This stimulus was unfiltered binary 2-D noise the contrast of which was uniform (25%) but the flicker rate (rate of replacement of the noise sample) of which was spatially modulated (between 0 and 33 Hz) by a circular square wave profile to produce rings of dynamic noise interleaved with rings of static noise. The spatial frequency was 0.4 c/°. Smooth motion was produced by incrementing the phase of the modulating square wave to move the boundaries between dynamic and static regions (see Fig. 2c). The drift speed was 8.8 °/sec (3.5 Hz). In this image, any one frame consists simply of uniform noise, and so all points are equally affected by any brightness nonlinearity. The low spatial frequency (0.4 c/°) was used because this type of motion was found to be hard to perceive at higher spatial frequencies.

For comparison, two types of first-order motion stimuli were used.

1stDyn. This stimulus was dynamic 2-D noise of contrast 25% the luminance of which was spatially modulated by a radially symmetrical sinusoid (i.e., the sum of a circular luminance grating and dynamic noise; see Figs. 1b, 2d). The spatial frequency and speed were the same as that for 2ndDyn.

1stFilt. This stimulus was the sum of a circular luminance grating and high-pass filtered noise of the type used for 2ndFilt (see Fig. 2e,f). Spatial frequency, drift speed, and noise contrast were the same as that for 2ndFilt.

The inclusion of noise in the first-order motion images was intended to provide a control for the noise that is present in the second-order motion images. Clearly, noise complicates the interpretation of the fMRI data, because part of the observed functional activity will be caused by the motion and part by the visual noise. Because this is unavoidable in the case of second-order motion, it was also incorporated in the case of first-order motion to provide a fair comparison.

For each type of first-order motion, two contrast levels were used. One was a high contrast (40%) and was designed to produce strong cortical activation. This is designated 1stDynHigh or 1stFiltHigh (Fig.2f). The other, designated 1stDynLow or 1stFiltLow (Fig. 2d,e), was a low contrast (6% for 1stDynLow and 3% for 1stFiltLow) and was chosen to have approximately the same visibility as the second-order stimulus of the same type (2ndDyn or 2ndFilt). Direction-identification thresholds for contrast-modulated dynamic noise are typically around 20% modulation depth (Smith and Ledgeway, 1997), so 100% modulation depth is only approximately five times threshold. The appropriate first-order comparison stimulus is therefore approximately five times its own detection threshold. This threshold is elevated by the presence of dynamic noise, hence the use of a higher contrast for 1stDynLow than for 1stFiltLow. The low-contrast first-order images are unlikely to cause response saturation. Even in area V5, only a minority of neurons saturate at such low contrasts (Sclar et al., 1990; Cheng et al., 1994), whereas contrast saturation of the fMRI response in human V5 appears to occur at ∼10% [Tootell et al. (1995), their Fig. 10]. Our high-contrast first-order stimuli, on the other hand, may well cause saturation in some visual areas, complicating the interpretation of fMRI activation magnitudes. Our intention was to provide, in different images, both a fair comparison with second-order motion (matched visibility) and a very strong test (high contrast). If any cortical region responds more strongly to second-order than to high-contrast first-order motion, a strong case can be made for a second-order motion preference.

In addition to the motion stimuli, four control stimuli were used. These were as follows.

2ndDynStat. This stimulus was identical to 2ndDyn except that the concentric rings were stationary and not expanding and contracting. The purpose was to allow assessment of the motion specificity of the responses elicited by 2ndDyn.

2ndFiltStat. This stimulus was identical to 2ndFilt except that the concentric rings were stationary.

Dyn. This stimulus was dynamic noise alone (25% contrast) and was identical to 1stDyn and 2ndDyn except that the noise was unmodulated.

Filt. This stimulus was high-pass filtered static noise alone (25% contrast) and was identical to 1stFilt and 2ndFilt except that the noise was unmodulated.

Visual stimuli for retinotopic mapping

Additional stimuli were used for mapping the boundaries of the various retinotopically organized visual areas of the occipital cortex. These were based on those used by others (Engel et al., 1994; Sereno et al., 1995). A high-contrast radial checkerboard pattern the contrast of which reversed at a frequency of 8 Hz was used (see Fig.1c). Check size was scaled with eccentricity to produce maximal activation of the visual areas. At any one moment, the flickering checkerboard filled half the visual field. The hemifield stimulus rotated about the central fixation point in steps of 20° (18 steps in a complete rotation). It remained in each position for 3 sec (the time taken to acquire one set of functional data; see below) before instantaneously rotating to the next position. [Sereno et al. (1995) used slow, continuous motion. Our method yields equivalent results but obviates the need to compensate for the different image positions during acquisition of the different functional slices.] In later tests, a smaller checkerboard wedge (20, 40, or 80°; Fig.1d) was used in place of the hemifield to provide improved resolution in higher cortical areas such as V3 and V3A (Tootell et al., 1997).

Data acquisition

Imaging was performed with a 1.5 T whole-body Siemens Magnetom (Vision) scanner equipped with a gradient system having 25 mT/m amplitude and 0.3 msec rise-time. The subject was positioned with his or her head in an RF receive-transmit full headcoil. Head motion was minimized with a vacuum cap, which was secured within the head coil. Local variations in blood oxygenation (BOLD response) were measured using susceptibility-based functional magnetic resonance imaging, applying gradient-recalled echoplanar imaging (EPI) sequences.

Ten parallel 4-mm-thick planes, positioned in the posterior cortex, were imaged every 3 sec using a T2*-weighted sequence (repetition time, 3000 msec; echo time, 84 msec; flip angle = 90°, 128 × 128 voxels, each 2 mm × 2 mm). The positions of the planes were between axial and coronal (see Fig. 6a) and were chosen with the aid of a midsagittal T1-weighted scout image to include the entire occipital lobe together with posterior portions of the parietal and temporal cortex.

Fig. 6.

Bottom. Illustrations of functional activation recorded in one subject. a, A 3-D-rendered view of the brain of the subject showing the volume in which data were acquired, together with a sagittal section (bottom) showing the locations of the individual slices. Three slices that are illustrated elsewhere in the figure are color-coded. Each linerepresents the center of a 4 mm slice. b, A single anatomical slice (slice 8; marked ingreen) is shown six times, with correlation coefficients indicating visual activation superimposed in color for six different visual stimuli. Each stimulus was interleaved with periods in which the screen was blank. Correlations in the range 0.5–1.0 are shown ascolors in the range red toyellow; correlations below 0.7 are not shown. Activity is evident in a medial area that reflects a mixture of V1 and V2v. On the lateral surface, bilaterally, activity is evident in the V5 complex (marked by red arrows). All six visual stimuli, including the three second-order motion stimuli in the second row, activate V5. Activation is weaker for dynamic noise (Dyn) than for motion. c, A different slice (slice 7; yellow) shown with correlations overlaid for two stimulus conditions. On theleft is the response to 2ndDyn(second-order motion; see text) interleaved with a blank field. Medially, activation is evident in a region corresponding mainly to V1. More laterally, activation is seen bilaterally in a region corresponding to V3 and an adjacent area that we refer to as V3B. The second image (on the right) shows the result of interleaving second-order motion with first-order motion. The medial activity (V1) evident on the left is completely absent, showing that this activity is not stimulus-specific. Activity in V3/V3B (red arrows) is reduced but is still evident, showing a preference for second-order over first-order motion. d, A more ventral slice (slice 9; red), showing activity in area VP (red arrows) under the same two stimulus conditions shown in c. Like V3/V3B, area VP (the ventral counterpart of V3) remains active when second-order motion is interleaved with first-order motion.

Stimulus presentation

Each experimental run lasted 162 sec, during which time the 10 slice volume was imaged repeatedly (54 volume acquisitions; 3 sec each). This period was divided into six epochs of duration 27 sec. In most runs, three epochs contained one of the visual stimuli described above, and these were interleaved with three epochs in which the screen was unpatterned but had the same mean luminance as the stimulus. The visual stimulus was shown continuously throughout each of the 27 sec epochs in which it was present (11 cycles of expansion and contraction in the case of motion stimuli). The interleaving of “on” and “off” epochs enabled the activity elicited by one of the stimuli to be compared with the baseline activity level for each voxel in the 10 slice volume. This procedure was repeated for each of a number of motion and control stimuli, with short breaks between runs. The order of testing the various stimuli was randomized. In additional conditions run in some subjects, two different visual stimuli were interleaved with no blank periods (e.g., first/second order or stationary/moving) to allow direct comparison of the activity levels elicited by the two patterns.

During the same session, T1-weighted images in the 10 planes used for functional imaging were acquired (resolution, 1 mm) to allow functional signal strengths to be superimposed on anatomical images.

Retinotopic mapping

To make it possible to map the regions activated by the motion stimuli onto the established set of retinotopically organized visual field maps in the cortex (V1, V2, etc.), additional functional data sets were acquired in which rotating hemifield or wedge stimuli were used (Sereno et al., 1995; Engel et al., 1997; Tootell et al., 1997). The rotating stimuli described earlier were used. In each run, four complete rotations of the flickering checkerboard were presented (total duration, 216 sec). Four such runs were conducted: two in which the rotation was clockwise and two in which it was counterclockwise. Functional data sets (again comprising 10 4-mm-thick slices) were acquired continuously (72 volumes). In some subjects this procedure was performed on a different occasion from the motion experiments, in which case a slightly different acquisition volume was inevitably used.

Anatomical imaging

For each subject, sagittal T1-weighted 3-D-MP-Rage images (magnetization-prepared rapid-acquisition gradient echo; Siemens AG, Erlangen, Germany) of the entire brain were acquired (voxel size, 1 × 1 × 1 mm³). When motion stimuli and retinotopic mapping stimuli were presented in different sessions, anatomical imaging was performed in both sessions to provide a means of coregistering the two sets of data. The anatomical data were used to determine the anatomical localization of functional responses. Such localization was performed principally using cortical flattening algorithms to obtain two-dimensional representations of cortical gray matter (Sereno et al., 1995; Engel et al., 1997). The Talairach bicommissural co-ordinate system (Talairach and Tournoux, 1988) was also used for specifying the locations of certain areas to allow comparison with other studies.

Data analysis

The data were analyzed and visualized using our own in-house software BrainTools (psyserver.pc.rhbnc.ac.uk/vision/BrainTools.html), with two exceptions (motion correction and cortical flattening) that are detailed below.

Responses to motion stimuli

Each functional volume was first processed using a 2-D motion correction program, Imreg, part of the AFNI package (Cox, 1996). This realigns each image in the time series to the average image position. This procedure minimizes the likelihood of correlated head motion introducing false positives into the functional analysis. The motion-corrected data were then analyzed using a correlation method based on methods established by Bandettini et al. (1993) and Friston et al. (1995). In such methods, analysis is based not on the absolute level of the BOLD response during visual stimulation but on the degree to which temporal changes in the BOLD response profile are correlated with the on–off cycle of visual stimulation. Before analysis, spatial smoothing of the functional signal within each slice was performed by convolution with a 2-D Gaussian function (Friston et al., 1995) of SD 1.7 mm. This smoothing reduces spatial noise, and because of the inherent spread of the BOLD effect, the cost in terms of spatial resolution is minimal. For each voxel in the acquisition volume, a correlation coefficient was then computed between the observed temporal response function obtained during a given run and a waveform representing the expected temporal response in an ideal voxel with a strong response to the visual stimulus. The expected response would be a square wave if the BOLD response were instantaneous, but in reality the hemodynamic response has a slower temporal characteristic and is retarded in phase. The waveform used for correlation was therefore a square wave that was temporally smoothed by convolution with a Gaussian of SD 3 sec and was retarded in phase by 6 sec (Friston et al., 1995). In addition, to maximize signal to noise, the BOLD response was also smoothed using a Gaussian convolution with SD of 3 sec. As Friston et al. (1995) indicate, this maximizes signal to noise at the expense of reducing the degrees of freedom in the statistical model. We have used the procedures of Friston et al. (1995) for calculating the effective degrees of freedom in the case of such smoothing; for the 54 volume acquisitions used in our study, the effective degrees of freedom in the model was approximately 20.

To obtain visual representations of the results, we constructed functional activation images as pseudocolor overlays on the corresponding T1-weighted anatomical slices. Voxels with correlation coefficients of <0.7 (p_voxel < 0.0003, where p_voxel is the probability of a false positive, per voxel) were not shown in the overlays. The overlays were used to identify the V5 complex for further analysis (all other areas were identified by retinotopic mapping) and for illustrative purposes (see Fig. 6).

Cortical flattening and retinotopic mapping

Although certain visual regions, such as the V5/MT complex, can be identified with reasonable certainty by inspection of functional overlays on cortical slices, other areas cannot. The posterior occipital cortex consists of several discrete representations of the visual field, and the boundaries between them cannot reliably be discerned from inspection of slices. To establish the responsiveness of visual areas V1, V2, V3/VP, V3A, and V4 to second-order motion, it was therefore necessary to map the boundaries of these areas, using established techniques (Engel et al., 1994; Sereno et al., 1995; Engel et al., 1997; Tootell et al., 1997). A two-dimensional representation of occipital cortex was derived from the three-dimensional (3-D) whole-brain anatomical data set, using an algorithm developed by Engel et al. (1997). The method involves extracting those voxels considered to be part of cortical gray matter using a segmentation procedure. The segmentation is based on the assumption that white matter can be separated from the rest of the image volume on the basis of voxel luminance. After identification of the white matter, the gray matter is assumed to be a connected sheet of voxels “grown” on top of the white matter volume. The gray matter is then represented as a single, convoluted surface. A “seed” is chosen in the center of the cortical subregion to be processed (typically in the fundus of the calcarine sulcus). The algorithm simulates a process of flattening the gray matter into a 2-D surface centered on the seed. It operates iteratively, minimizing spatial distortions of the gray matter.

Having obtained a flattened representation of the occipital cortex, the boundaries of the retinotopic visual areas were mapped onto it using a procedure based on that of Sereno et al. (1995). Four complete rotations of a flickering checkerboard (see Visual Stimulation) were used (rotation frequency, 0.02 Hz). The temporal phase of the fundamental Fourier component of the response was established for each voxel in the 10-slice acquisition volume. An adjustment was made for the acquisition time of each slice within the 3 sec volume acquisition. For each voxel, the phase obtained with clockwise rotation of the stimulus was averaged with that obtained with counterclockwise rotation. The averaged phase angle was then represented as a pseudocolor overlay on the flattened cortical surface. Because adjacent visual field representations are mapped in mirror-image manner (Sereno et al., 1995; Engel et al., 1997), boundaries between them appear in such an overlay as a reversal of the direction of change of phase angle.

Tootell et al. (1997) have recently reported that improved resolution of boundaries is obtained in regions that are broadly retinotopic but in which neurons have large receptive fields (e.g., V3, V3A) by using a thin rotating wedge in place of a rotating hemifield checkerboard. In the present study, this approach was adopted in later experiments. In this case, Fourier analysis of the temporal response function yields a spectrum that is spread in frequency and contains much-reduced power. Thus, there is a trade-off between improved resolution of visual field position and increased noise. We found that the optimum wedge size is 40–80°, rather larger than that used by Tootell et al. (1997).

Quantification of response strengths in different visual areas

Responses to the various motion stimuli were analyzed separately for each of several visual areas. Regions of interest (ROIs) corresponding to particular visual areas were subjected to a numerical analysis of response magnitude to compare the relative strength of activation across different stimulus conditions, within a given ROI. In the case of retinotopic areas, an ROI corresponding to each area was defined on the flattened cortical representation, based on boundaries specified by reversals in the direction of change of visual field position (see Fig. 4). A separate ROI was defined for each of the visual areas V1, V2d, V2v, etc. Each ROI was a quadrilateral on this 2-D map, chosen to best represent the relevant visual area. The irregularly shaped 3-D aggregation of voxels that covered the cortex represented by this 2-D ROI was identified, and the average activation of all voxels within this region was calculated. In the case of the V5 complex, the ROI was defined simply as a rectangular region bounding the significantly correlated voxels in the slice in which the complex was evident.

Fig. 4.

Top. Maps of the posterior cortex of three subjects obtained by simulating flattening of the gray matter.a–c, The left hemisphere is shown in all cases; similar results were obtained in the right hemispheres. Overlaid on the map is a pseudocolor representation of the phase of the fundamental component of the activation time course elicited by a rotating, flickering checkerboard (see Materials and Methods). Thecolors reflect visual field position (seekey in a) and show a smooth progression through the visual field within each visual area, with a reversal of the direction of change at the boundaries. Estimates of the locations of various boundaries are indicated. The dotted white line shows the approximate location of the fundus of the calcarine sulcus. The approximate position of the occipital pole is marked with a star.

Numerical activation strengths were calculated using the following method. First, the temporal response function of each voxel in the ROI was correlated with the smoothed and retarded ideal waveform, as described earlier, to give a correlation coefficient. The amplitude of the observed response time course was expressed in terms of the variance of the response, measured over the entire 162 sec record. To weight the computation of amplitude in favor of stimulus-related variance (as opposed to noise), we multiplied the variance by the correlation coefficient to give a measure of response strength (Bandettini et al., 1993). The resulting values were averaged across all voxels in the ROI, and the mean activation was normalized on a scale of 0–1, where 1 is the largest value that occurred during any experimental run in a given ROI in a given subject. The purpose of the normalization was to facilitate comparison across subjects. Finally, for each visual area, the average of the normalized activation values was calculated across all hemispheres in which an active ROI could be identified within the visual area in question.

The locations of the various ROIs identified were also established using the 3-D co-ordinate system of Talairach and Tournoux (1988). Talairach co-ordinates were based on the center of each ROI and were scaled to adjust for differences among the subjects in overall brain size.

RESULTS

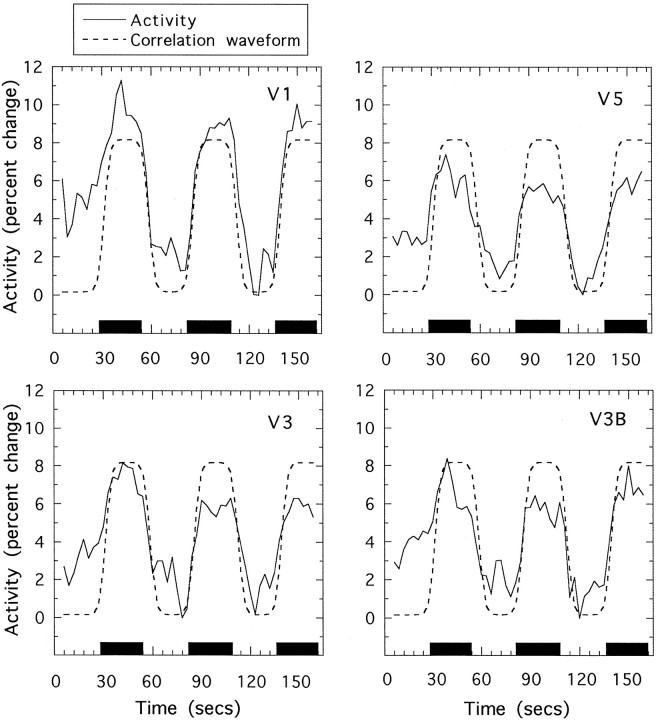
Consistent, stimulus-related changes in T2*-weighted activations were found in a variety of regions of the posterior cortex. A typical result is illustrated in Figure 3 that shows, for one subject, variations over time in several regions of cortex as a visual stimulus is alternately presented and then replaced by a blank screen of the same mean luminance. Also shown is the waveform that was used for correlation purposes (see Materials and Methods).

Fig. 3.

Sample temporal activation waveforms. Each plot shows (solid line) the percentage change in signal, averaged across a number of voxels in one region of interest, as a function of time. The periods during which a visual stimulus (2ndFlick) was present are shown by black bars; during the intervening periods, the screen was blank. Also shown (dashed line) is the theoretical waveform used for correlation; this is a square wave that has been smoothed and retarded in phase (see text) and has arbitrary amplitude. Results are shown for four different visual areas in the same subject.

Our experiments were conducted with two principal questions in mind. First, does the motion area V5/MT respond well to second-order motion? Second, what is the site of detection of second-order motion? It is usually thought that first-order motion signals are first made explicit in area V1 because, in primates, direction-sensitive neurons are common in V1 but absent in the retina and thalamus (Hubel and Wiesel, 1968). The site of detection of second-order motion is unknown. We therefore searched the posterior cortex for areas that respond more strongly to second-order than to first-order motion and that might be the site at which second-order motion is first represented explicitly. For this purpose, we relied initially on imaging experiments in which, instead of interleaving one stimulus with a blank field, first-order motion was interleaved with second-order motion of the same type (e.g., 1stFilt interleaved with 2ndFilt, 1stDyn with 2ndDyn, etc.). Such experiments are not suitable for deriving quantitative activation strengths because adaptation effects can cause interactions between the two phases of the stimulus cycle. But they give an immediate qualitative indication of areas that are differentially activated by the two stimuli that are interleaved. Subsequently, we estimated the sensitivity of each of the retinotopic areas V1, V2, V3, VP, and V3A to each of our stimuli, based on experiments in which each stimulus in turn was interleaved with a blank field.

We found no cortical region in any subject that responds exclusively to second-order motion. However, as will be seen, we found areas that, although responding well to first-order motion, have a clear and consistent preference for second-order motion. The results lead us to the tentative conclusion that the site at which second-order motion (and indeed second-order spatial structure) is made explicit may be V3 (lower hemifield) or VP (upper hemifield).

In all cases except for the V5/MT complex, analysis of activation in different functional regions was based on regions defined in 2-D space on a flattened representation of the posterior cortex. Results for retinotopic mapping will therefore be described first.

Retinotopic mapping

Flattened cortical representations for three subjects are shown in Figure 4. These show an approximately circular patch of flattened cortex (radius, 50 mm) centered on a seed in the fundus of the calcarine sulcus in one hemisphere. The phase of the fundamental component of the temporal response to the rotating checkerboard is shown as a pseudocolor overlay. The color code used is the same as that used by Engel et al. (1997). The overlay is thresholded (in terms of the amplitude of the fundamental) to remove unreliably noisy data. Continuous patches of color have been created from the relatively sparse functional data set by a process of interpolation that involves a degree of smoothing. The foveal representation, near to the occipital pole, forms an uncolored patch to the left of the image (marked with a star) that cannot be mapped because of resolution limitations and the effects of small eye movements. The images have been cropped at the edges of the colored overlay to remove uncolored areas beyond the region that could be retinotopically mapped and also areas representing eccentricities beyond that of the stimulus.

The results confirm the general organization reported by others (Sereno et al., 1995; Engel et al., 1997). In area V1, the horizontal meridian of the contralateral hemifield is represented in or near the fundus of the calcarine sulcus (Fig. 4, dotted lines). Moving away from the fundus in either direction results in a shift toward the vertical meridian, in the upper contralateral quadrant ventrally and the lower contralateral quadrant dorsally. At a distance of some 5–10 mm (depending on eccentricity) from the fundus, the vertical meridian is represented along two solid lines corresponding to the V1 and V2d border dorsally and the V1 and V2v border ventrally. These borders appear as green (lower vertical meridian) andblue (upper vertical meridian), respectively. Proceeding beyond these borders, away from the calcarine sulcus, visual field position moves smoothly back toward the horizontal meridian, representing the V2d and V3 border dorsally and the V2v and VP border ventrally (appearing as orange). At each of these borders, a further reversal occurs, and the representation moves back toward vertical meridian.

Beyond V3, our results confirm and also extend those reported previously. Tootell et al. (1997) report that beyond V3 lies V3A and that the retinotopic organization of V3A starts at the lower vertical meridian (at the border with V3), progresses to the horizontal meridian in the usual mirror-image manner, and then continues into the upper visual field toward the upper vertical meridian. Thus, whereas V2d and V3 represent only the lower quadrant (the corresponding representations of the upper quadrant being in V2v and VP), V3A represents the entire hemifield. We confirm this organization. A prominent patch ofmagenta/blue (representing the upper quadrant) can be seen in Figure 4 a short distance beyond the V3 and V3A border. We see this reliably in all hemifields in which retinotopic organization is distinct in this vicinity. However, V3A does not run the length of the V3 border but instead borders only the part of V3 representing peripheral visual field locations. Closer to the foveal V3 representation, a different pattern emerges. In this vicinity, the region beyond V3 seems to represent only the lower quadrant. Moreover, the lower quadrant representation is more extensive than that in V3A; in V3A, the representation shifts rapidly toward the upper quadrant with increasing distance from V3. It seems likely that this area is a distinct visual region from V3A, particularly because there is a sharp transition between it and V3A. Because, like V3A, this area adjoins V3, we refer to it as area V3B. The fact that V3A does not extend the full length of the V3 border was noted by Tootell et al. (1997). There is no conflict between their data and our own. Although they make no comment on the area we call V3B, in fact their data show signs of the same trend that we report in this area (e.g., Tootell et al., 1997, their Fig. 4).

Beyond VP ventrally, we sometimes see further retinotopic mapping, presumably corresponding to V4. But we do not see this consistently and have not attempted to measure activity in this region. Where V4 is in evidence, it seems to extend along the entire VP border. That is, we can see no sign of a division within V4 corresponding to that between V3A and V3B, although we cannot eliminate the possibility that such a division exists.

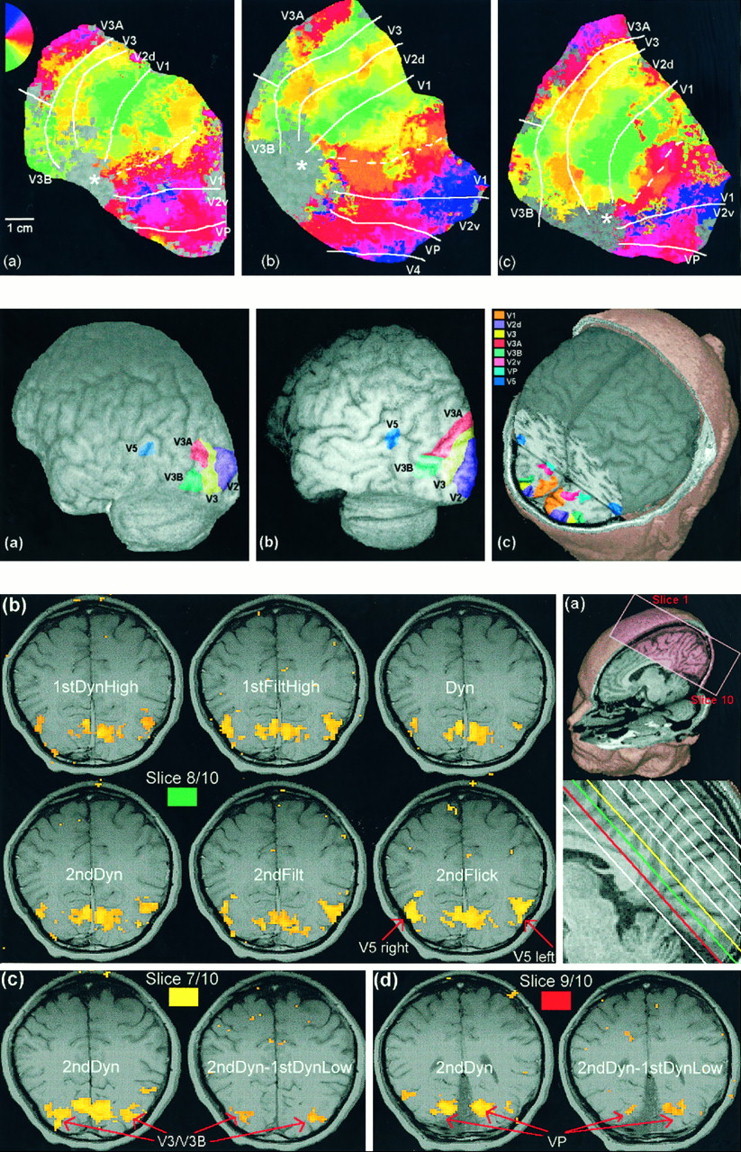
Figure 5 shows reconstructed 3-D views of the brains of two subjects. The cortical surface is volume-rendered using an integrated shading algorithm (Bomans et al., 1990). Figure 5,a and b, shows the locations of V2, V3, V3A, V3B, and V5 on the surface of the cortex. These images were created by plotting the boundary of each area determined on the flatmap onto the nearest point on the surface and then filling in. Comparison of Figure5a with b reveals considerable difference between the two subjects, even though the organization in 2-D cortical space is very similar in the two cases (Fig. 5a,b is from the same hemispheres shown in Fig. 4c,b, respectively). It should be remembered that the visual stimuli had a diameter of 30°, so only the central 15° of each area is shown. Areas V2, V3, and V3A presumably extend more dorsally and medially than is apparent in the figure. Figure 5c shows another 3-D-rendered image of the same brain shown in Figure 5b, this time with part of the cortex cut away to reveal a horizontal section through the various visual areas. The calcarine sulcus is oblique with respect to the horizontal cut, so that both V2d (above the calcarine) and V2v (below it) are revealed, as are both VP and V3.

Fig. 5.

Middle. 3-D rendered images of the brains of two subjects, showing the locations of some of the visual areas studied. a, b, The surface of the left hemisphere of the two brains. c, The same brain shown inb with part of the cortex cut away.

Activation by motion stimuli in retinotopic areas

Numerical activation strengths were measured in various cortical regions by defining ROIs on the cortical flatmap. Each ROI corresponds to one of the visual areas defined by retinotopic mapping. For each ROI, the voxels that correspond to that ROI were identified in the 3-D volume acquired during functional imaging with motion stimuli. For each motion stimulus, activation was averaged across these voxels (see Data Analysis). The same procedure was adopted for five subjects in whom both (1) satisfactory flatmaps were obtained and (2) a full set of motion conditions was run. As far as possible, the same regions of interest were defined in all these subjects. The results for each cortical area are described below. In each visual area, the results are averaged across all hemispheres (from a maximum of 10 in five subjects) in which the area in question could be unambiguously distinguished from the neighboring areas. The method of deriving these activation strengths is described in Data Analysis. The results (see Figs. 7-10) are based entirely on those experimental runs in which motion stimuli are interleaved with a blank field.

Fig. 7.

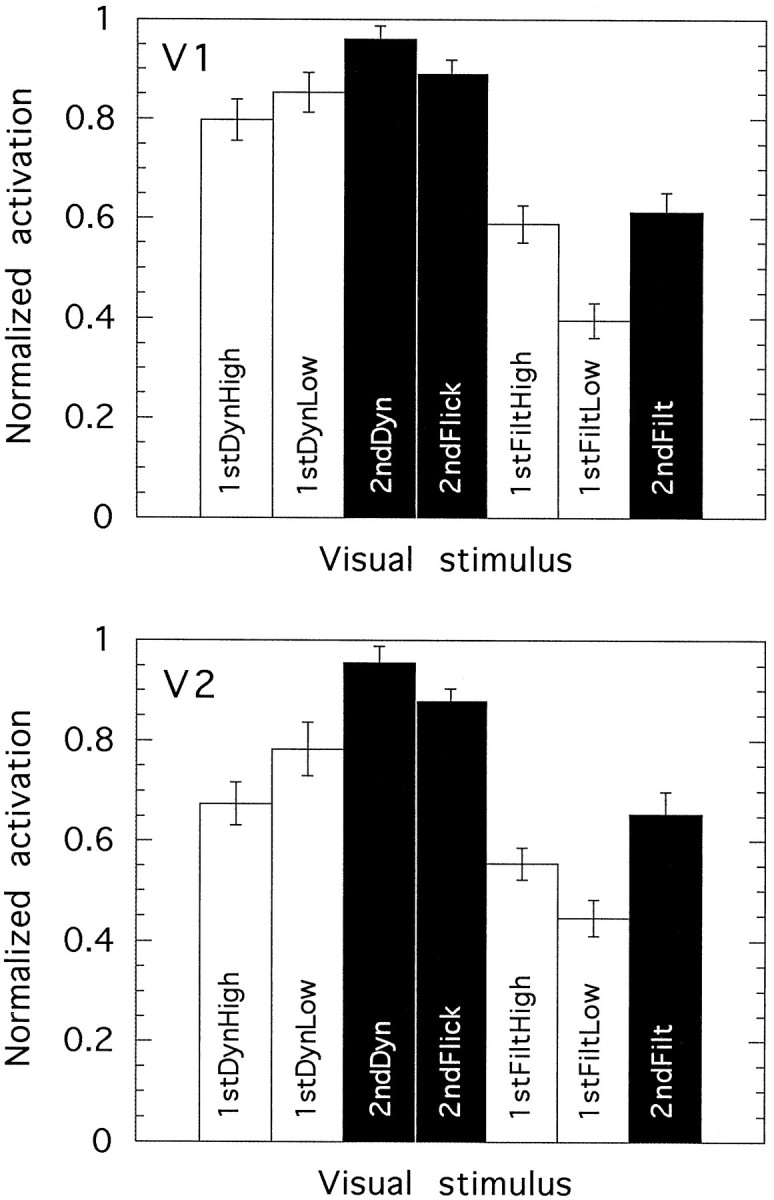
Normalized activation levels elicited by seven visual stimuli in each of two visual areas of the cortex:V1 (top) and V2(bottom). In both cases, data are pooled across upper and lower visual field representations. The data are averaged across 10 hemispheres (V1) or 8 hemispheres (V2) from five individuals. The three second-order motion stimuli are shadedblack; responses to the first-order stimuli are shown inwhite. Error bars show ±1 SEM.

Fig. 8.

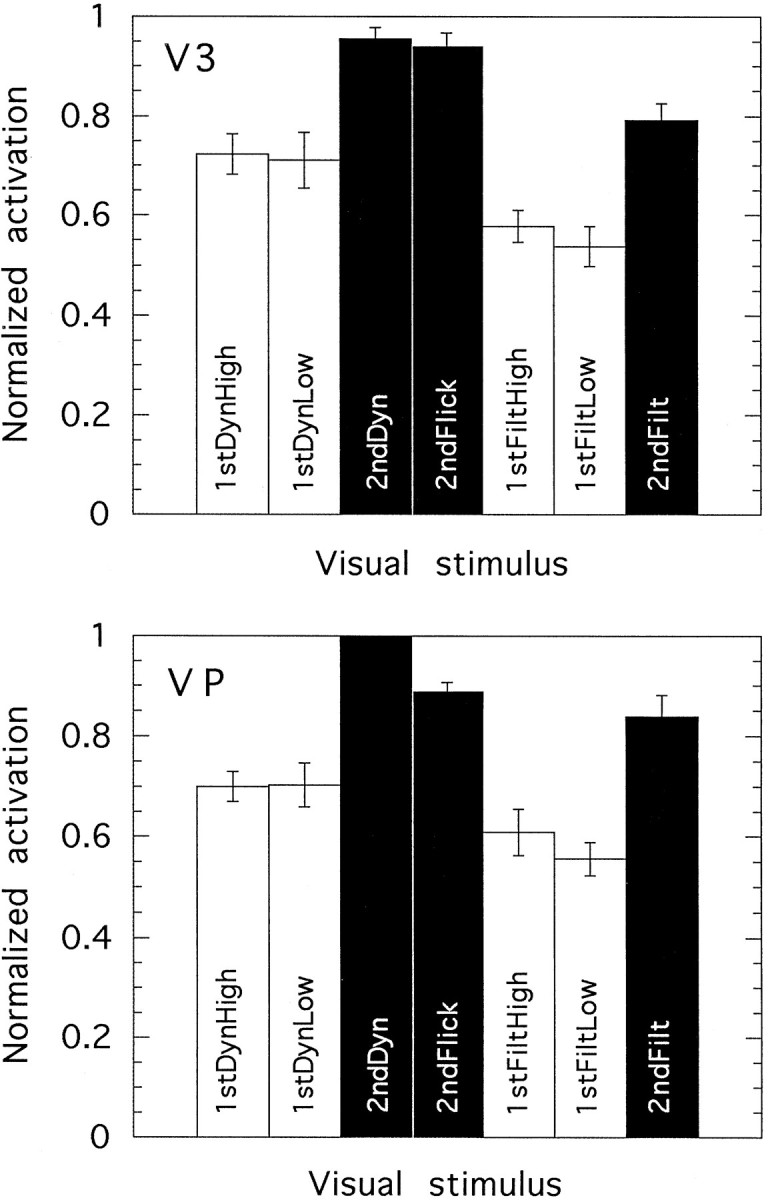
Normalized activation levels elicited by seven visual stimuli in each of two visual areas: V3(top) and VP (bottom). The data are averaged across 9 hemispheres (V3) or 10 hemispheres (VP) from five individuals. Error bars show ±1 SE.

Fig. 9.

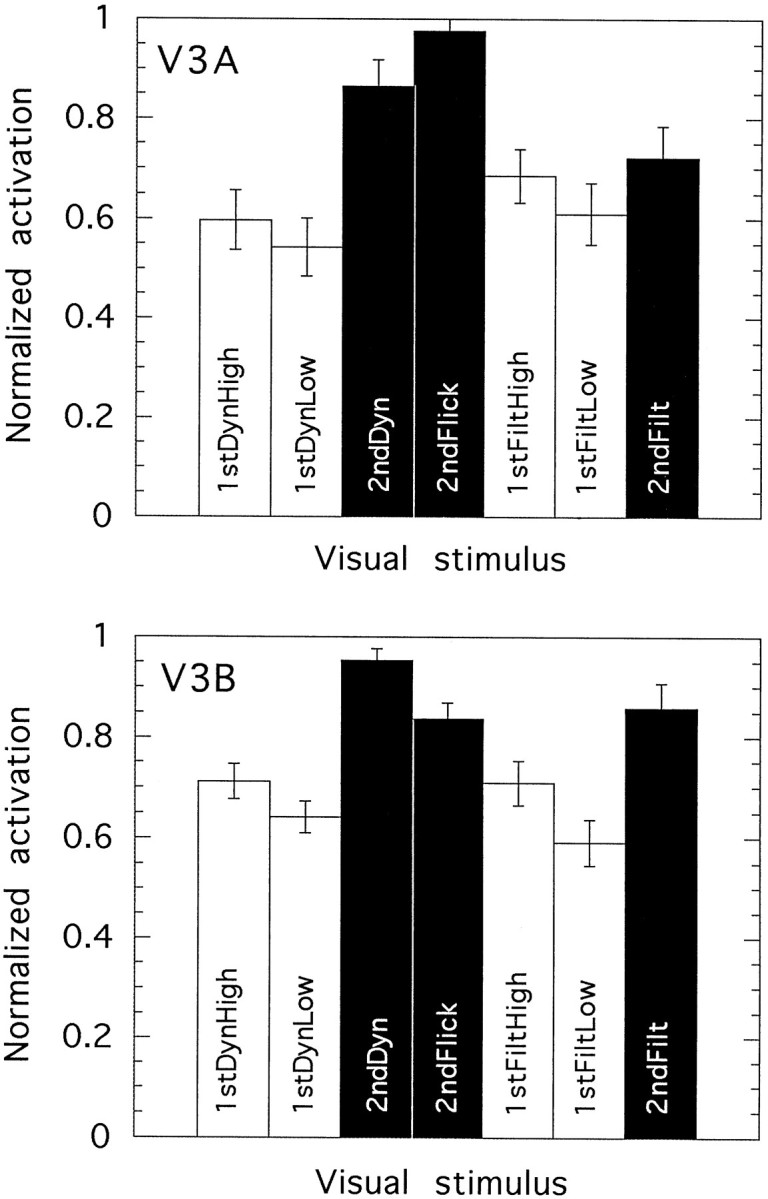
Normalized activation levels elicited by seven visual stimuli in each of two visual areas: V3A(top) and V3B (bottom). The data are averaged across six hemispheres (V3A) or eight hemispheres (V3B) from five individuals. Error bars show ±1 SE.

Fig. 10.

Normalized activation levels elicited by seven visual stimuli in area V5. The data are averaged across nine hemispheres from five individuals. Error bars show ±1 SE.

Area V1

As expected, visual area V1 (primary visual cortex) was activated by all of our visual stimuli. Examples of this activity can be seen as areas of high correlation with the stimulus profile superimposed on anatomical slices in Figure 6,b and c. Figure 7(top) shows normalized V1 activation levels for various visual stimuli, averaged across 10 hemispheres. First- and second-order motion stimuli produced similar levels of activation in V1. However, it must be remembered that all three second-order motion stimuli (including the one with a static carrier, 2ndFilt) contained temporal luminance modulations at every point in the image, even though they lack first-order motion. It is likely that much of the activation in V1 is not motion-specific, and in the case of second-order as well as first-order motion, much of it is presumably because of the first-order temporal structure (flicker) in the image. In support of this interpretation, it can be seen that those stimuli that contain dynamic noise (1stDyn, 2ndDyn, and 2ndFlick) give greater activations than do those that do not (1stFilt and 2ndFilt), irrespective of whether the motion is first- or second-order. This suggests that the response in V1 primarily reflects local spatiotemporal luminance modulations rather than responses to motion per se. Similarly, first-order motion with dynamic noise (1stDyn) gives similar activations irrespective of the contrast (high or low) of the motion stimulus, suggesting that most of the activation comes from the high-contrast dynamic noise and that any small difference because of the contrast of the moving grating is masked. For 1stFilt, the response is greater for high-contrast motion than for low, presumably because motion makes a proportionately greater contribution to the response in the absence of dynamic noise.

Because most of the V1 response to the stimuli seems not to reflect responses to the circular grating, it is impossible to compare the sensitivity of first-order with that of second-order motion.

Areas V2v and V2d

Normalized V2 activation levels are also shown in Figure 7(bottom). The data were initially analyzed separately for V2v (eight hemispheres) and V2d (seven hemispheres). The results were very similar. Because it is widely assumed that these two areas are functionally homologous and simply represent different quadrants of the visual field, the results from these two areas have been pooled in Figure 7. V2 shows the same trends as V1. As in V1, the main determinant of activation strength is whether or not the stimulus contains dynamic noise. First-order and second-order motion stimuli produce similar responses, but again it is likely that in neither case does the activity reflect responses to the moving gratings to more than a minor extent.

Areas V3 and VP

Figure 8 shows numerical activation levels elicited in response to the various visual stimulus conditions in areas V3 (nine hemispheres) and VP (10 hemispheres). As expected, in V3 only the lower quadrant of the contralateral hemifield is represented, whereas in VP only the upper contralateral quadrant is represented (see Fig. 4). Results for these two areas are very similar. The similarity between V3 and VP is consistent with the notion that the two areas are functionally identical and simply reflect the representations of different (upper and lower) hemifields. Whether this is truly the case in human cortex is unknown; there are some data from the primate cortex (e.g., Burkhalter et al., 1986; Felleman and van Essen, 1987) that suggest otherwise. Because it is uncertain whether they are functionally homologous in the sense that V2v and V2d are assumed to be, the results for V3 and VP are presented separately.

In V3 and VP, the pattern of results is quite different from that in V1 and V2. It is no longer the case that the stimuli containing dynamic noise elicit stronger responses than do those that do not contain dynamic noise. Instead, the visual stimuli that elicit the strongest responses are the second-order motion stimuli. This is true irrespective of which version (2ndDyn, 2ndFilt, and 2ndFlick) is compared with which first-order type. First-order motion stimuli elicit weaker responses, even in the case of the high-contrast versions. Statistical analysis shows that in V3, the response to 2ndDyn is significantly greater than that to either 1stDynLow (t= 4.1; df = 8; p < 0.005) or 1stDynHigh (t = 5.8; df = 8; p < 0.001). The same is true in VP (t = 6.7; df = 9;p < 0.0001; and t = 10.1; df = 9;p < 0.0001, respectively). Likewise, in V3, 2ndFilt produces greater activation than either 1stFiltLow (t = 4.8; df = 8; p < 0.002) or 1stFiltHigh (t = 4.9; df = 8; p < 0.002). Again, the same is true in VP (t = 10.0; df = 9;p < 0.0001; and t = 6.9; df = 9;p < 0.0001, respectively). The difference between first-order and second-order is therefore compelling. The fact that V3 and VP both show this difference and are so similar to each other adds to the reliability of the result.

In contrast to V1 and V2, the differences among the various motion conditions seem to reflect differences in the nature of the moving grating. The superior response to second-order motion in V3 and VP cannot easily be explained in terms of other differences between the images. The presence of dynamic noise, which has a powerful effect in V1 and V2, has much less effect in V3 and VP. The fact that 2ndFilt gives a stronger response than 1stDyn shows clearly that it is not the presence or otherwise of dynamic noise that is important but the nature of the motion stimulus itself. In both V3 and VP, the three most potent stimuli are the three second-order stimuli, even though in some respects these differ from each other more than they differ from their first-order counterparts. The fact that V3 and VP prefer second-order motion even when the comparison is with high-contrast first-order motion indicates that the preference is not a result of an inappropriate choice of contrast for the first-order patterns.

Thus, the enhanced responses seem genuinely to reflect the presence of the moving second-order grating. The only qualification to be made concerns the extent to which they reflect motion of the grating, as opposed to the mere presence of the grating. In other words, it is not obvious from Figure 8 whether the response is to second-order motion or to second-order form. This issue is discussed in a later section.

A strong and graphic test for a preference for second-order motion is provided by the experimental runs in which first-order and second-order motion were interleaved. The nature of the correlation procedure used for analysis is such that only a difference between the two activations will appear in the colored overlays in such conditions (qualitatively equivalent to a subtraction of the two responses). Figure 6,c and d, shows some results from runs of this type. Figure 6c shows the slice in which V3 appears in one subject. On the left is the response to 2ndDyn interleaved with a blank field. On the right is the result of interleaving the same stimulus 2ndDyn with its first-order counterpart 1stDyn. In the first case, regions in which 2ndDyn produces more activity than the blank field are shown inyellow/red. In each hemisphere, V1 is active on the medial surface. In addition, an area including the part of V3 closest to the foveal representation, together with part of the adjacent area V3B, is active (marked by red arrows). In the second case, in which the two types of motion are interleaved, only those areas that are more responsive to second-order than to first-order motion will survive the comparison. Area V1 is completely absent in this case. This is because although it is presumably active in response to both stimuli, the activity level is similar for both types of motion. However, a small active area corresponding to V3/V3B remains, indicating a preference for second-order motion. Figure6d shows a different slice in the same subject under the same two stimulus conditions. When second-order motion is interleaved with a blank field, an area of activation corresponding to part of VP can be seen in each hemifield. When second-order motion is interleaved with first-order motion, the activity in this area is still present, although weaker, indicating a preference for second-order motion.

Areas V3A and V3B

Figure 9 shows numerical activation levels elicited in response to the various visual stimuli in areas V3A (five hemispheres) and V3B (eight hemispheres). These two areas are adjacent, and both have a boundary with V3 (see Figs. 4 and 5). In V3A the entire contralateral hemifield is represented, whereas in V3B only the lower quadrant of the contralateral hemifield is represented. The results for V3A and V3B are fairly similar to each other and not unlike those seen in V3 and VP. The difference between results for those stimuli that contain dynamic noise and those that do not, prominent in V1 and V2 and still evident to a limited extent in V3 and VP, is completely absent in both V3A and V3B. In both areas, the three most active conditions are those in which second-order motion is present. It is not the case that the difference between the two is statistically significant for every possible comparison between a second-order and a first-order condition, as is the case in V3 and VP. Nonetheless, many such differences are significant. In V3B, the response to 2ndDyn is significantly greater than that to either 1stDynLow (t= 10.7; df = 7; p < 0.0001) or 1stDynHigh (t = 5.5; df = 7; p < 0.001). The same is true in V3A (t = 18.5; df = 5;p < 0.0001; and t = 4.3; df = 5;p < 0.01, respectively). Likewise, in V3B, 2ndFilt produces significantly greater activation than does either 1stFiltLow (t = 4.4; df = 7; p < 0.005) or 1stFiltHigh (t = 3.3; df = 7; p < 0.02). The same comparisons are nonsignificant in V3A. Thus, the preference for second-order motion is less striking in V3A and V3B than in V3 and VP but is still present. The most likely explanation for the preference is that V3A and V3B receive strong inputs from area V3 and (in the case of V3A only) VP.

Activation by motion stimuli in the V5/MT complex

The location of area V5 was identified in each subject simply by inspection of the anatomical slices with correlation data overlaid. In each subject, an isolated patch of activation appears bilaterally in a characteristic position the Talairach co-ordinates of which vary little among subjects. This region was readily identifiable in every subject included in the analysis. The mean Talairach co-ordinates of the center of V5, averaged across 15 hemispheres, are: x = ±46;y = −70; and z = 4. The co-ordinates for V5 show relatively little variance across subjects (SD = 7 mm) and are in general agreement with earlier studies (Watson et al., 1993;Tootell et al., 1995; Anderson et al., 1996; DeYoe et al., 1996). There is no doubt that the area we have identified is the same as the putative V5 identified in the human brain by others, and there seems to be little doubt that this area is homologous to V5/MT in monkeys, although it may be that important differences remain to be discovered.

Primate anatomical and neurophysiological results lead to the expectation that several additional motion-sensitive areas (e.g., MST, FST) should exist in the vicinity of human V5, and there is some preliminary evidence of at least one such area (e.g., Dale et al., 1995; Tootell et al., 1996). These additional areas are expected to lie in close proximity to V5. Of our sample of nine subjects the results of which were analyzed, five showed evidence of two separate motion areas in at least one hemisphere. In the remaining subjects/hemispheres, only one focus of activity could be resolved in the vicinity of V5. Because a complete picture of the identities and locations of the supplementary motion areas in human cortex is not yet available, it is probably unsafe to draw distinctions among these areas, and so we simply group them as the “V5 complex.” Where two regions were identified, both were analyzed, and in fact the results were in all cases similar in the two areas.

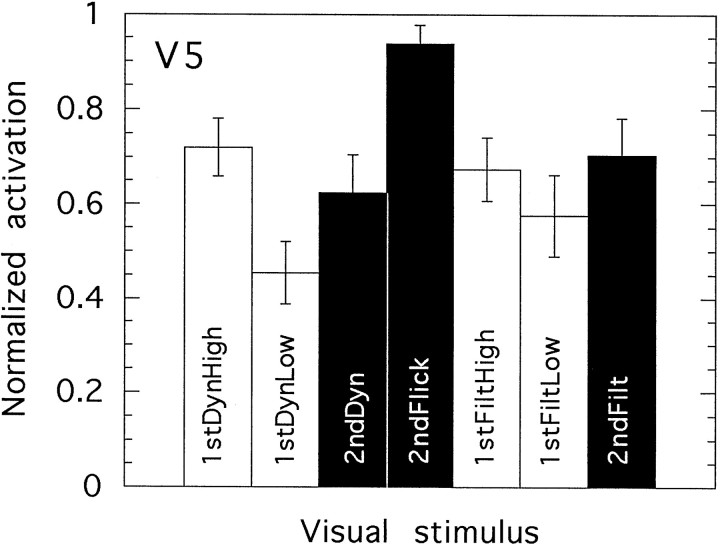
Figure 6b shows, for one subject, the anatomical slice in which V5 was located. Regions in which the activity is highly correlated with the stimulus profile are shown in color for two types of first-order motion, three types of second-order motion, and dynamic noise in separate images of the same slice. Also shown (Fig. 6a) is the location of this slice. The V5 complex (indicated by arrows) is visible bilaterally in all cases. It is clearly activated by second-order as well as by first-order motion. Dynamic noise alone also activates V5 but less effectively than any of the motion stimuli.

Figure 10 shows quantitatively the degree of activation evoked in the V5 complex by the various motion stimuli, averaged across subjects. The method for deriving these figures was the same as that used for the retinotopic areas except that the ROI was defined on slices such as those in Figure 6 rather than on flatmaps such as those in Figure 4. It can again be seen that V5 is activated by all classes of moving image, whether second-order or first-order motion. In common with V3A and V3B but not V1 and V2, the presence or absence of dynamic noise in the stimulus has no influence; if motion is present, the addition of dynamic noise does not increase the activation. In accord with earlier work (Tootell et al., 1995), high-contrast first-order motion yields somewhat greater activation than does low-contrast first-order motion. However, the difference is modest (particularly in the case of 1stFilt), consistent with the activity of neurons similar to those in primate MT that show high-contrast gain with response saturation at modest contrast levels (Sclar et al., 1990). The activity level evoked by second-order motion is numerically comparable with that evoked by first-order motion of either contrast level. However, in view of the contrast saturation that occurs in V5, it is unsafe to conclude that both stimulus types provide equal drive. To provide a full answer to this question, it would be necessary to measure contrast response functions for both types of motion.

It is thus quite clear that second-order motion provides a strong drive to area V5, but in contrast to some of the areas considered earlier, there is no evidence that it provides a stronger drive than does first-order motion. All motion stimuli produce similar activations except 1stDynLow, which is significantly lower than 1stDynHigh (t = 2.97; df = 8; p < 0.02), and 2ndFlick, which is significantly higher than 2ndDyn (t= 3.25; df = 8; p < 0.02). It should be remembered that the spatial frequency used for 2ndFlick was an octave lower than that used for all the other motion stimuli. To test the possibility that this accounts for the greater V5 response to this stimulus than to the others, we ran additional conditions in three subjects (six hemispheres) in which the response to 2ndDyn was compared with a version of 2ndDyn that had the same spatial frequency (0.4 c/°) as 2ndFlick. Similarly the response to 2ndFilt was compared with a version of 2ndFilt with spatial frequency 0.4 c/°. In both cases, the activation levels produced were very similar for the two spatial frequencies. (This was also true in the retinotopic areas.) Thus, the greater activation elicited in V5 by 2ndFlick compared with the other stimuli cannot be explained in terms of spatial frequency differences.

Dynamic noise alone (designated Dyn; not used in all subjects) also elicited significant activity in the V5 complex. The mean ratio of activation for 1stDynHigh to activation for Dyn was 2.4 (n = 6 hemispheres). For 1stDynLow compared with Dyn, the ratio was 1.7; for 2ndDyn compared with Dyn, it was 2.2. Thus, motion (whether first- or second-order) elicits rather more than twice the level of activation elicited by unmodulated dynamic noise. For 2ndFlick compared with Dyn (not strictly comparable because of different temporal frequencies), the mean ratio was 3.7. Filtered static noise alone elicited very little activity in V5. For example, the ratio for 1stFiltHigh compared to Filt was 11.6, and the ratios for 1stFiltLow to Filt and for 2ndFilt to Filt were 9.6 and 12.4, respectively.

In summary, comparisons with the control conditions (Dyn and Filt) indicate that (as expected) V5 activity is highly dependent on the presence of temporal structure in the image. Random spatiotemporally broadband structure yields about half the response produced by motion stimuli. This is true for both first-order and second-order motion. The response to second-order motion cannot be attributed to the presence of dynamic noise because (1) the response to noise alone is much less and (2) the response to 2ndFilt (which does not contain dynamic noise) is as strong as that to 2ndDyn and 2ndFlick (which do). Thus, the response is attributable in large part to the presence of the grating stimulus. The extent to which the response reflects specificity for motion of the grating is addressed in a later section.

Motion specificity

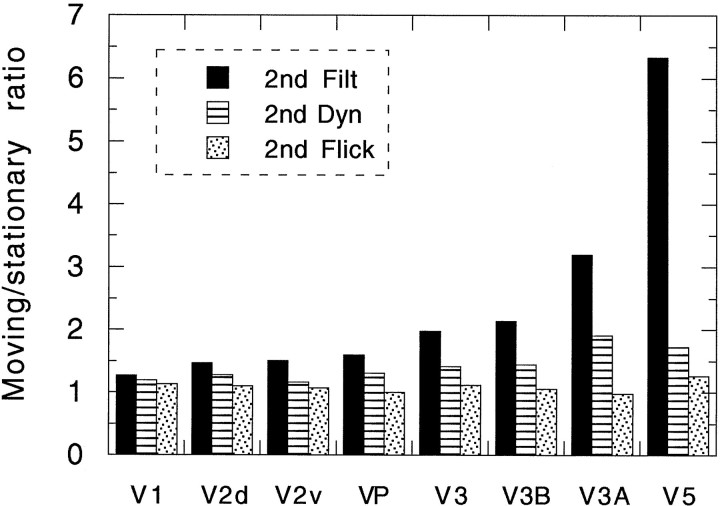
We have reported strong cortical activations in response to moving stimuli. We have used appropriate controls for the fact that, inevitably, part of the response reflects the activity of neurons that respond well to temporal structure (dynamic noise and local luminance modulations caused by movement). These controls enable us to assert that part, at least, of the activation observed is attributable to the presence of the moving circular grating in all areas except V1 and V2 (where, in reality, it is probably also true). However, it is also necessary to establish to what extent the activation results from the motion of the grating and to what extent from the mere presence of the grating. For example, it might be that V3/VP responds to second-order spatial structure (the radial grating itself) and is indifferent to whether or not the grating is moving, in which case it would be appropriate to consider this region as a candidate for the site of detection of second-order spatial structure rather than detection of second-order motion. To examine this issue, we conducted experiments in which stationary versions of each of our moving stimuli were presented, interleaved with a blank field. The activations obtained in this way in each cortical region were then compared with those obtained with moving stimuli, presented during the same experimental session. Specifically, 2ndDyn was compared with 2ndDynStat, 2ndFilt with 2ndFiltStat, and 2ndFlick with 2ndFlickStat.

Figure 11 shows the median ratio of the moving and stationary responses for each of the visual areas studied. The responses were calculated in the same way as were the numerical activations in Figures 7-10, and then a simple ratio was computed for each subject. Median ratios are plotted in preference to means because, particularly in V5, there were one or two very high ratios arising from near-zero activations for stationary stimuli. The best comparison with previously published motion specificity ratios is provided by the comparison between 2ndFilt and 2ndFiltStat, because here there is no temporal structure at all in the stationary case. Figure 11 shows the ratios in order of increasing motion specificity for this comparison. Motion specificity is least in V1 and V2, moving stimuli producing only slightly more activation than stationary stimuli. Motion specificity is a little higher but still modest in V3 and VP. V3B and particularly V3A are higher again, and V5 has the highest ratio of all. These results are qualitatively in line with those previously reported by Tootell et al. (1997) using first-order motion. In particular, we confirm that V3A is more motion-sensitive than is V3, the opposite of the situation that pertains in monkeys. However, whereas Tootell et al. (1997) report a striking difference between the two areas, the difference in our case is modest (∼3/1 in V3A and 2/1 in V3). It is possible that the discrepancy reflects a difference between first-order and second-order stimuli. To resolve this issue, a direct comparison of first-order and second-order motion ratios in the same laboratory is required.

Fig. 11.

Motion specificity of the various visual regions studied. The ratio of the activation produced by each of three second-order motion stimuli to that produced by images that are identical except that the grating is stationary are shown separately for each region. The regions are arranged in increasing order (left to right) of motion specificity.

The moving/stationary ratios for 2ndDyn and 2ndFlick are much less, particularly for V3A and V5. This could reflect genuine differences between different types of second-order motion, but it seems more likely that it occurs because of the presence of dynamic noise in these two images but not in 2ndFilt. In V5, motion elicits about twice the activity elicited by dynamic noise. The moving/stationary ratio can therefore never exceed two if dynamic noise is present. These ratios are arguably less meaningful, as a measure of motion specificity, than the 2ndFilt/2ndFiltStat ratio.

The high degree of motion selectivity in V5 obtained with second-order motion stimuli confirms that V5 genuinely responds to second-order motion. In the case of V3 and VP, however, the motion specificity (∼2/1) is more modest. Nonetheless, this ratio suggests that V3 and VP contain significant numbers of neurons that are truly sensitive to second-order motion, in addition to large numbers of other neurons that are not. This being the case, V3/VP is a good candidate for the site at which second-order motion is made explicit. An alternative interpretation is that second-order form is processed in V3/VP but that second-order motion is extracted from the image elsewhere, such as in V3A or V5 where motion specificity is higher. But on this view, the motion ratio for second-order stimuli in V3/VP would be expected to be 1/1 not 2/1. We therefore favor the former interpretation.

DISCUSSION

We have reported three principal findings. First, the human V5/MT complex is strongly activated by second-order motion. The three different types of second-order motion used all produced activations that were as strong as those produced by their first-order motion counterparts. The activity is primarily motion-specific, in accord with previous studies of V5. Second, area V3 and its ventral counterpart VP respond more strongly to second-order than to first-order motion. This result raises the possibility that V3 (lower hemifield) and VP (upper hemifield) are the first visual areas in which information about second-order motion is represented explicitly. The activity in these areas is only partially motion-specific, suggesting that functions other than motion processing are also fulfilled there. Third, we have identified a new visual area that we call area V3B. This area has borders with both V3 and V3A.

There was no cortical region that consistently responded better to first-order than to second-order motion. Superficially, this is surprising. However, it should be remembered that all our images, including the second-order motion stimuli, contained first-order spatial structure and that some (2ndDyn, 2ndFlick) contained strong first-order temporal structure. In primates (as in other mammals), most cortical areas contain a variety of neuron subtypes, many of which are not motion-sensitive. Functional imaging procedures cannot selectively tap motion-sensitive neurons. It may well be the case that a preference for first-order motion exists in, for example, V1, but that the motion-specific portion of the functional signal is swamped by responses to first-order spatial and temporal structure that are not related to motion processing. By the same token, we cannot assert that second-order motion is not detected in V1 or V2 simply because it does not cause differential activity until the level of V3 and VP. The notion that the earliest processing of second-order motion occurs in V3 and VP is speculative.

Relation to other imaging studies

This is the first neuroimaging study to be conducted on the sensitivity of the human cerebral cortex to second-order motion. However, it is of interest to draw comparison with the work of Dupont et al. (1997), Orban et al. (1995), and Van Oostende et al. (1997). The new area that we refer to as V3B has a similar location to an area identified by that group on the basis of strong responses to kinetic boundaries (boundaries between adjacent areas in which motion is in opposite directions). They have identified this area using both PET and fMRI methods. They refer to it as KO (for “kinetic occipital”), asserting that it is too lateral to be V3 and that it forms a distinct visual area. It seems that their KO and our V3B are probably the same area. The Talairach co-ordinates quoted by Orban et al. (1995) for KO are similar to those for V3B measured in our study. The mean co-ordinates for V3B based on the center of the region defined on the flattened cortical representation are: x = ±26;y = −89; and z = −2 (12 hemispheres; SD = 8mm). The most recent published Talairach co-ordinates for KO are: x = ±31; y = −91; andz = 0 (Van Oostende et al., 1997). The 3-D position in the unflattened brain as illustrated by Van Oostende et al. (1997) is also consistent with that of V3B shown in our Figure 5.

If it is indeed the case that V3B and KO are the same, it is not clear why Van Oostende et al. (1997) find a distinction between the functional properties of V3 and of KO or V3B, whereas our stimuli give quite similar results. Their stimuli have elements in common with ours. They used a grating formed from alternating columns of dots drifting in opposite directions to give motion boundaries. This stimulus can be regarded as a type of second-order spatial structure (though not as second-order motion because the boundaries so formed do not move). Our study shows that V3 and VP are the areas in which sensitivity to second-order stimuli is first evident and that V3A and V3B simply mirror this behavior. Van Oostende et al. (1997) claim that sensitivity to kinetic boundaries emerges in KO and is apparently absent in V3.

Whether V3B and KO are the same will not be resolved conclusively until responses from kinetic boundaries are mapped onto a flattened cortical representation in which KO is defined by retinotopic mapping. We assume, however, that they are the same. This being the case, we favor the nomenclature “V3B” rather than “KO” because (1) it is consistent with the numerical classification of all of the other retinotopic regions and (2) it may be unsafe to name areas based on assumed functions, in this case the detection of kinetic boundaries. Only after much more extensive study will the functions of this region be fully appreciated.

Relation to neurophysiological findings

A few studies of the responsiveness of MT neurons in macaques to second-order motion have been conducted. Albright (1992) used a bar stimulus defined by noise flicker frequency, a stimulus of the same class as our 2ndFlick stimulus. He found that most MT neurons responded well to motion of such a bar. Recently, O’Keefe and Movshon (1998)have conducted a more detailed study, using flicker-frequency-defined grating stimuli. They too obtained responses to second-order motion in MT neurons, although such responses were weaker than for first-order motion and were not obtained in all MT neurons. In light of these physiological findings, it is perhaps to be expected that human V5/MT is responsive to second-order motion. We cannot tell from our data whether fMRI activation of V5 by second-order motion and activation by first-order motion reflect the activity of the same neurons or of two distinct subpopulations, but the physiological data from primates make the former possibility more likely.

Chaudhuri and Albright (1997) recorded responses to flicker-defined bars in V1 neurons in macaques. Many cells responded to such stimuli, although less strongly, and these often showed a direction preference. This suggests that second-order motion is encoded in V1, although it is possible that these responses reflect descending inputs from higher areas. Certainly it seems likely that both types of motion are initially detected at an earlier stage of processing than in V5. In the case of first-order motion, V1 is the obvious candidate, but this is based entirely on expectations from primate neurophysiology. In the case of second-order motion, the site of detection is less clear. All we can say is that the site is not beyond V3 and VP. It seems clear that V5 is a site of additional processing, not initial detection, for both types of motion. Given that neurophysiological studies show that the same V5 neurons respond to both types of motion, it is likely that the two motion signals, although perhaps initially distinct, are merged in V5, perhaps to yield a single, maximally accurate estimate of motion.

Relation to psychophysics

There is now considerable psychophysical evidence that first-order and second-order motion are detected independently. First, if animation sequences are constructed in which perception of motion necessitates integration of first-order and second-order frames, motion perception fails (Mather and West, 1993; Ledgeway and Smith, 1994). Second, sensitivity to second-order motion differs from first-order motion sensitivity in important ways. For second-order motion, thresholds for identifying direction of motion are higher than those for identifying orientation (Smith and Ledgeway, 1997), whereas for first-order motion, both thresholds are the same. Temporal acuity is significantly worse for second-order than for first-order motion (Derrington et al., 1993;Smith and Ledgeway, 1998).

However, given the existence of two systems, it seems likely that they operate in parallel and that their outputs are later combined to give a single motion signal. This notion is embodied in at least one computational model of motion detection (Wilson et al., 1992). One piece of psychophysical evidence of combination of first- and second-order motion signals is that adaptation studies show strong interactions between motion signals of the two types (Ledgeway, 1994). Further psychophysical evidence for such combination comes from studies of perceived direction (Yo and Wilson, 1992). Thus, the conclusion from psychophysical studies is in accord with that from neurophysiological findings (previous section).

Relation to studies of brain damage

Zihl et al. (1983) have reported a striking case of motion blindness after bilateral lesions in the region of the tempero-occipitoparietal border. Unfortunately, the lesions are too large to permit accurate localization of the motion area(s) in this individual. Plant et al. (1993) and Plant and Nakayama (1993) have reported subtle differences in threshold sensitivity between the two types of motion and concluded that there must be a degree of anatomical dissociation between the two. In a recent study (Greenlee and Smith, 1997), we measured speed discrimination performance using each type of motion in a group of 21 former neurosurgery patients with much smaller, circumscribed, unilateral postsurgical lesions in various regions of the posterior cerebral cortex. The observed performance deficits showed a correlation between the two types of motion, indicating substantial overlap in the cortical areas involved. Yet subtle differences were found, indicating a partial dissociation. The picture of subtle differences only between the anatomical substrates of processing the two types of motion is very much in line with the present fMRI findings.

Conclusion

Our results provide the first direct evidence concerning the neuroanatomical substrates of the processing of second-order motion in the human brain. They indicate that such motion may be detected in V3/VP and then passed to V3A, V3B, and V5 for further processing.