Abstract
Molecular dynamics (MD) simulations that capture the spontaneous binding of drugs and other ligands to their target proteins can reveal a great deal of useful information, but most drug-like ligands bind on time scales longer than those accessible to individual MD simulations. Adaptive sampling methods―in which one performs multiple rounds of simulation, with the initial conditions of each round based on the results of previous rounds―offer a promising potential solution to this problem. No comprehensive analysis of the performance gains from adaptive sampling is available for ligand binding, however, particularly for protein–ligand systems typical of those encountered in drug discovery. Moreover, most previous work presupposes knowledge of the ligand’s bound pose. Here we outline existing methods for adaptive sampling of the ligand-binding process and introduce several improvements, with a focus on methods that do not require prior knowledge of the binding site or bound pose. We then evaluate these methods by comparing them to traditional, long MD simulations for realistic protein–ligand systems. We find that adaptive sampling simulations typically fail to reach the bound pose more efficiently than traditional MD. However, adaptive sampling identifies multiple potential binding sites more efficiently than traditional MD and also provides better characterization of binding pathways. We explain these results by showing that protein–ligand binding is an example of an exploration–exploitation dilemma. Existing adaptive sampling methods for ligand binding in the absence of a known bound pose vastly favor the broad exploration of protein–ligand space, sometimes failing to sufficiently exploit intermediate states as they are discovered. We suggest potential avenues for future research to address this shortcoming.
1. Introduction
A longstanding goal of molecular simulation has been to capture the binding process of a drug or other small-molecule ligand to its target. If unbiased, atomic-level molecular dynamics (MD) simulations of spontaneous ligand binding could be performed reliably, then they could determine not only ligand-binding sites and poses but also binding pathways and structural determinants of binding kinetics, all of which are topics of great interest in drug discovery.1,2 Thanks to improvements in algorithms, software, and computer hardware, individual all-atom simulations can now reach lengths of many microseconds (or even a millisecond with specialized hardware).3 This has enabled unguided simulations of the full binding process for a number of ligand–protein pairs, generating considerable excitement.4−8 The great majority of ligands, however, bind on time scales substantially longer than those currently accessible to individual MD simulations, making binding a rare event.
A number of methods exist for this problem of rare event sampling and appear in the literature under different names, beginning with “splitting” strategies introduced in the 1950s.9 Currently, many different path-sampling strategies have been applied to biomolecular systems,10 most notably the weighted ensemble method.11 These methods have the added benefit of producing unbiased data sets from which statistical mechanical observables can be calculated. However, the majority of path-sampling methods presuppose or require prior knowledge of the pathway of interest, requiring either start and ending points or some progress coordinate that must be defined prior to the run. Defining such coordinates for the binding of a ligand to an unknown location on a protein presents a significant challenge.
An alternative approach for sampling rare events is the use of heuristic methods, where the results may be biased by the choice of sampling strategy, but less information needs to be known beforehand about the desired result. One such class of heuristic method is sometimes referred to as adaptive sampling, in which multiple rounds of simulations are performed, initiating the simulations in each round from molecular system configurations deemed most promising based on the results of previous rounds.
In a typical adaptive sampling protocol, one runs many independent, simultaneous MD simulations (samplers) at each round. A subsequent machine-learning step uses available simulation trajectories to build a statistical model of what is currently known about what the ligand can do. The group of samplers is then restarted from the “most interesting” protein/ligand positions, as determined by the model, to begin a new round of adaptive sampling.
By iterating these two steps of sampling and machine learning, adaptive sampling explores the protein–ligand space in a parallelized manner. In principle, adaptive sampling may also offer speedups relative to traditional MD simulation by “wasting” less simulation time on uninteresting regions of the space of all possible configurations. The degree to which this is true in the case of protein–ligand binding, if at all, is the topic of this paper.
Adaptive sampling methods have been applied primarily to the problem of sampling protein conformations. For this application, a reasonable assumption is that any stable conformation that is different from those previously observed is interesting. Quantifying novelty in this way is relatively straightforward. Prior work uses metrics that aim to minimize redundant sampling,12 reduce the uncertainty of transitions,13 capture slow events,14 or explore free energy15 or other landscapes.16
Adaptive sampling has also been used to study ligand binding,17−19 but its performance relative to traditional MD simulation on protein–ligand systems typical of those encountered in drug discovery has not been determined. Existing implementations have been evaluated only on small test systems, present little justification for their choice of methods and parameters, and frequently rely on knowledge of the true bound pose to guide sampling.
In this Article, we evaluate the performance of adaptive sampling with no prior knowledge of both simple and complex protein–ligand systems using long unbiased MD simulations as a baseline. We introduce a suggested adaptive sampling protocol and implementation that requires no a priori knowledge of binding site, bound pose, or even that the ligand can bind at all—intended to be broadly transferable to ligand binding, in general. We provide the reasoning behind all design decisions to aid the reader in evaluating or implementing adaptive sampling for their own applications.
We find that current adaptive sampling methods as well as the improvements we present here do not usually sample bound poses faster than traditional MD simulation. However, they do excel at tasks requiring broad sampling of protein–ligand space, such as identifying possible interaction sites all over the protein, and they are able to accurately and efficiently characterize ligand pathways to a binding site even when the bound pose is not identified. We analyze our results by placing adaptive sampling in the context of the algorithmic exploration–exploitation dilemma, a class of problems featuring a trade-off between obtaining new knowledge (exploration) and using that knowledge (exploitation).20
2. Methods
2.1. Overview
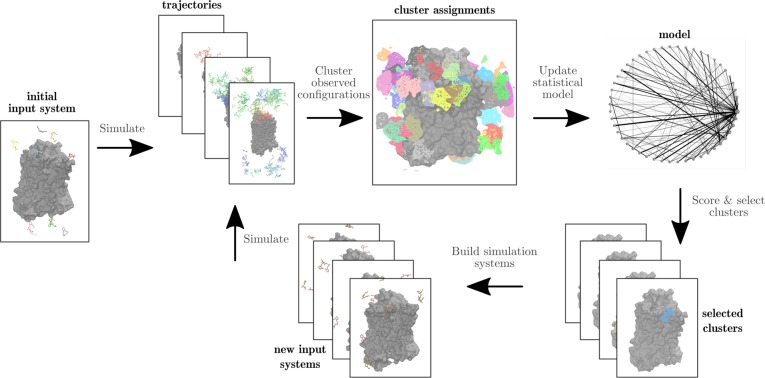
Adaptive sampling protocols generally consist of four main steps, as depicted in Figure 1.
Run multiple independent molecular dynamics simulations, generally starting from different configurations of the molecular system.
Cluster all configurations of the molecular system observed in simulation trajectories.
Select clusters for resampling in the next round. This involves assigning a score to each cluster, often on the basis of a statistical model that describes what is known about the dynamics of the molecular system given the simulations performed so far.
Build new molecular system configurations to serve as the starting points for another round of simulation, based on configurations from the selected clusters.
Figure 1.
Overview of the adaptive sampling protocol. Initially, multiple independent molecular dynamics simulations are run of an input system with multiple copies of the ligand in solution. All configurations of the molecular system observed in simulation trajectories are clustered, then used to update a statistical model. Clusters are selected for resampling in the next round by assigning a score to each cluster, and new molecular system configurations are built from selected clusters as starting points for another round of simulation.
Many design decisions and hyperparameters must be set to have a functional adaptive sampling implementation. In Sections 2.2–2.6, we introduce a recommended adaptive sampling protocol that requires no a priori knowledge of the ligand’s bound pose or even the neighborhood of its binding site, with well-defined, user-tunable parameters.
We allow a choice of several scoring functions, including the hub scores metric, which has not been previously used for adaptive sampling. Additionally, our implementation is the first to enable the effective use of multiple identical ligands in a single simulation to further enhance sampling, with a system building step to place them as efficiently as possible.
The source code for our implementation and configuration files used for test systems are publicly available at github.com/drorlab/adaptive_sampling.
2.2. Molecular Dynamics Simulation Step
Each round of adaptive sampling begins with running many simulations in parallel. For the initial round of sampling, one or more identical ligands are placed at random positions that are at least some minimum distance from the protein and from one another, typically in the water surrounding the protein. In subsequent runs, the ligands are placed in regions of interest, as defined by the scoring function (see Section 2.6).
Each simulation begins with a static structure with initial atom velocities assigned randomly. This diversifies sampling because initial random assignment of velocities may remove the system from low energy states, favoring exploration.21 The structure is minimized and equilibrated with restraints on the ligand and protein (see the Supporting Information (SI)).
Using nligands in each simulation rather than only one yields an nligands-fold increase in sampling but runs the risk of mischaracterizing molecular system behavior if the ligands frequently interact with one another or communicate through the protein. This parameter should be selected such that ligands have sufficient “room to roam” and do not exhibit a tendency to aggregate in simulation.
Two additional user-specified parameters determine the number N and length trun of samplers. Available computational resources and competing research priorities will place a realistic upper bound on N, but larger values are generally better because more samplers means greater exploration of configuration space in the same amount of wall-clock time.
The choice of trun requires some consideration. Individual trajectories need to be long enough to have a reasonable chance of capturing relevant events but short enough that one can perform multiple rounds of simulation, with the results of each guiding the next.
2.3. Clustering Ligand Positions
Raw simulation data specify the spatial coordinates of every atom for every frame in the trajectory. To select ligand coordinates for resampling in the next round, we must divide the system configurations sampled in simulations thus far into a discrete list of clusters, which can be used to construct a statistical model and then scored. In practice, each cluster will correspond roughly to a set of ligand locations, although clusters may also reflect the internal conformation of the ligand and protein.
To cluster effectively, this high-dimensional trajectory data set must be reduced to a lower-dimensional representation that captures the features of interest, particularly the position of each ligand relative to the protein. We wish to assign these features without prior knowledge of the binding site or pose, disqualifying the use of metrics like root-mean-square deviation (RMSD) to bound pose or distance to binding pocket residues.
Because multiple identical ligands may be in the system, we featurize each ligand independently. That is, for each frame of a simulation with 10 ligands, 10 feature vectors will be generated. We make the assumption that ligands do not interact substantially, which is moderately enforced at the system building phase by placing ligands far from each other.
Ligands are featurized according to the log of the minimum distance of each ligand heavy atom to each protein residue. The dimensionality of the vector is reduced to the slowest evolving components in time with time-structure-based Independent Components Analysis (tICA).22,23
Clustering on the tICA components produces “geometric” clusters because the only information present in the original feature vectors is spatial. Simple geometric clustering is insufficient to produce a good representation of the system. In particular, there are far more spatially distinct ligand positions in the bulk solvent than there are protein-interacting ones, but these solvent positions are not meaningful because ligands in solvent rapidly exchange between different geometric clusters and completely solvated ligands are not a priority for resampling.
We therefore apply a second clustering step in which geometric clusters that quickly interconvert are “lumped” into macrostates. The resulting macrostate clusters are geometrically distinct but of varying size due to this second, kinetic clustering step (see the SI). Clustering is done on the entire data set, not just the new trajectories from each round, because cluster assignments change when more of the configurational space is explored.
User-defined parameters in this step include the tICA lag time, the number of tICA components used for clustering, the number of geometric clusters, and the number of macrostates. Of these, the tICA lag time is of special importance because it determines the fastest dynamics that may be resolved in the final model, regardless of the frequency with which individual simulation frames are saved.
2.4. Model Construction
After clustering, observed transitions between macrostates are counted and a Markov state model (MSM) is constructed.24 This model represents each macrostate cluster as a node in a directed graph, where edges between nodes correspond to possible transitions from one ligand macrostate to another, with a “weight” specifying a transition rate estimated from the frequency of transition observed in simulation. This model can be used to estimate many different properties of the molecular system, including pathways, kinetics, equilibrium populations, and free energies.25
The construction of this model uses several user-defined parameters, including the number of macrostates and MSM lag time, which are further described in the SI. For a high-quality MSM suitable for further analysis, parameter selections are validated by observing convergence in the model’s implied time scales.26,27 However, this validation requires a significant amount of simulation data, creating a chicken-and-egg problem for adaptive sampling runs. We instead choose the model parameters somewhat arbitrarily, using the MSM only to guide sampling with the assumption that it is of dubious quality. Indeed, we find that even for successful adaptive sampling runs, our parameter selections are not ideal (Supplementary Figure 1).
2.5. Scoring Functions
The choice of which clusters from the macrostate model to resample is made by selecting clusters for resampling with a probability inversely proportional to their score, as determined by some scoring function. We apply a scoring function new to adaptive sampling, hub scores, and compare it to two simpler ones, populations and counts.
An ideal scoring function will be resistant to model uncertainty; that is, when the model is far from convergence, scores will still reflect useful states for resampling despite little data or an inaccurate picture of sampling. The scoring function should also be transferable between systems and should work regardless of the depth of the binding pathway, the presence or absence of a lipid bilayer, and so on.
The simplest scoring function we investigated is the counts function, where a state is selected with probability inversely proportional to the number of times the state has been sampled in simulation. This rewards the exploration of new or sparsely sampled states regardless of their context. It has been used in several previous studies.18,19,28
The populations scoring function selects states for resampling with probability inversely proportional to their predicted equilibrium population by the current MSM. This is equivalent to sampling states that the current model predicts have high free energy. This scoring function aims to both reduce uncertainty in the model, as poorly characterized states often have low predicted equilibrium population, and encourage resampling of higher energy transition states, such as those present in binding pathways. This scoring function has been previously implemented as the exploration phase of Free Energy Guided Sampling.15
Finally, we consider the use of hub scores, again with states selected for resampling with probability inversely proportional to their score. The hub score, originally applied to quantify protein folding networks,29 has not been used previously for adaptive sampling. This score is a measure of a state’s connectivity in the MSM, with a higher hub score specifying greater connectivity. More specifically, the hub score measures the probability that any given state will lie on a pathway between any two points in the configuration space, according to the MSM. In a typical protein–ligand MSM, the bulk solvent state has the highest hub score, and states more distant from it are lower.
Although the hub scores function has not been previously used for protein–ligand adaptive sampling, it appears promising due to its scoring of states in the context of the full model. When searching for bound poses, it makes sense to look for states that are at the end of pathways. Conversely, transient protein–ligand interactions intuitively should have a higher rate of interconversion with solvent, resulting in a higher hub score than a bound state at the end of a longer pathway.
In this study, we aimed to conduct a survey of broadly different scoring functions rather than a complete enumeration, and, as such, we omitted several previous implementations that have been either subsumed by or shown to be less useful than our selected three. For example, resampling uncertain transitions more13 is approximately equivalent to resampling uncertain states more with the counts function.
2.6. System Building
The final step of each adaptive sampling iteration is the construction of simulation systems for the next set of MD runs. This step is complicated by the fact that we typically use multiple ligands in each simulation, and we wish to place each of them preferentially in clusters that received low (i.e., good) scores. We therefore do not simply restart simulations from frames of previous simulations.
To ensure some diversity in cases where one cluster has a much lower score than others, the top-scoring N clusters are automatically sampled in the next round. A random simulation frame from each of these clusters is used to set the initial protein conformation and the position of a single ligand for one sampler. For each additional ligand, a cluster is selected at random with probability inversely proportional to its score. The ligand coordinates are set from a randomly chosen frame assigned to that cluster, provided that it is not too close to the protein or to other already-placed ligands, as determined by a user-configurable cutoff. Ligands that cannot be placed are positioned randomly in the bulk solvent.
Once each system is built, simulation begins, kicking off the next round of the adaptive sampling process.
2.7. Standard Test System: Trypsin–Benzamidine
The binding of the small molecular inhibitor benzamidine to the protein trypsin is frequently used as a model system for evaluating methods involving protein–ligand binding.5,30 The ligand-binding site is exposed to solvent, and little conformational change takes place upon binding. The high on-rate of benzamidine also enables easy sampling of multiple binding events, with an experimental association constant of 2.9 × 107 mol–1 s–131 and a computationally determined mean first passage time of 500 ns at a concentration of 0.0037 M.17
We ran six trials of adaptive sampling with N = 10 samplers with individual simulation length trun = 10 ns and two trials with each of the hubs, counts, or populations scoring metrics. We arbitrarily chose a maximum run time of 80 sampling rounds because this allowed all conditions to sample at least one binding event. An initial 10 ns of equilibration was omitted from each trajectory to avoid biasing the model; see the SI.
As a control, we ran six trials of traditional MD simulation, each with 10 samplers running for 800 ns each, which is equivalent to the total amount of simulation performed with adaptive sampling.
2.8. Realistic System: β2AR–Dihydroalprenolol
We also evaluated the performance of adaptive sampling on a more difficult system that represents a more typical real-world use case of the method. We selected the binding of the beta-blocker dihydroalprenolol to the β2 adrenergic receptor (β2AR) for this test because its binding process has previously been characterized by extensive traditional MD simulation.7
β2AR is a membrane-bound G-protein-coupled receptor (GPCR) where the ligand-binding pocket is removed over 15 Å from bulk solvent. The binding pathway requires the ligand to first enter the “extracellular vestibule” of the protein, at which point it has a >50% chance of continuing on to the binding site.7
This system is especially challenging because it contains a lipid bilayer, and the ligand is rather hydrophobic and will frequently partition into the bilayer. A previous unadaptive MD simulation study7 of this system cut short runs where all 10 dihydroalprenolol molecules entered the membrane because dihydroalprenolol leaves the membrane quite slowly once having entered.
We ran two trials of adaptive sampling using hub scores and two using population scores. In each case, we used N = 20 samplers with individual simulation length trun = 40 ns (with the initial 10 ns of equilibration omitted; see the SI) for 40 rounds of sampling.
The counts metric was not benchmarked on this system because initial attempts resulted in all ligands partitioning into the lipid in various locations. These ligands fail to bind to the protein without first partitioning back into solvent, which would require prohibitive amounts of simulation time to sample. Ligand positions in the membrane are geometrically distinct and do not rapidly interconvert, resulting in a unique cluster assignment at each membrane location. Because there are many possible places where the ligand may partition into the plane of the lipid, the probability of seeing one location many times is low, resulting in a low count for each membrane-bound cluster. The counts metric therefore ends up preferentially sampling all possible ligand locations in the membrane and fails to progress along actual binding pathways.
Although the hub scores function loosely correlates with observed counts, the proximity of membrane-partitioned locations to solvent results in these clusters having a higher hub score and therefore avoiding resampling. There is no correlation between clusters with low count and hub score (Supplementary Figure 2).
As a control, we ran two trials of traditional MD simulation, with each replicate running for an equivalent simulation time of 1.6 μs. We also obtained trajectories used in the previous binding study7 for additional validation.
Because adaptive sampling involves running a group of simulations simultaneously, all comparisons between our implementation and traditional MD simulation will be done using groups of independent simulations with equal total amounts of simulation time.
3. Results
3.1. Adaptive Sampling Correctly Identifies Binding Pathways and Intermediate States
Questions of whether or not adaptive sampling is faster or better than traditional MD simulation are moot if the results of adaptive sampling are not interpretable or fail to capture necessary information to describe binding. It is also possible that the pathways predicted by adaptive sampling do not represent the true predominant binding pathway, as the method could repeatedly resample states in such a way as to force the system to move over high-energy barriers while a lower energy transition state is missed. For both test systems, we evaluate if our method sampled the known bound pose and pathway.
We compared our β2AR adaptive sampling runs to the conclusions of a previous study where long MD simulations were used to characterize binding.7 That paper notes two entry pathways: In 11 of the 12 simulations where a ligand bound, it first entered the “extracellular vestibule” (a region enclosed by extracellular loops (ECLs) 2 and 3 and helices 5–7) and then proceeded into the binding pocket. In the remaining simulation, the ligand entered between ECL 2 and helices 2 and 7 before proceeding into the binding pocket.
All of our adaptive sampling trials captured both of these binding pathways (Figure 2). Moreover, they did so without requiring any manual analysis―to obtain binding pathways from these adaptive sampling runs, we simply queried the MSM for the top pathways from the bulk solvent cluster to the cluster corresponding to the bound pose. Interestingly, both pathways were obtained even from an adaptive sampling trial that did not sample the crystallographic bound pose; in this case, we queried for a pathway that reached the cluster closest to the bound pose.
Figure 2.
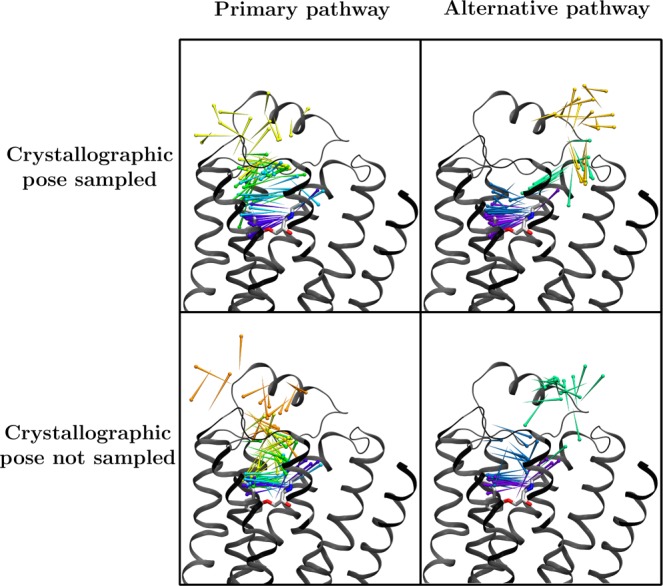
Primary (left) and alternative (right) pathways for ligand entry to the binding pocket of β2AR, as determined by 60 rounds of two adaptive sampling trials using the hub scores criteria. At the top are the predicted pathways from a trial where the crystallographic pose for the ligand was sampled, and at the bottom are those from a trial where the ligand entered the binding pocket but did not sample the crystallographic pose. In both cases, the model was queried for all paths from the most populous cluster (representing bulk solvent) to the cluster with the lowest mean RMSD to the crystallographic pose. The pathways shown were selected from the top ten highest flux paths based on the number of well-defined clusters visited. The crystallographic pose is shown as sticks, and ligand positions along the pathway are shown as pins, with the pinpoint at the nitrogen atom and the round end at the benzene ring center. The pins are colored by the cluster assignment within the pathway, with 20 pins shown per cluster.
By contrast, when we performed the same automated MSM-based analysis for the trajectories obtained by the same amount of traditional MD simulation, we did not identify both binding pathways. For the first traditional MD simulation trial, only the less common binding pathway was clearly identified by the MSM. Manual analysis of the trajectories from this run shows that only one pathway was sampled in the simulation. For the second traditional MD run, neither binding pathway was clearly identified because the clusters did not have sufficient spatial resolution; in particular, the pathway intermediates were lumped together with bulk solvent.
This marked difference in the quality of the predicted binding pathway suggests that by repeatedly placing the ligand in regions of interest, adaptive sampling may better characterize all available binding pathways. Traditional MD simulation may require significantly more simulation time to do this, because once the ligand is bound, it does not leave the pocket for some time.
For the trypsin–benzamidine system, our results support those of previous work17 in which adaptive sampling consistently samples the crystallographic pose of benzamidine. However, our featurization scheme, which neglects protein conformation, results in adaptive sampling’s failure to capture the protein’s metastable conformational states associated with binding, as the bound state, as reported by the final MSM, contains many different protein conformations (Supplementary Figure 3). The predicted binding pathway involves the ligand exploring the solvent and, once in the neighborhood of the binding site, quickly entering the pocket and binding. However, trypsin’s binding pocket is defined by three mobile protein loops, and the true binding pathway involves conformational changes that expose the binding site.32
These results suggest that for systems where the protein undergoes a conformational change associated with ligand binding, our adaptive sampling implementation fails to capture sufficient conformational hints from which to reconstruct an accurate pathway, even when the bound pose is sampled in the simulation. However, this limitation is not inherent to adaptive sampling methods, in general, and a more sophisticated featurization scheme could produce macrostates that capture both protein and ligand conformation and is an interesting topic for future work.
3.2. Adaptive Sampling Does Not Typically Sample the Bound Pose More Quickly, Especially for Realistic Systems
For both systems, both adaptive sampling and traditional MD simulations were successfully able to sample the bound state. For adaptive sampling, all of the benchmarked scoring functions obtained binding events on at least one test system, although the time to binding varied considerably between trials (Supplementary Figures 4 and 5). The only scoring function that failed to obtain binding on both test systems was counts, which resulted in all ligands partitioning into the membrane in the β2AR–dihydroalprenolol system. This result indicates that there is a significant opportunity to further refine scoring functions for adaptive sampling because counts is by far the most common metric used in prior work.
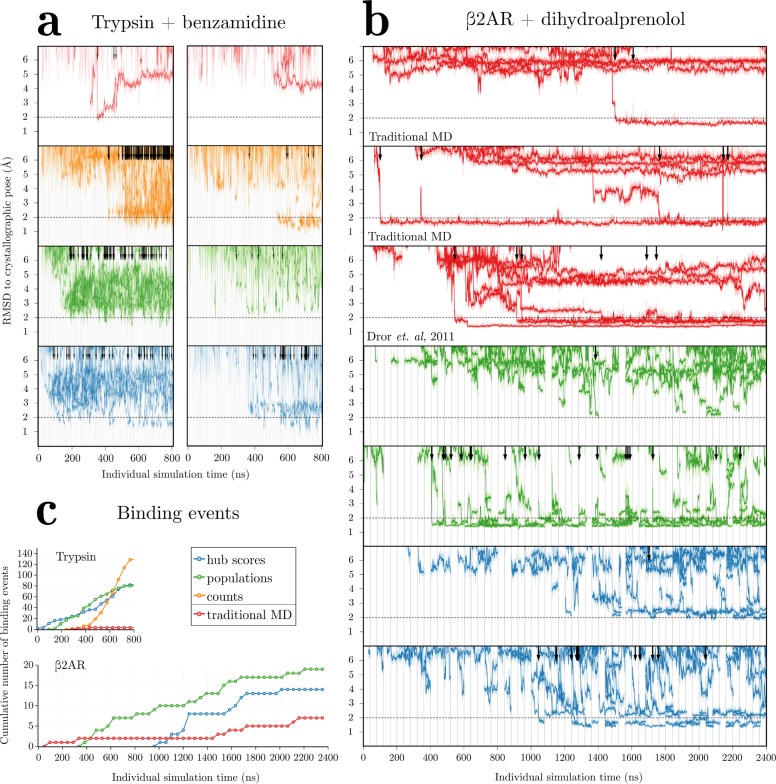
Surprisingly, adaptive sampling did not consistently sample the bound pose faster than traditional molecular dynamics simulation, especially for the β2AR system, where one traditional MD simulation samples a binding event in the first 200 ns of simulation (Figure 3b). By contrast, the fastest adaptive sampling run captured a binding event after 400 ns. Calculating the total simulation time per binding event shows that whereas adaptive sampling frequently makes more effective use of simulation time, high variance between runs prevents us from drawing stronger conclusions about the differences between adaptive sampling and traditional MD (Supplementary Figure 6).
Figure 3.
Root-mean-square deviation (RMSD) to the crystallographic pose for (a) the single benzamidine ligand present in the trypsin system for two selected trials and (b) the 10 dihydroalprenolol ligands present in the β2AR system over time for all trials, including data from a previous study.7 For adaptive sampling, vertical lines indicate resampling events every 10 (for trypsin–benzamidine) or 40 ns (for β2AR–dihydroalprenolol). All independent simulations are plotted simultaneously. Dark traces show RMSD values smoothed with a Savitsky–Golay filter with window size 5.8 ns, with unsmoothed RMSD traces shown behind in a lighter color. Binding events are defined as the ligand going from RMSD >3 Å to <2 Å and are indicated by arrows. A dotted horizontal line demarcates this 2 Å RMSD cutoff. (c) Cumulative number of binding events observed over all trials in this paper for the trypsin (top) and β2AR (bottom) systems.
It is important to note that by repeatedly resampling areas of interest and ignoring others, adaptive sampling yields trajectories that are correlated, and the number and type of binding events obtained are therefore not directly equivalent to those present in independent simulations. Researchers should perform additional validation on pathways predicted by adaptive sampling to check that these correlations did not unduly bias the results.
The performance difference between traditional MD simulation and adaptive sampling is not quite as extreme as these data suggest because traditional MD typically does not obtain a bound pose in 200 ns. Other simulations run obtained binding in anywhere from 800–2000 ns, with a total of 3/40 traditional MD runs and 5/20 previously published trajectories obtaining a ligand position with an RMSD <2 Å to the crystallographic pose in an equivalent amount of simulation time to our adaptive sampling trials.
However, unlike traditional MD, where all trajectories are wholly independent, adaptive sampling typically requires multiple simultaneous samplers that then exchange information. If there are cluster resources available for running 20 simulations simultaneously, for example, the odds of obtaining binding in at least one traditional MD simulation on this cluster are generally good, with a reasonable probability that a binding event is observed within the first microsecond or so. Adaptive sampling may not be worth the resources required if the only desired information about the protein–ligand system is the bound pose of the ligand.
3.3. Adaptive Sampling Cannot Reliably Identify Bound Poses without Follow-Up Analysis
Given that adaptive sampling seems to be able to sample the pose in simulation, we now address the issue of whether adaptive sampling can reliably identify bound poses.
Querying the final models after 60 rounds of sampling, the β2AR system finds that both runs using the hub scores criterion had the bound pose represented as one of the top three scoring clusters (of 50), whereas neither run with the populations criterion identified the pose in the top ten clusters despite repeatedly sampling the pose in the input trajectories. This agrees with previous suggestions33 that MSM predictions are highly sensitive to the parameters used to construct the model. In this case, the choice of scoring function affects result quality significantly, and other model parameters such as lag time or number of macrostates may have even more dramatic effects.
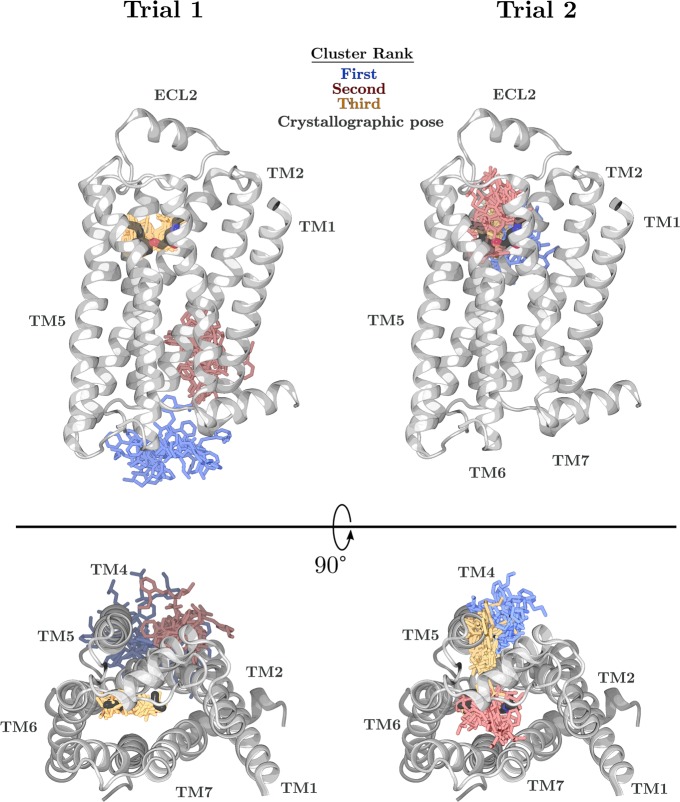
Our clustering scheme introduces an additional complication to identifying poses because the kinetic clustering step results in clusters that can be spread over large areas of the simulation box. Even if the bound pose is assigned to a given cluster, other frames assigned to that cluster could span the entire binding pocket, preventing pose identification. For example, of the three highest scoring clusters for one hub score run on β2AR, the top two have high spatial variance (Figure 4). Despite not representing the crystallographic pose, these two clusters may occupy possible binding sites because an intracellular agonist has been crystallized in approximately the same region as the top-scoring cluster,34 and the other cluster encompasses a location where cholesterol molecules are frequently present in crystal structures.
Figure 4.
Twenty ligand positions from each of the top three clusters (blue, red, and yellow, respectively) are shown for two trials of adaptive sampling on the β2AR system using the hub scores criteria for a total of 2.4 μs aggregate simulation. For each trial, the model built from 60 sampling rounds was queried for the top three scoring clusters, and the displayed frames assigned to each cluster were randomly chosen. The crystal structure is shown with the protein as gray ribbons and the ligand as black sticks.
The MSMs used in adaptive sampling are constructed primarily to inform subsequent rounds of sampling and are not intended to be high-quality models. Because the bound pose is indeed sampled in all of our adaptive sampling runs for the β2AR system, postrun analysis on the set of trajectories that uses geometric clustering only, incorporates knowledge of the expected binding site, or involves more sophisticated kinetic calculation would most likely be able to identify the pose. Future work could improve predictions by selecting clusters that have features likely to be characteristic of bound poses, such as low spatial variance or multiple hydrogen bonds.
3.4. Adaptive Sampling Better Characterizes Possible Allosteric Sites
Our benchmark simulations reveal another advantage of adaptive sampling: Binding sites away from the most ligand-accessible areas, such as the water-exposed regions of the β2AR system, are more rapidly sampled. Often, ligands may bind at locations on the protein other than the canonical, or orthosteric, binding site. These “allosteric” sites are of increasing interest as pharmaceutical targets, as differences in the orthosteric pocket between receptor subtypes can be subtle and targeting allosteric sites can thus allow for better subtype selectivity.35,36
In assessing the effectiveness of adaptive sampling at identifying allosteric sites, we quantify how frequently the ligand samples the allosteric sites found in our test systems. Because all possible or even all common allosteric sites are not characterized for β2AR, we use information about allosteric sites present in the entire family of GPCRs, of which β2AR is a member with the locations of possible allosteric sites approximated by the locations of crystallographically resolved cholesterol (and cholesterol hemisuccinate) molecules. This is reasonable because cholesterol is found in multiple, conserved binding sites on multiple GPCRs and is a hydrophobic molecule that is chemically similar to dihydroalprenolol.
Adaptive sampling using either population scores or hub scores achieves significantly greater sampling of all possible cholesterol sites compared with traditional MD simulation (Figure 5). In an equivalent amount of simulation time, the ligands in adaptive sampling simulations also sample the entire space within 5 Å of the protein more completely than traditional MD (Supplementary Figure 7).
Figure 5.
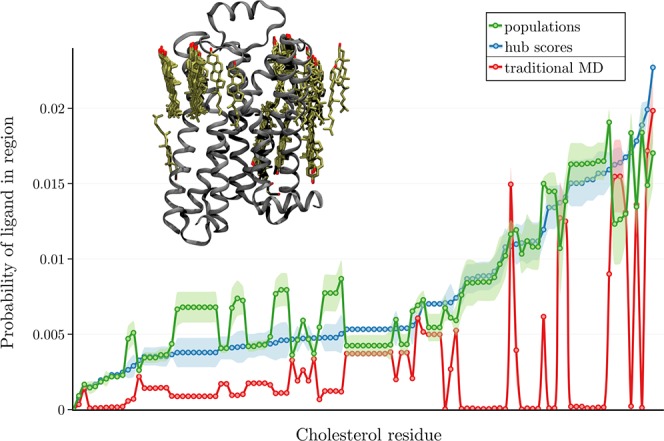
On the upper left, β2AR is shown as ribbons with sticks showing the locations of all resolved cholesterols (either as cholesterol or cholesterol hemisuccinate) in Class A GPCR structures deposited in the Protein Data Bank (PDB).48 Plotted is a sampling of each of those cholesterol locations in terms of the probability of any ligand atom occupying the region in a given frame. (See the SI.)
This improvement in sampling also holds true for the trypsin system. Again, the ligands in adaptive sampling simulations also sample the space within 5 Å of the protein more completely than an equivalent amount of traditional MD (Supplementary Figure 8).
4. Discussion
4.1. Thinking about Adaptive Sampling in the Context of the Exploration–Exploitation Dilemma
Adaptive sampling is most commonly used in the field of robotic remote sensing, where a robot or team of robots is tasked with finding a small number of interesting regions in a large, poorly characterized environment.37 When solving this exploration problem, the robots have the choice of either visiting regions in the neighborhood of the currently known best region (exploitation) or minimizing uncertainty in unknown parts of the space (exploration).38 A well known review by Thrun gives an overview of this trade-off in the context of reinforcement learning.39
Exploring the configuration space of a protein–ligand system with the goal of identifying (or at the very least, sampling) bound poses is a similar problem on a much smaller physical scale. Adaptive sampling methods here face the same exploration–exploitation dilemma, where a trade-off must be made between searching for new binding sites and interactions (exploration) or resampling already seen locations (exploitation) that may provide more accurate bound poses or progress further along binding pathways. This trade-off has been previously recognized in the context of protein conformational sampling16,40 but has not yet been discussed for the ligand-binding problem.
Some computational methods for the ligand-binding problem choose to emphasize exploration to an extreme, mapping out the entire protein surface probabilistically in terms of where the ligand can bind.41,42 Others employ a more exploitation-based approach using a knowledge-based metric such as RMSD to bound pose or ligand distance to binding pocket residues to determine which states should be resampled.21,32,43,44 Human intuition can also be used to manually determine which states are of interest for resampling.45
In cases where the binding site of the ligand is treated as an unknown, the scoring functions that have been used previously for adaptive sampling of protein–ligand binding tend to favor exploration over exploitation. This is also true of the hub score we have introduced, as newly discovered states frequently have the lowest hub score.
To encourage exploitation over exploration, one needs a scoring function that can recognize when a state is likely to be on the binding pathway. For our purposes, an effective scoring function (1) does not require any a priori knowledge of binding pose or site, (2) should avoid biasing the simulations toward the sampling of unlikely, or worse, unphysical pathways, and (3) produces superior sampling for the quantity of interest relative to traditional MD simulation.
The scoring function used is roughly equivalent to the progress coordinate used in path-sampling methods, but applications of these methods to protein–ligand systems42,46 require knowledge of the ligand-binding site. Designing a scoring or progress metric that does meet this first criterion is complicated by the inefficiency of these methods in sampling high-dimensional spaces,47 and reducing the dimensionality of this space requires the researcher to make some assumptions of the nature of the binding pathway.
Designing such a function for either adaptive or path-sampling contexts without prior knowledge of where the ligand binds is nontrivial but not impossible. For example, one might use the ligand’s solvent-accessible surface area (SASA), the variance of all ligand positions assigned to a macrostate, or the interaction energy between the ligand and the protein. Indeed, prior work has balanced exploration–exploitation trade-offs for sampling protein conformations by incorporating physical properties such as protein SASA, free energy, or experimental measurements.16,40
However, adaptive sampling algorithms that favor exploitation must have the ability to identify when exploitation has failed to know when more exploration is necessary,39 a challenging thing for a problem where even expert medicinal chemists cannot readily determine what differentiates true bound poses from decoys. Developing a scoring function that better handles this dilemma is an interesting subject for future work.
4.2. Rationalizing Adaptive Sampling’s Performance Relative to Traditional MD Simulation
It is no surprise that a method that favors exploration better explores possible ligand locations compared with traditional MD simulation. For systems where getting the ligand in the vicinity of the binding pocket is sufficient for binding, adaptive sampling can be expected to outperform traditional MD because it especially excels at obtaining ligand sampling broadly across the protein surface. This is why adaptive sampling is a win compared with traditional MD for the trypsin–benzamidine system (as seen in both our implementation and that of others). This binding process does not require consistent sampling of some intermediate state (exploitation). Instead, the ligand binds quickly once in the neighborhood of the binding site (exploration).
For β2AR and dihydroalprenolol, however, finding the exact bound pose requires considerable exploitation of an intermediate state in the binding pathway. In this system, the key intermediate in binding is in the extracellular vestibule,7 where the ligand may dwell for quite some time before finally assuming the bound pose (see traditional MD RMSD traces in Figure 3b). This intermediate state must therefore be sampled repeatedly to have a reasonable chance of seeing a binding event.
In addition to using scoring criteria that may fail to recognize relevant intermediate states, our adaptive sampling protocol enforces diversity among the samplers at the system building step when placing the first ligand. Although a perfect implementation might, in this case, have all samplers focusing on the intermediate state, in reality the models are quite underdetermined, and allowing all samplers to resample a single state results in a substantial chance of wasting sampling on irrelevant ligand positions.
In the β2AR test case, enforcing diversity in the built systems results in the ligand being removed from the vestibule to sample some other location of interest. As a result, adaptive sampling results in a much lower ligand dwell time in the vestibule and thus fewer binding events for β2AR (Supplementary Figure 9).
Although adaptive sampling is not consistently the best approach for quickly identifying bound states, it excels in sampling many binding events and characterizing pathways, even if the exact bound state is not found. Our adaptive sampling runs that obtained binding events sampled many more binding events than the traditional MD simulations.
In traditional MD simulation, once a ligand has bound, it rarely unbinds due to the higher energy barrier for unbinding. This prevents sampling of multiple binding events in a single simulation. During adaptive sampling, the ligand is frequently repositioned and can be removed from the binding site to sample other locations of interest, resulting in many more binding events. This results in a better characterization of the binding process, with less uncertainty in the transitions between states along the pathway but less time spent in the bound state, especially for β2AR (Supplementary Figure 10).
Additionally, adaptive sampling’s ability to better sample all ligand locations close to the protein means that it holds promise for identifying regions where the ligand has a reasonable dwell time. Docking, follow-up simulation, or other analyses may then be performed on those locations to produce possible bound poses of that ligand at that potential site.
5. Conclusions
Whereas it may be initially surprising that adaptive sampling may offer little benefit in terms of getting ligands to bind faster, putting the problem of ligand binding in the context of the exploration–exploitation dilemma provides an explanation. Getting ligands to bind in simulation is algorithmically equivalent to exploring some large, underdetermined space (in this case, the space consists of all possible protein–ligand interactions) to find a small number of regions of interest (ligand-binding sites), with a high cost of sampling (running simulations is slow).
Adaptive sampling with the scoring functions typically used in the absence of a known binding site is an inherently exploration-focused method. This results in a longer time to obtain binding for systems such as β2AR with a key intermediate state that must be resampled.
However, for scientific questions that require the broad exploration of protein–ligand configuration space, such as the identification of possible allosteric binding sites, adaptive sampling offers a substantial benefit to the researcher, as its focus on exploration results in much broader sampling of ligand locations near the protein, in general. Likewise, adaptive sampling methods excel at providing an accurate description of ligand-binding pathways.
Scoring functions that favor exploitation represent a promising area of future work. Indeed, one might be able to combine the ability of adaptive sampling methods to rapidly identify potential ligand-binding sites with sampling approaches that are better able to exploit these sites to get true bound poses within them.
Acknowledgments
We thank Greg Bowman and Naomi Latorraca for helpful suggestions and discussion.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00913.
Details of our methodology and additional figures (PDF)
This work was supported by NIH grant R01GM127359 (R.O.D.), NIH Biophysics Training Grant GM008294 (R.M.B.), National Science Foundation Graduate Research Fellowship award number DGE1656518 (R.M.B.), and an NVIDIA Fellowship (R.M.B.).
The authors declare no competing financial interest.
Supplementary Material
References
- Pan A. C.; Borhani D. W.; Dror R. O.; Shaw D. E. Molecular determinants of drug-receptor binding kinetics. Drug Discovery Today 2013, 18, 667–673. 10.1016/j.drudis.2013.02.007. [DOI] [PubMed] [Google Scholar]
- Schuetz D. A.; de Witte W. E. A.; Wong Y. C.; Knasmueller B.; Richter L.; Kokh D. B.; Sadiq S. K.; Bosma R.; Nederpelt I.; Heitman L. H.; Segala E.; Amaral M.; Guo D.; Andres D.; Georgi V.; Stoddart L. A.; Hill S.; Cooke R. M.; De Graaf C.; Leurs R.; Frech M.; Wade R. C.; de Lange E. C. M.; IJzerman A. P.; Müller-Fahrnow A.; Ecker G. F. Kinetics for Drug Discovery: an industry-driven effort to target drug residence time. Drug Discovery Today 2017, 22, 896–911. 10.1016/j.drudis.2017.02.002. [DOI] [PubMed] [Google Scholar]
- Klepeis J. L.; Lindorff-Larsen K.; Dror R. O.; Shaw D. E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009, 19, 120–127. 10.1016/j.sbi.2009.03.004. [DOI] [PubMed] [Google Scholar]
- Shan Y.; Kim E. T.; Eastwood M. P.; Dror R. O.; Seeliger M. A.; Shaw D. E. How does a drug molecule find its target binding site?. J. Am. Chem. Soc. 2011, 133, 9181–9183. 10.1021/ja202726y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buch I.; Giorgino T.; De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 10184–9. 10.1073/pnas.1103547108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decherchi S.; Berteotti A.; Bottegoni G.; Rocchia W.; Cavalli A. The ligand binding mechanism to purine nucleoside phosphorylase elucidated via molecular dynamics and machine learning. Nat. Commun. 2015, 6, 6155. 10.1038/ncomms7155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror R. O.; Pan A. C.; Arlow D. H.; Borhani D. W.; Maragakis P.; Shan Y.; Xu H.; Shaw D. E. Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 13118–13123. 10.1073/pnas.1104614108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror R. O.; Green H. F.; Valant C.; Borhani D. W.; Valcourt J. R.; Pan A. C.; Arlow D. H.; Canals M.; Lane J. R.; Rahmani R.; Baell J. B.; Sexton P. M.; Christopoulos A.; Shaw D. E. Structural basis for modulation of a G-protein-coupled receptor by allosteric drugs. Nature 2013, 503, 295–9. 10.1038/nature12595. [DOI] [PubMed] [Google Scholar]
- Kahn H.; Harris T. E. Estimation of Particle Transmission by Random Sampling. National Bureau of Standards Applied Mathematics Series 1951, 12, 27–30. [Google Scholar]
- Chong L. T.; Saglam A. S.; Zuckerman D. M. Path-sampling strategies for simulating rare events in biomolecular systems. Curr. Opin. Struct. Biol. 2017, 43, 88–94. 10.1016/j.sbi.2016.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuckerman D. M.; Chong L. T. Weighted Ensemble Simulation: Review of Methodology, Applications, and Software. Annu. Rev. Biophys. 2017, 46, 43–57. 10.1146/annurev-biophys-070816-033834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacci M.; Vitalis A.; Caflisch A. A molecular simulation protocol to avoid sampling redundancy and discover new states. Biochim. Biophys. Acta, Gen. Subj. 2015, 1850, 889–902. 10.1016/j.bbagen.2014.08.013. [DOI] [PubMed] [Google Scholar]
- Pronk S.; Bowman G. R.; Hess B.; Larsson P.; Haque I. S.; Pande V. S.; Pouya I.; Beauchamp K.; Kasson P. M.; Lindahl E. Copernicus: A New Paradigm for Parallel Adaptive Molecular Dynamics. 2011 International Conference for High Performance Computing, Networking, Storage and Analysis (SC) 2011, 1–10, 1–10. 10.1145/2063384.2063465. [DOI] [Google Scholar]
- Preto J.; Clementi C. Fast recovery of free energy landscapes via diffusion-map-directed molecular dynamics. Phys. Chem. Chem. Phys. 2014, 16, 19181–19191. 10.1039/C3CP54520B. [DOI] [PubMed] [Google Scholar]
- Zhou T.; Caflisch A. Free energy guided sampling. J. Chem. Theory Comput. 2012, 8, 2134–2140. 10.1021/ct300147t. [DOI] [PubMed] [Google Scholar]
- Zimmerman M. I.; Bowman G. R. FAST Conformational Searches by Balancing Exploration/Exploitation Trade-Offs. J. Chem. Theory Comput. 2015, 11, 5747–5757. 10.1021/acs.jctc.5b00737. [DOI] [PubMed] [Google Scholar]
- Doerr S.; De Fabritiis G. On-the-fly learning and sampling of ligand binding by high-throughput molecular simulations. J. Chem. Theory Comput. 2014, 10, 2064–2069. 10.1021/ct400919u. [DOI] [PubMed] [Google Scholar]
- Doerr S.; Harvey M. J.; Noe F.; De Fabritiis G. HTMD: High-Throughput Molecular Dynamics for Molecular Discovery. J. Chem. Theory Comput. 2016, 12, 1845–1852. 10.1021/acs.jctc.6b00049. [DOI] [PubMed] [Google Scholar]
- Lawrenz M.; Shukla D.; Pande V. S. Cloud computing approaches for prediction of ligand binding poses and pathways. Sci. Rep. 2015, 5, 7918. 10.1038/srep07918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger-Tal O.; Nathan J.; Meron E.; Saltz D. The exploration-exploitation dilemma: A multidisciplinary framework. PLoS One 2014, 9, e95693. 10.1371/journal.pone.0095693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tran D. P.; Takemura K.; Kuwata K.; Kitao A. Protein-Ligand Dissociation Simulated by Parallel Cascade Selection Molecular Dynamics. J. Chem. Theory Comput. 2018, 14, 404–417. 10.1021/acs.jctc.7b00504. [DOI] [PubMed] [Google Scholar]
- Pérez-Hernández G.; Paul F.; Giorgino T.; De Fabritiis G.; Noé F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Schwantes C. R.; Pande V. S. Improvements in Markov State Model construction reveal many non-native interactions in the folding of NTL9. J. Chem. Theory Comput. 2013, 9, 2000–2009. 10.1021/ct300878a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane T. J.; Bowman G. R.; Beauchamp K.; Voelz V. A.; Pande V. S. Markov State model reveals folding and functional dynamics in ultra-long MD trajectories. J. Am. Chem. Soc. 2011, 133, 18413–18419. 10.1021/ja207470h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan M. P.; Sultan M. M.; Hernández C. X.; Husic B. E.; Eastman P.; Schwantes C. R.; Beauchamp K. A.; McGibbon R. T.; Pande V. S. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophys. J. 2017, 112, 10–15. 10.1016/j.bpj.2016.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz J.-H.; Wu H.; Sarich M.; Keller B.; Senne M.; Held M.; Chodera J. D.; Schütte C.; Noé F. Markov models of molecular kinetics: generation and validation. J. Chem. Phys. 2011, 134, 174105. 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- Sarich M.; Noé F.; Schütte C. On the Approximation Quality of Markov State Models. Multiscale Model. Simul. 2010, 8, 1154–1177. 10.1137/090764049. [DOI] [Google Scholar]
- Weber J. K.; Pande V. S. Characterization and rapid sampling of protein folding Markov state model topologies. J. Chem. Theory Comput. 2011, 7, 3405–3411. 10.1021/ct2004484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson A.; Brooks C. L. Quantifying hub-like behavior in protein folding networks. J. Chem. Theory Comput. 2012, 8, 3044–3052. 10.1021/ct300537s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong C. F.; McCammon J. A. Dynamics and Design of Enzymes and Inhibitors. J. Am. Chem. Soc. 1986, 108, 3830–3832. 10.1021/ja00273a048. [DOI] [Google Scholar]
- Guillain F.; Thusius D. The use of Proflavin as an Indicator in Temperature-Jump Studies of the Binding of a Competitive Inhibitor to Trypsin. J. Am. Chem. Soc. 1970, 92, 5534–5536. 10.1021/ja00721a051. [DOI] [PubMed] [Google Scholar]
- Plattner N.; Noé F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015, 6, 7653. 10.1038/ncomms8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson A. Mapping the ligand binding landscape. Biophys. J. 2018, 115, 1707–1719. 10.1016/j.bpj.2018.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X.; Ahn S.; Kahsai A. W.; Meng K. C.; Latorraca N. R.; Pani B.; Venkatakrishnan A. J.; Masoudi A.; Weis W. I.; Dror R. O.; Chen X.; Lefkowitz R. J.; Kobilka B. K. Mechanism of intracellular allosteric β 2 AR antagonist revealed by X-ray crystal structure. Nature 2017, 548, 480–484. 10.1038/nature23652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christopoulos A. Allosteric Binding Sites on Cell-Surface Receptors: Novel Targets for Drug Discovery. Nat. Rev. Drug Discovery 2002, 1, 198–210. 10.1038/nrd746. [DOI] [PubMed] [Google Scholar]
- Rees S.; Morrow D.; Kenakin T. GPCR drug discovery through the exploitation of allosteric drug binding sites. Recept. Channels 2002, 8, 261–268. 10.1080/10606820214640. [DOI] [PubMed] [Google Scholar]
- Low K. H.; Gordon G. J.; Dolan J. M.; Khosla P. Adaptive Sampling for Multi-Robot Wide-Area Exploration. 2007 IEEE International Conference on Robotics and Automation 2007, 755–760. 10.1109/ROBOT.2007.363077. [DOI] [Google Scholar]
- Martinez-Cantin R.; De Freitas N.; Brochu E.; Castellanos J.; Doucet A. A Bayesian exploration-exploitation approach for optimal online sensing and planning with a visually guided mobile robot. Autonomous Robots 2009, 27, 93–103. 10.1007/s10514-009-9130-2. [DOI] [Google Scholar]
- Thrun S.The Role of Exploration in Learning Control. In Handbook of Intelligent Control: Neural, Fuzzy, and Adaptive Approaches; White D. A., Ed.; VanNostrand Reinhold: New York, 1992; pp 527–554. [Google Scholar]
- Perez A.; Morrone J. A.; Dill K. A. Accelerating physical simulations of proteins by leveraging external knowledge. Wiley Interdisciplinary Reviews: Computational Molecular Science 2017, 7, e1309. 10.1002/wcms.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guvench O.; MacKerell A. D. Computational fragment-based binding site identification by ligand competitive saturation. PLoS Comput. Biol. 2009, 5, e1000435. 10.1371/journal.pcbi.1000435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson A.; Lotz S. D. Ligand Release Pathways Obtained with WExplore: Residence Times and Mechanisms. J. Phys. Chem. B 2016, 120, 5377. 10.1021/acs.jpcb.6b04012. [DOI] [PubMed] [Google Scholar]
- Zwier M. C.; Pratt A. J.; Adelman J. L.; Kaus J. W.; Zuckerman D. M.; Chong L. T. Efficient Atomistic Simulation of Pathways and Calculation of Rate Constants for a Protein–Peptide Binding Process: Application to the MDM2 Protein and an Intrinsically Disordered p53 Peptide. J. Phys. Chem. Lett. 2016, 7, 3440–3445. 10.1021/acs.jpclett.6b01502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan M.; Liu N.; Zhou W.; Li D.; Yang M.; Hou T. Structural Diversity of Ligand-Binding Androgen Receptors Revealed by Microsecond Long Molecular Dynamics Simulations and Enhanced Sampling. J. Chem. Theory Comput. 2016, 12, 4611. 10.1021/acs.jctc.6b00424. [DOI] [PubMed] [Google Scholar]
- Stanley N.; Pardo L.; Fabritiis G. D. The pathway of ligand entry from the membrane bilayer to a lipid G protein-coupled receptor. Sci. Rep. 2016, 6, 22639. 10.1038/srep22639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teo I.; Mayne C. G.; Schulten K.; Lelièvre T. Adaptive Multilevel Splitting Method for Molecular Dynamics Calculation of Benzamidine-Trypsin Dissociation Time. J. Chem. Theory Comput. 2016, 12, 2983–2989. 10.1021/acs.jctc.6b00277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson A.; Brooks C. L. WExplore: Hierarchical exploration of high-dimensional spaces using the weighted ensemble algorithm. J. Phys. Chem. B 2014, 118, 3532–3542. 10.1021/jp411479c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The protein data bank. Nucleic acids research 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.