Pearl-Necklace-Like Local Ordering Drives Polypeptide Collapse

Abstract

The collapse of the polypeptide backbone is an integral part of protein folding. Using polyglycine as a probe, we explore the nonequilibrium pathways of protein collapse in water. We find that the collapse depends on the competition between hydration effects and intrapeptide interactions. Once intrapeptide van der Waal interactions dominate, the chain collapses along a nonequilibrium pathway characterized by formation of pearl-necklace-like local clusters as intermediates that eventually coagulate into a single globule. By describing this coarsening through the contact probability as a function of distance along the chain, we extract a time-dependent length scale that grows in a linear fashion. The collapse dynamics is characterized by a dynamical critical exponent z ≈ 0.5 that is much smaller than the values of z = 1–2 reported for nonbiological polymers. This difference in the exponents is explained by the instantaneous formation of intrachain hydrogen bonds and local ordering that may be correlated with the observed fast folding times of proteins.

Introduction

Changing the solvent condition from good to poor renders an extended polymer to undergo a collapse transition by forming a compact globule.^1,2 Both experiments^3,4 and simulations^5,6 indicate that a protein also experiences such a collapse transition while folding into its native state. However, the nonequilibrium dynamics of the collapse of proteins is only poorly understood and an active research topic.⁷ Most previous studies consider only the hydrophobicity of apolar side chains of amino acids in a protein as the driving force for its collapse.^8,9 In the present paper, we focus instead on the contributions by intrapeptide interactions, present even for residues with no or only weakly hydrophobic side chains¹⁰⁻¹³ where the collapse-driving forces are not necessarily proportional to the exposed surface. Our test system is polyglycine and has been chosen to connect our work with recent studies of homopolymer collapse dynamics¹⁴⁻¹⁷ that found nonequilibrium scaling laws as known for generic coarsening phenomena.¹⁸ Our hope is to establish such scaling laws also for the collapse of proteins. As a first stride toward this goal, here, we explore the kinetics of the collapse of polyglycine.

The collapse of homopolymers was first described by de Gennes’ seminal “sausage” model,¹⁹ but today, the phenomenological “pearl-necklace” picture by Halperin and Goldbart²⁰ is more commonly used, both for flexible^{14,16,17,21−25} and semiflexible polymer models.^26,27 In this picture, the collapse begins with nucleation of small local clusters (of monomers) leading to formation of an interconnected chain of (pseudo-) stable clusters, that is, the pearl-necklace intermediates. These clusters grow by eating up the unclustered monomers from the chain and subsequently coalesce, leading eventually to a single cluster. Finally, monomers within this final cluster rearrange to form a compact globule.

Of central interest in this context is the scaling of the collapse time τ_c with the degree of polymerization N (the number of monomers). While power-law scaling of the form

1

where z is the equilibrium dynamic critical exponent, has been firmly established, there is no consensus on the value of z. Molecular dynamics (MD) simulations provide much smaller values (z ≈ 1) than Monte Carlo (MC) simulations (z ≈ 2). This difference is often explained with the presence of hydrodynamics in the MD simulations, but a z value of 1 has been reported recently also for MC simulations.¹⁶ The pearl-necklace stage or the cluster growth kinetics can be understood by monitoring the time (t) dependence of the mean cluster size C_s(t), the relevant length scale. By drawing analogy with coarsening ferromagnets, it has been shown that scaling of the form

2

with growth exponent α_c = 1 holds for flexible homopolymers.^14,16

Protein collapse is much less understood. While it has been shown by modeling a protein as a semiflexible heteropolymer that the equilibrium scaling of the radius of gyration R_g with N is random-coil-like (R_g ∼ N^3/5) in a good solvent and globule-like (R_g ∼ N^1/3) in a poor solvent,^28,29 there have been few attempts to explore nonequilibrium collapse pathways,^30,31 and the corresponding scaling laws are not known. In order to probe the existence of such nonequilibrium scaling laws in protein collapse, we have simulated polyglycine chains (Gly)_N of various numbers N of residues. This choice allows us to probe in a systematic way the collapse of the polypeptide chain, considering only homopolymers built from the simplest amino acid, namely, glycine. Our results show that, in water, there is a tug of war between collapse-disfavoring hydration effects and collapse-favoring intrapeptide interactions. For longer chains (N ≥ 15), the intrapeptide interactions win over the hydration effect leading to a collapse, making water in practice a poor solvent. We use these longer polyglycine chains to shed light on the collapse kinetics, with an emphasis on the presence of nonequilibrium scaling laws. Our results from all-atom MD simulations in the NVT ensemble using a hydrodynamics preserving thermostat suggest a collapse mechanism that relies on fast local ordering by formation of pearl-necklace structures, which eventually merge into a single globule. This process is characterized by a dynamic critical exponent z ≈ 0.5 much smaller than the exponents z = 1–2 observed for nonbiological polymers, and we speculate that this quicker local ordering during collapse enables the fast folding times seen in proteins.

Model and Methods

We construct (Gly)_N molecules with hydrogenated N-terminus (−NH2) and C-terminus (−COOH). All-atom MD simulations are performed using standard GROMACS 5.0.2 tools, while CHARMM22 with CMAP corrections^32,33 is used for interactions between the atoms. For studying the collapse dynamics, we first prepare an extended chain in the random-coil phase at 1500 K. This follows solvation of this extended chain in a simple cubic box with water (modeled by the TIP3P model³⁴). The final MD run is performed at the desired quench temperature T_q = 290 K, which is lower than 310 K, roughly the collapse transition temperature of (Gly)_N in water. The size of the box and the number of water molecules, of course, are dependent on N and are so chosen that the number density of water molecules is the same for all N. For the smallest N, that is, for N = 20, the default box size is 4.2 nm. Subsequently, the box sizes for longer chains are determined using the scaling relation R_g ∼ N^3/5 for the radius of gyration discussed below. The size of the boxes should not have much role in the collapse provided that the two ends of the chain do not interact while using the periodic boundary condition. However, the number density of water molecules is supposed to play a role, which we keep the same for all N. For N = 20, the total number of water molecules used is 2000 giving a number density of 32 per nm^–3, which is maintained for all N. After the solvation, we run our MD simulations using the velocity Verlet integration scheme with a time step δt of 2 fs in the NVT ensemble using the Nosé–Hoover thermostat that conserves linear momentum and thus is believed to be sufficient for preserving hydrodynamic effects.³⁵ Here, we use chains of lengths N ∈ [20,50,75,100,150,200], and for each N, we generate 50 different initial configurations in the random-coil-like phase, except for N = 200 where this number is 15. Independent simulations starting from these different initial conditions are performed for every N. All these simulations are run up to time t_f, which is 10 ns for N = 20, 20 ns for N ∈ [50,150], and 25 ns for N = 200. Unless otherwise mentioned, the results presented subsequently are all averaged over the aforesaid number of independent simulations for respective N.

In the following, we briefly discuss three standard observables that we use for the analyses of our simulation data. (i) The squared radius of gyration for a polymer of length N (the number of monomers) is calculated as

3

For (Gly)_N, the chain length is determined from N, the number of residues or repeating units that contain a fixed set of atoms. Thus, R_g² for (Gly)_N is calculated considering all the atoms present in all the residues. However, the scaling can still be checked in terms N, as is done here. (ii) The static structure factor is calculated as

4

where is the scattering wave vector. In general, S() is the Fourier transform of the radial distribution function and is directly comparable with the experimentally observed X-ray scattering. For an isotropic system, as in the case here, everything depends on q = | |. As explained above, in the case for measuring R_g², for S(), too, we use all the atoms in all the residues. (iii) Hydrogen bonds are calculated using the standard GROMACS tool gmx hbond. It considers all possible donors and acceptors and decides for the existence of a hydrogen bond if the distance between them is less than 0.35 nm and the hydrogen-donor-acceptor angle is less than 30°.

Results

Evolution of Short Chains

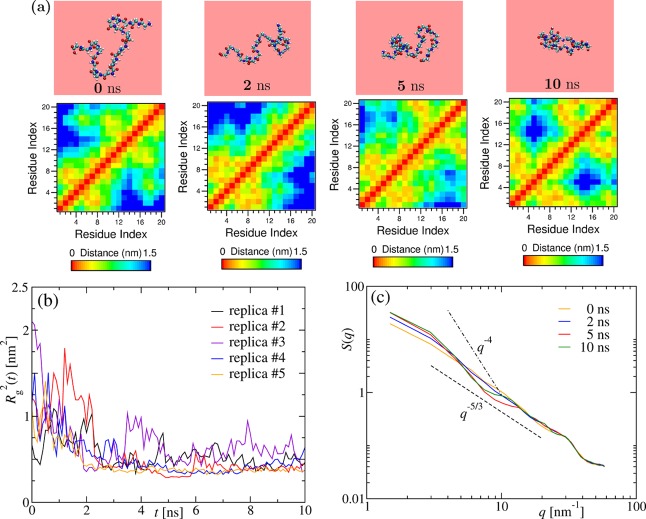
We begin our analysis with a rather short chain, that is, (Gly)₂₀. The time evolution snapshots during the collapse in water at a temperature T_q = 290 K, well below the corresponding collapse transition temperature, are shown in Figure 1a. In a protein, collapse leads eventually to folding characterized by formation of distinct native contacts among the residues. We show for this reason in the lower panel the residue contact maps where we define two residues as being in contact if they are within a distance of r_c = 1.5 nm. The red stripe along the diagonals depicts the self-contacts. The size of the extended (Gly)₂₀ chain is 2.0 nm; thus, almost all the mutual distances between the residues fall under r_c. This makes it difficult to capture segregation or formation of any local structures on length scales comparable to r_c. Only late in the trajectories do we find a signature for loop formation, which is also apparent in the snapshot at t = 10 ns. The emergence of such a loop is due to a competition between the hydration effects and the intrapeptide interactions leading to residue–residue contacts along the chain, although there are trapped water molecules. The interplay can be deduced from the nonmonotonous behavior of the squared radius of gyration R_g² as a function of time in Figure 1b, obtained from five different replicas chosen randomly out of the total 50 independent simulations. Note that, for all the cases, R_g² decays eventually to the equilibrium value.

Figure 1.

Time evolution of a short polypeptide. (a) The upper row shows typical representative snapshots from the time evolution [of replica #1 shown in panel (b)] for the collapse of the (Gly)₂₀ chain in water at T_q = 290 K, starting from an extended state at t = 0 ns. The lower row shows the corresponding residue contact maps where two residues along the chain are in contact if the distance between them is less than 1.5 nm. (b) Time dependence of the squared radius of gyration R_g²(t) shown for five different replicas chosen randomly out of the total 50 independent simulations for (Gly)₂₀. (c) Illustration of the structural evolution of the chain during the collapse shown via structure factors S(q) averaged over 50 independent simulations for (Gly)₂₀, as a function of the modulus q = || of the wave vector , at four different times as indicated. The dashed lines with power-law decay exponents 5/3 and 4 correspond to the expected behavior for an extended chain and crumpled globule, respectively.

In order to probe further the structural evolution of the chain along the collapse of (Gly)₂₀, we calculate the static structure factor S(q) at different times. Figure 1c shows S(q) for the times corresponding to the snapshots. At t = 0 ns, within the range q ∈ [3,30] nm^–1, the chain can be described as an extended coil with S(q) ∼ q^–1/ν,³⁶ where ν = 3/5 is the critical (Flory) exponent describing the scaling of R_g ∼ N^ν for a self-avoiding polymer. With time, the decay exponent should increase from −5/3 and is expected to approach −4 in order to be consistent with the globule-like behavior of S(q) ∼ q^–4.³⁶ Although the slope in our data in Figure 2c gradually increases with time, it does not appear to approach −4. This again could be due to the still ongoing interplay between the hydration effect and the intrapeptide interactions that hinders the chain to form a compact globule; however, extending the simulations up to 20 ns does not change the overall behavior. Similar observations are made for all systems (Gly)_N having a chain length of N < 50 residue units.

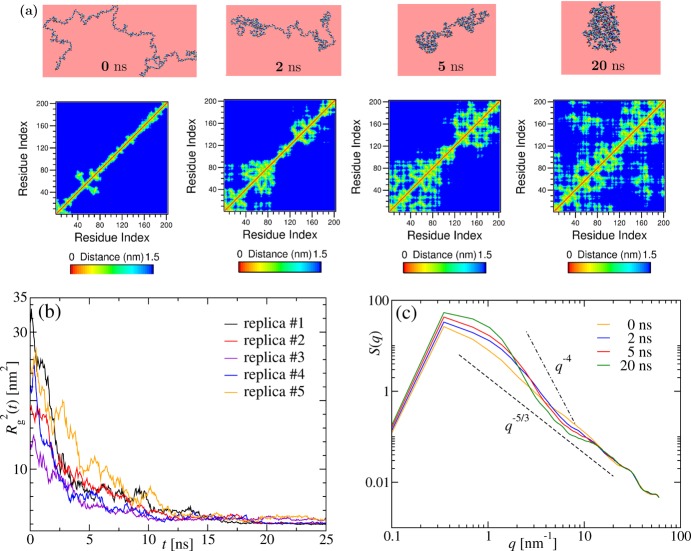
Figure 2.

Pearl-necklace formation during collapse of a long chain. (a) Same as in Figure 1a but for (Gly)₂₀₀ and correspondingly at different times, as mentioned. (b) Time dependence of the squared radius of gyration R_g²(t) obtained from five different replicas chosen randomly out of the total 15 independent simulations for (Gly)₂₀₀. (c) Structure factors S(q) averaged over the total 15 independent simulations for (Gly)₂₀₀ at times indicated in the figure. The dashed lines have the same meaning as in Figure 1c but are plotted with different prefactors.

Evolution of Long Chains

For longer chains, the collapse is more pronounced, and we finally encounter characteristic features reminiscent of the homopolymer collapse. For instance, in the upper row of Figure 2a, we present snapshots of the collapse of (Gly)₂₀₀ at T_q = 290 K. The sequence of these snapshots demonstrates a process that starts with local ordering of the residues along the chain. These local structures later merge with each other before finally forming a single globule at t = 20 ns. The emergence of these local arrangements is similar to the formation of local clusters in the pearl-necklace picture of homopolymer collapse.^{14,16,17,20,21} The resemblance becomes even more obvious when looking at the corresponding contact maps in the lower row of Figure 2a. The box-like clustering along the diagonal indicates formation of pearls along the chain (see particularly at t = 2 and 5 ns) that are reminiscent of the ones observed during the collapse of a semiflexible homopolymer in ref (27). However, we do not see the antiparallel hairpins that are associated with the diamond-shaped internal order within these boxes. An idea about the variation of these contact maps for different independent simulations and other chain lengths can be obtained from the Supporting Information.

In order to check for the presence of a competition between hydration effects and the intrapeptide interactions, we probe again the time dependence of R_g² as measured in five independent simulations. Data are presented in Figure 2b. Unlike for the shorter (Gly)₂₀ chain, the radius of gyration is now monotonically decreasing. This can be explained by the assumption that, for longer chains, the intrachain interactions overcome the hydration effects. A similar picture emerges from Figure 2c. The plots of the structure factor S(q) as a function of time demonstrate how the extended coil behavior of S(q) ∼ q^–5/3 at t = 0 ns gradually changes to a globule-like behavior of S(q) ∼ q^–4 at t = 20 ns.

Relaxation Dynamics

Next, we analyze the number of intramolecular (protein–protein n_pp) and intermolecular (protein–water n_pw) hydrogen (H) bonds. The time dependence of n_pp measured for different N and normalized by the respective values at t_f (the maximum time up to which the simulations are run; for details see the Model and Methods section) is plotted in the main frame of Figure 3a. Data for all N in Figure 3a attain a saturation value of 1 at the same time, demonstrating a reasonable overlap of the data. Similar observations can be made in panel (b), which shows that the decay of n_pw(t)/n_pw(0) to the saturation value happens at almost the same time for different N, leading again to nicely overlapping curves. In the inset of Figure 3a, the time dependence of n_pp for (Gly)₂₀ is nonmonotonous, whereas the n_pw data in the inset of Figure 3b exhibit a jump at an early time before reaching saturation. This again confirms the hydration effects for smaller chains. The overlap of the hydrogen-bond kinetics for large N (>20) implies that the collapse dynamics, that is, the presence of any scaling of the collapse time with respect to the chain length, shall not depend on the intrapeptide hydrogen bonds. Equilibrium studies, too, suggest that collapse is driven by the intrapeptide van der Waals interactions rather than the hydrogen-bond formation.⁷

Figure 3.

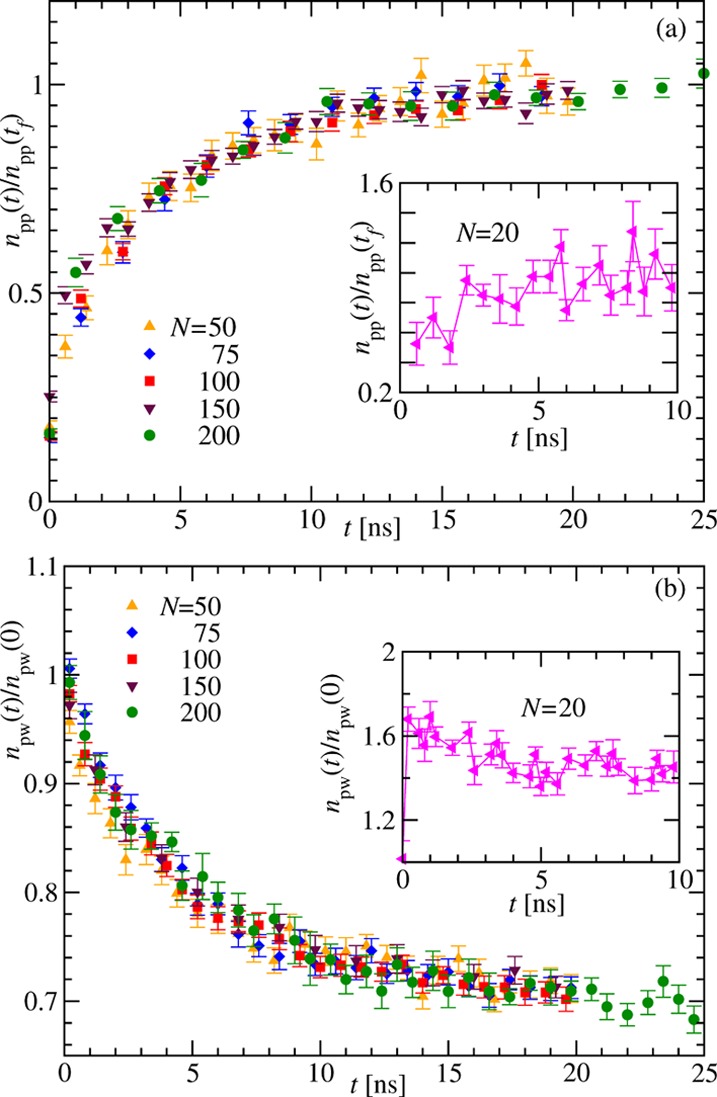
Kinetics of H bonding. (a) Time dependence of the number of protein–protein hydrogen bonds n_pp(t) during the collapse of (Gly)_N for different N. To make the curves fall within the same scale, the data is normalized with n_pp(t_f); t_f is the maximum run time the simulations are done. The inset shows the time dependence of n_pp(t) for (Gly)₂₀. (b) Same as in panel (a) but for the number of protein–water hydrogen bonds n_pw(t). Here, the normalization is done with n_pw(0). The inset shows the variation of n_pw(t) with time for (Gly)₂₀. The error bars in all the plots here correspond to the standard error of the mean calculated while averaging the data obtained from a number (mentioned in the Model and Methods section) of independent simulations.

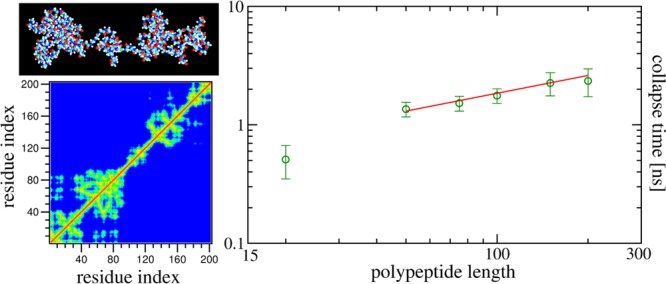
The overlap of the hydrogen-bond data does not allow one to calculate the collapse time τ_c from the time evolution of this quantity. More suitable for this purpose is the decay of the average squared radius of gyration R_g² depicted in Figure 4a. The nonoverlapping data are consistent with the respective solid lines obtained from the previously proposed fit^16,17

5

where b₀ corresponds to the value of R_g²(t) in the collapsed state and b₁ and β are associated nontrivial fitting parameters. The obtained values of β (see the inset of Figure 4a) indicate a very weak dependence on N, similar to the case of the earlier studied collapse of synthetic homopolymers.¹⁶ Although the above fit yields a collapse time τ_c, more accurate estimates can be calculated from the time when R_g²(t) has decayed to 50% of its total decay, that is, 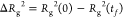. We plot the measured values of τ_c for different chain length N (including N = 20) in Figure 4b to check for scaling of the form in eq 1. Due to the competition between hydration effects and intrapeptide interactions that dominate for smaller N, one expects distinct scaling forms for small and large N. Our data indeed hint at the existence of two such scaling regions. Especially interesting is the consistency of our data for large N with the solid line having z = 0.5. This exponent suggests that the dynamics is faster than the one observed in MC simulations of nonbiological homopolymers.¹⁶ Surprisingly, it is even faster than in the case of homopolymer collapse in the presence of hydrodynamics.^22,23 We conjecture that the more rapid collapse is due to the almost instantaneous presence of intrachain hydrogen bonds that hasten local ordering; that is, once the intrachain hydrogen bonds are formed, the Cα atoms along the backbone come closer to form clusters, which in turn coalesce to finally form a single globule. This latter phase of the collapse is guided by the diffusive dynamics, which is certainly N-dependent. However, in combination with the initial N-independent phase of local pearl-necklace formation, one observes an overall collapse time that is weakly dependent on N. Simulations of longer chains would be desirable to confirm the value of z = 0.5 and the super-fast collapse mechanism in hydrogen-bonded polymers; however, such simulations were computationally too costly to be considered in the present study.

Figure 4.

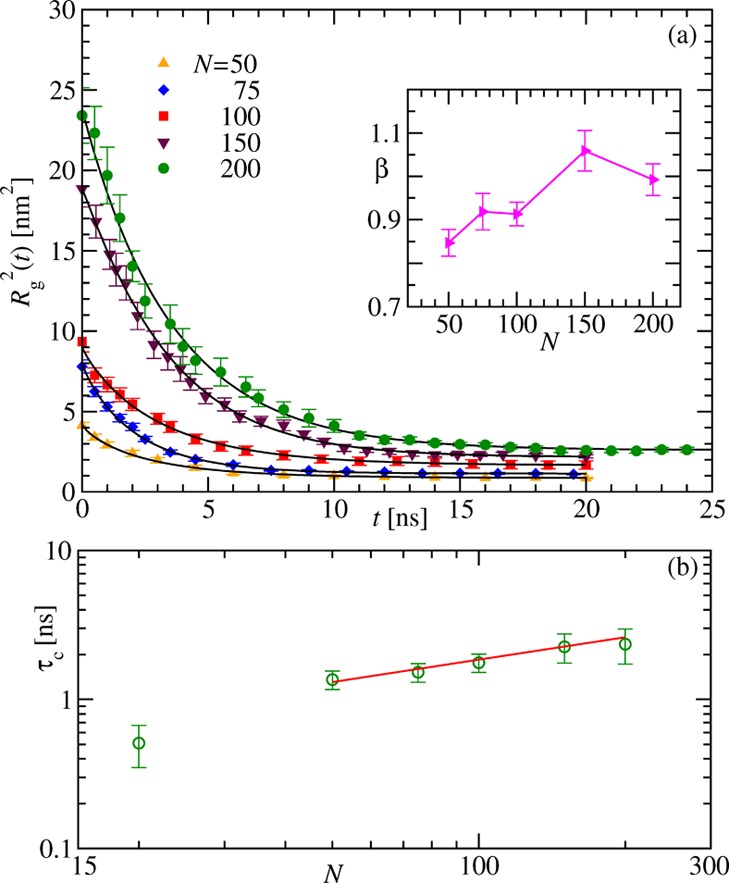
Scaling of the collapse time. (a) Variation of the average squared radius of gyration R_g²(t) with time for different chain lengths as indicated. The solid black lines are respective fits using eq 5, and the corresponding β obtained is shown as a function of N in the inset. (b) Dependence of the collapse times τ_c extracted from the time decay of R_g² on the number of residues N. The solid line represents the behavior τ_c ∼ N^z with z = 0.5. For all the data shown in the main frames, the error bars correspond to the standard error of the mean, while in the inset, they result from the fitting exercise.

Cluster Growth Kinetics

In a final step, we want to quantify the coarsening kinetics of the pearls observed in Figure 2a. A measure of the relevant length scale, that is, the mean cluster or pearl size C_s(t), can be obtained from a box plot analysis of the contact maps.²⁷ Conjecturing that the collapse is driven by the intrapeptide van der Waals attraction of the backbone, we extract C_s(t) from an analysis of the contact probability P(c_ij) as a function of the contour distance c_ij = | i – j| between any two Cα atoms at the ith and jth positions along the chain.³⁷ Two Cα atoms are said to have contact if they are within a cutoff distance r_c. Using r_c = 2.5 nm, we show in Figure 5a values of P(c_ij) calculated at different times during the collapse of (Gly)₂₀₀. These contact probabilities indicate indeed a growing length scale as their decay slows with time. At the beginning, for t = 0 ns, the chain is in the extended state and P(c_ij) decays according to a power law 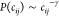with an exponent γ = 1.5, as expected in a good solvent.³⁸ As time progresses, this power-law behavior appears at larger c_ij after crossing over from a plateau-like behavior for small c_ij, which marks the local ordering along the chain. For any reasonable choice of r_c, the form of the curves stays unchanged as demonstrated in Figure 5b. Similarly, the form of the curve also does not depend on the chain length N as illustrated in the inset of Figure 5b where we use r_c = 2.5 nm and choose the point in time t = 2 ns. Results analogous to Figure 5a for N = 100 and N = 150 are presented in the Supporting Information.

Figure 5.

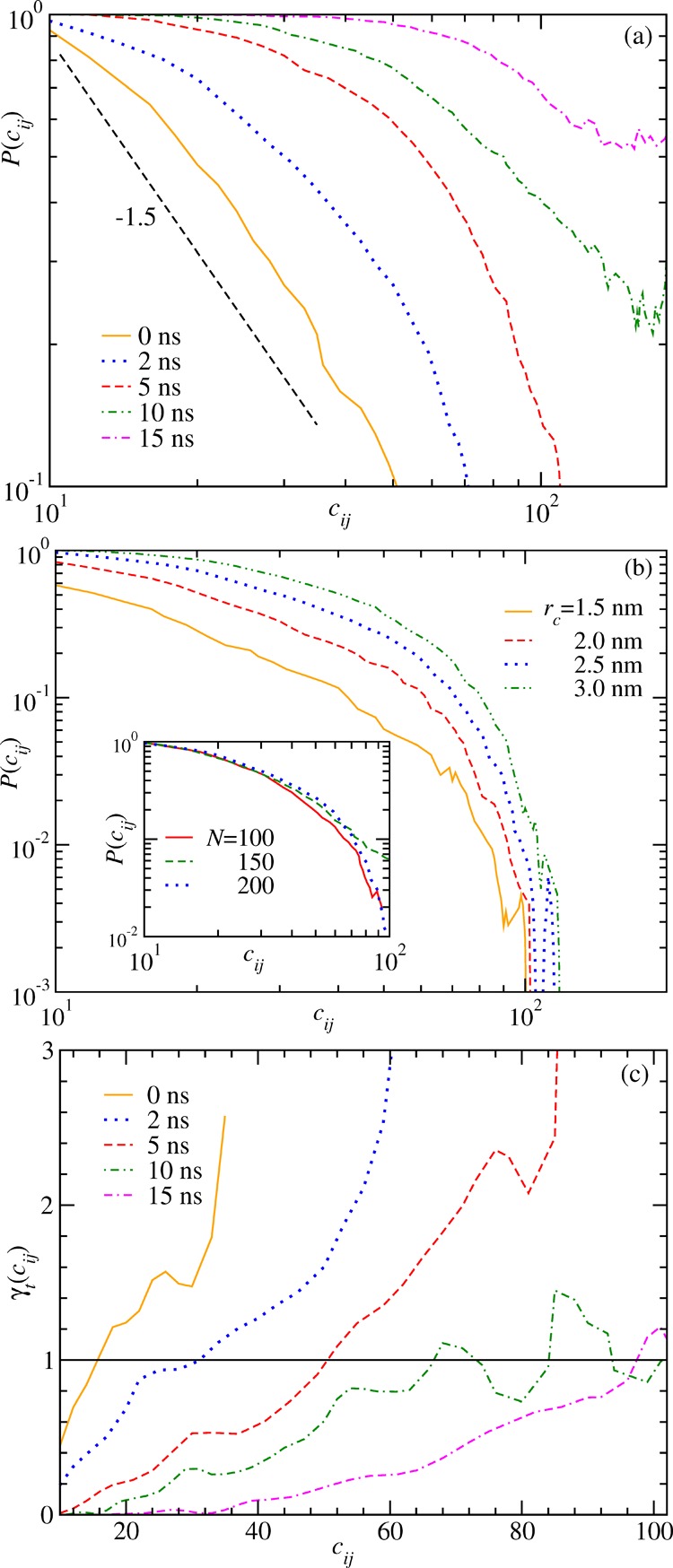
Contact probabilities along the contour of the chain. (a) Contact probability P(c_ij) calculated using the cutoff r_c = 2.5 nm as a function of the distance c_ij along the chain at five different times during collapse of (Gly)₂₀₀. The dashed line there represents a power-law decay with an exponent γ = 1.5 as expected in a good solvent.³⁸ (b) P(c_ij) at a fixed time t = 2 ns using different r_c as indicated, demonstrating the consistency of the proportionality behavior of the estimated contact probability. The inset shows P(c_ij) at t = 2 ns using r_c = 2.5 nm for different N. (c) Discrete slope γ_t obtained from eq 6 as a function of c_ij for the times presented in panel (a). The solid line is for γ_t = 1, marking the crossover value that gives the measure of the length scale C_s(t).

The crossover point in the decay of P(c_ij) as a function of c_ij is estimated from the discrete local slope calculated as³⁷

6

Plots of γ_t(c_ij) as a function of c_ij are shown Figure 5c for the data presented in Figure 5a. The crossing of the data with the γ_t = 1 line happens at larger c_ij as t increases, and thus, this crossover point gives a measure of the pearl size C_s(t). The obtained C_s(t) values for three different N are shown as a function of t on a double-log scale in the main frame of Figure 6. The flattening of the data for very large t is due to finite-size effects when no more ordering is possible due to the eventual formation of a single globule. For large t, before hitting finite-size effects, the growth resembles a power law C_s(t) = A_Nt^α_c, where the amplitude A_N depends still on the chain length N as the considered N is not large enough. Hence, P(c_ij) calculated using the same r_c will overlap with each other, a fact that is demonstrated in the inset of Figure 5b. However, since their form stays invariant in the large t regime, they apparently follow the same power law. To estimate the exponent α_c of the power-law growth (eq 2) on a double-log scale, one needs to have data ranging over several decades, which is not the case with our data for C_s(t). Thus, to distinguish the consistency of the data with either α_c = 2/3 or α_c = 1 behavior as shown in the main frame of Figure 6 by the dashed and the solid lines, respectively, is not so easy. In such cases, instead of eq 2, it is advantageous to describe the growth as

7

by considering a crossover time t₀ and cluster size C_s(t₀). This approach, originally developed for ferromagnets,³⁹ was already necessary in our earlier work for describing the collapse of nonbiological homopolymers.^14,16,17 Using the transformation

8

one finds 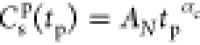, with the shifted time t_p = t – t₀. If α_c = 1 in eq 7, the transformation in eq 8 is invariant under any choice of t₀ in the post-crossover regime. This is demonstrated in the inset of Figure 4 where we plot C_s^p(t_p) as a function of t_p on a log–log scale for two different choices of t₀ as mentioned. The data for both the cases are consistent with a linear power-law behavior 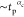having α_c = 1 as represented by the solid line there. This further consolidates our finding of a linear growth of clusters.

Figure 6.

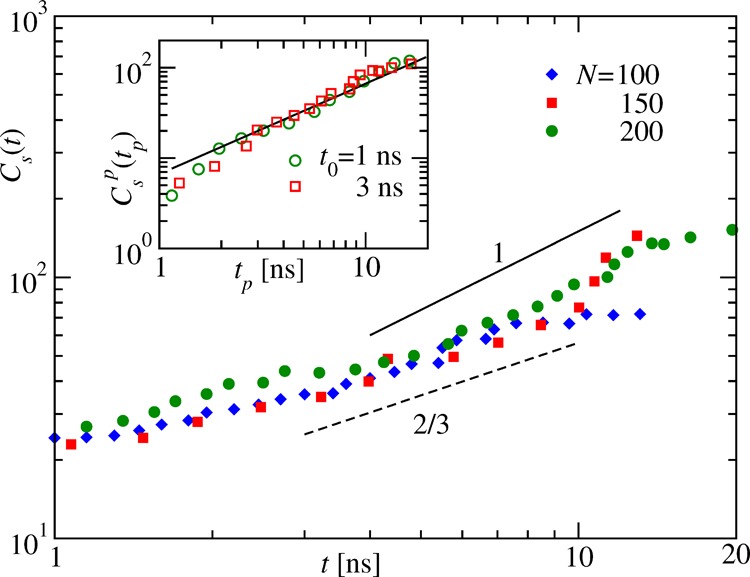
Cluster growth during the collapse. The main frame shows the growth of the mean cluster or pearl size C_s(t) with time for different N. The solid and the dashed lines represent power-law behavior C_s(t) ∼ t^α with α = 1 and 2/3, respectively. The inset shows the plot of C_s^p(t_p) as a function of the shifted time t_p = t – t₀ for N = 200 with two different choices of t₀. The solid line there represents a linear power-law behavior 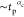with α_c = 1.

Discussion

In summary, we have investigated the nonequilibrium pathways by which polyglycine [(Gly)_N] collapses in water. For short chains, the pathway has few noticeable features and is driven by the competition between the hydration of the peptide, opposing the collapse, and the intrapeptide attractions, favoring the collapse.⁷ For chains with N > 20, the importance of hydration effects decreases, and the kinetics of hydrogen bonds indicates that van der Waals interactions of the backbone dominate⁷ and drive the collapse. The nonequilibrium intermediates seen during the collapse exhibit local ordering or clustering that is analogous to the phenomenological pearl-necklace picture known to be valid for the earlier studied coarse-grained homopolymer models.²⁰ Using the contact probability of the Cα atoms in the backbone, we extract a relevant dynamic length scale, that is, cluster size C_s, that as in simple homopolymer models grows linearly with time (C_s ∼ t).¹⁶ We believe that this linear growth is a result of the Brownian motion of the clusters and subsequent coalescence as in the case of droplet growth in fluids.⁴⁰

Especially intriguing is that the scaling of the collapse time with the length of the chain indicates a faster dynamics, with a critical exponent z ≈ 0.5 instead of z ≈ 1 that was seen in earlier homopolymer collapse studies,^22,23 which considered simplified models describing non-hydrogen-bonded polymers such as polyethylene and polystyrene.⁴¹ The smaller exponent found in this study may be connected with a mechanism that allows a more rapid collapse in amino acid based polymers than seen in nonbiological homopolymers such as poly(N-isoporpylacrylamide) and polystyrene where collapse times of 300 ms up to 350 s have been reported,^42,43 respectively. We conjecture that the smaller exponent z is characteristic of collapse transitions in amino acid based polymers where the presence of intrachain hydrogen bonding immediately seeds (transient) local ordering, while in non-hydrogen-bonded polymers such local ordering only happens as a consequence of diffusive motion.

This connection of rapid collapse with a quick appearance of local ordering would also have implications for possible folding mechanisms and may explain the fast folding times of proteins (typically in the μs–ms range for proteins with 100–200 residues). While the topology and roughness of protein folding funnels vary with sequence, making it difficult to establish the scaling laws observed for amino acid based homopolymers, we expect to see a comparable mechanism at work during protein folding. In this picture, the formation of the intermediate and transient secondary structures and other local ordering hasten the collapse of the protein chain, which in turn enables formation of the long-range contacts that stabilize the final fold. While the latter part would be modulated by the protein sequence, the fast collapse itself appears to be a polymer property involving only the backbone.

In order to test this conjecture, one would need to repeat first our above investigation for the other 19 amino acids verifying whether the scenario observed in this paper for polyglycine applies to all amino acids. Such studies and their extension to protein-like heteropolymers are beyond the scope of our current paper; however, the presented results demonstrate already that our approach provides a general platform to understand various conformational transitions that occur in biomolecules via local ordering. Another example would be, for instance, the helix–coil transition of polyalanine where the short-time dynamics has already been explored^44,45 or the study of two-time properties such as aging and dynamical scaling in collapse and folding^15,17 Hence, the main advantage of our approach is that it allows for a clearer separation between polymer properties and sequence-dependent factors in folding and structural changes of proteins.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.9b00562.

• Contact maps from four further independent simulations for chain lengths 20 and 200; contact maps for chain lengths 50, 75, 100, and 150; contact probabilities and their time-dependent discrete local slopes for chain lengths 100 and 150 (PDF)

The authors declare no competing financial interest.