Single-Electron Lanthanide-Lanthanide Bonds Inside Fullerenes toward Robust Redox-Active Molecular Magnets

Conspectus

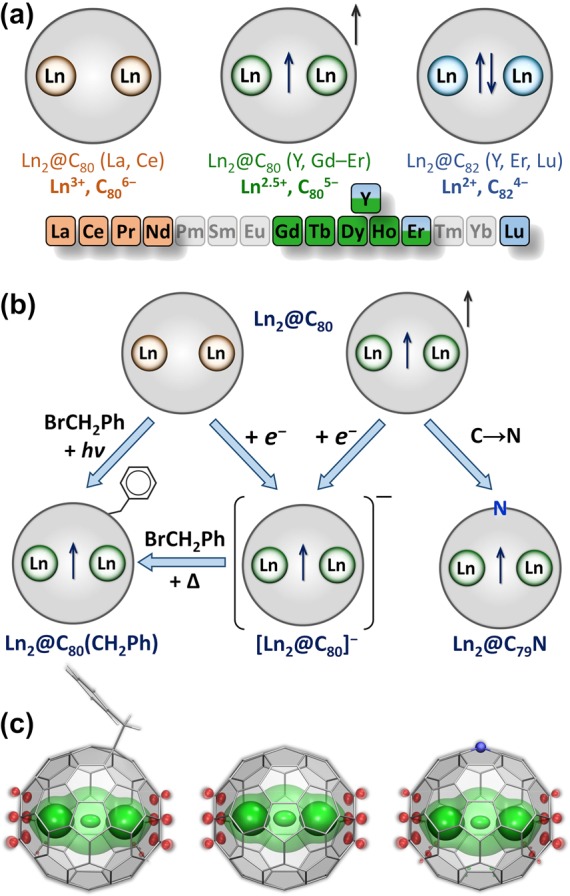
A characteristic phenomenon of lanthanide–fullerene interactions is the transfer of metal valence electrons to the carbon cage. With early lanthanides such as La, a complete transfer of six valence electrons takes place for the metal dimers encapsulated in the fullerene cage. However, the low energy of the σ-type Ln–Ln bonding orbital in the second half of the lanthanide row limits the Ln₂ → fullerene transfer to only five electrons. One electron remains in the Ln–Ln bonding orbital, whereas the fullerene cage with a formal charge of −5 is left electron-deficient. Such Ln₂@C₈₀ molecules are unstable in the neutral form but can be stabilized by substitution of one carbon atom by nitrogen to give azafullerenes Ln₂@C₇₉N or by quenching the unpaired electron on the fullerene cage by reacting it with a chemical such as benzyl bromide, transforming one sp² carbon into an sp³ carbon and yielding the monoadduct Ln₂@C₈₀(CH₂Ph). Because of the presence of the Ln–Ln bonding molecular orbital with one electron, the Ln₂@C₇₉N and Ln₂@C₈₀(R) molecules feature a unique single-electron Ln–Ln bond and an unconventional +2.5 oxidation state of the lanthanides.

In this Account, which brings together metallofullerenes, molecular magnets, and lanthanides in unconventional valence states, we review the progress in the studies of dimetallofullerenes with single-electron Ln–Ln bonds and highlight the consequences of the unpaired electron residing in the Ln–Ln bonding orbital for the magnetic interactions between Ln ions. Usually, Ln···Ln exchange coupling in polynuclear lanthanide compounds is weak because of the core nature of 4f electrons. However, when interactions between Ln centers are mediated by a radical bridge, stronger coupling may be achieved because of the diffuse nature of radical-based orbitals. Ultimately, when the role of a radical bridge is played by a single unpaired electron in the Ln–Ln bonding orbital, the strength of the exchange coupling is increased dramatically. Giant exchange coupling in endohedral Ln₂ dimers is combined with a rather strong axial ligand field exerted on the lanthanide ions by the fullerene cage and the excess electron density localized between two Ln ions. As a result, Ln₂@C₇₉N and Ln₂@C₈₀(CH₂Ph) compounds exhibit slow relaxation of magnetization and exceptionally high blocking temperatures for Ln = Dy and Tb. At low temperatures, the [Ln³⁺–e–Ln³⁺] fragment behaves as a single giant spin. Furthermore, the Ln–Ln bonding orbital in dimetallofullerenes is redox-active, which allows its population to be changed by electrochemical reactions, thus changing the magnetic properties because the change in the number of electrons residing in the Ln–Ln orbital affects the magnetic structure of the molecule.

Introduction

Increasing the single-ion magnetic anisotropy¹⁻⁵ and engineering the intramolecular coupling between magnetic ions⁶⁻⁹ are the two main strategies for improving the performance of single-molecule magnets (SMMs). Realization of both approaches is possible in endohedral metallofullerenes (EMFs) with lanthanide (Ln) ions.¹⁰⁻¹³ High magnetic anisotropy has been achieved in clusterfullerenes,¹⁴⁻¹⁸ i.e., EMFs combining metals with nonmetal ions in the endohedral species,¹¹ whereas dimetallofullerenes (di-EMFs) offer unprecedented possibilities for strong exchange coupling.¹⁹⁻²³

Metal–metal bonding is a well-known phenomenon in the chemistry of transition metals,²⁴ but lanthanide–lanthanide bonds in molecular compounds to date have been obtained only inside fullerene cages. Moreover, such Ln–Ln bonding interactions can be stabilized in di-EMFs in the form of a unique single-electron Ln–Ln bond, which is the main subject of this Account. The term single-electron Ln–Ln bond refers to the situation where the di-EMF molecule features a singly occupied Ln–Ln bonding molecular orbital (MO). The first di-EMFs featuring single-electron Ln–Ln bonds were the azafullerenes Ln₂@C₇₉N (Ln = Y, Tb, Gd), which were discovered in 2008 (it should be noted that because of the similarities in their electronic structures and oxidation states, Sc, Y, and La are considered on equal footing with 4f elements in this Account).^25,26 Density functional theory (DFT) studies of di-EMFs in 2012–2014 showed that single-electron Ln–Ln bonds can be obtained in other di-EMFs.^27,28 Stable La₂@C₈₀ monoadducts with single-electron Ln–Ln bonds were obtained in 2015 and 2016.^29,30 Giant exchange coupling and promising SMM properties were predicted for Ln₂@C₇₉N (Ln = Gd, Dy) in 2015.^31,32 These predictions for Gd₂@C₇₉N were confirmed experimentally in 2018^20,21 along with studies of the spin coherence properties of Gd₂@C₇₉N²¹ and its use for dynamical nuclear polarization at high fields.³³ Ln₂@C₈₀(CH₂Ph) monoadducts with a single-electron Ln–Ln bond were obtained for different lanthanides in 2017–2019, and excellent SMM performance was demonstrated for Dy and Tb di-EMFs.^22,23 A high blocking temperature of magnetization and giant coercivity were also reported for Tb₂@C₇₉N in 2019.¹⁹ This short and incomplete chronicle highlights the fast progress achieved by concerted computational and experimental studies of di-EMFs with single-electron Ln–Ln bonds during the past few years. In this Account, we summarize the current knowledge on these unique molecules.

Valence State of Lanthanides in Metallofullerenes

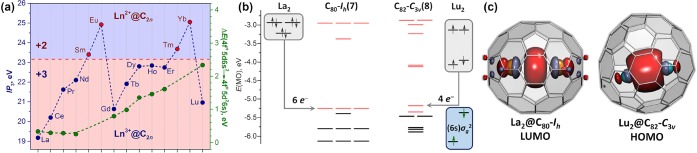
A transfer of metal valence electrons to the fullerene results in zwitterionic EMF molecules with an endohedral cation and anionic cage. In monometallofullerenes, the oxidation state of the lanthanide varies: Sm, Eu, Tm, and Yb are divalent, but other lanthanides prefer a trivalent state. This difference correlates with the third ionization potentials (IP₃) of lanthanide atoms (Figure 1a).³⁶ The metals with IP₃ exceeding 23 eV donate two electrons to the fullerene, whereas the IP₃ values for trivalent La, Ce, Pr, Nd, Gd, Tb, Dy, Ho, Er, and Lu are below the threshold of 23 eV.

Figure 1.

(a) Third ionization potentials (IP₃, blue dots) and energies of the 4fⁿ5d¹6s² → 4fⁿ5d²6s¹ excitations (green dots) of lanthanides.³⁴ The red dashed horizontal line marks the border between divalent and trivalent lanthanides in monometallofullerenes. (b) MO levels in C₈₀-I_h and C₈₂-C_3v cages (black, occupied MOs; pink, vacant MOs) as well as La₂ and Lu₂ dimers. Reproduced with permission from ref (35). Copyright 2018 Elsevier. (c) Molecules of La₂@C₈₀-I_h with the La–La bonding LUMO and Lu₂@C₈₂-C_3v with the Lu–Lu bonding HOMO.

Di-EMFs are well-known for the early lanthanides La and Ce and for heavier lanthanides such as Er and Lu. However, di-EMFs for metals in the middle of the lanthanide row could not be isolated until recently. Another puzzling phenomenon is the size and isomerism of fullerenes typical for di-EMFs with different lanthanides. The C₈₀-I_h cage has enhanced stability in the 6– state and is therefore typical for the endohedral species that donate six electrons. The high abundances of La₂@C₈₀-I_h and Ce₂@C₈₀-I_h thus agree with the 3+ oxidation state of La and Ce. For Lu and Er, however, the most abundant di-EMF cages are C₈₂-C_s(6) and C₈₂-C_3v(8), which are typical for EMFs with the fullerene charge of 4–,¹¹ and the spectroscopic properties of Ln₂@C₈₂ and the clusterfullerenes Ln₂S@C₈₂ and Ln₂C₂@C₈₂ are very similar.^37,38 These facts suggest the fullerene charge of 4– in Er₂@C₈₂ and Lu₂@C₈₂, implying the 2+ oxidation state of Er and Lu. The different behaviors of La/Ce and Er/Lu in di-EMFs cannot be explained by the IP₃ criterion and are rooted in the MO structure of the Ln₂ dimers.

Figure 1b compares the MO levels of C₈₀-I_h and C₈₂-C_3v(8) to those of La₂ and Lu₂.^27,35 The fourfold-degenerate orbital occupied by two electrons makes C₈₀-I_h unstable, but filling this MO with six more electrons produces a stable closed-shell electronic structure in C₈₀^6–. La₂ has a (6s)σ_g²(5d)π_u⁴ configuration with six valence electrons,³⁹ and since its occupied MO levels are considerably higher in energy than the LUMO in C₈₀-I_h, six electrons are transferred from La₂ to the fullerene in La₂@C₈₀-I_h, resulting in the charge distribution (La³⁺)₂@C₈₀^6–. La₂@C₈₀ has no valence electrons in the metal-localized orbitals, but its LUMO resembles the (6s)σ_g² orbital of the La₂ dimer (Figure 1c).

The orbitals of Lu₂ with configuration (6s)σ_g²(6s)σ_u²(5d)π_u² are spread in a broader energy range than those of La₂ (Figure 1b),³⁹ and the (6s)σ_g² level in Lu₂ has a lower energy than the LUMO of C₈₀-I_h. Therefore, the Lu₂ dimer in Lu₂@C₈₀-I_h does not transfer six electrons as required for the closed-shell electron configuration. The fullerene C₈₂-C_3v(8) with two low-energy unoccupied MOs is a more suitable host for Lu₂, as it is stabilized by the addition of four electrons.⁴⁰ In Lu₂@C₈₂, four electrons from the (6s)σ_u²(5d)π_u² levels of Lu₂ are transferred to the fullerene, whereas the low-energy (6s)σ_g² orbital of Lu₂ remains occupied. The formal charge distribution is (Lu²⁺)₂@C₈₂^4–, and the Lu–Lu bonding orbital resembling the (6s)σ_g² MO of Lu₂ is the HOMO of the di-EMF (Figure 1c).

In the middle of the lanthanide row, the energy of the (6s)σ_g² MO in the Ln₂ dimer is not low enough to stabilize the Ln²⁺ state but not high enough to ensure a transfer of six electrons in di-EMFs. Therefore, these lanthanides cannot produce di-EMFs with a closed-shell electronic structure. This seemingly simple conclusion was formulated only in 2014 in a computational study of Y₂@C₈₀-I_h,²⁸ which showed that Y₂@C₈₀-I_h is a triplet with one electron populating the Y–Y bonding orbital and the formal charge distribution (Y^2.5+)₂@C₈₀^5–. The same situation was also predicted for Gd and Lu.^28,41 With only one electron occupying the (6s)σ_g² Ln–Ln bonding orbital, such di-EMFs feature a single-electron Ln–Ln bond.

The valence states of lanthanides in di-EMFs are summarized in Figure 2a. Dimers of early lanthanides transfer six electrons to fullerenes, leading to a Ln³⁺ state and the Ln–Ln bonding orbital as the LUMO. Dimers of lanthanides at the end of the 4f row transfer only four electrons to fullerenes and keep the Ln–Ln bond in di-EMFs with a 2+ state of the Ln atoms. Finally, dimers of lanthanides in the middle of the row transfer five electrons to the hosting fullerene and form di-EMFs with a single-electron Ln–Ln bond and an oxidation state of Ln^2.5+. The valence state of lanthanides in di-EMFs is thus governed by the energy matching between unoccupied MOs of the fullerene and the (6s)σ_g² MO of the Ln₂ dimer. Whereas the IP₃ does not correlate with the (6s)σ_g² orbital energy, the 4fⁿ5d¹6s² → 4fⁿ5d²6s¹ excitation energy changes in accord with it (Figure 1a; see ref (27)). The state of the lanthanides in di-EMFs also depends on the fullerene host. For instance, Y and Er form both (Ln²⁺)₂@C₈₂ and (Ln^2.5+)₂@C₈₀ di-EMFs (Figure 2a), and computations showed that the (La^2.5+)₂@C_2n^5– state may be preferable for C₉₂–C₉₆.⁴²

Figure 2.

(a) Oxidation states of lanthanides in dimetallofullerenes; the color code for different states (light brown for Ln³⁺, light green for Ln^2.5+, and light blue for Ln²⁺) is used in subsequent figures. (b) Stabilization of di-EMFs with a single-electron Ln–Ln bond in the form of Ln₂@C₈₀(CH₂Ph), [Ln₂@C₈₀]⁻, and Ln₂@C₇₉N. (c) Spin density distributions in Gd₂@C₈₀(CH₂Ph), [Gd₂@C₈₀]⁻, and Gd₂@C₇₉N (“+”, green; “–”, red; transparent and solid isosurfaces have isovalues of 0.0012 and 0.014, respectively).

Stabilization of Single-Electron Ln–Ln Bonds in Dimetallofullerenes

Ions of Dimetallofullerenes

Depending on the nature of the frontier orbitals of Ln₂@C_2n, different strategies are required to stabilize single-electron Ln–Ln bonds (Figure 2b). For (Ln³⁺)₂@C_2n^6–, a single-electron Ln–Ln bond is created by addition of one electron to the Ln–Ln bonding LUMO. Indeed, reduction of La₂@C₈₀ leads to the radical anion [La₂@C₈₀]⁻ with a single-electron Ln–Ln bond.^43,44 In (Ln^2.5+)₂@C_2n^5–, the single-electron Ln–Ln bond is already present, but the fullerene has an unpaired electron, and addition of one electron produces an anion with a closed-shell structure of the cage, (Ln^2.5+)₂@C_2n^6–.^23,41,42 Formation of such anions is crucial for the extraction of (Ln^2.5+)₂@C_2n^5– from the carbon soot after arc-discharge synthesis. The radical nature results in high reactivity and polymerization of such di-EMFs, making them insoluble in CS₂ or aromatic solvents. However, dimethylformamide (DMF) extracts EMFs in the form of anions.⁴⁵⁻⁴⁷ Thus, single-electron reduction of both (Ln³⁺)₂@C_2n^6– and (Ln^2.5+)₂@C_2n^5– di-EMFs yields (Ln^2.5+)₂@C_2n^6– anions with a closed-shell electronic structure of the fullerene.

For (Ln²⁺)₂@C_2n^4– with a two-electron Ln–Ln bond, an obvious route to attain a single-electron Ln–Ln bond is a one-electron oxidation. Electrochemical studies of Ln₂@C₈₂ (Ln = Sc, Y, Er, Lu) proved that oxidation is a metal-based process forming (Ln^2.5+)₂@C_2n^4– cations.^37,48,49 Chemical oxidation of Sc₂@C₈₂ and Er₂@C₈₂ with [(4-BrC₆H₄)₃N]SbCl₆ gave corresponding cation radicals,³⁷ and an electron paramagnetic resonance (EPR) study of [Sc₂@C₈₂]⁺ revealed a giant ⁴⁵Sc hyperfine coupling constant of 19.9 mT, in agreement with the formation of a singly occupied Sc–Sc bonding MO. For the Er analogue, superconducting quantum interference device (SQUID) magnetometry showed considerable differences in the magnetization behaviors of Er₂@C₈₂ and its salt [Er₂@C₈₂]⁺SbCl₆^–.³⁷

Dimetallofullerene Derivatives

(Ln^2.5+)₂@C_2n^6– anions react with benzyl bromide to give noncharged benzyl monoadducts Ln₂@C_2n(CH₂Ph). A series of Ln₂@C₈₀(CH₂Ph) compounds ({Ln₂} hereafter) with Ln₂ = Y₂, Gd₂, Tb₂, Dy₂, Ho₂, Er₂, TbGd, and TbY were obtained by this approach.^22,23 A single-crystal X-ray diffraction study of {Dy₂} proved selective addition of the benzyl group to pentagon/hexagon/hexagon ([5,6,6]) junctions.²³ The reaction of La₂@C₈₀ with benzyl bromide under UV irradiation proceeds as a radical addition and also yields a [5,6,6] {La₂} monoadduct.²⁹ The unpaired electron formed when the benzyl radical is attached to the fullerene is transferred to the La–La bonding orbital and yields a single-electron La–La bond. Another monoadduct with single-electron La–La bond, La₂@C₈₀(C₃N₃Ph₂) (Figure 3b), was obtained by thermal reaction of La₂@C₈₀ with 3-chloro-5,6-diphenyltriazine.³⁰ Radical trifluoromethylation has been used to functionalize EMF mixtures, which among other products gave Ln₂@C₈₀(CF₃) monoadducts (Ln = Y,^28,50 Gd⁵¹).

Figure 3.

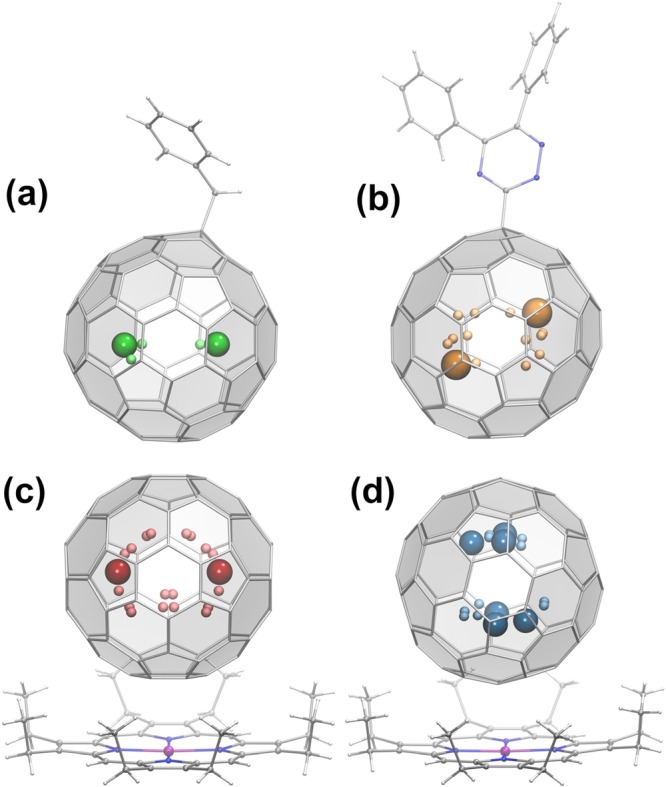
Molecular structures of di-EMFs with a single-electron Ln–Ln bond from single-crystal X-ray diffraction: (a) Dy₂@C₈₀(CH₂Ph);²³ (b) La₂@C₈₀(C₃N₃Ph₂);³⁰ (c) Tb₂@C₇₉N·Ni(OEP);²⁶ (d) Gd₂@C₇₉N·Ni(OEP).²¹ Large colored spheres show the Ln sites with the highest occupancies. The Ln···Ln distances are 3.896(1) Å (Dy), 3.784(2) Å (La), 3.902(1) Å (Tb), and 3.835(9) Å (Gd).

Azafullerenes Ln₂@C₇₉N

Since C₇₉N^5– is isoelectronic with C₈₀^6–, substitution of one carbon with nitrogen stabilizes (Ln^2.5+)₂@C₈₀^5– in the form of the azafullerene (Ln^2.5+)₂@C₇₉N^5–. Y₂@C₇₉N, Gd₂@C₇₉N, and Tb₂@C₇₉N were obtained by arc-discharge synthesis in the presence of nitrogen.^25,26 Single-crystal XRD studies of Tb₂@C₇₉N and Gd₂@C₇₉N cocrystallized with Ni(OEP) (Figure 3c,d)^21,26 proved that their fullerene cages are based on C₈₀-I_h, but the exact position of the nitrogen could not be determined. DFT computations showed that substitution of a [5,6,6] carbon in C₈₀-I_h by nitrogen gives the most stable Ln₂@C₇₉N structures.^19,26,31

Role of the Fullerene Cage

Despite the +2.5 oxidation state of the lanthanides, both Ln₂@C₈₀(CH₂Ph) and Ln₂@C₇₉N compounds are air-stable, which is not typical for compounds with lanthanides in unconventional oxidation states. Thus, the fullerene cage provides sufficient protection to the (Ln^2.5+)₂ species with a single-electron Ln–Ln bond. Another important aspect is the spatial confinement of Ln₂ dimers. Coulomb repulsion between lanthanide ions in di-EMFs is much stronger than the stabilization energy of the bonding interactions.²⁷ Therefore, Ln ions tend to maximize the Ln···Ln distance, but since the extent of the Ln₂ dimer is limited by the fullerene, metal ions remain at distances allowing bond formation. The bonding between strongly repulsive metal ions in di-EMFs has been identified as “oxymoron”²⁷ or “unwilling” bonding.⁵²

Magnetic Resonance Studies of Di-EMFs with Single-Electron Ln–Ln Bonds

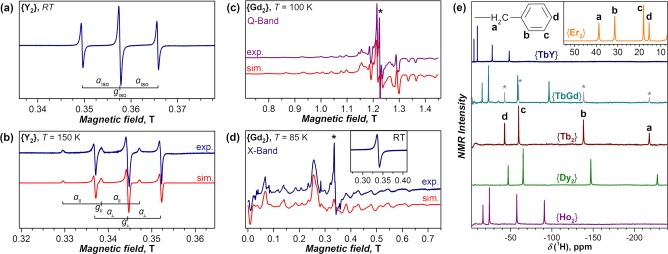
Figure 2c shows that {Gd₂}, [Gd₂@C₈₀]⁻, and Gd₂@C₇₉N have almost identical distributions of the spin density, with three maxima. Two of these are due to Gd 4f⁷ electrons, whereas the third one is associated with the unpaired electron in the Gd–Gd bonding orbital. A similar distribution is expected for other lanthanides with partially filled 4f shells, whereas for Y, La, and Lu only the spatial distribution of the unpaired valence electron in the Ln–Ln bonding MO will be seen. The experimental proof of such spin distributions is provided by magnetic resonance techniques.

For Y and La di-EMFs, spin properties are straightforwardly analyzed with EPR spectroscopy. The EPR spectrum of {Y₂} in toluene at room temperature (Figure 4a) shows a triplet isotropic hyperfine structure due to the two equivalent ⁸⁹Y nuclei (I_Y = ¹/₂). Very similar solution spectra were reported for Y₂@C₇₉N,²⁶ Y₂@C₈₀(CF₃),²⁸ and a mixture of [Y₂@C_2n]⁻ anions.²³ At low temperature, the spectra change to an axial hyperfine pattern (Figure 4b).²³ The EPR parameters (Table 1) prove the localization of the unpaired spin on the Y₂ dimer: The large a_iso(⁸⁹Y) values show that the s electrons of Y make a large contribution to the spin density, in agreement with DFT-calculated spin populations of 0.26 (s), 0.08 (p), and 0.16 (d) of each Y atom in {Y₂}. The A tensor anisotropy is caused by contributions from p and d orbitals of Y to the spin density. Finally, deviations of g_iso from the free electron value of 2.0023 and a considerable anisotropy of the g tensor also point to localization of the unpaired spin on the metal atoms. Likewise, localization of the spin density on the La₂ dimer in di-EMFs with single-electron La–La bonds also follows from the EPR studies of [La₂@C₈₀]⁻,^28,41 La₂@C₈₀(C₃N₃Ph₂),³⁰ and {La₂}²⁹ (Table 1).

Figure 4.

(a, b) X-band EPR spectra of {Y₂} in toluene at (a) room temperature and (b) 150 K. (c, d) Q-band (34 GHz) and X-band (9.4 GHz) EPR spectra of {Gd₂} in frozen toluene. The inset in (d) shows the room-temperature spectrum. (e) ¹H NMR spectra of {Ln₂} compounds in CS₂ at room temperature. Asterisks in the spectrum of {TbGd} denote the signals of {Tb₂}. Adapted with permission from (a, b) ref (23) and (c–e) ref (22). Copyright 2017 and 2019, respectively, Springer Nature.

Table 1. EPR Parameters of Y and La Di-EMFs with a Single-Electron Ln–Ln Bond.

	giso	aiso (mT)	g⊥, g∥	a⊥, a∥ (mT)
{Y2}23	1.9733	8.10	1.9620, 1.9982	7.57, 8.80
Y2@C79N26,53	1.9740	8.12	1.961, 1.999	7.60, 9.06
Y2@C80(CF3)28	1.9771	7.80
[La2@C80]−28,41			1.835, 1.972	31.5, 41.6
La2@C80(C3N3Ph2)30	1.899	35.9
{La2}29			1.840, 1.980	31.7, 43.1

EPR studies of 4f di-EMFs are complicated by fast relaxation and strong magnetic anisotropy, and successful measurements have been reported only for Gd₂@C₇₉N^21,25,33 and {Gd₂} to date.²² Coupling of the Gd 4f spins to the unpaired electron spin gives a large-spin ground state with a characteristic zero-field splitting (ZFS) pattern, which can be resolved in the EPR spectra of Gd₂@C₇₉N and {Gd₂} at low temperatures (Figure 4c,d). The ZFS can be ascribed to the spin S = ¹⁵/₂ originating from ferromagnetic coupling of the two 4f⁷ spins (S = ⁷/₂) and the unpaired electron spin (S = ¹/₂). The spin Hamiltonian takes the form

1

where the first two terms describe the ZFS and the last term represents the Zeeman effect. The X- and Q-band EPR spectra of {Gd₂} near 100 K are reproduced by the parameters D = 1.00(2) GHz, E = 0.22(4) GHz, and g_iso = 1.987 (Figure 4c,d).²² For Gd₂@C₇₉N, the analogous parameters are D = 0.96(6) GHz, E = 0.14(1) GHz, and g_iso = 1.99.⁵⁴ The spin coherence properties of Gd₂@C₇₉N solutions were studied by pulsed EPR experiments.²¹ Phase memory times (T_m) of up to 1.6 μs (5 μs with dynamic decoupling) were found at 5 K, and the possibility of coherent spin manipulation was confirmed by Rabi oscillations in echo-detected nutation experiments. The use of Gd₂@C₇₉N for improving dynamic nuclear polarization (DNP) at high fields was also demonstrated.³³

For lanthanides other than Gd, the localization of an unpaired spin on the metal dimers in {Ln₂} has been verified by NMR spectroscopy.²² Localization of the spin on the carbon cage would make the detection of ¹³C or ¹H NMR signals problematic. However, solution ¹H NMR spectra of {Ln₂} compounds exhibit well-defined resonances of benzyl protons (Figure 4e) strongly shifted from their positions in diamagnetic compounds (3–7 ppm). These paramagnetic ¹H shifts are caused by the dipolar magnetic field of the endohedral Ln₂ dimer. Since molecules in solution rotate, the isotropic contributions of the dipolar field average out, and paramagnetic shifts (δ^para) reflect the magnetic anisotropy of the endohedral Ln₂ dimer. In a point-dipole approximation, dipolar (or pseudocontact) paramagnetic shifts take the form⁵⁵

2

where R_i and θ_i are polar coordinates of the ith proton in the coordinate system centered on the Ln₂ dimer with the polar axis along the Ln–Ln bond, and χ_∥ (χ_⊥) is the longitudinal (transverse) magnetic susceptibility of the Ln₂ dimer. Since the first factor in eq 2 (the geometrical factor) is very similar for all {Ln₂} molecules, variation of the ¹H NMR spectra along the {Ln₂} series is mainly caused by the difference of χ_∥ and χ_⊥. Thus, ¹H chemical shifts reveal the sign and relative magnitude of the magnetic anisotropy. From a comparison of the ¹H NMR spectra in Figure 4e, we conclude that {Dy₂} and {Tb₂} have similar magnetic properties since their ¹H chemical shifts are almost identical. The {Ho₂} values are a factor of ca. 2 smaller, indicating a lower magnetic anisotropy. Substitution of one Tb in {Tb₂} by Y to obtain {TbY} expectedly results in a considerable decrease in the paramagnetic shift. For {TbGd}, a close similarity to the ¹H NMR spectra of {TbY} might be expected because isotropic spins do not produce dipolar paramagnetic shifts. However, the ¹H shifts in {TbGd} are 2 times larger than those in {TbY} (Figure 4e), which shows that the isotropic Gd³⁺ spin is locked to the anisotropic Tb³⁺ spin by strong exchange interactions. Finally, the ¹H resonances in {Er₂} are shifted in the opposite direction in comparison to other {Ln₂} molecules, revealing the opposite sign of the magnetic anisotropy.

Moving Electrons into and out of Ln–Ln Bonds

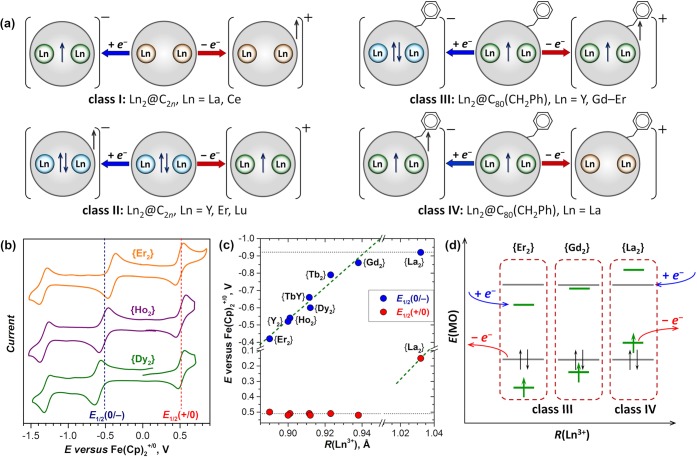
Since the Ln–Ln bonding MO in di-EMFs is either a LUMO, HOMO, or singly occupied MO, redox reactions of di-EMFs may populate or depopulate this orbital. According to their redox behavior, di-EMFs with Ln–Ln bonding MOs can be divided into four classes (Figure 5a). Ln₂@C_2n with La and Ce represent class I. They have a metal-based LUMO, and their reduction proceeds via the formation of a single-electron Ln–Ln bond. Oxidation of these di-EMFs is a cage-based process, and the corresponding redox potentials do not depend on the encapsulated metal. Class II is represented by di-EMFs of Y, Er, and Lu.^37,48,49,56 They have a doubly occupied metal-based HOMO, which loses one electron upon oxidation to form a single-electron Ln–Ln bond in the cation. The first oxidation potential is thus strongly metal-dependent. At the same time, reduction of these di-EMFs is a cage-based process with a metal-independent potential.

Figure 5.

(a) Four types of di-EMF redox behavior. (b) Cyclic voltammograms of {Ln₂} (Ln = Er, Ho, Dy) in o-dichlorobenzene (o-DCB). Vertical dashed lines denote the reduction (E_1/2(0/−)) and oxidation (E_1/2(+/0)) potentials of {Ho₂}. (c) Redox potentials in the {Ln₂} series. Horizontal dotted lines denote potentials of the fullerene-based redox processes, and dashed green lines show the variation of the potential of the redox-active Ln–Ln orbital. (d) Schematic description of the MO levels in {Er₂}, {Gd₂}, and {La₂}. Cage MOs are shown in gray and metal-based MOs in green.

Ln₂@C₈₀(CH₂Ph) adducts belong to class III or IV, and their redox behavior is illustrated in Figure 5b with {Er₂}, {Ho₂}, and {Dy₂};^22,23 the first redox potentials of the {Ln₂} series are summarized in Figure 5c. The reduction potential shifts from −0.4 to −0.9 V in going from Er to Gd, whereas the oxidation potential remains virtually constant at +0.5 V (potentials are referenced versus Fe(Cp)₂^+/0). A further increase in the Ln³⁺ ionic radius leads to a drop in the oxidation potential to +0.15 V in {La₂},²⁹ but the reduction potential of {La₂} is shifted from the {Gd₂} value by only −0.06 V. These changes in redox potentials can be rationalized using the MO scheme in Figure 5d. In {Y₂} and {Er₂}–{Gd₂}, assigned to class III, the LUMO is the vacant Ln–Ln bonding orbital, which is populated in the first reduction step, giving a two-electron Ln–Ln bond (Figure 5a). The reduction potential is therefore metal-dependent. At the same time, the HOMO of these {Ln₂} molecules is a cage-based orbital, whereas the singly occupied Ln–Ln bonding MO has lower energy and remains unaffected by oxidation. Both the occupied and vacant components of the Ln–Ln bonding MO increase in energy upon moving from heavier to lighter lanthanides. At a certain threshold, the order of the metal- and fullerene-cage-based orbitals changes (Figure 5d). Then the cage-based MO becomes the LUMO with a metal-independent reduction potential, whereas the metal-based MO becomes the HOMO, and the oxidation potential becomes metal-dependent and starts to shift negatively with increasing metal size. This is the situation in {La₂}, the only member of class IV to date.

The reduction mechanism of di-EMFs in class III has been confirmed by ¹H NMR spectroscopy.²² Population of the fullerene-based MO by the surplus electron in {Ln₂}⁻ would lead to delocalization of the unpaired spin over the fullerene cage, and ¹H NMR spectra of such anions would not be detectable. However, single-electron reduction of {Ln₂} with cobaltocene gave {Ln₂}⁻ anions with well-defined ¹H NMR resonances (Figure 6), proving the formation of a two-electron Ln–Ln bond.

Figure 6.

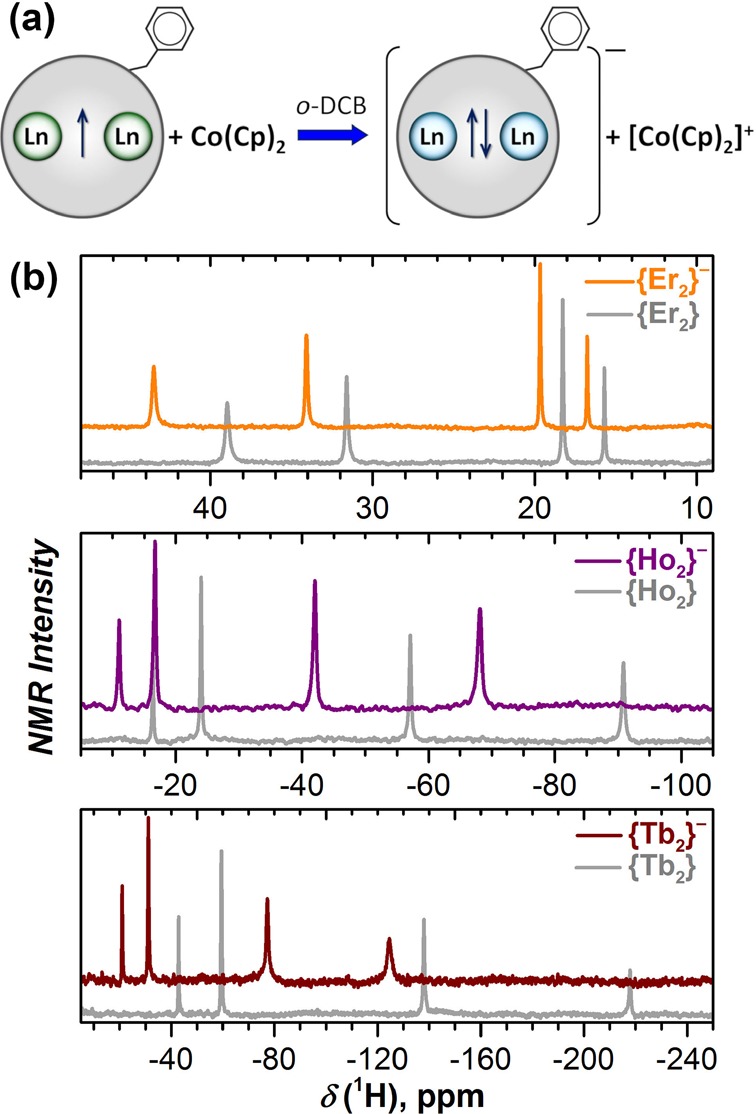
(a) Reaction of {Ln₂} with cobaltocene. (b) Room-temperature ¹H NMR spectra of {Er₂}⁻, {Tb₂}⁻, and {Ho₂}⁻ anions in o-DCB-d₄ solution (colored lines) compared with the spectra of pristine {Ln₂} compounds (gray lines). Reproduced with permission from ref (22). Copyright 2019 Springer Nature.

Single-Molecule Magnetism in Di-EMFs with Single-Electron Ln–Ln Bonds

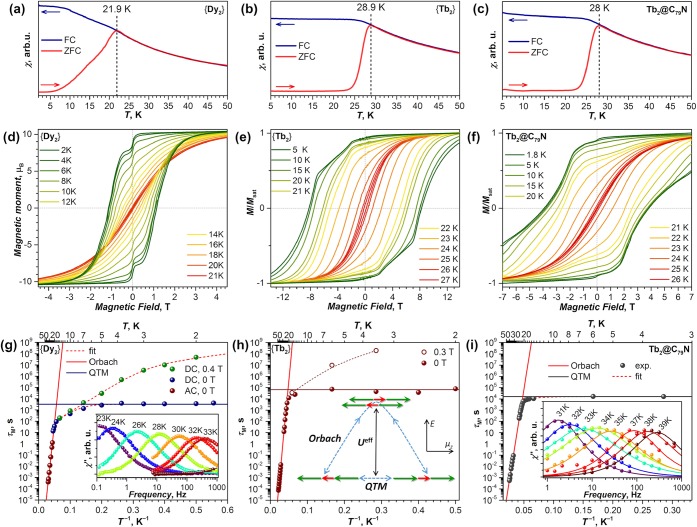
The core property of SMMs is slow relaxation of the magnetization, leading to blocking of the magnetization and magnetic hysteresis. Below the blocking temperature (T_B), the magnetic properties depend on the way that the current state of the sample was obtained, whereas above T_B the sample reaches thermodynamic equilibrium faster than the controlled parameter (temperature, magnetic field, etc.) is changed. With T_B values of 22, 29, and 28 K (Figure 7a–c), respectively, {Dy₂},²³ {Tb₂},²² and Tb₂@C₇₉N¹⁹ are the strongest SMMs among all EMF-SMMs.¹³ For comparison, the highest T_B values in nitride, carbide, sulfide, and oxide clusterfullerenes are 7–8 K (Dy₂ScN@C₈₀-I_h¹⁶ and DySc₂N@C₈₀-I_h¹⁴), 7 K (DyYTiC@C₈₀-I_h¹⁵), 4 K (Dy₂S@C₈₂-C_3v¹⁷), and 7 K (Dy₂O@C₈₂-C_3v¹⁸). {Ho₂} and {Er₂} do not show blocking of the magnetization above 2 K.²²

Figure 7.

(a–c) Magnetization blocking temperatures of (a) {Dy₂} (b), {Tb₂}, and (c) Tb₂@C₇₉N. The magnetic field was 0.2–0.3 T, and the temperature sweep rate was 5 K min^–1. (d–f) Magnetic hysteresis of (d) {Dy₂}, (e) {Tb₂}, and (f) Tb₂@C₇₉N. The magnetic field sweep rate was 3 mT s^–1 in (d) and (f) and 9.5 mT s^–1 in (e). (g–i) Magnetization relaxation times of (g) {Dy₂}, (h) {Tb₂}, and (i) Tb₂@C₇₉N. Adapted with permission from (a, d, g) ref (23), (b, e, h) ref (22), and (c, f, i) ref (19). Copyright 2017 and 2019 Springer Nature and 2019 Wiley-VCH, respectively.

Since T_B depends on the temperature sweep rate, it was suggested to use T_B100, the temperature at which the magnetization relaxation time is 100 s. The T_B100 values for {Dy₂} (18.2 K), {Tb₂} (25.2 K), and Tb₂@C₇₉N (24.1 K) are second only to those of Dy metallocenium cations, which hold the absolute records among all SMMs with T_B100 up to 53–65 K,³⁻⁵ and recently discovered Tb^II(Cp^iPr₅)₂ with T_B100 = 52 K.⁵⁷ We are not aware of other SMMs with T_B100 values higher than those of {Tb₂} and Tb₂@C₇₉N; at this moment, the closest follower with T_B100 of 20 K is the dinuclear Tb metallocene complex with a N₂^3– radical bridge.⁶

{Dy₂}, {Tb₂}, and Tb₂@C₇₉N exhibit magnetic hysteresis with large remanence below T_B (Figure 7d–f). The magnetic hysteresis of {Tb₂} is uniquely broad with giant coercive fields of 8 T at 5–10 K (Figure 7e).²² Similarly large coercivity was reported only in the aforementioned dinuclear-radical-bridged Tb complex⁶ and has no further analogues among molecular magnets. For Tb₂@C₇₉N, a 2-fold smaller but still large coercive field of 3.8 T is found between 2 and 10 K (Figure 7f).¹⁹

In order to identify the relaxation mechanisms of SMMs, magnetization relaxation times τ_M are measured at various temperatures and magnetic fields. The total relaxation rate (τ_M^–1) is a sum of the rates of contributing processes:

3

The first term in eq 3 describes relaxation of the magnetization via quantum tunneling of magnetization (QTM), which occurs when spin-up and spin-down levels are quasi-degenerate. Since QTM is not thermally activated, the relaxation rate τ_QTM^–1 is temperature-independent. However, QTM depends on the magnetic field and can be quenched completely when Zeeman splitting lifts the degeneracy of spin-up and spin-down levels. In the Orbach mechanism (the second term in eq 3), spin reversal involves overcoming the energy barrier U^eff, which corresponds to a certain excited state of the system, and hence follows the Arrhenius law. Finally, two power-law temperature terms describe the single-phonon direct mechanism (n₁ = 1) and the two-phonon Raman relaxation mechanism (n₂ = 4–9).

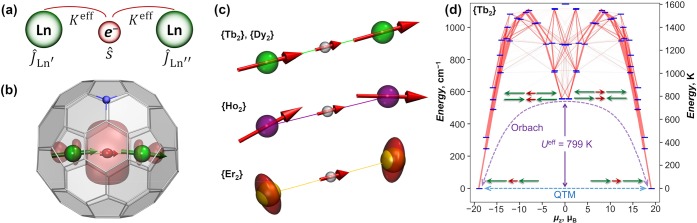
The magnetization relaxation times of {Dy₂}, {Tb₂}, and Tb₂@C₇₉N are plotted in Figure 7g–i in Arrhenius coordinates (log(τ_M) vs T^–1).^19,22,23 For {Ho₂} and {Er₂}, the relaxation times are orders of magnitude shorter and will not be discussed here.²² {Dy₂}, {Tb₂}, and Tb₂@C₇₉N show similar temperature dependences of τ_M. At low temperatures in zero field, the relaxation times are temperature-independent, which points to relaxation via QTM. In this regime, the combined spin of the [Ln³⁺–e–Ln³⁺] system flips as a single entity with rather long τ_QTM: 0.9 h in {Dy₂}, 18 h in {Tb₂}, and 4.5 h in Tb₂@C₇₉N. A magnetic field of 0.3–0.4 T quenches the QTM and slows the relaxation down to months or even years (Figure 7g,h). For {Dy₂}, dilution of the sample in a polystyrene matrix also resulted in a significant increase in the relaxation time,²³ showing that intermolecular dipolar fields play an important role in facilitating the QTM mechanism of EMF-SMMs.^14,23

Above 20 K, all three di-EMFs show a linear regime in Arrhenius coordinates, which points to the Orbach mechanism with the barriers U^eff of 613 ± 8 K in {Dy₂}, 799 ± 2 K in {Tb₂}, and 757 ± 4 K in Tb₂@C₇₉N. These energies are assigned to the pure exchange-excited states, in which the spin of one of the lanthanide ions is flipped (Figure 7h). In many SMMs showing zero-field QTM at the lowest temperatures, the temperature increase first activates the Raman mechanism, which then in turn gives way to the Orbach regime at higher temperatures. As a result, the Raman mechanism is often the main limiting factor reducing the blocking temperature of magnetization of SMMs with large Orbach barriers.⁵⁸ In {Tb₂} and Tb₂@C₇₉N, the strong coupling between the two Ln ions greatly suppresses the Raman mechanism, so that the QTM is superseded directly by the Orbach mechanism as the dominant mode of relaxation. As a result, although the Orbach barriers of {Tb₂} and Tb₂@C₇₉N are smaller than in a handful of SMMs with U^eff > 1000 K discovered during the past few years (including Dy₂ScN@C₈₀ with U^eff = 1735 K¹⁶), the T_B and T_B100 values of {Tb₂} and Tb₂@C₇₉N are higher than for many of those.

Coupling of Spins in Dimetallofullerenes with Single-Electron Ln–Ln Bonds

In designing a spin Hamiltonian describing di-EMFs with a single-electron Ln–Ln bond, the molecule is considered to be a three-center spin system [Ln³⁺–e–Ln³⁺] (Figure 8a). The lanthanides are treated as Ln³⁺ ions with corresponding ligand-field (LF) Hamiltonians and spin operators Ĵ_Ln, whereas the exchange Hamiltonian includes the direct Ln–Ln interaction with coupling constant j₁₂ and exchange interactions between the lanthanide spins and the unpaired electron spin ŝ with exchange constants K′ and K″:

4

Equation 4 implies the general case of two different lanthanides in one molecule (Ln′ and Ln″) and hence, two different Ln–e coupling constants (K′ and K″) are needed. For homometallic systems with nonsymmetric molecules, a small difference between K′ and K″ values can be ignored in the first approximation.

Figure 8.

(a) Schematic representation of di-EMFs with a single-electron Ln–Ln bond as a three-center [Ln³⁺–e–Ln³⁺] spin system. (b) Alignment of the Tb spins (green arrows) and the unpaired electron spin (red arrow) in Tb₂@C₇₉N. (c) Alignment of the Ln and unpaired electron spins (red arrows) in {Ln₂} molecules. The spins of Er ions are visualized as ellipsoids built upon the g tensors of their single-ion ground states. (d) Low-energy spectrum of the spin Hamiltonian (eq 6) for {Tb₂} with K^eff = 55 cm^–1. Red lines visualize transition probabilities. Tb and unpaired spins are shown with green and red arrows, respectively. Dashed arrows show the QTM and Orbach mechanisms.

Gd Dimetallofullerenes

As the LF terms for isotropic Gd spins can be neglected, the effective spin Hamiltonian of {Gd₂} or Gd₂@C₇₉N takes the form

5

DFT computations on {Gd₂},²³ Gd₂@C₇₉N,^31,32 and [Gd₂@C₈₀]^−41,59 showed that direct Gd–Gd interactions are antiferromagnetic with j₁₂ < −1 cm^–1, whereas the Gd–electron exchange is ferromagnetic with K′ and K″ values of 180–200 cm^–1. Taking into account the small difference between K′ and K″ and the small value of j₁₂ allows further simplification of the spin Hamiltonian to obtain the last equality in eq 5 with a single effective exchange constant K^eff, whose value can be estimated from a comparison of experimental and simulated χT curves. For Gd₂@C₇₉N^20,21 (Figure 9a) and {Gd₂},²² good agreement is achieved for K^eff = 170 ± 10 cm^–1 and 160 ± 10 cm^–1, respectively. These values are unprecedentedly large for lanthanide molecular magnets. The largest Gd–radical coupling constants in other compounds are 6 cm^–1 for Gd–nitroxide,^60,61 −10 cm^–1 for Gd–bipyrimidyl,⁶² and −27 cm^–1 for Gd–N₂^3– radical bridges.^8,63 The mechanism of the strong exchange interactions in the [Gd³⁺–e–Gd³⁺] system has been discussed in refs (31), (32), and (59) but is not fully understood at present.

Figure 9.

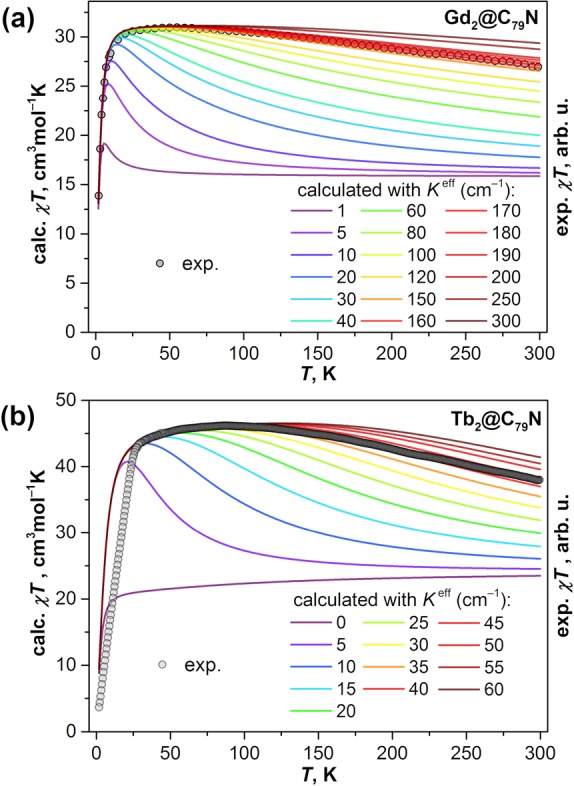
Comparison of experimental χT values (dots, arbitrary units) measured for (a) Gd₂@C₇₉N and (b) Tb₂@C₇₉N in a field of 1 T to the results of calculations for different values of the coupling constant K^eff. Adapted with permission from (a) ref (20) and (b) ref (19). Copyright 2018 Royal Society of Chemistry and 2019 Wiley-VCH, respectively.

Di-EMFs with Magnetically Anisotropic Lanthanides

The low-energy states of [Ln³⁺–e–Ln³⁺] systems with anisotropic lanthanides are described by the same Hamiltonian as in eq 5 but with the addition of ligand field terms:

6

Ab initio calculations at the CASSCF/RASSI-SO level revealed strong axiality of the ligand field for Tb³⁺ and Dy³⁺ ions in {Ln₂} and Ln₂@C₇₉N molecules (Figure 8b,c).^22,23 Dy³⁺ and Tb³⁺ have large-spin ground states with collinear quantization axes aligned parallel to the Ln–Ln bond (Figure 8c) and LF splittings of 900–1000 cm^–1. In the |J, m_J⟩ basis, the ground state Kramers doublet (KD) of Dy³⁺ is a pure state with |m_J| = ¹⁵/₂, but higher energy KDs have a more mixed character. In Tb³⁺, the four lowest-energy pseudo-Kramers doublets are essentially pure m_J states with 99–100% contributions of |m_J| = 6, 5, 4, and 3.²² Similar energies and m_J state compositions are found for Tb³⁺ in Tb₂@C₇₉N,¹⁹ but the magnetic axes of the Tb ions are tilted from the Tb–Tb bond by 7° (Figure 8b). A high-spin ground state is also predicted for Ho³⁺, but with a considerably smaller LF splitting, stronger tilting of the easy axes of the Ho ions (Figure 8c), and mixed m_J character with the leading term of 64% |±8⟩. For Er³⁺, an easy-plane ground state is predicted in agreement with NMR data (Figure 8c).²²

With Ĥ_LF parameters from ab initio calculations, the K^eff value can be estimated in a similar fashion as described for Gd₂@C₇₉N. Figure 9b shows that for Tb₂@C₇₉N the best match to the experimental χT curve is obtained for K^eff = 40–45 cm^–1.¹⁹ The K^eff values estimated from the χT curves are 48–53 cm^–1 for {Tb₂}, 30–35 cm^–1 for {Dy₂}, ca. 40 cm^–1 for {Ho₂}, and ca. 20 cm^–1 for {Er₂}.^22,23

Relaxation of the magnetization in di-EMFs can be understood using the spectrum of the spin Hamiltonian (eq 6), as shown in Figure 8d for {Tb₂}. [Ln³⁺–e–Ln³⁺] is a Kramers system for any lanthanide and has a rigorous twofold degeneracy of the spin states in zero field. In the ground-state doublet of {Tb₂}, all three spins are aligned along the Tb–Tb axis (Figure 8c). Negligible transverse components of the g tensor and the large total spin result in a low efficiency of QTM within this doublet, as transverse fields (e.g., from intermolecular interactions) cannot couple to increase the tunneling gap. Next follow the states with LF excitations in one or both lanthanides, forming branches with a gradual decrease of the moment at higher energies. These states do not provide efficient relaxation pathways. The first pure exchange-excited states, in which one of the Tb spins is flipped, appear at energies comparable to twofold LF excitations. In these states, Tb spins cancel each other out, leading to a small total moment with an almost free unpaired spin. As these states are very efficient for relaxation of the magnetization, the Orbach regimes found in the temperature dependence (Figure 7g–i) correspond to relaxation via these states. An assumption that U^eff corresponds to the energy of the first pure exchange-excited state (Figure 8d) allows an independent estimation of K^eff, which gives values of 55 cm^–1 for {Tb₂} and 32 cm^–1 for {Dy₂}, in good agreement with K^eff estimated from the χT curves.^22,23 For comparison, in dinuclear-radical-bridged Tb and Dy complexes, the largest Ln–radical coupling constants are −23.1 cm^–1 (Tb) and −7.2 cm^–1 (Dy).⁶ It should be noted that if the ground states of the lanthanide spins are of the Ising type with J_z = ±J, the energy of the pure exchange-excited state with the exchange-only Hamiltonian is 2JK^eff, which allows a very simple but less precise estimation of K^eff as U^eff/2J.

At the end of this section, we would like to note that comparison of the coupling constants between the compounds should be done cautiously because the values will depend on the definition of the exchange Hamiltonian. Whereas Ĥ_exchange in eq 6 is defined through the whole momentum Ĵ_Ln, another popular approach is based on the use of pseudospin (s̃_Ln = ¹/₂) to describe the ground state of lanthanides.^31,64,65 The same energy difference between ferromagnetically and antiferromagnetically coupled states in the −2K^effŝ·Ĵ_Ln and 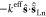exchange formalisms would require a k^eff that is 2J times larger than K^eff, where J is the total momentum of a lanthanide. Another option may be to use only the spin Ŝ_Ln without the angular momentum and to define the exchange term as −2j^effŝ·Ŝ_Ln. Likewise, j^eff can be obtained by scaling K^eff with the factor J/S. For Dy³⁺ with J = ¹⁵/₂ and S = ⁵/₂ as an example, the K^eff value of 32 cm^–1 for {Dy₂} is equivalent to k^eff = 960 cm^–1 or j^eff = 96 cm^–1. This substantial dependence of the coupling constant on the form of the exchange Hamiltonian should be taken into account carefully when comparing the values from different works.

Mixed-Metal Di-EMFs

Di-EMFs synthesized using two lanthanides at once comprise a mixture of Ln′₂, Ln″₂, and Ln′Ln″ species, and some such mixtures can be separated into individual components by recycling HPLC. In particular, separation of the Tb–Y system afforded pure {TbY}.²² Replacement of one Tb ion in {Tb₂} by Y dramatically increases the relaxation rates and changes the relaxation mechanism and hysteretic behavior (Figure 10a). {TbY} shows a narrow magnetic hysteresis below 5 K with an opening in the field of 0.1–1.0 T (Figure 10a). At 2 K in a magnetic field of 0.3 T, the relaxation time of {TbY} is 2.9 s (compared with ca. 6 years estimated for {Tb₂} at 3 K), and in zero field τ_M drops to only a few ms.²² Thus, the presence of two lanthanide spins with uniaxial anisotropy in {Ln₂} is essential for a good di-EMF SMM.

Figure 10.

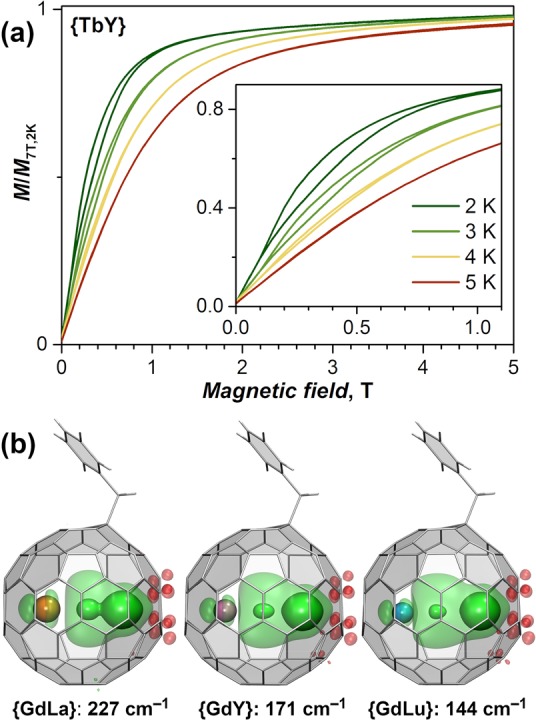
(a) Magnetization curves for {TbY} below 5 K. Reproduced with permission from ref (22). Copyright 2019 Springer Nature. (b) DFT-computed spin density distribution and Gd electron exchange coupling constants in {GdLa}, {GdY}, and {GdLu} (PBE0/DKH-TZVP level of theory; the isosurface visualization parameters are the same as in Figure 2).

Combining different lanthanides in one di-EMF is promising for the design of molecular magnets with tunable spin properties.⁶⁶ One of the unique aspects of this approach is the possibility to tune the Ln–electron exchange interactions by varying the relative size of the lanthanides, as illustrated in Figure 10b for {GdLa}, {GdY}, and {GdLu}. With the increase in the lanthanide size from Lu to Y and further to La, the maximum of the spin density due to the unpaired valence electron shifts closer and closer to Gd. Broken-symmetry DFT calculations show that this shift is accompanied by a strong variation of the Gd–electron exchange coupling constant from 144 cm^–1 in {GdLu} to 227 cm^–1 in {GdLa}.

Outlook

Although dedicated studies of dimetallofullerenes with single-electron lanthanide–lanthanide bonds with the focus on redox and magnetic properties have been pursued for only a few years, impressive advantages of dimetallofullerenes as molecular magnets are already clear. However, the field is still in its infancy, and further studies required to fully exploit the potential of these molecules are outlined below:

• 1.Only a few Ln′Ln″ combinations have been studied to date in di-EMFs. Further exploration of mono- and heterobimetallic systems may give exceptional control over the spin properties of dimetallofullerenes, such as spin–spin interactions, frontier orbital energies, and single-ion magnetic anisotropy.
• 2.Most of the studied di-EMFs with a single-electron Ln–Ln bond are based on the fullerene C₈₀-I_h. Comparison of the EPR and SMM properties of Ln₂@C₇₉N and Ln₂@C₈₀(CH₂Ph) shows a noticeable influence of the fullerene cage on the magnetic properties of di-EMFs,^19,20,22 which is not fully understood and should be studied further.
• 3.Endohedral fullerenes are able to undergo multiple derivatization reactions,⁶⁷ which affect the fullerene π system. The mutual influence of Ln–Ln bonds and exohedral chemistry and the variation of the spin properties of di-EMFs with functionalization have not been studied to date.
• 4.Ln–Ln bonds in fullerenes are redox-active,³⁵ and the electron transfer can dramatically change the magnetic properties of di-EMFs. Electron transfer can also be realized intramolecularly by creating donor–acceptor dyads with photoexcited electron transfer,⁶⁸ which may result in optically controlled magnetism.
• 5.Spins encapsulated within carbon cages are isolated from the environment but still can be manipulated externally, which has rich implications for quantum information processing.⁶⁹ The first experiments in this direction²¹ demonstrate the great potential of single-electron Ln–Ln bonds.
• 6.The chemical and thermal stability of fullerenes allow the design of EMF-based supramolecular architectures. One- and two-dimensional arrays of some EMF-SMMs have already been reported,¹³ and this should be feasible for di-EMFs as well. The strong interaction of core 4f electrons with the frontier Ln–Ln bonding orbital may give unique spin-transport properties. Thus, di-EMFs with a single-electron Ln–Ln bond have excellent perspectives in molecular spintronics.
• 7.The single-electron lanthanide–lanthanide bond in di-EMFs is challenging with regard to the development of a theoretical framework required for interpretation of experimental data. Although treating a single-electron Ln–Ln bond as a three-spin [Ln³⁺–e–Ln³⁺] system gives a reasonable description of the magnetic properties, the validity of this approach remains questionable. Implementation of more robust ab initio approaches and severe testing of model spin Hamiltonians are required for better modeling of the magnetic properties of di-EMFs.

Biographies

Fupin Liu received his Ph.D. in 2014 from the University of Science and Technology of China in Hefei, where he worked with Prof. S. Yang. In 2015 he joined the Fullerene group at IFW Dresden in Germany and is currently supervising synthetic and crystallographic studies of metallofullerenes.

Lukas Spree obtained his Master’s degree in applied natural science from Freiberg University in 2016 and then joined the Fullerene group at IFW Dresden to study the synthesis, chemical functionalization, and magnetic properties of metallofullerenes with F. Liu and A. A. Popov.

Denis S. Krylov obtained his Master’s degree in nanobiophysics in 2013 from TU Dresden. In 2014 he joined the Popov group at IFW Dresden to study the magnetic properties of EMFs by SQUID magnetometry, XMCD, and STM techniques. After his Ph.D. defense in 2018, he joined the Center for Quantum Nanoscience at Ewha Womans University (Seoul, Korea) to study spin properties of atoms and molecules on the nanoscale.

Georgios Velkos obtained his Master’s degree in nanosciences and nanotechnologies in 2017 from Aristotle University of Thessaloniki in Greece with an internship at Oxford University. Then he joined the Popov group at IFW Dresden to study the magnetic properties of metallofullerenes.

Stanislav M. Avdoshenko received M.S. (2007) and Ph.D. (2009) on computational studies of fullerene derivatives from Moscow State University. In 2009–2012 he was an Erasmus Fellow at TU Dresden, studying transport phenomena in complex systems. He then moved to the United States, first to the School of Materials Engineering at Purdue University (2012–2014) and then to the Institute for Computational Engineering and Sciences at UT Austin (2014–2016). In 2017 he received the prestigious Marie Skłodowska-Curie Fellowship to support his independent research at IFW Dresden. His group is now working on the theory of spin properties of lanthanide and transition metal systems, including those of metallofullerenes, and on quantum spin and charge dynamics in molecular materials.

Alexey A. Popov received M.S. (1999) and Ph.D. (2003) in chemistry from Moscow State University (MSU) in Russia. He was a Senior Researcher at MSU until 2008, when he received an Alexander von Humboldt Fellowship to work on endohedral metallofullerenes at IFW Dresden, where he now heads the Fullerene group. His research interests include experimental and computational studies of EMFs, including their synthesis, derivatization, magnetism, spectroelectrochemistry, and photophysics. He is a recipient of an ERC Consolidator Grant for the studies of bulk and surface magnetism of EMF-SMMs.

The authors declare no competing financial interest.