Summary
Digital pathology imaging of tumor tissues, which captures histological details in high resolution, is fast becoming a routine clinical procedure. Recent developments in deep-learning methods have enabled the identification, characterization, and classification of individual cells from pathology images analysis at a large scale. This creates new opportunities to study the spatial patterns of and interactions among different types of cells. Reliable statistical approaches to modeling such spatial patterns and interactions can provide insight into tumor progression and shed light on the biological mechanisms of cancer. In this article, we consider the problem of modeling a pathology image with irregular locations of three different types of cells: lymphocyte, stromal, and tumor cells. We propose a novel Bayesian hierarchical model, which incorporates a hidden Potts model to project the irregularly distributed cells to a square lattice and a Markov random field prior model to identify regions in a heterogeneous pathology image. The model allows us to quantify the interactions between different types of cells, some of which are clinically meaningful. We use Markov chain Monte Carlo sampling techniques, combined with a double Metropolis–Hastings algorithm, in order to simulate samples approximately from a distribution with an intractable normalizing constant. The proposed model was applied to the pathology images of 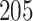 lung cancer patients from the National Lung Screening trial, and the results show that the interaction strength between tumor and stromal cells predicts patient prognosis (P =
lung cancer patients from the National Lung Screening trial, and the results show that the interaction strength between tumor and stromal cells predicts patient prognosis (P = 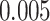 ). This statistical methodology provides a new perspective for understanding the role of cell–cell interactions in cancer progression.
). This statistical methodology provides a new perspective for understanding the role of cell–cell interactions in cancer progression.
Keywords: Double Metropolis–Hastings, Hidden Potts model, Lung cancer, Markov random field, Mixture model, Pathology image, Potts model, Spatial point pattern
1. Introduction
Cancer is a group of diseases characterized by the uncontrolled growth of tumor cells that can occur anywhere in the body. Current guidelines for diagnosing and treating cancer are largely based on pathological examination of hematoxylin and eosin (H&E)-stained formalin-fixed paraffin-embedded tissue section slides. A tumor pathology image harbors a large amount of information, such as growth patterns and interactions between tumor cells and the surrounding micro-environment. Cell growth pattern is associated with the survival outcome of cancer patients (Amin and others, 2002; Gleason and others, 2002; Borczuk and others, 2009; Barletta and others, 2010). Furthermore, a recent study shows that the cell growth pattern in tumor tissues predicts treatment response in lung cancer patients (Tsao and others, 2015). Different cell types, including lymphocyte (a type of immune cell), stromal, and tumor cells, are commonly seen in tumor tissue images. The interactions among these cells play vital roles in the progression and metastasis of cancer (Mantovani and others, 2002; Orimo and others, 2005; Merlo and others, 2006; Polyak and others, 2009; Hanahan and Weinberg, 2011; Gillies and others, 2012; Junttila and de Sauvage, 2013). Spatial variations among cell types and their association with patient prognosis have been previously reported in breast cancer (Mattfeldt and others, 2009). However, there is a lack of rigorous statistical methods to quantify the cell interactions due to the high complexity and heterogeneity of the disease.
With the advance of imaging technology, H&E-stained pathology imaging is becoming a routine clinical procedure. This process produces massive digital pathology images that capture histological details in a high resolution. Therefore, developing statistical methods for tumor pathology images has become essential to utilize the high-resolution images for patient prognosis and treatment planning. Recent studies have demonstrated the feasibility of using digital pathology image analysis to assist pathologists in clinical diagnosis and prognosis (Beck and others, 2011; Yuan and others, 2012; Luo and others, 2016; Yu and others, 2016). Furthermore, the application of computer vision and machine learning techniques allows for the identification and classification of individual cells in digital pathology image analysis (Yuan and others, 2012). Recent developments in deep-learning methods have greatly facilitated this process. We have developed a ConvPath pipeline (Figure S1 of supplementary material available at Biostatistics online, manuscript under review), which uses a convolutional neural network (CNN) to identify individual cells and predict the cell types (https://qbrc.swmed.edu/projects/cnn/). The CNN was trained using a large cohort of lung cancer pathology images manually labeled by pathologists. This pipeline can process tumor tissue images and determine the cell type and location for each individual cell. It creates new opportunities to study the spatial patterns of and interactions among different types of cells, which may reveal important information about tumor cell growth and its micro-environment. Spatial models, such as the Ising model and Potts model, have been used to extract spatial information for imaging data (Green and Richardson, 2002; Li, 2009; Ayasso and Mohammad-Djafari, 2010). Recently, Li and others (2017) proposed a variant of the Potts model to study pathology images, assuming that cell–cell interactions are homogeneous across the whole image. However, tumor cell growth patterns and their surrounding micro-environments are heterogeneous and vary across different spatial locations (see, e.g. Schnipper, 1986; Kirk, 2012; Longo, 2012; Shibata, 2012; Marte, 2013; McGranahan and Swanton, 2017).
In this article, we develop a novel Bayesian hidden Potts mixture model for the cell distribution maps, such as Figure 1(a) and (d), generated by our ConvPath pipeline. The proposed model has several advantages. First, it incorporates a hidden Potts model that projects irregularly distributed cells into a square lattice, which significantly reduces the complexity of the unstructured spatial data. Second, it integrates a Markov random field (MRF) prior model that accounts for the heterogeneity across the image, while partitioning the image into multiple regions with homogeneous cell–cell interactions. The interaction parameters of the Potts model, also called interaction energies, can be used to characterize the strengths of the spatial interactions among different types of cells. The double Metropolis–Hastings (DMH) algorithm (Liang, 2010) is used to sample from the posterior distribution with an intractable normalizing constant in the Potts model. The model performed well in simulated studies.
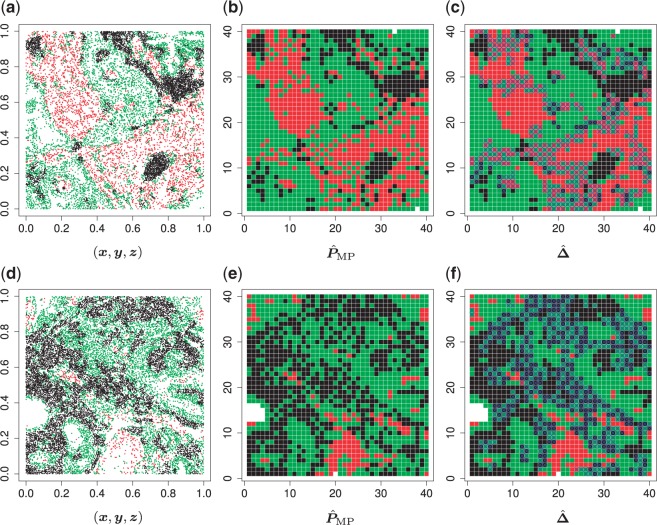
Fig. 1.
(a and d) The observed cell distribution maps for two sample images from different patients, where lymphocyte, stromal, and tumor cells are marked in black, red, and green, respectively. (b and e) The estimated hidden spins 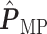 in the
in the 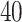 -by-
-by-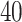 lattice. (c and f) The estimated AOI indicators
lattice. (c and f) The estimated AOI indicators 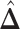 by choosing
by choosing 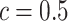 (median model), where the blue indicates
(median model), where the blue indicates 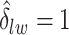 . For the first example, of which
. For the first example, of which 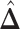 as shown in (c),
as shown in (c), 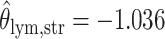 ,
, 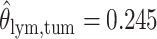 ,
, 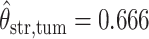 ,
, 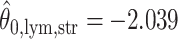 ,
, 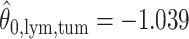 ,
, 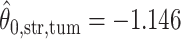 ; for the second example, of which
; for the second example, of which 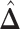 as shown in (f),
as shown in (f), 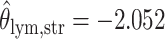 ,
, 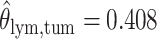 ,
, 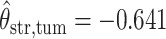 ,
, 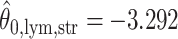 ,
, 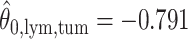 ,
, 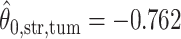 . Note that in the bottom-left of (d), (e), and (f), the empty region is the alveolus.
. Note that in the bottom-left of (d), (e), and (f), the empty region is the alveolus.
The proposed model was applied to the 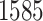 pathology images of
pathology images of 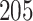 lung cancer patients from the National Lung Screening Trial (NLST), and the results show that the interaction strength between tumor and stromal cells is significantly associated with patient prognosis (P =
lung cancer patients from the National Lung Screening Trial (NLST), and the results show that the interaction strength between tumor and stromal cells is significantly associated with patient prognosis (P = 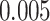 ). This statistical methodology provides a new perspective for understanding the role of cell–cell interactions in cancer progression. Last but not least, although this article is motivated by the analysis of tumor pathology images, the proposed model is generally applicable for other types of data from heterogeneous marked point processes. This article, to our best knowledge, is the first attempt to develop a rigorous statistical framework to model the heterogeneous spatial interactions among different types of cells in tumor pathology images.
). This statistical methodology provides a new perspective for understanding the role of cell–cell interactions in cancer progression. Last but not least, although this article is motivated by the analysis of tumor pathology images, the proposed model is generally applicable for other types of data from heterogeneous marked point processes. This article, to our best knowledge, is the first attempt to develop a rigorous statistical framework to model the heterogeneous spatial interactions among different types of cells in tumor pathology images.
The remainder of the article is organized as follows. Section 2 introduces the proposed modeling framework and discusses the MRF prior formulation. Section 3 describes the Markov chain Monte Carlo (MCMC) algorithm and discusses the resulting posterior inference. Section 4 assesses performance of the proposed model on simulated data and the results of a lung cancer case study. Section 5 concludes the article with some remarks on future research directions.
2. Models
We first review the Potts model and its interaction energy measurement in Section 2.1, and then we introduce the hidden Potts model in Section 2.2 and the hidden Potts mixture (HPM) model in Section 2.3. The graphical formulation of the HPM model is presented in Figure S2 of supplementary material available at Biostatistics online.
2.1. The Potts model
Let 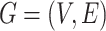 denote a graph
denote a graph 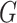 composed of a finite set
composed of a finite set 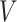 of vertices and a set
of vertices and a set 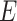 of edges joining pairs of vertices. In statistics, the Potts model can be considered as an undirected graph such that each vertex
of edges joining pairs of vertices. In statistics, the Potts model can be considered as an undirected graph such that each vertex 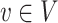 is geometrically regular assigned on a lattice (e.g. square, triangular, or honeycomb lattice) and each edge
is geometrically regular assigned on a lattice (e.g. square, triangular, or honeycomb lattice) and each edge 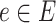 is at the same distance. Particularly, for an
is at the same distance. Particularly, for an 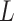 -by-
-by- square lattice graph in a Cartesian coordinate system, let
square lattice graph in a Cartesian coordinate system, let 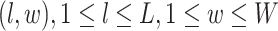 denote the coordinate of each vertex. Then, edges are connected between the vertex at location
denote the coordinate of each vertex. Then, edges are connected between the vertex at location 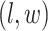 and its four neighbors at locations
and its four neighbors at locations 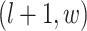 ,
, 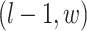 ,
, 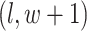 , and
, and 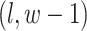 , if applicable. Every vertex will be assigned a spin, which is defined as an assignment of
, if applicable. Every vertex will be assigned a spin, which is defined as an assignment of 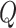
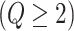 different classes. When
different classes. When 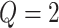 , the Potts model is known as the Ising model. Let an
, the Potts model is known as the Ising model. Let an 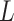 -by-
-by-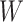 matrix
matrix 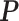 denote the collection of all spins, where each element
denote the collection of all spins, where each element 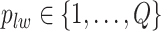 . Since the vertices are assigned different spins and react with their neighbors’ spins, there will be some measurement of overall energy, named Hamiltonian,
. Since the vertices are assigned different spins and react with their neighbors’ spins, there will be some measurement of overall energy, named Hamiltonian,
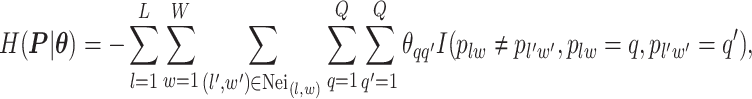 |
(2.1) |
where 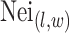 denotes the coordinate set of neighbors of vertex
denotes the coordinate set of neighbors of vertex  ,
, 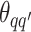 denotes the interaction energy between adjacent vertices, and
denotes the interaction energy between adjacent vertices, and 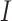 denotes the indicator function. Note that
denotes the indicator function. Note that  . According to Equation (2.1), only those edges between vertices that have different spins are counted. The negative value of
. According to Equation (2.1), only those edges between vertices that have different spins are counted. The negative value of 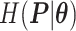 can be also considered as the weighted average of those edges connecting two different spins among the graph.
can be also considered as the weighted average of those edges connecting two different spins among the graph.
The Potts model probability mass function calculates the probability of observing the lattice in a particular state 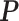 , where a state is a choice of spin at each vertex,
, where a state is a choice of spin at each vertex,
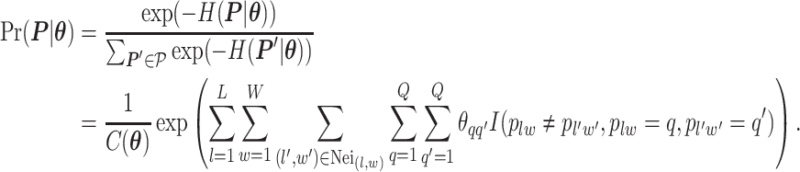 |
(2.2) |
Here, 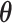 denotes the collection of interaction energy parameters between different classes, where each element
denotes the collection of interaction energy parameters between different classes, where each element 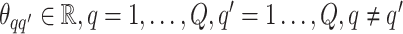 and
and 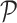 denotes the set of all possible states of the lattice. An exact evaluation of the normalizing constant
denotes the set of all possible states of the lattice. An exact evaluation of the normalizing constant 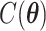 needs to sum over the entire space of
needs to sum over the entire space of 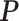 , which consists of
, which consists of 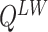 states. Thus,
states. Thus, 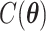 is intractable even for a small size model. Take
is intractable even for a small size model. Take 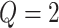 ,
, 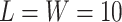 for example, it needs to sum over
for example, it needs to sum over 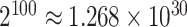 elements. To address this issue, we will employ the DMH algorithm (Liang, 2010) to estimate
elements. To address this issue, we will employ the DMH algorithm (Liang, 2010) to estimate 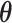 without calculating
without calculating 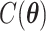 , which will be illustrated in Section 3. Equation (2.2) serves as the full likelihood of the Potts model, which satisfies the Markov property. Therefore, we can write the probability of observing
, which will be illustrated in Section 3. Equation (2.2) serves as the full likelihood of the Potts model, which satisfies the Markov property. Therefore, we can write the probability of observing 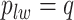 conditional on its neighbor spins, which is
conditional on its neighbor spins, which is
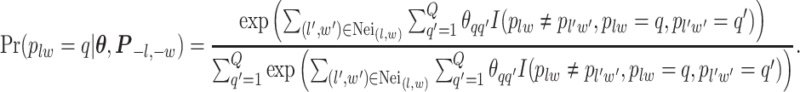 |
(2.3) |
Here, we use 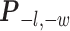 to denote all the spins excluding
to denote all the spins excluding 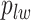 . According to Equation (2.3), the conditional probability that we observe the vertex
. According to Equation (2.3), the conditional probability that we observe the vertex 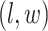 belonging to class
belonging to class 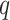 depends on the interaction energy parameters
depends on the interaction energy parameters 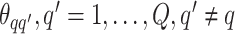 and the number of edges connecting two different spins. The larger the value of
and the number of edges connecting two different spins. The larger the value of 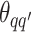 , the more likely that
, the more likely that 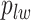 is discordant with the majority of its four neighboring spins.
is discordant with the majority of its four neighboring spins.
2.2. The hidden Potts model
Potts models have a wide range of applications in many areas since they provide an appealing representation of images and other types of spatial data. However, for images with irregularly distributed dots, it is impossible to apply a Potts model based on a lattice that forms a regular tiling. To overcome this limitation, Li and others (2017) proposed a hidden Potts model by introducing an auxiliary lattice to the image and defining a pre-specified projection parameter to control the similarity between the imputed lattice image and the original image. We develop a more flexible hidden Potts model by formulating a prior on the projection parameter. More importantly, our model takes into account the heterogeneity of the imaging data.
We consider a preprocessed pathology image, as shown in Figure 1(a) and (d), with 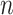 observed cells, where
observed cells, where 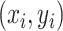 represents the location and
represents the location and 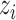 indicates the type of cell
indicates the type of cell 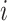 . We denote
. We denote 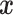 ,
, 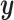 , and
, and 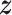 as the collection of
as the collection of 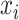 ,
, 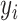 , and
, and  , respectively. Let an
, respectively. Let an 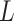 -by-
-by-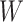 matrix
matrix 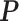 denote the hidden spins at the auxiliary lattice, which partitions the image into
denote the hidden spins at the auxiliary lattice, which partitions the image into 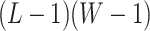 squares. The ratio
squares. The ratio 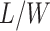 should approximate the ratio of
should approximate the ratio of 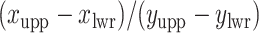 , where
, where 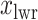 and
and 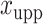 denote the lower and upper bounds of the horizontal axis, and
denote the lower and upper bounds of the horizontal axis, and 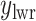 and
and 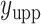 denote the lower and upper bounds of the vertical axis of the image. The bounds are usually known; if not, they can be estimated from the data itself by: (1) roughly setting
denote the lower and upper bounds of the vertical axis of the image. The bounds are usually known; if not, they can be estimated from the data itself by: (1) roughly setting 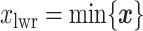 ,
, 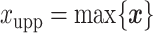 ,
, 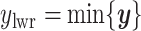 , and
, and 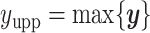 or (2) computing the Ripley–Rasson estimator (Ripley and Rasson, 1977) of a rectangle window given
or (2) computing the Ripley–Rasson estimator (Ripley and Rasson, 1977) of a rectangle window given 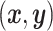 . To fit the imaging data into the square-lattice system, we normalize each coordinate
. To fit the imaging data into the square-lattice system, we normalize each coordinate 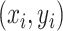 by performing a linear transformation
by performing a linear transformation 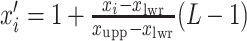 and
and 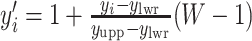 . Then we assume that the probability of assigning cell
. Then we assume that the probability of assigning cell 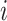 to type
to type 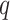 conditional on its adjacent spins at the hidden lattice is
conditional on its adjacent spins at the hidden lattice is
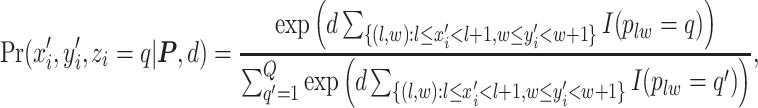 |
(2.4) |
where 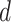 is the projection parameter. The larger the value of
is the projection parameter. The larger the value of 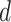 , the more likely a cell type is the same as the majority of its adjacent spins. If
, the more likely a cell type is the same as the majority of its adjacent spins. If 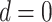 , then
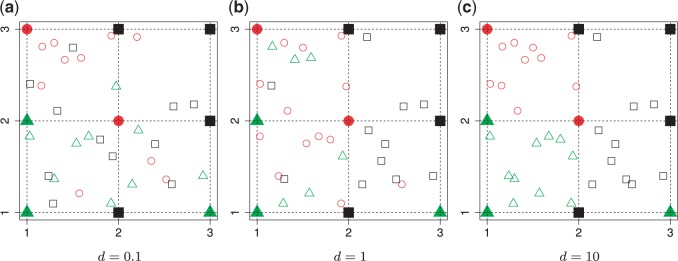
, then 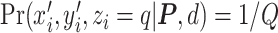 , which means the spatial distribution of the random cells is independent from the hidden spins. Figure 2 illustrates an example of the point emission process from a given
, which means the spatial distribution of the random cells is independent from the hidden spins. Figure 2 illustrates an example of the point emission process from a given 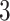 -by-
-by-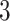 Potts model under different choices of
Potts model under different choices of 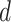 . In addition, we also demonstrate how
. In addition, we also demonstrate how 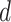 yields varying spin assignments of the hidden lattice conditional on the observed cells from a larger dataset in our simulation study (see Figure S5 of supplementary material available at Biostatistics online). Note that the cell types are independent and identically distributed within each lattice unit, conditional on the four nearby spins. Although this assumption is suitable for most cases, we discuss a location-dependent hidden Potts model in Section S1 of supplementary material available at Biostatistics online.
yields varying spin assignments of the hidden lattice conditional on the observed cells from a larger dataset in our simulation study (see Figure S5 of supplementary material available at Biostatistics online). Note that the cell types are independent and identically distributed within each lattice unit, conditional on the four nearby spins. Although this assumption is suitable for most cases, we discuss a location-dependent hidden Potts model in Section S1 of supplementary material available at Biostatistics online.
Fig. 2.
Illustration of a 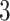 -by-
-by-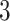 auxiliary lattice and the point emission process by different choices of
auxiliary lattice and the point emission process by different choices of 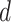 . The empty points represent the observed cells and the filled points represent the hidden spins in the lattice. The square, circle, and triangle shapes stand for class
. The empty points represent the observed cells and the filled points represent the hidden spins in the lattice. The square, circle, and triangle shapes stand for class 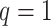 , 2, and 3, respectively.
, 2, and 3, respectively.
To summarize, the joint likelihood function of the hidden Potts model can be written as
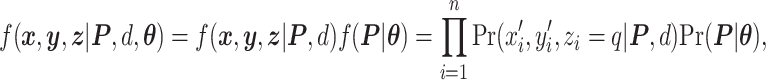 |
(2.5) |
where 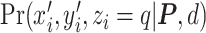 and
and 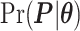 are given in Equations (2.4) and (2.2), respectively. The inference of spin
are given in Equations (2.4) and (2.2), respectively. The inference of spin 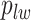 depends on: (1) the nearby observed cells within the square area included by coordinates
depends on: (1) the nearby observed cells within the square area included by coordinates 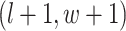 ,
, 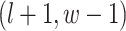 ,
, 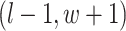 , and
, and 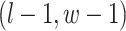 ; (2) the nearby spins at locations
; (2) the nearby spins at locations 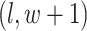 ,
, 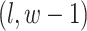 ,
, 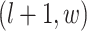 ,
, 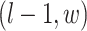 ; and (3) the underlying interaction parameters
; and (3) the underlying interaction parameters 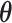 . We specify the prior distribution for
. We specify the prior distribution for  as
as 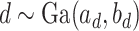 . One standard way of setting a weakly informative gamma prior is to choose small values for the two parameters, such as
. One standard way of setting a weakly informative gamma prior is to choose small values for the two parameters, such as 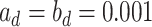 (Gelman, 2006). We conclude this subsection by discussing how to choose the tunable parameters
(Gelman, 2006). We conclude this subsection by discussing how to choose the tunable parameters 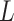 and
and 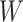 , which determine the size of the auxiliary lattice. Larger values of
, which determine the size of the auxiliary lattice. Larger values of 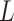 and
and 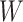 make the inference computationally expensive, while small values make a rough approximation to the interaction energy. We suggest choosing the values that correspond to
make the inference computationally expensive, while small values make a rough approximation to the interaction energy. We suggest choosing the values that correspond to 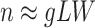 , where
, where 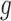 can be any integer between
can be any integer between 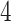 and
and 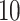 . This constraint generally requires observing
. This constraint generally requires observing 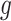 cells in each square.
cells in each square.
2.3. A proposal of the hidden Potts mixture model
Tumor tissues are heterogeneous. Spatial patterns of cell distributions may vary across different spatial regions. Applying a homogenous model described in Section 2.2 may obscure the recovery of the true values of interaction energy by averaging out the real signal from the “areas of interest” with other background areas. In this study, we propose a hidden Potts mixture model in order to take into account the heterogeneity of spatial point patterns observed in the pathology images. We first discuss the general case when the number of mixture components 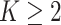 and then focus on the model when
and then focus on the model when 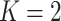 . From a biological point of view, these two regions can be referred to respectively: (1) The areas of interests (AOIs) with high interaction strengths among different types of cells. In AOIs, the different types of cells are highly mixed, which may reveal important information about cancer progression and (2) The background areas, in which the same type cells are aggregated into clusters.
. From a biological point of view, these two regions can be referred to respectively: (1) The areas of interests (AOIs) with high interaction strengths among different types of cells. In AOIs, the different types of cells are highly mixed, which may reveal important information about cancer progression and (2) The background areas, in which the same type cells are aggregated into clusters.
In the same auxiliary lattice described in Section 2.2, we envision that there are 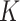 homogeneous regions with different interaction parameter settings,
homogeneous regions with different interaction parameter settings, 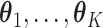 . With this assumption, an
. With this assumption, an 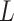 -by-
-by-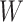 latent matrix
latent matrix 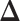 is introduced to indicate the
is introduced to indicate the 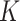 distinct regions, with
distinct regions, with 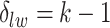 if the spin at location
if the spin at location 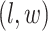 belongs to group
belongs to group 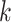 . According to Equation (2.2), the probability mass function of the mixture model given the partition
. According to Equation (2.2), the probability mass function of the mixture model given the partition 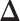 can be written as,
can be written as,
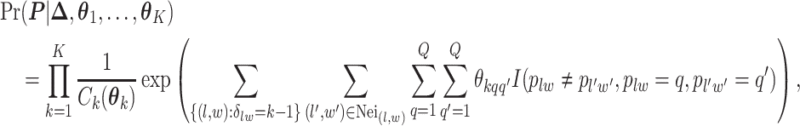 |
(2.6) |
where 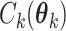 is the normalizing constants for region
is the normalizing constants for region 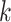 . To encourage two neighbor spins to be more likely in the same region (i.e. have the same
. To encourage two neighbor spins to be more likely in the same region (i.e. have the same 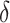 value), we incorporate the spatial dependency structure into the prior on
value), we incorporate the spatial dependency structure into the prior on 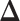 via a Potts model that satisfies a spatial Markov property. This prior model is a type of MRF, where the distribution of a set of random variables follows Markov properties that can be presented by an undirected graph. In our model, this graph is defined by the
via a Potts model that satisfies a spatial Markov property. This prior model is a type of MRF, where the distribution of a set of random variables follows Markov properties that can be presented by an undirected graph. In our model, this graph is defined by the 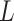 -by-
-by-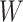 auxiliary lattice. The prior can be written as
auxiliary lattice. The prior can be written as
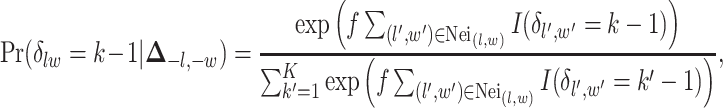 |
(2.7) |
where 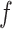 is a non-negative parameter that controls the spatial interaction and
is a non-negative parameter that controls the spatial interaction and 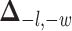 denotes the set of
denotes the set of 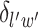 ’s excluding
’s excluding 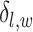 . A large value of
. A large value of 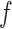 makes largely clustered configurations of
makes largely clustered configurations of 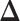 , while a small value corresponds to patterns that do not display any sort of spatial organization. Although the choice of
, while a small value corresponds to patterns that do not display any sort of spatial organization. Although the choice of 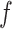 is very tricky, François and others (2006) suggests that the value
is very tricky, François and others (2006) suggests that the value 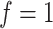 can be considered a high level of spatial interaction for
can be considered a high level of spatial interaction for  .
.
When 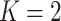 ,
, 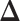 becomes a binary latent matrix that indicates the two distinct regions, with
becomes a binary latent matrix that indicates the two distinct regions, with 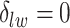 if the spin at location
if the spin at location 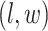 belongs to the background area, and
belongs to the background area, and 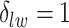 if the spin at location
if the spin at location 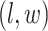 belongs to the AOI. Let
belongs to the AOI. Let 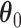 and
and 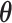 denote the interaction parameters in the background and AOI regions, respectively. According to Equation (2.6), the probability mass function of the two-component mixture model is written as,
denote the interaction parameters in the background and AOI regions, respectively. According to Equation (2.6), the probability mass function of the two-component mixture model is written as,
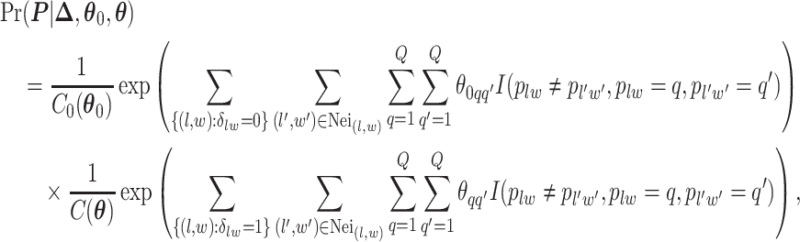 |
(2.8) |
where 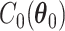 and
and 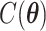 are the normalizing constants for the two regions. The prior model reduces to an Ising model, characterized by the following probability,
are the normalizing constants for the two regions. The prior model reduces to an Ising model, characterized by the following probability,
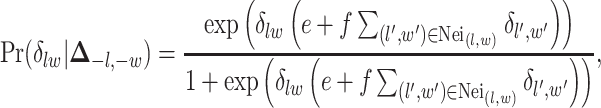 |
(2.9) |
where 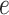 and
and 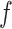 are hyperparameters to be chosen. Compared with Equation (2.7), the extra parameter
are hyperparameters to be chosen. Compared with Equation (2.7), the extra parameter 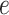 controls the number of
controls the number of 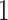 ’s in
’s in 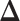 (i.e. the number of spins belonging to the AOI), while
(i.e. the number of spins belonging to the AOI), while 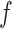 affects the probability of assigning a value according to its neighbor spins. Note that if a vertex does not have any neighbor in the AOI, its prior probability reduces to an independent Bernoulli prior with parameter
affects the probability of assigning a value according to its neighbor spins. Note that if a vertex does not have any neighbor in the AOI, its prior probability reduces to an independent Bernoulli prior with parameter 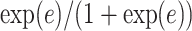 , which is a logistic transformation of
, which is a logistic transformation of 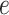 . Although the parameterization is somewhat arbitrary, some care is needed in deciding the value of
. Although the parameterization is somewhat arbitrary, some care is needed in deciding the value of 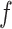 . In particular, a large value of
. In particular, a large value of 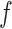 may lead to a phase transition problem; that is, the expected number of ones in
may lead to a phase transition problem; that is, the expected number of ones in 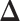 can increase massively for small increments of
can increase massively for small increments of 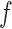 . This problem can happen because Equation (2.9) can only increase as a function of the number of
. This problem can happen because Equation (2.9) can only increase as a function of the number of 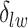 ’s equal to
’s equal to 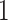 . An empirical estimate of the phase transition value can be obtained using the algorithm proposed by Propp and Wilson (1996) and the values of
. An empirical estimate of the phase transition value can be obtained using the algorithm proposed by Propp and Wilson (1996) and the values of 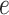 and
and 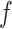 can then be chosen accordingly. In this article, we treat
can then be chosen accordingly. In this article, we treat 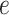 and
and 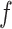 as fixed hyperparameters, following the articles by Li and Zhang (2010) and Stingo and others (2013). Table S1 of supplementary material available at Biostatistics online lists our recommendation for
as fixed hyperparameters, following the articles by Li and Zhang (2010) and Stingo and others (2013). Table S1 of supplementary material available at Biostatistics online lists our recommendation for 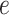 and
and 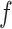 based on the size of the AOI a priori. As for
based on the size of the AOI a priori. As for 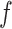 , any value between
, any value between 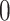 and
and 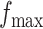 , as shown in Table S1 of supplementary material available at Biostatistics online, can be considered, with larger values closer to the phase transition point, leading to higher prior probabilities of selection for those nodes whose neighbors are already selected. In Section 4.1, we use simulated data to investigate the sensitivity to the specification of parameters
, as shown in Table S1 of supplementary material available at Biostatistics online, can be considered, with larger values closer to the phase transition point, leading to higher prior probabilities of selection for those nodes whose neighbors are already selected. In Section 4.1, we use simulated data to investigate the sensitivity to the specification of parameters 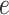 and
and 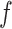 . For
. For 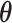 and
and 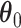 , we consider normal priors, and we set
, we consider normal priors, and we set 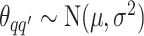 and
and 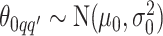 , where
, where 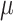 can be set to a positive number while
can be set to a positive number while 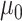 a negative number. This assumes the AOI has more interaction energy than the background a priori.
a negative number. This assumes the AOI has more interaction energy than the background a priori.
3. Model fitting
In this section, we describe the MCMC algorithm for posterior inference. Our inferential strategy allows us to simultaneously identify the AOI while quantifying the interaction parameters.
3.1. MCMC algorithm
Our primary interest lies in the identification of the AOI, via the matrix 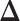 , and the inference of the interaction parameters within the AOI and the background area, via the vector
, and the inference of the interaction parameters within the AOI and the background area, via the vector 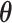 and
and 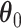 . We design a MCMC algorithm based on the DMH (Liang, 2010) and Metropolis search variable selection algorithms (George and McCulloch, 1997; Brown and others, 1998) to search the model space that consists of
. We design a MCMC algorithm based on the DMH (Liang, 2010) and Metropolis search variable selection algorithms (George and McCulloch, 1997; Brown and others, 1998) to search the model space that consists of 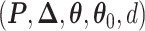 . We briefly describe why and how DMH is used in the model fitting as follows. The full details of our MCMC algorithm are given in Section S2 of supplementary material available at Biostatistics online.
. We briefly describe why and how DMH is used in the model fitting as follows. The full details of our MCMC algorithm are given in Section S2 of supplementary material available at Biostatistics online.
Take the update of 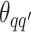 as an example. Within each MCMC iteration, we need to sample
as an example. Within each MCMC iteration, we need to sample 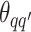 from its conditional distribution
from its conditional distribution 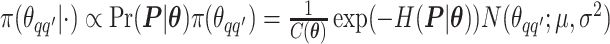 . Apparently, the Metropolis–Hastings (MH) algorithm cannot be directly applied to simulate from this distribution as the acceptance probability would involve an unknown normalizing constant ratio
. Apparently, the Metropolis–Hastings (MH) algorithm cannot be directly applied to simulate from this distribution as the acceptance probability would involve an unknown normalizing constant ratio 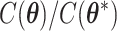 , where
, where 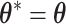 except the proposed element
except the proposed element 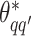 within. To address this issue, Liang (2010) proposed an auxiliary variable MCMC algorithm, which can make the normalizing constant ratio canceled by augmenting appropriate auxiliary variables through a short run of the MH algorithm initialized with the original observation. To do so, an auxiliary variable
within. To address this issue, Liang (2010) proposed an auxiliary variable MCMC algorithm, which can make the normalizing constant ratio canceled by augmenting appropriate auxiliary variables through a short run of the MH algorithm initialized with the original observation. To do so, an auxiliary variable 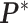 is simulated starting from
is simulated starting from 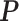 based on the new
based on the new 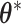 . Then, the proposed value
. Then, the proposed value 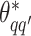 will be accepted with probability
will be accepted with probability 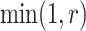 , where the Hastings ratio is computed as
, where the Hastings ratio is computed as
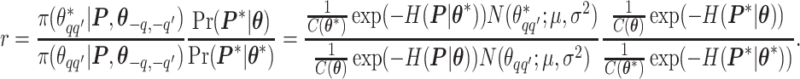 |
As we can see, the unknown normalizing constant ratio has been canceled.
3.2. Posterior estimation
We obtain the posterior inference by post-processing of the MCMC samples after burn-in. Suppose that two sequences of MCMC samples 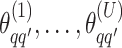 and
and 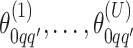 have been collected, where
have been collected, where 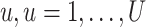 indexes the iteration after burn-in. An approximate Bayesian estimator of
indexes the iteration after burn-in. An approximate Bayesian estimator of 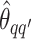 and
and 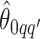 can be simply obtained by averaging over the samples,
can be simply obtained by averaging over the samples,
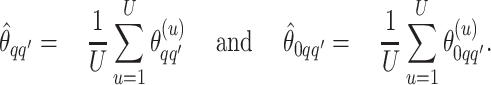 |
(3.1) |
For 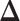 , we choose an estimate that relies on the marginal probability of inclusion (PPI) of single spins as the proportion of MCMC iterations in which the corresponding
, we choose an estimate that relies on the marginal probability of inclusion (PPI) of single spins as the proportion of MCMC iterations in which the corresponding 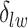 equal to
equal to 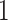 . That is
. That is
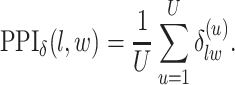 |
(3.2) |
A point estimate of 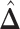 is then obtained by identifying those PPI values that exceed a given cut-off
is then obtained by identifying those PPI values that exceed a given cut-off 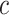 . A simple way is to choose
. A simple way is to choose 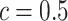 to obtain a median model. An alternative approach is based on a decision theoretic criterion, such as in Newton and others (2004), so that an expected rate of false detection (i.e. Bayesian FDR) smaller than a fixed threshold can be guaranteed. For the hidden spins
to obtain a median model. An alternative approach is based on a decision theoretic criterion, such as in Newton and others (2004), so that an expected rate of false detection (i.e. Bayesian FDR) smaller than a fixed threshold can be guaranteed. For the hidden spins 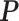 , we construct the estimate by selecting the most likely
, we construct the estimate by selecting the most likely 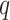 for each position
for each position 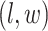 :
:
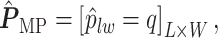 |
(3.3) |
if 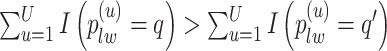 for any
for any 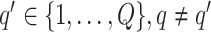 . We refer to the estimate obtained in this manner as the marginal probability (MP) estimate.
. We refer to the estimate obtained in this manner as the marginal probability (MP) estimate.
3.3. Label switching
In our finite mixture model, the invariance of the likelihood under permutation of the component labels may result in an identifiability problem, leading to symmetric and multimodal posterior distributions with up to 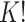 copies of each “genuine” model. For instance, for the case
copies of each “genuine” model. For instance, for the case 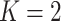 , we may obtain a model where
, we may obtain a model where 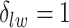 corresponds to the true background area, while
corresponds to the true background area, while 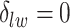 indicates the true AOI. This will also complicate inference on the parameters. To solve this problem, we simply impose an identifiability constraint on the interaction parameters,
indicates the true AOI. This will also complicate inference on the parameters. To solve this problem, we simply impose an identifiability constraint on the interaction parameters, 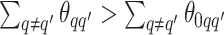 . For a more robust approach, we can also use the relabeling algorithm proposed by Stephens (2000).
. For a more robust approach, we can also use the relabeling algorithm proposed by Stephens (2000).
4. Results
We conducted simulation studies to assess the performance of the proposed Bayesian hidden Potts mixture model. The model was then applied to a large cohort of lung cancer pathology images, and it revealed novel potential imaging biomarkers for lung cancer prognosis.
4.1. Simulation
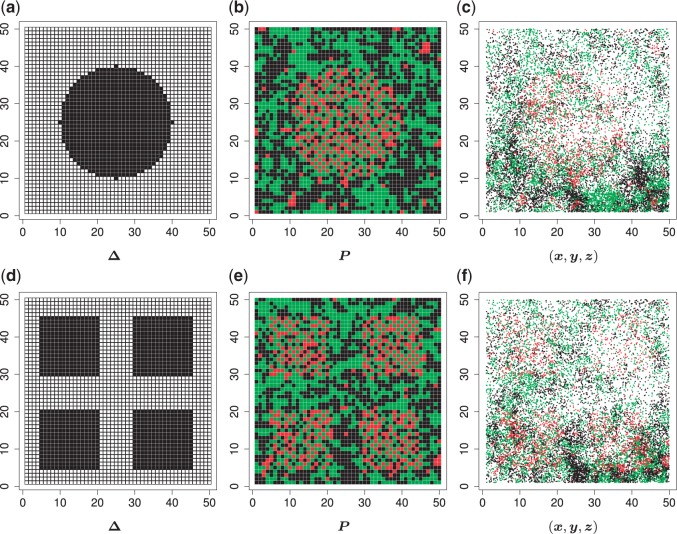
We used simulated data to investigate the performance of our strategy for posterior inference on the model parameters. All the generative models were based on a 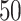 -by-
-by-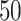 lattice unless otherwise noted. We considered two scenarios for the true structure of
lattice unless otherwise noted. We considered two scenarios for the true structure of 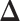 , as shown in Figure 3(a) and (d). For the first scenario the AOI is a single circle in the center of the image; for the second scenario the AOI is composed of four rectangles. The number of classes was set to
, as shown in Figure 3(a) and (d). For the first scenario the AOI is a single circle in the center of the image; for the second scenario the AOI is composed of four rectangles. The number of classes was set to 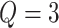 , and therefore, there were three interaction parameters in both
, and therefore, there were three interaction parameters in both 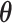 and
and 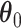 . We set
. We set 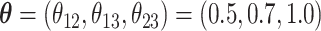 and
and 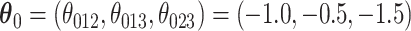 . For a given
. For a given 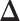 , we first simulated the hidden spins
, we first simulated the hidden spins 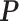 using the Gibbs sampler, running
using the Gibbs sampler, running 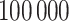 iterations with random starting configurations in both AOI and the background area. Next, we considered generating the points using two different point processes: (1) a homogeneous Poisson point process with a constant intensity
iterations with random starting configurations in both AOI and the background area. Next, we considered generating the points using two different point processes: (1) a homogeneous Poisson point process with a constant intensity  over the space
over the space 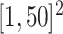 ; (2) a log Gaussian Cox process (LGCP) with an inhomogeneous intensity
; (2) a log Gaussian Cox process (LGCP) with an inhomogeneous intensity 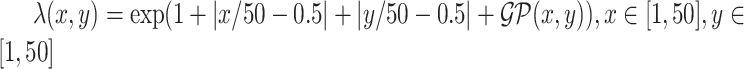 , where
, where 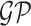 denotes a zero-mean Gaussian process with variance equal to
denotes a zero-mean Gaussian process with variance equal to 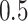 and scale equal to
and scale equal to 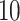 . Then, we assigned a class to each point according to its four nearest adjacent spins. Specifically, for point
. Then, we assigned a class to each point according to its four nearest adjacent spins. Specifically, for point 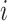 , its class
, its class 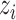 was drawn from a multinomial distribution
was drawn from a multinomial distribution 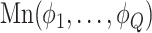 . The parameters
. The parameters 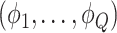 were inferred from a Dirichlet distribution
were inferred from a Dirichlet distribution 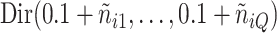 , where
, where 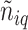 denotes the number of adjacent spins that belong to class
denotes the number of adjacent spins that belong to class 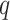 . Mathematically, it can be written as
. Mathematically, it can be written as 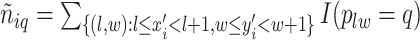 . Note that this mark formulation scheme is different from the model assumption, which is given in Equation (2.4). Figure 3(c) and (f) show examples of the observed data generated from LGCP. We repeated the above steps to generate
. Note that this mark formulation scheme is different from the model assumption, which is given in Equation (2.4). Figure 3(c) and (f) show examples of the observed data generated from LGCP. We repeated the above steps to generate 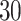 independent datasets for each setting of
independent datasets for each setting of 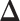 and each point process.
and each point process.
Fig. 3.
(a and d) The true maps of the 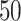 -by-
-by-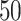 binary matrix
binary matrix 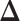 for scenarios 1 and 2, respectively. Each vertex in the lattice is represented by either an empty square if
for scenarios 1 and 2, respectively. Each vertex in the lattice is represented by either an empty square if 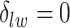 or a filled square if
or a filled square if 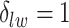 . (b and e) The true maps of the
. (b and e) The true maps of the  -by-
-by- hidden spins
hidden spins 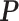 from one dataset generated from scenarios 1 and 2, respectively. The black, red, and green colors stand for class
from one dataset generated from scenarios 1 and 2, respectively. The black, red, and green colors stand for class 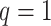 ,
, 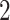 , and
, and 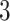 , respectively. (c and f) The observed cell distribution maps generated from the log Gaussian Cox process conditional on the hidden spins, as shown in (b and e), respectively.
, respectively. (c and f) The observed cell distribution maps generated from the log Gaussian Cox process conditional on the hidden spins, as shown in (b and e), respectively.
For the priors on 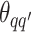 and
and 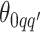 , we used normal distributions
, we used normal distributions 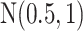 and
and 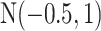 , respectively. We set the hyperparameters that control the MRF prior model to
, respectively. We set the hyperparameters that control the MRF prior model to 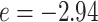 and
and 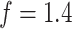 , which means that if a spin in the lattice does not have any neighbor in the AOI, its prior probability that it belongs to the AOI is
, which means that if a spin in the lattice does not have any neighbor in the AOI, its prior probability that it belongs to the AOI is 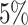 (For the first and second scenarios, the proportions of the AOI over the whole image are
(For the first and second scenarios, the proportions of the AOI over the whole image are 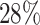 and
and 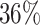 , respectively). As for the gamma prior on the projection parameter
, respectively). As for the gamma prior on the projection parameter 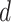 , we set
, we set 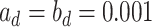 , which leads to a vague prior for
, which leads to a vague prior for 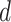 with expectation and variance equal to
with expectation and variance equal to 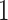 and
and 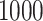 , respectively. This is one of the most commonly used weak gamma priors (Gelman, 2006). Results we report below were obtained by running the MCMC chain with
, respectively. This is one of the most commonly used weak gamma priors (Gelman, 2006). Results we report below were obtained by running the MCMC chain with 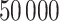 iterations, discarding the first
iterations, discarding the first 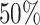 sweeps as burn in. We started the chain from a model by randomly choosing a
sweeps as burn in. We started the chain from a model by randomly choosing a 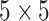 window in
window in  to be
to be 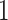 , drawing
, drawing 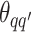 and
and 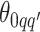 from their prior distributions, and assigning a random mark to each hidden spin
from their prior distributions, and assigning a random mark to each hidden spin 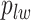 . We report the scalability of our methods in Section S3 of supplementary material available at Biostatistics online.
. We report the scalability of our methods in Section S3 of supplementary material available at Biostatistics online.
Figure S4 of supplementary material available at Biostatistics online displays the trace plots of the interaction parameters 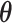 and the number of spins in the AOI from one simulated dataset generated from LGCP and scenario 2. It clearly shows that each chain converges and stabilizes around its true value in a very short run. Figure S5(a) and (b) of supplementary material available at Biostatistics online show the map of marginal posterior probabilities
and the number of spins in the AOI from one simulated dataset generated from LGCP and scenario 2. It clearly shows that each chain converges and stabilizes around its true value in a very short run. Figure S5(a) and (b) of supplementary material available at Biostatistics online show the map of marginal posterior probabilities 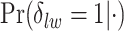 ’s and the median model by choosing
’s and the median model by choosing 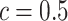 . Figure S5(c) of supplementary material available at Biostatistics online shows the map of the MP estimate of the hidden spins. It is evident from the maps that the inspection of the posterior probabilities of
. Figure S5(c) of supplementary material available at Biostatistics online shows the map of the MP estimate of the hidden spins. It is evident from the maps that the inspection of the posterior probabilities of 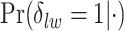 and
and 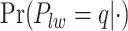 allows us to reconstruct the true structure of
allows us to reconstruct the true structure of 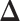 and
and 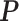 quite well. Figures S6 and S7 of supplementary material available at Biostatistics online show the density plots of MCMC samples of the six interaction parameters, collected from all
quite well. Figures S6 and S7 of supplementary material available at Biostatistics online show the density plots of MCMC samples of the six interaction parameters, collected from all 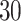 simulated datasets generated from each point process and scenario. Most of the true values were within the
simulated datasets generated from each point process and scenario. Most of the true values were within the 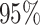 credible intervals. Next we evaluated the overall performance of recovery of the true
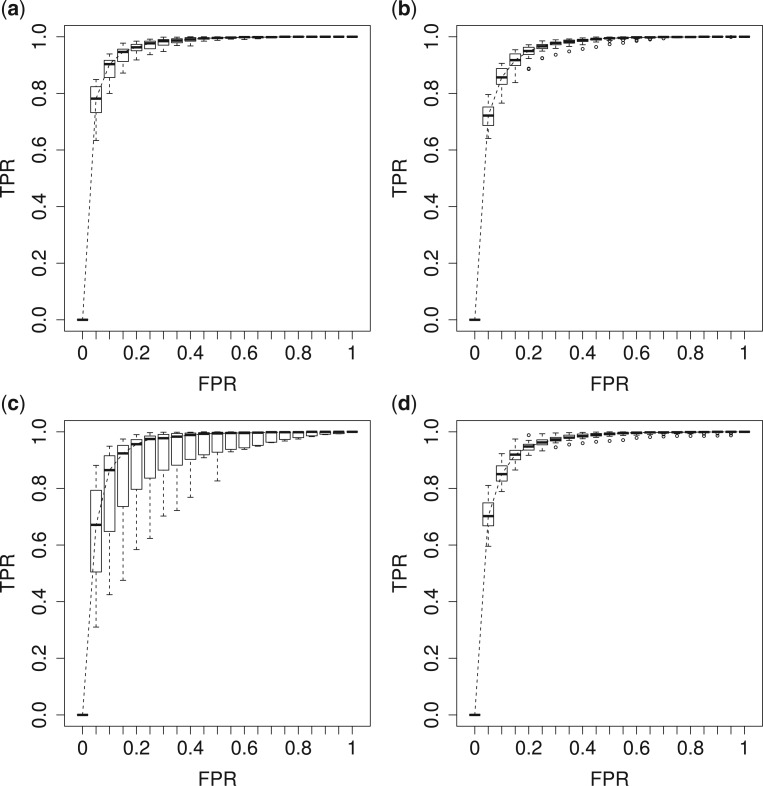
credible intervals. Next we evaluated the overall performance of recovery of the true 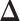 , in terms of average false positive rate (FPR) and true positive rate (TPR) achieved for different values of threshold
, in terms of average false positive rate (FPR) and true positive rate (TPR) achieved for different values of threshold 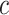 on the posterior probabilities of inclusion
on the posterior probabilities of inclusion 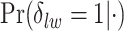 ’s. Results are reported in Figure 4 by drawing receiver operating characteristic (ROC) curves. The average areas under the ROC curves (AUC) range from
’s. Results are reported in Figure 4 by drawing receiver operating characteristic (ROC) curves. The average areas under the ROC curves (AUC) range from 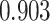 to
to 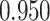 , indicating a satisfactory performance. We also reported the average FPRs, TPRs (i.e. recalls), precisions, and F-1 scores of the median model in Table S2 of supplementary material available at Biostatistics online. Lastly, we assessed the overall performance of recovery of the true hidden spins
, indicating a satisfactory performance. We also reported the average FPRs, TPRs (i.e. recalls), precisions, and F-1 scores of the median model in Table S2 of supplementary material available at Biostatistics online. Lastly, we assessed the overall performance of recovery of the true hidden spins 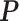 by plotting the ROC curves for different values of the threshold on the posterior probabilities of inclusion
by plotting the ROC curves for different values of the threshold on the posterior probabilities of inclusion 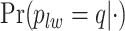 for each class
for each class 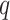 (See Figures S8 and S9 of supplementary material available at Biostatistics online). We compared our method with simply classifying each spin
(See Figures S8 and S9 of supplementary material available at Biostatistics online). We compared our method with simply classifying each spin 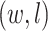 by a
by a 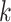 -nearest neighbor (
-nearest neighbor (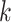 -NN) algorithm. The training set is the full set of the observed points in the corresponding dataset. Whichever
-NN) algorithm. The training set is the full set of the observed points in the corresponding dataset. Whichever 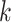 was chosen, the
was chosen, the 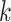 -NN algorithm produced a (FPR, TPR) point under the ROC curve that our method generated.
-NN algorithm produced a (FPR, TPR) point under the ROC curve that our method generated.
Fig. 4.
The ROC curves on the posterior probabilities of inclusion on 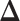 , in terms of the boxplots of TPRs under different FPRs, over
, in terms of the boxplots of TPRs under different FPRs, over 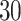 datasets generated from each point process and each setting of
datasets generated from each point process and each setting of 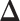 . (a) Homogeneous Poisson process - scenario 1; (b) Homogeneous Poisson process - scenario 2; (c) Log Gaussian Cox process - scenario 1; (d) Log Gaussian Cox process - scenario 2.
. (a) Homogeneous Poisson process - scenario 1; (b) Homogeneous Poisson process - scenario 2; (c) Log Gaussian Cox process - scenario 1; (d) Log Gaussian Cox process - scenario 2.
We conducted a sensitivity analysis on the choice of the MRF prior hyperparameters, 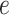 and
and 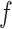 . In particular, we considered
. In particular, we considered 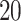 settings, by varying
settings, by varying 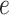 corresponding to the expected proportion of the AOI as
corresponding to the expected proportion of the AOI as 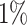 ,
, 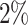 ,
, 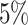 ,
,  , and
, and 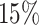 , and varying
, and varying 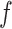 to
to 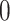 ,
, 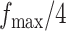 ,
, 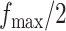 , and
, and 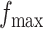 . Table S4 of supplementary material available at Biostatistics online shows the average AUC for each combination. The model is considerably insensitive to the choice of
. Table S4 of supplementary material available at Biostatistics online shows the average AUC for each combination. The model is considerably insensitive to the choice of 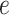 if the value of
if the value of 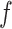 is equal to its maximum allowed value, as given in Table S1 of supplementary material available at Biostatistics online. The result suggests that employing the MRF prior model with a larger
is equal to its maximum allowed value, as given in Table S1 of supplementary material available at Biostatistics online. The result suggests that employing the MRF prior model with a larger 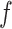 resulted in an increased ability to identify the true AOI, while the independent Bernoulli prior model (i.e.
resulted in an increased ability to identify the true AOI, while the independent Bernoulli prior model (i.e. 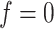 ) with no spatial information incorporated performed the worst. For those choices with
) with no spatial information incorporated performed the worst. For those choices with 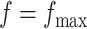 , we also calculated the average recalls, precisions, and F1-scores based on the PPI estimates of
, we also calculated the average recalls, precisions, and F1-scores based on the PPI estimates of 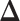 when choosing
when choosing 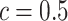 . Again, a close look at Table S3 of supplementary material available at Biostatistics online suggests that the proposed model was robust to the choice of hyperparameter
. Again, a close look at Table S3 of supplementary material available at Biostatistics online suggests that the proposed model was robust to the choice of hyperparameter 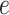 .
.
As the algorithm consists of two tunable parameters 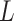 and
and 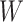 , we also conducted a sensitivity analysis by choosing different values of
, we also conducted a sensitivity analysis by choosing different values of 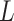 and
and 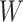 . We fit one dataset from the homogeneous Poisson process and scenario 2 into models with different lattice sizes
. We fit one dataset from the homogeneous Poisson process and scenario 2 into models with different lattice sizes 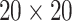 ,
, 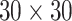 ,
, 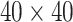 , and
, and 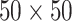 . Figure S10 of supplementary material available at Biostatistics online shows the maps of marginal posterior probabilities
. Figure S10 of supplementary material available at Biostatistics online shows the maps of marginal posterior probabilities 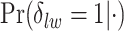 ’s and the median models for each setting. Generally speaking, the model was robust to the choice of
’s and the median models for each setting. Generally speaking, the model was robust to the choice of 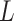 and
and 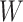 .
.
4.2. Application
Lung cancer is the leading cause of death from cancer in both men and women. Non-small-cell lung cancer (NSCLC) accounts for about 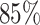 of deaths from lung cancer. In this case study, we applied the proposed method to the pathology images of
of deaths from lung cancer. In this case study, we applied the proposed method to the pathology images of 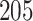 NSCLC patients in the NLST project (https://biometry.nci.nih.gov/cdas/nlst/). Each patient had one or more tissue slide(s) scanned at
NSCLC patients in the NLST project (https://biometry.nci.nih.gov/cdas/nlst/). Each patient had one or more tissue slide(s) scanned at 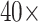 magnification. A lung cancer pathologist first determined and labeled the region of interest (ROI) within tumor region(s) from each tissue slide, and then we randomly chose five square regions per ROI as the sample images. The total number of sample images that we collected was
magnification. A lung cancer pathologist first determined and labeled the region of interest (ROI) within tumor region(s) from each tissue slide, and then we randomly chose five square regions per ROI as the sample images. The total number of sample images that we collected was 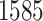 . For each sample image, we used the ConvPath pipeline, as shown in Figure S1 of supplementary material available at Biostatistics online, to generate the corresponding cell distribution map as the input of our model. The number of cells in each sample image ranged from
. For each sample image, we used the ConvPath pipeline, as shown in Figure S1 of supplementary material available at Biostatistics online, to generate the corresponding cell distribution map as the input of our model. The number of cells in each sample image ranged from 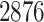 to
to 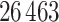 .
.
We applied the proposed model with a 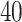 -by-
-by-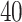 lattice to each preprocessed image. We used the same hyperparameter and algorithm settings as described in Section 4.1. Figure 1(a) and (d) are examples of the observed cell distribution maps from two patients’ sample images. Figure 1(b) and (e) visualize the MP estimates of the hidden spins
lattice to each preprocessed image. We used the same hyperparameter and algorithm settings as described in Section 4.1. Figure 1(a) and (d) are examples of the observed cell distribution maps from two patients’ sample images. Figure 1(b) and (e) visualize the MP estimates of the hidden spins 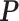 for the imaging data as shown in Figure 1(a) and (d). We can also consider them as the imputed images by projecting irregularly distributed cells into a
for the imaging data as shown in Figure 1(a) and (d). We can also consider them as the imputed images by projecting irregularly distributed cells into a 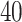 -by-
-by-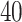 lattice. Figure 1(c) and (f) show the two regions, the AOIs (in blue shadow) and the background areas. The indicator matrix
lattice. Figure 1(c) and (f) show the two regions, the AOIs (in blue shadow) and the background areas. The indicator matrix 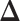 was estimated by a median model by choosing
was estimated by a median model by choosing 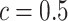 . As we can see, the imputed images are indeed good representations of the original cell distribution maps. Our method appears to separate those regions with intensive cell–cell interaction from a “freeze” background in which the cell–cell interaction energy is relatively low. This observation can be validated through Figure S13 of supplementary material available at Biostatistics online, which shows the density plots of
. As we can see, the imputed images are indeed good representations of the original cell distribution maps. Our method appears to separate those regions with intensive cell–cell interaction from a “freeze” background in which the cell–cell interaction energy is relatively low. This observation can be validated through Figure S13 of supplementary material available at Biostatistics online, which shows the density plots of 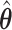 (red) and
(red) and 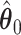 (green) via the hidden Potts mixture model and
(green) via the hidden Potts mixture model and 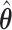 (black) via the hidden Potts model. It is clearly shown that the values of interaction energy of a homogeneous model are the roughly weighted average of the interaction energies of the AOI and the background regions from a mixture model, while the weight is determined by the
(black) via the hidden Potts model. It is clearly shown that the values of interaction energy of a homogeneous model are the roughly weighted average of the interaction energies of the AOI and the background regions from a mixture model, while the weight is determined by the 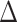 .
.
With the estimated interaction parameters in both AOI and the background area in each tissue slide, we conducted a downstream analysis to prove that proposing the hidden Potts mixture model as described in Section 2.3 is needed in practice, compared with its simpler version, which is the hidden Potts model as described in Section 2.2. Specifically, a Cox regression model was first fitted to evaluate the association between those estimated interaction parameters 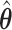 and
and 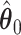 and patient survival outcomes, after adjusting for other clinical information, such as age, gender, tobacco history, and cancer stage. Multiple sample images from the same patient were modeled as correlated observations in the Cox regression model to compute a robust variance for each coefficient. The overall P-value for the Cox model is
and patient survival outcomes, after adjusting for other clinical information, such as age, gender, tobacco history, and cancer stage. Multiple sample images from the same patient were modeled as correlated observations in the Cox regression model to compute a robust variance for each coefficient. The overall P-value for the Cox model is 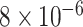 (Wald test), and the P-value and coefficient for each individual variable are summarized in Table 1 (P-values smaller than a 5% significance level are in boldface). The results imply that an increased interaction between stromal and tumor cells in the AOI (
(Wald test), and the P-value and coefficient for each individual variable are summarized in Table 1 (P-values smaller than a 5% significance level are in boldface). The results imply that an increased interaction between stromal and tumor cells in the AOI (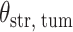 ) is associated with good prognosis in NSCLC patients (P =
) is associated with good prognosis in NSCLC patients (P = 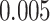 ). Interestingly, Beck and others (2011) also discovered that the morphological features of the stroma in the tumor region are associated with patient survival in a systematic analysis of breast cancer. Besides, the interaction between lymphocyte and stromal cells in the background area (P =
). Interestingly, Beck and others (2011) also discovered that the morphological features of the stroma in the tumor region are associated with patient survival in a systematic analysis of breast cancer. Besides, the interaction between lymphocyte and stromal cells in the background area (P = 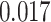 ) is also a prognostic factor, while the underlying biological mechanism is currently unknown. In comparison, we then fitted a homogeneous hidden Potts model, which is equivalent to our mixture model with all
) is also a prognostic factor, while the underlying biological mechanism is currently unknown. In comparison, we then fitted a homogeneous hidden Potts model, which is equivalent to our mixture model with all 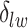 ’s fixed to
’s fixed to 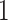 . The estimated interaction parameters
. The estimated interaction parameters 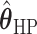 as well as other clinical variables were used as the predictors of the Cox regression model. The results are summarized in Table 1. As we can see, there is no significant predictor except cancer stage. This indicates that the homogeneous model tends to underestimate the true values of interaction energy between different types of cells. This example demonstrates the advantage of modeling the heterogeneous imaging data via a hidden Potts mixture model, rather than a hidden Potts model.
as well as other clinical variables were used as the predictors of the Cox regression model. The results are summarized in Table 1. As we can see, there is no significant predictor except cancer stage. This indicates that the homogeneous model tends to underestimate the true values of interaction energy between different types of cells. This example demonstrates the advantage of modeling the heterogeneous imaging data via a hidden Potts mixture model, rather than a hidden Potts model.
Table 1.
Survival analysis for NLST lung cancer pathology images. The overall P-value corresponding to a Wald test for the hidden Potts mixture model (heterogeneous) is 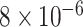 and for the hidden Potts model (homogeneous) is
and for the hidden Potts model (homogeneous) is 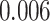
| Models | Parameters | Coefficient |
 (Coef.) (Coef.) |
SE | P-value |
|---|---|---|---|---|---|
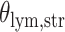
|
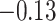
|
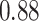
|
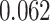
|
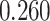
|
|
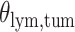
|
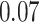
|
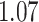
|
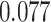
|
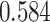
|
|
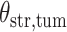
|
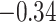
|
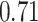
|
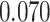
|
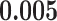
|
|
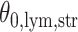
|
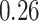
|
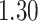
|
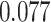
|
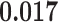
|
|
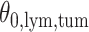
|
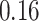
|
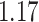
|
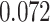
|
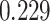
|
|
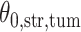
|
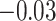
|
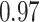
|
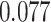
|
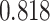
|
|
| Heterogeneous | Number of cells |
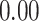
|
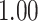
|
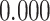
|
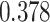
|
| Age |
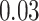
|
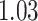
|
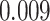
|
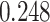
|
|
| Female vs. male |
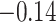
|
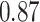
|
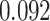
|
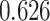
|
|
| Smoking vs. non-smoking |
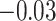
|
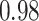
|
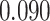
|
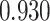
|
|
| Cancer stage I vs. II |
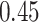
|
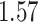
|
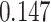
|
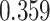
|
|
| Cancer stage I vs. III |
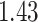
|
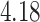
|
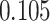
|
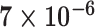
|
|
| Cancer stage I vs. IV |
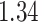
|
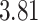
|
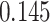
|
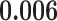
|
|
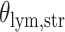
|
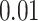
|
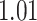
|
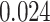
|
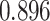
|
|
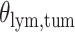
|
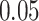
|
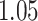
|
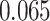
|
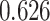
|
|
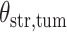
|
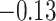
|
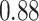
|
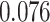
|
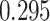
|
|
| Number of cells |
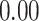
|
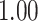
|
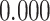
|
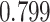
|
|
| Homogeneous | Age |
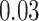
|
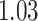
|
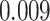
|
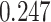
|
| Female vs. male |
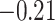
|
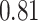
|
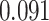
|
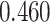
|
|
| Smoking vs. non-smoking |
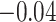
|
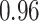
|
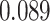
|
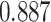
|
|
| Cancer stage I vs. II |
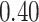
|
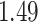
|
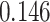
|
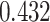
|
|
| Cancer stage I vs. III |
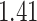
|
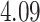
|
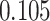
|
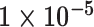
|
|
| Cancer stage I vs. IV |
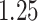
|
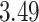
|
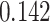
|
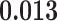
|
5. Conclusion
In this article, we focus on modeling cell distribution maps that arise in a lung cancer pathology image study. A hierarchical Bayesian framework was proposed in order to achieve three goals: (1) to reduce the complexity of the imaging data with thousands of irregularly distributed cells; (2) to quantify the interaction among different types of cells; and (3) to identify regions in the image where the interaction patterns significantly differ from each other. The proposed model utilizes the spatial information of thousands of irregularly distributed cells in the image. The introduction of auxiliary lattice helps to reduce the complexity of imaging data and defines a concise and explicit neighborhood for each spin in the Potts model. Our model is able to not only quantify the interaction energy between different types of cells, but also to distinguish clinically meaningful patterns from the background area via a Markov random field model.
For the lung cancer pathological imaging data, our study shows the interaction strength between stromal and tumor cells in the AOI is significantly associated with patient prognosis. This parameter can be easily measured using the proposed method and used as a potential biomarker for patient prognosis. This biomarker can be translated into real clinical tools at low cost because it is based only on tumor pathological slides, which are available in standard clinical care. In addition, this statistical methodology provides a new perspective to understand the biological mechanisms of cancer.
Several extensions of our model are worth investigating. First, the proposed model can be extended to more flexible finite mixture models by imposing a prior distribution on the number of components 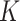 . Second, the correlation among interaction parameters could be taken into account by modeling them as a multivariate normal distribution. Third, we can learn about fixed hyperparameters, such as
. Second, the correlation among interaction parameters could be taken into account by modeling them as a multivariate normal distribution. Third, we can learn about fixed hyperparameters, such as 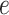 and
and 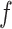 in the MRF prior by formulating its hyperpriors (see, e.g. Liang, 2010; Stingo and Vannucci, 2011). Fourth, although the use of MRF prior models encourages neighboring spins to clump together, there is no guarantee that the AOI is spatially contiguous, even if choosing,
in the MRF prior by formulating its hyperpriors (see, e.g. Liang, 2010; Stingo and Vannucci, 2011). Fourth, although the use of MRF prior models encourages neighboring spins to clump together, there is no guarantee that the AOI is spatially contiguous, even if choosing,  . How to generate a clinically useful and smooth AOI based on the MP matrix of inclusion
. How to generate a clinically useful and smooth AOI based on the MP matrix of inclusion 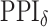 could be another future research direction. Last but not least, the proposed model provides a good opportunity to investigate the performance of other approximate Bayesian computation methods, such as variational Bayes, or even exact algorithms for sampling from distributions with intractable normalizing constants, such as Liang and others (2016). These could be future research directions.
could be another future research direction. Last but not least, the proposed model provides a good opportunity to investigate the performance of other approximate Bayesian computation methods, such as variational Bayes, or even exact algorithms for sampling from distributions with intractable normalizing constants, such as Liang and others (2016). These could be future research directions.
6. Software
Software in the form of R/C++ code is available on GitHub https://github.com/liqiwei2000/BayesHiddenPottsMixture. All the simulated datasets analyzed in Section 4.1 and two real datasets corresponding to the two sample images shown in Figure 1(a) and (d) of the manuscript are available on figshare https://figshare.com/projects/Bayesian_hidden_Potts_mixture_models/29659.
Supplementary Material
Acknowledgments
The authors would like to thank Jessie Norris for helping us in proofreading the manuscript. Conflict of Interest: None declared.
Funding
This work was partially supported by the National Institutes of Health [R01CA172211, P50CA70907, P30CA142543, R01GM115473, R01GM117597, R15GM113157, and R01CA152301], and the Cancer Prevention and Research Institute of Texas [RP120732].
References
- Amin, M. B., Tamboli, P., Merchant, S. H., Ordóñez, N. G., Ro, J., Ayala, A. G. and Ro, J. Y. (2002). Micropapillary component in lung adenocarcinoma: a distinctive histologic feature with possible prognostic significance. The American Journal of Surgical Pathology 26, 358–364. [DOI] [PubMed] [Google Scholar]
- Ayasso, H. and Mohammad-Djafari, A. (2010). Joint NDT image restoration and segmentation using Gauss–Markov–Potts prior models and variational Bayesian computation. IEEE Transactions on Image Processing 19, 2265–2277. [DOI] [PubMed] [Google Scholar]
- Barletta, J. A., Yeap, B. Y. and Chirieac, L. R. (2010). Prognostic significance of grading in lung adenocarcinoma. Cancer 116, 659–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck, A. H., Sangoi, A. R., Leung, S., Marinelli, R. J., Nielsen, T. O., van de Vijver, M. J., West, R. B., van de Rijn, M. and Koller, D. (2011). Systematic analysis of breast cancer morphology uncovers stromal features associated with survival. Science Translational Medicine 3, 108ra113. [DOI] [PubMed] [Google Scholar]
- Borczuk, A. C., Qian, F., Kazeros, A., Eleazar, J., Assaad, A., Sonett, J. R., Ginsburg, M., Gorenstein, L. and Powell, C. A. (2009). Invasive size is an independent predictor of survival in pulmonary adenocarcinoma. The American Journal of Surgical Pathology 33, 462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown, P. J., Vannucci, M. and Fearn, T. (1998). Multivariate Bayesian variable selection and prediction. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 60, 627–641. [Google Scholar]
- François, O., Ancelet, S. and Guillot, G. (2006). Bayesian clustering using hidden Markov random fields in spatial population genetics. Genetics 174, 805–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis 1, 515–534. [Google Scholar]
- George, E. I. and McCulloch, R. E. (1997). Approaches for Bayesian variable selection. Statistica Sinica 7, 339–373. [Google Scholar]
- Gillies, R. J., Verduzco, D. and Gatenby, R. A. (2012). Evolutionary dynamics of carcinogenesis and why targeted therapy does not work. Nature Reviews Cancer 12, 487–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gleason, D. F., Mellinger, G. T.; The Veretans Administration Cooperative Urological Research Group (2002). Prediction of prognosis for prostatic adenocarcinoma by combined histological grading and clinical staging. The Journal of Urology 167, 953–958. [PubMed] [Google Scholar]
- Green, P. J. and Richardson, S. (2002). Hidden Markov models and disease mapping. Journal of the American Statistical Association 97, 1055–1070. [Google Scholar]
- Hanahan, D. and Weinberg, R. A. (2011). Hallmarks of cancer: the next generation. Cell 144, 646–674. [DOI] [PubMed] [Google Scholar]
- Junttila, M. R. and de Sauvage, F. J. (2013). Influence of tumour micro-environment heterogeneity on therapeutic response. Nature 501, 346–354. [DOI] [PubMed] [Google Scholar]
- Kirk, R. (2012). Genetics: personalized medicine and tumour heterogeneity. Nature Reviews Clinical Oncology 9, 250–250. [DOI] [PubMed] [Google Scholar]
- Li, F. and Zhang, N. R. (2010). Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. Journal of the American Statistical Association 105, 1202–1214. [Google Scholar]
- Li, Q., Yi, F., Wang, T., Xiao, G. and Liang, F. (2017). Lung cancer pathological image analysis using a hidden Potts model. Cancer Informatics 16, 1176935117711910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, S. Z. (2009). Markov Random Field Modeling in Image Analysis. New York: Springer Science & Business Media. [Google Scholar]
- Liang, F. (2010). A double Metropolis–Hastings sampler for spatial models with intractable normalizing constants. Journal of Statistical Computation and Simulation 80, 1007–1022. [Google Scholar]
- Liang, F., Jin, I. H., Song, Q. and Liu, J. S. (2016). An adaptive exchange algorithm for sampling from distributions with intractable normalizing constants. Journal of the American Statistical Association 111, 377–393. [Google Scholar]
- Longo, D. L. (2012). Tumor heterogeneity and personalized medicine. New England Journal of Medicine 366, 956–957. [DOI] [PubMed] [Google Scholar]
- Luo, X., Zang, X., Yang, L., Huang, J., Liang, F., Canales, J. R., Wistuba, I. I., Gazdar, A., Xie, Y. and Xiao, G. (2016). Comprehensive computational pathological image analysis predicts lung cancer prognosis. Journal of Thoracic Oncology 12, 501–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantovani, A., Sozzani, S., Locati, M., Allavena, P. and Sica, A. (2002). Macrophage polarization: tumor-associated macrophages as a paradigm for polarized M2 mononuclear phagocytes. Trends in Immunology 23, 549–555. [DOI] [PubMed] [Google Scholar]
- Marte, B. (2013). Tumour heterogeneity. Nature 501, 327–327. [DOI] [PubMed] [Google Scholar]
- Mattfeldt, T., Eckel, S., Fleischer, F. and Schmidt, V. (2009). Statistical analysis of labelling patterns of mammary carcinoma cell nuclei on histological sections. Journal of Microscopy 235, 106–118. [DOI] [PubMed] [Google Scholar]
- McGranahan, N. and Swanton, C. (2017). Clonal heterogeneity and tumor evolution: past, present, and the future. Cell 168, 613–628. [DOI] [PubMed] [Google Scholar]
- Merlo, L. M. F., Pepper, J. W., Reid, B. J. and Maley, C. C. (2006). Cancer as an evolutionary and ecological process. Nature Reviews Cancer 6, 924–935. [DOI] [PubMed] [Google Scholar]
- Newton, M. A., Noueiry, A., Sarkar, D. and Ahlquist, P. (2004). Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics 5, 155–176. [DOI] [PubMed] [Google Scholar]
- Orimo, A., Gupta, P. B., Sgroi, D. C., Arenzana-Seisdedos, F., Delaunay, T., Naeem, R., Carey, V. J., Richardson, A. L. and Weinberg, R. A. (2005). Stromal fibroblasts present in invasive human breast carcinomas promote tumor growth and angiogenesis through elevated SDF-1/CXCL12 secretion. Cell 121, 335–348. [DOI] [PubMed] [Google Scholar]
- Polyak, K., Haviv, I. and Campbell, I. G. (2009). Co-evolution of tumor cells and their microenvironment. Trends in Genetics 25, 30–38. [DOI] [PubMed] [Google Scholar]
- Propp, J. G. and Wilson, D. B. (1996). Exact sampling with coupled Markov chains and applications to statistical mechanics. Random Structures and Algorithms 9, 223–252. [Google Scholar]
- Ripley, B. D. and Rasson, J. P. (1977). Finding the edge of a poisson forest. Journal of Applied Probability 14, 483–491. [Google Scholar]
- Schnipper, L. E. (1986). Clinical implications of tumor-cell heterogeneity. New England Journal of Medicine 314, 1423–1431. [DOI] [PubMed] [Google Scholar]
- Shibata, D. (2012). Heterogeneity and tumor history. Science 336, 304–305. [DOI] [PubMed] [Google Scholar]
- Stephens, M. (2000). Dealing with label switching in mixture models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 62, 795–809. [Google Scholar]
- Stingo, F. C., Guindani, M., Vannucci, M. and Calhoun, V. D. (2013). An integrative Bayesian modeling approach to imaging genetics. Journal of the American Statistical Association 108, 876–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stingo, F. C. and Vannucci, M. (2011). Variable selection for discriminant analysis with Markov random field priors for the analysis of microarray data. Bioinformatics 27, 495–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsao, M.-S., Marguet, S., Le Teuff, G., Lantuejoul, S., Shepherd, F. A., Seymour, L., Kratzke, R., Graziano, S. L., Popper, H. H., Rosell, R. and others. (2015). Subtype classification of lung adenocarcinoma predicts benefit from adjuvant chemotherapy in patients undergoing complete resection. Journal of Clinical Oncology 33, 3439–3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, K.-H., Zhang, C., Berry, G. J., Altman, R. B., Ré, C., Rubin, D. L. and Snyder, M. (2016). Predicting non-small cell lung cancer prognosis by fully automated microscopic pathology image features. Nature Communications 7, 12474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan, Y., Failmezger, H., Rueda, O. M., Ali, H. R., Gräf, S., Chin, S.-F., Schwarz, R. F., Curtis, C., Dunning, M. J., Bardwell, H. and others. (2012). Quantitative image analysis of cellular heterogeneity in breast tumors complements genomic profiling. Science Translational Medicine 4, 157ra143. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.