Kinetics and Chemistry of Hydrolysis of Ultrathin, Thermally Grown Layers of Silicon Oxide as Biofluid Barriers in Flexible Electronic Systems

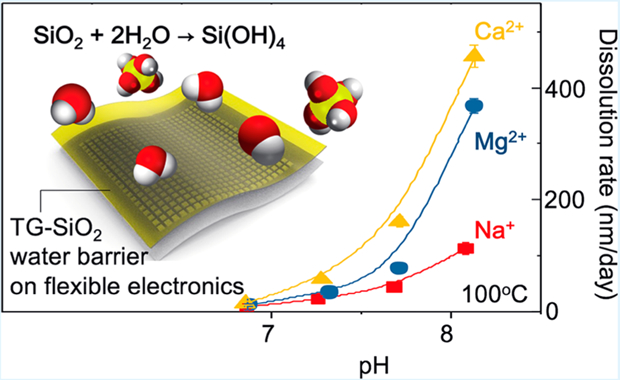
Abstract

Flexible electronic systems for bioimplants that offer long-term (multidecade) stability and safety in operation require thin, biocompatible layers that can prevent biofluid penetration. Recent work shows that ultrathin films of silicon dioxide thermally grown (TG-SiO₂) on device-grade silicon wafers and then released as transferrable barriers offer a remarkable set of attributes in this context. This paper examines the chemical stability of these materials in aqueous solutions with different combinations of chemistries that are present in biofluids. Systematic measurements reveal the dependence of the dissolution rate of TG-SiO₂ on concentrations of cations (Na⁺, K⁺, Mg²⁺, Ca²⁺) and anions (Cl⁻,HPO₄²⁻) at near-neutral pH. Certain results are consistent with previous studies on bulk samples of quartz and nanoparticles of amorphous silica; others reveal significant catalyzing effects associated with divalent cations at high pH and with specific anions at high ionic strength. In particular, Ca²⁺ and HPO₄²⁻ greatly enhance and silicic acid greatly reduces the rates. These findings establish foundational data of relevance to predicting lifetimes of implantable devices that use TG-SiO₂ as biofluid barriers, and of other classes of systems, such as environmental monitors, where encapsulation against water penetration is important.

Graphical Abstract:

1. INTRODUCTION

Recent advances in high-performance, flexible electronic/optoelectronic devices establish the foundations for physiological monitors and therapeutic systems capable of implantation in nearly any region of the body.^1–9 Examples range from devices for high-resolution electrophysiological mapping on the cardiac surfaces to injectable needles for optical stimulation and/or pharmacological manipulation of targeted neural circuits.^1,3 Because of the intrinsically low bending stiffnesses of the thin materials used in these platforms, such devices can establish conformal, minimally invasive interfaces to the curved, dynamic surfaces of soft biological systems while possessing many of the performance characteristics associated with rigid, planar, semiconductor-wafer-based integrated circuits. The absence of thin, flexible film barriers to biofluids has been a critical obstacle for use of such platforms as chronic implants, where the ultimate time scale for stable operation may reach into the realm of many decades. Recent work shows that physically transferred layers of silicon dioxide (TG-SiO₂) thermally grown on device-grade silicon wafers can provide defect-free isolation from biofluids without significantly compromising the flexible mechanics, suitable for integration onto broad classes of biocompatible electronic devices.^10,11 The dense, amorphous consolidated nature of the TG-SiO₂ and its nearly perfect nature (e.g., pinhole-free) follow from the controlled, high-temperature growth conditions and the single-crystalline, atomically smooth growth substrates. The resulting films can enable zero water penetration across macroscopic areas even at thicknesses in the range of only tens to hundreds of nanometers, thereby extending the use of this material beyond applications as a thin film dielectric or a flat substrate for small particle growth.^12,13 The ultimate failure mode is in gradual reductions in thickness caused by dissolution of SiO₂ through hydrolysis (SiO₂ + 2H₂O → Si(OH)₄) associated with immersion in biofluids.¹⁰ The rate of this dissolution and its dependence on chemical composition of the surrounding aqueous solution therefore represent issues of critical importance in selecting designs to match lifetime requirements.

Previous studies show that the thickness of TG-SiO₂ decreases in a linear fashion with time in near neutral aqueous buffer solutions such as phosphate buffered saline (PBS) at rates of 10⁻² to 10² nm/day in a temperature range from 25 to 100 °C, with Arrhenius scaling.^10,14 Thermal oxides formed using wet oxidation show slightly higher rates of dissolution compared to those formed by dry oxidation (by ~5%), consistent with their lower density.¹⁴ The results suggest that the hydrolysis of TG-SiO₂ proceeds by surface reactions without a significant role of reactive diffusion of water into the bulk SiO₂ or of water permeation through defect sites. The studies reported here focus on detailed, parametric investigations of the effects of the chemical composition of the surrounding solution, to establish essential aspects of the hydrolysis reaction and its role in determining the stability of implantable flexible electronic devices. As described in the following, the findings indicate that the compositional variance of different types of simulated biofluids (PBS, Hank’s balanced solution with and without Mg²⁺ and Ca²⁺, and artificial perspiration) can alter the dissolution rates to a significant degree. Silicic acid, another ubiquitous chemical in biofluids, can strongly decelerate the dissolution, depending on the concentration. Measurements of TG-SiO₂ dissolution in aqueous solutions with various types of ions (Na⁺, K⁺, Ca²⁺, Mg²⁺, Cl⁻, HPO ₄²⁻), ionic strengths (0−1 M), and pH (6−9) reveal accelerated dissolution at high ionic concentrations for all ion types, but with different acceleration factors and saturation levels. At similar ionic strength and pH, Ca²⁺ catalyzes the dissolution more effectively than monovalent cations (Na⁺, K⁺) and Mg²⁺, especially at higher pH. HPO ₄²⁻ leads to rates of dissolution that are faster than those associated with Cl⁻ at higher ionic strength. The discussion summarizes these results and compares them to previous studies of dissolution kinetics with other forms of silica such as quartz and amorphous polymorphs, with emphasis on underlying mechanistic reasoning.

2. RESULTS AND DISCUSSION

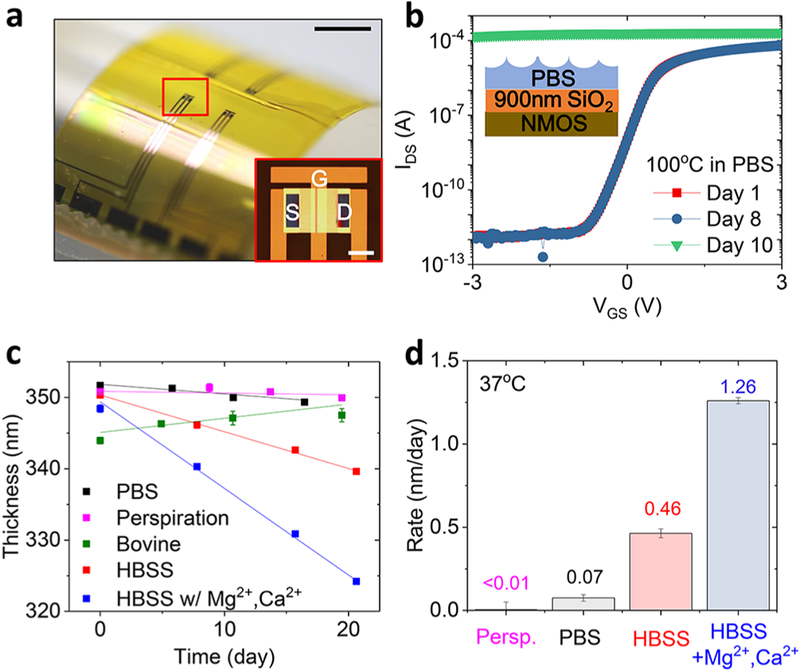
Figure 1a shows optical images of a piece of flexible electronics with four n-type metal-oxide-semiconductor (NMOS) transistors covered with an ultrathin layer of TG-SiO₂ (900 nm) for encapsulation. Transfer characteristics of a representative transistor are in Figure 1b in a log scale at a supply voltage V_DS = 0.1 V. Soaking these transistors in phosphate buffered saline (PBS, pH 7.4) at 100 °C accelerates the rate of hydrolysis of TG-SiO₂. The on/off current ratio remains ~10⁸ before a sudden failure at day 10 due to the complete dissolution of the TG-SiO₂ and subsequent exposure of the transistor to water. Figure 1c,d summarizes observations of spatially uniform thinning of layers of TG-SiO₂ by hydrolysis in simulated biofluids. The measurements involve immersing 5 mm × 5 mm pieces of Si wafer with a ~300 nm thick layer of TG-SiO₂ in 30 mL of each solution. Calculations based on the amount of dissolved SiO₂ and direct experimental measurements by inductively coupled plasma mass spectrometry analysis indicate that the silicic acid concentration remains <1 ppm throughout the course of these experiments. Figure 1c summarizes the changes in thickness associated with immersion in five types of simulated biofluids at 37 °C: PBS, Hank’s balanced saline solution (HBSS) with and without Mg²⁺ and Ca²⁺, artificial perspiration, and bovine serum. Table S1 (Supporting Information) summarizes the compositional differences of these solutions. The main difference between perspiration, PBS, and HBSS is in their pH levels (PBS, 7.4; HBSS, 8.3 (CO₂-sensitive); perspiration, 4.5). The viscosity of the serum is higher by ~10% compared to other solutions due to its protein content. Each solution yields a different dissolution rate: <0.01 nm/day (perspiration); 0.07 ± 0.02 nm/day (PBS);0.46 ± 0.03 nm/day (HBSS without Mg²⁺, Ca²⁺); 1.26 ± 0.02 nm/day (HBSS with Mg²⁺, Ca²⁺) (Figure 1d). The rates increase with pH, consistent with previous reports.¹⁴ Adding Mg²⁺ (0.9 mM) and Ca²⁺ (1.3 mM) to HBSS increases the rate by a factor of nearly 3. Binding of proteins in bovine serum to the surface of the TG-SiO₂ leads to an apparent increase in thickness, thereby frustrating an accurate measurement of dissolution. Prior studies show that proteins irreversibly adsorb on silica surface at room temperature, with an order of 10⁻¹ μg/cm².^15,16

Figure 1.

Flexible electronics encapsulated with thermally grown silicon dioxide (TG-SiO₂) and dissolution of TG-SiO₂ due to immersion in simulated biofluids at 37 °C. (a, b) Demonstration of electronic devices and flexible electronic systems encapsulated with TG-SiO₂. (a) Optical images of flexible n-type metal-oxide-semiconductor (NMOS) transistors (scale bar: 1 cm (black), 200 μm (white, inset)). (b) Results of soak tests of NMOS in PBS solutions at 100 °C. (c) Change in thickness of TG-SiO₂ as a function of time of immersion in simulated biofluids. (d) Measured dissolution rates (nm/day) for these fluids.

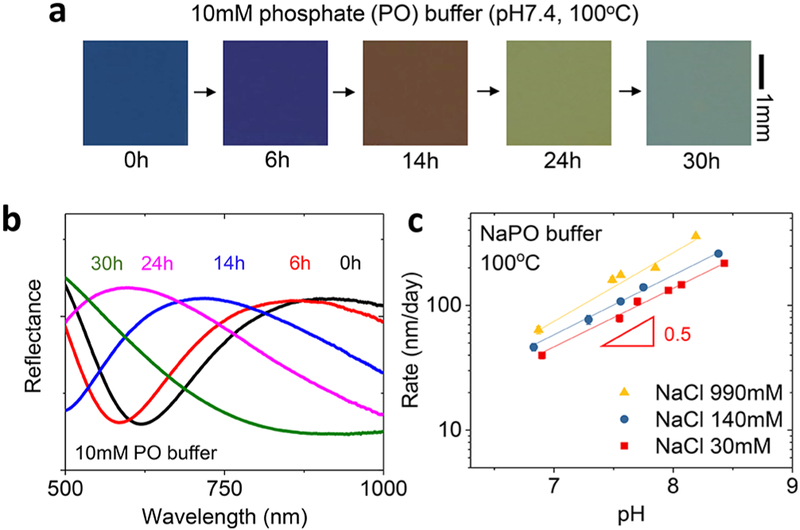
Optical images in Figure 2a highlight the changes in color that occur as the thickness of TG-SiO₂ decreases in phosphate buffer solution (Na₂HPO₄/NaH₂PO (NaPO) 10 mM, pH7.4) at 100 °C. (Here, the molar concentration of the phosphate buffer is the sum of NaH₂PO₄ and Na₂HPO₄ as conventionally used in the buffer description.) The uniformity in color during the dissolution is consistent with a high level of macroscopic uniformity in the hydrolysis reactions across the entire spatial extent of the sample. Figure 2b summarizes corresponding reflectance data that show a continuous shift of the peaks toward shorter wavelengths as the thickness decreases. Such measurements quantify the changes in thickness (from 320 nm at 0 h to 210 nm at 24 h) to yield the dissolution rate. Parametric studies at an elevated temperature (100 °C) yield data on the dependence of dissolution rate on ion concentration and pH. Biological and environmental fluids cover a range of pH values and concentrations of ions. For example, the pH of common natural water can be as low as 4.5 (urine, sweat) and as high as 8.4 (seawater). In terms of salinity, rivers and oceans contain 0.1 g to 100g/L solid contents mostly associated with dissolved cations (Na⁺, Mg²⁺, and Ca²⁺) and anions (Cl⁻, HCO⁻₃, SO₄²⁻, and silica) while extracellular biofluids contain strictly regulated amounts of salts within 8−20 g/L, mostly NaCl. Figure 2c summarizes the catalyzing effect of ions (NaCl) at various pH levels adjusted by ~3.3 mM NaPO. Since the ratio between NaH₂PO₄ and Na₂HPO₄ in phosphate buffer changes depending on the pH, we used formulations with constant ionic strength (IS, 10 mM NaPO), not concentration, for all pH values. The results show that at all NaCl concentrations (30, 140, and 990 mM), the dissolution rates increase with pH with a half-order dependence on OH⁻ concentration, consistent with previous studies of TG-SiO₂ in phosphate buffer solution.¹⁰ Rates are as follows: 40 ± 3 nm/day (30 mM), 46 ± 3 nm/day (140 mM), and 64 ± 4 nm/day (990 mM) at pH ~6.9; 218 ± 6 nm/day (30 mM), 260 ± 8 nm/day (140 mM), and 359 ± 8 nm/day (990 mM) at pH 8.2 (990 mM) to pH 8.4 (30 and 140 mM). The enhanced dissolution at high pH likely follows from deprotonation of the silanol groups on the silica surface and their enhanced reactivity toward hydrolysis, as observed in the relation between the silica surface charge and the dissolution rates for other types of silica.¹⁷ Although atomistic mechanisms of the accelerating effect of ions are not well understood, experimental results suggest that the presence of ions increases the frequency of the reactions without significantly decreasing the activation energy.¹⁸ Consistent with those prior results, the apparent activation energies for the hydrolysis of TG-SiO₂ extracted from measurements at three temperatures with Arrhenius scaling suggests that the average activation energies remain ~0.89 eV without significant differences between solutions with different ion concentrations (Figure S1). This value is similar to those for amorphous silica (0.85 eV for fused quartz and 0.79 eV for pyrolyzed silica).¹⁹

Figure 2.

Effects of ion concentration and pH on dissolution of TGSiO₂. (a) Optical images of TG-SiO₂ collected at several times of immersion in 10 mM sodium phosphate (Na₂HPO₄/NaH₂PO₄, NaPO) solution (pH 7.4) at 100 °C. (b) Reflectance curves at different times. (c) Effects of pH and NaCl concentration on the dissolution rate.

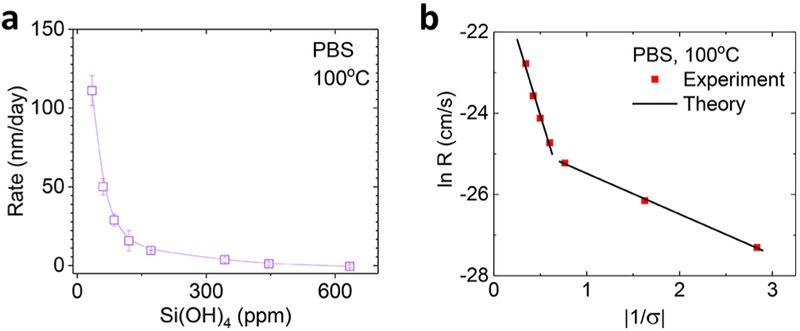
Although studies of dissolution in pure water with <1 ppm of Si(OH)₄ yield valuable kinetics information, investigations of dissolution in solutions with specified, non-negligible concentrations of Si(OH)₄ are important in the context of biological environments. Figure 3 shows the effects of silicic acid (Si(OH)₄), a product of SiO₂ hydrolysis and a ubiquitous presence in biological aqueous systems, typically at the 10⁰ to 10¹ ppm level. The formulations used Si(OH)₄ extracted from a 1000 ppm of Si standard solution (Sigma-Aldrich). The data in Figure 3a highlight the strong decrease of dissolution rate with increase in [Si(OH)₄] due to an increased rate of the reverse hydrolysis reaction, consistent with the dissolution behavior of quartz and other silica polymorphs.^20–22 The dissolution almost entirely stops at ~600 ppm of Si(OH)₄ at 100 °C.

Figure 3.

Effects of silicic acid on dissolution of TG-SiO₂. (a) Effect of silicic acid concentration on dissolution rate in PBS. (b) Comparisons to a polynuclear dissolution model.

Figure 3b presents fits of experiment data to a polynuclear dissolution model previously used to explain the dissolution of fused quartz/synthetic silica in solutions containing Si(OH)₄.²² This model describes the dependence of SiO₂ dissolution on [Si(OH)₄] by reduced rates of net detachment of Si(OH)₄ from the surface and increased activation energy for vacancy (or highly reactive site) formation where dissolution starts to spread. Specifically, the reactive sites refer to the surface silica tetrahedra with coordination numbers lower than those of bulk SiO₂, thereby yielding high surface energy. The model expresses the rate as

$$\text{ln}R=\text{ln}(hSA)-\frac{\pi {\alpha }^2\omega h}{{(kT)}^2}\frac{1}{\left|\sigma \right|}$$

where R is the volume of dissolution nuclei formed per unit area of surface and time, h is the height of the vacancy, S is the surface area affected by each nucleation event, A is a pre-exponential factor for nucleation rate, ω is the specific volume of molecule (cm³/molecule), α is the local interfacial free energy, k is the Boltzmann constant, and T is the temperature.²² σ = ln(C/Ce) is the degree of undersaturation, where C and Ce (630 ppm) are experimental and equilibrium concentrations of Si(OH)₄, respectively. The equation indicates that the logarithm of the rate of removing a unit of material from the surface has a squared dependence on the interfacial free energy (α) to create a new surface with highly reactive Si atoms exposed. We used these values for the following parameters, ω_TG‑SiO2 = 4.54⁻²³ cm/molecule, height h_TG‑SiO2 =2.17 Å, and T = 373.15 K.²² The polynuclear model applies to dissolution processes dominated by the detachment of SiO₂ units around nucleated reactive sites. The lines in Figure 3b show the model fit to the experiment data of TG-SiO₂ dissolution. The interfacial free energy α_I* = 80.2 mJ/m² is obtained for the higher-slope region at high undersaturation, and α_II* = 29.3 mJ/m² is obtained for the lower-slope region close to saturation. The interfacial energies of TG-SiO₂ are similar to the those of quartz, where two different slopes have been attributed to different regimes of the dissolution dominated either by nucleation of reactive surface Si atoms with fewer backbonds (undersaturation) or by reactive surface silicon atoms intrinsically present in the original structure (close to saturation).²²

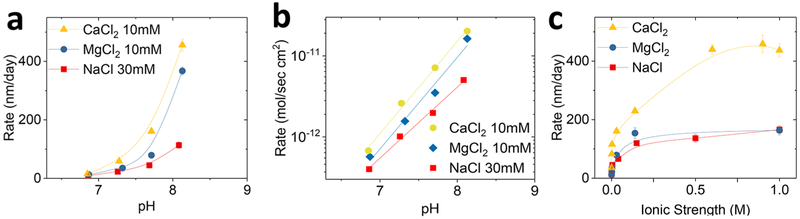
Since ions can accelerate the rates of dissolution (Figure 2c), studies of different cation and anion types that are present in biological or groundwater are important. Figure 4 summarizes the role of cation type. Here, the use of Tris buffer instead of phosphate buffer prevents precipitation reactions from interactions of divalent cations (Ca²⁺ and Mg²⁺) with the HPO₄²⁻. Figure 4a shows measured rates in CaCl₂, MgCl₂, and NaCl solutions at 30 mM ionic strength (IS) and near neutral pH. The results show that Ca²⁺ accelerates the dissolution more effectively than Mg²⁺ and Na⁺ in all pH ranges, as previously reported at low silicic acid concentrations.^21,22 The differences between Mg²⁺ and Na⁺ are insignificant for pH in the low part of this range (9 ± 4 nm/day (NaCl), 13 ± 3 nm/day (MgCl₂), and 15 ± 3 nm/day (CaCl₂) at pH 6.9), but become significant at higher pH (114 ± 11 nm/day (NaCl), 367 ± 13 nm/day (MgCl₂), and 456 ± 20 nm/day (CaCl₂) at pH 8.1). The underlying mechanisms likely relate to enhanced electrostatic interactions between more negatively charged SiO₂ surfaces and divalent cations at higher pH.^17,23 Since the [Cl⁻] is lower in CaCl₂ and MgCl₂ solutions than that in the NaCl solution at the same ionic strength, the observed acceleration can be attributed to the cations. The results are consistent with previous studies on quartz where faster rates occur with Ca²⁺ than with Mg²⁺.²⁴ Previous ab initio calculations suggest a quantum mechanical origin for the role of cations in accelerated dissolution of SiO₂. Here, bond paths can form between the divalent cations and bridging oxygen sites with partial negative charges on the silica surface.²⁵ This interaction weakens the surrounding Si−O bonds and enhances the susceptibility of the Si atoms to attack by water. According to these computational results, the differences between Ca²⁺ and Mg²⁺ arise from differences in water dynamics associated with these ions. Dissolution rates in KCl and NaCl solutions are similar (Figure S2).

Figure 4.

Dependence of TG-SiO₂ dissolution on cation type. (a) Rate of dissolution in solutions of NaCl, MgCl₂, and CaCl₂ at different pH. (b) Dissolution rates in mol/s·cm². (c) Dissolution rates in solutions with different ionic strengths.

Figure 4b presents the previous results in units of mol/s·cm² to facilitate comparisons with the rates associated with quartz and other amorphous forms of silica. The observed rates, 10⁻¹²−10⁻¹¹ mol/s·cm² at near neutral pH at 100 °C are all comparable for similar conditions: quartz, 10⁻¹⁵−10⁻¹⁴ mol/s· cm² at 70 °C and 10⁻¹¹−10⁻¹⁰ mol/s·cm² at 200 °C;^26,17 amorphous silica, 10⁻¹¹ at 150 °C.²² The reaction order on pH, which is independent of the units, is 0.88, 1.13, and 1.14 for Na⁺, Mg²⁺, and Ca²⁺, respectively, in Tris buffer. This dependence on pH is significantly larger than that for phosphate buffered solutions (0.5) as the values of the pH dependence depend on the buffer systems.¹⁸ The difference between phosphate and Tris buffers could result from interactions between the phosphate anion and the SiO₂ surface, as discussed later in the context of studies of effects of anions (Figure 5). Figure 4c describes the dependence of dissolution rates on the ionic strength at pH 7.7. The rate associated with Ca²⁺ is the highest at all concentrations. For all ion types, the rates increase initially at low concentrations, and then tend to saturate at high concentrations (from 13 ± 5 nm/day (without salts) to 166 ± 10 nm/day (NaCl), 164 ± 16 nm/day (MgCl₂), and 437 ± 22 nm/day (CaCl₂) at 1 M ionic strength, pH 7.7). This saturation behavior also occurs with quartz,¹⁹ and is generally believed to result from saturation of cations near the SiO₂ surface after effective screening of the negative SiO₂ surface charge.

Figure 5.

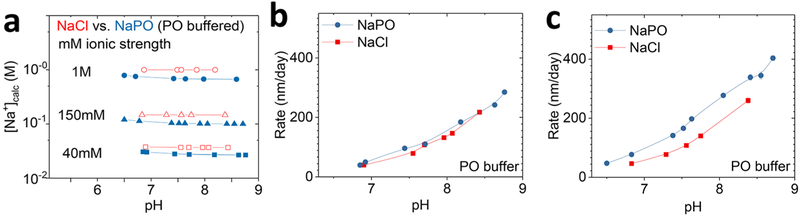
Dependence of TG-SiO₂ dissolution on anion type. (a) Na⁺ concentrations in solutions of NaCl and Na₂HPO₄/NaH₂PO₄ (NaPO). (b) Dissolution rates in solutions with 40 mM ionic strength. (c) Dissolution rates in solutions with 150 mM ionic strength.

Although the enhancements of dissolution rates in electrolyte solutions are typically attributed to cation−SiO₂ and cation−water interactions,^27,24 anion specificity can be observed in the case of Cl⁻ and HPO₄²⁻. Figure 5 compares dissolution rates in solutions of NaCl and Na₂HPO₄. The Na₂HPO₄ solutions also include a small amount of NaH₂PO₄ (Na₂HPO₄/NaH₂PO₄ <0.1) to adjust the solution pH while maintaining the total ionic strength at the desired level. Addition of 10 mM (by ionic strength) Na₂HPO₄/NaH₂PO₄ (NaPO) to the NaCl solutions maintains a constant pH. Figure 5a compares the concentration of Na⁺ in the NaCl and NaPO solutions at ionic strengths of 40 mM, 150 mM, and 1 M. In all cases, [Na⁺] is higher in NaCl solutions than in NaPO solutions at the same ionic strength. Figure 5b,c summarizes dissolution rates in NaCl and NaPO solutions at different ionic strengths. The results indicate that the difference in the dissolution rates with different anions is small at 40 mM (e.g., 40 ± 3 nm/day (NaCl) and 40 ± 4 nm/day (NaPO) at pH 6.9) but that the rates with phosphate anions become significantly faster than those with Cl⁻ at high ionic strengths for all pH levels (e.g., at pH 6.8, 46 ± 3 nm/day (NaCl) and 77 ± 3 nm/day (NaPO) in 150 mM and 64 ± 7 nm/day (NaCl) and 146 ± 9 nm/day (NaPO) in 1 M ionic strength). Such anion-specific dissolution behaviors may arise from screening of negative surface charge of SiO₂ by Na⁺ at high ionic strength and direct interaction between SiO₂ and anions. Strong hydrogen-bonding interactions between phosphate and the silica surface can be observed in sum frequency generation and FTIR spectroscopy.^28,29 Measurements of dissolution at different temperatures (Figure S3) suggest an activation energy with HPO₄²⁻ (0.6 eV) that is lower than that with Cl⁻ (0.8 eV) at 150 mM ionic concentration, thereby suggesting accelerating mechanisms that are different than those of cations.

3. CONCLUSION

This paper summarizes the results of systematic studies of the dissolution behaviors of ultrathin layers of TG-SiO₂ in aqueous solutions with compositions relevant to those in biofluids. The data reveal key factors in the dissolution kinetics: ion type and concentration, pH, and concentration of silicic acid. Some of the findings are consistent with the previous studies on quartz and amorphous silica. Additional results establish significant catalyzing effects from divalent cations at high pH and anion-specific features at high ionic strength. The insights into these chemistries are critically important in the context of the use of TG-SiO₂ as a water barrier layer for active, flexible electronic implants, and in other cases where long-term survivability is necessary in aqueous environments.

4. EXPERIMENTAL METHODS

The fabrication process for flexible NMOS transistors began with the isolation of silicon transistors on an SOI wafer (200 nm top Si/1 μm buried thermal oxide, SOITEC). Solid source doping with phosphorus yielded source and drain contacts at concentration level of ~10¹⁹ cm⁻³ with a channel length of 20 μm and width of 600 μm. Thermal oxidation and atomic layer deposition (ALD) yielded a dielectric stack of thermal SiO₂ (30 nm)/Al₂O₃ (13 nm) at ~1150 and 80 °C, respectively. A layer of Cr/Au (5 nm/100 nm) served as source, drain, gate electrodes, and metal interconnects. A transfer process bonded the front side of this substrate to a thin polymer film (Kapton, DuPont, 13 μm) laminated onto a glass substrate coated with a layer of dimethylsiloxane (PDMS; 10 μm) as a temporary support. The bonding involved application of a commercial adhesive (Kwik-Sil, World Precision Instruments). Reactive ion etching (RIE) with SF₆/O₂ (Plasma Therm) followed by inductively coupled plasma RIE (ICP-RIE, Surface Technology System) with SF₆ exposes the surface of the TG-SiO₂ (~900 nm, thinned by 100 nm during the etching process) as a biofluid barrier and biointerface. Peeling the device away from the substrate completed the process.

All dissolution experiments used commercially obtained Si wafers (P-type (Boron), 1−100 Ω·cm, (100), University Wafer). TG-SiO₂ was grown by wet thermal oxidation (1150 °C) on their surfaces. Soaking tests involved various types of simulated biofluids including PBS (Corning cellgro), Hank’s balanced salt solution (HBSS) (Thermo Fisher Scientific), bovine serum (RMBIO), and artificial perspiration (Pickering Laboratories) at 37 °C. Storage of these solutions occurred in PETE bottles, as purchased; experiments used high-density polyethylene (HDPE) bottles (United States Plastic Corp.). NaCl, KCl, and NaH₂PO₄/Na₂HPO₄ solutions were prepared by mixing the salts in deionized water. CaCl₂ and MgCl₂ solutions were diluted from their 1 M standard solution (Sigma-Aldrich). Si standard solution (1 g/L; Sigma-Aldrich) prepared by dissolving Si in 2% NaOH was added to PBS to include silicic acid. The pH of phosphate buffer was adjusted by changing the ratio between NaH₂PO₄ and Na₂HPO₄ while pH of Tris buffer was adjusted by adding HCl. After the soaking tests at 37 or 100 °C in each solution, the thickness of the TG-SiO₂ was measured by a reflectometer (MProbe, Semicon Soft). Dissolution rates indicated in the plots correspond to average values calculated from measurements on three separate pieces of TG-SiO₂.