Choice Set Formation in Residential Mobility and Its Implications for Segregation Dynamics

Abstract

We develop and estimate a statistical model of neighborhood choice that draws on insights from cognitive science and decision theory as well as qualitative studies of housing search. The model allows for a sequential decision process and the possibility that people consider a small and selective subset of all potential destinations. When combined with data from the Los Angeles Family and Neighborhood Survey, our model reveals that affordability constraints and households’ tendency toward short-distance moves lead blacks and Hispanics to have racially stratified choice sets in which their own group is disproportionately represented. We use an agent-based model to assess how racially stratified choice sets contribute to segregation outcomes. Our results show that cognitive decision strategies can amplify patterns of segregation and inequality.

Motivation

A persistent puzzle, especially in the sociological literature, is why racial segregation remains high despite reductions in more overt forms of discrimination and decades of liberalizing attitudes. The classic explanations highlight distinct features of the neighborhood selection process: (1) racial gaps in income and wealth mean that many minority households cannot afford predominantly white neighborhoods (Crowder and South 2005; Crowder et al. 2006); (2) enduring discriminatory practices on the part of real estate agents, lenders, and landlords limit what neighborhoods are available to racial minorities (Ross and Turner 2005); and (3) racial differences in preferences for neighborhoods, particularly whites’ unwillingness to be the local minority, imply that segregation will persist even in the absence of barriers (Clark and Fossett 2008).

In their efforts to adjudicate among these explanations, sociologists and demographers have devoted substantial attention to describing empirical patterns of neighborhood choice. In the 1990s, this work mostly took the form of locational attainment statistical models (e.g., Logan and Alba 1993), which regress sociodemographic attributes of census households onto univariate measures of neighborhood composition (e.g., median income, proportion black). In the 2000s, scholars used mobility data to examine correlations between people’s racial and economic status and the probability of moving into or out of a neighborhood characterized by its racial or economic composition (Crowder et al. 2006; South et al. 2011). The current state of the art is to use discrete choice models that allow neighborhoods to be characterized by distinct bundles of attributes (Bruch and Mare 2012; Logan and Shin 2016; Quillian 2015).¹

Typically, these statistical models do not provide a structural representation of the residential decision, instead capturing associations between neighborhood characteristics and attributes of individuals. As a result, quantitative studies of neighborhood mobility do not capture the behavioral or cognitive process underlying how people choose neighborhoods. Discrete choice models do provide an explicit representation of a decision process, but they assume a fully informed, utility-maximizing decision-maker who explicitly weighs the relative merits of hundreds, even thousands, of potential destinations within a metro area (c.f. McFadden 1978, 1999).

We know from qualitative studies of residential search that people typically look only within a small geographic area (Barrett 1976; Clark and Smith 1982) and have fragmentary knowledge of metro neighborhoods (Krysan and Bader 2009; Krysan and Crowder 2017). Thus, potential movers are unlikely to be informed about neighborhoods in geographically or socially distant areas (Carrillo et al. 2016; Havekes et al. 2016). Even if movers are informed, the set of neighborhoods they can realistically consider is limited by affordability, transportation, and other constraints (Krysan and Crowder 2017; Rosenblatt and DeLuca 2012). Thus, constraints are inherent in neighborhood choice: individuals rarely know about all possible destinations, and many options may be unattainable and therefore excluded from consideration.

Our understanding of the mechanisms that produce neighborhood segregation is hampered by the fact that existing quantitative models in the social sciences do a poor job representing the decision process underlying neighborhood mobility. In this study, we develop and estimate a behaviorally nuanced statistical model of neighborhood choice. Our model is anchored in qualitative studies of housing search and neighborhood choice, as well as a large body of work in cognitive science and decision theory.

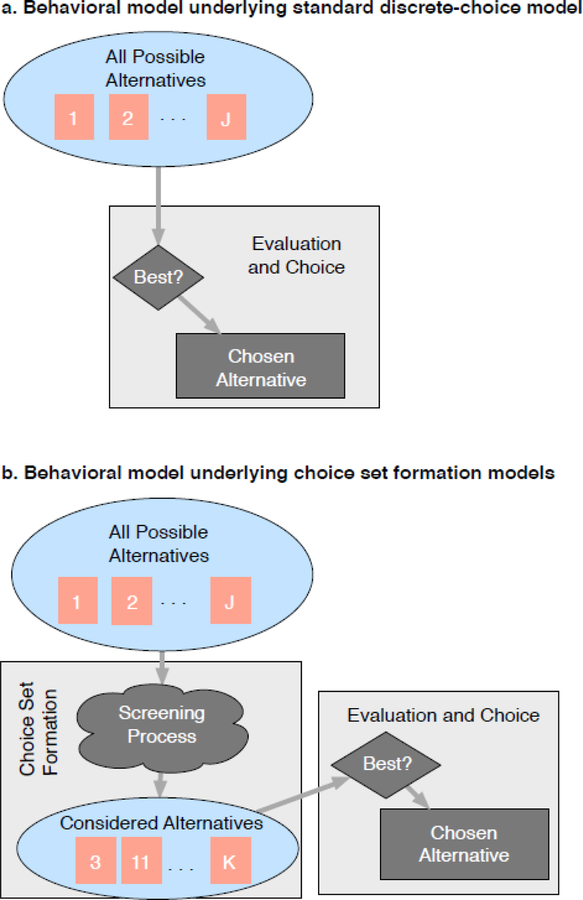
Figure 1 contrasts the model of decision-making typically used in quantitative social science analyses of choice (panel a) with the cognitively plausible framework proposed here (panel b). In conventional choice models (e.g., Ben-Akiva and Lerman 1985; Bruch and Mare 2012; McFadden 1974), the analyst assumes a single decision stage in which individuals evaluate all salient attributes of all potential choice alternatives using the same level of scrutiny. In contrast, a cognitively plausible choice model allows for heuristics—that is, simplifying problem-solving strategies—that reduce the cognitive complexity of the decision process. Choices may be made in multiple stages, with each stage reducing the number of alternatives under consideration and different rules governing evaluation at each stage. We refer to the process of identifying the set of considered alternatives as choice set formation.

Fig. 1.

Contrasting conventional choice models with choice set formation models

Using neighborhood mobility data from the Los Angeles Family and Neighborhood Survey (L.A.FANS), we demonstrate that our estimated statistical model provides a better structural representation of the underlying neighborhood choice process than more conventional choice models that assume all alternatives are given equal scrutiny.² We find that affordability constraints coupled with spatial limitations lead blacks and Hispanics to have choice sets that consist disproportionately of areas where their own group is overrepresented. This choice set formation process is not explicitly race-based, but because it unfolds in a segregated environment, the result is that individuals have racially stratified choice sets. Previous studies have documented divergent mobility patterns by race, even after controlling for income (e.g., Crowder et al. 2006; Fischer and Lowe 2015; Sampson and Sharkey 2008). In showing how cognitive strategies interact with unequal social landscapes, our analysis suggests how racially differentiated mobility patterns can be sustained even in the absence of race-based sorting.

A key takeaway from our empirical analysis is that the neighborhoods considered by potential movers differ markedly with their race and income. To better understand how demographically stratified choice sets of individuals affect larger-scale segregation dynamics, we implement a simple agent-based model that simulates residential mobility under different assumptions about (1) the extent to which choice sets expose movers to areas where their own-race group is overrepresented, and (2) the strength of racial preferences conditional on the set of neighborhoods considered. There is a long history of agent-based models exploring the aggregate outcomes implied by individuals’ preferences assuming fully informed, computationally efficient decision-makers (e.g., Bruch and Mare 2006, 2009; Fossett 2011; Schelling 1971). Our study broadens this literature by exploring how decision heuristics shape segregation dynamics. We show that even mild racial stratification of choice sets can amplify racial sorting. Our agent-based model suggests that decision processes—specifically, screeners used in the construction of choice sets—can be an important mechanism that helps sustain inequality and segregation.

The balance of the article is as follows. We first provide an overview of the literatures that motivate our multistage model of neighborhood choice. Building on this work, we specify a cognitively plausible statistical model of neighborhood choice. We then present our empirical analysis of neighborhood choice in Los Angeles County. We compare the fit of our selective consideration model with a standard choice model and discuss its substantive ramifications. Finally, we present our agent-based modeling results that explore the implications of racially stratified choice sets for segregation dynamics. We close with a discussion of how our findings refine and extend existing theories regarding the mechanisms sustaining racial residential segregation.

A Multistage Neighborhood Choice Process

Early work by cognitive scientists pegged our ability to process options for choice as being limited to seven alternatives (plus or minus two), but that estimate has since been revised to three or four (Cowan 2010; Miller 1956). Even with a relatively modest number of choice alternatives (e.g., less than 5), decision-makers need strategies to pare down the cognitive complexity of choice problems (Payne and Bettman 2004). To put this problem in perspective in the context of neighborhood choice, the focal region for our empirical analysis—Los Angeles County—has an area of 4,000 square miles encompassing 259 neighborhoods. People are unlikely to explicitly consider every possible area. Rather, the evidence from decision theory suggests that they initially engage in some sort of elimination process that results in only a few options for serious consideration.

A large literature in academic marketing, decision theory, and cognitive science demonstrates that a key strategy to reduce the cognitive complexity of these sorts of decisions is to engage in a multistage choice process, wherein the initial stage involves creating a choice set that is only a small subset of all potential choice options (Bruch and Feinberg 2017; Cohen and Lefebvre 2005; Payne et al. 1993; Roberts and Lattin 1991, 1997; Shugan 1980). Decision rules guiding what to include in the choice set are fundamentally different from the rules guiding the final choice (Salisbury and Feinberg 2012; Shocker et al. 1991). When identifying the choice set, people use less cognitively taxing screening rules that rely on only a small number of choice attributes. After the number of options has been whittled down to a manageable size, the decision-maker might expand on these criteria to consider trade-offs between, for example, the size of dwelling units and communing distance (Hauser et al. 2009). Thus, whereas the early decision processes are reductive, the later processes are refining.

From a behavioral standpoint, choice set formation (CSF) is the process of establishing the set of feasible or acceptable alternatives among those available to decision-makers (Swait and Ben Akiva 1987a:91). Scholars have historically focused on constraints as the central set of determinants that drive screening criteria in choice set formation—for instance, travel time, information gaps, affordability, cultural or social restrictions, and/or other phenomena that limit what options are available (e.g., Ben-Akiva and Lerman 1974; Meyer 1979; Swait 1984). Choice set formation also has been also viewed as the outcome of applying acceptability cutoffs on aspects of choice alternatives (Swait 2001). In the case of neighborhood choice, these might take the form of a threshold on maximum housing costs or minimum school quality.

Although empirical studies of residential mobility have rarely captured multiple decision stages, social researchers have accumulated substantial insights into the factors affecting choices at each stage. The initial stage of the residential mobility decision is simply whether to remain in the current housing unit. Prior work suggests that mobility decisions are often motivated by changes in life circumstances—for example, related to job, family, and/or housing needs—rather than neighborhood conditions (Ihrke 2014; Rossi 1980). Rates of mobility also differ by race and income (Lee et al. 1994; South and Deane 1993). In addition to intrinsic factors—such as the desire to be closer to work or the arrival of a new family member—decisions to move may also be prompted by extrinsic factors, such as a relationship breakup or eviction notice (Desmond 2012).

A decision-maker who opts to move must decide what neighborhoods to consider. A rich literature, largely from geography, demonstrates that housing searches are spatially bounded (e.g., Barrett 1973; Clark and Smith 1979; Huff 1986; Palm and Danis 2001; Rae and Sener 2016; Rogerson 1982; Smith and Clark 1982). Most moves are of very short distances, and affordability is a major constraint that shapes neighborhood consideration (Quillian 2017; Rosenblatt and DeLuca 2012; Talarchek 1982). Using data from a real estate website, Piazzesi et al. (2015) showed that geographic constraints and price range are far and away the most pervasive criteria used to restrict the scope of housing searches. This suggests that the neighborhood CSF process involves categorizing neighborhoods based on location and affordability and then selecting one or more sets for further consideration.

Finally, the mover selects the destination neighborhood from among the set of neighborhoods considered. At this stage, the decision-maker has reduced the choice set to a manageable size and may consider trade-offs on multiple attributes. A number of prior works have examined demographic correlates of neighborhood mobility—such as neighborhood racial composition, median income, and housing prices—assuming that the choice set is the entire metro area (e.g., Bayer et al. 2004; Bruch 2014; Quillian 2015; South and Crowder 1998). Our model allows for the possibility that these factors also, and potentially only, affect neighborhood consideration at the choice set formation stage.

Overall, this body of interdisciplinary work suggests that neighborhood selection is a multistage process in which a person who decides to leave the current neighborhood considers only a subset of available destinations based on affordability and location screeners. Having established a conceptual model of multistage neighborhood choice with selective consideration of neighborhoods, we now describe the statistical framework we use to implement it.

A Statistical Model of Neighborhood Choice With Choice Set Formation

Our model builds on earlier efforts to extend McFadden’s classic discrete choice model, which lays the microeconomic foundation for statistical models of choice behavior. McFadden’s approach is based on the assumption that individuals’ evaluation of alternatives can be characterized by a utility function in which individuals always select the alternative with maximum utility (McFadden 1974, 1978). The stochastic utility, U_i, associated with alternative i can be expressed as the sum of two components: (1) a systematic component, V_i, which accounts for the observable attributes of choice alternatives (and may vary systematically with observable attributes of alternatives and characteristics of choosers); and (2) a random component, ε_i, which accounts for unobserved factors. The probability that a person selects alternative i from a given choice set of alternatives, C, is $P(i|C)=P(U_i>U_j,\forall j\ne i\in C)$, where U_i, denotes the utility associated with an arbitrary alternative within choice set C.³

Choice modelers distinguish the universal set of possible alternatives from the choice set, which is the subset of alternatives explicitly under consideration that are both feasible and known to the decision-maker (Ben-Akiva and Lerman 1985:33). McFadden’s model is specified conditional on a given choice set; the process through which the choice set is generated is antecedent to model specification. Standard discrete choice models used in social science applications assume that the analyst knows the set of considered alternatives with absolute certainty. These studies typically ignore the details of the choice set, which is rarely known or explicated in practice.^4,5

Allowing for Choice Set Formation

The two-part nature of decision problems—first, the construction of the set of considered alternatives, and then the final decision conditional on this choice set—was first formally recognized by Charles Manski in his theoretical treatise on random utility models (Manski 1977). Manski specified that although a choice set is deterministic and known to the individual decision-maker, it is estimated as a probability by the analyst, who does not directly observe the process behind its generation.

Let M denote the universal set of all alternatives (i = 1,2, … I) from which the choice of the nth person is observed—for example, all neighborhoods within a metropolitan area. Define C_k as a choice set within Γ, the set of all possible subsets of M. Manski specified that the probability of the nth person choosing the ith choice alternative is written as follows:

$$P_n(i)={\sum }_{C_k\in \Gamma }{P}_n(i,C_k)={\sum }_{C_k\in \Gamma }{P}_n(i|C_k)Q_n(C_k),$$ (1)

where the subscript k indexes choice sets, Q_n(C_k) is the probability that C_k is the true choice set for person n, and P_n(i| C_k) is the conditional probability of the nth person choosing alternative i, given choice set C_k.⁶ Equation ((1) states that the probability of choosing an alternative is the conditional probability of the alternative in each set C_k in which it is contained, weighted by the likelihood of that choice set, and then summed over all possible choice sets. This formulation captures the analyst’s uncertainty about the true choice set by viewing choice as the expected probability of a joint choice of alternative and choice set (i, C_k) summed over all choice sets containing i.

Manski’s model was a theoretical effort to illuminate how the choice set formation process can be represented. Subsequently, scholars developed statistical models that implement choice set formation. Early formulations imposed deterministic constraints on choice sets based on assumptions about feasibility (e.g., a commuter cannot drive to work without access to a car). Later efforts allowed for probabilistic constraints that captured uncertainty in the analyst’s understanding of what options are available to a given decision-maker (Swait 1984, 2001; Swait and Ben-Akiva 1987b). These formulations also allowed analysts to include covariates that capture the formation of the choice set as well as the evaluation of the final choice, conditional on the choice set.⁷

We build on earlier modeling efforts in specifying our model of neighborhood choice, which hews closely to Eq. ((1).⁸ In the next section, we show how each component—the probability of choosing a particular neighborhood conditional on a choice set, P_n(i| C_k), and the probability of the choice set, Q_n(C_k)—is specified to capture the neighborhood selection process outlined in the section, A Statistical Model of Neighborhood Choice With Choice Set Formation.

Multistage Model of Neighborhood Choice With Choice Set Formation

Drawing from the residential search literature discussed in the previous section, the potential choice set, C_k, consists of all neighborhoods within a given price range located within one or more geographic regions.⁹ Let r = 1, …, R denote mutually exclusive and collectively exhaustive geographic regions of a metro area, such that each neighborhood maps into a unique region. In addition, let g = 1,. …,G denote mutually exclusive and collectively exhaustive price strata, such that each neighborhood maps into a single price stratum. In theory, we can have up to (2^R − 1) × G unique neighborhood choice sets, one for every combination of geographic regions within a given price stratum.¹⁰

Decision to Move

The choice sets are made up of two kinds of alternatives: (1) the potential destination neighborhoods (i = 1, …, I) nested within region-by-affordability choice sets, and (2) the option to remain in the current housing unit (i = 0). $\text{Let}\hspace{0.17em}{\Gamma }_{move}=\left\{\left\{i|i\in C_1\right\},\dots ,\left\{i|i\in C_K\right\}\right\}$ denote all possible region-by-affordability neighborhood choice sets for movers, and let Γ_Stay = {{0}} denote the current housing unit for stayers. The set of all possible choice sets in our model of neighborhood choice are the choice sets for movers, Γ_Move, crossed with the current housing unit contained in Γ_Stay. This doubles the (2^R − 1) × G original choice sets, such that half of the new choice sets include the option to remain in the current housing unit, and half of them do not.

This specification allows for the possibility that some movers may be forced to leave their current unit due to eviction or other circumstance beyond their control, in which case the set of all considered alternatives will not include the current unit. Among people who have the option to stay, the model implies that the probability of leaving the current unit depends not only on push factors, such as the birth of a child or change in employment status, but also the pull of potential destination neighborhoods. Accounting for these two types of elemental alternatives in the choice set, the unconditional probability that the nth person chooses the ith elemental alternative is as shown in Eq. ((1).

Choice of Destination, Given Choice Set

Now let $C_k^{\ast }$ denote a choice set that contains a region-by-affordability neighborhood choice set (C_k) and possibly also the current housing unit. The conditional probability that the nth person chooses the ith alternative given that choice set is

$$P_n(i│C_k^{\ast })=\{\begin{array}{ccc}\frac{\exp ({\mu }_k{V}_{in})}{{\sum }_{l\in C_k^{\ast }}\exp ({\mu }_k{V}_{ln})}& \forall \hspace{0.17em}i\in C_k^{\ast },& i=0,\dots ,I\\ 0& \forall \hspace{0.17em}i\notin C_k^{\ast }& \end{array},$$ (2)

where μ_k is a set-specific scale factor that reflects the degree of correlation in the stochastic component of utility of the alternatives within choice set $C_k^{\ast }$, and V_in is a linear-in-parameters combination of known and observed factors that influence neighborhood utility. Recall that the stochastic utility also contains the influence of factors unknown to the analyst, the aggregate magnitude of which must be accounted for relative to the known sources. Intuitively, the scale factors µ_k deflate or inflate the systematic utility to reflect the relative power of measured versus unmeasured factors to explain observed behavior. We allow different weighted sums of covariates in V_in to govern the decision to move or stay given that decisions about whether to move at all are motivated by different factors than decisions about what areas to consider if moving. The probability of choosing any neighborhood that is not in the choice set is 0.

Probability of Choice Set

A person’s probability of a given choice set $(C_k^{\ast })$ is the product of the probability that mover n considers neighborhoods within a given price range and the probability that mover n considers neighborhoods within a given set of geographic regions and possibly also the current housing unit.¹¹ The intuition behind this “independence” assumption is that affordability constraints work the same way in all geographic regions.¹² In the absence of data on how neighborhood decisions unfold, we prefer to remain agnostic about the sequencing of geographic and affordability restrictions—that is, whether people decide what areas they can afford and then consider possibilities within those areas based on geography; whether they decide what regions to consider and then look for affordable neighborhoods within that set; or whether such screening is actually simultaneous. Technical details about how we specify the choice set formation processes and incorporate affordability constraints are provided in the online appendix.

Our CSF model reduces to the conditional logit model (i.e., assumes neighborhoods receive equal consideration) when all scale factors are equal, all πs are 1 (i.e., all macro-regions are included in the choice set), and all affordability strata equally likely.¹³ Thus, the standard discrete choice mode is nested within our CSF model.¹⁴

Data

We estimate our model using data on adult respondents from Wave 2 of the L.A.FANS, a panel study of households living in 64 sampled neighborhoods in Los Angeles County (Sastry et al. 2006). These data include a six-year retrospective residential history. The L.A.FANS data show that 55 % of these respondents did not move at all over the entire observation period, 31 % moved once, and 14 % moved two or more times. Thus, consistent with prior work on residential mobility patterns (e.g., Long 1988), the majority of mobility decisions are decisions to remain in the current unit.

To reduce the disproportionate weight allotted to the stayer decisions in the likelihood function, we define a move as any change in residence that occurred within a two-year window over the six-year observation period. Thus, each individual has three potential move occasions. Note that if a respondent changed residence multiple times during the window, we register only where he or she was at the beginning and end of the two-year mobility window. Table 1 reports descriptive statistics for the sample population. Consistent with the composition of Los Angeles County, the sample is majority Hispanic (58 %), followed by white (26 %), black (10 %), and Asian (6 %). Because our sample underrepresents Asians and has only a small handful of moves by Asian households, we deemphasize these results in subsequent discussion.

Table 1.

Sample characteristics of adult respondents: L.A.FANS, Wave 2

	Hispanic	White	Black	Asian
Demographic Characteristics
Age	37.7	45.1	39.8	44
Income ($)	37,515	71,080	41,193	62,259
Education (years)	10	15.7	14.3	15.4
Number of children living at home	1.3	0.8	0.9	0.8
Mobility Triggers
Ended cohabitation	0.023	0.018	0.045	0.024
Started cohabitation	0.012	0.017	0.027	0.012
Changed cohabitation	0.008	0.003	0.003	0.008
Jobs lost	0.048	0.051	0.091	0.052
Jobs gained	0.056	0.042	0.094	0.036
Jobs changed	0.262	0.290	0.174	0.293
Mobility Patterns
Number of within-neighborhood moves	168	54	36	21
Number of between-neighborhood moves	240	82	52	25
N	763	325	128	79

Notes: Statistics are averaged over all person-years. The sample includes only person-year residential decisions of respondents who are not missing on any covariates.

Neighborhoods and Regions in Los Angeles

Rather than defining neighborhoods using administrative boundaries such as census tracts, we seek publicly recognized neighborhood boundaries. Within Los Angeles County, such boundaries are available through the Los Angeles Times’ Mapping L.A. project, which divides Los Angeles County into 259 neighborhoods containing an average of seven to eight census tracts. Beyond the neighborhood level, Los Angeles County is made up of recognized geographic regions. We identify seven regions using information from the Mapping L.A. project as well as the housing search areas defined by websites such as Craigslist, the Service Planning Areas used by community health organizations, and the boundaries of development zones. The macro-regions—shown in Fig. 2—reflect both natural boundaries and socially recognized distinctions. They contain between 22 and 58 census tracts. Demographic attributes of macro-regions are reported in Table 2.

Fig. 2.

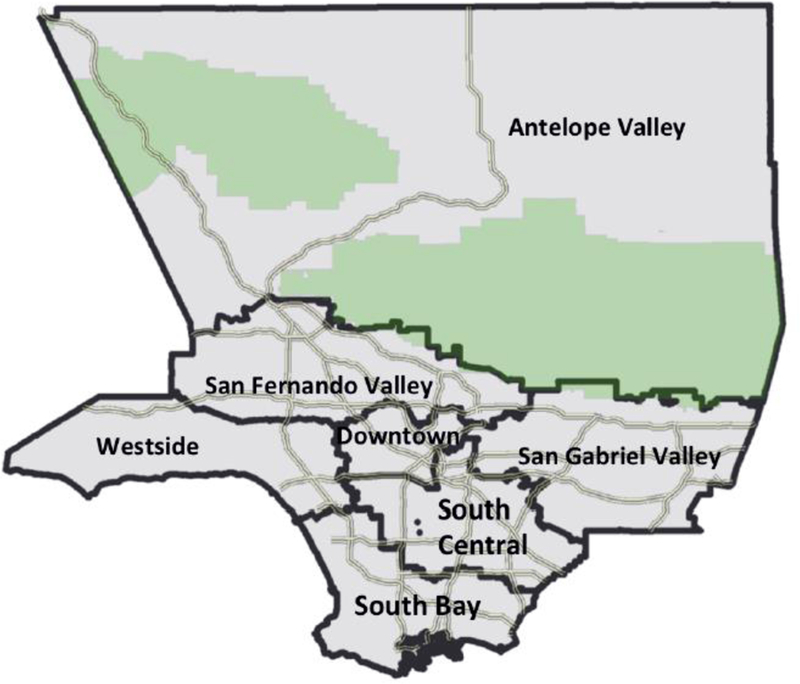
Geographic regions in Los Angeles County

Table 2.

Attributes of macro-region choice sets

	% Black	% Hispanic	% Asian	Median Income ($)	Total H Units (in 1,000s)
1. Antelope Valley	10	37	7	65,040	196
2. Downtown	7	47	18	39,300	402
3. San Fernando Valley	4	41	12	68,940	675
4. San Gabriel Valley	2	48	27	67,350	489
5. Westside	5	14	12	90,150	284
6. South Bay	13	38	16	67,140	572
7. South Central	14	73	5	44,520	611

We see pronounced differences in the makeup of macro-regions. South Central has the lowest median income, the least expensive housing, and the highest minority concentration: 73 % Hispanic and 14 % black residents. In contrast, the Westside is the wealthiest region, with the most expensive housing and highest concentration of white residents (at 69 %). Still, macro-regions exhibit a great deal of diversity, reflecting the geographic scale of segregation (Lee et al. 2008). For instance, South Central is home to most of Los Angeles’ predominantly black neighborhoods, but more than 30 % of the neighborhoods are less than 5 % black. Similarly, the median income of neighborhoods in South Bay ranges widely, from $37,937 to $187,777.¹⁵

Decision Factors at Different Stages

We model the utility associated with remaining in the current housing unit, V_0n, as a linear combination of individual attributes, including race, age, and education. Consistent with previous literature, we also specify that the utility associated with remaining in the current housing unit may vary over time as a function of duration of residence and whether the decision-maker experiences changes in the number of children or of school-aged children, the beginning or end of a live-in relationship, and a loss, gain, or change in employment.

The next set of covariates are conditional on deciding to move. To reflect people’s tendency to consider—that is, include in their choice set—neighborhoods they know relatively well, we add a covariate capturing the distance between the origin region and the potential destination region (Krysan and Crowder 2017; Quillian 2017). We also test whether (1) the set of geographic regions considered by individuals of a given race and income are a function of those regions’ racial and economic composition, net of housing costs; and (2) blacks and Hispanics respond differently than whites and Asians to affordability and distance. We specify that neighborhood affordability depends on a potential mover’s disposable income, which is a function of household income and size.

Finally, we model the utility associated with the nth person choosing with the ith neighborhood, conditional on the choice set. Covariates at this stage include neighborhood median income, income surplus and income deficit (the positive and negative difference between the nth person’s family income and the median income of the ith neighborhood), the median house price in the neighborhood, the proportion of neighborhood residents with less than a high school education interacted with whether the mover has less than high school education, and neighborhood racial composition interacted with the mover’s own race. We also include a dummy variable for whether the destination neighborhood is also the origin neighborhood as well as the linear and quadratic effects of distance between origin and destination.¹⁶

Statistical Results

We compare the fit and substantive interpretation of our CSF model that allows for selective consideration with a more conventional, conditional logit model that assumes people consider all 259 potential destination neighborhoods: that is, the choice set consists of the entire metro area. Table 3 reports summary fit statistics for the two models.

Table 3.

Goodness of fit for conventional choice model and choice set formation model

	Conditional Logit Model	Choice Set Formation Model
Log-Likelihood (0)	−21,058	−21,058
Log-Likelihood (convergence)	−3,759	−3,712
Rho Squared	.8215	.824
Akaike’s Rho Squared	.8198	.821
Number of Parameters	36	52
AIC	7,590	7,529
BIC	7,776	7,798

Based on a likelihood ratio test, our CSF model fits better than the standard conditional logit model, and this difference is statistically significant. Of course, the CSF model is also less parsimonious than the conditional logit model, with 52 parameters compared with 35 parameters, respectively. When we examine goodness-of-fit statistics that penalize complex models (i.e., AIC and BIC), we see that the CSF model is still preferred over the conditional logit model using AIC but not BIC. One likely reason for these mixed results is the relative dearth of moves in the sample. Among the 3,931 potential move occasions in the L.A.FANS data, only 695 of them resulted in a change of residence. Any model—including the conditional logit—that explains the high proportion of stayer decisions (82 %) in the data will be difficult to improve on. The real payoff to allowing for choice set formation comes once a person has decided to move.

In addition to being a better fit for the mobility data, the CSF model also tells a different substantive story than the conditional logit model. The standard conditional logit model assumes that movers consider all 259 neighborhoods in Los Angeles—that is, the probability of considering any given neighborhood is 1.0—but the CSF model implies that the average probability of consideration for any given neighborhood is around .15. In other words, movers are likely to never consider the vast majority of the potential destination neighborhoods because this probability will decrease with distance and affordability.¹⁷ In the rest of this section, we highlight differences in what the two models reveal about decision-making at different stages of neighborhood choice process.

The first panel in Table 4 reports the effect of respondent attributes on the probability of staying in the current housing unit. Both the CSF and the conditional logit models show similar patterns of mobility by race, age, family, duration of residence, and relationship status.^18,19 To facilitate comparison between the two models, the third column of Table 3 reports whether the CSF coefficient is outside the 95 % confidence interval for the conditional logit. It is not surprising that the conditional logit and CSF models produce similar results with regard to what factors are associated with the initial decision stage—to stay or go—given that the key difference between the two models is choice set formation. Although many of the coefficients for neighborhood choice (conditional on choice set) are statistically indistinguishable in the models, the different choice sets implied by the conditional logit and CSF models render them with different substantive implications. We now turn to understanding the implications of the CSF model for neighborhood sorting.

Table 4.

Coefficient estimates for conventional choice model and choice set formation model

	Conditional Logit (CL) Model	Choice Set Formation (CSF) Model	CSF Coefficient In/Out of CL 95 % Confidence Interval?
Staying in Current House
Household head is black	0.969**	0.115	Out
Household head is Asian	0.519	−0.24	In
Household head is Hispanic	2.966**	2.065**	Out
Household head has <high school education	0.519*	0.423	In
Household head’s age	1.440	1.428	In
Household head’s age squared	2.436	3.329	In
Number of children	−0.138*	−0.140*	In
Number of school-aged children	0.304*	0.311†	In
End of a cohabitation relationship	−0.436†	−0.603*	In
Start of a cohabitation relationship	−1.203**	−1.377**	In
Loss of job	−0.381*	−0.445†	In
Gain of job	−0.309	–0.190	In
Job change	−0.316**	–0.357**	In
Ln[Duration of tenure (days)]	0.176**	0.164*	In
What Neighborhoods to Consider
Region consideration likelihood
Average propensity to consider any geographic region		2.756**
Average propensity to include current housing unit in choice set		10 (––)a
Distance in miles from origin region		−11.776**
Affordability stratum likelihood
Tau 1		0 (––)a
Tau 2		1.764**
Tau 3		3.711**
Household income		3.400**
Ratio of household income to household size		1.1
Region scale factors (natural logarithm)
Antelope Valley		–0.502**
Downtown		0.351**
San Fernando Valley		−0.007
San Gabriel Valley		−0.043
Westside		−0.011
South Bay		−0.04
South Central		0.229*
Stay at current residence		0 (––)a
Affordability stratum scale factors (natural logarithm)
Stratum 1		−0.215
Stratum 2		−0.144
Stratum 3		−0.097
Stratum 4		0 (––)a
Neighborhood Choice Conditional on Choice Set
Intercept	−11.298**	−10.660**	In
Median income	5.824**	2.894†	Out
Income surplus	−1.483*	−1.234	In
Income deficit	1.099	3.015**	Out
Median housing unit price	−5.211**	0.235	Out
% <High school education	2.375*	1.509	In
<High school education × % <high school education	1.978**	1.595*	In
% Black	−5.985**	−2.239	Out
% Black, squared	5.488*	1.268	In
% Hispanic	−0.555	0.113	In
% Hispanic, squared	−2.321	−1.783	In
% Asian	−4.795**	−1.459	Out
% Asian, squared	5.628*	1.717	In
Household head is black × % Black	10.698**	4.543	Out
Household head is black × % Black, squared	−10.819*	−2.165	In
Household head is Hispanic × % Hispanic	9.024**	5.788**	In
Household head is Hispanic × % Hispanic, squared	−5.998**	−3.247†	In
Household head is Asian × % Asian	7.747*	1.698	In
Household head is Asian × % Asian, squared	−10.760†	−0.702	In
Origin	1.540**	1.367**	In
Distance from origin community area	−25.428**	−27.906**	In
Distance from origin community area, squared	30.219**	34.945**	In
Size	1 (––)a	1 (––)a
N	1,298	1,298

Note: Observations are individual two-year interval-potential destinations.

^aThe coefficient is fixed by the analyst.

^†p ≤ .10;

^*p ≤ .05;

^**p ≤ .01

Choice Set Formation

The second panel of coefficients in Table 4, by definition available only for the CSF model, captures the likelihood that a given neighborhood is included in the choice set. We first examine coefficients describing the pattern of spatial selection into the choice set (Region Consideration Likelihood).²⁰ Distance from the region of origin is a strong and statistically significant predictor of which regions are included in the choice set. This is consistent with past work finding that most moves occur over short distances (e.g., Clark and Smith 1982).

Turning to the coefficients describing the probability of considering neighborhoods within a given affordability range (Affordability Consideration Likelihood), we see that household income is a strong predictor: higher-income households consider more expensive neighborhoods. Figure 3 presents a LOWESS plot of the average probability of a given neighborhood being in the choice set (i.e., consideration) based on median housing price for respondents whose incomes fall at the 5th, 25th, 75th, and 95th percentiles of the family income distribution. Data points are jittered to improve resolution. Not surprisingly, respondents in the 5th percentile of the income distribution ($5,490/year) tend to consider the least expensive neighborhoods, with a number of very low-income neighborhoods that have an unusually high (.4) probability of being considered by this group. Among higher-income households, the response curve flattens out, suggesting that affordability constraints play a lesser role in the decision about what areas to consider. As one might expect, the households at the 95th percentile of income ($183,900) are more likely to consider moderate- to high-priced neighborhoods.

Fig. 3.

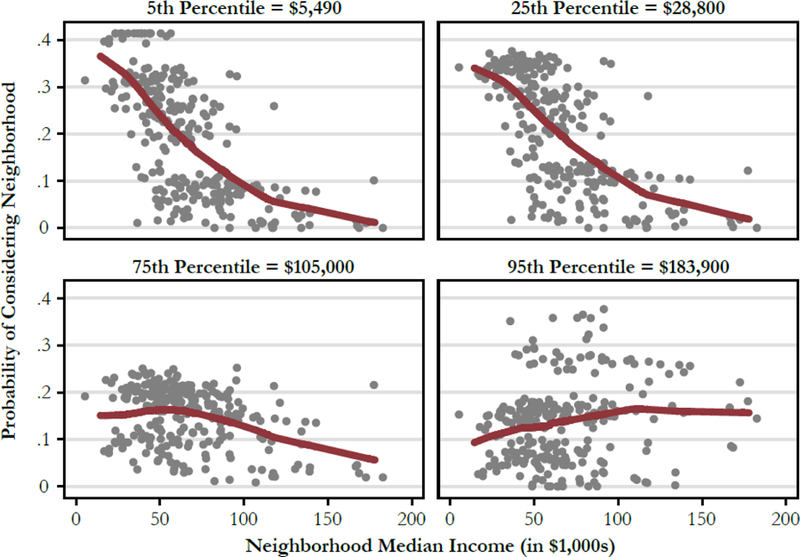
Average probability of neighborhoods being in choice set by median price, for individuals at varying percentiles of family income

We tested for but did not find evidence that the racial and economic composition of a given region affects the probability that the region is included in the choice set, net of prices and distance. Nor did we find that affordability and/or geographic constraints in the formation of choice sets operate differently for members of different race groups. Our model suggests that all race groups respond similarly to spatial and affordability constraints. Nevertheless, geographic and affordability screeners have important implications for racial differences in choice sets, especially for blacks and Hispanics.

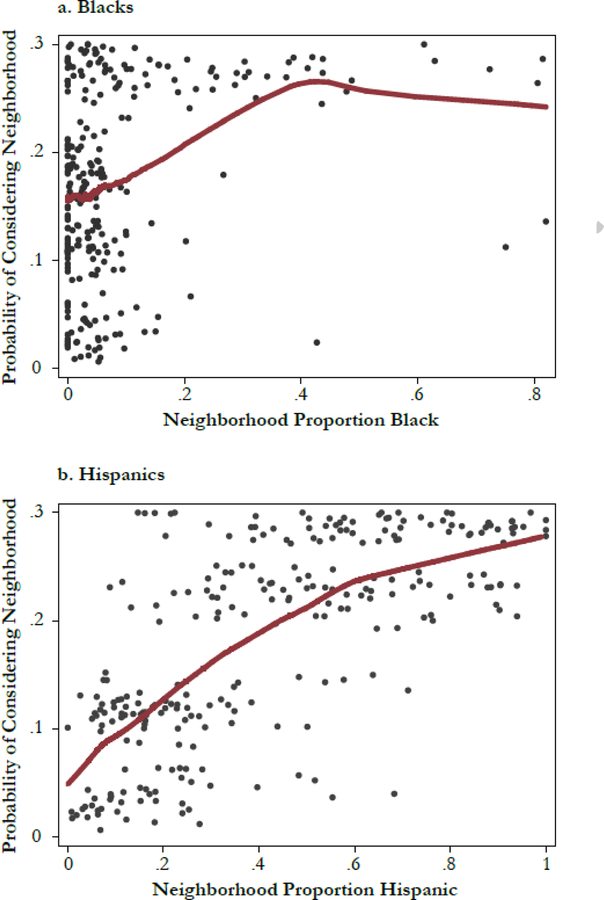
Figure 4 shows how a neighborhood’s proportion of residents being one’s own racial/ethnic group affects the probability that neighborhood will be explicitly considered (i.e., in the choice set) of blacks and Hispanics. Data points are jittered to improve resolution. Both blacks and Hispanics are more likely to consider areas that contain a high proportion of one’s own group. As a result, the choice sets of blacks and Hispanics disproportionately include neighborhoods with higher fractions of their own group relative to the metropolitan area as a whole.²¹ Comparing the choice sets of blacks and Hispanics to neighborhoods in Los Angeles as a whole, we find that blacks and Hispanics consider neighborhoods that are, on average, 27 % less white and about 20 % more Hispanic than Los Angeles neighborhoods as a whole. We do not find evidence that whites and Asians are more likely to consider areas where their own racial/ethnic group is overrepresented.²²

Fig. 4.

Probability of neighborhood being in choice set by proportion own race/ethnicity, blacks and Hispanics

Choice of Neighborhood Destination

The final panel in Table 4 shows the probability of moving to a particular neighborhood conditional on the choice set. Because the models include identical covariates predicting the probability of choice conditional on choice set, any difference in the substantive and statistical significance can be attributed to the different composition of the choice sets. Conditional on the choice set, neighborhoods with higher median incomes are more attractive, all else equal. Having a family income above the median neighborhood income (Income Surplus) has a negative effect for both models (although significant only in the CL model), suggesting that people tend to avoid neighborhoods where the median income is less than their own. Having an income below the median income (Income Deficit) has a statistically significant and positive effect only for the CSF model. In other words, people sort more strongly on income—in terms of seeking out the highest-income neighborhood in their choice set—once we condition on their choice sets. The effect of median housing price is statistically significant and negative in the conditional logit model—implying that, all else equal, movers avoid costly areas—but is not statistically significant from 0 in the CSF model. This suggests that the CSF model effectively captures affordability constraints at the choice set formation stage.

With regard to the effects of racial composition on choice outcomes, almost all coefficients in the standard conditional logit model are statistically significant, and their magnitude and direction are consistent with past studies (e.g., Bruch 2014; Bruch and Mare 2012). In the CSF model, only two main effects are statistically significant: the linear terms on percentage black and percentage Asian. Both these coefficients are large and negative, suggesting that conditional on the choice set, nonblacks avoid black neighborhoods, and non-Asians avoid Asian neighborhoods. All the interaction terms in the conditional logit model are statistically significant; in the CSF model, only a small handful of terms are significant. The fact that the majority of racial composition variables are not statistically significant in the CSF, conditioning on the choice set, is likely a result of the fact that CSF creates more homogeneous choice sets than the city as a whole.

Figure 5 displays variation in the odds of a person who is black, white, Hispanic, or Asian choosing a final destination neighborhood by own-group composition, with all other neighborhood attributes held at their mean values. This encompasses both the effects of race at the choice set formation stage and the choice of final neighborhood conditional on the choice set. To avoid making out-of-sample predictions, each line is plotted over only ranges of racial composition for which there are sufficient data in Los Angeles County. These odds are computed relative to a white person choosing a 100 % white neighborhood. We see that racial sorting among blacks and Hispanics is more pronounced in the CSF model. For example, the odds that a Hispanic household will choose a 40 % Hispanic neighborhood are twice as high in the CSF model than in the conditional logit model.²³

Fig. 5.

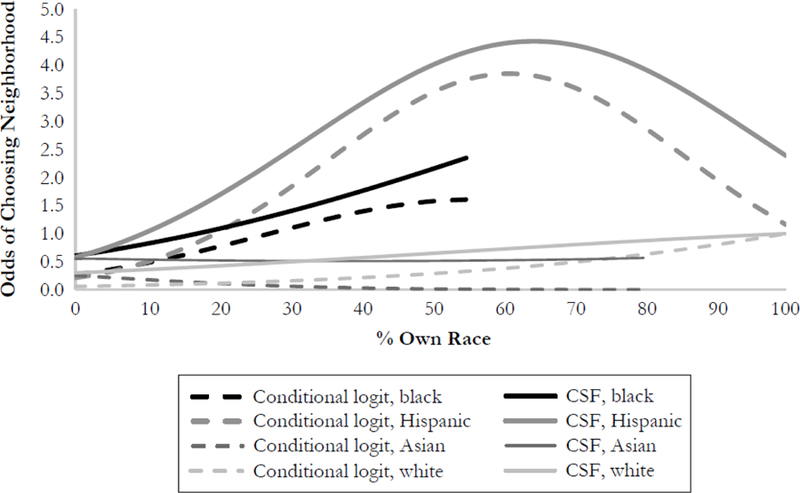
Conditional probability of choosing a neighborhood by percentage own race/ethnicity, given on areas considered

Thus, in contrast to a standard conditional logit model that assumes all neighborhoods receive equal consideration, we find that the CSF model fits the data better and tells a different empirical story. The CSF model suggests that people consider, on average, less than one-quarter of all available destinations. Although our model reveals no racial differences in how potential movers respond to affordability constraints and spatial considerations, neighborhood segregation in Los Angeles is such that the same decision process has very different implications for the choice sets of different racial/ethnic groups. Specifically, blacks and Hispanics are more likely to consider areas with higher proportions of their own racial/ethnic group. Overall, the CSF model suggests that by assuming that people explicitly consider every neighborhood in a metropolitan area standard choice models used in demographic research underestimate levels of racial/ethnic and economic sorting.

How Stratified Choice Sets Affect Segregation Dynamics

A central finding from our empirical analysis is that neighborhood choice sets are stratified by race and income. Blacks and Hispanics are exposed disproportionately to neighborhoods where their own group is overrepresented relative to the city as a whole, and low-income households disproportionately consider poorer neighborhoods. To what extent do these stratified choice sets contribute to segregation outcomes? To answer this question, we develop a simple agent-based model in which agents engage in a two-stage residential choice process: first deciding what neighborhoods to consider, and then deciding where to move conditional on consideration. Although our current model focuses on racial sorting, it is straightforward to extend it to other attributes, such as income. We assess how segregation outcomes vary with different assumptions about (1) the extent to which choice sets expose movers to areas where their own racial/ethnic group is overrepresented, and (2) the strength of racial/ethnic preferences conditional on the set of neighborhoods considered.

The model consists of a 40 × 40 lattice inhabited by 1,350 agents who are evenly divided into two race groups. The agents are initially distributed at random across the lattice. Only one agent can occupy each cell, and approximately 15 % of the cells are vacant. Each cell has a unique neighborhood defined by a radius around it. For example, a radius of 1 implies that neighborhoods are the 8 surrounding cells, whereas a radius of 2 implies that the neighborhood consists of the 24 surrounding cells. All results reported here assume a radius of 2. After the model is initialized, agents are randomly sampled with replacement and given the opportunity to either remain in their current cell or move to an empty cell on the lattice. Each step of the model denotes a unique move opportunity for one agent.

Once sampled for a move opportunity, agents decide where to move based on a two-step utility function. First, the agent decides what neighborhoods to consider. Consideration is based on a threshold proportion own race, which we refer to in the model as c*. For example, if c* = .2, the agent will consider only those neighborhoods where at least 20 % of the occupants are members of own race. The agent then chooses one destination from among the set of neighborhoods considered $(C_{c^{\ast }})$ The probability that the ith agent chooses destination $d\in C_{c^{\ast }}$ is denoted as $P_i(d|C_{c^{\ast }})$. We specify that this probability is a function of the proportion own race in the neighborhood of d, X_d, and the weight given to that proportion (β). Formally, this can be written as a choice function that, assuming independent and identical Gumbel distributions on the error term, results in the following equation for the probability $P_i(d|d\in C_{c^{\ast }})=e^{\beta X_d}/{\sum }_{a\in C_{c^{\ast }}}{e}^{\beta X_a}$, where the denominator sums over all vacant cells whose neighborhoods meet the consideration set cutoff. Figure 6 shows what this choice function implies for varying βs, assuming c* = .2.

Fig. 6.

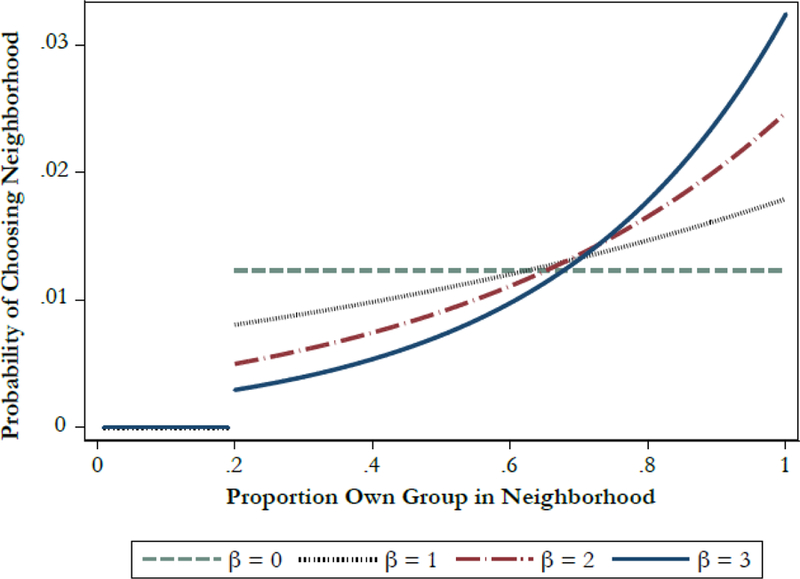
Choice functions for simulation models, with C* = .2 and varying βs

We conduct a series of experiments in which we vary the proportion own race that agents use in deciding what neighborhoods to consider (c*) as well as the strength of own-race preferences conditional on considering a neighborhood (β). We vary c* from 0 to .4, in intervals of .05. We vary β from 0 to 3. (A beta value of 0 implies that agents choose a destination at random from those neighborhoods they consider.) The model is run for 70,000 ticks, which is more than enough time for it to reach equilibrium. We measure segregation using a simple metric: the percentage of agents who live in neighborhoods that are entirely occupied by agents of like race such that they are racially isolated in their own neighborhoods. All reported results represent average outcomes over 10 runs of the model keeping model parameters constant but using a different random seed.

Figure 7 summarizes the final segregation outcomes produced by the simulation model for different values of c* and β. The error bars denote 95 % confidence intervals. We see that when own-group preferences conditional on consideration are mild (i.e., β = 1) and racially stratified choice set formation is also mild, the fraction of isolated agents is close to 0. However, c* values of .2 are sufficient to create a substantial uptick in segregation. A c* of .2 implies that agents will consider neighborhoods only if their race group is at least 20 % of the local population, which is entirely plausible based on what we know of whites’ and blacks’ willingness to live in neighborhoods of varying racial composition (Charles 2003). Moreover, segregation increases nonlinearly with the fraction own race considered in choice set formation. When own-race preferences are more pronounced (e.g., β = 2), segregation increases more sharply with an uptick in c*. When agents have a strong racial preferences (i.e., β = 3) conditional on consideration, even a very small c* value, such as .05, is sufficient to produce a large uptick in segregation.

Fig. 7.

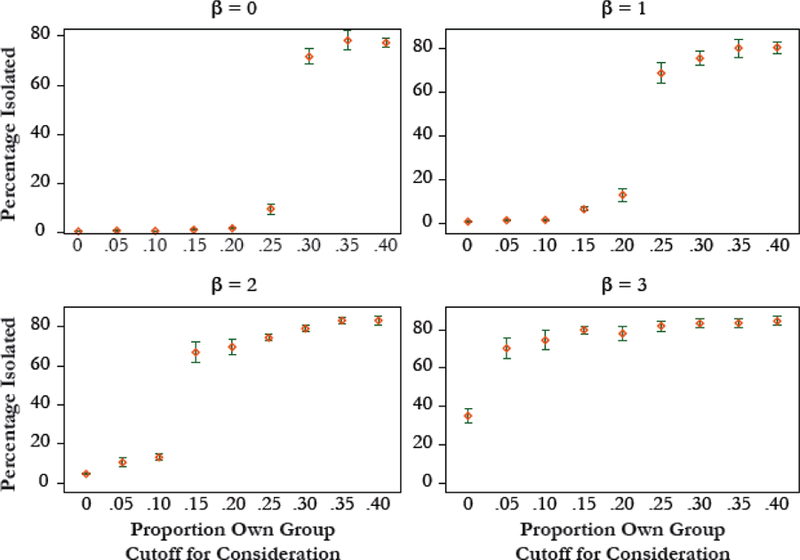
Segregation outcomes from agent-based models

These simulations demonstrate that choice sets can amplify the effects of racial preferences and sorting. Even relatively mild tendencies for racially stratified choice sets—for example, assuming movers consider areas only where their own group is at least 20 % of the local area—produce substantial effects on segregation outcomes. One possible explanation for this is that racially stratified choice sets imply that people have zero probability of moving to areas where their own group is less prevalent. This limits the extent to which even low probability moves can occur, which is one mechanism through which stable segregation can be achieved (Bruch and Mare 2006, 2009). Overall, our results suggest that decision processes—specifically screeners used in the construction of choice sets—may be an important mechanism in sustaining inequality and segregation.

Discussion

Despite a growing body of qualitative work on the strategies people use to choose neighborhoods (e.g., Carrillo et al. 2016; Darrah and DeLuca 2014; Krysan and Bader 2009; Krysan and Crowder 2017; Pattillo 2015; Rhodes and DeLuca 2014), quantitative analyses of neighborhood choice are hampered by the fact that conventional statistical models of choice behavior used in the social sciences are rooted in a rational actor framework, which assumes a fully informed decision maker who explicitly considers every salient attribute of every choice alternative (McFadden 1974, 1999). In reality, decision-makers have limited time, cognitive capacity, and working memory for learning about choice alternatives (Koehler and Harvey 2004; Simon 1990). As a result, people are often unaware of their full range of available options, and access to information is highly stratified by socioeconomic status (Lareau and Goyette 2014; Phillippo and Griffin 2016). The fact that quantitative models of choice do not represent even basic details of people’s neighborhood choice process hampers our ability to pinpoint mechanisms that govern residential mobility patterns.

In this study, we develop and estimate a cognitively plausible and statistically tractable choice model suitable for social science research. Our model of neighborhood choice captures key features of the underlying choice process: first, that neighborhood selection unfolds in multiple stages with potentially different decision criteria at each stage; and second, that the initial stage of neighborhood choice involves selecting a reduced set of options for more detailed consideration. We find that our model with selective consideration fits the residential mobility data better than conventional models that assume all neighborhoods receive equal consideration.²⁴ Because they incorrectly assume that all racial groups consider the same set of neighborhoods, conventional models of neighborhood choice appear to underestimate the importance of race-related factors in residential mobility decisions.²⁵

To better understand the role of choice sets in shaping segregation dynamics, we develop a simple agent-based model of two-stage neighborhood choice. The results suggest that even a choice set formation process that is mild in its effect on what neighborhoods agents consider can affect segregation outcomes. The extremity of screeners at the choice set formation stage and the strength of own-race preferences also interact when people evaluate considered neighborhoods. The stronger the agents’ own-race preferences when evaluating considered neighborhoods, the more marked the effect of even a small tendency toward racially stratified choice sets. Although more work is needed to evaluate the role of choice sets in shaping empirical patterns of segregation, our simulations suggest that decision processes are an important and underrecognized mechanism that contribute to persistent segregation.

Students of segregation have long been puzzled about why neighborhood mobility patterns continue to reproduce concentrated racial inequality despite substantial legal, social, and cultural changes in the past half-century. Prior studies have revealed that differences in socioeconomic status explain only a portion of the differences in the neighborhood mobility patterns of whites and nonwhites (Alba and Logan 1993; Crowder et al. 2006; Logan and Alba 1993). This has led scholars of segregation to emphasize the importance of place stratification—that certain minorities (i.e., blacks and Hispanics) cannot convert income into neighborhood upward mobility as readily as whites (Logan 1978; Pais et al. 2012). But it is unclear how place stratification is produced. The traditional approach highlights both supply-side barriers, such as racial steering and discrimination, as well as demand-side factors, such as the preferences of whites to live in same-race neighborhoods. Still, scholars have struggled to explicate how and to what extent to which these factors contribute to mobility patterns.

Our work suggests that choice set formation (i.e., multistage decision processes that involve screening rules and selective consideration) is an important mechanism through which place stratification occurs. Our choice models reveal that a racially segregated urban landscape coupled with affordability constraints produces racially homogeneous choice sets. In other words, even if racial steering and discrimination were eliminated, the combined implications of affordability and geography may be sufficient to create distinct and racialized submarkets for housing (see also Fischer and Lowe 2015). Our models, by aiming to better capture residential mobility process, provide a more nuanced explanation for the root causes of residential segregation. Of course, our analyses focus on a single metropolitan area with a unique geographic layout. Our approach can be extended to other cities for which mobility information is available. We view this as an important direction for future research.

The cognitively plausible choice model presented here can be straightforwardly extended to other domains in which people identify viable choice from among a larger set of alternatives. For example, women who anticipate starting a family are more likely to consider college majors that lead to careers with flexible hours (Alon and DiPrete 2015). Students from disadvantaged backgrounds applying for college focus on schools that are close to home or that they have heard of (Hoxby and Avery 2013). Recent evidence suggests that when seeking a partner online, mate-seekers invoke noncompensatory screeners or “deal-breakers” that rule out large swaths of options based on a small number of criteria (Bruch et al. 2016). By providing a more structurally sophisticated and behaviorally nuanced model of choice behavior, our study offers a strategy for understanding how cognitive processes shape socially relevant decisions.