The Effects of Electrostatic Correlations on the Ionic Current Rectification in Conical Nanopores

Abstract

Ion-ion electrostatic correlations are recognized to play a significant role in the presence of concentrated multivalent electrolytes. To account for their impact on ionic current rectification phenomenon in conical nanopores, we use the modified continuum Poisson-Nernst-Planck (PNP) equations by Bazant et al. (Phys. Rev. Lett. 2011, 106, 046102). Coupled with the Stokes equations, the effects of the electroosmotic flow are also included. We thoroughly investigate the dependence of the ionic current rectification ratios as a function of the double layer thickness and the electrostatic correlation length. By considering the electrostatic correlations, the modified PNP model successfully captures the ionic current rectification reversal in nanopores filled with lanthanum chloride LaCl₃. This finding qualitatively agrees with the experimental observations that cannot be explained by the standard PNP model, suggesting that ion-ion electrostatic correlations are responsible for this reversal behavior. The modified PNP model not only can be used to explain the experiments, but also go beyond to provide a design tool for nanopore applications involving multivalent electrolytes.

1. Introduction

Ionic channels are important in living cells. Synthetic nanopores are important model systems for studying ionic channels [1–7]. Indeed, one of the best ways to investigate alive organ activities is to explore transportation of ions in synthetic nanopores [8–10]. Besides the implications in living cells, due to the unique phenomena occurred at nanoscale, synthetic nanopores themselves currently attract great interests as well [11]. For example, electrical measurements of nanopores show interesting properties of ion transport such as ion permselectivity [12], ion enrichment and depletion [13–15] and ion current rectification [16]. In addition, DNA and proteins can be identified or studied by synthetic nanopores via monitoring the ionic current since they change the current magnitude when translocating through the nanopore [2, 4, 6, 17–22]. Nanopores have numerous applications in biotechnology since they can be used in many separations and sensing processes [16–18, 23–29].

The current-voltage curves through the conical nanopore pose the asymmetric behavior generally. The ionic current magnitude depends on the direction of the applied voltage across the nanopore, leading to the ionic current rectification [30]. In ionic current rectification, the magnitude of the ionic current with the electric field direction from the tip side to the base side is different from the one with the opposite electric field. The ionic current rectification can be used to make a gate inside the pore that is related to voltage fluctuation [31], transfer ions in the conical nanopore in different electrochemical characteristics [32, 33], enhance and exhaust ions [30].

Even more interestingly, in the presence of multivalent electrolytes, i.e., lanthanum chloride LaCl₃, the ionic current rectification can even reverse in comparison to that in the monovalent electrolyte, i.e., KCl [34], where the magnitude of the ionic current with the electric field from the tip side to the base side is smaller than that with the electric field from the base side to the tip side. The reversal was attributed to charge inversion. Charge inversion is an inclusive incident which attracts a lot of scientific researchers from theory to applications [1, 24, 25]. It happens when there is deep interference between ions in a solution so that interfacial charges absorb ions with different charges much more than their existing charges [1]. This incident happens a lot in biological process like DNA and proteins. Charge inversion is also considered for large biological channels like Lysenin and OmpF channels [3–5]. For these channels, to act like a diode, using various pH solutions is helpful [6–8]. Although charge inversion is used to explain the ionic current rectification reversal, no detailed numerical simulations without many assumptions were carried out to thoroughly understand the underlying physics.

Overscreening or charge oscillation where the layer of excess counterions is immediately compensated by a charged layer with excess co-ions has been used to explain charge inversion [35]. The charge oscillation inside the double layer is due to Coulomb short-range electrostatic correlations which are prominent in concentrated multivalent electrolytes [36–38]. Recently, Bazant et al. incorporated the electrostatic correlations into a Landau-Ginzburg-typed free energy by using Cahn-Hilliard gradient-based expansions and derived a modified Poisson-Nernst-Planck (PNP) model [35]. This model not only successfully predicted the overscreening but also explained the electro-osmotic flow reversal [39], electrophoretic mobility reversal [40], and dielectrophoretic polarization reversal [41]. The modified PNP model has also been implemented to study electro-convective instability, nano electro-osmotic flow, and electro-convective flow on a curved surface [42]. However, it has not been used to study the ionic current in a conical nanopore where there is a clear qualitative discrepancy between the experimental results and the predictions from the standard PNP model. To bridge this qualitative discrepancy, it is worthwhile to quantitatively investigate the impact of electrostatic correlations on ionic currents in conical nanopores and examine if electrostatic correlations alone can explain the ionic current rectification reversal without invoking other assumptions. The main contribution of our work is to use a simple continuum model and demonstrate that the model can adequately capture essential physics and explain the reversal of the ionic current rectification in the multivalent electrolyte LaCl₃. By capturing the underlying physics in multivalent electrolytes, this continuum model can also be used to study other electrokinetic phenomena related with nanopores. Although more complex models have been proposed to study electrostatic correlations [43], these models are usually non-local and involve coupled integral equations. Therefore, they are typically intractable for complex dynamic problems or complicated geometries like here. In contrast, the modified PNP model used here is simple enough to be directly applied to dynamic electrokinetic problems.

In this manuscript, we will employ the modified Poisson-Nernst-Planck (PNP) model accounting for ion-ion electrostatic correlations with the Stokes equation since recent studies suggest that the electro-osmotic flow contributing to the convection current is important and can’t be negligible at high imposed voltages and large surface charges [44].

2. Mathematical Model

In this study, we consider a conical nanopore with a length of L* (Figure 1). The nanopore has a narrow tip radius R_t* and wider base radius R_b*. Two large reservoirs with a size of L_R* are connected to the end sides of the nanopore. The reservoirs and the nanopore are filled with an electrolyte solution with density ρ*, viscosity μ*, and permittivity ε*. The reservoirs are set to be so large that the concentration far from the nanopore remains a constant. The nanopore has a uniform negative surface charge σ* and we assume that the reservoirs’ walls are not charged. The charged nanopore attracts counterions and repels co-ions, forming the electric double layer. An applied electric field across the nanopore can induce an ionic current consisting of migration, convection, and diffusion through the nanopore. Consider the axis-symmetry of the system. We use the cylindrical coordinate. The radial r is at a right angle, and the axial z is collateral with the axis of the nanopore. The origin of the coordinate lies at the center of the nanopore.

Figure 1.

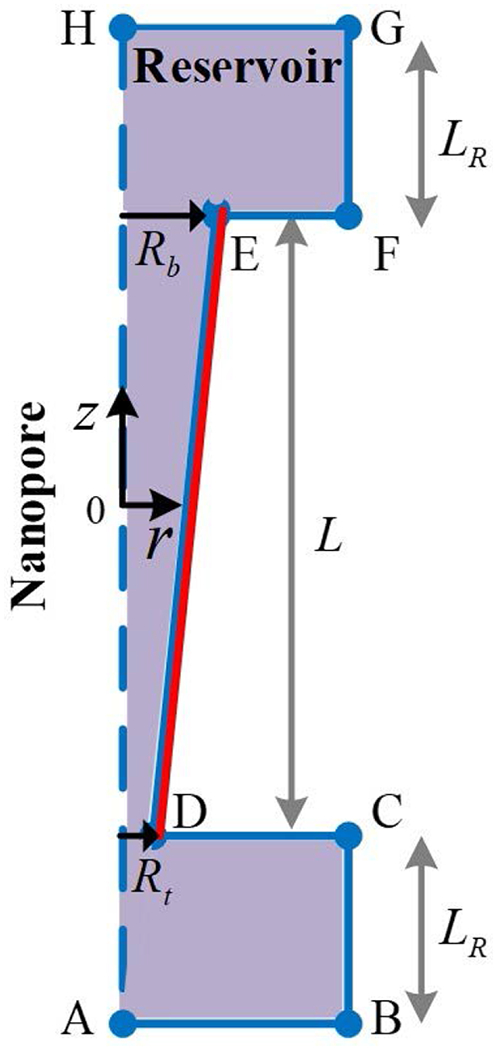
A schematics of the simulated system and the cylindrical coordinates.

Next, we present the mathematical model in the dimensionless form. Here, we use the superscript * to denote the dimensional forms. The variables without superscript * are dimensionless. Due to the nature of the low Reynolds number, we employ the Stokes equation to describe the flow motion,

$$-\nabla p-\frac{1}{2{\lambda }_D^2}(z_{+}{C}_{+}+z_{-}{C}_{-})\nabla \varphi +{\nabla }^2\overrightarrow{u}=0$$ (1)

For incompressible fluid:

$$\nabla •\overrightarrow{u}=0$$ (2)

In the above, $\overrightarrow{u}$ is the velocity vector in which u_r and u_z are the r and z velocity components; p is the pressure; ϕ is the electric potential; C₊ and C₋ are cation and anion concentration, respectively; z₊ and z₋ are the valences of cation and anion; and ${\lambda }_D=\frac{1}{{R_t}^{\ast }}\sqrt{\frac{{\epsilon }^{\ast }{R}^{\ast }{T}^{\ast }}{2F^{\ast 2}{C}_0^{\ast }}}$ is the dimensionless double layer thickness where $C_0^{\ast }$ is the cation bulk concentration; R* is the ideal gas constant; F* is the Faraday constant; and T* is the temperature.

For nondimensionalization, we chose R_t*, the tip radius, as the length scale; R*T*/F* as the electrical potential scale; ε*R*²T*²/(μ*F*²R_t*) as the velocity scale; $C_0^{\ast }$ as the concentration scale; ε*R*²T*²/(F*²R_t*²) as the pressure scale; ε*R*T*/(F*R_t*) as the surface charge scale.

We apply the symmetric condition on the boundary AH, the non-slip boundary conditions on the nanopore’s wall DE and the segment CD and EF. For other boundaries, we specify p = 0.

To account for the impact of ion-ion electrostatic correlations, we employ the modified PNP model developed by Bazant et al. [35]:

$$l_c^2{\nabla }^4\varphi -{\nabla }^2\varphi =\frac{1}{2{\lambda }_D^2}(z_{+}{C}_{+}+z_{-}{C}_{-})$$ (3)

Here l_c is the electrostatic correlation length.

For ions’ flux including convection, diffusion, and migration, we have:

$${\overrightarrow{N}}_{\pm }=C_{\pm }\overrightarrow{u}-{\Lambda }_{\pm }\nabla C_{\pm }-z_{\pm }{\Lambda }_{\pm }{C}_{\pm }\nabla \varphi .$$ (4)

Here ${\Lambda }_{\pm }=\frac{{D_{\pm }}^{\ast }}{{D_0}^{\ast }}$ in which $D_0=\frac{{\epsilon }^{\ast }{R}^{\ast 2}{T}^{\ast 2}}{{\mu }^{\ast }{F}^{\ast 2}}$, D₊* and D₋* are the molecular diffusivity of cation and anion.

The Nernst-Planck equations govern the ions’ transport:

$$\nabla •N_{\pm }=0$$ (5)

In terms of boundary conditions, we apply the axisymmetric conditions along the boundary AH. For the nanopore’s wall DE, the segment CD, EF, and reservoirs’ walls BC and FG, we apply

$$n•N_{\pm }=0$$ (6)

For the boundary AB and GH, the concentrations are equal to the bulk concentration:

$$C_{+}=1\text{and}{C}_{-}=z_{+}.$$ (7)

To compute the ionic current rectification ratio IR, we need to apply the electric fields both from the tip to the base and from the base to the tip. Here, the boundary condition on the GH is

$$\varphi =0,$$ (8)

and the boundary condition on the AB is

$$\varphi =\pm V_0,$$ (9)

depending on the direction of the electric field.

The boundary condition on the nanopore’s surface DE is given by

$$-\frac{\partial \varphi }{\partial n}=\sigma .$$ (10)

Here for simplicity, we do not consider the charge regulation and their impact in the multivalent ions. For the remaining boundaries, we apply the insulated condition for the electrical potential.

The resulting ionic current through the nanopore can be obtained by integrating the current density consisting of migration, convection, and diffusion along any cross section in the computational domain. Here we integrate the current density along AB. We also integrated along other cross section areas and found out that the difference is negligible.

$$I=\int (z_{+}{N}_{+}+z_{-}{N}_{-})•\mathit{nds}$$ (11)

The following values are used in our simulations: ρ* = 10³ kg/m³, μ* = 10⁻³ Pa•s, T* = 298 K, the diffusivities of La³⁺, K⁺, Cl⁻ are, respectively, 6.16×10⁻⁹ m²/s, 1.95×10⁻⁹ m²/s, and 2.03×10⁻⁹ m²/s, and R_t* = 5 nm. Here throughout the manuscript, the tip radius R_t* is fixed to be 5 nm. The coupled nonlinear equations (Eqs. 1–5) are numerically solved by the commercial finite element software COSMOL 5.2^® (Comsol is a product of Comsol™, Boston). The computational domain is given in Figure 1. Here, R_b = 6,L = 200,L_R = 40. Further increasing L does not change the results, indicating the computational domain is sufficiently large. Quadratic triangular elements are used for discretization. Nonuniform elements are employed adjacent to the nanopore’s wall with at least 40 elements to capture the details of the double layer. We refined the meshes a few times to make sure that the results are mesh-independent.

Furthermore, when l_c = 0, Eq. (3) turns to be the standard PNP model. By letting l_c << 1 and z_± = ±1, we can compare the predictions from the modified PNP model with the ones from the standard PNP model for monovalent electrolyte KCl for various double layer thicknesses and surface charges [44]. The I-V curves of three different double layer thicknesses and three different surface charge densities are plotted in Figure 2. There are good agreements between the PNP model and the modified PNP model for KCl, validating the computational algorithm. In addition, it is seen that the negative and positive parts of the I − V curve are not symmetric and behave like a diode, consistent with experimental observations in conical nanopores.

Figure 2.

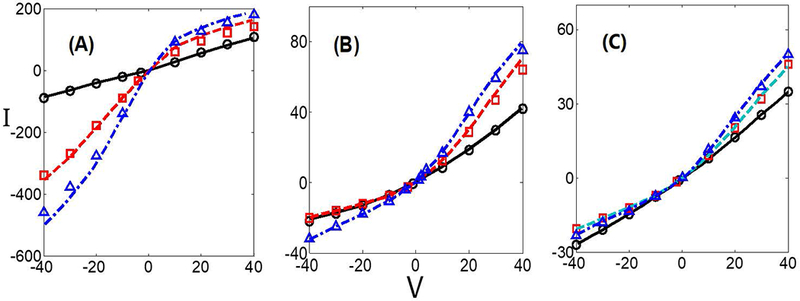
The I − V curves for a monovalent solution KCl in a conical nanopore. (A) λ_D = 1, (B) λ_D = 0.17, (C) λ_D = 0.1. The different lines stand for the PNP model from [44] and the different symbols represent the modified PNP model with l_c = 10⁻³. The solid line (circles), dashed line (squares), and dash-dotted line (triangles) are for surface charge densities σ = −2.73 (−10 mC/m²), σ = −13.66 (−50 mC/m²) and σ = −27.32 (−100 mC/m²).

3. Results and Discussion

To characterize the ionic current rectification, we can define an ionic current rectification ratio $\mathit{IR}=\mid \frac{I(V_0)}{I(-V_0)}\mid$. First, we examine the impact of electrostatic correlations on the ionic current rectification ratio IR. Figure 3 shows the ionic current rectification ratio as a function of the electrostatic correlation length l_c, when λ_D = 0.2, corresponding to the bulk concentration C₀* = 100 mM, σ = −40, and V₀ = 100. Interestingly, the IR first increases, reaches the maximum, and then decreases below 1, indicating that the ionic current rectification reversal occurs.

Figure 3.

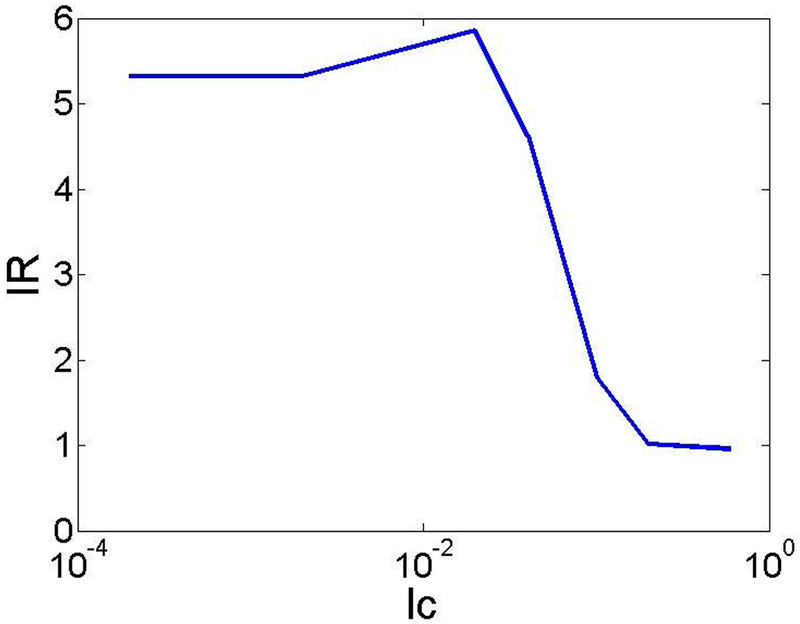
Current rectification ratio IR as a function of the electrostatic correlation length l_c when λ_D = 0.2, σ = −40, and V₀ = 100.

To understand this behavior, Figure 4 plots the averaged cross-sectional ionic concentrations of La³⁺ and Cl⁻ and the electric potentials cross the nanopore for different l_c and V₀. When l_c = 2×10⁻³, the ionic distributions and the electrical potential are similar to those in the absence of electrostatic correlations. Due to the asymmetry of the conical nanopore, the relative double layer thickness at the tip side is larger than that of the base side. The variation of the relative double layer thickness creates a cation trap near the tip side in the absence of the external electric field [16, 45] (Figure 4A II).

Figure 4.

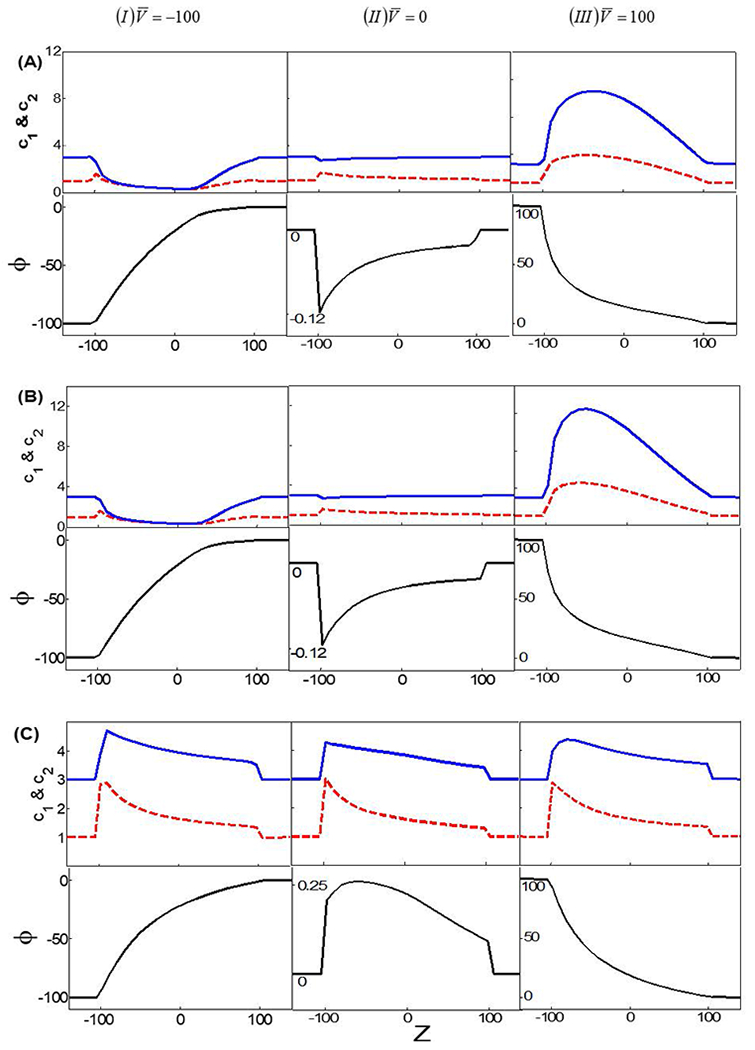
The averaged cross-sectional ionic concentrations in which the solid line and the dashed line correspond, respectively, to anion Cl⁻ and cation La³⁺ (the top) and the averaged electrical potentials (the bottom) for λ_D = 0.2 and σ = −40 when l_c = 2×10⁻³ (A); l_c = 0.02 (B); and l_c = 0.6 (C). The left, the middle, and the right column represent, respectively, the applied voltage of V₀ = −100, V₀ = 0, and V₀ = 100.

When V₀ is positive, the applied electric field drives positive ions into the nanopore from the tip side and these ions are trapped inside the nanopore, leading to a higher concentration or a higher ionic current. In contrast, when V₀ is negative, the electric field is from the base to the tip. Positive ions are pulled out from the tip side of the nanopore and enter from the base side. Since the electric field at the tip side is larger than the one at the base side, fewer ions are present inside the nanopore, leading to a lower ionic current. Accordingly, the ionic current rectification ratio is larger than 1.

When l_c = 0.6, the impact of electrostatic correlations is prominent, causing the charge to oscillate. Without the external electric field, the charge oscillation induced by electrostatic correlations results in anion trap instead of cation trap. This anion trap leads to a larger ionic current when V₀<0. Hence, the ionic current rectification ratio becomes less than 1 or the ionic current rectification reversal occurs, which is successfully predicted by the modified PNP model.

Interestingly, Figure 3 also suggests that when l_c = 0.02, the ionic current rectification ratio increases slightly compared to the smaller l_c. It can be understood: due to the charge oscillation induced by ion-ion electrostatic correlations, more negative ions are stored inside the nanopore. At the same time, since l_c is still small or l_c / λ_D = 0.1, cation concentration does not change significantly. As a consequence, the net ionic current increases slightly, resulting in an increase of the current rectification ratio. Recent experiments showed that by adding LaCl₃ into the KCl solution, the rectification ratio slightly increases and then decreases to less than 1 [36]. Our theoretical predictions are qualitatively consistent with the experimental observations: small ion-ion electrostatic correlations can slightly increase the anion or Cl⁻ concentration without significantly decreasing the cation concentration, leading to a slight increase of ionic current rectification ratio.

We examine the impact of the surface charge and double layer thickness on the ionic current rectification in the presence of the electrostatic correlations. Figure 5 plots the ionic current rectification ratio as a function of 1/λ_D for both σ = −40 and σ = −20 when l_c = 0.6 and V₀ = 100. Both rectification ratios are less than 1, suggesting that electrostatic correlations are important to induce the anion trap near the tip region of the nanopore. In addition, the rectification ratio of σ = −40 is generally smaller than that of σ = −20 since the impact of the electrostatic correlations is more significant at a larger surface charge. It is not surprising that the ratio is smaller. In addition, as the relative double layer thickness increases, the ionic rectification ratio decreases. This trend is consistent with the one without the electrostatic correlations. This is attributed to the overlapping of the double layers [44].

Figure 5.

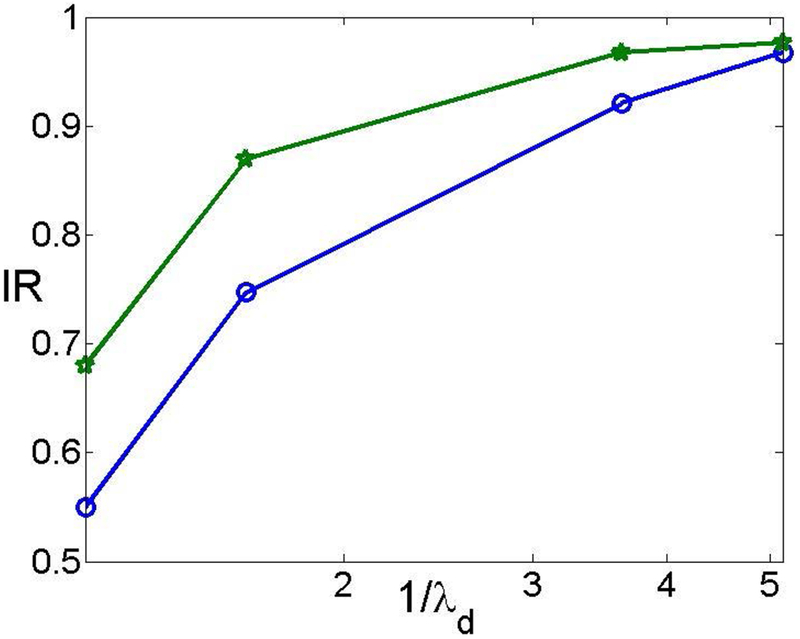
The current rectification ratio IR as a function of 1/λ_D when l_c = 0.6 and V₀ = 100. The line with stars and that with circles represent, respectively, to σ = −20 and σ = −40.

Next, we examine the impact of the electrostatic correlations on the induced electroosmotic flow. Figure 6 plots the flow rate Q as a function of the electrostatic correlation length l_c when λ_D = 0.2, V₀ = −100, and σ = −40. Consistent with the impact of electrostatic correlations on the electro-osmotic flow near a flat surface [39], a flow reversal is observed with the increase of l_c and the flow rate is proportional to l_c when l_c is large. Figure 7 shows the flow field for different l_c. A flow reversal is clearly demonstrated.

Figure 6.

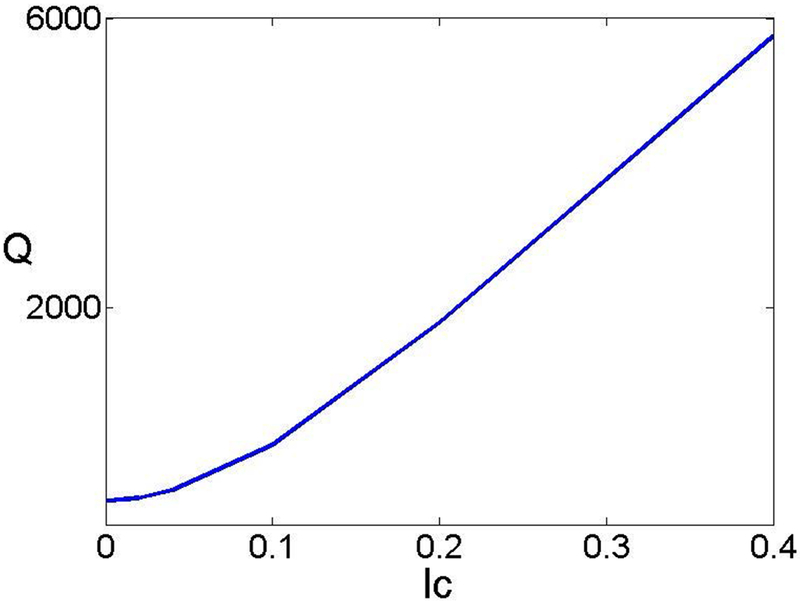
The flow rate as a function of l_c when λ_D = 0.2, V₀ = −100, and σ = −40.

Figure 7.

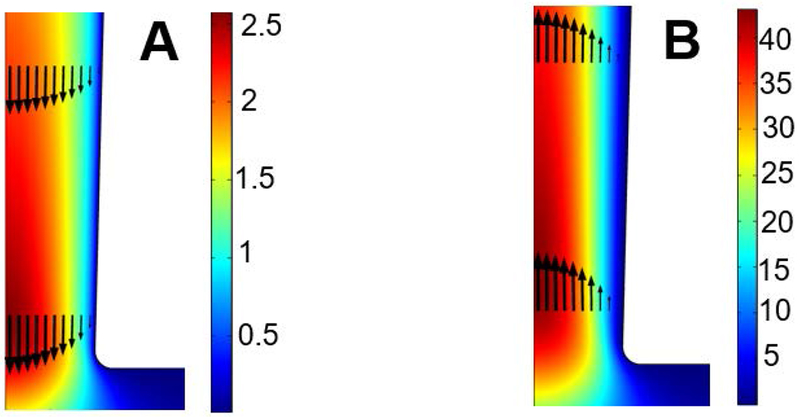
The flow field near the tip of the conical nanopore for (A) l_c = 2×10⁻³ and (B) l_c = 0.6 when λ_D = 0.2, V₀ = −100, and σ = −40.

Finally, Figure 8 plots the cation concentration distribution near the tip regions for l_c = 2×10⁻³ and l_c = 0.6 when λ_D = 0.2, V₀ = −100, and σ = −40. Interestingly, at l_c = 2×10⁻³, the concentration is depleted outside the tip region. In contrast, when l_c = 0.6, the concentration is enriched outside the tip region. In other words, at large electrostatic correlations, the concentration polarization is reversed as well, similar to the flow reversal.

Figure 8.

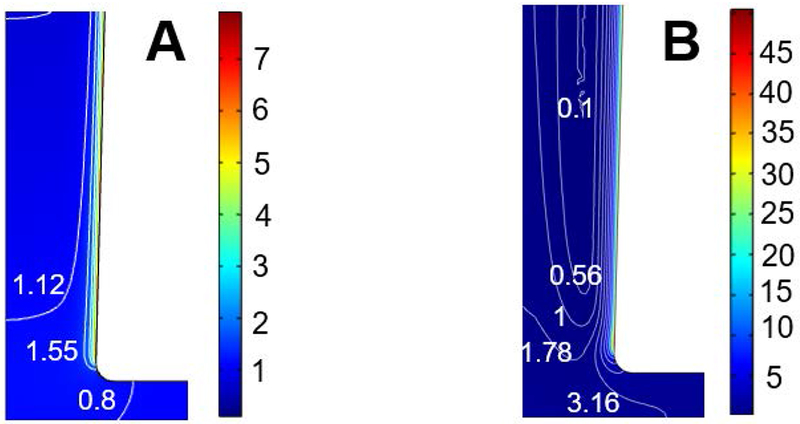
Distribution of the concentration of cation (La³⁺) near the tip region of the conical nanopore for (A) l_c = 2×10⁻³ and (B) l_c = 0.6 when λ_D = 0.2, V₀ = −100, and σ = −40.

4. Concluding remarks

By considering the effects of ion-ion electrostatic correlations, we investigated the ionic current rectification in a conical nanopore in the presence of multivalent electrolytes by using the modified continuum Poisson-Nernst-Planck (PNP) equations presented by Bazant et al. [35]. Here we chose the trivalent cation solutions consisting of lanthanum chloride as the electrolyte solution and focused on the high salt concentration (~100 mM), where the double layer thickness is smaller than the nanopore radius. It is recognized that ion-ion electrostatic correlations are prominent in concentrated multivalent electrolytes and can lead to the charge oscillation. Our numerical results showed that at larger electrostatic correlation lengths, the ionic current rectification reverses, leading to the ratio less than 1. By examining the electrical potential distribution in the absence of external electric fields, we showed that the cation trap at the tip side with a smaller electrostatic correlation length turns to be the anion trap with a larger electrostatic correlation length, explaining the ionic current rectification reversal. Our studies concluded that ion-ion electrostatic correlations inducing the charge oscillation are responsible for the ionic current rectification reversal. In addition, our studies also suggested flow reversal and concentration polarization reversal induced by ion-ion electrostatic correlations. Our studies can help to better understand experimental results and the modified continuum PNP model can also be used to design various nanopore based devices with multivalent electrolytes.

Abbreviations:

(PNP)

Poisson-Nernst-Planck