Summary
Bayesian additive regression trees (BART) is a flexible prediction model/machine learning approach that has gained widespread popularity in recent years. As BART becomes more mainstream, there is an increased need for a paper that walks readers through the details of BART, from what it is to why it works. This tutorial is aimed at providing such a resource. In addition to explaining the different components of BART using simple examples, we also discuss a framework, the General BART model, that unifies some of the recent BART extensions, including semiparametric models, correlated outcomes, statistical matching problems in surveys, and models with weaker distributional assumptions. By showing how these models fit into a single framework, we hope to demonstrate a simple way of applying BART to research problems that go beyond the original independent continuous or binary outcomes framework.
Keywords: semiparametric models, spatial, Dirichlet process mixtures, machine learning, Bayesian nonparametrics
1 ∣. INTRODUCTION
Bayesian additive regression trees (BART; Chipman et al.1) has gained popularity in the recent years among the research community with numerous applications including biomarker discovery in proteomic studies2, estimating indoor radon concentrations3, estimation of causal effects4,5, genomic studies6, hospital performance evaluation7, prediction of credit risk8, predicting power outages during hurricane events9, prediction of trip duration in transportation10, and somatic prediction in tumor experiments11. BART has also been extended to survival outcomes12,13, multinomial outcomes14,15, and semi-continuous outcomes16. In the causal inference literature, notable papers that promote the use of BART include Hill5 and Green and Kern17. BART has also been consistently among the best performing methods in the Atlantic causal inference data analysis challenge18,19,20. In addition, BART has been making inroads in the missing data literature. For the imputation of missing covariates, Xu et al. 21 proposed a way to utilize BART for the sequential imputation of missing covariates, while Kapelner and Bleich22 proposed to treat missingness in covariates as a category and set up the splitting criteria so that the eventual likelihood in the Metropolis-Hasting (MH) step of BART is maximized. For the imputation of missing outcomes, Tan et al.23 examined how BART can improve the robustness of existing doubly robust methods in situations where it is likely that both the mean and propensity models could be misspecified. Other more recent attempts to utilize or extend BART include applying BART to quantile regression24, extending BART to count responses25, using BART in functional data26, applying BART to recurrent events27, identifying subgroups using BART28,29,30, using BART as a robust model to impute missing principal strata to account for selection bias due to death31, decision making and uncertainty quantification for individualized treatment regimes32, as well as competing risks33.
The widespread use of BART has resulted in many researchers starting to use BART as a reference model for comparison when proposing new statistical or prediction methods. A few recent examples include Liang et al.34, Nalenz and Villani35, and Lu et al.36. This growing interest for BART raises a need for an in-depth tutorial paper to help researchers better understand the method. The first portion of this paper is aimed at addressing this.
The second portion of our work revolves around extensions of BART beyond the original independent continuous or binary outcomes setup. Recent papers involved extensions of BART to semiparametric models37, correlated outcomes38, statistical matching problems in surveys39, and more flexible outcome distributions40. Although these papers were written separately, they share a common feature in their framework. In brief, when estimating the posterior distribution, they subtract a latent variable from the outcome and then model this residual as BART. This idea, although simple, is powerful because this can allow researchers to easily extend BART to problems that they may face in their data set without having to rewrite or re-derive the Monte Carlo Markov Chain (MCMC) procedure for drawing the regression trees in BART. We summarize this idea in a framework unifying these models that we call, the General BART model. We believe that by presenting our General BART model framework and linking it with the models in these four papers as examples, it will be a valuable tool for researchers who are trying to incorporate and extend BART to solve their research problems.
Our in-depth review of BART in Section 2 focuses on three commonly asked questions regarding BART: What gives BART flexibility? Why is it called a sum of regression trees? What are the mechanics of the BART algorithm? In Section 3, we demonstrate the superior performance of BART compared to the Bayesian linear regression (BLR) when data are generated from a complicated model. We then describe the application of BART to two real-life data sets, one with continuous outcomes and the other with binary outcomes. Section 4 lays out the framework for our General BART model that allows BART to be extended to semiparametric models, correlated outcomes, survey, and situations where a more robust assumption for the error term is needed. In each of these examples, we describe how the prior distributions are set and how the posterior distribution is obtained. We conclude with a discussion in Section 5.
2 ∣. BAYESIAN ADDITIVE REGRESSION TREES
We begin our discussion with the independent continuous outcomes BART. We argue that BART is flexible because it is able to handle non-linear main effects and multi-way interactions without much input from researchers. To demonstrate how BART handles these model features, we explain using a visual example of a regression tree. We then illustrate the concept of a sum of regression trees using a simple example with two regression trees. We next show how a sum of regression trees accommodate non-linear main and multi-way interaction effects. We provide two perspectives to show how BART determines these non-linear effects automatically. First, we discuss the BART mechanism using a visual and detailed breakdown of the BART algorithm at work with a simple example, providing the intuition for each step along the way. Second, we provide a more rigorous explanation of the BART MCMC algorithm by discussing the prior distribution used for BART and how the posterior distribution can be calculated. Finally, we show how BART handles independent binary outcomes.
2.1 ∣. Continuous outcomes
2.1.1 ∣. Single regression tree
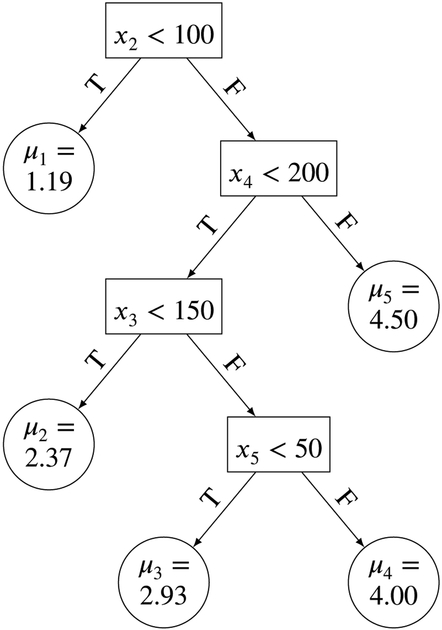
To understand BART we first introduce regression trees. Suppose we have covariates x = (x1,…, x5) and outcome y. A regression tree represents the conditional expectation of y given x. We provide a visual representation of a hypothetical, simple regression tree in Figure 1. Each place where there is a binary decision split is called a node. At the top node (root), there is a condition x2 < 100. If x2 < 100 is true, we follow the path to the left, otherwise we follow the path to the right. Assuming that x2 < 100 is true, we see that we arrive at a node which is not split upon. This is called a terminal node and the parameter μ1 = 1.19 is the assigned value of E[y∣x] for any x where x2 < 100. Suppose instead that x2 < 100 is not true. Then, moving along the right side, another internal node with condition x4 < 200 is encountered. This condition would be checked and, if this condition is true (false), we follow the path to the left (right). This process continues until we reach a terminal node and the parameter μi in that terminal node is assigned as the value of E[y∣x], where μi is the mean parameter of the ith node for the regression tree. So, for example, a subject k with xk1 = 30, xk2 = 120, xk3 = 115, xk4 = 191, and xk5 = 56 would be assigned a value of μ2 = 2.37 for E[y∣x]. The value would be exactly the same for another subject k′ who instead had covariates xk′1 = 130, xk′2 = 135, xk′3 = 92, xk′4 = 183, xk′5 = 10.
FIGURE 1.
Example of a regression tree g(x; T, M) where μi is the mean parameter of the ith node for the regression tree.
We denote by T the binary tree structure itself - the various binary split decision rules of the form {xq < c} versus {xq > c}, . The vector of parameters associated with T, i.e. the collection of terminal node parameters, is denoted by M ={μ1,…,μb}, where b is the number of terminal nodes. Defining a regression tree as g(x; T, M), we can view g(x; T, M) as a function that assigns the conditional mean E[y∣x] to the parameter μi ∈ M i.e. μi = g(x; T, M) ↦ E(y∣x) via binary decision rules denoted as T. Note that we have not discussed how these binary decision rules in a regression tree are created by BART and how uncertainty about which covariate to split on and which value to split on, is quantified. We will address that when we introduce the BART priors and algorithms.
Regression tree as an analysis of variance (ANOVA) model
Another way to think of the regression tree in Figure 1 is to view it as the following analysis of variance (ANOVA) model:
where I{.} is the indicator function and ε ~ N(0, σ2). We can see that the term μ1 I{x2 < 100} corresponds to the terminal node on the top left corner of Figure 1, μ2I{x2 ≥ 100}I{x4 < 200}I{x3 < 150} corresponds to the terminal node just below μ1 = 1.19, and so on. We can think of μ1I{x2 < 100} as a main effect, because it only involves the second variable x2, while μ2I{x2 ≥ 100}I{x4 < 200}I{x3 < 150} is a three way interaction effect involving the second (x2), fourth (x4), and third variable (x3). By viewing a regression tree as an ANOVA model, we can easily see why a regression tree and hence, BART, which is made up of a sum of regression trees, is able to handle main and multi-way interaction effects.
2.1.2 ∣. Formal definition
We now formally define BART. Suppose we have a continuous outcome y and p covariates x = (x1,…, xp). The goal is a model that can capture complex relationships between x and y, with the aim of using it for prediction. BART attempts to estimate f(x) from models of the form y = f(x)+ε, where, for now, ε ~ N(0, σ2). To estimate f(x), a sum of m regression trees is used i.e. . Thus, BART is often presented as
| (1) |
where Tj is the jth binary tree structure (recall T from Section 2.1.1) and Mj = {μj1,…, μjbj} is the vector of terminal node parameters associated with Tj. The number of trees m, is usually fixed at a large number, e.g., 50, 100, or 200. For example Bleich et al.41 suggests that 50 is often adequate. Note that some authors may also refer to the BART prior in the model setup as f ~BART. In addition, some readers may recognize that using y = μ + f(x) + ε may be more appropriate because by using (1), some form of centering for the y’s would be required. In fact, a transformation of y to center it at 0 is often done in the background of the BART algorithm (details given in the Appendix). We adopted (1) to be consistent with the definition used by most of the literature.
2.1.3 ∣. Sum of regression trees
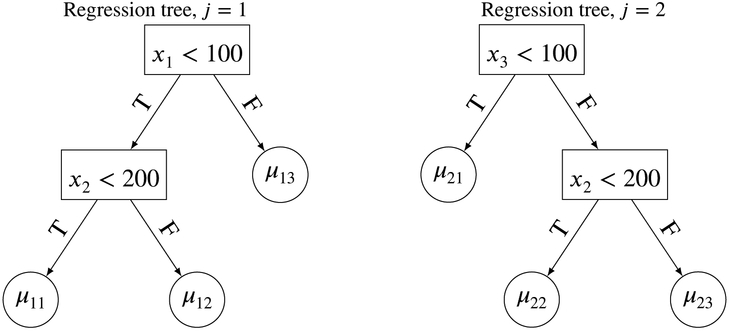
We next focus on the sum of regression trees, . We begin by using an example with m = 2 trees and p = 3 covariates. Suppose we were given the two trees in Figure 2. The resulting conditional mean of y given x is . Consider the hypothetical data from n = 10 subjects given in Table 1. We can see that the quantity that is being ‘summed’ and eventually allocated to E(y∣x) is not the regression tree or tree structure, but the value that each jth tree structure assigns to the subject. This is one way to think of a sum of regression trees. It allocates a sum of parameters μji to E[y∣x] of the subject. Note that contrary to initial intuition, it is the sum of μji’s that are allocated rather than the mean of the μji’s. This is mainly because BART calculates each posterior draw of the regression tree function g(x; Tj, Mj) using a leave-one-out concept, which we shall elaborate shortly.
FIGURE 2.
Illustrating the sum of regression trees using a simple two regression tree example.
TABLE 1.
The values of from the regression trees in Figure 2.
| Subject | y | x1 | x2 | x3 | g(x; T1, M1) | g(x; T2, M2) | f(x) |
|---|---|---|---|---|---|---|---|
| 1 | y1 | −182 | 235 | −333 | μ12 | μ21 | μ12 + μ21 |
| 2 | y2 | 54 | 339 | 244 | μ12 | μ23 | μ12 + μ23 |
| 3 | y3 | −106 | −50 | −682 | μ11 | μ21 | μ11 + μ21 |
| 4 | y4 | −80 | −62 | −320 | μ11 | μ21 | μ11 + μ21 |
| 5 | y5 | −123 | 198 | −77 | μ11 | μ21 | μ11 + μ21 |
| 6 | y6 | 175 | 108 | −46 | μ13 | μ21 | μ13 + μ21 |
| 7 | y7 | −44 | 11 | 136 | μ11 | μ22 | μ11 + μ22 |
| 8 | y8 | −131 | −10 | −70 | μ11 | μ21 | μ11 + μ21 |
| 9 | y9 | −56 | 68 | 257 | μ11 | μ22 | μ11 + μ22 |
| 10 | y10 | 7 | 324 | 282 | μ12 | μ23 | μ12 + μ23 |
Another way to view the concept of a sum of regression trees is to think of the regression trees in Figure 2 as ANOVA models (recall our single regression tree example). Then, the sum of regression trees for this simple example is just the following ANOVA model:
Note that this does not imply that BART is an ANOVA model. This is because, in BART, each MCMC iteration produces a possibly different ANOVA model. These models are posterior draws from the target model distribution f(x).
Non-linearity of BART
From this simple example, we can see how BART handles non-linearity. Each single regression tree is a simple step-wise function or ANOVA model. When we sum regression trees together, we are actually summing together these ANOVA models or step-wise functions, and as a result, we eventually obtain a more complicated step-wise function which can approximate the non-linearities in the main effect and multiple-way interactions. It is this ability to handle non-linear main and multiple-way interaction effects that makes BART a flexible model. But unlike many flexible models, BART does not require the researcher to specify the main and multi-way interaction effects.
Prior distributions
In the examples above, we have taken the trees as a given, including which variables to split on, the splitting values, and the mean parameters at each terminal node. In practice, each g(x; Tj, Mj) is unknown. We therefore need prior distributions for these functions. Thus, we can also think of BART as a Bayesian model where the mean function itself is unknown. A major advantage of this approach is that uncertainty about both the functional form and the parameters will be accounted for in the posterior predictive distribution of y.
Before getting into the details of the prior distributions and MCMC algorithm, we will first walk through a simple example to build the intuition.
2.1.4 ∣. BART machinery: a visual perspective
In our simple example, we have three covariates x = (x1, x2, x3) and a continuous outcome y. We will now run the BART MCMC algorithm with m = 4 regression trees for 5 iterations on this data set. At each iteration, we present the regression tree structures to illustrate how the algorithm works at each step. As mentioned previously, we typically would choose a large number for m, for example, 50. Here we are using just 4 trees to illustrate the key ideas.
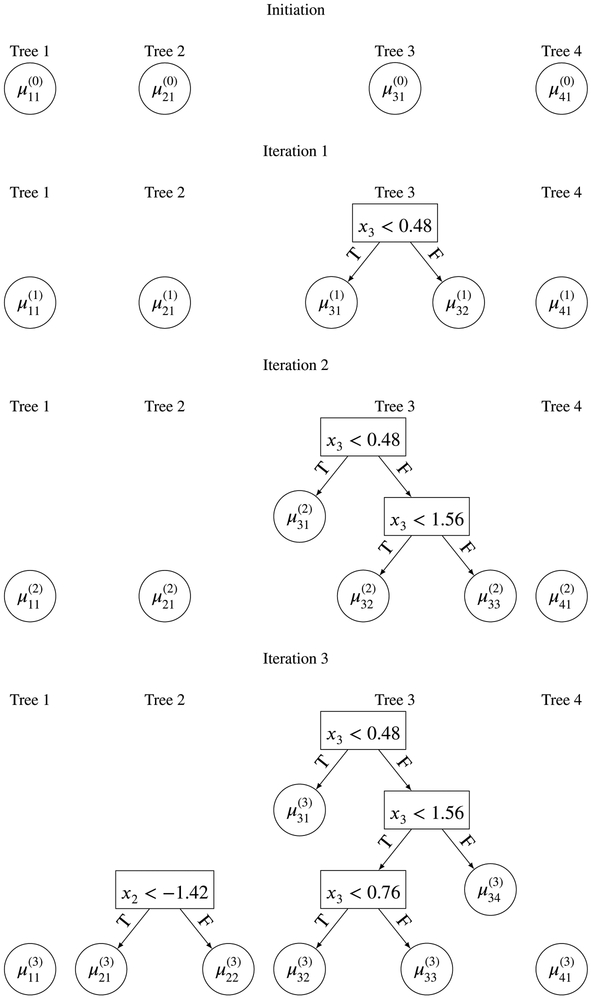
The first step in the algorithm is initialization of the four regression trees to single root nodes (See “Initiation” in Figure 3). Since all four regression trees are single root nodes, the parameters initialized for these nodes would be .
FIGURE 3.
Initiation of BART to iteration 3 of the MCMC steps within BART with m = 4.
With this initialization in place, BART starts to draw the tree structures for each regression tree in the first MCMC iteration. Without loss of generality, let us start with determining (T1, M1), the first regression tree. This is possible because the ordering of the regression tree calculation does not matter when computing the posterior distribution. We first calculate . Then a MH algorithm is used to determine the posterior draw of the tree structure, T1 for this iteration. The basic idea of MH is to propose a new tree structure from T1, call this , and then calculate the probability of whether should be accepted, taking into consideration: (the likelihood of the residual given the new tree structure), r1∣T1 (the likelihood of the residual given the previous tree structure), the probability of observing , the probability of observing T1, the probability of moving from to T1, and the probability of moving from T1 to . For example, if the new tree proposed consists of a single root node of x2 < 100, then the likelihood of would be (recall the ANOVA representation of a regression tree) and the likelihood of would be . More rigorous and technical details are provided in the Appendix. We describe the different types of moves from T1 to in detail in the next subsection. If is accepted, T1 is updated to become i.e. . Else, nothing would be changed for T1. From Figure 3, we can see that was not accepted in the first iteration so the tree structure remains as a single root node. The algorithm then updates M1 based on the new updated regression structure for T1, in our context draw from , r1, σ, and moves on to determine (T2, M2). Details of how to calculate , rj, σ where b is the iteration index can be found in the Appendix.
To determine (T2, M2), again the algorithm calculates , where is the updated parameter for regression tree 1. Similarly, MH is used to propose a new and r2 is used to calculate the acceptance probability to decide whether should be accepted. Again, we see from Figure 3 that was not accepted. For (T3, M3), the MH iteration result is more interesting because the newly proposed was accepted and we can see from Figure 3 that a new tree structure was used for T3 in Iteration 1. This new tree structure produces two terminal node parameters and which can be drawn from , r3, σ and , r3, σ respectively. As a result, when calculating r4, this becomes . was not accepted and a single node was updated as the tree structure for (T4, M4). Once the regression tree draws are complete, BART then proceeds to draw the posterior distribution of σ2, the variance of the error term in (1). More details will be given in the next subsection.
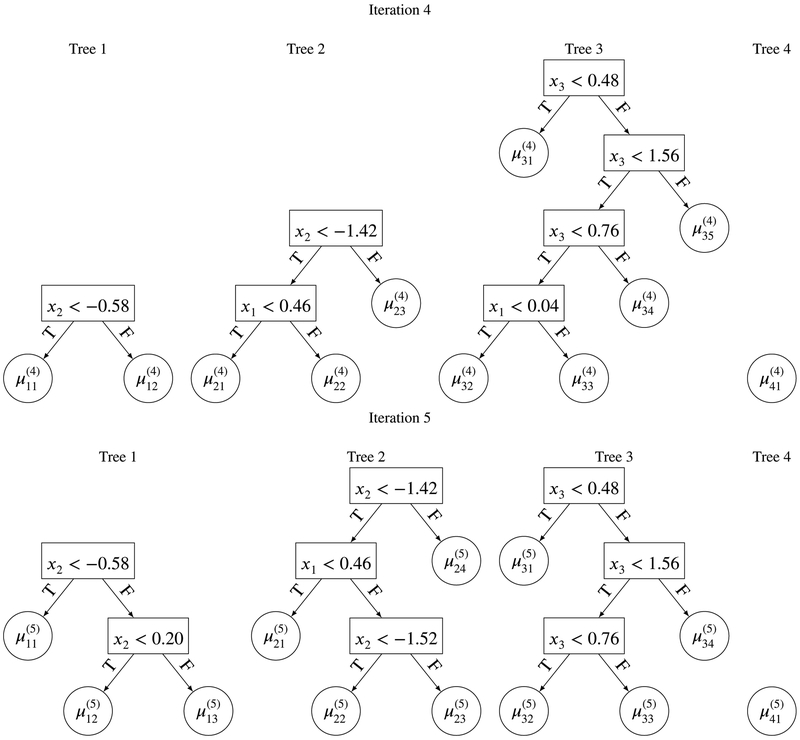
Figures 3 and 4 give the full iterations from initiation to iteration 5. From these figures we can see how the four regression trees grow and change from one iteration of the MCMC to another. This iterative process runs for a burn-in period (typically 100 to 1 000 iterations), before those draws are discarded, and then run for as long as needed to obtain a sufficient number of draws from the posterior distribution of f(x). After any full iteration in the MCMC algorithm, we have a full set of trees. We can therefore obtain a predicted value of y for any x of interest (simply by summing the terminal node μji’s). By obtaining predictions across many iterations, we can easily obtain a 95% prediction interval. Another point to note is how shallow the regression trees are in Figures 3 and 4 with a maximum depth of 3. This is because the regression trees are heavily penalized (via the prior) to reduce the likelihood for a single tree to grow very deep. This concept (boosting) is similar to that found in the machine learning literature, where many weak models (learners) combined together can outperform a single strong model.
FIGURE 4.
Iterations 4 and 5 of the MCMC steps within BART with m = 4.
2.1.5 ∣. A rigorous perspective on the BART algorithm
Now that we have a visual understanding of how the BART algorithm works, we shall give a more rigorous explanation. First, we start with the prior distributions for BART. The prior distribution for (1) is p[(T1, M1), …, (Tm, Mm), σ]. The assumption is that {(T1, M1), …, (Tm, Mm)} and σ are independent and that (T1, M1), …, (Tm, Mm) are independent of each other. Then the prior distribution can be written as
| (2) |
For the third to fourth line in (2)recall that Mj = {μj1,…, μibj} is the vector of terminal node parameters associated with Tj and each node parameter μji is usually assumed to be independent of each other. Equation (2) implies that we need to specify priors μji∣Tj, σ, and Tj. The priors for μji∣Tj and σ are usually given as and respectively, where IG(a, b) is the Inverse-Gamma distribution with shape parameter a and rate parameter b. Note that the representation of the prior for σ2 is a slight departure from most BART literature which often use the Inverse-Chisquare to represent the same prior distribution. We employed the Inverse-Gamma representation here because it is a more convenient form for the benefit of the reader.
The prior for p(Tj) is more interesting and can be specified using:
The probability that a node at depth d = 0, 1, … would split, which is given by . The parameter a ∈ {0, 1} controls how likely a node would split, with larger values increasing the likelihood of a split. The number of terminal nodes is controlled by parameter β > 0, with larger values of β reducing the number of terminal nodes. This aspect is important as this is the penalizing feature of BART which prevents BART from overfitting and allowing convergence of BART to the target function f(x)42.
The distribution used to select the covariate to split upon in an internal node. The default suggested distribution is the uniform distribution. Recent work by Ročková and van der Pas43 and Linero44 have argued that the uniform distribution does not promote variable selection and should be replaced if variable selection is desired.
The distribution used to select the cutoff point in an internal node once the covariate is selected. The default suggested distribution is the uniform distribution.
The setting of the other parameters for the BART priors is rather technical, so we refer interested readers to the Appendix.
The prior distribution would induce the posterior distribution:
which can be simplified into two major posterior draws using Gibbs sampling. First, draw m successive
| (3) |
for j = 1,…, m, where T−j and M−j consist of all the tree structures and terminal nodes except for the jth tree structure and terminal node; then, draw
| (4) |
from .
To obtain a draw from (3), note that this distribution depends on (T−j, M−j, y, σ) through
the residuals of the m–1 regression sum of trees fit excluding the jth tree (recall our visual example in the previous subsection). Thus (3) is equivalent to the posterior draw from a single regression tree rj = g(x; Tj, Mj) + ε or
| (5) |
We can obtain a draw from (5) by first integrating out Mj to obtain p(Tj∣rj, σ). This is possible since a conjugate normal prior on μji was employed. We draw p(Tj∣rj, σ) using a MH algorithm where, first, we generate a candidate tree for the jth tree with probability distribution . The details of the new tree proposal are given in the next paragraph. We then accept with probability
| (6) |
where is the ratio of the probability of how the previous tree moves to the new tree against the probability of how the new tree moves to the previous tree, is the likelihood ratio of the new tree against the previous tree, and is the ratio of the probability of the new tree against the previous tree.
A new tree can be proposed given the previous tree Tj using four local steps: (i) grow, where a terminal node is split into two new child nodes; (ii) prune, where two terminal child nodes immediately under the same non-terminal node are combined together such that their parent non-terminal node becomes a terminal node; (iii) swap, the splitting criteria of two non-terminal nodes are swapped; (iv) change, the splitting criteria of a single non-terminal node is changed. Once we have the draw of p(Tj∣rj, σ), we then draw , where rji is the subset of elements in rj allocated to the terminal node parameter μji and ni is the number of rji’s allocated to μji. We derive p(μji∣Tj, rj, σ), (4), and (6) for the grow and prune steps as an example in the Appendix. Other possible moves have also been proposed in literature. Interested readers can refer to the following papers45,46,47,48.
2.2 ∣. Binary outcomes
For binary outcomes, BART can be extended using a probit model. Specifically, we may write
| (7) |
where Φ[.] is the cumulative distribution function of a standard normal distribution. With such a setup, only priors for (T1, M1),…, (Tm, Mm) are needed. The same decomposition in (2) without σ can be employed and the similar prior specifications for μji∣Tj and Tj can be used. An important note that some readers may not notice is that such a setup in (7) shrinks f(x) toward 0 and hence shrinking Φ[f(x)] toward 0.5. This may not be what researchers want nor anticipate and hence, if it is more desirable to shrink Φ[f(x)] toward a value p0 ∈ (0, 1) that is not 0.5, the strategy is to replace f(x) in (7) with fc = f(x) + c where the offset c = Φ−1[p0]. The setup of the remaining parameters are slightly different from that of continuous outcomes and we describe the details in the Appendix.
To estimate the posterior distribution, data augmentation49 can be used. We assume that y = I(z > 0) where z is a latent variable drawn as follows:
with N(a,b))[μ, σ2] being a truncated normal distribution with mean μ and variance σ2 truncated at (a, b). Next, we can treat z as the continuous outcome for a BART model with
| (8) |
where ε ~ N(0, 1) because we employed a probit link. The usual posterior estimation for a continuous outcome BART with σ ≡ 1 can now be employed on (8) for one iteration in the MCMC. The updated f(x) can then be used to draw a new z and this new z can be used to draw another iteration of f(x). The process can then be repeated until convergence.
3 ∣. ILLUSTRATING THE PERFORMANCE OF BART
3.1 ∣. Posterior performance via synthetic data
We generated a synthetic data set with p = 3, n = 1000 and, the true model for y is
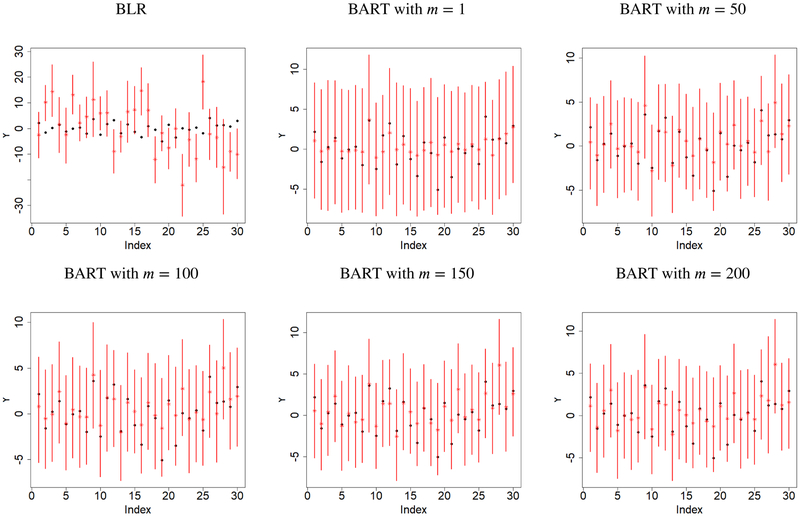
with each xp ~ N(0, 1) and ε ~ N(0, 2). The goal is to demonstrate that BART can predict y’s effectively even in complex, non-linear models, and also properly account for prediction uncertainty. We will compare results of BART against that of a parametric Bayesian linear regression (BLR) model. To this end, we randomly selected 970 samples as the training set and then use the remaining 30 samples as the testing set. Note that in practice, we commonly see a 60(training)-40(testing) or a 70(training)-30(testing) split being used although more rigorous splits have been suggested50. We employed a different split because a graphical presentation of 300 or 400 results would not be feasible. We also varied the number of trees used by BART to illustrate how varying m affects the performance of BART. We plotted the point estimate and 95% credible interval of the 30 randomly selected testing data points and compared them with their true values in Figure 5. The code to implement this simulation can be found in our Supporting Information.
FIGURE 5.
Posterior mean and 95% credible interval of Bayesian linear regression (BLR) and BART with m = 1, 50, 100, 150, 200 for 30 randomly selected testing set outcomes. n = 1000, black=true value, red=model estimates.
We can see from Figure 5 that most of the point estimates of BLR were far away from their true values and many of the true values were not covered by the 95% credible interval. For BART with a single tree, although the true values were mostly covered by the 95% credible interval, the point estimates were far from their true values. When we increased the number of trees to 50 in BART, we see a significant improvement in terms of bias (closeness to the true values) compared to both BLR and BART with m = 1. In addition, we see a narrowing of the 95% intervals. As we increase the number of trees, the point estimate and 95% intervals stabilize. In other words, we might see a big difference between m = 1 and m = 50, and virtually no difference between m = 200 and m = 20 000. In practice, the idea is to choose a large enough value for m so that BART approximates the results that would have been obtained if more trees were used. Although as we increase m, the computation efficiency would decrease, the fact that each regression tree is a weak learner still allows BART to finish computation within a reasonable amount of time. Hence, Chipman et al.1 suggested m = 200 originally but later researchers agree that m = 50 is often adequate41. Alternatively, one could determine a sufficiently large m using cross validation1, but that would be computationally expensive.
3.2 ∣. Predicting the Standardized Hospitalization Ratio from the 2013 Centers for Medicare and Medicaid Services Dialysis Facility Compare data set
We next present an example to demonstrate how BART can be applied to a data set to improve prediction over the usual multiple linear regression (MLR) model. The 2013 Centers for Medicare and Medicaid Services Dialysis Facility Compare data set contains information regarding 105 quality measures and 21 facility characteristics of all dialysis facilities in the US, including US territories. This data set is available publicly. We provide the data set we downloaded and code in our Supporting Information. We are interested in finding a model that can better predict the standardized hospitalization ratio (SHR). This quantity is important because a large portion of dialysis cost for End Stage Renal Disease (ESRD) patients can be attributed to patient hospitalizations.
Table 2 shows some descriptive statistics for this data set. SHR was adjusted for a patient’s age, sex, duration of ESRD, comorbidities, and body mass index at ESRD incidence. We removed 463 facilities (7%) with missing SHR values because of small patient numbers. We also removed peritoneal dialysis (PD) removal greater than 1.7 Kt/V because of the high proportion of missingness (80%). We combined pediatric hemodialysis (HD) removal greater than 1.2 Kt/V with adult HD removal greater than 1.2 Kt/V because most facilities (92%) do not provide pediatric HD. We re-categorized the chain names to “Davita”, “Fresenius Medical Care (FMC)”, “Independent”, “Medium”, and “Small”. “Medium” consists of chains with 100-500 facilities while “Small” are chains with less than 100 facilities. To estimate patient volume, we used the maximum of the number of patients reported by each quality measure group: Urea Reduction Ratio (URR), HD, PD, Hemoglobin (HGB), Vascular Access, SHR, SMR, STR, Hypercalcemia (HCAL), and Serum phosphorus (SP). We also logarithm-transformed (log) SHR, SMR, and STR so that the theoretical range for these log standardized measures will be −∞ to ∞.
TABLE 2.
Descriptive statistics of dialysis facility characteristics and quality measures (n=5,774).
| Parameters (% missing) | Mean (s.d)/Frequency (%) | Parameters (% missing) | Mean (s.d)/Frequency (%) |
|---|---|---|---|
| Arterial Venous Fistula (3) | 63.27 (11.22) | Number of stations | 18.18 (8.27) |
| Avg. Hemoglobin<10.0 g/dL (5) | 12.86 (10.32) | Serum P. (2) | 28.52 (5.13) |
| Chain name: | Shift after 5pm? | ||
| Davita | 1,812 (31) | Yes | 1,097 (19) |
| FMC | 1,760 (30) | No | 4,677 (81) |
| Independent | 820 (14) | SHR | 1.00 (0.31) |
| Medium | 740 (13) | SMR (2) | 1.02 (0.29) |
| Small | 642 (12) | STR (7) | 1.01 (0.54) |
| Patient volume* | 100.07 (60.93) | Type: | |
| Facility Age (years) | 14.47 (9.81) | All (HD, Home HD, & PD) | 1,443 (25) |
| For profit? | HD & PD | 1,897 (33) | |
| Yes | 4,967 (86) | HD & Home HD | 103 (2) |
| No | 806 (14) | HD alone | 2,331 (40) |
| HD≥1.2 Kt/V (4) | 88.52 (9.85) | URR≥65% (7) | 98.77 (3.04) |
| Hypercalcemia (3) | 2.37 (3.20) | Vas. Catheter>90 days (3) | 10.74 (6.66) |
Estimated
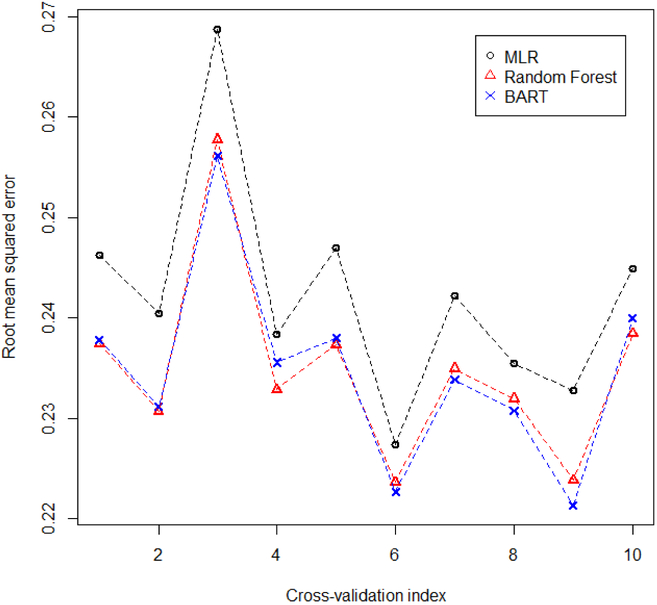
For our analysis, we used the log-transformed SHR as the outcome and the variables in Table 2 as the predictors. We used the root mean squared error (RMSE) of a 10-fold cross-validation to compare the prediction performance from multiple linear regression (MLR), Random Forest (RF), and BART. For RF and BART, we used the default settings from the R packages randomForest and BayesTree respectively. The 10 RMSEs produced by each method from the 10-fold cross validation is provided in Figure 6. It is clear from this figure that BART and RF produce very similar prediction performances and are better compared to MLR. The mean of these 10 values also suggested a similar picture with MLR producing a mean of 0.24 while RF and BART produced a mean of 0.23.
FIGURE 6.
Root mean squared error (RMSE; y-axis) for the 10-fold cross-validation of multiple linear regression (MLR), random forest, and Bayesian additive regression trees of log transformed standardized hospitalization ratio (SHR). x-axis indicates the RMSE for the xth fold.
3.3 ∣. Predicting left turn stops at an intersection
We next present another illustration of BART on a real example, but this time with a binary outcome. In Tan et al.51, the authors were interested in predicting whether a human driven vehicle would stop at an intersection before making a left turn. Left turns are important in countries with right side driving because most vehicle conflicts including crashes at intersections occur during left turns. Accurate predictions about whether a human driven vehicle would stop before executing a left turn could help driverless vehicles improve decision making at intersections. More details about this data set can be found in Tan et al.51. In brief, the data comes from the Integrated Vehicle Based Safety System (IVBSS) study conducted by Sayer et al.52. This study collected driving data from 108 licensed drivers in Michigan between April 2009 and April 2010. Each driver drove one of the 16 research vehicles fitted with various recording devices to capture the vehicle dynamics while the subject is driving on public roads for 12 days.
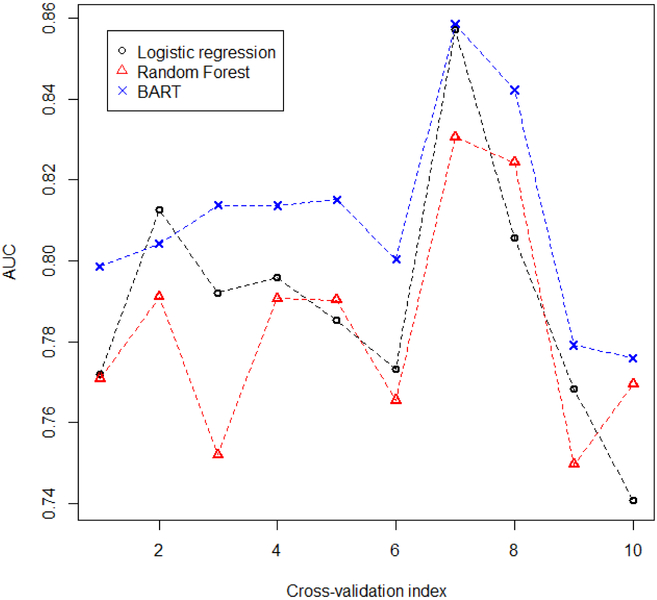
For this example, we focused on the vehicle speed at 50, 51, …, 56 meters away from the center of an intersection and whether we could utilize this vehicle dynamic to predict whether the driver would stop (vehicle speed < 1m/s) in the future (0, 1, …, 49 meters from the center of an intersection). Similar to Tan et al.51, we performed a principal components analysis (PCA) on the vehicle speeds (50, 51,…, 56 meters) and took the first 3 principal components (PCs) as the predictors. Tan et al.51 took the first 3 PCs as predictors because they found that using the first 3 PCs as predictors improved prediction performance compared to using the original vehicle speeds. In addition, adding more PCs beyond the first 3 did not improve prediction performance. We ran a 10-fold cross-validation on this data set and compared the binary prediction results of logistic regression, RF, and BART. Since the outcome of interest for this data set was binary, we used the area under the receiver operating curve (AUC) to determine the prediction performance instead of the RMSE, which is more suited for continuous outcomes.
Figure 7 shows the results of the 10 AUCs produced by each method from the 10-fold cross validation. BART performed better than either logistic regression or RF in predicting whether the human-driven vehicle would stop in the future at an intersection before making a left turn. This is also evident from the mean of the 10 cross validation AUC values produced by each method. BART produced a mean of 0.81 compared to 0.79 from logistic regression, and 0.78 from RF.
FIGURE 7.
Area under the receiver operating characteristic curve (AUC; y-axis) for the 10-fold cross-validation of logistic regression, random forest, and Bayesian additive regression trees of left turn stop probabilities at an intersection. x-axis indicates the AUC for the xth fold.
4 ∣. GENERAL BART MODEL
Recently researchers have extended or generalized BART to a wider variety of settings, including clustered data, spatial data, semiparametric models, and to situations where more flexible distributions for the error term is needed. Taking a closer look at these recent extensions, we found a common and unifying theme. It enables the proposed models to be fitted without having to do extensive re-derivation for the posterior algorithm described in Section 2. By unifying the models in these various papers into one single approach, we believe it will aid the application of BART to a wider variety of situations. In addition, we hope the discussion of our approach would be able to spark inspiration for further, possibly more complicated extensions of BART.
To set up our General BART model, suppose once again that we have a continuous outcome y and p covariates x = {x1,…, xp}. Suppose also that we have another set of q covariates w = {w1,…,wq}, such that no two columns in x and w are the same. Then, we can extend (1) as follows:
| (9) |
where h(.) is a function that works on w using parameter Θ, and ε ~ G(Σ) can be any distribution with parameter Σ.
Assuming that {(T1, M1), …, (Tm, Mm)}, Θ, and £ are independent, the prior distribution for (9) would be p[(T1, M1),…, (Tm, Mm)]p(Θ)p(Σ). Assuming again that the (Tj, Mj)’s are independent of each other, p[(T1, M1),…, (Tm, Mm)] can be decomposed into . The priors needed are thus p(μji∣Tj), p(Tj), p(Θ), and p(Σ). Note that it is possible to model Θ and Σ jointly so that the prior distribution becomes instead. We shall see this in Example 4.4.
To obtain the posterior distribution of p[(T1, M1),…, (Tm, Mm), Θ, Σ∣y], Gibbs sampling can be used. For P[(T1, M1),…, (Tm, Mm)∣Θ, Σ, y], this can be seen as drawing from the following model
| (10) |
where , which is just a BART model with a modified outcome . Hence, the BART algorithm presented in Section 2 can be used to draw {(T1, M1),…, (Tm, Mm)}. Similarly, p[Θ∣(T1, M1),…, (Tm, Mm), Σ, y] can be obtained by drawing from the model
| (11) |
where y′ = y – f(x). This posterior draw depends on the function h(.) being used as well as the prior distribution specified for Θ. As there are many possibilities where we can set up h(.) and Θ, we shall not discuss the specifics here. The examples we present in the subsequent subsections will highlight a few of these possibilities we have seen in the literature thus far. Finally, drawing from p[Σ∣(T1, M1),…, (Tm, Mm), Θ, y] is just drawing from the model
| (12) |
Again, many possibilities are available for setting up the prior distribution for Σ and hence the distributional assumption for ε. The default is usually ε ~ N(0, σ2) where . Example 4.4 shows a plausible alternative. Iterating through these Gibbs steps will give us the posterior draw of p[(T1, M1),…, (Tm, Mm), Θ, Σ∣y].
For binary outcomes, the probit link can once again be used where
Under this framework, we will only need priors for p[(T1, M1),…, (Tm, Mm)] and p(Θ). p[(T1, M1),…, (Tm, Mm)] can be decomposed once again into if we are willing to assume that the m trees are independent of one another, and data augmentation53 can be used obtain the posterior distribution. Again with the assumption that y = I(z > 0), we can draw
and then treat z as the outcome for the model in (9). This implies ε ~ N(0, 1) and we can apply the Gibbs sampling procedure we described for continuous outcomes using z instead of y with Σ = σ = 1. Iterating through the latent draws and Gibbs steps will produce the posterior distribution that we require.
With the general framework and model for BART in place, we are now equipped to consider how Zeldow et al.37, Tan et al.38, Zhang et al.39, and George et al.40 extended BART to solve their research problems in the next four subsections.
4.1 ∣. Semiparametric BART
The semiparametric BART approach was first developed by Zeldow et al.37. Their work was motivated by observational studies where there are many confounders, an exposure, and a small number of variables that are of interest as exposure-covariate interaction (heterogenity of treatment effect). While a flexible model such as BART could handle the potential complex confounding and main effects relationship with the outcome, there is some loss of interpretability relative to a parametric model. On the other hand, fully parametric models rely on strong assumptions.
Therefore, their idea was to have a semiparametric model, where the exposure and exposure-covariate interactions had parametric specification, and the nuisance or confounder variables were modeled nonparametrically (using BART). In its simplest form, we can reconstruct this idea under the framework of (9) as follows. The x covariates are the confounders that have to be controlled for, but are not of primary interest. The variables w include the exposure and covariates that are of substantive interest as possible effect modifiers. Then,
where w = {w1,…, wq}, Θ = {θ0,…, θq}, and ε ~ N(0, σ2) with Σ = σ. Prior distributions for μji∣Tj, Tj, and σ2 follow the usual distributions we use for BART while Θ ~ MVN (β, Ω). Posterior estimation follows the procedure we described in Section 4 using Gibbs Sampling. For (10) and (12), since they suggested using the default BART priors, the usual BART mechanisms can be applied to obtain the posterior draws. For (11), Θ ~ MVN(β, Ω) implies that we can treat this as the usual BLR and standard Bayesian methods could be used to obtain the posterior draw for Θ. The framework for binary outcomes follows easily using the data augmentation step we describe in Section 4.
4.2 ∣. Random intercept BART for correlated outcomes
Random intercept BART (riBART) was proposed by Tan et al.38 as a method to handle correlated continuous or binary outcomes with correlated binary outcomes as the main focus. In this work, the authors wanted to predict whether a human driven vehicle would stop at an intersection before making a left turn. They used a data set that contained about 100 drivers with each driver making numerous turns. In a preliminary analysis, they found that BART produced better prediction performance. However, BART was designed for independent outcomes and not correlated binary outcomes. Hence, they proposed to extend BART to handle the correlated binary outcomes in their data set by using a random intercept (extensions to random intercept and slope is straight forward).
To re-formulate riBART under the framework of (9), we set h(w, Θ) = wa, where Θ = (a, τ) and
i. e. w is a n × K matrix, where k indexes the subjects, , with the first column being a vector of , the second column , and so on until the last column , where 1i and 0j are row vectors of 1s and 0s with size i and j respectively. Let a = {a1,…, aK} where a∣τ2 ~ N(0, τ2), ε ~ N(0, σ2) where Σ = σ, and specify the usual BART priors for σ, μji∣Tj, and Tj. a and ε are assumed to be independent. A simple prior of τ2 ~ IG(1, 1) could be used although more robust or complicated priors are possible. Posterior estimation and binary outcomes then follow the procedure described in Section 4 easily.
4.3 ∣. Spatially-adjusted BART for a statistical matching problem
The spatially-adjusted BART approach of Zhang et al.39 was proposed to handle statistical matching problems54 that occur in surveys. In statistical matching problems, inference is desired for the relationship between two different variables collected from two different studies. For example, survey A may collect information on income but survey B collects information on health status. Often, subjects in both surveys do not overlap. The relationship between income and health status is then desired. To solve this, Zhang et al.39 proposed to use the geographical information or information aggregated at the geographical level to impute the missing variables. They set up two different models for surveys A and B separately but with a shared spatial random effects which takes into account the geographical location of each individual. This spatial random effects allow correlation among subjects living in adjacent geographical locations to be employed to improve inference. Although their approach is specifically set up to handle statistical matching problems, a simpler version can be formulated to handle more general spatial data.
To do so, we once again use the general BART model with w and a being the same setup as Section 4.2 but with
| (13) |
where C = ckl is a K × K adjacency matrix, l = 1,…, K, with ckl = 1 if group k and group l are (spatial) neighbors for k ≠ l; ckl = 0 otherwise; and ckl = 0 if k = l. H is a diagonal K × K matrix with diagonals , ρ is a parameter with range (−1, 1), and δ2 is the variance component for (13). The parameters ρ and δ2 are prespecified. Finally, ε ~ N(0, σ2) and (9) is completed by placing the usual BART priors for σ, μji∣Tj, and Tj. Posterior draws again follow the procedures we outline in Section 4.
4.4 ∣. Dirichlet Process Mixture BART
Similar to how BART can be used as a prior for unknown function f(·), Dirichlet process (DP) priors are often used as priors for unknown distributions55. We use notation D ~ DP(D0, α) if a random distribution D follows a DP prior with base measure D0 and concentration parameter α.
For the General BART Model in (9), it is the distribution of ε that is unknown. The following DP Mixture BART was proposed by George et al40:
Although the assumption of suggests that each subject will have their own mean and variance for the error term, draws from a DP are discrete with probability 1. Therefore, the number of unique values for (ak, ) at any step in the posterior algorithm will be much less than n. Essentially, the distribution of ε can be viewed as a mixture of normals, where the number of mixture components is not specified. Lower values of the concentration parameter α favor fewer mixture components. Therefore, it is common to specify a prior for α that puts more weight on smaller values (i.e., our prior guess is that we will not need many mixture components).
Viewing DPMBART as a form of (9), we have h(w, Θ) = wa where w and a have the same structure as riBART and . Note here that we are no longer assuming that ak and εk are independent unlike in some of our previous examples.
DPMBART requires specification of D0 and a prior for α. For D0, the commonly employed form is p(μ, σ∣ν, λ, μ0, h0) = p(σ∣ν, λ)p(μ∣σ, μ0, h0). George et al.40 specified their priors as
The parameter ν is set at 10 to make the spread of error for a single component h tighter. The parameter λ is chosen using the idea from how λ is determined in BART with the quantile set at 0.95 instead of 0.9 (See Appendix for how λ is determined in BART). For μ0, because DPMBART subtracts from y, μ0 = 0. For h0, the residuals of a multiple linear regression fit is used to place μ into the range of these residuals, r. The marginal distribution of is , where tν is a t distribution with ν degrees of freedom. Let hs be the scaling for μ. Given hs = 10, h0 can be chosen by solving
For α, the prior used by DPMBART is the same as in Section 2.5 of Rossi56, where the idea is to relate α to the number of unique components in (ak, ).
The posterior draw for DPMBART follows most of the ideas discussed in General BART where first, the idea of (10) is used to draw (T1, M1),…, (Tm, Mm)∣ak, . The slight difference is to view this as a weighted BART draw with . The second draw, (ak, σ2)∣(T1, M1),…, (Tm, Mm) follows (11) which can be solved by using draws (a) and (b) of the algorithm in Section 1.3.3 of Escobar and West57. The final draw is α∣(ak, σ2). This is obtained by putting α on a grid and using Bayes’ theorem with where H is the number of unique (ak, )’s. Another way of generating these posterior draws (DPM portion) can be found in Neal58.
5 ∣. DISCUSSION
In this tutorial, we walked through the BART model and algorithm in detail, and presented a general model based on recent extensions. We believe this is important because of the growing use of BART in research applications. By clarifying the various components of BART, we hope that researchers will be more comfortable using BART in practice.
Despite the success of BART, there are a number of papers that point out some of its limitations and propose modifications. One such limitation is the suboptimal performance of BART with high-dimensional data due to the use of the uniform prior to select the covariate to be split upon in the internal nodes. A solution is to allow researchers to place different prior probabilities on each covariate59. More sophisticated solutions include using a DP prior for selecting covariates44 or using a spike-and-slab prior60. Other solutions have also been proposed61,41. Another commonly addressed limitation is the computational speed of BART. Due to the many MH steps that BART requires, computation speed of BART can often be slow, especially when the sample size n and/or the number of covriates p is large. One direction is to parallelize the computational steps in BART, for example, Pratola et al.62, Kapelner and Bleich59, and Entezari et al.63 The other direction is to improve the efficiency of the MH steps which leads to the reduction in the number of trees needed. Notable examples include Lakshminarayanan et al.64, where particle Gibbs sampling was used to propose the tree structure Tj’s; Entezari et al.63, where likelihood inflated sampling was used to calculate the MH steps, and more recently He et al.48, where they proposed to use a different tree-growing algorithm which grows the tree from scratch (root node) at each iteration. Other less discussed issues with BART include the problem of under estimation of the uncertainty of BART caused by inefficient mixing when the true variation is small47, inability of BART to handle smooth functions65, and inclusion of many spurious interactions when the number of covariates is large66. Finally, the posterior concentration properties of BART have also been discussed recently by Ročková and van der Pas43, Ročková and Saha42, and Linero and Yang65. These works provide theoretical proof of why BART has been successful in many data applications we have seen thus far.
A second component we focused on was how we can extend BART using a very simple idea without having to re-write the whole MCMC algorithm to draw the regression trees. We term this framework General BART. Special cases of this model have already been used by various authors to extend BART to a variety settings. By unifying these methods under a single framework and showing how these methods are related to the General BART model, we hope to provide researchers with the start of a roadmap for new extensions. For example, researchers working with longitudinal data may want a more flexible modeling portion for the random effects and hence may want to model h(w, Θ) as BART. Another possibility is to combine the ideas in Examples 4.1, 4.2, and 4.4, i.e. correlated outcomes with an interpretable linear model portion and robust error assumptions.
We do note that the critical component of our General BART framework is re-writing the model in such a way that the MCMC draw of the regression trees can be done separately from the rest of the model. In situations where this is not possible, re-writing of the MCMC procedure for the regression trees may be needed. An example of this would occur if, rather than mapping the outcome to a parameter at the terminal node of a regression tree, it is mapped to a regression model. However, we feel that the general BART model is flexible enough to handle many of the extensions that might be of interest to researchers.
Supplementary Material
ACKNOWLEDGMENTS
We thank the two anonymous reviewers for their constructive comments which have greatly improved this article. This work was supported through grant R01GM112327 from the National Institutes of Health.
References
- 1.Chipman H, George E, McCulloch R. BART: Bayesian Additive Regression Trees. The Annals of Applied Statistics 2010; 4(1): 266–298. [Google Scholar]
- 2.Hernández B, Pennington S, Parnell A. Bayesian methods for proteomic biomarker development. EuPA Open Proteomics 2015; 9: 54–64. [Google Scholar]
- 3.Kropat G, Bochud F, Jaboyedoff M, et al. Improved predictive mapping of indoor radon concentrations using ensemble regression trees based on automatic clustering of geological units. Journal of Environmental Radioactivity 2015; 147: 51–62. [DOI] [PubMed] [Google Scholar]
- 4.Leonti M, Cabras S, Weckerle C, Solinas M, Casu L. The causal dependence of present plant knowledge on herbals – Contemporary medicinal plant use in Campania (Italy) compared to Matthioli (1568). Journal of Ethnopharmacology 2010; 130(2): 379–391. [DOI] [PubMed] [Google Scholar]
- 5.Hill J Bayesian nonparametric modeling for causal inference. Journal of Computational and Graphical Statistics 2011; 20:217–240. [Google Scholar]
- 6.Liu Y, Shao Z, Yuan G. Prediction of Polycomb target genes in mouse embryonic stem cells. Genomics 2010; 96(1): 17–26. [DOI] [PubMed] [Google Scholar]
- 7.Liu Y, Traskin M, Lorch S, George E, Small D. Ensemble of trees approaches to risk adjustment for evaluating a hospital’s performance. Health Care Management Science 2015; 18(1): 58–66. [DOI] [PubMed] [Google Scholar]
- 8.Zhang J, Härdle W. The Bayesian Additive Classification Tree applied to credit risk modelling. Computational Statistics and Data Analysis 2010; 54(5): 1197–1205. [Google Scholar]
- 9.Nateghi R, Guikema S, Quiring S. Comparison and validation of statistical methods for predicting power outage durations in the event of hurricanes. Risk analysis 2011; 31(12): 1897–1906. [DOI] [PubMed] [Google Scholar]
- 10.Chipman H, George E, Lemp L, McCulloch R. Bayesian flexible modeling of trip durations. Transportation Research Part B 2010; 44(5): 686–698. [Google Scholar]
- 11.Ding J, Bashashati A, Roth A, et al. Feature based classifiers for somatic mutation detection in tumour-normal paired sequencing data. Bioinformatics 2012; 28(2): 167–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bonato V, Baladandayuthapani V, Broom B, Sulman E, Aldape K, Do K. Bayesian ensemble methods for survival prediction in gene expression data. Bioinformatics 2011; 27(3): 359–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sparapani R, Logan B, McCulloch R, Laud P. Nonparametric survival analysis using Bayesian Additive Regression Trees (BART). Statistics in Medicine 2016; 35(16): 2741–2753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kindo B, Wang H, Pena E. Multinomial probit Bayesian additive regression trees. Stat 2016; 5(1): 119–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Agarwal R, Ranjan P, Chipman H. A new Bayesian ensemble of trees approach for land cover classification of satellite imagery. Canadian Journal of Remote Sensing 2013; 39(6): 507–520. [Google Scholar]
- 16.Linero A, Sinhay D, Lipsitz S. Semiparametric Mixed-Scale Models Using Shared Bayesian Forests. arXiv preprint 2018: 1809.08521. [DOI] [PubMed] [Google Scholar]
- 17.Green D, Kern H. Modeling Heterogeneous Treatment Effects in Survey Experiments with Bayesian Additive Regression Trees. Public Opinion Quarterly 2012; 76(3): 491–511. [Google Scholar]
- 18.Hill J Atlantic Causal Inference Conference Competition results. New York University, New York: (Available from http://jenniferhill7.wixsite.com/acic-2016/competition). 2016. [Google Scholar]
- 19.Hahn P, Murray J, Carvalho CM. Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects. arXiv preprint 2017: 1706.09523. [Google Scholar]
- 20.Dorie V, Hill J, Shalit U, Scott M, Cervone D. Automated versus do-it-yourself methods for causal inference: lessons learned from a data analysis competition. arXiv preprint 2017: 1707.02641. [Google Scholar]
- 21.Xu D, Daniels M, Winterstein A. Sequential BART for imputation of missing covariates. Biostatistics 2016; 17(3): 589–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kapelner A, Bleich J. Prediction with missing data via Bayesian additive regression trees. The Canadian Journal of Statistics 2015; 43: 224–239. [Google Scholar]
- 23.Tan Y, Flannagan A, Elliott M. “Robust-squared” Imputation Models using Bart. Journal of Survey Statistics and Methodology 2019; 4: ahead of print. [Google Scholar]
- 24.Kindo B, Wang H, Hanson T, Pena E. Bayesian quantile additive regression trees. arXiv preprint 2016: 1607.02676. [Google Scholar]
- 25.Murray J Log-Linear Bayesian Additive Regression Trees for Categorical and Count Responses. arXiv preprint 2017: 1701.01503. [Google Scholar]
- 26.Starling J, Murray J, Carvalho C, Bukowski R, Scott J. BART with Targeted Smoothing: An analysis of patient-specific stillbirth risk. arXiv preprint 2018: 1805.07656. [Google Scholar]
- 27.Sparapani R, Rein L, Tarima S, Jackson T, Meurer J. Non-parametric recurrent events analysis with BART and an application to the hospital admissions of patients with diabetes. Biostatistics 2018: Ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sivaganesan S, Muller P, Huang B. Subgroup finding via Bayesian additive regression trees. Statistics in Medicine 2017; 36(15): 2391–2403. [DOI] [PubMed] [Google Scholar]
- 29.Schnell P, Tang Q, Offen W, Carlin B. A Bayesian Credible Subgroups Approach to Identifying Patient Subgroups with Positive Treatment Effects. Biometrics 2016; 72(4): 1026–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schnell P, Muller P, Tang Q, Carlin B. Multiplicity-adjusted semiparametric benefiting subgroup identification in clinical trials. Clinical Trials 2018; 15(1): 75–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tan Y, Flannagan C, Pool L, Elliott M. Accounting for selection bias due to death in estimating the effect of wealth shock on cognition for the Health and Retirement Study. arXiv preprint 2018: 1812.08855. [DOI] [PubMed] [Google Scholar]
- 32.Logan B, Sparapani R, McCulloch R, Laud P. Decision making and uncertainty quantification for individualized treatments using Bayesian Additive Regression Trees. Statistical Methods in Medical Research 2019; 28(4): 1079–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sparapani R, Logan B, McCulloch R, Laud P. Nonparametric competing risks analysis using Bayesian Additive Regression Trees. Statistical Methods in Medical Research 2019; 1: ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liang F, Li Q, Zhou L. Bayesian Neural Networks for Selection of Drug Sensitive Genes. Journal of the American Statistical Association 2018; 113(523): 955–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nalenz M, Villani M. Tree ensembles with rule structured horseshoe regularization. The Annals of Applied Statistics 2018; 12(4): 2379–2408. [Google Scholar]
- 36.Lu M, Sadiq S, Feaster D, Ishwarana H. Estimating Individual Treatment Effect in Observational Data Using Random Forest Methods. Journal of Computational and Graphical Statistics 2018; 27(1): 209–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zeldow B, Lo Re V 3rd, Roy J A semiparametric modeling approach using Bayesian Additive Regression Trees with an application to evaluate heterogeneous treatment effects. Annals of Applied Statistics 2019: in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tan Y, Flannagan C, Elliott M. Predicting human-driving behavior to help driverless vehicles drive: random intercept Bayesian additive regression trees. Statistics and its Interface 2018; 11(4): 557–572. [Google Scholar]
- 39.Zhang S, Shih Y, Müller P. A Spatially-adjusted Bayesian Additive Regression Tree Model to Merge Two Datasets. Bayesian Analysis 2007; 2(3): 611–634. [Google Scholar]
- 40.George E, Laud P, Logan B, McCulloch R, Sparapani R. Fully Nonparametric Bayesian Additive Regression Trees. arXiv preprint 2018: 1807.00068. [Google Scholar]
- 41.Bleich J, Kapelner A, George E, Jensen S. Variable Selection for BART: An Application to Gene Regulation. The Annals of Aplied Statistics 2014; 8(3): 1750–1781. [Google Scholar]
- 42.Ročková V, Saha E. On Theory for BART. arXiv preprint 2018: 1810.00787. [Google Scholar]
- 43.Ročkovα V, Pas v. dS. Posterior Concentration for Bayesian Regression Trees and their Ensembles. arXiv preprint 2017: 1708.08734. [Google Scholar]
- 44.Linero A Bayesian Regression Trees for High-Dimensional Prediction and Variable Selection. Journal of the American Statistical Association 2018; 113(522): 626–636. [Google Scholar]
- 45.Denison D, Mallick B, Smith A. A Bayesian CART Algorithm. Biometrika 1998; 85(2): 363–377. [Google Scholar]
- 46.Wu Y, Tjelmeland H, West M. Bayesian CART: Prior Specification and Posterior Simulation. Journal of Computational and Graphical Statistics 2007; 16(1): 44–66. [Google Scholar]
- 47.Pratola M Efficient Metropolis-Hastings Proposal Mechanisms for Bayesian Regression Tree Models. Bayesian Analysis 2016; 11(3): 885–911. [Google Scholar]
- 48.He J, Yalov S, Hahn R. XBART: Accelerated Bayesian Additive Regression Trees. arXiv preprint 2019: 1810.02215v3. [Google Scholar]
- 49.Albert J, Chib S. Bayesian Analysis of Binary and Polychotomous Response Data. Journal of the American Statistical Association 1993; 88(422): 669–679. [Google Scholar]
- 50.Guyon I A scaling law for the validation-set training-set size ratio. AT & T Bell Laboratories, Berkeley, CA: 1997. [Google Scholar]
- 51.Tan Y, Elliott M, Flannagan C. Development of a real-time prediction model of driver behavior at intersections using kinematic time series data. Accident Analysis & Prevention 2017; 106: 428–436. [DOI] [PubMed] [Google Scholar]
- 52.Sayer J, Bogard S, Buonarosa M, et al. Integrated Vehicle-Based Safety Systems Light-Vehicle Field Operational Test Key Findings Report DOT HS 811 416. National Center for Statistics and Analysis, NHTSA, U.S. Department of Transportation, Washington, DC: (Available from http://www.nhtsa.gov/DOT/NHTSA/NVS/Crash%20Avoidance/Technical%20Publications/2011/811416.pdf). 2011. [Google Scholar]
- 53.Albert J, Chib S. Bayesian modeling of binary repeated measures data with application to crossover trials In Bayesian Biostatistics, Berry DA and Stangl DK, eds. New York: Marcel Dekker; 1996. [Google Scholar]
- 54.Rässler S Statistical matching: A frequentist theory, practical applications and alternative bayesian approaches Lecture Notes in Statistics, Springer Verlag, New York: 2002. [Google Scholar]
- 55.Escobar M, West M. Bayesian Density Estimation and Inference Using Mixtures. Journal of the American Statistical Association 1995; 90: 577–588. [Google Scholar]
- 56.Rossi P Bayesian Non- and Semi-parametric Methods and Applications. Princeton University Press, Princeton, New Jersey: 2014. [Google Scholar]
- 57.Dey D, Müller P, Sinha D. Practical Nonparametric and Semiparametric Bayesian Statistics. Springer-Verlag, New York, New York. 1998. [Google Scholar]
- 58.Neal R Markov Chain Sampling Methods for Dirichlet Process Mixture Models. Journal of Computational and Graphical Statistics 2000; 9(2): 249–265. [Google Scholar]
- 59.Kapelner A, Bleich J. bartMachine: Machine Learning with Bayesian Additive Regression Trees. Journal of Statistical Software 2016; 70(4): 1–40. [Google Scholar]
- 60.Liu Y,, Ročková V, Wang Y ABC Variable Selection with Bayesian Forests. arXiv preprint 2018: 1806.02304. [Google Scholar]
- 61.Chipman H, George E, McCulloch R. Bayesian Regression Structure Discovery. Oxford University Press, USA: 2013. [Google Scholar]
- 62.Pratola M, Chipman H, Gattiker J, Higdon D, McCulloch R, Rust W. Parallel Bayesian Additive Regression Trees. Journal of Computational and Graphical Statistics 2014; 23(3): 830–852. [Google Scholar]
- 63.Entezari R, Craiu R, Rosenthal J. Likelihood inflating sampling algorithm. The Canadian Journal of Statistics 2018; 46(1): 147–175. [Google Scholar]
- 64.Lakshminarayanan B, Roy D, Teh Y. Particle Gibbs for Bayesian Additive Regression Trees. arXiv preprint 2015: 1502.04622. [Google Scholar]
- 65.Linero A, Yang Y. Bayesian regression tree ensembles that adapt to smoothness and sparsity. Journal of the Royal Statistical Society - Series B 2018; 80(5): 1087–1110. [Google Scholar]
- 66.Du J, Linero A. Interaction Detection with Bayesian Decision Tree Ensembles. arXiv preprint 2018: 1809.08524. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.